An evaluation of common methods for dichotomization of continuous variables to discriminate disease status

Abstract

Dichotomization of continuous variables to discriminate a dichotomous outcome is often useful in statistical applications. If a true threshold for a continuous variable exists, the challenge is identifying it. This paper examines common methods for dichotomization to identify which ones recover a true threshold. We provide mathematical and numeric proofs demonstrating that maximizing the odds ratio, Youden’s statistic, Gini Index, chi-square statistic, relative risk and kappa statistic all theoretically recover a true threshold. A simulation study evaluating the ability of these statistics to recover a threshold when sampling from a population indicates that maximizing the chi-square statistic and Gini Index have the smallest bias and variability when the probability of being larger than the threshold is small while maximizing Kappa or Youden’s statistics is best when this probability is larger. Maximizing odds ratio is the most variable and biased of the methods.

2 Introduction

Dichotomization of continuous variables is frequently used in medical applications to stratify patients according to risk, make determinations about the necessity of additional diagnostic testing, and to allocate physician resources according to patient need (Perkins and Schisterman, 2006; MacCallum et al., 2002; Kannel and McGee, 1979). For example, elevated low-density lipoprotein cholesterol (LDL-C) is a known cardiovascular disease risk factor. Determining a risk-benefit threshold LDL-C level of ≥ 190 mg/dL was instrumental in the development of guidelines for initiating statin therapy for primary prevention of cardiovascular disease (Wilson et al., 1998; Ray et al., 2014). Additionally, in statistical modeling, dichotomizing continuous variables often results in a simpler interpretation, and some statistical models, such as decision tree methods, require that all variables be dichotomized prior to or during implementation (Ruczinski et al., 2003; Contal and O’Quigley, 1999; Mazumdar et al., 2003; Royston et al., 2000; Breiman et al., 1984; Hansen, 2000).

If a true threshold exists that discriminates between two groups, the challenge is identifying it. Many methods are available for dichotomizing continuous predictors to discriminate between two groups. Some of these methods are based on expert opinion and epidemiological studies, such as with cholesterol level (Wilson et al., 1998; Goodman et al., 1988; Goodman, 1991). There are also many data-driven methods that select a threshold based on maximizing or minimizing a specific statistic. For example, the threshold could be chosen such that it maximizes the odds ratio between dichotomized predictor and the dichotomous outcome.

Although the primary purpose of all methods is to find a dichotomy that effectively discriminates between two groups, because the dichotomy is defined using a threshold, the problem reduces to effectively finding that threshold. This paper examines which of the most commonly used methods for dichotomization effectively recover a “true” threshold given that one exists. Section 2 of this paper defines the statistics to be maximized for dichotomization in terms of 2×2 contingency tables. Additionally, in this section, mathematical and numerical proofs regarding which of the methods recover the true threshold are also provided. Section 3 describes a simulation study that evaluates the impacts of location of the threshold, sample size, and strength of association between a continuous predictor and a dichotomous outcome on the ability to recover the true threshold to provide guidance on which statistics are most effective and when these statistics are likely to fail. Section 4 presents the results of the simulation study. Section 5 provides a discussion of the implication of the results and offers recommendations regarding the appropriateness of a method of dichotomization for different scenarios.

3 Criteria for Dichotomization

Methods that can be used for dichotomizing a continuous predictor to discriminate between two groups can be separated into three main categories. Methods in the first category are clinically motivated using prior knowledge or experience (Naggara et al., 2011; Schäfer, 1989; Vermont et al., 1991; Gallop et al., 2003; Bortheiry et al., 1994; Hoffman et al., 2000; Alvarez-Garcıa et al., 2003) and are not supported by statistical theory. A second category of methods used for dichotomization is based on the prevalence of a condition in a population, such as observed prevalence which chooses a threshold, t, closest to the observed prevalence (i.e. $\frac{t}{{\mathit{\text{max}}}_t\Vert t-p\Vert }$ where p is the prevalence) (Manel et al., 2001; Kelly et al., 2008). Although methods based on prevalence are data-driven, the observed prevalence in the sample is dependent on the selected sample and may not reflect the population level disease prevalence. For example, in a 1:1 case-control scenario, the observed prevalence is determined by the study design rather than the natural prevalence in the population, in which case these methods will fail (Lalkhen and McCluskey, 2008; Kelly et al., 2008). Thus, methods based on prevalence, such as mean prevalence, matching prevalence, and observed prevalence, are not considered in this paper. Methods in the third category, the main focus of this paper, are data driven algorithms where the choice of threshold is selected by maximizing or minimizing a statistic, specifically Youden’s statistic (Youden, 1950), odds ratio (Kraemer, 1992), ROC curve (Greiner et al., 2000; Boehning et al., 2011; Greiner, 1995), relative risk (Greiner et al., 2000), Gini Index (Strobl et al., 2007), sensitivity and specificity (Lopez-Raton et al., 2014) among others (Aoki et al., 1997; Vermont et al., 1991; Hand, 1987; Breiman et al., 1984). Relative risk is only considered in the cohort study design where the sample is designed to mimic disease distribution in the population.

3.1 Numerical evaluation of the “best” threshold

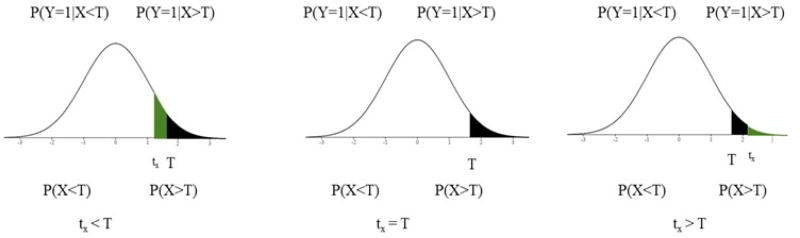
This section provides an empirical examination of which of the common methods of dichotomization correctly identifies the true threshold, T. For the numerical investigation, the threshold, T, is specified such that for a continuous random variable X and a binary random variable Y, P(Y = 1|X ≥ T) > P(Y = 1|X < T). We set P(X > T) = 0.05, P(Y = 1) = 0.1, and P(Y = 1|X > t) = 0.4. Then X is dichotomized for varying thresholds in a specified interval. For simplicity, we let X ~ N(0, 1) and consider the range of X from [−4, 4] in the increments of 0.001 with the true threshold included in the interval. Each value in [−4, 4] is considered as a possible threshold for dichotomizing X to discriminate values of Y. For each possible threshold, t_x, there is a corresponding 2×2 contingency table between the dichotomized random variable X and Y with cell probabilities a, b, c, d as shown in Table 1. All statistics considered in this paper are defined in Table 2 using a, b, c, d and P(Y = 1). Using the 2×2 table, the statistics defined in Table 2 are calculated using the probabilities depicted in Figure 1. The cell probabilities for t_x < T, t_x = T, and t_x > T are shown below.

1. t_x < T

   $$a=P(X\ge T)P(Y=1|X\ge T)+(P(X<T)-P(X<t_x))P(Y=1|X<T)$$

   $$b=P(X\ge t_x)-(P(X\ge T)P(Y=1|X\ge T)-(P(X<T)-P(X<t_x))P(Y=1|X<T))$$ (1)

   $$c=(P(X<t_x))P(Y=1|X<T)$$

   $$d=(P(X<t_x))-(P(X<t_x))P(Y=1|X<T)$$
2. t_x = T,

   $$a=P(X\ge T)P(Y=1|X\ge T)$$

   $$b=P(X\ge T)-P(X\ge T)P(Y=1|X\ge T)$$ (2)

   $$c=P(X<T)P(Y=1|X<T)$$

   $$d=P(X<T)-P(X<T)P(Y=1|X<T)$$
3. t_x > T

   $$a=P(X\ge t_x)P(Y=1|X\ge T)$$

   $$b=P(X\ge t_x)-P(X\ge t_x)P(Y=1|X\ge T)$$ (3)

   $$c=P(X<T)P(Y=1|X<T)+(P(X<t_x)-P(X<T))P(Y=1|X\ge T)$$

   $$d=(P(X<t_x)-(P(X<T)P(Y=1|X<T)-(P(X<t_x)-P(X<T))P(Y=1|X\ge T))$$

Table 1.

Probabilities for a 2×2 contingency table for a binary outcome Y and a continuous variable X thresholded at T

	Y = 1	Y = 0
X ≥ T	$\begin{array}{cc}a\hfill & =P(Y=1,X>T)\hfill \\ \hfill & =P(X\le t)P(Y=1|X\ge T)\hfill \end{array}$	$\begin{array}{cc}b\hfill & =P(Y=0,X>T)\hfill \\ \hfill & =P(X\ge T)-P(X\ge T)P(Y=1|X\ge T)\hfill \end{array}$	P(X ≥ T)
X < T	$\begin{array}{cc}c\hfill & =P(Y=1,X<T)\hfill \\ \hfill & =(1-P(X\ge T))P(Y=1|X<T)\hfill \end{array}$	$\begin{array}{cc}d\hfill & =P(Y=0,X<T)\hfill \\ \hfill & =(1-P(X\ge T))-(1-P(X\ge T))P(Y=1|X<T)\hfill \end{array}$	P(X < T)
	P(Y = 1)	1 − P(Y = 1)

Table 2.

Formulas for statistics for selecting a threshold for a continuous variable X to discriminate a binary outcome Y based on the probabilities in Table 1

Odds Ratio	Youden’s Statistic	Chi-Square
$\frac{\mathit{\text{ad}}}{\mathit{\text{bc}}}$	$\frac{a}{a+c}+\frac{d}{b+d}-1$	$\frac{{(\mathit{\text{ad}}-\mathit{\text{bc}})}^2}{(a+b)(c+d)(b+d)(a+c)}$
Kappa Statistic	Relative Risk*	Gini Index
$\frac{(a+d)-((a+b)(a+c)+(c+d)(b+d))}{1-((a+b)(a+c)+(c+d)(b+d))}$	$\frac{a/(a+b)}{c/(c+d)}$	$(P_y(1-P_y))-(\frac{\mathit{\text{ab}}}{a+b}+\frac{\mathit{\text{cd}}}{c+d})$
Specificity	Misclassification	Sensitivity
$\frac{d}{b+d}$	$1-\frac{a+d}{N}$	$\frac{a}{a+c}$
Accuracy Area	Minimax	Minimum ROC**
$\frac{a}{a+c}·\frac{d}{b+d}$	max (b, c)	$\sqrt{{(1-\frac{a}{a+c})}^2+{(1-\frac{d}{b+d})}^2}$

^*For cohort study

^**Measures the distance from the ROC curve to the point (0,1)

Figure 1.

Graphical representation of possible thresholds for X presented in equations 1–3.

The numerical values for the statistics in Table 2 calculated over the interval [−4, 4] are shown in Figure S1 in the Supplemental. Methods for which the maximum absolute value for the statistic occurs at the true threshold are considered successful. There are six statistics for which the maximum value occurs at T, namely chi-square, kappa, Youden’s, Gini Index, relative risk and odds ratio.

3.2 Theoretical confirmation

Based on the numerical evidence presented in section 2.1, the following theorem is conjectured for functions in the first 2 rows of Table 2 which include the six statistics for which the maximum occurs at the true threshold.

Theorem 1

For a continuous random variable X and dichotomous variable Y, given a prevalence of Y (P(Y = 1)), and a threshold T such that, P(Y = 1|X ≥ T) > P(Y = 1|X < T), the inequality g(t) < g(T) for all t ≠ T holds. Here g(t) is any one of the functions shown in the first two rows of Table 2. That is, if there exists a true threshold T, the maximum odds ratio, Youden’s statistic, chi-square statistic, Gini Index, kappa statistic, or relative risk will occur at T.

Proof

We first consider the case where P(X > t_x) > P(X ≥ T).

Consider the case where multiplying both sides of the condition P(Y = 1|X ≥ T) > P(Y = 1|X < T) by P(t_x < X < T) yields,

$$P(t_x<X<T)P(Y=1|X\ge T)>P(t_x<X<T)P(Y=1|X<T).$$

Replacing P(t_x < X < T) on the LHS with P(t_x > X) − P(X > T) and adding P(X > T)P(Y = 1|X ≥ T) to both sides yields,

$$P(t_x>X)P(Y=1|X\ge T)>P(t_x<X<T)P(Y=1|X<T)+P(X>T)P(Y=1|X\ge T).$$

Subtracting P(X > T)P(Y = 1|X ≥ T)² + P(t_x < X < T)P(Y = 1|X ≥ T)P(Y = 1|X < T) from both sides and factoring yields,

$$P(Y=1|X\ge T)(P(t_x>X)-P(X>T)P(Y=1|X\ge T)-P(t_x<X<T)P(Y=1|X<T))>(1-P(Y=1|X\ge T))(P(X>T)P(Y=1|X\ge T)+P(t_x<X<T)P(Y=1|X<T)).$$

Dividing both sides by (P(t_x > X) − P(X > T)P(Y = 1|X ≥ T) − P(t_x < X < T)P(Y = 1|X < T)) and (1 − P(Y = 1|X ≥ T)) we have,

$$\frac{P(Y=1|X\ge T)}{(1-P(Y=1|X\ge T))}>\frac{(P(X>T)P(Y=1|X\ge T)+P(t_x<X<T)P(Y=1|X<T))}{(P(t_x>X)-P(X>T)P(Y=1|X\ge T)-P(t_x<X<T)P(Y=1|X<T))}.$$

Multiplying both sides by (1 − P(Y = 1|X < T)) yields,

$$\frac{P(Y=1|X\ge T)(1-P(Y=1|X<T))}{(1-P(Y=1|X\ge T))}>\frac{(P(X>T)P(Y=1|X\ge T)+P(t_x<X<T)P(Y=1|X<T))(1-P(Y=1|X<T))}{(P(t_x>X)-P(X>T)P(Y=1|X\ge T)-P(t_x<X<T)P(Y=1|X<T))}.$$

Finally, dividing both sides by P(Y = 1|X < T) yields,

$$\frac{P(Y=1|X\ge T)(1-P(Y=1|X<T))}{(1-P(Y=1|X\ge T))P(Y=1|X<T)}>\frac{(P(X>T)P(Y=1|X\ge T)+P(t_x<X<T)P(Y=1|X<T))(1-P(Y=1|X<T))}{(P(t_x>X)-P(X>T)P(Y=1|X\ge T)-P(t_x<X<T)P(Y=1|X<T))P(Y=1|X<T)}$$

which means $\frac{a_T{d}_T}{b_T{c}_T}>\frac{a_{t_x}{d}_{t_x}}{b_{t_x}{c}_{t_x}}$ and ${\mathit{\text{OR}}}_{t_x=T}>{\mathit{\text{OR}}}_{t_x>T}.$

Now consider the case where multiplying both sides of the condition P(Y = 1|X ≥ T) > P(Y = 1|X < T) by P(X > t_x) < P(X > T) yields the equation,

$$(P(X>t_x)-P(X\ge T))·P(Y=1|X\ge T)>(P(X<T)-P(X<t_x))P(Y=1|X<T)$$

Distributing P(Y = 1|X ≥ T) on the LHS and adding P(X ≥ T)P(Y = 1|X ≥ T) to both sides yields,

$$P(X>t_x)·P(Y=1|X\ge T)>P(X\ge T)P(Y=1|X\ge T)+(P(X<T)-P(X<t_x))P(Y=1|X<T).$$

Next, subtracting P(Y = 1|X ≥ T)(P(X ≥ T)P(Y = 1|X ≥ T)+(P(X < T)−P(X < t_x))P(Y = 1|X < T)) from both sides and dividing by (1 − P(Y = 1|X ≥ T)) and (P(X ≥ T)P(Y = 1|X ≥ T) + (P(X < T) − P(X < t_x)) yields,

$$\frac{P(Y=1|X\ge T)}{(1-P(Y=1|X\ge T))}>\frac{(P(X\ge T)P(Y=1|X\ge T)+(P(X<T)-P(X<t_x))P(Y=1|X<T))}{(P(X>t_x)-P(X\ge T)P(Y=1|X\ge T)+(P(X<T)-P(X<t_x))P(Y=1|X<T))}.$$

Multiplying both sides by $\frac{(1-P(Y=1|X<T))}{P(Y=1|X<T)}$ we have,

$$\frac{P(Y=1|X\ge T)·(1-P(Y=1|X<T))}{(1-P(Y=1|X\ge T))·P(Y=1|X<T)}>\frac{(P(X\ge T)P(Y=1|X\ge T)+(P(X<T)-P(X<t_x))P(Y=1|X<T))·(1-P(Y=1|X<T))}{(P(X>t_x)-P(X\ge T)P(Y=1|X\ge T)+(P(X<T)-P(X<t_x))P(Y=1|X<T))·(P(Y=1|X<T))}.$$

Thus OR_tx=T > OR_tx<T. If the expression for OR_tx=T is greater than the expression for OR_tx<T and the expression for OR_tx=T is greater than the expression for OR_tx>T then it shows that the odds ratio is the highest when t_x = T.

The proofs of this theorem for the other five statistics are provided in the Appendix here.

4 Simulations Study

In Section 2, six statistics that are maximized at the true threshold T, were identified. However, if a sample is drawn from a population, it is not clear which of these statistics will most accurately identify the true threshold. To evaluate the ability of the six statistics to recover the true threshold, a simulation study was performed. Sample data sets were generated by first generating a continuous normal random variable X ~ N(0, 1). A binary variable Y was then generated according to the relationship defined in Equation 4.

$$P(Y=1)=P(X\ge T)P(Y=1|X\ge T)+P(X<T)P(Y=1|X<T)$$ (4)

where P(Y = 1|X > T) > P(Y = 1|X < T) and T is the true threshold for dichotomizing X.

Simulations were performed under various scenarios arising from combinations of the parameters: the number of observations in the sample, N = 250, 500, or 1000, the overall prevalence of Y defined by P(Y = 1), the choice of threshold T for X, strength of association between predictor X and response Y defined by an odds ratio, and case-control or cohort study designs. The probabilities P(Y = 1|X ≥ T) and P(Y = 1|X < T) were calculated based on the choice of T, the odds ratio, and the prevalence of Y. For cohort study scenarios, we generated N values of X and Y. For the 1:1 case:control scenarios, we generated 20,000 X and Y values and selected $\frac{N}{2}$ cases and $\frac{N}{2}$ controls. All simulation scenarios are described in Table 3. The true parameter values and simulation scenario for each method for n = 250 can be found in Supplemental Table S1.

Table 3.

Simulation Scenarios

OR	P(X ≥ T)	P(Y = 1)	P(Y = 1|X ≥ T)	Scenario
1.5	0.05	0.2	0.268	1
		0.4	0.495	2
	0.2	0.2	0.255	3
		0.4	0.479	4
	0.5	0.2	0.232	5
		0.4	0.448	6
3	0.05	0.2	0.411	7
		0.4	0.654	8
	0.2	0.2	0.363	9
		0.4	0.614	10
	0.5	0.2	0.283	11
		0.4	0.528	12
6	0.05	0.2	0.569	13
		0.4	0.786	14
	0.2	0.2	0.475	15
		0.4	0.735	16
	0.5	0.2	0.326	17
		0.4	0.6	18

For each simulation scenario and sample size, we generated 500 datasets. The choice of threshold for each method was estimated by calculating the probabilities of a,b,c, and d as described in Table 1 for all possible thresholds for X. These probabilities were converted into cell counts by multiplying by the sample size N. We then calculated the associated odds ratio, kappa statistic, chi-square statistic, Youden’s statistic, and Gini Index for the 2×2 table corresponding to each unique threshold for X in the observed data. Any threshold for X that resulted in a cell count of less than 1 was eliminated from consideration in order to minimize the influence of extreme values. Across simulation scenarios less than 6% of observations on average were eliminated from consideration in the cohort setting and less than 2% in the case-control setting. The thresholds that corresponded to the maximum value obtained for each statistic were selected as the “best” thresholds. Assessment of how well the maximum of each statistic recovered the true threshold, T, was determined by examining the mean squared error and the bias squared for the estimated threshold across all simulated datasets for all scenarios. All simulations were conducted in R v. 3.2.1 (R Core Team)

5 Simulation Results

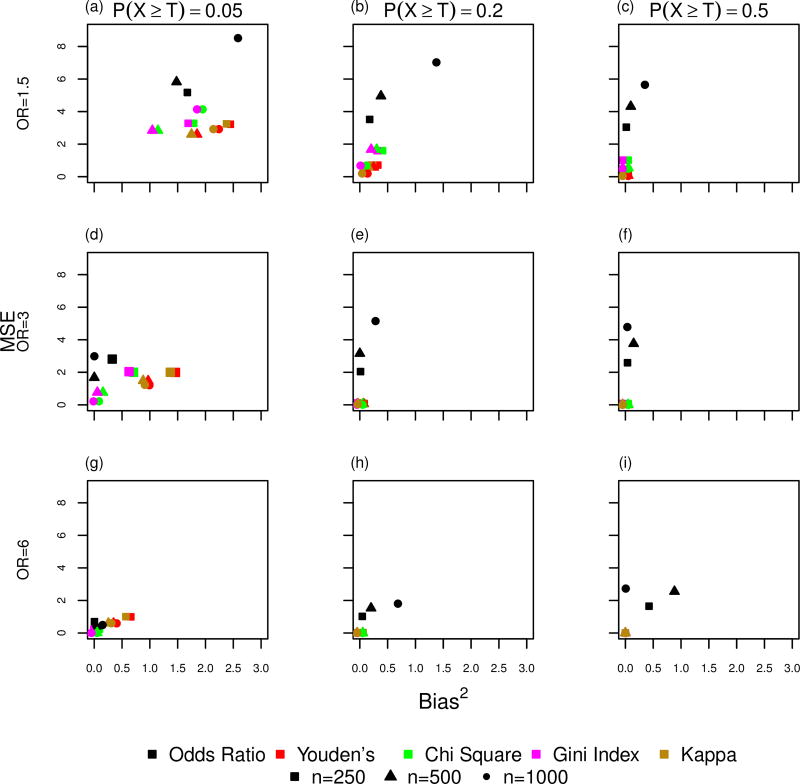
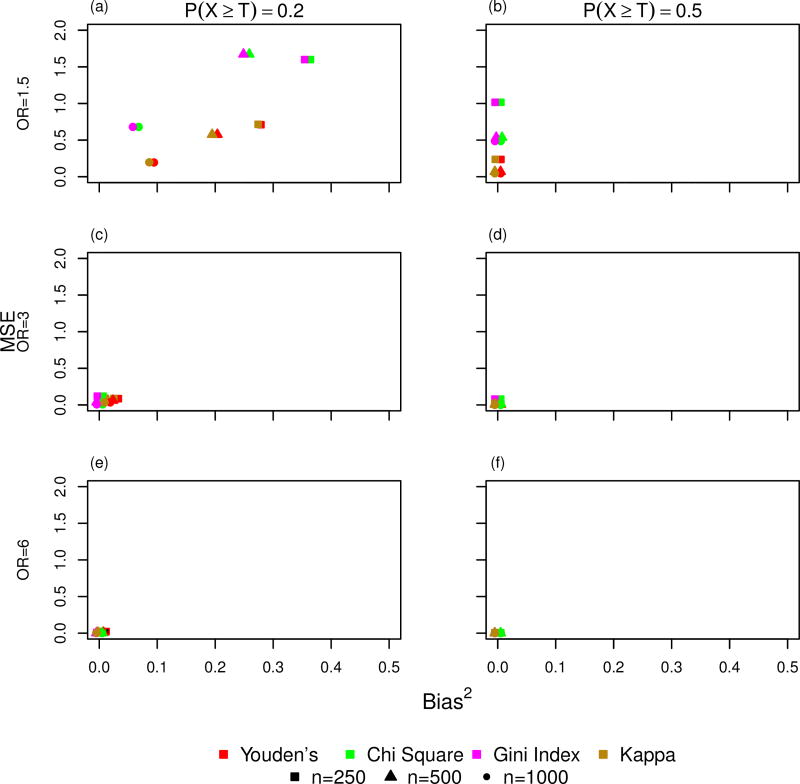
Figure 2 shows the results from the simulation study for the case-control study design scenario. Each graph shows the mean squared error (MSE) by bias squared for all statistics described in Table 3 for the different combinations of P(X ≥ T) and strength of association with Y. The columns in Figure 2 show the impact of increasing values for P(X ≥ T) and the rows show the impact of increasing strength of association with Y. Three different sample sizes, 250, 500, and 1000, are represented by the different shapes, square, triangle, and circle, respectively and each statistic is represented by a different color. As the strength of association between X and Y increases (OR=1.5 to OR=6), all statistics exhibit smaller MSE and bias squared for the estimated threshold indicating that the estimate threshold based on each statistic becomes less variable and biased. As the probability of observing values of X above the true threshold increases, a majority of the methods show a reduction in bias squared and MSE of the estimated threshold as P(X ≥ T) increases from 0.05 to 0.5. The main exception is the odds ratio which does show a decrease in bias for weaker strength of association (OR = 1.5, Figure 2 a–c), but which has worse bias as P(X ≥ T) increases when the strength of association with Y is large (Figure 2 g–i). Additionally, the odds ratio also exhibits an increase in MSE as P(X ≥ T) increases with a stronger association between X and Y (Figure 2 d–i). As sample size increases, most of the methods show a reduction in MSE and bias². The only exception occurs when the strength of association is the weakest and P(X ≥ T) is the smallest (Figure 2a). Figure 3 shows the results for P(X ≥ T)= 0.2 and P(X ≥ T) = 0.5 excluding the odds ratio as it is the least effective at recovering the true threshold. When the strength of association is large and P(X ≥ T) is > 0.2, the chi-square statistics, Youden’s statistic, Gini Index, and kappa statistic all exhibit minimal MSE and bias² (Figure 3 c–f).

Figure 2.

Simulation results showing mean-squared error (MSE) by Bias² under the case-control study design for the estimated threshold obtained by maximizing the statistics: odds ratio, Youden’s, chi-square, Gini Index, and kappa. Rows represent strength of association between X and Y and columns represent the probability that the independent variable X is greater than the true threshold T.

Figure 3.

Simulation results showing mean-squared error (MSE) by Bias² under the case-control study design for the estimated threshold obtained by maximizing the statistics: Youden’s, chi-square, Gini Index, and kappa, excluding P(X ≥ T)=0.05. Rows represent strength of association between X and Y and columns represent the probability that the independent variable X is greater than the true threshold T.

Among the 5 statistics, the odds ratio statistic exhibits the largest MSE and often the largest bias² across all simulation scenarios (Figure 2 a–i). The bias² in the estimated threshold is largest for the odds ratio when the strength of association between X and Y is large (OR=6) and P(X ≥ T) ≥ 0.2 (Figure 2h and i). The Gini Index and chi-square statistic perform similarly to one another for all simulation scenarios. In general, both statistics perform well in comparison to the three other statistics when P(X ≥ T)=0.05 irrespective of the strength of association (OR=1.5, 3, or 6) with the exception of the weakest strength of association between X and Y (OR=1.5) where the kappa and Youden’s statistics perform slightly better (Figure 2a). The kappa and Youden’s statistics also perform similarly to one another across all simulation scenarios and their performance is better than chi-square and Gini Index when P(X ≥ T)=0.2 or 0.5 The chi-square statistic, Gini Index, Youden’s statistic, and kappa statistic all have a squared bias and MSE very near 0 when P(X ≥ T) ≥ 0.2 and the strength of association between X and Y is large (OR> 3).

We also investigated the direction of the bias. Across most of the simulation scenarios, the chi-square statistic, Gini Index, kappa statistic, and Youden’s statistic are negatively biased. The only exception is Youden’s statistic which has a small positive bias when P(X ≥ T) = 0.5 and OR = 6.0. Bias is more variable for the odds ratio. The odds ratio is negatively biased at all sample sizes when the strength of association is small (OR = 1.5). Odds ratio also tends to exhibit negative bias when P(X ≥ T)=0.5, although this is inconsistent for n = 1000 as strength of association increases. Once P(X ≥ T) is at least 0.2, all methods exhibit negligible bias except for the odds ratio, which has a bias that varies between −0.94 and 0.82.

Simulation scenarios assuming a cohort study design produced very similar results to the case-control scenarios. The relative risk, rather than the odds ratio, was evaluated in the cohort scenarios. Similar to the case-control scenario, the chi-square statistic, Youden’s statistics, Gini Index, and kappa statistic all exhibited a reduction in MSE and bias for the estimated threshold as P(X ≥ T) increase, strength of association between X and Y increase, and with increasing sample size (Supplemental Figures S2 and S3). Similar to what was observed for the odds ratio in the case-control scenario, the relative risk tended to have larger MSE and bias relative to the other four methods with the largest differences observed as strength of association and P(X ≥ T) increased. Also similar to the results in the case-control scenario, the chi-square statistic, Gini Index, Youden’s statistic, and kappa statistic all have a bias and MSE very near 0 when P(X ≥ T) ≥ 0.2 and the strength of association between X and Y is large (OR≥ 3) (Figure S3 c–f). One notable difference between the case-control and cohort scenarios is the performance of the kappa statistic. In the cohort scenarios the kappa statistic selects an estimated threshold with similar or smaller MSE relative to the other four statistics in all scenarios.

5.1 Summary of Results

The simulation study examined the performance of the odds ratio, Youden’s statistic, chi-square statistic, Gini Index, relative risk and kappa statistic to recover a true threshold, T, for continuous predictor X to discriminate a binary outcome Y. All of these statistics improve on average at finding the true threshold as sample size increases, strength of association between X and Y increases, and as P(X ≥ T) increases. The statistic with the most variability in all scenarios is the odds ratio. When the strength of association between X and Y is small, all methods exhibit a larger MSE and bias relative to the truth. When the population odds ratio increases to OR≥ 3, Youden’s statistic and kappa statistic exhibit the lowest MSE and bias relative to the odds ratio, chi-square statistic, and Gini Index. Study design had little effect on the performance of the methods.

6 Conclusions

Continuous variables are often dichotomized in medical applications to discriminate disease status of a patient population and thereby assist in directing the treatment of a patient. For example, a continuous laboratory value might be dichotomized in order to stratify patients in to disease risk categories in order to make a determination about medication a patient should receive. Additionally, dichotomization of a continuous predictor might be utilized in statistical modeling to simplify interpretation.

Numerous methods have been described in the literature for dichotomizing a continuous variable to discriminate a binary outcome. In this paper, we provided numerical evidence followed by mathematical proofs that maximizing the odds ratio, relative risk, Youden’s statistic, chi-square statistic, Gini Index, and kappa statistic theoretically recover a true threshold for a continuous random variable X, when one exists. In the simulation study, these six statistics exhibited lower MSE and bias as sample size, strength of association, and P(X ≥ T) increased. The odds ratio and relative risk statistics were the most variable and exhibited a higher MSE and bias relative to the other methods. If the event is rare (i.e P(X ≥ T)=0.05), chi-square statistic and Gini Index have the smallest MSE and Bias regardless of strength of association (OR=1.5, 3, or 6). But when P(X ≥ T) > 0.2, then kappa and Youden’s statistic has the smallest MSE and bias. Once there is both a large strength of association (OR=3 or 6) and a high probability for the event (P(X ≥ T)=0.2 or 0.5), all four are similar. It is our recommendation that odds ratio and relative risk should not be used as they provide the least optimal results and most variable.

We are not discounting the use of other statistics to dichotomize variables. Depending on the situation and type of variable, statistics other than the ones discussed in this paper may be appropriate. Sometimes, it is necessary to use a clinically defined threshold, especially if the focus is on developing a diagnostic test with high sensitivity.

The mixture of binomials for Y defined in equation 4 describes a scenario where there is a steep sigmoidal relationship between a continuous predictor X and dichotomous outcome Y. If the relationship between X and Y is sigmoidal over a large range of X, such as in the case where the probability that Y is 1 follows a logistic relationship with X, the threshold selected by these methods occurs in the most steeply increasing portion of the logistic curve and we would expect greater variability in the selection of a threshold.