IWTomics: testing high-resolution sequence-based ‘Omics’ data at multiple locations and scales

Abstract

Summary

With increased generation of high-resolution sequence-based ‘Omics’ data, detecting statistically significant effects at different genomic locations and scales has become key to addressing several scientific questions. IWTomics is an R/Bioconductor package (integrated in Galaxy) that, exploiting sophisticated Functional Data Analysis techniques (i.e. statistical techniques that deal with the analysis of curves), allows users to pre-process, visualize and test these data at multiple locations and scales. The package provides a friendly, flexible and complete workflow that can be employed in many genomic and epigenomic applications.

Availability and implementation

IWTomics is freely available at the Bioconductor website (http://bioconductor.org/packages/IWTomics) and on the main Galaxy instance (https://usegalaxy.org/).

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Detecting genomic features associated with the presence of particular DNA elements, or the occurrence of certain events, is a common task in sequence-based ‘Omics’ research—e.g. when studying integration preferences of transposable elements, the landscape of mutations, or epigenomic profiles around Transcription Start Sites (TSS). A possible approach is to measure features in windows of fixed size around the elements or events of interest (e.g. regions with high mutation rates, or surrounding the elements under study) and compare them with controls using univariate hypothesis tests and/or regressions (see Chiaromonte and Makova, 2015, and references therein). The size of the windows defines the scale of the analysis. Large sizes incorporate neighboring effects, but hinder the detection of localized differences since the signal is usually cumulated or averaged over the window. Small sizes map the signal at finer scales, but miss neighboring effects. Another approach is to consider high-resolution feature profiles in the vicinity of the elements or events (e.g. histone modification read coverages around TSSs) and plot average profiles across the whole genome (e.g. Young et al., 2011). Although this approach visualizes both local and neighboring effects of the features, it is specific to coverage data and lacks a rigorous assessment of observed differences.

Here, we present IWTomics, an R/Bioconductor package that implements Functional Data Analysis (FDA) and graphical tools to analyze and compare ‘Omics’ data measured at high resolution over groups of genomic regions. IWTomics provides a data structure to manage several groups of regions and several features, and includes functions for pre-processing, visualization and statistical testing. It implements an extended version of Interval-Wise Testing (IWT) (Pini and Vantini, 2017) designed for sequence-based ‘Omics’ applications, and does not require any pre-specified location or scale. Indeed, the procedure performs each test at multiple locations and scales, and provides in output those at which the considered feature shows significant effects. In doing so, it adjusts P-values taking into account the multiple contiguous locations, and the multiple scales tested. A simplified version of the package is available as a Galaxy tool (Afgan et al., 2016).

2 Statistical background and workflow

To perform hypothesis testing on a high-resolution feature, we treat measurements in small, contiguous windows within each genomic region as evaluations of curves on a discrete grid—embedding the problem in an FDA framework (Fig. 1a). IWT is an inferential procedure to test the null hypothesis that the distributions of two stochastic curves (e.g. the profiles of a feature along two groups of regions) are equal, versus the alternative that they differ. Testing is performed non-parametrically via permutations—making IWT suitable for data which often violate normality. The objects tested are the entire curves, and IWT performs a functional P-value adjustment that considers all locations and scales tested. This procedure differs from multiple testing corrections such as Bonferroni or Benjamini–Hochberg, because it exploits the ordered nature of the measurements along the genome, increasing statistical power (more details below and in Supplementary Section S1). Importantly, IWT has better power and accuracy when the test statistic employed (e.g. the mean difference curve) is smooth. However, while the package includes functions to smooth the data if desired, individual observed ‘Omics’ curves need not to be smooth. A detailed description of the types of ‘Omics’ data that can be analyzed with IWTomics, and of the resolution requirements for the features, is provided in the R/Bioconductor package vignette (Subsection 1.4).

Fig. 1.

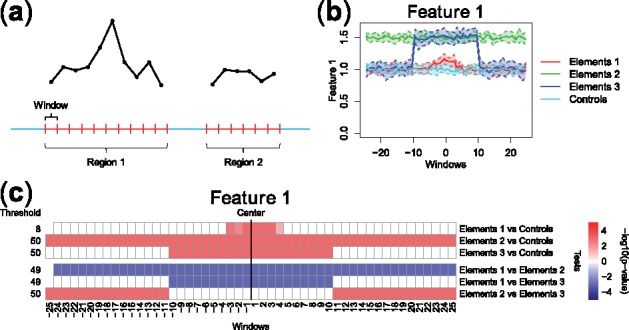
(a) FDA framework for sequence-based ‘Omics’ data: each genomic region is associated to a curve made of measurements in small, contiguous windows (a curve for each feature considered). (b) Example of pointwise boxplots, for a simulated dataset comprising curves corresponding to one high-resolution feature (Feature 1) in four different groups of genomic regions (visualized with different colors). Regions comprise up to 50 windows (windows –25 to +25), and they are aligned at their center (x-axis). (c) Summary graphical representation of IWT results on the simulated dataset in panel (b). Each row shows the adjusted P-values related to one comparison, at the selected scale threshold. Locations with significant differences between the two groups of curves are shown in red (feature over-represented in the first group) and blue (feature under-represented in the first group). Detailed IWT results and an illustration of adjusted P-value curves can be found in Supplementary Figure S1. An example using real biological data is described in Supplementary Section S3

Let $y_{1,i}\left(x\right),\hspace{0.17em}i=1,\dots ,n_1$ and $y_{2,j}\left(x\right),\hspace{0.17em}j=1,\dots ,n_2$ be random samples from the two stochastic curves, defined on the interval I. IWT performs a functional permutation test on every subinterval $S=(x_a,x_b)\subseteq I$ and its complement $S=I\mathrm{\setminus }(x_a,x_b)$ obtaining a P-value p^S. Then, an adjusted P-value curve $\tilde{p}\left(x\right)$ is computed controlling the interval-wise error rate, i.e. the probability of rejecting the null on every S where it is true (for details, see Pini and Vantini, 2017, and Supplementary Section S1). $\tilde{p}\left(x\right)$ allows the user to identify locations in I where the two curve distributions differ significantly. The extended version of IWT implemented in IWTomics computes an adjusted P-value curve ${\tilde{p}}_s\left(x\right)$ for any given scale s, controlling the interval-wise error rate on every S of length $\left|S\right|\le s$ and allowing the user to identify also scales at which significant differences unfold (Supplementary Section S1). For illustration purpose, consider the simulated data in Figure 1b, and in particular the comparison Element 1 versus Controls (red and cyan boxplots, respectively). IWT performs the test over all 50 possible locations and provides a P-value curve ${\tilde{p}}_s\left(x\right)$ for each possible scale $s=1,2,\dots ,50$. The adjusted P-value curve ${\tilde{p}}_8\left(x\right)$ at scale 8, shown in the first row of the summary plot in Figure 1c, controls the false positive rates among all intervals (made of contiguous windows) of length $1,2,\dots ,8$.

IWTomics has an efficient, user-friendly implementation based on the R object oriented programming framework. It comprises the S4 data class IWTomicsData to collect information about several features (possibly corresponding to diverse types of sequence-based ‘Omics’ data) in several groups of genomic regions. Data can be supplied through BED or text files, and the import method allows the user to choose from multiple curve alignment options (center, right, left or scale), depending on nature of the data and analysis objectives. IWTomics also allows the user to pre-process data using FDA techniques (e.g. smoothing) and to visualize them with various types of plots (e.g. pointwise boxplots, Fig. 1b). The main function of the package, IWTomicsTest, is a versatile implementation of IWT which includes independent, paired-samples and one-sample tests (center of symmetry of one stochastic curve, e.g. the profile of a feature in a single group of regions). In addition, different test statistics are available (e.g. mean difference, quantile difference). A single run of IWTomicsTest can perform several tests at once (e.g. comparisons concerning different groups of regions and/or features). However, each test is performed independently; adjusted P-value curves in output account for multiple locations and scales in each test, but no correction is applied across tests. Test results can be inspected through adjusted P-value curves and a number of informative graphical representations (Supplementary Fig. S1). A function producing a graphical summary of test results is also provided (Fig. 1c). The workflow of the IWTomics Galaxy tool is shown in Supplementary Figure S2.

3 Application examples

Campos-Sánchez et al. (2016) employed a beta version of IWTomics to investigate how features of the genomic landscape affect integration and fixation of endogenous retroviruses (ERVs), based on their profiles around ERVs integration sites. Using the Interval Testing Procedure (ITP, Pini and Vantini, 2016), of which the IWT is an extension, they were able to disentangle integration versus fixation preferences and to gain important insights into the mechanisms underlying the uneven distribution of ERVs along the genome.

In another application, Guiblet et al. (2017) used IWTomics to analyze DNA polymerization kinetics and the effects of non-B DNA motifs and microsatellites (sequences where DNA may adopt a three-dimensional conformation different from the canonical double-stranded structure) on the time of incorporation of consecutive bases in PacBio sequencing. They found that DNA polymerization kinetics is affected not only by the particular nucleotide being incorporated, but also by the presence of non-B DNA structures.

In Supplementary Section S3, we demonstrate the performance of IWTomics comparing it to alternative methods, using both real biological data (a subset of the ERV dataset analyzed in Campos-Sánchez et al., 2016) and simulated data. Details about computation time are provided in Supplementary Section S4.

4 Conclusion

IWTomics is one of the first tools employing rigorous and sophisticated FDA techniques for the analysis of high-resolution sequence-based ‘Omics’ data. It is easy to use and broadly applicable, since it does not require assumptions on the curve distributions, nor pre-specification of effect locations or scales. We expect it to provide critical insights into many genomic and epigenomic analyses.