Sources of Error in IRT Trait Estimation

Abstract

In item response theory (IRT), item response probabilities are a function of item characteristics and latent trait scores. Within an IRT framework, trait score misestimation results from (a) random error, (b) the trait score estimation method, (c) errors in item parameter estimation, and (d) model misspecification. This study investigated the relative effects of these error sources on the bias and confidence interval coverage rates for trait scores. Our results showed that overall, bias values were close to 0, and coverage rates were fairly accurate for central trait scores and trait estimation methods that did not use a strong Bayesian prior. However, certain types of model misspecifications were found to produce severely biased trait estimates with poor coverage rates, especially at extremes of the latent trait continuum. It is demonstrated that biased trait estimates result from estimated item response functions (IRFs) that exhibit systematic conditional bias, and that these conditionally biased IRFs may not be detected by model or item fit indices. One consequence of these results is that certain types of model misspecifications can lead to estimated trait scores that are nonlinearly related to the data-generating latent trait. Implications for item and trait score estimation and interpretation are discussed.

In psychometric modeling, nontrivial errors in latent trait estimates are unavoidable for a variety of reasons, including a limited number of available items, time restrictions, and test-taker fatigue. Nevertheless, those who design, administer, and score tests aim to achieve the most reliable trait estimates possible. In other words, a primary psychometric concern is minimizing the errors associated with trait estimates. Within an item response theory (IRT) framework, estimated latent trait scores are computed based on a series of examinee item responses and characteristics of the items. Errors in the resulting estimated trait scores result from random error, the trait score estimation method, errors in item calibration, and model misspecification. The purpose of this study was to identify the relative consequence of each error source on trait score estimates. This study focuses in particular on misspecification of the item response function (IRF) functional form.

Error Sources

It is common practice in IRT analyses to estimate latent trait scores using a two-stage approach. In the first stage, item calibration, item parameters are estimated using methods such as marginal maximum likelihood (MML; Bock & Aitkin, 1981). In the second stage, trait score estimates are typically computed using methods such as maximum-likelihood estimation or expected a posteriori (EAP) prediction and treating the item parameter estimates as fixed. Because MML produces consistent and computationally efficient estimates of IRT item parameters, this approach is considered the gold standard technique for item parameter estimation.

Under a two-stage approach, errors in IRT trait estimation can be attributed to four nested sources. These error sources (Jones, Wainer, & Kaplan, 1984, p. 2-3) are (a) random error due to the probabilistic nature of the model, (b) errors in trait estimation due to the estimation method, (c) errors in item parameter estimation, and (d) model misspecification. These error sources are ordered hierarchically; the existence of a higher numbered error source implies the existence of all lower numbered error sources. Strictly speaking, error sources (a) and (b) are inseparable because trait estimates are only obtained using a particular trait estimation method. Furthermore, when using estimated item parameters, errors due to the trait estimation method persist. Finally, when the model is misspecified, errors in item parameter estimates and errors due to the trait estimation method are all present. Because models are imperfect representations of reality, it is reasonable to expect that all four error sources are present in any IRT analysis.

With regard to the first error source, errors may be attributed to random variation resulting from the fact that IRT models are probabilistic rather than deterministic. The effect of random error decreases as the number of administered test items increases, and so there are practical limitations on the extent to which random error can be reduced. With regard to the second error source, different methods for estimating latent trait scores introduce different types of errors. In this article, three trait estimation methods—maximum likelihood (ML), Bayesian EAP (Bock & Mislevy, 1982), and weighted likelihood (WL; Warm, 1989)—are considered. Details of the properties of these methods and their standard errors (ses) are provided in Online Appendix A. In brief, ML estimates are outwardly biased (Lord, 1983), EAP estimates are biased toward the mean of the prior distribution, and WL estimates are unbiased (Warm, 1989).

A third source of error results from imperfect estimation of item parameters. Because item parameter estimates need not equal their true values, errors in item calibration may affect the accuracy of trait estimates. To complicate the issue, accurate item parameter estimates are often difficult to obtain, particularly for highly parameterized models such as the three-parameter (3PL; see Thissen & Wainer, 1982) and four-parameter (4PL; Culpepper, 2016; Waller & Feuerstahler, 2017) IRT models. Accurate item parameter estimates are particularly difficult to obtain when the calibration sample is small. In two-stage estimation, the uncertainty associated with the item parameter estimates is typically ignored and as a result, the asymptotic properties of the ML, EAP, and WL trait estimators do not necessarily hold when estimated item parameters are treated as known. For instance, WL is no longer unbiased when item parameters are estimated instead of known (Zhang, 2005). Moreover, errors in item parameter estimation can lead to increased bias of trait estimates (Zhang, Xie, Song, & Lu, 2011) and underestimated standard errors (Cheng & Yuan, 2010), particularly when using small item calibration samples (Tsutakawa & Johnson, 1990). Various corrections have been proposed to adjust $\hat{\mathrm{\theta }}$ and $\mathrm{se}(\hat{\mathrm{\theta }})$ for the effects of item parameter estimation error (e.g., Patton, Cheng, Yuan, & Diao, 2014; Tsutakawa & Johnson, 1990), but it is still common practice to treat estimated item parameters as fixed when estimating trait scores. When item parameter estimation error is not accounted for, the properties of the ML, EAP, and WL trait estimators should hold approximately for highly accurate item parameter estimates. Moreover, the accuracy of item parameter estimates depends on the size and trait distribution of the calibration sample. Calibration samples of at least several hundred examinees are recommended for the one-parameter (1PL) and two-parameter (2PL) IRT models (e.g., Drasgow, 1989), and several thousand examinees are recommended for the 3PL (Thissen & Wainer, 1982) and 4PL (Culpepper, 2016; Waller & Feuerstahler, 2017).

In the majority of applications, latent trait estimates are computed assuming correct model specification. Model misspecification in IRT, broadly speaking, occurs when an item response model cannot accurately characterize item response probabilities. Under this definition, model misspecification necessarily leads to incorrect item parameter estimates. In other words, correct item parameters do not exist when the model is misspecified because the estimated IRFs can never perfectly trace the true IRFs. One type of model misspecification not considered in this article occurs when multidimensional data are fit to unidimensional models (e.g., Drasgow & Parsons, 1983). In contrast, this manuscript is focused on one specific type of functional form misspecification. Specifically, the author of the present study focuses on the effects of ignoring the need for an IRF upper asymptote parameter less than 1; that is, fitting the 1PL, 2PL, or 3PL, when the 4PL is the data-generating model.

Few studies have explicitly investigated the effects of functional form misspecification on trait estimation error. Jones et al. (1984) generated item responses from a complex and nonstandard IRT model, and fit the resulting data sets to the 1PL, 2PL, and 3PL. They then generated item response vectors using the nonstandard model, and estimated ML trait scores using the estimated 1PL, 2PL, and 3PL item parameters. The authors found that trait estimates computed from the estimated 3PL parameters led to the least bias but highest mean squared error at low trait values, and that ML trait estimates were severely biased for the 1PL and 2PL. Wainer and Thissen (1987) simulated data in a similar manner to Jones et al. (1984) but focused on several latent trait estimators. They found that in sufficiently long tests (≥20 items), the 3PL led to more accurate trait estimates than the 1PL and 2PL at all trait levels. More recently, Markon and Chmielewski (2013) studied the effects of model misspecification on the bias, variance, mean squared error, and confidence interval coverage rates of IRT trait estimates. The authors generated data according to the 3PL and estimated ML trait scores using the true 3PL item parameters and the estimated 1PL, 2PL, and 3PL item parameters. At all trait values, they found that trait estimates computed from the 1PL and 2PL were higher than trait scores estimated from the true and estimated 3PL item parameters. They also found that at moderate to low trait values, trait estimates computed from the 1PL and 2PL had lower variance but higher mean squared error than either set of 3PL trait estimates. However, at high trait values, trait estimates computed from the true and estimated 3PL item parameters had small variance relative to the misspecified trait estimates. The authors also found that confidence interval coverage rates were higher for the correctly specified model than for the misspecified models. Moreover, for both correct and incorrect model specifications, they found substantial differences in coverage rates across trait values. Specifically, under model misspecification, coverage rates tended to be lower than their nominal rate at low $\mathrm{\theta }$ values and higher than their nominal rate at high $\mathrm{\theta }$ values. The authors emphasized that both the bias and variance of a trait estimate—both of which affect confidence intervals—can be severely affected by model misspecification.

Confidence Intervals for Trait Estimates

Many IRT trait recovery studies consider bias, variability, or correlation statistics that are functions only of the true and estimated trait scores. Fewer studies incorporate the estimated standard errors. As suggested by Markon and Chmielewski (2013), “The applied literature on misspecification has focused much more extensively on bias effects than variance effects, which can be misleading given that overall error is a function of both” (p. 108). One way to assess the combined accuracy of the estimate and its standard error is by comparing the nominal and observed confidence interval coverage rates.

A primary use of trait standard errors, denoted $\mathrm{se}(\hat{\mathrm{\theta }})$, is to construct confidence intervals around $\hat{\mathrm{\theta }}$. Asymptotically, the ML $\hat{\mathrm{\theta }}$ is unbiased and normally distributed with standard deviation equal to $\mathrm{se}(\hat{\mathrm{\theta }})$. Thus, a 95% confidence interval constructed around trait estimate equals

$$\begin{array}{c}\hat{\mathrm{\theta }}\pm 1.96\times \mathrm{se}\left(\hat{\mathrm{\theta }}\right).\hfill \end{array}$$

Notably, confidence intervals are traditionally constructed using the formula in Equation 1, even for trait estimates computed with methods other than ML (see De Ayala, Schafer, & Sava-Bolesta, 1995). Standard errors and confidence intervals play a central role in CAT (Weiss, 1982). If obtaining point estimates of $\mathrm{\theta }$, the computerized adaptive testing (CAT) might be terminated once the observed standard error is sufficiently small (e.g., $\mathrm{se}(\hat{\mathrm{\theta }})<.30$). Instead, to classify an individual as being above or below some predetermined threshold, the CAT may be terminated when the threshold is no longer in the confidence interval around $\hat{\mathrm{\theta }}$ (Waller & Reise, 1989).

Although it has been shown that trait scores estimated from misspecified models are often inaccurate (Jones et al., 1984; Markon & Chmielewski, 2013; Wainer & Thissen, 1987), the relative contribution of model misspecification is unclear. For instance, it is not clear whether misestimated trait scores result from a lack of test information, the trait estimation method, inaccurate item parameter estimates, or model misspecification. In the next section, a Monte Carlo simulation study is described that elucidates the relative contributions of each of these error sources.

As noted earlier, our simulation study is limited to one type of functional form misspecification, namely fitting data generated from the 4PL to the 3PL, 2PL, and 1PL. This type of functional form misspecification was selected for this study first for its simplicity. Because the 4PL extends the 3PL by adding a single upper asymptote parameter, any differences in trait estimation accuracy under this type of model misspecification are attributable to the omission of the upper asymptote parameter. In addition, recent interest in the 4PL suggests that an upper asymptote is needed to avoid biased trait scores at the upper end of the trait continuum in the context of computerized adaptive testing (Rulison & Loken, 2009). Finally, although the results of this study will be limited to one type of functional form misspecification, the author hopes to provide a general framework in which the magnitude of functional form misspecification—the form of which is unknown in real data—can be understood and assessed.

Method

A series of Monte Carlo simulations were conducted to gauge the effects of trait estimation error, item parameter estimation error, and model misspecification on the bias and confidence interval coverage rates for latent trait estimates. In all cases, item responses were generated according to the four-parameter model (4PL; Barton & Lord, 1981). For item $i$ and person $j$, the 4PL models the probability of a keyed response $y_{\mathrm{ij}}=1$ as follows:

$$\begin{array}{c}P(y_{\mathrm{ij}}=1|{\mathrm{\theta }}_{j,}{\mathbf{\xi }}_i)=c_i+(d_i-c_i)\frac{1}{1+\exp [-a_i({\mathrm{\theta }}_j-b_i)]},\hfill \end{array}$$

where ${\mathbf{\xi }}_i=(a_i,b_i,c_i,d_i)$ indicates a vector of item parameters, and ${\mathrm{\theta }}_j$ indicates a latent trait value. Importantly, the 3PL, 2PL, and 1PL are nested submodels of the 4PL. The 3PL is a restriction of the 4PL, wherein all $d_i=1$; the 2PL is a restriction of the 3PL, wherein all $c_i=0$; and the 1PL is a restriction of the 2PL, wherein a common $a_i$ value is estimated for all items (i.e., $a_1=a_2=a_3=\cdots$).

To simulate data, 4PL parameters for 100 items were generated by drawing parameter values from the following distributions: $a~\mathrm{LN}(0,.5)$, $b~\mathrm{Unif}(-2.5,2.5)$, $c~\mathrm{Beta}(2,40)$, and $d~\mathrm{Beta}(40,2)$. This generating distribution for $a$ provides a majority of moderately discriminating items in the range of those reported for the 3PL (e.g., Table 1 of Zhang, 2012) and 4PL (e.g., Loken & Rulison, 2010; Waller & Reise, 2010). A uniform generating distribution for $b$ provides high test information at a wide range of $\mathrm{\theta }$ values. Finally, narrow generating distributions for $c$ and $d$ ensure that many items have $c_i$ and $d_i$ values close to 0 and 1. Researchers have suggested that it is unlikely that ${\hat{c}}_i>>0$ and ${\hat{d}}_i<<1$ for the same item (Reise & Waller, 2003), and few reported sets of estimated 4PL item parameters report both estimated asymptotes far from their boundaries (Loken & Rulison, 2010; Waller & Reise, 2010). A plot of the test information function (TIF) and expected standard errors for this item bank, as well as the specific item parameter values, is available upon request. For this item bank, there was slightly more information at low $\mathrm{\theta }$ values than at high $\mathrm{\theta }$ values, but the asymptotic standard error was less than 0.30 for $-2.5\le \mathrm{\theta }\le 2.0$. This standard error value is similar to standard error termination criteria often used in computerized adaptive testing (e.g., Dodd, Koch, & De Ayala, 1993). All item responses used in this study were generated according to these model parameters.

Table 1.

Conditional $\mathbf{\theta }$ Bias Using True Item Parameters, Estimated Item Parameters, and Misspecified Models.

		$\mathrm{\theta }$
		Estimator	−3.0	−2.5	−2.0	−1.5	−1.0	−0.5	0.0	0.5	1.0	1.5	2.0	2.5	3.0
1		ML	−.08	−.02	−.01	−.01	.00	.00	.02	.00	−.01	.01	.00	.03	.08
2		WL	.01	.01	.00	−.01	−.01	.00	.01	.00	−.01	.00	.00	.00	.01
3		EAP1	.26	.16	.12	.09	.06	.04	.02	−.03	−.08	−.10	−.15	−.20	−.29
4		EAP2	.02	−.01	.02	.02	.02	.02	.02	−.01	−.03	−.01	−.03	−.01	−.03
	N	Model	−3.0	−2.5	−2.0	−1.5	−1.0	−0.5	0.0	0.5	1.0	1.5	2.0	2.5	3.0
5	1,000	4PL	−.05	−.10	.00	.05	.05	.03	.02	−.02	−.05	−.03	−.01	.07	.04
6			(−.21)	(−.27)	(.16)	(.19)	(.16)	(.13)	(.12)	(−.10)	(−.14)	(−.15)	(−.15)	(.26)	(.22)
7	5,000	4PL	−.10	−.14	−.03	.02	.03	.03	.02	−.02	−.04	−.02	.02	.10	.08
8			(−.20)	(−.25)	(−.11)	(.08)	(.08)	(.07)	(.05)	(−.06)	(−.09)	(−.07)	(.12)	(.22)	(.15)
9	20,000	4PL	−.09	−.11	−.01	.02	.03	.02	.02	−.01	−.04	−.01	.01	.09	.07
10			(−.14)	(−.17)	(−.06)	(.04)	(.05)	(.05)	(.04)	(−.03)	(−.06)	(−.04)	(.05)	(.14)	(.12)
	N	Model	−3.0	−2.5	−2.0	−1.5	−1.0	−0.5	0.0	0.5	1.0	1.5	2.0	2.5	3.0
11	20,000	3PL	−.35	−.41	−.26	−.10	.01	.06	.07	.02	−.06	−.12	−.23	−.33	−.47
12			(−.41)	(−.49)	(−.32)	(−.13)	(.03)	(.09)	(.09)	(.04)	(−.08)	(−.15)	(−.27)	(−.38)	(−.53)
13	20,000	2PL	−.03	−.07	−.04	−.01	.02	.03	.02	−.01	−.04	−.01	−.01	−.01	−.08
14			(−.06)	(−.10)	(−.07)	(−.03)	(.04)	(.05)	(.05)	(−.03)	(−.06)	(−.04)	(−.04)	(−.04)	(−.11)
15	20,000	1PL	−.03	−.09	−.06	−.01	.02	.03	.03	−.01	−.04	−.03	−.04	−.04	−.12
16			(−.06)	(−.11)	(−.08)	(−.04)	(.05)	(.06)	(.05)	(−.03)	(−.06)	(−.06)	(−.08)	(−.08)	(−.16)

Note. Quantities not in parentheses give the bias values averaging (where applicable) across 100 sets of estimated item parameters. Quantities in parentheses give the bias values that are largest in absolute value among 100 sets of estimated item parameters. Rows 1 to 4 correspond to trait estimates computed from the data-generating item parameters. Rows 5 to 16 correspond to trait estimates computed with the EAP2 estimator. ML = maximum likelihood; WL = weighted likelihood; EAP = expected a posteriori. 1PL, 2PL, 3PL, 4PL = one-parameter, two-parameter, three-parameter, four-parameter model.

A sequence of 13 $\mathrm{\theta }$ values ranging from −3 to 3 was next considered in increments of 0.5. At each $\mathrm{\theta }$ value, 2,000 response vectors were randomly generated from the true item parameters $\mathbf{\xi }$ for a total of 26,000 response vectors. For each response vector, $\hat{\mathrm{\theta }}$ and $\mathrm{se}(\hat{\mathrm{\theta }})$ were computed using ML, WL, and EAP estimation conditioning on the true item parameters $\mathbf{\xi }$. The EAP trait estimation method was used twice with each response vector: once using a N(0,1) prior (EAP1) and again using a N(0,2) prior (EAP2), where “2” indicates the prior standard deviation. All trait estimates were obtained using the catR package (Magis & Raiche, 2012) in R (R Core Team, 2016), and 33 quadrature points were used for the EAP trait estimates. For all conditions and trait estimation methods, trait estimates were truncated at −4 and 4.

The simulation proceeded in three stages: In the first stage, trait estimates were computed from the 26,000 response vectors and the data-generating 4PL item parameters. By using a long 100-item test, this simulation design allowed us to explore the accuracy of each trait estimation method while minimizing the effects of random error. The results for this first set of simulations should reflect the properties of the ML, EAP, and WL estimators that were described earlier. Specifically, ML trait estimates should demonstrate a slight outward bias, WL trait estimates should be unbiased, EAP1 estimates should demonstrate a strong inward bias, and EAP2 estimates should demonstrate a mild inward bias.

In the second stage of simulation, trait estimates were computed from the 26,000 response vectors and 100 sets of estimated 4PL item parameters. This second stage allowed us to explore the error introduced by uncertainty in item parameter estimation. To obtain 4PL item parameter estimates, 100 vectors of $\mathrm{\theta }$ values were drawn from standard normal distributions at each of three sample sizes $N=1,000$, $5,000$, and $20,000$. Using each vector of $\mathrm{\theta }$ values and the true item parameters, a total of 100 binary data sets were generated at each sample size. Note that these binary data sets were only used to estimate item parameters; trait scores were estimated for the 26,000 response vectors described earlier. Previous research (Culpepper, 2016) has concluded that a sample size of $N>2,500$ is usually sufficient for accurate 4PL item parameter estimation, whereas $N=1,000$ may be too small. The sample sizes of (a) $N=1,000$, (b) $N=5,000$, and (c) $N=20,000$ were chosen to represent sample sizes that were, respectively, (a) too small for accurate parameter estimation, (b) sufficient for accurate parameter estimation, and (c) large enough to minimize any effects of item parameter estimation. The author of the present study then estimated 300 sets of 4PL item parameters (three sample sizes × 100 replications) using marginal Bayes modal estimation (Mislevy, 1986) as implemented by the mirt package (Chalmers, 2012) in R (R Core Team, 2016). Item parameter estimates were obtained by integrating over a N(0,1) latent trait distribution and by specifying a convergence tolerance of .0001. To aid model convergence, the following priors were used: $\mathrm{logit}(c)~N(-1.8,1)$ and $\mathrm{logit}(d)~N(1.8,1)$. These 300 sets of estimated item parameters were then treated as known parameters to obtain latent trait estimates. In this second set of simulations, the WL estimator was no longer expected to be unbiased (Zhang, 2005), and increased bias in trait estimates was also expected for particular sets of item parameter estimates (i.e., within calibrations; Zhang et al., 2011). Moreover, prior research suggests that ignoring item parameter estimation error can result in underestimated standard errors (Cheng & Yuan, 2010; Tsutakawa & Johnson, 1990). As a result, reduced confidence interval coverage rates might be expected for these conditions in our simulations, especially for smaller calibration samples.

In the third stage of simulation, trait estimates were computed from the 26,000 response vectors and estimated 1PL, 2PL, and 3PL item parameters. To obtain estimated item parameters from these misspecified models, the same 100 data sets were used with $N=20,000$ subjects that were used in the second stage. Trait estimates were then computed for the 26,000 4PL-generated response vectors by conditioning on each set of estimated 1PL, 2PL, and 3PL item parameters. In the third stage, item parameters were only estimated for these misspecified models using $N=20,000$ subjects, so as to isolate the unique effects of model misspecification (i.e., to avoid conflation with item parameter estimation errors). As in the second stage of simulations, item parameter estimates were computed using mirt. For the 3PL item parameter estimates, the prior $\mathrm{logit}(c)~N(-1.8,1)$ was included to aid model convergence but no priors were used for the $a$ or $b$ parameters for any models. With these specifications, all models converged according to the criteria used in the mirt software.

Results

Effects of Trait Estimation

The combined effects of random error and trait estimation error are first evaluated. For the four trait estimation methods, the observed conditional bias values are reported in rows 1 to 4 of Table 1, and the observed conditional confidence interval coverage rates are reported in rows 1 to 4 of Online Table A. At almost all $\mathrm{\theta }$ values, the ML, WL, and EAP2 estimators are essentially unbiased, although as expected (Lord, 1983), the ML estimator is outwardly biased at extreme $\mathrm{\theta }$ values. Correspondingly, these three trait estimators have confidence interval coverage rates that are very close to the nominal rate of .95 at all $\mathrm{\theta }$ values. In contrast, but also as expected (Bock & Mislevy, 1982), the EAP1 estimator exhibits a strong inward bias. The strong inward bias of the EAP1 estimator, combined with the smaller standard errors associated with Bayesian trait estimates (1982), leads to relatively low coverage rates for the EAP1 estimator for extreme $\mathrm{\theta }$ values ($|\mathrm{\theta }|>1.5)$. This result emphasizes that constructing confidence intervals using Equation 1 is inappropriate for Bayesian estimates with highly informative priors, and might lead to inappropriate classification decisions (De Ayala et al., 1995). Overall, apart from the EAP1 estimator, trait estimation has only a small effect on person parameter bias or confidence interval coverage rates. Although the results for this stage of our simulation are not novel, they support previous research on the ML, WL, and EAP trait estimators, and provide useful benchmark statistics against which to evaluate the effects of other error sources.

Effects of Item Parameter Estimation

The effect of item parameter estimation on latent trait estimates was evaluated using the same sets of 13 ($\mathrm{\theta }$ levels) ×2,000 (replications) response vectors used in the previous section. At this step, only the results for the EAP2 estimator are reported. Only the EAP2 estimator was considered because, in the first set of results, EAP2 was associated with coverage rates that were closest to the nominal rate of .95 and the smallest bias values apart from WL. Moreover, EAP2 has elsewhere demonstrated better bias values and confidence interval coverage rates than the ML or EAP1 estimators (Rulison & Loken, 2009). Results for the other three trait estimators are available upon request.

At each of the three sample sizes, average conditional bias and confidence interval coverage rates were computed both across and within the 100 replications (i.e., the 100 sets of estimated item parameters). Bias values are presented in rows 5 to 10 of Table 1. Here, the numbers outside parentheses are the bias values averaged across replications, and the numbers within parentheses are the maximum absolute bias values (sign reintroduced) within replications. Notice that the three sample sizes lead to similar patterns and magnitudes of bias. Note also that the conditional biases do not strictly increase as $\mathrm{\theta }$ increases (as one might expect from an inwardly biased Bayesian trait estimator). Moreover, the direction of bias (inward vs. outward) is not constant for moderate ranges of the $\mathrm{\theta }$ continuum. This result was also observed, although to a lesser extent, when conditioning on the data-generating item parameters (Table 1, row 4). This unexpected phenomenon appears to be unique to the EAP2 trait estimator. Although it is not clear why the direction of bias is not a monotonic function of $\mathrm{\theta }$, the across-replication magnitude of bias is small ($\left|\mathrm{bias}\right|<.15$) for all trait values and very small ($\left|\mathrm{bias}\right|\le .05$) for central trait values ($|\mathrm{\theta }|\le 2$). Furthermore, although the maximum absolute bias within replications decreases somewhat with larger sample sizes, there is not a consistent reduction in bias with larger sample sizes.

Confidence interval coverage rates are presented in rows 5 to 10 of Online Table A. Here, the numbers outside parentheses are the coverage rates averaged across replications, and the numbers within parentheses are the minimum coverage rates within replications. Notice that across replications, coverage is high for all three sample sizes and closest to the nominal rate of .95 for central $\mathrm{\theta }$ values (high coverage at $\mathrm{\theta }=\{-3,3\}$ may be attributed to large standard errors in these conditions). However, at $N=1,000$, minimum within-replication coverage rates dip below .90 for several $\mathrm{\theta }$ values, with $\mathrm{\theta }=-1.5$ exhibiting a minimum coverage rate of only .859. Because standard errors are underestimated when item parameter estimation error is ignored (Cheng & Yuan, 2010), some reduction in confidence interval coverage rates, particularly at small sample sizes, is expected. Previous research also suggests that a calibration sample of $N=1,000$ is too small to accurately estimate 4PL item parameters (Waller & Feuerstahler, 2017). Thus, it is not surprising that confidence interval coverage rates are far below .95 in the $N=1,000$ conditions. Although coverage rates at $N=1,000$ are still relatively high, they are far below the nominal rate of .95. Furthermore, at the two larger sample sizes, both minimum and average coverage rates are close to the nominal rate of .95. This finding suggests that, when using the 4PL, samples larger than $N=1,000$ are needed to obtain accurate estimates of both the trait score and its standard error.

Effects of Model Misspecification

The effects of model misspecification on bias are shown in rows 11 to 16 of Table 1. As in the previous set of analyses, the quantities outside parentheses indicate the average bias across the 100 replications, and the quantities within parentheses give the (signed) maximum absolute bias observed within replications. The effects of model misspecification on confidence interval coverage are shown in rows 11 to 16 of Online Table A. Here, the quantities outside parentheses give the coverage rates across replications, and the quantities within parentheses give the minimum coverage rate within replications. When interpreting these results, bear in mind that each set of 1PL, 2PL, and 3PL item parameter estimates was computed with the very large sample size of $N=20,000$. A large sample size was chosen to minimize the effects due to item parameter estimation errors; when using smaller item calibration samples, the bias and coverage rate statistics would likely be more variable due to the added variability of the item parameter estimates.

Table 1 and Online Table A reveal that both the 1PL and 2PL lead to relatively unbiased trait estimates ($\left|\mathrm{bias}\right|>.15$) that have coverage rates close to .95 (and always above .90) across the $\mathrm{\theta }$ continuum. Notably, the bias of trait estimates is not much (or even consistently) worse for the 1PL and 2PL conditions compared with the 4PL conditions with $N=20,000$. Coverage rates for the 1PL and 2PL trait estimates are slightly lower at most $\mathrm{\theta }$ values than the 4PL trait estimates with $N=20,000$, but the magnitudes of these differences are small. In contrast, the 3PL leads to trait estimates with a strong negative bias at both the lower and upper ends of the $\mathrm{\theta }$ continuum. The magnitude of bias is only slightly larger at high $\mathrm{\theta }$ values than at low $\mathrm{\theta }$ values; average bias at $\mathrm{\theta }=3$ equals −.47, and average bias at $\mathrm{\theta }=-3$ equals −.35. As a result, coverage rates at high $\mathrm{\theta }$ values are far below the nominal rate and dip as low as .546 at $\mathrm{\theta }=3$ (as low as .480 within replications). At the lower end of the $\mathrm{\theta }$ continuum, coverage rates are also far below the nominal rate of .95, but rates are still above .80 at these lower $\mathrm{\theta }$ values. Although both high and low $\mathrm{\theta }$ estimates are biased under the 3PL, low $\mathrm{\theta }$ values have higher coverage rates than high $\mathrm{\theta }$ values because low $\mathrm{\theta }$ values also have larger standard errors. Although not reported in this article, this pattern of results for the 3PL was also observed for the other three trait estimators (coverage at $\mathrm{\theta }=3$ with the EAP1 estimator dipped as low as .276 within replications!). These results suggest that, if the data were generated from the 4PL, less biased trait estimates with better coverage rates would be obtained by using the 1PL or 2PL instead of the more flexible 3PL. This surprising result deserves further exploration. In the following section, our attention is focused on the bias of IRT trait estimates under the 3PL.

A Closer Look at Biased Trait Estimates

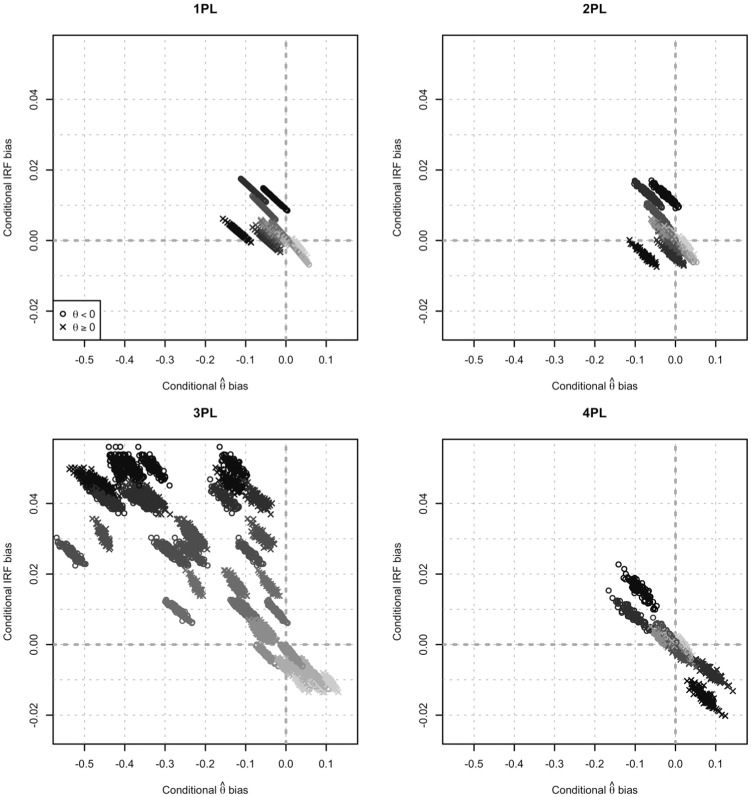
In the previous section, it was found that, for responses generated under the 4PL, trait estimates computed from the misspecified 3PL were heavily biased at extreme trait levels. Unexpectedly, trait estimates computed from misspecified 1PL or 2PL item parameter estimates were nearly unbiased. The fact that this result occurred for the 3PL but not for the 1PL or 2PL—which are submodels of the 3PL—suggests that some aspect of 3PL item parameter estimation causes biased trait estimates. As a first step, then, it is necessary to identify the ways in which the 3PL item parameter estimates differ from the 1PL, 2PL, and 4PL item parameter estimates. In previous studies of item parameter recovery, various indices have been used to evaluate item parameter recovery, including parameter bias and root mean square error (e.g., Hulin, Lissak, & Drasgow, 1982) and overall IRF recovery (e.g., Ramsay, 1991). Parameter recovery is explored by comparing the data-generating 4PL item parameters with the 100 sets each of 1PL, 2PL, 3PL, and 4PL item parameter estimates (i.e., the same sets of item parameters and estimates used in the simulation study described earlier). First, the recovery of item difficulties $b$ (the only parameter estimated for each item in all four models) is considered. Considering only those item parameters estimated with $N=20,000$ subjects, it was found that $b$ parameters are indeed more biased under the 3PL than under 1PL, 2PL, and 4PL: across items and replications, the $b$ parameter bias equals .00, −.02, .15, and .01 for the 1PL, 2PL, 3PL, and 4PL. Alternatively, the $b$ parameter root mean square errors across items and replications equal .57, .42, .53, and .29 for the 1PL, 2PL, 3PL, and 4PL. Although these numbers indicate that the 3PL $b$ recovery is not as good as using the correct 4PL model, 3PL $b$ recovery is comparable with $b$ recovery for the other models. In fact, $b$ parameter root mean square errors are larger for the 1PL than for the 3PL. Rather than $b$ parameter recovery, perhaps trait estimation bias can be better predicted by response function recovery, such as the root integrated mean square error (RIMSE; Ramsay, 1991). Across items and replications, the average RIMSE equaled .026, .022, .028, and .009 for the 1PL, 2PL, 3PL, and 4PL, respectively. Although the 3PL is associated with slightly larger RIMSEs than the other models, this index does not reflect the magnitude of bias observed only in the 3PL. One reason why the RIMSE only weakly predicts 3PL trait estimation bias may be because the RIMSE places greatest weight on central $\mathrm{\theta }$ values. In our simulation results, central $\mathrm{\theta }$ values were recovered fairly well for all models, but extreme $\mathrm{\theta }$ values were poorly estimated for the 3PL. To capture these conditional effects, IRF recovery is next evaluated as the IRF bias conditional on $\mathrm{\theta }$. The relationships between $\hat{\mathrm{\theta }}$ bias and conditional IRF bias averaged across the 100 test items are displayed in Figure 1 for the 1PL, 2PL, 3PL, and 4PL. The four panels of this figure correspond to the four item response models, and each panel includes 13 $\mathrm{\theta }$ values crossed with 100 sets of item parameter estimates computed with $N=20,000$ subjects. In this figure, darker colored points represent more extreme $\mathrm{\theta }$ values (i.e., closer to $\left|\mathrm{\theta }\right|=3$), lighter colored points represent $\mathrm{\theta }$ values closer to 0, “o” points represent data-generating $\mathrm{\theta }<0$, and “×” points represent data-generating $\mathrm{\theta }\ge 0$. Notice in this figure that each panel displays a number of clustered points that appear to have strong linear relationships within clusters. Further investigation reveals that these clusters correspond to different data-generating $\mathrm{\theta }$ values. Across $\mathrm{\theta }$ values and replications, conditional IRF bias predicts .38, .26, .96, and .83 of the variance in conditional $\hat{\mathrm{\theta }}$ bias for the 1PL, 2PL, 3PL, and 4PL, respectively. Moreover, the 3PL estimated IRFs have greater conditional bias than the 1PL and 2PL. Recall that each dot represents an average across 100 test items. This means that the 3PL item parameter estimates are systematically conditionally biased. It is not necessarily that each estimated 2PL IRF reproduces the true 4PL IRF better than each estimated 3PL IRF. Instead, across test items, the conditional IRF biases tend to be in the same direction for the 3PL, whereas they cancel out for the 2PL. These results provide convincing evidence that (a) conditional IRF bias causes trait estimation bias, and (b) our simulation results showed greatest bias for 3PL trait estimates because the 3PL conditional IRFs exhibit greater systematic bias than the 1PL, 2PL, or 4PL conditional IRFs.

Figure 1.

Scatter plot of conditional EAP2 $\hat{\mathbf{\theta }}$ bias versus conditional IRF bias.

Note. Results are displayed for 100 sets each of 1PL, 2PL, 3PL, and 4PL estimated item parameters computed with $N=20,000$. Lighter colored dots correspond to data-generating $\left|\mathbf{\theta }\right|$ values closer to 0, and darker colored dots correspond to data-generating $\left|\mathbf{\theta }\right|$ values closer to 3. In addition, “0” points represent data-generating, and “×” points represent data-generating $\mathbf{\theta }\ge 0$. EAP = expected a posteriori; IRF = item response functions.

Before exploring why the 3PL estimated IRFs and trait scores are conditionally biased, it should be noted that sets of estimated item parameters that lead to biased trait estimates do not necessarily exhibit poor model–data fit. To illustrate this point, absolute model fit, relative model fit, and item fit statistics are computed for the sets of 1PL, 2PL, 3PL, and 4PL estimated item parameters described earlier. All fit results are reported in Table 2. Recall that each model was fit to the same 100 data sets, where each data set was generated under the 4PL with $N=20,000$ subjects. Absolute model fit was first considered as indexed by the M₂ limited-information goodness-of-fit statistic (Maydeu-Olivares & Joe, 2005) and the RMSEA₂ (root mean square error approximation) limited-information goodness-of-approximation measure (Maydeu-Olivares & Joe, 2014). For the M₂ statistic with α = .05, 94% of the 4PL models fit (close to the expected rate of 95%), 81% of the 3PL models fit, and none of the 2PL or 1PL models fit. These results show that in the majority of data sets generated from a 4PL and a very large sample size ($N=20,000$), the M₂ statistic will indicate acceptable model fit for the 3PL. The average $\mathrm{RMSE}{\mathrm{A}}_2$ indices also indicate close model fit for the 3PL. Across replications, the average RMSEA₂ value for the 3PL equals .0008, far below the $\mathrm{RMSE}{\mathrm{A}}_2<.05$ cutoff recommended by Maydeu-Olivares and Joe (2014) for assessing close model fit in IRT models. Moreover, the RMSEA₂ values for the 3PL are, on average, only .0004 larger than the RMSEA₂ values for the 4PL. In fact, in 20% of data sets, the 3PL resulted in a lower RMSEA₂ value for the 3PL than for the 4PL. Although across replications these absolute model fit measures show slightly better fit for the correct 4PL than for the 3PL, they do not suggest any major problems with 3PL absolute model fit for most data sets. Relative model fit was next considered as indexed by the deviance information criterion (DIC; Spiegelhalter, Best, Carlin, & van der Linde, 2002),¹ which selects an appropriate model by balancing improvements in model fit with the costs of increased model complexity. For each of the 100 data sets of $N=20,000$, the DIC selected the 4PL as the best fitting model. When the 4PL DICs were omitted from the model comparison, the DIC selected the 3PL for every data set. These relative model fit results indicate that the 3PL fits substantially better than the 2PL or the 1PL for data generated under the 4PL. Next, for each set of estimated item parameters, the proportion of items that fit according to the $S-X^2$ statistic (Orlando & Thissen, 2000) was looked at. Setting a Type I error rate of α = .05, 7%, 51%, 76%, and 94% of the 1PL, 2PL, 3PL, and 4PL items fit. Although more items fit under the 4PL than under the other models, the 3PL still leads to a majority of items that fit and many more items that fit than the 2PL or 1PL. Although these fit results are not surprising—the data-generating model is more complex than the 1PL, 2PL, and 3PL, and the 3PL is more complex than the 1PL or 2PL—they also show that assessing fit does not detect items that produce biased trait estimates.

Table 2.

Absolute and Relative Model and Item Fit Statistics.

	M2 model fit proportiona	RMSEA2 mean (min, max)b	RMSEA2 lowestc	DIC lowestd	S− X2 item fit proportion overall (min, max)e
4PL	.94	.0004 (.0000, .0015)	.80	1.00	.94 (.90, .99)
3PL	.81	.0008 (.0000, .0018)	.20	.00	.76 (.71, .83)
2PL	.00	.0060 (.0057, .0063)	.00	.00	.51 (.44, .55)
1PL	.00	.0216 (.0210, .0221)	.00	.00	.07 (.03, .11)

Note. This table represents model and item fit statistics for 100 data sets (replications), each with 100 items and $N=20,000$ subjects fit to the 1PL, 2PL, 3PL, and 4PL. RMSEA = root mean square error approximation.

^aProportions of estimated models that fit according to the M₂ statistic with α = .05.

^bAverage, minimum, and maximum RMSEA₂ index across the 100 replications.

^cProportion of data sets for which each model provides the lowest RMSEA₂ value among the four competing models.

^dProportion of data sets for which each model provides the lowest DIC value among the four competing models.

^eProportion of items that fit according to the S−X² statistic with α = .05. This proportion is reported across test items and replications, and the minimum and maximum proportions within replications are reported in parentheses.

Above, it was established that biased trait estimates are the result of systematically biased IRF estimates, and that conditionally biased IRFs need not be detected by fit indices. The effects of item elimination based on the $S-X^2$ statistic (see Online Appendix B) were also considered, but it was found that this strategy only reduces trait estimation bias in extremely large calibration samples. These results suggest that the added bias of 3PL IRFs leads to better model–data fit than 3PL IRFs that are less systematically biased (e.g., the 2PL IRFs, which are identical to 3PL IRFs with $c=0$). However, it may also be that biased item parameter estimates stem from suboptimal choices in item parameter estimation. Perhaps different item calibration choices—in particular, different Bayesian priors—might produce different bias results. To evaluate the extent to which the choice of $c$ prior affects bias results, the 3PL simulations were ran at $N=20,000$ four more times with four different priors on $\mathrm{logit}(c)$ (recall that mirt places a prior on $\mathrm{logit}(c)$ rather than on $c$ itself). The studied priors were as follows: (a) a flat prior on $\mathrm{logit}(c)$, (b) a N(−5, .1) prior that is highly informative at $c=0$ when logits are transformed to the $c$ metric, (c) a N(−1.09, .01) prior that is highly informative at $c=.25$, and (d) a N(0, 1.5) prior that is relatively flat across the $[0,1]$ interval on the $c$ (probability) metric. Each of these priors led to different amounts of EAP2 $\hat{\mathrm{\theta }}$ bias when averaged across replications. At $\mathrm{\theta }=3$, bias equaled −.50 for the original N(−1.8, 1) prior, −.48 for the flat prior, .14 for the N(−5, .1) prior, and −1.08 for the N(−1.09, .01) prior. Full bias results are available upon request. These results suggest that even at very large sample sizes, the bias of trait estimates computed from estimated 3PL item parameter estimates is highly sensitive to the choice of Bayesian priors. Finally, to establish that these results are not specific to the mirt software, these results are successfully reproduced using Hamiltonian Monte Carlo in the rstan (Stan Development Team, 2016) package for R. Results are reported in Online Appendix C.

Implications

The finding that trait estimates are biased under the misspecified 3PL suggests that the metric of the estimated trait differs from the metric of the data-generating trait. The fact that the 3PL is negatively biased at both low and high trait scores implies a nonlinear relationship between $\mathrm{\theta }$ and $\hat{\mathrm{\theta }}$. This result stands in stark contrast to the theoretical result that parametric item response models—including the 3PL—are identified up to linear transformations of the latent trait. In terms of Stevens’s (1946) taxonomy, the IRT latent trait is interval-level when using parametric models. It is true that for parametric IRT models, the units and interval spacing of the latent trait are determined, up to linear transformations, by the functional form of the IRF (Lord, 1975). However, if the latent trait is transformed by a nonlinear but monotonic function, an item response model exists that makes identical predictions only with a different IRF shape (Lord, 1975). If the IRF functional form is misspecified, then the units and interval spacing are not determined by the correct IRF functional form. Thus, there is no reason to believe that the latent trait determined by the misspecified functional form should be linearly related to the latent trait determined by the correct functional form. Put another way, if the IRT latent trait is interval-level conditional on the fitted IRF shape (e.g., 4PL), then if the fitted IRF shape deviates from the data-generating IRF shape, the fitted latent trait need not retain the units and interval spacing of the data-generating latent trait. Although fitting the 3PL to 4PL-generated data should introduce some degree of model misfit, it is entirely plausible that the best fitting IRT model under the misspecified IRF form implies a latent trait that is nonlinearly related to the data-generating latent trait.

It is worth noting that this is not the first time that systematic biases in trait estimates—implying a nonlinear distortion of the latent trait metric—have been found with regard to the 3PL. A similar result was found by Yen (1981) in a slightly different context. She found that, when analyzing 3PL-generated data with the 2PL and 3PL, the two models fit equally well, but that the two sets of trait estimates were curvilinearly related, with “the [2PL] trait estimates more stretched out at the high end than the [3PL] traits” (p. 259). Yen explained her results in terms of model misspecification and the ability of the 2PL parameters to compensate for the lack of lower asymptote. Our results add nuance to this understanding of trait estimation under misspecified models. Rather than attempting to find and fit the true data-generating model, simpler IRT models may perform well so long as they make relatively unbiased test-level predictions conditional on all $\mathrm{\theta }$ values of interest. To be more precise, it is not necessary that all IRFs are conditionally unbiased; it is good enough if the test response function (i.e., the sum of IRFs) is conditionally unbiased. One way to achieve unbiased IRFs is to fit nonparametric item response models (e.g., Ramsay, 1991). Nonparametric models fit item response curves that are less conditionally biased than those of parametric models. However, nonparametric IRT trait estimates should only be interpreted as ordinal quantities, and so this solution will not provide the user with trait estimates with meaningful units. Ultimately, if one aims to develop a scale with meaningful units, the units should either be referenced against an external variable (e.g., grade levels), or a measurement approach should be taken that permits interval-level interpretations (see, for example, Perline, Wright, & Wainer, 1979).

Perhaps the most important implications of these findings might relate to how the latent trait metric is interpreted. In fact, many of the statistics and procedures used on IRT trait estimates imply an interval-level metric. For instance, linear item linking, evaluating change or growth over time, and even the use of confidence intervals based on normally distributed standard errors all depend on the idea that intervals on the latent trait are fixed and meaningful. Furthermore, distributional statements about the latent trait and parametric statistics applied to latent trait scores imply an interval-level latent trait. One may argue that interval-level interpretations are justified so long as the same procedures are applied to all individuals (i.e., so long as all individuals are scored using the same set of estimated item parameters). The trouble with this idea is that the units and spacing of the trait scores are then inextricably bound to the estimated item parameters of the test. If the test’s item parameters were to be validated with independent data, small differences in methodology, such as a change in Bayesian prior, could lead to different substantive conclusions.

Solutions to the problem of biased trait estimates are not obvious, partly because it is not easy to detect bias when the data-generating model is unknown. As demonstrated above, item elimination based on item fit statistics might reduce trait estimation bias in extremely large item calibration samples, but these methods are less effective in moderate to small item calibration samples. Trait estimation methods that adjust for both the bias and variability associated with item parameter estimation (e.g., Lewis, 1985, 2001; Tsutakawa & Johnson, 1990) might result in less biased trait estimates, although these methods assume correct model specification and have not yet been tested on misspecified IRT models. At minimum, researchers can perform additional checks when calibrating item parameters to detect whether the estimated latent trait is unstable. For instance, when calibrating item parameters, researchers could fit additional models with other methodological choices, and check whether methodological differences lead to test response functions that predict very different scores for some ranges of the latent trait continuum.² An example of such a check was demonstrated in the previous section, in which the 3PL model was refit using several choices of Bayesian priors. In this example, it was found that trait estimates at extremes of the latent trait had very different average values depending on the choice of Bayesian priors. If these robustness checks suggest that item calibration is indeed sensitive to methodological choices, either a less malleable (but still well-fitting) model should be chosen, or caution should be exercised to avoid interval-level score interpretations.

Conclusion

The goal of this study was to determine the relative impact of trait estimation error, item parameter estimation error, and model misspecification on the bias and confidence interval coverage rates of IRT latent trait estimates. Our results clearly showed that, assuming sufficiently large data sets, the greatest errors in latent trait estimates result from model misspecification. However, it was found that not all misspecified models introduce estimation errors, and the effect of model misspecification is not directly related to the complexity of the fitted model. Specifically, it was found that when 4PL data were fit to the 3PL, trait estimates were heavily biased and had poor coverage at extreme trait levels. Surprisingly, when 4PL data were fit to the 2PL or 1PL, trait estimate bias statistics and confidence interval coverage rates were similar to those from the correctly specified model. Follow-up analyses demonstrated that bias in latent trait estimates can be predicted from systematic conditional bias in the estimated item response functions.

Our simulation study was limited to only one type of model misspecification, and so the specific results reported in this article may not directly apply to other types of functional form misspecifications or misspecified dimensionality. However, the results of this study clearly demonstrate that seemingly minor model misspecification can have large effects on the scaling of the latent trait metric. Put another way, it was demonstrated that there is not a direct relationship between model/item fit and parameter estimation bias, a result which ought to be explored for other types of IRT model misspecification. Our results show that estimated models that demonstrate acceptable fit are not necessarily immune from the effects of model misspecification, especially when item calibration samples are not extremely large.

In this article, it was found that item parameter estimation methods that systematically underestimate or overestimate response probabilities can lead to trait estimates that are nonlinearly related to the true latent trait. Systematic bias could also occur if, for example, guessing behavior is not taken into account (low ability examinees will have systematically underestimated trait scores, even if a guessing parameter is fixed to a certain value but is inappropriate for the data). It is recommended that researchers routinely evaluate the sensitivity of estimated item parameters and response functions to small methodological choices. Researchers are also encouraged to draw interval-level score interpretations with great caution and only after evaluating the sensitivity of their fitted models.