On-chip Heaters for Tension Tuning of Graphene Nanodrums

Abstract

For the study and application of graphene membranes, it is essential to have means to control their resonance frequency and temperature. Here, we present an on-chip heater platform for local tuning of in-plane tension in graphene mechanical resonators. By Joule heating of a metallic suspension ring we show thermomechanical resonance frequency tuning in a few-layer (FL) graphene nanodrum, which is accompanied by an increase in its quality factor, which we attribute to the increase of the in-plane tension. The in situ control of temperature, in-plane tension, resonance frequency, and quality factor of suspended two-dimensional (2D) nanodrums makes this device a unique platform for investigating the origin of dissipation in these ultrathin structures and can be of fundamental importance for studying the thermal properties of 2D materials. Moreover, by simultaneously controlling the heater and the backgate voltage, we can independently control the resonance frequency and quality factor, which is of great importance for applications in sensors and resonant mechanical filters.

Since the first realization of graphene mechanical resonators,¹ there have been many technological achievements showcasing their successful electrical readout,² constructing tunable mechanical oscillators³ and voltage-controlled variable capacitors.⁴ Graphene- and 2D material-based nanoelectromechanical systems (NEMS) usually exhibit high and tunable resonance frequencies, which make them attractive candidates as mechanical RF filters, mixers, and voltage controlled oscillators. Frequency tunability is also of major importance for tuning the dynamic range of graphene-based pressure^5,6 and gas sensors,⁷⁻⁹ and in more fundamental studies, for tuning the nonlinear coupling between mechanical resonance modes^10,11 or coupling superconducting microwave cavities to graphene nanodrums.¹²⁻¹⁴

To achieve tuning, graphene-based NEMS usually incorporate a local gating scheme, where a voltage difference is applied between the suspended membrane and a bottom electrode. The resulting electrostatic force exerted on the membrane increases the tension in the membrane and can be used as a tuning knob for the mechanical resonance frequency. An interesting observation is that the tunability, in such cases, comes at a cost of increased dissipation, i.e., a decrease in the quality factor.¹⁵⁻¹⁷ This is unusual since increased tensile stress in nanomechanical devices is usually associated with a decrease in dissipation.¹⁸⁻²¹ However, when strain is applied externally, e.g., by cooling down the sample to cryogenic temperatures^2,15−17 or by using a piezo crystal underneath the sample,²² the frequency increase is accompanied by an increase of the quality factor. Consequently, the ability to mimic this effect with an on-chip tensioning mechanism is of great interest because it allows reaching higher f–Q products, and it is important for low loss sensing, low phase-noise oscillators²³ and for reaching the quantum ground state of nanomechanical resonators.²¹ Achieving this will also provide new insights on the dissipation mechanisms in 2D nanomechanical resonators.

In this work, we present an on-chip heater device that is capable of tuning the in-plane tension of graphene nanodrums by Joule heating. Using a ring-shaped structure that undergoes thermal expansion, we demonstrate tuning of tensile strain in a suspended FL graphene nanodrum, which results in an increase of its mechanical resonance frequency, while at the same time reducing mechanical dissipation. In addition to the usually employed electrostatic^2,3 and optothermal actuation mechanisms,^1,24 it is shown that the device design also allows for electrothermal actuation, where the motion of the drum is excited by a thermal ac signal. The dynamic characterization of the FL graphene drum is supported by in situ atomic force microscopy (AFM) measurements that show the effects of in-plane biaxial tension on the morphology of suspended 2D materials.

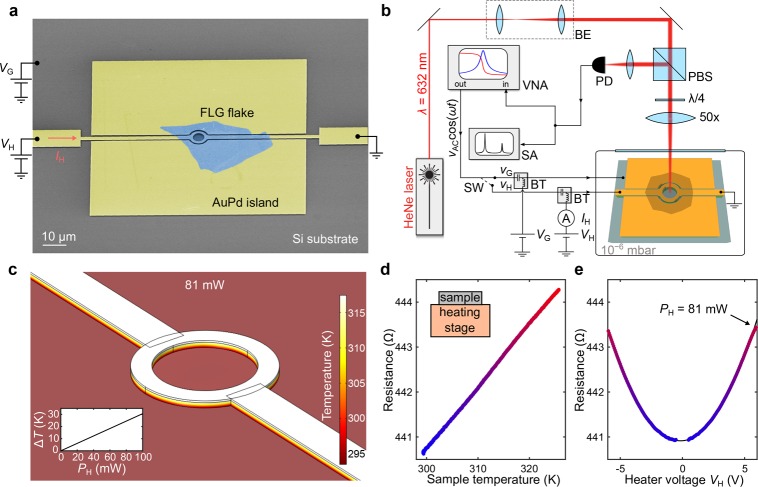
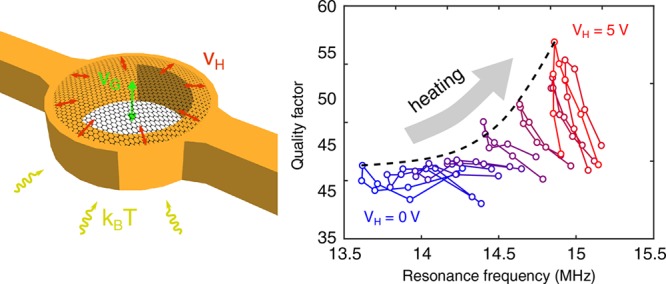
The device is shown in Figure 1a. The heater consists of a narrow (2 μm wide), long AuPd electrode with a circular ring structure in the middle (inner diameter, 5 μm; outer diameter, 7 μm). The width of the heater ring is exactly one-half of the width of the rest of the electrode, such that the resistance per unit length is constant, resulting in a spatially uniform heat flux. On both sides of the heater there are AuPd metallic islands that serve as mechanical support for the graphene flake. All metallic structures are supported by a SiO₂ layer (the thickness of the SiO₂–AuPd stack is 385 nm). The flake shown in Figure 1a is 4 nm thick FL graphene. When a voltage V_H is applied across the heater, a current I_H runs through the heater ring, causing Joule heating. As a consequence, tensile stress is generated in the suspended graphene flake due to the positive thermal expansion of the supporting heater ring and the negative thermal expansion of the graphene.^15,25 In addition, a more conventional way of tensioning the graphene drum is available, by an out-of-plane electrostatic force that can be generated using the silicon backgate.

Figure 1.

(a) False-colored scanning electron micrograph of the device. The FL graphene flake (blue) is suspended over the AuPd (yellow) heater and supported by the surrounding AuPd islands (electrically floating). Voltage is applied to one end of the heater (V_H), and the other end is grounded. The resulting dissipated power (V_HI_H) causes a temperature increase in the narrow heater structure. (b) Measurement setup: a HeNe laser is focused on the suspended graphene drum, which is mounted in a high-vacuum chamber. The motion of the drum modulates the reflected intensity of the laser, which is captured using a photodiode (PD). The drum can be driven both electrothermally (using the heater, v_H) and electrostatically (using the backgate, v_G), depending on the switch (SW) configuration. The driven motion is measured using a Vector Network Analyzer (VNA), and the undriven (Brownian) motion is measured using a Spectrum Analyzer (SA). (c) Finite element model of the temperature profile across the heater structure for an input Joule heating power of 81 mW. The inset shows the temperature increase (ΔT) as a function of the heater power. (d,e) Measured heater resistance when heating the entire sample using an external stage heater (d) and when applying a voltage on the heater (e). Resistance, as found in the calibration measurement (d), is used to estimate the heater temperature during Joule heating (e), as indicated by assigning identical colors to data points of identical resistance.

A detailed schematic of the measurement setup is shown in Figure 1b. A HeNe laser is focused onto the graphene drum, which is mounted in a vacuum chamber. The reflected laser light is interferometrically modulated by the motion of the drum and its intensity is measured by a photodiode (PD). The ac driving voltage can be applied to the heater electrode (v_H) or to the gate electrode (v_G). In both configurations, the two bias-tees (BT) also enable dc biasing of the heater (V_H) and/or of the silicon gate (V_G). Both the driven and the undriven motion of the drum is measured using a vector network analyzer (VNA) and a spectrum analyzer (SA), respectively.

In Figure 1c we show a finite-element simulation of the temperature profile of the heater at a fixed input power. The details of the finite-element model are outlined in the Supporting Information Section I. The image shows the temperature profile for a thermal power of P_H = V_H²/R_H = 81 mW. In this case, the temperature of the heater is 25 K higher than the ambient temperature. As expected, the calculated temperature difference ΔT is proportional to the heater power (see inset of Figure 1c). The temperature of the heater is also determined experimentally, by measuring the temperature-dependent resistance change of the heater itself (under laser illumination). To calibrate it we use a heating stage to warm up the entire sample and measure the heater resistance (see Supporting Information Section II for details). The resulting R–T curve is shown in Figure 1d. The measured resistance as a function of heater voltage is shown in Figure 1e. Using the calibration data, we convert the measured resistance into temperature, which is color-coded in the data points in (d) and (e). The measured temperature increase is comparable to the simulated one (Figure 1c).

The added functionality of the heater allows for three different actuation methods, which are schematically shown in Figure 2a. At finite temperature the motion of the drum is excited by thermal noise. A measurement of the resulting Brownian motion of the drum is shown in Figure 2b. From this measurement, we extract the displacement sensitivity, 1.1 × 10⁶V/m, and the noise floor of the measurement setup, 72 fm/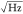. These numbers are comparable to our previously reported values,²⁶ which show that the presence of the heater structure does not deteriorate the performance of the measurement setup. Conventionally, the drum can also be driven using an out-of-plane force by applying a voltage on the backgate: V_G + v_G cos ωt, where ω = 2πf. An example of such measurement is shown in Figure 2c. The top panel shows the phase, and the bottom panel shows the magnitude of the motion.

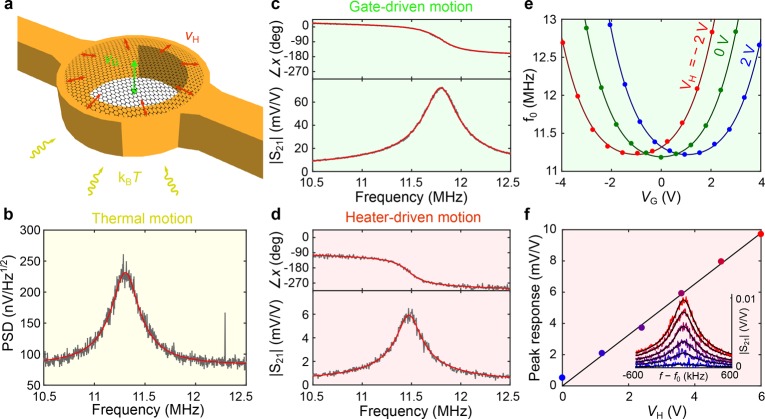
Figure 2.

(a) Schematic of the three actuation mechanisms used. The color of each of the arrows corresponds to the background of each panel. The Brownian motion occurs due to the finite temperature of the environment (yellow arrows). The drum can be driven using electrostatic driving via the gate (V_G, green arrow) or using electrothermal driving via the heater (V_H, red arrows). (b) Thermal (undriven) motion of the drum measured using the spectrum analyzer. (c) Phase (top) and magnitude (bottom) of the gate-driven motion at zero heater power (V_H = 0 V) with v_G,RMS = 25.2 mV. (d) Phase (top) and magnitude (bottom) of the heater-driven motion at zero gate voltage (V_G = 0 V) with v_H,RMS = 25.2 mV. (e) Extracted resonance frequency (f₀) as a function of the gate voltage V_G for three different heater voltages. The black lines are polynomial fits of the f₀ vs V_G curves, as a guide to the eye. The temperature increase at V_H = ±2 V is 2.2 K. The drive amplitude is v_G,RMS = 25.2 mV. (f) Extracted amplitude at resonance as a function of the dc voltage on the heater. The black line is a linear fit. The inset shows the data and fits for each of the color-coded points. The drive amplitude is v_H,RMS = 25.2 mV.

The design of the device also allows for exciting the motion of the drum with an in-plane force resulting from the thermal expansion of the heater (electrothermal driving). Although, assuming a perfectly flat membrane, an in-plane periodic force should not be able to excite out-of-plane motion, structural irregularities in the membrane (ripples, slack, wrinkles) will always give a net out-of-plane component to the in-plane force. Electrothermal actuation is performed by applying the driving voltage across the heater: V_H + v_H cos ωt, causing the heater ring to expand and contract periodically, which results in a modulation of the tension of the drum. The heat transport at a driving frequency ω can be modeled as

1

where C and κ are the thermal capacitance and conductance of the system, ΔT is the temperature difference with respect to the steady-state temperature, and p_H is the applied ac heating power. The expected thermal-expansion-induced amplitude is then given by

2

where x_ω is the motion amplitude at ω, α_eff is the effective thermal expansion coefficient of the AuPd–graphene system, and τ is the characteristic thermal delay time of the system (τ = C/κ). A measurement using this actuation method is shown in Figure 2d. The bottom panel shows the measured magnitude and the top panel shows the phase. Compared with Figure 2c, where the drive is purely electrostatic, the resonance frequency of both measurements is roughly the same; the slight difference in resonance frequency of 0.3 MHz can be explained by the different dc values of the voltage applied to the heater V_H and the gate V_G (cf. Figure 2e). A striking difference between the two is the measured phase. Using electrothermal driving, we observe a phase difference of approximately −π/2 between the heater-driven motion and the gate-driven motion, which is indicative of a thermal delay in the system.^27,28 Using the phase difference at resonance, the characteristic delay time is estimated to be τ ≫ 14 ns (∠x_ω = −π/2 for ω ≫ 1/τ, see eq 2). This value is in accordance with what was previously reported on graphene nanodrums.²⁸ This provides evidence for high-frequency driving of graphene drums by Joule heating.

By applying a dc voltage on the backgate (V_G), we can also tune the resonance frequency of the drum. Due to the out-of-plane deflection of the drum, this results in an electrostatically induced tension, which manifests itself as an increase in the resonance frequency. Such a measurement is shown in Figure 2e (green points). The location of the minimum of this curve is determined by the condition at which the gate voltage equals the potential of the graphene flake, which may sometimes deviate from zero due to trapped charges on the graphene or a difference in the workfunctions of the graphene and the contacting electrode.² In our experiment, for V_H = 0 V, the parabola is centered around V_G = 0 V, indicating that the effect of trapped charge is negligible. For V_H ≠ 0 V, however, we use the location of this minimum to estimate the effective potential of the graphene drum. Due to the symmetric design of the heater structure, the potential of the graphene drum is expected to raise by half of the voltage applied across the heater (V_H). The red and blue data points in Figure 2e represent measurements using V_H = −2 and 2 V, respectively. The fact that the minima of these curves are shifted by half of the applied heater voltage (by −1 and 1 V) confirms that the potential at the graphene drum is V_H/2. By combining voltage shifts due to the applied gate and heater voltages, the effective gate voltage across the gap that causes electrostatic forces becomes V_G,eff = V_G – V_H/2. This is used in subsequent measurements to decouple the influence of the heater-induced and backgate-induced tension.

To establish that the resonance in Figure 2d is indeed excited by high-frequency heating, a set of measurements is performed at different ac heating powers p_H by varying V_H, while keeping V_G,eff = 0 V to eliminate the possibility of residual electrostatic forces. In Figure 2f, we show the dependence of the resonance peak height of the electrothermally driven motion on the dc heater voltage (V_H). In such a configuration, if the drive was due to capacitive cross-coupling to the gate, the measured amplitude would not depend on the value of V_H. Since the ac heating power is proportional to V_Hv_H and the ac electrostatic force is proportional to V_G,eff(v_G + γv_H), γ being a cross-talk factor, the observation that the amplitude increases linearly with the dc heater voltage proves that the nature of the driving is electrothermal (cf. Figure 2d).

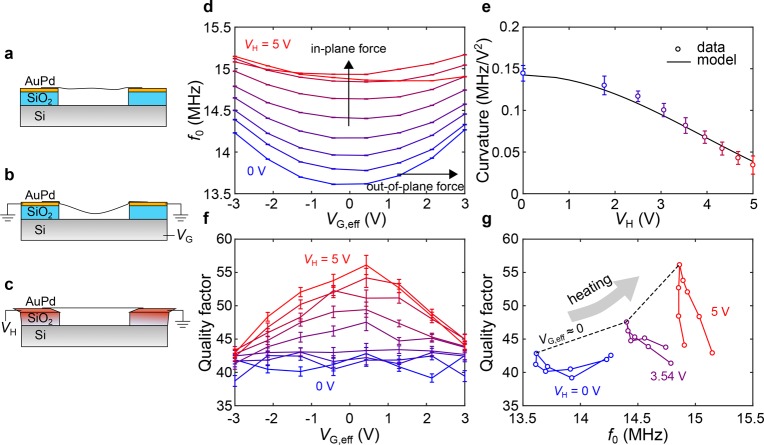
A differentiating advantage of the presented device is that it provides an alternative tensioning mechanism: the force resulting from the thermal expansion of the heater causes in-plane biaxial tension in the membrane, parallel to the substrate, in contrast to electrostatic forces, which have a significant out-of-plane component. This concept is illustrated in Figure 3a–c. Figure 3a represents the device as-fabricated, rippled,²⁹ and slightly adhered to the walls.^30,31 When using electrostatic force (Figure 3b), the drum is pulled downward, promoting sidewall adhesion but still contributing to the tension due to the geometrical deformation of the structure.³² When using the heater, the drum is expected to stretch in-plane (Figure 3c), which increases the stiffness and flattens the membrane.

Figure 3.

(a–c) Artist impression of the tensioning mechanisms. (a) Device as-fabricated. (b) Electrostatically induced vertical deflection. When using the heater, (c) the graphene is stretched in-plane due to the thermal expansion of the ring and contraction of the graphene flake. Resonance frequency (d) and quality factor (f) as a function of V_G,eff for increasing V_H. The color of each curve denotes the heater voltage (see x-axis of (e) for the values). (e) Extracted curvature (d²f₀/dV_G²) of the V_G vs f₀ curve around V_G,eff = 0 V. The black line shows the modeled response. (g) Quality factor vs resonance frequency plot for gate sweeps at different heater voltages. The middle point of each curve represents the case where V_G,eff ≈ 0 V (points are connected by a black dashed line).

To compare the two tensioning mechanisms, we look at the frequency tuning using both the backgate (out-of-plane force) and the heater (in-plane force) and how each mechanism affects the mechanical dissipation of the resonator. In Figure 3d, we look at the frequency tuning curves using the backgate centered around V_G,eff = 0 V. The different colors correspond to different heater voltages from zero to 5 V. Two effects can be observed: first, the resonance frequency at V_G,eff = 0 V increases with increasing heater voltage, indicating an increase in tension with V_H; second, we observe a decrease in the tunability of the frequency with the backgate for increasing heater voltage. The latter can be quantified by extracting the curvature of each curve at V_G,eff = 0 V, as shown in Figure 3e. This decrease in gate tunability can be explained by a model that takes into account the added tension due to the electrostatic force as a function of the in-plane tension. The observed trend is another confirmation that the heater-induced tension is in-plane. The mathematical model of this behavior, which was used to fit the data in Figure 3e, is shown in the Supporting Information Section III. The model takes into account a circular membrane under an electrostatic load. The resonance frequency of the membrane is calculated as a function of electrostatic load for increasing values of the pretension, which is analogous to adding in-plane tension by means of thermal expansion of the ring. Using this model, we also extract the effective thermal expansion coefficient of the graphene-heater system: α_eff = 1. 64 × 10^–6 K^–1 (see eq 1).

Dissipation in 2D mechanical resonators is still poorly understood and is a subject of debate.^2,15,33 It is well-known that the electrostatically induced shift in resonance frequency is usually accompanied by a decrease in the quality factor,^15,16 and this has been attributed to electronic Joule dissipation of the displacement current through the resonator.¹⁶ Surprisingly, when tuning the tension electrothermally, the frequency increase of ∼10% (at V_H = 5 V) is accompanied by a 33% increase in the quality factor (from Q_0 V = 42 to Q_5 V = 56), as shown in Figure 3f. This is unexpected and cannot be explained in the framework of the usually observed temperature-dependence of the quality factor, which decreases with increasing temperature.^2,15,16,34 Similar to our observations, simultaneous reduction in dissipation and increase in resonance frequency was observed by Kramer et al. when using a piezo crystal to apply in-plane tensile strain in MoS₂ nanodrums.²² It can be inferred that the increase in quality factor is directly connected with the increase of in-plane tension, as reported in refs (18−21).

To illustrate this better, Figure 3g shows an f₀–Q plot. Each color represents a sweep of V_G centered around V_G – V_H/2 = 0 V at a different heater voltage. The black dashed line connects the points of the curves where the effective gate voltage is close to zero to show the simultaneous increase of both the resonance frequency (i.e., tension) and the quality factor upon increasing the heater voltage. The same effect was observed in two other samples, shown in the Supporting Information Section IV. It is interesting to note that, using two control inputs, V_G and V_H, we gain access to a large portion of the f₀–Q parameter space and show that this allows independent tuning of the resonance frequency and the quality factor (see Supporting Information Section V). The ability to control the quality factor and the frequency of the resonator independently is a rather unique feature of our device, enabling applications in, for example, tunable filters, where both bandwidth and frequency need to be controlled.

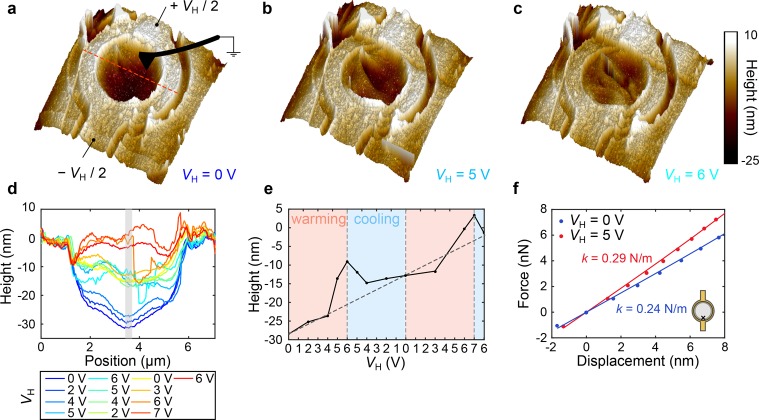
Atomic force microscopy is a powerful tool for studying the mechanical properties of 2D materials.³⁵ To gain more insight into the topography of the resonator and how it is affected by tension, we perform a series of AFM measurements in peak-force mode (using a Bruker FastScan AFM) while varying the heater voltage, shown in Figure 4. For these measurements, the heater is connected symmetrically to a bipolar voltage source to ensure that V_G,eff = 0 V, such that no electrostatic force is exerted between the AFM tip and the resonator. The gate electrode and the AFM tip are electrically grounded. Measurements at three different heater voltages are shown in Figure 4 a–c. Two qualitative observations can be made. First, the measured membrane height in the center of the drum increases with increasing heater voltage, indicative of a higher in-plane tension that flattens the membrane. Second, at high heater voltages V_H, the morphology of the drum changes substantially through the formation of what appears to be a wrinkle. Upon careful inspection, a point-like imperfection at the edge of the membrane, also observed at V_H = 0 V (Figure 4a), seems to be the cause for the formation of this wrinkle. The presented data demonstrate, to our knowledge, the first direct observation of in situ wrinkle formation under biaxial tension. Such measurements can be used for investigating the delicate dynamics of morphological imperfections in suspended 2D materials and their influence on the mechanical properties of these ultrathin membranes.³⁶⁻³⁹

Figure 4.

(a–c) AFM images of the flake taken at three different heater voltages. (d) Extracted height profiles along the central cutline (dashed red line in (a)) of the drum for a sequence of heater voltages. Each color represents a different voltage, and the order of the measurements matches the order of the colors. (e) Extracted average height of the center of the drum (gray region in (d)) as a function of V_H. The x-axis represents the measurement sequence and shows the value of V_H (axis is not monotonic). The dashed line is a guide to the eye. (f) Force–deflection curves taken near the edge of the drum (black cross in the inset) at two heater voltages: 0 V (blue) and 5 V (red).

A total of 13 images is recorded while sweeping the heater voltage up and down in the sequence shown in Figure 4d. Figure 4d shows a horizontal cutline of the AFM height maps. It can be seen that the position of the center of the drum moves upward with increasing heater voltage, which is accompanied by a decrease in the membrane slack (amount of wall adhesion). The decreased wall adhesion can be the reason for the observed increase in the Q-factor of the resonator upon heating (Figure 3f), due to the reduced area of the wall-adhered surface and therefore reduced coupling to the substrate.⁴⁰

The extracted height at the center of the drum is shown in Figure 4e. The height is taken from the horizontal cutlines, averaging over five points just to the left of the wrinkle (gray region in Figure 4e). The x-axis shows the sequence of heater voltages applied. The height of the drum increases when heating up and decreases when cooling down, which is suggestive of increasing tension in the drum. Moreover, we also observe a displacement of the center of the drum upon a complete warm-up–cool-down cycle at zero heater power. This permanent upward deformation can be a consequence of the dynamics of wrinkle formation, given that there is an energy cost associated with wrinkle unzipping. Figure 4f shows two AFM force-deflection curves taken near the edge of the drum (position shown in the inset) at two different heater voltages. The slope of each curve represents the linear spring constant of the drum, which is related to the pretension.³⁵ In accordance with the frequency response measurements (Figure 3) and the measurements from Figure 4e, an increase of the tension of the drum is observed upon increasing the heater voltage. It is important to note that the ratio between the extracted spring constants (k_5 V/k_0 V = 1.21) matches the ratio of the pretension extracted from the measured resonance frequencies in Figure 3d, .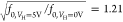

With the experiments shown in Figure 4, we show that even in nanodrums that are initially flat, wrinkles appear upon the application of tensile strain. Small imperfections at the clamping edge of the drum or small anisotropies in the applied strain can be potential seeds for the wrinkles. It might very well be that even the smallest imperfections or anisotropies will eventually lead to the formation of wrinkles, as long as the tensile strain is large enough. We therefore anticipate that the observation of these wrinkles in our system is not an artifact related to the device construction, but rather a phenomenon that will occur at a certain tensile stress value in any nanodrum, sooner or later, depending on the size of the imperfections or asymmetries in the system.

In conclusion, we realized an on-chip heater device capable of tuning the in-plane tension of suspended 2D material membranes. Using dc Joule heating, we show tuning of the in-plane tension of suspended graphene membranes, which results in a resonance frequency increase of 10%. In contrast to the case of electrostatic gating, the increase in frequency is accompanied by an increase in the quality factor of 32%, which we attribute to the increase in in-plane tension of the graphene nanodrum. We also demonstrate that this device concept provides a new way of actuation of 2D resonators, by means of ac electrothermal modulation of the tension in the suspended structure. The presented device can serve as a platform for fundamental studies on nonlinear dynamics and thermal properties of suspended 2D materials, as well as a tool for independently tuning the resonance frequency and the quality factor in next-generation NEMS RF filters, modulators, and voltage controlled oscillators.

Methods

The device is fabricated onto a Si/SiO₂ wafer (SiO₂ thickness: 285 nm) using one e-beam lithography step to define all the metallic features (heater, electrodes, and metallic support islands). This is followed by evaporation of Ti/AuPd (5 nm/95 nm). The metal is then used as a hard mask to etch away the SiO₂ by reactive ion etching (50 sccm CHF₃, 2.5 sccm Ar, 7 μbar). The resulting cavity depth is 385 nm. The graphene flakes are exfoliated from natural crystals of highly oriented pyrolytic graphite and transferred on top of the heater electrode using a dry-transfer technique.⁴¹ The thickness of the graphene is determined by AFM. All measurements were performed using 0.5 mW incident laser power.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.7b05358.

• Temperature profile simulations; calibration of the resistance–temperature curves; modeling the frequency response as a function of in-plane and out-of-plane tension; measurements on two other devices; independent tuning of f₀ and Q (PDF)

Author Contributions

^⊥ These authors contributed equally.

The authors declare no competing financial interest.