Abstract
Background and Aims
Many African genera of the Amaranthaceae exhibit unique inflorescences that include sterile flowers modified to hooks or spines. Considering that the abundance of large terrestrial herbivores increased on the African continent with the expansion of grassland and savannah ecosystems, modified sterile flowers could have been an innovation that boosted the diversification of an African achyranthoid clade of Amaranthaceae, with large animals serving dispersal.
Methods
We generated an extensively sampled phylogeny comprising 26 of the 31 achyranthoid genera as well as representatives of all other lineages of Amaranthaceae. Phylogenetic tree inference employed four genomic regions, using parsimony, likelihood and Bayesian inference methods. We estimated divergence times, evaluated trait-dependant changes and species diversification rates using state-dependent speciation and extinction models, and reconstructed ancestral character states for modified sterile flowers.
Key Results
The achyranthoids were found to be a major clade of the Amaranthaceae, comprising mostly African members. Phylogenetic relationships within this clade were well resolved and supported two main subclades. Several genera were found to be polyphyletic. Our results indicate that the achyranthoids started to diversify ~28 million years ago, and that modified sterile flowers evolved multiple times. An asymmetry in transition rates towards the gain of sterile flowers was observed, whereas no trait-dependent increase in species diversification rates was detected. Bayesian rate heterogeneity analyses indicated that the achyranthoids diversified without significant rate shifts.
Conclusions
The accumulation of modified sterile flowers within achyranthoids appears to result from the higher transition rates in favour of modified sterile flowers. Multiple gains suggest an adaptive value for this trait. However, epizoochory does not appear to fuel species diversification, possibly due to extensive gene flow through regularly migrating mammals, which limits the possibility of speciation by isolation.
Keywords: Africa, Amaranthaceae, BiSSE, Caryophyllales, character evolution, epizoochory, floral morphology, HiSSE, phylogeny, species diversification
INTRODUCTION
The Amaranthaceae constitute a nearly cosmopolitan family of flowering plants within the order Caryophyllales, forming a well-supported lineage with the Chenopodiaceae (Cuénoud et al., 2002; Schäferhoff et al., 2009). In the strict sense (excluding Chenopodiaceae), the Amaranthaceae contain ~800 species in 79 genera (Hernández-Ledesma et al., 2015), comprising a variety of life forms (herbs, shrubs, lianas and trees) that inhabit a wide range of habitats (from deserts to rainforests). Most of the diversity of the Amaranthaceae is found in the neotropics as well as in eastern and southern Africa (Townsend, 1993).
Müller and Borsch (2005a) found the subfamily Amaranthoideae and most of the tribes and subtribes in the classification of Schinz (1934) and Townsend (1993) to be para- or polyphyletic. A newly recovered achyranthoid clade included several genera of the subtribe Aervinae, while the genera Aerva, Nothosaerva and Ptilotus were identified as part of a separate lineage (the ‘aervoid clade’; Müller and Borsch 2005b). The achyranthoid clade was estimated to comprise ~134–150 species in 31 genera, if currently accepted genera were upheld. However, adequate support for the clade was lacking due to limited character and taxon sampling. We assume that, next to the mostly neotropical gomphrenoids (Sánchez-del Pino et al., 2009), which comprise about 380 species, the achyranthoid clade constitutes the second main radiation within the Amaranthaceae. The majority of achyranthoid taxa occur in Africa, except the Hawaiian genus Nototrichium, species of Achyranthes from Asia and the Pacific, and certain species of Cyathula distributed in China and the Himalaya.
Members of the achyranthoid clade (Müller and Borsch, 2005b) and of many Aervinae in the pre-phylogenetic circumscription of the subtribe possess cymose inflorescence structures. In several taxa, sterile modified flowers appear within partial florescences, which fall off completely at maturity as burr-like units (Acosta et al., 2009). The sterile flowers are modified to hooks, spines or barbs, which provide adhesive structures serving epizoochory. In some genera (e.g. Achyranthes), which do not exhibit sterile flowers, the midribs of bracteoles are thickened to spines, which also form adhesive appendages.
Epizoochory occurs in <5 % of seed plants (Sorensen, 1986) but is frequent in achyranthoids (>80 % of the genera). Ridley (1930) suggested that the evolution of plants exhibiting burrs as dispersal units in Africa was primarily promoted through epizoochory by herds of ungulates covering large areas of the African continent between the Eocene and the Pleistocene. He reported species of Cyathula, Achyranthes and Pupalia to be animal-dispersed by adhesion and described the diaspores of Pupalia as ‘the most persistently adhesive burrs’ he knows. Agnew and Flux (1970) as well as Mori and Brown (1998) showed that several achyranthoid species had been dispersed over long distances in the fur of animals. Most African achyranthoids occur in Acacia–Commiphora wood- and bushlands, dry evergreen afromontane forests, grassland vegetation complexes or semi-desert scrublands, all of which are vegetation types with open spaces (White, 1983; Friis et al., 2011) and are thus suitable for long-distance dispersal via epizoochory.
In the present investigation, we hypothesize that the modified sterile flowers present in many African Amaranthaceae evolved during time periods when African habitats changed to more open conditions and the local diversity of terrestrial mammals increased. We propose that the diversification of the African achyranthoid clade may have been fuelled by these adaptations to epizoochory. To evaluate this hypothesis, we conducted a series of phylogenetic analyses of the Amaranthaceae by following three primary aims. First, we aimed to generate a robust molecular phylogenetic hypothesis for the achyranthoids to evaluate the composition of the achyranthoid clade initially found by Müller and Borsch (2005b). Second, we aimed to estimate divergence times and to reconstruct the evolution of modified sterile flowers based on our new phylogenetic trees. This second aim would allow us to identify the number of origins of modified sterile flowers within the achyranthoids. Third, we aimed to evaluate the influence of morphological traits that may have an adaptive value for epizoochory in speciation and extinction in the achyranthoids. In this third goal, we specifically aimed to understand (1) whether speciation and extinction rates are significantly different in the presence of the character ‘modified sterile flowers’ (and the more inclusive functional trait of ‘adhesive appendages’, which can be considered as any part of a dispersal unit with an adhesive property and an adaptive value for epizoochory, regardless of whether a taxon possess sterile flowers) than in their absence, (2) whether transition rates between character states are strongly asymmetrical, and (3) whether net diversification is higher in the presence of these features than in their absence. The specific research questions of the third aim were evaluated through a trait-dependent as well as a trait-independent approach. In the trait-dependant approach, we estimated and compared speciation, extinction and character transition rates in relation to morphological traits with a potential adaptive value for epizoochory. In the trait-independent approach, we explored possible diversification rate shifts across the entire family Amaranthaceae. Taken together, these analyses will allow us to evaluate whether the diversification of the African achyranthoid clade may have been fuelled by the emergence of modified sterile flowers in this group.
MATERIALS AND METHODS
Collection of plant material and taxon sampling
Plant material was primarily collected during field trips to Ethiopia and Kenya in 2012 and 2013. Taxon sampling focused on the whole subtribe Aervinae sensuSchinz (1934). We included almost half of all known species belonging to the achyranthoid clade in our analyses, representing 26 of 31 genera. Our sampling was thus guided to best represent the morphological diversity in the group, independently of the current classification into genera. Also, the very few species occurring outside Africa were represented in our sampling; sampling statistics are provided in Table 1. Taxa that were recovered with minimal support or in unexpected phylogenetic positions were supplemented by additional samples of the same species from different localities to verify the inferred positions. Species names, geographical origin and herbarium voucher information for all taxa under study are given in Supplementary Data Table S1.
Table 1.
Number and proportions of genera and species sampled for the present investigation
| Genera (approximate sampling proportions) | Species (approximate sampling proportions) | |
|---|---|---|
| Estimated taxon numbers of achyranthoids | 31 | ~134–150 |
| Taxa in dataset A | 26 (84 %) | 69 (51 %) |
| Taxa in dataset B | 26 (84 %) | 65 (49 %) |
| Taxa in dataset C | 23 (74 %) | 63 (47 %) |
Construction of datasets
For the present investigation, we generated a total of 396 new DNA sequences. In addition, we included 112 sequences from Müller and Borsch (2005a, b) in our datasets. Three different DNA matrices were assembled: (1) a combined plastid dataset (hereafter dataset A), which consisted of the chloroplast regions trnK/matK, rpl16 and trnL-F and comprised 130 samples with a focus on the achyranthoid clade but also a representative coverage of subfamily Amaranthoideae; (2) a broader plastid dataset (dataset B), which consisted of the chloroplast region trnK/matK only and comprised a total of 189 samples from across the Caryophyllales (134 samples of Amaranthaceae, 40 of Chenopodiaceae and 15 representing clades within the Caryophyllales); and (3) a nuclear ribosomal dataset (dataset C), which consisted of internal transcribed spacer (nrITS) sequences of 105 taxa with a focus on achyranthoids plus representatives of other main Amaranthaceae clades.
We used dataset A to reconstruct detailed relationships of the achyranthoid clade; dataset B was employed for divergence dating, as it allowed (1) the placement of three fossil specimens assigned to the Chenopodiaceae as primary calibration points, and (2) the definition of three secondary calibration points by using age estimates of Bell et al. (2010). Dataset C allowed a comparison of tree topologies inferred from nuclear ribosomal data with those inferred from plastid DNA regions.
DNA isolation, amplification and sequencing
Total genomic DNA was isolated as described in Müller and Borsch (2005a). Primer sequences and details of the PCR protocols are listed in Supplementary Data Table S2. Upon amplification, all PCR products were sequenced by standard Sanger sequencing at Macrogen Europe (Amsterdam, The Netherlands). Chromatograms were inspected by eye, corrected for erroneous nucleotide calls and assembled using PhyDE 0.9971 (Müller et al., 2010). Final DNA sequences were submitted to ENA (http://www.ebi.ac.uk/ena/) upon conversion to checklist files with custom Python scripts (https://github.com/michaelgruenstaeudl/annonex2embl). ENA/GenBank accession numbers for all taxa under study are given in Supplementary Data Table S1.
Sequence alignment, indel coding and model selection
Initial alignment files generated with Muscle 3.6 (Edgar, 2004) were further refined under a motif-based approach (Löhne and Borsch, 2005) using PhyDe. Areas of uncertain homology were subsequently excluded from matrices. Insertions and deletions in datasets A and C were coded according to the ‘simple indel coding’ scheme (Simmons and Ochoterena, 2000) as implemented in SeqState 1.4.0 (Müller, 2005). Inversions were reverse-complemented and coded manually. Best-fitting models of nucleotide substitution were selected via the Akaike information criterion (AIC; Akaike, 1974) using the software jModeltest 2.1.7 (Darriba et al., 2012). The substitution model GTR+G was found to display the best fit for DNA sequences of matK, the trnL intron and the trnL-F intergenic spacer. The model GTR+G+I was found to display the best fit for DNA sequences of ITS1, ITS2, rpl16 and the trnK intron, and the model HKY+I for the 5.8S ribosomal DNA.
Phylogenetic analysis
Phylogenetic inference was performed via maximum parsimony (MP), maximum likelihood (ML) and Bayesian inference (BI). Parsimony analyses were conducted in PAUP* 4.0b10 (Swofford, 2002), with 10 000 jackknife (JK) replicates to calculate node support. Likelihood analyses were conducted in RAxML 7.4.2 (Stamatakis, 2006), with node support calculated via 1000 rapid bootstrap (BS) replicates, using the RAxMLGui 1.3 as input interface (Silvestro and Michalak, 2012). BI was performed with MrBayes 3.2.2 (Ronquist et al., 2012), with node support calculated as posterior probabilities. Four independent Markov chain Monte Carlo (MCMC) runs with four chains and 10 000 000 generations each were conducted, with trees sampled every 1000th generation. The burn-in was set to 50 %, resulting in a combined posterior tree distribution of 20 000 trees. Majority-rule consensus trees were calculated from the combined posterior tree distribution subsampled to 1000 trees. We rated BS/JK values of 70–84 % and posterior probability of 0.9–0.94 as moderate support, and BS/JK values of 85–100 % and posterior probability of 0.95–1 as strong support. For BI and ML analyses, datasets were partitioned to allow independent parameter estimation for each partition. For analyses in RAxML, the model MULTIGAMMAI was employed as the nearest approximation to the model GTR+I+G. The binary character model (Lewis, 2001) was applied to indel partitions. DNA sequence alignments and the main phylogenetic trees inferred were submitted to TreeBASE (number 21912).
For all trait-dependent and -independent analyses of speciation and extinction rates as well as our ancestral character state reconstructions, we reduced multiple samples of the same species in our phylogenetic trees to a single representative by randomly selecting one sequence. In cases of non-monophyly of multiple samples per taxon, one representative per phylogenetic position was kept. This strategy ensured that taxa were properly represented and simultaneously prevented species duplicates biasing the final results.
Molecular clock calibration
To calibrate the molecular clock, three fossils were assigned to different clades of the Chenopodiaceae. These fossils were: Chenopodipollis multiplex, Salicornites massalongoi and Parvangula randeckensis. Chenopodipollis multiplex had been found in a marine influence assemblage alongside other marine organisms (Nichols and Traverse, 1971) and was assigned to Chenopodiaceae by Kadereit et al. (2003). Although habitats close to coastal environments are typical of Chenopodiaceae, this is rarely the case for Amaranthaceae or Caryophyllaceae with similar pollen. Thus, we implemented a conservative calibration point for this fossil and used it as a minimum constraint on the stem node of Chenopodiaceae (excluding subfamily Polycnemoideae). The fossil S. massalongoi had been described as a fragment of a plant stem (Principi, 1926; Collinson et al., 1993) and was since assigned to the Salicornioideae (Hohmann et al., 2006; Kadereit et al., 2012). Here, we used it as a minimum constraint for the stem node of Salicornioideae, assuming that the succulent stem features appeared with the split of Salicornioideae and have fostered its diversification into dry and saline habitats. The fossil P. randeckensis had been described as Chenopodium-like seeds (Gregor, 1982) but, considering seed evolution in the Chenopodioideae (Sukhorukov and Zhang 2013), these seeds may belong to a lineage after divergence of the Axyris–Krascheninnikovia clade. The fossil was placed in different positions by different authors (Kadereit et al., 2003, 2012; Hohmann et al., 2006). We designated this fossil as a minimum age constraint for the stem of the Axyris–Krascheninnikovia clade. Maximum ages for all three fossils were set to 125 million years (Ma), which represents the mean age of the core eudicots [corresponding to node 29 of Appendix S5 in Bell et al. (2010)]. The age distribution of each of these primary calibration points was modelled as an exponential prior distribution (Ho and Philips, 2009), with an offset equal to the minimum age of the respective fossil and a mean such that the median age of the exponential distribution equalled the maximum age of the fossil. A fossil calibration so constrained renders the age estimate of the fossil the likely divergence time of the calibrated node, but also allows the inference of older ages. A summary of the primary calibration points employed in this investigation as well as their respective age ranges is given in Table 2.
Table 2.
Fossils and their age ranges used for primary calibration of the molecular clock
| No. | Fossil name | Description | Origin | Age (Ma) | Epoch | Publication |
|---|---|---|---|---|---|---|
| 1 | Chenopodipollis multiplex | Pollen record | USA | 65–56 | Palaeocene | Nichols and Traverse (1971) |
| 2 | Salicornites massalongoi | Part of an axis | Italy | 35–23 | Oligocene | Principi (1926) |
| 3 | Parvangula randeckensis | Chenopodium-Like seeds | Germany | 23–16 | Early Miocene | Gregor (1982) |
Additionally, we defined three secondary calibration points by using age estimates of Bell et al. (2010): the age for the crown group of the Caryophyllales (their node 39); the age for the crown group of the polygonoid clade (their node 41); and the maximum estimated age of the entire tree, corresponding to Gunneridae (their node 31). The age distribution of each of these secondary calibration points was modelled as a normal prior distribution and was equal to the 95 % highest posterior density (HPD) interval of the ages inferred by Bell et al. (2010), which were based on lognormal prior age distributions.
Estimation of divergence times
Divergence times were estimated using a Bayesian relaxed molecular clock model in BEAST 1.8.0 (Drummond et al., 2012). A preliminary evaluation of the nucleotide substitution rates across dataset B indicated that the rates did not conform to a strict molecular clock (Peterson, 2006). Hence, a relaxed molecular clock with uncorrelated substitution rates sampled from an exponential distribution for the estimation of divergence times was applied (Drummond et al., 2006). Lineage diversification was modelled as a birth–death process, and a random starting tree was employed. Two MCMC runs with 50 000 000 generations each were performed for the estimation of divergence times, with trees sampled every 1000 generations. We confirmed adequate parameter sampling (effective sample size >200) and the mixing of Markov chains in both runs through visual inspection of the MCMC samples using Tracer 1.4 (Rambaut and Drummond, 2007). Given the results of our sampling and convergence diagnostics, the first 50 % of the MCMC generations were removed as burn-in. The remaining trees were subsampled to every fifth generation, generating a post-burn-in posterior tree distribution of 500 trees per run. The post burn-in MCMC samples of both runs were combined via LogCombiner 1.8.0 (Drummond et al., 2012), and the combined tree distribution was summarized as a maximum clade credibility (MCC) tree via TreeAnnotator 1.8.0 (Drummond et al., 2012).
Analyses of state-dependent speciation and extinction
To evaluate the influence of morphological traits with a potential adaptive value for epizoochory in speciation and extinction rates in the achyranthoids, we employed a trait-dependent analysis approach using two morphological characters: modified sterile flowers and the more inclusive trait of adhesive appendages (Fig. 1). Presence (noted as 1) and absence (0) of both characters was coded for the achyranthoid taxa included in dataset B, using the same specimens as in the molecular phylogenetic analyses. Additional assessment and confirmation of the traits in the study taxa were conducted via extraction of morphological descriptions from the literature (e.g. protologues of taxa, genus and species descriptions of floras, morphological treatments) or via the examination of herbarium material. The complete character matrix is provided in Supplementary Data Table S3.
Fig. 1.
Flower morphology of achyranthoids. (A, B) Inflorescences of Pupalia lappacea (Di Vincenzo et al., 301, B) and Cyathula cylindrica (Wondafrash et al., 3332, B) exhibiting modified sterile flowers. (C) Adhesive dispersal unit of Cyathula orthacantha (Di Vincenzo et al., 21, B) with sterile flowers modified to spines. (D) Inflorescence of Achyranthes aspera (Di Vincenzo et al., 9, B), with bracteoles having a thickened spine-like midrib. (E) Partial inflorescence of Cyathula uncinulata (Wondafrash et al., 3199, B) with terminal parts of sterile and fertile flowers modified to hooks. (F) Cyathula cylindrica (Wondafrash et al., 3332, B); cyme of one fertile flower and two lateral modified sterile flowers. (G) Inflorescence of Chionothrix latifolia (Di Vincenzo et al., 236, B) with hairs growing at maturity and serving wind dispersal. (H) Inflorescence of Psilotrichum gnaphalobryum (Di Vincenzo et al., 239B, B) with solitary fertile flowers. Scales bars: (A, B, D, G, H) = 1 cm; (C, E, F) = 2 mm.
To estimate speciation and extinction rates in the achyranthoids in relation to the morphological traits, two types of statistical analysis were conducted via the application and comparison of two sets of state-dependent speciation and extinction (SSE) models: binary-state speciation and extinction (BiSSE) models (Maddison et al., 2007) as implemented in the R package ‘diversitree’, and hidden-state speciation and extinction (HiSSE) models (Beaulieu and O’Meara, 2016) as implemented via the R package ‘hisse’. Specifically, we conducted analyses of state-dependent speciation and extinction rates under (1) a detailed group of hierarchical BiSSE models and (2) a combined group of SSE models selected from the BiSSE and HiSSE concepts. The aim of applying model group (1) was to evaluate which of the modelled combinations of speciation, extinction and character transition rates could best explain character distribution and phylogenetic diversification of the achyranthoids. The aim of model group (2) was to evaluate whether the inclusion of an additional, unaccounted (i.e. hidden) character state may better explain the fit of the speciation, extinction and character transition rates than the BiSSE models alone.
For model group (1), we estimated trait-dependent rates of speciation (λ), extinction (μ) and character transition (q) under 20 different BiSSE models and compared the fit of each model, given our inferred phylogenetic trees. Each of these models had six different parameters (i.e. the rates of speciation, extinction and character transition under character state 0 and character state 1) and differed in the number of constraints applied to the parameters. Two sets of models were hereby defined: models in which one or more parameters were constrained to be equal (e.g. λ0 = λ1; hereafter ‘BiSSE model set 1’), and models in which one or more parameters were constrained to be zero (e.g. λ0 = 0; hereafter ‘BiSSE model set 2’). The trait-dependent rates were estimated for both states of modified sterile flowers and adhesive appendages. In addition, we calculated the net effect for each model (de Vos et al., 2014), which represents the difference between speciation and extinction rate under character state 1 (i.e. the net diversification under state 1) minus the difference between speciation and extinction rate under character state 0 (i.e. the net diversification under state 0). Relative model fit was evaluated within each BiSSE model set but not among the two sets. All parameter estimations and comparisons of model fit also included a model with unconstrained parameters (i.e. λ, μ and q were allowed to vary; hereafter ‘unconstrained model’), which was used as a null hypothesis. A summary of all BiSSE models employed for the analysis of the character ‘modified sterile flowers’ is provided in Table 3 and a summary of all BiSSE models employed for the more inclusive trait ‘adhesive appendages’ is provided in the Supplementary Data Table S4.
Table 3.
Model fit of different binary state-dependent speciation and extinction models regarding the presence of modified sterile flowers (0 = absent; 1 = present). In the models evaluated, parameters were set as equal (BiSSE model set 1) and to zero (BiSSE model set 2) across character states. Relative model fit was evaluated via the AIC and AICc; a comparison of model fit between the unconstrained and each constrained model was performed via the LRT. Parameter estimates and test statistics were calculated on the MCC tree that summarizes 1000 post-burn-in MCMC trees of the posterior tree distribution inferred during the estimation of divergence times
| Model specification | Model fit | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Speciation (λ) | Extinction (μ) | Character transition rate (q) | d.f. | lnLik | AIC | AICc | LRT χ2 | LRT P-value | |
| Unconstrained – all rates free | 6 | −251.656 | 515.311 | 516.494 | NA | NA | |||
| BiSSE model set 1 | free | μ 0 = μ1 | Free | 5 | −252.745 | 515.491 | 516.324 | 2.179 | 0.140 |
| free | free | q 01 = q10 | 5 | −251.877 | 513.753 | 514.587 | 0.442 | 0.506 | |
| λ 0 = λ1 | Free | Free | 5 | −253.045 | 516.091 | 516.924 | 2.779 | 0.096 | |
| free | μ 0 = μ1 | q 01 = q10 | 4 | −253.325 | 514.651 | 515.199 | 3.340 | 0.188 | |
| λ 0 = λ1 | free | q 01 = q10 | 4 | −253.373 | 514.745 | 515.293 | 3.434 | 0.180 | |
| λ 0 = λ1 | μ 0 = μ1 | free | 4 | −253.340 | 514.679 | 515.227 | 3.368 | 0.186 | |
| λ 0 = λ1 | μ 0 = μ1 | q 01 = q10 | 3 | −253.380 | 512.760 | 513.084 (best) | 3.448 | 0.328 | |
| BiSSE Model set 2 | λ 0 = 0 | Free | Free | 5 | −276.098 | 562.196 | 563.029 | 48.884 | <0.01* |
| free | μ 0 = 0 | Free | 5 | −251.847 | 513.693 | 514.527 | 0.382 | 0.536 | |
| free | μ 1 = 0 | Free | 5 | −254.647 | 519.295 | 520.128 | 5.983 | 0.014* | |
| free | Free | q 01 = 0 | 5 | −252.394 | 514.789 | 515.622 | 1.477 | 0.224 | |
| free | Free | q 10 = 0 | 5 | −252.754 | 515.508 | 516.341 | 2.196 | 0.138 | |
| λ 0 = 0 | μ 0 = 0 | Free | 4 | −273.762 | 555.525 | 556.073 | 44.214 | <0.01* | |
| λ 0 = 0 | μ 1 = 0 | Free | 4 | −276.098 | 560.196 | 560.743 | 48.884 | <0.01* | |
| λ 0 = 0 | Free | q 01 = 0 | 4 | −286.815 | 581.629 | 582.177 | 70.318 | <0.01* | |
| Free | μ 0 = 0 | q 01 = 0 | 4 | −253.201 | 514.402 | 514.950 | 3.091 | 0.213 | |
| Free | μ 0 = 0 | q 10 = 0 | 4 | −252.755 | 513.509 | 514.057 (best) | 2.198 | 0.333 | |
| Free | μ 1 = 0 | q 01 = 0 | 4 | −254.647 | 517.295 | 517.843 | 5.983 | 0.050 | |
| Free | μ 1 = 0 | q 10 = 0 | 4 | −257.465 | 522.930 | 523.478 | 11.619 | <0.01* | |
Asterisks indicate LRT results at P < 0.05. lnLik, natural logarithm of the likelihood.
For model group (2), we estimated speciation, extinction and character transition rates under selected SSE models and again compared the fit of each model given our inferred phylogenetic trees. Parameters of the HiSSE models were set up according to the recommendations of Beaulieu and O’Meara (2016) for defining character-independent models (CIDs). Models with four diversification process parameters were set up, with the most parameterized CID model containing 13 free parameters (CID2 with unconstrained net turnover, extinction fraction and character transition rates among and between the two observed and the two hidden states) and the least parameterized CID model containing six free parameters (CID2 with unconstrained net turnover and extinction fraction parameters among and between the two observed and the two hidden states, but character transitions constrained to be equal). Relative model fit was evaluated among the selected SSE models, with the most parameterized CID and the most parameterized BiSSE model acting as null hypothesis. A summary of all CID and BiSSE models of model group (2) employed for the analysis of the character ‘modified sterile flowers’ is provided in Table 4, and a summary of all CID and BiSSE models of model group (2) employed for the more inclusive trait ‘adhesive appendages’ is provided in the Supplementary Data Table S4.
Table 4.
Comparisons of model fit of different CID models of the HiSSE model concept and of BiSSE models regarding the presence of modified sterile flowers. Two two-state and two four-state CID models as well as four BiSSE models were evaluated. Dual transitions between character states (e.g. q0A ↔ q1B; q0B ↔ q1A) were not included in any CID model. Relative model fit was evaluated via the AIC and AICc; the difference in model fit between the most parameterized CID or BiSSE model and all others was evaluated via the LRT
| Model specification | Model fit | Comparison with CID-2 unconstrained |
Comparison with BiSSE unconstrained |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Net turnover (τ) |
Extinction fraction (ε) |
Character transition rate (q) |
d.f. | lnLik | AIC | AICc | LRT χ2 | LRT P-value | LRT χ2 | LRT P-value | ||
| HiSSE models | CID-2 | Free | Free | Free | 13 | −212.593 | 449.185 | 455.185 | NA | NA | 0.183 | 1.000 |
| Free | Free | Equal | 6 | −218.105 | 446.209 | 447.226 | 0.0705 | 1.000 | 0.026 | 1.000 | ||
| CID-4 | Free | Free | Three rates | 11 | −215.528 | 453.057 | 458.038 | 0.0201 | 1.000 | 0.082 | 1.000 | |
| Free | Free | Equal | 9 | −215.826 | 449.651 | 452.924 | 0.0244 | 1.000 | 0.074 | 1.000 | ||
| BiSSE models | Free | Free | Free | 7 | −221.510 | 455.019 | 456.467 | 0.1832 | 1.000 | NA | NA | |
| Equal | Free | Free | 6 | −221.545 | 454.108 | 453.091 | 0.1846 | 1.000 | <0.001 | 1.000 | ||
| Free | Equal | Free | 6 | −221.714 | 454.445 | 453.428 | 0.1916 | 1.000 | <0.001 | 1.000 | ||
| Equal | Equal | Free | 5 | −221.504 | 451.675 | 451.008 | 0.1829 | 0.999 | <0.001 | 1.000 | ||
lnLik, natural logarithm of the likelihood; NA, not applicable.
Model fit was evaluated by two different procedures. First, we applied likelihood ratio tests (LRTs) between the unconstrained model and each constrained model to determine whether any of the constrained models was significantly different from the unconstrained model; this comparison was enabled by a hierarchical setup of the parameter constraints. Second, we evaluated the relative fit of each model by ML optimization, using the AIC as well as an AIC corrected for small sample size (AICc; Hurvich and Tsai, 1989) to identify best-fitting models. Parameter estimates for each model and test statistics were calculated and then averaged over 100 randomly selected trees of the posterior tree distribution generated during the estimation of divergence times in order to accommodate the phylogenetic uncertainty of the tree distribution. In addition to the comparison of model fit via ML optimization, we also applied MCMC sampling to estimate marginal posterior probability densities for the diversification rate parameters of the unconstrained model. We thus conducted MCMC sampling for 10 000 generations, with 95 % HPD intervals calculated for each parameter.
To allow the application of a global sampling fraction for SSE models to correct for incomplete taxon sampling (Table 1), our analyses were conducted exclusively on the achyranthoid clade of our ultrametric trees inferred from dataset B. This clade comprised a total of 65 taxa. We bioinformatically extracted the achyranthoid clade from each of the 100 randomly selected trees of the posterior tree distribution using the R package ‘phyloch’ 1.5–5 (Heibl, 2008). For modified sterile flowers, we assumed a sampling proportion of 0.44/0.41 (absence/presence); for adhesive appendages we assumed a ratio of 0.63/0.34 (Supplementary Data Table S5).
Ancestral character state reconstruction
We conducted ancestral character state reconstruction (ACSR) for modified sterile flowers under three different BiSSE models. The second trait, adhesive appendages, was not reconstructed, as their functionality is achieved by different, non-homologous organs (sterile flowers and bracteoles). The same matrix for presence and absence of sterile flowers was applied for ACSR as for model testing (Supplementary Data Table S3).
We performed ACSR with the function ‘asr-bisse’ of the R package diversitree 0.9–7 (FitzJohn et al., 2009). Reconstruction was performed under the unconstrained binary-state speciation and extinction model and those BiSSE models with the smallest AICc value out of BiSSE model sets 1 and 2 (Table 3). To average out phylogenetic uncertainty, final ACSR was conducted over the post-burn-in posterior tree distribution as inferred during divergence dating. Inferred ancestral character states were visualized on the MCC tree. To evaluate the significance of the reconstruction results, we followed Schluter et al. (1997) and used likelihood ratios as measures of relative weight of evidence and the ratio 1:7.4 (i.e. 0.86) as indication for significance of a particular character state.
Analyses of shifts in diversification rates
In the trait-independent approach, we evaluated rate shifts across the entire family Amaranthaceae. The software BAMM 2.5.0 (Rabosky, 2014) was employed to calculate the rate heterogeneity of speciation and extinction on the MCC tree inferred during the estimation of divergence times. To apply a more confident sampling fraction in BAMM, our analyses were conducted exclusively on the clade of Amaranthaceae. Sampling fractions for the main clades of the Amaranthaceae are listed in Supplementary Data Table S5.
Analyses were conducted in four independent runs with 10 000 000 MCMC generations each, and results were sampled every 1000 generations. Post-run analyses and visualizations were performed using the R package BAMMtools 2.1.5 (Rabosky et al., 2014) and run convergence was tested with the R package CODA 0.19–1 (Plummer et al., 2006). Upon removal of the first 10 % of all sampled MCMC generations as burn-in, we inferred the posterior probabilities of rate-shift configurations under different numbers of rate shifts and calculated Bayes factors (BFs) to compare all rate-shift configurations with prior and posterior probabilities greater than zero with a model without shifts. We considered BF > 20 to be substantial evidence for one model over another, and BF > 50 was considered very strong evidence in support of the model under analysis. The 95 % credible set of distinct rate-shift configurations and the single best-shift configuration with the highest posterior probabilities were generated as final results.
RESULTS
Molecular datasets
The aligned matrix of dataset A comprised 4747 bp (trnK/matK, 2474 bp; rpl16, 1069 bp; trnL-F, 1204 bp), of which 373 bp were excluded as mutational hotspots (trnK/matK, five hotspots with a total of 67 bp; rpl16, eight hotspots with a total of 158 bp; trnL-F, ten hotspots with a total of 148 bp). Simple indel coding of dataset A resulted in an additional matrix of 573 characters. Six inversions (in total 39 bp) were found in trnK/matK, two inversions (in total 58 bp) in rpl16 and three inversions (in total 34 bp) in trnL-F of dataset A. Dataset B included a total of 2474 aligned positions of the trnK/matK region, and five mutational hotspots with a total of 145 bp were excluded from this dataset. Eight inversions with a total of 61 bp were found in dataset B. Dataset C included a total of 706 aligned positions for nrITS, from which four mutational hotspots with a total of 83 bp were excluded. Simple indel coding of dataset C resulted in an additional matrix of 122 characters.
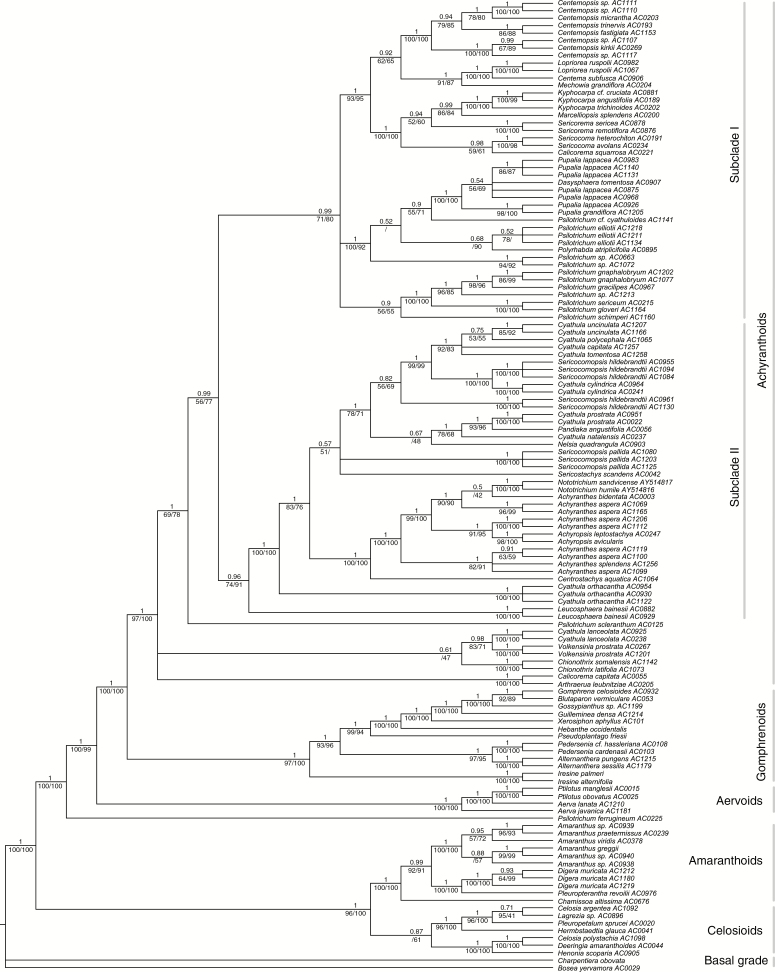
Phylogenetic analyses of dataset A
Reconstructions under BI, ML and MP yielded identical tree topologies, only differing in node support (Fig. 2). Monophyly of the achyranthoid clade was confirmed with high support. Five of the 26 genera were identified as polyphyletic: Psilotrichum was inferred as four separate lineages (in addition to P. ferrugineum outside the clade), Cyathula as six separate lineages, Sericocomopsis as three separate lineages, Achyranthes as three separate lineages, and Calicorema as two separate lineages. The genera Centrostachys, Chionothrix, Dasysphaera, Lopriorea, Mechowia, Nelsia, Polyrhabda and Volkensinia have been included in a molecular phylogenetic analysis for the first time and were identified as part of the achyranthoid clade. The two endemic Madagascan genera Henonia and Lagrezia were resolved within the celosioid clade, and Digera as well as Pleuropterantha within the amaranthoid clade.
Fig. 2.
Phylogeny of the Amaranthaceae with a focus on the achyranthoid clade inferred by Bayesian inference on dataset A. Posterior probabilities of the Bayesian inference are given above branches, jackknife percentages of the maximum parsimony (left) and bootstrap percentages of the maximum likelihood analyses (right) are given below branches.
Furthermore, we found two strongly supported major subclades that diverged after a grade of three early diverging achyranthoid lineages (Fig. 2). These three lineages are: (1) Arthraerua plus Calicorema capitata; (2) Cyathula lanceolata plus the genus Volkensinia; and (3) the genus Chionothrix. Subclade I comprises the genera Polyrhabda, Pupalia, Dasysphaera, Sericocoma, Sericorema, Marcelliopsis, Kyphocarpa, Centema and Lopriorea, Centemopsis, the species Calicorema squarrosa and several lineages of Psilotrichum. Subclade II comprises the genera Nototrichium, Achyranthes, Achyropsis, Centrostachys, Sericocomopsis, Sericostachys, Nelsia, Pandiaka and Leucosphaera, and several lineages of Cyathula (except C. lanceolata).
Phylogenetic analyses of dataset C
Reconstructions under BI, ML and MP recovered the achyranthoid clade as well as most internal nodes also found in the plastid tree (Supplementary Data Fig. S1). The core of subclade II of achyranthoids was inferred with maximum support, whereas the genus Leucosphaera was inconsistently recovered as sister to Cyathula lanceolata rather than as sister to all other taxa in subclade II. The species that were recovered as subclade I under the plastid data were inferred as a grade of three independent lineages under nrITS data.
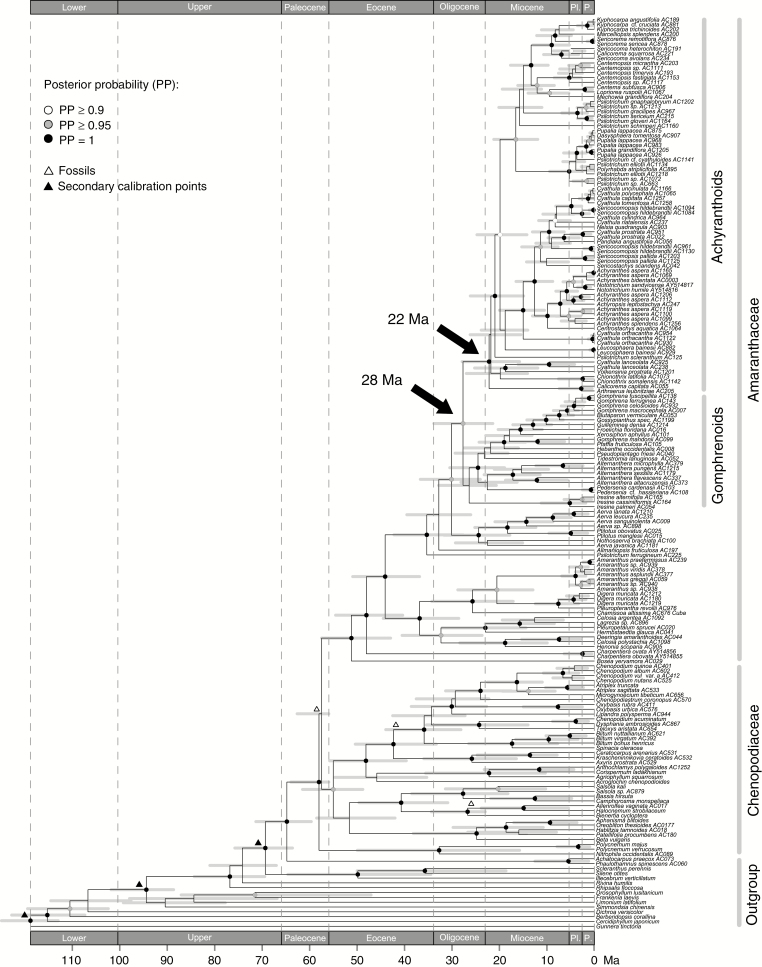
Divergence dating
The age of the crown group of the Amaranthaceae was estimated to be 51.25 Ma (95 % HPD 42.97–57.55 Ma) (node number 56 in Supplementary Data Fig. S7). The achyranthoid clade split from the gomphrenoid clade ~27.7 million years ago (Mya) (95 % HPD 21.42–33.86 Mya) and started to diversify 22.2 Mya (95 % HPD 15.79–27.89 Mya) (Fig. 3; node numbers 88 and 112 in Supplementary Data Fig. S7). The diversification of most subclades within the achyranthoids was inferred to have occurred within the past 10 Ma (Fig. 3). A list of all inferred ages including their 95 % HPD intervals is provided in Supplementary Data Fig. S7.
Fig. 3.
Chronogram of the Amaranthaceae–Chenopodiaceae alliance inferred from dataset C. Fossil (white triangles) and secondary (black triangles) calibration points as well as 95 % HPD intervals (grey bars) are visualized on the MCC tree. Epoch abbreviations: Lower, Lower Cretaceous; Upper, Upper Cretaceous; Pl., Pliocene; P., Pleistocene.
Analyses of state-dependent speciation and extinction
In our analyses of different state-dependent SSE models using model group (1), none of the models of BiSSE model set 1 was found to be significantly different from the unconstrained model regarding the character ‘modified sterile flowers’ (Table 3). Among the models of BiSSE model set 2, the LRTs indicated six models to be significantly different from the unconstrained model, but the fit of each of these models was worse than that of the unconstrained model. Comparisons of relative model fit via the AICc indicated that the model with all parameters constrained to be equal between state 0 and state 1 (λ0 = λ1, μ0 = μ1, q01 = q10) had the best fit among models of BiSSE model set 1. By contrast, the model that constrained the extinction rate under state 0 as well as the character transition from state 1 to state 0 to zero (μ0 = 0, q10 = 0) was found to have the lowest AICc value within BiSSE model set 2.
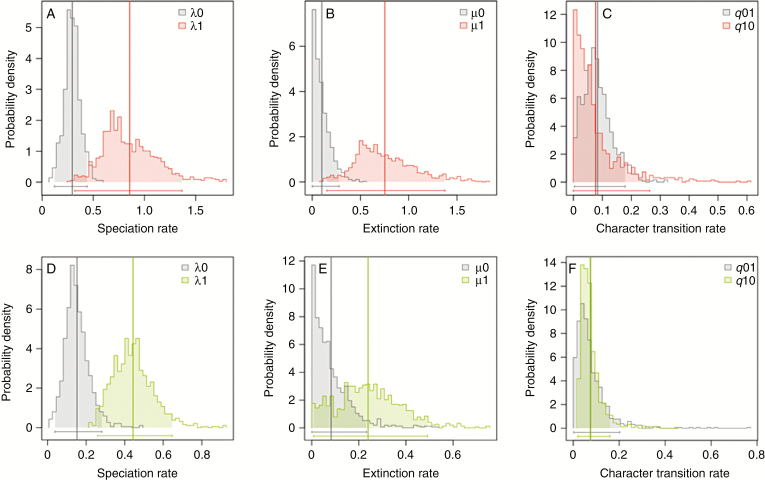
Since no model was significantly better compared with the null model and AICc values were similar across most models, we calculated the parameter values for speciation, extinction and character state transitions as well as the net effect under the unconstrained model (Table 5). For all other models, parameter values are provided in Supplementary Data Table S8. In the unconstrained model, both speciation and extinction rates for taxa with modified sterile flowers were found to be higher than for taxa lacking sterile flowers. However, the net effect under the unconstrained model was slightly negative, pointing to lower net diversification rates for taxa with than without modified sterile flowers. Rates for gains of modified sterile flowers were higher than for their loss (Table 5, Fig. 4). The accumulation of modified sterile flowers within achyranthoid taxa therefore results from the higher transition rates in favour of modified sterile flowers.
Table 5.
Median rates of speciation (λ), extinction (μ) and character transition (q) and the net effect of diversification for modified sterile flowers (0 = absent; 1 = present) under the unconstrained model. Median rate values were calculated across 100 post-burn-in MCMC trees of the posterior tree distribution as inferred during the estimation of divergence times. Each median value is followed by the interquartile range in parentheses. A negative net effect indicates a lower diversification rate for taxa with modified sterile flowers
| Model specification | Parameterization | Net effect | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Speciation (λ) | Extinction (μ) | Character transition rate (q) | λ 0 | λ 1 | μ 0 | μ 1 | q 01 | q 10 | (λ1 − μ1) − (λ0 − μ0) |
| Unconstrained – all rates free | 0.28 (0.26, 0.32) | 0.94 (0.76, 1.14) | 0.05 (0, 0.13) | 0.87 (0.64, 1.09) | 0.08 (0.02, 0.11) | 0.03 (0, 0.05) | −0.12 (−0.28, −0.06) | ||
Fig. 4.
Posterior probability distributions of speciation (λ), extinction (μ) and character transition rates (q) under the unconstrained BiSSE model regarding the presence (1) and absence (0) of modified sterile flowers (A–C) and adhesive flower appendages (D–F). Vertical lines represent mean values; horizontal bars and shaded areas represent the 95 % credibility intervals of posterior probability distributions.
Concerning adhesive flower appendages as a more inclusive functional trait, our LRT evaluations indicated that none of the models of BiSSE model set 1 was found to be significantly different from the unconstrained model (Supplementary Data Table S4). Comparisons of relative model fit via the AICc indicated that the model that constrained extinction and character transition rates to be equal between state 0 and state 1 (μ0 = μ1, q01 = q10) had the best fit among models of BiSSE model set 1. Among the models of BiSSE model set 2, the LRTs indicated a total of seven models to be significantly different from the unconstrained model. However, none of these seven models had a better fit to our data than the null model according to the AICc values. Comparisons further indicated that the model that constrained the extinction rate under state 1 as well as the character transition from state 0 to state 1 (μ1 = 0, q01 = 0) was found to have the best relative model fit.
Similar to the results for modified sterile flowers, our analyses regarding the presence of adhesive appendages indicated that no model was significantly better than the null model, and AICc values were quite similar across most BiSSE models. We calculated the parameter values for speciation, extinction and character transition as well as the net effect under all models (Supplementary Data Table S8). In the unconstrained model, we found higher speciation and extinction rates for taxa with adhesive appendages than for taxa without them. Here, the net effect was found to be positive, indicating that diversification rates for taxa with adhesive appendages were higher than for taxa without them. Character transition rates were found to be equal for both gains and losses (Supplementary Data Table S8, Fig. 4).
In our analyses of different state-dependent SSE models using model group (2), none of the evaluated models was found to be significantly different from the unconstrained model (Table 4, Supplementary Data Table S4). This finding was true for both morphological traits evaluated. For both traits, neither the BiSSE models nor the constrained CID models of the HiSSE concept displayed a significantly better model fit to the data than the null CID model when evaluated using an LRT. Comparisons of relative model fit via the AICc indicated that the least parameterized CID model had the best relative fit among models of model group (2). Again, this result was observed for both morphological traits evaluated. In summary, the results of our analyses of different state-dependent SSE models using model group (2) indicated that the inclusion of an additional, hidden character state did not explain the fit of the speciation, extinction and character transition rates significantly better than the BiSSE models alone.
Ancestral character state reconstruction
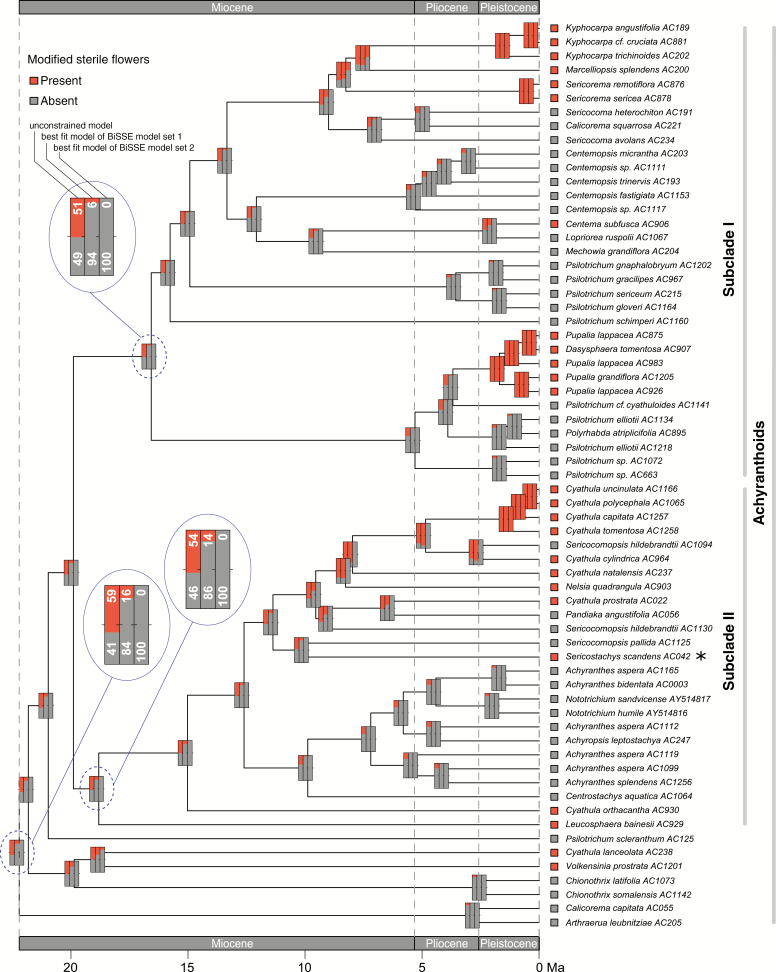
Since model testing did not infer a single best BiSSE model, we reconstructed ancestral character states for modified sterile flowers under three different BiSSE models: the unconstrained model and the two best-fitting models from BiSSE model sets 1 and 2 as inferred through the AICc (Fig. 5). The best-fitting BiSSE models yielded very similar reconstructions for the majority of the early divergences in the achyranthoid clade but were distinctly different from the reconstructions under the unconstrained model. The best-fitting BiSSE models inferred the absence of modified sterile flowers in the most recent common ancestor (MRCA) of the achyranthoids as more likely than the presence (BiSSE model set 1, 16 % presence, 84 % absence; BiSSE model set 2, 0 % presence, 100 % absence) and, indicated multiple origins of this trait within the clade: 14 independent origins for modified sterile flowers are inferred within the achyranthoids under the best-fit model of BiSSE model set 1, and 15 independent origins under the best-fit model of BiSSE model set 2 (according to the significance level of 86 % for a particular character state). The unconstrained model, by contrast, inferred the presence of modified sterile flowers in the MRCA of the achyranthoids as more likely than the absence (59 % presence, 41 % absence). Similarly, the reconstruction results for the MRCA of subclades I and II of the achyranthoids under the best-fit BiSSE models indicated the absence of modified sterile flowers as more likely than their presence (subclade I, BiSSE model set 1, 6 % presence, 94 % absence; BiSSE model set 2, 0 % presence, 100 % absence; subclade II, BiSSE model set 1, 14 % presence, 86 % absence; BiSSE model set 2, 0 % presence, 100 % absence), whereas the reconstruction results under the unconstrained model were uncertain, indicating equal probability for both character states (subclade I, 51 % presence, 49 % absence; subclade II, 54 % presence, 46 % absence).
Fig. 5.
Reconstruction of ancestral character states for modified sterile flowers under three different BiSSE models (bars from left to right): the unconstrained model; the best fit model of BiSSE model set 1 with parameters set as equal across the character states; and the best fit model of BiSSE model set 2 with parameters set to zero across states. The asterisk marks a species that bears sterile flowers that are not modified to adhesive appendages, but instead are modified to long hairs that serve wind dispersal. Percentages in the magnified nodes represent character state probabilities.
Analyses of shifts in diversification rates
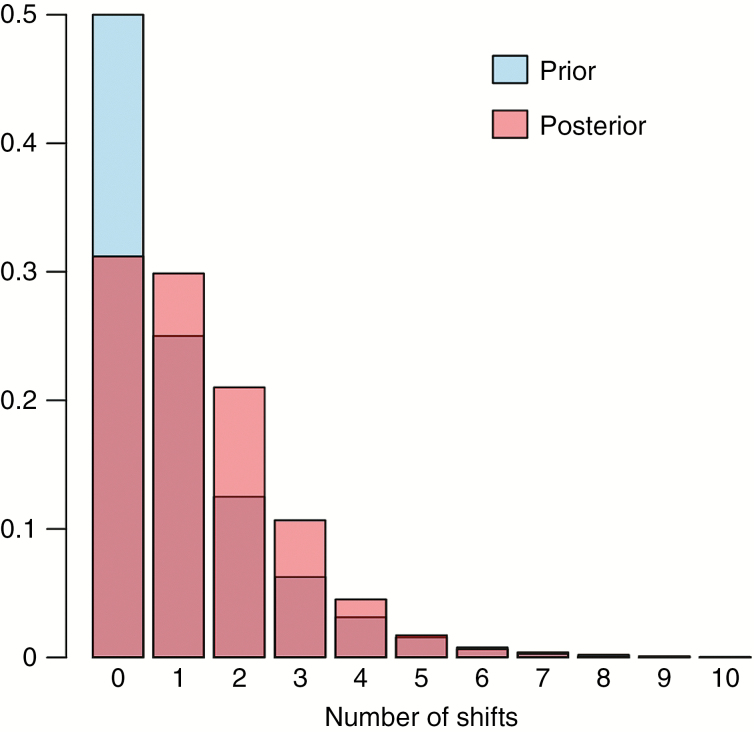
Convergence of BAMM analyses was assessed in four independent runs via effective sample size (ESS) values (ESS log-likelihood, 481.59–699.76; ESS number of shifts, 824.84–1151.58). Our analyses via BAMM indicated that the zero-shift configuration (null model) had the highest prior and posterior probability (posterior probability = 0.31; Fig. 6). Model comparison via BFs did not show evidence in favour of a model with one or more shifts relative to the null model, as BFs for all models with one or more shifts were <20, ranging from 0.37 to 2.73. Computing the 95 % credible set of macroevolutionary rate shifts yielded a set of 11 distinct shift configurations, out of which three accounted for 72 % of the posterior probability (Supplementary Data Fig. S9). The first configuration accounted for 40 % of the probability of the data, the second for 26 % and the third for ~6 %. The null model with zero shifts was the one with the highest posterior probability (0.40). None of the other configurations had sampling frequencies >0.06 and are therefore not shown. A phylorate plot that displays the most frequently sampled configuration out of the credible shift set is given in Supplementary Data Fig. S9.
Fig. 6.
Prior and posterior probability distributions of the number of rate shifts as inferred via BAMM on the MCC tree inferred during the estimation of divergence times.
DISCUSSION
Monophyly and overall phylogenetic structure of the achyranthoid clade
Under our increased sampling of taxa and molecular characters, the achyranthoid clade originally evidenced by Müller and Borsch (2005a, b) has been found strongly supported. In addition, the genera Centrostachys, Chionothrix, Dasysphaera, Lopriorea, Mechowia, Nelsia, Polyrhabda, Sericocomopsis and Volkensinia of the subtribe Aervinae sensuTownsend (1993), which had not been included in any phylogenetic study so far, have been identified as part of the achyranthoid clade.
Compared with the sole analyses of trnK/matK (Müller and Borsch 2005a, b), the internal relationships of achyranthoids are much better resolved in this study, except for the first diverging lineages. While Cyathula lanceolata and Volkensinia appear in a medium-supported subclade, at least in the plastid tree (Fig. 2), their relationships to Chionothrix and the Calicorema capitata plus Arthraerua subclade remain unclear. However, the relationship of C. capitata with Arthraerua leubnitziae is confirmed with maximum support in plastid and nuclear trees (Fig. 2, Supplementary Data Fig. S6). The affinities of both South African taxa are further supported by similar pollen morphology (Müller and Borsch, 2005b).
Our analysis also confirms the position of the achyranthoid clade as sister to the Gomphrenoideae, both of which are the sister to an aervoid clade (Müller and Borsch 2005a, b). Four other genera of the paraphyletic Amaranthoideae sensuTownsend (1993) that were newly included in our phylogenetic analysis appear outside of the achyranthoids: Digera and Pleuropterantha are close relatives of Amaranthus (extending the amaranthoid clade of Müller and Borsch 2005a). Henonia and Lagrezia belong to the celosioids (Fig. 2), indicating that tribe Celosieae in the circumscription of Schinz (1934) is not monophyletic unless Lagrezia [classified to Amaranthineae (Schinz, 1934; Townsend, 1993)] is included.
The two lineages of achyranthoids initially found by Müller and Borsch (2005b) appear as two major subclades with our more representative taxon sampling (subclades I and II; Fig. 2). Plastid and nrITS trees are largely congruent. Topological differences only occur among samples of Psilotrichum in subclade I and concerning the placement of Cyathula orthacantha.
Species of Psilotrichum are found in several different lineages. The Asian P. ferrugineum is confirmed in a position outside the achyranthoid clade (Müller and Borsch, 2005b) and P. scleranthum (= P. africanum) is now resolved as isolated sister to subclades I plus II in the combined plastid dataset (Fig. 2). Psilotrichum gnaphalobryum, P. gracilipes, P. gloveri and P. sericeum form a well-supported subclade in all trees (Fig. 2, Supplementary Data Fig. S6). Psilotrichum schimperi is also included in this subclade based on plastid data (Fig. 2), but its position is unresolved under nrITS (Supplementary Data Fig. S6). Another lineage with the remaining species of Psilotrichum (P. elliotii, P. cyathuloides) appears close to a Dasysphaera–Pupalia subclade. Interestingly, the Somalian monotypic genus Polyrhabda is suggested as a close relative of P. elliotii. The Dasysphaera–Pupalia subclade is highly supported in all analyses and is one of the youngest groups that have evolved modified sterile flowers with hooks forming adhesive diaspores (Figs 1 and 5). Calicorema squarrosa is now well supported as sister to Sericocoma (Fig. 2, Supplementary Data Fig. S6), and not to Sericorema as depicted in the Bayesian trnK/matK tree (posterior probability = 0.81; Müller and Borsch 2005b).
In subclade II of the achyranthoids, the genus Achyranthes appears paraphyletic to Achyropsis and Nototrichium (Fig. 2, Supplementary Data Fig. S6). All species of Nototrichium are small trees, indicating insular gigantism in these Hawaiian endemics. Centrostachys aquatica is sister to all other species in this subclade. It morphologically resembles the herbaceous species of Achyranthes but has bigger flowers and occurs in swampy habitats. All four genera are characterized by spiciform inflorescences with solitary fertile flowers. In Centrostachys and Achyranthes (Fig. 1D) the flowers with their bracts and bracteoles are deflexed at maturity and bracteoles possess strongly thickened, spine-like midribs that serve for adhesion in diaspores. This feature was obviously lost in Achyropsis and Nototrichium. Furthermore, elaborate stamen tube appendages characteristic of Achyranthes and relatives are absent in Nototrichium. Different samples of Achyranthes aspera are found in at least three lineages, paralleling a considerable morphological variation (e.g. plant size from 10 to 150 cm, presence or absence of woodiness, dense or very sparse indumentum). The Asian Achyranthes bidentata is depicted close to Ethiopian and Kenyan plants of Achyranthes aspera, and the Hawaiian endemic Achyranthes splendens is found distantly from Nototrichium. Further taxon and character sampling is necessary to understand the complex evolutionary history in Achyranthes.
The species of Cyathula appear scattered across subclade II (Fig. 2, Supplementary Data Fig. S6), except for C. lanceolata, which belongs to the early diverging achyranthoids. The deviating position of C. lanceolata in Müller and Borsch (2005b) is an artefact because their sequence (AC022) was mislabelled and in fact is C. prostrata. Cyathula orthacantha is isolated and diverges after Leucosphaera within subclade II (Fig. 2). Cyathula uncinulata (Fig. 1E), C. polycephala, C. tomentosa and C. capitata constitute a subclade of taxa with very dense and partly subglobose synflorescences that is sister to C. cylindrica (Fig. 1B) plus three samples of the polyphyletic Sericocomopsis hildebrandtii (Fig. 2, Supplementary Data Fig. S6). Cyathula natalensis, C. prostrata and Pandiaka form a lineage with elongate, lax inflorescences. Since the genus concept of Cyathula is based on the presence of sterile flowers (Townsend, 1993; Hérnandez-Ledesma et al., 2015), now shown as homoplastic, it is not surprising that the genus does not appear as a natural group. Sericocomopsis currently has two accepted species (Townsend, 1993), distinguished by simple versus stellate hairs. They are resolved in three different lineages (Fig. 2, Supplementary Data Fig. S6), indicating that the simple-haired individuals currently circumscribed as S. hildebrandtii constitute more than one species.
Diversification of the achyranthoid clade through time
Compared with the gomphrenoids, which are a Neotropical radiation (Sánchez-Del Pino et al., 2009) that started 26.4 Mya (95 % HPD 20.68–32.85 Mya) and resulted in the largest clade within the Amaranthaceae, we estimate the crown group age of the achyranthoids as 22.2 Ma (95 % HPD 15.79–27.89 Ma) (node numbers 89 and 112 in Supplementary Data Fig. S7). Most achyranthoids occur in open habitats, mainly semi-desert scrubland, Acacia–Commiphora wood- and bushland as well as dry evergreen afromontane forest and grassland complexes. Characteristic plant groups of these habitats are Acacia (Fabaceae, subfamily Mimosoideae), Commiphora (Burseraceae) and different C4 grasses, such as Sporobolus (subfamily Chloridoideae), Hyparrhenia, Heteropogon and Panicum (subfamily Panicoideae). As shown by Bouchenak-Khelladi et al. (2014), these C4 grass lineages originated around 35 Mya. The crown age of the genus Commiphora was estimated to be ~30 Ma by Becerra et al. (2012). The earliest split of an African Acacia clade with species occurring in open environments from its American sister group is dated to early Miocene times by Bouchenak-Khelladi et al. (2010) but was estimated to even have occurred from around 33 Mya onward by Miller et al. (2013).
Since the above-mentioned genera are dominant in the vegetation in which achyranthoids occur, we may assume that those habitats evolved from ~30 Mya onward. These findings are in line with our age estimation for the achyranthoids. The inferred origins of all these plants, being indicators of open arid and semi-arid habitats, furthermore coincide with the assumed stepwise aridification of East Africa since Eocene–Oligocene times in conjunction with the uplift of the East African Rift system (e.g. Sepulchre et al., 2006).
As shown in our chronogram (Fig. 3) the two major subclades of achyranthoids started to diversify in the early Miocene 16.6 Mya (95 % HPD 11.94–21.22 Mya) and 18.8 Mya (95 % HPD 14.05–23.87 Ma), respectively (node numbers 155 and 121 in Supplementary Data Fig. S7). Achyranthoid species are mostly herbs and small shrubs which are not competitive in broad-leaved forests. Thus, the opening of forests is likely to have offered new niches for achyranthoid species to diversify. Many achyranthoid taxa, such as the Dasysphaera–Pupalia lineage or the Cyathula species with dense inflorescences (node number 152 in Supplementary Data Fig. S7), evolved in Pliocene–Pleistocene times, shortly after C4 grasslands became ecologically dominant in large parts of East Africa (8–6 Mya; Bouchenak-Khelladi et al., 2014).
Evolution of modified sterile flowers
At the selected significance level, the reconstruction of ancestral character states suggests that modified sterile flowers originated at least 14 times independently in the achyranthoids (Fig. 5). Reconstruction results for deeper nodes under the unconstrained model are uncertain, indicating almost equal probabilities for both character states. The transition rates under the unconstrained model were found to favour gains of modified sterile flowers during the evolution of achyranthoids (Table 5). This is in line with our ACSR (Fig. 5), which suggests more gains than losses of this character over time. For the more inclusive functional trait of adhesive appendages, by contrast, transition rates are equal in both directions (Supplementary Data Table S8). This also suggests that a reversal of the bracteole midrib morphology [from thickened and thorn-like, as in Achyranthes (Fig. 1D), to the unmodified state] is more probable than the loss of sterile flowers, which would require a change in inflorescence architecture.
The first occurrence of modified sterile flowers above the significance level was inferred to the early Pliocene under the constrained model of BiSSE model set 1. However, it seems more parsimonious regarding the number of independent origins that the first achyranthoid lineages with modified sterile flowers originated in the second half of the Miocene (once in the stem node incorporating Nelsia quadrangula and several species of Cyathula, and a second time in the ancestor of Kyphocarpa, Marcelliopsis and Sericorema). Several independent origins of this trait occurred during the Pleistocene in subclades I and II. Our reconstructions also indicated that sterile flowers in several early-diverging taxa (e.g. Volkensinia, Leucosphaera, Cyathula lanceolata and Cyathula orthacantha) could have evolved on terminal branches, and therefore dating the origin of the trait is not possible. We assume that the asymmetries in transition rates contributed highly to the prevalence of modified sterile flowers in many achyranthoid species.
Species diversification and epizoochory in achyranthoid evolution
To illustrate the effect of modified sterile flowers (and the more inclusive functional trait of adhesive appendages) on achyranthoid diversification, we evaluated the rates of speciation, extinction and net diversification by comparing lineages with and without these traits under several BiSSE models (Table 5, Supplementary Data Table S8). Speciation as well as extinction rates were found to be higher in the presence than in the absence of both traits (Fig. 4, Table 5, Supplementary Data Table S8). Thus, net diversification was only slightly different in the presence than in the absence of these traits.
The reliability of analyses with SSE models on datasets with <300 terminals has been evaluated in several investigations (e.g. Davis et al., 2013; Rabosky and Goldberg, 2015). Even though the sample size in this investigation was <300, it is well in line with recently recommended sample sizes for SSE models (Gamisch, 2016). Beaulieu and O’Meara (2016) developed proper null models (CID-2 and CID-4), which we used to validate our data and which confirmed the lack of diversification signal in the observed traits. Additionally, we employed BAMM to test for trait-independent rate heterogeneity among the Amaranthaceae, specifically within certain subclades of the achyranthoids or the clade as a whole. The idea was to look for diversification rate shifts that, if present, could be correlated to the dated origins of modified sterile flowers. However, our results indicate the absence of diversification rate shifts within the diversification of the achyranthoids (Fig. 6, Supplementary Data Fig. S9).
Beaulieu and Donoghue (2013) argued that ‘the origin of a trait may not, in itself, be sufficient to increase diversification rate, but rather, requires the right combination of traits’. This view is shared by different authors (e.g. de Queiroz, 2002; Maddison et al., 2007; Beaulieu and O’Meara, 2016). In achyranthoids there is no significant boost of diversification after the acquisition of traits that can serve epizoochory. Nevertheless, the high number of independent origins of sterile flowers, connected with biased transition rates, suggests an adaptive value. The evolution of open habitats in East Africa has probably been an ecological opportunity for the achyranthoids. Nearly all members of this clade occur in habitats with large animals (with a few exceptions, such as Sericostachys, which evolved a liana habit secondarily). Our inferred divergence times indicate that the evolution of achyranthoid diversity coincides with times in which habitats changed and appropriate dispersal agents became abundant (Fig. 3). Large terrestrial mammals started to diversify in the Oligocene. Fossil evidence pointed to a further increase in diversity of large herbivores (including bovids, which represent the largest group of herbivores in Africa today) during the Late Miocene (8–6 Mya) due to a well-established Eurasian connection that allowed massive migration to Africa. A peak of diversity was reached in the Pliocene due to the global transition from C3 to C4 vegetation (Bobe, 2006; Charles-Dominique et al., 2016).
Several investigations developed models to measure and predict the adhesive ability of different diaspore types. Factors such as retention times and separation forces strongly influence the persistence of diaspores in fur and, by extension, dispersal distances (Gorb and Gorb, 2002; Will et al., 2007; Couvreur et al., 2008; Will and Tackenberg 2008; Bullock et al., 2011). Animals migrate between similar habitats, leading to directed dispersal of plants to habitats with optimal conditions for their offspring (Stebbins, 1971). Since most animals use the same route during migration and have been shown to be mobile links between fragmented and therefore isolated ecosystems (Couvreur et al., 2004), there is only a limited possibility for populations to become isolated due to an interruption in gene flow. In achyranthoids, epizoochory may therefore be a successful dispersal mechanism, but rapid diversification may be counteracted by regular interchange of gene pools. More work is needed to evaluate this possibility, particularly by analysing the phylogeography and population structure of widespread achyranthoid species.
SUPPLEMENTARY DATA
Supplementary data are available online at https://academic.oup.com/aob and consist of the following. Table S1: list of analysed taxa of (a) Amaranthaceae and (b) Caryophyllales. Table S2: (a) PCR protocol used for amplification of the plastid trnK/matK, rpl16, trnL-F and the nrITS genomic regions, and (b) primers used for amplification and sequencing of the plastid trnK/matK, rpl16, trnL-F and the nrITS genomic regions. Table S3: character matrix coding the presence and absence of traits within the achyranthoids. Table S4: (a) model fit of different binary state-dependent speciation and extinction models regarding the presence of adhesive flower appendages, and (b) comparisons of model fit of different CID models of the HiSSE model concept and of BiSSE models regarding the presence of adhesive flower appendages. Table S5: (a) global sampling fractions specified for BiSSE analyses, and (b) clade-specific sampling fractions specified for BAMM analyses and species numbers assumed for Amaranthaceae. Figure S6: phylogeny of the achyranthoid clade based on nrITS sequences inferred via BI. Figure S7: chronogram and summary of age estimates of the Amaranthaceae–Chenopodiaceae alliance inferred from dataset C via divergence dating. Table S8: median rates of speciation, extinction and character transition as well as the net effect of diversification for modified sterile flowers under all models. Figure S9: the shift configurations with the highest posterior probabilities out of the 95 % credible set of distinct shift configurations.
ACKNOWLEDGEMENTS
This study was carried out in partial fulfilment of a doctoral thesis by V.D.V. We thank the Ethiopian Biodiversity Institute, Itambo Malombe (East African Herbarium) and the Kenyan authorities for support and collection permits. We also acknowledge the assistance of Assefa Hailu (Addis Ababa University) and Mathias Mbale (National Museums of Kenya) during fieldwork. Additional assistance was provided by staff from the Botanical Garden und Botanical Museum Berlin, especially by Kim Govers, Bettina Giesicke, Julia Pfitzner and Doreen Weigel for laboratory work and by Susy Fuentes Bazan regarding the placement of Chenopodiaceae fossils, as well as by Michael Rodewald for graphically processing the photographic plate. This study was supported by computer resources from the HPC Service of ZEDAT of the Freie Universität Berlin. This work was supported by Deutsche Forschungsgemeinschaft (BO1815/1–4 to T.B. and S.D.)
LITERATURE CITED
- Acosta JM, Perreta M, Amsler A, Vegetti AC. 2009. The flowering unit in the synflorescences of Amaranthaceae. Botanical Review 75: 365–376. [Google Scholar]
- Agnew ADQ, Flux JEC. 1970. Plant dispersal by hares (Lepus capensis L.) in Kenya. Ecology 51: 735–737. [Google Scholar]
- Akaike H. 1974. A new look at the statistical model identification. IEEE Transactions on Automatic Control 19: 716–723. [Google Scholar]
- Beaulieu JM, Donoghue MJ. 2013. Fruit evolution and diversification in campanulid angiosperms. Evolution 67: 3132–3144. [DOI] [PubMed] [Google Scholar]
- Beaulieu JM, O’Meara BC. 2016. detecting hidden diversification shifts in models of trait-dependent speciation and extinction. Systematic Biology 65: 583–601. [DOI] [PubMed] [Google Scholar]
- Becerra JX, Noge K, Olivier S, Venable DL. 2012. The monophyly of Bursera and its impact for divergence times of Burseraceae. Taxon 61: 333–343. [Google Scholar]
- Bell CD, Soltis DE, Soltis PS. 2010. The age and diversification of the angiosperms re-revisited. American Journal of Botany 97: 1296–1303. [DOI] [PubMed] [Google Scholar]
- Bobe R. 2006. The evolution of arid ecosystems in eastern Africa. Journal of Arid Environments 66: 564–584. [Google Scholar]
- Bouchenak-Khelladi Y, Maurin O, Hurter J, van der Bank M. 2010. The evolutionary history and biogeography of Mimosoideae (Leguminosae): an emphasis on African acacias. Molecular Phylogenetics and Evolution 57: 495–508. [DOI] [PubMed] [Google Scholar]
- Bouchenak-Khelladi Y, Slingsby JA, Verboom GA, Bond WJ. 2014. Diversification of C-4 grasses (Poaceae) does not coincide with their ecological dominance. American Journal of Botany 101: 300–307. [DOI] [PubMed] [Google Scholar]
- Bullock JM, Galsworthy SJ, Manzano P, et al. . 2011. Process-based functions for seed retention on animals: a test of improved descriptions of dispersal using multiple data sets. Oikos 120: 1201–1208. [Google Scholar]
- Charles-Dominique T, Davies TJ, Hempson GP, et al. . 2016. Spiny plants, mammal browsers, and the origin of African savannas. Proceedings of the National Academy of Sciences of the USA 113: E5572–E5579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collinson ME, Boulter MC, Holmes PL. 1993. Magnoliophyta (‘Angiospermae’). In: The fossil record 2. London: Chapman & Hall, 809–840 [Google Scholar]
- Couvreur M, Christiaen B, Verheyen K, Hermy M. 2004. Large herbivores as mobile links between isolated nature reserves through adhesive seed dispersal. Applied Vegetation Science 7: 229–236. [Google Scholar]
- Couvreur M, Verheyen K, Vellend M, et al. . 2008. Epizoochory by large herbivores: merging data with models. Basic and Applied Ecology 9: 204–212. [Google Scholar]
- Cuénoud P, Savolainen V, Chatrou LW, Powell M, Grayer RJ, Chase MW. 2002. Molecular phylogenetics of Caryophyllales based on nuclear 18S rDNA and plastid rbcL, atpB, and matK DNA sequences. American Journal of Botany 89: 132–144. [DOI] [PubMed] [Google Scholar]
- Darriba D, Taboada GL, Doallo R, Posada D. 2012. jModelTest 2: more models, new heuristics and parallel computing. Nature Methods 9: 772–772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis MP, Midford PE, Wayne Maddison W. 2013. Exploring power and parameter estimation of the BiSSE method for analyzing species diversification. BMC Evolutionary Biology 13: 38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drummond AJ, Ho SYW, Phillips MJ, Rambaut A. 2006. Relaxed phylogenetics and dating with confidence. PLOS Biology, 4: e88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drummond AJ, Suchard MA, Xie D, Rambaut A. 2012. Bayesian phylogenetics with BEAUti and the BEAST 1.7. Molecular Biology and Evolution 29: 1969–1973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edgar RC. 2004. MUSCLE: multiple sequence alignment with high accuracy and high throughput. Nucleic Acids Research 32: 1792–1797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- FitzJohn RG, Maddison WP, Otto SP. 2009. Estimating trait-dependent speciation and extinction rates from incompletely resolved phylogenies. Systematic Biology 58: 595–611. [DOI] [PubMed] [Google Scholar]
- Friis I, Demissew S, van Breugel P. 2011. Atlas of the potential vegetation of Ethiopia. Addis Ababa, Ethiopia: Addis Ababa University Press, Shama Books. [Google Scholar]
- Gamisch A. 2016. Notes on the statistical power of the binary state speciation and extinction (BiSSE) model. Evolutionary Bioinformatics 12: EBO.S39732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorb E, Gorb S. 2002. Contact separation force of the fruit burrs in four plant species adapted to dispersal by mechanical interlocking. Plant Physiology and Biochemistry 40: 373–381. [Google Scholar]
- Gregor HJ. 1982. Die ‘Parvangulae’ und ‘Guttulae’ Hiltermann & Schmitz 1968 aus dem Randecker Maar – Samenreste von Centrospermae. Paläontologische Zeitschrift 56: 11–18. [Google Scholar]
- Heibl C. 2008. PHYLOCH: R language tree plotting tools and interfaces to diverse phylogenetic software packages http://www.christophheibl.de/Rpackages.html.
- Hernández-Ledesma P, Berendsohn WG, Borsch T, et al. . 2015. A taxonomic backbone for the global synthesis of species diversity in the angiosperm order Caryophyllales. Willdenowia 45: 281–383. [Google Scholar]
- Ho SYW, Phillips MJ. 2009. Accounting for calibration uncertainty in phylogenetic estimation of evolutionary divergence times. Systematic Biology 58: 367–380 [DOI] [PubMed] [Google Scholar]
- Hohmann S, Kadereit JW, Kadereit G. 2006. Understanding Mediterranean-Californian disjunctions: molecular evidence from Chenopodiaceae-Betoideae. Taxon 55: 67–78. [Google Scholar]
- Hurvich CM, Tsai C-L. 1989. Regression and time series model selection in small samples. Biometrika 76: 297–307. [Google Scholar]
- Kadereit G, Borsch T, Weising K, Freitag H. 2003. Phylogeny of Amaranthaceae and Chenopodiaceae and the evolution of C-4 photosynthesis. International Journal of Plant Sciences 164: 959–986. [Google Scholar]
- Kadereit G, Ackerly D, Pirie MD. 2012. A broader model for C-4 photosynthesis evolution in plants inferred from the goosefoot family (Chenopodiaceae s.s.). Proceedings of the Royal Society B Biological Sciences 279: 3304–3311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis PO. 2001. A likelihood approach to estimating phylogeny from discrete morphological character data. Systematic Biology 50: 913–925. [DOI] [PubMed] [Google Scholar]
- Löhne C, Borsch T. 2005. Molecular evolution and phylogenetic utility of the petD group II intron: a case study in basal angiosperms. Molecular Biology and Evolution 22: 317–332. [DOI] [PubMed] [Google Scholar]
- Maddison WP, Midford PE, Otto SP. 2007. Estimating a binary character’s effect on speciation and extinction. Systematic Biology 56: 701–710. [DOI] [PubMed] [Google Scholar]
- Miller JT, Murphy DJ, Ho SYW, Cantrill DJ, Seigler D. 2013. Comparative dating of Acacia: combining fossils and multiple phylogenies to infer ages of clades with poor fossil records. Australian Journal of Botany 61: 436–445. [Google Scholar]
- Mori SA, Brown JL. 1998. Epizoochorous dispersal by barbs, hooks, and spines in a lowland moist forest in central French Guiana. Brittonia 50: 165–173. [Google Scholar]
- Müller K. 2005. SeqState – primer design and sequence statistics for phylogenetic DNA data sets. Applied Bioinformatics 4: 65–69. [DOI] [PubMed] [Google Scholar]
- Müller K, Borsch T. 2005a Phylogenetics of Amaranthaceae based on matK/trnK sequence data – evidence from Parsimony, likelihood, and Bayesian analyses. Annals of the Missouri Botanical Garden 92: 66–102. [Google Scholar]
- Müller K, Borsch T. 2005b Multiple origins of a unique pollen feature: stellate pore ornamentation in Amaranthaceae. Grana 44: 266–281. [Google Scholar]
- Müller J, Müller K, Neinhuis C, Quandt D. 2010. PhyDE: Phylogenetic Data Editor v 0.9971 www.phyde.de.
- Nichols DJ, Traverse A. 1971. Palynology, petrology, and depositional environments of some early tertiary lignites in Texas. Geoscience and Man 3: 37–48. [Google Scholar]
- Peterson AT. 2006. Application of molecular clocks in ornithology revisited. Journal of Avian Biology 37: 541–544. [Google Scholar]
- Plummer M, Best N, Cowles K, Vines K. 2006. CODA: Convergence Diagnosis and Output Analysis for MCMC. R News 6: 7–11. [Google Scholar]
- Principi P. 1926. La flora oligocenica de Chiavon e Salcedo. Memorie della Carta Geologica d’Italia 10: 1–127. [Google Scholar]
- de Queiroz A. 2002. Contingent predictability in evolution: key traits and diversification. Systematic Biology 51: 917–929. [PubMed] [Google Scholar]
- Rabosky DL. 2014. Automatic detection of key innovations, rate shifts, and diversity-dependence on phylogenetic trees. PLoS ONE 9: e89543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabosky DL, Goldberg EE. 2015. Model inadequacy and mistaken inferences of trait-dependent speciation. Systematic Biology 64: 340–355. [DOI] [PubMed] [Google Scholar]
- Rabosky DL, Grundler M, Anderson C, et al. . 2014. BAMMtools: an R package for the analysis of evolutionary dynamics on phylogenetic trees. Methods in Ecology and Evolution 5: 701–707. [Google Scholar]
- Rambaut A, Drummond AJ. 2007. Tracer v1.4.http://tree.bio.ed.ac.uk/software/tracer/.
- Ridley HN. 1930. The dispersal of plants throughout the world. Ashford, UK: Reeve & Co. [Google Scholar]
- Ronquist F, Teslenko M, van der Mark P, et al. . 2012. MrBayes 3.2: efficient Bayesian phylogenetic inference and model choice across a large model space. Systematic Biology 61: 539–542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sánchez-Del Pino I, Borsch T, Motley TJ. 2009. trnL-F and rpl16 sequence data and dense taxon sampling reveal monophyly of unilocular anthered Gomphrenoideae (Amaranthaceae) and an improved picture of their internal relationships. Systematic Botany 34: 57–67. [Google Scholar]
- Schäferhoff B, Müller KF, Borsch T. 2009. Caryophyllales phylogenetics: disentangling Phytolaccaceae and Molluginaceae and description of Microteaceae as a new isolated family. Willdenowia 39: 209–228. [Google Scholar]
- Schluter D, Price T, Mooers AØ, Ludwig D. 1997. Likelihood of ancestor states in adaptive radiation. Evolution 51: 1699–1711. [DOI] [PubMed] [Google Scholar]
- Schinz H. 1934. Amaranthaceae. In: Engler A, Prantl K, eds. Die natürlichen Pflanzenfamilien, Vol. 16c, 2nd edn Leipzig: W. Engelmann. [Google Scholar]
- Sepulchre P, Ramstein G, Fluteau F, Schuster M, Tiercelin JJ, Brunet M. 2006. Tectonic uplift and Eastern Africa aridification. Science 313: 1419–1423. [DOI] [PubMed] [Google Scholar]
- Simmons MP, Ochoterena H. 2000. Gaps as characters in sequence-based phylogenetic analyses. Systematic Biology 49: 369–381. [PubMed] [Google Scholar]
- Sorensen AE. 1986. Seed dispersal by adhesion. Annual Review of Ecology and Systematics 17: 443–463. [Google Scholar]
- Silvestro D, Michalak I. 2012. raxmlGUI: a graphical front-end for RAxML. Organisms Diversity & Evolution 12: 335–337. [Google Scholar]
- Stamatakis A. 2006. RAxML-VI-HPC: maximum likelihood-based phylogenetic analyses with thousands of taxa and mixed models. Bioinformatics 22: 2688–2690. [DOI] [PubMed] [Google Scholar]
- Stebbins GL. 1971. Adaptive radiation of reproductive characteristics in angiosperms, II: Seeds and seedlings. Annual Review of Ecology and Systematics 2: 237–260. [Google Scholar]
- Sukhorukov AP, Zhang ML. 2013. Fruit and seed anatomy of Chenopodium and related genera (Chenopodioideae, Chenopodiaceae/Amaranthaceae): implications for evolution and taxonomy. PLoS ONE 8: e61906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swofford DL. 2002. PAUP* Phylogenetic Analysis Using Parsimony (*and other methods). Version 4. Sunderland, MA: Sinauer Associates. [Google Scholar]
- Townsend CC. 1993. Amaranthaceae. In: Kubitzki K, Rohwer JG, Bittrich V, eds. Families and genera of vascular plants, Vol. 2 Berlin: Springer. [Google Scholar]
- de Vos JM, Hughes CE, Schneeweiss GM, Moore BM, Conti EC. 2014. Heterostyly accelerates diversification via reduced extinction in primroses. Proceedings of the Royal Society B Biological Sciences 281: 20140075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White F. 1983. The vegetation of Africa. A descriptive memoir to accompany the UNESCO/AETFAT/UNSO vegetation map of Africa. Natural Resources Research, No. 20. Paris: UNESCO. [Google Scholar]
- Will H, Maussner S, Tackenberg O. 2007. Experimental studies of diaspore attachment to animal coats: predicting epizoochorous dispersal potential. Oecologia 153: 331–339. [DOI] [PubMed] [Google Scholar]
- Will H, Tackenberg O. 2008. A mechanistic simulation model of seed dispersal by animals. Journal of Ecology 96: 1011–1022. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.