Transition from Actin-Driven to Water-Driven Cell Migration Depends on External Hydraulic Resistance

Abstract

Cells in vivo can reside in diverse physical and biochemical environments. For example, epithelial cells typically live in a two-dimensional (2D) environment, whereas metastatic cancer cells can move through dense three-dimensional matrices. These distinct environments impose different kinds of mechanical forces on cells and thus potentially can influence the mechanism of cell migration. For example, cell movement on 2D flat surfaces is mostly driven by forces from focal adhesion and actin polymerization, whereas in confined geometries, it can be driven by water permeation. In this work, we utilize a two-phase model of the cellular cytoplasm in which the mechanics of the cytosol and the F-actin network are treated on an equal footing. Using conservation laws and simple force balance considerations, we are able to describe the contributions of water flux, actin polymerization and flow, and focal adhesions to cell migration both on 2D surfaces and in confined spaces. The theory shows how cell migration can seamlessly transition from a focal adhesion- and actin-based mechanism on 2D surfaces to a water-based mechanism in confined geometries.

Introduction

Animal cell migration is a complex process orchestrated by actin dynamics, focal adhesions, and also water flux (1, 2). However, how these elements are added together to obtain the observed cell speed is less clear. For example, cell migration on two-dimensional (2D) surfaces is mostly driven by forces from actin polymerization and focal adhesions (3), and there has been extensive work on modeling actin-driven cell migration on 2D surfaces (4, 5, 6), whereas cells in confined geometries can be driven by water permeation (7). Moreover, cells in confined channels show a diversity of behavior: some cells such as MDA-MB-231 (human breast cancer cell line) show reduced migration speed when actin is disrupted (8, 9), whereas for others such as S180 (mouse sarcoma cell line), the migration speed is unaffected (7). In addition to varying responses to actin inhibition, cell movement in confinement appears to be sensitive to hydraulic resistance (10). Even more complex are cells in three-dimensional (3D) collagen matrices, where they develop long protrusions that interact with the collagen fibers, pores, and interstitial fluid (11, 12, 13, 14, 15). Depending on the cell shape, the nucleus may also play a significant role in propelling the cell (16). Thus, there are diverse mechanisms driving cell migration (17). We would like to understand whether there are unified physical principles and mechanisms giving rise to the wide range of observed cell behavior. Can we explain the impact of the physical environment on the speed of cell migration? In this work, by focusing on the combined contributions from actin dynamics and water flow, we develop a general model to understand mechanisms of cell migration in 3D, 2D, and one-dimensional (1D) environments (Fig. 1, A–C). In all these cases, we examine an effective one-dimensional volume element of a cell and compute the leading-edge cell speed for different actin- and water-flow dynamics. We find that the hydraulic environment of the cell potentially has a counterintuitive impact on the cell speed and determines the contribution of actin and water to the observed cell movement. In particular, cells can speed up if the coefficient of external hydraulic resistance increases, even when there is no change in the molecular elements driving migration. These results explain the diversity of observed cell-migration mechanisms and suggest that cells moving in 3D matrices are not only influenced by collagen fibers but also the hydrodynamic environment.

Figure 1.

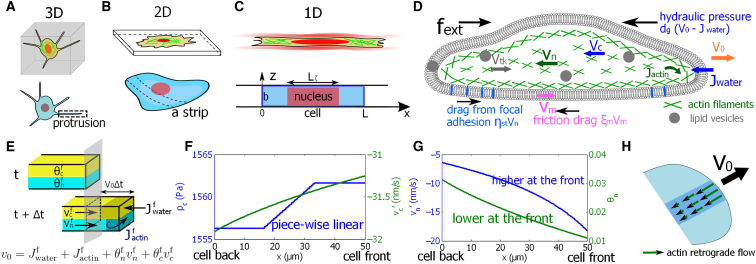
A two-fluid-phase cell-migration model. (A) The schematics of a cell in a 3D collagen gel are shown. The thin protrusion can be regarded as a 1D structure. (B) The schematics of a cell on a 2D substrate are shown. A strip of a cell on a 2D substrate can be regarded a 1D structure. (C) The schematics of a cell in a confined space are shown. In this case, the cell is essentially 1D. The model represents a cell (or a strip) with length L and width b. (D) A diagram of the relevant forces that contribute to cell migration is given. $v_{n,c}$ is the actin network and cytosol phase velocity, respectively. $v_{\text{tk}}$ is the possible vesicle trafficking rate from the back to the front. The actin phase forms focal adhesion with the environment, resulting in a frictional drag force ${\eta }_{\text{st}}{v}_n$. Membrane movement also generates frictional force $\left({\xi }_m{v}_m\right)$. As the cell displaces external water, the hydraulic resistance can be expressed as $d_g\left(v_0-J_{\text{water}}\right)$, where $v_0$ is the cell boundary velocity. (E) A unit cross-sectional area of the cell leading edge is given. An exact kinematic relation for two-phase cell migration from time t to t + Δt can be derived from mass balance. Each phase is attached to the cell leading edge (no void space) so that the cell velocity is related to the velocity of each phase. $J_{\text{actin}}^{\text{f}}$ is the actin polymerization rate at the leading edge. $J_{\text{water}}^{\text{f}}$ is the water influx rate at the leading edge. ${\theta }_{c,n}$ is the volume fraction of the cytosol actin network phase, respectively. $v_c^{\text{f}}$ and $v_n^{\text{f}}$ are the intracellular fluid velocities at the leading edge for the cytosol and actin phase, respectively. (F) The computed intracellular hydrostatic pressure field (left axis) and cytosol velocity field with respect to the cell frame (right axis) are shown. $v_c^{\prime }=v_c-v_0$. (G) The computed intracellular actin velocity field with respect to the cell frame (left axis) and its volume fraction (right axis) are shown. $v_n^{\prime }=v_n-v_0$. (H) A diagram of the actin retrograde flow predicted by the model is given. To see this figure in color, go online.

Materials and Methods

A two-phase model of cell migration

To avoid complications associated with cell geometry, in this work, we mainly discuss a 1D-volume element of a moving cell. For example, for cells in 3D collagen matrices (Fig. 1 A), the thin protrusions can be regarded as 1D structures. For cells on 2D substrates (Fig. 1 B), we model a 1D strip of the cell. In this case, we only consider velocities and forces perpendicular to the cell leading edge. The effect of external bulk fluid flow in 2D is not considered in the model. For cells in a confined space (Fig. 1 C), the actin network and water flows can be directly modeled in 1D. In this case, the cell nucleus provides additional drag forces on the cytoplasm as the flows pass around or through (for the water phase) the nucleus. Within the 1D framework, the cell boundary is reduced to a front (“f”) and a back (“b”). We use superscripts “f” and “b” to denote quantities associated with the cell front (leading edge) and back (trailing edge), respectively. In the following, we discuss briefly the 1D two-phase model of cell migration; more details and explanations can be found in the Supporting Materials and Methods.

In our model, we treat the cytosol (c, which is essentially water) and the actin network (n) as two fluid phases interacting with each other (18) and with the environment. The essential elements in the model are illustrated in Fig. 1 D. The volume fraction and velocity of the cytosol (actin network) phase are ${\theta }_c\left({\theta }_n\right)$ and $v_c\left(v_n\right)$, respectively. In the frame of the cell body when the flow is steady, mass conservation conditions of the two phases are

$$\frac{d}{dx}\left[{\theta }_n{v}_n^{\prime }\right]=0$$ (1)

and

$$\frac{d}{dx}\left[{\theta }_c{v}_c^{\prime }\right]=0,$$ (2)

where $v_n^{\prime }=v_n-v_0$ and $v_c^{\prime }=v_c-v_0$ are the velocities of the two phases in the frame of the moving cell and $v_0$ is the steady migration velocity of the leading edge and the cell.

For moving cells, new actin filaments are polymerized at the cell boundary with a rate $J_{\text{actin}}^{\text{f}/\text{b}}$. Similarly, water influx, $J_{\text{water}}^{\text{f}/\text{b}}$, also occurs at the cell boundary. In this model, $J_{\text{actin}}^{\text{f}/\text{b}}$ is a parameter, and $J_{\text{water}}^{\text{f}/\text{b}}$ is calculated from the chemical potential difference of water, i.e., $J_{\text{water}}^{\text{f}/\text{b}}=-{\alpha }^{\text{f}/\text{b}}\left(\mathit{\Delta }{P}^{\text{f}/\text{b}}-\mathit{\Delta }{\mathit{\Pi }}^{\text{f}/\text{b}}\right)$, where $\mathit{\Delta }{P}^{\text{f}/\text{b}}$ and $\mathit{\Delta }{\mathit{\Pi }}^{\text{f}/\text{b}}$ are, respectively, the hydrostatic and osmotic pressure differences across the cell membrane and ${\alpha }^{\text{f}/\text{b}}$ is a coefficient of membrane water permeability. The cell can control $\mathit{\Delta }{\mathit{\Pi }}^{\text{f}/\text{b}}$ by generating ion fluxes at the cell boundary, and therefore we take it as a parameter. $\mathit{\Delta }{P}^{\text{f}/\text{b}}$ must be computed from mechanical considerations.

Because there are no void spaces, the cell boundary velocity is closely related to the boundary velocity of each phase. At the leading edge of the cell, as illustrated in Fig. 1 E, boundary kinematic relations read as ${\theta }_c^{\text{f}}{v}_c^{\text{f}}+J_{\text{water}}^{\text{f}}=v_0{\theta }_c^{\text{f}}$ and ${\theta }_n^{\text{f}}{v}_n^{\text{f}}+J_{\text{actin}}^{\text{f}}=v_0{\theta }_n^{\text{f}}$. Therefore, the velocity of the cell boundary is

$$v_0=J_{\text{water}}^{\text{f}}+J_{\text{actin}}^{\text{f}}+{\theta }_n^{\text{f}}{v}_n^{\text{f}}+{\theta }_c^{\text{f}}{v}_c^{\text{f}},$$ (3)

where we have used ${\theta }_c+{\theta }_n=1$. Eq. 3 suggests that both water flux and actin polymerization can potentially contribute to cell migration (19). In a steady state with constant cell volume, $J_{\text{actin}}^{\text{f}}=-J_{\text{actin}}^{\text{b}}$ and $J_{\text{water}}^{\text{f}}=-J_{\text{water}}^{\text{b}}$; we thus use the notations $J_{\text{actin}}=J_{\text{actin}}^{\text{f}}$ and $J_{\text{water}}=J_{\text{water}}^{\text{f}}$ to represent the magnitude of these fluxes in the cell.

During cell migration, the cell membrane has a translational velocity, $v_m$, with respect to the surroundings. This motion leads to a frictional force between the cell and the surroundings. This force can be expressed as $f_m=-{\xi }_m{v}_m$, where ${\xi }_m$ is the coefficient of frictional drag. $v_m$ and $v_0$ are typically equivalent, but they can also be different if we include the velocity of membrane growth or extension from vesicle trafficking (20), $v_{\text{tk}}$. In this case, the apparent velocity of the cell boundary, $v_0$, is formally a sum of the translational velocity of the lipid membrane and the velocity from vesicle trafficking, i.e., $v_0=v_m+v_{\text{tk}}$. $v_{\text{tk}}$ depends on the cell membrane tension, τ (21, 22). Note that vesicle trafficking does not affect Eq. 3, which is only based on the assumption that the actin network phase is always attached to the membrane. This assumption holds during typical tissue-cell migration. One violation of such a condition is blebbing motility (23), in which the membrane extends without actin. Although blebbing motility can be analyzed within the two-phase framework, the details are more complicated. We will not discuss this case here.

If we regard the actin network as isotropic, it then also has an effective pressure that is different from the cytosol phase because of active contractions from myosin. The actin network is linked to the underlying substrate through focal adhesions and integrins (24). As the actin network flows, this linkage transmits a force from the environment to the actin network and thus onto the entire cell. For low actin-flow velocities, the force from focal adhesions is approximately proportional to the velocity of actin flow (25), i.e., $f_{\text{st}}=-{\eta }_{\text{st}}{v}_n$, where ${\eta }_{\text{st}}$ is the coefficient of focal adhesion friction. Factors that can influence ${\eta }_{\text{st}}$ include the substrate stiffness (26, 27) and the size (28) and density (29) of adhesions. In this work, we restrict ourselves to understanding the mechanism of cell migration for a linear force-velocity relation for the focal adhesions. Experiments (25) and theory (27, 30, 31) have shown that the adhesion force-velocity relationship is generally complex and nonlinear. This can be incorporated into our model, but the details are not analyzed here.

To predict the cell velocity from Eq. 3, we need to know intracellular velocities $v_n^{\text{f}}$ and $v_c^{\text{f}}$. These must be solved from mechanical force balance. When all of the forces are considered, the conservation of momentum for the two cytoplasmic fluid phases are

$$0=-{\theta }_c\frac{d}{dx}{P}_c+\eta {\theta }_n{\theta }_c\left(v_n^{\prime }-v_c^{\prime }\right)-{\zeta }_c{\theta }_c{v}_c^{\prime }$$ (4)

and

$$0=-{\theta }_n\frac{d}{dx}{P}_c-{\eta }_n{\theta }_n\left[v_n^{\prime }+\left(v_0-v_m\right)\right]+\eta {\theta }_n{\theta }_c\left(v_c^{\prime }-v_n^{\prime }\right)$$

$$-\frac{d}{dx}\left({\theta }_n{\varphi }_n\right)-{\eta }_{\text{st}}{\theta }_n\left(v_n^{\prime }+v_0\right)-{\zeta }_n{\theta }_n{v}_n^{\prime },$$ (5)

where η is the coefficient of interphase viscous drag, ${\eta }_n$ is the effective viscosity of the actin phase, and ${\zeta }_c\left(x\right)$ and ${\zeta }_n\left(x\right)$ are the coefficients of frictional drag from the nucleus on the cytosol and on the actin phases, respectively; these are only defined in the region where the nucleus is present. $P_c$ and $P_n=P_c+{\varphi }_n$ are the cytosol and network phase pressures, respectively. We write the excess pressure in the network phase as ${\theta }_n{\varphi }_n$, which is also related to active contraction generated by myosin.

As the cell boundary moves at velocity $v_0$, the cell may experience an extracellular hydraulic resistance (in units of pressure, because this force is exerted on an area element). When $v_0\ne J_{\text{water}}$, the cell boundary must push the external fluid at velocity $v_{\ast }=v_0-J_{\text{water}}$. In the extreme case of a cell in a confined channel, the cell must push the complete column of water in front of the cell at the velocity $v_{\ast }$, and the friction between the extracellular fluid and the channel wall generates a large hydraulic resistance. This hydraulic resistance can be expressed as a linear function of $v_{\ast }$, i.e., $P_{\ast }=d_g\left(v_0-J_{\text{water}}\right)$, where d_g is a coefficient to be determined by the extracellular geometry and flow properties. In addition, the cell may experience external forces from extracellular objects such as mounted cantilever (32). We use $f_{\text{ext}}$ to account for this effective force per unit area (again in units of pressure). Therefore, the force balance of the cell membrane is

$$b\left[\left(P_{\text{in}}^{\text{f}}-P_{\ast }^{\text{f}}\right)-\left(P_{\text{in}}^{\text{b}}-P_{\ast }^{\text{b}}\right)\right]+b{f}_{\text{ext}}^{\text{f}}-b{f}_{\text{ext}}^{\text{b}}=-b{\eta }_n{\int }_0^L{\theta }_n\left[v_n^{\prime }+\left(v_0-v_m\right)\right]dx+2{\xi }_m{v}_{m}L.$$ (6)

The cell boundary velocity $v_0$ can be solved by integrating the sum of Eqs. 4 and 5 and adding that to Eq. 6. In the limit of $v_m=v_0$, $v_0$ can be solved analytically as follows (see Supporting Materials and Methods for more information):

$$v_0=\frac{L{\eta }_{\text{st}}{J}_{\text{actin}}+f_{\text{ext}}^{\text{f}}-f_{\text{ext}}^{\text{b}}}{L{\eta }_{\text{st}}{\text{Θ}}_n+2{\xi }_{m}L/b+d_g}+\frac{L_{\zeta }\left({\zeta }_c{J}_{\text{water}}+{\zeta }_n{J}_{\text{actin}}\right)+d_g{J}_{\text{water}}}{L{\eta }_{\text{st}}{\text{Θ}}_n+2{\xi }_{m}L/b+d_g},$$ (7)

where L and b are the length and width of the cell (or a strip of cell), respectively, $L_{\zeta }$ is the length of the nucleus (Fig. 1 C), and ${\text{Θ}}_n$ is the average volume fraction of the actin phase, satisfying ${\int }_0^L{\theta }_n\left(x\right)dx=L{\text{Θ}}_n$. The approximation $v_m=v_0$ is valid when the net flux of vesicle trafficking is negligible. This can occur when the membrane-tension gradient across the cell is negligible or when the rate of vesicle formation is low. We will show that the membrane-tension gradient is indeed very small for the underlying physics included in the model. In this work, we also have not considered membrane blebbing and thus also neglect any membrane-tension changes due to blebbing (33).

The numerical values of parameters for the model are listed in Table 1. Unless otherwise specified or varied, these parameters are used throughout the work. More details on the physical interpretation of each parameter can be found in the Supporting Materials and Methods.

Table 1.

Parameters Used in the Models

Parameters	Description	Values	Sources
R (J/mol K)	ideal gas constant	8.31451	constant
T (K)	absolute temperature	300	room temperature
L (μm)	cell length	50	generic
$L_{\zeta }$ (μm)	nucleus length	L/2	generic
b (μm)	cell width	3	generic
h (μm)	membrane thickness	0.5	(48)
η (Pa ⋅ s/μm2)	drag coefficient between two phases	1	(49)
${\eta }_n$ (Pa ⋅ s/μm2)	effective viscosity in the actin phase	1.3	see text
${\zeta }_c$ (Pa ⋅ s/μm2)	effective drag coefficient from the nucleus to the cytosol phase	10	assumed
${\zeta }_n$ (Pa ⋅ s/μm2)	effective drag coefficient from the nucleus to the actin network phase	100	assumed
${\xi }_m$ (Pa ⋅ s/μm)	coefficient of friction of the channel wall	1	(7)
${\eta }_{\text{st}}$ (Pa ⋅ s/μm2)	coefficient of drag from focal adhesion	1 × 104	(25)
$d_g$ (Pa ⋅ s/μm)	coefficient of hydraulic pressure	1 × 103	see text
$f_{\text{ext}}^{\text{f}}$ (Pa)	external force per unit area at the front	0	generic
$f_{\text{ext}}^{\text{b}}$ (Pa)	external force per unit area at the back	0	generic
${\alpha }^{\text{f}}$ (μm/(Pa ⋅ s))	water permeability constant at the front	1.0 × 10−4	(7)
${\alpha }^{\text{b}}$ (μm/(Pa ⋅ s))	water permeability constant at the back	1.0 × 10−4	(7)
${\gamma }_{\text{tk}}^0$ (nm/s)	maximal rate of vesicle trafficking	10	assumed
${\tau }_{\text{max}}$ (Pa m)	maximal membrane tension when vesicle trafficking stops	5 × 10−2	assumed
${\text{Θ}}_n$	average volume fraction of the actin phase	0.02	(50)
${\varphi }_n$ (Pa)	excess pressure in the actin network	−1000 (back) to −5000 (front)	assumed
$J_{\text{actin}}$ (nm/s)	actin flux at the two boundaries	10${\text{Θ}}_n$	assumed
$P_0^{\text{f}}$ (Pa)	extracellular hydrostatic pressure at the front	0	generic
$P_0^{\text{b}}$ (Pa)	extracellular hydrostatic pressure at the back	0	generic
$c_0^{\text{f}}$ (mM)	extracellular ion concentration at the front	340	(7)
$c_0^{\text{b}}$ (mM)	extracellular ion concentration at the back	340	(7)
$c_{\text{in}}^{\text{f}}$ (mM)	intracellular ion concentration at the front	340.75	generic
$c_{\text{in}}^{\text{b}}$ (mM)	intracellular ion concentration at the back	340.5	generic

These are the default parameters unless otherwise specified.

Results and Discussion

The nucleus can increase the intracellular pressure difference

Fig. 1, F and G show a typical distribution of the intracellular hydrostatic pressure, volume fraction of the actin phase, and velocities of the two phases for a migrating cell with respect to the cell moving frame (see Supporting Materials and Methods for parameters). The velocity of the cell edge and the membrane translation are predicted to be the same, $v_0=v_m=12$ nm/s. Therefore, in this case, vesicle trafficking has a negligible effect. This is because the membrane tension difference between the cell front and back is negligible (see Supporting Materials and Methods and a later section). For the assumed osmotic pressure gradient, the water flux into the cell at the front is $J_{\text{water}}=31$ nm/s, whereas the actual cell velocity is much smaller. Because $v_0\ne J_{\text{water}}$, the cell displaces the extracellular fluid as it migrates.

The average intracellular hydrostatic pressure, $P_c$, is determined by the average osmolarity difference across the cell. In confined channels, the nucleus also influences $P_c$, giving rise to a piece-wise linear pressure profile. Larger effective drag from the nucleus on the cytosol, i.e., larger ${\zeta }_c$, induces higher pressure difference between the front and back of the cell. When ${\zeta }_c=0$, then $P_c$ is a smooth function over the entire cell length, and the difference of $P_c$ across the cell is reduced (see Fig. S2). This result is consistent with the “nuclear piston” mode of migration, in which the pressure gradient of the nucleus can influence cell speed (16). With the nucleus, the model predicts the same average intracellular cytosol pressure as the case without the nucleus; only $\mathit{\Delta }{P}_c=P_c^{\text{f}}-P_c^{\text{b}}$ is different. The relative velocity of the cytosol, $v_c^{\prime }=v_c-v_0$ (shown in Fig. 1 F), is determined mostly by the boundary condition, i.e., $v_c^{\prime }\left(L\right)=-J_{\text{water}}/{\theta }_c\left(L\right)$. Higher $\left|v_c^{\prime }\right|$ at the back of the cell is consistent with the lower cytosolic volume fraction, because the product ${\theta }_c{v}_c^{\prime }$ must be a constant from the mass conservation.

Retrograde flow is prominent at the cell leading edge

The relative velocity of the actin network, $v_n^{\prime }=v_n-v_0$ (shown in Fig. 1 G), is largely determined by the rate of actin (de)polymerization at the boundaries, i.e., $v_n^{\prime }\left(L\right)=-J_{\text{actin}}/{\theta }_n\left(L\right)$. In this example, the actin velocity at the cell front in the fixed frame is $v_n^{\text{f}}=v_n^{\prime \text{f}}+v_0=-6$ nm/s. This negative velocity pointing inwards is the actin retrograde-flow motion commonly seem during cell migration (34). Our model also predicts a decrease of the retrograde velocity toward the back of the cell (Fig. 1 G) as seen in experiments (35). A cartoon depiction of actin retrograde flow is shown in Fig. 1 H. Because of the boundary condition specified in the model, we do not consider an anterograde actin flow at the back of the cell (6).

Cell migration on 2D substrates relies on actin dynamics and focal adhesion

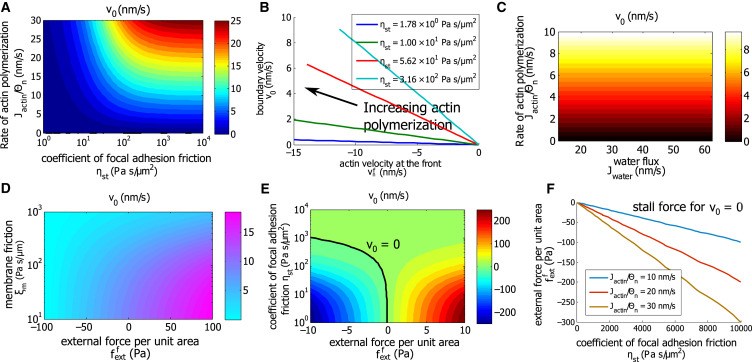
For cells on 2D substrates, the coefficient of hydraulic resistance is negligible ($d_g^{2\text{D}}=0$; see the Supporting Materials and Methods for more information), and the effective drag from the nucleus on the two phases can be neglected as well (${\zeta }_c={\zeta }_n=0$). Hence, Eq. 7 is reduced to a simpler form in which $v_0$ is independent of $J_{\text{water}}$. The model predicts that $v_0$ scales with the rate of actin polymerization, $J_{\text{actin}}/{\text{Θ}}_n$, and the coefficient of focal adhesions, ${\eta }_{\text{st}}$ (Fig. 2 A). In the limit of large ${\eta }_{\text{st}}$ (for example, along the line ${\eta }_{\text{st}}={10}^4$ Pa ⋅ s/μm²), the effect of ${\xi }_m$ and $f_{\text{ext}}^{\text{f}/\text{b}}$ diminishes and $v_0\simeq J_{\text{actin}}/{\text{Θ}}_n$, suggesting that when the strength of focal adhesion is high (no slip), the cell velocity is determined by the rate of actin polymerization. On the other hand, when the force from focal adhesions is abolished (along the line ${\eta }_{\text{st}}=1$ Pa ⋅ s/μm²), $v_0$ does not increase as $J_{\text{actin}}$ increases. This is consistent with the finding that for actin polymerization to be effective, there must be sufficient focal adhesion friction (24).

Figure 2.

Cell migration on 2D substrates. (A) The contours of the cell boundary velocity, $v_0$, are shown as functions of actin polymerization rate $J_{\text{actin}}$ and focal adhesion friction coefficient ${\eta }_{\text{st}}$. $J_{\text{actin}}/{\text{Θ}}_n$ is a measure of actin velocity at the cell boundary generated by actin polymerization. In the calculation, $J_{\text{actin}}$ varies and ${\text{Θ}}_n$ remains unchanged. (B) The cell boundary velocity $v_0$ is given as a function of $v_n^{\text{f}}$ for different coefficient of focal adhesion ${\eta }_{\text{st}}$. (C) The contours of $v_0$ as $J_{\text{actin}}$ and $J_{\text{water}}$ vary as shown. In 2D, $J_{\text{water}}$ does not influence cell boundary velocity. (D) The contours of $v_0$ as ${\xi }_m$ and $f_{\text{ext}}^{\text{f}}$ vary as shown. (E) The contours of $v_0$ as $f_{\text{ext}}^{\text{f}}$ and ${\eta }_{\text{st}}$ vary as shown. (F) The stall force per unit area for different ${\eta }_{\text{st}}$ is given. As expected, the magnitude of the stall force increases with increasing coefficients of focal adhesion friction or the rate of actin polymerization. To see this figure in color, go online.

Fig. 2 B shows the predicted relation between $v_0$ and actin retrograde velocity as $J_{\text{actin}}$ varies for different ${\eta }_{\text{st}}$. A higher rate of actin polymerization results in a higher cell velocity and also a higher magnitude of actin retrograde flow, because $\left|v_n^{\text{f}}\right|$ increases faster than $v_0$. For the same actin velocity $v_n$, the model predicts a higher $v_0$ for higher ${\eta }_{\text{st}}$.

Although the cell boundary velocity is in general influenced by the water flux through the membrane (Eq. 3), the model predicts that under negligible hydraulic resistance $\left(d_g^{2\text{D}}=0\right)$, the boundary velocity is independent of $J_{\text{water}}$. This can also be seen from Eq. 7, in which $J_{\text{water}}$ does not contribute to $v_0$ when d_g = 0. More discussion is given in a later section.

Influence of external force on cell migration

The cell boundary moves faster if the membrane friction with the environment, ${\xi }_m{v}_m$, is low or the combination of the external forces (per unit area), $f_{\text{ext}}^{\text{f}}-f_{\text{ext}}^{\text{b}}$, points in the direction of cell migration (Fig. 2 D). Contour plots of $v_0$ as a function of ${\eta }_{\text{st}}$ and $f_{\text{ext}}^{\text{f}}$ show a similar story (Fig. 2 E). We predict that when the friction force from focal adhesion is small (low ${\eta }_{\text{st}}$), $v_0$ scales linearly with $f_{\text{ext}}^{\text{f}}$; when the force from focal adhesion is large (high ${\eta }_{\text{st}}$), then the external forces have a negligible effect on cell velocity. Therefore, Fig. 2 E also implies an external force-cell velocity relation for cell migration. Similar calculations can be obtained for different rates of actin polymerization. We can extract the stall force when $v_0=0$ for each ${\eta }_{\text{st}}$ and $J_{\text{actin}}$. As expected, the magnitude of the stall force increases as ${\eta }_{\text{st}}$ or $J_{\text{actin}}$ increases (Fig. 2 F). For a 2D cell’s boundary element of 3 μm width and 200 nm height, the predicted stall force is on the order of 1 nN, which is of the same order as the stall force for cell boundary lamellipodium (32).

The spatial variation of the cell-membrane tension is set partially by the membrane friction with the environment and partially by the external force: larger ${\xi }_m$ and $f_{\text{ext}}^{\text{f}}-f_{\text{ext}}^{\text{b}}$ can generate a membrane tension difference up to 10% from the back to the front of the cell (see Fig. S3). In other cases, the membrane tension is almost uniform across the cells, and thus the velocity contributed by the membrane trafficking is negligible. This result validates the assumption of $v_m=v_0$ that is used to approximate $v_0$ in Eq. 7. The viscosity of each phase or the friction between two phases has little contribution to $v_0$ (see Fig. S3), showing that for cells on 2D substrates, migration is mostly driven by actin polymerization, focal adhesion, and external forces acting on the cell.

Confined 1D cells migrate faster under higher coefficients of hydraulic resistance

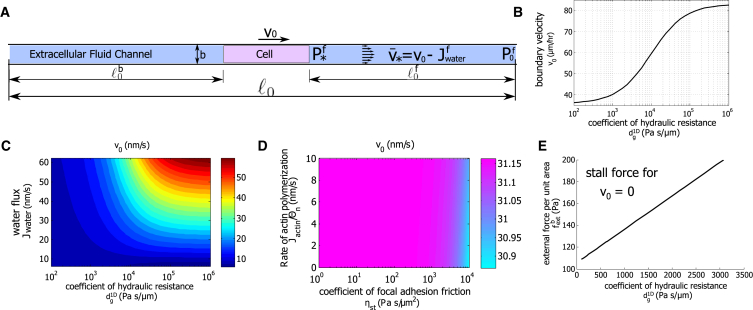
For cells in confined channels (Fig. 3 A), the coefficient of hydraulic resistance is $d_g^{1\text{D}}=12{\mu }_f{\ell }_0/b^2$, where ${\ell }_0$ is the total length of the channel and ${\mu }_f$ is the extracellular fluid viscosity in the channel (see the Supporting Materials and Methods for more information). A longer channel or a higher extracellular fluid viscosity leads to a higher coefficient of hydraulic resistance. In a typical channel in this work or in (7), for example, $b=5\mu$ m, ${\ell }_0=500\mu$ m, and ${\mu }_f={10}^{-3}$ Pa ⋅ s, then $d_g^{1\text{D}}$ is about 2.5 × 10⁻¹ Pa ⋅ s/μm. In reality, $d_g^{1\text{D}}$ can be much higher than this estimate because the channel walls are not smooth. Fig. 3 B shows the model prediction that $v_0$ increases with $d_g^{1\text{D}}$ while the other parameters remain the same. The cell velocity saturates at low and high $d_g^{1\text{D}}$. For intermediate $d_g^{1\text{D}}$, one order of magnitude change of $d_g^{1\text{D}}$—for example, from 5 × 10³ Pa ⋅ s/μm to 5 × 10⁴ Pa ⋅ s/μm—results in an increase in cell velocity (from ∼54 μm/h to ∼75 μm/h) by ∼40%.

Figure 3.

Confined 1D cells migrate faster under higher coefficients of hydraulic resistance. (A) A diagram of the cell and the external fluid flow in a 1D channel is shown. (B) A model prediction of the cell boundary velocity $v_0$ as $d_g^{1\text{D}}$ varies is shown. Here, $c_{\text{in}}^{\text{f}}=340.7$ mM, which corresponds to a water flux of $J_{\text{water}}=82\mu$ m/h. (C) The velocity of the cell edge $v_0$ as $J_{\text{water}}$ and $d_g^{1\text{D}}$ vary as shown. We let $c_{\text{in}}^{\text{f}}$ vary from 340.6 to 341 mM and obtain $J_{\text{water}}$ accordingly. Cell velocity increases with increasing $J_{\text{water}}$ and $d_g^{1\text{D}}$. (D) The contours of $v_0$ as $J_{\text{actin}}$ and ${\eta }_{\text{st}}$ vary as shown. Here, $d_g^{1\text{D}}={10}^6$ Pa$\cdot$s/μm. For confined channels with high hydraulic resistance, neither actin polymerization nor focal adhesion friction influence the cell speed significantly. (E) Stall force per unit area increases with $d_g^{1\text{D}}$. To see this figure in color, go online.

This prediction, showing that cells move faster in an environment with a higher coefficient of hydraulic resistance, is rather counterintuitive. This result can be understood by considering the flow of the extracellular fluid. In Fig. 3 B, with constant $J_{\text{water}}$, $v_0$ increases as $d_g^{1\text{D}}$ increases, meaning that the cell utilizes more of the water flux in $v_0$. This means the fluid velocity in the channel, $v_{\ast }=v_0-J_{\text{water}}$, decreases with $d_g^{1\text{D}}$, which is expected under higher hydraulic resistance. In addition, the cytosol velocity $v_c$ must be continuous with extracellular fluid velocity and decrease for larger $d_g^{1\text{D}}$. Therefore, the cell boundary velocity increases.

On the other hand, increased velocity of cell migration under a higher coefficient of hydraulic resistance, $d_g^{1\text{D}}$, helps to reduce the otherwise high hydraulic resistance, $d_g^{1\text{D}}{v}_{\ast }$: although the coefficient of hydraulic resistance varies from 10² to 10⁶ Pa ⋅ s/μm, as shown in Fig. 3 C, the actual hydraulic resistance experienced by the cell remains in the same order of magnitude when the cell velocity $v_0$ increases (see Fig. S4). Note that in this work, we have assumed that the network phase is always attached to the cell boundary during continuous (de)polymerization, and the velocity of polymerization $J_{\text{actin}}$ is constant. Experiments have shown that actin polymerization can adapt against mechanical resistance to grow at a constant velocity (36), which justifies this assumption, although, in principle, any dependence of $J_{\text{actin}}$ on force can be incorporated in our model.

Transition between actin-driven and flow-driven cell migrations depends on the external coefficient of hydraulic resistance

Equation 3 suggests that $v_0$ increases with $J_{\text{water}}$; indeed, the model predicts that the cell migrates faster under larger water flux. Fig. 3 C shows the dependence of $v_0$ with $J_{\text{water}}$ and $d_g^{1\text{D}}$. When $d_g^{1\text{D}}$ is small ($d_g^{1\text{D}}<{10}^2$ Pa ⋅ s/μm), the cell velocity is low and is almost independent of $J_{\text{water}}$, suggesting that water flux does not contribute to cell migration in this regime. This is the situation for cells on a 2D substrate (also see Fig. 2 C). When $d_g^{1\text{D}}$ is large ($d_g^{1\text{D}}>{10}^5$ Pa ⋅ s/μm), the cell velocity equals to $J_{\text{water}}$; this is the situation for a cell in a confined space where cell migration is mostly facilitated by water flux, i.e., an osmotic engine model (7). In this regime, the boundary velocity saturates with $d_g^{1\text{D}}$.

For a high coefficient of hydraulic resistance, for example, $d_g^{1\text{D}}={10}^6$ Pa ⋅ s/μm, the predicted cell velocity $v_0$ is independent of $J_{\text{actin}}$ or ${\eta }_{\text{st}}$ (Fig. 3 D). This result, together with Fig. 3 C, indicates that under a high coefficient of hydraulic resistance, $v_0$ is dominated by water flux, not the actin network, whereas under a low coefficient of hydraulic resistance, $v_0$ is dominated by the actin network, not water flux. Our model shows that the transition from actin-driven cell migration to water-driven cell migration can result from the physical effects of fluid flow, not from a change in the mechanism of migration signaled by the cell.

Similar to the 2D case in which higher external forces are needed to stop cell migration under higher strength of focal adhesion (Fig. 2 F), in 1D, higher external forces are needed to stop cell migration under a higher coefficient of hydraulic resistance (Fig. 3 E). The magnitude of the stall force is therefore also a measure of the strength of the “driving force,” which is focal adhesion and actin polymerization in 2D and water flux in 1D.

Hydraulic resistance in 3D matrices

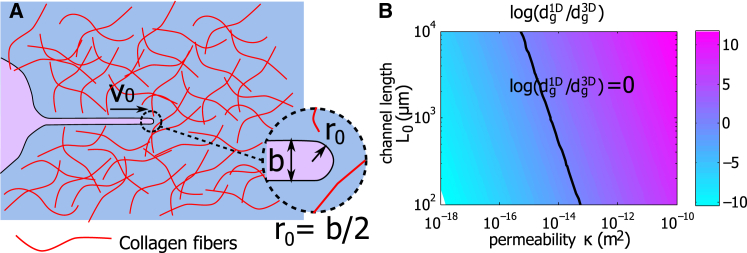
The model can be extended to understand the influence of the hydraulic environment on cell migration in 3D matrices (hydrogels such as collagen) (Fig. 4 A). The front of the protrusion interacts with the matrix and the interstitial fluid. As the protrusion extends, it exerts a force on its environment and changes the hydrodynamic pressure distribution in the matrix. The extracellular matrix is a viscoelastic material with high porosity. The gel component, i.e., the collagen-fiber network, deforms as the cell protrudes and therefore exerts an external force on the migrating cell. In the case of collagen gels, the matrix is also disassembled as the cell migrates and secretes matrix metalloproteinases (37). We have seen in the previous sections that the coefficients of hydraulic resistance can vary significantly in 1D versus 2D. This difference can determine the relative contribution of different mechanisms of cell migration. In vivo, the mechanical properties of the collagen matrix are complex. Although much has been studied to understand the viscoelastic property and the porosity of the collagen matrix, it remains unclear what types of hydraulic resistance the cell experiences in 3D matrices and how this compares to the d_g in 1D and 2D. In this section, we explore how d_g in 3D depends on the mechanical properties of the collagen matrix.

Figure 4.

Cell movement in 3D collagen matrix. (A) A diagram of a cell protrusion and the surrounding collagen matrix is shown. Collagen fibers are distributed in the matrix. The tip of the protrusion has a radius $r_0=b/2$, where b is the width of the protrusion. (B) The contour of $\text{ln}\left(d_g^{1\text{D}}/d_g^{3\text{D}}\right)$ as the 1D channel length ${\ell }_0$ and the permeability of the collagen matrix κ vary is shown. The line is where $d_g^{1\text{D}}=d_g^{3\text{D}}$. To see this figure in color, go online.

Using a poroelastic theory, we estimate the effective coefficient of hydraulic resistance to be $d_g^{3\text{D}}={\mu }_{f}b/2\kappa$ (see the Supporting Materials and Methods for more information), where ${\mu }_f$ is the effective viscosity of the fluid phase in the collagen matrix, κ is the permeability of the collagen matrix, and b is still the width of the cell protrusion. To differentiate the notation used in 1D, we will add “3D” or “1D” to the corresponding quantities in each geometry, i.e., $d_g^{3\text{D}}={\mu }_f^{3\text{D}}{b}^{3\text{D}}/2\kappa$ and $d_g^{1\text{D}}=12{\mu }_f^{1\text{D}}{\ell }_0/{\left(b^{1\text{D}}\right)}^2$. We assume ${\mu }_f^{3\text{D}}={\mu }_f^{1\text{D}}$. Depending on the values of $b^{3\text{D}}/2\kappa$ and $12{\ell }_0/{\left(b^{1\text{D}}\right)}^2$, the coefficient of hydraulic resistance in 3D can be either larger or smaller than that in 1D. For example, when κ = 10⁻¹⁶ m² (38), $b^{3\text{D}}=b^{1\text{D}}=3\mu$ m, and ${\ell }_0={10}^3$ μm, then $d_g^{3\text{D}}>d_g^{1\text{D}}$. But when κ = 10⁻¹² m², then $d_g^{3\text{D}}<d_g^{1\text{D}}$. Fig. 4 B shows the phase diagram of the ratio $\text{ln}\left(d_g^{1\text{D}}/d_g^{3\text{D}}\right)$ as the 1D channel length ${\ell }_0$ and the permeability of the collagen matrix κ vary. The line $\text{ln}\left(d_g^{1\text{D}}/d_g^{3\text{D}}\right)=0$ indicates $d_g^{1\text{D}}=d_g^{3\text{D}}$.

Depending on the viscosity of the interstitial fluid in the collagen matrix and the matrix hydraulic permeability, which is related to the collagen density, the coefficient of hydraulic resistance in 3D can be comparable to 1D (Fig. 4 B). This suggests that the hydraulic effects could play an important role in 3D cell protrusion, including morphogenesis and cancer cell metastasis. In experiments, it is found that cell velocity has a biphasic dependence on the collagen density (13), which may be attributed to collagen fiber alignment, matrix pore size (13), cell-matrix biochemical interaction, or the effect of the hydraulic resistance, which can occur when there is a large water flux through the cell surface and the hydraulic resistance starts to dominate at low matrix permeability. To fully study 3D cell migration, other matrix properties should be considered, including strain-stiffening (39), stress relaxation (40), collagen fiber alignment, matrix pore size, and production of matrix metalloproteinases (13). More extensive studies, both experimental and theoretical, are needed to address this complexity.

Conclusions

Understanding the mechanism of cell migration in different physical environments helps to uncover pathophysiological mechanisms. Using a two-phase modeling framework, we derived a general expression that is applicable to a wide range of physical conditions to compute the cell boundary velocity as a function of actin polymerization rate and water influx rate. The model incorporates known mechanics of important motility components and includes effects of focal adhesion and membrane friction force as well as hydraulic resistance from flow outside of the cell. Depending on the environmental properties, the coefficient of hydraulic resistance can be substantial, especially in 1D channels and 3D matrices. The coefficient of hydraulic resistance can influence the relative contribution of water influx to migration speed. In 2D environments, the hydraulic resistance is negligible so that even if the water influx is large, it does not contribute to cell speed as long as the cell maintains constant volume. In 1D confined channels with a high coefficient of hydraulic resistance, water influx enhances migration speed. In 3D matrices, the hydraulic resistance depends on the local environment of the cell and can be as large as the 1D case. This result suggests that in 3D, knocking out the cell components responsible for water flux would have major effects in cell motility.

In this work, we mainly focus on how cell migration may perturb the extracellular fluid environment and generate a hydraulic resistance back onto the cell; we have not considered bulk fluid flow from the environment, which can be relevant for cell migration on a 2D surface, e.g., endothelial cells in blood flow. When this bulk flow is in a confined geometry such as a blood vessel, we also expect a pressure drop in the flow and also across the cell. This hydrodynamic pressure difference across the cell can also influence cell migration. In unconfined geometries, the pressure drop across the cell is negligible during bulk flow. Instead, fluid shear stress on the cell surface is more important. This shear stress on the cell will activate membrane channels and further promote cell migration (41). A complete model incorporating effects from external bulk flow has not been developed.

Our results express the cell speed for given actin-polymerization and water-influx rates. However, exactly how these fluxes are controlled is not addressed and requires additional study and modeling. For example, the contraction of the actomyosin network is mediated by the strength of the focal adhesion. Biochemical feedback among the focal adhesion, actin flow, and actomyosin contraction can also generate traction oscillations within the adhesion (42, 43). To resolve these effects, a more complicated model is needed to couple the contraction in the actomyosin network, actin flow, and the strength of adhesions. In addition, there is likely substantial cross talk between actin polymerization and water flux. Actin polymerization is linked to the polarity of the cell (44) and likely influences ion channels and pumps that set up the osmotic gradient (45). There are also direct interactions between ion channels and the cytoskeleton (46). Water and ion fluxes could also reorganize the cytoskeleton. This is especially true for calcium, which is implicated in activating myosin contraction (47). Therefore, examining the interplay between actin dynamics and water flux would yield new insights.

Author Contributions

Y.L. and S.X.S. designed the theory and model, and Y.L. performed the calculations. Y.L. and S.X.S. wrote the manuscript.

Editor: Celeste Nelson.