Gating Currents in the Hv1 Proton Channel

Abstract

The Hv1 proton channel shares striking structural homology with fourth transmembrane helical segment-type voltage-sensor (VS) domains but manifests distinctive functional properties, including a proton-selective “aqueous” conductance and allosteric control of voltage-dependent gating by changes in the transmembrane pH gradient. The mechanisms responsible for Hv1’s functional properties remain poorly understood, in part because methods for measuring gating currents that directly report VS activation have not yet been described. Here, we describe an approach that allows robust and reproducible measurement of gating-associated charge movements in Hv1. Gating currents reveal that VS activation and proton-selective aqueous conductance opening are thermodynamically distinct steps in the Hv1 activation pathway and show that pH changes directly alter VS activation. The availability of an assay for gating currents in Hv1 may aid future efforts to elucidate the molecular mechanisms of gating cooperativity, pH-dependent modulation, and H⁺ selectivity in a model VS domain protein.

Introduction

The voltage-gated proton channel Hv1 is a member of a large superfamily of voltage-sensor- (VS) domain-containing proteins that function as voltage-gated ion channels (VGCs) and voltage-sensitive lipid phosphatases (VSPs) (1, 2, 3, 4). Despite lacking a canonical ion-channel-pore domain, Hv1 mediates an activated-state H⁺-selective “aqueous” conductance (G_AQ) that is believed to utilize a water-wire pathway for H⁺ transfer within the hydrated VS-domain central crevice (1, 2, 5, 6, 7, 8, 9). Although residues that alter ion selectivity in Hv1 have been identified (10, 11), it remains unclear why G_AQ is observed in Hv1 but not related VS domains (5, 6). New methods that isolate VS activation from G_AQ opening are therefore needed.

A generally accepted model of VS activation posits that changes in membrane potential act on gating charges to drive conformational rearrangement of the fourth transmembrane helical segment (S4) in the VS domain (12). The phenomenological similarities between time- and voltage-dependent gating in dimeric Hv1 channels and the gating of cation currents through the pore domains of tetrameric VGCs strongly suggest that VS activation operates by a similar mechanism (1, 2, 9, 13, 14, 15). However, Hv1 also manifests biophysical features, such as allosteric control of voltage-dependent gating by changes in the transmembrane pH gradient (ΔpH = pH_I − pH_O), that are evidently unique among VGCs and VSPs (1, 2, 7, 9, 16, 17). The structural and mechanistic bases for functional differences between Hv1 and related VS-domain-containing proteins are incompletely understood.

In VGCs and VSPs, depolarization-dependent S4 movement reorganizes protein-associated charges within the electrical field, producing a capacitive gating-associated current (I_G) that is integrated in time to yield the total “on” gating charge (Q_ON) (18). Under appropriate experimental conditions (i.e., when permeant ions are removed or an inactivating pore mutation is introduced), I_G can be directly measured using voltage-clamp electrophysiology (18, 19, 20). In VGCs, the shapes and positions of the gating charge versus voltage (Q-V) and conductance versus voltage (G-V) relations are different, indicating that they represent thermodynamically distinct events in the channel activation pathway (18, 21). Studies have begun to elucidate the molecular mechanisms of “electromechanical” coupling in tetrameric VGCs (21, 22, 23, 24, 25), but it remains unclear whether a similar phenomenon occurs in Hv1 channels. To directly address this question, gating current measurements are needed. However, the intrinsic G_AQ-mediated H⁺ current in Hv1 is likely to confound efforts to record I_G in isolation.

Compared to ionic currents, gating-current amplitudes are small; removal of the permeant ion or pore block thus serves to reduce or eliminate ionic current and experimentally isolate I_G (18, 19, 20). Abolishing G_AQ-mediated current in Hv1 by ion substitution would likely require that the recording-solution pH be raised (i.e., [H⁺] lowered) beyond the range that is permissive for voltage-clamp electrophysiology in biological membranes, limiting the utility of this approach. N214R (N4R) and N214K substitutions were previously shown to attenuate steady-state outward currents carried by G_AQ, but inward “tail” currents (I_TAIL) remain measurable (7, 9, 26). Introducing N4R into the background of R205H (R1H) permits isolation of the resting-state H⁺ “shuttle” conductance (G_SH) without substantially perturbing G_AQ gating (9), suggesting that N214R could also be useful for revealing I_G in Hv1. Here, we show that incorporating N214R into the background of rapidly activating Hv1 mutants (W207A or R205A) enables direct measurement of gating currents in human Hv1 channels expressed in mammalian cells.

Materials and Methods

Cell culture and electrophysiology

Wild-type (WT) or mutant human Hv1 cDNA (NM_032369) in the pcDNA5/FRT/TO vector was used to create isogenic tetracycline-inducible FlpIn293-TREx stable cell lines as previously described (9). Cells were plated onto glass coverslips, and expression of mutant Hv1 proteins was induced by addition of tetracycline (1.0 μg/mL) to the culture medium 24–72 h before electrophysiology. Whole-cell currents were measured at 22–24°C using an A-M Systems model 2400 amplifier (A-M Systems, Sequim, WA) as described previously (9). Currents are elicited by voltage-step protocols from a holding potential (V_HOLD) to the prepulse step potential (V_STEP) for the indicated time and subsequently to the test potential (V_TEST; typically +100 mV). Data were low-pass filtered at 2–5 kHz and digitized at 10–20 kHz using a National Instruments USB-5251 DAQ (National Instruments, Austin, TX) interfaced to a PC computer running a custom LabVIEW 7-based data acquisition and amplifier control program (C. A. Villalba-Galea; details and software distribution available on request). Data were analyzed using Clampfit9 (Molecular Devices, San Jose, CA) and Origin 8.1 (OriginLab, Northampton, MA). The standard intracellular and extracellular solutions contained the following (in mM): 100 Bis (2-hydroxyethyl)amino-tris(hydroxymethyl) methane (Bis-Tris), 1 ethylene glycol tetraacetic acid (EGTA), and 8 HCl; pH was adjusted to 6.5 and a final osmolality of 310–320 mOsm by the addition of tetramethylammonium hydroxide (TMAOH) and methanesulfonic acid (HMeSO₃). pH_O-dependent gating was measured in bath solutions containing 100 mM 2-(N-morpholino)ethanesulfonic acid (MES, pH 5.5) in place of Bis-Tris, as previously described (7). Series resistance is routinely compensated ∼80%, and liquid-junction potential corrections are not applied.

Data analysis

Unless otherwise indicated, data represent means ± standard error (SE) of values measured in n cells. I_STEP represents the peak current during steps to the indicated potential (V_STEP). The activated state “aqueous” conductance in Hv1 (G_AQ) was calculated from G_AQ = I_STEP/V-E_REV, where E_REV is the zero-current potential determined from inspection of the I_STEP-V relation. Tail current (I_TAIL) amplitude is measured by fitting the decaying current to a monoexponential function of the form I_TAIL = I₀ + Ae^−V/t (where I₀ is the minimal current after decay of I_TAIL, A is current amplitude, V is membrane potential, and t is time) and extrapolating fits to the instant the voltage was changed. Leak currents were subjected to offline linear subtraction. To estimate voltage-dependent gating parameters, I_TAIL-V relations are fitted to a Boltzmann function of the following form: $I_{TAIL}=\left(\left(I_{TAIL\max }\right)-\left(I_{TAIL\min }\right)/1+e^{V-V_{\raisebox{1ex}{$0.5$}\!\left/ \!\raisebox{-1ex}{$dx$}\right.}}\right)+I_{TAIL\min }$, where V_0.5 is the voltage at which 50% of the maximal current is reached, dx is a slope factor, and I_{TAIL max} and I_{TAIL min} represent the maximal and minimal tail-current amplitudes, respectively. G_AQ-V relations are fitted to a single Boltzmann of the form $G_{AQ}=\left(\left(G_{AQ\max }\right)-\left(G_{AQ\min }\right)/1+e^{V-V_{\raisebox{1ex}{$0.5$}\!\left/ \!\raisebox{-1ex}{$dx$}\right.}}\right)+G_{A{Q}_{\min }}$, where V_0.5, dx, G_{AQ max}, and G_{AQ min} have the same meanings as defined for I_TAIL. In some cases, effective gating valence (z_G) was calculated from Boltzmann fits, where z_G = RT/F × dx, where F, R, and T have their usual meanings (i.e., RT/F = 25.3 mV at 20°C, the approximate temperature at which experiments were conducted). Curve fits reported in figure legends represent the best fit to the mean data; Table 1 reports mean ± SE of fitted or calculated values determined separately in the indicated number of individual experiments.

Table 1.

Fitted and Calculated Gating Parameters

		QON			ITAIL			ITAIL-QON
Construct	Parameter	Mean	SE	n	Mean	SE	n	Difference
	VM (mV)	−38.9	0.8	6	−31.6	0.8	6	7.3a
W207A-N214R	V0.5 (mV)	−40.0	1.1	6	−31.4	0.6	6	8.6b
	zG (e0)	2.80	0.06	6	3.21	0.11	6	0.41NS
	VM (mV)	−24.1	0.3	12	−11.3	0.4	12	12.8c
W207A-N214R-ΔC	V0.5 (mV)	−24.6	0.3	12	−15.7	0.4	12	8.9d
	zG (e0)	1.75e	0.01	12	1.52f	0.02	12	−0.23g
	VM (mV)	17.8	0.8	3	25.7	1.6	3	8.0NS
R205A-N214R	V0.5 (mV)	25.1	2.3	3	26.4	1.3	3	1.3NS
	zG (e0)	2.14h	0.12	3	1.89i	0.07	3	−0.25NS

Data represent calculated V_M or Boltzmann-fitted V_0.5 and zδ parameters for Q_ON-V and I_TAIL-V relations measured at pH_O 6.5 in the indicated number of cells.

^aW207A-N214R: I_TAIL V_M vs. Q_ON V_M, p = 0.03.

^bW207A-N214R: I_TAIL V_0.5 vs. Q_ON V_0.5, p = 0.02.

^cW207A-N214R-ΔC: I_TAIL V_M vs. Q_ON V_M, p = 1.6 × 10⁻⁷.

^dW207A-N214R-ΔC: I_TAIL V_0.5 vs. Q_ON V_0.5, p = 2.2 × 10⁻⁵.

^eQ_ONz_G: W207A-N214R vs. W207A-N214R-ΔC, p = 2.3 × 10⁻⁷.

^fI_TAILz_G: W207A-N214R vs. W207A-N214R-ΔC, p = 5.6 × 10⁻⁷.

^gW207A-N214R-ΔC: I_TAILz_G vs. Q_ONz_G, p = 0.01.

^hQ_ONz_G: W207A-N214R vs. R205A-N214R, p = 0.01.

ⁱI_TAILz_G: W207A-N214R vs. R205A-N214R, p = 0.02.

The G_AQ activation time course (see Fig. 1, A and B) is fitted to a single exponential function of the form $I=I_{max}\left(1-e^{\raisebox{1ex}{$-\left(t-d\right)$}\!\left/ \!\raisebox{-1ex}{$\tau $}\right.}\right)$, where I is the measured I_TAIL at time t and I_max is I_TAIL at t = ∞, d is the delay, and τ is the activation time constant (i.e., τ_ACT). G_AQ activation in W207A-N214R-ΔC (see Fig. S3) is fitted to a monoexponential function of the form $I_{TAIL}=I_{TAILmax}\left(1-e^{\raisebox{1ex}{$-\left(t\right)$}\!\left/ \!\raisebox{-1ex}{$\tau $}\right.}\right)$. The fitted exponential time course is then scaled to the amplitude of the steady-state I_STEP at each voltage (i.e., I_{TAIL max} = I_STEP) and subtracted from the measured I_STEP to yield transient outward I_G at each V_STEP. Channel number (N) is calculated by dividing the total gating charge (Q_ON) by the unitary gating valences (zδ = 6 e₀ for full-length Hv1 channels and zδ = 3 e₀ for ΔC truncated channels) estimated from variance analysis (27). Unitary conductance (γ_AQ) is calculated from the slope of a plot of G_{AQ max} (determined from I_TAIL) versus N (i.e., G_{AQ max} = N × γ_AQ). The “on” gating charge (Q_ON) is determined by the trapezoidal integration of I_G.

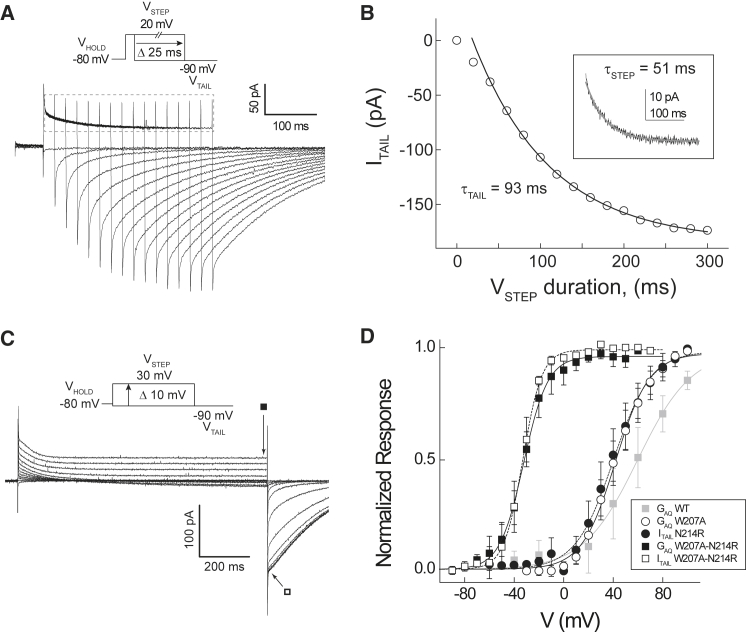
Figure 1.

G_AQ-V and I_TAIL-V relations in Hv1 W207A-N214R. (A) Representative currents elicited by the indicated voltage step protocol (inset: V_HOLD = −80 mV; V_STEP = +20, 0–300 ms duration in 25 ms increments; V_TAIL = −90 mV) in a cell expressing in W207A-N214R are shown. Current measured during the 300-ms-duration V_STEP is magnified in (B, inset). (B) I_TAIL amplitude (current shown in (C)) is plotted as a function of V_STEP duration. The solid black line represents a fit of the data to a single exponential decay function (τ_TAIL = 93 ms) after a delay (18 ms). The inset shows current elicited by V_STEP = +20 mV, duration 300 ms; the solid gray line represents a fit of the data to a single exponential decay function (τ_STEP = 51 ms). (C) Representative currents elicited by the indicated voltage protocol (inset: V_HOLD = −80 mV; V_STEP = −90 to +30 mV in 10-mV increments, 1-s duration; V_TAIL = −90 mV) in a cell expressing W207A-N214R are shown. Symbols indicate times at which I_STEP (filled square) and I_TAIL (open square) are measured. (D) Steady-state currents measured at the end of V_STEP (I_STEP) are used to calculate G_AQ (see Materials and Methods), and data are normalized to their respective maxima in each cell to generate G_AQ-V relations for WT (filled gray squares; n = 4), W207A (open circles; n = 4), and W207A-N214R (filled squares; n = 7). Mean normalized I_TAIL-V relations are shown for N214R (filled circles; n = 4) and W207A-N214R (open squares; n = 9). Solid lines indicate Boltzmann fits to the mean G_AQ-V (WT, gray line: V_0.5 = +59.7 mV, z_G = 1.2 e₀; W207A: V_0.5 = +41.9 mV, z_G = 1.9 e₀; W207A-N214R: V_0.5 = −32.3 mV, z_G = 2.6 e₀) and dashed lines indicate Boltzmann fits to mean I_TAIL-V (N214R: V_0.5 = +40.1 mV, z_G = 1.7 e₀; W207A-N214R: V_0.5 = −33.0 mV, z_G = 3.3 e₀) relations.

Requests for biological materials (i.e., cDNA constructs used for this study) should be directed to the corresponding author. Additional information and requests for software used for integration of gating currents may be directed to Carlos A. Villalba-Galea (cvillalbagalea@pacific.edu).

Results

To measure gating-charge movement in Hv1, we hypothesized that it would be necessary to identify a mutant channel in which 1) the time course of G_AQ activation is greatly accelerated and 2) current carried by G_AQ is greatly diminished. A mutation of a conserved Trp residue in the S4 helix of Hv1 (W207) is reported to greatly speed the time course of G_AQ activation (28). Mutations at R205 (R1) also exhibit rapid G_AQ activation by membrane depolarization (1, 2, 7, 9, 27, 29), but the effects of this and other S4 Arg mutations to decrease the apparent gating-charge valence (z_G) (27) represent a potential limitation for their use in measuring gating current. Introducing an additional Arg residue into the S4 helix of Hv1 (N214R) was previously shown to block outward steady-state currents carried by G_AQ (7, 9, 26). We therefore combined W207A and N214R mutations (W207A-N214R) and induced expression of mutant channels in a modified HEK-293 cell line by addition of tetracycline to the culture medium (see Materials and Methods).

W207A-N214R alters G_AQ activation kinetics and steady-state voltage-dependent gating

We previously reported that nontransfected cells and cells that were not exposed to tetracycline do not exhibit voltage-dependent currents under the recording conditions used here (7). However, robust voltage-gated currents are measured under whole-cell voltage clamp in cells expressing N-terminally tagged EGFP-hHv1 W207A-N214R (Fig. 1 A). Increasing the duration of the voltage step (V_STEP) to +20 mV causes the amplitude of the subsequent, inwardly directed tail current (I_TAIL) measured at −90 mV to increase and eventually plateau (Fig. 1, A and B). Peak I_TAIL rises sigmoidally with V_STEP duration and is fitted to a single-exponential function after a delay (Fig. 1 B), similar to WT Hv1 channels (1, 2, 28, 30). The fitted time constant for I_TAIL activation (τ_TAIL = 93 ms) is substantially faster than WT Hv1 but slower than W207A (28). Unlike W207A and WT Hv1, which pass outward G_AQ-mediated currents that display sigmoid activation kinetics during a fixed voltage step (1, 2, 28), W207A-N214R exhibits a complex biphasic time course (Fig. 1 A). A rapidly activating transient outward current decays to an apparent steady state with a fitted time course (τ_STEP = 51 ms) that is almost two times faster than I_TAIL (Fig. 1 B). The kinetic difference between I_STEP and I_TAIL activation time courses suggests that the transient-current decay may report a conformational change that precedes the opening of G_AQ.

Next, we sought to establish experimental conditions under which I_G and I_TAIL are measured under apparent steady-state conditions. Q_ON and I_TAIL are each time and voltage dependent (Fig. S1, A–D), and Boltzmann fits to the data show that the fitted V_0.5 and slope factors (apparent z_G) also depend on the duration of the preceding voltage step (Fig. S1, E and F). A voltage step (V_STEP, before I_TAIL measurement) or prepulse (V_PP, before Q_ON measurement) of 1-s duration is evidently sufficient to achieve apparent equilibrium conditions, because a longer voltage pulse elicits no additional changes in either the fitted V_0.5 or z_G (Fig. S1, E and F). We therefore measure I_STEP at the end of a 1-s depolarization and calculate conductance to determine the G_AQ-V relation; I_TAIL is measured after a subsequent hyperpolarizing step as described previously (1, 9).

As expected, the I_TAIL-V and G_AQ-V relations in W207A-N214R are highly similar, indicating that they report the same conformational transition, namely, G_AQ activation. Compared to WT Hv1 and W207A and N214R single mutants, G_AQ gating is shifted toward negative potentials in W207A-N214R (Fig. 1 D). The fitted midpoint (V_0.5) of the G_AQ-V and I_TAIL-V relations in W207A-N214R are ∼90 mV more negative than WT Hv1 and ∼70 mV more negative than either W207A or N214R (Fig. 1 D). Interestingly, the slopes of Boltzmann fits to the G_AQ-V and I_TAIL-V relations are shallower in WT Hv1 than in W207A, N214R, or W207A-N214R mutant channels (Fig. 1 D). The similarity in z_G calculated from Boltzmann fits suggests that the kinetically fast mutant channels tested here are likely to move a similar quantity of gating charge during VS activation. Although measurement of the limiting slope suggests that z_G = ∼6 e₀ in WT Ciona intestinalis Hv1, indicating that G_AQ-V and I_TAIL-V relations may significantly underestimate z_G (27), z_G estimates in mutant channels measured here may nonetheless be usefully compared (Table 1).

Gating currents in Hv1 W207A-N214R

Because G_AQ is not substantially open at early times after depolarization, we hypothesize that rapidly activating transient outward currents could represent I_G in Hv1. As in WT Hv1, the kinetics of G_AQ opening in W207A-N214R are both time and voltage dependent (Fig. S1, A and B). The decay of the transient outward current measured at various potentials is also evidently voltage dependent (Fig. 2 A). Although it should be possible to subtract the G_AQ-mediated component of current from the aggregate I_STEP to yield I_G in isolation (Fig. 1, A and B), the time course of G_AQ activation follows a complex sigmoidal time course (31). Determining the amplitude of H⁺-current I_STEP contributed by G_AQ at each time and voltage depends on accurate kinetic modeling of the activation pathway, which is impractical in W207A-N214R because outward H⁺ currents are blocked. Instead, we opt to record transient outward currents at a fixed potential (i.e., V_STEP = +100 mV) after stepping through a range of prepulse voltages (V_PP). A step to +100 mV from a large negative V_PP (i.e., −120 mV), at which the open probability for G_AQ is evidently close to its minimum (Fig. 1 D), elicits a large transient outward current with a complex rising and falling kinetic profile (Fig. 2 A). The initial spike of outward current seen in Fig. 2 A is attributed to incomplete compensation of the membrane capacitance and is not analyzed further here. As expected, the amplitude of the transient outward current measured at +100 mV saturates at both positive and negative V_PP (Fig. 2 A), suggesting that it represents an authentic I_G in Hv1.

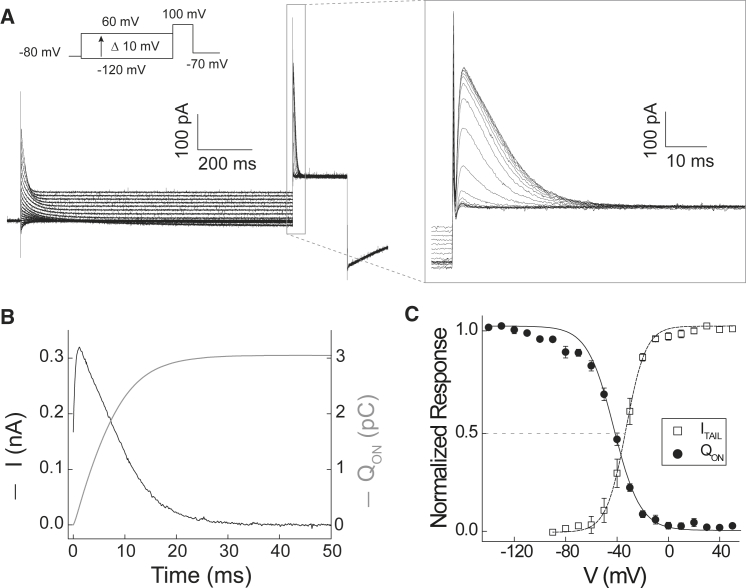
Figure 2.

Integration of transient outward current reveals “on” gating charge (Q_ON) movement. (A) Representative currents elicited by the indicated voltage protocol (V_HOLD = −80 mV; V_PP = −120 to +60 mV in 10-mV increments, 1-s duration; V_STEP = +100 mV, 200-ms duration; V_TAIL = −70 mV) are shown. Transient outward currents at V_STEP = +100 mV within the dashed box are magnified in the boxed inset. Steady-state currents measured at the end of V_PP are attributed to G_AQ (see also Figs. S3 and S4). (B) The transient outward current (V_PP = −100 mV, V_STEP = +100 mV, black line) is plotted together with its time integral (Q_ON, gray line). The timescale is adjusted to reflect the rise in transient outward current after a brief initial current that we attribute to uncompensated capacitance. In this example, gating current integration begins 1.75 ms after the V_STEP voltage command is applied. (C) Q_ON (filled circles) measured at V_STEP = +100 mV (V_PP = −120 mV, 1000 ms duration) is normalized to its maximum in each cell and mean data (n = 9 cells) are plotted in function of V_PP. The mean I_TAIL-V relation (open circles; data from Fig. 1B) is replotted for comparison. Lines represent fits to Boltzmann functions (Q_ON, solid line: V_0.5 = −42.5 mV; z_G = 2.5 e₀; I_TAIL, dashed line: V_0.5 = −33.0 mV, z_G = 3.3 e₀). Median voltages (V_M) calculated for the normalized mean Q_ON-V and I_TAIL-V relations shown here are V_M = −44.9 mV and V_M = −33.2 mV, respectively.

Integrating I_G yields a direct measure of the gating charge generated by functional Hv1 channels in the plasma membrane (Q_ON). As expected, Q_ON rises exponentially and saturates in time, as illustrated in a representative experiment in which I_STEP is measured at +100 mV (Fig. 2 B). Integrating I_STEP over a range of V_PP yields a highly nonlinear Q_ON-V relation that clearly saturates at large positive and negative potentials (Figs. 2 C and S1). Q_ON is maximal after V_PP to hyperpolarizing voltages that are expected to drive occupancy of resting-state VS conformations and Q_ON falls toward zero as the driving force for gating-charge translocation decreases (Figs. 2 C and S1). To compare I_TAIL-V and Q_ON-V gating parameters, we initially compared Boltzmann fits of the data (Fig. S1). Surprisingly, V_0.5 for the Q_ON-V relation is consistently 8–10 mV more negative than the I_TAIL-V relation (Figs. 2 C and S1; Table 1), suggesting that gating-charge movement and G_AQ opening represent thermodynamically distinct transitions in the Hv1 activation pathway.

In contrast to our expectations, the slopes of Boltzmann functions fitted to Q_ON-V relations are evidently shallower than I_TAIL-V relations (Figs. 1 D and 2 C; Table 1). Previous studies in both Hv1 and tetrameric VGCs show that Boltzmann fits to I_TAIL-V or G-V relations typically yield smaller estimates of z_G than limiting-slope or Q-V relations (1, 2, 27, 32, 33, 34). Closer inspection reveals that although the I_TAIL-V relations are well described by single Boltzmann distributions (Fig. 1 D), the Q_ON-V relation characteristically deviates from the Boltzmann fit between −100 and −70 mV (Fig. 2 C). The data therefore suggest that gating-charge movement in Hv1 requires more than one transition, similar to tetrameric VGCs for which complex Q-V relations are not described by simple Boltzmann distributions and fitted-slope values often appear to underestimate z_G (14, 20, 21, 35, 36, 37, 38). We therefore calculated the median voltages (V_M) for Q_ON-V and I_TAIL-V relations to compare thermodynamic gating parameters in a model-independent fashion (38). Similar to V_0.5, we find that V_M is consistently ∼10 mV more negative for Q_ON than for I_TAIL (Table 1), indicating that G_AQ opening requires an additional gating transition.

Estimating channel number and unitary conductance from Hv1 gating currents

A straightforward expectation is that Q_ON and I_TAIL similarly depend on the number of functional channels (N) in the plasma membrane; maximal Q_ON (Q_{ON max}) is therefore expected to be tightly correlated with maximal I_TAIL amplitude (I_{TAIL max}). If Q_ON = N × z_G × P_ACT, where P_ACT is the probability that z_G has been moved (i.e., the VS domain is activated), and I_{TAIL max} = N × i × P_OPEN, where i is the unitary current and P_OPEN is the probability that G_AQ is open, the slope of the Q_{ON max} vs. I_{TAIL max} relation thus reports charge movement per “conducting unit” (i.e., Q_{ON max}/I_{TAIL max} = z_G/i). Consistent with expectations, the plot of Q_{ON max} vs. I_{TAIL max} is well fitted to a straight line with slope = 5.9 pC/nA (Fig. 3 A). Limiting-slope analysis of G_AQ-V relations provides an independent estimate of the gating valence (z_G = 6 e₀/conducting unit) in WT, presumably dimeric C. intestinalis Hv1 channels (27), allowing us to calculate N from the Q_{ON max} data. To accurately measure G_AQ, each cell must express ∼0.5 × 10⁶ W207A-N214R conducting units, and Q_ON measurements are ideally measured in cells that appear to express >2 × 10⁶ channels (Fig. 3 B). Using the z_G-values determined from our Boltzmann fits of Q_ON-V or I_TAIL-V relations (Table 1) would approximately double the number of channels needed to generate the measured current or charge movement. Alternatively, if z_G-values reported for C. intestinalis Hv1 underestimate the actual gating valence, we might overestimate N somewhat. Given that even highly similar channels like Kv1.2 and Drosophila Shaker can manifest dramatically different gating valences (39), some caution is warranted in the interpretation of absolute channel numbers reported here. Nonetheless, our data suggest that mutant Hv1 channels are highly overexpressed in our studies, and robust protein expression is probably an important prerequisite for I_G measurement in Hv1.

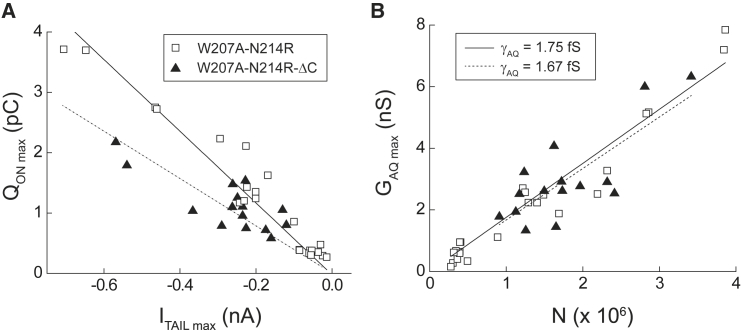
Figure 3.

Estimating unitary conductance in Hv1 W207A-N214R. (A) Plots of maximal Q_ON (Q_{ON max}) versus maximal I_TAIL (I_{TAIL max}) measured in individual cells expressing W207A-N214R (open squares) or W207A-N214R-ΔC (filled triangles) are shown. Mean (± SE) Q_{ON max} = 1.25 ± 0.22 pC, and I_{TAIL max} = 197 ± 40 pA (n = 24 cells). Lines indicate linear fits of the data (W207A-N214, solid line: slope = 5.9 pC/nA; R² = 0.97; W207A-N214R-ΔC, dashed line: slope = 3.9 pC/nA; R² = 0.87. (B) The apparent number of channels (N) is calculated from the total charge (Q_{ON max}) divided by the previously reported (27) gating valences for full-length (squares; z_G = 6 e₀) or truncated (triangles; z_G = 3 e₀) channels’ limiting-slope analyses. Linear fits of maximal G_AQ (G_{AQ max}) determined from Boltzmann fits to G_AQ-V relations in each cell (see Fig. 1D) versus calculated channel number yield estimates of the G_AQ unitary conductances for W207A-N214R (solid line: γ_AQ = 1.75 fS) and W207A-N214R-ΔC (dashed line: γ_AQ = 1.67 fS). To see this figure in color, go online.

Standard ion channel theory posits that G_{AQ max} = N × γ_AQ × P_OPEN (where P_OPEN is the probability of G_AQ being open), so γ_AQ can readily be calculated from the slope of the G_{AQ max} vs. N plot (Fig. 3 B). Because N214R blocks G_AQ-mediated current by occupying a site at the intracellular entrance to the G_AQ-meditated H⁺ transfer pathway (5, 7, 9, 26), we calculated γ_AQ from I_TAIL measured at negative voltages at which the block is less evident. However, the estimated unitary conductance in W207A-N214R (γ_AQ = 1.75 fS) is still ∼20-fold smaller than a previous estimate based on variance analyses of native voltage-gated H⁺ currents in human eosinophils (γ = 36 fS) measured under similar experimental conditions (40). Our data are consistent with a previous study showing that N214R exerts a pronounced blocking effect on outward H⁺ transfer (9) but suggest that both outward and inward H⁺ currents are smaller in W207A-N214R than in WT Hv1.

Effect of mutations on gating-charge movement in Hv1

The effects of charge-neutralizing mutations indicate that conserved S4 Arg residues function as gating charges in Hv1 and other VS domain-containing proteins. We therefore combined N214R with a second-site mutation (R205A) that eliminates the most extracellular Arg in S4 (R1) and measured gating currents as described earlier. R205A-N214R exhibits rapid G_AQ activation kinetics, prominent G_AQ-mediated tail currents at negative voltages, and transient outward gating currents that are similar to W207A-N214R (Fig. S2, A and B). Although the steady-state I_STEP attributed to G_AQ appears to be larger in R205A-N214R than W207A-N214R, the G_AQ contribution is readily subtracted to yield transient outward currents that can be integrated to estimate Q_ON (Fig. S2, A and C). The positions of the R205A-N214R I_TAIL-V and Q_ON-V relations are shifted positively by ∼57 mV compared to W207A-N214R, consistent with previous reports showing that S4 mutations have dramatic effects on gating kinetics and the steady-state thermodynamic properties but nonetheless retain most or all of the essential biophysical properties of voltage-gated H⁺ channels (1, 2, 9, 28). The fitted V_0.5-values for Q_ON-V and I_TAIL-V relations in R205A-N214R are not significantly different, but like in W207A-N214R, V_M-values are separated by 8 mV (Fig. S2 C; Table 1). z_G-values estimated from Boltzmann fits to Q_ON-V (z_G = 2.1 ± 0.1 e₀) and I_TAIL-V (z_G = 1.9 ± 0.1 e₀) relations are 0.7 e₀ and 1.3 e₀ smaller, respectively, in R205A-N214R than W207A-N214R (Table 1).

To determine whether C-terminal deletion alters z_G, we next measured gating currents in W207A-N214R-ΔC. Limiting-slope analyses indicate that z_G is ∼50% smaller in Hv1-ΔC (z_G ≈ 3 e₀) than full-length channels, possibly because the conducting unit is a monomer rather than a dimer (14, 27). If monomeric Hv1-ΔC channels function similarly to dimeric WT channels, z_G/i is not expected to be different. However, we find that the slope of the Q_{ON max}/I_{TAIL max} relation is significantly smaller in W207A-N214R-ΔC than it is in full-length W207A-N214R channels (Fig. 3 A). We observe a similar decrease in the apparent z_G/i ratio in R205A-N214R (Fig. S2 D), consistent with the hypothesis that R1 neutralization decreases the total gating-charge valence (1, 2, 9, 27). The effect of ΔC on Q_ON max/I_{TAIL max} therefore suggests that C-terminal truncation alters a unitary channel property (z_G and/or i) in addition to its effects on dimer stability and gating cooperativity.

Using the gating valence previously determined for C. intestinalis Hv1-ΔC channels (z_G = 3 e₀/conducting unit) (27), we estimated that the unitary conductances in W207A-N214-ΔC (γ_AQ = 1.67 fS) and R205A-N214R (γ_AQ = 2.21 fS) are not significantly different from W207A-N214R (γ_AQ = 1.75 fS; Figs. 3 B and S1 E). This result is consistent with an earlier study showing that the two pores in dimeric Hv1 channels are independent and each contributes equally to the total current (41). A straightforward interpretation of the data is that the reduction in Q_{ON max}/I_{TAIL max} ratio, and thus z_G/i, observed in R1- and ΔC-mutant channels is mainly due to a decrease in gating valence. Consistent with this interpretation, we find that, like R205A-N214R, the Boltzmann slopes of both the Q_ON-V and I_TAIL-V relations are shallower in W207A-N214R-ΔC than in W207A-N214R (Table 1). In ΔC channels, apparent z_G from the Q_ON-V (z_G = 1.8 ± 0.1 e₀) and I_TAIL-V (z_G = 1.5 ± 0.1 e₀) are 0.9 and 1.8 e₀ smaller, respectively, than W207A-N214R (Table 1).

In addition to the effects of ΔC on steady-state properties of unitary Hv1 channels, C-terminal truncation apparently reduces complexity in the Hv1 activation pathway, as evidenced by a switch from sigmoid (WT) to exponential (ΔC) G_AQ activation time courses (14, 26). We also find that although the time course for I_TAIL activation in W207A-N214R is sigmoidal (Fig. 1 B), I_TAIL evidently rises exponentially in W207A-N214R-ΔC (Fig. S3, A–C). We therefore scaled single-exponential fits of the I_TAIL time course to the amplitude of the current at the end of each I_STEP (Fig. S3 B) and then subtracted the G_AQ-mediated component of current at each voltage from the aggregate I_STEP. Integrating the G_AQ-subtracted transient currents measured at a range of V_STEP yields a family of transient currents with the expected voltage and time dependence for gating current (Fig. S3 D). V_0.5 for the Q_ON-V relation in W207A-N214R-ΔC, which is well fitted to a single Boltzmann distribution, is shifted positively by ∼+15 mV compared to W207A-N214R (Fig. S3 E; Table 1). Consistent with expectations for a gating current, the τ_DEACT-V relation of the G_AQ-subtracted transient current is bell-shaped, and the peak is located close to the fitted V_0.5 (Fig. S3, E and F). Consistent with the previously noted differences in the Q_{ON max}/I_{TAIL max} relations forW207A-N214R and W207A-N214R-ΔC, we find that the mean Boltzmann slope of Q_ON-V relations measured at +100 mV are shallower in W207A-N214R-ΔC (z_G = 1.75 ± 0.01 e₀) than W207A-N214R (z_G = 2.80 ± 0.06 e₀, p < 0.01; Table 1). The mean Boltzmann slope of the W207A-N214R I_TAIL-V relation (z_G = 3.21 ± 0.11 e₀) is also steeper than W207A-N214R-ΔC (z_G = 1.52 ± 0.02 e₀, p < 0.01; Table 1). In summary, gating currents suggest that both R1 neutralization and C-terminal truncation decrease the gating valence but do not appreciably alter unitary conductance.

Gating-charge movement in W207A-N214R is sensitive to changes in pH_O

To determine whether W207A-N214R exhibits the hallmark sensitivity to changes in the pH gradient that is characteristic of Hv1 channel gating (1, 2, 17), we simultaneously measured I_TAIL and I_G at pH_O 6.5 and pH_O 5.5 (Figs. 4 A and S4, A and B). G_AQ begins to activate at voltages that are negative to the Nernst potential for H⁺ (E_H⁺), and W207A-N214R mediates steady-state inward currents that are distinct from WT Hv1 (Fig. S4, A and B). Similar to WT Hv1, however, lowering pH_O in the physiological range (i.e., pH_O < 8) shifts both the position of the G_AQ-V relation and the I_STEP reversal potential (ΔE_REV = 49.7 ± 4.1 mV, n = 5 cells; see also Fig. S4). ΔE_REV measured between pH_O 6.5 and pH_O 5.5 (pH_I 6.5) is close to the Nernst prediction for a H⁺-selective channel (ΔE_H+ = 56 mV at 20°C), suggesting that W207A-N214R remains reasonably H⁺-selective under our recording conditions, consistent with a previous study of W207 single-mutant channels (28). As expected from the effect of extracellular acidification on the driving force for H⁺ current, I_STEP and I_TAIL amplitudes are altered by pH_O changes (Fig. S4, A and B); lowering pH_O also speeds I_TAIL decay in W207A-N214R (Fig. S4, A and B), consistent with previous reports (1, 9, 17, 28).

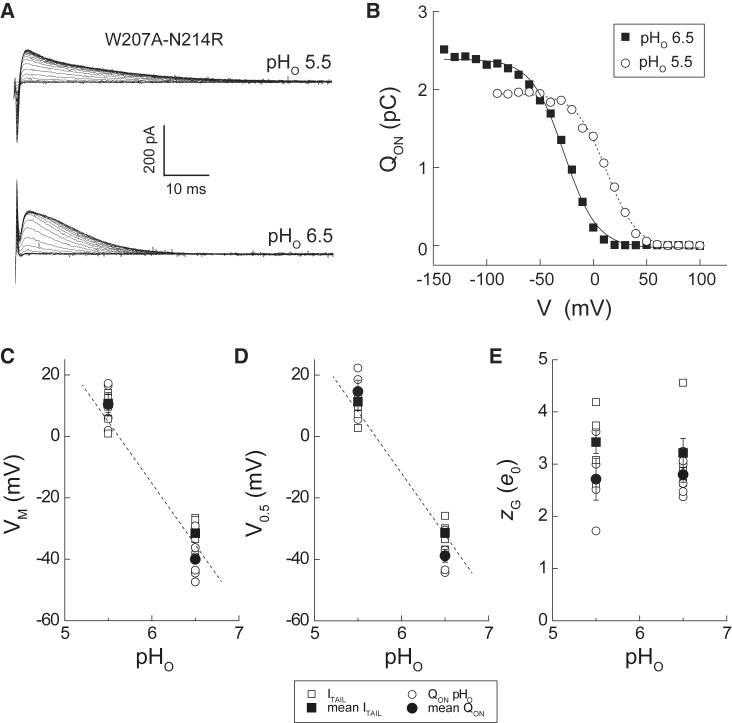
Figure 4.

pH_O dependence of Q_ON-V and I_TAIL-V relations in W207A-N214R. (A) Representative outward transient current traces recorded at pH_O 5.5 (top) or pH_O 6.5 (bottom) in a cell expressing W207A-N214R are shown. Currents at +100 mV are elicited by a series of voltage steps between −140 and +100 mV (10-mV increments, duration = 200 ms; data not shown). (B) Representative Q_ON-V relations are generated by integrating the currents (data shown in (A): open circles, pH_O 5.5; filled squares, pH_O 6.5). Lines represent Boltzmann fits to the data (dashed line, pH_O 5.5: Q_{ON max} = 1.9 pS, V_0.5 = 11.8 mV, z_G = 1.83 e₀; solid line, pH_O 6.5: Q_{ON max} = 2.4 pS, V_0.5 = −27.7 mV, z_G = 1.70 e₀). (C–E) V_M (C), V_0.5 (D), and z_G (E) parameters determined for I_TAIL-V (squares) and Q_ON-V relations (circles) at pH_O 6.5 or pH_O 5.5 are shown. Mean values are indicated by filled symbols, and data from individual experiments are indicated by open symbols. Dashed lines in (C and D) indicate slope = −40 mV/pH unit. To see this figure in color, go online.

We demonstrate here for the first time, to our knowledge, that gating-charge movement in Hv1 is also pH sensitive. First, we show that the rate of I_G decay at +100 mV is faster at pH_O 6.5 compared to pH_O 5.5 (Fig. 4 A), indicating that the “on” gating charge moves faster at more alkaline pH. Raising pH_O reciprocally slows the time course of I_TAIL decay at −90 mV (Figs. 4 A and S4, A and B). The kinetic effects of pH_O changes on I_G and I_TAIL in W207A-N214R are consistent with the effect of pH_O changes on the G_AQ activation time course in WT Hv1, in which extracellular alkalization both speeds opening and slows closing (1, 2, 17, 42). Consistent with the effects of pH_O changes on the G_AQ-V relation, V_0.5 and V_M-values determined for Q_ON-V relations at pH_O 6.5 and pH_O 5.5 are displaced by ∼40 mV (Fig. 4, B–D). The magnitude of the pH-dependent shift in gating-charge movement in W207A-N214R is therefore comparable to the response measured in WT and other Hv1 mutant channels, including the W207A single mutant (7, 28). In contrast to V_0.5 and V_M, z_G-values estimated from the slopes of Boltzmann fits to Q_ON-V and I_TAIL-V relations are not significantly different at pH_O 6.5 and pH_O 5.5 (Fig. 4, B and E; Table 1). Finally, we find that Q_{ON max} is smaller at pH_O 5.5 than at pH_O 6.5 (Fig. 4 B). On average, the quantity of gating charge moved at pH_O 5.5 is 29% smaller than at pH_O 6.5 (Q_{ON max pH5.5/}Q_{ON max pH 6.5} = 0.71 ± 0.05; mean ± SE, n = 5 cells, p = 0.02 by Student’s paired t-test).

Discussion

Although Hv1 shares structural and functional homology with other voltage-dependent cation channels and phosphatases, its VS domain is evidently unique in mediating an intrinsic, activated-state “aqueous” H⁺ conductance (1, 2, 7). G_AQ gating in Hv1 is also strongly modulated by changes in ΔpH (1, 2, 17), but the molecular mechanism(s) responsible for pH-dependent gating remain unknown (7, 28). Strikingly, neutralization of candidate ionizable residues in Hv1 is insufficient to abrogate either pH_O-dependent gating or H⁺-selective ion permeation (5, 6, 7), but neutralization of H168 was shown to attenuate sensitivity to changes in pH_I (16). So far, only one nonfunctional mutant Hv1 channel (D112V) has been described (11), but it remains unclear whether this mutation exerts its effect by 1) causing a reorganization of the H⁺ transfer pathway to block G_AQ-mediated H⁺ transfer or 2) preventing a voltage-dependent conformational rearrangement that is necessary for G_AQ opening. To understand the mechanisms of VS activation and G_AQ gating independently from H⁺ transfer, new experimental tools are needed.

Here, we show that for the first time, to our knowledge, gating currents associated with the movement of protein-associated charge can be measured in mutant Hv1 channels. We attribute the success of our experimental strategy to three factors: 1) high expression of mutant proteins driven in stable, tetracycline-inducible cell lines; 2) incorporation of mutations (W207A or R205A) that dramatically speed the normally slow G_AQ activation kinetics in mammalian Hv1 channels; and 3) partial block of G_AQ-mediated ionic current by N214R. Together, these experimental manipulations reveal the existence of transient currents with gating properties that are distinct from the ionic H⁺ current. I_G directly reports VS activation, and its integral yields the quantity of charge moved, which is directly proportional to G_AQ. I_G measurements in the Hv1 mutants tested here exhibit all the expected features of authentic gating currents, including time- and voltage-dependent gating and saturable dependence on membrane potential. One limitation of our study is that we have so far been unable to cleanly separate the relative contributions of G_AQ and the “off” gating charge (Q_OFF) to the measured I_TAIL, and the expectation that Q_ON = Q_OFF remains to be demonstrated. Additional studies are thus needed to identify mutant Hv1 channels in which inwardly directed H⁺ currents carried by G_AQ are selectively blocked.

Hv1 gating currents reveal several previously unknown biophysical properties of Hv1 channels. First, the Q_ON-V relation is nonidentical to the G_AQ-V (or I_TAIL-V) relation, indicating that G_AQ opening requires a thermodynamic transition that is distinct from VS activation per se. “Electromechanical” coupling between VS activation and pore opening is a well-established phenomenon in tetrameric voltage-gated cation channels (18, 21, 22, 23, 25) but has not been described for Hv1, which lacks the canonical pore domain and instead utilizes the VS domain for both gating and H⁺-selective ion conduction (1, 2). Our results are consistent with the possibility that a conformational rearrangement that follows VS activation (i.e., the movement of gating charge in the transmembrane electrical field) is necessary to open the H⁺ transfer pathway. Gating hysteresis measured in the related VSP from C. intestinalis (CiVSP) is attributed to a voltage-independent transition (43), and evidence for a similar step in the Hv1 activation pathway has also been described previously (31). The ability to measure gating currents in Hv1 may be useful for dissecting the molecular bases of gating hysteresis and thermodynamic coupling of VS activation and G_AQ-mediated “gating pore” opening in a simple model protein.

The shape of the Q_ON-V relation appears to reveal gating complexity that has not been previously measured in Hv1 channels. Although both resting-state currents in the R1H mutant (9) and fluorescence signals measured under voltage clamp (29) suggest that VS activation in Hv1 does not proceed in a single gating transition, we previously lacked an experimental approach to directly measure how changes in membrane potential drive gating-charge movement in Hv1. Combined with simultaneous measurements of ionic current and an estimate of the elementary gating valence (z_G), gating-charge measurements provide new insight into the unitary conductance of the G_AQ pathway and the absolute number of functional Hv1 channel subunits in the membrane. Previously, N and γ_AQ have been amenable to estimation using current-variance analysis (40). As expected from previous studies (1, 27, 44, 45), neutralization of a highly conserved S4 Arg side chain in Hv1 (R205) decreases the quantity of gating charge per conducting unit (z_G/i). Unexpectedly, however, we find that C-terminal truncation also appears to decrease z_G/i in Hv1 W207A-N214R, suggesting that in addition to its role in stabilizing dimerization (41, 46, 47), the C-terminus may intimately interact with the voltage-dependent gating machinery. Having the ability to both measure gating current and estimate z_G from the limiting slope on the same protein will enable direct measurement of z_G and γ_AQ, allowing researchers to experimentally test hypotheses about VS activation, pH-dependent gating, and H⁺ conduction mechanisms in Hv1 that have so far remained mysterious.

pH-dependent gating, which is manifested by an ∼40 mV/pH unit shift in the position of the G_AQ-V relation, is one of the hallmark biophysical features of Hv1 channels (1, 2, 7, 17). Both V_M and V_0.5-values determined for I_TAIL-V relations are similarly pH-dependent (Fig. 4), indicating that pH_O sensitivity is not perturbed in W207A-N214R, at least under the experimental conditions tested here. At physiological pH (i.e., pH < 8), the W207A single mutant is also sensitive to changes in pH_I (28), suggesting that W207A-N214R probably also senses and transduces changes in ΔpH. pH_O sensitivity in W207A-N214R therefore appears to be similar to WT Hv1 and a large number of other mutants reported previously (1, 2, 7, 11, 17, 28). This conclusion is reinforced by the observation that apparent z_G estimated from Boltzmann fits to the I_TAIL-V and Q_ON-V relations is not discernably pH-sensitive between pH_O 5.5 and pH 6.5_O (Fig. 4 B).

Although Boltzmann fits to the Q_ON-V curves suggest that the unitary gating valence, z_G, is insensitive to changes in pH_O, caution is warranted in the interpretation of z_G-values determined from Boltzmann fits to the data. First, Q_ON-V relations in W207A-N214R are evidently complex (Fig. 2 C), suggesting that gating-charge movement does not proceed in a single gating step. Boltzmann fitting of G-V curves is known to underestimate z_G, particularly when VS activation requires multiple state transitions and is therefore not well described by a two-state model (35, 38). Indeed, z_G estimated using the limiting-slope method in C. intestinalis Hv1 (∼6 e₀) is two to three times larger than values derived from fits to G_AQ-V relations in mammalian Hv1 channels (1, 2, 14, 27, 32). We therefore use limiting-slope estimates of z_G for the purpose of calculating channel number and unitary conductance in full-length (6 e₀; i.e., W207A-N214R) and truncated (3 e₀; i.e., W207A-N214R-ΔC) Hv1 channels in this study. Our estimates of N and γ_AQ would therefore differ by a factor of only ∼2 if values from Boltzmann fits to our data (Table 1) were used.

Although W207A dramatically alters G_AQ activation and deactivation kinetics, its effect on estimated unitary conductance was not reported previously (28), and it remains unknown whether mutations of this residue alter the size or structure of the H⁺ permeation pathway in Hv1. Resting- and activated-state model and x-ray structures predict that the W207 side chain probably faces away from the hydrated VS central crevice (7, 8, 9, 32, 48, 49, 50, 51), suggesting that if W207 mutations alter γ_AQ, they probably do so indirectly. On the other hand, the basic side chain of N214R was previously shown to occupy a site that can selectively block outwardly directed H⁺ transfer from an intracellular site that lies within the electrical field (9). Because the γ_AQ estimated for W207A-N214R (Fig. 3 B) is >10-fold smaller than a previous estimate for WT Hv1 (40), we conclude that the N214R side chain probably reduces the amplitudes of both I_STEP and I_TAIL. Stated differently, the positive charge introduced at the R4 position appears to reduce γ_AQ in a voltage-dependent fashion that is reminiscent of pore block by permeant ions in VGCs (52, 53).

In summary, we report a method for reliably and reproducibly measuring gating currents in mammalian cells by expressing a human Hv1 double mutant that displays fast activation kinetics and selective block of the outwardly directed ionic H⁺ current. I_G in Hv1 displays many of the biophysical features previously reported for other VS-domain proteins, including thermodynamic coupling of VS activation and pore opening. Gating currents also enable new methods for estimating Hv1 unitary conductance and channel number. The ability to directly measure VS activation in Hv1 may be helpful for testing a variety of unresolved hypotheses about the mechanisms of voltage- and pH-dependent gating and H⁺ conduction in Hv1. Gating currents are also likely to be useful for addressing fundamental questions about VS activation that are common to Hv1, VSPs, and VGCs. For example, it remains unclear why Hv1 channels are evidently unique among VS-domain proteins in mediating an intrinsic, activated-state G_AQ. Gating-current measurements should enable experimental separation of mutagenic effects on VS activation versus pore structure and potentially help to clarify why specific mutations (i.e., D112V in human Hv1) render channels nonfunctional, whereas other substitutions at the same position act mainly to erode H⁺ selectivity (11).

Author Contributions

V.D.L.R. designed and executed experiments, analyzed results, and prepared figures and tables. I.S.R. designed and executed experiments, analyzed results, prepared figures and tables, and wrote the manuscript.

Editor: Baron Chanda.