Minimal Network Topologies for Signal Processing during Collective Cell Chemotaxis

Abstract

Cell-cell communication plays an important role in collective cell migration. However, it remains unclear how cells in a group cooperatively process external signals to determine the group’s direction of motion. Although the topology of signaling pathways is vitally important in single-cell chemotaxis, the signaling topology for collective chemotaxis has not been systematically studied. Here, we combine mathematical analysis and simulations to find minimal network topologies for multicellular signal processing in collective chemotaxis. We focus on border cell cluster chemotaxis in the Drosophila egg chamber, in which responses to several experimental perturbations of the signaling network are known. Our minimal signaling network includes only four elements: a chemoattractant, the protein Rac (indicating cell activation), cell protrusion, and a hypothesized global factor responsible for cell-cell interaction. Experimental data on cell protrusion statistics allows us to systematically narrow the number of possible topologies from more than 40,000,000 to only six minimal topologies with six interactions between the four elements. This analysis does not require a specific functional form of the interactions, and only qualitative features are needed; it is thus robust to many modeling choices. Simulations of a stochastic biochemical model of border cell chemotaxis show that the qualitative selection procedure accurately determines which topologies are consistent with the experiment. We fit our model for all six proposed topologies; each produces results that are consistent with all experimentally available data. Finally, we suggest experiments to further discriminate possible pathway topologies.

Introduction

Collective cell migration plays an important role in many biological processes, including development, wound healing, and cancer metastasis, and it has been the focus of much recent experimental and theoretical work (1, 2, 3, 4, 5, 6, 7). Interestingly, collective migration is not merely the result of many independent cells moving around but can exhibit unique behavior. For example, measurements of several different cell types have shown that cells cooperate to sense a gradient such that cell clusters follow gradients whereas single cells are unable to detect this gradient (8, 9). Furthermore, expanding cell monolayers often reveal the spontaneous formation of finger-like instabilities with specialized leader cells at their tips (10, 11). These results point toward the important role that cell-cell interactions can play in collective migration. Here, we are particularly interested in collective chemotaxis, or how clusters of cells work together to follow a chemical gradient, as measured in malignant lymphocytes (8), neural crest migration in developing embryos (9), and border cell migration in Drosophila (12, 13, 14).

Collective chemotaxis problems have been modeled by many groups, with widely varying assumptions for cell-cell interactions. These include a focus on intercellular forces such as cell-cell repulsion and adhesion (15), mechanical communication via contact inhibition of locomotion (16, 17, 18, 19), or biochemical communication through a diffusible inhibitor (20, 21). In particular, several earlier theoretical studies show that, depending on the biochemical details of how the cluster processes the signal, cluster speeds and directionalities can be profoundly different (20, 21, 22, 23). Current experiments have not yet provided a way to clearly determine these signal-processing mechanisms, and most studies have assumed only a minimal multicellular local excitation global inhibition (LEGI) signal-processing mechanism (20, 21, 23).

In this article, we develop a method to use existing experimental data to constrain possible multicellular signaling networks. Our approach is a qualitative perturbation analysis in which we use mathematical analysis to determine how experimental interventions such as photoactivation of one element of the signaling network will affect measured outcomes. These behaviors will often only depend on the topology of the signaling network—which elements are connected to which—and not the biochemical details. We use this technique to determine potential minimal network topologies for border cell cluster migration in the Drosophila egg chamber. We can show that existing experimental data rule out all networks with five or fewer interactions (including the aforementioned LEGI model), and we can deduce that only six possible six-link topologies are able to explain the experimental data. In this process, we introduce two methods to circumvent the complexity caused by a stochastic, spatially extended problem like border cell chemotaxis. We first use analytical methods for the selection of possible topologies to avoid exhaustively simulating all topologies. Then, for selected topologies, we carry out quantitative simulations in which we solve nonlinear stochastic differential equations using a master equation approach instead of direct numerical integration. We verify through explicit numerical sampling that these networks are fully consistent with the data and carry out a parameter fit for the six topologies. Finally, we propose additional experiments to further narrow down the possible options.

Methods

The ordinary differential equation (ODE) for Rac is:

$$\frac{\text{d}\left[{\text{R}}_{\text{i}}\right]}{\text{dt}}=\frac{\left({\text{basal}}_{\text{AR}}+{\text{k}}_{\text{SR}}\left[{\text{S}}_{\text{i}}\right]+{\text{k}}_{\text{GR}}\left[\text{G}\right]\right)}{1+{\text{PI}}_{\text{i}}}\left({\text{R}}^{\text{tot}}-\left[{\text{R}}_{\text{i}}\right]\right)-\left({\text{basal}}_{\text{DR}}+{\text{k}}_{-\text{GR}}\left[\text{G}\right]\right)\left[{\text{R}}_{\text{i}}\right]\text{.}$$

Here, $\left[{\text{R}}_{\text{i}}\right]$ represents the concentration of Rac in cell i, and $\left[{\text{S}}_{\text{i}}\right]$ is the signal sensed by cell i. No matter what the signal profile across the whole egg chamber looks like, as the size of the cluster is small compared to the length of the egg chamber, it is reasonable to approximate the $\left[{\text{S}}_{\text{i}}\right]$ within the cluster in a linear form as follows: $\left[{\text{S}}_{\text{i}}\right]={\text{S}}_{\text{mean}}\left(1+{\text{S}}_{\text{grad}}\text{cos}{\mathit{\theta }}_{\text{i}}\right)$, with ${\mathit{\theta }}_{\text{i}}$ as the angle of cell i in the cluster. In this equation, the first term is the activation of Rac, and the second term is the deactivation of Rac. ${\text{basal}}_{\text{AR}}$ and ${\text{basal}}_{\text{DR}}$ are the basal activation and deactivation rates, respectively. The activation or deactivation terms with $\left[{\text{S}}_{\text{i}}\right]$ or $\left[\text{G}\right]$ are the rates regulated by the signal or the global factor. ${\text{PI}}_{\text{i}}$ is the photoinhibition effect implemented on Rac in cell i. The photoinhibition works with a photoactivatable form of the dominant-negative mutants of Rac (PA-RacT17N). RacT17N strongly binds to upstream guanine nucleotide exchange factors and blocks wild-type Rac from being activated. We thus divide the activation term in this equation by $\left(1+{\text{PI}}_{\text{i}}\right)$ to describe the photoinhibition effect.

The ODE for the global factor G is:

$$\frac{\text{d}\left[\text{G}\right]}{\text{dt}}=\left({\text{basal}}_{\text{AG}}+{\text{k}}_{\text{RG}}\left({\left[\text{R}\right]}_{\text{avg}}+{\text{PA}}_{\text{avg}}\right)+{\text{k}}_{\text{SG}}{\left[\text{S}\right]}_{\text{avg}}+{\text{k}}_{\text{PG}}\times \text{NP}\right)-\left({\text{basal}}_{\text{DG}}+{\text{k}}_{-\text{RG}}\left({\left[\text{R}\right]}_{\text{avg}}+{\text{PA}}_{\text{avg}}\right)+{\text{k}}_{-\text{SG}}{\left[\text{S}\right]}_{\text{avg}}+{\text{k}}_{-\text{PG}}\times \text{NP}\right)\left[\text{G}\right]\text{.}$$

Here, ${\left[\text{R}\right]}_{\text{avg}}$ and ${\left[\text{S}\right]}_{\text{avg}}$ are the average concentrations of Rac and signal over all the cells. In this equation, the first term is the production of the global factor, and the second term is the degradation of this factor. ${\text{basal}}_{\text{AG}}$ and ${\text{basal}}_{\text{DG}}$ are the basal rates of G. ${\text{PA}}_{\text{i}}$ is the photoactivation effect on Rac in cell i. In the photoactivatable form of Rac, the binding site of downstream effector on Rac is blocked without light of certain wavelength, and light-induced conformational change would release this block and make Rac available to the effectors (24). This means light treatment provides more activated Rac available to induce downstream event. This photoactivation effect does not go into the equation of $\left[\text{R}\right]$. Instead, we add the additional activated Rac (PA) provided by the light treatment to wherever there is $\left[\text{R}\right]$ in the equations of $\left[\text{G}\right]$ and $\left[\text{P}\right]$ in the form of $\left[\text{R}\right]+\text{PA}$. ${\text{PA}}_{\text{avg}}$ is the average effect of photoactivation and is defined as ${\text{PA}}_{\text{avg}}=\left(1/\text{n}\right){\sum }_{\text{i}}{\text{PA}}_{\text{i}}$, where n is the number of cells in a cluster. In addition, we have not introduced ${\text{G}}^{\text{tot}}$ in the $\left[\text{G}\right]$ equations, as we assume that $\left[\text{G}\right]$ is far from saturation.

The stochastic differential equation (SDE) for protrusion is:

$$\frac{\text{d}\left[{\text{P}}_{\text{i}}\right]}{\text{dt}}=\left({\text{k}}_{\text{RP}}\left(\left[{\text{R}}_{\text{i}}\right]+{\text{PA}}_{\text{i}}\right)+{\text{k}}_{\text{GP}}\left[\text{G}\right]+{\text{k}}_{\text{SP}}\left[{\text{S}}_{\text{i}}\right]\right)\frac{{\left[{\text{P}}_{\text{i}}\right]}^2}{{\left[{\text{P}}_{\text{i}}\right]}^2+1^2}\left({\text{P}}^{\text{tot}}-\left[{\text{P}}_{\text{i}}\right]\right)-\left({\text{basal}}_{\text{DP}}+{\text{k}}_{-\text{GP}}\left[\text{G}\right]+{\text{k}}_{-\text{RP}}\left(\left[{\text{R}}_{\text{i}}\right]+{\text{PA}}_{\text{i}}\right)+{\text{k}}_{-\text{SP}}\left[{\text{S}}_{\text{i}}\right]\right)\left[{\text{P}}_{\text{i}}\right]+\mathit{\eta }\left(\text{t}\right)\text{.}$$

Here, the first term is the activation of P, and the second-order Hill function represents the self-activation of P. The second term is the deactivation of P, and the basal deactivation rate ${\text{basal}}_{\text{DP}}$ is normalized to 1 in the simulation. The third term is the Gaussian noise term.

If we assume that the equations for $\left[\text{R}\right]$ and $\left[\text{G}\right]$ reach equilibrium quickly compared to the timescale of protruding (20–30 min) (13, 25), we can get the steady states for [R] and [G] as follows and then plug them into the $\left[\text{P}\right]$ equations:

$${\left[{\text{R}}_{\text{i}}\right]}^{\text{s}}=\frac{{\text{basal}}_{\text{AR}}+\left[{\text{S}}_{\text{i}}\right]+{\text{k}}_{\text{GR}}{\left[\text{G}\right]}^{\text{s}}}{{\text{basal}}_{\text{AR}}+\left[{\text{S}}_{\text{i}}\right]+{\text{k}}_{\text{GR}}{\left[\text{G}\right]}^{\text{s}}+\left({\text{basal}}_{\text{DR}}+{\text{k}}_{-\text{GR}}{\left[\text{G}\right]}^{\text{s}}\right)\left(1+{\text{PI}}_{\text{i}}\right)}{\text{R}}^{\text{tot}}$$

$${\left[\text{G}\right]}^{\text{s}}=\frac{{\text{k}}_{\text{RG}}\left({\left[\text{R}\right]}_{\text{avg}}^{\text{s}}+{\text{PA}}_{\text{i}}\right)+{\text{k}}_{\text{SG}}{\left[\text{S}\right]}_{\text{avg}}+{\text{k}}_{\text{PG}}\times \text{NP}+{\text{basal}}_{\text{AG}}}{{\text{k}}_{-\text{RG}}\left({\left[\text{R}\right]}_{\text{avg}}^{\text{s}}+{\text{PA}}_{\text{i}}\right)+{\text{k}}_{-\text{SG}}{\left[\text{S}\right]}_{\text{avg}}+{\text{k}}_{-\text{PG}}\times \text{NP}+{\text{basal}}_{\text{DG}}}\text{.}$$

With this fast equilibrium assumption, we are only interested in the steady states of $\left[\text{R}\right]$ and $\left[\text{G}\right]$ so that we can normalize ${\text{basal}}_{\text{DR}}$, ${\text{R}}^{\text{tot}}$, ${\text{basal}}_{\text{AG}}$, and ${\text{basal}}_{\text{DG}}$ to 1.

It is worth noting that these equations are the general forms, including all the possible interactions, and given a certain network, only the parameters related to the existing interactions are nonzero. For networks with five or six interactions, three of the interactions are fixed, and their related parameters are listed in Table 2. The rest of the parameters related to the undetermined interactions are represented by ${\text{k}}_1$, ${\text{k}}_2$, and ${\text{k}}_3$ in Table 2. For one specific network, such as network A in Fig. 2 c, ${\text{k}}_1\equiv {\text{k}}_{\text{SG}}$, ${\text{k}}_2\equiv {\text{k}}_{\text{RG}}$, and ${\text{k}}_3\equiv {\text{k}}_{-\text{GP}}$.

Table 2.

Range of Model Parameters Used in Sampling Simulations

Name	Range in log10 Space	Comment	Name	Range in log10 Space	Comment
${\text{S}}_{\text{grad}}$	(−3, 0)		${\text{S}}_{\text{mean}}$	(−2, 1)
${\text{basal}}_{\text{AR}}$	(−2, 1)		${\text{k}}_1$	(−2, 2)	parameters corresponding to the links, except the three fixed ones; ${\text{k}}_3$ is only used in the six-link network
${\text{P}}^{\text{tot}}$	(−2, 2)		${\text{k}}_2$	(−2, 2)
${\text{k}}_{\text{RP}}$	(−2, 2)		${\text{k}}_3$	(−2, 2)
PI	(−2, 2)	photoinhibition strength	PA		photoactivation strength (only used in fitting, not sampling tests)

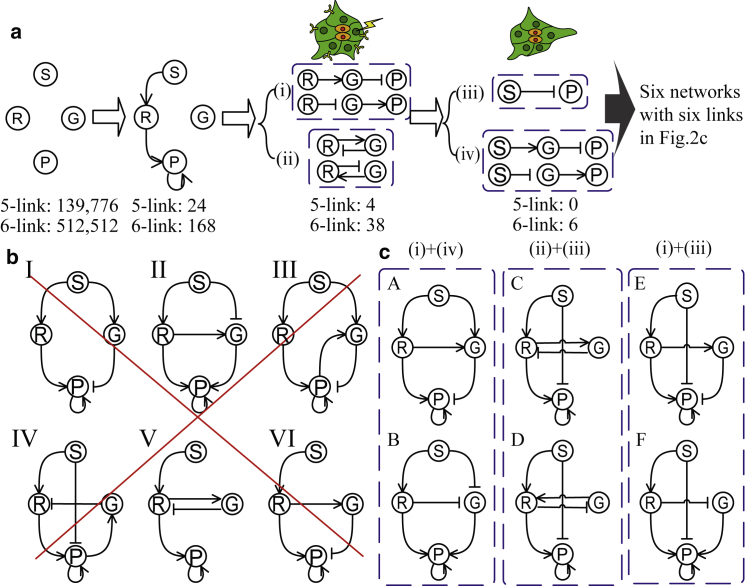
Figure 2.

Network selection procedure. (a) A schematic flow of the qualitative selection procedure is shown. In the first step, the number of candidates is reduced by fixing three links based on other experimental results and by the requirement of at least one input to G and one output from G. In the second and third steps, photoinhibition of Rac and Receptor^DN experiments are used, respectively, to further reduce the number of candidates. (b) Examples of networks that are excluded using our qualitative selection procedure are shown. Networks I–IV are excluded based on photoinhibition of Rac, whereas the exclusion of V and VI is based on Receptor dominant-negative mutant experiments. Positive interactions are shown as arrows, and negative interactions are shown as bars. For further details, see the text. (c) Final results are shown of the qualitative selection procedure, consisting of six networks each with six links. To see this figure in color, go online.

Results

Border cell migration: available experimental data

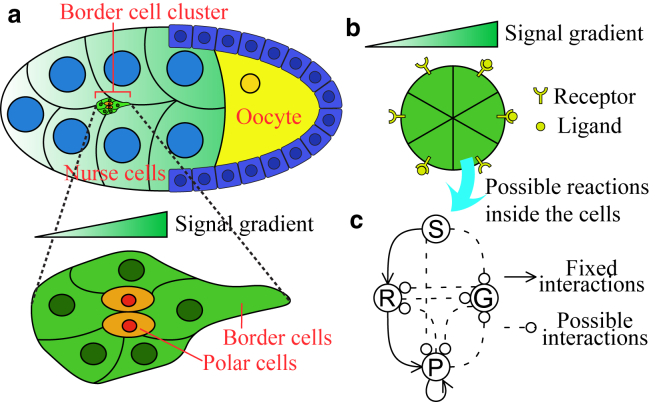
We study a characteristic example of collective chemotaxis: the guided movement of border cell clusters during the embryonic stage of Drosophila (26, 27, 28). A border cell cluster consists of two polar cells and 4–8 border cells (Fig. 1 a) and migrates during development between the nurse cells toward the oocyte as an interconnected group. During this migration, only the border cells show protrusions, whereas the polar cells do not protrude and remain at the center of the cluster. The directional migration of the cluster is essential for Drosophila oogenesis and is guided by chemoattractant gradients (29, 30). Using genetic manipulations of the signal receptors and photoactivatable Rac, a Rho GTPase known to be pivotal in the control and formation of protrusions during cell migration (31), experiments show that the change of signaling state in one cell of the cluster can guide the movement of the whole cluster (32). Light-mediated activation and inhibition of Rac in a single cell can not only change the direction of the cluster but also inhibit or promote the protrusion of other cells in the cluster (13).

Figure 1.

Border cell cluster in Drosophila egg chamber and model simplification. (a) A schematic drawing shows a Drosophila egg chamber and a border cell cluster composed of border cells and polar cells. The cluster moves toward the oocyte guided by chemical signals. (b) Our simplified model of a border cell cluster consists of six nondeformable cells arranged in a rigid array. (c) The basic structure of the signal-processing network consists of four nodes, three fixed positive interactions (solid arrows), and seven possible interactions (dashed arrows with round heads, meaning that the sign of the interactions is undetermined). To see this figure in color, go online.

We use experimental data obtained from (13), which is summarized in Table 1. These data quantify the number of border cells protruding and the directionality index of the cluster, which can be either positive, corresponding to more protruding cells at the front of the cluster, or negative, corresponding to more protruding cells located away from the highest chemoattractant concentration (13) (a detailed definition of the directionality index will be given later). In wild-type clusters, the average number of cells containing a protrusion is about two, whereas the directionality index is large and positive. The authors of (13) also obtained additional data using transgenic flies in which Rac can be selectively and locally activated or inhibited using light. Photoinhibition of Rac of a border cell at the front of the cluster, for example, results in a larger number of average protrusions in the noninhibited cells and a directionality close to zero. In addition, the number of protrusions was quantified in cells expressing dominant negative forms of the chemoattractant receptors, denoted here by ${\text{Receptor}}^{\text{DN}}$. In these cells, ligands can still bind to receptors but fail to deliver a downstream signal. Clusters expressing ${\text{Receptor}}^{\text{DN}}$ were found to have more protrusions on average than wild-type clusters but with a roughly zero directionality index, as would be expected in the absence of any directional signal.

Table 1.

Summary of Experimental Data, Uncertainties Indicate SD

Experiment (Shorthand)	Number of Protruding Cells	Directionality Index	Comments
Wild-type (WT)	$2.0\pm 0.2$	$0.435\pm 0.035$
Photoinhibition of WT (inhibit)	$4.5\pm 0.6$	$-0.025\pm 0.095$	photoinhibition of Rac in the cell at the front of the wild-type cluster
ReceptorDN (RecDN)	$4.15\pm 0.35$	$0.015\pm 0.085$	cells expressing the dominant negative form of the chemoattractant receptors
Photoactivation of WT (activateback)	$2.0\pm 0.3$	$-0.405\pm 0.055$	photoactivation of Rac in the cell at the back of the wild-type cluster
Photoactivation of ReceptorDN (activateRecDN)	$2.1\pm 0.4$	$0.245\pm 0.045$	photoactivation of Rac in one cell of the ReceptorDN cluster

The SD was extracted from the figures in (13).

Model

To construct our model, because the experimental measurements we study are the protrusions in the cluster measured over a relatively short time, we will not consider cell deformation, cluster motion, or cluster rearrangement. Furthermore, because polar cells do not protrude and remain at the center of the cluster, we will only consider border cells in our simulations. We fix the number of these cells to six but note that the analytical methods do not rely on the number of cells in a cluster, and we have verified that the numerical simulation results remain similar for clusters with more or fewer cells. The resulting model is schematically shown in Fig. 1 b and consists of a rigid cluster with cells making an angle of ${\mathit{\theta }}_{\text{i}}=\left(\mathit{\pi }/3\right)\text{i}$, i = 1,..,6 with the gradient direction. Each border cell i contains an identical pathway, and our goal is to determine a minimal set of components or nodes required to capture experimental findings. Because the cell is responding to an external chemoattractant in the form of protrusions and because the activation and inhibition of Rac affect the cell’s response, we assume that the pathway has as local components the input chemoattractant signal S_i, the protrusion level P_i, and the Rac activation level R_i. In addition, we introduce a fourth global component, G, representing cell-cell communication. We do not specify the nature of this communication but note that it can be in the form of a small molecule, as suggested by experiments on branching morphogenesis (20) or in the form of mechanical interactions (12, 33, 34). Because in either case communication between cells is fast compared to protrusion dynamics, which occur on timescales of 20–30 min (13, 25), we will assume that all cells in the cluster share the same value of G. Note that this assumption is valid as long as the degradation of G is not too fast (21, 22). The output of the model and the quantities that can be compared to experimental data include the total number of cells with protrusions, represented by NP, and the direction of the protrusions, quantified by a directionality index specified in Further Discrimination between the Six Minimal Networks with Six Interactions.

We will consider three possible interactions or links between each node of the network, including self-interactions: 1) positive, in which the output of one node increases the activity of the other node or of itself; 2) negative, corresponding to a repression of the activity; and 3) no interaction. As a result, we have to consider 3¹⁶ possible topologies for the model network. One potential technique to determine if these networks are consistent with the data would be to follow the approach of (35), in which the researchers exhaustively searched three-node networks, sampling a broad range of parameters for each to find those with perfect adaptation to a changing signal. However, this is not computationally feasible given the more than 40,000,000 possibilities at hand. Such an approach is further complicated by the fact that our model describes a stochastic, spatially extended system. Thus, although we describe the pathway as a four-node network in which one node is the (fixed) chemotactic input, the equations for the entire cluster contain 13 variables and 13 equations (two local equations for each cell and one global equation). Instead of the sampling approach of (35), we will pursue a qualitative perturbation analysis method.

Qualitative selection approach

We will now reduce the number of possible topologies based on experimental data and without specifying specific functional forms of the interactions. In this qualitative selection procedure, we do not take into account the precise number of protrusions after a specific experimental perturbation. Instead, we only take into account if the perturbation increases or decreases the number of protrusions along with the location of the protrusions. The flow of this procedure is schematically shown in Fig. 2 a. As we will see below, we only have to consider topologies with fewer than seven links. Therefore, we start with all possible network configurations with five-link (amounting to 139,776) and six-link (totaling 512,512) topologies.

Before addressing the detailed results in Wang et al., we can already rule out a large amount of these topologies. First, we note the general result that Rac is known to be activated by an external signal and activates downstream effectors of cell protrusion (31). Consequently, positive interactions from S to R and from R to P are required. Second, experiments have shown that positive feedback loops that are downstream of activated Rac help maintain the protrusion (31). These loops will be captured by a positive self-activation link for P. In addition, as there is no experimental evidence for the amplification of R or G and as we are trying to find the minimal topologies, we assume that there is no self-activation or self-inhibition for these nodes. Furthermore, because S represents the external signal, we assume that there is no feedback to S. This reduction results in the networks that are shown in Fig. 1 c, where the three fixed positive interactions are shown as black solid arrows and where the seven remaining possible interactions are shown using black dotted arrows with round heads, meaning that the sign of the interactions is undetermined. Finally, we note that the experiments of Wang et al. show that local photoactivation and inhibition affect the protrusion number of the entire cluster. This automatically implies that there must be cell-cell communication. In our model, this communication is achieved through the global factor G, and we thus need at least two more links in addition to the three shown in Fig. 1 c: one input to G and one output from G. Taking into account the restrictions mentioned above, we find that we have 24 possible five-link topologies and 168 possible six-link topologies, schematically indicated by the second step in Fig. 2 a. Of course, there will be even more topologies with a larger number of links. However, as we will see below, several six-link topologies are consistent with the experimental data, and because we are searching for minimally complex networks, we will not consider topologies with more than six links.

Photoinhibition experiment requires one of four possible interaction motifs

Photoinhibition of Rac in the front cell of a wild-type cluster decreases the probability of that cell protruding but increases the protrusion probability of the other cells in the cluster (13). This information creates two requirements for the network. First, because inhibiting Rac in one cell affects a separate cell’s protrusions, there should be an interaction from one cell’s R to the other cell’s P through the global factor G. This gives us four possible motifs within the network ($\text{R}\to \text{G}\to \text{P}$, $\text{R}\to \text{G}\to \text{R}\to \text{P}$, $\text{R}\to \text{P}\to \text{G}\to \text{P}$, and $\text{R}\to \text{P}\to \text{G}\to \text{R}\to \text{P}$), and topologies lacking these motifs can be excluded. An example of such an excluded network is shown in Fig. 2 b, I. Second, because inhibition corresponds to a reduction of R, the interaction between R and P through G should be negative. Thus, the product of the signs of the links in these four possible motifs should be negative. We will not consider the possibility of having more than one motif, as this would be redundant, and we are trying to find the minimal number of possible networks. For instance, in the $\text{R}\to \text{G}\to \text{P}$ motif, if both links are positive, the net effect from one cell’s R to another cell’s P will be positive, which contradicts the experiments. Network II in Fig. 2 b is an example of a network that can be excluded using this logic. The other three motifs contain more than two links, including a direct link between R and P. Because this $\text{R}\to \text{P}$ interaction is required by other experimental results to be positive (31, 36), there are also only two possibilities of sign assignments. For example, for the pathway $\text{R}\to \text{G}\to \text{R}\to \text{P}$, the sign assignment can only be either $\text{R}\stackrel{+}{\to }\text{G}\stackrel{-}{\to }\text{R}\stackrel{+}{\to }\text{P}$ or $\text{R}\stackrel{-}{\to }\text{G}\stackrel{+}{\to }\text{R}\stackrel{+}{\to }\text{P}$.

After further analysis, we can rule out both the (a) $\text{R}\to \text{P}\to \text{G}\to \text{P}$ and the (b) $\text{R}\to \text{P}\to \text{G}\to \text{R}\to \text{P}$ motifs entirely. Two examples including these two excluded motifs are shown in Fig. 2 b as III and IV. In these motifs, communication from one cell to another occurs through G using protrusion as an intermediate step. The photoinhibition experiments show that Rac inhibition in one cell leads to a significant increase of protrusions in other cells (see Table 1). Within these motifs, this implies that a protrusion decrease in one cell $\left({\text{P}}_{\text{i}}\right)$ promotes protrusions in other cells $\left({\text{P}}_{\text{j}}\right)$. As the signal S does not change in the photoinhibition experiments, the following logic holds regardless of how S is connected to the other components of the network. So, in the following analysis, when we rule out a motif, we mean that all the networks containing this motif (without redundant motifs) are ruled out. And as $\text{R}\to \text{P}$ is fixed to be a positive effect by experiments, we only need to consider the signs of the following two motifs: $\left({\text{a}}^{\prime }\right)\text{P}\to \text{G}\to \text{P}$ and $\left({\text{b}}^{\prime }\right)\text{P}\to \text{G}\to \text{R}$.

As is mentioned in the first paragraph of this section, the phenomenon that inhibiting ${\text{R}}_{\text{i}}$ leads to a decrease in ${\text{P}}_{\text{j}}$ has ruled out the possibility that the effect of motif $\left({\text{a}}^{\prime }\right)$ is positive. On the other hand, if the effect of motif $\left({\text{a}}^{\prime }\right)$ is negative (as in Fig. 2 b, III), we take $\text{P}\stackrel{+}{\to }\text{G}\stackrel{-}{\to }\text{P}$ as an example because the logic is similar if we switch the signs. After photoinhibition, the experiments show that more cells display protrusions. This results in an increase in the global factor G because the sign of the link between P and G is positive. However, because G to P is negative, this will lead to lower ${\text{P}}_{\text{j}}$, which contradicts the experimental results. So for motif $\left({\text{a}}^{\prime }\right)$, neither positive nor negative effects match the experiments, and thus, motif (a) is excluded.

We can follow a similar line of logic to exclude motif (b). For this motif, the positive effect is also ruled out in the first paragraph of this section by the phenomenon that inhibiting ${\text{R}}_{\text{i}}$ promotes ${\text{P}}_{\text{j}}$. Consider the case in which the effect of motif $\left({\text{b}}^{\prime }\right)$ is negative; we take $\text{P}\stackrel{+}{\to }\text{G}\stackrel{-}{\to }\text{R}$ (as in Fig. 2 b, IV) as an example because switching the signs does not influence the logic. As the number of protrusions increases after photoinhibition, G increases, and thus, ${\text{R}}_{\text{j}}$ decreases. The decrease in ${\text{R}}_{\text{j}}$, however, will lead to a decrease in ${\text{P}}_{\text{j}}$ decrease, which contradicts the experiments. So motif (b) is also excluded.

Therefore, only two of the four possible motifs remain. These motifs, when taking into account the different sign assignments, result in four possibilities listed in (i) and (ii) in Fig. 2 a. If combined with the fixed links mentioned earlier, they generate four five-link and 38 six-link networks.

Receptor ^DN experiment requires one of three possible interaction motifs

Wang et al. found that clusters expressing ${\text{Receptor}}^{\text{DN}}$ have more protrusions on average than wild-type clusters (13). We model ${\text{Receptor}}^{\text{DN}}$ by taking the signal to be zero, meaning that all cells will see identical environments. The comparison to wild-type protrusion numbers will be simpler if we similarly assume that wild-type clusters see a constant but nonzero signal. This will be reasonable in predicting the number of protrusions if the gradient is relatively small. This assumption is supported by measurements of the chemoattractant PVF1 along the border cell cluster’s migration path that do not show a steep gradient (12). Furthermore, as we will show below, numerical simulations that take the gradient into account give consistent results.

In the absence of a gradient, the problem is reduced into a homogeneous one, and the average number of protrusions is simply given by $\langle \text{NP}\rangle =\left(\text{number}\text{of}\text{cells}\right)\times \text{Prob}$, where Prob is the probability of a protrusion in any cell. The result of the ${\text{Receptor}}^{\text{DN}}$ experiment (protrusion number increases when [S] decreases) can be translated into an inequality: $\left(\text{dProb}/\text{d}\left[\text{S}\right]\right)<0$. Using the total derivative’s chain rule, we can express $\left(\text{dProb}/\text{d}\left[\text{S}\right]\right)$ in terms of partial derivatives and total derivatives that are experimentally known (see Supporting Materials and Methods for a detailed derivation):

$$\left(1-\frac{\partial \text{Prob}}{\partial \left[\text{G}\right]}\frac{\partial \left[\text{G}\right]}{\partial \text{Prob}}\right)\frac{\text{dProb}}{\text{d}\left[\text{S}\right]}=\frac{\partial \text{Prob}}{\partial \left[\text{S}\right]}+\frac{\partial \text{Prob}}{\partial \left[\text{G}\right]}\frac{\partial \left[\text{G}\right]}{\partial \left[\text{S}\right]}+\left(1-\frac{\partial \text{Prob}}{\partial \left[\text{G}\right]}\frac{\partial \left[\text{G}\right]}{\partial \text{Prob}}\right)\frac{\text{dProb}}{\text{d}\left[\text{R}\right]}\frac{\text{d}\left[\text{R}\right]}{\text{d}\left[\text{S}\right]}.$$ (1)

Experiments indicate that both total derivatives appearing in the last term are positive: fluorescence resonance energy transfer measurements show that Rac activity increases after adding epidermal growth factor (13), implying $\left(\text{d}\left[\text{R}\right]/\text{d}\left[\text{S}\right]\right)>0$, whereas experiments using photoactivatable Rac show that Rac activation induces cell protrusion (24), implying $\left(\text{dProb}/\text{d}\left[\text{R}\right]\right)>0$. To get $\left(\text{dProb}/\text{d}\left[\text{S}\right]\right)<0$ in Eq. 1, there are two options:

$$\text{a})\left(1-\frac{\partial \text{Prob}}{\partial \left[\text{G}\right]}\frac{\partial \left[\text{G}\right]}{\partial \text{Prob}}\right)<0\text{and}\left(\frac{\partial \text{Prob}}{\partial \left[\text{S}\right]}+\frac{\partial \text{Prob}}{\partial \left[\text{G}\right]}\frac{\partial \left[\text{G}\right]}{\partial \left[\text{S}\right]}\right)>0\text{or}$$

$$\text{b})\left(1-\frac{\partial \text{Prob}}{\partial \left[\text{G}\right]}\frac{\partial \left[\text{G}\right]}{\partial \text{Prob}}\right)>0\text{and}\left(\frac{\partial \text{Prob}}{\partial \left[\text{S}\right]}+\frac{\partial \text{Prob}}{\partial \left[\text{G}\right]}\frac{\partial \left[\text{G}\right]}{\partial \left[\text{S}\right]}\right)<0.$$

Option a) requires at least three links, namely i) $\text{G}\to \text{P}$, $\text{P}\to \text{G}$, and $\text{S}\to \text{P}$ or ii) $\text{G}\to \text{P}$, $\text{P}\to \text{G}$, and $\text{S}\to \text{G}$ as $\left(\partial \text{Prob}/\partial \left[\text{G}\right]\right)\left(\partial \left[\text{G}\right]/\partial \text{Prob}\right)$, should be nonzero. Combining the links in these two possibilities with the five links already determined above and taking into account possible redundant links lead to networks that have either seven or eight links. Thus, these networks will not be further considered. Option b) requires $\left(\partial \text{Prob}/\partial \left[\text{S}\right]\right)<0$ or $\left(\partial \text{Prob}/\partial \left[\text{G}\right]\right)\left(\partial \left[\text{G}\right]/\partial \left[\text{S}\right]\right)<0$, which can be accomplished with either one or two additional links shown in Fig. 2 a (iii) and (iv). Two examples of excluded networks based on the ${\text{Receptor}}^{\text{DN}}$ experiments are shown in Fig. 2 b as V and VI.

Final construction of possible topologies

We can now assemble the simplest possible networks by choosing one possible motif mandated by the photoinhibition experiment and one possible motif mandated by the ${\text{Receptor}}^{\text{DN}}$ experiment. Specifically, combining motifs from group (i) and motifs from group (iv) of Fig. 2 a results in the two networks A and B shown in the first group of Fig. 2 c. Similarly, combining motifs from (ii) and (iii) leads to networks C and D in Fig. 2 c, and combining motifs from groups (i) and (iii) produces networks E and F. All of these candidate networks have six links: our qualitative selection procedure has ruled out any five-link networks. Choosing motifs from group (ii) and group (iv) will result in networks with seven links, which we will ignore, as we have found that six-link networks are sufficient to meet our requirements. In the Discussion, we will discuss briefly networks with more links. Finally, it’s worth emphasizing again that the above analysis did not specify functional forms of the interactions in the networks; the results will hold regardless of the quantitative details of the interactions.

Simulation results are consistent with selection analysis

In the above analysis of the ${\text{Receptor}}^{\text{DN}}$ experiment, we made one key approximation: we assumed that the gradient is shallow enough that protrusion numbers are independent of the gradient. To verify that this approximation does not influence our results and to study the selected networks in a quantitative way, we cast our candidate networks into ODEs and SDEs. Specifically, we have one deterministic equation for R in each cell and a single global deterministic equation for G. These equations are listed in Methods. The equation for the protrusion in cell i, $\left[{\text{P}}_{\text{i}}\right]$, is cast as an SDE of the form

$$\frac{\text{d}\left[{\text{P}}_{\text{i}}\right]}{\text{dt}}=\text{F}\left(\left[\text{G}\right],\left[{\text{P}}_{\text{i}}\right],\left[{\text{R}}_{\text{i}}\right],\left[{\text{S}}_{\text{i}}\right]\right)+\mathit{\eta }\left(\text{t}\right),$$

where F represents a nonlinear function, and $\mathit{\eta }$ is a Gaussian noise term with zero mean and SD $\mathit{\sigma }$: $\langle \mathit{\eta }\left({\text{t}}_1\right)\mathit{\eta }\left({\text{t}}_2\right)\rangle =2{\mathit{\sigma }}^2\mathit{\delta }\left({\text{t}}_1-{\text{t}}_2\right)$. We have chosen F to be such that P is bistable and can be either in a low state, ${\left[\text{P}\right]}_{\text{a}}$, corresponding to a nonprotruding state, or in a high state, ${\left[\text{P}\right]}_{\text{c}}$, representing the protruding state (details in Methods). Using a bistable equation for P results in a clear distinction between cells that are protruding (in the high state) and those that are not (low state). To solve the resulting set of 13 coupled equations, we assume that all seven deterministic equations reach equilibrium quickly compared to the timescale of protruding (20–30 min) (13, 25). The resulting stable states for R and G can then be substituted into the six SDEs for P_i.

To solve the SDEs, one could in principle use an SDE solver to determine the steady state of the cluster and thus the average protrusion number. However, this would require capturing a large number of transitions between the high and low states. These transitions could become prohibitively slow, especially if the barrier in the bistable protrusion state is large compared to the strength of fluctuations, requiring an excessive amount of computational resources. Therefore, rather than directly solving the SDEs, we treat the problem as a transition between the low state ${\left[\text{P}\right]}_{\text{a}}$ and high state ${\left[\text{P}\right]}_{\text{c}}$ and compute transition rates between these two states. This is possible because the equation for P can be written as follows:

$$\frac{\text{d}\left[\text{P}\right]}{\text{dt}}=-{\text{U}}^{\text{'}}\left(\left[\text{P}\right]\right)+\mathit{\eta }\left(\text{t}\right),$$

which is precisely the equation of an overdamped particle in a double-well potential $\text{U}\left(\left[\text{P}\right]\right)$. Thus, we can calculate the transition rates between states ${\left[\text{P}\right]}_{\text{a}}$ and ${\left[\text{P}\right]}_{\text{c}}$ using the Kramers approximation as follows:

$${\text{k}}_{\text{on}}=\frac{\sqrt{-{\text{U}}^{\text{''}}\left({\left[\text{P}\right]}_{\text{a}}\right){\text{U}}^{\text{''}}\left({\left[\text{P}\right]}_{\text{b}}\right)}}{2\mathit{\pi }}{\text{e}}^{-\frac{\text{U}\left({\left[\text{P}\right]}_{\text{b}}\right)-\text{U}\left({\left[\text{P}\right]}_{\text{a}}\right)}{{\mathit{\sigma }}^2}}$$

$${\text{k}}_{\text{off}}=\frac{\sqrt{-{\text{U}}^{\text{''}}\left({\left[\text{P}\right]}_{\text{c}}\right){\text{U}}^{\text{''}}\left({\left[\text{P}\right]}_{\text{b}}\right)}}{2\mathit{\pi }}{\text{e}}^{-\frac{\text{U}\left({\left[\text{P}\right]}_{\text{b}}\right)-\text{U}\left({\left[\text{P}\right]}_{\text{c}}\right)}{{\mathit{\sigma }}^2}}.$$

Here, ${\left[\text{P}\right]}_{\text{b}}$ is the maximum of the potential $\text{U}\left(\left[\text{P}\right]\right)$ between ${\left[\text{P}\right]}_{\text{a}}$ and ${\left[\text{P}\right]}_{\text{c}}$ (see also Fig. S1). Note that the Kramers approximation needs the prerequisites that $\mathit{\Delta }\text{U}\gg {\mathit{\sigma }}^2$, where $\mathit{\Delta }\text{U}\equiv \text{U}\left({\left[\text{P}\right]}_{\text{b}}\right)-\text{U}\left({\left[\text{P}\right]}_{\text{a}\text{or}\text{c}}\right)$. When this prerequisite does not hold, we use a more accurate method based on the mean first passage time in a one-dimensional potential to calculate the transition rates (details are in Supporting Materials and Methods). Because the transition rates depend on the ratio of $\mathit{\Delta }\text{U}$ and ${\mathit{\sigma }}^2$ rather than the specific value of ${\mathit{\sigma }}^2$ and because the value of $\mathit{\Delta }\text{U}$ is controlled by other parameters, we can fix $\mathit{\sigma }=0.1$ in our simulation without losing generality.

Given the transition rates between the two states, we can compute the average number of protrusions under many circumstances. Each cell can be either protruding or not; there are then $2^6=64$ possible states for a cluster with six cells, and each state $\mathit{\alpha }$ (with $\mathit{\alpha }=1,2,\dots ,64$) then has a total number of protrusions, ${\text{NP}}_{\mathit{\alpha }}$. Associated with each state is a probability ${\text{W}}_{\mathit{\alpha }}$, which can be computed using a master equation

$$\frac{{\text{dW}}_{\mathit{\alpha }}}{\text{dt}}=\sum _{\mathit{\beta }=1}^{64}{\text{q}}_{\mathit{\alpha \beta }}{\text{W}}_{\mathit{\beta }}.$$

Here, q is a matrix with ${\text{q}}_{\mathit{\alpha \beta }}$ ($\mathit{\alpha }\ne \mathit{\beta }$) describing the transition rate from state $\mathit{\beta }$ to state $\mathit{\alpha }$, whereas ${\text{q}}_{\mathit{\alpha \alpha }}$ represents the transition rate out of state $\mathit{\alpha }$, which can be defined as ${\text{q}}_{\mathit{\alpha \alpha }}=-{\sum }_{\beta =1,\beta \ne \alpha }^{64}{q}_{\beta \alpha }.$ The transition rates are given by the escape rates ${\text{k}}_{\text{on}}$ and ${\text{k}}_{\text{off}}$ shown above. We will only consider transitions in which one cell changes its state. In the long-time limit, the probabilities tend to the stationary solution, that is $\left({\text{dW}}_{\mathit{\alpha }}/\text{dt}\right)=0$, resulting in a set of 64 coupled linear equations that can be easily solved (37). Once these probabilities are found, it is straightforward to find the average number of protrusion, computed as $\langle \text{NP}\rangle ={\sum }_{\mathit{\alpha }}{\text{NP}}_{\mathit{\alpha }}{\text{W}}_{\mathit{\alpha }}$, the number of protrusions in the direction of the gradient, or other relevant experimental measurements.

To reduce the computational expense, we study all 24 networks with five links resulting from our initial qualitative selection (shown in the second step of Fig. 2 a) but limit ourselves to a subset of 12 six-link networks out of 168 possible networks, including the ones shown in Fig. 2 c. In our simulations, we use Latin hypercube sampling to generate 500,000 sets of parameters; because parameters correspond to positive rates, we sample uniformly over the log of the parameters. The parameters and their sampling ranges are listed in Table 2. Then, we apply the same perturbations corresponding to the ${\text{Receptor}}^{\text{DN}}$ and photoinhibition experiments and compare the pre- and postperturbation protrusion numbers.

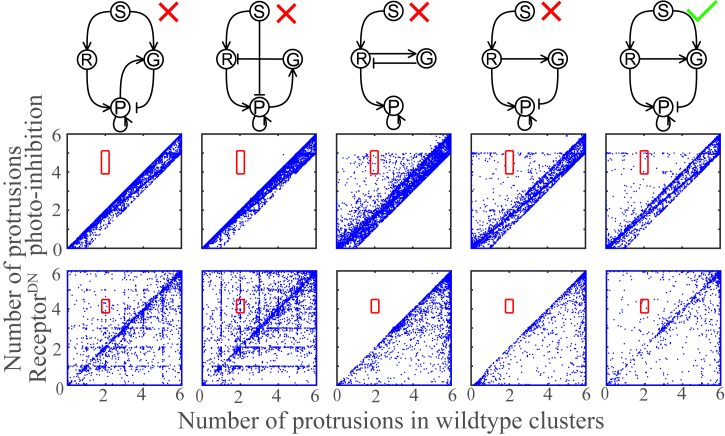
In Fig. 3, we show the sampling results for the five networks illustrated in the upper row. The first four (two five-link and two six-link topologies) were ruled out by our selection procedure, whereas the rightmost network is not excluded by the qualitative selection. The results of the numerical sampling are shown in the middle and lower rows, where each dot corresponds to one set of parameters. The x axis represents the number of protrusions in wild-type clusters, whereas the y axis represents the protrusion number for the lead cell photoinhibition (middle row) and the ${\text{Receptor}}^{\text{DN}}$ experiments (lower row). The red box shows the experimentally observed protrusion number with the center as the mean and the length and width as the observed SDs. The existence of dots within the red box means that the network is consistent with the experimental data. We see that the first four networks fail to meet the requirements for one of the two experiments, whereas the last network shows parameter combinations that can satisfy both.

Figure 3.

Parameter sampling results of five networks. The x axes show the number of protrusions for wild-type clusters, and the y axes show the number of protrusions for the photoinhibition case (middle row) and the Receptor^DN case (lower row). The rectangular boxes show the region quantitatively consistent with the experimental data, whereas a dot represents the output of one set of parameters. To see this figure in color, go online.

We emphasize that in Fig. 3 and in the networks from which we have sampled explicitly, we find results that are consistent with our qualitative models. Models that fail the ${\text{Receptor}}^{\text{DN}}$ test qualitatively fail it in sampling, whereas models that can be ruled out by the qualitative selection procedure based on the photoinhibition experiments are also inconsistent with these experiments when analyzing the sampling results. It is worth noting that the points within the red box in the middle row may not be the same sets of parameters as those in the lower row; having points in both red boxes is necessary but not sufficient to be consistent with the experiment. Below, we will fit the parameters for the six selected networks to make sure that we can find at least one set of parameters for each network that is consistent with the experimental results listed in Table 1. More sampling results can be found in Figs. S2–S4, and the sampling results for networks B–F of Fig. 2 c are shown in Fig. S4.

Further discrimination between the six minimal networks with six interactions

After finding the six minimal networks with six interactions, the remaining question is how to discriminate between these six networks or these three groups. In addition to the protrusion statistics we have already used, Wang et al. also defined and measured a directionality index defined as ${\text{D}}_{\exp }=\left({\sum }_{\text{i}}{\overrightarrow{\text{P}}}_{\text{i}}\cdot \overrightarrow{\text{d}}/{\sum }_{\text{i}}\Vert {\overrightarrow{\text{P}}}_{\text{i}}\Vert \right)$, where $\overrightarrow{\text{d}}$ is the unit vector in the signal gradient direction, and ${\overrightarrow{\text{P}}}_{\text{i}}$ is the protrusion vector for cell i determined from experimental images. To compare this to our model results, we take the direction of the protrusion in the model to be normal to the edge of the round cluster and of length 1 for the protruding state and 0 for the nonprotruding state. Thus, we can define a directionality index for the model using the equation ${\text{D}}_{\text{mod}}=\left({\sum }_{\text{i}=1}^6{\text{P}}_{\text{i}}\cos {\mathit{\theta }}_{\text{i}}/{\sum }_{\text{i}=1}^6{\text{P}}_{\text{i}}\right)$, which can range from +1 (only the front cell shows a protrusion) to −1 (only the back cell protrudes).

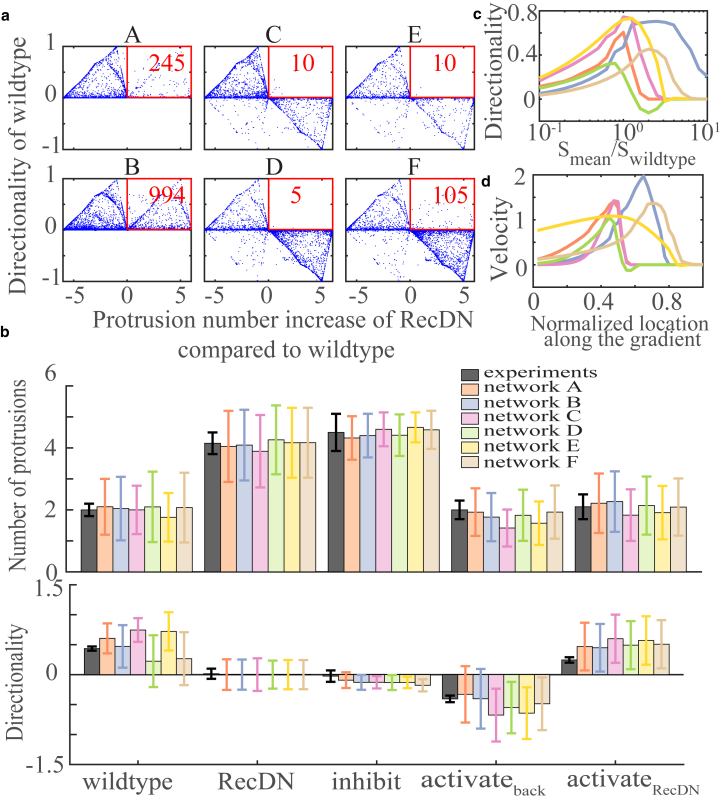
Among the six possible networks in Fig. 2 c, networks C, D, E, and F have a negative $\text{S}\to \text{P}$ interaction, whereas networks A and B do not. This negative $\text{S}\to \text{P}$ interaction is determined by the ${\text{Receptor}}^{\text{DN}}$ experiments requiring $\langle {\text{NP}}_{{\text{Rec}}^{\text{DN}}}\rangle -\langle {\text{NP}}_{\text{wild}}\rangle >0$. However, if the chemoattractant suppresses protrusions, it would tend to make the cluster move against the signal gradient, contradicting the experiments. This is not a critical problem, as there is also a positive effect $\text{S}\to \text{R}\to \text{P}$ to balance the negative effect. But for networks C, D, E, and F, positive chemotaxis of the cluster is not a robust feature but one requiring fine-tuning of the parameters. In contrast, for networks A and B, the negative effect from S to P is through the global factor G, which has the same value for all the cells, leading to robust chemotaxis. This difference is shown in Fig. 4 a by plotting the results of 500,000 samples with the y axis as the directionality for the wild-type cluster and the x axis as the difference between the average protruding number for ${\text{Receptor}}^{\text{DN}}$ clusters and that for wild-type clusters $\left(\langle {\text{NP}}_{{\text{Rec}}^{\text{DN}}}\rangle -\langle {\text{NP}}_{\text{wild}}\rangle \right)$. Within Fig. 4 a, parameters that pass the ${\text{Receptor}}^{\text{DN}}$ standard are in the right half of the plot, whereas parameters with positive directionality are in the top half of the plot; ideally, models should have points in the top right quadrant. Fig. 4 a shows more dots in the upper half for networks A, B, and F, which means that it is more likely to obtain good parameters for these three networks compared to the others. More importantly, there are no dots below the x axis in networks A and B, meaning that regardless of parameters, these two networks always make the wild-type cluster follow the gradient. In other words, networks A and B robustly have positive directionality. The absence of robust directionality in networks C–F suggests that, if these are correct, further experimental interventions could convert chemotaxis to chemorepulsion.

Figure 4.

Simulation results. (a) Parameter sampling results for the six selected networks show am average increase of protrusion number under the Receptor^DN condition compared to the wild-type cluster in the x axes and the wild-type cluster’s directionality in the y axes. The square box shows the region that is qualitatively consistent with the experimental results, and the number represents the number of parameter sets (out of 500,000) that produce results that are consistent with the experiments. (b) A comparison of the experimental data reported in Table 1 and simulation results for the six selected networks with fitted parameters are shown. A–F correspond to networks A through F in Fig. 2c. Error bars show the SDs. (c) Trends of the cluster’s directionality are shown for the six selected networks with fitted parameters when the mean signal is changed. (d) Trends of the cluster’s velocity are shown for the six selected networks with fitted parameters along the migration path. To see this figure in color, go online.

In addition, we are able to suggest experiments to help further discriminate between the six selected networks. One significant difference between networks C and D of Fig. 2 c and the other networks is how the protrusion of one cell is affected by the activation of R in another cell. For networks C and D, this control is through R, which means changing R in one cell influences not only the protrusions of other cells but also the level of R. Therefore, measurement of Rac activation simultaneously with photoactivation would show whether R’s activity can be controlled by light treatment on other cells. The results of these experiments can then be used to further discriminate between topologies.

Parameter fitting

To make sure that parameters exist to meet the requirement of all the experiments simultaneously and as a prerequisite to making predictions, we fit 10 parameters for each of the six networks using a simulated annealing algorithm. We fit not only the ${\text{Receptor}}^{\text{DN}}$ and photoinhibition experiments but also the other protrusion number data found in Table 1. We also mandate that our fits display signs of directionality that are consistent with the experimental results listed in Table 1. Details of the procedure can be found in the Supporting Materials and Methods. The comparison of protrusion number and directionality between the simulation results with fitted parameters and the experimental data for the six networks under all five conditions listed in Table 1 are shown in Fig. 4 b. Clearly, our best-fit parameters are able to produce results that are within similar levels of accuracy for each of the six networks. The values of the fitted parameters for the six networks are listed in Supporting Materials and Methods. It is worth mentioning that we can find more than one set of parameters for each network that can fit the experimental data similarly well, as the parameter space has lots of local minima. Our fitting procedure typically produces multiple parameter sets, and here, for illustrative purposes, we choose the set that has the lowest total error, as defined by our error function. Note, however, that this parameter set might not represent the global minimum and might not be the most optimal one. As a simple robustness check, we perturb one parameter by $\pm 10\text{\%}$ while keeping the other parameters constant and quantify the outcomes of the model with the modified parameter. We find that the sensitivity of the model depends on the parameter and on the network topology. For example, for all the six topologies, we find that the results are not sensitive to the parameters ${\text{S}}_{\text{mean}}$, ${\text{S}}_{\text{grad}}$, PI, and PA; a change in these parameters results in a change in the number of protrusions of less than 10%. Changes in other parameters, including ${\text{k}}_{\text{RP}}$ and ${\text{k}}_{-\text{IP}}$, lead to larger changes in protrusion numbers for some specific network topologies. Note, however, that our goal is not to find specific parameter values or parameter values that are robust to changes. Instead, we aim to find possible topologies that are consistent with experimental data using strategies that are independent of parameter values. Robustness may be used later as a useful criterion for further distinguishing models (38).

One interesting feature of this figure is that for most conditions, the SDs of the simulations are much larger than those of the experiment. For all the six minimal networks, there is no feedback from P to G so that the protrusion of one cell is independent of the protruding states of other cells. With this independence prerequisite, as the signal for every cell is the same in the ${\text{Receptor}}^{\text{DN}}$ case, the protruding probabilities for all the cells in a cluster of n cells are given by $\text{Prob}=\left(4.15/\text{n}\right)$, as the experimental measurement shows an average of 4.15 protrusions under this condition. Now, we can calculate the SD for protrusion number easily, as the probability of having n protrusions is simply $\left(\begin{array}{c}\text{n}\\ \text{i}\end{array}\right){\left(\text{Prob}\right)}^{\text{i}}{\left(1-\text{Prob}\right)}^{\text{n}-\text{i}}$, where $\left(\begin{array}{c}\text{n}\\ \text{i}\end{array}\right)$ is the binomial coefficient. Therefore, $\text{SD}=\sqrt{\sum _{\text{i}=0}^{\text{n}}{\left(\text{i}-4.15\right)}^2\left(\begin{array}{c}\text{n}\\ \text{i}\end{array}\right){\left(\text{Prob}\right)}^{\text{i}}{\left(1-\text{Prob}\right)}^{\text{n}-\text{i}}}$, giving $\text{SD}=1.13$ for $\text{n}=6$. This is consistent with our simulation result and is much larger than the experimental SD, which is ∼0.35. This means that within a model with six cells in which the probability of a cell protruding is independent of whether other cells have protruded, the SD of the protrusion number cannot be reduced by merely changing the fit parameters. To get an SD close to the experimental result, we have to change either the cell number or the network topology to remove independence. When $\text{n}=5$, $\text{SD}\approx 0.84$, and when $\text{n}=4$, to get an average protrusion number close to 4, $\text{Prob}=1$ and thus $\text{SD}=0$. Usually, there are 4–8 border cells in the cluster (27), so one possible reason for the small SD in the experiment is that a significant fraction of cluster samples has only four border cells. The other possibility is to change the independence prerequisite by adding a link from P to G to form negative feedback between P and G on the six selected networks. Networks with a $\text{P}\to \text{G}$ link show reduced variance because the feedback can constrain the average number of protrusions to be very close to a whole number. This is clear in the sampling results of ${\text{Receptor}}^{\text{DN}}$ for the first two networks in Fig. 3 showing a pattern with grids at the whole numbers. If the variance is to be tightly constrained in this way, however, we need at least seven interactions for the minimal networks. We give an example of this kind of seven-link network by adding a positive arrow from P to G to network A, shown as network 2 in Fig. S6. The simulation results show that adding this additional feedback can reduce the SD for the number of protrusions but not necessarily for the directionality.

Model predictions

Although we do not know which of the six selected networks is the real one, we can still make some reasonable predictions based on their common simulation results with the fitted parameters. By changing the mean value of the signal while keeping the relative gradient constant, we can get the trends of the directionality. This is shown in Fig. 4 c, which reveals that all networks display a maximal directionality near the original mean value of signal. This result is qualitatively robust regardless of network topologies or parameters as long as they meet the requirements of our selecting process. Fig. 4 c also shows that the directionality of network D (green curve) can become negative for some range of signal strengths. This is consistent with our previous conclusion that the networks, except networks A and B, do not guarantee chemotaxis. We note that a direct quantitative comparison between experimental and model results is difficult. First, experiments have not established the concentration and gradient strength of chemoattractant in vivo. Secondly, we did not consider the length of the protrusion in our model—our protrusions were either on or off. For example, in our model, if all the cells in the cluster have protrusions, the directionality is exactly zero, but in reality, it is possible that the protrusions of the cells at the front half of the cluster are larger, resulting in a positive directionality.

Despite the lack of quantitative comparison, we can still compare our model prediction of Fig. 4 c with experimental data. Increasing the mean of signal in a wild-type cluster while keeping the relative gradient constant is similar to PVF1 overexpression. This overexpression was found to decrease the directionality of the cluster (39). Furthermore, experiments have measured the speed profile of the cluster along its path, during which the mean signal is assumed to increase (19). To compare with this experimental data, we define a velocity $V={\sum }_{\text{i}}{\overrightarrow{\text{P}}}_{\text{i}}\cdot \overrightarrow{\text{d}}$, where $\overrightarrow{\text{d}}$ is the unit vector in the signal gradient direction, and ${\overrightarrow{\text{P}}}_{\text{i}}$ is the protrusion vector for cell i. Note that in this definition, we do not consider the length of the protrusion nor do we include any mechanical aspect of migration. We assume that the signal profile across the egg chamber is exponential, as suggested in (19), and the signal profile for a cluster at location $\text{Lx}$ is $\text{S}\left(\text{x}\right)={\text{S}}_{\text{mean}}{\text{e}}^{-{\text{S}}_{\text{grad}}\left(\text{C}-\text{Lx}\right)}\left(1+{\text{S}}_{\text{grad}}\cos {\mathit{\theta }}_{\text{i}}\right).$ Here, L is the total length of the migration path, and x is the normalized location. We set the radius of the cluster to be 1, and by rough measurement of the length of the cluster’s travel path from the images in (26), we will take L = 20. For C, the location at which the data in (13) are measured, we will take C = 8, corresponding to measurements around 1/3–1/2 region of the cluster’s travel path (X. Wang, personal communication). ${\text{S}}_{\text{mean}}$ and ${\text{S}}_{\text{grad}}$ are the parameters fitted in the previous part for the six selected networks and correspond to the mean and relative gradient of the signal at the measured position in the experiments. We plot V vs. x curves for all the six networks in Fig. 4 d. We can see that the main trend that velocity first accelerates and then decelerates is consistent with the experimental curves in (19). This behavior emerges from our model, which has been fitted to the perturbation experiments but uses no information from (19) other than the proposed exponential signal profile.

We also examine the role of cell-cell communication in the cluster’s chemotaxis by making the global factor G purely local. In the simulation, we use the same sets of parameters we have fitted for the six networks as in Fig. 4 b and get negative or zero cluster velocities (Fig. S5 a), indicating that cell-cell communication increases the chemotactic ability of the cluster. To verify that these results are not sensitive to the precise choice of parameters, we use the same sets of randomly generated parameters as in Figs. 3 and 4 a but reject those with negative velocity. We find that for all six networks, blocking cell-cell communication by making G local results in decreased and sometimes negative cluster velocities (Fig. S5 b). In fact, for networks C and D, abolishing global communication always results in clusters that have negative velocities. It should be noted that clusters of mammary epithelial cells with decreased cell-cell communication have been shown to lose their directional response to shallow gradients (20). It would be interesting to examine this prediction in experiments in which gap junctions between border cells are blocked.

Discussion

In this study, we used mathematical analysis combined with sampling simulations and parameter fitting to determine the simplest network topology that is consistent with a set of in vivo experiments on border cell migration. The mathematical analysis relied solely on qualitative experimental observations and is thus independent of specific functional forms of the interactions between the pathway nodes. Key to this analysis is the fact that specific experimental perturbations, either in the form of photoinhibition, photoactivation, or mutations, resulted in clear phenotypic changes. Using these changes, we were able to reduce the amount of possible simple networks from a very large number to only six.

The complexity of our problem makes application of standard approaches infeasible. A number of existing techniques exist to infer network topologies from experimental data on single cells (20, 21, 22). Often, it is possible to gain insight into the topology on the basis of mutant analysis, drug responses, or clever experimentation (40, 41). Furthermore, for topologies that contain a limited number of components, it is feasible to perform an exhaustive numerical search through parameter space to determine all possible topologies that are consistent with a particular feature observed in experimental data (35). We have not directly applied these approaches to our problem because inferring network topologies for collective migration is more challenging for multiple reasons. First, cells communicate with each other to sense signal gradient, resulting in a spatially extended system. Second, the output of the system is often a stochastic variable and is only known as an average quantity. In addition to these system-specific challenges, the number of network components might be too large to carry out exhaustive numerical searches. Therefore, we have developed a qualitative perturbation analysis method that can greatly reduce the number of candidate topologies. We then carried out numerical simulations only on the remaining networks for further study.

The final result, i.e., the six possible six-link pathways shown in Fig. 2 c, was verified using both sampling simulations and by a fitting procedure that produced parameter sets for which the model results are fully consistent with all experimental data. We should point out that obtaining a satisfactory fit was not necessarily expected. Our fitting procedure takes into account directionality data (Table 1) that was not used in our qualitative selective procedure. Because we found parameter sets for all topologies that were consistent with the experimental data, we are not able to further distinguish between the six networks. However, additional sampling simulations show that some topologies may be more robust than others (Fig. 4 a). Furthermore, we propose additional experiments, such as combining light treatment with Rac activity measurement, that should be able to further discriminate between possible topologies.

Our study has a number of limitations. First, our analysis provides the simplest four-node topologies that are able to reproduce the experimental data, which turn out to be topologies with six links. Within this class of four-node networks, it is likely that topologies with more than six links can also be consistent with the data. Determining all possible four-node topologies, however, would be computationally prohibitive. Second, it is possible that more complex networks containing more nodes are also able to conform to the data. We show the simulation results for two networks with seven links in Fig. S6. Network 1 is obtained from a combination of the motifs in groups (ii) and (iv) in Fig. 2 a and adds negative feedback from G to R in network A (Fig. 2 c). We again fitted the parameters of this new network and found that the simulation results are similar to the ones obtained in our six-link networks (Fig. S6 and Fig. 4 b). Network 2 is obtained by adding a positive interaction from P to G in network A (Fig. 2 c). Simulations of this network show that the error bars for the number of protrusions are smaller than the ones for the six-link networks (Fig. S6 and Fig. 4 b). The results of network 2 show that new phenomena (smaller error bars in the example) are possible with more links. We do not view the minimal networks with four nodes and six links as the final word on the subject but suggest them as a reasonable start for further research, much as minimal LEGI models have proved useful for studying chemotaxis in other contexts. In summary, our goal in this study was to find minimally complex networks that can then be further selected with additional experiments. It is conceivable that these experiments, which to our knowledge are new, will result in the elimination of all six networks, in which case more complex networks or networks with more links need to be considered. Procedures similar to the ones we used here should then be able to provide possible signaling-pathway architectures.

Despite these limitations, our results provide valuable information about the multicellular signal-processing network in the collective migration of border cells, showing the defect of the multicellular LEGI model (network I in Fig. 2 b) that was studied in (20, 21, 22, 23) and narrowing the topology to only six possibilities. These models may be interesting candidate models to further study collective migration in the border cell system as well as in other systems. For example, in (14, 42), Rab11 and Cdc42’s functions in cell-cell communication are studied using mutations and light treatment of Rac. With their results, we can check which roles they may play in our topologies, and further discrimination of the six topologies may be possible; otherwise, we may need a larger network including some new components. The six topologies that we have found are also potential candidates to study in contexts in which minimal multicellular LEGI models have been previously applied (20, 21, 22, 23). These topologies may potentially provide more gradient-sensing accuracy than the LEGI scheme (20, 21) or may have different chemotactic dependence on cluster sizes (19, 22, 23). In addition, the photoactivatable Rac has been used in other cell types, such as mesendoderm cells (33) and neural crest cells (34), that also show collective cell migration. Application of our approach combined with Rac activation experiments in these systems could show whether the topologies we have found for the border cell cluster migration are robust across different cell types or whether different topologies are optimal for differential biological circumstances. We should point out that if photoactivatable Rac, an excellent tool for the reversible manipulation of proteins, is not practicable, traditional genetic methods may also provide data that can be analyzed by our qualitative approach. For example, in (43), DNA-programmed epithelial cell assembly is used to study multicellular protrusions when Ras is activated in all or some of the cells. The comparison of homogeneous and heterogeneous Ras activity can provide a similar kind of information as that of the ${\text{Receptor}}^{\text{DN}}$ (homogeneous inhibition) and the local light treatment of Rac (heterogeneous activation or inhibition) experiments we use in our work. Thus, our work provides a starting point for future research on signaling networks of collective chemotaxis, and the methods we have developed here may be applied in other collective migrating systems as well.

Author Contributions

H.Y. designed the research, performed the research, analyzed the data, and wrote the manuscript. B.A.C. and W.-J.R. designed the research, analyzed the data, and wrote the manuscript.

Editor: Cynthia Reinhart-King.

Supporting Citations

Reference (44) appears in the Supporting Material.