Abstract
Understanding and optimizing spacing of learning events is a central topic in basic research in learning and memory and has widespread and substantial implications for learning and instruction in real-world settings. Spacing memory retrievals across time improves memory relative to massed practice – the well-known spacing effect. Most spacing research has utilized fixed (predetermined) spacing schedules. Some findings indicate advantages of expanding spacing intervals over equal spacing (e.g., Landauer & Bjork, 1978); however, evidence is mixed (e.g., Karpicke & Roediger, 2007). One potential account of differing findings is that spacing per se is not the primary determinant; rather learning may depend on interactions of spacing with an underlying variable of learning strength that varies for learners and items. If so, learning may be better optimized by adaptive schedules that change spacing in relation to a learner’s ongoing performance. In two studies, we investigated an adaptive spacing algorithm, Adaptive Response-Time-based Sequencing (ARTS; Mettler, Massey & Kellman, 2011) that uses response time along with accuracy in interactive learning to generate spacing. In Experiment 1, we compared adaptive scheduling with fixed schedules having either expanding or equal spacing. In Experiment 2, we compared adaptive scheduling to two fixed “yoked” schedules that were copied from adaptive participants; these equated average spacing and trial characteristics across conditions. In both experiments, adaptive scheduling outperformed fixed conditions at immediate and delayed tests of retention. No evidence was found for differences between expanding and equal spacing. The advantage of adaptive spacing in yoked conditions was primarily due to adaptation to individual items and learners. Adaptive spacing based on ongoing assessments of learning strength for individual items and learners yields greater learning gains than fixed schedules, a finding that helps to understand the spacing effect theoretically and has direct applications for enhancing learning in many domains.
Keywords: adaptive learning, spacing effect, memory, learning
Among the most influential and consequential efforts in the science of learning in recent years have been studies of spacing in learning. Over a century of research on conditions of practice has determined that spacing, or distributing the study of learning material over time, improves long-term retention relative to massing or cramming the material in the short term (Dempster, 1989; Ebbinghaus, 1913; Glenberg, 1976; Rumelhart, 1967; Tsai, 1927). Spacing improves learning across a variety of materials and learning modes. Although item memorization has been most frequently studied, spacing effects have been shown for other types of learning, such as learning of perceptual classifications (Kornell & Bjork, 2008; Mettler & Kellman, 2014; Wahlheim, Dunlosky & Jacoby, 2011). Effects of spacing are robust, affecting long-term retention at multiple timescales of practice (Cepeda, Pashler, Vul, Wixted & Rohrer, 2006; Cepeda, Vul, Rohrer, Wixted & Pashler, 2008), and they are phylogenetically broad, extending beyond human cognition (Zhang et al., 2011).
Spacing has the potential to drive substantial improvements in learning for students in real educational settings (Carpenter, Cepeda, Rohrer, Kang, & Pashler, 2012; Mettler, Massey & Kellman, 2011), and it has been endorsed as a primary recommendation for organizing instruction in an Institute of Education Sciences-sponsored practice guide based on reviews of evidence by a national panel of experts (Pashler et al., 2007). However, the insights derived from both classic and recent work have largely failed to penetrate curriculum and instruction in either K-12 or higher education. The most common formats for organizing curriculum, such as “layer cake” sequences (e.g., studying biology, physics and chemistry in successive grades), massed practice (e.g., studying a given math topic, completing a set of similar problems for homework and then moving on to a new topic the next day), and spiral curricula (studying fractions every year in elementary and middle school math, with long gaps in between) use learning schedules that are associated with poor outcomes in terms of long-term durability of learning (Rohrer & Taylor, 2006; Snider, 2004). Instruction in many education and training settings typically fails to make the critical distinction between performance during or immediately after instruction and long-term retention and recall (Bjork & Bjork, 2011). Further, it fails to recognize that even adult learners have little insight into their own learning processes, typically overestimating the likelihood that they will remember something in the future and not recognizing which study methods improve retention and retrieval in the long run (Bjork, 1999; Bjork, Dunlosky, & Kornell, 2013; Kornell & Bjork, 2007). While knowledgeable teachers can to some degree make up for the metacognitive weaknesses of their students, it is logistically difficult for educators to customize schedules of practice for individual students and topics.
The advent of learning technologies that can track and implement learning schedules brings an entirely new set of tools to the enterprise—tools that can off-load from both students and instructors the difficult task of optimally pacing practice during learning. However, to fully realize their benefit, it is necessary for them to incorporate scientifically sound principles to guide schedules of practice to support learning over meaningful time spans. This paper explores which schedules of practice improve learning outcomes and investigates a novel hypothesis for why they might do so. The findings have important theoretical implications for understanding spacing in fixed and adaptive schedules and have direct potential application for the development of new learning resources and technologies across many domains of learning, including K-12 and college education, medical and other professional education, and training in industry.
If spacing fosters greater learning, a natural question arises: Which spacing intervals are most useful? Further, if items are repeatedly presented, as is typical in real-world learning contexts, what characteristics of spacing across repeated presentations most improve learning? Answering these questions requires some understanding of the mechanisms that make spacing effective.
Why Is Spacing Effective?
A variety of explanations for spacing benefits in learning have been suggested; indeed, within and across various learning tasks, there may be a family of spacing phenomena and explanations for them (Mettler & Kellman, 2014; Glenberg, 1979).
Some proposed explanations for the spacing effect include encoding variability and deficient processing accounts. In encoding variability accounts, adding space between item presentations facilitates variability of the encoding context. That is, the conditions of practice are likely to be different at subsequent presentations of an item as more time elapses between presentations. Differences in context lead to an increase in the probability that memories are encoded in different ways, thus strengthening the memories that are formed (Glenberg, 1979). In deficient processing accounts, it is thought that learners do not process repeated instances of items when spacing intervals are too short. That is, when items are massed, or repeated rapidly in time, learners reduce the amount of attention given to subsequent presentations. Spacing, in contrast, encourages greater attention to repeated presentations of items, thus benefiting memory (Hintzman, 1974). A variant of this idea is that long term learning benefits from periodic retrievals from long term memory but not from recovering information that still resides in working memory (Baddeley, 1986). More recent accounts highlight the role of representations of prior practice, the memorability of initial presentations, or the ease of recognition of items in understanding spacing (e.g., Benjamin & Tullis, 2010; Delaney, Verkoeijen & Spirgel, 2010).
A strong candidate explanation for some of the major benefits of spaced practice in this context is that the value of a learning event differs depending on how well-learned an item is, i.e., an internal variable of learning strength. Learning strength will tend to decline over time, making successful retrieval more difficult as the time since the last presentation or retrieval increases, and as suggested by many studies of spacing, it is likely influenced by a number of other variables. The optimal time to practice an item is when retrieval is difficult but can still succeed. This retrieval effort hypothesis follows from the desirable difficulty framework of Bjork & Bjork (1992), and has been supported by a number of studies (Pyc & Rawson, 2009; Thios & D’Agostino, 1976; Johnston & Uhl, 1976). Results show that the difficulty of retrieval can be induced in a number of ways—for example, by interleaving difficult tasks between retrieval attempts (Bjork & Allen, 1970), changing the amount of memory interference that retrieval attempts encounter (Storm, Bjork & Storm, 2010), or manipulating the number of retrieval attempts that an item receives before a test (Pyc & Rawson, 2009). Retrieval effort can also be induced by stretching the spacing intervals over which retrievals are attempted. The variety of variables shown in research to influence retrieval effort suggests that fluctuations of learning strength in a learning session arise from numerous and subtle influences that would be difficult to capture in an a priori model.
Fixed schedules incorporating expanding intervals of retrieval practice (Landauer & Bjork, 1978; Cull, Shaughnessy & Zechmeister, 1996) may improve learning because the schedule of retrievals is congruent with changes in the strength of learning items in memory. In expanding practice, initial spacing intervals are short since learning strength is initially low, but spacing intervals gradually grow, under the expectation that information can be retrieved at longer delays. Further, the greatest benefits to learning strength will be gained from difficult retrievals at the largest possible delays—temporally close to, but not past, the point of forgetting. If the intervals are felicitously chosen, expanding the retrieval interval thus can ensure that retrievals remain difficult and widely spaced, improving long-term learning.
Despite intuitions that expanding retrieval practice is beneficial for learning, the evidence for benefits of expanding spacing relative to other spacing schedules, such as equal interval spaced presentation, is mixed (Karpicke & Roediger 2007, 2010). Karpicke & Roediger (2007) reported that equal interval practice is actually superior to expanding practice when measured at a delayed test, and further, that there were no differences in learning outcomes between equal or expanding schedules when the size of their initial spacing interval was equated. Other studies have demonstrated similar equivocal results. Karpicke & Bauernschmidt (2011) found no evidence for or against expanding interval practice in a study where learners were trained to an initial criterion of proficiency, similar to other research (Carpenter & DeLosh, 2005). Contrary to these results, Storm, Bjork and Storm (2010) have reported that memory was better for an expanding schedule of practice, but only when items that intervened during spacing were highly related to spaced items, suggesting that expanding intervals are most beneficial when the potential for forgetting is high.
Spacing Intervals and Learning Strength
From the standpoint of the retrieval effort hypothesis (or any perspective that relates spacing to changing learning strength), the mixed results of research testing fixed schedules of spacing are not surprising. Fixed spacing intervals may be poorly suited to variations in the learning strength of items for a given learner. Some items may, across learners, be more difficult to learn, but learning strengths for various items in the course of learning seem likely to reflect individual interactions of learners and items. Although a preset schedule of expanding spacing intervals across trials will tend to correlate with increasing learning strength for a typical item, the match may be far from perfect. Even if learning strength increases monotonically, preset intervals may expand too much or not enough. In some cases, learning strength may actually be a non-monotonic function of trials, depending on item difficulty and relations among items being learned. From the standpoint of the retrieval difficulty hypothesis, the use of predetermined intervals may be less effective than flexible spacing arrangements that match current learning strength to spacing intervals.
Adaptive Schedules of Practice
Ideal schedules of spacing for each item would be based on learning strength at particular times for each individual learner. How might we get ongoing measures of learning strength during a learning session? Adaptive learning methods have been proposed that determine recurrence of learning items based on accuracy (Atkinson, 1972; Pavlik & Anderson, 2008; Mozer, Pashler, Cepeda, Lindsey & Vul, 2009). However, spacing based on accuracy alone does not distinguish between easier and more difficult retrievals. Adaptive systems that estimate learning parameters for different items by carrying out a prior study with the learning materials and a similar group of learners (Atkinson, 1972; Pavlik & Anderson, 2008) may capture some of the variations in learning strength, but do so by relying on binary accuracy information alone. A more direct method of tracking learning strength might be possible using an ongoing indicator of learning strength—one that might vary for different learners, items, and their interactions. Such a system could adjust spacing schedules in response to the ongoing behavior of each learner.
The ARTS system.
Evidence indicates that response time (RT) is a useful indicator of retrieval difficulty, and thus of an item’s current learning strength (Pyc & Rawson 2009; Benjamin & Bjork, 1996; Karpicke & Bauernschmidt, 2011). This relationship offers a useful way of updating spacing to track underlying learning strength: Adaptive methods can use an individual’s accuracy and RT performance data for learning items to dynamically schedule spacing intervals. Mettler, Massey, and Kellman (2011) showed that a system that determines spacing dynamically based on each learner’s accuracy and speed in interactive learning trials (the Adaptive Response-Time-based Sequencing or ARTS system) produced highly efficient learning and compared favorably with a classic adaptive learning system (Atkinson, 1972).
Unlike other adaptive systems that compute a model of memory strength for individual items (Atkinson, 1972) or a model of memory improvement per unit of practice time (Pavlik & Anderson, 2008), the ARTS algorithm does not model learning strength so much as attempt to read it directly through reaction time measures. ARTS uses a priority score system, in which the priority for an item to reappear on each learning trial is computed dynamically as a function of accuracy, response time, and trials since the last presentation. Priority scores for items can increase at different rates, and the item with the highest priority is always selected for presentation on the next trial. Therefore, priority scores represent competition for presentation rather than a direct model of learning strength.
Because all items compete for presentation on any trial through their priority scores, the system concurrently implements adaptive spacing for all learning items. As learning strength increases, as reflected in performance, delay intervals automatically expand in this system. Errors in accuracy or increases in RT can also cause the delay interval to contract. Also, in some previous implementations, the system enforces mastery criteria based on both accuracy and speed. Since it is expected that benefits to memory should be greatest when retrieval is difficult but also correct, performance during learning in terms of accuracy should stay high. Combined with the goal of improving speed of learners’ responses, ARTS thus enforces efficient learning in terms of memory gain per unit time (as in Pavlik & Anderson, 2008).
Comparing Fixed vs. Adaptive Spacing
In the current studies, we compared an adaptive scheduling algorithm, ARTS, to fixed schedules of practice. We focused on several questions. First, do adaptive schedules of practice outperform fixed schedules (of either the equal spacing or expanding spacing types)? We tested this in Experiment 1 by directly comparing fixed and adaptive schedules. Second, if adaptive schedules are better, how are these benefits attained? In particular, can we uncover evidence indicating whether it is adaptation to individual learners versus adaptation relating to particular learning items that confers more benefit? We tested this question in Experiment 2 using methods designed to distinguish between these influences.
We know of no previous work comparing adaptive schedules to fixed schedules. The research literature on fixed schedules of spacing and the literature on adaptive learning have been largely distinct. Substantial work has explored scheduling based on adaptive techniques (Mozer, et al., 2009; Pavlik & Anderson, 2008; Wozniak & Gorzelanczyk, 1994), and a separate large literature addresses issues related to the scheduling of a few fixed trials of practice; however no prior study has attempted to compare fixed and adaptive schedules to assess the comparative benefits of each.1
Carrying out experimental research comparing fixed spacing and adaptive schemes raises some interesting collateral issues. Studies of adaptive learning and typical studies of item memory tend to have different structures, related to different goals. Perhaps the most important difference for present purposes is whether learning sessions have fixed or variable duration. In some adaptive systems, including ARTS, learning proceeds, not for a fixed number of trials or presentations, but to criteria of mastery. An important benefit of adaptive, interactive learning when applied to real-world learning situations is that each component of learning (e.g., each item in fact learning or each category in perceptual learning; Mettler & Kellman, 2014) can be tracked in terms of an individual learner’s performance, with each learner guided to objective mastery criteria (in ARTS, both accuracy and speed of response criteria). Components that have been mastered may be dropped out (retired) from the learning set, and the course of learning ends when each component has been mastered.
In contrast, studies of predetermined equal vs. expanding spacing intervals have almost all used a fixed number of item presentations, often 3 or 4. This approach provides better experimental control for condition comparisons, although it seldom results in mastery of all of the learning material in any condition (see Rawson & Dunlosky, 2011 for criticism of the reliance on fixed amounts of practice in studies of the spacing effect).
In the experiments described here, we adopted experimental protocols that resemble prior studies of spacing intervals in memory; specifically, each condition involved 4 presentations of an item in all cases. This approach provided comparability to earlier spacing work and allowed direct comparison of accuracy gains in learning across conditions, without having to factor in variable numbers of trials for individual learners to reach mastery criteria. One drawback of this approach is that adaptive learning schemes may have most value when learning to criterion is used. In fact, prior work with the ARTS system (e.g., Mettler et al, 2011; Mettler & Kellman, 2014) raises the question of whether the advantages of adaptive learning are even manifest in the first several presentations of an item. In forthcoming work, we take up the comparison of fixed and adaptive spacing schedules when learning to criterion is used (Mettler, 2014).
Experiment 1
To compare adaptive and fixed spacing schedules, we used a geography learning task. Participants learned 24 country names and locations on a map of Africa. Each item was presented 4 times and all items were presented in a single session. The primary experimental manipulation was the method of determining spacing intervals between the 4 presentations of each item. There were 3 different types of delay schedule: The adaptive group of participants received items using the ARTS adaptive algorithm (see below), which dynamically spaces item presentation intervals based on real-time performance data. Another group of participants received a fixed schedule of practice where half of their learning items were scheduled according to an equal schedule of practice (5–5–5 intervening items) and the other half of their items were scheduled according to an expanding schedule of practice (1–5–9 intervening items). These particular fixed intervals were chosen from those commonly used in the literature on spacing schedules.
In the learning session, every presentation consisted of a test trial on which a participant was shown a map of Africa with national boundaries drawn in but without names (see Figure 1). One country was highlighted and the participant was asked to pick the correct name from a list of 38 country names. Participants were given accuracy feedback and, in the case of an incorrect response, they were shown the correct answer. Participants were given a pretest before the learning session and an immediate posttest immediately after the learning session. The pre and posttests were identical to training trials except that there was no feedback given after a response. Each country was tested once in pretest and once in posttest. Finally, participants returned for a delayed posttest after one week. The delayed posttest was identical to the immediate posttest. The order of test items was randomized for each test. If adaptive scheduling produces better learning than fixed scheduling, we expected that participants would perform better on measures of recall at both immediate and delayed posttests.
Figure 1.
Example of trial format used in learning and assessment phases of the experiments. Each trial displayed a map of Africa with a target country highlighted, and a list of response choices on the right side of screen.
Planned Analyses
The primary dependent measures were accuracy and response times (RTs) across items. In addition to these performance measures, the actual spacings generated by adaptive scheduling were compared to those chosen for fixed schedules. This experiment also served as a baseline for determining the individual item intervals for Experiment 2 (adaptive sequencing vs. fixed yoked schedules).
Method
Participants.
Participants were 72 undergraduate psychology students who received course credit for completing the experiment. The stopping rule for data collection in both experiments was when there were at least 16 participants in each condition, allowing for more if in a week cycle of participant pool signups there were more than 16. We decided to run twice as many participants in the fixed condition due to the within subject design, for a total of 36 participants in each condition.
Materials.
The learning materials consisted of 24 African countries that participants were required to identify on a map of Africa. 14 additional countries were used as ‘filler’ items in order to space presentations appropriately, especially at the end of learning sessions (see note on filler items in ‘Filler items and jitter in fixed schedules’). All material was presented on a computer within a web-based application. Participants saw a 500 pixel by 800 pixel map of Africa on the left side of the screen and a two-column list of African countries alphabetically organized by column then row (Figure 1). Each list label was a software button that could be independently selected using a computer mouse.
Design.
There were two between-subject conditions, adaptive spacing and fixed spacing. There were two within-subject fixed spacing conditions, fixed-equal spacing and fixed-expanding spacing. In the fixed spacing conditions, one random half of learning items were assigned to the fixed-equal condition and the other half were assigned to the fixed-expanding spacing condition.
Adaptive Response-Time-based Sequencing (ARTS).
The ARTS sequencing algorithm calculated a priority score for each learning item, where, on any subsequent trial, priority scores were compared across items to determine the likelihood of an item being presented on that trial. Details of the priority score calculation are given in Equation 1 (and below) and parameters are given in the appendix (Table A.1)2.
| (1) |
Priority P for item i was determined as a function of the number of trials since that item was last presented Ni, an enforced delay D (a constant, which was set to 1 in the experiments here), and the accuracy (αi) and response time (RTi) on the previous presentation of that item. Accuracy (αi) was a binary variable determined by the correctness of the user’s response: 0 if the question was answered correctly, 1 otherwise. This binary accuracy variable acted as a switch activating either the error part of the equation (for an incorrect answer) or the RT part of the equation (for a correct answer). The rationale was that RTs for incorrect answers were not considered informative for spacing. An incorrectly answered item was given a large priority increment (W) that typically ensured re-presentation after a delay of one trial. Correctly answered items were assigned a priority score that was a log function of RT (where the logarithm was used to weight small differences among RTs more heavily for shorter RTs than for longer ones). Item presentation on a given trial was always decided by choosing the item with the largest priority score (P) in the set. In addition, the introduction of new items was controlled by the assignment of default priority scores to all items, allowing for the introduction of new items once previously introduced items became better learned and had lower priority scores than the default. Parameters a, b, r, were weighting constants: a controlled the rapidity with which priority accumulated as a function of elapsed trials; b and r modulated the relation between RTs and spacing intervals.
Although priority score equations using response time and accuracy can take many forms, the parameters here were fixed and identical in both Experiment 1 and 2, and were also similar to those used in previously published research on item learning (Mettler, Massey & Kellman, 2011) and perceptual category learning (Mettler & Kellman, 2014). It is important to note that priority scores generated by Equation 1 are related to but do not directly reflect learning strength. Priority scores indicate the degree to which items need practice and will differ from accuracy and RT based measures of learning strength in certain situations. For instance, priority scores for incorrect responses reflect the importance of re-presentation of missed items rather than estimates of their learning strength. In addition, priority scores can go beyond the information available in an individual response, such as incorporating the effects of trial feedback on estimates of learning strength.
Taken together, the elements of the priority score equation given here implement a number of principles of learning that have been derived in memory research, including rapid recurrence of missed items; but enforcing at least some delay in re-presenting an item, in order to make sure the answer does not still reside in working memory; and stretching the retention or recurrence interval as learning strength, indicated by accuracy and RT, increases.
Procedure.
In all sessions of the experiment, learning items were presented singly, in the form of test trials. Participants were shown a map of Africa featuring an outlined country and were asked to select, from a list of labels containing country names, the name that matched the highlighted country. Participants used the computer mouse to select from the list of names.
Participants attended two sessions, separated by one week. In the first session, participants initially took a pretest on all items, then completed a training phase, followed by an immediate posttest. The entire session took no more than one hour for each participant. Pretests contained all 38 target and filler items, presented in random order. During the pretest, participants were not given feedback. The pretest was followed by a learning phase that consisted of the same type of trial as the pretest, except that participants were given feedback after each response showing the correctness of their response as well as a label indicating the correct answer. The learning phase took up the majority of the first session of the experiment. After every ten trials in the learning phase, participants received block feedback indicating their average response accuracy and average response speed for the previous block of 10 trials and every previous block up to 10 prior blocks. After the learning phase, an immediate posttest was administered, identical to that given in the pretest. After the posttest participants were instructed to return in one week and were asked not to study or reflect on the information learned. A delayed posttest, identical to the immediate posttest, was administered after one week. No feedback was given on either posttest.
Spacing conditions.
Participants were randomly assigned to fixed or adaptive scheduling conditions, with 36 participants in each condition. In the adaptive condition, all learning trials were adaptively sequenced according to the response-time-based ARTS algorithm. In the fixed condition, one random half of each participant’s items were scheduled according to an equal spacing scheme, and the other random half were scheduled according to an expanding spacing scheme. Thus, in the fixed condition, every participant received two within-subject conditions that manipulated fixed scheduling in either an expanding or equal spacing scheme. This interleaving of conditions was done primarily to avoid the problem of excessive filler items in the expanding spacing condition.
In the fixed spacing group, spacing intervals between presentations were pre-determined and constant. Items in the fixed-equal condition received spacing of 5 trials between items. Items in the fixed-expanding condition received first 1, then 5, then 9 trials between presentations of each item. For every participant in the fixed condition, the order of presentation was pre-set so that every participant received the same number and order of fixed equal or expanding trials. Items in the fixed condition did not strictly alternate between equal and expanding schedules, but every attempt was made to balance the number of equal and fixed schedules across position in the entire learning phase, so as not to confound serial position with schedule type. Although the order of presentation of items in the fixed condition was fixed, the assignment of individual items to either of the two schedule types was randomized for each participant. In addition, the order of introduction of individual items was shuffled across possible positions in the pre-set schedule for each participant before the learning phase began.
For every participant in the adaptive condition, the total schedule order was dynamically decided during the learning session, and the order of introduction of new items was chosen randomly from the remaining items in a learning set for each participant.
In all conditions in Experiment 1, each learning item was presented a total of four times.
Filler items and jitter in fixed schedules.
There are two problems that arise when applying the same fixed schedule of practice to every item in a learning sesession. First, the structure of fixed spacing intervals does not allow continuous presentation of items without conflicts in the intended interval schedule for each item. Imagine 4 items (labeled A through D) each presented first with a 1-trial interval, then a 3-trial interval. The layout of this presentation sequence would appear as follows: A, B, A, B, C, D, [A or C?]. The 7th presentation indicates a conflict between the first and third item. These conflicts appear most frequently with fixed-expanding schedules, and less frequently with fixed-equal schedules or with adaptive schedules. One solution to this type of conflict is to allow for a degree of “jitter” in any given fixed schedule. We added jitter to fixed schedules using a simple rule: Each set of 3 spacing intervals between the four presentations of an item in the fixed condition was allowed to deviate from its pre-set interval (e.g., 1–5–9) by one position, smaller or larger, at any interval except the first. For example, 1–6–9, 1–5–9, 1–5–10 would all be valid “jittered” versions of the 1–5–9 expanding interval. In addition to jitter, conflicts were reduced naturally as a result of mixing expanding and equal fixed schedules.
A second problem with interleaving fixed schedules is that there are inevitably gaps, or trials where no item is scheduled to be presented. Filler items can be used to support the interleaving of items with fixed schedules while preventing gaps, and also to maintain appropriate spacing intervals at the end of a learning session, when no target learning items remain in the set. Filler items in the current study consisted of presentations of 14 additional countries, randomly selected whenever filler items were needed. Filler items were necessary in the fixed conditions and the adaptive presentation conditions; in both cases the final few presentations of items occur at larger and larger spacing intervals, requiring filler items when no new target items are available.
By combining expanding and equal schedule presentations into the same session, and by applying jitter as well as adding filler items, we were able to design a single fixed session that used limited filler items. Thus, filler items were utilized primarily to fill expanding schedules at the end of training and their use was equated across both adaptive and fixed conditions.
Sequencing parameters.
The default adaptive sequencing parameters are described in the Appendix, Table A.1. In this study, the default parameters were used for the adaptive algorithm, with some modifications. It was found in pilot testing that our default parameters were less effective when applied to a learning session limited by a total number of presentations per item, rather than a learning session where learners continue until meeting a learning criterion. The following parameters were changed to better support the current type of study : “RT weight,” r = 3.0; “enforced delay,” D = 1.
Results
The primary results of Experiment 1 are shown in Figure 2, which shows mean accuracy across phase. The adaptive condition showed higher accuracy than both fixed spacing conditions in the learning phase and also at delayed posttest, where fixed-equal and fixed-expanding conditions showed similar performance. In the immediate posttest, the adaptive condition produced higher performance than fixed-equal, with fixed-expanding scores intermediate between the other two conditions.
Figure 2.

Mean proportion correct by experiment phase across 3 scheduling conditions in Experiment 1. Error bars show +/− 1 standard error of the mean.
These observations were confirmed by the analyses. At pretest, adaptive accuracies were highest (M = 0.076, SD = 0.27), followed by fixed expanding (M = 0.051, SD = 0.22) and fixed equal (M = 0.042, SD = 0.20). Comparisons between conditions showed a significant difference for adaptive vs. fixed equal (t(70) = 2.19, p = .032), but not for adaptive vs. fixed expanding (t(70) = 1.54, p = .13), or fixed equal vs. fixed expanding (t(35) = 0.73, p = .47). These differences indicate some pretest differences in performance across groups, despite random assignment of participants to conditions. Overall mean pretest scores (M = 0.056, SD = 0.072) were significantly different from chance responding (one sample t test: t(107) = 4.13, p < .01), suggesting that some participants possessed some prior knowledge of some countries. (Chance responding would have been 1 correct item out of 38, or .026.) Because it is not clear whether pretest scores reflected random variation or modest systematic differences between conditions, we considered in the analyses below both posttest accuracies as well as change scores between pretest and posttests.
Accuracy.
Performance results were not analyzed using a standard one-way ANOVA due to the special combination of between- and within-subjects factors. (Only the adaptive vs. fixed comparisons were between subjects.) Three ANOVAs were used, one for each comparison of pairs of conditions, with test-phase as a within subjects factor.
A 2×2 mixed factor ANOVA with factors of adaptive vs. fixed-equal conditions and posttest phase (immediate vs. delayed) found a significant main effect of condition (F(1,70) = 4.63, p = .035, = .062), a main effect of test phase (F(1,70) = 110.56, p < .001, = .612) and no interaction of test phase and condition (F(1,70) = 1.06, p = .31, = .015). These results indicate significantly higher accuracies in the posttests for the adaptive condition vs. the fixed-equal condition. For adaptive vs. fixed-expanding conditions, a 2×2 mixed factor ANOVA on condition and test phase found no significant main effect of condition (F(1,70) = 2.37, p = .13, = .033), a significant main effect of test phase (F(1,70) = 147.0, p < .001, = .677), and a significant condition by test phase interaction (F(1,70) = 5.1, p = .027, = .068). For the two fixed conditions, a 2×2 condition by posttest phase repeated measures ANOVA found a marginal main effect of condition (F(1,70) = 3.13, p = .081, = .043), a main effect of test phase (F(1,35) = 126, p < .001, = .783), and no condition by test phase interaction (F(1,70) = 1.18, p = .28, = .017). A Bartlett’s test confirmed homogeneity of variance for accuracies at both posttests (immediate: p = .64, delayed: p = .31).
At immediate posttest, average accuracies were highest for the adaptive condition (M = 0.61, SD = 0.21), lower for the fixed-expanding condition (M = 0.58, SD = 0.23), and lowest for the fixed-equal condition (M = 0.52, SD = 0.24). Individual comparisons showed that accuracies did not differ significantly at immediate posttest between the adaptive and fixed conditions (adaptive vs. fixed-equal: t(70) = 1.63, p = .11; adaptive vs. fixed-expanding: t(70) = 0.55, p = .58). A paired t test showed that the two within-subject fixed conditions differed significantly (t(35) = 2.15, p = .039, Cohen’s d = 0.24).
At delayed posttest, accuracies were highest in the adaptive condition (M = 0.42, SD = 0.20), and lower for the two fixed conditions: fixed-expanding (M = 0.31, SD = 0.19) and fixed-equal (M = 0.30, SD = 0.24). Individual comparisons showed average accuracies for the adaptive condition were significantly greater than both of the fixed spacing conditions (adaptive vs. fixed-expanding: t(70) = 2.41, p = .019, Cohen’s d = 0.56; adaptive vs. fixed-equal: t(70) = 2.38, p = .02, Cohen’s d = 0.57). A paired t test showed that the fixed-expanding and fixed-equal spacing means were not significantly different from each other (t(35) = 0.45, p = .65).
Change and gain scores.
Because there were detectable differences between conditions at pretest, we examined posttest results in terms of scores that looked at posttest accuracy in relation to pretest scores. We computed two types of change score for each participant, which we labeled change scores and gain scores. Change scores were computed by subtracting average pretest accuracies from average posttest accuracies.
Immediate posttest change scores were computed by subtracting a participant’s average pretest accuracy from their average posttest accuracy, and delayed posttest change scores were computed by subtracting average pretest accuracy from average delayed posttest accuracy. Posttest and delayed posttest change scores are shown in Figure 3.
Figure 3.
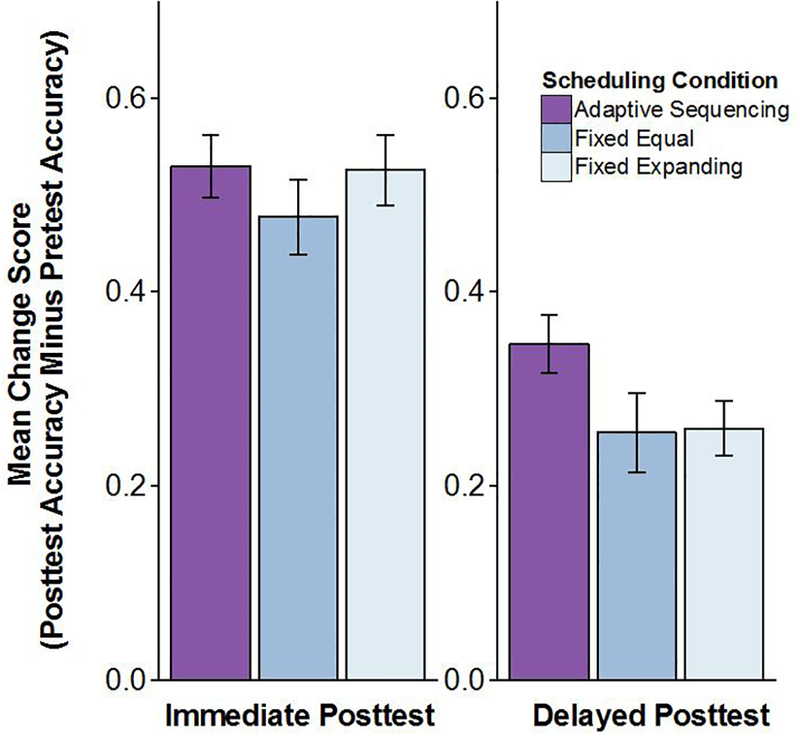
Mean change in accuracy from pretest to posttests across 3 scheduling conditions in Experiment 1. Left panel shows difference between immediate posttest and pretest. Right panel shows difference between delayed posttest and pretest. Error bars show +/− 1 standard error of the mean.
The ANOVAs conducted on change scores were parallel to those carried out for accuracy scores above. For adaptive vs. fixed-expanding, a 2×2 mixed factor ANOVA on condition and test phase found no main effect of condition (F(1,70) = 1.21, p = .28, = .017), a main effect of test phase (F(1,70) = 147.13, p < .001, = .678), and a significant condition by test phase interaction (F(1,70) = 5.03, p = .028, = .067). For adaptive vs. fixed-equal spacing, there was no significant main effect of condition (F(1,70) = 2.37, p = .13, = .032), a main effect of test phase (F(1,70) = 110.68, p < .001, = .613), and no significant condition by test phase interaction (F(1,70) = 1.03, p = .31, = .015). For fixed-expanding vs. fixed-equal spacing, there was no main effect of condition (F(1,70) = 1.29, p = .26, = .018), a main effect of test phase (F(1,35) = 126, p < .001, = .783), and no significant condition by test phase interaction (F(1,70) = 0.88, p = .35, = .012).
Individual comparisons at immediate test showed that change scores were similar for all schedules and did not differ significantly (adaptive vs. fixed-equal: t(70) = 1.03, p = .30, Cohen’s d = 0.02; adaptive vs. fixed-expanding: t(70) = 0.076, p = .94, Cohen’s d = 0.25; paired t test between fixed-equal and fixed-expanding conditions: t(35) = 1.58, p = .12, Cohen’s d = 0.22). At delayed-test, change scores appeared to be higher in the adaptive condition (M = 0.35, SD = 0.18) than in either the fixed-equal condition (M = 0.25, SD = 0.24) or the fixed-expanding condition (M = 0.26, SD = 0.17). There was a significant difference between the adaptive and fixed-expanding condition (t(70) = 2.11, p = .04, Cohen’s d = 0.50) and a marginally significant difference between the adaptive and fixed-equal condition (t(70) = 1.81, p = .07, Cohen’s d = 0.43). A paired t test between the two fixed conditions showed no significant difference (fixed-equal vs. fixed-expanding: t(35) = 0.13, p = .90, Cohen’s d = 0.02).
In addition to change scores, we computed gain scores by subtracting pretest scores from posttest scores, but did not include items that were accurate at pretest but inaccurate at posttest. Gain scores were computed to address the possibility that differences in pretest scores were primarily due to chance. Gain scores showed similar results to change scores, with the following differences: an ANOVA found a marginally significant main effect of condition between adaptive and fixed-equal conditions (p=0.08) and t-tests at delayed posttest showed significant differences between adaptive and both fixed conditions (adaptive vs. fixed-equal, p=0.03; adaptive vs. fixed-expanding, p=0.02).
Response times.
Average response times (RTs) are shown in Figure 4 for each condition and for three experimental phases: the learning phase, immediate posttest and delayed posttest. RT data only include RTs from trials that were answered correctly. Pretests are ignored owing to the few items that were answered correctly in that phase. Of most interest were RTs at training and at immediate and delayed posttests.
Figure 4.
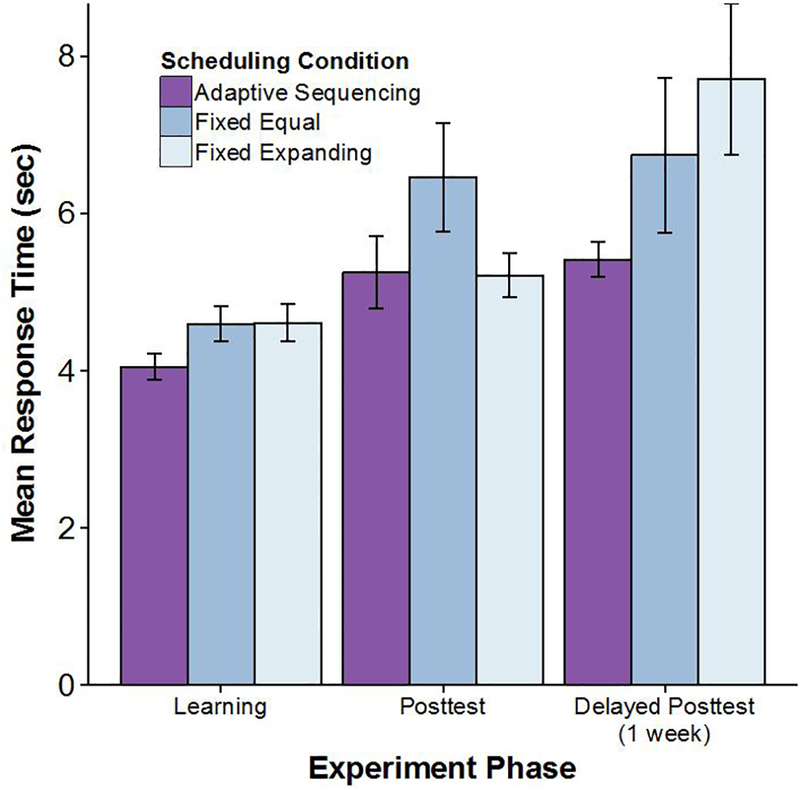
Mean response times (in seconds) at each test phase across 3 scheduling conditions in Experiment 1. Response times are from correctly answered trials only. Error bars show +/− 1 standard error of the mean.
ANOVAs were not carried out on RTs, due to missing data for 4 participants who answered no items correctly at either immediate or delayed posttest3. During training, adaptive RTs were lowest (M = 4.04 sec, SD = 0.99) followed by fixed-equal (M = 4.59, SD = 1.34), then fixed-expanding (M = 4.61, SD = 1.4). Individual comparisons showed that the difference between the adaptive and the two fixed conditions was marginally significant (adaptive vs. fixed-expanding: t(70) = 1.97, p = .052, Cohen’s d = 0.47; adaptive vs. fixed-equal: t(70) = 1.97, p = .053, Cohen’s d = 0.47), but a paired t test between the two fixed conditions showed no significant difference (t(35) = 0.11, p = .9, Cohen’s d = 0.012). At immediate posttest, t tests between conditions showed no significant difference between adaptive and the two fixed conditions (adaptive vs. fixed-expanding: t(69) = 0.07, p = .94, Cohen’s d = 0.02; adaptive vs. fixed-equal: t(70) = 1.46, p = .15, Cohen’s d = 0.35) and a paired t test between the two fixed conditions showed no significant difference (t(34) = 1.39, p = .17, Cohen’s d = 0.43). At the delayed posttest there was a significant difference between the adaptive and fixed-expanding conditions (t(69) = 2.3, p = .02, Cohen’s d = 0.64), but other RTs were not significantly different from one another (adaptive vs. fixed-equal: t(66) = 1.31, p = .19, Cohen’s d = 0.36; fixed-equal vs. fixed-expanding: t(30) = 1.48, p = .15, Cohen’s d = 0.166). Comparing RTs across posttest phases, only the difference between the fixed-expanding condition at posttest vs. delayed posttest was significant (t(33) = 2.8, p = .008; all other ps > .70).
We also examined the RTs at each presentation in learning across the three schedules. Response times during the learning phase are shown in Figure 5 by scheduling condition and presentation number.
Figure 5.
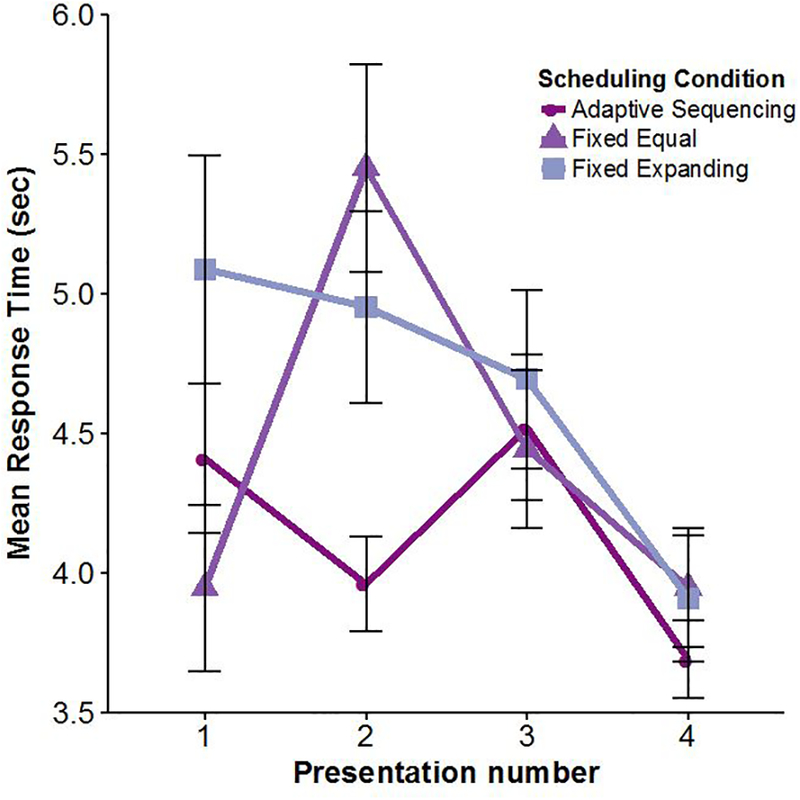
Mean response times (in seconds) at each presentation (1–4) during learning, across the 3 scheduling conditions in Experiment 1. Response times are from correctly answered trials only. Error bars show +/− 1 standard error of the mean.
Examination of response times revealed that conditions did not differ in response times at the first, third, or fourth presentation: only the two fixed conditions differed (fixed-equal vs. fixed-expanding: t(13) = 3, p = .01; all other t test ps > .05). Other conditions showed differences at the second presentation. There were significant differences between the adaptive and fixed conditions (adaptive vs. fixed-expanding: t(70) = 2.59, p = .01; adaptive vs. fixed-equal: t(69) = 3.64, p < .001) but not between the two fixed conditions (t(34) = 1.06, p = .29, paired t test).
Analyses of average spacing intervals.
We define the spacing interval (or shorthand, interval) as the number of trials intervening between two presentations of the same learning item. Adaptive and fixed conditions differed in the size of spacing intervals for individual items during learning sessions. The mean spacing interval per learner was calculated by averaging the mean presentation interval for each item and averaging over all items. In the fixed-equal and fixed-expanding conditions, the intervals chosen in the experiment (1–5–9 and 5–5–5) ensured that mean intervals were always 5 trials in length. Average adaptive schedule intervals were close in length but with some variance (M = 6.7, SD = 2.033)4. We also looked at the size of intervals conditional on whether the presentation before the interval was responded to correctly or not. The mean interval size by scheduling condition and conditional on response accuracy are shown in Figure 6. Although the mean adaptive interval size was similar to the mean interval size for fixed schedules, adaptive spacing intervals after incorrect responses were short (M = 1.01, SD = 0.09) owing to the enforced delay mechanism, and they were longer following correct responses (M = 10.88, SD = 6.50).
Figure 6.
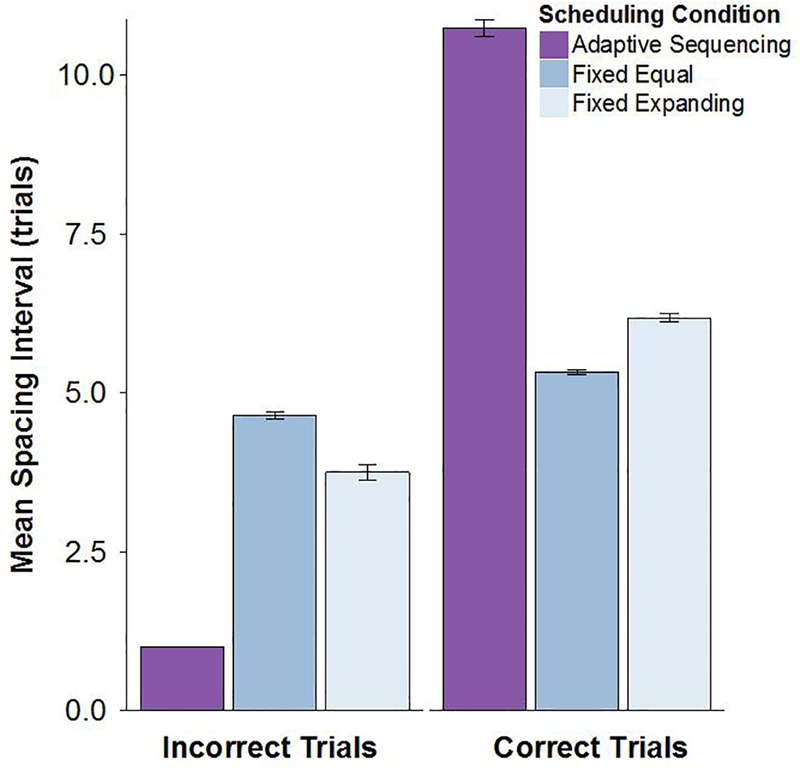
Mean spacing interval (in trials) across 3 scheduling conditions in Experiment 1 conditional on whether the trial preceding the interval was answered correctly or not. Error bars show +/− 1 standard error of the mean.
Finally, we examined the average spacing intervals at each presentation number for the adaptive condition. Because each item was presented 4 times, there were three spacing intervals. The mean sizes of the three intervals in the adaptive condition are shown in Figure 7. The mean initial interval was the smallest (M = 1.62, SD = 0.71), the second interval largest (M = 10.95, SD = 4.46), and the third interval smaller than the second interval (M = 7.52, SD = 2.20).
Figure 7.
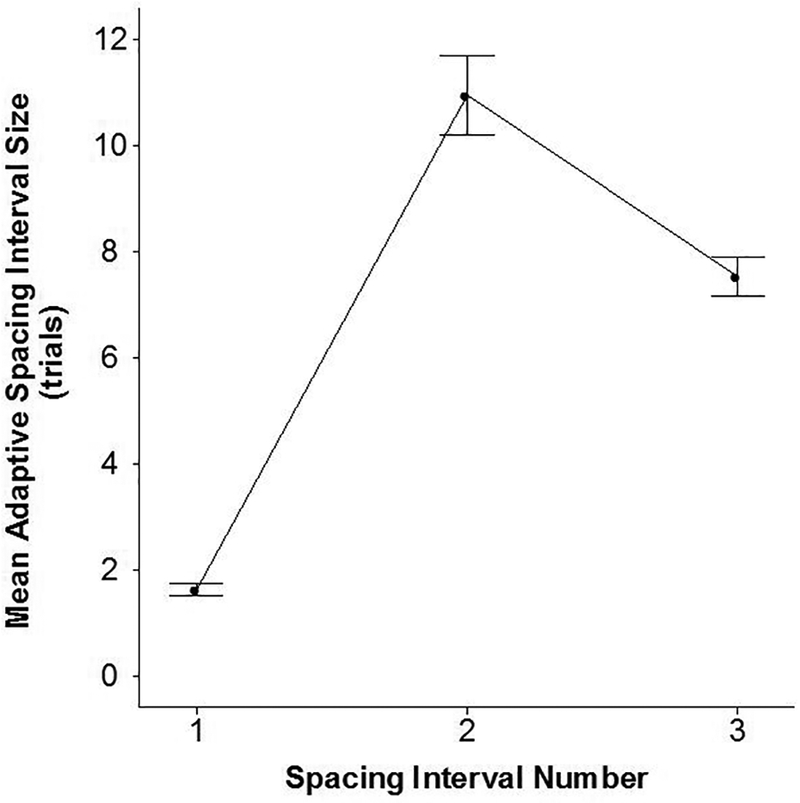
Mean spacing interval size (in trials) across 3 spacing intervals in the adaptive scheduling condition in Experiment 1. Error bars show +/− 1 standard error of the mean.
While it appears that the pattern of retrievals was not expanding, but expanding-then-contracting, in fact, a line of best fit to these points still yields a positive slope. There were also 4 adaptive participants who showed strictly expanding profiles, positively increasing interval sizes at each presentation.
Discussion
As demonstrated by a variety of measures, an adaptive sequencing algorithm outperformed pre-determined schedules of practice. These patterns were clear in posttest accuracy as well as two derived measures of accuracy that discounted prior knowledge from measures of learning. Change scores were computed by subtracting pretest accuracy from posttest accuracy for each participant, and gain scores were computed by subtracting from posttest accuracy only those items that were known at both pretest and posttest. Both measures showed significant differences in learning across scheduling conditions. Change scores showed that learners experienced significantly greater learning in the adaptive condition than in the fixed-equal condition. Gain scores showed significantly stronger gains in the adaptive condition than in either of the fixed scheduling conditions. In addition, these improvements were present with medium to large effect sizes, and gains were retained across a considerable delay (1 week), suggesting that adaptive scheduling techniques produce greater and more durable learning.
In addition to learning gains measured by accuracy, there was a trend for greater fluency (faster responding) for participants who learned using an adaptive scheduling algorithm than for participants who learned using fixed-expanding schedules of practice. Our expectations for RT differences between conditions were consistent with these trends. Since ARTS generates larger spacing delays when responses are faster, it was hoped that responses would become faster, and thus spacing delays longer, over time. It appears that adaptive scheduling may produce better fluency, an important learning goal that relates not only to the durability of learning but the ability to use learned information or skills in complex tasks (Kellman & Garrigan, 2009).
These results are consistent with mechanisms that have been proposed to explain the benefits of spacing in learning. Retrieval difficulty, a major driver of spacing effects, may depend on underlying learning strength, an internal variable that is likely to vary from trial to trial, between individuals, and among learning items. Study-phase retrieval accounts of the spacing effect posit that retrieval difficulty depends on access to representations of prior practice, the memorability of initial presentations, or the ease of recognition of items (see Benjamin & Tullis, 2010; Delaney, Verkoeijen & Spirgel, 2010; or Johnston & Uhl, 1976). Given that the determinants of retrieval difficulty may be numerous, pre-determined intervals of spacing, even when based on elaborate cognitive models, are likely unable to consistently match the requirements of optimal practice. Fluctuations in learning strength, in the ability to access previous memory traces, or in the difficulty of item recognition or recall may preclude consistent, predictable levels of retrieval difficulty.
The ARTS system used here adds RT to accuracy as an ongoing measure of learning strength for each learning item, specific to each learner, at each point in learning at which the next spacing interval needs to be determined. Though RTs may have other determinants – such as lapses in attention – RTs are at least a reasonable proxy for learning strength; a connection supported by other research (Pyc & Rawson, 2009). Relative differences in RTs can reflect changes that occur in learning strength of individual items as learning progresses and can be used to optimize spacing for each item. The advantages of adaptive spacing in the current study further confirms that response times can serve as useful measures of learning strength (Benjamin & Bjork, 1996; Pyc & Rawson 2009; Karpicke & Bauernschmidt, 2011) and potentially of fluctuations in the characteristics of item retrieval during the study-phase, such as item recognition, or changes in context (Mozer et al., 2009; Raaijmakers, 2003). It is also possible that ARTS is sensitive to the combined effect of learning strength and study-phase retrieval characteristics. More of these distinctions could be explored in future research.
These results are among the first to show that adaptive learning systems, specifically the ARTS system, are capable of producing learning gains under circumstances similar to that of standard memory studies. Learning with a preset, total number of presentations (3 or 4 in many memory studies) is not comparable to most real-world learning situations. It provides learners with few chances to retain knowledge, and usually results in learning gains that are far from what would be sufficient for real learners to achieve mastery in a real learning domain. We chose to study adaptive spacing under these conditions for reasons that have motivated their use by many researchers: experimental control and comparability to other studies. Doing so allows the present data to help bridge two research literatures—studies of spacing schedules on one hand and adaptive learning on the other. At the same time, it is possible that an adaptive system designed to individualize learning and bring each learner to objective mastery criteria for each item (e.g., Mettler, Massey, & Kellman, 2011; Mettler & Kellman, 2014) would not show its full effects under these conditions. Despite the limitation of four total presentations per item, differences between adaptive and fixed conditions were evident in a learning session. In addition to demonstrable learning gains, differences persisted across a delay, speaking to the effectiveness of adaptive strategies to promote durable learning even without learning to criterion.
Connections with prior research.
Initial spacing intervals.
Unlike some prior research, we found evidence that initial intervals in a spacing schedule are not powerful enough to dictate long-term learning outcomes for any particular schedule. In our experiment, items in the adaptive condition received an “enforced delay” of one trial whenever items were answered incorrectly (c.f. Pavlik & Anderson, 2008, who used an enforced delay of two trials). Thus, the vast majority of initial intervals in the adaptive condition possessed a 1-trial spacing interval (due to most items being responded to incorrectly on the initial trial). This 1-trial delay was equivalent to the 1-trial delay in the fixed-expanding condition (where the delay applied to all items regardless of response). Nevertheless, performance at a delayed test was still greater in the adaptive condition than in the fixed-expanding condition. This differential degree of learning despite a rough equivalence of initial intervals suggests that short initial intervals do not convey as much power to learning as other features of spacing—specifically, the pattern of spacing intervals after the initial interval. While this result is contrary to the claims of some research (Karpicke & Roediger, 2007), we do not think it necessarily diminishes those prior researchers’ conclusions as applied to fixed schedules of practice. However, it is not clear whether those conclusions also apply to adaptive schedules of practice. Initial intervals of practice remain an important and potentially potent locus of scheduling consideration in many different scheduling schemes, including adaptive ones.
Expanding vs. equal spacing.
The fixed spacing intervals tested here did not show consistent learning advantages for expanding spaced practice over equal spaced practice. This finding is similar to some results in the spaced practice literature and different from others. However, the advantages of adaptive spacing shown here are consistent with the hypothesis that there is no simple, general answer to the question of whether fixed or expanding spacing is superior. Optimal spacing intervals may vary with learning items, overall difficulty of learning material, and learners. They may fluctuate differently for different learners for each specific item during the course of learning. Optimal spacing would seem to require adaptive systems that can assess learning strength in a specific and ongoing manner.
In this experiment, fixed schedules appeared to be somewhat equally suboptimal in their ability to respond to fluctuations in learning strength. Despite the similarity in learning outcomes across fixed schedules, we found that the patterns of spacing intervals generated in adaptive schedules tended to increase in size during learning (although spacing sometimes flattened out or contracted across later presentations). As we found a general trend toward expanding patterns in the adaptive condition, and as fixed-expanding schedules resulted in greater raw accuracy at immediate posttest, our results do not contradict the idea that expanding retrieval practice is often an effective arrangement for learning. We investigate this issue further in Experiment 2.
Limitations of this experiment.
There are limitations in interpreting the current results. Spacing intervals were slightly longer on average in the adaptive case; perhaps greater spacing alone led to greater learning benefits in the adaptive condition. While possible, this theoretical concern points out the practical limitations of fixed spacing intervals and the advantages of adaptive schedules. Without prior knowledge of the ideal spacing, it is impossible to choose optimal intervals before the start of learning. Investigating the issue of whether average spacing intervals were responsible for the effects seen in Experiment 1 was one of the goals of Experiment 2, in which spacing interval sizes were equated across fixed and adaptive conditions.
Experiment 2: Adaptive Sequencing vs. Yoked-Adaptive Fixed Spacing
Experiment 1 provided clear evidence that adaptive sequencing produces better learning than some common fixed spacing schedules that have been shown to benefit learning in prior research. In Experiment 2, we attempted to determine the locus of learning effects in adaptive schedules. To do this, we compared adaptive schedules with new, specially devised fixed schedules that were matched to have patterns of spacing intervals similar to those generated by adaptive schedules.
What drives the benefits of adaptive scheduling? We have suggested that the power of adaptive intervals rests on adaptation to ongoing learning strength. If so, there are at least two possible sources of this advantage – adaptation to individual items and adaptation to individual learners. In order to assess each of these influences, we compared adaptive learning to two new kinds of fixed schedules. These fixed ‘yoked’ schedules had spacing intervals that were identical to those participants had generated using adaptive schedules in Experiment 1.
Yoking fixed schedules to adaptive schedules was accomplished in the following way: A participant in a “yoked” condition received the same schedule of spacing intervals that a prior participant in an adaptive condition had received. Yoked schedules were predetermined (fixed) and had no relation to participants’ ongoing pattern of performance during learning. One of the yoked conditions (the yoked-item condition) was designed to preserve spacing intervals that were found for individual items. In this condition, a learner received the same schedule of intervals that a prior adaptive participant had received. Each item was presented in the same order, and the pattern of intervals given to each item was retained. To give a concrete example, if a prior adaptive learner had received the country “Angola” with a 1–5–15 series of intervals, with the first appearance of Angola occurring on trial 12, a yoked-item user would get Angola at the same point in their learning session with the same spacing intervals.
In the other yoked condition (the yoked-random condition), a learner received the same schedule of spacing intervals that a prior participant received, but items were shuffled across the pre-specified schedule of spacing intervals. If a prior adaptive learner had received Angola as described above, a yoked-random learner would receive the same series of spacing intervals (1–5–15), beginning with the same trial number for initial appearance, but for a different item (e.g., “Botswana”). 5
The yoking manipulations served multiple purposes. First, if the advantages of adaptive learning found in Experiment 1 resulted merely from the distributions of spacing intervals that occurred in the adaptive condition, or interleaving or variability of retrieval contexts that occurred from adaptive spacing, we would expect that those advantages would be fully preserved in both yoked conditions. If, on the other hand, adaptive scheduling is responsive to learning strength for particular learners and items, simply duplicating the kinds of intervals produced by adaptive spacing for other users should not produce learning results at the level given by individualized adaptive learning. The yoked-random condition tests this possibility, as it uses spacing intervals characteristic of performance with the adaptive algorithm but not based on the current participant’s responses.
The yoked-item condition tests the possibility that beneficial spacing can be predicted to some degree, across learners, by variations in individual learning items. It is possible that the advantages evident with adaptive sequencing in Experiment 1 occurred because some items are in general more difficult than others, and the adaptive algorithm detected this from learners’ performance. If so, the “magic” of adaptive sequencing might reside in adjusting spacing to fit item difficulty. This possibility would have potential practical consequences: adaptive systems that track individual responses and adjust spacing dynamically might not be needed if item difficulties are similar across learners and can be somehow determined in advance. If, on the other hand, learning strengths differ as a function of interactions of individual learners and items, then we would expect that replicating the item spacings from previous participants would not be as effective as adaptive scheduling.
Method
Participants.
The participants were 48 undergraduate psychology students who received course credit for completing the experiment. The stopping rule for data collection was when there were at least 16 participants in each condition, allowing for more if in a week cycle of participant pool signups there were more than 16.
Materials.
The learning materials were identical to Experiment 1—that is, 24 African countries as well as filler items.
Design.
Experiment 2 retained the pretest, posttest, delayed posttest design of Experiment 1. There were three between-subject conditions (16 participants per condition): learning items were presented to participants in either an adaptive schedule (identical to Experiment 1), or in one of two “yoked” fixed schedules. Each participant in the fixed conditions was assigned a single adaptive yoked “target” participant, usually the participant who had last run in the adaptive condition. An adaptive participant was run first, followed by two fixed participants. Participants were thus effectively randomly assigned to condition. In every condition during the learning phase, each learning item was presented a total of four times.
Yoking conditions.
For participants in the adaptive condition, scheduling of item presentation was dynamically determined by the ARTS system, as in Experiment 1. For participants in both yoked conditions, items were presented on a fixed, pre-set schedule. Each participant’s schedule was based on a prior adaptive participant’s trial record. In the yoked-item condition, the trial record was simply copied, so that a new yoked participant received a duplicate version of the trial record of the prior adaptive participant including the order of introduction of items, the size of the spacing intervals delivered to items, and the number and schedule of filler items. In the yoked-random condition, the trial record of the previous adaptive participant was retained but the mapping of items to sets of spacing intervals was shuffled, so that new yoked participants received for each item the same sequence of spacing intervals that an earlier participant had generated adaptively, but the specific item was different. For example, if a prior participant in the adaptive scheduling condition received three spacing intervals of 2–4–10 for the item “Angola,” a participant in the yoked-item condition would get the same item, at the same point in the learning session with the same intervals; whereas a participant in the yoked-random condition would receive the same series of intervals but for a different item (e.g., “Botswana”). For both yoked conditions, then, every series of spacing intervals (e.g., 2–4–10) occupied the same serial position in the learning session as had been generated by a prior adaptive learner, but for the yoked-random group, items were shuffled across the pre-set series of intervals. The yoking design, as noted above, aimed to have each participant in a yoked condition copy a unique adaptive participant’s trial schedule. However due to instances of errors with participant login to the system, 4 participants in the yoked-random condition shared 2 yoked schedules, and 2 participants in the yoked-item condition shared the same yoked schedule.
Procedure.
The order of the pretest, learning phase, posttest and delayed posttests were identical to Experiment 1. Trial presentations were identical to Experiment 1.
Results
The primary results of Experiment 2 are shown in Figure 8, which depicts mean accuracy by condition in all phases of the experiment. The adaptive condition showed higher accuracy than both yoked conditions in the learning phase, immediate posttest, and delayed posttest. There appears to be a trend for the yoked-item condition to outperform the yoked-random condition in the learning phase and in both posttests.
Figure 8.
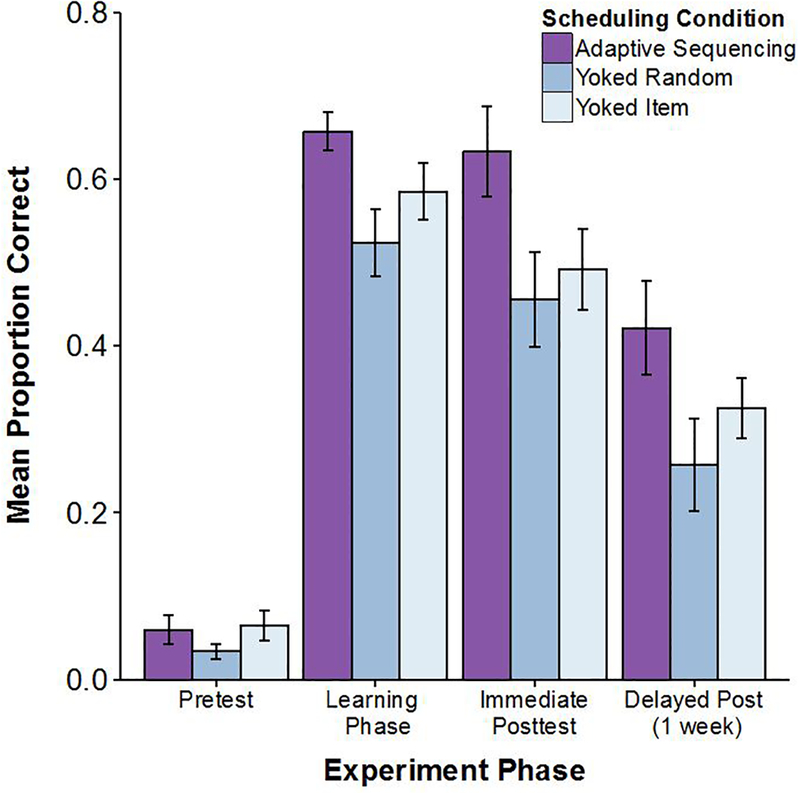
Mean proportion correct by phase across the 3 scheduling conditions in Experiment 2. Error bars show +/− 1 standard error of the mean.
These observations were confirmed by the analyses.
Pretest scores.
Mean accuracies did not differ significantly at prestest as shown by a a one-way ANOVA with condition as the between-subjects factor (F(2,45) = 1.23, p = .30, = .052). Mean pretest scores (M = 0.053, SD = 0.061) did differ significantly from chance responding (one sample t test: t(47) = 2.88, p < .01), suggesting that some participants possessed prior knowledge of some countries. As a result, we computed change and gain scores between pretest and posttest in addition to comparing average accuracies.
Posttest accuracy.
Accuracy data were analyzed by a 3×2 mixed factor ANOVA with condition (adaptive vs. yoked-random vs. yoked-item) as a between-subjects factor and test phase (immediate vs. delayed posttest) as a within-subjects factor. There was a significant main effect of condition (F(2,45) = 3.3, p = .046, = .128), a significant main effect of test phase (F(1,45) = 77.09, p < .001, = .631), and no condition by test phase interaction (F(2,45) = 0.36, p = .7, = .016). A Bartlett’s test confirmed homogeneity of variance for accuracies at both posttests (immediate: p = .80, delayed: p = .19). At the immediate posttest, average accuracies were highest for the adaptive condition (M = 0.63, SD = 0.22), lower for the yoked-item condition (M = 0.49, SD = 0.19), and lowest for the yoked-random condition (M = 0.46, SD = 0.23). Comparing means at the immediate posttest, t tests showed average accuracies for the adaptive condition were significantly greater than the yoked-random condition (t(30) = 2.24, p = .032, Cohen’s d = 0.80) and adaptive spacing marginally exceeded the yoked-item condition (t(30) = 1.94, p = .062, Cohen’s d = 0.69). The two yoked conditions did not differ significantly from one another (t(30) = 0.49, p = .63, Cohen’s d = 0.17). Accuracies at the delayed posttest were highest in the adaptive condition (M = 0.42, SD = 0.22), lower for the yoked-item condition (M = 0.326, SD = 0.144) and lowest for the yoked-random condition (M = 0.26, SD = 0.22). Similar to the immediate posttest, at the delayed posttest, average accuracies for the adaptive spacing condition were significantly greater than the yoked-random condition (t(30) = 2.09, p = .045, Cohen’s d = 0.74), but did not significantly exceed the yoked-item condition (t(30) = 1.45, p = .16, Cohen’s d = 0.53). The two yoked conditions did not differ (t(30) = 1.03, p = .31, Cohen’s d = 0.37).
Change and gain scores.
Since there was measurable prior knowledge, we examined posttest results in terms of change scores computed between pretest and posttests. We computed the same two types of change scores as in Experiment 1: change scores and gain scores. Change scores were computed by subtracting average pretest accuracies from average posttest accuracies. Gain scores were computed by subtracting pretest scores from posttest scores, ignoring items that were accurate at pretest and inaccurate at posttest.
Immediate posttest change scores and delayed posttest change scores are shown Figure 9.
Figure 9.
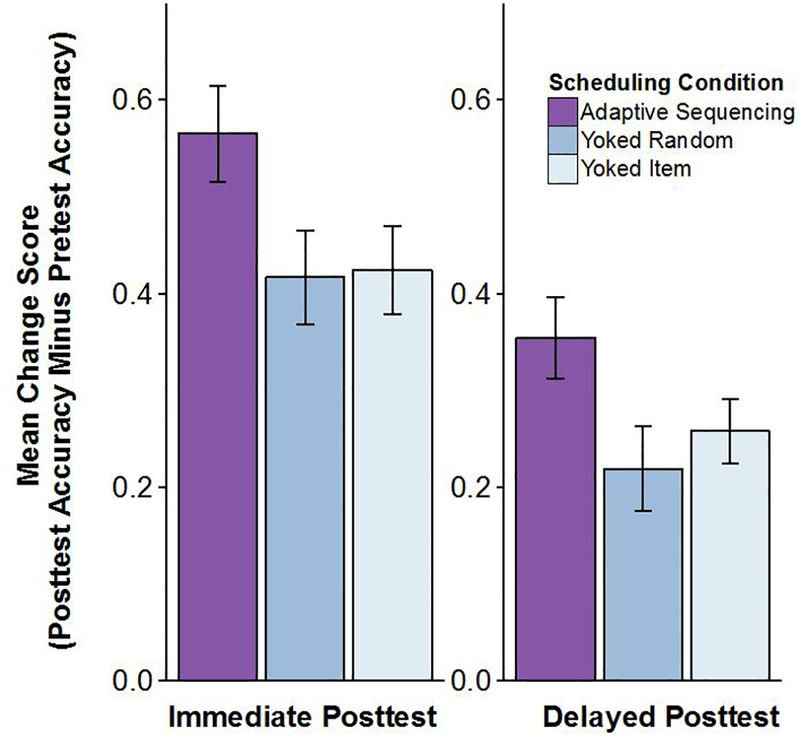
Mean change score at immediate and delayed posttests in Experiment 2. Error bars show +/− 1 standard error of the mean.
A 3×2 mixed factor ANOVA on condition and test phase revealed a significant main effect of condition (F(2,45) = 3.64, p = .034, = .139), a significant main effect of test phase (F(1,45) = 77.09, p < .001, = .631), and no condition by test phase interaction (F(2,45) = 0.36, p = .7, = .016). Change scores at immediate posttest were highest in the adaptive condition (M = 0.57, SD = 0.20), lowest in the yoked-random condition (M = 0.42, SD = 0.20) and nearly as low in the yoked-item condition (M = 0.42, SD = 0.18). Comparing means, t tests were significantly different between the adaptive and both of the two yoked conditions (adaptive vs. yoked-item: t(30) = 2.09, p = .045, Cohen’s d = 0.74; adaptive vs. yoked-random: t(30) = 2.14, p = .04, Cohen’s d = 0.76) but the two yoked conditions did not differ significantly (t(30) = 0.12, p = .91, Cohen’s d = 0.04). Delayed posttest change scores were lower but similar: average scores were highest in the adaptive condition (M = 0.35, SD = 0.17), lowest in the yoked-random condition (M = 0.22, SD = 0.17) and nearly as low in the yoked-item condition (M = 0.26, SD = 0.13). Comparing means, t tests showed significant differences between the adaptive and the yoked-random conditions (t(30) = 2.23, p = .033, Cohen’s d = 0.78), and a marginally significant difference between adaptive and yoked-item (t(30) = 1.79, p = .08, Cohen’s d = 0.63). The difference between the two yoked conditions was not significant (t(30) = 0.71, p = .48, Cohen’s d = 0.25).
In addition to change scores, we also computed gain scores. Pretest scores were subtracted from posttest scores, excluding items that were accurate at both posttest and pretest. Gain score results were different from change score results in the following ways: the paired comparisons between adaptive and the two yoked conditions at immediate posttest were only marginally significant (adaptive vs. yoked-random: p=.057; adaptive vs. yoked-item: p=.058), and the paired comparison at delayed posttest between adaptive and yoked-item conditions was not significant (p=.12).
Response times.
Mean response times (RTs) are shown in Figure 10 for each condition and each experimental phase except pretests. (Pretest RTs are ignored owing to the few items that were answered correctly in that phase). RT data include only RTs from trials on which correct answers were given.
Figure 10.
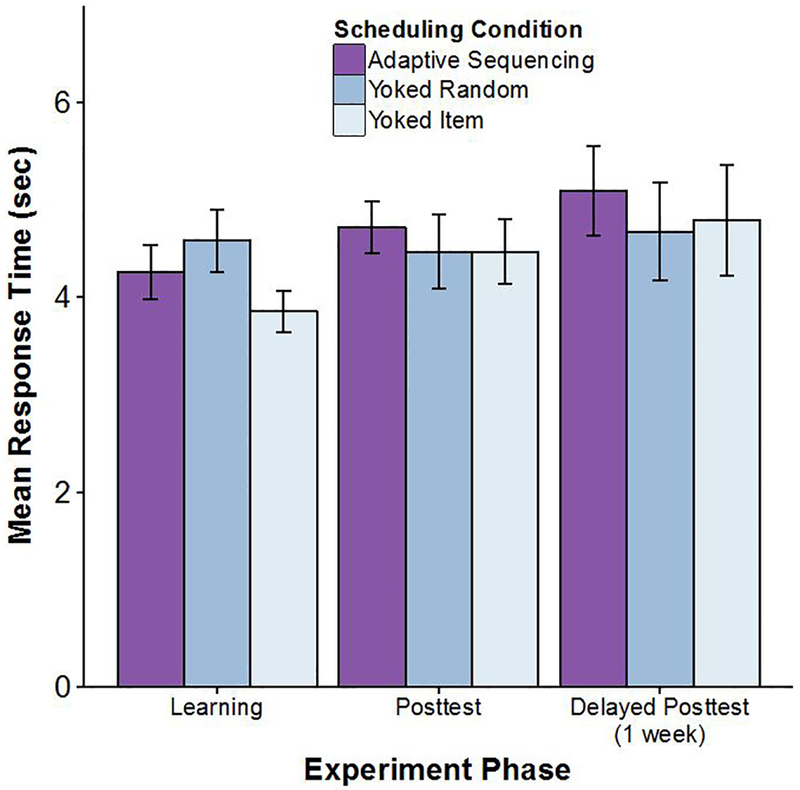
Mean response time (in seconds) at learning and test phases across 3 scheduling conditions in Experiment 2. Response times are from correctly answered trials only. Error bars show +/− 1 standard error of the mean.
In the learning phase, a one-way ANOVA showed no significant differences between conditions (p > .18). A 3×2 ANOVA with scheduling condition and posttest phases as factors found no significant effect of condition (F(2,45) = 0.26, p = .77, = .011), no effect of test phase (F(1,45) = 1.12, p = .29, = .024), and no interaction of scheduling condition with posttest phase (F(2,45) = 0.03, p = .97, = .001). Individual comparisons showed that RTs at each phase were not significantly different from one another (all ps >.05). Comparing RTs across posttest phases, no conditions showed significantly different RTs across the two posttests (all ps >.05).
Analyses of spacing intervals.
Adaptive and yoked conditions differed only slightly in the size of spacing intervals delivered to individual items during the learning session. The mean spacing interval per learner was calculated by averaging the mean spacing intervals for every item for that learner and averaging over items. Mean adaptive spacing intervals were close in length to the adaptive condition in Experiment 1 (adaptive: M = 6.77, SD = 1.46, yoked-random: M = 6.81, SD = 1.40, yoked-item: M = 6.89, SD = 1.43). We also looked at the size of spacing intervals conditional on whether the presentation before the spacing interval was responded to correctly in order to distinguish the sizes of adaptive vs. enforced delay spacing intervals. Mean spacing intervals by presentation are shown in Figure 11.
Figure 11.
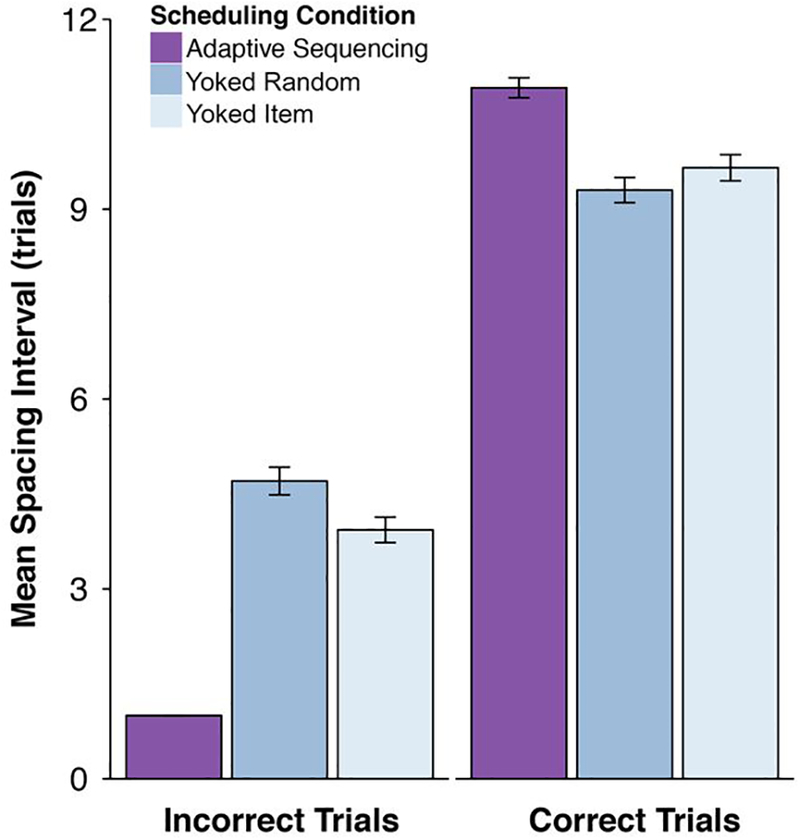
Mean spacing interval size (in trials) across 3 scheduling conditions in Experiment 2 conditional on whether the trial preceding the interval was answered correctly or not. Error bars show +/− 1 standard error of the mean.
As in Experiment 1, the conditional values revealed that adaptive spacing interval sizes were bimodal: larger for correct responses (M = 10.92, SD = 5.04) and smaller for incorrect ones (M = 1.0, SD = 0.0).
Finally we examined the average spacing interval at each presentation number for the adaptive condition to see if interval sizes corresponded to those generated in Experiment 1. Figure 12 shows mean sizes of spacing intervals in the adaptive condition as similar to Expt. 1: mean initial interval was the smallest (M = 1.67, SD = 0.98), the second interval largest (M = 10.42, SD = 2.12), and the third interval smaller than the second interval (M = 8.22, SD = 1.82).
Figure 12.
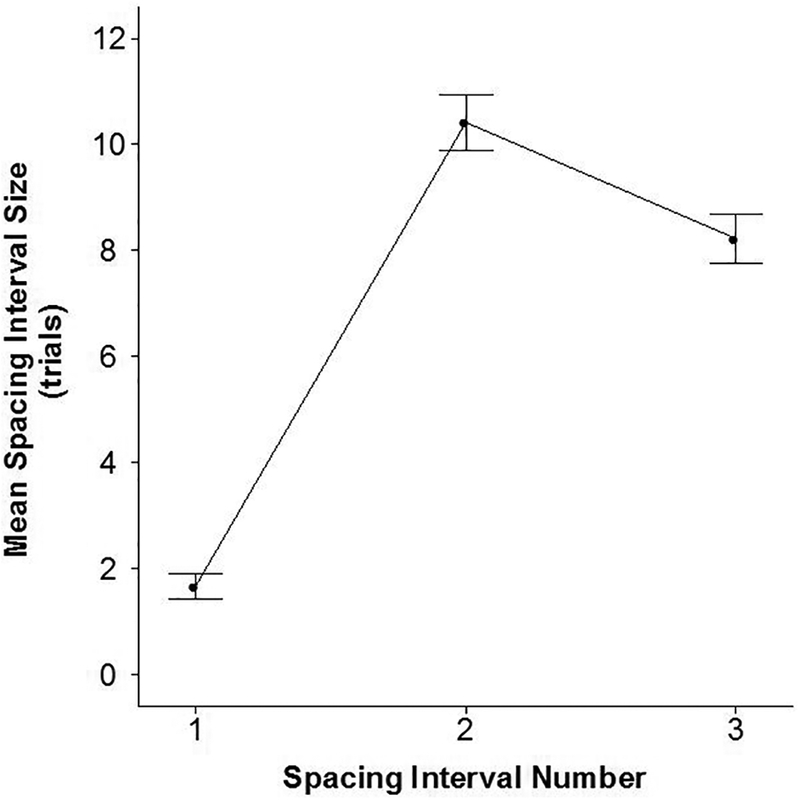
Exp 2. Mean spacing interval size (in trials) across 3 intervals in the adaptive scheduling condition of Experiment 2. Error bars show +/− 1 standard error of the mean.
Discussion
In Experiment 2 adaptive scheduling led to larger learning improvements than fixed schedules at both an immediate and delayed posttest. Adaptive schedules performed better despite the fact that the fixed schedules in this study possessed highly similar spacing intervals to adaptive schedules. These fixed schedules were “yoked” to mimic the spacing interval characteristics of schedules generated by an adaptive algorithm. In the yoked-item condition intervals were tuned to individual items: Participants received the exact schedule that a prior adaptive participant received, where spacing intervals associated with each item were exactly duplicated. In the yoked-random condition, intervals were not attached to individual items: participants received a prior adaptive schedule but items were introduced in a random order so that each item received the schedule of intervals appropriate for some different item. This schedule tested for effects of the distribution of spacing intervals overall, apart from specific effects of particular items.
Adaptive scheduling showed significantly greater learning as measured by change scores between pretest and posttest than both yoked conditions at an immediate posttest. Adaptive scheduling also significantly outperformed the yoked-random condition, both in terms of greater learning accuracy at both posttests, and in terms of change-scores and gain scores at a delayed test. There were several marginal effects of adaptive over both yoked-item and yoked-random conditions: gain scores were marginally better at immediate posttest, and accuracies were marginally better at delayed posttest for the adaptive condition than the yoked-item condition, and in all cases, yoked-item performance trended numerically lower than performance in the adaptive condition. Even the weakest statistical (marginally significant) comparisons between adaptive and the fixed conditions showed effect sizes from .57 to .70; these are considered medium to large effect sizes.
In no case, neither at immediate nor delayed posttest, nor for any measure of performance, did the two yoked conditions differ significantly from each another. The numerical advantage in the yoked-item condition over the yoked-random condition may suggest that tuning intervals to the spacing requirements of individual items could be of some value in generating a predetermined schedule. However, the present results suggest that such schedules perform more poorly than adaptive schedules, indicating that knowledge of item difficulty is not the primary driver of gains in adaptive scheduling.
These results echo and extend the results of Experiment 1. Learning is better when spacing intervals are a function of ongoing learner performance. The results support the hypothesis that optimizing spacing requires attunement to learning strength, which varies for learners and items in a dynamic way. Since there is no way to predict the pattern of learning strength changes for items for a new learner, adaptive spacing offers the only avenue toward optimizing spacing intervals for sets of items across a learning session.
General Discussion
The spacing effect is a powerful driver of human learning. It is also a major focus of research, with 7250 entries appearing on Google Scholar and 4010 entries between 2005 and 2015. A significant portion of work on this effect has been aimed at determining what spacing schedules promote the best learning. Most of that work, and most explicit implementations of spacing in learning applications, have utilized fixed arrangements of spacing intervals.
The present work provides evidence that fixed intervals of spacing, in general, cannot be optimal. Experiment 1 showed that adaptive spacing based on ongoing assessment of learning strength for individual items and learners outperforms typical fixed spacing schedules. Experiment 2 probed more deeply the reasons for the advantages of adaptive spacing. Even when overall properties of spacing distributions were matched across adaptive and yoked fixed conditions, the adaptive condition produced better learning outcomes. This experiment also revealed that the advantages of adaptive spacing cannot be captured in a fixed, predetermined schedule based on data about the differential difficulty of various learning items: The yoked-item condition of Experiment 2 preserved spacing characteristics for individual items that adaptive learners had produced. These did indeed vary somewhat across items, but replicating those differences with new learners did not produce learning outcomes comparable to those obtained with an adaptive system that used response times to track learning strength for particular learners and items.
These results cohere with an emerging account of spacing effects. Although spacing likely benefits learning for multiple reasons, the explanation that may be most relevant for determining the optimal recurrence interval for a learning item (or category; see Mettler & Kellman, 2014) involves the importance of retrieval difficulty and its relation to learning strength. A new learning trial confers optimal benefit for learning a given item when that item can be retrieved with greatest difficulty but has not yet been forgotten (Pyc & Rawson, 2009; Bjork & Bjork, 1992). The difficulty of retrieving an item will generally increase with trials or time elapsed since its last presentation, due to decay in learning strength, interference from intervening learning trials, or presentation of confusable items. The specific relations between these variables and difficulty are likely mediated by learning strength. Not all effects of intervening trials and items reduce learning strength; some influences that may increase learning strength are reminders or cues that may be provided by other items, or presentation of other items or feedback that help differentiate items. Also intervening items that are unrelated to learning items probably have less effect on learning strength than items closely related to learning items (Storm, Bjork & Storm, 2010). Fluctuations in effort or arousal could influence learning strength in either direction. All of these influences reduce the effectiveness of predetermined schedules relative to adaptive systems that gauge learning strength in an ongoing manner.
The present data indicate that use of response times together with accuracy in adaptive learning, as in the ARTS system used here, allows dynamic assessment of ongoing learning strength. ARTS outperformed typical fixed spacing schemes often employed in the literature on the spacing effect. Although the assessment and mastery features of ARTS are designed to guide learners to mastery criteria, implying that the time to mastery will vary for different learners, here we omitted the mastery features and tested ARTS under conditions typically used in spacing experiments. In both experiments, items were presented a limited number of times. It was possible that the benefits of ARTS would not be apparent with only 4 presentations; continuing adaptive learning to mastery would have likely led to differing numbers of presentations for each item, higher levels of performance, and may have been particularly valuable for retention after a delay. However, despite imposing on the adaptive system the limitations of a small, equal set of presentations for each item, adaptively scheduling the spacing proved more beneficial than presenting items with fixed schedules. The benefit of adaptive scheduling over fixed schedules was substantial, with medium to large effect sizes that persisted across a 1-week delay. In no condition and at no test were fixed schedules found to perform better than adaptive schedules.
Theoretical Implications
Results from studies of adaptive scheduling offer a window onto theoretical debates about the optimal schedule of practice in learning and memory, specifically, debates about equal or expanding spacing (Karpicke & Roediger, 2007; Landauer & Bjork, 1978; Storm, Bjork, & Storm, 2010; Carpenter & Delosh, 2005) and research investigating the locus of learning effects in spaced practice (Karpicke & Bauernschmidt, 2011; Pashler, Zarow, & Triplett, 2003). We comment on each in turn.
Is expanding practice optimal for retention?
A major controversy in the spacing literature has been whether fixed schedules of equal intervals or schedules of expanding spacing intervals produce better learning. Expanding retrieval practice is sometimes thought to be the most effective distributed scheduling technique (Landauer & Bjork, 1978; Pimsleur, 1967; Storm, Bjork, & Storm, 2010); however other evidence indicates there is no difference between expanding and equal schedules of practice (Karpicke & Bauernschmidt, 2011) or even that equal interval practice is superior to expanding practice (Karpicke & Roediger, 2007; Logan & Balota, 2008) or superior at a delay (Cull, 2000).
Our results have several implications for this issue. First, as we suggested above, there will not be a single, general answer to the question of the best fixed schedule. Variations in published results using varied material, conditions of learning, and learners can be explained by effects of these variables on retrieval difficulty as mediated by learning strength (c.f. Storm, Bjork & Storm, 2010). That said, our results with adaptive learning do offer some support for expanding schedules in the learning domain we studied. Our retrospective analyses of the patterns of spacing intervals generated in adaptive conditions showed that these tended to be expanding. We also found some evidence that long-term performance correlates with expanding trial spacing rather than equal or contracting spacing. When spacing intervals expanded for an item, as measured by successively increasing interval sizes across presentations, delayed posttest scores for those items were greater. (See Supplemental Materials, Figure 3). While not causal, the evidence is indicative of an advantage for expanding schedules of spaced practice. It should be noted that, although expanding spacing was often the actual spacing outcome of adaptive scheduling, not all participants or items experienced expanding spacing intervals. In fact, while the trend across presentations in the adaptive condition was on the whole expanding, only a few participants experienced strictly expanding spacing for all learning items across all presentations. These findings further confirm the operation of influences on learning strength that are not predictable in advance by predetermined schedules having either equal or expanding spacing intervals.
Further debate between choices of optimal fixed spacing schedules is likely to remain equivocal. When spacing is decided in advance of dynamic assessment of learner performance, retrievals may fail due to exceedingly long delays, or initial retrievals may be too easy and fail to add much to learning strength. Karpicke and Roediger (2007) commented: “Considering the widespread belief in the utility of expanding retrieval, it is surprising that there is not a larger base of research with consistent evidence showing expanding retrieval practice to be the superior spaced practice technique for improving long-term retention.” We would argue instead that the lack of consistent evidence for any fixed spacing scheme is unsurprising, given that fixed schedules lack the flexibility to match spacing parameters to specific materials, items and learners across a variety of situations.
What makes spacing beneficial?
Our experiments also reflect on hypothesized drivers of spacing advantages – for example, characteristics of spacing interval size such as absolute delay length (Karpicke & Baeurnschmidt, 2011). If generic characteristics of absolute spacing intervals were crucial, we would have expected equivalent performance in two conditions that received the same pattern and size of delays. In fact, a different outcome occurred: Even when schedule characteristics were equated, learning suffered in comparison to a condition where spacing intervals did adapt to individual learners’ interactions with items. The primary reason to alter spacing intervals during practice is to match the characteristics of ongoing learning strength, not to meet particular delay characteristics or criteria of spacing schedules in the abstract. Because ARTS can measure learning strength as learning progresses, it can optimize learning events to a degree that fixed spacing schedules cannot match, no matter the specific delay characteristics of the fixed intervals.
This point applies to considerations regarding initial and later intervals of practice. Evidence suggests that optimizing initial retrievals when learning strength is low for poorer learners or for difficult material can improve learning (Cull, Shaughnessy & Zechmeister, 1996). It has also been suggested that after appropriate initial intervals, later intervals have very little effect on learning (Karpicke & Roediger, 2010). In our results, differences in learning emerged from manipulations of spacing intervals even when schedules were matched on their initial intervals (Experiment 2). Specifically, when spacing intervals were adaptive, learning benefits can accrue despite matches with fixed spacing conditions in the size of the initial spacing interval. The results suggest that appropriately adjusting spacing throughout learning—not just at the beginning—is an important and effective way to generate learning gains.
Comparison with other adaptive systems.
The present results suggest that these benefits of adaptively arranged spacing might be relatively easy to realize in real-world learning settings and improve upon techniques used in other adaptive systems. The ARTS system was able to extract useful assessments of ongoing learning strength while in use by learners. Extraction of response time data along with accuracy is relatively simple and unobtrusive. Adaptive systems have commonly required prior studies with particular learning content and similar participants to obtain model parameters (Atkinson, 1972; Pavlik & Anderson, 2008), or attempt to find optimal scheduling without relying on prior studies, but do not adapt to ongoing changes in learning strength (Khajah, Lindsey, & Mozer, 2014). In real-world learning settings, it would often be impractical to run a prior experiment with similar learners and the same learning material. There are advantages to an adaptive learning system that does not require such prerequisites. Moreover, some results of the current studies indicate there are limits to the efficiencies attainable using data obtained from other learners; optimal spacing may require personalized, ongoing attunement to each learner’s performance during learning.
In addition to efficiencies in implementation, ARTS’s use of reaction time measures in addition to accuracy provides a potentially more accurate assessment of learning strength than other systems. Prior adaptive systems have relied primarily on accuracy alone, in some cases informed by theoretical models about how learning strength might grow or decay (Pavlik & Anderson, 2005). These represent important efforts, but such efforts are unlikely to reflect the individual nuances of an individual’s learning through a learning session, inter-item interactions in learning sessions, or the individual interactions of learners and items. Although ARTS was not directly compared with adaptive systems in the current research, some evidence indicates that use of ongoing reaction time data provides a better measure of learning strength and thus translates to greater learning performance and delayed retention than other systems (see Mettler, Massey & Kellman, 2011).
Bridging Studies of Fixed and Adaptive Spacing.
The present work compared an adaptive learning system with the fixed schedules of spacing typically studied in the memory literature. To our knowledge, this has not been done in any previous work. In bridging two research literatures that have been largely separate, the present work, and future work of this kind, has substantial potential to clarify major issues in understanding learning in general and spacing in particular. First and foremost, as described above, comparing fixed and adaptive schedules offers a window into the mechanisms of spacing. The present results help illuminate prior findings and disagreements in the fixed spacing literature, as well as the advantages of adaptive spacing. They converge on an understanding of much of the value of spacing in terms of three ideas: the retrieval difficulty hypothesis, the connection between retrieval difficulty and learning strength, and the value of up-to-the-moment assessment of learning strength from accuracy combined with response times. This emerging understanding may clarify a number of issues in the field, such as why theories that attempt to explain why and which fixed schedules are effective appear to be in conflict with the scheduling outcomes of some adaptive schemes (for example, adaptive schedules tend to be contracting rather than expanding in Pavlik & Anderson, 2008; see Lindsey, et al., 2009). Secondly, comparisons between fixed and adaptive spacing would appear to be important threshold tests for adaptive systems. An adaptive schedule should be more effective than fixed schedules, else the theoretical assumptions and the practical implications of that adaptive model are suspect. In addition, connecting these lines of research may be relevant to other features of learning systems. Adaptive schedules often use learning to mastery criteria, an important element in many real-world settings. In the studies here, we used a fixed number of presentations for items, but further comparisons of adaptive and fixed presentations might be useful where the number of presentations is not set in advance and mastery criteria are employed. In general, unifying these research areas may connect each with the theoretical tools and insights of the other. In particular, the current research suggests an important conclusion: that predetermined (fixed) schedules cannot be optimal, as they do not adjust to ongoing fluctuations in learning strength – involving individual items, learners, and times in a learning session – and thus cannot determine the best spacing in terms of retrieval effort and successful retrieval.
Practical Applications.
The techniques discussed here have important implications and relevance in many domains including theories of optimal educational practice, the cognitive science of learning, and the psychological understanding of learning and memory processes. The techniques developed here have already been applied to real world learning problems such as mathematics learning (Mettler, Massey & Kellman, 2011) and extend to perceptual or category learning (Mettler & Kellman, 2014), such as the training of expertise in perceptual learning in domains like aviation and a number of medical learning domains, such as echocardiography, radiology, dermatology and pathology (Krasne, Hillman, Kellman, & Drake, 2013; Krasne, Rimoin, Altieri, Craft & Kellman, 2015; Thai, Krasne & Kellman, 2015). It is important to note that there will likely be some differences when laboratory studies such as those in this paper are generalized to large scale, real-world educational domains. However, the techniques described in this paper have already been successfully deployed in large scale studies, with longterm consequences for learning. In work applying the adaptive learning system described here to perceptual category learning in medical domains, for example, learning gains in a Histopathology perceptual adaptive learning module (PALM) were substantially preserved in delayed posttests given 6–7 weeks later (Krasne et al, 2013); in a Dermatology PALM, advantages for students who completed the module over those who did not were clearly evident in delayed tests given a year later (Krasne et al, 2015), and in an Echocardiography PALM, 3rd-year medical students who invested about 45 minutes per day for two days to complete the module outperformed second year emergency medicine residents, for whom ECG interpretation is a centrally important skill, with the learning gains for the PALM group being substantially preserved in delayed posttest given a year later (Neiman, Stevens, Kellman & Krasne, submitted). Adaptive systems based on ongoing assessment of learning strength can likely enhance learning in any domain where spacing and scheduling are important moderators of long-term learning strength. As such, they are likely to be valuable tools in many future applications of learning technology.
Acknowledgements
The authors gratefully acknowledge support from the US National Science Foundation (NSF) Research on Education and Evaluation in Science and Engineering (REESE) Program award 1109228; the US Department of Education, Institute of Education Sciences (IES), Cognition and Student Learning (CASL) Program awards R305A120288 and R305H060070; the National Institute of Child Health and Human Development (NICHD) award 5RC1HD063338; and US Department of Education, IES SBIR award ED-IES-10-C-0024 to Insight Learning Technology, Inc. Any opinions, findings, and conclusions or recommendations expressed in this article are those of the authors and do not necessarily reflect the views of NSF, the US Department of Education, or other agencies.
The authors thank Robert Bjork, Alan Castel, Jim Stigler, Ed Stabler, and members of the Human Perception Lab and CogFog Seminar at UCLA for helpful comments and insight. Systems that use learner speed and accuracy to sequence learning events are covered by US Patent #7052277, assigned to Insight Learning Technology, Inc. For information, please contact Info@insightlt.com.
Appendix
Appendix Table 1.
Parameters for the adaptive sequencing algorithm in Experiments 1 and 2.
| Parameter | Value |
|---|---|
| a – Counter weight | 0.1 |
| b – Default weight | 1.1 |
| r – RT weight | 3.0 |
| W – Incorrect priority increment | 20 |
| D – Delay constant | 1 |
Footnotes
Techniques do not always agree on the goals of learning. Some techniques aim primarily to reduce the amount of total time spent practicing items, thus targeting the learning of items most likely to benefit from extra practice in the long term, but at a sacrifice to items deemed too difficult to learn quickly (Pavlik & Anderson, 2008). Other studies fix total time but prescribe differing numbers of presentations and differing durations of practice at each repetition (Lindsey, Shroyer, Pashler, & Mozer, 2014). Few adaptive schedules attempt explicitly to maximize the duration of spacing delays to optimize learning for each item, and we know of no other techniques that rely on ongoing measures of response speed during learning.
Parameters were borrowed from prior work and loosely tuned using pilot data, to better match the format of 4 total presentations, which differed from prior work where learning proceeded to mastery criteria.
We considered these data missing not at random (MNAR) (see Howell (2007)); however we conducted t tests in an effort to further explore the data.
Across items, in the fixed conditions there was also minor variation in spacing interval size due to the use of ‘jitter’ as described above in the Method section.
Another variation would involve averaging across all item delays for participants in an adaptive condition and yoking new participants’ delays to these averages. Of many possible variations along these lines we chose direct yoking because of the power it gave us in generating subconditions that examine aspects of item vs. learner differences in learning.
Portions of this work were submitted as a dissertation by the first author.
Contributor Information
Everett Mettler, University of California, Los Angeles.
Christine M. Massey, University of Pennsylvania
Philip J. Kellman, University of California, Los Angeles
References
- Atkinson RC (1972). Optimizing the learning of a second-language vocabulary. Journal of Experimental Psychology, 96(1), 124–129. [Google Scholar]
- Baddeley AD (1986). Working memory. Oxford, England: Clarendon Press. [Google Scholar]
- Benjamin AS & Bjork RA (1996). Retrieval fluency as a metacognitive index In Reder L (Ed.), Implicit memory and metacognition (pp. 309–338). Hillsdale, NJ: Erlbaum. [Google Scholar]
- Benjamin AS & Tullis JG (2010). What makes distributed practice effective? Cognitive Psychology, 61(3), 228–247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bjork RA & Allen TW (1970). The spacing effect: Consolidation or differential encoding? Journal of Verbal Learning and Verbal Behavior, 9(5), 567–572. [Google Scholar]
- Bjork EL, & Bjork RA (2011). Making things hard on yourself, but in a good way: Creating desirable difficulties to enhance learning In Gernsbacher MA, Pew RW, Hough LM, & Pomerantz JR (Eds.), Psychology and the real world: Essays illustrating fundamental contributions to society (pp. 56–64). New York: Worth. [Google Scholar]
- Bjork RA & Bjork EL (1992). A new theory of disuse and an old theory of stimulus fluctuation In Healy A, Kosslyn S, & Shiffrin R (Eds.), From learning processes to cognitive processes: Essays in honor of William K. Estes (Vol. 2, pp. 35–67). Hillsdale, NJ: Erlbaum. [Google Scholar]
- Bjork RA, Dunlosky J, & Kornell N (2013). Self-regulated learning: Beliefs, techniques, and illusions. Annual Review of Psychology, 64, 417–444. [DOI] [PubMed] [Google Scholar]
- Carpenter SK & DeLosh EL (2005). Application of the testing and spacing effects to name learning. Applied Cognitive Psychology, 19, 619–636. [Google Scholar]
- Carpenter SK, Cepeda NJ, Rohrer D, Kang SH, & Pashler H (2012). Using spacing to enhance diverse forms of learning: Review of recent research and implications for instruction. Educational Psychology Review, 24(3), 369–378. [Google Scholar]
- Cepeda NJ, Pashler H, Vul E, Wixted JT, & Rohrer D (2006). Distributed practice in verbal recall tasks: A review and quantitative synthesis. Psychological Bulletin, 132(3), 354. [DOI] [PubMed] [Google Scholar]
- Cepeda NJ, Vul E, Rohrer D, Wixted JT, & Pashler H (2008). Spacing effects in learning: A temporal ridgeline of optimal retention. Psychological Science, 19(11), 1095–1102. [DOI] [PubMed] [Google Scholar]
- Cull WL (2000). Untangling the benefits of multiple study opportunities and repeated testing for cued recall. Applied Cognitive Psychology, 14(3), 215–235. [Google Scholar]
- Cull WL, Shaughnessy JJ, & Zechmeister EB (1996). Expanding understanding of the expanding-pattern-of-retrieval mnemonic: Toward confidence in applicability. Journal of Experimental Psychology: Applied, 2(4), 365–378. [Google Scholar]
- Delaney PF, Verkoeijen PP, & Spirgel A (2010). Spacing and testing effects: A deeply critical, lengthy, and at times discursive review of the literature. Psychology of Learning and Motivation, 53, 63–147. [Google Scholar]
- Dempster FN (1989). Spacing effects and their implications for theory and practice. Educational Psychology Review, 1(4), 309–330. [Google Scholar]
- Ebbinghaus H (1913). Memory: A contribution to experimental psychology. New York: Teachers College, Columbia University. [Google Scholar]
- Glenberg AM (1976). Monotonic and nonmonotonic lag effects in paired-associate and recognition memory paradigms. Journal of Verbal Learning and Verbal Behavior, 15(1), 1–16. [Google Scholar]
- Glenberg AM (1979). Component-levels theory of the effects of spacing of repetitions on recall and recognition. Memory & Cognition, 7(2), 95–112. [DOI] [PubMed] [Google Scholar]
- Hintzman DL (1974). Theoretical implications of the spacing effect In Solso RL (Ed.), Theories in cognitive psychology: The Loyola Symposium. (pp. 77–99). Potomac, MD: Erlbaum. [Google Scholar]
- Howell DC (2007). The analysis of missing data In Outhwaite W & Turner S Handbook of Social Science Methodology. London: Sage. [Google Scholar]
- Johnston WA & Uhl CN (1976). The contributions of encoding effort and variability to the spacing effect on free recall. Journal of Experimental Psychology: Human Learning & Memory, 2(2), 153–160. [Google Scholar]
- Lindsey R, Mozer M, Cepeda NJ, & Pashler H (2009). Optimizing memory retention with cognitive models. In Howes A, Peebles D, Cooper R(Eds.), 9th International Conference on Cognitive Modeling – ICCM2009, Manchester, UK. [Google Scholar]
- Karpicke JD & Bauernschmidt A (2011). Spaced retrieval: absolute spacing enhances learning regardless of relative spacing. Journal of Experimental Psychology: Learning, Memory, and Cognition, 37(5), 1250–1257. [DOI] [PubMed] [Google Scholar]
- Karpicke JD & Roediger HL III, (2007). Expanding retrieval practice promotes short-term retention, but equally spaced retrieval enhances long-term retention. Journal of Experimental Psychology: Learning, Memory, and Cognition, 33(4), 704–719. [DOI] [PubMed] [Google Scholar]
- Karpicke JD & Roediger HL III, (2010). Is expanding retrieval a superior method for learning text materials? Memory & Cognition, 38(1), 116–124. [DOI] [PubMed] [Google Scholar]
- Kellman PJ & Garrigan P (2009). Perceptual learning and human expertise. Physics of Life Reviews, 6(2), 53–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khajah MM, Lindsey RV, & Mozer MC (2014). Maximizing students’ retention via spaced review: Practical guidance from computational models of memory. Topics in Cognitive Science, 6, 157–169. [DOI] [PubMed] [Google Scholar]
- Krasne S, Hillman JD, Kellman PJ & Drake TA (2013). Applying perceptual and adaptive learning techniques for teaching introductory histopathology. Journal of Pathology Informatics, 4, 34–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krasne S, Rimoin L, Altieri L, Craft N & Kellman P (2015). Training pattern recognition of skin lesion morphology, configuration and distribution. Journal of the American Academy of Dermatology, 72(3):489–95. doi: 10.1016/j.jaad.2014.11.016. Epub 2015 Jan 13. [DOI] [PubMed] [Google Scholar]
- Kornell N & Bjork RA (2007). The promise and perils of self-regulated study. Psychonomic Bulletin & Review, 14(2), 219–224. [DOI] [PubMed] [Google Scholar]
- Kornell N & Bjork RA (2008). Learning concepts and categories: Is spacing the “enemy of induction”? Psychological Science, 19(6), 585–592. [DOI] [PubMed] [Google Scholar]
- Landauer TK & Bjork RA (1978). Optimum rehearsal patterns and name learning In Gruneberg M, Morris P, & Sykes R (Eds.), Practical aspects of memory (pp. 625–632). London: Academic Press. [Google Scholar]
- Lindsey RV, Shroyer JD, Pashler H, & Mozer MC (2014). Improving students’ long-term knowledge retention through personalized review. Psychological Science, 25(3), 639–647. [DOI] [PubMed] [Google Scholar]
- Mettler E (2014). Studies of Adaptive and Fixed Schedules in Factual and Perceptual Learning. Retrieved from Proquest. #3605425.
- Mettler E, & Kellman PJ (2014). Adaptive response-time-based category sequencing in perceptual learning. Vision Research, 99, 111–123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mettler E, Massey CM, & Kellman PJ (2011). Improving adaptive learning technology through the use of response-times In Proceedings of the 33rd Annual Meeting of the Cognitive Science Society. Boston, MA: Cognitive Science Society; (pp. 2532–7). [Google Scholar]
- Mozer MC, Pashler H, Cepeda N, Lindsey RV, & Vul E (2009). Predicting the optimal spacing of study: A multiscale context model of memory. In Advances in Neural Information Processing Systems, Vol. 22 (pp. 1321–1329). [Google Scholar]
- Niemann JT, Stevens CD, Kellman PJ & Krasne S Mastering ECG interpretation skills through a perceptual and adaptive learning module. Under review, Advances in Health Science Education. [DOI] [PMC free article] [PubMed]
- Pavlik PI & Anderson JR (2005). Practice and forgetting effects on vocabulary memory: An activation-based model of the spacing effect. Cognitive Science, 29, 559–586. [DOI] [PubMed] [Google Scholar]
- Pavlik PI & Anderson JR (2008). Using a model to compute the optimal schedule of practice. Journal of Experimental Psychology: Applied, 14(2), 101–117. [DOI] [PubMed] [Google Scholar]
- Pimsleur P (1967). A memory schedule. The Modern Language Journal, 51(2), 73–75. [Google Scholar]
- Pyc MA & Rawson KA (2009). Testing the retrieval effort hypothesis: Does greater difficulty correctly recalling information lead to higher levels of memory? Journal of Memory and Language, 60(4), 437–447. [Google Scholar]
- Raaijmakers JGW (2003). Spacing and repetition effects in human memory: Application of the SAM model. Cognitive Science, 27, 431–452. [Google Scholar]
- Rawson KA, & Dunlosky J (2011). Optimizing schedules of retrieval practice for durable and efficient learning: How much is enough? Journal of Experimental Psychology: General, 140(3), 283–302. [DOI] [PubMed] [Google Scholar]
- Rohrer D & Taylor K (2006). The effects of overlearning and distributed practice on the retention of mathematics knowledge. Applied Cognitive Psychology, 20, 1209–1224. [Google Scholar]
- Rumelhart DE (1967). The effects of interpresentation interval on performance in a continuous paired-associate task Technical Report 116, Institute for Mathematical Studies in Social Sciences, Stanford University. [Google Scholar]
- Snider VE (2004). A comparison of spiral versus strand curriculum. Journal of Direct Instruction, 4(1), 29–39. [Google Scholar]
- Storm BC, Bjork RA, & Storm JC (2010). Optimizing retrieval as a learning event: When and why expanding retrieval practice enhances long-term retention. Memory & Cognition, 38(2), 244–253. [DOI] [PubMed] [Google Scholar]
- Thai KP, Krasne S & Kellman PJ (2015). Adaptive perceptual learning in electrocardiography: The synergy of passive and active classification In Noelle DC, Dale R, Warlaumont AS, Yoshimi J, Matlock T, Jennings CD, & Maglio PP (Eds.) Proceedings of the 37th Annual Meeting of the Cognitive Science Society. Austin, TX: Cognitive Science Society, 2350–2355. [Google Scholar]
- Thios SJ & D’Agostino PR (1976). Effects of repetition as a function of study-phase retrieval. Journal of Verbal Learning and Verbal Behavior, 15(5), 529–536. [Google Scholar]
- Tsai L (1927). The relation of retention to the distribution of relearning. Journal of Experimental Psychology, 10(1), 30. [Google Scholar]
- Wahlheim CN, Dunlosky J, & Jacoby LL (2011). Spacing enhances the learning of natural concepts: An investigation of mechanisms, metacognition, and aging. Memory & Cognition, 39(5), 750–763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wozniak PA & Gorzelanczyk EJ (1994). Optimization of repetition spacing in the practice of learning. Acta neurobiologiae experimentalis, 54, 59–62. [PubMed] [Google Scholar]
- Zhang Y, Liu R-Y, Heberton GA, Smolen P, Baxter DA, Cleary LJ, & Byrne JH (2012). Computational design of enhanced learning protocols. Nature Neuroscience, 15(2), 294–297. [DOI] [PMC free article] [PubMed] [Google Scholar]


