Group testing case identification with biomarker information

Abstract

Screening procedures for infectious diseases, such as HIV, often involve pooling individual specimens together and testing the pools. For diseases with low prevalence, group testing (or pooled testing) can be used to classify individuals as diseased or not while providing considerable cost savings when compared to testing specimens individually. The pooling literature is replete with group testing case identification algorithms including Dorfman testing, higher-stage hierarchical procedures, and array testing. Although these algorithms are usually evaluated on the basis of the expected number of tests and classification accuracy, most evaluations in the literature do not account for the continuous nature of the testing responses and thus invoke potentially restrictive assumptions to characterize an algorithm’s performance. Commonly used case identification algorithms in group testing are considered and are evaluated by taking a different approach. Instead of treating testing responses as binary random variables (i.e., diseased/not), evaluations are made by exploiting an assay’s underlying continuous biomarker distributions for positive and negative individuals. In doing so, a general framework to describe the operating characteristics of group testing case identification algorithms is provided when these distributions are known. The methodology is illustrated using two HIV testing examples taken from the pooling literature.

1. Introduction

Testing individual specimens in pools, which is known as group testing (or pooled testing), is widespread in disease screening applications. Individuals in pools that test negatively are declared to be negative, and positive pools are resolved (or “decoded”) to determine which individuals are positive. The origins of group testing are usually traced back to Dorfman (1943), who proposed that it be used to screen World War II soldiers for syphilis. Since this seminal work, group testing has been applied to numerous infectious disease applications. A literature review reveals recent public health and surveillance applications for HIV (Krajden et al., 2014), HBV and HCV (Page-Shafer et al., 2008; Candotti and Allain, 2009), chlamydia and gonorrhea (Lewis et al., 2012), West Nile virus (Busch et al., 2005), and influenza (Edouard et al., 2015). Group testing is also routinely used by national organizations around the world to screen blood and plasma donations for HIV/HBV/HCV and other diseases (see, e.g., Schmidt et al., 2010; O’Brien et al., 2012; Stramer et al., 2013).

The original procedure proposed by Dorfman (1943) is a two-stage hierarchical algorithm; i.e., non-overlapping pools are tested in the first stage and individuals from positive pools are tested in the second. Hierarchical algorithms using a larger number of stages can reduce the number of tests needed when the disease prevalence is small. For example, Mehta et al. (2011) describe a three-stage algorithm for HIV testing in San Diego that uses master pools of size 10 in the first stage, subpools of size 5 in the second stage, and individual testing in the third. The most common non-hierarchical algorithm is two-dimensional array testing (Phatarfod and Sudbury, 1994; Hudgens and Kim, 2011; McMahan et al., 2012b), where individuals are tested in the rows and columns of an array. A recent HIV application in New Jersey (Martin et al., 2013) illustrates how array testing can even be used in higher dimensions (Kim and Hudgens, 2009). Comprehensive summaries of group testing algorithms and their operating characteristics are found in Kim et al. (2007) and Westreich et al. (2008).

When faced with the task of choosing an appropriate case identification algorithm for screening purposes, public health officials and lab technicians are interested in cost and accuracy. Laboratories with large budgets may opt to test specimens individually as pooling can reduce an assay’s sensitivity. In the group testing literature, this reduction is known as “the dilution effect” and can result in an increased number of false negative diagnoses. Group testing algorithms can be selected on the basis of minimizing the expected number of tests per individual to minimize costs (Kim et al., 2007; Westreich et al., 2008) or perhaps in a way that incorporates both the expected number of tests and classification accuracy (see, e.g., Malinovsky et al., 2016). Of course, additional practical considerations such as testing platform constraints, the time needed for testing, and the availability of individuals to pool should also be carefully considered.

When an individual or pooled specimen is tested, an assay typically elicits a binary diagnosis (positive/negative) that is derived from measuring a continuous biomarker; large values of this continuous measurement are usually evidence that the disease is present. Although it is widely known that dichotomizing a continuous outcome can lead to a loss in information, previous evaluations in group testing have largely ignored this underlying aspect and instead have relied explicitly on binary results. Doing so helps to facilitate the derivation of closed-form expressions for the expected number of tests and classification accuracy probabilities; however, this also usually requires one to make assumptions such as (a) the sensitivity and specificity are unaffected by pool size; i.e., there is no dilution effect, and (b) testing outcomes on pools containing common individuals are independent conditional on the true pool statuses. An important contribution of this article is to provide a general framework for case identification evaluation where these assumptions are not needed.

In offering this framework, our approach exploits the underlying continuous biomarker distributions associated with positive and negative individuals. In other words, we do not dichotomize testing outcomes into “positive” or “negative” categories, but instead we make our evaluations in terms of the biomarker distributions themselves. Our work is related to the methodology in Wein and Zenios (1996), who proposed using biomarker concentrations to determine an optimized Dorfman algorithm for HIV testing. However, our article takes a somewhat different perspective. We are not focused on determining optimal designs for specific group testing procedures per se; instead, our goal is to enhance previous case identification algorithm evaluations, such as those in Kim et al. (2007) and Westreich et al. (2008), in group testing applications where biomarker distributions are known. Our evaluations can be performed for any group testing procedure, including Dorfman testing, higher-stage hierarchical algorithms, and array testing. We obtain closed-form expressions for operating characteristics for normally distributed biomarkers in specific algorithms; however, even these expressions may be of limited utility for practitioners. We therefore use simulation to overcome the computational challenges when incorporating biomarker information.

2. Notation and Preliminaries

We modify the notation from Wang et al. (2015), who used biomarker distributions to acknowledge the dilution effect in group testing regression. Let T_i = 1 if the ith individual is truly positive; T_i = 0 otherwise. We assume the T_i’s are independent and identically distributed statuses with pr(T_i = 1) = p, the prevalence of the population. Generalizing our evaluation framework to allow for unequal individual disease probabilities (McMahan et al., 2012a; 2012b) or correlated individuals (Lendle et al., 2012) is straightforward; see Section 6. Let 𝒞̃_i denote the true biomarker level of the ith individual (e.g., viral load, optical density reading, antibody concentration, etc.). We assume the 𝒞̃_i’s are mutually independent random variables and that the conditional probability density function of 𝒞̃_i given the true status T_i = t is

$$f_{{\stackrel{\sim }{\mathcal{C}}}_i\mid T_i=t}(u)=t{f}_{{\stackrel{\sim }{\mathcal{C}}}^{+}}(u)+(1-t)f_{{\stackrel{\sim }{\mathcal{C}}}^{-}}(u),$$

where f_𝒞̃⁺ and f_𝒞̃⁻ denote the true biomarker density functions for positive and negative individuals, respectively. In other words, positive individuals in the population have true biomarker levels described by the common density f_𝒞̃⁺; similarly, negative individuals’ true biomarker levels are described by f_𝒞̃⁻.

We are interested in calculating quantities like the expected number of tests per individual and classification accuracy probabilities commonly seen in the group testing case identification literature (i.e., pooling sensitivity, pooling specificity, predictive values). To set our ideas, we assume a hierarchical group testing algorithm is used in S ≥ 2 stages, although we later modify our notation to account for array testing in two dimensions (Phatarfod and Sudbury, 1994; Hudgens and Kim, 2011; McMahan et al., 2012b); see Section 3.3. An S-stage hierarchical algorithm begins by testing a master pool of individual specimens. If the master pool tests negatively, all individuals are declared to be disease-free and no further testing is performed. Otherwise, non-overlapping subpools are formed and are tested in the second stage. Any second-stage subpool that tests positively is split again while subpools that test negatively in the second stage are declared to be disease-free. This process continues until all subpools in a particular stage test negatively or until individual testing (in stage S) is performed.

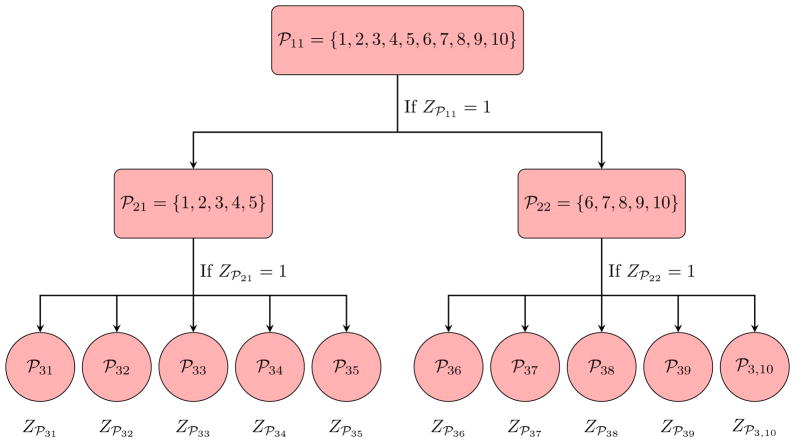
For an S-stage hierarchical algorithm, let ℘_sl denote the index set of individuals in the lth pool formed at the sth stage of testing, for l = 1, 2, …, n₁/n_s and s = 1, 2, …, S, where n_s = |℘_sl| is the number of individuals in ℘_sl. To illustrate this notation, Figure 1 displays the S = 3 stage hierarchical algorithm described in Mehta et al. (2011) from Section 1. In this example, the master pool is ℘₁₁ = {1, 2, …, 10}, the two second-stage pools are ℘₂₁ = {1, 2, …, 5} and ℘₂₂ = {6, 7, …, 10}, and the singleton pools ℘₃₁ = {1},℘₃₂ = {2}, …,℘_3,10 = {10} are for individual testing in the third stage. These pools are of size n₁ = 10, n₂ = 5, and n₃ = 1. Additional examples of hierarchical algorithms used in HIV testing are found in Sherlock et al. (2007). Henceforth, a general S-stage hierarchical algorithm is denoted by H(n₁: n₂: ⋯: n_S), where n_S = 1. Note that Dorfman’s seminal strategy uses S = 2 stages.

Figure 1.

S = 3 stage hierarchical group testing algorithm H(n₁ = 10: n₂ = 5: n₃ = 1).

Let T_℘sl = 1 if the lth pool in the sth stage is truly positive; i.e., ℘_sl contains at least one truly positive individual, T_℘sl = 0 otherwise. Similarly, let Z_℘sl = 1 if ℘_sl tests positively, Z_℘sl = 0 otherwise. To acknowledge the continuous nature of the diagnostic assay, we assume that Z_℘sl = I(𝒞_℘sl > τ_℘sl); i.e., the pool ℘_sl tests positively if 𝒞_℘sl, the measured biomarker level of the pool, exceeds a threshold τ_℘sl which potentially depends on the pool size n_s at stage s. To acknowledge the potential of error when measuring the true biomarker level 𝒞̃_℘sl, we assume that 𝒞_℘sl | 𝒞̃_℘sl ~ f_ε, where f_ε = f_ε(·| 𝒞̃_℘sl) is a known probability density function. Therefore, our framework utilizes three distributions: the true biomarker distributions for positive and negative individuals, f_𝒞̃⁺ and f_𝒞̃⁻, respectively, and f_ε, which incorporates the effect of assay measurement error. Threshold selection for τ_℘sl is discussed in Section 4.

As noted in Section 1, previous evaluations of case identification algorithms have largely assumed the sensitivity and specificity are constant and hence are unaffected by pool size. Although this assumption may be reasonable when testing negative pools (i.e., constant specificity), it is potentially more dubious when testing positive pools. Using the Law of Total Probability, note that the sensitivity associated with testing ℘_sl can be written as

$$\text{pr}(Z_{{\mathcal{P}}_{sl}}=1\mid T_{{\mathcal{P}}_{sl}}=1)=\frac{{\sum }_{m=1}^{n_s}\text{pr}(Z_{{\mathcal{P}}_{sl}}=1\mid {\sum }_{i\in {\mathcal{P}}_{sl}}{T}_i=m)\text{pr}({\sum }_{i\in {\mathcal{P}}_{sl}}{T}_i=m)}{\text{pr}(T_{{\mathcal{P}}_{sl}}=1)},$$

where the random variable Σ_i∈℘sl T_i counts the number of positive individuals in ℘_sl. Therefore, for the sensitivity to remain constant throughout the testing process, one would have to require that pr(Z_℘sl = 1| Σ_i∈℘sl T_i = m) are equal for each m = 1, 2, …, n_s, l = 1, 2, …, n₁/n_s and s = 1, 2, …, S. Clearly, this requirement may be unsuitable−especially when testing results are heavily influenced by dilution.

On the other hand, when written in terms of the true biomarker distributions, f_𝒞̃⁺ and f_𝒞̃⁻, and the measurement error density f_ε, the sensitivity of ℘_sl is given by

$$\begin{gathered} S_e(n_s)=\text{pr}(Z_{{\mathcal{P}}_{sl}}=1\mid T_{{\mathcal{P}}_{sl}}=1)=\text{pr}\left({\mathcal{C}}_{{\mathcal{P}}_{sl}}>{\tau }_{{\mathcal{P}}_{sl}}|\sum _{i\in {\mathcal{P}}_{sl}}{T}_i>0\right) \\ =\frac{{\sum }_{m=1}^{n_s}\left(\begin{array}{c}{n}_s\\ m\end{array}\right)p^m{q}^{n_s-m}{S}_e(n_s:m)}{1-q^{n_s}}, \end{gathered}$$

where q = 1 − p and

$$S_e(n_s:m)={\int }_{{\tau }_{{\mathcal{P}}_{sl}}}^{\infty }{\int }_{-\infty }^{\infty }{f}_{\epsilon }(u\mid v)n_s{f}_{{\sum }_{i\in {\mathcal{P}}_{sl}}{\stackrel{\sim }{\mathcal{C}}}_i}^{m(n_s-m)}(n_{s}v)\mathit{dvdu},$$ (1)

where

$$f_{{\sum }_{i\in {\mathcal{P}}_{sl}}{\stackrel{\sim }{\mathcal{C}}}_i}^{m(n_s-m)}(v)={\int }_{{\sum }_{i=1}^{n_s}{v}_i=v}\prod _{i=1}^m{f}_{{\stackrel{\sim }{\mathcal{C}}}^{+}}(v_i)\prod _{i=m+1}^{n_s}{f}_{{\stackrel{\sim }{\mathcal{C}}}^{-}}(v_i)d{v}_{1}d{v}_2\dots d{v}_{n_s}.$$ (2)

The expression in Equation (2) is the density of Σ_i∈℘sl 𝒞̃_i, the sum of the mutually independent biomarker levels in ℘_sl when ℘_sl contains exactly m ≥ 1 positive and n_s − m negative individuals; we obtain this density by convolving the true individual biomarker densities f_𝒞̃⁺ and f_𝒞̃⁻ m and n_s − m times, respectively.

In writing Equation (1), we assume the true biomarker level 𝒞̃_℘sl is the arithmetic average of the individual biomarker levels in ℘_sl; i.e., ${\stackrel{\sim }{\mathcal{C}}}_{{\mathcal{P}}_{sl}}=n_s^{-1}{\sum }_{i\in {\mathcal{P}}_{sl}}{\stackrel{\sim }{\mathcal{C}}}_i$. This assumption is often viewed as sacrosanct in the biomarker pooling literature (see, e.g., Zhang and Albert, 2011; Malinovsky et al., 2012; Mitchell et al., 2014; Delaigle and Hall, 2015) and is likely reasonable when pools are formed from aliquots of equal volume. Under this assumption, the specificity of ℘_sl is given by

$$\begin{gathered} S_p(n_s)=\text{pr}(Z_{{\mathcal{P}}_{sl}}=0\mid T_{{\mathcal{P}}_{sl}}=0)=\text{pr}\left({\mathcal{C}}_{{\mathcal{P}}_{sl}}<{\tau }_{{\mathcal{P}}_{sl}}|\sum _{i\in {\mathcal{P}}_{sl}}{T}_i=0\right) \\ ={\int }_{-\infty }^{{\tau }_{{\mathcal{P}}_{sl}}}{\int }_{-\infty }^{\infty }{f}_{\epsilon }(u\mid v)n_s{f}_{{\sum }_{i\in {\mathcal{P}}_{sl}}{\stackrel{\sim }{\mathcal{C}}}_i}^{0(n_s-0)}(n_{s}v)\mathit{dvdu}, \end{gathered}$$ (3)

where $f_{{\sum }_{i\in {\mathcal{P}}_{sl}}{\stackrel{\sim }{\mathcal{C}}}_i}^{0(n_s-0)}(·)$ is the density that convolves f_𝒞̃⁻ n_s times−once for each of the negative individuals in ℘_sl. Note that Equations (1) and (3) are similar in form to the analogous expressions found in McMahan et al. (2013) and Delaigle and Hall (2015), both of whom incorporate biomarker and measurement error distributions in group testing regression.

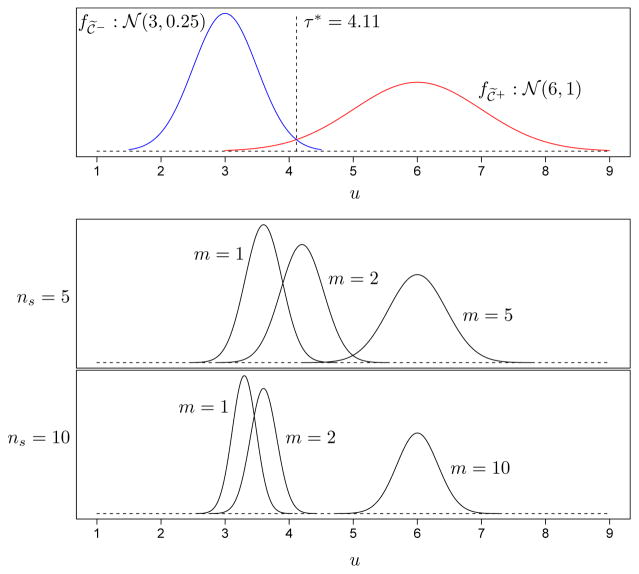
As an example, suppose the true individual biomarker distributions for negative and positive individuals are 𝒞̃⁻ ~ 𝒩(3, 0.25) and 𝒞̃⁺ ~ 𝒩(6, 1), respectively, and that the measurement error density is 𝒩(𝒞̃, 0.0025). For these distribution choices, the threshold that maximizes Youden’s index (Youden, 1950) for individual testing is τ^* = 4.11, which provides values of sensitivity and specificity (for individual testing) equal to 0.970 and 0.987, respectively. To illustrate the effect of pooling, Figure 2 displays the densities of the measured biomarker level on ℘_sl; i.e., $f_{{\mathcal{C}}_{{\mathcal{P}}_{sl}}}(u)={\int }_{-\infty }^{\infty }{f}_{\epsilon }(u\mid v)n_s{f}_{{\sum }_{i\in {\mathcal{P}}_{sl}}{\stackrel{\sim }{\mathcal{C}}}_i}^{m(n_s-m)}(n_{s}v)dv$, for different values of m when the pool size is n_s = 5 and n_s = 10. This figure illustrates how relevant operating characteristics in group testing could ultimately depend on the individual biomarker distributions, the pool size, the threshold used for pools (see Section 4), and the number of positive individuals in each pool. In other words, once one moves beyond treating pool and individual diagnoses as binary, case identification evaluation becomes far more complicated. Note that we have created Figure 2 assuming normality for 𝒞̃⁻, 𝒞̃⁺, and the measurement error so that f_𝒞℘sl</sub></sub> (u) can be calculated exactly. However, biomarkers in real applications are rarely normally distributed and calculating f_𝒞℘sl</sub></sub> (u) for non-normal biomarkers, if it is even possible to do so, potentially involves high-dimensional integration (i.e., of dimension equal to the pool size).

Figure 2.

Top panel: Individual biomarker densities for 𝒞̃⁻ ~ 𝒩(3, 0.25) and 𝒞̃⁺ ~ 𝒩(6, 1). Under our measurement error density assumption, 𝒞|𝒞̃ ~ 𝒩(𝒞̃, 0.0025), the threshold τ^* = 4.11 maximizes Youden’s index for individual testing. Middle and bottom panels: Densities of the pooled biomarker measurements, $f_{{\mathcal{C}}_{{\mathcal{P}}_{sl}}}(u)={\int }_{-\infty }^{\infty }{f}_{\epsilon }(u\mid v)n_s{f}_{{\sum }_{i\in {\mathcal{P}}_{sl}}{\stackrel{\sim }{\mathcal{C}}}_i}^{m(n_s-m)}(n_{s}v)dv$, for different m (the number of positive individuals in ℘_sl) when the pool size is n_s = 5 and n_s = 10.

3. Operating Characteristics

3.1. Efficiency

The most important characteristic of a group testing case identification algorithm is its expected number of tests per individual, or efficiency. Because the cost of screening is usually highly correlated with the number of tests expended, algorithms with lower values of this expectation are generally preferred. For example, an algorithm whose efficiency is 0.5 is twice as efficient as individual testing. An algorithm whose efficiency is larger than 1 uses more tests than individual testing on average. In the group testing literature, optimal algorithms are usually identified as those that are the most efficient.

Unfortunately, within the general framework we have outlined in this article, calculating the efficiency quickly becomes unmanageable−even for simple algorithms. For example, consider the S = 3 stage algorithm H(10: 5: 1) depicted in Figure 1. It is easy to see that the efficiency of this algorithm is $\frac{1}{10}+\frac{1}{5}\text{pr}(Z_{{\mathcal{P}}_{11}}=1)+\text{pr}(Z_{{\mathcal{P}}_{11}}=1,Z_{{\mathcal{P}}_{21}}=1)$, where recall Z_℘11 and Z_℘21 denote the (binary) testing responses of ℘₁₁ and ℘₂₁, respectively. When written in terms of the biomarker distributions, the first-stage probability is

$$\begin{gathered} \text{pr}(Z_{{\mathcal{P}}_{11}}=1)=\text{pr}({\mathcal{C}}_{{\mathcal{P}}_{11}}>{\tau }_{{\mathcal{P}}_{11}}\mid T_{{\mathcal{P}}_{11}}=1)\text{pr}(T_{{\mathcal{P}}_{11}}=1)+\text{pr}({\mathcal{C}}_{{\mathcal{P}}_{11}}>{\tau }_{{\mathcal{P}}_{11}}\mid T_{{\mathcal{P}}_{11}}=0)\text{pr}(T_{{\mathcal{P}}_{11}}=0) \\ =\sum _{m=1}^{10}\left(\begin{array}{c}10\\ m\end{array}\right)p^m{q}^{10-m}{S}_e(10:m)+\{1-S_p(10)\}{q}^{10}, \end{gathered}$$

where S_e(10: m) is calculated using Equations (1) and (2) and S_p(10) is calculated using Equation (3) with n_s = n₁ = 10, τ_℘sl = τ_℘11, and ℘_sl = ℘₁₁. Even more daunting, a second-stage pool tests positively with probability pr(Z_℘11 = 1, Z_℘21 = 1), which equals

$$\begin{gathered} \sum _{m_1=0}^5\sum _{m_2=0}^5\left(\begin{array}{c}5\\ m^2\end{array}\right)p^{m_2}{p}^{5-m_2}\left(\begin{array}{c}5\\ m_1\end{array}\right)p^{m_1}{q}^{5-m_1}{\int }_{{\tau }_{{\mathcal{P}}_{11}}}^{\infty }{\int }_{{\tau }_{{\mathcal{P}}_{21}}}^{\infty }\{{\int }_{{ℝ}^{10}}\prod _{s=1}^2{f}_{\epsilon }\left(u_s\mid \frac{1}{n_s}\sum _{i=1}^{n_s}{v}_i\right) \\ \times \prod _{i=1}^{m_2}{f}_{{\stackrel{\sim }{\mathcal{C}}}^{+}}(v_i)\prod _{i=m_2+1}^5{f}_{{\stackrel{\sim }{\mathcal{C}}}^{-}}(v_i)\prod _{i=6}^{m_1+5}{f}_{{\stackrel{\sim }{\mathcal{C}}}^{+}}(v_i)\prod _{i=m_1+6}^{10}{f}_{{\stackrel{\sim }{\mathcal{C}}}^{-}}(v_i)d{v}_{1}d{v}_2\cdots d{v}_{10}\}d{u}_{2}d{u}_1, \end{gathered}$$

where n₁ = 10 and n₂ = 5. In this expression, it is understood that products of the form ${\prod }_{i=a}^b{f}_{{\stackrel{\sim }{\mathcal{C}}}^{+}}(v_i)$ and ${\prod }_{i=a}^b{f}_{{\stackrel{\sim }{\mathcal{C}}}^{-}}(v_i)$, a > b, are vacuous.

As this simple example illustrates, offering a biomarker-based framework for group testing case identification presents nearly overwhelming computational challenges. Unfortunately, this is the price one must pay when relaxing assumptions used in previous evaluations. For example, under classical assumptions in Kim et al. (2007) and Westreich et al. (2008), the probabilities we have just presented reduce to pr(Z_℘11 = 1) = S_e(1 − q¹⁰) + (1 − S_p)q¹⁰ and

$$\text{pr}(Z_{{\mathcal{P}}_{11}}=1,Z_{{\mathcal{P}}_{21}}=1)=S_e^2(1-q^5)+S_e(1-S_p)(q^5-q^{10})+{(1-S_p)}^2{q}^{10},$$

respectively, where S_e and S_p are the assumed common sensitivity and specificity for pools of size n₁ = 10 and n₂ = 5. The simplified formula for pr(Z_℘11 = 1, Z_℘21 = 1) above arises only when the testing responses Z_℘11 and Z_℘21 are conditionally independent given the true pool statuses T_℘11 and T_℘21. This assumption is required under classical evaluations because ℘₁₁ and ℘₂₁ contain common individuals.

In Appendix A in the Supplementary Material, we have derived a general expression for the efficiency of an S-stage hierarchical algorithm. This derivation has been described previously in the group testing literature; see, e.g., Kim et al. (2007) and the references therein. In our notation, the efficiency can be expressed as

$$\text{EFF}\{H(n_1:n_2:\cdots :n_S)\}=\frac{1}{n_1}+\sum _{s=1}^{S-1}\frac{1}{n_{s+1}}\text{pr}\left(\prod _{s^{\prime }=1}^s{Z}_{{\mathcal{P}}_{s^{\prime }1}}=1\right),$$

where the random variable ${\prod }_{s^{\prime }=1}^s{Z}_{{\mathcal{P}}_{s^{\prime }1}}$ equals 1 if and only if the first pool in each of the first s stages tests positively. Calculating $\text{pr}({\prod }_{s^{\prime }=1}^s{Z}_{{\mathcal{P}}_{s^{\prime }1}}=1)$ within our framework involves accounting for the joint uncertainty that arises in the correlated, error-laden biomarker measurements 𝒞_℘11, 𝒞_℘21, …, 𝒞_℘s1, an extremely difficult problem analytically. Although this probability can be calculated exactly under normal biomarker assumptions, in general we recommend using Monte Carlo simulation and estimating EFF{H(n₁: n₂: ⋯: n_S)} instead. Such a strategy is flexible and will accommodate any biomarker and measurement error distributions. In addition, one can quickly estimate the variance of the number of tests per individual (Kim et al., 2007), which would otherwise be an intractable calculation. A description of our simulation procedure is now given.

SIMULATION PROCEDURE

1. Generate T₁, T₂, …, T_n1~ iid Bernoulli(p). Generate 𝒞̃_i ~ f_𝒞̃i|Ti=t (u) = tf_𝒞̃⁺(u) + (1 − t)f_𝒞̃⁻(u), i = 1, 2, …, n₁.

2. (Stage 1). Calculate ${\stackrel{\sim }{\mathcal{C}}}_{{\mathcal{P}}_{11}}=n_1^{-1}{\sum }_{i\in {\mathcal{P}}_{11}}{\stackrel{\sim }{\mathcal{C}}}_i$ and generate 𝒞_℘11 from f_ε(·| 𝒞̃_℘11).

   1. If Z_℘11 = I(𝒞_℘11 > τ_℘11) = 0, stop and classify the n₁ individuals in ℘₁₁ as negative.

   2. If Z_℘11 = I(𝒞_℘11 > τ_℘11) = 1, divide 𝒞̃_i ∈ ℘₁₁ into subgroups of size n₂.

3. (Stage 2). Calculate ${\stackrel{\sim }{\mathcal{C}}}_{{\mathcal{P}}_{2l}}=n_2^{-1}{\sum }_{i\in {\mathcal{P}}_{2l}}{\stackrel{\sim }{\mathcal{C}}}_i$ for each subgroup in Step 2(b) and generate 𝒞_℘2lfrom f_ε(·| 𝒞̃_℘2l). Calculate Z_℘2l= I(𝒞_℘2l> τ_℘2l). For each l,

   1. if Z_℘2l= I(𝒞_℘2l> τ_℘2l) = 0, classify the n₂ individuals in ℘_2l as negative (stop if all second-stage subgroups are negative).

   2. if Z_℘2l= I(𝒞_℘2l> τ_℘2l) = 1, divide 𝒞̃_i ∈ ℘_2l into subgroups of size n₃.

4. (Stage 3). For each subgroup in Step 3(b), calculate ${\stackrel{\sim }{\mathcal{C}}}_{{\mathcal{P}}_{3l}}=n_3^{-1}{\sum }_{i\in {\mathcal{P}}_{3l}}{\stackrel{\sim }{\mathcal{C}}}_i$, generate 𝒞_℘3lfrom f_ε(·| 𝒞̃_℘3l), and calculate Z_℘3l= I(𝒞_℘3l> τ_℘3l). Continue this overall process until all subgroups in a particular stage test negatively or until individual testing (in stage S) is performed.

We implement this procedure B times and estimate the efficiency of H(n₁: n₂: ⋯: n_S) using

$$\widehat{\text{EFF}}\{H(n_1:n_2:\cdots :n_S)\}=\frac{1}{n_{1}B}\sum _{b=1}^B{M}_b,$$

where M_b is the number of tests observed in the bth replication. The variance of the number of tests per individual, denoted by var{H(n₁: n₂: ⋯: n_S)}, can be estimated using the sample variance of M₁/n₁,M₂/n₁, …,M_B/n₁. Our simulation procedure is extremely fast and thus can be performed using very large values of B. Under normal biomarker assumptions, we show in Appendix B in the Supplementary Material that the difference between calculating EFF{H(n₁: n₂: ⋯: n_S)} exactly and estimating it using a large number of replications is negligible.

3.2. Classification Accuracy

Although the efficiency of a group testing case identification algorithm is its most important characteristic, being able to quantify an algorithm’s classification accuracy is also critical. Two commonly used measures of accuracy in the case identification literature are pooling sensitivity and pooling specificity. For an S-stage hierarchical algorithm, the pooling sensitivity

$$\text{PSE}\{H(n_1:n_2:\cdots :n_S)\}=\text{pr}\left(\prod _{s=1}^S{Z}_{{\mathcal{P}}_{s1}}=1|T_1=1\right)$$

is the probability a truly positive individual is classified positively. Analogously, the pooling specificity

$$\text{PSP}\{H(n_1:n_2:\cdots :n_S)\}=1-\text{pr}\left(\prod _{s=1}^S{Z}_{{\mathcal{P}}_{s1}}=1|T_1=0\right)$$

is the probability a truly negative individual is classified negatively. Values of PSE and PSP close to unity are preferred as this translates to a small percentage of false negative and false positive diagnoses. Simple formulae for PSE and PSP are available under classical assumptions (see, e.g., Kim et al., 2007). For example, $\text{PSE}\{H(n_1:n_2:\cdots :n_S)\}=S_e^S$ implies that a larger number of stages decreases pooling sensitivity. Of course, this formula no longer applies in our more general framework.

We derive expressions for PSE{H(n₁: n₂: ⋯: n_S)} and PSP{H(n₁: n₂: ⋯: n_S)} in terms of f_𝒞̃⁺, f_𝒞̃⁻, and f_ε in Appendix B in the Supplementary Material. However, as with the efficiency, these expressions may ultimately be too complicated for practical use. Therefore, simulation details to estimate PSE and PSP for an S-stage hierarchical algorithm are also provided. With these estimates in hand, one can also estimate the pooling positive predictive value

$$\text{PPV}=\frac{p\text{PSE}}{p\text{PSE}+(1-p)(1-\text{PSP})}$$

and the pooling negative predictive value

$$\text{NPV}=\frac{(1-p)\text{PSP}}{(1-p)\text{PSP}+p(1-\text{PSE})}.$$

These probabilities measure how likely an individual is truly positive (negative) given that the individual has been classified positively (negatively).

3.3. Array Testing

Our simulation methodology can be extended to estimate the operating characteristics of array testing algorithms. In two-dimensional array testing, individuals are first assigned to the cells of an array with R rows and C columns (Phatarfod and Sudbury, 1994; McMahan et al., 2012b). In the first stage, the rows and the columns of the array are tested. The second stage uses individual testing for individuals not classified as negative after the first stage. When the prevalence p is small, two-dimensional array testing can be more efficient than hierarchical algorithms (Kim et al., 2007; Westreich et al., 2008).

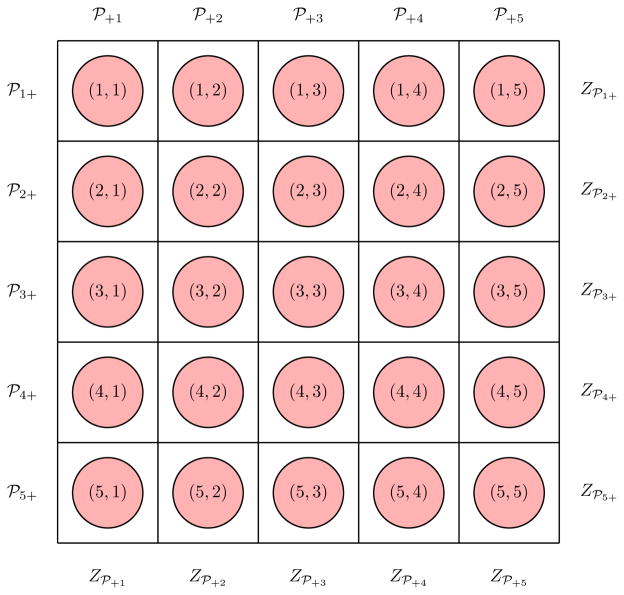
We modify our notation from Section 2 to accommodate array testing in two dimensions. Let T_r,c denote the true binary status of the individual in the (r, c)th position, and let 𝒞̃_r,c denote this individual’s true biomarker level so that f_{𝒞̃r,c|Tr,c=t}(u) = tf_𝒞̃⁺(u) + (1 − t)f_𝒞̃⁻(u), for r = 1, 2, …,R and c = 1, 2, …,C. The rth row and cth column pools are denoted by ℘_r+ = {(r, 1), (r, 2), …, (r,C)} and ℘_+c = {(1, c), (2, c), …, (R, c)}, respectively. Let ${\stackrel{\sim }{\mathcal{C}}}_{{\mathcal{P}}_{r+}}=C^{-1}{\sum }_{c=1}^C{\stackrel{\sim }{\mathcal{C}}}_{r,c}$ and 𝒞_℘r+ denote the true and measured biomarker level of ℘_r+, respectively. Let ${\stackrel{\sim }{\mathcal{C}}}_{{\mathcal{P}}_{+c}}=R^{-1}{\sum }_{r=1}^R{\stackrel{\sim }{\mathcal{C}}}_{r,c}$ and 𝒞_℘+cbe defined analogously for ℘_+c. In the first stage, row and column testing provide Z_℘r+ = I(𝒞_℘r+ > τ_℘r+) and Z_℘+c= I(𝒞_℘+c > τ_℘+c), where τ_℘r+ and τ_℘+care first-stage thresholds (see Section 4) and where 𝒞_℘r+| 𝒞̃_℘r+ ~ f_ε(·| 𝒞̃_℘r+) and 𝒞_℘+c| 𝒞̃_℘+c~ f_ε(·| 𝒞̃_℘+c). We follow the convention in Kim et al. (2007) when identifying which individuals to test in the second stage; i.e., those individuals in

$$\mathcal{M}=\left\{(r,c):Z_{{\mathcal{P}}_{r+1}}=Z_{{\mathcal{P}}_{+c}}=1\text{or}{Z}_{{\mathcal{P}}_{r+1}}=1,\sum _{c^{\prime }=1}^C{Z}_{{\mathcal{P}}_{+c^{\prime }}}=0\text{or}\sum _{r^{\prime }=1}^R{Z}_{{\mathcal{P}}_{r^{\prime }+}}=0,Z_{{\mathcal{P}}_{+c}}=1\right\}.$$

The event {Z_℘r+ = Z_℘+c= 1} occurs at the intersection of the rth row and cth column. The other two events in ℳ represent ambiguous first-stage outcomes that could arise from testing error. Second-stage testing observes Z_r,c = I(𝒞_r,c > τ) for each individual in ℳ, where 𝒞_r,c| 𝒞̃_r,c ~ f_ε(·| 𝒞̃_r,c) and τ is a threshold for individual testing. Figure 3 illustrates this notation when R = C = 5 (i.e., for a square array). Complete simulation details to estimate the efficiency and accuracy probabilities are provided in Appendix C in the Supplementary Material.

Figure 3.

Two-dimensional array testing with R = C = 5. First-stage testing results on row pools are Z_℘1+,Z_℘2+, …,Z_℘5+, where Z_℘r+ = I(𝒞_℘r+ > τ_℘r+), for r = 1, 2, …, 5. Testing results on column pools are Z_℘+1,Z_℘+2, …,Z_℘+5, where Z_℘+c= I(𝒞_℘+c> τ_℘+c), for c = 1, 2, …, 5. Second-stage testing is performed on individuals as described in Section 3.3.

4. Threshold Selection

There are different types of assays used for infectious disease detection, including antibody tests (e.g., ELISA, Western Blot, combination tests which also detect antigens, etc.) and more modern tests which utilize amplification methods. Before an assay is approved for commercial use, it is usually applied to known positive and known negative specimens to determine suitable thresholds for individual testing. Ideally, these thresholds provide high levels of sensitivity and specificity when testing individual specimens. A complete list of screening assays for HIV/HBV/HCV and other infectious agents in the United States is available at www.fda.com. An approved assay’s product insert typically recommends which threshold should be used to identify positive individuals.

When an assay is applied to pooled specimens, choosing the appropriate threshold can be more subjective. Early work in group testing estimation (see, e.g., Chen and Swallow, 1990; Tu et al., 1994) suggested that individual testing assay thresholds might also be used for pools; see Stephens et al. (2000) and Currie et al. (2004) for specific applications. In the infectious disease pooling literature, a common strategy is to take the individual testing threshold, say τ, and divide it by the number of individuals in the pool; e.g., τ_℘11 = τ/n₁ for a master pool in an S-stage hierarchical algorithm H(n₁: n₂: ⋯: n_S), τ_℘2l= τ/n₂ for a second-stage pool, and so on. Note that selecting a pooled threshold inappropriately large will decrease the pooling sensitivity, thereby increasing the number of false negative diagnoses. On the other hand, a pooled threshold that is too small will provide far too many false positive pools, thereby weakening the efficiency of group testing.

For individual testing with threshold τ, it is easy to see that the sensitivity is a decreasing function of τ while the specificity is an increasing function of τ. Therefore, one way to choose an individual testing threshold is to maximize Youden’s index (Youden, 1950); i.e., τ^* = arg max_τ∈ℝ{S_e(τ) + S_p(τ) − 1}, as this offers a balance between maximizing both sensitivity and specificity. For a pool generically denoted by ℘ consisting of individuals whose true disease statuses are denoted by T_i, we propose a pooled threshold that is similar in spirit to Youden’s index for individual testing; i.e.,

$${\tau }_{\mathcal{P}}^{\ast }=arg\underset{\tau \in ℝ}{max}\left\{{\int }_{\tau }^{\infty }{f}_{{\mathcal{C}}_{\mathcal{P}}\mid {\sum }_i{T}_i=1}(u)du+{\int }_{-\infty }^{\tau }{f}_{{\mathcal{C}}_{\mathcal{P}}\mid {\sum }_i{T}_i=0}(u)du-1\right\}.$$

The conditional density f_{𝒞℘| ΣiTi=1}(·) describes the distribution of the measured biomarker level of pool ℘ when there is exactly one positive individual in it. We have selected this density for two reasons. First, in low disease prevalence applications, it is almost always true that a truly positive pool is positive because there is only one positive individual in the pool. Therefore, ${\tau }_{\mathcal{P}}^{\ast }$ will be the appropriate threshold for a large majority of the positive pools. Second, as positive pools could conceivably contain more than one positive individual, ${\tau }_{\mathcal{P}}^{\ast }$ favors the adoption of a smaller-than-necessary threshold. Although this may inflate the efficiency slightly, it also promotes the detection of positive individuals.

5. Applications

We illustrate our simulation methodology using two examples taken from the HIV pooling literature. The first example is from Wein and Zenios (1996) and Zenios and Wein (1998), who consider HIV testing with an antibody assay. The second example from May et al. (2010) is not an classical HIV screening application, but instead describes a virological assay to detect treatment failure among HIV patients. The salient feature of each application is that biomarker distributions for 𝒞⁺ and 𝒞⁻ are presented as well as posited distributions for the assay measurement error. We illustrate our biomarker-based evaluations in each application using Dorfman testing, an S = 3 stage hierarchical algorithm using halving (Black et al., 2012), and two-dimensional array testing.

For Application 1 (Wein and Zenios, 1996; Zenios and Wein, 1998), the biomarker distributions provided by the authors are ln 𝒞⁺ ~ 𝒩(0.958, 0.865²), 𝒞⁻ ~ I(𝒞⁻ = 0.086), and the measurement error distribution is 𝒞_℘|𝒞̃_℘ ~ 𝒩{ 𝒞̃_℘/(1+ 𝒞̃_℘), 0.0088× 𝒞̃_℘/(1+ 𝒞̃_℘)²}. The use of a degenerate distribution for negative individuals is described in Zenios and Wein (1998). For this collection of distributions, the threshold that maximizes Youden’s index for individual testing is τ^* = 0.0485, which provides values of S_e > 0.999 and S_p > 0.999; i.e., individual testing is nearly perfect. For Application 2 (May et al., 2010), log₁₀ 𝒞⁺ is specified to have a two-component mixture 0.93G₁ +0.07G₂, where G₁(G₂) is a three-parameter gamma random variable with shape parameter 1.6 (3.2), scale parameter 0.5 (0.5), and location parameter 2.7 (2.7). For negative individuals, 𝒞⁻ ~ 0.85U₁ +0.05U₂ +0.10U₃, where U₁ ~ 𝒰(0, 50), U₂ ~ 𝒰(50, 100), and U₃ ~ 𝒰(100, 500), where 𝒰(a, b) denotes a uniform distribution from a to b. The measurement error distribution is specified as log₁₀ 𝒞_℘| 𝒞̃_℘ ~ 𝒩(log₁₀ 𝒞̃_℘, 0.12²). The threshold that maximizes Youden’s index for individual testing in Application 2 is τ^* = 436.11, which provides values of S_e = 0.989 and S_p = 0.980.

For both applications, we illustrate the differences between our biomarker-based calculations of efficiency, variability, and classification accuracy and the same calculations which rely on classical assumptions (Kim et al., 2007; Westreich et al., 2008); i.e., constant S_e(S_p) and conditional independence of testing responses given the true statuses. In doing so, we consider values of p ∈ {0.01, 0.05, 0.10} while utilizing the three threshold options described in Section 4: τ^* (same for individual testing and pools), τ^* divided by pool size, and our proposed Youden index threshold for pools ${\tau }_{\mathcal{P}}^{\ast }$. For each combination of p and the threshold used, we calculate the efficiency, the standard deviation of the number of tests per individual, and the four accuracy probabilities in Section 3.2. All of our biomarker-based characteristics are estimated using B = 1,000,000 Monte Carlo data sets. Operating characteristics under classical assumptions are calculated exactly using the expressions in Kim et al. (2007).

Our results when p = 0.05 are provided in Table 1; the same tables for p = 0.01 and p = 0.10 are given in Appendix D in the Supplementary Material. In each table, we first determine the most efficient Dorfman algorithm H(n₁: 1), three-stage halving algorithm H(n₁: n₁/2: 1), and square array algorithm A(n₁ × n₁) under the classical assumptions in Kim et al. (2007) and then compare our biomarker-based evaluations to this optimal setting. Our goal is not to try to outperform the operating characteristics under classical assumptions per se, but instead to illustrate the differences between these calculations and those which exploit underlying biomarker distributions and measurement error, and, more pointedly, how these differences depend on the threshold used. This comparison simultaneously allows one to assess how robust group testing characteristics are under classical assumptions. To the best of knowledge, this is the first assessment of this type in the case identification literature.

Table 1.

Operating characteristics for Application 1 (Zenios and Wein, 1998) and Application 2 (May et al., 2010) when p = 0.05. Efficiency (EFF), standard deviation of the number of tests per individual (SD), and accuracy probabilities (PSE, PSP, PPV, and NPV) are provided. The threshold τ^* maximizes Youden’s index for individual testing. The threshold ${\tau }_{\mathcal{P}}^{\ast }$ is calculated as in Section 4. Classical operating characteristics are calculated exactly from Kim et al. (2007). Biomarker-based characteristics are estimated using B = 1,000,000 Monte Carlo data sets. For each application, individual testing values of S_e and S_p are provided. The same tables for p = 0.01 and p = 0.10 are in Appendix D in the Supplementary Material.

			Biomarker-based evaluations			Classical
			τ*	τ*/pool size	${\tau }_{\mathcal{P}}^{\ast }$
Application 1 Se > 0.999; Sp > 0.999	H(5: 1)	EFF (SD)	0.426 (0.418)	0.788 (0.492)	0.426 (0.418)	0.426 (0.418)
		PSE	0.996	>0.999	0.997	>0.999
		PSP	>0.999	>0.999	>0.999	>0.999
		PPV	>0.999	>0.999	>0.999	>0.999
		NPV	>0.999	>0.999	>0.999	>0.999
	H(8: 4: 1)	EFF (SD)	0.391 (0.388)	0.704 (0.450)	0.393 (0.391)	0.395 (0.389)
		PSE	0.986	0.999	0.993	>0.999
		PSP	>0.999	>0.999	>0.999	>0.999
		PPV	>0.999	>0.999	>0.999	>0.999
		NPV	0.999	>0.999	>0.999	>0.999
	A(9 × 9)	EFF (SD)	0.374 (0.115)	0.835 (0.161)	0.378 (0.116)	0.380 (0.117)
		PSE	0.973	0.999	0.986	>0.999
		PSP	>0.999	>0.999	>0.999	>0.999
		PPV	>0.999	>0.999	>0.999	>0.999
		NPV	0.999	>0.999	>0.999	>0.999
Application 2 Se = 0.989; Sp = 0.980	H(5: 1)	EFF (SD)	0.337 (0.344)	0.588 (0.487)	0.458 (0.437)	0.439 (0.426)
		PSE	0.633	0.987	0.952	0.978
		PSP	0.998	0.983	0.991	0.996
		PPV	0.931	0.756	0.853	0.930
		NPV	0.981	>0.999	0.997	0.999
	H(8: 4: 1)	EFF (SD)	0.258 (0.302)	0.575 (0.424)	0.406 (0.397)	0.396 (0.387)
		PSE	0.513	0.986	0.920	0.967
		PSP	0.999	0.985	0.994	0.997
		PPV	0.947	0.776	0.894	0.948
		NPV	0.975	0.999	0.996	0.998
	A(10 × 10)	EFF (SD)	0.253 (0.053)	0.751 (0.169)	0.394 (0.121)	0.385 (0.120)
		PSE	0.412	0.989	0.892	0.967
		PSP	0.999	0.981	0.994	0.997
		PPV	0.964	0.733	0.889	0.948
		NPV	0.970	0.999	0.994	0.998

From Table 1 and the additional tables in Appendix D, it is clear that the efficiency (EFF), the standard deviation of the number of tests per individual (SD), and the pooling sensitivity (PSE) of group testing are the most heavily influenced by the choice of threshold. One should not be deceived by the osten-sibly efficient results that arise when the threshold for individual testing τ^* is also used with pools, as this is also accompanied by a decrease in PSE−sharply so in Application 2 where S_e and S_p are lower. On the other hand, dividing τ^* by the pool size leads to a threshold that is too small. This results in too many negative pools testing positively which inflates the efficiency. Our proposed threshold for pools ${\tau }_{\mathcal{P}}^{\ast }$ offers a nice compromise between these two extremes by providing approximately the same efficiency as under classical assumptions. Both applications show that accuracy probabilities under classical assumptions may be slightly optimistic, an important finding for practitioners who are concerned about classification accuracy. This is seen more noticeably in Application 2 where the error rates for individual testing are comparatively larger and also for lower values of p in both applications (e.g., p = 0.01, shown in Appendix D).

6. Discussion

We have proposed a simulation-based methodology to evaluate the operating characteristics of group testing case identification algorithms when individual biomarker distributions are known. Our approach allows the investigator to incorporate the effect of assay measurement error and proposes a new strategy for selecting thresholds when testing pools. Our research web site www.chrisbilder.com/grouptesting contains R programs that implement our simulation methods for hierarchical algorithms and two-dimensional array testing with normally distributed biomarkers. These programs can be changed to include other biomarker distributions; e.g., gamma, lognormal, or nonstandard choices like those found in Section 5. In addition, these programs can be modified to include other group testing strategies, such as array testing designs that include master pools (Kim et al., 2007), higher dimensional arrays (Kim and Hudgens, 2009), and other algorithms outside the H(n₁: n₂: ⋯: n_S) family described in Section 2.

Our evaluations of case identification algorithms do not require one to assume anything about the sensitivity and specificity of testing pools, because operating characteristics are estimated directly from the biomarker distributions themselves. Our approach also does not force one to assume that testing results are conditionally independent given the true statuses of the individuals being tested. This assumption is required under classical evaluations because pools formed throughout the testing process can contain common individuals. Litvak et al. (1994) have described scenarios where the conditional independence assumption is reasonable empirically; however, there is a large body of evidence in the diagnostic testing literature suggesting that this assumption may be too restrictive. Finally, because the framework described in this article incorporates Monte Carlo simulation, it would be straightforward to generalize our evaluations to allow for unequal disease probabilities p_i, say, which may arise when covariate information is available on individuals (McMahan et al., 2012a; 2012b). For this same reason, our approach could also be extended to accommodate individual disease statuses that are correlated (Lendle et al., 2012) or to applications where biomarkers are measured for multiple diseases (Tebbs et al., 2013).

Throughout this article, we have assumed that the biomarker distributions for positive and negative individuals, f_𝒞̃⁺ and f_𝒞̃⁻, respectively, and the measurement error density f_ε are known exactly. This assumption may be prohibitive in applications where biomarker and measurement error information is not available (e.g., in surveillance studies, etc.). It should be possible to estimate these distributions with continuous group testing responses on pools and individuals, although this would require the development of new deconvolution methods and hence we leave this to future work. In lieu of perfect knowledge about these distributions, an anonymous referee has suggested that one could perform a sensitivity analysis to assess the impact of misspecifying f_𝒞̃⁺, f_𝒞̃⁻, or f_ε. This is straightforward to accomplish within the framework outlined in this article because our methods make use of Monte Carlo simulation. In Appendix E in the Supplementary Material, we provide an example showing how such an analysis could be implemented.