A voltage change across a membrane protein moves charges or dipoles producing a gating current that is an electrical expression of a conformational change.
Abstract
Many membrane proteins sense the voltage across the membrane where they are inserted, and their function is affected by voltage changes. The voltage sensor consists of charges or dipoles that move in response to changes in the electric field, and their movement produces an electric current that has been called gating current. In the case of voltage-gated ion channels, the kinetic and steady-state properties of the gating charges provide information of conformational changes between closed states that are not visible when observing ionic currents only. In this Journal of General Physiology Milestone, the basic principles of voltage sensing and gating currents are presented, followed by a historical description of the recording of gating currents. The results of gating current recordings are then discussed in the context of structural changes in voltage-dependent membrane proteins and how these studies have provided new insights on gating mechanisms.
Introduction
The landmark work of Hodgkin and Huxley (1952) showed for the first time that the sodium and potassium permeabilities of the squid giant axon depended on membrane voltage and not on membrane current. Their series of papers using the voltage-clamp technique demonstrated that the sodium conductance had such a steep dependence on membrane potential that the conductance was increased e-fold with only 4 mV of membrane potential change. In the last paper of the series (Hodgkin and Huxley, 1952), when referring to this voltage dependence, they wrote: “Details of the mechanisms will probably not be settled for some time, but it is difficult to escape the conclusion that the changes in ionic permeability depend on the movement of some component of the membrane which behaves as though it had a large charge or dipole moment.”
With this statement, Hodgkin and Huxley predicted the existence of gating currents. The idea is physically sound: To detect a voltage change, a sensor is needed, which could be magnetic or electric charges or dipoles. When the voltage is modified, the sensor moves producing an electric current. As this current is responsible for turning the ionic conductance on or off, it is called gating current. Their writing continued as follows: “If such components exist it is necessary to suppose that their density is relatively low and that a number of sodium ions cross the membrane at a single active patch.”
This statement is remarkable, because it is the prediction that ionic conductances are made up of ion channels. Therefore, in their view, the gating charges relocate under the influence of the electric field, which in turn allows conduction through the ion channel. An overwhelming amount of evidence (from electrophysiology, site-directed mutagenesis, and structural determinations) has confirmed these proposals.
Hodgkin and Huxley did not report gating currents, but they wrote: “We cannot set a definite upper limit to this hypothetical current, but it could hardly have been more than a few percent of the maximum sodium current without producing a conspicuous effect at the sodium potential.”
What Hodgkin and Huxley meant here is that, at the sodium equilibrium potential, the driving force for the ionic current is zero, so no ionic current should be recorded, whereas the gating current should still be present. However, because they were unable to detect it, they concluded that it must be small. This prediction was also correct, because when the sodium gating currents were recorded, they were ∼1/50th of peak sodium currents.
In this Journal of General Physiology Milestone, I will first make some general remarks on the origin and recording of gating currents. These will be followed by a description of gating currents in a historical context and a general overview of the correlation between gating currents and structural changes observed in membrane proteins.
Voltage sensing and gating currents
To sense the electric field, translocation of charges or movement of dipoles within the membrane field is required. The necessary condition is that those charges or dipoles must be within the electric field, which is normally within and perpendicular to the plane of the membrane. However, the electric field in a membrane protein may not span the whole membrane and might be oriented in a different direction. Upon changes in membrane voltage, the electric field within the membrane changes, moving those gating charges or dipoles, which in turn generates a current. Because this movement is confined to the membrane electric field, these small currents are capacitive in nature. Consequently, the total charge transported (the time integral of the current) during a voltage change must be equal to charge transported when the voltage is returned to its initial value. This condition has been called the equality of the OFF and ON charge.
One may ask, how is it possible to detect a movement that takes place within a space not exceeding 50 Å? Fig. 1 is a schematic representation of a membrane under voltage clamp connected to a display (green circle) that measures current as a function of time. In part a, the clamp is maintaining the internal (bottom) side of the membrane negative, attracting a positive, movable charge. In part b, the clamp suddenly reverses the voltage so that now the charge is attracted to the top part of the membrane and starts moving, as shown in part c. When it reaches the far end of the membrane, it stops, and the current subsides. Therefore, the current recorded is transient, which is a basic property of gating currents. The actual time course of the transient will depend on the mobility and the path of the gating charge. For example, if the charge can only be on either side of the membrane (a two-state model), then the transient will look like a delta function. All this is possible because of the continuity equation, derived from Ampere’s law of Maxwell equations, which show that we can record that current in the circuit even if the recording apparatus is far away.
Figure 1.
Schematic representation of the external recording of the time course of a charge moving in the membrane field. The letters indicate evolution in time. The polarity of the voltage clamp is suddenly reversed in b.
Ampere’s law relates the curl () of the magnetic field () with current density () and the electric field () as follows:
| (1) |
where ε is the dielectric constant and t is time. Taking the divergence of both sides and considering that , we get
| (2) |
which tells us that the total current is always the same in any part of the circuit in closed circuits and that at any point, it can be made of either conductive or displacement components (Eisenberg, 2016).
Recording gating currents
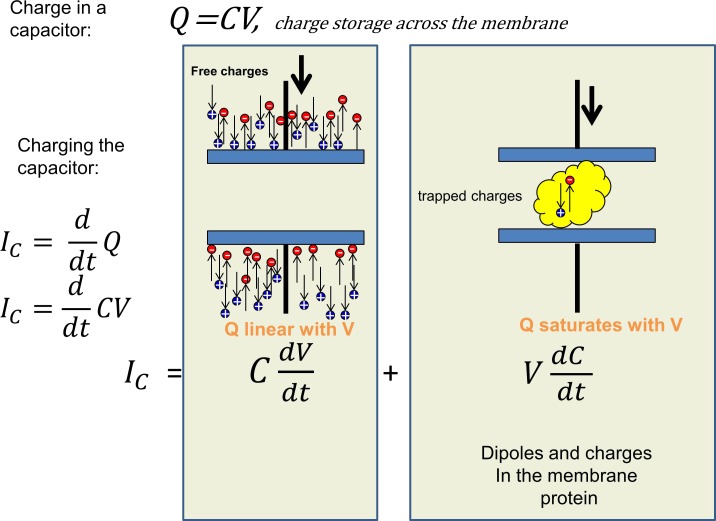
How, then, is it possible to record the actual gating current in a real membrane that contains voltage-dependent channels? Typically, we start from a holding potential where the gating charges are all in one position and apply a pulse of voltage to move them to their far-end position. In doing so, the current recorded will typically be a transient that corresponds to charging of the membrane capacitance followed by ionic currents from channels that are already open or turn on with the pulse. The ionic currents must be eliminated by ion replacement or specific blockers or using nonconducting mutants, because they are normally much larger than the gating currents. In the virtual absence of ionic currents, we have the situation pictured in Fig. 2. The capacitive current IC corresponds to the time derivative of the charge. As the charge Q is Q = CV, where C is the capacitance and V is the voltage, we get for the capacitive current
| (3) |
The first term of Eq. 3 considers a fixed capacitor where unlimited number of charges can reorient. When there are a limited number of trapped charges within the capacitor that do not move instantly when the electric field is changed, the capacitance is no longer constant, and its time derivative is not zero. In fact, the second term is the gating current. In Fig. 2, the first term is shown pictorially on the left, where the mobile ions in the bath solution rearrange to decorate the surfaces of the membrane with an asymmetric charge. As the voltage is increased, more charge separation may occur. The voltage dependence of the charge separation is linear, because the bulk solution provides essentially unlimited charges to the surface of the membrane. This linearity extends to large positive or negative voltages and is only limited by the membrane breakdown. In contrast, the gating charges pictured on the right side of the figure are limited, and, because they cannot escape the membrane, at large voltages, they go to their extreme positions. Consequently, the movement of these charges saturate at extreme voltages. The differences in voltage dependence between the free and trapped charges can then be used to separate them, because the current elicited by pulses of equal magnitude in different voltage ranges is equal for the free charges. This means that adding the currents produced by two pulses equal in size but in opposite directions should cancel the linear component of the capacitive currents. The same addition will not cancel the current produced by the charges trapped within the membrane, provided the voltage range of the first pulse is selected to be in the region where the trapped charges move and the other pulse where they are in their extreme position. The pulse protocols to extract the gating currents are based on this principle. If there are ionic currents left after blocking and ion replacement, these pulses will also subtract all the linear ionic currents, but any nonlinear ionic current will remain.
Figure 2.
The capacitive current and its components. The current needed to charge or discharge the membrane capacitance has two components. The charging of the capacitor plates is provided by the mobile ions in solution, and the charge carried by the current is a linear function of the voltage (left panel), whereas inside the membrane (right panel), the charge is a nonlinear function of voltage because the mobile dipoles or charges reach their extreme positions at high voltages.
Analysis and interpretation of gating currents
A simple approximation to analyze and interpret the experimentally recorded gating currents is based on the two-state model. In a two-state model, the gating charge can be in only two positions (1 and 2), representing two energy wells of a more complex “energetic landscape.” The two wells are separated by an energy barrier that makes it unlikely that the gating charge could spontaneously transition between them. To go from 1 to 2, the gating charge must overcome the barrier. As the gating particle is charged, imposing a transmembrane potential can modulate the probability of crossing the barrier. This means, for example, that given the voltage is measured with respect to 2 and that the gating charge is positive α, the rate to move from 1 to 2 increases as the voltage is made more positive, whereas the backward rate β increases as the voltage is made more negative. These rates are normally expressed following kinetic theory, and they are instantaneous functions of membrane potential V:
| (4) |
where α0 and β0 are constants, W is the energy barrier height, W0 is the difference of energy between the wells, V is the membrane potential, z is the valence of the particle, e0 is the electronic charge, and kB and T are Boltzmann constant and temperature, respectively. The value of x is the fraction of the electric field where the peak of the barrier is located. Typically, the field is assumed to be constant (but this need not be the case).
Gating current
Using these definitions for the rate constants, it is easy to solve the first-order differential equation for the time-dependent probability of a gating charge being in state 2 (p2) or state 1 (p1 = 1 − p2) when starting at a potential Vi and going to potential V:
| (5) |
where p2(0) is the initial condition of p2 just before the pulse. If starting from a steady voltage Vi, then The time course of the gating current Ig(V,t) for a pulse to voltage V, is the net flux of charge computed as the flux from 1 to 2 minus the flux from 2 to 1:
| (6) |
and replacing the time courses for p1 and p2 gives
| (7) |
which is a simple exponential decay with no rising phase. In most biological systems, gating currents normally exhibit decays with several exponential components, including a rising phase (Armstrong and Bezanilla, 1977; White and Bezanilla, 1985). The extra components may come either from charges moving among several (more than two) positions or from several subunits contributing to the recorded current (see Gating current activation and deactivation). These mechanisms have been quantitatively detailed in several proposed kinetic models (Bezanilla et al., 1994; Zagotta et al., 1994; Sigg et al., 1999). The rising phase of gating currents also requires more than two states or more than one gating particle (Sigg and Bezanilla, 2003). It should be noted, however, that these models are not based on physical parameters of the structure that generate the gating currents, and they are not self-consistent in the sense that the movement of the gating particle does not affect the distribution of the electric field or other charged species in the system. A physical self-consistent model based on the known structure of a voltage sensor has been recently developed, and it gives insight on the interaction of the gating charges, electric field, and displacement currents (Horng et al., 2016, 2017).
Charge versus voltage
We can derive the distribution of the charge as a function of voltage (the Q–V curve) by solving p2 in the steady state. The total charge will be proportional to the charge transported by each sensor (ze0) multiplied by the number of sensors (N):
| (8) |
which is a sigmoid function that saturates at extreme voltages and has been misnamed as a Boltzmann. Typically, the Q–V curve is more complicated than the equation above, because there are several steps in the gating charge movement and/or the molecule in question has several sensors.
An important parameter of a voltage sensor is its valence, z, a parameter linked to the number of charges translocated per gating transition. In the equation above, the valence appears as a factor and also within the exponential. If the number of sensors N is known, then z can be calculated when computing the Q–V curve between the two extreme voltages. However, N must be determined with additional experiments that include noise analysis to estimate the number of channels (Sigworth, 1977), counting them with labeled toxin (Levinson and Meves, 1975; Aggarwal and MacKinnon, 1996), or estimating the charge per channel using the limiting slope method (Almers, 1978; Sigg and Bezanilla, 1997). A fit of the normalized Q–V curve to the above equation determines the valence, but only if the gating charge moves between two states. If the charge moves among several states, the slope of the Q–V curve decreases and the estimated valence using the two-state equation will be in error (Bezanilla and Villalba-Galea, 2013).
The search for gating currents
After the Hodgkin and Huxley (HH) prediction, several investigators tried to record gating currents from the squid giant axon under voltage clamp, but they were unsuccessful because, at that time, the membrane currents were viewed in an oscilloscope and photographed, seriously limiting the resolution required to see the small gating currents. I remember a failed attempt we did with Clay Armstrong while Eduardo Rojas was visiting us in Woods Hole in 1971 using perfused squid axons and recording capacity transients on film. Around that time, Martin Schneider and Knox Chandler (Schneider and Chandler, 1973) obtained recordings of a nonlinear charge movement that had decays in the tens of milliseconds from frog skeletal muscle fibers under voltage clamp. They interpreted these currents as related to the excitation–contraction coupling. In their experiments, they used a transient recorder that could sample every 0.5 ms to subtract traces obtained with pulses of equal magnitude but different holding potentials. Returning to Woods Hole in 1972, Clay and I designed a circuit that alternated pulses of equal magnitude but different polarity superimposed on a constant holding potential of approximately −70 mV, which we called the ±P procedure. The idea was to use an internally perfused axon with impermeant ions while externally perfused with impermeant ions plus tetrodotoxin. Then, the +P pulse takes the membrane potential to a region that moves the gating charge to open the sodium channels while the −P pulse does not move the charge but can be used to subtract all the linear components of leak and capacity transient. Thus, adding the currents produced by the +P and −P pulses should give the nonlinear charge movement plus any residual nonlinear conductance. We needed to sample at a much higher rate than that used by Schneider and Chandler, because the expected sodium gating currents are ∼100 times faster than the charge movement in muscle. We borrowed a waveform eductor from Paul Horowicz from the University of Rochester, which is a device with 100 capacitors that are sequentially connected to the input so that one obtains 100 samples in time, accumulating in each capacitor the input signal synchronized in time with the ±P command pulse. With this device, we were successful in recording the currents that had the correct voltage dependence and time dependence expected from sodium gating currents (Armstrong and Bezanilla, 1973).
Although the original gating currents were small and noisy, during subsequent years, technical improvements increased the resolution significantly. In the first five years since the first measurements, at least two other groups made important contributions to our understanding and characterization of gating currents of the sodium channel (Keynes and Rojas, 1974; Meves, 1974). In only two years, the classical squid axon was no longer the only biological preparation to record gating currents, as detailed measurements and analysis were also obtained from the node of Ranvier in myelinated fibers (Nonner et al., 1975).
When voltage-gated channels were cloned in the late 1980s, it was possible to express channels in Xenopus laevis oocytes at high surface density. This expression system combined with the patch-clamp technique (Hamill et al., 1981) and the cut-open oocyte technique (Taglialatela et al., 1992; Stefani and Bezanilla, 1998) allowed clean recording of gating currents (Bezanilla et al., 1991; Stühmer et al., 1991) with minimum interference from other channels. It also allowed for the possibility of modifying the channel sequence using site-directed mutagenesis, thus initiating the search for structural correlates of gating currents. In addition, the introduction of site-directed fluorimetry (also called voltage-clamp fluorimetry; Mannuzzu et al., 1996; Cha and Bezanilla, 1997), allowed, for the first time, the simultaneous recording of gating currents with fluorescence changes that could be correlated to conformational changes.
Characterization of sodium gating currents
Gating currents from the squid giant axon
To expand on the gating current results obtained in the first successful season in Woods Hole, we needed a better sampling system than the waveform eductor. Therefore, when we returned to Rochester, we designed and built a signal averager that had a 12-bit A/D converter that could sample every 5 µs and had digital adders connected to a recirculating memory built with shift registers. This device allowed us to record and synchronously add 256 samples at the speed of the A/D converter and, subsequently, reconvert the stored signal to analogue form, via a D/A converter at slower speed for data to be plotted. The circuit diagram of this signal averager (“la maquina”) was published in (Bezanilla and Armstrong, 1977b).
There was, however, the unanswered question of whether the currents we recorded were indeed gating currents of the sodium channels. Therefore, in the next season at Woods Hole, we used this new device and recorded gating currents in conditions where we could correlate them to sodium currents. To this end, we found three ways to block gating currents and sodium currents with voltage protocols and by addition of internal zinc (Bezanilla and Armstrong, 1974). During the same season, we characterized the sodium gating currents in more detail, and the results were published in the Journal of General Physiology (Armstrong and Bezanilla, 1974).
To be able to apply large depolarizations without destroying the axon with the subtracting pulse, we developed the divided pulse procedure that used a subtracting pulse of one fourth of the amplitude of the test pulse while the preamplifier at the input of the signal averager changed its gain by a factor of four during the subtracting pulse. We found two properties of gating currents that were not predicted by a simple interpretation of the HH equations, one related to activation and deactivation and the other to inactivation.
Gating current activation and deactivation
The top panels of Fig. 3 show the original recordings of ON gating currents (a), OFF gating currents (c), ON ionic currents (b), and OFF ionic currents (d; Armstrong and Bezanilla, 1974). These currents can be directly compared with the HH formulation (Fig. 3, bottom), because the HH equations have specific predictions for the voltage dependence and time courses of gating and ionic currents. In the HH formulation, the sodium current INa at a voltage V is given by
| (9) |
where is open-channel conductance (a constant), VNa is the sodium equilibrium potential, and m3 and 1 − h are the voltage- and time-dependent probabilities of activation and inactivation, respectively. The parameter m represents the probability that one of the gating particles is in the correct position for the channel to conduct and, as the channel will open only if all three are in the correct position, the open probability is m3. The gating particle with probability m is assumed to have only two states with forward rate that increases as V becomes more positive and backward rate that increases when V becomes more negative. Starting from a negative voltage VH where m is zero and applying a more positive voltage VD for maximum activation, m and m3 will increase as a function of time t as follows:
Figure 3.
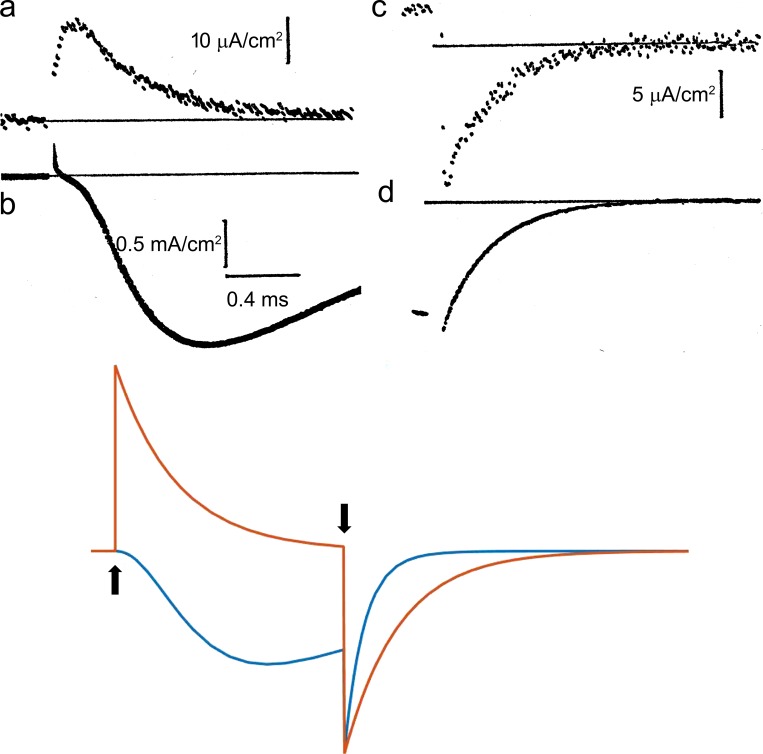
Comparison of ionic and gating currents with the HH model. (a–d, top) Sodium gating currents (a and c) and sodium ionic currents (b and d) for a depolarizing pulse (a and b) and during repolarization (c and d). Adapted from Armstrong and Bezanilla (1974). Superimposed and scaled gating current (orange trace) and sodium current (blue trace) computed with the HH equations (bottom). The axon was held at V = −70 mV, and V was stepped to 0 at the up arrow and returned to −70 mV at the down arrow. Computed gating curents have been scaled so that the peak of computed ionic and gating currents coincide at pulse OFF.
| (10) |
where for V=VD. The conductance follows m3, which rises in time after a delay, as shown in the HH simulation (Fig. 3, bottom panel, blue trace) and experimentally (Fig. 3 b). On the other hand, the movement of the gating particle is represented by m. The gating current is given by Eq. 7, where p2(t) in this case is represented by m. Therefore, the gating current is predicted to be a single exponential decay (Fig. 3, bottom panel, orange trace). In contrast, the experimentally recorded gating current (Fig. 1 a) shows a fast rising phase and decay with at least two time constants. We will address those two issues later.
When the voltage is returned to a negative value VH where m = 0, from a potential VD where m = 1 (deactivation), using Eq. 7, the HH predictions for Ig and m3 are
| (11) |
and
| (12) |
where for V = VH. This result is because one gating particle is enough to close the channel but the gating current is contributed by all three particles. Eqs. 11 and 12 provide a clear prediction for deactivation kinetics: that the time constant of the gating current would be three times slower than that of the ionic current, as shown clearly in Fig. 3 (bottom) by comparing the time course of the blue and orange traces after the time when the voltage was returned to the holding potential (down arrow). However, the experimental result showed that the gating current is at most 1.2 times slower than the ionic current (Fig. 3, c and d). This result rules out the original HH model and indicates that channel closure does not follow the return of three independent gating particles. Across the Atlantic, similar experiments were performed on Loligo forbesi squids by Richard Keynes and Eduardo Rojas (Keynes and Rojas, 1974), but their results led them to the opposite conclusion, when they proposed that their experimental gating currents precisely followed the HH model. This discrepancy was cleared by one of the authors in a later paper (Keynes and Kimura, 1983).
The time course of the sodium gating currents show a clear rising phase at short times. By changing the subtraction pulse to regions where there is no gating charge movement, the rising phase decreased but did not disappear. The time course of charging the membrane capacitance is critical in determining the early phase of gating currents. This issue was addressed by us (Stimers et al., 1987) by looking at the effect of the distributed series resistance on sodium gating current. By using hypertonic solutions to expand the cleft spaces in between Schwann cells and in between the Schwann cell and the axolemma, the membrane capacitance could be charged with essentially one time constant, and as a consequence, the sodium gating currents did not show a rising phase. We concluded that most of the observed rising phase of the sodium gating currents was an artifact produced by a region of the membrane that was charged more slowly. We will see below that, in contrast, potassium gating currents do exhibit a marked rising phase.
Gating currents and sodium inactivation
In the HH formulation, the gating current produced by a depolarizing pulse is not affected by a previous depolarizing pulse if there is a repolarizing interval in between the two pulses. In contrast, the experiments reported in 1974 (Armstrong and Bezanilla, 1974; Bezanilla and Armstrong, 1974) revealed that a depolarizing prepulse preceding a depolarizing test pulse, after a 0.7 ms return to the holding potential, reduces the magnitude of the gating currents during the test pulse.
In the following Woods Hole seasons, we studied in detail how a depolarizing prepulse decreased gating currents during the pulse, and we found that it correlated with sodium current inactivation. Several technical improvements were required to carry out the experiments with more complicated pulse procedures and better resolution. To this end, we interfaced our analogue to digital acquisition electronics to a minicomputer (PDP8), and we also used this computer to generate pulses via a D/A converter under program control. The divided pulse procedure was replaced by the P/4 procedure where the subtracting pulses were one fourth the amplitude of the test pulse but repeated four times, thus improving the signal-to-noise ratio with respect to the divided pulse procedure. In addition, we could apply the subtracting pulses from a voltage different from the holding potential (usually more negative). This was an important conceptual advance, because at sufficiently negative potentials, the subtracting pulses did not elicit any nonlinear charge movement, and thus, the gating currents revealed the actual charge movement of the test pulse (Bezanilla and Armstrong, 1977a).
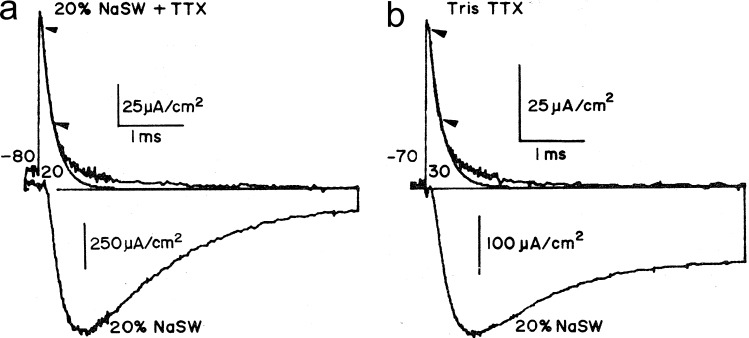
Gating currents recorded with the improved system are shown in Fig. 4. In Fig. 4 a, gating current is shown (upward noisy transient) together with the ionic current (downward noisy trace). The gating current has been fitted by a single exponential (smooth trace) between the two arrows, showing that the gating current exhibits a slow component. Because the inactivation of the sodium current is voltage dependent, it was natural to ask whether this slower component would correspond to the charge movement of the inactivation process. However, it was found that the slow component of the gating current is much faster than the time course of inactivation.
Figure 4.
Two components of sodium gating currents. (a and b) Gating currents (upward noisy traces) and ionic currents (downward traces) without pronase (a) and after pronase treatment (b). The smooth traces are fits to the gating current traces in between the indicated arrows. TTX, tetrodotoxin. Adapted from Armstrong and Bezanilla (1977).
Pronase, a proteolytic enzyme, perfused internally removes inactivation of the sodium current (Armstrong et al., 1973), and when the ionic currents were recorded after pronase treatment (Fig. 4 b), the inactivation was incomplete. Interestingly, however, the slow component was not affected, consistent with the idea that the slow component was not the inactivation gating current. We will see below that with site-directed fluorimetry, we could trace the origin of the slow component.
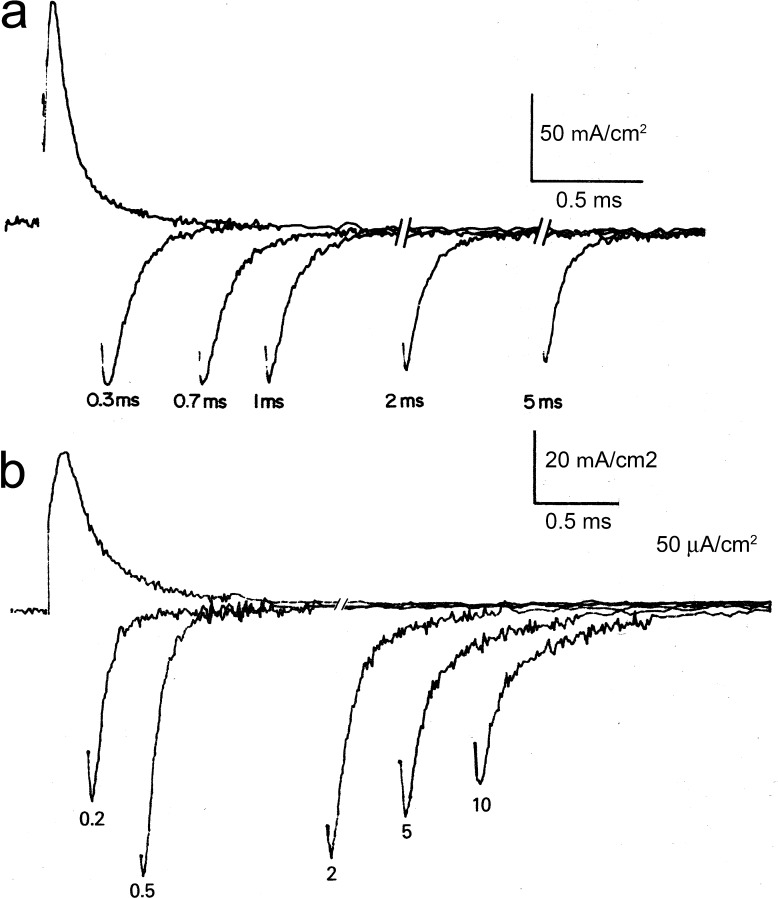
When the holding potential was −70 mV and the depolarizing pulse was varied in duration, the OFF gating currents changed drastically. As the pulse was lengthened, the area of the OFF decreased to approximately one third of the area of the ON (Fig. 5 a), and the time course of the charge decrease coincided with the time course of sodium current inactivation at the same potential. One of the hallmark features of the gating current is that the ON area must be the same as the OFF area, because all the charges that move in one direction must return to their initial position when the voltage is reestablished. The explanation for this charge reduction (immobilization) is that there must be another kinetic component that is too slow to be detected. When the experiment is repeated with a holding potential of −140 mV, that second component is revealed (Fig. 5 b). Notice that at short pulse durations, before inactivation has developed, the OFF gating current is a single fast exponential, whereas when the duration is increased, a slow component develops and the fast component decreases while the ratio of the OFF/ON areas is approximately maintained. The slow component of the OFF was found to have the same time course as the recovery from inactivation, which is extremely voltage dependent and becomes accelerated at more negative potentials. Therefore, when inactivation develops, upon repolarization, some of the gating charge cannot return to its initial position until inactivation is recovered. At −70 mV, the recovery from inactivation is so slow that the charge returns at a rate that is not distinguishable from the noise of the baseline, whereas at −140 mV, it becomes fast enough (∼0.6 ms) so that it becomes visible as a slow component of the OFF. This charge immobilization was verified at different voltages, and it followed the voltage dependence of inactivation. In other words, the inactivation of the sodium channel is not produced by an independent gating particle, as it was predicted by the HH formulation where activation and inactivation are independent because their probabilities are multiplied (Eq. 1). In contrast, our results indicated that the two processes are coupled and that the voltage dependence of inactivation is inherited from the voltage dependence of the activation process.
Figure 5.
Charge immobilization and remobilization. Gating currents for pulses of different durations, as indicated. (a) Starting and return potential is −70 mV. (b) Starting and return potential is −140 mV. Adapted from Armstrong and Bezanilla (1977).
Based on the effect of pronase that removed inactivation and also removed charge immobilization, we postulated the original ball and chain model (Armstrong and Bezanilla, 1977) whereby a portion of the channel protein has access to the pore, blocking it and, in so doing, immobilizing the gating charge. The action of the ball to block the channel depends on the activation of the channel, so that when the gating charge has not moved, the putative receptor of the ball is not available; hence, the interaction of the ball with its receptor gives origin to the voltage dependence of inactivation. It was found later that the last step of inactivation has a shallow voltage dependence (Vandenberg and Bezanilla, 1991b). It is interesting to note that not all the charge that moves during the activation is affected by inactivation because one third of the charge moves independent of inactivation (it is not immobilized), indicating that there is more than one gating charge involved in activating the channel. The distinction of these two charge components of the sodium channel gating has been unraveled by site-directed fluorimetry, as I will describe in the following paragraphs.
Kinetic models of the squid giant axon sodium channel
The HH model (Hodgkin and Huxley, 1952) reproduced the ionic currents quite accurately, but as we have seen, it was not compatible with the results on gating currents. Coupling between activation and inactivation was an important feature revealed by gating currents, but it was also seen by other types of experiments (Goldman and Schauf, 1972). As gating current activation did not follow HH either, new models were proposed to account for all the features of ionic and gating currents (Armstrong and Bezanilla, 1977; Armstrong and Gilly, 1979).
In the early 1980s, analysis of single sodium channel recordings (Aldrich et al., 1983; Horn and Vandenberg, 1984) allowed detailed gating models that showed that the channel could go to the inactivated state from closed states as well as from the open state and confirmed the coupling of activation with inactivation. Maximum likelihood methods using single-channel data selected coupled models that fared better than the uncoupled HH model. A limitation of single-channel data is that it is quite insensitive to transitions between closed states not near the open state; therefore, the models obtained by single-channel data did not predict gating currents. Ideally, the models should be built with single-channel, macroscopic ionic and gating currents. This became possible when the cut-open axon technique allowed the recording of single channels in the squid giant axon (Bezanilla, 1987). In fact, using this technique, it was possible to record not only single channels but also ionic and gating currents from the same preparation (Vandenberg and Bezanilla, 1991a). The best kinetic model based on single-channel recordings and selected from maximum likelihood analysis was expanded and constrained by fitting simultaneously the first latency of single-channel recordings together with ionic and gating current recordings in a range of voltages from −98 to 2 mV, including deactivation tails at different durations (Vandenberg and Bezanilla, 1991b). The model obtained is shown in Fig. 6 with the expressions that defined the rate constants. Inactivated states could be reached from a closed and/or the open states; the branch at the top of the model corresponds to the inactivated states that immobilize the charge. The actual step between the open and inactivated state had a charge of 0.91 e0. The rate constants between the first four closed states are all the same, and attempts at making them different did not fit the data better. Although this is a linear model, it is possible to interpret it as several gating particles as was done originally by Richard FitzHugh (in a paper by C. M. Armstrong; Armstrong, 1969) with the HH equations when he demonstrated that the m3 formulation can be written as a linear sequential model where the forward rates are 3α, 2α, and α, whereas the backward rates are β, 2β, and 3β. When the forward rates are all equal among them and the backward rates are also equ
Figure 6.
Kinetic model of the sodium channel fitted from single-channel, macroscopic ionic, and gating currents data. Adapted from Vandenberg and Bezanilla (1991b). The arrow next to rate g is rate j.
al among them, the three particles are not independent anymore, but they interact among each other with positive cooperativity. As this model did not have the 3β, 2β, and β closing sequence, the ratio of the time constants of gating currents to ionic currents was not 3 but close to 1.2, as experimentally recorded (Vandenberg and Bezanilla, 1991b).
Sodium gating currents from cloned channels in heterologous expression systems
When the sequence of the brain and skeletal muscle sodium channels became available, it was possible to express sodium channels at high surface density in Xenopus oocytes. The sequence of the sodium channels coded for a large polypeptide with four homologous repeats, called domains, with each one having six transmembrane segments (Fig. 7 a). The landmark paper by Stühmer and collaborators (Stühmer et al., 1989), combining electrophysiology and site-directed mutagenesis clearly pointed to the arginine residues in the fourth segments (S4) of the sodium channel as the gating charges involved in voltage sensing. It also provided evidence that the region between domains III and IV was important in sodium current inactivation. The function of domain IV was studied in detail by several authors (Chen et al., 1996; Kontis and Goldin, 1997).
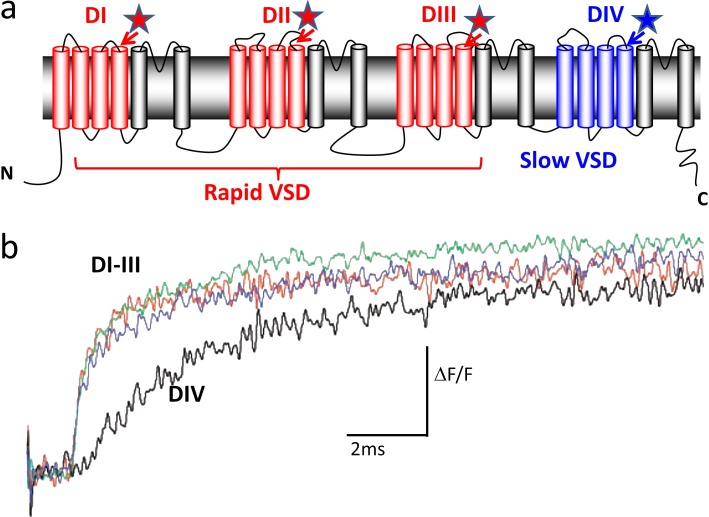
Figure 7.
The four domains of the sodium channel and their gating kinetics. (a) Sodium channel topology. Stars represent where the fluorophore was inserted. Domains are labeled from DI through DIV. VSD, voltage sensing domain. (b) Kinetics of the fluorescence changes of each domain S4 segment. Adapted from Chanda and Bezanilla (2002).
The correlation between charge immobilization and conformational changes in the sodium channel was done in human skeletal muscle sodium channel hNav1.4. Using the cut-open axon oocyte technique, it was possible to obtain sodium currents under voltage control, and large gating currents could be recorded in the presence of impermeant ions and tetrodotoxin (Cha et al., 1999a). We verified that gating charge was immobilized by inactivation very much in the same way that was found before in the squid axon. Then, we took advantage of site-directed fluorescent labeling to examine conformational changes in the S4 segment of each domain of the sodium channel concomitant with the ionic current recorded. Each of the four S4 segments was mutated to cysteine near their extracellular side, and tetramethylrhodamine-maleimide was conjugated to the cysteine residues one segment at a time (Fig. 7 a, stars). The fluorescence signals from S4 segments of domains I and II followed activation and were not affected as fast inactivation developed during the depolarizing pulse, nor were they affected by an inactivating depolarizing prepulse. In contrast, the fluorescence signals from S4 segments in domain III and especially in domain IV showed kinetic components that were affected as fast inactivation developed and by inactivating depolarizing prepulses. This result suggested that domains in the sodium channel display specific functions. The S4 segments in domains III and IV are responsible for voltage-sensitive conformational changes linked to fast inactivation and are immobilized by fast inactivation, whereas the S4 segments in domains I and II are unaffected by fast inactivation. A simple interpretation of these results is that the inactivating particle, identified to be a sequence if Ile-Phe-Met (Patton et al., 1992; West et al., 1992), interacts with the S4 segments of domains III and IV to induce charge immobilization.
To trace the role of each one of the S4 segments in the activation of the sodium channel, we compared the time course of the fluorescence change of each domain with the time course of the gating currents recorded simultaneously. The time course of the fluorescence change of domains I, II, and III were much faster than that of domain IV (Fig. 7 b; Chanda and Bezanilla, 2002). As was the case for the squid sodium gating currents (Fig. 4), the decay of the gating currents of the Nav1.4 channel also showed fast and slow components, with the fast component of the gating currents having the same time course of the fluorescence changes of domains I, II, and III and the slow component of the gating current having the same time course of the fluorescence change of domain IV. Therefore, the origin of the slow component of the sodium gating currents was the movement of the sensor of domain IV. Interestingly, when simultaneously recording the sodium ionic current with domain IV fluorescence, we found that the current developed even before domain IV fluorescence started, indicating that the channel conducts before domain IV is activated. This is consistent with the idea that domain IV contributes to a second open state of the sodium channel as was characterized before in the squid axon (Correa and Bezanilla, 1994). More recently, Goldschen-Ohm et al. (2013) were able to combine single-channel recordings and voltage-clamp fluorimetry to show that kinetics of activation of domain IV correlated with appearance of a distinct pore conformation in the absence of inactivation. However, experiments that neutralized the charges of each of the S4 of the sodium channel indicated that the movement of domain IV voltage sensor is the rate-limiting step for development of and recovery from fast inactivation (Capes et al., 2013). This result makes the sensor of domain IV involved in charge immobilization and thus the primary voltage sensor of inactivation. A verification of this finding was done by mutations that accelerated exclusively the kinetics of S4 of domain IV resulting in faster kinetics of inactivation (Lacroix et al., 2013). Therefore domains I, II, and III contain the voltage sensors for activation whereas domain IV has the voltage sensor of inactivation, but inactivation proper is done by the inactivating region containing the triad isoleucine, phenylalanine, and methionine in the linker between domains III and IV.
Further experiments with site-directed fluorescence in the sodium channel were done to test how each domain may interact with other domains during voltage sensing. This was done by introducing a modification in the voltage dependence of a particular domain and testing with fluorescence whether another domain was affected by that modification (Chanda et al., 2004). The results of these experiments showed that all domains cooperate positively with each other such that if one domain activates in response to depolarization, the activation probability of the other domains is increased. This positive cooperativity is a factor in the fast kinetics of the sodium channel (appendix in Chanda et al., 2004.)
Potassium channel gating currents
Potassium gating currents from the squid giant axon
When attempts are made at recording gating currents, there is an optimal kinetic window to observe them. This is because when the gating charge moves fast, it produces a large current, whereas a slow-moving charge produces a small current. Given a level of noise from the combination of the biological preparation, electrodes, and electronics, a fast gating process is easier to detect than a slow one. On the other hand, when gating processes are extremely fast, gating currents become difficult to measure accurately, if at all, because the gating current gets buried within the capacitive transient and does not correspond to the set voltage applied (during the capacity transient the membrane potential is changing). However, if the gating process is too slow, it likely becomes indistinguishable from the noise and the uncertainty of the recorded baseline.
This last case often corresponds to the kinetics of potassium channels (approximately 10 times slower than that of sodium currents). To partially overcome this problem, the temperature of the preparation can be increased to accelerate the kinetics and bring the gating currents within the recording window. Typically, the sodium gating currents were recorded at ∼6°C, and under those conditions the potassium gating currents cannot be observed, except perhaps as the OFF component of long pulses (returning at −140 mV) where the OFF/ON ratio seemed to increase slightly above one (Fig. 3 b). By raising the temperature to 20°C, kinetics were accelerated approximately five times, the sodium gating current became too fast to record, and a new gating current component appeared that correlated with the kinetics of the potassium channel conductance at that temperature (Bezanilla et al., 1982b).
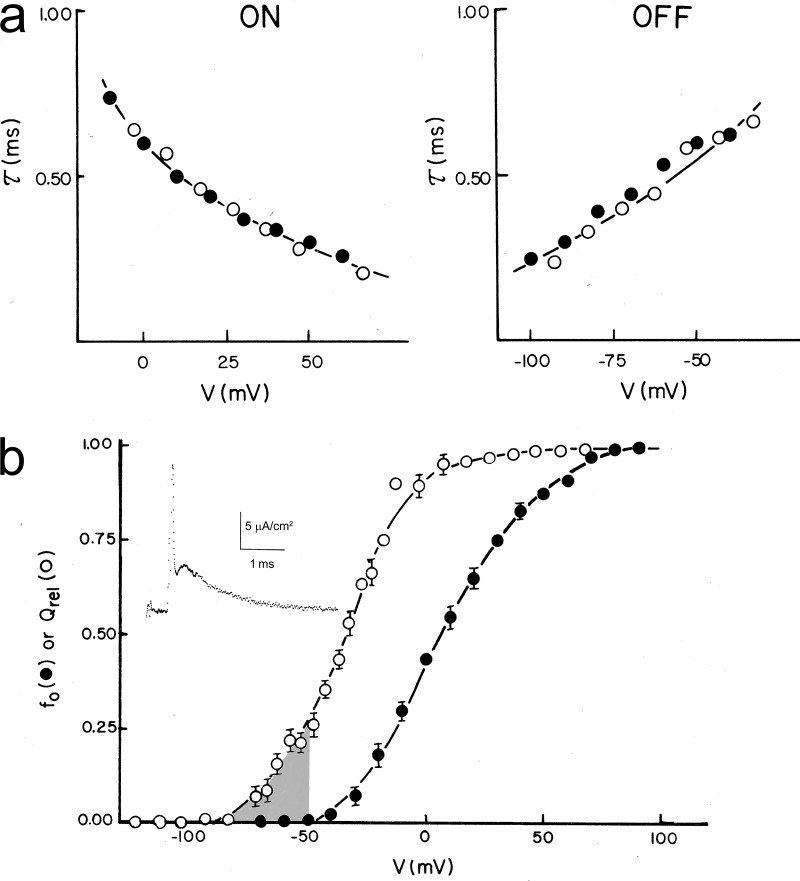
A detailed study of the potassium gating currents in the squid giant axon was published in the Journal of General Physiology (White and Bezanilla, 1985) and required several improvements in the techniques. The potassium gating current originally reported had a substantial contribution of sodium gating currents, and this contamination was drastically decreased with three manipulations. In the first publication, we held the membrane at −60 mV, which induces slow inactivation of sodium gating currents (see below); we also used the local anesthetic dibucaine that blocks sodium ionic and gating currents without affecting potassium conductance. Detailed analysis was possible because we could decrease the sodium contribution even more by replacing the external chloride ion by nitrate that decreased sodium ionic and gating currents to approximately one half without affecting potassium currents. With all these experimental improvements, we recorded potassium gating currents in single sweeps with good signal–to-noise ratio and with kinetics that coincided with the ionic current kinetics for the ON and the OFF currents (Fig. 8 a).
Figure 8.
Potassium gating currents from squid axon. (a) Time constants (τ) of ionic and gating currents during (ON) and after the pulses (OFF) of the indicated voltages. (b) Normalized Q–V (Qrel) and G–V (fo) curves. Inset shows a representative potassium gating current showing a rising phase after the partially blocked sodium gating currents. Adapted from White and Bezanilla (1985).
When a negative prepulse preceded the depolarizing test pulse, a delay is induced in the activation of the potassium ionic current known as the Cole–Moore shift (Cole and Moore, 1960). This was reflected in a clear separation between the sodium gating and potassium gating currents that revealed an obvious rising phase in the potassium gating current (Fig. 8 b, inset). Contrary to what is seen in the sodium gating currents, the rising phase of the potassium gating currents is not a consequence of the slow charging of the membrane capacitance (it is much slower than the slow component of the capacity transient); rather, it is a bona fide kinetic component of the gating current. This rising phase is inconsistent with the n4 model of potassium gating from the HH equations, which predicts a single exponential decay. In addition, the OFF gating current should be four times slower than the ionic currents (Eq. 3, but n4 instead of m3), but the experimental results show that they have approximately the same time constant for an extended range of voltages (Fig. 8 a, right).
A comparison of the Q–V curve with the G–V curve (Fig. 8 b) shows a significant separation in the voltage axis indicating that a large amount of charge moves in between nonconducting (closed) states (Fig. 8, shaded region). Indeed, the linear kinetic model we used to fit simultaneously the ionic and gating currents had a total of 16 states (15 closed and 1 open). To generate the rising phase, the first step was made the slowest.
Gating currents from Shaker potassium channels
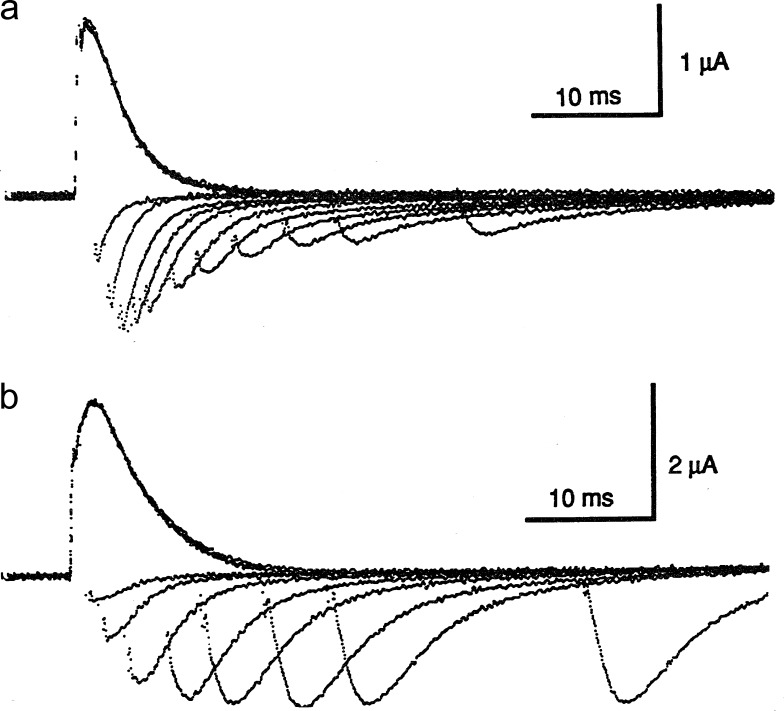
The currents from the potassium channel encoded by the Drosophila melanogaster Shaker gene (Papazian et al., 1987) activate with depolarization and rapidly inactivate while depolarization is maintained. The classical experiments done by Hoshi et al. (1990) demonstrating that the N-terminal portion of the channel was responsible for the inactivation provided the first structural support for a ball and chain type of mechanism.
This channel, which expressed at high densities in oocytes, was therefore a good candidate to record potassium gating currents in a heterologous system. Using a modified cut-open oocyte technique where we perfused the internal oocyte to accelerate the washout of potassium ions, we could record large gating currents as shown in Fig. 9 A (Bezanilla et al., 1991). These showed that the OFF gating current carries less charge than the ON gating currents for pulse durations that correspond to full development of inactivation. When the membrane potential was returned to more negative potentials, the charge returned in two components very much like it was described in the case of the sodium channel in the squid axon. In contrast, when the channel had the N-terminal region removed, the OFF currents recovered all the charge moved during the ON of the pulse (Fig. 9 B). Therefore, this experiment showed that in the Shaker potassium channel, the N-terminal region of the channel protein not only is responsible for fast inactivation but also produces the charge immobilization of the gating current.
Figure 9.
Gating currents of Shaker potassium channels for pulses of different durations. (a) Wild-type Shaker channel showing charge immobilization. (b) Mutant Shaker potassium channel with an N terminus removed shows no charge immobilization. Adapted from Bezanilla et al. (1991).
Experiments with Shaker potassium channels confirmed many of the properties of potassium gating currents observed in the squid axon, and, because the channel density was very large in the oocytes, gating currents were visible even before subtraction. In addition, there was no interference from currents of other channels, making a more detailed analysis possible (Stefani et al., 1994). Similar to the potassium channels in the squid, the voltage dependence of the Q–V curve was shifted to the left with respect to the G–V, showing that a large amount of charge moves among closed states. The rising phase of the potassium gating currents was confirmed and was found to be increased by hyperpolarizing prepulses that induce the Cole–Moore shift. This result was in agreement with a detailed study done in the squid giant axon where we described a Cole–Moore shift in sodium gating and ionic currents that enhanced the rising phase of the gating currents as a result of hyperpolarizing prepulses (Taylor and Bezanilla, 1983). Also, the main decay of the OFF gating current followed the same kinetics of the ionic currents. Detailed kinetic models of Shaker potassium channel were soon published (Bezanilla et al., 1994; Zagotta et al., 1994) based on gating and ionic currents and the finding that the fully functional channel was made of four identical subunits, as shown by MacKinnon (1991).
Since these initial studies, the Shaker potassium channel has become the best model to study gating current properties. The discovery of the W434F mutation in the pore region, a mutation that makes the channel nonconducting but preserves the gating currents, made available a powerful tool to study gating currents (Perozo et al., 1993). This channel does not conduct because the slow inactivation becomes extremely fast (Yang et al., 1997). In this mutant, the Q–V curve is unaltered, but there are small differences in the kinetics, especially in the OFF currents. In a few cases, the modification of the pore has made large changes in the apparent gating currents (Carvalho-de-Souza and Bezanilla, 2018), but for the majority of the studies of gating currents, the W434F has become the standard tool. The Shaker potassium channel with inactivation removed, together with its W434F, has been the main channel used to make correlations of structure with function using site-directed mutagenesis and spectroscopy either with site-directed fluorometry or FRET.
Gating current is affected by prolonged depolarization
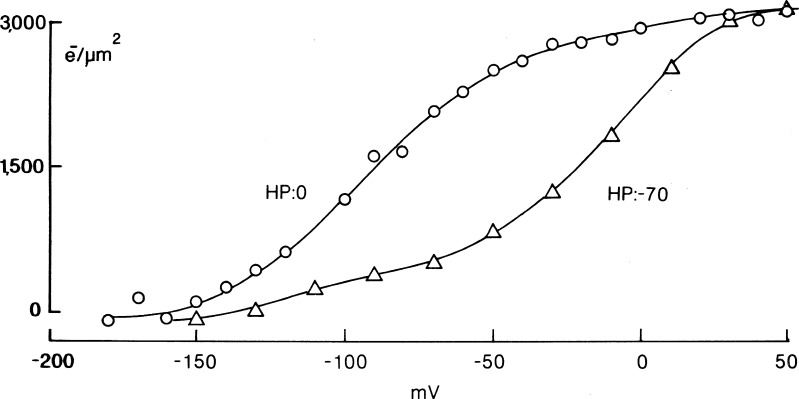
The early observation that holding the membrane depolarized eliminated the recorded sodium gating currents (Bezanilla and Armstrong, 1974) was the result of the ±P procedure. The actual charge movement did not get abolished by depolarization, as was demonstrated later using the P/4 procedure with subtraction at large positive or negative potentials. In that study published in the Journal of General Physiology (Bezanilla et al., 1982a), we found that holding the membrane potential at 0 mV shifted the Q–V curve toward more negative potentials with respect to the Q–V curve obtained at a holding potential of −70 mV, whereas the total amount of charge moved was the same for both holding potentials (Fig. 10). Short depolarizations that correlate with fast inactivation also shift the Q–V curve (Armstrong and Bezanilla, 1977), but not as much as prolonged depolarization.
Figure 10.
The shift of the sodium channel Q–V curve by prolonged depolarization. Q–V curves shown for holding potentials (HPs) of −70 and 0 mV. Adapted from Bezanilla et al. (1982a).
It was known that prolonged depolarization induces another type of inactivation in sodium currents called slow inactivation (Adelman and Palti, 1969; Rudy, 1978) that settles in seconds and also takes seconds to remove. If after prolonged depolarization a 50-ms hyperpolarized prepulse is given, the shift of the Q–V is partially recovered, as expected from the recovery of fast sodium inactivation, but the remaining shift requires longer recovery periods. The large shift of the Q–V curve induced by prolonged depolarization was found to be correlated with the sodium current slow inactivation in the squid giant axon (Bezanilla et al., 1982a).
The relaxed state
When gating currents were measured from cloned channels, it was found that the shift of the Q–V curve by prolonged depolarization was a property shared by all the S4-based voltage sensors. As is the case for voltage-gated channels (Shirokov et al., 1992; Olcese et al., 1997; Larsson and Elinder, 2000; Piper et al., 2003; Kuzmenkin et al., 2004; Männikkö et al., 2005; Bruening-Wright and Larsson, 2007), it is also the case for the voltage-dependent phosphatase CiVSP (Villalba-Galea et al., 2008). Our detailed study of gating current kinetics and steady-state properties, together with site-directed fluorimetry, revealed that prolonged depolarization leads the voltage sensor to a different kinetic state called the relaxed state, adding a third distinct major state to the well-known resting and active states (Villalba-Galea et al., 2008). Although in many cases there was a correlation between the relaxed state and slow inactivation of the ionic currents as described originally for the sodium channel, it was found that the two processes were in general independent, because relaxation developed even when no inactivation was present. Additionally, under certain conditions, the two phenomena had different kinetics or voltage dependences. Finally, relaxation also occurred in the CiVSP voltage sensor, where there was no channel to inactivate.
The shift of the Q–V curve with a steady depolarization implies some sort of hysteresis in the gating charge movement. A simple two-state model cannot reproduce this fundamental property of the gating charge because it is based on a memoryless process. A minimal extension of the two-state model is to add a third state that gets populated only after the activated state is reached. A physical interpretation of this phenomenon is that as the sensor evolves from resting to active, it may interact with another structure to become relaxed. A model was initially proposed for the sodium channel (Bezanilla et al., 1982a), and it was extended in more quantitative terms for the relaxed state using the CiVSP as an example in Villalba-Galea et al. (2008).
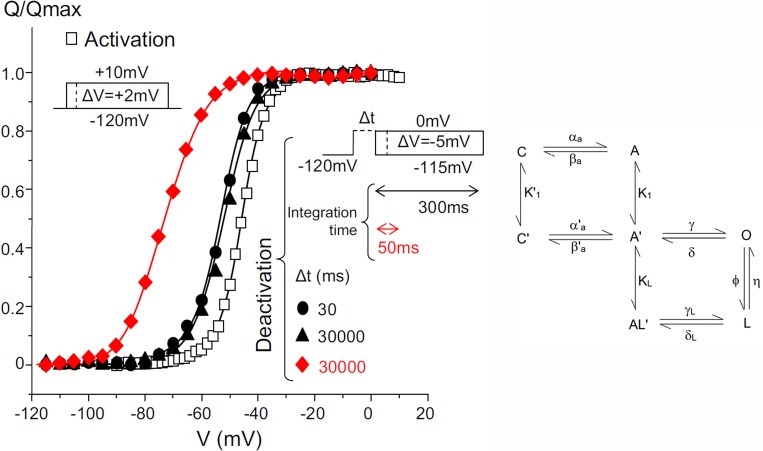
High resolution and high expression of gating currents of Shaker potassium channels with fast inactivation removed and with the W434F mutation gave us the opportunity to look into the relaxed state in more detail, because the integration times to extract the charge moved could be extended from tens of milliseconds to hundreds of milliseconds (Lacroix et al., 2011). We found that after prolonged depolarization (30 s), when the integration time was 50 ms, the Q–V showed a large shift, as reported before (Fig. 11, left, red curve). However, when the integration time was extended to 300 ms, the large shift of the Q–V curve disappeared, and only a 10- to 15-mV shift remained (Fig 11, left, filled triangles). This result is indeed expected, and it is similar to the apparent immobilization of the sodium gating current when returning the pulse to −70 mV (Fig. 3 a) that was remobilized when returning to −140 mV (Fig. 3 b). In other words, the large observed shift of the Q–V curve is only a consequence of missing gating charge caused by the extremely slow kinetics, requiring a very long integration time to recover all the moved charge. However, the 10- to 15-mV shift remains, regardless of the integration period, indicating that the main deactivation pathway is different from the main activation pathway. Using 4-aminopyridine to block the last step to open the channel, we found that the small shift is still present. A simple kinetic model that can explain these results is shown in the state diagram in Fig. 11 (right). For brief depolarizations, when the gating charge gets to the active state A, even before going into the open state O, it evolves into a different state A′; therefore, the return pathway is A′ to C′ to C. We speculated that the moved charged introduced a bias in the voltage seen by the gating charges, and that was represented by the new state, A′. For longer depolarizations, the gating charge evolves to the open state O and for even longer depolarizations to the relaxed state L by a slow step between the O and L states.
Figure 11.
Shifts of Q–V curves of the Shaker potassium channel with fast inactivation removed depends on the integration times. Protocols and results (left). Activation protocol is in the left inset, and the charge is plotted as open squares. The deactivation protocol is the inset on the right, and the charge is plotted as red symbols for integration time of 300 ms and black symbols for integration time of 50 ms. Δt represents the pulse duration for deactivation. Minimum kinetic model that accounts for the experimental data (right). See text for details. Adapted from Lacroix et al. (2011).
The relaxed state of the voltage-sensing domain stabilizes the open pore, whereas slow inactivation decreases ion conduction. We found that in the Shaker potassium channel, inactivation and relaxation show similar kinetics; therefore, they compete with each other. On the other hand, in Kv1.2, the slow inactivation develops slower than relaxation (Labro et al., 2012); therefore, relaxation slows down the closure of potassium conduction, which may play a role in repetitive firing.
Gating currents are capacitive currents
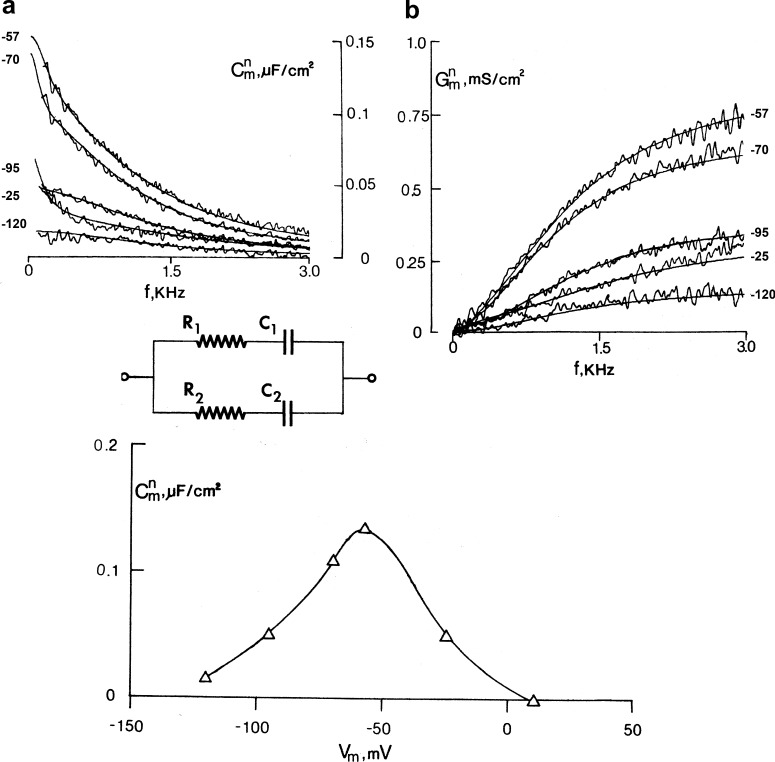
We studied the voltage dependence of capacitance using a frequency domain analysis of the admittance of the squid axon in the absence of permeant ions and in the presence of tetrodotoxin. The membrane potential was held constant, and we applied a small pseudo–binary noise signal perturbation and computed the ratio of the Fourier transform of the recorded current over the Fourier transform of the applied voltage signal. This analysis revealed the nature of the voltage- and time-dependent capacitance that results from the gating charge of the sodium channels (Fernández et al., 1982a). The frequency dependence of the capacitance and conductance, after subtraction of the voltage-independent part, are shown in Fig. 12, and they are typical of a lossy dielectric, which may be represented by a capacitor and a resistor in series. The continuous curves are the fits to the circuit in Fig. 12, which has two lossy capacitors representative of the two time constants observed in the sodium gating currents, with all parameters being voltage dependent. The bell-shaped capacitance as a function of voltage at 100 Hz is shown in Fig. 12 (bottom) and corresponds to the first derivative of the Q–V curve. This C versus V curve is the real stationary voltage dependence of the capacitance resulting from the gating charge of the sodium channel.
Figure 12.
Frequency domain analysis of gating currents. Top: Capacitance (a) and conductance (b) as a function of frequency for several voltages. The fits to the circuit are the smooth curves. Bottom: Capacitance as a function of voltage. Adapted from Fernández et al. (1982a).
High-resolution recordings of gating currents reveal new features
The squid axon voltage clamp can settle in ∼10 µs. Forster and Greeff (1992), using a fast voltage clamp, reported a very fast transient from sodium gating current in the squid giant axon. Using cell-attached macropatches in oocytes, it is possible to also obtain a fast clamp, and after we modified the electronics, a bandwidth of 200 KHz could be achieved that is comparable to the squid axon voltage clamp. Using this technique in oocytes expressing high density of Shaker potassium channels, we recorded a similar fast transient of a few microseconds preceding the main gating charge movement (Sigg et al., 2003). This initial fast gating current (“el piquito”) corresponds to the relocation of the gating charges within the wells of energy before they jump across the main energy barrier, and a simple diffusion model in an energy landscape could account for this fast transient. A possible interpretation, which still needs experimental confirmation, is that the fast transient is the result of the relocation within the field of the side chains of the arginines when they pile up against the main energy barrier.
Gating current at the single-channel level is a jump process
The two extreme possibilities for the gating currents of a single channel are (1) gating currents at the single-molecule level have the same time course of the macroscopic gating currents from a large number of channels, or (2) the gating current at the single-molecule level is a jump process between discrete states across a barrier, as illustrated in the simulation of Fig. 13. In both cases, the size of the current is below the resolution of present electrophysiological techniques, but the prediction of the fluctuations produced by an ensemble of channels is quite different. In the case of a jump process, the noise is higher, and, as can be seen in the mean gating current in Fig. 13, maximum fluctuations occur after the peak of the gating current. This suggests that measuring the ensemble mean and variance of several channels should reveal the time course of the fluctuations. The breakthrough experiment by Conti and Stühmer (1989) used patches expressing a large number of sodium channels in oocytes. The fluctuations of the gating currents had the properties of a jump process, and they determined the elementary charge transported as 2.3 e0. The background noise of the patch clamp and biological preparation required heavy filtering that turned out to be limiting for the fast sodium channels. We studied the gating current fluctuation of Shaker potassium channels (Sigg et al., 1994) using an appropriate bandwidth for their kinetics, which are much slower than sodium channels. Interestingly, the elementary charge was 2.4 e0, but there was experimental evidence that this main charge was preceded in time by charge that was not resolved from the background noise, indicating an additional smaller gating charge. These results indicated that there were more than two states in the movement of the elementary charge, consistent with the measurement of total charge per channel done by Schoppa et al. (1992) that gave 13.2 e0 instead of 9.6 e0 (2.4 × 4; see below).
Figure 13.
Simulation of gating current as a jump process. The top blue trace corresponds to a pulse of voltage that activates the sensor. This pulse is repeated many times, and some of the resulting currents are plotted in the red traces; the bottom trace illustrates the mean of hundreds of trials.
How many charges move in the voltage sensor?
The number of charges moving in the voltage sensor could be estimated measuring the total gating charge and the total number of molecules contributing to the gating charge. The variability in channel density makes the estimate very uncertain when the number of channels and gating charge are measured in separate experiments. In the case of the squid axon, the charge per channel of sodium channels could be anywhere between 4 and 12 electronic charges. The problem was solved by Schoppa et al. (1992) when they measured the number of Shaker potassium channels in a membrane patch using nonstationary fluctuation analysis. Then, after blocking ion conduction, they measured the total gating charge in the same membrane patch. This method gave a total 12.3 e0 for the Shaker potassium channel. For the skeletal muscle sodium channel, the estimated charge was a total of 12 e0 per channel (Hirschberg et al., 1995).
The procedure of dividing the gating charge by the number of active molecules counts all of the moving charges, including the nonessential charge, which is charge that does not open the channel. There is, however, a different method that measures only the essential charge based on the voltage dependence of the conductance called the limiting slope method. The method was originally formulated by Almers (1978) for the special case of a linear sequential model of channel activation, and it was extended to a general activation model by Sigg and Bezanilla (1997) using a partition function approach.
It is important to note that the total charge per channel is not necessarily equivalent the total number of physical charges moved. Rather, it represents the number of charges times the fraction of the electric field across which the charges move. For example, if two positive charges move half of the electric field, the number determined would be one electric charge, and, of course, it would be not possible to discriminate between one positive charge moving or one negative charge moving in the opposite direction. In other words, electrical measurements are blind to the polarity and distance traveled by the gating charge; therefore, other types of measurements are required to determine these parameters.
Finally, it should be remembered that the current measured in the external circuit as gating current has a component of an actual physical charge movement that generates a current density within the electric field and, also, a displacement current that is proportional to the first derivative in time of the electric field (Eq. 2). This means that even if one knew how many physical charges move and how much they move in the field, the gating charge obtained by integration of the gating current may not account for all those charges, because a fraction of the measured currents may be a displacement current. Kinetic models have been the typical way to explain gating currents, and they are based on the assumptions that charges cross energy barriers (Eqs. 4–8) and do not include displacement currents. Therefore, with this type of model, the prediction of the physical charges moving may not reflect the actual charge moving. On the other hand, a physical model based on the structure of a voltage sensor like that developed by Horng et al. (2016, 2017 is self-consistent and includes both current density and displacement currents. Using this model, it was shown that even though all the physical charges translocate across the entire electric field, the charge estimated in the external circuit is less than the physical charge moved, because some of the total current is displacement current in the sensor.
What part of the protein generates the gating currents?
S4-based voltage sensors
Gating currents can provide high-resolution data on the magnitude and time course of charge movement, but they provide no information about how those currents are generated by the structure. It is a requirement that a dipole or charge moves in the changing electric field. In the context of the known structures of voltage sensor domains, the obvious candidates for the gating charges are the acidic and basic residues in proteins as well as residues that have dipole moments (or even the dipole moment of an α-helix). Since the initial structures of channels became available, several investigators speculated on what part of the protein was generating the gating current. The special sequence of basic residues (mainly arginines) that are located in the fourth transmembrane segment, each separated by two uncharged residues in sodium, potassium, and calcium channels, were identified early on as possible candidates for charge sensors. The initial mutagenesis experiments in sodium channels (Stühmer et al., 1989) or potassium channels (Papazian et al., 1991) showed that changing the charged residues in the S4 segment produced significant alterations in the voltage dependence of the channels. However, a shift of the G–V curve or a change in the apparent slope (far from the limiting slope) as a consequence of an arginine neutralization does not prove that such an arginine is part of the gating charge. Even changes in gating currents after neutralization of an arginine or a glutamate do not prove that said charge is a gating charge, because voltage shifts can be induced by changes of noncharged residues and slope changes in gating currents reveal not only the number of charges but also the number of states of the charges.
On the other hand, if a charged residue is suspected to be a gating charge and its neutralization decreases the limiting slope or decreases the charge per channel measured as described in the previous section, then one can say with confidence that that particular charge is part of the voltage sensor. This is the procedure followed by two groups. Aggarwal and MacKinnon (1996) estimated the number of channels in each oocyte with radiolabeled toxin and then estimated the charge in same oocyte by integrating the capacity transient as a function of voltage followed by subtraction of the linear component. Seoh et al. (1996) used patch clamp to first estimate the number of channels with noise analysis and the gating charge by direct measurement of the charge after blockage of the ionic current. In addition, Seoh et al. (1996) estimated the number of channels with the limiting slope method. The result of these two groups was that, starting from the extracellular side, the first four arginines of the S4 segment and the most intracellular glutamate of the S2 segment of the Shaker potassium channel contribute to the gating charge. This is the most complete survey of charges and their role in gating done so far. It is frequently assumed that in other S4-based voltage sensors, a similar result holds.
The large-conductance calcium-activated potassium channel (BK) is also an S4-based sensor, but it has an extra membrane segment (S0) and its gating currents are extremely fast compared with other S4-based sensors, as was initially reported by Stefani et al. (1997). In this seminal paper, the number of charges per channel was found to be lower (between four and five), suggesting that in BK, the gating mechanism may differ from voltage-gated potassium or sodium channels. A detailed understanding of the BK channel gating was done by Horrigan and Aldrich (2002) by combining gating current measurements with analysis of ionic currents for different voltages and calcium concentrations culminating in a complete allosteric model of BK activation.
Other types of voltage sensors
There are large number of membrane proteins whose function is voltage dependent but do not have the classical S1–S4 voltage sensor found in voltage-gated sodium, potassium, calcium, and proton channels or in the voltage-dependent phosphatases (Bezanilla, 2008). Although in many cases the gating charges have not been identified, there are a few proteins where their voltage dependence is fairly well understood.
One example is the sodium/potassium pump that shows voltage dependence that has been traced to the movement of the same ions that are transported by the pump. The sodium/potassium pump exhibits a gating current with at least three components in the sodium part of the cycle that has been analyzed in detail (Holmgren et al., 2000; Gadsby et al., 2012). This gating current has been traced to the entry of sodium ions into an access channel that is in the electric field, and once inside, the ions get occluded. Therefore, the gating charges are the ions themselves. In the case of the potassium part of the cycle, there is also a gating current, much faster and smaller than in the sodium part of the cycle, that is produced by the entry of potassium ions into the access channel with their subsequent occlusion (Castillo et al., 2015). Another example of this type of mechanism is found in chloride channels.
Another protein that is voltage dependent and has no S4-like sensor is the M2 receptor, a G-protein–coupled receptor. Fast gating currents with a shallow Q–V curve have been recorded from the M2 receptor (Ben-Chaim et al., 2006). Site-directed fluorimetry studies correlated the gating currents with conformational changes in the region where the putative voltage sensor may be located (Dekel et al., 2012), and recent studies proposed that the voltage sensor is made by tyrosine residues, where their dipole moments get reoriented in the field to produce the gating currents (Barchad-Avitzur et al., 2016).
Gating currents as a direct probe of channel gating energetics
A new advance has been the introduction of the important concept that the charge voltage (Q–V) curves can be used to extract thermodynamic parameters such as the net-free energy of activation and allosteric interaction energies without building detailed kinetic models (Chowdhury and Chanda, 2012, 2013; Sigg, 2013). This analysis relies on the principle that the gating charge and applied voltage are paired conjugate variables that can describe the energy of the system (analogous to force displacement curve in a mechanical device). Chowdhury and Chanda (2012) showed that the net-free energy of activation of a voltage-dependent process can be obtained by simply taking the product of the total gating charge and a parameter called median voltage activity, which is defined as the mean voltage of the capacitance distribution function. Median voltage activity is analogous to the “median activity” parameter of a binding curve, which was first described by Wyman (1967). This discovery of median voltage activity as a model-free metric of free energy allows one to combine the power of linkage analysis with molecular perturbation studies to provide new insights about the molecular forces driving channel gating (Chowdhury and Chanda, 2013; Fernández-Mariño et al., 2018). The emergence of these approaches to understand the mechanisms of channel gating is just beginning to be appreciated (Sigg, 2014).
Where are the sensing charges moving?
Once the arginines were found to be the gating charges in S4-containing voltage sensor domains, the big question was: How do they move in response to changes in the membrane voltage?
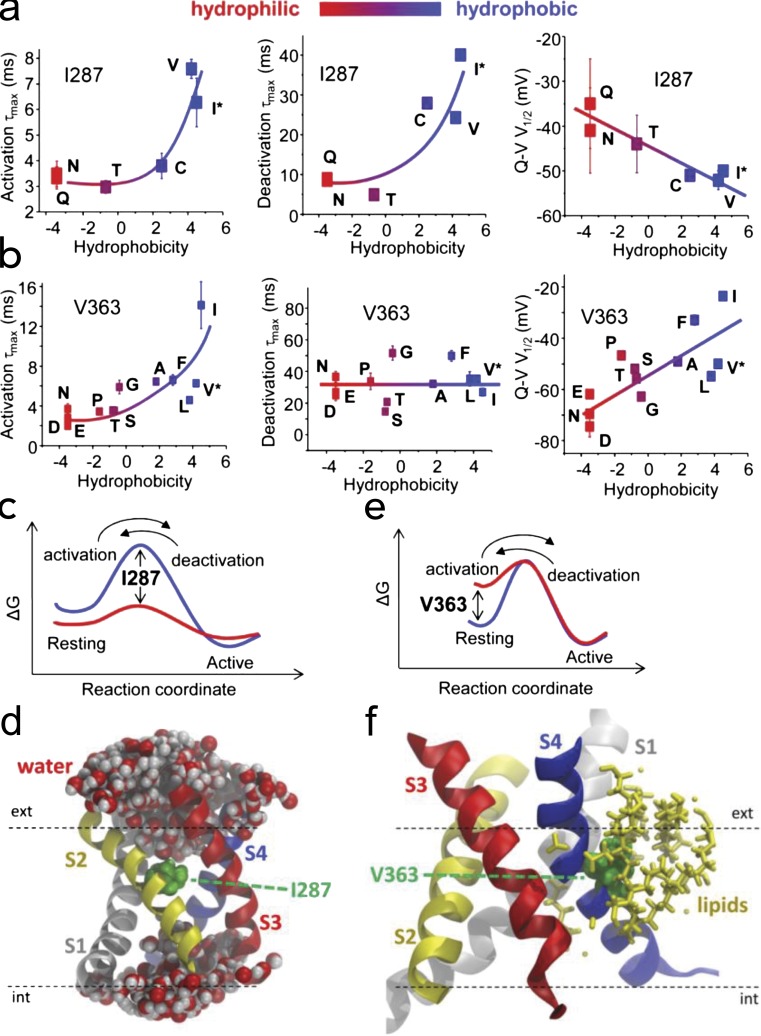
The pioneer work of Yang and Horn (1995) in the sodium channel was the first to establish that a cysteine-mutated charged residue of the S4 segment changes its exposure with changes in the membrane potential. They showed that in Nav1.4, the mutant R1448C, a charge in the S4 of domain IV, has a slowed rate of inactivation, verifying that domain IV is involved in inactivation. Then, they conjugated MTSET to that cysteine and found that the inactivation rate recovered. The remarkable result was that the rate of modification depended on the voltage applied while MTSET was present and with the same dependence of the Q–V curve. This indicates that the exposure of position 1448 in Nav1.4 follows the activation of the voltage sensor, and the simplest interpretation was that part of the S4 segment (or some other region of the protein nearby) moves with the voltage dependence of the sensor. (Of course, other interpretations are possible, such as that the ionization of the sulfhydryl is changing as a result of changing the membrane potential.) A more detailed study of the other charged residues in the S4 segment of domain IV (Yang et al., 1996) showed that the second and third charges can be accessed from the inside at hyperpolarized potentials and from the outside at depolarized potentials, whereas the first charge was only accessible from the outside at depolarized potentials and not accessible to the inside with hyperpolarization. These experiments suggest that the first three charges traverse a hydrophobic region that is narrow, suggesting a concentrated field. These experiments were followed by a similar approach in the Shaker potassium channel (Larsson et al., 1996; Yusaf et al., 1996; Baker et al., 1998), where they showed that also the S4 moves as detected by exposure changes of residues in the S4 segment when changing the membrane potential.
We designed a different approach to test for changes in exposure from the inside to the outside as a function of voltage and time (Starace et al., 1997; Starace and Bezanilla, 2001, 2004), where the gating arginines were changed to histidines to look for proton currents under a proton gradient. In these experiments, voltage-dependent proton currents were obtained while recording gating currents. Fig. 14 shows the logic of the experiments and the results obtained for the first six charges of the Shaker potassium channel. There were three possible results. The most trivial one was that there was no titration either because the histidines are not accessible to the solutions or because they do not move. This was found for the fifth and sixth charge of the S4 segment, in agreement with earlier findings that those two charges do not participate in voltage sensing (Fig. 14 c). Another possible result was that the histidine gets alternatively exposed to the inside or the outside media depending on the membrane potential. In that case, the sensor acts like a proton transporter with a maximum rate of transport at the voltage where the Q–V relation is 0.5, where there is equal probability of the sensor being exposed to either side of the membrane (Fig. 14 a). This was the case for the second, third, and fourth charges of the S4 segment (Fig. 14 c). Finally, a third possibility was that at one voltage, the histidine spans a narrow region between the inside and outside media so that the voltage sensor becomes a proton pore (Fig. 14 b). This situation was found for the first charge (R362H) for the resting state and for the fourth charge (R371H) for the active state (Fig. 14 c).
Figure 14.
Histidine scanning of the gating charges. (a) Transporter case. (b) Pore case. (c) Results for the first six charges of the S4 segment of Shaker potassium channel.
All these experiments that tested exposure either by cysteine or histidine scanning showed that the gating charges can get alternatively exposed to inside or outside solutions depending on the membrane potential. At the same time, the formation of proton pores indicates that the field is concentrated in a narrow region. In fact, it was later found that replacing the first charge by a small amino acid leads to an ionic current at hyperpolarized potentials, confirming the existence of a narrow region inside the sensor (Tombola et al., 2005). These pores suggest that the S4 segment moves between water-filled vestibules in a concentrated electric field. This was also found by manipulations that changed the electrostatics around the voltage sensor (Islas and Sigworth, 2001) and by our experiments where we attached to different points of the channel protein an electrochromic fluorophore. In these experiments, we found that the field was at least three times more intense in the region where S4 is located (Asamoah et al., 2003). Considering that the hydrophobic part of the bilayer is ∼28 Å, the field seen by the gating charges would span a region of ∼10 Å. When the first crystal structure of a voltage-gated potassium channel became available, it showed a canonical pore region surrounded by an arrangement of transmembrane segments (the voltage sensor) that did not agree with many previous results. The authors (Jiang et al., 2003a) then combined the pore region with the structure of the isolated sensor proposing a model where S3 and S4 crossed the bilayer with changing voltage (Jiang et al., 2003b). The movement of the arginines across the lipid bilayer was inconsistent with the histidine scanning results (Starace and Bezanilla, 2004) and with the effects of chloroform on the sodium currents in the squid axons, which showed a decrease of gating current without a change in kinetics, whereas movement of the hydrophobic ion dipicrylamine in the bilayer was accelerated (Fernández et al., 1982b). This discrepancy disappeared when the crystal structure of Kv1.2 and the crystal structure of a chimera between Kv1.2 and Kv2.1 (Long et al., 2005, 2007) showed water-filled crevices and the gating charges pointing toward them.
More recently, several papers dealing with the detailed movement of the gating charges have been made, including experimental (Henrion et al., 2012) and computational studies (Delemotte et al., 2011; Jensen et al., 2012).
The hydrophobic plug
Based on the previous discussion, the emerging consensus is that, in response to voltage changes, the gating currents are generated by the movement of S4 arginines between two aqueous regions separated by a hydrophobic region (where most of the electric field resides). The refined crystal structure of Kv1.2 (Chen et al., 2010) in the presumably open-relaxed state shows from the extracellular side that the charges are indeed in an aqueous medium and that there is a region made by ∼10 residues, contributed by S1, S2, and S3 segments, that completely block the access from the extracellular to the intracellular solution. Therefore, one expects that most of the field will be in this region that has been named the hydrophobic plug or gating pore (Islas and Sigworth, 2001; Campos et al., 2007; Tao et al., 2010). It is then natural to ask: What is the influence of this plug on the gating currents? We did a detailed study of the plug by making a systematic replacement of all the residues of the plug and characterizing the gating currents for each of these mutations (Lacroix et al., 2014). This study showed several critical residues that control the shape of the field (S240), the stability of the open state (F290, F244, and I237), and the hydrophobicity of the plug (I287) that controls the main energy barrier for gating charge movement. This last residue (Fig. 15 C) was found as an isoleucine or another hydrophobic amino acid in many slow voltage sensors, including the S4 of domain IV of eukaryotic sodium channels. In contrast, the first three domains of the sodium channel have that residue replaced by a hydrophilic threonine, lowering the energy barrier of the gating particles of the first three domains and making their gating currents faster (Fig. 15).
Figure 15.
Two residues that control speed of the sensor. (a) Activation, deactivation time constants and midpoint of the Q–V curve as a function of the hydrophobicity of residue 287 in Shaker. (c) Energy diagram: a replacement of the isoleucine (blue barrier) by an hydrophilic residue (red barrier) lowers the energy barrier for arginines crossing the hydrophobic plug, as indicated in d. (d) The position of the I287 in the middle of the plug. (b, e, and f) For the case of residue V363 in S4, activation and deactivation time constants and midpoint of the Q–V curve are shown as a function of hydrophobicity (b); in this case, the main effect of making the residue hydrophilic is to lift the resting well (e), which is because in the resting state, that residue faces the lipid bilayer (f). Adapted from Lacroix et al. (2013).
There is another residue immediately after the first charges of the S4 segments (V363 in Shaker) that must be hydrophilic to accelerate the gating current; the same is also found in the first three domains of the sodium channels (see the proposed mechanism in Fig. 15). When those two residues are made hydrophobic in the first three domains of the sodium channel (without β subunit), it becomes as slow as the Shaker potassium channel. Along the same lines, as was mentioned before, inactivation can be made faster by replacing the hydrophobic residue in the I287-equivalent position in the S4 of domain IV by a hydrophilic residue (Lacroix et al., 2013)
The movement of the sensor
The original helical screw model of the voltage sensor (Catterall, 1986; Guy and Seetharamulu, 1986), published after the first sequences of voltage-gated channels were obtained, has survived over many other possible models that propose a large range of S4 translation (Cha et al., 1999b; Ruta et al., 2005; Henrion et al., 2012; Jensen et al., 2012). In its present version, the total travel of the S4 segment perpendicular to the membrane is more limited (∼7 Å) than originally thought, as can be inferred from multiple experiments including FRET, the lanthanide-based variant LRET, and cross-linking (Bezanilla, 2008). Recently, putative active and resting states crystal structures of the CiVSP confirm a small (∼5 Å) S4 translation with rotation (Li et al., 2014). In the case of the potassium channel Kv1.2, no closed structure has been reported, but a consensus model that puts together many experimental constraints indicates that upon activation, the S4 has limited outward translation (7–10 Å) with some rotation and a change in tilting, in agreement with experimental data (Vargas et al., 2012).
Outlook
Our knowledge of the structural changes during voltage sensing is not nearly as detailed as gating current recordings. Once we find how the arginines penetrate through the hydrophobic plug and their actual trajectories as they move within the protein as well as their interaction with the side chains of the hydrophobic plug, then we will start having a real physical picture of voltage sensor operation. There are many other parts of the protein that seem to be moving in addition to the S4 segment, and their trajectories should also be delineated. A physical understanding will include also how the electric field is distributed and how it changes in different parts of the sensor. We expect that progress will be made combining kinetic experiments that include changing the arginines to charged fluorophores with local detection of the electric field with physical models of the landscape of energy that consider the electric field interaction with the charges, ions, amino acid side chains, and everything else in the sensor, in addition to direct detection of conformational changes caused by electric field in crystal structures (Hekstra et al., 2016).
To the long list of gating currents recorded to date from many voltage-dependent proteins (for brevity, not mentioned here), we expect that gating currents of many other channels, transporters, GPCR-coupled receptors, pumps, and voltage-dependent enzymes will be added, thus enriching our understanding of voltage sensing in its many different forms while adding to our knowledge of how other proteins function within the confines of the intense electric fields common in all biological membranes.
Acknowledgments
Many thanks to Drs. Carlos Bassetto, Joao Carvalho-de-Souza, Baron Chanda, Ana M. Correa, Eduardo Perozo, Jeremy Treger, and the reviewers for reading this manuscript and for their important and useful suggestions.
This work was supported by the National Institutes of Health (grant GM030376).
The author declares no competing financial interests.
Olaf S. Andersen served as editor.
References
- Adelman W.J. Jr., and Palti Y.. 1969. The effects of external potassium and long-duration voltage conditioning on the amplitude of sodium currents in the giant axon of the squid, Loligo pealei. J. Gen. Physiol. 54:589–606. 10.1085/jgp.54.5.589 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aggarwal S.K., and MacKinnon R.. 1996. Contribution of the S4 segment to gating charge in the Shaker K+ channel. Neuron. 16:1169–1177. 10.1016/S0896-6273(00)80143-9 [DOI] [PubMed] [Google Scholar]
- Aldrich R.W., Corey D.P., and Stevens C.F.. 1983. A reinterpretation of mammalian sodium channel gating based on single channel recording. Nature. 306:436–441. 10.1038/306436a0 [DOI] [PubMed] [Google Scholar]
- Almers W. 1978. Gating currents and charge movements in excitable membranes. Rev. Physiol. Biochem. Pharmacol. 82:96–190. 10.1007/BFb0030498 [DOI] [PubMed] [Google Scholar]
- Armstrong C.M. 1969. Inactivation of the potassium conductance and related phenomena caused by quaternary ammonium ion injection in squid axons. J. Gen. Physiol. 54:553–575. 10.1085/jgp.54.5.553 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armstrong C.M., and Bezanilla F.. 1973. Currents related to movement of the gating particles of the sodium channels. Nature. 242:459–461. 10.1038/242459a0 [DOI] [PubMed] [Google Scholar]
- Armstrong C.M., and Bezanilla F.. 1974. Charge movement associated with the opening and closing of the activation gates of the Na channels. J. Gen. Physiol. 63:533–552. 10.1085/jgp.63.5.533 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armstrong C.M., and Bezanilla F.. 1977. Inactivation of the sodium channel. II. Gating current experiments. J. Gen. Physiol. 70:567–590. 10.1085/jgp.70.5.567 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armstrong C.M., and Gilly W.F.. 1979. Fast and slow steps in the activation of sodium channels. J. Gen. Physiol. 74:691–711. 10.1085/jgp.74.6.691 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Armstrong C.M., Bezanilla F., and Rojas E.. 1973. Destruction of sodium conductance inactivation in squid axons perfused with pronase. J. Gen. Physiol. 62:375–391. 10.1085/jgp.62.4.375 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asamoah O.K., Wuskell J.P., Loew L.M., and Bezanilla F.. 2003. A fluorometric approach to local electric field measurements in a voltage-gated ion channel. Neuron. 37:85–97. 10.1016/S0896-6273(02)01126-1 [DOI] [PubMed] [Google Scholar]
- Baker O.S., Larsson H.P., Mannuzzu L.M., and Isacoff E.Y.. 1998. Three transmembrane conformations and sequence-dependent displacement of the S4 domain in shaker K+ channel gating. Neuron. 20:1283–1294. 10.1016/S0896-6273(00)80507-3 [DOI] [PubMed] [Google Scholar]
- Barchad-Avitzur O., Priest M.F., Dekel N., Bezanilla F., Parnas H., and Ben-Chaim Y.. 2016. A Novel Voltage Sensor in the Orthosteric Binding Site of the M2 Muscarinic Receptor. Biophys. J. 111:1396–1408. 10.1016/j.bpj.2016.08.035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ben-Chaim Y., Chanda B., Dascal N., Bezanilla F., Parnas I., and Parnas H.. 2006. Movement of ‘gating charge’ is coupled to ligand binding in a G-protein-coupled receptor. Nature. 444:106–109. 10.1038/nature05259 [DOI] [PubMed] [Google Scholar]
- Bezanilla F. 1987. Single sodium channels from the squid giant axon. Biophys. J. 52:1087–1090. 10.1016/S0006-3495(87)83304-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezanilla F. 2008. How membrane proteins sense voltage. Nat. Rev. Mol. Cell Biol. 9:323–332. 10.1038/nrm2376 [DOI] [PubMed] [Google Scholar]
- Bezanilla F., and Armstrong C.M.. 1974. Gating currents of the sodium channels: three ways to block them. Science. 183:753–754. 10.1126/science.183.4126.753 [DOI] [PubMed] [Google Scholar]
- Bezanilla F., and Armstrong C.M.. 1977a Inactivation of the sodium channel. I. Sodium current experiments. J. Gen. Physiol. 70:549–566. 10.1085/jgp.70.5.549 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezanilla F., and Armstrong C.M.. 1977b A low-cost signal averager and data-acquisition device. Am. J. Physiol. 232:C211–C215. 10.1152/ajpcell.1977.232.5.C211 [DOI] [PubMed] [Google Scholar]
- Bezanilla F., and Villalba-Galea C.A.. 2013. The gating charge should not be estimated by fitting a two-state model to a Q-V curve. J. Gen. Physiol. 142:575–578. 10.1085/jgp.201311056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezanilla F., Taylor R.E., and Fernández J.M.. 1982a Distribution and kinetics of membrane dielectric polarization. 1. Long-term inactivation of gating currents. J. Gen. Physiol. 79:21–40. 10.1085/jgp.79.1.21 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezanilla F., White M.M., and Taylor R.E.. 1982b Gating currents associated with potassium channel activation. Nature. 296:657–659. 10.1038/296657a0 [DOI] [PubMed] [Google Scholar]
- Bezanilla F., Perozo E., Papazian D.M., and Stefani E.. 1991. Molecular basis of gating charge immobilization in Shaker potassium channels. Science. 254:679–683. 10.1126/science.1948047 [DOI] [PubMed] [Google Scholar]
- Bezanilla F., Perozo E., and Stefani E.. 1994. Gating of Shaker K+ channels: II. The components of gating currents and a model of channel activation. Biophys. J. 66:1011–1021. 10.1016/S0006-3495(94)80882-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruening-Wright A., and Larsson H.P.. 2007. Slow conformational changes of the voltage sensor during the mode shift in hyperpolarization-activated cyclic-nucleotide-gated channels. J. Neurosci. 27:270–278. 10.1523/JNEUROSCI.3801-06.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campos F.V., Chanda B., Roux B., and Bezanilla F.. 2007. Two atomic constraints unambiguously position the S4 segment relative to S1 and S2 segments in the closed state of Shaker K channel. Proc. Natl. Acad. Sci. USA. 104:7904–7909. 10.1073/pnas.0702638104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Capes D.L., Goldschen-Ohm M.P., Arcisio-Miranda M., Bezanilla F., and Chanda B.. 2013. Domain IV voltage-sensor movement is both sufficient and rate limiting for fast inactivation in sodium channels. J. Gen. Physiol. 142:101–112. 10.1085/jgp.201310998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carvalho-de-Souza J.L., and Bezanilla F.. 2018. Nonsensing residues in S3-S4 linker’s C terminus affect the voltage sensor set point in K+ channels. J. Gen. Physiol. 150:307–321. 10.1085/jgp.201711882 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castillo J.P., Rui H., Basilio D., Das A., Roux B., Latorre R., Bezanilla F., and Holmgren M.. 2015. Mechanism of potassium ion uptake by the Na(+)/K(+)-ATPase. Nat. Commun. 6:7622 10.1038/ncomms8622 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catterall W.A. 1986. Molecular properties of voltage-sensitive sodium channels. Annu. Rev. Biochem. 55:953–985. 10.1146/annurev.bi.55.070186.004513 [DOI] [PubMed] [Google Scholar]
- Cha A., and Bezanilla F.. 1997. Characterizing voltage-dependent conformational changes in the Shaker K+ channel with fluorescence. Neuron. 19:1127–1140. 10.1016/S0896-6273(00)80403-1 [DOI] [PubMed] [Google Scholar]
- Cha A., Ruben P.C., George A.L. Jr., Fujimoto E., and Bezanilla F.. 1999a Voltage sensors in domains III and IV, but not I and II, are immobilized by Na+ channel fast inactivation. Neuron. 22:73–87. 10.1016/S0896-6273(00)80680-7 [DOI] [PubMed] [Google Scholar]
- Cha A., Snyder G.E., Selvin P.R., and Bezanilla F.. 1999b Atomic scale movement of the voltage-sensing region in a potassium channel measured via spectroscopy. Nature. 402:809–813. 10.1038/45552 [DOI] [PubMed] [Google Scholar]
- Chanda B., and Bezanilla F.. 2002. Tracking voltage-dependent conformational changes in skeletal muscle sodium channel during activation. J. Gen. Physiol. 120:629–645. 10.1085/jgp.20028679 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chanda B., Asamoah O.K., and Bezanilla F.. 2004. Coupling interactions between voltage sensors of the sodium channel as revealed by site-specific measurements. J. Gen. Physiol. 123:217–230. 10.1085/jgp.200308971 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L.Q., Santarelli V., Horn R., and Kallen R.G.. 1996. A unique role for the S4 segment of domain 4 in the inactivation of sodium channels. J. Gen. Physiol. 108:549–556. 10.1085/jgp.108.6.549 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X., Wang Q., Ni F., and Ma J.. 2010. Structure of the full-length Shaker potassium channel Kv1.2 by normal-mode-based X-ray crystallographic refinement. Proc. Natl. Acad. Sci. USA. 107:11352–11357. 10.1073/pnas.1000142107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chowdhury S., and Chanda B.. 2012. Estimating the voltage-dependent free energy change of ion channels using the median voltage for activation. J. Gen. Physiol. 139:3–17. 10.1085/jgp.201110722 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chowdhury S., and Chanda B.. 2013. Free-energy relationships in ion channels activated by voltage and ligand. J. Gen. Physiol. 141:11–28. 10.1085/jgp.201210860 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole K.S., and Moore J.W.. 1960. Potassium ion current in the squid giant axon: dynamic characteristic. Biophys. J. 1:1–14. 10.1016/S0006-3495(60)86871-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conti F., and Stühmer W.. 1989. Quantal charge redistributions accompanying the structural transitions of sodium channels. Eur. Biophys. J. 17:53–59. 10.1007/BF00257102 [DOI] [PubMed] [Google Scholar]
- Correa A.M., and Bezanilla F.. 1994. Gating of the squid sodium channel at positive potentials: II. Single channels reveal two open states. Biophys. J. 66:1864–1878. 10.1016/S0006-3495(94)80980-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dekel N., Priest M.F., Parnas H., Parnas I., and Bezanilla F.. 2012. Depolarization induces a conformational change in the binding site region of the M2 muscarinic receptor. Proc. Natl. Acad. Sci. USA. 109:285–290. 10.1073/pnas.1119424109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delemotte L., Tarek M., Klein M.L., Amaral C., and Treptow W.. 2011. Intermediate states of the Kv1.2 voltage sensor from atomistic molecular dynamics simulations. Proc. Natl. Acad. Sci. USA. 108:6109–6114. 10.1073/pnas.1102724108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eisenberg B. 2016. Conservation of current and conservation of charge. Available on arXiv as https://arxiv.org/abs/1609.09175.
- Fernández J.M., Bezanilla F., and Taylor R.E.. 1982a Distribution and kinetics of membrane dielectric polarization. II. Frequency domain studies of gating currents. J. Gen. Physiol. 79:41–67. 10.1085/jgp.79.1.41 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernández J.M., Bezanilla F., and Taylor R.E.. 1982b Effect of chloroform on charge movement in the nerve membrane. Nature. 297:150–152. 10.1038/297150a0 [DOI] [PubMed] [Google Scholar]
- Fernández-Mariño A.I., Harpole T.J., Oelstrom K., Delemotte L., and Chanda B.. 2018. Gating interaction maps reveal a noncanonical electromechanical coupling mode in the Shaker K+ channel. Nat. Struct. Mol. Biol. 25:320–326. 10.1038/s41594-018-0047-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forster I.C., and Greeff N.G.. 1992. The early phase of sodium channel gating current in the squid giant axon. Characteristics of a fast component of displacement charge movement. Eur. Biophys. J. 21:99–116. 10.1007/BF00185425 [DOI] [PubMed] [Google Scholar]
- Gadsby D.C., Bezanilla F., Rakowski R.F., De Weer P., and Holmgren M.. 2012. The dynamic relationships between the three events that release individual Na+ ions from the Na+/K+-ATPase. Nat. Commun. 3:669 10.1038/ncomms1673 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman L., and Schauf C.L.. 1972. Inactivation of the sodium current in Myxicola giant axons: Evidence for coupling to the activation process. J. Gen. Physiol. 59:659–675. 10.1085/jgp.59.6.659 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldschen-Ohm M.P., Capes D.L., Oelstrom K.M., and Chanda B.. 2013. Multiple pore conformations driven by asynchronous movements of voltage sensors in a eukaryotic sodium channel. Nat. Commun. 4:1350 10.1038/ncomms2356 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guy H.R., and Seetharamulu P.. 1986. Molecular model of the action potential sodium channel. Proc. Natl. Acad. Sci. USA. 83:508–512. 10.1073/pnas.83.2.508 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamill O.P., Marty A., Neher E., Sakmann B., and Sigworth F.J.. 1981. Improved patch-clamp techniques for high-resolution current recording from cells and cell-free membrane patches. Pflugers Arch. 391:85–100. 10.1007/BF00656997 [DOI] [PubMed] [Google Scholar]
- Hekstra D.R., White K.I., Socolich M.A., Henning R.W., Šrajer V., and Ranganathan R.. 2016. Electric-field-stimulated protein mechanics. Nature. 540:400–405. 10.1038/nature20571 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henrion U., Renhorn J., Börjesson S.I., Nelson E.M., Schwaiger C.S., Bjelkmar P., Wallner B., Lindahl E., and Elinder F.. 2012. Tracking a complete voltage-sensor cycle with metal-ion bridges. Proc. Natl. Acad. Sci. USA. 109:8552–8557. 10.1073/pnas.1116938109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirschberg B., Rovner A., Lieberman M., and Patlak J.. 1995. Transfer of twelve charges is needed to open skeletal muscle Na+ channels. J. Gen. Physiol. 106:1053–1068. 10.1085/jgp.106.6.1053 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin A.L., and Huxley A.F.. 1952. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117:500–544. 10.1113/jphysiol.1952.sp004764 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmgren M., Wagg J., Bezanilla F., Rakowski R.F., De Weer P., and Gadsby D.C.. 2000. Three distinct and sequential steps in the release of sodium ions by the Na+/K+-ATPase. Nature. 403:898–901. 10.1038/35002599 [DOI] [PubMed] [Google Scholar]
- Horn R., and Vandenberg C.A.. 1984. Statistical properties of single sodium channels. J. Gen. Physiol. 84:505–534. 10.1085/jgp.84.4.505 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horng T.-L., Eisenberg R.S., Liu C., and Bezanilla F.. 2016. Gating Current Models Computed with Consistent Interactions. Biophys. J. 110:102a–103a. 10.1016/j.bpj.2015.11.611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horng T.-L., Eisenberg R.S., Liu C., and Bezanilla F.. 2017. Continuum gating current models computed with consistent interactions. arXiv:1707.02566. [DOI] [PMC free article] [PubMed]
- Horrigan F.T., and Aldrich R.W.. 2002. Coupling between voltage sensor activation, Ca2+ binding, and channel opening in large-conductance (BK) potassium channels. J. Gen. Physiol. 120:267–305. 10.1085/jgp.20028605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoshi T., Zagotta W.N., and Aldrich R.W.. 1990. Biophysical and molecular mechanisms of Shaker potassium channel inactivation. Science. 250:533–538. 10.1126/science.2122519 [DOI] [PubMed] [Google Scholar]
- Islas L.D., and Sigworth F.J.. 2001. Electrostatics and the gating pore of Shaker potassium channels. J. Gen. Physiol. 117:69–89. 10.1085/jgp.117.1.69 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen M.O., Jogini V., Borhani D.W., Leffler A.E., Dror R.O., and Shaw D.E.. 2012. Mechanism of voltage gating in potassium channels. Science. 336:229–233. 10.1126/science.1216533 [DOI] [PubMed] [Google Scholar]
- Jiang Y., Lee A., Chen J., Ruta V., Cadene M., Chait B.T., and MacKinnon R.. 2003a X-ray structure of a voltage-dependent K+ channel. Nature. 423:33–41. 10.1038/nature01580 [DOI] [PubMed] [Google Scholar]
- Jiang Y., Ruta V., Chen J., Lee A., and MacKinnon R.. 2003b The principle of gating charge movement in a voltage-dependent K+ channel. Nature. 423:42–48. 10.1038/nature01581 [DOI] [PubMed] [Google Scholar]
- Keynes R.D., and Kimura J.E.. 1983. Kinetics of activation of the sodium conductance in the squid giant axon. J. Physiol. 336:621–634. 10.1113/jphysiol.1983.sp014601 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keynes R.D., and Rojas E.. 1974. Kinetics and steady-state properties of the charged system controlling sodium conductance in the squid giant axon. J. Physiol. 239:393–434. 10.1113/jphysiol.1974.sp010575 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kontis K.J., and Goldin A.L.. 1997. Sodium channel inactivation is altered by substitution of voltage sensor positive charges. J. Gen. Physiol. 110:403–413. 10.1085/jgp.110.4.403 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuzmenkin A., Bezanilla F., and Correa A.M.. 2004. Gating of the bacterial sodium channel, NaChBac: Voltage-dependent charge movement and gating currents. J. Gen. Physiol. 124:349–356. 10.1085/jgp.200409139 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Labro A.J., Lacroix J.J., Villalba-Galea C.A., Snyders D.J., and Bezanilla F.. 2012. Molecular mechanism for depolarization-induced modulation of Kv channel closure. J. Gen. Physiol. 140:481–493. 10.1085/jgp.201210817 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lacroix J.J., Labro A.J., and Bezanilla F.. 2011. Properties of deactivation gating currents in Shaker channels. Biophys. J. 100:L28–L30. 10.1016/j.bpj.2011.01.043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lacroix J.J., Campos F.V., Frezza L., and Bezanilla F.. 2013. Molecular bases for the asynchronous activation of sodium and potassium channels required for nerve impulse generation. Neuron. 79:651–657. 10.1016/j.neuron.2013.05.036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lacroix J.J., Hyde H.C., Campos F.V., and Bezanilla F.. 2014. Moving gating charges through the gating pore in a Kv channel voltage sensor. Proc. Natl. Acad. Sci. USA. 111:E1950–E1959. 10.1073/pnas.1406161111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larsson H.P., and Elinder F.. 2000. A conserved glutamate is important for slow inactivation in K+ channels. Neuron. 27:573–583. 10.1016/S0896-6273(00)00067-2 [DOI] [PubMed] [Google Scholar]
- Larsson H.P., Baker O.S., Dhillon D.S., and Isacoff E.Y.. 1996. Transmembrane movement of the shaker K+ channel S4. Neuron. 16:387–397. 10.1016/S0896-6273(00)80056-2 [DOI] [PubMed] [Google Scholar]
- Levinson S.R., and Meves H.. 1975. The binding of tritiated tetrodotoxin to squid giant axons. Philos. Trans. R. Soc. Lond. B Biol. Sci. 270:349–352. 10.1098/rstb.1975.0014 [DOI] [PubMed] [Google Scholar]
- Li Q., Wanderling S., Paduch M., Medovoy D., Singharoy A., McGreevy R., Villalba-Galea C.A., Hulse R.E., Roux B., Schulten K., et al. 2014. Structural mechanism of voltage-dependent gating in an isolated voltage-sensing domain. Nat. Struct. Mol. Biol. 21:244–252. 10.1038/nsmb.2768 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long S.B., Campbell E.B., and Mackinnon R.. 2005. Crystal structure of a mammalian voltage-dependent Shaker family K+ channel. Science. 309:897–903. 10.1126/science.1116269 [DOI] [PubMed] [Google Scholar]
- Long S.B., Tao X., Campbell E.B., and MacKinnon R.. 2007. Atomic structure of a voltage-dependent K+ channel in a lipid membrane-like environment. Nature. 450:376–382. 10.1038/nature06265 [DOI] [PubMed] [Google Scholar]
- MacKinnon R. 1991. Determination of the subunit stoichiometry of a voltage-activated potassium channel. Nature. 350:232–235. 10.1038/350232a0 [DOI] [PubMed] [Google Scholar]
- Männikkö R., Pandey S., Larsson H.P., and Elinder F.. 2005. Hysteresis in the voltage dependence of HCN channels: Conversion between two modes affects pacemaker properties. J. Gen. Physiol. 125:305–326. 10.1085/jgp.200409130 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mannuzzu L.M., Moronne M.M., and Isacoff E.Y.. 1996. Direct physical measure of conformational rearrangement underlying potassium channel gating. Science. 271:213–216. 10.1126/science.271.5246.213 [DOI] [PubMed] [Google Scholar]
- Meves H. 1974. The effect of holding potential on the asymmetry currents in squid gaint axons. J. Physiol. 243:847–867. 10.1113/jphysiol.1974.sp010780 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nonner W., Rojas E., and Stämpfli H.. 1975. Displacement currents in the node of Ranvier. Voltage and time dependence. Pflugers Arch. 354:1–18. 10.1007/BF00584499 [DOI] [PubMed] [Google Scholar]
- Olcese R., Latorre R., Toro L., Bezanilla F., and Stefani E.. 1997. Correlation between charge movement and ionic current during slow inactivation in Shaker K+ channels. J. Gen. Physiol. 110:579–589. 10.1085/jgp.110.5.579 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papazian D.M., Schwarz T.L., Tempel B.L., Jan Y.N., and Jan L.Y.. 1987. Cloning of genomic and complementary DNA from Shaker, a putative potassium channel gene from Drosophila. Science. 237:749–753. 10.1126/science.2441470 [DOI] [PubMed] [Google Scholar]
- Papazian D.M., Timpe L.C., Jan Y.N., and Jan L.Y.. 1991. Alteration of voltage-dependence of Shaker potassium channel by mutations in the S4 sequence. Nature. 349:305–310. 10.1038/349305a0 [DOI] [PubMed] [Google Scholar]
- Patton D.E., West J.W., Catterall W.A., and Goldin A.L.. 1992. Amino acid residues required for fast Na(+)-channel inactivation: charge neutralizations and deletions in the III-IV linker. Proc. Natl. Acad. Sci. USA. 89:10905–10909. 10.1073/pnas.89.22.10905 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perozo E., MacKinnon R., Bezanilla F., and Stefani E.. 1993. Gating currents from a nonconducting mutant reveal open-closed conformations in Shaker K+ channels. Neuron. 11:353–358. 10.1016/0896-6273(93)90190-3 [DOI] [PubMed] [Google Scholar]
- Piper D.R., Varghese A., Sanguinetti M.C., and Tristani-Firouzi M.. 2003. Gating currents associated with intramembrane charge displacement in HERG potassium channels. Proc. Natl. Acad. Sci. USA. 100:10534–10539. 10.1073/pnas.1832721100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudy B. 1978. Slow inactivation of the sodium conductance in squid giant axons. Pronase resistance. J. Physiol. 283:1–21. 10.1113/jphysiol.1978.sp012485 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruta V., Chen J., and MacKinnon R.. 2005. Calibrated measurement of gating-charge arginine displacement in the KvAP voltage-dependent K+ channel. Cell. 123:463–475. 10.1016/j.cell.2005.08.041 [DOI] [PubMed] [Google Scholar]
- Schneider M.F., and Chandler W.K.. 1973. Voltage dependent charge movement of skeletal muscle: a possible step in excitation-contraction coupling. Nature. 242:244–246. 10.1038/242244a0 [DOI] [PubMed] [Google Scholar]
- Schoppa N.E., McCormack K., Tanouye M.A., and Sigworth F.J.. 1992. The size of gating charge in wild-type and mutant Shaker potassium channels. Science. 255:1712–1715. 10.1126/science.1553560 [DOI] [PubMed] [Google Scholar]
- Seoh S.A., Sigg D., Papazian D.M., and Bezanilla F.. 1996. Voltage-sensing residues in the S2 and S4 segments of the Shaker K+ channel. Neuron. 16:1159–1167. 10.1016/S0896-6273(00)80142-7 [DOI] [PubMed] [Google Scholar]
- Shirokov R., Levis R., Shirokova N., and Ríos E.. 1992. Two classes of gating current from L-type Ca channels in guinea pig ventricular myocytes. J. Gen. Physiol. 99:863–895. 10.1085/jgp.99.6.863 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigg D. 2013. A linkage analysis toolkit for studying allosteric networks in ion channels. J. Gen. Physiol. 141:29–60. 10.1085/jgp.201210859 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigg D. 2014. Modeling ion channels: Past, present, and future. J. Gen. Physiol. 144:7–26. 10.1085/jgp.201311130 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigg D., and Bezanilla F.. 1997. Total charge movement per channel: The relation between gating charge displacement and the voltage sensitivity of activation. J. Gen. Physiol. 109:27–39. 10.1085/jgp.109.1.27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigg D., and Bezanilla F.. 2003. A physical model of potassium channel activation: from energy landscape to gating kinetics. Biophys. J. 84:3703–3716. 10.1016/S0006-3495(03)75099-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigg D., Stefani E., and Bezanilla F.. 1994. Gating current noise produced by elementary transitions in Shaker potassium channels. Science. 264:578–582. 10.1126/science.8160016 [DOI] [PubMed] [Google Scholar]
- Sigg D., Qian H., and Bezanilla F.. 1999. Kramers’ diffusion theory applied to gating kinetics of voltage-dependent ion channels. Biophys. J. 76:782–803. 10.1016/S0006-3495(99)77243-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigg D., Bezanilla F., and Stefani E.. 2003. Fast gating in the Shaker K+ channel and the energy landscape of activation. Proc. Natl. Acad. Sci. USA. 100:7611–7615. 10.1073/pnas.1332409100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sigworth F.J. 1977. Sodium channels in nerve apparently have two conductance states. Nature. 270:265–267. 10.1038/270265a0 [DOI] [PubMed] [Google Scholar]
- Starace D.M., and Bezanilla F.. 2001. Histidine scanning mutagenesis of basic residues of the S4 segment of the shaker K+ channel. J. Gen. Physiol. 117:469–490. 10.1085/jgp.117.5.469 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Starace D.M., and Bezanilla F.. 2004. A proton pore in a potassium channel voltage sensor reveals a focused electric field. Nature. 427:548–553. 10.1038/nature02270 [DOI] [PubMed] [Google Scholar]
- Starace D.M., Stefani E., and Bezanilla F.. 1997. Voltage-dependent proton transport by the voltage sensor of the Shaker K+ channel. Neuron. 19:1319–1327. 10.1016/S0896-6273(00)80422-5 [DOI] [PubMed] [Google Scholar]
- Stefani E., and Bezanilla F.. 1998. Cut-open oocyte voltage-clamp technique. Methods Enzymol. 293:300–318. 10.1016/S0076-6879(98)93020-8 [DOI] [PubMed] [Google Scholar]
- Stefani E., Toro L., Perozo E., and Bezanilla F.. 1994. Gating of Shaker K+ channels: I. Ionic and gating currents. Biophys. J. 66:996–1010. 10.1016/S0006-3495(94)80881-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stefani E., Ottolia M., Noceti F., Olcese R., Wallner M., Latorre R., and Toro L.. 1997. Voltage-controlled gating in a large conductance Ca2+-sensitive K+channel (hslo). Proc. Natl. Acad. Sci. USA. 94:5427–5431. 10.1073/pnas.94.10.5427 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stimers J.R., Bezanilla F., and Taylor R.E.. 1987. Sodium channel gating currents: Origin of the rising phase. J. Gen. Physiol. 89:521–540. 10.1085/jgp.89.4.521 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stühmer W., Conti F., Suzuki H., Wang X.D., Noda M., Yahagi N., Kubo H., and Numa S.. 1989. Structural parts involved in activation and inactivation of the sodium channel. Nature. 339:597–603. 10.1038/339597a0 [DOI] [PubMed] [Google Scholar]
- Stühmer W., Conti F., Stocker M., Pongs O., and Heinemann S.H.. 1991. Gating currents of inactivating and non-inactivating potassium channels expressed in Xenopus oocytes. Pflugers Arch. 418:423–429. 10.1007/BF00550881 [DOI] [PubMed] [Google Scholar]
- Taglialatela M., Toro L., and Stefani E.. 1992. Novel voltage clamp to record small, fast currents from ion channels expressed in Xenopus oocytes. Biophys. J. 61:78–82. 10.1016/S0006-3495(92)81817-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tao X., Lee A., Limapichat W., Dougherty D.A., and MacKinnon R.. 2010. A gating charge transfer center in voltage sensors. Science. 328:67–73. 10.1126/science.1185954 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor R.E., and Bezanilla F.. 1983. Sodium and gating current time shifts resulting from changes in initial conditions. J. Gen. Physiol. 81:773–784. 10.1085/jgp.81.6.773 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tombola F., Pathak M.M., and Isacoff E.Y.. 2005. Voltage-sensing arginines in a potassium channel permeate and occlude cation-selective pores. Neuron. 45:379–388. 10.1016/j.neuron.2004.12.047 [DOI] [PubMed] [Google Scholar]
- Vandenberg C.A., and Bezanilla F.. 1991a Single-channel, macroscopic, and gating currents from sodium channels in the squid giant axon. Biophys. J. 60:1499–1510. 10.1016/S0006-3495(91)82185-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vandenberg C.A., and Bezanilla F.. 1991b A sodium channel gating model based on single channel, macroscopic ionic, and gating currents in the squid giant axon. Biophys. J. 60:1511–1533. 10.1016/S0006-3495(91)82186-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vargas E., Yarov-Yarovoy V., Khalili-Araghi F., Catterall W.A., Klein M.L., Tarek M., Lindahl E., Schulten K., Perozo E., Bezanilla F., and Roux B.. 2012. An emerging consensus on voltage-dependent gating from computational modeling and molecular dynamics simulations. J. Gen. Physiol. 140:587–594. 10.1085/jgp.201210873 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villalba-Galea C.A., Sandtner W., Starace D.M., and Bezanilla F.. 2008. S4-based voltage sensors have three major conformations. Proc. Natl. Acad. Sci. USA. 105:17600–17607. 10.1073/pnas.0807387105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- West J.W., Patton D.E., Scheuer T., Wang Y., Goldin A.L., and Catterall W.A.. 1992. A cluster of hydrophobic amino acid residues required for fast Na(+)-channel inactivation. Proc. Natl. Acad. Sci. USA. 89:10910–10914. 10.1073/pnas.89.22.10910 [DOI] [PMC free article] [PubMed] [Google Scholar]
- White M.M., and Bezanilla F.. 1985. Activation of squid axon K+ channels: Ionic and gating current studies. J. Gen. Physiol. 85:539–554. 10.1085/jgp.85.4.539 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wyman J. 1967. Allosteric Linkage. J. Am. Chem. Soc. 89:2202–2218. 10.1021/ja00985a037 [DOI] [Google Scholar]
- Yang N., and Horn R.. 1995. Evidence for voltage-dependent S4 movement in sodium channels. Neuron. 15:213–218. 10.1016/0896-6273(95)90078-0 [DOI] [PubMed] [Google Scholar]
- Yang N., George A.L. Jr., and Horn R.. 1996. Molecular basis of charge movement in voltage-gated sodium channels. Neuron. 16:113–122. 10.1016/S0896-6273(00)80028-8 [DOI] [PubMed] [Google Scholar]
- Yang Y., Yan Y., and Sigworth F.J.. 1997. How does the W434F mutation block current in Shaker potassium channels? J. Gen. Physiol. 109:779–789. 10.1085/jgp.109.6.779 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yusaf S.P., Wray D., and Sivaprasadarao A.. 1996. Measurement of the movement of the S4 segment during the activation of a voltage-gated potassium channel. Pflugers Arch. 433:91–97. 10.1007/s004240050253 [DOI] [PubMed] [Google Scholar]
- Zagotta W.N., Hoshi T., and Aldrich R.W.. 1994. Shaker potassium channel gating. III: Evaluation of kinetic models for activation. J. Gen. Physiol. 103:321–362. 10.1085/jgp.103.2.321 [DOI] [PMC free article] [PubMed] [Google Scholar]