A fast fiducial marker tracking model for fully automatic alignment in electron tomography

Abstract

Motivation

Automatic alignment, especially fiducial marker-based alignment, has become increasingly important due to the high demand of subtomogram averaging and the rapid development of large-field electron microscopy. Among the alignment steps, fiducial marker tracking is a crucial one that determines the quality of the final alignment. Yet, it is still a challenging problem to track the fiducial markers accurately and effectively in a fully automatic manner.

Results

In this paper, we propose a robust and efficient scheme for fiducial marker tracking. Firstly, we theoretically prove the upper bound of the transformation deviation of aligning the positions of fiducial markers on two micrographs by affine transformation. Secondly, we design an automatic algorithm based on the Gaussian mixture model to accelerate the procedure of fiducial marker tracking. Thirdly, we propose a divide-and-conquer strategy against lens distortions to ensure the reliability of our scheme. To our knowledge, this is the first attempt that theoretically relates the projection model with the tracking model. The real-world experimental results further support our theoretical bound and demonstrate the effectiveness of our algorithm. This work facilitates the fully automatic tracking for datasets with a massive number of fiducial markers.

Availability and implementation

The C/C ++ source code that implements the fast fiducial marker tracking is available at https://github.com/icthrm/gmm-marker-tracking. Markerauto 1.6 version or later (also integrated in the AuTom platform at http://ear.ict.ac.cn/) offers a complete implementation for fast alignment, in which fast fiducial marker tracking is available by the ‘-t’ option.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Nowadays, three-dimensional (3D) structural analysis based on electron microscopy plays an important role in the field of structural biology. Among the various applications, electron tomography (ET) acts as a bridge between high-resolution structural analysis and cellular imaging (Phan et al., 2012; Wan and Briggs, 2016). In ET, the 3D ultrastructure is reconstructed from a series of micrographs (tilt series) taken in different orientations. Generally, the projection parameters can be recorded from the goniometer and used for further reconstruction. However, due to mechanical instability and specimen transformation, the recorded micrographs do not exactly align with the recorded parameters. To obtain high-quality 3D density from the tilt series, it is thus necessary to recalculate the projection parameters (i.e. tilt series alignment) before reconstruction.

Tilt series alignment is one of the most important stages in ET process, which can be classified into two categories: (i) marker-free alignment and (ii) marker-based alignment. Marker-free alignment uses the intrinsic ultrastructures from specimens to calibrate the projection parameters. The current available marker-free alignment methods include cross-correlation (Guckenberger, 1982), common-lines (Liu et al., 1995), iterative alignment methods combining cross-correlation with reconstruction and reprojection (Winkler and Taylor, 2006, 2013) and feature-based alignment methods (Brandt et al., 2001a; Brandt and Ziese, 2006; Castaño-Díez et al., 2007, 2010; Han et al., 2014; Phan et al., 2009; Sorzano et al., 2009). Though marker-free alignment does not need any additional information of the specimen, it suffers from the low signal-to-noise ratio of electron micrographs, especially in cryo-ET datasets. The other alignment category, fiducial marker-based alignment, which requires gold beads to be embedded in the specimens (Frank, 2008; Kremer et al., 1996; Lawrence, 1992), is more robust to noise owing to the high contrast of the gold beads. Currently, fiducial marker-based alignment is the most widely used method in high-resolution ET. Moreover, for the large-field datasets with obvious lens distortions, the non-straight electron beam trajectory model is preferred (Lawrence et al., 2006; Phan et al., 2012) and thus the fiducial marker-based alignment becomes the only option.

The rapid development of electron microscopy technologies has caused the explosion of data in ET. A large number of researchers began to use subtomogram averaging to analyze high-resolution structures in situ (Wan and Briggs, 2016). In addition, large-field micrographs have become widely used. The exploding size of data necessitates the development of more efficient and automatic alignment algorithms.

A number of automatic marker-based alignment algorithms have been proposed (Amat et al., 2008; Han et al., 2015; Mastronarde and Held, 2017). Based on their tracking strategies, we categorize them into two groups: (i) spatial marker-based automatic alignment and (ii) model-based automatic alignment. IMOD’s latest automatic alignment (Mastronarde and Held, 2017) is a classic spatial marker-based alignment. IMOD’s scheme begins with the selection of initial micrographs near the zero tilt angle and the detection of fiducial marker positions. These fiducial markers are then tracked and pre-reconstructed in the 3D spatial space, from which two-dimensional (2D) reprojections are generated and used as references for further fiducial marker tracking in the entire tilt series. Though spatial marker-based alignment tracks the fiducial markers exactly according to the projection model, it still requires the determination of the correspondence between the 2D predicted fiducial marker reprojections and the measured fiducial marker positions (for convenience, we denote this operation as ‘motion prediction’). On the other hand, model-based alignment (Amat et al., 2008; Han et al., 2015) directly uses the information of measured fiducial marker positions to achieve fiducial marker tracking. Naturally, the tracking in model-based alignment is based on a predefined mathematical model, such as the Markov random field used by Amat et al. (2008) or the random sample consensus (RANSAC) (Fischler and Bolles, 1981) used by Han et al. (2015). The fiducial marker tracking strategy used in model-based automatic alignment is simpler but not exactly accordant with the projection model.

Despite the aforementioned efforts, several concerns still remain. Potential failures have been observed in spatial marker-based alignment (Mastronarde and Held, 2017) due to its long workflow, in which the neighbor searching used in motion prediction is a weak point. Compared with the spatial marker-based alignment (Mastronarde and Held, 2017), model-based alignment (Amat et al., 2008; Han et al., 2015) has a simpler workflow and has been proven to be successful in applications like cryo-ET. However, the relationship between the model-based alignment’s mathematical model and the real projection model still remains to be elucidated. Execution time is another issue for automatic marker-based alignment. Markov random field (Amat et al., 2008) is a good attempt for fiducial marker tracking but costs too much time in local information analysis. The RANSAC model (Han et al., 2015) utilizes the global information of fiducial marker positions but encounters an increasing computational cost when the number of fiducial marker increases.

Focusing on the fiducial marker tracking problem, this paper makes the following contributions. Firstly, we theoretically prove the upper bound of the transformation deviation of aligning the positions of fiducial markers on two micrographs by affine transformation, which theoretically reveals the relationship of model-based alignment and the projection model. To our knowledge, this is the first theoretical work to relate the projection model to a tracking model. The given upper bound of the deviation is an instructive guide for further algorithm design and is useful in both model-based alignment and motion prediction of spatial marker-based alignment. Secondly, we introduce Gaussian mixture model (GMM) into this field and design an automatic algorithm based on it to make fiducial marker tracking more effective and efficient. Finally, we propose a divide-and-conquer strategy against lens distortions to ensure the reliability of our scheme. The real-world experimental results further support the theoretical bound and demonstrate the effectiveness of our algorithm. This work makes the fully automatic tracking for datasets with a massive number of fiducial markers possible.

2 Materials and methods

A scheme of marker-based alignment typically includes three stages: (i) fiducial marker detection, (ii) fiducial marker tracking and (iii) parameter optimization. In this work, we will focus on the fiducial marker tracking and assume that the fiducial marker positions have already been detected. In this section, the relationship between a 2D model-based tracking and the 3D projection model is demonstrated for the first time. A consequent upper bound of the deviation is proved, within which the fiducial markers can be tracked in an affine transformation constrained model. Then a series of solutions is proposed to cope with the fiducial marker tracking problem.

2.1 Affine relationship of two micrographs

We begin with the projection model. Typically, the projection is modeled as an affine or orthogonal projection. A classic orthogonal model is described as follows (in this section, the bold font is used to indicate vectors or matrices; a 2D point is represented by a 2 × 1 vector):

$$\left(\begin{array}{c}u\\ v\end{array}\right)=s{\mathbf{R}}_{\gamma }\mathbf{P}{\mathbf{R}}_{\beta }{\mathbf{R}}_{\alpha }\left(\begin{array}{c}X\\ Y\\ Z\end{array}\right)+\mathbf{t},$$ (1)

where (X, Y, Z)^T is the spatial location of the ultrastructure or fiducial markers, s is the image scale change, γ is the inplane rotation angle, α is the pitch angle of the tilt axis of the projection, β is the tilt angle of the sample, $\mathbf{t}={(t_0,t_1)}^T$ is the translation of the view, (u, v)^T is the measured projection point and P denotes the orthogonal projection matrix. ${\mathbf{R}}_{\alpha },\hspace{0.17em}{\mathbf{R}}_{\beta }$, P and R_γ are defined as follows:

$$\begin{array}{c}{\mathbf{R}}_{\alpha }=\left(\begin{array}{ccc}1& 0& 0\\ 0& \hspace{0.17em}\text{cos}\hspace{0.17em}\alpha & \hspace{0.17em}\text{sin}\hspace{0.17em}\alpha \\ 0& -\text{sin}\hspace{0.17em}\alpha & \hspace{0.17em}\text{cos}\hspace{0.17em}\alpha \end{array}\right),\\ {\mathbf{R}}_{\beta }=\left(\begin{array}{ccc}\hspace{0.17em}\text{cos}\hspace{0.17em}\beta & 0& -\text{sin}\hspace{0.17em}\beta \\ 0& 1& 0\\ \hspace{0.17em}\text{sin}\hspace{0.17em}\beta & 0& \hspace{0.17em}\text{cos}\hspace{0.17em}\beta \end{array}\right),\\ \mathbf{P}=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\end{array}\right),\\ {\mathbf{R}}_{\gamma }=\left(\begin{array}{cc}\hspace{0.17em}\text{cos}\hspace{0.17em}\gamma & \hspace{0.17em}\text{sin}\hspace{0.17em}\gamma \\ \hspace{0.17em}-\text{sin}\hspace{0.17em}\gamma & \hspace{0.17em}\text{cos}\hspace{0.17em}\gamma \end{array}\right).\end{array}$$

For two arbitrary views (micrographs), we can always construct a single transformation that aligns all the corresponding fiducial markers within a limited deviation. We will first prove a Lemma that theoretically guarantees the upper bound of deviation on any arbitrary fiducial marker, and then apply this Lemma to prove a Theorem which guarantees the upper bound over all the fiducial markers.

Lemma:

Suppose the pitch angle is fixed during tilt, for any arbitrary fiducial marker ${(X_j,Y_j,Z_j)}^T$ and its arbitrary two projections (denoted as p_ij and ${\mathbf{p}}_{i\prime j}$), there is always a transformation A and t which is independent of j (Equation 3 and Equation 4) that can be applied to this fiducial marker (${\mathbf{p}}_{ij}^{\prime }=\mathbf{A}{\mathbf{p}}_{ij}+\mathbf{t}$) to make the deviation $\left|\right|{\Delta }_j\left|\right|=\left|\right|{\mathbf{p}}_{ij}^{\prime }-{\mathbf{p}}_{i\prime j}\left|\right|\le s_{i\prime }\left|\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}\Delta \beta }{\hspace{0.17em}\text{cos}\hspace{0.17em}\alpha \hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_i}\right(Z_j-Z_{\mathit{\mu }}\left)\right|$, where α is the fixed pitch angle, $s_{i\prime }$ is the scale change of the $i\prime$ th micrograph, β_i and ${\beta }_{i\prime }$ are the tilt angles of the corresponding projections, $\Delta \beta ={\beta }_{i\prime }-{\beta }_i$ and $Z_{\mathit{\mu }}=\frac{1}{N}{\sum }_{j=1}^N{Z}_j$.

Proof.

We give the detailed proof in Supplementary Material Section S1. Here we only provide the outline of the proof. The main idea is to construct such a transformation that is independent of j and prove that the deviation of this transformation is exactly $s_{i\prime }\left|\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}\Delta \beta }{\hspace{0.17em}\text{cos}\hspace{0.17em}\alpha \hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_i}\right(Z_j-Z_{\mathit{\mu }}\left)\right|$ as given in the Lemma. Therefore, the optimal transformation will always be upper bounded by this value.

Firstly, by substituting P, R_β and R_α into Equation (1), the orthogonal projection can be rewritten as:

$$\begin{array}{c}\left(\begin{array}{c}u\\ v\end{array}\right)=s{\mathbf{R}}_{\gamma }\left(\begin{array}{cc}\hspace{0.17em}\text{cos}\hspace{0.17em}\beta & \hspace{0.17em}\text{sin}\hspace{0.17em}\alpha \hspace{0.17em}\text{sin}\hspace{0.17em}\beta \\ 0& \hspace{0.17em}\text{cos}\hspace{0.17em}\alpha \end{array}\right)\left(\begin{array}{c}X\\ Y\end{array}\right)\\ +s{\mathbf{R}}_{\gamma }\left(\begin{array}{c}-\text{sin}\hspace{0.17em}\beta \hspace{0.17em}\text{cos}\hspace{0.17em}\alpha \\ \hspace{0.17em}\text{sin}\hspace{0.17em}\alpha \end{array}\right)Z+\left(\begin{array}{c}{t}_0\\ t_1\end{array}\right).\end{array}$$ (2)

Now consider the jth fiducial marker ${(X_j,Y_j,Z_j)}^T$ (j = 1, 2,…, N), by writing out its projections in the ith and $i\prime$ th views [${\mathbf{p}}_{ij}={(u_{ij},v_{ij})}^T$ and ${({\mathbf{p}}_{i\prime j}=u_{i\prime j},v_{i\prime j})}^T$] according to Equation (2) and define ${\Delta }_j={\mathbf{p}}_{ij}^{\prime }-{\mathbf{p}}_{i\prime j}$, we can construct transformation A and t as follows:

$$\mathbf{A}=\frac{s_{i\prime }}{s_i}{\mathbf{R}}_{{\gamma }_{i\prime }}\left(\begin{array}{cc}\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_{i\prime }& \hspace{0.17em}\text{sin}\hspace{0.17em}{\alpha }_{i\prime }\hspace{0.17em}\text{sin}\hspace{0.17em}{\beta }_{i\prime }\\ 0& \hspace{0.17em}\text{cos}\hspace{0.17em}{\alpha }_{i\prime }\end{array}\right)\left(\begin{array}{cc}\frac{1}{\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_i}& \frac{-\text{sin}\hspace{0.17em}{\alpha }_i\hspace{0.17em}\text{sin}\hspace{0.17em}{\beta }_i}{\hspace{0.17em}\text{cos}\hspace{0.17em}{\alpha }_i\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_i}\\ 0& \frac{1}{\hspace{0.17em}\text{cos}\hspace{0.17em}{\alpha }_i}\end{array}\right){\mathbf{R}}_{-{\gamma }_i},$$ (3)

and

$$\mathbf{t}={\mathbf{t}}_{i\prime }-\mathbf{A}{\mathbf{t}}_i-\mathbf{w}{Z}_{\mathit{\mu }},$$ (4)

where $Z_{\mathit{\mu }}=\frac{1}{N}\sum _{j=1}^N{Z}_j$ and $\mathbf{w}=s_{i\prime }{\mathbf{R}}_{{\gamma }_{i\prime }}{(\Delta u,\Delta v)}^T$. Here,

$$\begin{array}{c}\Delta u=-\frac{\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_{i\prime }\hspace{0.17em}\text{sin}\hspace{0.17em}{\beta }_i\hspace{0.17em}\text{cos}\hspace{0.17em}{\alpha }_i}{\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_i}-\frac{{(\text{sin}\hspace{0.17em}{\alpha }_i)}^2\hspace{0.17em}\text{sin}\hspace{0.17em}{\beta }_i\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_{i\prime }}{\hspace{0.17em}\text{cos}\hspace{0.17em}{\alpha }_i\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_i}\\ +\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}{\alpha }_{i\prime }\hspace{0.17em}\text{sin}\hspace{0.17em}{\beta }_{i\prime }\hspace{0.17em}\text{sin}\hspace{0.17em}{\alpha }_i}{\hspace{0.17em}\text{cos}\hspace{0.17em}{\alpha }_i}+\text{sin}\hspace{0.17em}{\beta }_{i\prime }\hspace{0.17em}\text{cos}\hspace{0.17em}{\alpha }_{i\prime },\\ \Delta v=\frac{\hspace{0.17em}\text{cos}\hspace{0.17em}{\alpha }_{i\prime }\hspace{0.17em}\text{sin}\hspace{0.17em}{\alpha }_i-\text{sin}\hspace{0.17em}{\alpha }_{i\prime }\hspace{0.17em}\text{cos}\hspace{0.17em}{\alpha }_i}{\hspace{0.17em}\text{cos}\hspace{0.17em}{\alpha }_i}=\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}({\alpha }_i-{\alpha }_{i\prime })}{\hspace{0.17em}\text{cos}\hspace{0.17em}{\alpha }_i}.\end{array}$$

Note that our construction of A and t is independent of j. In most ET systems, the micrographs are taken with the pitch angle fixed, which means that ${\alpha }_i\approx {\alpha }_{i\prime }$. Suppose ${\alpha }_i={\alpha }_{i\prime }=\alpha$, and let ${\beta }_{i\prime }-{\beta }_i=\Delta \beta ,\hspace{0.17em}\Delta u$ and Δv can be rewritten as:

$$\begin{array}{c}\Delta u=\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}{\alpha }^2}{\hspace{0.17em}\text{cos}\hspace{0.17em}\alpha }·\left(\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}{\beta }_{i\prime }·\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_i-\text{cos}\hspace{0.17em}{\beta }_{i\prime }·\hspace{0.17em}\text{sin}\hspace{0.17em}{\beta }_i}{\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_i}\right)\\ +\frac{\hspace{0.17em}\text{cos}\hspace{0.17em}{\alpha }^2}{\hspace{0.17em}\text{cos}\hspace{0.17em}\alpha }·\left(\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}{\beta }_{i\prime }·\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_i-\text{cos}\hspace{0.17em}{\beta }_{i\prime }·\hspace{0.17em}\text{sin}\hspace{0.17em}{\beta }_i}{\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_i}\right)\\ =\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}{\alpha }^2+\text{cos}\hspace{0.17em}{\alpha }^2}{\hspace{0.17em}\text{cos}\hspace{0.17em}\alpha }·\left(\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}({\beta }_{i\prime }-{\beta }_i)}{\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_i}\right)=\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}\Delta \beta }{\hspace{0.17em}\text{cos}\hspace{0.17em}\alpha ·\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_i},\\ \Delta v=\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}(\alpha -\alpha )}{\hspace{0.17em}\text{cos}\hspace{0.17em}\alpha }=0.\end{array}$$ (5)

The deviation Δ_j can thus be derived as:

$${\Delta }_j=s_{i\prime }{\mathbf{R}}_{{\gamma }_{i\prime }}\left(\begin{array}{c}\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}\Delta \beta }{\hspace{0.17em}\text{cos}\hspace{0.17em}\alpha \hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_i}\\ 0\end{array}\right)(Z_j-Z_{\mathit{\mu }}).$$ (6)

By taking the norm of $\left|\right|{\Delta }_j\left|\right|$, we get $\left|\right|{\Delta }_j\left|\right|=s_{i\prime }\left|\right|{\mathbf{R}}_{{\gamma }_{i\prime }}\left|\right|\left|\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}\Delta \beta }{\hspace{0.17em}\text{cos}\hspace{0.17em}\alpha \hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_i}\right(Z_j-Z_{\mathit{\mu }}\left)\right|=s_{i\prime }\left|\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}\Delta \beta }{\hspace{0.17em}\text{cos}\hspace{0.17em}\alpha \hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_i}\right(Z_j-Z_{\mathit{\mu }}\left)\right|$. Since the transformation we constructed in Equation (3) and Equation (4) always exists, and is just one of all the possible transformations, the deviation of the optimal transformation will thus always be upper bounded by $s_{i\prime }\left|\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}\Delta \beta }{\hspace{0.17em}\text{cos}\hspace{0.17em}\alpha \hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_i}\right(Z_j-Z_{\mathit{\mu }}\left)\right|$.

Typically, $s\prime$ is around 1; the value of the tilt angle β is between $-{60}^{°}$ and ${60}^{°}$; and the pitch angle α is between $-5^{°}$ and $5^{°}$. Therefore, the value of $\left|\right|\Delta \mathbf{t}\left|\right|$ will not be more than $2s_{i\prime }\hspace{0.17em}\text{sin}\hspace{0.17em}\Delta \beta (Z_j-Z_{\mathit{\mu }})$. If all the fiducial markers are located on one surface of the specimen, $Z_j-Z_{\mathit{\mu }}$ will be very small (almost equal to zero). In this case, the distributions of the fiducial markers on different projections can be constrained by the affine transformation between two arbitrary micrographs in the tilt series. If the fiducial markers are located on two surfaces of the specimen, $Z_j-Z_{\mathit{\mu }}$ will not be more than half of the thickness of the specimen (denoted as T). If a large tilt angle offset occurs, a coordinate transformation can be applied to the system to keep the fiducial markers horizontal. We give a more generalized case of the proof in Part 2 of Supplementary Material Section S1 to support our bound when the tilt angle offset is considered. A micrograph with well-distributed fiducial markers will not contain overlapping fiducial markers. Therefore, the distance between two measured fiducial marker positions will be more than the diameters of the fiducial markers. Now denoting the diameter of a fiducial marker as D, we can conclude that if the tilt angle difference is $\Delta \beta <\frac{D}{T}$, the distributions of the fiducial markers on two views can be constrained by the affine transformation without any ambiguity. For example, if the diameter of fiducial markers is 20 pixels and the thickness of the specimen is 200 pixels, the maximum $\Delta \beta$ is around 6° (0.1 Radian), which is satisfied by almost all the tilt series.

Theorem:

Suppose the pitch angle is fixed during tilt, for any arbitrary two projections (denoted as ${\mathbf{p}}_i$ and ${\mathbf{p}}_{i\prime }$), there is always a transformation A and t that can be applied to ${\mathbf{p}}_i$ such that the total deviation over all the fiducial markers is upper bounded by ${\sum }_{j=1}^N{s}_{i\prime }\left|\frac{\hspace{0.17em}\text{sin}\hspace{0.17em}\Delta \beta }{\hspace{0.17em}\text{cos}\hspace{0.17em}\alpha \hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_i}\right(Z_j-Z_{\mathit{\mu }}\left)\right|$, where $Z_{\mathit{\mu }}=\frac{1}{N}\sum _{j=1}^N{Z}_j$.

Proof.

By applying the construction of the transformation according to Equation (3) and Equation (4), both of which are independent of any specific fiducial marker, the upper bound can be derived by summing the upper bound in the Lemma over all the fiducial markers.

The upper bound infers that the measured fiducial marker positions from a tilt series’ different views can be related by the affine transformation within a very small deviation, which indicates that fiducial marker tracking based on a predefined mathematical model can achieve comparable results as the spatial marker-based tracking. The proved upper bound has two direct applications: first, it offers an affine prior to the prediction of fiducial marker positions, which will be useful for motion prediction (Mastronarde and Held, 2017) and missing fiducial marker recovery (Amat et al., 2008; Han et al., 2015); second, it can serve as the guide for the development of fast tracking algorithms.

2.2 Fiducial marker tracking by GMM

We proved that the affine transformation assumption between two micrographs can be satisfied within a very small deviation, which makes the design of a fast and reliable fiducial marker tracking algorithm possible. In this section, a GMM (Jian and Vemuri, 2011) will be used to represent a point set, and a point set registration solution from the view of probability distribution will be provided.

2.2.1 GMM presentation of a point set

We would denote the positions of fiducial markers from a micrograph as the fixed ‘scene’ point set $\mathcal{X}=\{{\mathbf{x}}_n,n=1,\dots ,N\}$ and the positions of fiducial markers from another micrograph as the moving ‘model’ point set $\mathcal{Y}=\{{\mathbf{y}}_m,m=1,\dots ,M\}$. Our aim is to find an affine transformation $\mathcal{T}(·)$ so that there is a subset of $\mathcal{T}\left(\mathcal{Y}\right)$ with the maximum cardinality in which the points are corresponding to the points from a subset of the fixed ‘scene’ set $\mathcal{X}$ under a selected measure of distance (or equivalently, similarity).

For a point y, the probability density function that a point x is corresponding to y can be measured by a Gaussian kernel (Jian and Vemuri, 2011):

$$p\left(\mathbf{x}\right|\mathbf{y})=\frac{1}{2\pi {\sigma }^2}\text{exp}\hspace{0.17em}\left(-\frac{\left|\right|\mathbf{x}-\mathbf{y}|{|}^2}{2{\sigma }^2}\right),$$ (7)

where σ is a punishment parameter for similarity. If point x is located in the same coordinate of y, the probability reaches its maximum. Given the point set $\mathcal{Y}$, its GMM presentation can be defined as $p\left(\mathbf{x}\right|\mathcal{Y})={\sum }_{j=1}^{m}P\left(m\right)p\left(\mathbf{x}\right|{\mathbf{y}}_m)$, where P(m) represents the prior probability of the mth point ${\mathbf{y}}_m$. The set to set case ($\mathcal{X}$ to $\mathcal{Y}$) can be generalized from the one point to set case as $\frac{1}{2\pi {\sigma }^2}{\sum }_{n=1}^N{\sum }_{m=1}^M{w}_m{e}^{-\frac{\left|\right|{\mathbf{x}}_n-\mathcal{T}\left({\mathbf{y}}_m\right)|{|}^2}{2{\sigma }^2}}$, where w_m is the weight specified by the prior. It is clear that the sum of the probability density function has the robust similarity form of $si{m}_{robust}=\sum \sum g\left(\right||\mathbf{x}-\mathbf{y}|{|}^2)$, where $g(·)$ is the M-estimator (Stewart, 1999) in Gaussian shape. Robust similarity is not a convex function (Jian and Vemuri, 2011). An heuristic solution such as simulated annealing may overcome some local maximums, but it is unable to guarantee a globally optimal solution.

Since the fiducial marker distribution is prone to be corrupted by missing markers or the appearance of markers in high tilt angles, a feasible similarity punishment should ensure that the global solution of sim_robust equals to the correct corresponding relationship of the point sets. The shape of the cost function is also determined by σ. Our solution starts from the determination of the similarity punishment σ. We borrow the concept of the point-spread function (PSF) to explain the criteria in σ value determination. The PSF describes how blurry a single point-like emitter will appear when it is diffracted through a microscope and the full width at half maximum value of the PSF is used to characterize the resolution (Betzig et al., 2006; Nieuwenhuizen et al., 2013). The Gaussian kernel is just like the PSF here and the resolution of the fiducial marker positions is determined by the similarity and σ. We should ensure that almost all the fiducial markers are distinguishable under a given σ, which means that the peak of the Gaussian function should be retained under summation. Therefore, σ can be determined as:

$$\sigma =\beta \min (\frac{1}{M}\sum _{m=1}^{M}dist({\mathbf{y}}_m,\mathcal{Y}),\frac{1}{N}\sum _{n=1}^{N}dist({\mathbf{x}}_n,\mathcal{X})),$$ (8)

where $\beta \in [0.2,0.5]$ is the parameter to control the distance interpretation and $dist(\mathbf{x},\mathcal{X})$ refers to the minimum distance between the point x to the points belonging to $\mathcal{X}$ (except itself).

2.2.2 Fast parameter refinement by CPD

Coherent point drift (CPD) (Myronenko and Song, 2010) is introduced for the estimation of transformation $\mathcal{T}(·)$. The view of CPD is from the aspect of assignment and CPD introduces a representation of the outliers. Given a point x, it has P(m) probability corresponding to the mth point ${\mathbf{y}}_m$, thus its total probability that belongs to the point set $\mathcal{Y}$ is denoted as $\sum _{j=1}^{m}P\left(m\right)p\left(\mathbf{x}\right|{\mathbf{y}}_m)$. Considering the probability that point x may represent an outlier, let w denote the outlier probability. Assuming x is sampled from the point set $\mathcal{X}$ randomly and the points in $\mathcal{Y}$ share an equal prior probability, the mixture model takes the form as:

$$p\left(\mathbf{x}\right)=w\frac{1}{N}+(1-w)\sum _{j=1}^m\frac{1}{M}p\left(\mathbf{x}\right|{\mathbf{y}}_m).$$ (9)

The cost function in CPD is defined as the minimization of the negative log-likelihood function:

$$E\left(\mathcal{T}\right(·),{\sigma }^2)=-\sum _{n=1}^N\hspace{0.17em}\text{log}\hspace{0.17em}\sum _{m=1}^{M+1}P\left(m\right)p\left(\mathbf{x}\right|{\mathbf{y}}_m),$$ (10)

where P(m) is the reweighted prior and $p\left(\mathbf{x}\right|{\mathbf{y}}_{M+1})=\frac{w}{N}$ represents the probability of outliers. The negative likelihood function has an obvious advantage that it can be effectively solved by an expectation–maximum (EM) algorithm.

According to Jensen’s inequality, the upper bound of the negative log-likelihood function used in the EM algorithm can be defined as:

$$Q=-\sum _{n=1}^N\sum _{m=1}^{M+1}{p}^{old}\left(m\right|{\mathbf{x}}_n)\hspace{0.17em}\text{log}\hspace{0.17em}\left(P^{new}\left(m\right)p^{new}\left({\mathbf{x}}_n\right|{\mathbf{y}}_m)\right),$$ (11)

where $p\left(m\right|{\mathbf{x}}_n)=P(m\left)p\right({\mathbf{x}}_n\left|{\mathbf{y}}_m\right)/p\left({\mathbf{x}}_n\right)$ is the corresponding probability between ${\mathbf{y}}_m$ and ${\mathbf{x}}_n$, the ‘old’ parameters indicate the guess of values in the E-step and the ‘new’ parameters are determined by minimizing the expectation of the complete negative log-likelihood function in the M-step. The algorithm iterates the E-step and M-step until convergence.

E-step:

Ignoring the constants, the objective function in the E-step can be rewritten as:

$$\begin{array}{c}Q(\mathbf{A},\mathbf{t},{\sigma }^2)=\frac{1}{2{\sigma }^2}\sum _{n=1}^N\sum _{m=1}^M{p}^{old}\left(m\right|{\mathbf{x}}_n\left)\right||{\mathbf{x}}_n-\mathcal{T}({\mathbf{y}}_m;\mathbf{A},\mathbf{t}\left)\right|{|}^2\\ +\frac{N_{p}D}{2}\text{log}\hspace{0.17em}{\sigma }^2,\end{array}$$ (12)

where $\mathcal{T}({\mathbf{y}}_m;\mathbf{A},\mathbf{t})=\mathbf{A}{\mathbf{y}}_m+\mathbf{t},\hspace{0.17em}{N}_p={\sum }_{n=1}^N{\sum }_{m=1}^M{p}^{old}\left(m\right|{\mathbf{x}}_n)\le N$ (with N = N_p only if w = 0), and $p^{old}\left(m\right|{\mathbf{x}}_n)$ denotes the posterior probabilities of GMM components calculated using the previous parameter values:

$$p^{old}\left(m\right|{\mathbf{x}}_n)=\frac{\hspace{0.17em}\text{exp}\hspace{0.17em}\left(-\frac{1}{2}\left|\right|\frac{{\mathbf{x}}_n-\mathcal{T}({\mathbf{y}}_m,{\mathbf{A}}^{old},{\mathbf{t}}^{old})}{{\sigma }^{old}}|{|}^2\right)}{\sum _{k=1}^M\hspace{0.17em}\text{exp}\hspace{0.17em}\left(-\frac{1}{2}\left|\right|\frac{{\mathbf{x}}_n-\mathcal{T}({\mathbf{y}}_k,{\mathbf{A}}^{old},{\mathbf{t}}^{old})}{{\sigma }^{old}}|{|}^2\right)+c}.$$ (13)

Here $c=2\pi {\sigma }^2\frac{w}{1-w}\frac{M}{N}$. Within a feasible local interval, minimizing the objective function Q in the E-step is equal to solving the negative log-likelihood function E in Equation (10).

M-step:

In the M-step, our aim is to find the affine matrix A and t in $\mathcal{T}(·)$ that minimizes the objective function Q. It is clear that Q has a closed-form expression (Myronenko and Song, 2010). For the convenience of the following discussion, several representations of variables are introduced:

1. ${\mathbf{X}}_{N\times 2}={({\mathbf{x}}_1\cdots {\mathbf{x}}_N)}^T$—matrix presentation of the point set $\mathcal{X}$;

2. ${\mathbf{Y}}_{M\times 2}={({\mathbf{y}}_1\cdots {\mathbf{y}}_M)}^T$—matrix presentation of the point set $\mathcal{Y}$;

3. $\mathbf{1}$—the column vector of all ones;

4. $\mathrm{d}\left(\mathbf{a}\right)$—the diagonal matrix formed from vector a;

5. P—the matrix that is composed by $p_{mn}=p^{old}\left(m\right|{\mathbf{x}}_n)$.

The solution is to firstly find the root of the partial derivative Q with respect to t and then substitute t back into the objective function to obtain the matrix A. Here the equation of $\frac{\partial Q}{\partial \mathbf{t}}$ takes the form as:

$$\frac{\partial Q}{\partial \mathbf{t}}=\frac{1}{{\sigma }^2}\sum _{n=1}^N\sum _{m=1}^M{p}^{old}\left(m\right|{\mathbf{x}}_n)\left({\mathbf{x}}_n-\mathbf{A}{\mathbf{y}}_m+\mathbf{t}\right)=0,$$ (14)

in which the root t is

$$\mathbf{t}=\frac{1}{N_p}\sum _{n=1}^N\sum _{m=1}^M{p}^{old}\left(m\right|{\mathbf{x}}_n\left)\right({\mathbf{x}}_n-\mathbf{A}{\mathbf{y}}_m).$$ (15)

By introducing the variables 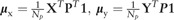, t can be rewritten as $\mathbf{t}={\mathit{\mu }}_x-\mathbf{A}{\mathit{\mu }}_y$.

Substitute t back into Q and solve the equation of partial derivative $\frac{\partial Q}{\partial \mathbf{A}}$, the root A is

(16)

where $\widehat{\mathbf{X}}=\mathbf{X}-\mathbf{1}{\mathit{\mu }}_x^T,\hspace{0.17em}\widehat{\mathbf{Y}}=\mathbf{Y}-\mathbf{1}{\mathit{\mu }}_y^T$. ${\sigma }^2$ is also updated according to the result of $\frac{\partial Q}{\partial {\sigma }^2}$:

$${\sigma }^2=\frac{1}{N_{p}D}\left(\text{tr}\right({\widehat{\mathbf{X}}}^T\mathrm{d}\left({\mathbf{P}}^T\mathbf{1}\right)\widehat{\mathbf{X}})-\text{tr}({\widehat{\mathbf{X}}}^T{\mathbf{P}}^T\widehat{\mathbf{Y}}{\mathbf{A}}^T\left)\right).$$ (17)

After solving the matrix A and t, the moving ‘model’ point set $\mathcal{Y}$ is then updated by $\mathcal{T}\left({\mathbf{y}}_m\right)=\mathbf{A}{\mathbf{y}}_m+\mathbf{t}$.

2.2.3 Divide-and-conquer strategy against lens distortion

The most severe problem in fiducial marker tracking is that the shape context of fiducial markers on a micrograph can be easily corrupted. Although the affine transformation relationship can serve as a global constraint and suppress the effect of outliers, spherical aberration of the lens and non-uniform magnetic fields will result in non-uniform magnification of the micrographs (Lawrence et al., 2006), which may increase the deviation of the global affine constraint. Furthermore, as an algebraic solution to the point set registration, CPD still has problems in local convergence, which will lead to incorrect correspondence. Our method tries to overcome the local convergence issue. The procedure of fiducial marker matching based on the GMM is illustrated in Algorithm 1, where the threshold d is used to determine whether two points from different point sets are close enough.

Algorithm 1 .

Recover correspondence between $\mathcal{X}$ and $\mathcal{Y}$.

input:$\mathcal{X},\hspace{0.17em}\mathcal{Y}$

1: Generate initial estimation of $\mathcal{T}(·;\mathbf{A},\mathbf{t})$ by grid search;

2: Select several $\left\{\mathcal{T}\right(·\left)\right\}$ as initial inputs

3: for all${\mathcal{T}}_i\in \left\{\mathcal{T}\right(·\left)\right\}$do

4:  Estimate ${\mathcal{T}}_i$ by CPD as in Section 2.2.2

5:  Apply ${\mathcal{T}}_i$ to $\mathcal{Y}$

6:  Calculate $si{m}_{robust}(\mathcal{X},{\mathcal{T}}_i(\mathcal{Y}\left)\right)$

7:  ifsim_robust is large enough then

8:   Use ${\mathcal{T}}_i$ and stop trying

9:  end if

10: end for

11: $\mathcal{T}(·)\leftarrow {\mathcal{T}}_i(·)$

12: return$\mathcal{T}(·)$

In our solution, the initial value of σ is assigned according to Equation (8). As a compensation, a grid search of the applicable value of the transformation matrix A and t with a step size of $2.5\sigma$ is conducted at the beginning. The initial values of A and t with a high value of the robust similarity measure are fed into CPD. Under the assumption that the pitch angle almost remains unchanged, we can get the simplified version of A according to Equation (3):

$$\mathbf{A}=\frac{s_{i\prime }}{s_i}{\mathbf{R}}_{{\gamma }_{i\prime }}\left(\begin{array}{cc}\frac{\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_{i\prime }}{\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_i}& \frac{\hspace{0.17em}\text{tan}\hspace{0.17em}\alpha \hspace{0.17em}\text{sin}\hspace{0.17em}\Delta \beta }{\hspace{0.17em}\text{cos}\hspace{0.17em}{\beta }_i}\\ 0& 1\end{array}\right){\mathbf{R}}_{-{\gamma }_i}.$$ (18)

It should be noted that the values of $s_{i\prime }$ and s_i are very close to each other. The values of ${\beta }_{i\prime }$ and β_i can be assigned from the recorded tilt angles when designing the search range of A. Considering the real pitch angle in a tilt series, $\text{tan}\hspace{0.17em}\alpha$ is a very small value and can be neglected. Therefore, the search range of A is indeed very small. If the tilt angle interval is not too large, the affine matrix A will degenerate to a rotation matrix. However, it is enough for an initial estimation of A. The search range of t is limited in half the width of the micrographs, which is enough considering the actual shift. The transformation which has a high rank of $si{m}_{robust}(\mathcal{X},{\mathcal{T}}_i(\mathcal{Y}\left)\right)$ will be used as the initial seed for further estimation. The fine estimation of transformation $\mathcal{T}(·)$ is then carried out by CPD. The refined value $\mathcal{T}(·)$ with the highest $si{m}_{robust}(\mathcal{X},{\mathcal{T}}_i(\mathcal{Y}\left)\right)$ is outputted as the final result.

The affine transformation relationship cannot cover all the correspondence of two sets of fiducial markers under the effect of lens distortion. Fortunately, we notice that the divide-and-conquer strategy can solve this issue well. Our proposed algorithm that is against the lens distortion is illustrated in Algorithm 2.

Algorithm 2 .

Refine transformation $\mathcal{T}(·)$ against lens distortion.

input:$\mathcal{X},\hspace{0.17em}\mathcal{Y},\hspace{0.17em}\mathcal{T}$, and distance threshold d

1: $\mathcal{C}\leftarrow \varnothing$; $\Phi \leftarrow \varnothing$

2: while$dist(\mathcal{X},\mathcal{T}(\mathcal{Y}\left)\right)<d$do

3:  Apply $\mathcal{T}(·)$ to $\mathcal{Y}$

4:  for all$x\in \mathcal{X}$ and $y\in \mathcal{Y}$do

5:   if$dist(x,\mathcal{T}(y\left)\right)<0.75d$then

6:    $\mathcal{C}\leftarrow \mathcal{C}\cup (x,y)$

7:   end if

8:   $\mathcal{M}\leftarrow \varnothing$

9:   if$dist(x,\mathcal{T}(y\left)\right)<d$then

10:    $\mathcal{M}\leftarrow \mathcal{M}\cup (x,y)$

11:   end if

12:  end for

13:  $\Phi \leftarrow \Phi \cup \mathcal{T}$

14:  Recalculate transformation $\mathcal{T}$ by $\mathcal{M}$

15: end while

16: return$\mathcal{C}$ and $\Phi$

In our implementation, a coarse distance threshold d is used, such as the diameter of the used fiducial markers. The input is the result from Algorithm 1. Firstly, the transformation $\mathcal{T}(·)$ is applied to $\mathcal{Y}$ and then the peer distance with $\mathcal{X}$ is calculated. If the distance of two points from different point sets is less than the distance threshold d, the point pair is considered as a matched pair. If the distance is less than $0.75d$, the matched pair will be directly outputted; if not, the matched pair will be used to recalculate the transformation $\mathcal{T}(·)$. Here we assume that the distortion is mild and continuous. In the next iteration, we rerun the procedure to generate the satisfied correspondence until no matched point pair can be found between $\mathcal{X}$ and $\mathcal{T}\left(\mathcal{Y}\right)$. Finally, multiple $\mathcal{T}\prime s$ will be outputted to describe the distortion in the micrographs.

3 Results

3.1 Test datasets

Three datasets are used in our experiments. The first dataset, VEEV, is a tilt series with the fiducial markers located sparsely on the surfaces (Fig. 1A). In this specimen, cryo-EM grids were prepared by depositing 5 μL of VEEV mixed with gold beads on 200 mesh Quantifoil copper grids with a holey carbon support. An additional thin carbon film was overlaid on the grids before specimen deposition. The tilt series was taken by a DE20 camera (Direct Electron, LP, San Diego, CA) with a cumulative dose of $\sim 55-70\mathrm{e}/{\AA }^2$ per tilt series. The tilt angles of the projection images range from $-{50.0}^{°}$ to $+{50.0}^{°}$ at $5^{°}$ intervals. In total, there are 21 images in the tilt series. The size of each tilt image is $3K\times 4K$ with a pixel size of 0.1 nm. Because this dataset has about $40\sim 50$ fiducial markers sparsely located on one surface, it is feasible to be used to assess the tracking deviation in real datasets.

Fig. 1.

Example images from the three test sets. (A) VEEV, (B) Hemocyanin and (C) Adhesion belt

The second dataset, Hemocyanin, is a tilt series of vitrified keyhole limpet hemocyanin solution (Fig. 1B). Hemocyanin was bought from Sigma-Aldrich (USA) and buffered in phosphate-buffered saline solution with a protein concentration of 1 mg/ml. The 300 mesh copper EM grids with holey carbon film (Quantifoil R2/1) were bought from EMS (Electron Microscopy Sciences, USA). Protein solution was applied to glow discharged grids and blotted in Vitrobot IV (FEI, the Netherlands) using 4 s blotting time under blotting force 2. The blotting chamber conditions were kept at 4% and 100% humidity. After blotting, the grids were plunge-frozen in liquid ethane cooled by liquid nitrogen. The cryo-ET data were collected by FEI Titan Krios (operated at 300 kV) with a Gatan US4000 camera. The total dose used during data collection was around 8000 e/nm². There are 95 images with the tilt angles ranging from $-{70.0}^{°}$ to $+{70.0}^{°}$ at $1^{°}\sim 2^{°}$ intervals. The size of each tilt image is $2K\times 2K$ with a pixel size of 0.4 nm. This is a dataset that we have used in our previous work (Han et al., 2015).

The third dataset, Adhesion belt, is a tilt series of adhesion belt structure (Fig. 1C). The Adhesion belt dataset was provided by the National Institute of Biological Sciences of China. The data were collected by an FEI Titan Krios (operated at 300 kV) with a Gatan camera. There are 111 images, with tilt angles ranging from $-{50.0}^{°}$ to $+{60.0}^{°}$ at $1^{°}\sim 2^{°}$ intervals. The size of each tilt image is $2K\times 2K$, with a pixel size of 2.03 nm (2 magnitude-binned). The initial orientation of the tilt azimuth with respect to the vertical direction of the image is ${2.4}^{°}$. This dataset has a mass of fiducial markers embedded in the specimen, which provides a proper dataset to compare the runtime of our previous work and the current algebraic solution.

3.2 Experimental performance

3.2.1 Verification of the theoretical bound

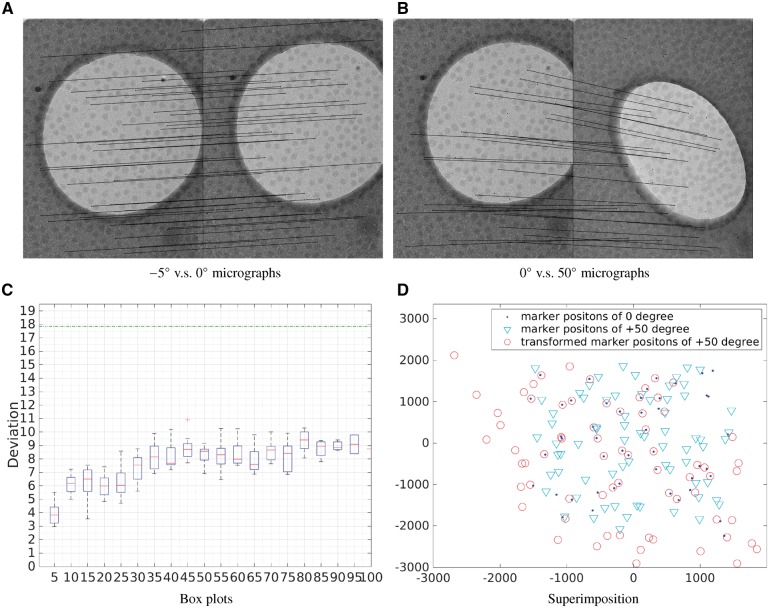
We first test whether the theoretical upper bound given in Section 2.1 holds in real-world datasets. Since the VEEV dataset was taken in a large zoom scale and has a good distribution of fiducial markers, it is used in this experiment. Firstly, the fiducial marker positions were extracted by our automatic fiducial marker detection method (Han et al., 2015) and then the fiducial marker positions belonging to different micrographs were matched. According to the angle values of the VEEV dataset, we matched the ith and the $(i+n)$ th micrographs ($n=1,\mathrm{2\dots }N-i$) and obtained the corresponding point set registration results. All the fiducial marker positions were matched by the GMM-based solution. In case of notable difference between $\text{cos}\hspace{0.17em}\beta \prime$ and $\text{cos}\hspace{0.17em}\beta$ (i.e. $\text{cos}\hspace{0.17em}(\beta \prime )/\hspace{0.17em}\text{cos}\hspace{0.17em}(\beta )>1.2$), the full implementation of Equation (18) is used for the coarse estimation. Since in practice $\text{cos}\hspace{0.17em}\beta \prime$ and $\text{cos}\hspace{0.17em}\beta$ are almost always similar, Equation (18) is seldom needed, but rather to guarantee the completeness of the method. Figure 2 illustrates the fiducial marker match results. Figure 2A presents the relationship of fiducial marker positions between the micrographs from $-5^{°}$ and $0^{°}$ tilt angles. We can see that the links used to mark the correspondent relationship are almost parallel to each other, which indicates that the fiducial marker positions have not changed a lot between these two views. Figure 2B presents the relationship between the fiducial markers from $0^{°}$ and ${50}^{°}$ tilt angles in which the tilt angle difference is ${50}^{°}$. As expected, the related positions of the fiducial markers have changed a lot due to the tremendous difference of tilt angles. Figure 2C gives the match error of micrographs with different intervals of the tilt angle. It can be noticed that the deviation is the smallest when the tilt angle interval is $5^{°}$ and the average deviation increases when the tilt angle interval increases. Figure 2C is very useful for the design of tracking methods. According to the values of the average deviation, when the tilt angle interval is less than ${20}^{°}$, the deviation is <6 pixels, which is much smaller than the fiducial marker diameter value (18 pixels). Therefore, when designing tracking algorithms, we can just match the micrographs whose tilt angle interval is less than ${20}^{°}$ and then combine the match results together (Amat et al., 2008; Brandt and Ziese, 2006; Han et al., 2015).

Fig. 2.

(A) The match of fiducial markers that belong to micrographs of $-5^{°}$ and $0^{°}$ tilt angles. (B) The match of fiducial markers that belong to micrographs of $0^{°}$ and ${50}^{°}$ tilt angles. (C) For each interval, the box plot indicates the distribution of the registration error for the point set registration: firstly, the average deviation of each point set registration result is calculated and then the box plot is drawn based on this average deviation. According to the tilt angle values, the first box plot contains 20 average deviations, the second contains 19 and so on. (D) Superimposition of fiducial marker positions from the micrographs with $0^{°}$ and ${50}^{°}$ tilt angles (labeled by ‘dot’ and ‘inverted triangle’, respectively), and the affine transformed marker positions from the micrograph with ${50}^{°}$ tilt angle (labeled by ‘circle’)

3.2.2 Effectiveness of the divide-and-conquer strategy

Figure 2D shows the superimposition of fiducial marker positions from the micrographs with $0^{°}$ and ${50}^{°}$ tilt angles (labeled by ‘dot’ and ‘inverted triangle’, respectively), and the affine transformed marker positions from the micrograph with ${50}^{°}$ tilt angle (labeled by ‘circle’). We can see that the GMM-based fiducial marker tracking algorithm (Algorithm 1) can reasonably well recover the correspondence between fiducial markers in the two micrographs, but the lens distortion issue is obvious. Figure 3 illustrates the transformed fiducial marker positions in Figure 2D after applying the divide-and-conquer refinement to resolve the lens distortion issue (Algorithm 2). According to our strategy, we firstly matched the two datasets by threshold $0.75d$ and labeled the matched points. Then the remaining unmatched points were reformed into two new point sets and were matched by d. This procedure was repeated until no more matched points could be labeled. In this dataset, we used the fiducial marker diameter as a strict distance threshold. After applying our divide-and-conquer algorithm, the fiducial markers from the ${50}^{°}$ micrograph were divided into three separate point sets. As shown in Figure 3, the divide-and-conquer algorithm ran for three rounds, and two affine transformation parameters were calculated and applied to the fiducial markers. The transformed fiducial markers denoted by red ‘circle’ and green ‘circle’ are the ones matched correctly with the fixed fiducial markers, whereas the fiducial markers that are labeled by black ‘circle’ belong to the third point set for which a uniform transformation to the fixed point set was difficult to be found. There are 28 matched pairs of fiducial markers detected after the divide-and-conquer algorithm, whereas there are only 22 matched pairs without this refinement step (Fig. 2D).

Fig. 3.

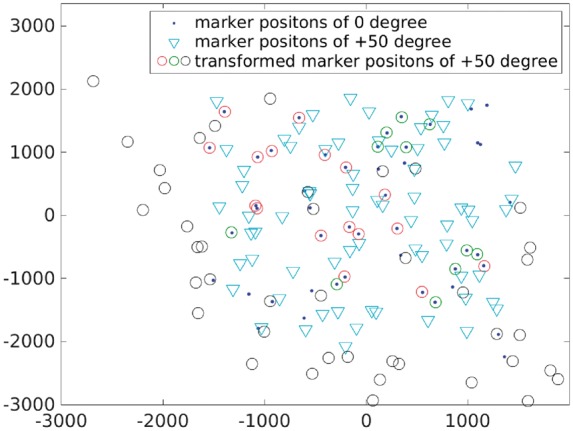
Result illustration of the VEEV dataset. Superimposition of fiducial marker positions from the micrographs with $0^{°}$ and ${50}^{°}$ tilt angles (labeled by ‘dot’ and ‘inverted triangle’, respectively), and the affine transformed marker positions from the micrograph with ${50}^{°}$ tilt angle (labeled by ‘circle’). Divide-and-conquer algorithm is used to reduce the effect of lens distortion: the fiducial markers labeled by red ‘circle’ and green ‘circle’ are the ones matched correctly with the fixed fiducial markers from $0^{°}$; and the fiducial markers labeled by black ‘circle’ are regarded as outliers

In practice, a tilt series alignment module does not need to be applied to match the whole set of micrographs. Instead, only the adjacent micrographs or micrographs within several intervals are matched. Keeping the tilt angle interval smaller than ${20}^{°}$ and using the transitivity of fiducial marker positions on different micrographs can lead to more reliable fiducial marker tracking (Amat et al., 2008; Han et al., 2015). Therefore, the effect of lens distortion is difficult to be observed in the matching result of two micrographs with a small tilt angle interval. However, according to the deviation value in Equation (6), a relatively large deviation may still be observed in the high tilt angles. Under this circumstance, the effect of lens distortion will be enlarged. Our divide-and-conquer algorithm can be used to obtain better fiducial marker tracking. Here, the Hemocyanin dataset is used as an illustration. The adjacent micrographs and the micrographs with one interval apart are matched. Because the interval of tilt angles is very small in the Hemocyanin dataset, almost all the fiducial markers can be tracked with high quality without lens distortion correction. However, micrographs with high tilt angles still encounter lens distortion issues, which require the divide-and-conquer refinement. Figure 4 shows the matching results from the micrographs with ${67}^{°}$ and ${70}^{°}$ tilt angles. For each micrograph, 180 fiducial marker positions were detected and used in fiducial marker matching. Figure 4A shows the result directly matched by the affine transformation model, in which the majority of the fiducial markers were correctly matched, but some markers still have relatively large deviation (e.g. the fiducial markers in the green ellipse region). Figure 4B shows the result in which the lens distortion is resolved by the divide-and-conquer algorithm. It is clear that the fiducial markers located in the green ellipse region have much smaller deviation compared to the previous result. By directly applying the affine transformation, we obtained 155 pairs of the correctly tracked fiducial markers, whereas after the application of the divide-and-conquer algorithm, 161 pairs were correctly tracked. The results prove the effectiveness of the lens distortion refinement.

Fig. 4.

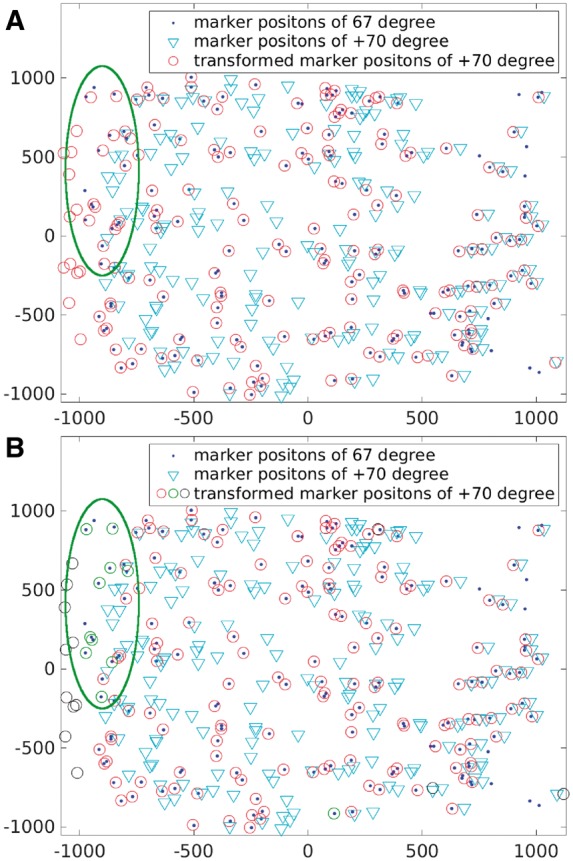
Result illustration of the Hemocyanin dataset. Superimposition of fiducial marker positions from the micrographs with ${67}^{°}$ and ${70}^{°}$ tilt angles (labeled by ‘dot’ and ‘inverted triangle’, respectively), and the affine transformed marker positions from the micrograph with ${70}^{°}$ tilt angle (labeled by ‘circle’). (A) The direct fiducial marker match result by affine transformation. (B) Divide-and-conquer algorithm is used to reduce the effect of lens distortion: the fiducial markers labeled by red ‘circle’ and green ‘circle’ are the ones matched correctly with the fixed fiducial markers; and the fiducial markers labeled by black ‘circle’ are concerned as outliers

3.2.3 Computational efficiency

Another merit of our solution is the speedup gained from the application of the GMM. Though our previous work (Han et al., 2015) can align a classic cryo-ET dataset in about $3\sim 5$  min, the process of a large-field dataset which has hundreds of fiducial markers embedded in still remains a problem. With our new solution, the model-based fiducial marker tracking can be solved in a simpler way. According to our derivation, if the micrographs’ tilt angle interval is not too large, the coarse estimation of the transformation matrix A can be simplified as a rigid matrix. If the coarse estimation in Algorithm 1 is replaced by rigid transformation, we can gain a significant speedup without the loss of accuracy. Figure 5 illustrates the comparison of the runtime between our algebraic tracking algorithm and the previous random sampling work (Han et al., 2015). Here, for the Hemocyanin dataset and the Adhesion belt dataset, the fiducial marker positions in the nth and (n+1)th, and nth and (n+2)th micrographs are matched. Both the algebraic solution and the random sampling solution were run on a Fedora 25 system with 128 Gb memory and two E5-2667v4 (3.2 GHz) CPU. In Figure 5, the x-axis represents the average number of fiducial marker positions for each matching operation, and the y-axis represents the runtime (ms) in the log scale. It can be seen that if the number of fiducial marker positions is less than 110, there is no obvious difference between our current GMM-based algebraic solution and our previous random sampling solution (both of the two methods can finish the fiducial marker matching of two micrographs in 1000 ms). It complies with the fact that the random sampling solution will not cost too much time for cryo-ET datasets with a small number of fiducial markers. When the number of fiducial marker increases (e.g. >150), the previous random sampling solution needs about $2000\sim 5000$ ms to finish a fiducial marker matching of two micrographs, whereas the current GMM-based solution only needs $200\sim 500$ ms. The total tracking time is consistent with the above results. For the Hemocyanin dataset, to generate the whole track model, the random sampling solution and the GMM-based solution cost 263 196 ms (4.38 min) and 41 164 ms (0.68 min), respectively. For the Adhesion belt dataset, to generate the whole track model, the random sampling solution and the GMM-based solution cost 2 325 557 ms (38.76 min) and 176 987 ms (2.95 min), respectively. Because for the Hemocyanin dataset, most of the micrographs only have $80\sim 120$ fiducial markers, the total runtime for random sampling is not too long. On the contrary, most of the micrographs have $195\sim 255$ fiducial markers in the Adhesion belt dataset, so the runtime cost by the random sampling solution is about 10 times longer than that of the GMM-based solution. The trend will continue if the number of fiducial markers increases. Therefore, the GMM-based solution is much faster for the datasets with a large number of fiducial markers.

Fig. 5.

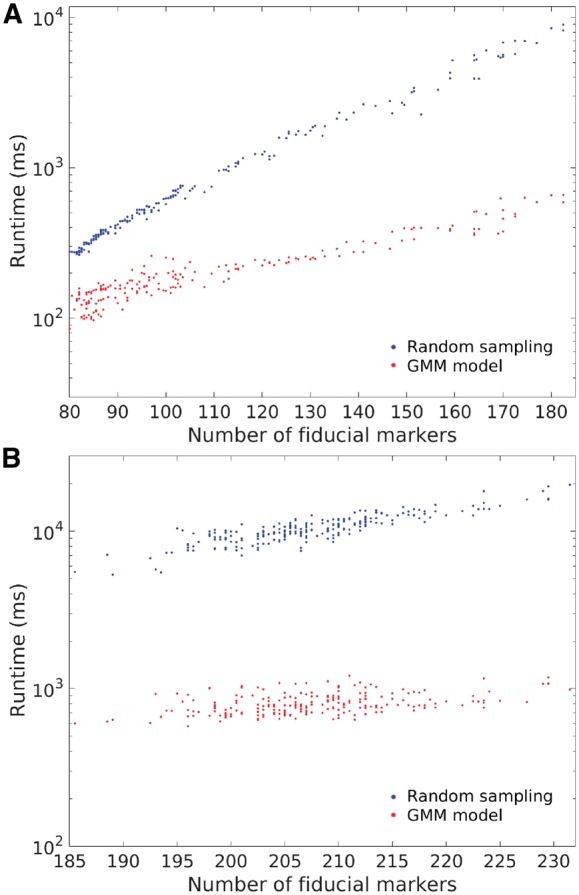
Runtime of the proposed GMM-based method (in red) and the previous random sampling-based method (Han et al., 2015) (in blue) on (A) the Hemocyanin dataset and (B) the Adhesion belt dataset. The x-axis represents the average number of fiducial markers and the y-axis represents the runtime (ms) in the log scale

3.2.4 Performance in marker-based alignment

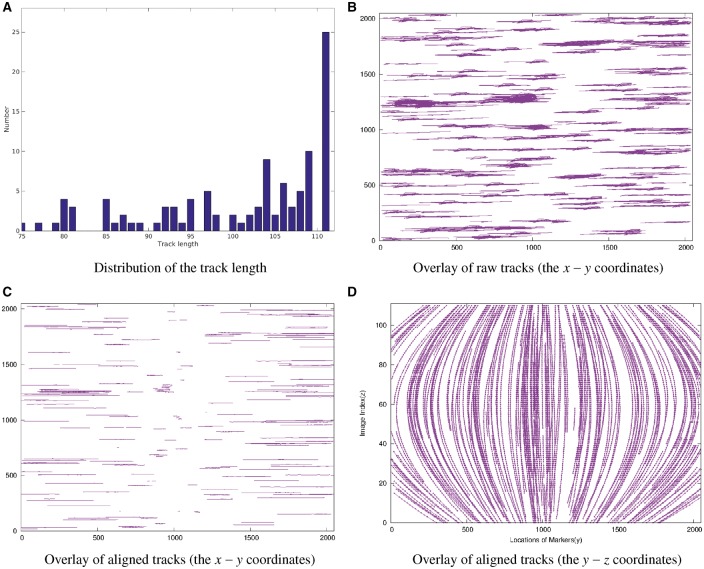
To test the correctness of the proposed GMM-based tracking model, we integrated it to our previous fully automatic alignment scheme (Han et al., 2015, 2017) and obtained the alignment result for the Adhesion belt dataset (Fig. 6). It can be seen that after the assembly of peer matching, there are 105 tracks that cover more than 77 micrographs in the Adhesion belt dataset (∼70% of the entire tilt series). Only the tracks that are long enough are used for projection parameter estimation. As shown in Figure 6A, all the 105 tracks are used and the average length of tracks used for parameter optimization is 96.4, while the mean alignment residual is 0.37 pixel. Figure 6C and D shows the aligned tracks of the Adhesion belt dataset from different directions. We can notice that the alignment is successful. We also compared the results with the ones of random sampling and found that there was no significant difference in the tracking accuracy. To achieve the approximate alignment, our random sampling method took 43.5 min in total, whereas the GMM-based method took only 6.7 min. Overall, the experimental results demonstrate that the theoretical upper bound is very useful for tracking algorithm design and our GMM-based tracking model can dramatically improve the tracking efficiency with good accuracy.

Fig. 6.

Illustration of the marker-based alignment with the GMM-based model used for fiducial marker tracking on the Adhesion belt dataset. (A) The histogram of the length of assembled fiducial marker tracks. (B) Overlay of the raw fiducial marker tracks in the image space (x–y coordinates in pixel). (C) Overlay of the aligned fiducial marker tracks in the image space (x–y coordinates). (D) Overlay of the aligned fiducial marker tracks in the image space (y–z coordinates)

4 Discussion and conclusion

In this work, our focus is the fiducial marker tracking in fully automatic tilt series alignment. We begin our work by discussing the projection model in ET and then giving and proving a theoretical upper bound of the deviation that allows the positions of fiducial markers in two micrographs to be aligned by affine transformation. This theoretical bound is very useful for the design of tracking methods, which can ensure that tracking using only 2D positions of the fiducial markers can be successful for most of the general tilt series. Then, the tracking of fiducial markers is reduced to an incomplete point set registration problem. We introduce a GMM and design an automatic algorithm based on it to make fiducial marker tracking more effective and efficient. Finally, we propose a divide-and-conquer algorithm to resolve the lens distortion issue to ensure the reliability of our scheme. The real-world experimental results further support our proposed bound and demonstrate the effectiveness of our algorithms. This work makes the fully automatic tracking for datasets with a large number of fiducial markers possible. However, to achieve more reliable and accurate fully automatic fiducial marker-based alignment, several future works should be done.

Firstly, we should make efforts on making the algebraic solution more robust for complex situations. Compared with the random sampling method (Han et al., 2015), the algebraic method is much faster. However, the algebraic method is sensitive to outliers compared to the random sampling method (Supplementary Material Section S2). The current version may stuck in datasets with extremely irregular fiducial marker distributions. This situation often happens when aligning tilt series for subtomogram averaging, in which the motion of views may be large and may result in many fiducial markers outside the focus area, for example, 60 abruptly introduced outside markers versus 10 inside markers. Because the fiducial markers are randomly distributed on the specimen and do not indicate a certain shape context, these abruptly introduced fiducial markers will appear as outliers and degenerate the probability distribution in our analysis. Fortunately, usually the subtomogram averaging applications do not use many fiducial markers and thus our previous random sampling method can handle such irregular datasets fast enough. In the future, analysis based on the marker density may be added to the model to cope with such situations.

Secondly, a more mature fiducial marker detection method is needed for a robust fully automatic fiducial marker-based alignment. For datasets that have hundreds of fiducial markers embedded in, the algebraic solution is obviously a better choice. Better performance of marker detection could offer a better fiducial marker distribution and further improve the tracking result. There are various studies that describe the fiducial marker detection algorithms (Amat et al., 2008; Brandt et al., 2001b; Cao et al., 2011; Han et al., 2015; Mastronarde and Held, 2017; Ress et al., 1999). Trampert et al. (2015) made a comparison of several state-of-the-art fiducial marker detection algorithms and drew the conclusion that none of them is superior to the others in all cases, which suggests that the choice of a marker detection algorithm depends on the properties of the dataset to be analyzed. Considering the difference between a cryo-ET micrograph and a negative-stained micrograph, a feasible and accurate fiducial marker detection algorithm should fully use the intrinsic properties in the dataset. Recent development of machine learning techniques such as deep learning (Wang et al., 2016) and bioimaging signal processing techniques such as NMR peak picking (Abbas et al., 2013; Alipanahi et al., 2009; Cannistraci et al., 2015; Cheng et al., 2014; Liu et al., 2012) would be a promising direction for fiducial marker detection.