Temporally and spatially adaptive Doppler analysis for robust handheld optical coherence elastography

Abstract

Optical coherence elastography (OCE), a functional extension of optical coherence tomography (OCT), can be used to characterize the mechanical properties of biological tissue. A handheld fiber-optic OCE instrument will allow the clinician to conveniently interrogate the localized mechanical properties of in vivo tissue, leading to better informed clinical decision making. During handheld OCE characterization, the handheld probe is used to compress the sample and the displacement of the sample is quantified by analyzing the OCT signals acquired. However, the motion within the sample inevitably varies in time due to varying hand motion. Moreover, the motion speed depends on spatial location due to the sample deformation. Hence, there is a need for a robust motion tracking method for manual OCE measurement. In this study, we investigate a temporally and spatially adaptive Doppler analysis method. The method described here strategically chooses the time interval (δt) between signals involved in Doppler analysis to track the motion speed v(z,t) that varies temporally and spatially in a deformed sample volume under manual compression. Enabled by temporally and spatially adaptive Doppler analysis, we report the first demonstration of real-time manual OCE characterization of in vivo tissue to the best of our knowledge.

1. Introduction

Optical coherence tomography (OCT) allows structural and functional imaging of biological tissue with high resolution and high speed [1]. The imaging capability of OCT can be integrated into handheld instruments using fiber optic components [2–4]. A compact, lightweight handheld OCT probe allows a clinician to interrogate tissue characteristics at different anatomical locations [5, 6]. Therefore, handheld OCT imaging instrument is attractive for many clinical applications, including guiding vitreous-retinal surgery, delineating tumor margin for surgical excision, and guiding tissue biopsy for the diagnosis of breast or prostate cancer. A handheld OCT instrument can use the magnitude of OCT signal to reveal morphological features of the tissue. With further signal processing, other characteristics of the tissue related to its physiological and pathological status can be extracted. One feature of clinical interest is the mechanical properties of tissue. For diseases such as breast cancer and prostate cancer, cancerous tissue has a larger stiffness compared to normal tissue [7]. Therefore, manual palpation as well as elastography technologies, have been used in assessing the stiffness of these diseases in clinic [8–10]. Optical coherence elastography (OCE), a functional extension of OCT, has been used to characterize the mechanical properties of biological tissue, by measuring the response (deformation, resonant frequency, elastic wave propagation, etc) of biological tissues under external or internal mechanical excitations [11–14]. Compared to elastography techniques based on ultrasound imaging and magnetic resonance imaging, OCE has advantages in motion sensitivity and spatial resolution.

Despite great challenge in quantifying mechanical properties through OCE measurement, depth resolved displacement obtained by analyzing OCT signal can be used as an effective surrogate for sample stiffness. With the assumption of uniform distribution of stress (σ that remains constant for different spatial locations), the strain is directly related to the stiffness of the sample (ε = σ/E where E indicates the Young’s modulus and quantifies the stiffness of the sample). Therefore, under the same stress σ, the strain (ε = $\frac{d\delta L\left(z\right)}{dz}$ evaluated by the spatial derivative of displacement δL(z) [15]) is larger for a soft material with a smaller E and is smaller for a hard material with a larger E, as indicated in Fig. 1. Tissue under different pathophysiological conditions has different stiffness, hence OCE measurement of displacement and strain allows in situ tissue characterization. For example, cancerous tissue has a larger stiffness compared to normal tissue. A positive margin at the site of tumor excision with residual cancerous tissue can thus be identified by evaluating the displacement generated through manual OCE measurement. The displacement is expected to increase as the depth, and the position where the slope of displacement changes abruptly implies the boundary between the cancerous tissue and the normal tissue. Therefore, OCE characterization can reveal highly localized mechanical contrast and hence lead to better informed clinical decision making, without fully quantifying the mechanical properties of the tissue.

Fig. 1.

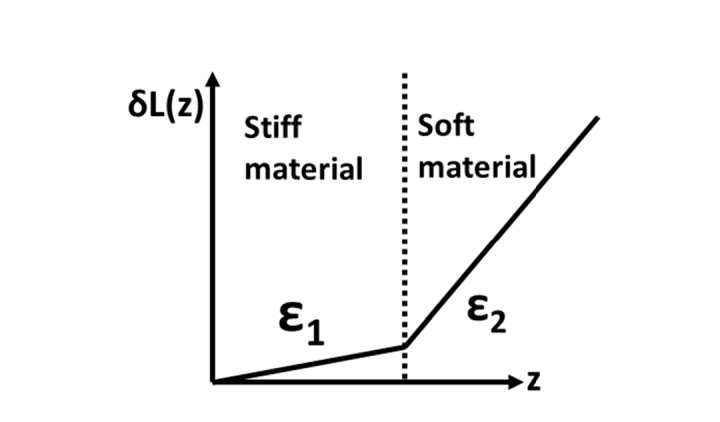
Illustration of depth resolved displacement for a sample with different stiffness at different depth. Here, ε₁ < ε₂.

OCE characterization enables augmented tissue differentiation capability for a variety clinical application [16–20]. Recent advancement in OCE technology includes 3D elastography that revealed in vivo mechanical contrast and demonstrated quantitative mechanical properties of human skin in vivo [21], as well as M-mode OCE measurement based on a miniature fiber-optic probe. Particularly, a compact fiber-optic OCE instrument can be used in a similar manner as a conventional clinical handheld instrument. The tissue can be manually compressed by the OCE device and the motion of the tissue can be tracked by analyzing OCT signal. A handheld OCE instrument hence performs high sensitivity virtual palpation of the tissue with great convenience and flexibility. Moreover, fiber optic OCE instruments can be integrated into a needle device, further delivering the capability of mechanical characterization to tissue that is deeply embedded. However, the major challenge for manual OCE characterization of tissue is the unpredictable and unstable motion within the tissue. The deformation of the sample under the known pattern of mechanical excitation can be reliably tracked by analyzing OCT signal. In conventional compression OCE measurement, the sample has a well-defined geometry and undergoes quasi-static compression. Alternatively, the mechanical excitation can be impulse or sinusoidal function [22, 23]. In previous studies of 1D or 3D OCE for the mapping of mechanical properties, an actuator was often used to deform the sample. However, the need to use an actuator for mechanical loading limits the development of a light-weight and compact OCE probe. For a handheld, manually actuated OCE instrument, it is challenging to impose mechanical excitations that are quasi-static, impulse or sinusoidal. The manual loading process often generates a motion speed that varies with time. The quality of in vivo OCE signal is also affected by involuntary motion from the subject and from the user who holds the probe. In addition, the sample deforms under compression, implying spatial variation of motion characteristics. Our software approach of adaptive Doppler analysis enables 1D OCE measurement based on a manual loading process, and allows the acquisition of high quality in vivo OCE signal from a handheld probe.

Motion tracking in OCE can be achieved through Doppler analysis or speckle decorrelation analysis. Speckle analysis has a smaller dynamic range and is more appropriate to track motion with larger magnitude [24, 25]. In this study, Doppler analysis is used to quantify the axial motion speed and displacement. A simple and effective method for temporally and spatially adaptive Doppler analysis is investigated here. The adaptive Doppler analysis method strategically chooses the time interval (δt) between signals involved in Doppler analysis, to track the motion speed v(z,t) that varies temporally in a manual compression process and spatially in a deformed sample volume. The method is validated in an OCE system with a handheld single fiber probe and real-time signal processing software based on graphic processing units (GPU). To achieve robust motion tracking, we calculate high density (HD) Doppler phase shift that is most unlikely to have phase wrapping artifact and average the HD Doppler signal to estimate the speed of axial motion from which we derive a time interval to achieve a large yet artifact free Doppler phase shift. The premise of this method is that (1) directional motion affects larger scale characteristics of the Doppler signal and can be estimated through averaging; (2) noise characteristics in estimated Doppler phase shift are independent of the time interval δt while the signal due to directional motion does. Enabled by high signal acquisition and processing speed, we perform an online estimation of the motion speed, select an optimal δt adaptively, and perform robust motion tracking for OCE measurement.

The manuscript describes the first handheld fiber optic instrument that allows in vivo real-time OCE characterization, to the best of our knowledge. The manuscript is organized as follows. First, we introduce the principle of the adaptive Doppler analysis method. Afterwards, the imaging system and data acquisition are described. We then show results obtained from phantom experiments and in vivo tissue characterization, to demonstrate the effectiveness of the adaptive Doppler analysis for motion tracking in a dynamic manual loading process.

It is worth mentioning that we do not intend to extract quantitative mechanical properties of the sample through OCE measurement in this study. Instead, we acquired one dimensional data to reveal depth resolved sample displacement. By observing the variation of the displacement, particularly the slope, mechanical contrast of the sample can be revealed. The spatial variation of stress, 3D nature of displacement, as well as viscoelastic behavior of the sample are not considered. Moreover, OCE is referred to the application of OCT technology for mechanical characterization. In this manuscript, OCE signal indicates depth resolved displacement of the sample under compression, although the strain (derivative of displacement) is more directed related to the mechanical properties of the sample.

2. Principle for adaptive Doppler analysis

In OCE characterization, the loaded sample deforms and has displacement dependent on spatial location (δL(z)). With local displacement δL(z) extracted by analyzing OCT signal, localized axial strain, the spatial derivative of the displacement (Eq. (1)), is calculated as the surrogate of sample stiffness. For sampled discrete OCT image, local strain can be estimated either through finite difference approach or least square estimation.

$$\epsilon \left(z\right)=\frac{d}{dz}\left[\delta L\left(z\right)\right]$$ (1)

It is worth mentioning that the motion within a deformed sample under axial compression is generally 3D with axial and lateral components. However, Doppler phase analysis is only sensitive to axial motion. Therefore, motion in transverse plane is not considered in this study, as in most previous OCE studies based on Doppler analysis. Furthermore, our measurement geometry has cylindrical symmetry, and the light beam propagates along the axis of cylindrical symmetry. Hence the lateral displacement of an isotropic sample seen by the incident light beam is expected to be minimum.

To obtain 1D depth resolved OCE signal (δL(z)), Doppler phase shifts between OCT A-scans are calculated. Consider the OCT signal with complex value at the k^th pixel at depth kδz of an A-scan (m^th A-scan) and that at the k^th pixel of another A-scan ((m + Δ_k,m)^th A-scan). Here δz indicates the depth sampling interval by individual pixels in an A-scan. A non-zero Doppler phase shift (δϕ_k,m = δϕ(kδz,mT₀)) is expected because of axial displacement at depth z = kδz within the time interval δt = Δ_k,mT₀, where T₀ indicates the time interval between the acquisitions of adjacent A-scans. δϕ_k,m is linearly related to the speed of axial motion v_k,m (assuming a constant axial motion within the observation time: v_k,m = v(kδz,mT₀) at depth kδz within time interval from mT₀ to (m + Δ_k,m)T₀, as shown in Eq. (2) where λ₀ is the central wavelength of the light source [26].

$$\delta {\varphi }_{k,m}=4\pi \frac{v_{k,m}\delta t}{{\lambda }_0}=4\pi \frac{v_{k,m}{\Delta }_{k,m}{T}_0}{{\lambda }_0}$$ (2)

The Doppler phase shift δϕ_k,m is calculated using Eq. (3) [27], where I_k,m = I(kδz,mT₀) indicates the complex OCT signal at the k^th pixel of an A-scan obtained at time mT₀; I_{k,m + Δ(k,m)} = I (kδz,(m + Δ_k,m)T₀) indicates the complex OCT signal at the k^th pixel of an A-scan obtained at time (m + Δ_k,m)T₀; atan(∙) indicates to take the arctangent; Im(∙), Re(∙) and (∙)* indicate to take the imaginary part, the real part and the complex conjugate of a complex value.

$$\delta {\hat{\varphi }}_{k,m}=a\tan \left[\frac{\mathrm{Im}\left(I_{k,m}^{*}{I}_{k,m+{\Delta }_{k,m}}\right)}{\mathrm{Re}\left(I_{k,m}^{*}{I}_{k,m+{\Delta }_{k,m}}\right)}\right]$$ (3)

The relationship between the estimated Doppler phase shift δ${\hat{\varphi }}_{k,m}$ and the actual phase shift δϕ_k,m due to directional motion is shown in Eq. (4), where n_k,m is the random phase noise deriving from various noise sources in OCT measurement (shot noise, thermal noise, excess noise, speckle noise, etc). On the other hand, N_k,m is an integer and is non-zero when |δϕ_k,m|>π/2: N_k,m = . $\frac{\delta {\varphi }_{k,m}+sign\left(\delta {\varphi }_{k,m}\right)\frac{\pi }{2}}{\pi }$ Here ${}^{\lfloor \rfloor }$ indicates to take the integer part of a real number. In other words, for |δϕ_k,m|>π/2, δ${\hat{\varphi }}_{k,m}$ fails to provide an unbiased estimation of δϕ_k,m, which is known as the phase wrapping artifact. Phase wrapping artifact arises, because the arctangent (atan) function used to calculate the phase shift in Eq. (3) does not have the ability to differentiate an arbitrary phase shift δϕ_k,m and δϕ_k,m + N_k,mπ [28,29]. Clearly, N_k,m depends on time (t = mT₀) and spatial location (z = kδz).

$$\delta {\hat{\varphi }}_{k,m}=\delta {\varphi }_{k,m}-N_{k,m}\pi +n_{k,m}$$ (4)

With the Doppler phase obtained using Eq. (3), we will be able to estimate the speed of axial motion: ${\hat{v}}_{k,m}$ = $\frac{{\lambda }_0}{4\pi T_0{\Delta }_{k,m}}\delta {\hat{\varphi }}_{k,m}$ for the k^th pixel in the m^th A-scan, and further estimate the depth resolved displacement (δ${\hat{L}}_k$ = δ$\hat{L}$(kδz)) over the entire compression process: δ${\hat{L}}_k={\displaystyle \sum }_{m=1}^M\left({\hat{v}}_{k,m}{T}_0\right)$ where M indicates the total number of A-scans acquired during the sample compression process. δ${\hat{L}}_k$ can thus be expressed using Eq. (5).

$$\delta {\hat{L}}_k=\delta L_k-{\displaystyle \sum _{m=1}^M\left(\frac{{\lambda }_0}{4{\Delta }_{k,m}}{N}_{k,m}\right)}+{\displaystyle \sum _{m=1}^M\left(\frac{{\lambda }_0}{4\pi {\Delta }_{k,m}}{n}_{k,m}\right)}$$ (5)

On the right hand side (RHS) of Eq. (5), the first term represents the actual displacement; the second term represents the phase wrapping artifact and the third term denotes the contribution from random phase noise. To improve the sensitivity, SNR and dynamic range for OCE characterization, it is desirable to have a smaller variance (Var(δ${\hat{L}}_k$-δL_k)) for the estimated displacement. It is assumed that n_k,m (m = 1, 2, 3, …, M) is Gaussian, and independent in different A-scans. The variance of n_k,m is shown in Eq. (6), where SNR is the signal to noise ratio of the OCT signal and β is a constant [30–32]. With the above assumption and with N_k,m≡0, the variance in displacement tracking is given by Eq. (7).

$$Var\left(n_{k,m}\right)=\beta \frac{1}{SNR}$$ (6)

$$Var\left(\delta L_k\right)={{\displaystyle \sum _{m=1}^M\left(\frac{{\lambda }_0}{4\pi {\Delta }_{k,m}}\right)}}^{2}Var\left(n_{k,m}\right)$$ (7)

In Eq. (7), λ₀ depends on the OCT system used for the imaging study; M depends on the time period of the sample loading process; Var(n_k,m) is determined by the OCT system as well as the optical characteristics of the sample. Hence Δ_k,m is the only parameter that can be varied to improve the displacement tracking, and noise in displacement tracking for a given compression process can be reduced with a larger value of Δ_k,m.

On the other hand, for unbiased displacement tracking, it requires N_k,m≡0. Therefore, the time interval between A-scans used for Doppler phase calculation (δt = Δ_k,mT₀) has to be sufficiently small, such that |δϕ_k,m| = |4πv_k,mΔ_k,mT₀/λ₀|≤ π/2. To prevention phase wrapping artifact in Doppler analysis, the following condition has to be satisfied.

$${\Delta }_{k,m}\le \frac{{\lambda }_0}{8v_{k,m}{T}_0}$$ (8)

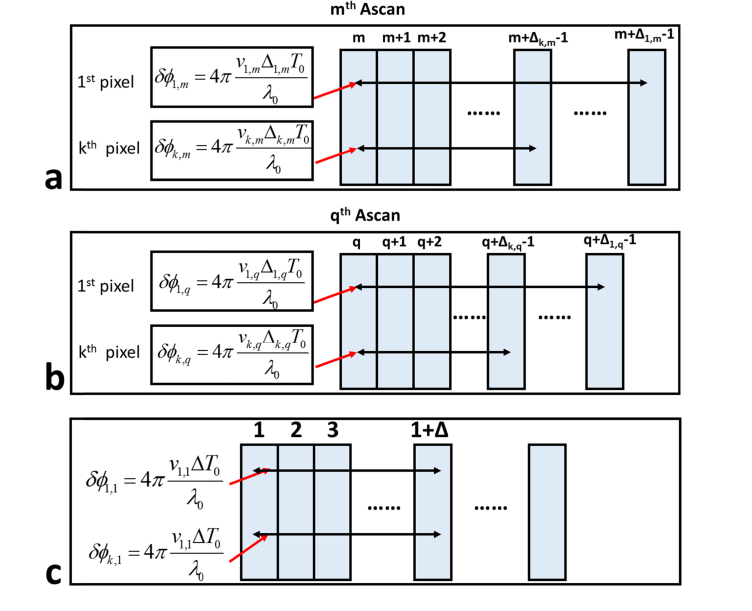
Equation (8) implies the optimal choice of Δ_k,m depends on the speed of the motion (v_k,m). For a handheld OCE instrument used to exert manual compression, the motion speed within the sample depends on the depth because the sample is axially deformed. The motion speed also varies as time due to the non-constant compression speed. Therefore, v_k,m = v(kδz,mT₀) and there is a need to have a time interval adaptive to the spatial location and time (δt(z,t) = Δ(kδz,mT₀)T₀ = Δ_k,mT₀ where Δ_k,m is an integer) for Doppler analysis. In other words, different values are chosen for Δ_k,m at different depth (z = kδz) and at different time (t = mT₀) (Fig. 2(a) and 2(b)). In comparison, conventional Doppler analysis tracks displacement by comparing OCT signals acquired with a constant time interval (Fig. 2(c)) regardless of time and spatial location. Therefore, the results of Doppler analysis are susceptible to phase wrapping artifact and suboptimal signal-to-noise ratio, particularly for a manual OCE characterization process.

Fig. 2.

(a) and (b) demonstrate adaptive selection of time intervals for Doppler analysis: (a) Time intervals used to calculate Doppler phase shift for the same A-scan (m^th A-scan) are different for pixels at different depth (1^st pixel and k^th pixel); (b) Time intervals used to calculate Doppler phase shift for the same pixel in different A-scans are different (1st pixel in the m^th A-scan and in the q^th A-scan and k^th pixel in the m^th A-scan and in the q^th A-scan); (c) time interval remains the same for conventional Doppler analysis.

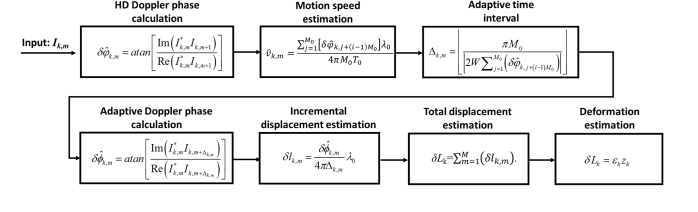
To determine the value of Δ_k,m adaptive to spatial location (z = kδz) and time (t = mT₀), we first estimate the motion speed v_k,m by calculating the high density (HD) Doppler phase shift. For discrete OCT signals acquired frame by frame, each frame of OCT data consists of multiple (M₀) A-scans acquired with a time interval of T₀. Hence the k^th pixel in the j^th A-scan of the i^th frame is I_k,m, where m = j + (i-1)M₀. The HD Doppler phase shift δ${\hat{\phi }}_{k,m}$ is calculated between I_k,m and I_k,m+1 using Eq. (3) with Δ_k,m≡1. We then calculate the mean HD Doppler phase shift for the i^th frame of OCT data ($\delta {\overline{\phi }}_{k,i}$ = $\frac{1}{M_0}{\displaystyle \sum }_{j=1}^{M_0}\left[\delta {\hat{\phi }}_{k,j+\left(i-1\right)M_0}\right]$) and estimate the speed of axial motion at the k^th pixel at depth kδz to be $\frac{\delta {\overline{\phi }}_{k,i}}{4\pi T_0}{\lambda }_0$. As A-scans in a whole frame are involved, the estimation of motion speed has a temporal resolution determined by the time needed to acquire a frame of OCT data (M₀T₀), and the motion speed for the m^th A-scan is thus approximately ${\hat{v}}_{k,m}=\frac{\delta {\overline{\phi }}_{k,i}}{4\pi T_0}{\lambda }_0$ where i = $\frac{m}{M_0}$ + 1 and ${}^{\lfloor \rfloor }$indicates to take the integer part of a rational number. With the estimated motion speed, the Doppler phase shift accumulated within a time interval δt is thus $4\pi \frac{{\hat{v}}_{k,m}}{{\lambda }_0}$δt_. As discussed above, it requires |$4\pi \frac{{\hat{v}}_{k,i}}{{\lambda }_0}\delta t$ |≤ $\frac{\pi }{2}$ to prevent phase wrapping from happening. For discrete OCT signal, δt = δt_k,m = Δ_k,mT₀ where the integer Δ_k,m can be obtained by (9) with W>1. W is a coefficient that we introduce to scale the magnitude of phase shift δϕ_k,m with regard to π/2, to make sure that δϕ_k,m is large enough while free of phase wrapping artifact. Δ_k,m is assigned to have a value of 1, if the result obtained by Eq. (9) is smaller than 1. Moreover, to calculate phase shift using A-scans within the same frame of OCT data, it requires Δ_k,m to be smaller than M₀/2. If the value calculated using Eq. (9) is larger than M₀/2, Δ_k,m = M₀/2.

$${\Delta }_{k,m}=\lfloor \frac{\pi M_0}{\left|2W{\displaystyle {\sum }_{j=1}^{M_0}\left(\delta {\hat{\phi }}_{k,j+\left(i-1\right)M_0}\right)}\right|}\rfloor$$ (9)

Notably, we choose the value of W to be larger than 1, such that the method is robust against phase wrapping when phase noise exists. As validated in previous studies including our recent work [30–32], the level of phase noise in the OCT imaging system is inversely proportional to the signal to noise ratio (SNR) of amplitude OCT signal. Consider a shot noise limited OCT system with noise level determined by the power of reference light. For such an OCT system, the phase noise is small for a sample that generates large amplitude OCT signal and the value of W can be close to 1. In comparison, the phase noise is large for a sample that generates small amplitude OCT signal and the value of W has to be sufficiently larger than 1. In this study, other than specifically mentioned, W = 2 for the calculation of adaptive time interval for Doppler analysis.

Using adaptively determined time interval for Doppler analysis (δt_k,m = Δ_k,mT₀ with Δ_k,m obtained from Eq. (9)), Doppler phase shift (δ${\hat{\varphi }}_{\text{k,m}}$) between A-scan pairs I_k,m and I_k,m+Δ(k,m) is calculated according to Eq. (3). δ${\hat{\varphi }}_{\text{k,m}}$ is then converted to the incremental displacement (δl_k,m = (λ_{0$\delta {\hat{\varphi }}_{\text{k},\text{m}}$})/(4πΔ_k,m)). Therefore, the displacement accumulated over the entire compression process with M A-scans acquired is calculated for a specific depth (k^th pixel) during the entire compression process: δL_k = ${\displaystyle {\sum }_{m=1}^M\left(\delta l_{k,m}\right)}$. By calculating the displacement within the entire compression process, M Doppler phases are averaged and the value of M is several orders of magnitude larger than 1. Therefore, the displacements obtained are orders of magnitude larger than the wavelength of the light source (Figs. 6, 8, 9–11). With depth resolved displacement, we then estimate the depth resolved strain of the loaded sample to evaluate its stiffness.

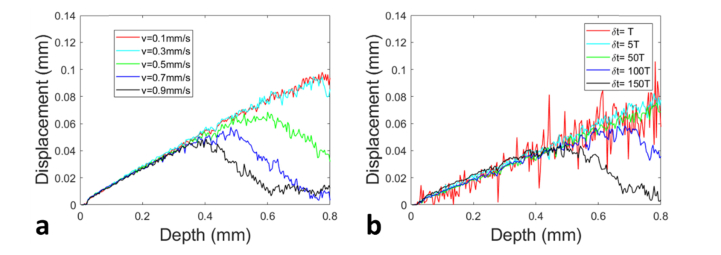
Fig. 6.

Depth resolved displacement (a) obtained with different motor speeds and the same time interval (δt = ΔT₀, where T₀ = 16μs and Δ = 50) for Doppler analysis; (b) obtained with the same motor speed (v_motor = 0.25mm/s) and different time intervals for Doppler analysis.

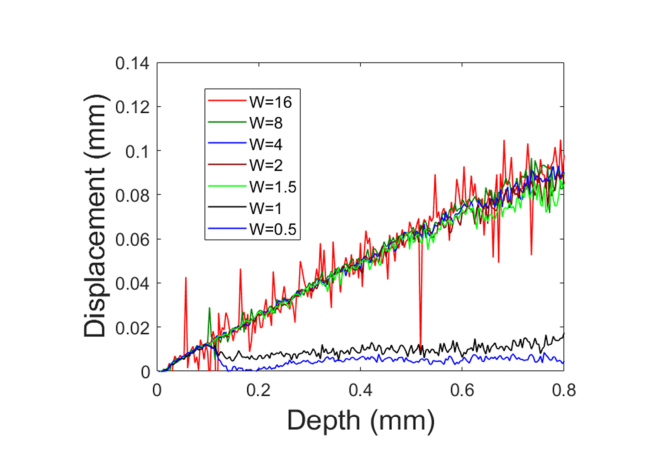
Fig. 8.

Depth resolved displacements obtained through adaptive Doppler analysis when different values of W were used to determine the time interval according to Eq. (9).

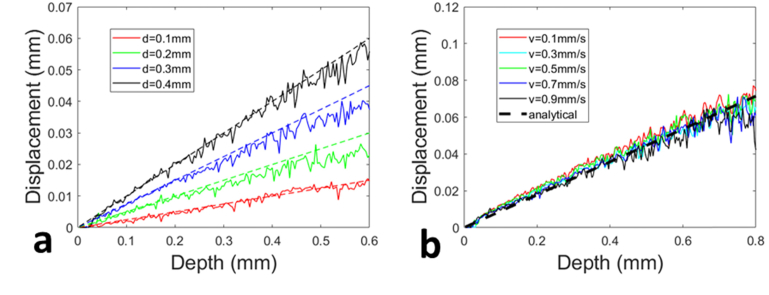
Fig. 9.

Depth resolved displacement extracted through adaptive Doppler analysis, (a) with the motor translated at the same speed for different displacements; (b) with the motor translated at different speeds for the same displacement.

Fig. 11.

(a) Displacement (blue) obtained from adaptive Doppler tracking and magnitude OCT signal (red) of Sample 1; (b) displacement (blue) obtained from adaptive Doppler tracking and magnitude OCT signal (red) of Sample 2.

In summary, we have implemented the adaptive Doppler analysis illustrated in Fig. 3 in real-time through GPU accelerated parallel computation. The software acquires spectral interferograms frame by frame, performs fast Fourier transform on the spectral interferograms, calculates the HD Doppler phase shift to estimate the speed of axial motion, adaptively determines the optimal time interval for each frame of OCT data to perform Doppler analysis, and tracks depth resolved displacement for sample mechanical characterization.

Fig. 3.

Block diagram for adaptive Doppler analysis.

3. Experimental setup

The spectral domain OCT system used in this study has been described in our previous publications [19, 20]. Briefly, a super-luminescent diode centered at 1310nm is used as the broadband source for OCT imaging. The interferometric signal is detected by a line scan CMOS camera (SUI1024LDH2, Goodrich), and streamed to the host computer (Dell Precision T7600) for image reconstruction and analysis. A general purpose graphic processing units (GeForce 780) is used for signal processing. The OCT engine provides a 7.5μm axial resolution and 2.5mm depth imaging range.

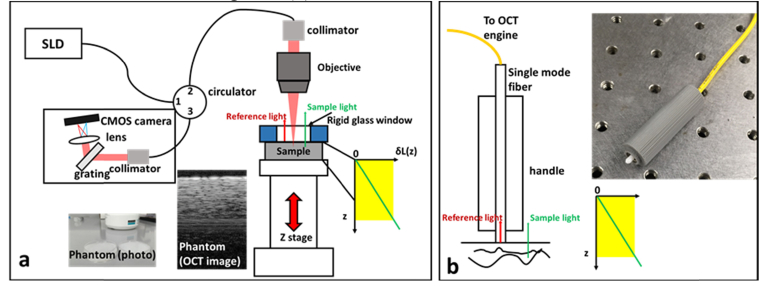
To validate the method of adaptive Doppler analysis under well controlled loading conditions, we conducted OCE experiment on the setup shown in Fig. 4(a) where the sample was sandwiched between two rigid places. One of the plates was a window (5mm sapphire window) that allowed broadband light to incident into the sample for OCT imaging, and the other plate was attached to a high precision vertical translation stage actuated by a linear motor. Here, we implemented OCT imaging in a common path configuration where the reference light was derived from a constant reflector at the probe arm and shared the same optical path as the sample light. With the shared optical path for reference and sample light, random phase variation due to environmental perturbation was minimized. The phase noise predominantly came from variation of optical signal and was determined by Eq. (6). In Fig. 4(a), the bottom surface of the glass window provides a reference light that interferes with sample light to generate interferometric OCT signal. The reference light and sample light were combined and routed by a circulator for spectral domain detection. The rigid bottom surface of the window provided a constant optical path length (z = 0) and did not move under compression. Hence the displacement (δL(z)) increased as depth starting from the value of 0, as shown in the inset of Fig. 4(a).

Fig. 4.

(a) Benchtop setup for experimental validation of the method for adaptive Doppler analysis; (b) fiber optic probe for handheld OCE characterization.

A Thorlabs scanning lens (LSM02, Thorlabs, with 11μm beam diameter on the focal plane and 70μm depth of field) was used as the imaging objective. The scanning lens is specifically designed for OCT imaging that uses a broadband light source for illumination, and has minimal chromatic aberration. The objective is also optimized in spherical aberration to achieve large field of view. Therefore, the quality of signal was not significantly affected by the aberration of the imaging system. Our imaging system has a pair of galvo mirror for lateral scanning. By driving one of the galvo mirrors with a sawtooth wave, B-mode images can be obtained (Fig. 12(a), 12(b), 12(d) and 12(e)). However, lateral scanning was not performed in obtaining data for Doppler analysis, to minimize decorrelation due to lateral beam displacement.

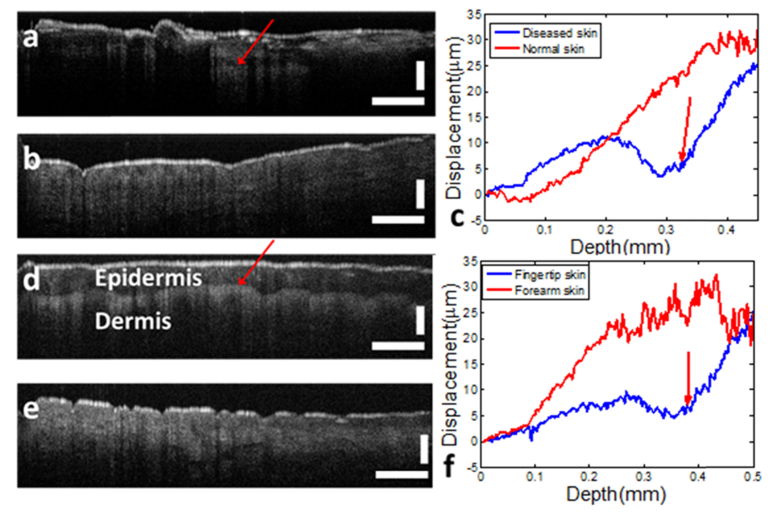
Fig. 12.

(a) in vivo OCT image of diseased skin at the back of the hand; (b) in vivo OCT image of normal skin at the back of the hand; (c) displacement measured through adaptive Doppler analysis of OCT signal for diseased skin and normal skin; (d) in vivo OCT image of fingertip skin; (e) in vivo OCT image of forearm skin; (f) displacement measured through adaptive Doppler analysis of OCT signal for fingertip skin and forearm skin. Scale bars represent 500μm.

The elastic phantom used in this study was prepared by curing silicone rubber, RTV-22 purchased from Raw Material Suppliers. Details on this phantom can be found in our previous publication [20]. Titanium dioxide particles were added into the silicone gel before curing to provide light scattering. The sample is considered as having homogeneous mechanical (stiffness) and optical (light scattering and absorption) properties. The elastic phantom used in this study is shown in Fig. 4(a) (photo and OCT image).

We further demonstrated robust mechanical characterization through a handheld probe shown in Fig. 4(b). The probe was simply a single mode fiber with a flat fiber tip and a 3D printed handle. The fiber probe is simply attached to the second port of the circulator for sample illumination and OCT signal acquisition. The Fresnel reflection at the fiber tip provided the reference light for common path OCT imaging. Therefore, the fiber tip is considered as the origin of the spatial coordinate for OCT imaging (z = 0) and did not deform under compression, similar to the reference surface in Fig. 4(a). The displacement extracted by analyzing OCT signal gradually increased as the depth starting from the value of 0, as shown in the inset of Fig. 4(b).

4. Results

We used NVIDEA Nsight to evaluate the speed of the algorithm implemented in CUDA. The software processed approximately 288k A-scans per second, and the signal processing speed was much faster than the maximum data acquisition rate of the camera (92k A-scans per second). Moreover, the time required to perform adaptive Doppler analysis on a frame of OCT data was approximately 0.1ms.

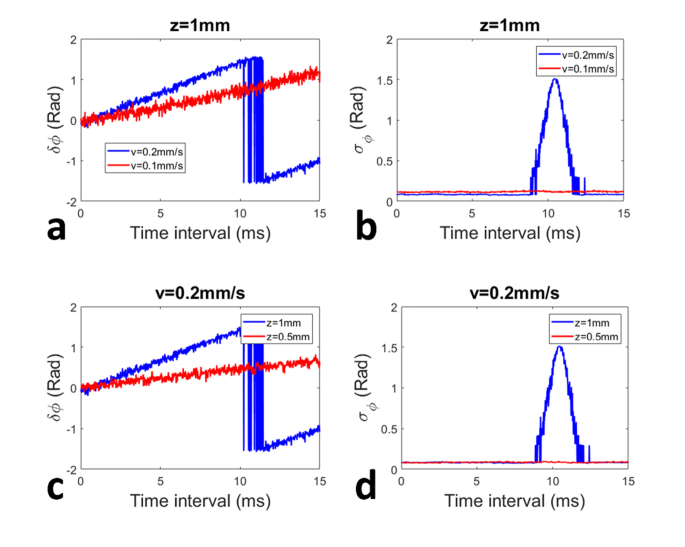
To demonstrate the need for an adaptive time interval (δt) in OCE measurement through a manual compression process, we acquired experimental data from the benchtop setup shown in Fig. 4(a). We translated the z-stage at different speeds (v_motor = 0.2mm/s and v_motor = 0.1mm/s) to compress the elastic sample sandwiched between the two rigid plates. At each motor translation speed, we acquired a frame of OCT data (with 1024 A-scans, i.e., M₀ = 1024) with a time interval of 16μs between adjacent A-scans (T₀ = 16μs). We first demonstrate how the Doppler signal and the phase noise are determined by the time interval between OCT signals involved in phase shift calculation. For each frame of OCT data, we selected the pixel at the depth z = 1mm (z = kδz = 1mm) from an A-scan (j^th A-scan); calculated the phase shift between this pixel (I_k,j) and a pixel in subsequent A-scans acquired with different time delays (I_k,j+Δ, Δ = 1, 2, 3, …): $\delta {\hat{\varphi }}_j\left(\delta t\right)=\text{arg}\left(I_{k,j}^{*}{I}_{k,j+\Delta }^{*}\right)$; averaged the resultant phases: $\delta \hat{\varphi }\left(\delta t\right)=\frac{1}{M_0-\Delta }{\displaystyle {\sum }_{j=1}^{M_0-\Delta }\delta {\hat{\varphi }}_j\left(\delta t\right)}$. Doppler phase shifts ($\delta \overline{\varphi }\left(\delta t\right)$) at the specific depth obtained with different time intervals (δt = ΔT₀) are shown in Fig. 5(a) as blue (v_motor = 0.2mm/s) and red (v_motor = 0.1mm/s) curves. In Fig. 5(a), $\delta \overline{\varphi }\left(\delta t\right)$ initially increases linearly with δt. This is consistent with that fact that displacement and Doppler phase increase as time (Eq. (2)). However, with a larger motor translation speed (blue curve in Fig. 5(a) with v_motor = 0.2mm/s), phase wrapping artifact arises when $\delta \overline{\varphi }\left(\delta t\right)$ approaches and exceeds π/2. In comparison, data obtained with a smaller motor translation speed (red curve in Fig. 5(a) with v_motor = 0.1mm/s) are free of phase wrapping artifact for the same δt. Figure 5(a) suggests that the selection of time interval for Doppler analysis has to be adaptive to the mechanical excitation, i.e., the translation speed of the compressor during OCE characterization. In addition, the phase calculated using Eq. (3) also fluctuates randomly due to noise. Using $\delta {\hat{\varphi }}_j$ (δt) obtained, we assessed the random noise of the estimated Doppler phase σ_ϕ(δt) = $\sqrt{\frac{1}{M_0-\Delta -1}{\displaystyle {\sum }_{j=1}^{M_0-\Delta }{\left[\delta {\hat{\varphi }}_j\left(\delta t\right)-\delta \hat{\varphi }\left(\delta t\right)\right]}^2}}$, for phase obtained with different time intervals (δt = ΔT₀). σ_ϕ(δt) are shown in Fig. 5(b) as blue (v_motor = 0.2mm/s) and red (v_motor = 0.1mm/s) curves. A peak can be observed in the blue signal in Fig. 5(b), because Doppler signal varies drastically when phase wrapping appears (blue signal in Fig. 5(a)). Other than the peak due to phase wrapping, the noise in Doppler phase estimation remains approximately constant for different values of δt. This is because random phase variation in OCT signal originates from factors (noise in OCT measurement and random environmental perturbations) that can be considered as temporally independent and identically distributed random variables, as indicated by Eq. (6). Therefore, the results of Doppler analysis are expected to have a similar level of noise, despite different time interval of δt. According to Eq. (7), a larger value of Δ_k,m is desirable to achieve a reduced error in displacement tracking, because the phase noise does not increase with time (Fig. 5(b)) while the phase shift due to directional motion increases with time (Fig. 5(a)).

Fig. 5.

Doppler phase shift (a) and phase noise (b) obtained from the sample at the same depth with different motor translation speeds; Doppler phase shift (c) and phase noise (d) obtained from the sample at the different depths with the same motor translation speed.

In addition, the displacement within the sample under OCE characterization varies as spatial location due to the sample deformation under compression. The deformation is quantified as axial strain (Eq. (1)) to reveal the mechanical properties of the sample. Therefore, Doppler analysis also has to be adaptive to the spatial location. To demonstrate this, one frame of OCT data acquired in the above described experiment (v_motor = 0.2mm/s) was analyzed. We calculated Doppler phase shift between pixels at depth z = 1mm, as well as Doppler phase shift at a smaller depth (z = 0.5mm). The mean Doppler phase shifts for different δt are shown in Fig. 5(c) as blue (z = 1mm) and red (z = 0.5mm) curves. Similar to results shown in Fig. 5(a), the Doppler phase shift in Fig. 5(c) initially increases linearly with δt. For Doppler phase shift calculated for a larger depth (blue curve in Fig. 5(c) corresponding to z = 1mm), phase wrapping artifact arises when δϕ approaches and exceeds π/2. In comparison, data obtained from a smaller depth (red curve in Fig. 5(c) with z = 0.5mm) are not affected by phase wrapping artifact for the same range of time interval. Therefore, it is necessary to select time interval adaptive to spatial location for Doppler analysis for robust Doppler analysis. Using the same set of OCT data obtained with v_motor = 0.2mm/s, we also evaluated the random noise for Doppler phase shift for different depths. The results are shown in Fig. 5(d) as blue (z = 1mm) and red (z = 0.5mm) curves. Despite a peak observed in the blue curve due to the phase wrapping, the Doppler signals show a constant noise level for different values of δt.

Next we demonstrated the impact of time interval selection for Doppler analysis on the tracking of depth resolved displacement. Using the benchtop configuration shown in Fig. 4(a), we translated the motor at different speeds (v_motor = 0.1mm/s, 0.3mm/s, 0.5mm/s, 0.7mm/s and 0.9mm/s) to deform the sample sandwiched between two rigid plates. At the same time, we used the OCT engine to acquire spectral interferograms continuously from the phantom undergone compression. We calculated the Doppler phase shift (δ${\hat{\varphi }}_{k,m}$ where k is the index of pixel in an A-scan and m is the A-scan index) between complex OCT signals at pixels in the m^th A-scan (I_k,m) and in the (m + Δ)^th A-scan (I_k,m+Δ). We converted the phase shift to the displacement δl_k,m = (λ₀δ${\hat{\varphi }}_{k,m}$)/(4π), and calculated the displacement over the entire compression process: δL_k = δL(kδz) = ${\displaystyle {\sum }_{m=1}^M\left(\delta l_{k,m}\right)}$. To obtain results shown in Fig. 6(a), the time interval for Doppler analysis was chosen to be a constant value: δt = ΔT₀, where Δ = 50 and T₀ = 16μs. When the motor was translated at a larger speed (v_motor = 0.5mm/s, 0.7mm/s and 0.9mm/s) to compress the sample, the obtained displacements show phase wrapping artifact. This is because the Doppler phase shift between A-scans acquired with interval δt has a magnitude larger than π/2 and could not be accurately estimated using Eq. (3). Results in Fig. 6(a) suggest that the time interval for Doppler analysis has to be selected adaptively to the speed of motion. In a different set of experiments, with benchtop experimental setup shown in Fig. 4(a), we translated the motor at the same speed (v_motor = 0.25mm/s) to compress the sample, acquired OCT data, performed Doppler analysis, and obtained displacements shown in Fig. 6(b). Notably, the Doppler phase shift used to track the displacement was calculated between A-scans with different time intervals: δt = ΔT₀, where T₀ = 16μs and Δ = 1, 2, 5, 50, 100, 150. In Fig. 6(b), when Doppler analysis was performed by comparing A-scans acquired with a small time interval (δt = ΔT₀ with Δ = 1, 5, 50), the extracted displacement increases with depth as anticipated. The random variation of the extracted displacement is larger for a smaller δt and is smaller for a larger δt, which is constant with Eqs. (6) and (7), as well as results shown in Fig. 5. However, further increasing the time interval (δt = ΔT₀ with Δ = 100, 150) between A-scans involved in Doppler analysis leads to phase wrapping artifact. Instead of increasing with depth as expected, the displacement starts to decrease at a larger depth (blue and black curves in Fig. 6(b)). As suggested by Fig. 6(b), the axial speed is different at different spatial locations within a deformed sampled and it requires different optimal time intervals for Doppler tracking.

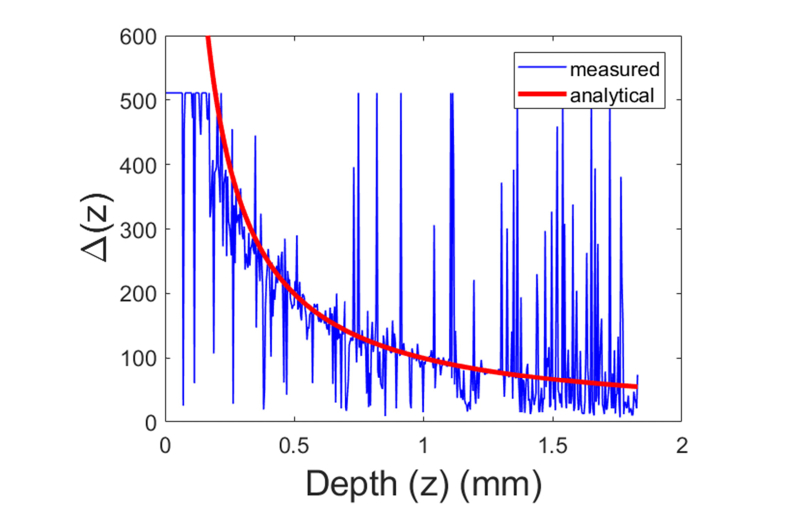
We then demonstrated real-time estimation of motion speed and the calculation of adaptive time interval for Doppler analysis through HD Doppler phase calculation. With the setup shown in Fig. 4(a), we compressed the sample by translating the motor at a speed of v_motor = 0.1 mm/s. Using one frame of OCT data acquired, we calculated the HD Doppler phase shift between adjacent A-scans, assessed the mean speed of axial motion at different depths, and estimated the optimal time interval (δt(z) = Δ(z)T₀) for adaptive Doppler analysis according to Eq. (9) with W = 4. Integer values of Δ obtained for different depths are shown in Fig. 7 as the blue curve. On the other hand, we assumed uniform axial deformation, and linearly displacement: δL(z) = εz with ε = δL_motor/L_sample. Here δL_motor = v_motorδt, and the thickness of the sample L_sample = 4mm. Therefore, the time required for OCT signal at depth z to achieve a phase shift of π/(2W) can be estimated: δt = λ₀L_sample/(8Wv_motorz), and the depth dependent integer Δ(z) can be obtained analytically: Δ = $\frac{{\lambda }_0{L}_{sample}}{8T_{0}W{v}_{\text{motor}}z}$, plotted as the red curve in Fig. 7. The consistency between analytical result and time interval obtained in real-time can be observed.

Fig. 7.

Adaptive time interval (δt(z) = Δ(z)T₀) selected for a sample under compression.

The time interval for Doppler analysis is determined using Eq. (9) that involves a pre-defined parameter W in the software. For Doppler signal free of phase wrapping artifact, the noise in the estimated phase is independent of the time interval between signals involved in Doppler analysis, as shown in Fig. 5(b) and 5(d), as well as Eqs. (6) and (7). On the other hand, a smaller value of W in Eq. (9) implies a larger value of time interval between A-scans for Doppler phase calculation and a larger phase shift due to accumulated displacement. Therefore, a smaller value of W leads to a higher SNR in displacement tracking. However, for W≤1, the result of displacement tracking is distorted, because the actual phase shift $\left|\frac{\pi }{2W}\right|\ge \frac{\pi }{2}$ cannot be effectively estimated using Eq. (3). To demonstrate how the value of W affects motion tracking, we used the benchtop experimental setup shown in Fig. 4(a) to compress the sample by translating the motor in axial direction with the same speed (0.25mm/s) and the same total displacement (0.5mm). With different values of W, we calculated time intervals using Eq. (9) and obtained depth resolved displacements from the compression processes shown in Fig. 8. Consistent with the above analysis, the noise in displacement tracking reduces as the value of W decreases, and phase wrapping artifact appears when W = 1 and 0.5. Therefore, a smaller value of W is preferred to optimize the SNR of displacement tracking, but W has to be sufficiently large (W>1) to prevent phase wrapping artifact in adaptive Doppler analysis.

We then validated that the adaptive Doppler analysis method allowed an accurate and robust displacement tracking. Using the benchtop setup shown in Fig. 4(a), we compressed the sample by translating the motor with different displacements (δL_motor = 0.1mm, 0.2mm, 0.3mm and 0.4mm) at the same speed (v_motor = 0.1mm/s). We obtained depth resolved displacements (solid curves) shown in Fig. 9(a) from the real-time software that performed the adaptive Doppler analysis (time interval was calculated using Eq. (9) with W = 2). With the assumption of uniform axial deformation, the displacement established within the sample is expected to increase linearly with the depth: δL(z) = εz, and ε can be estimated: ε = δL_motor/L_sample (L_sample indicates the thickness of the sample and L_sample = 4mm). Hence, we were able to generate the depth resolved sample displacement accordingly under different motor displacements, and the results are shown as dashed lines in Fig. 9(a). The displacements extracted by performing adaptive Doppler analysis on OCT signal are consistent with the analytical results based on the known motor displacement and sample geometry, suggesting the adaptive Doppler analysis accurately tracks the magnitude of axial displacement at different depths of the deformed sample. We also varied the motor translation speeds (v_motor = 0.1mm/s, 0.3mm/s, 0.5mm/s, 0.7mm/s and 0.9mm/s), and translated the motor for 0.5mm (δL_motor = 0.5mm) to compress the sample. Depth resolved sample displacements obtained through the adaptive Doppler analysis are shown in Fig. 9(b). We also generated displacement that increases linearly as depth (δL(z) = εz and ε = δL_motor/L_sample) based on the assumption of uniform deformation, and show the results in Fig. 9(b) as the dashed black line. Despite different motor translation speeds, our results show depth resolved displacements that have comparable signal quality and are free of phase wrapping artifacts. In comparison, Fig. 6(a) shows that Doppler analysis based on a fixed time interval resulted in different noise levels in displacement tracking and phase wrapping artifacts.

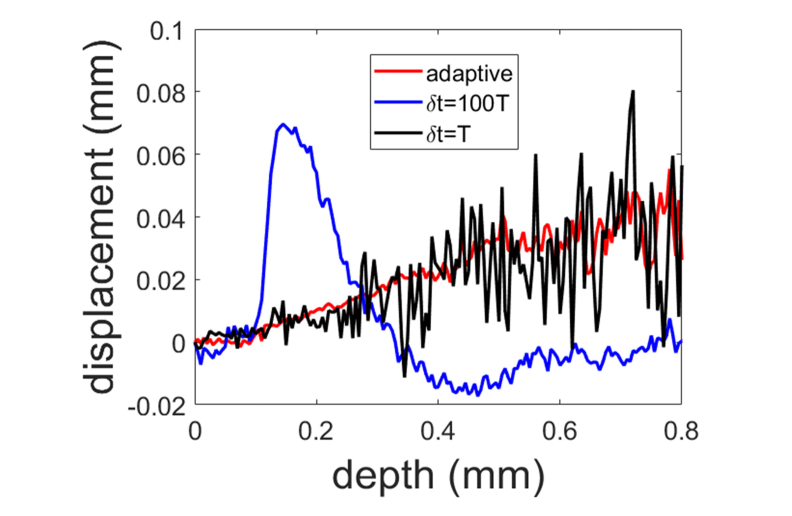
Following the validation of adaptive Doppler analysis on the benchtop setup, we performed OCE measurement using a handheld probe (Fig. 4(b)). During OCE characterization, the sample was manually compressed by the probe, while OCT signals were acquired. Depth resolved displacements were obtained, by calculating Doppler phase shift between OCT signal acquired with adaptive (Eq. (9)), large (δt = 100T₀) and small (δt = T₀) time intervals, where T₀ indicates the time interval between the acquisition of consecutive A-scans and T₀ = 16μs. Figure 10 shows the displacements obtained at the end of the manual compression processes and Visualization 1 ^{(545KB, avi)} (adaptive time), Visualization 2 ^{(723KB, avi)} (δt = 100T₀) and Visualization 3 ^{(634KB, avi)} (δt = T₀) show how the displacement fields were established throughout the compression processes. Clearly, when displacement tracking was performed with a large time interval (δt = 100T₀), the displacement does not increase monotonically with depth as expected (blue signal in Fig. 10), due to the phase wrapping artifact. The phase wrapping phenomenon can be observed more clearly in Visualization 2 ^{(723KB, avi)} . On the other hand, displacement tracking performed with δt = T₀ (black signal in Fig. 10) is quite noisy, which is consistent with Eqs. (6) and (7). The displacement obtained through adaptive Doppler analysis (red signal in Fig. 10) is less noisy and free from phase wrapping artifact. Results in Fig. 10 indicate that adaptive Doppler analysis is crucial for a manual device used to perform OCE characterization because hand maneuver is inevitably associated with varying compression speed.

Fig. 10.

Depth resolved displacement extracted from manual compression process with adaptive (red), large (blue) and small (black) time intervals between A-scans involved in Doppler analysis (see Visualization 1 ^{(545KB, avi)} , Visualization 2 ^{(723KB, avi)} and Visualization 3 ^{(634KB, avi)} ).

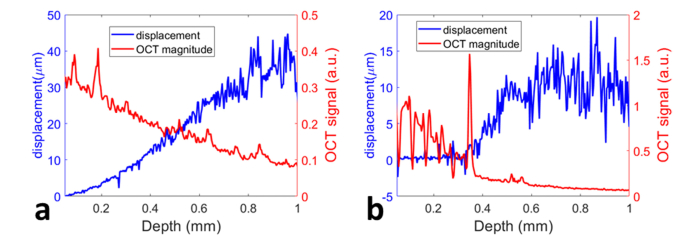
We further demonstrated that manual OCE characterization based on adaptive Doppler analysis could reveal the spatial variation of mechanical properties. Two samples were prepared (Sample 1: silicon phantom; Sample 2: silicon phantom with multiple layers of cellophane tape stacked on top). We used the handheld probe to compress both samples manually, and performed the real-time adaptive Doppler analysis on OCT signals to obtain the displacement from Sample 1 (blue signal in Fig. 11(a)) and Sample 2 (blue signal Fig. 11(b)). In Fig. 11(a) and 11(b), we also show the magnitude OCT signals (red signals) from Sample 1 and Sample 2, respectively. The silicon phantom (Sample 1) was optically and mechanically homogeneous. Therefore, the A-scan (red signal in Fig. 11(a)) decays with depth due to the absorption and scattering of light, while the depth resolved displacement (blue signal in Fig. 11(a)) extracted from adaptive Doppler analysis increases mononically with depth. In comparison, the magnitude OCT signal obtained from Sample 2 clearly shows the tape layers (red signal up to around 0.36mm depth in Fig. 11(b)). The displacement obtained from Sample 2 (blue signal in Fig. 11(b)) remains approximately the same until reaching the boundary between the tape layers and the silicon phantom because the tape layers did not deform under compression. Results in Fig. 11 suggest that adaptive Doppler analysis allows mechanical contrast between different materials to be revealed, although the motion within the sample generated by manual compression varies with time and spatial location.

To demonstrate in vivo OCE characterization of tissue based on adaptive Doppler analysis, we used the handheld probe to compress the skin tissue of a volunteer. The skin region with a wart at the back of the hand (Fig. 12(a), OCT image) is compressed by the probe, and the displacement extracted through adaptive Doppler analysis is shown in Fig. 12(c) as the blue curve. A neighboring region with healthy skin (Fig. 12(b)) was also characterized by handheld OCE, resulting in the displacement shown as the red curve in Fig. 12(c). Different strain characteristics can be observed in Fig. 12(c) for healthy and diseased skin. Due to the heterogeneous properties of the diseased skin, the displacement shows different slopes (red arrow indicates the starting of displacement for another slope), suggesting different axial strain within different depth range. In comparison, the displacement of the healthy skin increases approximately with the same slope. With the assumption of uniformly distributed stress, results in Fig. 12(c) indicate the elasticity of the diseased skin varies as depth and the healthy skin has homogeneous elasticity within the depth range interrogated by OCT. We also performed OCE characterization on the fingertip (Fig. 12(d)) and the forearm (Fig. 12(e)) skin of the same subject. Displacements were obtained through manual compression and adaptive Doppler analysis, as shown in Fig. 12(f). Due to the relatively thicker epidermis layer and the clear epidermal-dermal junction (red arrow in Fig. 12(d)) in fingertip skin, the displacement measured from compressed fingertip skin shows different slopes within different depth regions. A smaller slope is observed within the layer of epidermis, and a larger slope is observed within the layer of dermis, suggesting a smaller strain in epidermis and a larger strain in dermis. This is consistent with results reported by Kennedy et. al in [33]. With the assumption of uniform spatial distribution of stress, results in Fig. 12 (f) suggest a larger stiffness of epidermis compared to dermis,. Scale bars in Fig. 12 represent 500μm.

5. Conclusion and discussion

In summary, we developed and validated a Doppler analysis method that is adaptive to time and spatial location, for robust manual OCE characterization based on a handheld instrument. Enabled by this adaptive Doppler tracking strategy, real-time, manual mechanical characterization of in vivo tissue was demonstrated for the first time to the best of our knowledge.

It is worth mentioning that our goal is to reveal local mechanical contrast of the tissue (Fig. 11(b), Fig. 12(c) and 12(f)). Absolute measurement of tissue mechanical properties in vivo is a much more challenging task. Quantification of tissue mechanical property requires to know the 3D spatial distribution of the stress and the strain. In addition, the measurement boundary condition determined by the probe as well as the sample structure/heterogeneity has to be known. Moreover, for biological tissue that is generally viscoelastic, the force and displacement generated in the compression process depends not only on the intrinsic properties of the tissue but also on the dynamic loading process. However, quantitative measurement of tissue mechanical properties is beyond the scope of this study. Doppler analysis only tracks motion in axial direction. Therefore, we simply used the slope of axial displacement to represent the magnitude of sample deformation. We also assumed the stress to have a uniform spatial distribution. Hence the displacement has a linear dependency on the depth within a mechanically homogeneous volume from which OCT signal is acquired. This is validated by our experimental data (Fig. 9). Currently, we neglect the viscoelastic behavior of the sample. Without force/stress quantification, the strain was used as a surrogate for the stiffness of the sample. Despite the above simplifications, our measurement has the capability to reveal local mechanical heterogeneity, as shown in Fig. 11(b), Fig. 12(c) and Fig. 12(f).

To improve the dynamic range of Doppler tracking, previous effort has been focused on tracking fast motion, through unwrapping algorithm or exciting the sample with a crawling wave [34]. However, when the Ascan acquisition rate was high and the manual compression speed was slow, it is essential to track small Doppler phase shift that might be overwhelmed by random phase noise. Therefore, our method improves the dynamic range of motion tracking mainly by using a longer time window (Δ_k,m>1) to track slow motion. Consider the smallest measurable motion speed (v_min) to be equivalent to the noise magnitude in speed estimation. With Eqs. (6) and (7), we can estimate the minimal speed for the compression process, and v_min takes its smallest value when Δ_k,m takes its largest value (Δ_k,m = M₀/2). Assuming constant SNR, we have: $v_{min}=\frac{{\lambda }_0}{2\pi M_0{T}_0}\sqrt{\frac{\beta }{SNR}}$. On the other hand, a smaller Δ_k,m is selected for a greater motion speed until phase wrapping artifact arises. When the Doppler analysis is performed with Δ_k,m = 1 and is just free of phase wrapping (|δ${\hat{\varphi }}_{k,m}$| = π/2), the maximum trackable motion speed is $v_{max}=\frac{{\lambda }_0}{8T_0}$. The dynamic range (DR$=\frac{{\overline{v}}_{max}}{{\overline{v}}_{min}}$) in Doppler motion tracking (axial speed) is thus $DR=\sqrt{\frac{SNR}{\beta }}\frac{\pi \left(M_0/2\right)}{2}$. Compared to non-adaptive Doppler tracking (DR = $\sqrt{\frac{SNR}{\beta }}\frac{\pi }{2}$), the adaptive Doppler analysis achieves a M₀/2 fold improvement in the dynamic range for motion tracking, where M₀ is the number of A-scans in a frame of OCT data acquired. In our experiments, M₀ = 1024, suggesting a 512 fold improvement in linear dynamic range for motion tracking. With our camera running at its highest data acquisition rate (92kHz), a central wavelength of the light source of 1.3μm, β in Eq. (6) to be 3 [32], $v_{min}$ is approximately 0.003mm/s and $v_{max}$ is approximately 120mm/s, which provides a sufficient dynamic range to track manual compression process.

The adaptive motion tracking method described here uses a longer time window (Δ_k,m>1) to observe the change of signal by calculating the Doppler phase shift. This allows more accurate quantification of the motion but also reduces the temporal resolution of the measurement. However, with the assumption of quasi-static compression on elastic sample, we only consider the final accumulated displacement within the sample. Therefore, the compromised temporal resolution does not affect the characterization of local mechanical heterogeneity.

The potential benefit of using non-adjacent Ascans for Doppler analysis was noted by Adie et al [35]. However, in [35], there lacked detailed discussion and experimental validation for adaptive Doppler analysis. The authors of [35] either varied the data acquisition rate to track motion within the sample at different excitation frequencies, or chose sampling interval to be 1 or 2 depending on the known excitation frequency. The study described in this manuscript offers a practical solution for robust OCE characterization through a simple handheld device.

Compared to Eq. (3) that extracts Doppler phase using two-quadrant arctangent, the maximum phase free of phase wrapping artifact can be doubled by using four-quadrant arctangent function. Two-quadrant arctangent function was adopted in this study to simplify algorithm implementation for the analysis of noisy signal. Consider a complex OCT signal I(t). To obtain Doppler phase shift δϕ within a time interval δt, Z(t) = I(t + δt)I*(t) = X + jY is calculated and δϕ is estimated using the inverse of the tangent function: $\delta \hat{\varphi }$= tan⁻¹(Y/X). The inverse of the tangent function can be obtained using either two-quadrant arctangent atan(Y/X), or four-quadrant arctangent (atan2(Y,X)) that calculates atan(Y/X) and uses the signs of both arguments to determine the quadrant of the resultant phase. Four-quadrant arctangent function is based on two-quadrant arctangent and hence has similar noise characteristics. When X is small and Y is significantly larger, the absolute value of atan(Y/X) is close to π/2 and can be overwhelmed by noise, because the small value (X) in the denominator effectively amplifies the noise. Therefore, when atan is used to extract δϕ, two Ascans are chosen to generate a Doppler phase shift (absolute value) that is sufficiently smaller than π/2 to prevent phase wrapping artifact as well as amplified noise. When atan2 is used to achieve improved performance of Doppler analysis, the desirable Doppler phase shift (absolute value) has to be sufficiently larger than π/2 to prevent amplified noise and has to be sufficiently smaller than π to prevent phase wrapping artifact. Therefore, with Doppler phase shift calculated using four-quadrant arctangent function, the choice of time interval between Ascans depends on the noise of the amplitude OCT signal and is a non-trivial task.

Funding

National Institutes of Health (NIH) (1R15CA213092-01A1).

Disclosures

The authors declare that there are no conflicts of interest related to this article.