Abstract
A natural Bayesian approach for mixture models with an unknown number of components is to take the usual finite mixture model with symmetric Dirichlet weights, and put a prior on the number of components—that is, to use a mixture of finite mixtures (MFM). The most commonly-used method of inference for MFMs is reversible jump Markov chain Monte Carlo, but it can be nontrivial to design good reversible jump moves, especially in high-dimensional spaces. Meanwhile, there are samplers for Dirichlet process mixture (DPM) models that are relatively simple and are easily adapted to new applications. It turns out that, in fact, many of the essential properties of DPMs are also exhibited by MFMs—an exchangeable partition distribution, restaurant process, random measure representation, and stick-breaking representation—and crucially, the MFM analogues are simple enough that they can be used much like the corresponding DPM properties. Consequently, many of the powerful methods developed for inference in DPMs can be directly applied to MFMs as well; this simplifies the implementation of MFMs and can substantially improve mixing. We illustrate with real and simulated data, including high-dimensional gene expression data used to discriminate cancer subtypes.
Keywords: Bayesian, nonparametric, clustering, density estimation, model selection
1 Introduction
Mixture models are used in a wide range of applications, including population structure (Pritchard et al., 2000), document modeling (Blei et al., 2003), speaker recognition (Reynolds et al., 2000), computer vision (Stauffer and Grimson, 1999), phylogenetics (Pagel and Meade, 2004), and gene expression profiling (Yeung et al., 2001), to name a few prominent examples. A common issue with finite mixtures is that it can be difficult to choose an appropriate number of mixture components, and many methods have been proposed for making this choice (e.g., Henna, 1985; Keribin, 2000; Leroux, 1992; Ishwaran et al., 2001; James et al., 2001).
From a Bayesian perspective, perhaps the most natural approach is to treat the number of components k like any other unknown parameter and put a prior on it. When the prior on the mixture weights is Dirichletk(γ, …, γ) given k, we refer to such a model as a mixture of finite mixtures (MFM), for short. Several inference methods have been proposed for this type of model (Nobile, 1994; Phillips and Smith, 1996; Richardson and Green, 1997; Stephens, 2000; Nobile and Fearnside, 2007; McCullagh and Yang, 2008), the most commonly-used method being reversible jump Markov chain Monte Carlo (Green, 1995; Richardson and Green, 1997). Reversible jump is a very general technique, and has been successfully applied in many contexts, but it can be difficult to use since applying it to new situations requires one to design good reversible jump moves, which is often nontrivial, particularly in high-dimensional parameter spaces. Advances have been made toward general methods of constructing good reversible jump moves (Brooks et al., 2003; Hastie and Green, 2012), but these approaches add another level of complexity to the algorithm design process and/or the software implementation.
Meanwhile, infinite mixture models such as Dirichlet process mixtures (DPMs) have become popular, partly due to the existence of relatively simple and generic Markov chain Monte Carlo (MCMC) algorithms that can easily be adapted to new applications (Neal, 1992, 2000; MacEachern, 1994, 1998; MacEachern and Müller, 1998; Bush and MacEachern, 1996; West, 1992; West et al., 1994; Escobar and West, 1995; Liu, 1994; Dahl, 2003, 2005; Jain and Neal, 2004, 2007). These algorithms are made possible by the variety of computationally-tractable representations of the Dirichlet process, including its exchangeable partition distribution, the Blackwell–MacQueen urn process (a.k.a. the Chinese restaurant process), the random discrete measure formulation, and the Sethuraman–Tiwari stick-breaking representation (Ferguson, 1973; Antoniak, 1974; Blackwell and MacQueen, 1973; Aldous, 1985; Pitman, 1995, 1996; Sethuraman, 1994; Sethuraman and Tiwari, 1981).
It turns out that there are MFM counterparts for each of these properties: an exchangeable partition distribution, an urn/restaurant process, a random discrete measure formulation, and in certain cases, an elegant stick-breaking representation. The main point of this paper is that the MFM versions of these representations are simple enough, and parallel the DPM versions closely enough, that many of the inference algorithms developed for DPMs can be directly applied to MFMs. Interestingly, the key properties of MFMs hold for any choice of prior distribution on the number of components.
There has been a large amount of research on efficient inference methods for DPMs, and an immediate consequence of the present work is that most of these methods can also be used for MFMs. Since several DPM sampling algorithms are designed to have good mixing performance across a wide range of applications—for instance, the Jain–Neal split-merge samplers (Jain and Neal, 2004, 2007), coupled with incremental Gibbs moves (MacEachern, 1994; Neal, 1992, 2000)—this greatly simplifies the implementation of MFMs for new applications. Further, these algorithms can also provide a major improvement in mixing performance compared to the usual reversible jump approaches, particularly in high dimensions.
This work resolves an open problem discussed by Green and Richardson (2001), who noted that it would be interesting to be able to apply DPM samplers to MFMs:
“In view of the intimate correspondence between DP and [MFM] models discussed above, it is interesting to examine the possibilities of using either class of MCMC methods for the other model class. We have been unsuccessful in our search for incremental Gibbs samplers for the [MFM] models, but it turns out to be reasonably straightforward to implement reversible jump split/merge methods for DP models.”
The paper is organized as follows. In Sections 2 and 3, we formally define the MFM and show that it gives rise to a simple exchangeable partition distribution closely paralleling that of the Dirichlet process. In Section 4, we describe the Pólya urn scheme (restaurant process), random discrete measure formulation, and stick-breaking representation for the MFM. In Section 5, we establish some asymptotic results for MFMs. In Section 6, we show how the properties in Sections 3 and 4 lead to efficient inference algorithms for the MFM. In Section 7, we compare the mixing performance of reversible jump versus our proposed algorithms, then apply the model to high-dimensional gene expression data, and finally, provide an empirical comparison between MFMs and DPMs.
2 Model
We consider the following well-known model:
| (2.1) |
Here, H is a prior or “base measure” on Θ ⊂ ℝℓ, and {fθ : θ ∈ Θ} is a family of probability densities with respect to a sigma-finite measure ζ on 𝒳 ⊂ ℝd. (As usual, we give Θ and 𝒳 the Borel sigma-algebra, and assume (x, θ) ↦ fθ(x) is measurable.) We denote x1:n = (x1, …, xn). Typically, X1, …, Xn would be observed, and all other variables would be hidden/latent. We refer to this as a mixture of finite mixtures (MFM) model.
It is important to note that we assume a symmetric Dirichlet with a single parameter γ not depending on k. This assumption is key to deriving a simple form for the partition distribution and the other resulting properties. Assuming symmetry in the distribution of π is quite natural, since the distribution of X1, …, Xn under any asymmetric distribution on π would be the same as if this asymmetric distribution was replaced by its symmetrization, i.e., if the entries of π were uniformly permuted (although this would no longer necessarily be a Dirichlet distribution). Assuming the same γ for all k is a genuine restriction, albeit a fairly natural one, often made in such models even when not strictly necessary (Nobile, 1994; Phillips and Smith, 1996; Richardson and Green, 1997; Green and Richardson, 2001; Stephens, 2000; Nobile and Fearnside, 2007). Note that prior information about the relative sizes of the weights π1, …, πk can be introduced through γ—roughly speaking, small γ favors lower entropy π’s, while large γ favors higher entropy π’s. Also note that sometimes it is useful to put a hyperprior on the parameters of H (Richardson and Green, 1997).
Meanwhile, we put very few restrictions on pK, the distribution of the number of components. For practical purposes, we need the infinite series to converge to 1 reasonably quickly, but any choice of pK arising in practice should not be a problem. For certain theoretical purposes, it is desirable to have pK(k) > 0 for all k ∈ {1, 2, …}, e.g., this is necessary to have consistency for the number of components (Nobile, 1994).
For comparison, the Dirichlet process mixture (DPM) model with concentration parameter α > 0 and base measure H is defined as follows, using the stick-breaking representation (Sethuraman, 1994):
3 Exchangeable partition distribution
The primary observation on which our development relies is that the distribution on partitions induced by an MFM takes a form which is simple enough that it can be easily computed. Let 𝒞 denote the partition of [n] := {1, …, n} induced by Z1, …, Zn; in other words, 𝒞 = {Ei : |Ei| > 0} where Ei = {j : Zj = i} for i ∈ {1, 2, …}.
Theorem 3.1
Under the MFM (Equation 2.1), the probability mass function of 𝒞 is
| (3.1) |
where t = |𝒞| is the number of parts/blocks in the partition, and
| (3.2) |
Here, x(m) = x(x+1) ··· (x+m−1) and x(m) = x(x−1) ··· (x−m+1), with x(0) = 1 and x(0) = 1 by convention; note that x(m) = 0 when x is a positive integer less than m. Theorem 3.1 can be derived from the well-known formula for p(𝒞|k), which can found in, e.g., Green and Richardson (2001) or McCullagh and Yang (2008); we provide a proof for completeness. All proofs have been collected in the supplementary material. We discuss computation of Vn(t) in Section 3.2. For comparison, under the DPM, the partition distribution induced by Z1, …, Zn is where t = |𝒞| (Antoniak, 1974). When a prior is placed on α, as in the experiments in Section 7, the DPM partition distribution becomes
| (3.3) |
where .
Viewed as a function of the block sizes (|c| : c ∈ 𝒞), Equation 3.1 is an exchangeable partition probability function (EPPF) in the terminology of Pitman (1995, 2006), since it is a symmetric function of the block sizes. (Some authors also require EPPFs to have self-consistent marginals—see Section 3.3—but we follow the usage of Pitman (2006), who does not require this.) Consequently, 𝒞 is an exchangeable random partition of [n]; that is, its distribution is invariant under permutations of [n] (alternatively, this can be seen directly from the definition of the model, since Z1, …, Zn are exchangeable). In fact, Equation 3.1 induces an exchangeable random partition of the positive integers; see Section 3.3.
Further, Equation 3.1 is a member of the family of Gibbs partition distributions (Pitman, 2006); this is also implied by the results of Gnedin and Pitman (2006) characterizing the extreme points of the space of Gibbs partition distributions. Results on Gibbs partitions are provided by Ho et al. (2007), Lijoi et al. (2008), Cerquetti (2011), Cerquetti (2013), Gnedin (2010), and Lijoi and Prünster (2010). However, the utility of this representation for inference in mixture models with a prior on the number of components does not seem to have been previously explored in the literature.
Due to Theorem 3.1, we have the following equivalent representation of the model:
| (3.4) |
where ϕ = (ϕc : c ∈ 𝒞) is a tuple of t = |𝒞| parameters ϕc ∈ Θ, one for each block c ∈ 𝒞.
This representation is particularly useful for doing inference, since one does not have to deal with component labels or empty components. (If component-specific inferences are desired, a method such as that provided by Papastamoulis and Iliopoulos (2010) may be useful.) The formulation of models starting from a partition distribution has been a fruitful approach, exemplified by the development of product partition models (Hartigan, 1990; Barry and Hartigan, 1992; Quintana and Iglesias, 2003; Dahl, 2009; Park and Dunson, 2010; Müller and Quintana, 2010; Müller et al., 2011) and the loss-based approach of Lau and Green (2007).
3.1 Basic properties
We list here some basic properties of the MFM model. See the supplementary material for proofs. Denoting xc = (xj : j ∈ c) and m(xc) = ∫Θ [Πj∈c fθ(xj)] H(dθ) (with the convention that m(x∅) = 1), we have
| (3.5) |
While some authors use the terms “cluster” and “component” interchangeably, we use cluster to refer to a block c in a partition 𝒞, and component to refer to a probability distribution fθi in a mixture . The number of components K and the number of clusters T = |𝒞| are related by
| (3.6) |
| (3.7) |
where in Equation 3.6, the sum is over partitions 𝒞 of [n] such that |𝒞| = t. Note that p(t|k) and p(k|t) depend on n. Wherever possible, we use capital letters (such as K and T) to denote random variables as opposed to particular values (k and t). The formula for p(k|t) is required for doing inference about the number of components K based on posterior samples of 𝒞; fortunately, it is easy to compute. We have the conditional independence relations
| (3.8) |
| (3.9) |
3.2 The coefficients Vn(t)
The following recursion is a special case of a more general result for Gibbs partitions (Gnedin and Pitman, 2006).
Proposition 3.2
The numbers Vn(t) (Equation 3.2) satisfy the recursion
| (3.10) |
for any 0 ≤ t ≤ n and γ > 0.
This is easily seen by plugging the identity
into the expression for Vn+1(t + 1). In the case of γ = 1, Gnedin (2010) has discovered a beautiful example of a distribution on K for which both pK(k) and Vn(t) have closed-form expressions.
In previous work on the MFM model, pK has often been chosen to be proportional to a Poisson distribution restricted to the positive integers or a subset thereof (Phillips and Smith, 1996; Stephens, 2000; Nobile and Fearnside, 2007), and Nobile (2005) has proposed a theoretical justification for this choice. Interestingly, the model has some nice mathematical properties if one instead chooses K − 1 to be given a Poisson distribution, that is, pK(k) = Poisson(k − 1|λ) for some λ > 0. For instance, it turns out that if pK(k) = Poisson(k − 1|λ) and γ = 1 then .
However, to do inference, it is not necessary to choose pK to have any particular form—we just need to be able to compute p(𝒞), and in turn, we need to be able to compute Vn(t). To this end, note that k(t)/(γk)(n) ≤ kt/(γk)n, and thus the infinite series for Vn(t) (Equation 3.2) converges rapidly when t ≪ n. It always converges to a finite value when 1 ≤ t ≤ n; this is clear from the fact that p(𝒞) ∈ [0, 1]. This finiteness can also be seen directly from the series since kt/(γk)n ≤ 1/γn, and in fact, this shows that the series for Vn(t) converges at least as rapidly (up to a constant) as the series converges to 1. Hence, for any reasonable choice of pK (i.e., not having an extraordinarily heavy tail), Vn(t) can easily be numerically approximated to a high level of precision. In practice, all of the required values of Vn(t) can be precomputed before MCMC sampling, and this takes a negligible amount of time relative to MCMC (see the supplementary material).
3.3 Self-consistent marginals
For each n = 1, 2, …, let qn(𝒞) denote the MFM distribution on partitions of [n] (Equation 3.1). This family of partition distributions is preserved under marginalization, in the following sense.
Proposition 3.3
If m < n then qm coincides with the marginal distribution on partitions of [m] induced by qn.
In other words, drawing a sample from qn and removing elements m + 1, …, n from it yields a sample from qm. This can be seen directly from the model definition (Equation 2.1), since 𝒞 is the partition induced by the Z’s, and the distribution of Z1:m is the same when the model is defined with any n ≥ m. This property is sometimes referred to as consistency in distribution (Pitman, 2006).
By Kolmogorov’s extension theorem (e.g., Durrett, 1996), it is well-known that this implies the existence of a unique probability distribution on partitions of the positive integers ℤ>0 = {1, 2, …} such that the marginal distribution on partitions of [n] is qn for all n ∈ {1, 2, …} (Pitman, 2006).
4 Equivalent representations
4.1 Pólya urn scheme / Restaurant process
Pitman (1996) considered a general class of urn schemes, or restaurant processes, corresponding to exchangeable partition probability functions (EPPFs). The following scheme for the MFM falls into this general class.
Theorem 4.1
The following process generates partitions 𝒞1, 𝒞2, … such that for any n ∈ {1, 2, …}, the probability mass function of 𝒞n is given by Equation 3.1.
Initialize with a single cluster consisting of element 1 alone: 𝒞1 = {{1}}.
-
For n = 2, 3, …, element n is placed in …
an existing cluster c ∈ 𝒞n−1 with probability ∝ |c| + γ
a new cluster with probability
where t = |𝒞n−1|.
Clearly, this bears a close resemblance to the Chinese restaurant process (i.e., the Blackwell–MacQueen urn process), in which the nth element is placed in an existing cluster c with probability ∝ |c| or a new cluster with probability ∝ α (the concentration parameter) (Blackwell and MacQueen, 1973; Aldous, 1985).
4.2 Random discrete measures
The MFM can also be formulated starting from a distribution on discrete measures that is analogous to the Dirichlet process. With K, π, and θ1:K as in Equation 2.1, let
where δθ is the unit point mass at θ. Let us denote the distribution of G by ℳ(pK, γ,H). Note that G is a random discrete measure over Θ. If H is continuous (i.e., H({θ}) = 0 for all θ ∈ Θ), then with probability 1, the number of atoms is K; otherwise, there may be fewer than K atoms. If we let X1, …, Xn|G be i.i.d. from the resulting mixture, i.e., from
then the distribution of X1:n is the same as in Equation 2.1. So, in this notation, the MFM model is:
This random discrete measure perspective is connected to work on species sampling models (Pitman, 1996) in the following way. When H is continuous, we can construct a species sampling model by letting G ~ ℳ(pK, γ,H) and modeling the observed data as β1, …, βn ~ G given G. We refer to Pitman (1996), Hansen and Pitman (2000), Ishwaran and James (2003), Lijoi et al. (2005, 2007), and Lijoi et al. (2008) for more background on species sampling models and further examples. Pitman derived a general formula for the posterior predictive distribution of a species sampling model; the following result is a special case. Note the close relationship to the restaurant process (Theorem 4.1).
Theorem 4.2
If H is continuous, then β1 ~ H and the distribution of βn given β1, …, βn−1 is proportional to
| (4.1) |
where are the distinct values taken by β1, …, βn−1, and .
For comparison, when G ~ DP(αH) instead, the distribution of βn given β1, …, βn−1 is proportional to , since (Ferguson, 1973; Blackwell and MacQueen, 1973).
4.3 Stick-breaking representation
The Dirichlet process has an elegant stick-breaking representation for the mixture weights π1, π2, … (Sethuraman, 1994; Sethuraman and Tiwari, 1981). This extraordinarily clarifying perspective has inspired a number of nonparametric models (MacEachern, 1999, 2000; Hjort, 2000; Ishwaran and Zarepour, 2000; Ishwaran and James, 2001; Griffin and Steel, 2006; Dunson and Park, 2008; Chung and Dunson, 2009; Rodriguez and Dunson, 2011; Broderick et al., 2012), has provided insight into the properties of related models (Favaro et al., 2012; Teh et al., 2007; Thibaux and Jordan, 2007; Paisley et al., 2010), and has been used to develop efficient inference algorithms (Ishwaran and James, 2001; Blei and Jordan, 2006; Papaspiliopoulos and Roberts, 2008; Walker, 2007; Kalli et al., 2011).
In a certain special case—namely, when pK(k) = Poisson(k − 1|λ) and γ = 1—we have noticed that the MFM also has an interesting representation that we describe using the stick-breaking analogy, although it is somewhat different in nature. Consider the following procedure:
Take a unit-length stick, and break off i.i.d. Exponential(λ) pieces until you run out of stick.
In other words, let , define , let π̃i = εi for i = 1, …, K̃ − 1, and let .
Proposition 4.3
The stick lengths π̃ have the same distribution as the mixture weights π in the MFM model when pK(k) = Poisson(k − 1|λ) and γ = 1.
This is a consequence of a standard construction for Poisson processes. This suggests a way of generalizing the MFM model: take any sequence of positive random variables (ε1, ε2, …) (not necessarily independent or identically distributed) such that with probability 1, and define K̃ and π̃ as above. Although the distribution of K̃ and π̃ may be complicated, in some cases it might still be possible to do inference based on the stick-breaking representation. This might be an interesting way to introduce different kinds of prior information on the mixture weights, however, we have not explored this possibility.
5 Asymptotics
In this section, we consider the asymptotics of Vn(t), the asymptotic relationship between the number of components and the number of clusters, and the approximate form of the conditional distribution on cluster sizes given the number of clusters.
5.1 Asymptotics of Vn(t)
Recall that (Equation 3.2) for 1 ≤ t ≤ n, where γ > 0 and pK is a p.m.f. on {1, 2, …}. When an, bn > 0, we write an ~ bn to mean an/bn → 1 as n→∞.
Theorem 5.1
For any t ∈ {1, 2, …}, if pK(t) > 0 then
| (5.1) |
as n→∞.
In particular, Vn(t) has a simple interpretation, asymptotically—it behaves like the k = t term in the series. All proofs have been collected in the supplementary material.
5.2 Relationship between the number of clusters and number of components
In the MFM, it is perhaps intuitively clear that, under the prior at least, the number of clusters T = |𝒞| behaves very similarly to the number of components K when n is large. It turns out that under the posterior they also behave very similarly for large n.
Theorem 5.2
Let x1, x2, … ∈ 𝒳 and k ∈ {1, 2, …}. If pK(1), …, pK(k) > 0 then
as n→∞.
5.3 Distribution of the cluster sizes under the prior
Here, we examine one of the major differences between the MFM and DPM priors. Roughly speaking, under the prior, the MFM prefers all clusters to be the same order of magnitude, while the DPM prefers having a few large clusters and many very small clusters. In the following calculations, we quantify the preceding statement more precisely. (See Green and Richardson (2001) for informal observations along these lines.) Interestingly, these prior influences remain visible in certain aspects of the posterior, even in the limit as n goes to infinity.
Let 𝒞 be the random partition of [n] in the MFM model (Equation 3.1), and let A = (A1, …, AT) be the ordered partition of [n] obtained by randomly ordering the blocks of 𝒞, uniformly among the T! possible choices, where T = |𝒞|. Then
where t = |𝒞|. Now, let S = (S1, …, ST) be the vector of block sizes of A, that is, Si = |Ai|. Then
for s ∈ Δt, t ∈ {1, …, n}, where Δt = {s ∈ ℤt : Σi si = n, si ≥ 1 ∀i} (i.e., Δt is the set of t-part compositions of n). For any x > 0, by writing x(m)/m! = Γ(x + m)/(m! Γ(x)) and using Stirling’s approximation, we have x(m)/m! ~ mx−1/Γ(x) as m→∞. This yields the approximations
(using Theorem 5.1 in the second step), and
for s ∈ Δt, where κ is a normalization constant. Thus, p(s|t) has approximately the same shape as a symmetric t-dimensional Dirichlet distribution, except it is discrete. This would be obvious if we were conditioning on the number of components K, and it makes intuitive sense when conditioning on T, since K and T are essentially the same for large n.
It is interesting to compare p(s) and p(s|t) to the corresponding distributions for the Dirichlet process. For the DP with a prior on α, we have by Equation 3.3, and pDP(A) = pDP(𝒞)/|𝒞|! as before, so for s ∈ Δt, t ∈ {1, …, n},
and
which has the same shape as a t-dimensional Dirichlet distribution with all the parameters taken to 0 (noting that this is normalizable since Δt is finite). Asymptotically in n, pDP(s|t) puts all of its mass in the “corners” of the discrete simplex Δt, while under the MFM, p(s|t) remains more evenly dispersed.
6 Inference algorithms
Many approaches have been used for posterior inference in the MFM model (Equation 2.1). Nobile (1994) approximates the marginal likelihood p(x1:n|k) of each k in order to compute the posterior on k, and uses standard methods given k. Phillips and Smith (1996) and Stephens (2000) use jump diffusion and point process approaches, respectively, to sample from p(k, π, θ|x1:n). Richardson and Green (1997) employ reversible jump moves to sample from p(k, π, θ, z|x1:n). In cases with conjugate priors, Nobile and Fearnside (2007) use various Metropolis–Hastings moves on p(k, z|x1:n), and McCullagh and Yang (2008) develop an approach that could in principle be used to sample from p(k, 𝒞|x1:n).
Due to the results of Sections 3 and 4, much of the extensive body of work on MCMC samplers for DPMs can be directly applied to MFMs. This leads to a variety of MFM samplers, of which we consider two main types: (a) sampling from p(𝒞|x1:n) in cases where the marginal likelihood m(xc) = ∫Θ [Πj∈c fθ(xj)] H(dθ) can easily be computed (typically, this means H is a conjugate prior), and (b) sampling from p(𝒞, ϕ|x1:n) (in the notation of Equation 3.4) in cases where m(xc) is intractable or when samples of the component parameters are desired.
When m(xc) can easily be computed, the following Gibbs sampling algorithm can be used to sample from the posterior on partitions, p(𝒞|x1:n). Given a partition 𝒞, let 𝒞 \ j denote the partition obtained by removing element j from 𝒞.
Initialize 𝒞 = {[n]} (i.e., one cluster).
-
Repeat the following steps N times, to obtain N samples.
-
For j = 1, …, n: Remove element j from 𝒞, and place it …
in c ∈ 𝒞 \ j with probability
in a new cluster with probability
where t = |𝒞 \ j|.
-
This is a direct adaptation of “Algorithm 3” for DPMs (MacEachern, 1994; Neal, 1992, 2000). The only differences are that in Algorithm 3, |c| + γ is replaced by |c|, and γVn(t + 1)/Vn(t) is replaced by α (the concentration parameter). Thus, the differences between the MFM and DPM versions of the algorithm are precisely the same as the differences between their respective urn/restaurant processes. In order for the algorithm to be valid, the Markov chain needs to be irreducible, and to achieve this it is necessary that {t ∈ {1, 2, …} : Vn(t) > 0} be a block of consecutive integers containing 1. It turns out that this is always the case, since for any k such that pK(k) > 0, we have Vn(t) > 0 for all t = 1, …, k.
Note that one only needs to compute Vn(1), …, Vn(t*) where t* is the largest value of t visited by the sampler. In practice, it is convenient to precompute these values using a guess at an upper bound tpre on t*, and this takes a negligible amount of time compared to running the sampler (see the supplementary material). Just to be clear, tpre is only introduced for computational expedience—the model allows unbounded t, and in the event that the sampler visits t > tpre, it is trivial to increase tpre and compute the required values of Vn(t) on demand.
When m(xc) cannot easily be computed, a clever auxiliary variable technique referred to as “Algorithm 8” can be used for inference in the DPM (Neal, 2000; MacEachern and Müller, 1998). Making the same substitutions as above, we can apply Algorithm 8 for inference in the MFM as well, to sample from p(𝒞, ϕ|x1:n).
A well-known issue with incremental Gibbs samplers such as Algorithms 3 and 8, when applied to DPMs, is that mixing can be somewhat slow, since it may take a long time to create or destroy substantial clusters by moving one element at a time. With MFMs, this issue seems to be exacerbated, since compared with DPMs, MFMs tend to put small probability on partitions with tiny clusters (see Section 5.3), making it difficult for the sampler to move through these regions of the space.
To deal with this issue, split-merge samplers for DPMs have been developed, in which a large number of elements can be reassigned in a single move (Dahl, 2003, 2005; Jain and Neal, 2004, 2007). In the same way as the incremental samplers, one can directly apply these split-merge samplers to MFMs as well, by simply plugging-in the MFM partition distribution in place of the DPM partition distribution. More generally, it seems likely that any partition-based MCMC sampler for DPMs could be applied to MFMs as well. In Section 7, we apply the Jain–Neal split-merge samplers, coupled with incremental Gibbs samplers, to do inference for MFMs in both conjugate and non-conjugate settings.
As usual in mixture models, the MFM is invariant under permutations of the component labels, and this can lead to so-called “label-switching” issues if one naively attempts to estimate quantities that are not invariant to labeling—such as the mean of a given component—by averaging MCMC samples. In the experiments below, we only estimate quantities that are invariant to labeling, such as the density, the number of components, and the probability that two given points belong to the same cluster. Consequently, the label-switching issue does not arise here. If inference for non-invariant quantities is desired, methods for this purpose have been proposed (Papastamoulis and Iliopoulos, 2010).
In addition to the partition-based algorithms above, several DPM inference algorithms are based on the stick-breaking representation, such as the slice samplers for mixtures (Walker, 2007; Kalli et al., 2011). Although we have not explored this approach, it should be possible to adapt these to MFMs using the stick-breaking representation described in Section 4.3.
7 Empirical demonstrations
In Section 7.1, we compare the mixing performance of reversible jump MCMC versus the Jain–Neal split-merge algorithms proposed in Section 6 for inference in the MFM. Section 7.2 applies an MFM model to discriminate cancer subtypes based on gene expression data. In Section 7.3, we illustrate some of the similarities and differences between MFMs and DPMs. All of the examples below happen to involve Gaussian component densities, but of course our approach is not limited to mixtures of Gaussians.
7.1 Comparison with reversible jump MCMC
We compare two methods of inference for the MFM: the usual reversible jump MCMC (RJMCMC) approach, and our proposed approach based on the Jain–Neal split-merge algorithms. This purpose of this is (1) to compare the mixing performance of our method versus RJMCMC, and (2) to demonstrate the validity of our method by showing agreement with results obtained using RJMCMC. In addition to having better mixing performance, our method has the significant advantage of providing generic algorithms that apply to a wide variety of component distributions and priors, whereas RJMCMC requires one to design specialized reversible jump moves.
RJMCMC is a very general framework and an enormous array of MCMC algorithms could be considered to be a special case of it. The most commonly-used instantiation of RJMCMC for mixtures seems to be the original algorithm of Richardson and Green (1997) for univariate Gaussian mixtures, so it makes sense to compare with this. For multivariate Gaussian mixtures, several RJMCMC algorithms have been proposed (Marrs, 1998; Zhang et al., 2004; Dellaportas and Papageorgiou, 2006), however, the model we consider below uses diagonal covariance matrices, and in this case, the Richardson and Green (1997) moves can simply be extended to each coordinate. More efficient algorithms almost certainly exist within the vast domain of RJMCMC, but the goal here is to compare with “plain-vanilla RJMCMC” as it is commonly-used.
7.1.1 Comparison with RJMCMC on the galaxy dataset
The galaxy dataset (Roeder, 1990) is a standard benchmark for mixture models, consisting of measurements of the velocities of 82 galaxies in the Corona Borealis region. To facilitate the comparison with RJMCMC, we use exactly the same model as Richardson and Green (1997). The component densities are univariate normal, fθ(x) = fμ,λ(x) = 𝒩(x|μ, λ−1), and the base measure (prior) H on θ = (μ, λ) is , λ ~ Gamma(a, b) independently (where Gamma(λ|a, b) ∝ λa−1e−bλ). Further, a hyperprior is placed on b, by taking b ~ Gamma(a0, b0). The remaining parameters are set to μ0 = (max{xi} + min{xi})/2, σ0 = max{xi} − min{xi}, a = 2, a0 = 0.2, and . Note that the parameters μ0, σ0, and b0 are functions of the observed data x1, …, xn, making this a data-dependent prior. Note further that taking μ and λ to be independent results in a non-conjugate prior; this is appropriate when the location of the data is not informative about the scale (and vice versa). See Richardson and Green (1997) for the rationale behind these parameter choices. (Note: This choice of σ0 may be a bit too large, affecting the posteriors on the number of clusters and components, however, we stick with it to facilitate the comparison.) Following Richardson and Green (1997), we take K ~ Uniform{1, …, 30} and set γ = 1 for the finite-dimensional Dirichlet parameters.
To implement our proposed inference approach, we use the split-merge sampler of Jain and Neal (2007) for non-conjugate priors, coupled with Algorithm 8 of Neal (2000) (using a single auxiliary variable) for incremental Gibbs updates to the partition. Specifically, following Jain and Neal (2007), we use the (5,1,1,5) scheme: 5 intermediate scans to reach the split launch state, 1 split-merge move per iteration, 1 incremental Gibbs scan per iteration, and 5 intermediate moves to reach the merge launch state. We use Gibbs sampling to handle the hyperprior on b (i.e., append b to the state of the Markov chain, run the sampler given b as usual, and periodically sample b given everything else). More general hyperprior structures can be handled similarly. We do not restrict the parameter space in any way (e.g., forcing the component means to be ordered to obtain identifiability, as was done by Richardson and Green, 1997). All of the quantities we consider are invariant to the labeling of the clusters; see Jasra et al. (2005) for discussion on this point.
Results for RJMCMC were obtained using the Nmix software provided by Peter Green,1 which implements the algorithm of Richardson and Green (1997).
Results
First, we demonstrate agreement between inference results obtained using RJMCMC and using our method based on the Jain–Neal algorithm. Table 1 compares estimates of the MFM posterior on the number of components k using both Jain–Neal and RJMCMC. Each algorithm was run for 106 iterations, the first 105 of which were discarded as burn-in. The two methods are in very close agreement, empirically verifying that they are both correctly sampling from the MFM posterior.
Table 1.
Estimates of the MFM posterior on k for the galaxy dataset.
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Jain–Neal | 0.000 | 0.000 | 0.060 | 0.134 | 0.187 | 0.194 | 0.158 |
| RJMCMC | 0.000 | 0.000 | 0.059 | 0.131 | 0.187 | 0.197 | 0.160 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|
| 0.110 | 0.069 | 0.040 | 0.023 | 0.012 | 0.007 | 0.004 | 0.002 |
| 0.110 | 0.068 | 0.039 | 0.022 | 0.012 | 0.006 | 0.003 | 0.002 |
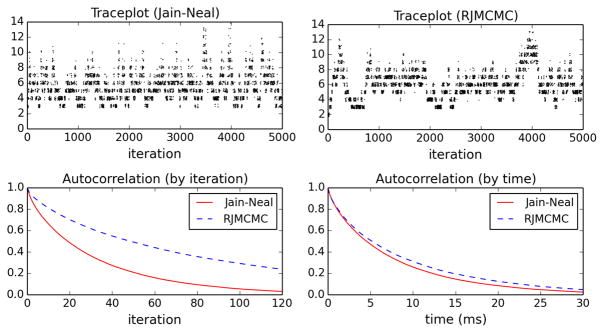
To compare the mixing performance of the two methods, Figure 1 (top) shows traceplots of the number of clusters over the first 5000 iterations. The number of clusters is often used to assess mixing, since it is usually one of the quantities for which mixing is slowest. One can see that the Jain–Neal split-merge algorithm appears to explore the space more quickly than RJMCMC. Figure 1 (bottom left) shows estimates of the autocorrelation functions for the number of clusters, scaled by iteration. The autocorrelation of Jain–Neal decays significantly more rapidly than that of RJMCMC, confirming the visual intuition from the traceplot. This makes sense since the Jain–Neal algorithm makes splitting proposals in an adaptive, data-dependent way. The effective sample size (based on the number of clusters) is estimated to be 1.6% for Jain–Neal versus 0.6% for RJMCMC; in other words, 100 Jain–Neal samples are equivalent to 1.6 independent samples (Kass et al., 1998).
Figure 1.
Results on the galaxy dataset. Top: Traceplots of the number of clusters at each iteration. Bottom: Estimated autocorrelation function of the number of clusters, scaled by iteration (left) and time in milliseconds (right).
However, each iteration of the Jain–Neal algorithm takes approximately 2.9 × 10−6 n seconds, where n = 82 is the sample size, compared with 1.3 × 10−6 n seconds for RJM-CMC, which is a little over twice as fast. (All experiments in this paper were performed using a 2.80 GHz processor with 6 GB of RAM.) In both algorithms, one iteration consists of a reassignment move for each datapoint, updates to component parameters and hyperparameters, and a split or merge move, but it makes sense that Jain–Neal would be a bit slower per iteration since its reassignment moves and split-merge moves require a few more steps. Nonetheless, it seems that this is compensated for by the improvement in mixing per iteration: Figure 1 (bottom right) shows that when rescaled to account for computation time, the estimated autocorrelation functions are nearly the same. Thus, in this experiment, the two methods perform roughly equally well.
7.1.2 Comparison with RJMCMC as dimensionality increases
In this subsection, we show that our approach can provide a massive improvement over RJMCMC when the parameter space is high-dimensional. We illustrate this with a model that will be applied to gene expression data in Section 7.2.
We simulate data of increasing dimensionality, and assess the effect on mixing performance. Specifically, for a given dimensionality d, we draw , where , and then normalize each dimension to have zero mean and unit variance. The purpose of the factor is to prevent the posterior from concentrating too quickly as d increases, so that one can still see the sampler exploring the space.
To enable scaling to the high-dimensional gene expression data in Section 7.2, we use multivariate Gaussian component densities with diagonal covariance matrices (i.e., for each component, the dimensions are independent univariate Gaussians), and we place independent conjugate priors on each dimension. Specifically, for each component, for i = 1, …, d, dimension i is given (μi, λi), and λi ~ Gamma(a, b), μi|λi ~ 𝒩(0, (cλi)−1). We set a = 1, b = 1, c = 1 (recall that the data are zero mean, unit variance in each dimension), K ~ Geometric(r) (pK(k) = (1 − r)k−1r for k = 1, 2, …) with r = 0.1, and γ = 1. We compare the mixing performance of three samplers:
Collapsed Jain–Neal. Given the partition C of the data into clusters, the parameters can be integrated out analytically since the prior is conjugate. Thus, we can use the split-merge sampler of Jain and Neal (2004) for conjugate priors, coupled with Algorithm 3 of Neal (2000). Following Jain and Neal (2004), we use the (5,1,1) scheme: 5 intermediate scans to reach the split launch state, 1 split-merge move per iteration, and 1 incremental Gibbs scan per iteration.
Jain–Neal. Even though the prior is conjugate, we can still use the Jain and Neal (2007) split-merge algorithm for non-conjugate priors, coupled with Algorithm 8 of Neal (2000). As in Section 7.1.1, we use the (5,1,1,5) scheme.
RJMCMC. For reversible jump MCMC, we use a natural multivariate extension of the moves from Richardson and Green (1997). Specifically, for the split move, we propose splitting the mean and variance for each dimension i according to the formulas in Richardson and Green (1997), using independent variables u2i and u3i. For the birth move, we make a proposal from the prior. The remaining moves are essentially the same as in Richardson and Green (1997).
Results
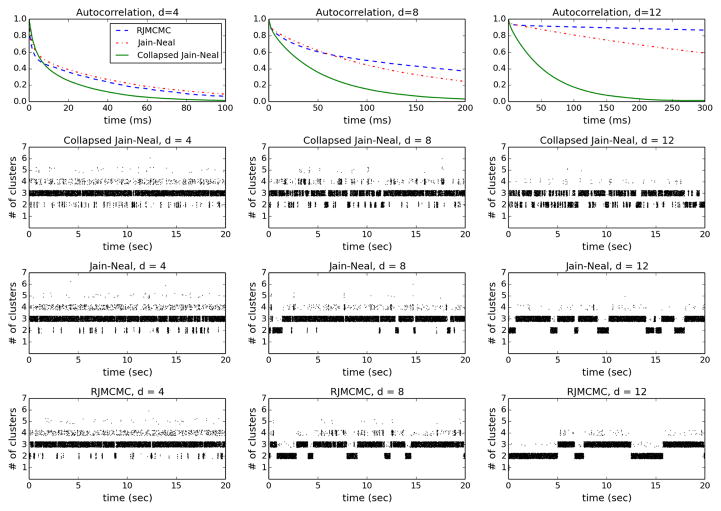
For each d ∈ {4, 8, 12}, a dataset of size n = 100 was generated as described above, and each of the three algorithms was run for 106 iterations. For each algorithm and each d, Figure 2 shows the estimated autocorrelation function for the number of clusters (scaled to milliseconds), as well as a traceplot of the number of clusters over the first 20 seconds of sampling. We see that as the dimensionality increases, mixing performance degrades for all three algorithms, which is to be expected. However, it degrades significantly more rapidly for RJMCMC than for the Jain–Neal algorithms, especially the collapsed version. This difference can be attributed to the clever data-dependent split-merge proposals in the Jain–Neal algorithms, and the fact that the collapsed version benefits further from the effective reduction in dimensionality resulting from integrating out the parameters.
Figure 2.
Top: Estimated autocorrelation functions for the number of clusters, for each algorithm, for each d ∈ {4, 8, 12}. Bottom: Traceplots of the number of clusters over the first 20 seconds of sampling.
As the dimensionality increases, the advantage over RJMCMC becomes ever greater. This demonstrates the major improvement in performance that can be obtained using the approach we propose. In fact, in the next section, we apply our method to very high-dimensionality gene expression data on which the time required for RJMCMC to mix becomes unreasonably long, making it impractical. Meanwhile, our approach using the collapsed Jain–Neal algorithm still mixes well.
7.2 Discriminating cancer subtypes using gene expression data
In cancer research, gene expression profiling—that is, measuring the amount that each gene is expressed in a given tissue sample—enables the identification of distinct subtypes of cancer, leading to greater understanding of the mechanisms underlying cancers as well as potentially providing patient-specific diagnostic tools. In gene expression datasets, there are typically a small number of very high-dimensional data points, each consisting of the gene expression levels in a given tissue sample under given conditions.
One approach to analyzing gene expression data is to use Gaussian mixture models to identify clusters which may represent distinct cancer subtypes (Yeung et al., 2001; McLachlan et al., 2002; Medvedovic and Sivaganesan, 2002; Medvedovic et al., 2004; de Souto et al., 2008; Rasmussen et al., 2009; McNicholas and Murphy, 2010). In fact, in a comparative study of seven clustering methods on 35 cancer gene expression datasets with known ground truth, de Souto et al. (2008) found that finite mixtures of Gaussians provided the best results, as long as the number of components k was set to the true value. However, in practice, choosing an appropriate value of k can be difficult. Using the methods developed in this paper, the MFM provides a principled approach to inferring the clusters even when k is unknown, as well as doing inference for k, provided that the components are well-modeled by Gaussians.
The purpose of this example is to demonstrate that our approach can work well even in very high-dimensional settings, and may provide a useful tool for this application. It should be emphasized that we are not cancer scientists, so the results reported here should not be interpreted as scientifically relevant, but simply as a proof-of-concept.
7.2.1 Setup: data, model, and inference
We apply the MFM to gene expression data collected by Armstrong et al. (2001) in a study of leukemia subtypes. Armstrong et al. (2001) measured gene expression levels in samples from 72 patients who were known to have one of two leukemia types, acute lymphoblastic leukemia (ALL) or acute myelogenous leukemia (AML), and they found that a previously undistinguished subtype of ALL, which they termed mixed-lineage leukemia (MLL), could be distinguished from conventional ALL and AML based on the gene expression profiles.
We use the preprocessed data provided by de Souto et al. (2008), which they filtered to include only genes with expression levels differing by at least 3-fold in at least 30 samples, relative to their mean expression level across all samples. The resulting dataset consists of 72 samples and 1081 genes per sample, i.e., n = 72 and d = 1081. Following standard practice, we take the base-2 logarithm of the data before analysis, and normalize each dimension to have zero mean and unit variance.
We use the same model as in Section 7.1.2. Note that these parameter settings are simply defaults and have not been tailored to the problem; a careful scientific investigation would involve thorough prior elicitation, sensitivity analysis, and model checking.
The collapsed Jain–Neal algorithm described in Section 7.1.2 was used for inference. The sampler was run for 1,000 burn-in iterations, and 19,000 sample iterations. This appears to be many more iterations than required for burn-in and mixing in this particular example—in fact, only 5 to 10 iterations are required to separate the clusters, and the results are indistinguishable from using only 10 burn-in and 190 sample iterations. The full state of the chain was recorded every 20 iterations. Each iteration took approximately 1.3 × 10−3 n seconds, where n = 72 is the number of observations in the dataset.
7.2.2 Results
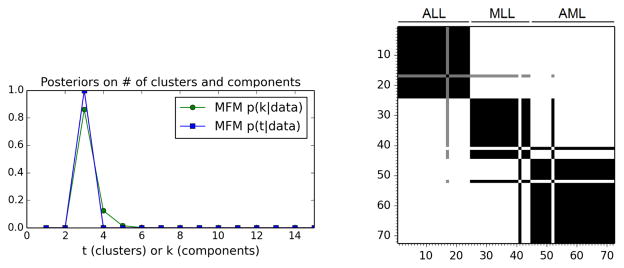
The posterior on the number of clusters t is concentrated at 3 (see Figure 3), in agreement with the division into ALL, MLL, and AML determined by Armstrong et al. (2001). The posterior on k is shifted slightly to the right because there are a small number of observations; this accounts for uncertainty regarding the possibility of additional components that were not observed in the given data.
Figure 3.
Results on the leukemia gene expression dataset. Left: Posteriors on the number of clusters and components. Right: Posterior similarity matrix. See the text for discussion.
Figure 3 also shows the posterior similarity matrix, that is, the matrix in which entry (i, j) is the posterior probability that data points i and j belong to the same cluster; in the figure, white is probability 0 and black is probability 1. The rows and columns of the matrix are ordered according to ground truth, such that 1–24 are ALL, 25–44 are MLL, and 45–72 are AML. The model has clearly separated the subjects into these three groups, with a small number of exceptions: subject 41 is clustered with the AML subjects instead of MLL, subject 52 with the MLL subjects instead of AML, and subject 17 is about 50% ALL and 50% MLL. Thus, the MFM has successfully clustered the subjects according to cancer subtype. This demonstrates the viability of our approach in high-dimensional settings.
7.3 Similarities and differences between MFMs and DPMs
In the preceding sections, we established that MFMs share many of the mathematical properties of DPMs. Here, we empirically compare MFMs and DPMs, using simulated data from a three-component bivariate Gaussian mixture. Our purpose is not to argue that either model should be preferred over the other, but simply to illustrate that in certain respects they are very similar, while in other respects they differ. In general, we would not say that either model is uniformly better than the other; rather, one should choose the model that is best suited to the application at hand—specifically, if one believes there to be infinitely many components, then an infinite mixture such as a DPM is more appropriate, while if one expects finitely many components, an MFM is likely to be a better choice. See Section A.1 for further discussion. For additional empirical analysis of MFMs versus DPMs, we refer to Green and Richardson (2001), who present different types of comparisons than we consider here.
7.3.1 Setup: data, model, and inference
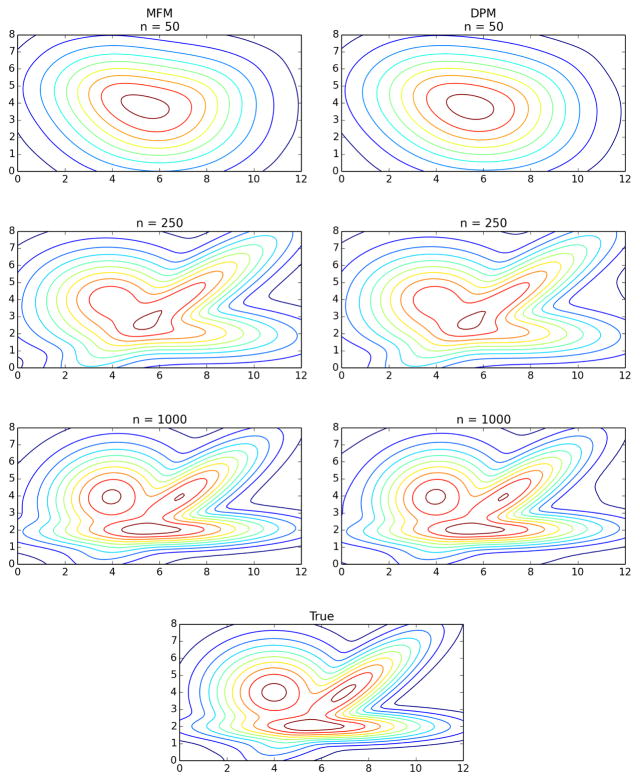
Consider the data distribution where w = (0.45, 0.3, 0.25), where with ρ = π/4, and . See Figure 4 (bottom).
Figure 4.
Density estimates for MFM (left) and DPM (right) on increasing amounts of data from the bivariate example (bottom). As n increases, the estimates appear to be converging to the true density, as expected.
For the model, we use multivariate normal component densities fθ(x) = fμ,Λ(x) = 𝒩(x|μ,Λ−1), and for the base measure H on θ = (μ, Λ), we take μ ~ 𝒩 (μ̂, Ĉ), Λ ~ Wishartd(V, ν) independently, where μ̂ is the sample mean, Ĉ is the sample covariance, ν = d = 2, and V = Ĉ −1/ν. Here, .
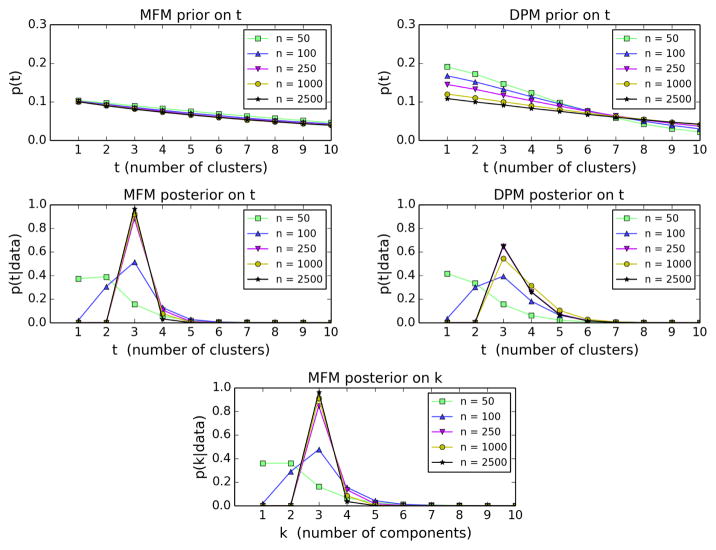
For the MFM, we take K ~ Geometric(0.1) and γ = 1. For the DPM, we put an Exponential(1) prior on the concentration parameter, α. This makes the priors on the number of clusters t roughly comparable for the range of n values considered below; see Figure 7.
Figure 7.
Prior and posterior on the number of clusters t for the MFM (left) and DPM (right), and the posterior on the number of components k for the MFM (bottom), on increasing amounts of data from the bivariate example. Each prior on t is approximated from 106 samples from the prior.
For both the MFM and DPM, we use the split-merge sampler of Jain and Neal (2007) for non-conjugate priors, coupled with Algorithm 8 of Neal (2000), as in Section 7.1.1. The same inference algorithm as in Section 7.1.1 is used, with the sole exception that in this case there is no hyperprior on the parameters of H. Gibbs updates to the DPM concentration parameter α are made using Metropolis–Hastings moves.
Five independent datasets were used for each n ∈ {50, 100, 250, 1000, 2500}, and for each model (MFM and DPM), the sampler was run for 5,000 burn-in iterations and 95,000 sample iterations (for a total of 100,000). Judging by traceplots and running averages of various statistics, this appeared to be sufficient for mixing. The cluster sizes were recorded after each iteration, and to reduce memory storage requirements, the full state of the chain was recorded only once every 100 iterations. For each run, the seed of the random number generator was initialized to the same value for both the MFM and DPM. The sampler used for these experiments took approximately 8 × 10−6 n seconds per iteration.
7.3.2 Density estimation
For certain nonparametric density estimation problems, both the DPM and MFM have been shown to exhibit posterior consistency at the minimax optimal rate, up to logarithmic factors (Kruijer et al., 2010; Ghosal and Van der Vaart, 2007). In fact, even for small sample sizes, we observe empirically that density estimates under the two models are remarkably similar; for example, see Figure 4. (See the supplementary material for details on computing the density estimates.) As the amount of data increases, the density estimates for both models appear to be converging to the true density, as expected. Indeed, Figure 5 indicates that the Hellinger distance between the estimated density and the true density is going to zero, and further, that the rate of convergence appears to be nearly identical for the DPM and the MFM. This suggests that for density estimation, the behavior of the two models seems to be essentially the same.
Figure 5.
Left: Hellinger distance between the estimated and true densities, for MFM (red, left) and DPM (blue, right) density estimates, on the bivariate example. Right: Bayes factors in favor of the MFM over the DPM. For each n ∈ {50, 100, 250, 1000, 2500}, five independent datasets of size n were used, and the lines connect the averages for each n.
On the other hand, Figure 5 shows that the Bayes factors p(x1:n|MFM)/p(x1:n|DPM) are increasing as n grows, indicating that the MFM is a better fit to this data than the DPM, in the sense that it has a higher marginal likelihood. This makes sense, since the MFM is correctly specified for data from a finite mixture, while the DPM is not. See Section A.2 for details on computing these Bayes factors.
7.3.3 Clustering
Frequently, mixture models are used for clustering and latent class discovery, rather than for density estimation. MFMs have a partition distribution that takes a very similar form to that of the Dirichlet process, as discussed in Section 3. Despite this similarity, the MFM partition distribution differs in two fundamental respects.
The prior on the number of clusters t is very different. In an MFM, one has complete control over the prior on the number of components k, which in turn provides control over the prior on t. Further, as the sample size n grows, the MFM prior on t converges to the prior on k. In contrast, in a Dirichlet process, the prior on t takes a particular parametric form and diverges at a log n rate.
Given t, the prior on the cluster sizes is very different. In an MFM, most of the prior mass is on partitions in which the sizes of the clusters are all the same order of magnitude, while in a Dirichlet process, most of the prior mass is on partitions in which the sizes vary widely, with a few large clusters and many very small clusters (see Section 5.3).
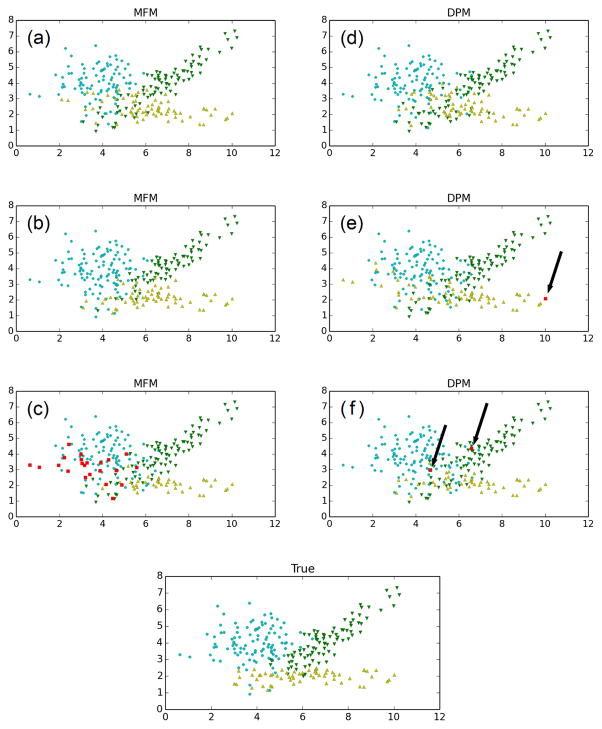
These prior differences carry over to noticeably different posterior clustering behavior. Figure 6 displays a few representative clusterings sampled from the posterior for the three-component bivariate Gaussian example. When n = 250, around 92% of the MFM samples look like (a) and (b), while around 2/3 of the DPM samples look like (d). Since the MFM is consistent for k, the proportion of MFM samples with three clusters tends to 100% as n increases, however, we do not expect this to occur for the DPM (see Section 7.3.4); indeed, when n = 2500, it is 98% for the MFM and still around 2/3 for the DPM. Many of the DPM samples have tiny “extra” clusters consisting of only a few points, as seen in Figure 6(e) and (f). Meanwhile, when the MFM samples have extra clusters, they tend to be large, as in (c). All of this is to be expected, due to items (1) and (2) above, along with the fact that these data are drawn from a finite mixture over the assumed family, and thus the MFM is correctly specified, while the DPM is not.
Figure 6.
Representative sample clusterings from the posterior for the MFM and DPM, on n = 250 data points from the bivariate example. The bottom plot shows the true component assignments. See discussion in the text. (Best viewed in color.)
7.3.4 Number of components and the mixing distribution
Assuming that the data are from a finite mixture, it is also sometimes of interest to infer the number of components or the mixing distribution, subject to the caveat that these inferences are meaningful only to the extent that the component distributions are correctly specified and the model is finite-mixture identifiable. (In the notation of Section 4.2, the mixing distribution is G, and we say the model is finite-mixture identifiable if for any discrete measures G, G′ supported on finitely-many points, fG = fG′ a.e. implies G = G′.) While Nguyen (2013) has shown that under certain conditions, DPMs are consistent for the mixing distribution (in the Wasserstein metric), Miller and Harrison (2013, 2014) have shown that the DPM posterior on the number of clusters is typically not consistent for the number of components, at least when the concentration parameter is fixed; the question remains open when using a prior on the concentration parameter, but we conjecture that it is still not consistent. On the other hand, MFMs are consistent for the mixing distribution and the number of components (for Lebesgue almost-all values of the true parameters) under very general conditions (Nobile, 1994); this is a straightforward consequence of Doob’s theorem. The relative ease with which this consistency can be established for MFMs is due to the fact that in an MFM, the parameter space is a countable union of finite-dimensional spaces, rather than an infinite-dimensional space.
These consistency/inconsistency properties are readily observed empirically—they are not simply large-sample phenomena. As seen in Figure 7, the tendency of DPM samples to have tiny extra clusters causes the number of clusters t to be somewhat inflated, apparently making the DPM posterior on t fail to concentrate, while the MFM posterior on t concentrates at the true value (by Section 5.2 and Nobile, 1994). In addition to the number of clusters t, the MFM also permits inference for the number of components k in a natural way (Figure 7), while in the DPM the number of components is always infinite. One might wonder whether the DPM would perform better if the data were drawn from a mixture with an additional one or two components with much smaller weight, however, this doesn’t seem to make a difference; see the supplementary material. On the other hand, on data from an infinite mixture, one would expect the DPM to perform better than the MFM. See the supplementary material for the formulas used to compute the posterior on k.
Although the MFM enables consistent inference for k in principle (Nobile, 1994), there are several issues that need to be carefully considered in practice; see Section A.3.
Supplementary Material
A Appendix
A.1 Examples where MFMs may be more suitable than DPMs
In many real-world situations, it is clear a priori that there is a finite (but unknown) number of components, due to the physics of the data generating process. In neural spike sorting, for instance, the observed spikes come from a mixture in which each spike is generated by one of many neurons/units, and “regardless of the number of putative spikes detected, the number of different single units one could conceivably discriminate from a single electrode is upper bounded due to the conductive properties of the tissue” (Carlson et al., 2014). In genetics, “a straightforward statistical genetics argument shows that the problem of haplotype inference can be formulated as a mixture model, where the set of mixture components corresponds to the pool of ancestor haplotypes, or founders, of the population… however, the size of this pool is unknown; indeed, knowing the size of the pool would correspond to knowing something significant about the genome and its history” (Xing et al., 2006). In cancer tumor phylogenetics, each datapoint corresponds to a locus in the genome, and the data come from a mixture of tumor cell populations within a single tissue sample. The number of cell populations (k) should not increase indefinitely as the number of loci assayed (n) grows (Landau et al., 2013).
Furthermore, the DPM is often mistakenly described in the literature as a mixture with a prior on the number of components, i.e., it is mistakenly described as an MFM. For instance, da Silva (2007) writes, “the DP mixture model is a Bayesian nonparametric methodology that relies on Markov chain Monte Carlo simulations for exploring mixture models with an unknown number of components.” Medvedovic and Sivaganesan (2002) write, “this [DPM] model does not require specifying the number of mixture components, and the obtained clustering is a result of averaging over all possible numbers of mixture components.” Xing et al. (2007) write, “methods for fitting the genotype mixture must crucially address the problem of estimating a mixture with an unknown number of mixture components… we present a Bayesian approach to this problem based on a nonparametric prior known as the Dirichlet process.” We suspect that in many such cases an MFM is a more natural model.
There are a variety of examples where researchers initially used an MFM, and later began using a DPM only because it was more computationally convenient. For instance, Tadesse et al. (2005) used MFMs with RJMCMC for a novel Bayesian variable selection method, but in follow-on work (Kim et al., 2006) they used DPMs because “with the Dirichlet process mixture models, the creation and deletion of clusters is naturally taken care of in the process of updating the sample allocations.” Meanwhile, in some cases, researchers have attempted to force DPMs to behave more like MFMs by choosing the DPM concentration parameter as a function of n to prevent the number of clusters from growing with n (Landau et al., 2013). With our new MFM algorithms, researchers need not default to DPMs for computational considerations; they can use the model that is best suited to the application at hand.
A.2 Computing Bayes factors for MFM versus DPM
In principle, the Bayes factor for the MFM versus the DPM could be used as an empirical criterion for choosing between the two models, and in fact, it is quite easy to compute an approximation to the Bayes factor using importance sampling. However, at this time we are not comfortable with using this as a method for choosing between MFM and DPM because when n is small, this Bayes factor can be sensitive to the choice of hyperparameters, and when n is large, the importance sampling approximation might have high variance since the two partition distributions could be concentrating in different regions of the space. Nonetheless, we include the details of the calculation here, since it may be of interest.
Given a pair of partition distributions f(C) = f̃(C)/Zf and g(C) = g̃(C)/Zg with common support, importance sampling can be used to approximate the ratio of normalization constants: where C1,…, CN ~ g. In particular, if f̃(C) = p(x1:n|C)pMFM(C) and g̃(C) = p(x1:n|C)pDP(C), then f is the MFM posterior and g is the DPM posterior, and we can use samples C1, …, CN from g to approximate the Bayes factor in favor of the MFM over the DPM:
where we have used the fact that f̃(C)/g̃(C) = pMFM(C)/pDP(C) since the likelihood p(x1:n|C) is the same in the MFM and the DPM. This approximation to the Bayes factor is easy to compute using the output of an MCMC sampler for the DPM, since all we need to do is compute the ratio of the prior probabilities pMFM(Ci)/pDP(Ci) for each partition Ci sampled from the DPM posterior. Alternatively, one could use the output of an MCMC sampler for the MFM, by swapping the roles of the DPM and the MFM throughout.
A.3 Issues with estimating the number of components
Due to the fact that inference for the number of components is a topic of high interest in many communities, it seems prudent to make some cautionary remarks in this regard. Many approaches have been proposed for estimating the number of components (Henna, 1985; Keribin, 2000; Leroux, 1992; Ishwaran et al., 2001; James et al., 2001; Henna, 2005; Woo and Sriram, 2006, 2007). In theory, the MFM model provides a Bayesian approach to consistently estimating the number of components, making it a potentially attractive method of assessing the heterogeneity of the data. However, there are several possible pitfalls to consider, some of which are more obvious than others.
An obvious potential issue is that in many applications, the clusters which one wishes to distinguish are purely notional (for example, perhaps, clusters of images or documents), and a mixture model is used for practical purposes, rather than because the data are actually thought to arise from a mixture. Clearly, in such cases, inference for the “true” number of components is meaningless. On the other hand, in some applications, the data definitely come from a mixture (for example, extracellular recordings of multiple neurons), so there is in reality a true number of components, although usually the form of the mixture components is far from clear.
More subtle issues are that the posteriors on k and t can be (1) strongly affected by the base measure H, and (2) sensitive to misspecification of the family of component distributions {fθ}. Issue (1) can be seen, for instance, in the case of normal mixtures: it might seem desirable to choose the prior on the component means to have large variance in order to be less informative, however, this causes the posteriors on k and t to favor smaller values (Richardson and Green, 1997; Stephens, 2000; Jasra et al., 2005). The basic mechanism at play here is the same as in the Bartlett–Lindley paradox, and shows up in many Bayesian model selection problems. With some care, this issue can be dealt with by varying the base measure H and observing the effect on the posterior—that is, by performing a sensitivity analysis—for instance, see Richardson and Green (1997).
Issue (2) is more serious. In practice, we typically cannot expect our choice of {fθ: θ ∈ Θ} to contain the true component densities (assuming the data are even from a mixture). When the model is misspecified in this way, the posteriors of k and t can be severely affected and depend strongly on n. For instance, if the model uses Gaussian components, and the true data distribution is not a finite mixture of Gaussians, then the posteriors of k and t can be expected to diverge to infinity as n increases. Consequently, the effects of misspecification need to be carefully considered if these posteriors are to be used as measures of heterogeneity. Steps toward addressing the issue of robustness have been taken by Woo and Sriram (2006, 2007) and Rodríguez and Walker (2014), however, this is an important problem demanding further study.
Despite these issues, sample clusterings and estimates of the number of components or clusters can provide a useful tool for exploring complex datasets, particularly in the case of high-dimensional data that cannot easily be visualized. It should always be borne in mind, though, that the results can only be interpreted as being correct to the extent that the model assumptions are correct.
Footnotes
Currently available at http://www.maths.bris.ac.uk/~peter/Nmix/.
Contributor Information
Jeffrey W. Miller, Department of Biostatistics, Harvard University.
Matthew T. Harrison, Division of Applied Mathematics, Brown University
References
- Aldous DJ. Exchangeability and related topics. Springer; 1985. [Google Scholar]
- Antoniak CE. Mixtures of Dirichlet processes with applications to Bayesian nonparametric problems. The Annals of Statistics. 1974;2(6):1152–1174. [Google Scholar]
- Armstrong SA, Staunton JE, Silverman LB, Pieters R, den Boer ML, Minden MD, Sallan SE, Lander ES, Golub TR, Korsmeyer SJ. MLL translocations specify a distinct gene expression profile that distinguishes a unique leukemia. Nature Genetics. 2001;30(1):41–47. doi: 10.1038/ng765. [DOI] [PubMed] [Google Scholar]
- Barry D, Hartigan JA. Product partition models for change point problems. The Annals of Statistics. 1992:260–279. [Google Scholar]
- Blackwell D, MacQueen JB. Ferguson distributions via Pólya urn schemes. The Annals of Statistics. 1973:353–355. [Google Scholar]
- Blei DM, Jordan MI. Variational inference for Dirichlet process mixtures. Bayesian Analysis. 2006;1(1):121–143. [Google Scholar]
- Blei DM, Ng AY, Jordan MI. Latent Dirichlet allocation. Journal of Machine Learning Research. 2003;3:993–1022. [Google Scholar]
- Broderick T, Jordan MI, Pitman J. Beta processes, stick-breaking and power laws. Bayesian Analysis. 2012;7(2):439–476. [Google Scholar]
- Brooks SP, Giudici P, Roberts GO. Efficient construction of reversible jump Markov chain Monte Carlo proposal distributions. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2003;65(1):3–39. [Google Scholar]
- Bush CA, MacEachern SN. A semiparametric Bayesian model for randomised block designs. Biometrika. 1996;83(2):275–285. [Google Scholar]
- Carlson DE, Vogelstein JT, Wu Q, Lian W, Zhou M, Stoetzner CR, Kipke D, Weber D, Dunson DB, Carin L. Multichannel electrophysiological spike sorting via joint dictionary learning and mixture modeling. IEEE Transactions on Biomedical Engineering. 2014;61(1):41–54. doi: 10.1109/TBME.2013.2275751. [DOI] [PubMed] [Google Scholar]
- Cerquetti A. Conditional α-diversity for exchangeable Gibbs partitions driven by the stable subordinator. 2011 arXiv:1105.0892. [Google Scholar]
- Cerquetti A. Marginals of multivariate Gibbs distributions with applications in Bayesian species sampling. Electronic Journal of Statistics. 2013;7:697–716. [Google Scholar]
- Chung Y, Dunson DB. Nonparametric Bayes conditional distribution modeling with variable selection. Journal of the American Statistical Association. 2009;104(488) doi: 10.1198/jasa.2009.tm08302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- da Silva ARF. A Dirichlet process mixture model for brain MRI tissue classification. Medical Image Analysis. 2007;11(2):169–182. doi: 10.1016/j.media.2006.12.002. [DOI] [PubMed] [Google Scholar]
- Dahl DB. An improved merge-split sampler for conjugate Dirichlet process mixture models. Technical Report, Department of Statistics, University of Wisconsin – Madison. 2003 [Google Scholar]
- Dahl DB. Sequentially-allocated merge-split sampler for conjugate and nonconjugate Dirichlet process mixture models. Journal of Computational and Graphical Statistics. 2005;11 [Google Scholar]
- Dahl DB. Modal clustering in a class of product partition models. Bayesian Analysis. 2009;4(2):243–264. [Google Scholar]
- de Souto MC, Costa IG, de Araujo DS, Ludermir TB, Schliep A. Clustering cancer gene expression data: a comparative study. BMC Bioinformatics. 2008;9(1):497. doi: 10.1186/1471-2105-9-497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dellaportas P, Papageorgiou I. Multivariate mixtures of normals with unknown number of components. Statistics and Computing. 2006;16(1):57–68. [Google Scholar]
- Dunson DB, Park JH. Kernel stick-breaking processes. Biometrika. 2008;95(2):307–323. doi: 10.1093/biomet/asn012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durrett R. Probability: Theory and Examples. Vol. 2. Cambridge University Press; 1996. [Google Scholar]
- Escobar MD, West M. Bayesian density estimation and inference using mixtures. Journal of the American Statistical Association. 1995;90(430):577–588. [Google Scholar]
- Favaro S, Lijoi A, Pruenster I. On the stick-breaking representation of normalized inverse Gaussian priors. Biometrika. 2012;99(3):663–674. [Google Scholar]
- Ferguson TS. A Bayesian analysis of some nonparametric problems. The Annals of Statistics. 1973:209–230. [Google Scholar]
- Ghosal S, Van der Vaart A. Posterior convergence rates of Dirichlet mixtures at smooth densities. The Annals of Statistics. 2007;35(2):697–723. [Google Scholar]
- Gnedin A. A species sampling model with finitely many types. Elect Comm Probab. 2010;15:79–88. [Google Scholar]
- Gnedin A, Pitman J. Exchangeable Gibbs partitions and Stirling triangles. Journal of Mathematical Sciences. 2006;138(3):5674–5685. [Google Scholar]
- Green PJ. Reversible jump Markov chain Monte Carlo computation and Bayesian model determination. Biometrika. 1995;82(4):711–732. [Google Scholar]
- Green PJ, Richardson S. Modeling heterogeneity with and without the Dirichlet process. Scandinavian Journal of Statistics. 2001 Jun;28(2):355–375. [Google Scholar]
- Griffin JE, Steel MJ. Order-based dependent Dirichlet processes. Journal of the American Statistical Association. 2006;101(473):179–194. [Google Scholar]
- Hansen B, Pitman J. Prediction rules for exchangeable sequences related to species sampling. Statistics & Probability Letters. 2000;46(3):251–256. [Google Scholar]
- Hartigan JA. Partition models. Communications in Statistics – Theory and Methods. 1990;19(8):2745–2756. [Google Scholar]
- Hastie DI, Green PJ. Model choice using reversible jump Markov chain Monte Carlo. Statistica Neerlandica. 2012;66(3):309–338. [Google Scholar]
- Henna J. On estimating of the number of constituents of a finite mixture of continuous distributions. Annals of the Institute of Statistical Mathematics. 1985;37(1):235–240. [Google Scholar]
- Henna J. Estimation of the number of components of finite mixtures of multivariate distributions. Annals of the Institute of Statistical Mathematics. 2005;57(4):655–664. [Google Scholar]
- Hjort NL. Technical Report. University of Oslo; 2000. Bayesian analysis for a generalised Dirichlet process prior. [Google Scholar]
- Ho M-W, James LF, Lau JW. Gibbs partitions (EPPF’s) derived from a stable subordinator are Fox H and Meijer G transforms. 2007 arXiv:0708.0619. [Google Scholar]
- Ishwaran H, James LF. Gibbs sampling methods for stick-breaking priors. Journal of the American Statistical Association. 2001;96(453) [Google Scholar]
- Ishwaran H, James LF. Generalized weighted Chinese restaurant processes for species sampling mixture models. Statistica Sinica. 2003;13(4):1211–1236. [Google Scholar]
- Ishwaran H, Zarepour M. Markov chain Monte Carlo in approximate Dirichlet and beta two-parameter process hierarchical models. Biometrika. 2000;87(2):371–390. [Google Scholar]
- Ishwaran H, James LF, Sun J. Bayesian model selection in finite mixtures by marginal density decompositions. Journal of the American Statistical Association. 2001;96(456) [Google Scholar]
- Jain S, Neal RM. A split-merge Markov chain Monte Carlo procedure for the Dirichlet process mixture model. Journal of Computational and Graphical Statistics. 2004;13(1) [Google Scholar]
- Jain S, Neal RM. Splitting and merging components of a nonconjugate Dirichlet process mixture model. Bayesian Analysis. 2007;2(3):445–472. [Google Scholar]
- James LF, Priebe CE, Marchette DJ. Consistent estimation of mixture complexity. The Annals of Statistics. 2001:1281–1296. [Google Scholar]
- Jasra A, Holmes C, Stephens D. Markov chain Monte Carlo methods and the label switching problem in Bayesian mixture modeling. Statistical Science. 2005:50–67. [Google Scholar]
- Kalli M, Griffin JE, Walker SG. Slice sampling mixture models. Statistics and Computing. 2011;21(1):93–105. [Google Scholar]
- Kass RE, Carlin BP, Gelman A, Neal RM. Markov chain Monte Carlo in practice: a roundtable discussion. The American Statistician. 1998;52(2):93–100. [Google Scholar]
- Keribin C. Consistent estimation of the order of mixture models. Sankhya Ser A. 2000;62(1):49–66. [Google Scholar]
- Kim S, Tadesse MG, Vannucci M. Variable selection in clustering via Dirichlet process mixture models. Biometrika. 2006;93(4):877–893. [Google Scholar]
- Kruijer W, Rousseau J, Van der Vaart A. Adaptive Bayesian density estimation with location-scale mixtures. Electronic Journal of Statistics. 2010;4:1225–1257. [Google Scholar]
- Landau DA, Carter SL, Stojanov P, McKenna A, Stevenson K, Lawrence MS, Sougnez C, Stewart C, Sivachenko A, Wang L, Wan Y, Zhang W, Shukla SA, Vartanov A, Fernandes SM, Saksena G, Cibulskis K, Tesar B, Gabriel S, Hacohen N, Meyerson M, Lander ES, Neuberg D, Brown JR, Getz G, Wu CJ. Evolution and impact of subclonal mutations in chronic lymphocytic leukemia. Cell. 2013;152(4):714–726. doi: 10.1016/j.cell.2013.01.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lau JW, Green PJ. Bayesian model-based clustering procedures. Journal of Computational and Graphical Statistics. 2007;16(3):526–558. [Google Scholar]
- Leroux BG. Consistent estimation of a mixing distribution. The Annals of Statistics. 1992;20(3):1350–1360. [Google Scholar]
- Lijoi A, Prünster I. Models beyond the Dirichlet process. Bayesian Nonparametrics. 2010;28:80. [Google Scholar]
- Lijoi A, Mena RH, Prünster I. Hierarchical mixture modeling with normalized inverse-Gaussian priors. Journal of the American Statistical Association. 2005;100(472):1278–1291. [Google Scholar]
- Lijoi A, Mena RH, Prünster I. Bayesian nonparametric estimation of the probability of discovering new species. Biometrika. 2007;94(4):769–786. [Google Scholar]
- Lijoi A, Prünster I, Walker SG. Bayesian nonparametric estimators derived from conditional Gibbs structures. The Annals of Applied Probability. 2008;18(4):1519–1547. [Google Scholar]
- Liu JS. The collapsed Gibbs sampler in Bayesian computations with applications to a gene regulation problem. Journal of the American Statistical Association. 1994;89(427):958–966. [Google Scholar]
- MacEachern SN. Estimating normal means with a conjugate style Dirichlet process prior. Communications in Statistics – Simulation and Computation. 1994;23(3):727–741. [Google Scholar]
- MacEachern SN. Practical nonparametric and semiparametric Bayesian statistics. Springer; 1998. Computational methods for mixture of Dirichlet process models; pp. 23–43. [Google Scholar]
- MacEachern SN. Dependent nonparametric processes. ASA Proceedings of the Section on Bayesian Statistical Science; 1999. pp. 50–55. [Google Scholar]
- MacEachern SN. Unpublished manuscript. Department of Statistics, The Ohio State University; 2000. Dependent Dirichlet processes. [Google Scholar]
- MacEachern SN, Müller P. Estimating mixture of Dirichlet process models. Journal of Computational and Graphical Statistics. 1998;7(2):223–238. [Google Scholar]
- Marrs AD. An application of reversible-jump MCMC to multivariate spherical Gaussian mixtures. Advances in Neural Information Processing Systems. 1998:577–583. [Google Scholar]
- McCullagh P, Yang J. How many clusters? Bayesian Analysis. 2008;3(1):101–120. [Google Scholar]
- McLachlan GJ, Bean RW, Peel D. A mixture model-based approach to the clustering of microarray expression data. Bioinformatics. 2002;18(3):413–422. doi: 10.1093/bioinformatics/18.3.413. [DOI] [PubMed] [Google Scholar]
- McNicholas PD, Murphy TB. Model-based clustering of microarray expression data via latent Gaussian mixture models. Bioinformatics. 2010;26(21):2705–2712. doi: 10.1093/bioinformatics/btq498. [DOI] [PubMed] [Google Scholar]
- Medvedovic M, Sivaganesan S. Bayesian infinite mixture model based clustering of gene expression profiles. Bioinformatics. 2002;18(9):1194–1206. doi: 10.1093/bioinformatics/18.9.1194. [DOI] [PubMed] [Google Scholar]
- Medvedovic M, Yeung KY, Bumgarner RE. Bayesian mixture model based clustering of replicated microarray data. Bioinformatics. 2004;20(8):1222–1232. doi: 10.1093/bioinformatics/bth068. [DOI] [PubMed] [Google Scholar]
- Miller JW, Harrison MT. A simple example of Dirichlet process mixture inconsistency for the number of components. Advances in Neural Information Processing Systems. 2013;26 [Google Scholar]
- Miller JW, Harrison MT. Inconsistency of Pitman–Yor process mixtures for the number of components. Journal of Machine Learning Research. 2014;15:3333–3370. [Google Scholar]
- Müller P, Quintana F. Random partition models with regression on covariates. Journal of Statistical Planning and Inference. 2010;140(10):2801–2808. doi: 10.1016/j.jspi.2010.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müller P, Quintana F, Rosner GL. A product partition model with regression on covariates. Journal of Computational and Graphical Statistics. 2011;20(1) doi: 10.1198/jcgs.2011.09066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neal RM. Maximum Entropy and Bayesian Methods. Springer; 1992. Bayesian mixture modeling; pp. 197–211. [Google Scholar]
- Neal RM. Markov chain sampling methods for Dirichlet process mixture models. Journal of Computational and Graphical Statistics. 2000;9(2):249–265. [Google Scholar]
- Nguyen XL. Convergence of latent mixing measures in finite and infinite mixture models. The Annals of Statistics. 2013;41(1):370–400. [Google Scholar]
- Nobile A. PhD thesis. Department of Statistics, Carnegie Mellon University; Pittsburgh, PA: 1994. Bayesian Analysis of Finite Mixture Distributions. [Google Scholar]
- Nobile A. Technical Report. Department of Statistics, University of Glasgow; 2005. Bayesian finite mixtures: a note on prior specification and posterior computation. [Google Scholar]
- Nobile A, Fearnside AT. Bayesian finite mixtures with an unknown number of components: The allocation sampler. Statistics and Computing. 2007;17(2):147–162. [Google Scholar]
- Pagel M, Meade A. A phylogenetic mixture model for detecting pattern-heterogeneity in gene sequence or character-state data. Systematic Biology. 2004;53(4):571–581. doi: 10.1080/10635150490468675. [DOI] [PubMed] [Google Scholar]
- Paisley JW, Zaas AK, Woods CW, Ginsburg GS, Carin L. A stick-breaking construction of the beta process. Proceedings of the 27th International Conference on Machine Learning; 2010. pp. 847–854. [Google Scholar]
- Papaspiliopoulos O, Roberts GO. Retrospective Markov chain Monte Carlo methods for Dirichlet process hierarchical models. Biometrika. 2008;95(1):169–186. [Google Scholar]
- Papastamoulis P, Iliopoulos G. An artificial allocations based solution to the label switching problem in Bayesian analysis of mixtures of distributions. Journal of Computational and Graphical Statistics. 2010;19(2):313–331. [Google Scholar]
- Park J-H, Dunson DB. Bayesian generalized product partition model. Statistica Sinica. 2010;20:1203–1226. [Google Scholar]
- Phillips DB, Smith AFM. Markov chain Monte Carlo in Practice. Springer; 1996. Bayesian model comparison via jump diffusions; pp. 215–239. [Google Scholar]
- Pitman J. Exchangeable and partially exchangeable random partitions. Probability Theory and Related Fields. 1995;102(2):145–158. [Google Scholar]
- Pitman J. Some developments of the Blackwell-MacQueen urn scheme. Lecture Notes- Monograph Series. 1996:245–267. [Google Scholar]
- Pitman J. Combinatorial Stochastic Processes. Springer–Verlag; Berlin: 2006. [Google Scholar]
- Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155(2):945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quintana FA, Iglesias PL. Bayesian clustering and product partition models. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2003;65(2):557–574. [Google Scholar]
- Rasmussen CE, de la Cruz BJ, Ghahramani Z, Wild DL. Modeling and visualizing uncertainty in gene expression clusters using Dirichlet process mixtures. IEEE/ACM Transactions on Computational Biology and Bioinformatics. 2009;6(4):615–628. doi: 10.1109/TCBB.2007.70269. [DOI] [PubMed] [Google Scholar]
- Reynolds DA, Quatieri TF, Dunn RB. Speaker verification using adapted Gaussian mixture models. Digital Signal Processing. 2000;10(1):19–41. [Google Scholar]
- Richardson S, Green PJ. On Bayesian analysis of mixtures with an unknown number of components. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 1997;59(4):731–792. [Google Scholar]
- Rodriguez A, Dunson DB. Nonparametric Bayesian models through probit stick-breaking processes. Bayesian Analysis. 2011;6(1) doi: 10.1214/11-BA605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodríguez CE, Walker SG. Univariate Bayesian nonparametric mixture modeling with unimodal kernels. Statistics and Computing. 2014;24(1):35–49. [Google Scholar]
- Roeder K. Density estimation with confidence sets exemplified by superclusters and voids in the galaxies. Journal of the American Statistical Association. 1990;85(411):617–624. [Google Scholar]
- Sethuraman J. A constructive definition of Dirichlet priors. Statistica Sinica. 1994;4:639–650. [Google Scholar]
- Sethuraman J, Tiwari RC. Technical Report. Department of Statistics, Florida State University; 1981. Convergence of Dirichlet measures and the interpretation of their parameter. [Google Scholar]
- Stauffer C, Grimson WEL. IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Vol. 2. IEEE; 1999. Adaptive background mixture models for real-time tracking. [Google Scholar]
- Stephens M. Bayesian analysis of mixture models with an unknown number of components—An alternative to reversible jump methods. The Annals of Statistics. 2000;28(1):40–74. [Google Scholar]
- Tadesse MG, Sha N, Vannucci M. Bayesian variable selection in clustering highdimensional data. Journal of the American Statistical Association. 2005;100(470):602–617. [Google Scholar]
- Teh YW, Görür D, Ghahramani Z. Stick-breaking construction for the Indian buffet process. International Conference on Artificial Intelligence and Statistics; 2007. pp. 556–563. [Google Scholar]
- Thibaux R, Jordan MI. Hierarchical beta processes and the Indian buffet process. International Conference on Artificial Intelligence and Statistics; 2007. pp. 564–571. [Google Scholar]
- Walker SG. Sampling the Dirichlet mixture model with slices. Communications in Statistics – Simulation and Computation. 2007;36(1):45–54. [Google Scholar]
- West M. ISDS Discussion Paper #92-A03. Duke University; 1992. Hyperparameter estimation in Dirichlet process mixture models. [Google Scholar]
- West M, Müller P, Escobar MD. Hierarchical priors and mixture models, with application in regression and density estimation. In: Freeman P, Smith AF, editors. Aspects of Uncertainty: A Tribute to DV Lindley. Wiley; 1994. pp. 363–386. [Google Scholar]
- Woo M-J, Sriram TN. Robust estimation of mixture complexity. Journal of the American Statistical Association. 2006;101(476) [Google Scholar]
- Woo MJ, Sriram TN. Robust estimation of mixture complexity for count data. Computational Statistics and Data Analysis. 2007;51(9):4379–4392. [Google Scholar]
- Xing EP, Sohn KA, Jordan MI, Teh YW. Bayesian multi-population haplotype inference via a hierarchical Dirichlet process mixture. Proceedings of the 23rd International Conference on Machine Learning; 2006. pp. 1049–1056. [Google Scholar]
- Xing EP, Jordan MI, Sharan R. Bayesian haplotype inference via the Dirichlet process. Journal of Computational Biology. 2007;14(3):267–284. doi: 10.1089/cmb.2006.0102. [DOI] [PubMed] [Google Scholar]
- Yeung KY, Fraley C, Murua A, Raftery AE, Ruzzo WL. Model-based clustering and data transformations for gene expression data. Bioinformatics. 2001;17(10):977–987. doi: 10.1093/bioinformatics/17.10.977. [DOI] [PubMed] [Google Scholar]
- Zhang Z, Chan KL, Wu Y, Chen C. Learning a multivariate Gaussian mixture model with the reversible jump MCMC algorithm. Statistics and Computing. 2004;14(4):343–355. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.