Spherical Caps in Cell Polarization

Abstract

Intracellular symmetry breaking plays a key role in wide range of biological processes, both in single cells and in multicellular organisms. An important class of symmetry-breaking mechanisms relies on the cytoplasm/membrane redistribution of proteins that can autocatalytically promote their own recruitment to the plasma membrane. We present an analytical construction and a comprehensive parametric analysis of stable localized patterns in a reaction-diffusion model of such a mechanism in a spherical cell. The constructed patterns take the form of high-concentration patches localized into spherical caps, similar to the patterns observed in the studies of symmetry breaking in single cells and early embryos.

Main Text

Many important processes in cell and developmental biology are controlled by highly nonuniform intracellular distributions of protein concentrations and enzymatic activities (1, 2). Examples include polarized patterns of membrane localization observed in studies of mating responses in yeast (3, 4, 5, 6, 7) and early embryogenesis in Caenorhabditis elegans (8, 9, 10). In both cases, patterns take the form of a localized cap on a cell membrane and play an instructive role, leading to the formation of a budding protrusion in yeast and asymmetric localization of cell determinants in the C. elegans embryo, respectively.

The formation of such cap-like patterns can rely on autocatalytic membrane recruitment of a diffusible cytoplasmic protein. The molecular and cellular bases for this mechanism have been established in several cases, motivating an impressive number of mathematical models that are being used to explore the quantitative requirements for the formation of robust localized patterns (5, 8, 11, 12, 13, 14, 15, 16, 17, 18). The simplest of such models has a single chemical species that interconverts between membrane and cytoplasmic states (13, 14, 17). One critical aspect is that self-promoted membrane recruitment can give rise to bistability, whereby the membrane can be in two states with very different levels of accumulated protein. This is the model considered in this Letter (Fig. 1).

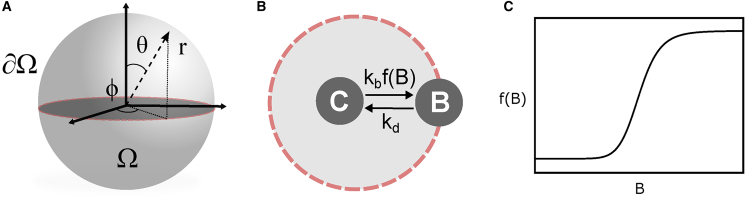
Figure 1.

(A) Schematic of a spherical cell. (B) The membrane association and dissociation processes are shown. (C) The function modeling the autocatalytic membrane recruitment is shown. To see this figure in color, go online.

In the system under consideration, the species with concentration C moves freely with diffusivity D_C in the cell interior and reversibly binds to the cell membrane. The cell interior and the membrane are denoted by Ω and ∂Ω, respectively. The dissociation-rate constant is denoted by k_d. The membrane-bound species, with surface density B, has diffusivity D_B and promotes its own recruitment to the membrane. This is described by making the forward-binding rate a sigmoidal function of protein concentration at the membrane. The binding rate is modeled as a sum of two terms: the first term describes constitutive binding; the second term reflects autocatalytic recruitment, which follows a Hill-like dependence. These are characterized by the rate constant k_b, constitutive rate β, threshold value Γ, and cooperativity parameter ν. The joint dynamics of the cytoplasmic and membrane species in a spherical cell of radius r is then governed by the following equations:

$$\frac{\partial B}{\partial t}=D_B{\mathit{\nabla }}_{r{\mathbb{S}}^2}^{2}B+k_b\left(\beta +\frac{B^{\nu }}{B^{\nu }+{\mathit{\Gamma }}^{\nu }}\right)C-k_{d}B,$$ (1)

$$\frac{\partial C}{\partial t}=D_C{\mathit{\nabla }}^{2}C,$$ (2)

and

$${D_C\left(\mathit{\nabla }C\cdot \hat{n}\right)|}_{r{\mathbb{S}}^2}=-k_b\left(\beta +\frac{B^v}{B^v+{\mathit{\Gamma }}^v}\right)C+k_{d}B.$$ (3)

In these equations, $\hat{n}$ is the outward unit normal to $\partial \mathit{\Omega }=r{\mathbb{S}}^2$, ${\mathit{\nabla }}^2$ is the spherical Laplacian in Ω, and ${\mathit{\nabla }}_{r{\mathbb{S}}^2}^2$ is the Laplace-Beltrami operator on ∂Ω:

$${\mathit{\nabla }}_{r{\mathbb{S}}^2}^2=\frac{1}{r^2\text{sin}\theta }\frac{\partial }{\partial \theta }\left(\text{sin}\theta \frac{\partial }{\partial \theta }\right)+\frac{1}{r^2{\text{sin}}^2\theta }\frac{{\partial }^2}{\partial {\varphi }^2},$$ (4)

where θ ∈ [0, π] and ϕ ∈ [0, 2π] are the angular variables of the standard spherical coordinates.

This model and many of its relatives considered in the context of cell polarization belong to a broad class of reaction-diffusion systems with spatially segregated compartments of different dimensionality (15, 18, 19, 20, 21, 22). In combination with diffusion on the membrane, autocatalytic membrane recruitment can result in the formation and progressive expansion of a domain with high membrane concentration (11, 13, 14, 15, 16, 17, 18, 19, 20, 23, 24). However, it is counteracted by total mass conservation and fast cytoplasmic diffusion (12, 13, 14). For a proper choice of model parameters, localized accumulation on the membrane depletes concentration in the cytoplasm and can stabilize the expanding domain, resulting in a stable pattern.

Because the total amount of protein in the system is constant, the membrane and bulk protein concentrations are globally coupled by mass conservation. Although the general phenomenology associated with the formation of localized patterns in globally coupled reaction-diffusion problems is well understood (19, 20, 23), the number of results in the context of intracellular symmetry breaking is very limited (4, 16, 24). In fact, all existing analytical results are limited to one-dimensional “cells” and are based on ad hoc descriptions of nonlocal coupling of membrane dynamics by cytoplasmic diffusion (12, 13, 14, 17, 25). Here, we report exact analytical solutions for the spherical cap patterns constructed in the regime of large cytoplasmic diffusion that properly take into account the three-dimensional geometry of the cell.

We start by considering the conservation equation for the total amount of a protein, which is not synthesized or degraded but only redistributed between cytoplasm and membrane (5, 12, 13):

$$\underset{\mathit{\Omega }}{\int }C\text{ d}V+\underset{\partial \mathit{\Omega }}{\int }B\text{ d}S=\frac{4}{3}\pi r^3{C}_0,$$ (5)

where C₀ is the total amount of protein in the cell divided by cell volume. Because cytoplasmic diffusivity is typically much larger than membrane diffusivity, the cytoplasmic concentration may be assumed to be uniform throughout the cell (see Supporting Materials and Methods for further discussion):

$$C=C_0-\frac{3}{4\pi r^3}\underset{\partial \text{Ω}}{\int }B\text{ d}S.$$ (6)

Upon substitution of this expression into Eq. 1, our model is reduced to a single equation for the membrane species (26). This equation is rendered dimensionless by the following transformations: $\tau \equiv k_{d}t$ and $u\equiv k_{d}B/\left(k_b{C}_0\right)$. This leads to the following problem for the spatiotemporal dynamics of the dimensionless cell surface concentration, u = u (θ, ϕ, τ):

$$\begin{array}{c}\frac{\partial u}{\partial \tau }={\delta }^2{\mathit{\nabla }}_{{\mathbb{S}}^2}^{2}u-u\\ +\left(1-\frac{\alpha }{2\pi }{\int }_0^{2\pi }{\int }_0^{\pi }u\text{sin}\theta \text{ d}\theta \text{ d}\varphi \right)\left(\beta +\frac{u^{\nu }}{u^{\nu }+{\gamma }^{\nu }}\right).\end{array}$$ (7)

The rescaled problem has five dimensionless groups: ν and β are inherited directly from the original model; $\gamma \equiv k_d\mathit{\Gamma }/\left(k_b{C}_0\right)$ is the dimensionless threshold for the membrane recruitment nonlinearity; ${\delta }^2\equiv D_B/\left(k_d{r}^2\right)$ is the ratio of characteristic times for dissociation from the membrane and surface diffusion; and finally, $\alpha \equiv 3k_b/\left(2k_{d}r\right)$ may be interpreted as the ratio of the maximal fluxes to and from the cell membrane and quantifies the strength of the global coupling essential for the formation of localized patterns.

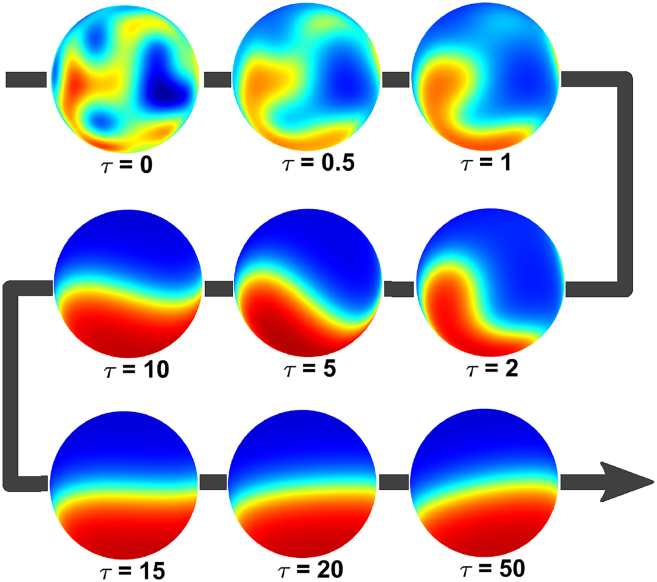
We started our analysis of this problem by solving it numerically using a spectral discretization implemented in the Chebfun package (27, 28). In all cases, the system converged to one of two types of behaviors: uniform steady state profiles and nonuniform axisymmetric cap-like patterns. Fig. 2 shows the snapshots from a representative numerical solution that eventually converges to such a pattern. Our numerical experiments indicate that such solitary caps, although placed at different locations on the surface, are the only spatially nonuniform attractors of Eq. 7.

Figure 2.

Snapshots of cell surface concentration from a representative numerical solution of Eq. 7 with α = 1, β = 0.1, γ = 0.3, δ² = 0.05, and ν = 20. To see this figure in color, go online.

The axial symmetry of the cap-like patterns allows us to reduce the dimensionality of the problem. Without loss of generality, we may place the cap center at the North Pole of the sphere and focus only on the ϕ-independent solutions. Furthermore, when the membrane-recruitment nonlinearity is sharp $\left(\nu \gg 1\right)$, it can be approximated by the Heaviside function. Using a common coordinate transformation, η = −cosθ ∈ [−1,1], we obtain the following ordinary differential equation for the axially symmetric steady state solution $u=\overline{u}\left(\eta \right)$:

$${\delta }^2\frac{d}{d\eta }\left[\left(1-{\eta }^2\right)\frac{d\overline{u}}{d\eta }\right]=\overline{u}-\left(1-\alpha {\int }_{-1}^1\overline{u}\text{ d}\eta \right)\left(\beta +H\left(\overline{u}-\gamma \right)\right).$$ (8)

This equation is piecewise linear, which greatly simplifies the analysis of localized patterns. One can readily check that this equation may have at most two spatially uniform stable steady states, in which the membrane concentration is either above or below the threshold value:

$$u_{-}=\frac{\beta }{1+2\alpha \beta }\mathrm{and}{u}_{+}=\frac{1+\beta }{1+2\alpha \left(1+\beta \right)}.$$

In addition to these uniform steady states, we found patterned solutions that correspond to spherical caps. In constructing these solutions, we assumed that they decrease monotonically from η = −1 to η = 1, crossing the threshold at some value of the longitudinal coordinate: $\overline{u}\left({\eta }_c\right)=\gamma$. In other words, the autocatalytic membrane recruitment is “on” for η < η_c and “off” for η > η_c. As shown in the Supporting Material, such steady states can be found analytically in terms of the Legendre function P_μ(η), where $\mu =\left(1/2\right)\left(\sqrt{1-4{\delta }^{-2}}-1\right)$:

$$\overline{u}\left(\eta >{\eta }_c\right)=\left(\gamma -\beta k\right)\frac{P_{\mu }\left(\eta \right)}{P_{\mu }\left({\eta }_c\right)}+\beta k$$ (9)

and

$$\overline{u}\left(\eta <{\eta }_c\right)=\left(\gamma -\left(1+\beta \right)k\right)\frac{P_{\mu }\left(-\eta \right)}{P_{\mu }\left(-{\eta }_c\right)}+\left(1+\beta \right)k,$$ (10)

where

$$k=\frac{\gamma \left(1+\frac{P_{\mu }^{\prime }\left({\eta }_c\right)}{P_{\mu }^{\prime }\left(-{\eta }_c\right)}\frac{P_{\mu }\left(-{\eta }_c\right)}{P_{\mu }\left({\eta }_c\right)}\right)}{1+\beta \left(1+\frac{P_{\mu }^{\prime }\left({\eta }_c\right)}{P_{\mu }^{\prime }\left(-{\eta }_c\right)}\frac{P_{\mu }\left(-{\eta }_c\right)}{P_{\mu }\left({\eta }_c\right)}\right)}.$$

To evaluate these expressions, one must find the position η_c where $\overline{u}\left({\eta }_c\right)=\gamma$. This position can be found from the dimensionless form of the conservation law for the total amount of protein, leading to the following implicit function that relates η_c to the dimensionless parameters of the problem:

$$\gamma =\frac{1+\beta \left(1+\frac{P_{\mu }^{\prime }\left({\eta }_c\right)}{P_{\mu }^{\prime }\left(-{\eta }_c\right)}\frac{P_{\mu }\left(-{\eta }_c\right)}{P_{\mu }\left({\eta }_c\right)}\right)}{\left(1+\frac{P_{\mu }^{\prime }\left({\eta }_c\right)}{P_{\mu }^{\prime }\left(-{\eta }_c\right)}\frac{P_{\mu }\left(-{\eta }_c\right)}{P_{\mu }\left({\eta }_c\right)}\right)\left(1+\alpha \left(1+{\eta }_c\right)+2\alpha \beta \right)}.$$ (11)

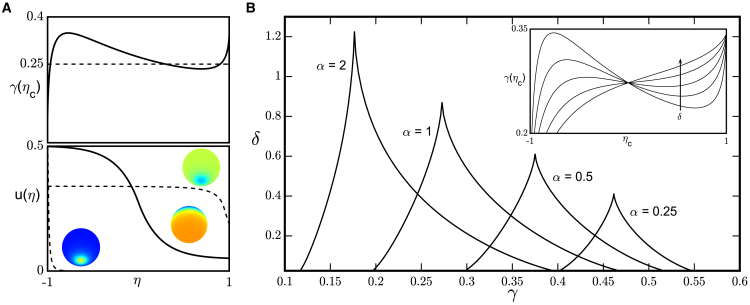
Graphical analysis of this equation reveals that it can have up to three roots, corresponding to three different values of η_c for which $\overline{u}\left({\eta }_c\right)=\gamma$ (Fig. 3). Each of these values gives rise to a different spatially nonuniform steady state. In particular, in the biologically significant regime of $\delta \ll 1$, there exists one solution in the form of a large spherical cap, for which

$$\gamma \left({\eta }_c\right)\simeq \frac{2\beta +1}{2\left(1+\alpha \left(2\beta +1+{\eta }_c\right)\right)},$$ (12)

Figure 3.

(A) Construction of spatially nonuniform steady states. The graphical solution of Eq. 11, for α = 1, β = 0.1, γ = 0.25, and δ = 0.3, reveals three roots (top panel), giving rise to three different spatial profiles (bottom panel). (B) Two-dimensional cuts through the four-dimensional domain of model parameters that support the formation of stable localized patterns for β = 0.1 are shown. The boundaries of the cusps correspond to the extrema of the γ(η_c) function; this function becomes monotonic at the tip of the cusp (inset). Here, the inset shows γ(η_c) for β = 0.1, α = 1, and δ = {0.1, 0.25, 0.5, 1, 2}. To see this figure in color, go online.

and two small spherical cap solutions, for which $\sqrt{1-{\eta }_c^2}\sim \delta$ whenever $\gamma \in \left(\frac{2\beta +1}{2\left(1+2\alpha \left(\beta +1\right)\right)},\frac{2\beta +1}{2\left(1+2\alpha \beta \right)}\right)$. Stability analysis of these solutions (see Supporting Materials and Methods) shows that for $\delta \ll 1$, a spherical cap solution is stable if and only if α >α_c, where

$${\alpha }_c\simeq \frac{\delta }{2\left(2\beta +1\right){\left(1-{\eta }_c^2\right)}^{3/2}}.$$ (13)

According to this formula, for all δ sufficiently small and γ in the above range, the small-cap solutions are linearly unstable, whereas the large cap is linearly stable. We note that, as expected, the stable solutions constructed analytically above persist in the problem with ν finite, even for ν ≈ 5.

Equation 11 may be used to delineate the four-dimensional domain of parameters α, β, γ, and δ that can support states with broken symmetry. Fig. 3 shows a series of two-dimensional cuts through this domain, computed at a constant value of constitutive membrane recruitment and four different strengths of the global coupling parameter. For each of these cuts, the localized patterns exist in a cusp-like region that is characterized by an upper limit for dimensionless surface diffusivity δ. Beyond this value, the right-hand side of Eq. 11 becomes a single-valued function of γ_c (see the inset of Fig. 3 B), which corresponds to the disappearance of stable patterns. Our analysis also reveals how reducing the strength of global coupling moves the system outside of the domain corresponding to the symmetry-broken stable steady states.

Our results provide insights into the parametric dependence and robustness of the localized patterns. For instance, changes in the cell radius affect two dimensionless groups: the dimensionless-cell-surface diffusivity, δ ∼ 1/r, and the strength of global coupling, α ∼ 1/r. Because the existence of patterned states is promoted by small values of surface diffusivity and strong global coupling, patterned states are realized for an intermediate range of cell sizes (see Fig. S2).

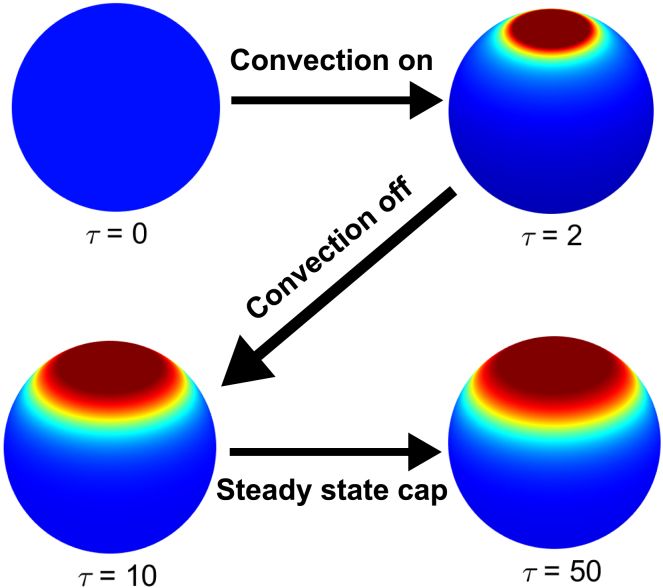
Further research is required to understand how cells can not only form the localized patterns but also direct them to specific positions. Studies in the early C. elegans embryo suggest that such control may be provided by cortical flows that transiently localize the diffusible species at a specific location on the cell membrane (1, 8, 10). Our model can be readily modified to account for such flows. As an illustration, Fig. 4 shows the results of a numerical experiment in which a model cell starts from a steady state in which most of the protein is cytoplasmic. A transient unidirectional flow then creates a region of high membrane concentration, triggering the formation of a self-sustained localized pattern.

Figure 4.

Directed control of pattern formation by a transient unidirectional flow. The system starts from a uniform “off” steady state. The flow is from the South to North Pole. α = 1, β = 0.1, γ = 0.35, and δ² = 0.05. See the Supporting Materials and Methods for details. To see this figure in color, go online.

An additional layer of control may be provided by variations in the curvature of the cell surface. Our preliminary simulations in spheroid geometries indicate that large spherical cap solutions persist under perturbations of spherical symmetry but at the same time are guided to specific locations by variations of curvature. Analyzing the effects of such variations, which can be either static or dynamic, should provide additional insights into the mechanisms of intracellular symmetry breaking (1, 2).

Author Contributions

S.Y.S. and C.B.M. designed the research. C.B.M. and R.D. performed analytical and numerical studies. H.M. provided software and numerical analysis.

Editor: Anatoly Kolomeisky.

Supporting Citations

References (29, 30, 31, 32, 33, 34, 35, 36) appear in the Supporting Material.