TraceSpecks: A Software for Automated Idealization of Noisy Patch-Clamp and Imaging Data

Abstract

Experimental records of single molecules or ion channels from fluorescence microscopy and patch-clamp electrophysiology often include high-frequency noise and baseline fluctuations that are not generated by the system under investigation and have to be removed. Moreover, multiple channels or conductance levels can be present at a time in the data that need to be quantified to accurately understand the behavior of the system. Manual procedures for removing these fluctuations and extracting conducting states or multiple channels are laborious, prone to subjective bias, and likely to hinder the processing of often very large data sets. We introduce a maximal likelihood formalism for separating signal from a noisy and drifting background such as fluorescence traces from imaging of elementary ${\text{Ca}}^{2+}$ release events called puffs arising from clusters of channels, and patch-clamp recordings of ion channels. Parameters such as the number of open channels or conducting states, noise level, and background signal can all be optimized using the expectation-maximization algorithm. We implement our algorithm following the Baum-Welch approach to expectation-maximization in the portable Java language with a user-friendly graphical interface and test the algorithm on both synthetic and experimental data from the patch-clamp electrophysiology of ${\text{Ca}}^{2+}$ channels and fluorescence microscopy of a cluster of ${\text{Ca}}^{2+}$ channels and ${\text{Ca}}^{2+}$ channels with multiple conductance levels. The resulting software is accurate, fast, and provides detailed information usually not available through manual analysis. Options for visual inspection of the raw and processed data with key parameters are provided, in addition to a range of statistics such as the mean open probabilities, mean open times, mean close times, dwell-time distributions for different number of channels open or conductance levels, amplitude distribution of all opening events, and number of transitions between different number of open channels or conducting levels in asci format with a single click.

Introduction

Recent advances in total internal reflection fluorescence microscopy (TIRFM) provide a powerful tool for the functional study of thousands of ${\text{Ca}}^{2+}$ release channels simultaneously at single channel resolution in a minimally invasive manner, maintaining the physiological environment of the channels (1, 2, 3). This technique, called “optical patch-clamp,” has been used to study ${\text{Ca}}^{2+}$ flux through several individual channels, including N-type voltage-gated ${\text{Ca}}^{2+}$ channels (1, 4, 5), nicotinic acetylcholine receptors (2, 5), and L-type ${\text{Ca}}^{2+}$ channels in cardiac muscle (5). Optical patch-clamp was also used to resolve the quantal substructure of elementary ${\text{Ca}}^{2+}$ puffs and sparklets arising from concerted opening of multiple channels in a cluster of inositol 1,4,5-trisphosphate $\left({\text{IP}}_3\right)$ receptors $\left({\text{IP}}_3\text{R}\text{s}\right)$ and dihydropyridine-sensitive voltage-gated ${\text{Ca}}_{\text{V}}1.2$ channels, respectively, by directly resolving the opening and closing of individual channels in the cluster (6, 7). Recently, the same technique was employed to resolve the conductance levels in a single ion channel while simultaneously imaging thousands of ${\text{Ca}}^{2+}$-permeable plasma membrane (PM) pores formed by β-amyloid $\left(\text{A}{\beta }_{1-42}\right)$ in the cells with Alzheimer’s disease pathology (8, 9).

Optical patch-clamp generates thousands of time traces representing the gating of individual channels in a single experiment. However, manual analysis of the data generated is extremely tedious and challenging, which hinders the full utility of this powerful technique. The analysis of fluorescence traces from single channels with single or multiple conductance levels or concerted opening of multiple channels in a cluster of channels (such as ${\text{IP}}_3\text{R}\text{s}$, ryanodine receptors, and dihydropyridine-sensitive voltage-gated ${\text{Ca}}_{\text{V}}1.2$ channels) obtained from TIRFM requires the removal of background noise and baseline fluctuations in the data records that are not generated by the channels under study. These fluctuations could arise either from the saturation of dye molecules or the drift in measuring equipment itself. Because the data are expected to exhibit quantized steps, the signal and the data (and possibly the noise) have significant autocorrelation times; simple filtering may not yield a clear separation of signal from background and may fail to make use of the known quantal character of the data.

A similar situation arises when using other techniques such as single-channel patch-clamp and single-molecule fluorescence and photobleaching experiments, where analysis of the experimental data first requires the removal of noise and varying background that are not generated by the phenomenon under study (10, 11, 12, 13, 14, 15). In the patch-clamp experiments (16), instabilities in the gigaohm seal formed between the biological membrane patch and the patch-clamp microelectrode often result in substantial fluctuations in the magnitude of the observed current and a drift in the recorded signal. Such baseline fluctuations are usually significantly slower than the abrupt changes in current magnitude caused by opening and closing of the channel and have to be removed before the current traces can be analyzed further by standardized software such as Quantifying Unknown Biophysics (QUB) (17, 18) and Hawkes, Jalali & Colquhoun Fit (HJCFIT) (19) that model the channel gating characteristics based on idealized data.

Existing baseline subtraction algorithms can require substantial time and/or user interaction on ion channel data, as the program forces users to check each individual fit by eye. Without a robust baseline subtraction algorithm, some experimentalists perform this laborious task by hand by following the quantal jumps by eye and subtracting the drifting background. Such a manual background-subtraction procedure requires eyeballing and mouse clicking to indicate the background trajectory, which is time-consuming and susceptible to subjective bias. Although QUB provides three different methods for automated background subtraction, it could over- or underestimate the signal in situations in which the drift is significant. In such a scenario, one can resort to manually selecting the baseline, which can be subjective and time-consuming. Another source of subjectivity arises when the conductance levels are not clearly defined because the user has to specify the number of conductance levels or channels present in the trace and amplitude of each conductance level. Such examples are also frequently observed in the fluorescence traces.

To overcome these obstacles, we previously developed a minimally parameterized likelihood (20) approach for separating the signal from noisy and drifting background, which gives results that agree with the mouse-based method and is much faster (21). However, the requirement to compile and execute the algorithm for processing the data proved to be a major hurdle for experimentalists not familiar with compiled languages. Although the main goal of this study was to extend the algorithm so that it can be used for both patch-clamp electrophysiology and fluorescence data, we develop a user-friendly graphical user interface (GUI) that is easy to use, flexible, and portable. Furthermore, we incorporate several new features in the software that were not included in the previous version. In addition to extracting idealized trace and drifting background, the software extracts many features from the data, including the mean open probabilities (P_O); open times $\left({\tau }_O\right)$; close times $\left({\tau }_C\right)$; dwell-time distributions for different conductance levels or number of open channels; overall P_O, ${\tau }_O$, and ${\tau }_C$ in the trace; amplitude distribution of all events; and transition frequencies between different conductance levels or channels open with a few simple steps. We demonstrate the utility of our software by processing patch-clamp data containing single and multiple channels per trace, fluorescence traces from TIRFM representing ${\text{Ca}}^{2+}$ signals generated by concerted opening and closing of several channels in a cluster of ${\text{IP}}_3\text{R}\text{s}$, and fluorescence traces representing the ${\text{Ca}}^{2+}$ flux through PM pores with multiple conductance levels, formed by $\text{A}{\beta }_{1-42}$ oligomers associated with Alzheimer’s disease pathology.

We would like to point out that TraceSpecks is not a substitute for QUB, HJCFIT, or other similar algorithms (14, 22, 23). It is rather a front-end application that we believe will enhance the utility of these programs, enabling them to model the kinetics of ion channels and single molecules when the time traces are either more challenging or recorded in native environment through tools such as fluorescence microscopy. Furthermore, the source code included with the software provides an opportunity to customize TraceSpecks according to personal preferences.

Methods

In this section, we first outline the main points of the algorithm (detailed derivation of the algorithm can be found in (21)) followed by details of how we generate synthetic records representing patch-clamp electrophysiology of a single ion channel with varying signal-to-noise ratio (SNR) as well as synthetic fluorescence traces representing the concerted opening and closing of multiple channels in a cluster of ${\text{IP}}_3\text{R}\text{s}$. A brief description of sample experimental methods and the data used to demonstrate the utility of the software are also given toward the end of this section.

Theory

We use the expectation-maximization (EM) algorithm to estimate the number of open channels or conductance levels, which are treated as missing data. The EM algorithm was originally developed by Baum, Welch et al. in the 1960s and formalized by Dempster et al. (24, 25, 26, 27). Readers interested only in using the software can safely skip this part and move to the user manual included in the online supplement. Readers interested in reproducing the algorithm in another programing language (note that Java source code is included in the online supplement and that Fortran 90 and C versions are available from the authors upon request) can move to the three steps summarizing the algorithm at the end of this section. Those interested in understanding the theory behind the software and modifying the algorithm should read this section and (21) for more details.

Assuming that $n_t$ is the number of channels open or the conductance level in which the channel is gating and that i is the current passing through the channel at time t, the observed signal at time t is given by $d_t$ = $b_t$ + i$n_t$ + ${\sigma }_{\xi }{\xi }_t$, where ${\xi }_t$ is the zero-mean discrete-time Gaussian white noise and ${\sigma }_{\xi }$ is the level of noise. We further assume that the baseline is undergoing a discrete-time random walk, $b_t$ = $b_{t-1}$ + ${\sigma }_b{\tilde{\xi }}_t$, where ${\tilde{\xi }}_t$ is the discrete-time white noise like ${\xi }_t$. Under these assumptions, it follows that $d_t-b_t$ + i$n_t$ and $b_t-b_{t-1}$ are zero-mean Gaussian-distributed random variables with variances ${\sigma }_{\xi }^2$ and ${\sigma }_b^2$, respectively.

The joint distribution for d, b, and n is given as

$$p\left(d,b,n;\theta \right)=\mathcal{N}{e}^{-\mathcal{H}\left(d,b,n;\theta \right)}.$$ (1)

$\mathcal{H}$ is given by

$$\mathcal{H}\left(d,b,n;\theta \right)=\frac{1}{2{\sigma }_b^2}\sum _{t=1}^{T-1}{\left(b_{t+1}-b_t\right)}^2+\frac{1}{2{\sigma }_{\xi }^2}\sum _{t=1}^T{\left(d_t-b_t-i{n}_t\right)}^2,$$ (2)

where T is the number of data points, $d=\left(d_1,d_2,\dots \mathrm{..},d_T\right)$, $b=\left(b_1,b_2,\dots \mathrm{..},b_T\right)$, $n=\left(n_1,n_2,\dots \mathrm{..},n_T\right)$, and θ represents the parameters ${\sigma }_{\xi }^2$, ${\sigma }_b^2$, and i. $\mathcal{N}$ is the normalization factor:

$$\mathcal{N}=\frac{1}{{\sum }_n\int e^{-\mathcal{H}\left(d,b,n,\theta \right)}dddb}.$$ (3)

${\sum }_n\equiv {\sum }_{n_1=0}^{N_{ch}}{\sum }_{n_2=0}^{N_{ch}}\dots {\sum }_{n_T=0}^{N_{ch}}$, and $N_{ch}$ is an upper bound on the number of channels contained in the trace (number of channels patched or number of channels in a cluster of channels). For a single ion channel (or molecule) with multiple equally spaced conductance levels, $N_{ch}$ represents the total number of conductance levels that the system can have, where the closed state of the channel is represented by level 0. $dd$ and $db$ represent the differentials of all the variables being integrated over, e.g., $db={\prod }_{t=1}^{T}d{b}_t$. In principle, we would like to maximize the likelihood of the data given the model, $L\left(d;\theta \right)$, as follows:

$$L\left(d;\theta \right)\equiv \sum _n\underset{b}{\int }p\left(d,b,n;\theta \right)db,$$ (4)

but this is unwieldy. Although the integral over T dimensions can be dealt with, the sum is over at least $2^T$ values and cannot be maximized in one step. Thus, we employ the iterative EM procedure that attempts to find the maximal likelihood estimate of L by first making an initial guess for $\theta =\tilde{\theta }$ and then iterating the following steps:

$$Q\left({\theta }^{\prime },\tilde{\theta }\right)={\langle \text{log}p\left(d,b,n;{\theta }^{\prime }\right)\rangle }_{p\left(b,n|d;\tilde{\theta }\right)}$$ (5)

$$\theta =\underset{{\theta }^{\prime }}{\text{argmax}}Q\left({\theta }^{\prime },\tilde{\theta }\right)$$

$$\tilde{\theta }=\theta .$$

In the above, ${\langle \text{log}p\left(d,b,n;{\theta }^{\prime }\right)\rangle }_{p\left(b,n|d;\tilde{\theta }\right)}$ denotes the expectation of $\text{log}p\left(d,b,n;{\theta }^{\prime }\right)$ with respect to the distribution $p\left(b,n|d;\tilde{\theta }\right)$. The EM iteration is known to converge to, at worst, a local maximal likelihood estimate for $L\left(d|\theta \right)$.

Because of the simple dependence that the likelihood function has on b, we can integrate b out and then employ a slightly modified version of the EM algorithm to solve the remaining maximal likelihood problem (see (21) for the derivation), as follows:

$$p\left(d,n;\theta ,b^{\text{∗}}\right)\equiv \int p\left(d,b,n;\theta \right)\prod _{t=1}^{T}d{b}_t=\mathcal{N}\int e^{-\mathcal{H}\left(d,b,n;\theta \right)}\prod _{t=1}^{T}d{b}_t=\mathcal{N}{e}^{-\mathcal{H}\left(d,b^{\text{∗}},n;\theta \right)}$$ (6)

where $b^{\text{∗}}$ is the maximal likelihood estimate of b found by minimizing $\mathcal{H}$,

$$-\frac{\partial \mathcal{H}}{\partial b}{|}_{b=b^{\text{∗}}}=\frac{1}{{\sigma }_b^2}\mathit{\Delta }{b}^{\text{∗}}+\frac{1}{{\sigma }_{\xi }^2}\left(d-b^{\text{∗}}-in\right)=0,$$

and $\mathit{\Delta }$ is the finite difference Laplacian: $\mathit{\Delta }{b}_t\equiv b_{t+1}+b_{t-1}-2b_t$. Thus,

$$b^{\text{∗}}\left(d,n,\theta \right)={\left(-\mathit{\Delta }+R^2\right)}^{-1}\left(d-in\right),$$ (7)

where $R^2={\sigma }_b^2/{\sigma }_{\xi }^2$. As written, $b^{\text{∗}}$ in the argument of $p\left(d,n;\theta ,b^{\text{∗}}\right)$ in Eq. 6 is redundant because $b^{\text{∗}}$ is a known function of d, n, and θ. The reason we have employed this seemingly redundant notation is just to make clear in the algorithm which value of $b^{\text{∗}}$ (old or updated) we used to compute the current expected values of n.

The normalization constant $\mathcal{N}$ is given by (see (21) for the derivation)

$$\mathcal{N}\approx \frac{1}{{\left(1+N_{ch}\right)}^T}{\left(\frac{1}{2\pi }\right)}^{T/2-1/2}{\left(\frac{1}{{\sigma }_{\xi }^2}\right)}^{T/2-1/2}\frac{2^{T/2}R}{{\left(2+R^2+\sqrt{R^4+4R^2}\right)}^{T/2}}.$$ (8)

The distribution $p\left(b,n|d;\tilde{\theta }\right)$ needed for Q in Eq. 5 becomes $p\left(n|d,\tilde{\theta },{\tilde{b}}^{\text{∗}}\right)$ after integrating out b. Here, ${\tilde{b}}^{\text{∗}}$ is the initial guess for the background signal. To find $p\left(n|d,\tilde{\theta },{\tilde{b}}^{\text{∗}}\right)$, we note that in general, $p\left(x|y\right)=p\left(x,y\right)/p\left(y\right)$. Thus,

$$p\left(n|d,\tilde{\theta },{\tilde{b}}^{\text{∗}}\right)=\frac{p\left(d,n;\tilde{\theta },{\tilde{b}}^{\text{∗}}\right)}{{\sum }_{n}p\left(d,n;\tilde{\theta },{\tilde{b}}^{\text{∗}}\right)}=\frac{e^{-\mathcal{H}\left(d,{\tilde{b}}^{\text{∗}},n;\tilde{\theta }\right)}}{{\sum }_n{e}^{-\mathcal{H}\left(d,{\tilde{b}}^{\text{∗}},n;\tilde{\theta }\right)}}=\prod _{t=1}^{T}p\left(n_t|d_t,\tilde{\theta },t\right).$$ (9)

The quantity $p\left(n_t|d_t,\tilde{\theta },t\right)$ is the conditional probability that there are $n_t$ channels open at a single time point t. To simplify the notation, we write $p\left(j|d_t,\tilde{\theta },t\right)$ to indicate the conditional probability that there are j channels open at time t:

$$p\left(j|d_t,\tilde{\theta },t\right)=\frac{\text{exp}\left(-\frac{{\left(d_t-{\tilde{b}}_t^{\text{∗}}-\tilde{i}j\right)}^2}{{\tilde{\sigma }}_{\xi }^2}\right)}{{\sum }_{k=0}^{N_{ch}}\text{exp}\left(-\frac{{\left(d_t-{\tilde{b}}_t^{\text{∗}}-\tilde{i}k\right)}^2}{{\tilde{\sigma }}_{\xi }^2}\right)}=\frac{1}{{\sum }_{k=0}^{N_{ch}}{e}^{{\eta }_{jt}-{\eta }_{kt}}},$$ (10)

where ${\eta }_{mt}\equiv {\left(d_t-{\tilde{b}}_t^{\text{∗}}-m\tilde{i}\right)}^2/2{\tilde{\sigma }}_{\xi }^2$ and $m=\mathrm{0,1,2,3},\dots N_{ch}$. We will use angle brackets without subscripts to denote expectations with respect to $p\left(j|d_t,\tilde{\theta },t\right)$ so that

$$\langle n_t^s\rangle \equiv \sum _{j=0}^{N_{ch}}{j}^{s}p\left(j|d_t,\tilde{\theta },t\right).$$ (11)

For a single channel or single-molecule recording, $N_{ch}=1$, and Eq. 11 results in $\langle n_t\rangle =1/e^{{\eta }_{1t}-{\eta }_{0t}}+1$.

At this point we can write Q explicitly:

$$Q\left(\theta ,\tilde{\theta }\right)=\text{log}\mathcal{N}-\frac{1}{2{\sigma }_b^2}\sum _{t=1}^{T-1}{\left(b_{t+1}^{\text{∗}}-b_t^{\text{∗}}\right)}^2-\frac{1}{2{\sigma }_{\xi }^2}\sum _{t=1}^T\langle {\left(d_t-b_t^{\text{∗}}-i{n}_t\right)}^2\rangle .$$ (12)

The dependence on $\tilde{\theta }$ is only through $b^{\text{∗}}$ and the angle brackets. The end result of this calculation is that we replace the dependence in $\mathcal{H}$ on powers of $n_t$ with the expected value of those powers: $n_t\to \langle n_t\rangle$ and $n_t^2\to \langle n_t^2\rangle$. We maximize $Q\left(\theta ,\tilde{\theta }\right)$ by updating θ iteratively in the following steps.

• Step 0: (Initialization) Make initial guess for ${\tilde{b}}_t^{\text{∗}},{\sigma }_{\xi }^2,i$, and $R^2$: $\tilde{\theta }=\left({\sigma }_{\xi }^2,i,R^2\right)$.

• Step I: (Estimate or Expectation) Update the expected values of $n_t$ and $n_t^2$ with respect to $p\left(j|d_t,\theta ,t\right)$, which we will denote as $\langle n_t\rangle$ and $\langle n_t^2\rangle$:

$$\langle n_t^s\rangle =\sum _{j=0}^{N_{ch}}{j}^{s}p\left(j|d_t,\theta ,t\right).$$ (13)

At the end of this step, $n_t$ and $n_t^2$ in $\mathcal{H}$ will be replaced by $\langle n_t\rangle$ and $\langle n_t^2\rangle$, respectively.

• Step II: (Maximize).

Update baseline signal

$$b^{\text{∗}}={\left(-\mathit{\Delta }+{\tilde{R}}^2\right)}^{-1}\left(d-\tilde{i}\langle n\rangle \right)$$

We obtain $b^{\text{∗}}$ with a standard tridiagonal matrix solver, which is very fast. Note the dependence in $b^{\text{∗}}$ is on $\tilde{\theta }$ rather than on θ. In steps B, C, and D, we update the parameters i, ${\sigma }_{\xi }^2$, and $R^2$ while keeping $b^{\text{∗}}$ fixed.

Update i

The derivative of Q with respect to i is

$$\frac{\partial Q}{\partial i}=\frac{1}{{\sigma }_{\xi }^2}\sum _{t=1}^T\left(\langle n_t\rangle \left(d_t-b_t^{\text{∗}}\right)-i\langle n_t^2\rangle \right).$$

To maximize Q with respect to i, we set the above equation to zero, which yields

$$i=\frac{{\sum }_{t=1}^T\left(d_t-b_t^{\text{∗}}\right)\langle n_t\rangle }{{\sum }_{t=1}^T\langle n_t^2\rangle }.$$

Update ${\sigma }_{\xi }^2$

The derivative of Q with respect to $1/{\sigma }_{\xi }^2$ is

$$\frac{\partial Q}{\partial \frac{1}{{\sigma }_{\xi }^2}}=\frac{T{\sigma }_{\xi }^2}{2}-\frac{1}{2R^2}\sum _{t=1}^T{\left(b_t^{\text{∗}}-b_{t-1}^{\text{∗}}\right)}^2-\frac{1}{2}\sum _{t=1}^T\left({\left(d_t-b_t^{\text{∗}}\right)}^2-2\left(d_t-b_t^{\text{∗}}\right)i\langle n_t\rangle +i^2\langle n_t^2\rangle \right)$$

To maximize Q with respect to ${\sigma }_{\xi }^2$, we set the above equation to zero, which yields

$${\sigma }_{\xi }^2=\frac{1}{T}(\frac{1}{R^2}\sum _{t=1}^T{\left(b_t^{\text{∗}}-b_{t-1}^{\text{∗}}\right)}^2+\sum _{t=1}^T\left({\left(d_t-b_t^{\text{∗}}\right)}^2-2\left(d_t-b_t^{\text{∗}}\right)i\langle n_t\rangle +i^2\langle n_t^2\rangle \right).$$ (14)

Update $R^2$

The derivative of Q with respect to $R^2$ is $\partial Q/\partial R^2=\left(\mathcal{B}/2{\sigma }_{\xi }^2{R}^4\right)-T\left(1+\left(2+R^2/\sqrt{4R^2+R^4}\right)/2+R^2+\sqrt{4R^2+R^4}\right)$, where $\mathcal{B}\equiv {\sum }_{t=1}^{T-1}{\left(b_{t+1}^{\text{∗}}-b_t^{\text{∗}}\right)}^2$. The updated $R^2$ is the single real positive root of $\partial Q/\partial R^2=0$. At this point, $\tilde{\theta }=\left({\sigma }_{\xi }^2,i,R^2\right)$.

Return to step I

To summarize, we iterate the steps described above in the order of step 0 $\to$ step I $\to$ step II $\to$ step I. In the E step, we compute the $N_{ch}$ expectation values of $n_t$ for each t, and in the M step, we update the parameters based on maximizing Q in Eq. 6.

The algorithm is implemented in widely portable Java language in a user-friendly GUI with options to set up initial parameters and graphical display of raw and processed traces. Options to store statistics on the processed data are provided, including mean P_O, ${\tau }_O$, ${\tau }_C$, dwell-time distributions for different conductance levels, or number of open channels for the processed trace. Information regarding the amplitude distribution of all opening events as well as the frequency of transitions between different numbers of open channels or conductance levels are also provided. An example of algorithm’s GUI is shown in Fig. 1. A compiled and portable Java program with the GUI that performs these calculations and the user manual for the software is provided in the online supplement. A Java source code is also included in the online supplement for those interested in customizing the software for their personal use. Fortran 90 and C versions of the software are also available from the authors on request.

Figure 1.

Graphical user interface of TraceSpecks. Various controls for reading, displaying, and saving data sets are provided. Text controls are used to provide input parameters for the algorithm as well as displaying the optimal parameters and results determined by the algorithm. Raw trace, background noise signal, and idealized signals can be viewed in the graphical panel of the GUI for visual inspection and can be zoomed in and out as needed. To see this figure in color, go online.

We remark that TraceSpecks suggests initial values for the four parameters (i, ${\sigma }_{\xi }^2$, $R^2$, and background) based on the nature of the data. In our experience, the software gives good results for fluorescence traces when the initial parameter values suggested by the algorithm are used. However, these are mere suggestions and might result in over- or underestimation of the channel’s activity. We recommend selecting different initial values if the user is not satisfied with the results. We noticed that sometimes the results can be improved by playing with the initial values of the BackgroundFactor (the raw data multiplied by BackgroundFactor gives the initial background) and Current (i) in the case of patch-clamp data. This is the rare weakness of the algorithm, as it requires some intuition about the data. However, by playing with these parameters for a few minutes or running the algorithm at command line (see user manual provided in the online supplement), one gets a good idea for the initial values. Furthermore, the fact that the algorithm allows the initial values to be relatively crude makes this initial phase easier.

Data records

We apply our method to synthetic and experimental data sets from both TIRFM experiments and patch-clamp recordings. Our synthetic data sets comprise two examples, one representing patch-clamp experiments with variable SNR and another one mimicking fluorescence traces from a cluster of ${\text{IP}}_3\text{R}\text{s}$ (28). The experimental data set consists of nuclear patch-clamp recordings from ${\text{IP}}_3$ in Sf9 cells (29), fluorescence recordings from ${\text{IP}}_3$-induced ${\text{Ca}}^{2+}$ puffs (30), and Aβ-induced ${\text{Ca}}^{2+}$-permeable PM pores (8) in Xenopus oocytes.

Synthetic data sets. Details of patch-clamp synthetic data generation can be found in our previous article (21). Briefly, we use 10,000 open and closed events with the duration of these events drawn randomly from a uniform distribution. The range of distribution for closed events is five times that of open events. A channel’s P_O is controlled by varying the range of the distribution from which the closed time is drawn. We construct background signal b_t = ${\text{b}}_{t-1}$ + ${\sigma }_b{\tilde{\xi }}_t$ to get final simulated channel trace d_t = b_t + i n_t + ${\sigma }_{\xi }{\xi }_t$, where ${\tilde{\xi }}_t$ and ${\xi }_t$ are zero-mean Gaussian noise with deviations ${\sigma }_b$ and ${\sigma }_{\xi }$, respectively. In addition to background and signal noise, channel current i is also treated as a normal random variable of mean $\langle i\rangle$ and deviation ${\sigma }_{\xi }$. n_t is the number of channels open at time t, which is 0 or 1 for the current case but can be higher for the synthetic data of multichannel/multiconductance levels. Although we only use white noise here, the algorithm handles data with correlated noise equally well. We refer readers interested in a detailed discussion on the treatment of correlated noise by the algorithm to (21).

To test the robustness and accuracy of the software toward noise levels present in the experimental data, we generated single-channel synthetic patch-clamp data with SNRs ranging from 2.1 to 12.6, as described below.

As mentioned above, there are two noise sources in our model, ${\xi }_t$ and ${\tilde{\xi }}_t$:

$${\text{SNR}}_{\xi }\equiv \frac{i}{{\sigma }_{\xi }}$$ (15)

$${\text{SNR}}_{\text{b}}\equiv \frac{i}{{\sigma }_b\sqrt{max\left(N_O,N_C\right)}}$$ (16)

$$SNR=\frac{i}{{\sigma }_{\xi }}\sqrt{\frac{1}{1+R^{2}max\left(N_O,N_C\right)}},$$ (17)

where $N_O$ and $N_C$ are the mean number of sampling intervals for open and closed events, respectively. ${\text{SNR}}_{\xi }$ is a standard SNR. ${\text{SNR}}_{\text{b}}$ indicates how much the baseline drifts relative to the current during the average open or closed event. $SNR$ is the combined SNR: $SNR=\sqrt{SN{R}_{\xi }^2+SN{R}_b^2}$. Using ${\sigma }_{\xi }^2=5$ and ${\sigma }_b^2=2$, we vary mean current i from 20 to 120 (arbitrary current units) to get an SNR from 2.1 to 12.6.

We also process fluorescence data from a simulated cluster composed of 10 ${\text{IP}}_3\text{R}$ ${\text{Ca}}^{2+}$ channels. Details about simulating a single cluster have been published before (28, 31, 32). Briefly, channels were arranged in a two-dimensional array on a patch of endoplasmic reticulum (ER) membrane with an interchannel spacing of $120\mathrm{nm}$. The gating of each channel is given by a four-state Markov chain model with rest (R), active (A), open (O), and inactivate (I) states connected in a loop (Fig. 2 of (28)). The channel is open when in state O and closed otherwise. The state of each channel was determined by using a stochastic scheme outlined in (33).

${\text{Ca}}^{2+}$ concentration on the cytosolic side of the cluster was controlled by diffusion, flux through ${\text{IP}}_3\text{R}\text{s}$, free stationary buffers, mobile buffers, and imaging dye. We considered slow mobile buffer mimicking EGTA. The propagation of ${\text{Ca}}^{2+}$ and buffers was solved implicitly using the Laplacian of ${\text{Ca}}^{2+}$ and buffers in spherical coordinates on a hemispherical volume of radius $5\mu \mathrm{m}$ and a spatial grid size of $5\mathrm{nm}$. We estimated the fluorescence changes $\left(\mathit{\Delta }F/F_0\right)$ from TIRFM by following the procedure in (34, 35), i.e.,

$$\mathit{\Delta }F/F_0=\sum _j\int \int \int dxdydz{b}_d^{\text{∗}j}\left(r_j\left(x,y,z\right)\right)$$

$$\times \left(-\frac{{\left(x-x_0\right)}^2}{{\sigma }_x^2}-\frac{{\left(y-y_0\right)}^2}{{\sigma }_y^2}\right)exp\left(-\frac{z}{{\gamma }_z}\right),$$ (18)

where $b_d^{\text{∗}j}$ is the ${\text{Ca}}^{2+}$-bound dye at distance $r_j\left(x,y,z\right)$ due to ${\text{Ca}}^{2+}$ released by the $j^{th}$ channel at $x_0=0,y_0=0$, ${\sigma }_x^2={\sigma }_y^2=0.0225\mu m^2$, and ${\gamma }_z=0.15\mu m$. The integration in Eq. 18 was performed over a cubic volume of $1.5\times 1.5\times 0.15\mu \mathrm{m}$. To make the simulated TIRFM signal as close to the experiment as possible, we added experimental noise and drifting background extracted from TIRFM of puff sites in Xenopus oocytes to the simulated fluorescence data.

Experimental data sets

Experimental traces of current passing through single ${\text{IP}}_3\text{R}$ channels, which are ubiquitous intracellular ${\text{Ca}}^{2+}$-release channels localized mainly to the ER and outer nuclear membranes (36), were acquired by nuclear patch-clamp electrophysiology, as described in (29, 37, 38). Currents passing through outer nuclear membrane patches isolated at the tips of micropipettes were amplified using an Axopatch 200B patch-clamp amplifier (Molecular Devices, Sunnyvale, CA) and filtered either at 1 kHz using a tunable low-pass four-pole Bessel filter (Frequency Devices, Ottawa, IL) or at 5 or 10 KHz using the internal tunable low-pass four-pole Bessel filter of the Axopatch amplifier. The current signals were digitized at 5 kHz using an ITC16 interface (HEKA Instruments, Bellmore, NY) and recorded directly onto a data acquisition computer using the Pulse + PulseFit software (HEKA Instruments).

Full details of TIRFM experiments on ${\text{IP}}_3$-induced puffs are given in (30). Briefly, records of ${\text{IP}}_3$-induced puffs were obtained from ${\text{Ca}}^{2+}$ imaging of Xenopus laevis oocytes at room temperature by widefield epifluorescence microscopy using an Olympus inverted microscope (IX 71) equipped with a $60\times$oil-immersion objective, a 488 nm argon ion laser for fluorescence excitation, and a charge-coupled device camera (Cascade 128+; Roper Scientific, Vianen, the Netherlands) for imaging fluorescence emission (510–600 nm) at frame rates of 30–100 $s^{-1}$. Fluorescence was imaged within a 40$\times$ 40 μm region within the animal hemisphere of the oocyte, and measurements are expressed as a ratio $\left(\mathit{\Delta }\text{F}/{\text{F}}_0\right)$ of the mean change in fluorescence ($\mathit{\Delta }$F) at a given region of interest $\left(1.5\times 1.5\mu \mathrm{m}\right)$ centered on the putative ${\text{IP}}_3\text{R}$ cluster to the resting fluorescence at that region before stimulation $\left({\text{F}}_0\right)$. Mean values of ${\text{F}}_0$ were obtained by averaging over several frames before stimulation. MetaMorph (Molecular Devices) was used for preliminary image processing. Fluorescence traces representing ${\text{Ca}}^{2+}$ release events due to channel gating in the cluster were extracted from the image sequences using a previously developed software called CellSpecks that can detect all ${\text{Ca}}^{2+}$ events in a video sequence recorded from a cell’s membrane and extracts fluorescence time traces for individual clusters. Further details about CellSpecks can be found in (8).

Detailed experimental methods for imaging the activity of PM pores formed by $\text{A}{\beta }_{1-42}$ oligomers are given in (8). Briefly, solution containing soluble oligomers prepared from human recombinant Aβ_1-42 peptide and aliquots were applied using a glass pipette with a tip diameter of ∼30 μm to voltage-clamped oocytes of defolliculated stage VI Xenopus treated with fluo-4 dextran. For imaging, oocytes were placed animal hemisphere down in a chamber whose bottom is formed by a fresh ethanol-washed microscope cover glass (type-545-M; Thermo Fisher Scientific, Waltham, MA) and were bathed in Ringer solution (110 mM NaCl, 1.8 mM CaCl2, 2 mM KCl, and 5 mM Hepes (pH 7.2)) at room temperature (∼23°C) continually exchanged at a rate of ∼0.5 mL/min by a gravity-fed superfusion system. The membrane potential was clamped at a holding potential of 0 mV using a two-electrode voltage clamp (Gene Clamp 500; Molecular Devices) and was stepped to a more negative potential of −100 mV when imaging ${\text{Ca}}^{2+}$ flux through amyloid pores to increase the driving force for ${\text{Ca}}^{2+}$ entry into the cytosol. The video sequences generated by TIRFM were processed by CellSpecks to extract fluorescence traces for individual $\text{A}{\beta }_{1-42}$ pores.

Results and Discussion

We use TraceSpecks to idealize experimental time traces from patch-clamp experiments with single and multiple channels in the patch, TIRFM of ${\text{Ca}}^{2+}$ puffs generated by clusters of ${\text{IP}}_3\text{R}\text{s}$, fluorescence traces representing the gating of ${\text{Ca}}^{2+}$-permeable pores formed by $\text{A}{\beta }_{1-42}$ oligomers in the PM, simulated TIRFM signals from a cluster of ${\text{IP}}_3\text{R}$ channels, and synthetic patch-clamp data with variable SNR. In this section, we first demonstrate the robustness and accuracy of our software using synthetic data with variable SNR and then apply it to other data sets mentioned above.

Before presenting our results, we would like to point out that the software uses two different schemes for reporting the dwell-time distributions, mean P_O, ${\tau }_O$, and ${\tau }_C$ for different conductance levels or number of open channels in the trace as shown in Fig. 2. Although we only present the dwell-time distributions and other statistics from the first scheme (Fig. 2 a) in the article, TraceSpecks saves the results from both schemes in ascii format in separate files.

Figure 2.

TraceSpecks uses two schemes for calculating open and closed dwell times. As an example, we show an idealized trace with three channels/open conductance levels. (a) In scheme 1, ${\text{t}}_{\text{oij}}$ and ${\text{t}}_{\text{cij}}$ represent the ${\text{j}}^{\text{th}}$ dwell time when a minimum of i channels are open (or the channel is gating in conductance level i or above) and the ${\text{j}}^{\text{th}}$ dwell time when a minimum of i channels are not open, respectively. (b) In scheme 2, ${\text{t}}_{\text{oij}}$ represents the ${\text{j}}^{\text{th}}$ dwell time when i channels are open (or the channel is gating in conductance level i), and ${\text{t}}_{\text{c}1\text{j}}$ represents the ${\text{j}}^{\text{th}}$ dwell time when no channel is open (or the channel is in closed level). To see this figure in color, go online.

Synthetic data

As described in Methods, using ${\sigma }_{\xi }^2=5$ and ${\sigma }_b^2=2$ and varying mean current i from 20 to 120 (arbitrary units), we have generated synthetic data sets with SNRs ranging from 2.1 to 12.6. As shown in Fig. 3, TraceSpecks idealized these noisy synthetic patch-clamp traces with drifting and variable background and accurately determined various parameters of interest for almost all values of SNR. A sample noisy trace with the background separated by the software and the idealized trace are shown in Fig. 3, a and c, respectively. We also show the actual trace without the noise and background for comparison in Fig. 3 b. We repeat this experiment for many traces with varying SNRs, estimate different features, and compare these estimates with the actual values of these features. In Fig. 3, d–f, we show the mean-square error for ${\tau }_O$, ${\tau }_C$, and P_O. Even for SNR as small as 2.1, the estimates for these parameters are very good. It is worth mentioning that the SNR in TIRFM experiments is close to 8 (39), whereas that for the patch-clamp electrophysiology is even higher (40). TraceSpecks extracts the exact values for different parameters of interest for traces with SNRs of five or above (Fig. 3, d–f).

Figure 3.

Processing synthetic patch-clamp data with variable SNR of 2.1–12.6. (a) Sample raw trace is shown with noisy and drifting background (dashed line) and background separated by TraceSpecks (solid line), (b) actual trace, and (c) idealized trace. Mean-square errors are shown for mean ${\tau }_O$ (d), mean ${\tau }_C$ (e), and mean P_O (f). To see this figure in color, go online.

Application to fluorescence data from a simulated cluster composed of 10 ${\text{IP}}_3\text{R}$ channels demonstrates (Fig. 4 a, dashed line) that the software works well for multichannel data too. The drifting background separated from the signal by the software is shown by the solid line in Fig. 4 a. The idealized signal representing the expected number of open channels in the cluster at time t is shown in Fig. 4 b. For simulations shown in Fig. 4 a, we also recorded the number of open channels in the cluster that are shown in Fig. 4 c for comparison. It is clear from Fig. 4, b and c that the processed signal closely compares with the actual number of open channels. It should be noted that our method also reports ${\tau }_O$, ${\tau }_C$, and P_O as well as the dwell-time distributions for different numbers of open channels and interchannel transitions (transition from X number of channels open to Y number of channels open at a time t, where Y can be less than or larger than X) for the given trace (data not shown).

Figure 4.

Processing simulated puffs. (a) A noisy and drifting fluorescence time series is generated by a simulated single ${\text{IP}}_3\text{R}$ cluster with added background extracted from the raw experimental data (dashed line) and the drifting background estimated by the software (solid line). (b) Idealized signal is generated by the software. (c) Number of open channels in the cluster as a function of time from simulation is shown for comparison.

Experimental data

In this section, we demonstrate the application of our method to fluorescence time traces representing ${\text{IP}}_3$-induced ${\text{Ca}}^{2+}$ puffs by ${\text{IP}}_3\text{R}$ clusters in the ER membrane and the gating of PM pores formed by $\text{A}{\beta }_{1-42}$ oligomers, both observed through TIRFM in Xenopus oocytes as well as traces from nuclear patch-clamp electrophysiology of ${\text{IP}}_3\text{R}\text{s}$ in Sf9 cells with single and multiple channels per patch.

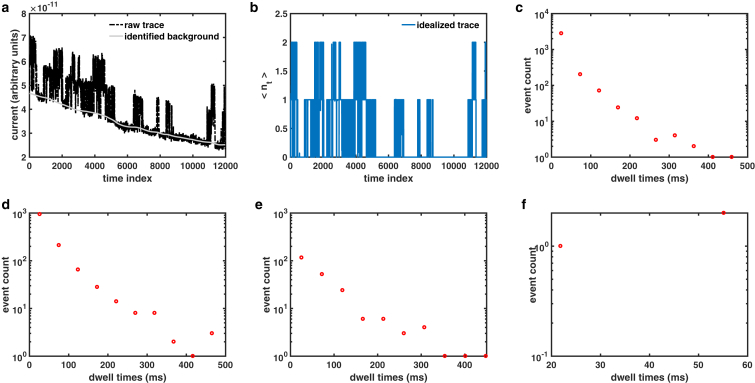
First, we idealize traces from nuclear patch-clamp electrophysiology of ${\text{IP}}_3\text{R}\text{s}$. Although the method works equally well for traces with a single channel per patch (see for example Fig. 3), we only show slightly complex examples of multiple channels per patch. A summary of eight traces with two to four channels per patch is shown in Fig. 5 and Table 1. A sample raw trace with two channels along with the separated background and idealized trace identified by the algorithm is shown in Fig. 5, a and b, respectively. Dwell-time distributions when at least one, two, three, or four channels are open in all eight traces are shown in Fig. 5, c–e, respectively. Our method also provides mean ${\text{P}}_{Oi}$, ${\tau }_{Oi}$, and ${\tau }_{Ci}$ for at least i channels open for the eight traces (Table 1). For example, ${\text{P}}_{O1}$ and ${\tau }_{O1}$ are the mean probability and mean open time that at least one channel is open. Similarly, ${\tau }_{C1}$ is the mean time when none of the channels are open (a minimum of one channel is not open), and ${\tau }_{C2}$ is the mean time when either one or zero channels are open (a minimum of two channels are not open).

Figure 5.

Processing current time traces that record the gating of ${\text{IP}}_3\text{R}$ channels during single-channel patch-clamp electrophysiological experiments using nuclei isolated from Sf9 cells. (a) A typical raw current trace (black) in which two channels were active and the background leak current level (gray) were identified by our software. (b) The number of open channels at any time during the experiment in (a) is shown. Dwell-time distributions when at least one (c), two (d), three (e), or four (f) channels are open in all eight traces processed are shown. To see this figure in color, go online.

Table 1.

Channel Statistics for Eight Traces from Nuclear Patch-Clamp Electrophysiology of ${\text{IP}}_3\text{R}$s in Sf9 Cells with Two, Three, and Four Active Channels per Patch

Trace	${\text{P}}_{O1}$	${\text{P}}_{O2}$	${\text{P}}_{O3}$	${\text{P}}_{O4}$	${\tau }_{O1}$$ms$	${\tau }_{O2}$$ms$	${\tau }_{O3}$$ms$	${\tau }_{O4}$$ms$	${\tau }_{C1}$$ms$	${\tau }_{C2}$$ms$	${\tau }_{C3}$$ms$	${\tau }_{C4}$$ms$
1	0.91	0.67	–	–	166	271	–	–	17	128	–	–
2	0.41	0.16	–	–	642	163	–	–	927	8017	–	–
3	0.82	0.52	–	–	505	790	–	–	111	722	–	–
4	0.93	0.86	0.38	–	113	138	171	–	9	23	278	–
5	0.41	0.14	0.003	–	187	275	160	–	265	1683	36,525	–
6	0.36	0.14	0.02	–	29	53	75	–	51	321	3558	–
7	0.69	0.41	0.11	0.002	49	72	91	77	22	105	714	21,639
8	0.81	0.60	0.30	0.002	911	1566	2166	1100	219	1048	4922	253,520

Columns 2–5 and 6–9 are the mean probabilities and mean open times, respectively, when at least one, two, three, and four channels are open. Columns 10–13 are the mean closed times when a minimum of one, two, three, and four channels are not open.

We also processed many fluorescence records from TIRFM of ${\text{IP}}_3$-induced ${\text{Ca}}^{2+}$ puffs in Xenopus oocytes with varying amplitudes (in terms of peak fluorescence or number of open channels during the puff) and duration. We identified up to ten channels in the traces processed and show a range of parameters and statistics extracted from the fluorescence traces by our software in Fig. 6. Fig. 6, a1 and a2 show a raw trace representative of ${\text{IP}}_3$-induced puffs (black) with background noise (gray) and the number of channels identified by TraceSpecks, respectively. The raw TIRFM signal is the relative fluorescence change due to the cluster activity, averaged over a $1.5\times 1.5\mu \mathrm{m}$ area surrounding the cluster. As pointed out above, the software allows us to store the mean P_O, ${\tau }_O$, ${\tau }_C$, and dwell-time distributions for different numbers of channels open in the cluster and amplitudes of all puffs in a trace in ascii format for plotting and postprocessing. As an example, we show the distribution of puff amplitudes represented as the maximal number of channels opened simultaneously in a puff from all traces processed in (a3) of Fig. 6.

Figure 6.

Processing fluorescence records from TIRFM of ${\text{IP}}_3$-induced ${\text{Ca}}^{2+}$ puffs in Xenopus oocytes. The first column on the left shows a sample raw trace (black) and the background separated by the software (gray) (a1), the corresponding idealized trace (a2), amplitude (maximal number of channels open simultaneously) (a3), distribution of all puffs in all traces processed, and the transition between different numbers of channels open/closed (a4). The remaining four columns show distributions of dwell times (first row), mean P_O (second row), mean ${\tau }_O$ (third row), and mean ${\tau }_C$ (fourth row) when at least one (b1–b4), two (c1–c4), three (d1–d4), and four channels (e1–e4) are open in all traces processed. Mean ${\tau }_C$ for channel i represents the mean time when the number of open channels is less than i. To see this figure in color, go online.

Another key piece of information about the traces representing the activity of multiple channels or single channels with multiple conductance levels is determining the probability of transitions between different numbers of channels opened or different conducting states. For example, what is the likelihood that Y channels will be open at time t$+\delta$t given that there are X channels open at time t, where X and Y do not have to be consecutive digits? Or what is the probability that a channel in conductance level X at time t will be in conductance level Y at time t$+\delta$t? This information can be used for modeling the kinetics of a single channel with multiple conductance levels or a cluster with multiple channels using programs such as QUB and HJCFIT. We report this information as an interstate or interchannel transition graph, as shown in (a4). In this graph, the point at location (X,Y) = (2,1) indicates that there is a transition from two simultaneous open channels to one open channel (one of the open channels closed). The size of the circle is proportional to the number of such transitions found in all traces that we processed. Similarly, the point at location (X,Y) = (1,2) indicates that another channel opened between time t and t$+\delta$t, and the total number of open channels is now two. We also observed transitions in which the total number of channels at time t and t$+\delta$t are not consecutive digits. The dwell-time distributions (first row), mean P_O (second row), mean ${\tau }_O$ (third row), and mean ${\tau }_C$ (fourth row) when at least one (b1–b4), two (c1–c4), three (d1–d4), and four (e1–e4) channels are open in all traces are also shown in Fig. 6. The software saves this information for all channels identified (10 in this case), but the statistics for the remaining six channels are skipped for clarity.

The method also works for fluorescence traces representing the function of ion channels having multiple levels with quantal conductances and traces with very low SNR. As an example, we process fluorescence traces from TIRFM of many $\text{A}{\beta }_{1-42}$-induced ${\text{Ca}}^{2+}$-permeable pores in the PM of Xenopus oocyte and summarize our results in Fig. 7. We observe a closed level in which no ${\text{Ca}}^{2+}$ flux is passing through the pore (represented by level 0) and up to five open conductance levels (represented by level 1, 2, 3, 4, and 5) (9). In Fig. 7, we show a sample raw trace; the separated background; idealized trace; the distribution of dwell times; mean P_O, mean ${\tau }_O$, mean ${\tau }_C$ when the channel is gating in a conductance level equal to or larger than 1, 2, 3, and 4; and the number of transitions between different conductance levels. We skip the distributions for conductance level 5, as there were only a few instances in which the channel opened in that level. The details about the data for $\text{A}{\beta }_{1-42}$ pores are similar to that of ${\text{IP}}_3$-induced puffs except that the number of open channels from the puffs discussion is replaced by conducting levels in the case of $\text{A}{\beta }_{1-42}$ pores. We would like to point out that there is a significantly larger number of transitions between levels 0 and 1 in comparison to the puffs data, indicating that $\text{A}{\beta }_{1-42}$ pores prefer to gate in low conductance levels. Also, in comparison to ${\text{IP}}_3$-induced puffs, we observed a larger number of transitions in which the levels involved are not immediately next to each other (for example, transitions from level 0 to level 2 and vice versa) (Fig. 7 a4).

Figure 7.

Processing fluorescence records from TIRFM of $\text{A}{\beta }_{1-42}$-induced pores in the PM of Xenopus oocytes. The first column on the left shows a sample raw trace (black) and the background separated by TraceSpecks (gray) (a1), the corresponding idealized trace representing the conductance level in which the pore is gating (a2), amplitude (the highest conductance level in which the channel is gating during a single opening event) distribution (a3), and the transition between different conductance levels (a4) for all opening and closing events in all traces processed. The remaining four columns show distributions of dwell times (first row), mean P_O (second row), mean ${\tau }_O$ (third row), and mean ${\tau }_C$ (fourth row) when the pore is gating in level 1 or above (b1–b4), level 2 or above (c1–c4), level 3 or above (d1–d4), and level 4 or above (e1–e4) in all traces processed. Mean ${\tau }_C$ for conductance level i represents the mean time when the conductance level is less than i. To see this figure in color, go online.

Conclusions

Data from fluorescence imaging as well as the routinely employed electrophysiological patch-clamp techniques are contaminated with noise and drifting background that does not arise from the system under study. Removing this noise and fluctuating background is usually the first step in the analysis of the data. In the absence of an automated method, experimentalists adhere to the eye and the mouse-based approach for processing noisy imaging and patch-clamp data. This laborious manual procedure could cost experimentalists more time processing the data than conducting the actual experiment.

One example of where the lack of efficient algorithm for separating the signal from background noise could limit the full utilization of very powerful experimental techniques is the high-resolution imaging of ${\text{Ca}}^{2+}$ signals. Recent advances in imaging techniques such as TIRFM offer a paradigm-shifting improvement in our ability to study thousands of ion channels in parallel within their native environment (1, 2). This technique, called “optical patch-clamp,” generates fluorescence time traces from thousands of ion channels in a single experiment. Although an algorithm to automatically detect, localize, and measure fluorescence changes during localized ${\text{Ca}}^{2+}$ signals imaged through optical patch-clamp has been recently developed (41), the lack of efficient algorithms to extract signal out of the noise and idealize the fluorescence traces remains the main hurdle in accessing a wide range of information about the system under investigation and developing single-channel/molecule models based on huge data sets collected from thousands of channels/molecules in their native environment in these experiments.

In this work, we developed a minimally parameterized likelihood method that can process both noisy patch-clamp and imaging data with drifting background. The robustness and accuracy of our algorithm is demonstrated by closely recovering the signal from noisy synthetic patch-clamp data with variable SNR and fluorescence traces representing ${\text{Ca}}^{2+}$ puffs generated by a cluster of ${\text{IP}}_3\text{R}$ channels. This was followed by the processing of significant data from both TIRFM experiments as well as patch-clamp recordings and extracting many important features from the data.

We implemented our algorithm in the very portable Java language with options to set up initial parameters; display optimized parameters, raw trace, and separated background; and idealize trace, mean P_O, ${\tau }_O$, and ${\tau }_C$ for all channels/conductance levels in the trace as well as the overall mean P_O, ${\tau }_O$, and ${\tau }_C$ of the trace (Fig. 1). The option to store all these traces and statistics is also provided in addition to dwell times for the channel gating in different conducting states or different numbers of open channels in a cluster or a patch, amplitude distribution of all events in terms of the highest number of channels open/conductance level and peak fluorescence in which the channel is gating during the event, and the number of transitions between different states in ascii format for plotting and later use. A compiled Java program with a user-friendly GUI that performs all these tasks and that is portable to Mac, personal computer, and Unix platforms with user manual and source code is provided in the online supplement.

As pointed out above, our labs have completed the development of another software program called CellSpecks that can detect and extract fluorescence traces for thousands of channels in a membrane patch recorded simultaneously in their native environment at single-channel and millisecond resolutions using TIRFM. Merging TraceSpecks and CellsSpecks will result in a comprehensive software capable of detecting thousands of channels in a video sequence recorded through high-resolution fluorescence microscopy, idealizing, and analyzing traces from all channels. Developing such a comprehensive software is beyond the scope of this work and will be the subject of our future research.

Author Contributions

S.I.S. performed the research, contributed analytic tools, analyzed the data, and wrote the article. A.D. performed the research, analyzed the data, and wrote the article. D.-O.D.M. performed the research and analyzed the data. I.P. designed the research. J.E.P. designed the research and contributed analytic tools. G.U. designed the research, contributed analytic tools, analyzed the data, and wrote the article.

Editor: James Sneyd.