Spatiotemporal Network Markers of Individual Variability in the Human Functional Connectome

Abstract

Functional connectivity (FC) analysis has revealed stable and reproducible features of brain network organization, as well as their variations across individuals. Here, we localize network markers of individual variability in FC and track their dynamical expression across time. First, we determine the minimal set of network components required to identify individual subjects. Among specific resting-state networks, we find that the FC pattern of the frontoparietal network allows for the most reliable identification of individuals. Looking across the whole brain, an optimization approach designed to identify a minimal node set converges on distributed portions of the frontoparietal system. Second, we track the expression of these network markers across time. We find that the FC fingerprint is most clearly expressed at times when FC patterns exhibit low modularity. In summary, our study reveals distributed network markers of individual variability that are localized in both space and time.

Introduction

Complex human cognitive functions such as memory, language, or logical reasoning depend on the architecture of brain networks (Petersen and Sporns 2015; Sporns et al. 2005). The architecture of networks derived from intrinsic (resting-state) functional connectivity (FC) has been widely studied (Bassett and Bullmore 2009; Buckner et al. 2013), with FC most commonly estimated from the similarity or linear correlation of the time courses of pairs of brain regions defined by a voxel- or template-based parcellation (Bullmore and Sporns 2009). Numerous studies have focused on identifying network characteristics that are common across individuals (Damoiseaux et al. 2006; Biswal et al. 2010) and on characterizing the long-time average of FC (Friston 2011). Recently, there is growing interest in identifying markers of individual variability in brain networks (Poldrack et al. 2015; Dubois and Adolphs 2016) as well as in characterizing temporal patterns of FC (Hutchison et al. 2013).

Markers of individual variability have been investigated in several recent studies (Mueller et al. 2013; Miranda-Dominguez et al. 2014; Finn et al. 2015; Airan et al. 2016). Miranda-Dominguez et al. (2014) proposed a model for predicting the subject-level activity of a given brain region based on knowing the activity of other brain regions at a particular time point. Finn et al. (2015) used individual connectivity profiles to accurately identify subjects across several scan sessions including task and rest conditions, with the frontoparietal network (FP) emerging as most distinctive. Studying the effects of various acquisition parameters (sampling frequency) and analysis methods (parcellation) to characterize individual differences, Airan et al. (2016) found that the precuneus as well as prefrontal parietotemporal cortices were among those brain regions that contributed most to identify subjects.

These prior studies investigated individual variability as expressed in long-time averages of FC. Recent studies have suggested that FC exhibits temporal variability over shorter time scales. Several computational models simulating spontaneous neuronal dynamics have shown that brain dynamics are not time-invariant, but instead exhibit fluctuations at multiple time scales (Honey et al. 2007; Ghosh et al. 2008; Deco et al. 2009). Experimental studies have demonstrated dynamical variations of FC estimated from functional magnetic resonance imaging (fMRI) resting-state recordings (Chang and Glover 2010; Hutchison et al. 2013; Allen et al. 2014; Calhoun et al. 2014). For instance, some studies have shown fluctuations in the modularity of FC within short temporal windows (“snapshots”), with highly modular patterns displaying a consistent topology characterized by disconnection of task-positive from task-negative systems (Betzel et al. 2016). Changes in the patterns of FC have also been observed in relation to the level of awareness (Barttfeld et al. 2015) and in sleep-wakefulness transitions (Laumann et al. 2016) suggesting a potential relationship to brain state and neuromodulation (Shine et al. 2016). These observations of time- and state-dependence of FC raise the important question whether markers of individual variability are differentially expressed across brief FC snapshots.

Our study proceeds along 2 interconnected aims. The first aim was to determine the optimal set of brain nodes needed to reliably identify individual subjects across separate resting-state sessions. We utilized 2 independent multi-session data sets (DSs) and compared patterns of FC across individuals and across sessions. We found that FC patterns in different resting-state networks afforded different levels of accuracy, and that highly accurate identification of individuals depended on the granularity of the cortical parcellation. Using a simulated annealing (SA) probabilistic optimization algorithm applied to whole-brain FC we then identified the minimal set of cortical nodes needed to optimally identify individuals. Our second aim was to determine whether the level at which network markers of individuality were expressed fluctuated across time. We extracted brief FC snapshots across individuals and across 2 separate imaging sessions and then determined the accuracy with which each snapshot allowed individuals to be identified. Selecting the least and the most characteristic FC patterns, we characterized specific features of network topology associated with the FC fingerprint as expressed across time.

Materials and Methods

For a summary illustration of the workflow  (see Supplementary Fig. S1).

Data Sets

We used 2 independently acquired multi-session resting-state fMRI DSs. DSs 1 and 2 were acquired under resting state conditions with subjects instructed to remain still, stay awake and with their eyes open. None of the participants of DS 1 and 2 had a history of substance abuse, neurological, or psychiatric disorders.

DS 1 was comprised of 30 healthy young subjects (50% males, mean age = 24) that were scanned every 3 days during 1 month, yielding 10 scans per subject (Chen et al. 2015). In our study, we used the first and last scanning sessions. DS 1 has been released (http://dx.doi.org/10.15387/fcp_indi.corr.hnu1) as part of the Consortium for Reliability and Reproducibility (CoRR) (Zuo et al. 2014). MRI Imaging sessions were acquired in a GE M850 3.0 Tesla scanner (GE Medical Systems, Waukesha, WI) at CCBD, Hangzhou Normal University. For the brain structural analyses, a T1-weighted Fast Spoiled Gradient echo (FSPGR: TR = 8.1 ms, TE = 3.1 ms, TI = 450 ms, flip angle = 8°, field of view = 256 × 256 mm, matrix = 256 × 256, voxel size = 1.0 × 1.0 × 1.0 mm, 176 sagittal slices) was carried out. To minimize head movement, straps, and foam pads were used to fix the head securely during each scan. For the FC analyses, a T2-weighted echo-planar imaging (EPI: TR = 2000 ms, TE = 30 ms, flip angle = 90°, field of view = 220 × 220 mm, matrix = 64 × 64, voxel size = 3.4 × 3.4 × 3.4 mm, 43 slices) sequence was performed to acquire resting state fMRI images for 10 min.

Details on fMRI preprocessing can be found in Xu et al. (2015). Briefly, processing consisted of: (1) removing the first 5 EPI volume (10 s) to avoid possible effects T1 stabilization; (2) temporal despiking to limit extreme values from hardware instability or head motion (including scrubbing procedures, Power et al. 2014); (3) slice timing correction and volume realignment; (4) mean-based intensity normalization to 10.000; (5) matching spatial correspondences between individual functional images and anatomical images by employing white surface boundary-based registration algorithm (Greve and Fischl 2009); (6) regress out the estimated Friston's 24-parameter motion curves (Yan et al. 2013) and nuisance signals from the white matter and cerebrospinal fluid to reduce physiologic noise; (7) temporally band-pass filter (0.01–0.08 Hz) and removing of linear and quadratic trends; and (8) global signal regression and spatial smoothing using a 6 mm FWHM Gaussian kernel.

DS 2 comprised 40 healthy young subjects’ (62% males, mean age = 24.5) test–retest with 1 month of difference recruited as part of the Brain Genomic Superstruct Project (Holmes et al. 2015). Scans were acquired on a 3 Tesla TimTrio system (Siemens) using a 12-channel phased-array head coil supplied by the vendor. High-resolution 3D T1-weighted magnetization multiecho images for structural anatomic reference (multiecho MPRAGE) (van der Kouwe et al. 2008) and a gradient-echo echo-planar pulse sequence sensitive to blood oxygenation level-dependent (BOLD) contrast for functional imaging data were obtained. Multi echo MPRAGE parameters were as follows: TR, 2200 ms; TI, 1100 ms; TE, 1.54 ms for image 1–7.01 ms for image 4; flip angle, 7°; 1.2 × 1.2 × 1.2 mm; FOV, 230. EPI parameters were as follows: TR, 3000 ms; TE, 30 ms; flip angle, 85°; 3 × 3 × 3 mm voxels; FOV, 216; 47 slices (each run lasted 6.2 min, 124 time points).

Details on fMRI preprocessing can be found in Sepulcre et al. (2012). Briefly, processing consisted of: (1) removal of first 4 volumes (12 s) to allow T1-equilibration effects; (2) slice-timing correction, volume realignment, and motion correction; (3) temporally band-pass filter (0.01–0.08 Hz) and removing of constant offsets and linear trends; (4) removing of nuisance signals, along with their temporal derivatives, through linear regression including: 6 parameters obtained from correction for rigid-body head motion, averaged white matter signal from the centrum semiovale and averaged cerebrospinal fluid signal from the body of the lateral ventricles; and (5) global signal regression and spatial smoothing using a 6 mm FWHM Gaussian kernel.

For both DSs, individual correlation matrices were false discovery rate (FDR)-corrected at 0.05 significance level (Benjamini and Hochberg 1995). The FDR step in our analysis was aiming to remove the very weak (and unreliable) connections. The percentage of edges removed were approximately ~22% in average in both sessions. We also performed additional analyses without the FDR correction step resulting in identical results in all cases.

Parcellations

For DS 1, we created a set of 10 random (spatially continuous and non-overlapping) parcellations over a broad range of coarseness [18 levels, ranging from 30 to 3198 nodes or regions of interest (ROIs)] using pyClusterROI (Craddock et al. 2012). All the parcels were required to fit into a gray matter mask and into a common mask across all the subjects. All ROIs that did not meet these conditions were discarded; as a result, the number of ROIs across random parcellations within a given level varied slightly.

Similarity of FC across Sessions

The static FC analyses were performed by calculating the Pearson correlation of the time series (intrinsic activity) of every pair of brain regions. Thus, for each subject we obtained a set of square symmetric weighted FC matrices of varying sizes n_i, where n_i is the number of ROIs defined by the random parcellation. We transformed the upper triangle of each matrix into a functional connectome vector (FCv) of length n_i(n_i − 1)/2, containing the complete individual pattern of FC. This procedure was performed separately for each subject and each session, resulting in 2 sets of FCv₁(s_i) and FCv₂(s_i), where the subindex on FCv denotes the session and s_i identifies the subjects. Then, these vectors were compared across all M subjects and across both sessions. We tested 2 measures of similarity, the Pearson correlation (adopted for most of the results reported in this paper) and the cosine vector angle; both measures yielded qualitatively highly similar results. The final output was a similarity matrix S of size M × M. It is expected that maximum similarity values are to be found on the diagonal of this matrix, representing the similarity between corresponding single subject's FCs across the 2 sessions. Hence, we define the accuracy of matrix S as the number of diagonal elements S_i,i that are maximal with respect to all other elements S_i,j (j = 1,…,M) in the jth column of S. Note that the similarity matrix is not symmetric. Here, we report the analyses both column-wise (similarity from 1 to 2) as well as the average of column- and row-wise similarity.

Accuracy was determined on whole-brain FC, as well as on specific brain networks (Yeo et al. 2011), specifically the visual network (VIS), the auditory and somatosensory network (ASM), the dorsal-attention network (DAN), the saliency network (SAL), the orbito-frontal-temporopolar network (ORB), the FP, and the default mode network (DMN), referred to here as resting state networks (RSNs). In addition, we used the accuracy score to guide optimization runs (see below).

Optimization

We implemented optimization algorithms to identify the minimum set of nodes needed for optimal identification of subjects across sessions. To do so, we defined a cost function based on the similarity matrix, computed as the average across the values along the main diagonal minus the average of the off-diagonal values. We impose the additional constraint that the identification accuracy must increase or remain constant at each step. We explored 2 strategies. The first is a deterministic “greedy algorithm” (GA) strategy which maximizes the cost function by removing, at each step, 1 node such that the increase in the cost function is maximal. The drawback of this strategy is that it may lead to suboptimal solutions that represent local maxima. An alternative strategy is to apply SA, a probabilistic search algorithm (Kirkpatrick et al. 1983), which implements the Metropolis criterion (Metropolis et al. 1953) to guide optimization. SA proceeds by probabilistically removing nodes, including occasionally nodes whose removal results in lower accuracy, in the service of identifying a globally optimum. As the algorithm proceeds, the probability of accepting suboptimal solutions gradually decreases (a computational analog to “cooling” or lowering the temperature). The initial temperature was set to T₀ = 1, determined analytically using formulas proposed on the basis of different prior studies (Ben-Ameur 2004) as well as with pilot runs.

Optimization runs are carried out on whole-brain FC data as well as on FC from individual resting-state networks. The minimal set of “survivor nodes” resulting from optimization runs on whole-brain or individual network FC is defined as the “global fingerprint” and “network-specific fingerprint”, respectively.

To address the generalizability of our results, we performed additional optimization analyses using a cross-validation procedure. First, we merged DS 1 (30 subjects) and DS 2 (40 subjects) into 1 single DS of 70 subjects. As DS 1 was sampled with a TR = 2 and DS 2 with a TR = 3, we resampled DS 1 at 3 s. Then, we randomly divided the subjects into training DS (58 subjects) and testing DS (12 subjects) using a 5-fold cross-validation. We run the optimization analyses on the whole-brain (using a random partition of 200 ROIs) in the training DS. Then, the survivor nodes (SNs) were used to perform identification analyses on the testing DS. The optimizations were run 10 times for each 1 of the 5 subdivisions (5-fold) of the merged DS. Afterwards, we determined which of the 7 RSNs (Yeo et al. 2011) accounted for the largest number of SNs. This network was then used to carry out another set of optimization and cross-validation analyses.

FC Snapshots and Dynamic Expression

To examine possible fluctuations in the expression of the fingerprint over time, we subdivided each scan session into brief FC snapshots (40 s non-overlapping windows, 14 windows per subject-session), using a fine-grained parcellation of 1739 nodes. For each window t_q, we estimated the FC [FC(t_q)] by calculating the Pearson correlation of the corresponding time series. Each FC matrix FC(t_q) was converted to a vector (FCv(s_i, t_q), s₁ = 1,…,M, t_q = 1,…,t_max) of length n_i(n_i − 1)/2, comprising 1 511 191 connections (n_i = 1739). FC snapshots of subject s_i, window t_q and session 1/2 were denoted as FCv₁(s_i,t_q) and FCv₂(s_i,t_q), respectively. Within each session, we compared the pairwise correlations of all patterns FCv₁(s_i,t_q) with all other patterns FCv₁(s_j,t_r) (j = 1,…,M; r = 1,…,14) and identified the time intervals t_q, t_r that yielded the maximal similarity score

$${\langle {\max }_{t_r}\{S(\mathrm{F}\mathrm{C}{\mathrm{v}}_1(s_i,t_q),\mathrm{F}\mathrm{C}{\mathrm{v}}_1(s_j,t_r))\}\rangle }_{s_j},$$

where ${⟨⟩}_{s_j}$ denotes the average across all subjects and S (·,·) is the similarity. Thus, for each subject s_i and a time interval t_q, we find the functional connectome FCv₁(s_j,t_r) corresponding to subject s_j and time interval t_r, such that the similarity between FCv₁(s_i,t_q) and FCv₁(s_j,t_r) is maximal. Then, we compute the average across all maximum similarity values between FCv₁(s_i,t_q), and all FCv₁(s_j,t_r) j = 1,…,M. This process is repeated for all FCvs of subject s_i and all subject pairs, yielding a row vector of length 14, whose qth element represents the average maximal similarity scores between FCv1(s_i,t_q) and all other FC snapshots of all other subjects. Finally, we repeat this process for all M subjects, resulting in M row vectors of average maximum similarities.

The same process was carried out to identify minimum similarities between all FCvs of all subjects, that is:

$${\langle {\min }_{t_r}\{S({\mathrm{FCv}}_1(s_i,t_q),{\mathrm{FCv}}_1(s_j,t_r))\}\rangle }_{s_j}$$

This resulted in 2 sets of M row-vectors of length 14: 1 set containing average maximum similarity values and the second set containing the average minimum similarity values. Because these values have been averaged across subjects, maximum similarity values are associated with patterns that are more common (“least unique”) across subjects, whereas minimum average similarity values are associated with less common (“more unique”) patterns. The least commonly shared connections across time are defined as the “dynamic fingerprint” because they represent characteristic fluctuations of FC across time.

We statistically tested average connectivity strength displayed on the 30 most unique and 30 least unique dynamical FC snapshots of each subject. This comparison accounted for the number of differential functional connections between most and least unique pattern. Briefly, we performed a paired t-test between most and least unique patterns for each link. Subsequently, paired t-test matrices were FDR-corrected (P < 0.05), yielding a P-value matrix. To increase reliability, this procedure was repeated for sessions 1 and 2 of DS 1. Then we quantified the overlap between the significant connections from the 2 sessions performing a spatial cross correlation of the 2 maps.

Furthermore, given that the comparison between the more and less common patterns may facilitate the emergence of significant differences we generated null FC data using a stationary vector autoregressive (VAR) model as described by Zalesky et al. (2014) to perform additional comparisons. The surrogate regional time series were generated with the VAR model under the null hypothesis of a linearly correlated and stationary process. The order of the VAR model was set to 4 to use a maximum lag of approximately 8 s (Zalesky et al. 2014; Fukushima et al. 2016). The VAR models were estimated from the experimental resting state fMRI (DS 1) and then used to individually simulate time series for each pair of regions. VAR model was simulated using an approach used previously (Zalesky et al. 2014; Fukushima et al. 2016). Briefly, the initial values for the simulation are randomly sampled from contiguous blocks of resting state fMRI time series data while the innovation terms are randomly sampled residuals of the VAR estimation. Approximately, a total of 2500 null samples (30 subjects × 84 samples) were generated from actual data as in Zalesky et al. (2014) and Fukushima et al. (2016). The FC matrices obtained from the null data were compared with the common patterns (least unique patterns) using the same procedure as described above.

We used 2 metrics to investigate the topology of the most unique and least unique FC snapshots. We computed the average of the absolute magnitude of FC across the whole network, which provides an indication of the overall FC amplitude. In addition, we performed modularity maximization (Sporns and Betzel 2016) using the Louvain algorithm (Blondel et al. 2008) to search for optimal module partitions (Newman and Girvan 2004). We ran 1000 repetitions of the algorithm and selected the partition that yielded the maximum modularity metric.

We performed an analogous analysis between sessions. More specifically, We performed a similarity analysis across subjects and across time by correlating, for each subject s_i and a given time interval t_q from session 1, the pattern FCv₁(s_i,t_q), with all other patterns FCv₂(s_j,t_r) of session 2, and found the best matching patterns along time intervals in session 1 and session 2:

$${\max }_{t_t}\{S({\mathrm{FCv}}_1(s_i,t_q),{\mathrm{FCv}}_2(s_j,t_r))\}$$

We carried out this analysis using the nodes from the whole brain, the SNs extracted from the optimization analyses (explained below) and the 7 RSNs.

Gyrification and Temporal Signal-to-Noise Ratio

Gyrification and Temporal Signal-to-Noise Ratio (TSNR) analyses were both performed to rule out any potential confounds associated with the individual pattern of gyrification on the cortical mantle. Specifically, in order to evaluate the individual cortex curvature as a potential confounding factor for identification accuracy we computed the local cortical folding (Schaer et al. 2012) in DS 1. Briefly, we first created cortical mesh models (~150 000 vertices) for each subject from the MRI structural image using a standard Freesurfer pipeline procedure (Dale et al. 1999; Fischl et al. 1999). Then, we compute the local gyrification index (lGI) which measures the amount of cortex buried within the sulcal folds compared to the amount of visible cortex. The lGl ranges from 1 to 5, with 1 indicating a flat surface and 5 indicating a highly folded cortex (Schaer et al. 2012). As a final step, we resampled the lGI individual data to an average subject (using the fsaverage template comprising 163 842 vertices) and smoothed the data on the cortical surface (full-width at half-maximum of 10 mm). Then, we compute the vertex-wise mean values for each hemisphere and assign each vertex to 1 of the 7 RSNs after registering a RSN mask provided by freesurfer to the fsaverage template.

BOLD variance could be influenced by partial volume effects induced by variation in regional volumes as well as gyral cortical folding. To account for this potential confound we computed the TSNR on DSs 1 and 2, as the temporal mean BOLD signal of each voxel divided by its standard deviation. TSNR was computed in DS 1 in both sessions, and the resulting measurements were correlated with the values of SNs coming from the global fingerprints on parcellations A and B. The relationship between TSNR, gyrification and the SNs was assessed using the non-parametric correlation measure Goodman–Kruskal Gamma (γ), where γ = 1 and γ = −1 indicate a perfect positive and negative association, respectively.

We wanted to rule out the possibility that the node volume could predict node survivability in the optimization procedure. Since SNR is proportional to the square root of volume this suggests that node volume could be a potential confounding variable. Although the parcellations were generated in such a way that ROIs were designed to contain similar numbers of voxels we compared specifically the node volume of the SNs versus non-SNs. The node volume was computed for each ROI (node) quantifying the number of voxels comprising the ROI. Then, we averaged and compared (via t-test) the number of voxels from the survivor and non-SNs on different parcellations.

Results

Identification Accuracy is Network and Parcellation Dependent

As a first step in identifying network markers of individual variability, we performed analyses on whole-brain FC data in a parcellation of 1739 nodes acquired from a set of 30 individuals (DS 1). For the whole brain, 29 out of 30 individuals are identifiable across 2 sessions (accuracy = 0.96). We tested which RSN contributed most. Highest accuracy was found for 2 heteromodal networks, the DMN (30/30 = 1) and the FP (30/30 = 1), and for 2 multimodal networks, the SAL (30/30 = 1) and the DAN (29/30 = 0.97). Lower accuracy was associated with 2 unimodal networks, the ASM (24/30 = 0.8), the VIS (25/30 = 0.83) and 1 multimodal network, the ORB (22/30 = 0.73). A similar pattern of results was obtained for DS 2 (40 subjects, 1739 nodes). We found an accuracy of 0.85 (34/40) for the whole brain, with strongest contributions from the DMN (39/40 = 0.98), FP (39/40 = 0.98), and SAL (38/40 = 0.95), intermediate contributions from the DAN (35/40 = 0.88), and weaker contributions from ORB (27/40 = 0.68), ASM (31/40 = 0.78), and VIS (30/40 = 0.75).

These data were derived from a 1-way (session 1–session 2, or “column-wise”) match. We also performed an identification analysis by averaging across both directions (1–2 and 2–1). The analyses performed on DS 1/2 revealed similar results as described above: VIS (0.76/0.8), ASM (0.76/087), DAN (0.93/0.82), SAL (0.93/0.92), ORB (0.63/0.65), FP (1.00/1.00), DMN (0.96/0.97), and WB (0.96/0.85). These results suggest that different resting-state networks express different degrees of individual variability that afford different levels of accuracy in identifying individuals across sessions.

To ensure robustness of our findings, we employed an alternative measure of similarity, the cosine vector angle, on DS 1. We found very similar results to those reported above based on a Pearson correlation metric. For a 1-way match the accuracy was 29/30 for the whole-brain, with lower accuracy associated with 2 unimodal networks, the VIS (23/30 = 0.77), the ASM (24/30 = 0.8), and 2 multimodal networks, the ORB (24/30 = 0.8), and the SAL (25/30 = 0.83). Highest accuracy was achieved by 2 heteromodal networks, the DMN (28/30 = 0.93) and the FP (30/30 = 1) and 1 multimodal network, the DAN (27/30 = 0.9). The 2-way match yielded VIS (0.66), ASM (0.5), DAN (0.73), SAL (0.76), ORB (0.5), FP (0.9), and DMN (0.86).

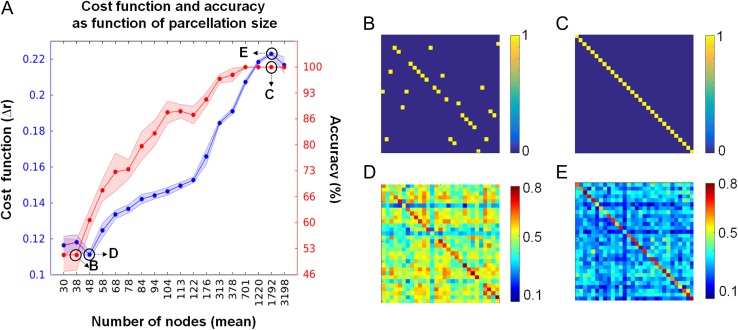
Next, we investigated whether our results depended on the “granularity” (number of ROIs) of the random parcellation. In DS 1, we found a strong effect of parcellation size on the accuracy with which individuals could be detected, and on the quality of the cost function used to estimate correspondence between FC patterns across sessions (Fig. 1A). Figure 1B,C show examples of 2 maximum filtered similarity matrices (from networks of 38 and 1792 nodes) of low and high accuracy, respectively. Figure 1D,E show examples of 2 similarity matrices (from networks of 48 and 1792 nodes) of low and high value of the cost function, respectively. Averaged over 10 runs of random parcellations, the accuracy reached a plateau (at 100%) at 701 nodes and the cost function at around 1220 nodes. For parcellations at or below 100 nodes, the accuracy with which individuals could be identified across sessions was markedly diminished.

Figure 1.

Cost function and accuracy in relation to parcellation size. (A) Red markers (right y-axis) show mean accuracy, measured as the fraction of correctly identified subjects (average of 10 random parcellations). Red-shaded areas correspond to +/− 1 standard deviation. Blue markers (left y-axis) show the mean cost function, measured as the difference between the main diagonal and the off-diagonal of the similarity matrix, normalized by the number of elements in the matrix (average of 10 random parcellations). Blue-shaded areas correspond to +/− 1 standard deviation. Black upper-case letters within the graph refer to panels on the right (data from 1 random parcellation). (B–E) Similarity matrices obtained by correlating the subjects’ FCv of session 1 and 2. Accuracy was computed as the number of elements that fall within the main diagonal of the similarity matrix. In panels (B) and (C) the accuracy is at 50 and 100%, respectively. Panels (D) and (E) show the Pearson correlation matrices corresponding to networks of 48 and 1792 nodes (low and high values of the cost function), respectively.

Optimization Identifies a Minimal Set of Nodes for Fingerprinting

The network-specificity of fingerprinting shown above, in line with previous work (Finn et al. 2015), suggests that certain portions of the cerebral cortex contain more reliable networks markers of individuality than others. We attempted to identify these locales using an optimization approach applied to the whole cerebral cortex (“global fingerprint”). We implemented a SA algorithm searching for nodes that allow optimal identifiability of individuals across sessions. The algorithm was run on 3 different random parcellations. Two were of comparable granularity (322 nodes, parcellation A; 382 nodes, parcellation B) and a third parcellation comprised 701 nodes (parcellation C). These parcellation sizes were chosen since they allowed identification accuracy approaching 100% (Fig. 1) while also permitting computationally tractable optimization runs. The goal of the optimization algorithm was to gradually reduce the number of nodes used for identifying individual subjects across sessions while maintaining optimal levels (100%) of accuracy.

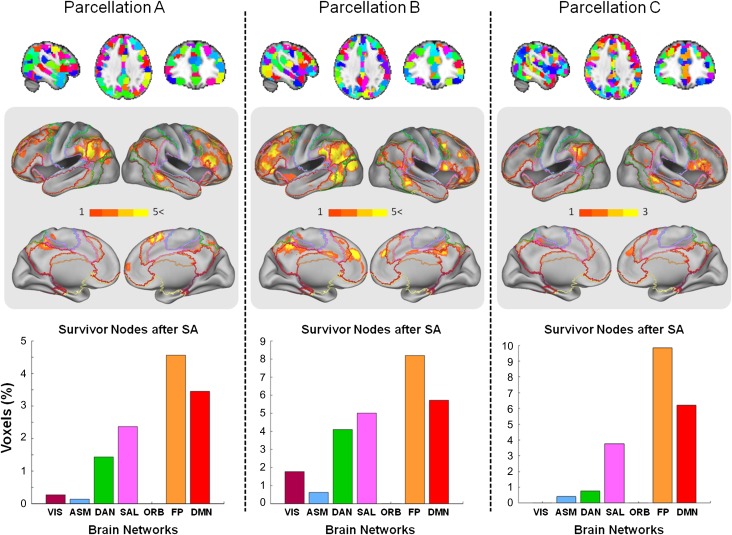
Ten separate runs were conducted for parcellations A and B to ascertain convergence onto a common neural substrate. SNs were aggregated to show patterns of localization (Fig. 2, light gray panels) and were found to be localized mainly in medial and dorsolateral prefrontal cortex as well as in the left parietal cortex. We calculated the percentage of SNs localized within each 1 of the 7 RSNs, correcting for network size. The largest proportion of SNs was encountered in the FP network, with the DMN containing the second highest proportion, followed by SAL and DAN. In both parcellations, the unimodal networks VIS and ASM, and ORB contained significantly fewer SNs.

Figure 2.

SNs (global fingerprints) obtained from SA on whole-brain data. Columns show results from 3 different whole-brain parcellations. Parcellations A, B, and C comprising 382, 322, and 701 parcels, respectively, are shown in the upper row. The middle row shows surface projections of the SNs (fingerprints) on the brain aggregated over ten SA runs on parcellations A and B, and 3 SA runs on parcellation C. The color bar represents the number of runs that a given brain node survived the SA procedure. Surface projections of the 7 RSNs from Yeo et al. (2011) are superimposed as outlines. The histograms in the bottom row indicate the fraction of SNs (normalized by size of network) averaged across all the repetitions of the SA. Surface projections use the PALS approach of Van Essen (2005). See text for abbreviations of brain networks.

For coarser parcellations, random parcels may straddle the boundaries of several RSNs preventing unambiguous assignment to a single RSN. To improve spatial resolution, we ran 3 SA optimizations on a finer partition of 701 nodes (Fig. 2, parcellation C) with each node comprising approximately 110 voxels. The results show that, once again, the highest proportion of survivor is found in the FP network, followed by DMN and SAL. Other RSNs make much smaller contributions to the global fingerprint.

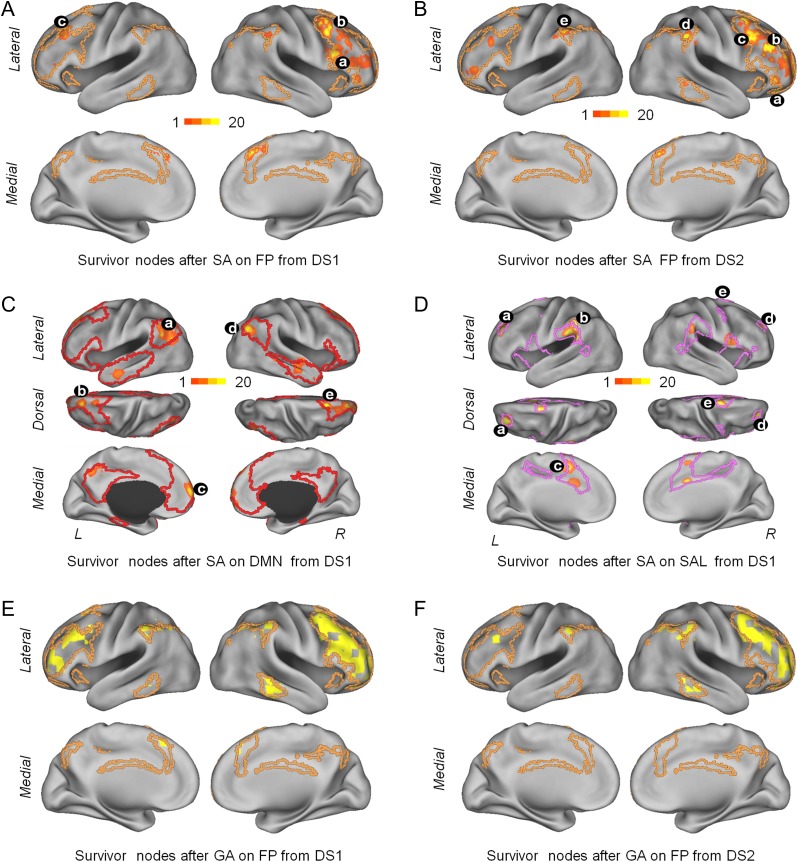
To determine if the optimization approach can also improve identification of subjects across sessions when applied to specific networks (i.e., on subsets of nodes selected from whole-brain FC) we ran the SA algorithm separately on FC (both DSs) from the 7 RSNs. Successful optimizations were possible for the DMN, FP, and SAL network on DS 1; only the FP showed improvement on DS 2. Figure 3 shows the spatial localization of the network-specific fingerprint from DSs 1 and 2 (SA and GA algorithms) for the FP network (Table 1 summarizes the results).

Figure 3.

Surface projections of network-specific fingerprints. Panels (A) and (B) show SNs obtained from 20 runs of the SA algorithm on the FP on data set (DS) 1 (panel A) and DS 2 (panel B). Panels (C) and (D) show SNs obtained from 20 runs of the SA algorithm on the DMN and the SAL on DS 1. Panels (E) and (F) shows SNs obtained from a single run of the GA algorithm on the FP on DS 1 and DS 2 (compare to panels (A) and (B)). Color map in panels (A)–(D) indicates the number of times that a node was found within the SN set across 20 optimization runs. Black symbols with lower-case letters indicate the location of nodes that were consistently encountered in the network-specific fingerprint. (A) a (50, 18, 24 MNI; BA44, inferior frontal gyrus) was found in 12 runs, b (42, 10, 56 MNI; BA8, middle frontal gyrus) was found in 15 runs and c (−38, 26, 40 MNI; BA9, middle frontal gyrus) was found in 12 runs. (B) a (26, 42, −16 MNI; BA47, frontal pole) was found in 17 runs, b (42, 34, 24 MNI; BA9, middle frontal gyrus) was found in 15 runs, c (42, 18, 48 MNI; BA8 middle frontal gyrus) was found in 17 runs, d (58, −38, 40 MNI; BA40, supramarginal gyrus) was found in 12 runs, and e (−54, −38, 48 MNI; BA40, supramarginal gyrus) was found in 7 runs (left hemisphere). (C) a (−46, −54, 32 MNI; BA39, angular gyrus) and d (42, 62, 32; BA39, angular gyrus) was found in 19 runs, c (−14, 26, 56 MNI; BA8, superior frontal gyrus) was found in 7 runs, b (−6, 66, 8 MNI; BA10, frontal pole) was found in 10 runs, and e (18, 26, 56; BA6, superior frontal gyrus) was found in 13 runs. (D) a (−30, 42, 24 MNI; BA10, lateral frontopolar cortex) was found in 18 runs, b (−60, −38, 40; BA40, supramarginal gyrus) was found in 16 runs, c (−6, 2, 48 MNI; BA6, supplementary cortex) was found in 13 runs, d (26, 42, 24 MNI; BA9, dorsolateral prefrontal cortex) and e (18, 2, 72 MNI; BA6, superior frontal gyrus) were found in 17 runs each.

Table 1.

Algorithm performance by network

Networks nodes	DS 1						DS 2
	GA			SA			GA			SA
	Acci–f	Cfi–f	Rn	Acci–f	Cfi–f	Rn	Acci–f	Cfi–f	Rn	Acci–f	Cfi–f	Rn
DMN-418	30–30	0.28–0.62	400	30–30	0.28–0.62	401 ± 0	39–39	0.27–0.27	0	39–39	0.27–0.27	0
FP-192	30–30	0.32–0.39	72	30–30	0.32–0.62	181 ± 1.7	39–40	0.32–0.45	61	39–40	0.32–0.55	176 ± 3.4
ORB-185	22–22	0.22–0.23	9	22–22	0.22–0.23	85 ± 9.2	27–28	0.17–0.17	4	27–31	0.17–0.37	171 ± 3
SAL-124	28–28	0.27–0.27	0	30–30	0.27–0.51	111 ± 1.5	38–38	0.27–0.27	0	38–38	0.27–0.27	0
DAN-76	29–29	0.28–0.28	0	29–29	0.28–0.48	63 ± 2	35–37	0.27–0.34	29	35–37	0.27–0.34	52 ± 4
ASM-394	24–24	0.21–0.22	9	24–24	0.21–0.34	347 ± 4	31–33	0.23–0.26	90	31–34	0.23–0.44	381 ± 2.8
VIS-350	25–25	0.19–0.21	28	25–25	0.19–0.25	140 ± 10	30–30	0.17–0.17	0	30–30	0.17–0.17	0

Acc: Accuracy, Cf: Cost function, Rn: Removed nodes. Subindices i and f denote the values before and after running the algorithm, respectively. Values (mean ± std) from the SA algorithm were obtained after averaging across multiple runs (20). Names and total number of nodes comprising each network are listed on the leftmost column. See text for abbreviations of brain networks.

The cross-validation analyses performed after merging the 2 DSs revealed identical results as those reported independently in each DS. More specifically, the analyses carried out on the whole brain revealed that the FP aggregated most of the SNs (see Supplementary Fig. S2). In addition, the distribution of the SNs across the cortical mantle followed a highly similar distribution compared to that shown in Figure 2 (compared with bar graphs of Supplementary Fig. S2). The largest proportion of the SNs fell within the FP, the second largest was in the DMN, followed by SAL and DAN. Again, the primary areas (VIS and ASM) and the ORB network contained the lowest percentage of SNs (see Supplementary Fig. S2). Further analysis revealed an increase in the identification accuracy (except in 1 case) using the SNs obtained from the training DS on the testing DS (see Supplementary Fig. S3, first column). Once, we determined that the FP network accounted for most of the SNs we conducted an optimization analysis within the FP network. The distribution of the SNs followed a similar pattern as the patterns shown in Figure 3 (cf. see Supplementary Fig. S4).

Contributions of Local and Long-Distance Connections

We were interested to investigate the relative contributions of the spatial distances spanned by functional connections to identifying subjects across sessions. We classified local and long-distant connections following Sepulcre et al. (2010). Local and long-distance connections were distinguished by introducing physical distance restrictions in the voxel-by-voxel FC network. The contiguous neighborhood of a given voxel was considered as local connectivity while the voxels outside of this neighborhood were considered as distant connections. To define the local neighborhood we used spheres of different radii, spanning 14, 16, and 18 mm. These distance thresholds provide information about the connectivity between local areas and also minimize correlation that reflect smoothing between adjacent voxels (Sepulcre et al. 2010). We run the analyses independently for each radius.

We then approached the analysis in 2 ways. First, we performed the identification analysis separately for local and long-distance connections on the whole brain and on each individual RSN. We did not observe any strong differential contribution of either local or long-distance connections. Second, we tested whether local and long-distance connections contributed differentially as part of the functional network maintained among the SNs. Again, local and long-distance functional connections contributed equally (49/51%, respectively).

Role of TSNR and Gyrification

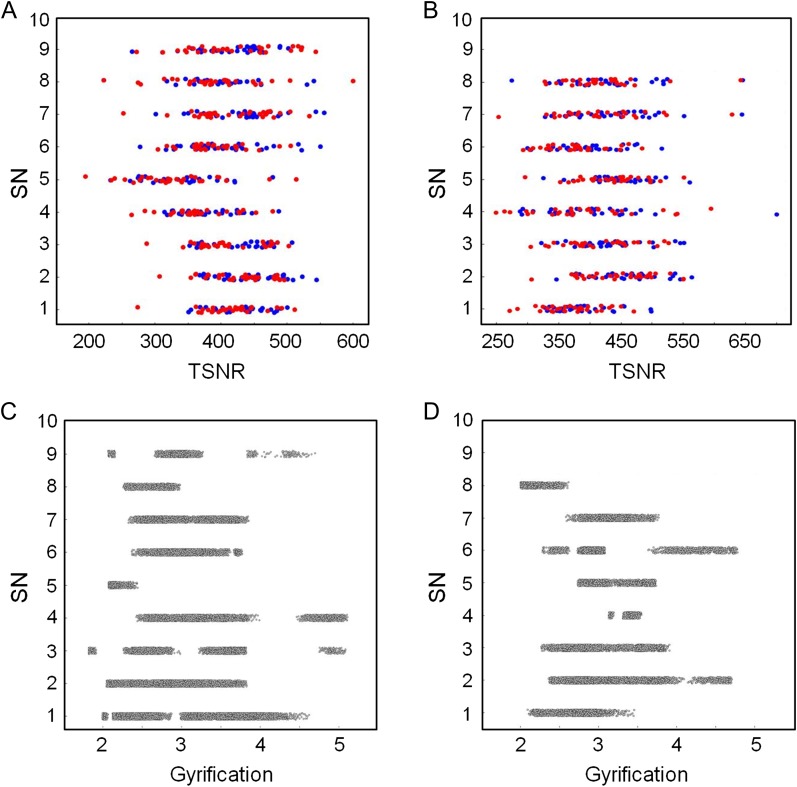
Regional differences in the TSNR may impact estimates of FC and fingerprinting. TSNR (mean_SN−1 = 423, mean_R−1 = 391, mean_SN−2 = 409, mean_R−2 = 376, from parcellation A; mean_SN−1 = 407, mean_R−1 = 389, mean_SN−2 = 396, mean_R−2 = 374, from parcellation B; indices 1, 2, SN, R denote session 1, session 2, SNs and non-SNs, respectively) was computed on the SNs obtained from 2 parcellations of DS 1 (see Fig. 2). No significant correlation between the TSNR values and the propensity of the nodes to be included in the survivor set was found on both sessions (Fig. 4A: γ₁ = 0.01, P₁ = 0.69, γ₂ = 0.01, P₂ = 0.66 for parcellation A; Fig. 4B: γ₁ = 0.01, P₁ = 0.25, γ₂ = 0.02, P₂ = 0.16, parcellation B). As a surrogate index of the SNR, the comparison between the node volume from SNs and non-survivors nodes resulted in nonsignificant differences (P-values = 0.23, 0.24 corresponding to the parcellations A and B).

Figure 4.

Scatter plots of frequency (out of 10 runs total) of SN as a function of TSNR (panels (A) and (B)) and gyrification (panels (C) and (D)). Red and blue markers in panels (A) and (B) correspond to data from sessions 1 and 2, respectively. Panels (A) and (C) show data computed from parcellation A. Panels (B) and (D) show data computed from parcellation B. There is no significant correlation between TSNR or gyrification and the frequency of a node being designated as SN. Data points are jittered along the y-axis to improve legibility (SN values are integers).

Local differences in gyrification (mean_SN = 3.04, mean_R = 3.03, parcellation A; mean_SN = 3.02, mean_R = 3.11, parcellation B) across the cortical mantle may have an impact on the computation of FC by biasing the contribution of cortical regions to between-session identifiability of subjects. To address this issue, we extracted the gyrification across the brain for 2 parcellations of the DS 1 (Fig. 4). No significant correlation between the gyrification values and the propensity of the nodes to be included in the survivor set was found (Fig. 4C; γ = 0.01, P = 0.95 for parcellation A; Fig. 4D; γ = 0.01, P = 0.85 for parcellation B).

Expression of Fingerprints across Time

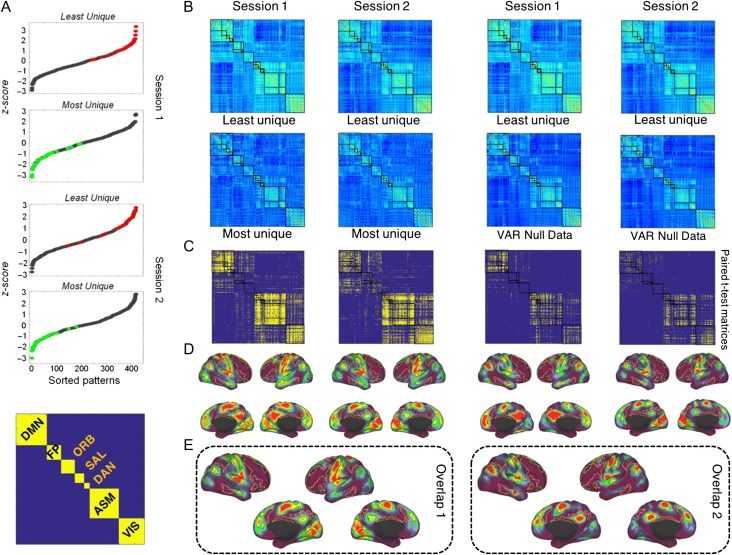
Next, we investigated the temporal expression of fingerprints by examining brief FC snapshots, computed for non-overlapping 40 s windows from 30 subjects (DS 1). We identified those patterns that, within a single session, exhibited the most/least unique features, that is, the weakest/strongest between-session similarity across all windows and all subjects, respectively. Figure 5A shows the distributions of the sorted averaged maximum/minimum correlation magnitudes for each subject and time window. Figure 5A (bottom) shows the matrix organization of the RSNs that was used to show the FC patterns and the statistical maps. Figure 5B shows the FC patterns that exhibited the lowest average correlations (“most unique”) and the highest correlations (“least unique”), aggregated across all subjects. The 2 patterns exhibit different network topologies. The “most unique” patterns display relatively low absolute FC magnitude (FC = 0.39, +/− 0.03 session 1; FC = 0.40, +/− 0.04 session 2) and low modularity (Q = 0.37, +/− 0.03 session 1; Q = 0.38, +/− 0.04 session 2), while the “least unique” patterns display higher absolute FC magnitude (FC = 0.45, +/− 0.05 session 1; FC = 0.44, +/− 0.04 session 2) and higher modularity (Q = 0.41, +/− 0.03 session 1; Q = 0.42, +/− 0.04 session 2). These differences were statistically significant (P < 0.01) and were reproducible across sessions. Figure 5B also shows the average FC null data patterns generated using the VAR models.

Figure 5.

Temporal expression of fingerprints. (A) Sorted similarity z-score values of FC patterns of all 14 time windows of each subject for sessions 1 and 2. Green and red markers indicate the minimum and maximum similarity values, respectively. In the bottom, it is shown the matrix organization of the RSN used to display the FC patterns and the statistical maps. (B) Most unique and least unique FC snapshots, corresponding to patterns with lowest and highest similarities across all windows and all subjects, respectively. The average of most/least unique features corresponds to the green and red markers in panel A. In the second row (third and fourth columns), are shown the average FC patterns corresponding generated by the VAR model. (C) Significant differences (P < 0.05, FDR-corrected, paired t-test) of the links between the most and least unique patterns in both sessions (first and second columns) and the most and null data patterns (third and fourth columns) in both sessions. The color map represents P-values. Hot colors indicate that FC connections (averaged across subjects) are greater for the least unique compared with the most unique patterns and compared with the null data. (D) Brain projection of the significant links in both sessions for both comparisons. The color map indicates the extent of similarity of FC connections across subjects. Hot colors indicate a high degree of similarity. The FP network is outlined on the surface. It exhibits low values, indicating (consistent with previous analyses; see Figs 2 and 3) that this network aggregates a large number of dissimilar (less consistent, more variable) links across subjects. (E) Overlapping maps of the sessions from the comparisons between “least unique” versus “most unique” (overlap map 1, spatial correlation value of 0.68) and from the comparisons between “least unique” versus “null data” (overlap map 2, spatial correlation value of 0.93). The overlapping maps show that highly similar significant connections are mainly located outside of the FP and ORB network.

Figure 5C shows a statistical map comparing the set of “least unique” and “most unique” patterns (first and second columns) as well as the set of “least unique” and “null data” patterns (third and fourth columns) across all of the 30 subjects (paired t-test, P < 0.05, FDR-corrected), with hot colors indicating greater FC in the “least unique” versus the “most unique” and “least unique” versus “null data” patterns. We note that the sharpest positive differences are seen within the DMN, VIS, ASM, DAN, and SAL network (in contrast to the FP and ORB networks) This suggests that less unique network patterns are associated with FC that is internally strong within DMN, VIS, ASM, DAN, and SAL networks. Figure 5D shows a projection of the density of connections that are significantly stronger in the “most unique” versus “least unique” and versus “VAR null data” patterns within each network. All results replicate across sessions 1 and 2.

We note that most of the highly similar significant connections are not falling within the FP and ORB networks. It is also worth noting the high similarity in both contrasts comparing the “least unique” versus “most unique” and “least unique” versus “null data” (Fig. 5D). While the number of significant connections is diminished in the null data comparison, their pattern is highly similar (Fig. 5C,D).

Figure 5E shows 2 overlapping maps, 1 showing the overlap across sessions from the comparisons between “least unique” versus “most unique” (Fig. 5E overlap 1) and the other showing the overlap across sessions from the comparisons between “least unique” versus “null data” (Fig. 5E overlap 2). In addition, we quantified the overlap between the 2 sessions for each 1 of the 2 comparisons. The spatial cross correlation value for overlap 1 was 0.68 while for overlap 2 it was 0.93. Once again it can be seen that highly similar significant connections are mainly outside of the FP and ORB network.

It is worth noting that these differences are independent of the size of the network and the underlying node degree. Specifically, the SAL and DAN which are smaller networks than the FP and ORB (see Fig. 5A bottom), aggregate significantly more highly similar connections across subjects (see Fig. 5C). Instead, the FP and ORB, while containing nodes of very high degree (cortical hubs), do not contain many highly similar connections.

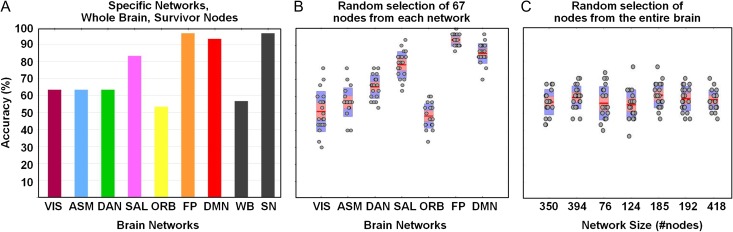
Finally, we attempted to identify patterns that best allowed the identification of subjects across the 2 sessions (30 subjects, DS 1), by computing the similarities of FC snapshots obtained from all subjects across the 2 sessions. This was performed for the whole brain, network-by-network (VIS, ASM, DAN, SAL, ORB, FP, and DMN) and for the set of SNs identified by SA (Fig. 6A). Then, we generated 20 networks comprising 67 nodes selected at random from each one of the functional networks (Fig. 6B). The number 67 was chosen because it is the number of SNs after 20 runs of SA in the FP. Accuracy is very similar to that achieved when using each individual network as a whole (compare Fig. 6A). However, when generating 20 networks comprising an equivalent numbers of nodes to the 7 network partition (but randomly selected from the whole brain; Fig. 6C), we did not observe an effect of network size and accuracy levels were similar to levels seen for the whole brain (compare Fig. 6A).

Figure 6.

Fingerprint expression across sessions separated one month apart on DS 1. (A) Accuracy levels on specific RSNs, SNs (obtained by SA optimization) and the whole-brain network (WB). (B) Accuracy levels of networks constructed using 67 randomly selected nodes from each RSN (20 repeats). (C) Accuracy levels of networks constructed using randomly selected nodes from the entire brain, with the number of nodes corresponding to the sizes of the seven RSNs (20 repeats).

Discussion

In this study, we identified network markers of individual variability in FC, both in space, by localizing them to specific regions in the human brain, and in time, by characterizing how expression varies across brief FC snapshots. Our spatial analysis indicated that these markers were aggregated within heteromodal and multimodal regions. An optimization analysis carried out on specific networks as well as the whole brain determined a specific set of key nodes mainly located within the FP that allowed identification of individuals with high accuracy. In these spatial identification analyses, we found a strong effect of parcellation size, with finer parcellations resulting in better accuracy. Looking across shorter time windows, we classified and compared connectivity snapshots according to high similarity (“least unique”) and low similarity (“most unique”) across individuals. Importantly, these patterns exhibited different network topology as measured by modularity, with least unique patterns showing higher modularity than most unique patterns.

Previous studies have reported on the spatial localization of potential individual FC fingerprints in the human brain (Miranda-Dominguez et al. 2014, Finn et al. 2015, Airan et al. 2016). For instance, Finn et al. (2015) identified subjects using cross-session Pearson correlations of FC mapped into a 268-node parcellation. To investigate the role of parcellation size on identification accuracy, we created 10 random parcellations on 18 levels of granularity, with 6 of these levels (313, 378, 701, 1220, 1792, and 3198) exceeding the spatial resolution of the 268-node atlas. We found that increasing the number of parcels generally improved identification accuracy, with maximal performance reached at ~700 nodes (see Fig. 1). Consistent with our findings, Airan et al. (2016) pointed out that a higher number of ROIs in the parcellation increases the ability to differentiate between individuals, and Finn et al. (2015) reported an increase in accuracy after changing the parcellation from 68 nodes to 268 nodes.

Regarding localization, Finn et al. (2015) found that the medial frontal network and the “FP” yielded higher accuracy for individual identification. In our study, we ran an optimization algorithm on the whole brain allowing us to prune the network and identify the minimal set of nodes needed for fingerprinting. In accordance with Finn et al. (2015), our analyses indicated that the FP contributed most to this minimal set. Further, in partial accordance with their “medial prefrontal network”, we found that the SAL network also made significant contributions. However, the authors’ definition of the medial prefrontal network includes the ORB network which in our analyses performed poorly for identification purposes. Notwithstanding, it is worth noting that orbitofrontal cortex is a known area susceptible to signal dropout which may partially account for the areas poor performance in identification analyses. In parallel, we ran the same analysis on each one of the RSNs reducing the number of nodes needed to identify individuals, creating a network-specific fingerprint for each RSN. Among these, we found that the fingerprint of the FP allowed highest identification accuracy.

Miranda-Dominguez et al. (2014) found that the most variable connections between individuals were located within higher-order heteromodal association areas. It is worth noting that their results are consistent with the results presented by Finn et al. (2015) regarding the “FP” but not the “medial frontal network”. Airan et al. (2016) used a non-parametric statistical test for individual differentiation. Consistent with our results, these authors found that the FP contributes substantially toward individual subject identification, with additional significant contributions of the precuneus and posterior cingulate, both key components of the DMN. This corresponds to our finding that the DMN allowed for highly accurate identification of subjects. However, the optimization analyses pinpointed the FP as an individual marker in both DSs while localization of additional SNs to the DMN occurred only in DS 1. Our study together with previous investigations strongly suggests that FP is the strongest candidate carrying network markers of individuality. We add additional support by applying a whole-brain optimization approach that localizes network markers of individual variations in FC to a small number of key nodes within the FP network.

The neurobiological mechanisms that determine the location of the human brain FC fingerprint remain largely unknown. In this context, it is worth noting that Mueller et al. (2013) showed a specific topographic distribution of FC variability, with greater variability in heteromodal or association areas of cortex. Corresponding to their results, we found greater interindividual variability associated with heteromodal association areas than unimodal areas. Notably, these areas are associated with higher order cognitive functions (Goldman-Rakic 1988) such as intelligence (Cole et al. 2012), memory, and learning (Fuster 2001), mental rotation (Kosslyn et al. 1998) or problem solving (Christoff et al. 2001). The function of the FP network has been linked to the integration and processing of different kinds of information. The possibility to reorganize, recombine, and integrate information in a variety of ways to solve different problems might confer an evolutionary advantage. Regions which experienced the largest cortical surface expansion across evolution coincide with the FP (Van Essen and Dierker 2007) with specific hot spots in the DLPFC and the temporo-parietal junction (TPJ). Interestingly, these areas (DLPFC and TPJ) also stand out in our optimization analysis (see Fig. 2). In contrast, areas that experienced less cortical expansion such as visual and motor systems (unimodal networks) correspond in our analyses with areas or networks which had lower accuracy in identification analyses.

In addition to the function of the FP as a higher cognitive or control network, other characteristics have been described associated with the topological properties within the network. For instance, the FP has been described to be a member of an anatomically defined rich club (van den Heuvel and Sporns 2011). However, other areas that are also members of the structural rich club, such as the precuneus, do not appear to be strong network markers of individual differences in FC (see Fig. 5). This suggests only partial overlap between FC fingerprints and underlying structural connectivity. In addition to clarifying the anatomical substrate, other open issues concern developmental patterns, cross-species comparisons, and relation to cognitive function and genetics. Regarding development, future studies across different ages may illuminate the developmental mechanisms through which fingerprints emerge. Cross-species comparisons would be essential to clarify their association with phylogenetically late-developing regions, for example, in the FP system. Regarding cognitive function, future studies might investigate whether variations in FC fingerprints can predict individual differences in cognitive and behavioral performance, and whether they are selectively disrupted in the course of brain disorders. Finally, the role of genetic factors and patterns of heritability on FC fingerprints remain to be examined.

In addition to spatial localization, our study also tracked the expression of FC functional fingerprints across time. Within single scanning sessions, we classified and compared the least unique and most unique patterns for each of the subjects. The analysis revealed that the least unique connection patterns across subjects were found outside of the FP. Consistent with our identification and optimization analysis that focused on spatial localization, the FP aggregates the most dissimilar connections when examining dynamic patterns that unfold across the subjects’ actual time series as well as using a surrogate null FC data (Fig. 5). These results have several implications. First, using independent approaches we have shown convergent evidence pointing to the FP as the most reliable marker of individual variations in FC. Second, we have shown that during a single scanning these markers are expressed at different levels. The latter finding resonates with recent work on dynamical variations of FC that has shown fluctuations in specific topological network characteristics such as modularity, with highly modular patterns characterized by disconnection of task-positive from task-negative systems (Betzel et al. 2016). In our analysis, we find that most unique snapshots are characterized by lower modularity as well as lower average FC, compared to more commonly shared FC patterns. Third, we showed that this is a robust phenomenon observed across different scanning sessions separated by one month (Fig. 5D,E). Furthermore, using FC snapshots of the fingerprint network identified by whole-brain optimization we were able to identify the subjects across sessions with the highest accuracy in comparison with other networks (Fig. 6A).

Our study is subject to several limitations. The scope of the study was focused on functional fingerprints measured at the macroscale, corresponding to large neural populations aggregated into voxel clusters. Working at finer scales, for example at the single voxel level (or below), would likely allow pinpointing network markers of individual variability with greater spatial accuracy. Currently, limits on computational time prohibit the use of the voxel scale for the optimization approach used in our study to identify network markers from whole-brain data. Other limitations include the modest sizes of our 2 subject cohorts, the brief duration of the resting-state scans, boundaries on window sizes used for creating FC snapshots, and choices of preprocessing parameters. Additional studies will be needed to address these limitations more comprehensively.

In summary, our study takes an additional step toward the characterization of individual differences in human FC, by examining these individual differences in both space and time. Using network-specific and whole-brain optimization approaches we identify a specific subset of nodes corresponding to network markers of individual variability. This fingerprint is not only localized in space, but differentially expressed across time. By identifying neural substrates of individual differences in brain architecture our study opens new avenues for mapping brain-behavior relations in basic and clinical research.

Supplementary Material

Supplementary material are available at Cerebral Cortex online.

Funding

The authors acknowledge funding from the J.S. McDonnell Foundation (22002082 to O.S.) and the National Institutes of Health (R01 AT009036 to C.P.-G. and O.S.).