Monitoring molecular nonadiabatic dynamics with femtosecond X-ray diffraction

Significance

X-ray crystallography has long been used to determine the structure of crystals and molecular samples. More recent advancements in light sources and computational methods made it possible to routinely determine the structure of large proteins. The introduction of X-ray free-electron lasers opens up the possibility to track the dynamics of molecular structures on a femtosecond time scale and to create molecular movies of chemical reactions. The theory of time-independent diffraction is well known. However, time-resolved diffraction techniques pose not only new challenges to experiments but also to their interpretation. In this work, we present a unified theoretical framework that will aid experimental interpretations as well as predictions of types of X-ray diffraction experiments.

Abstract

Ultrafast time-resolved X-ray scattering, made possible by free-electron laser sources, provides a wealth of information about electronic and nuclear dynamical processes in molecules. The technique provides stroboscopic snapshots of the time-dependent electronic charge density traditionally used in structure determination and reflects the interplay of elastic and inelastic processes, nonadiabatic dynamics, and electronic populations and coherences. The various contributions to ultrafast off-resonant diffraction from populations and coherences of molecules in crystals, in the gas phase, or from single molecules are surveyed for core-resonant and off-resonant diffraction. Single-molecule $\propto N$ scaling and two-molecule $\propto N^2$ scaling contributions, where $N$ is the number of active molecules, are compared. Simulations are presented for the excited-state nonadiabatic dynamics of the electron harpooning at the avoided crossing in NaF. We show how a class of multiple diffraction signals from a single molecule can reveal charge-density fluctuations through multidimensional correlation functions of the charge density.

The term diffraction denotes the interference of waves elastically scattered from different positions in space (1). Since the phase difference between waves originating from different spatial locations encodes the sample geometry, the diffraction of waves can be used to infer the spatial pattern of the arrangement of scatterers. This technique has long been used with off-resonant X-rays to reveal the atomic structure of crystalline solids, where the long-range order amplifies the diffraction signal for certain values of the momentum transfer scattering vector $\mathbf{q}$, known as the Bragg peaks. The location pattern of the Bragg peaks then reveals the long-range crystal structure, while their intensity pattern reflects the unit-cell structure through the classical diffraction signal $S\left(\mathbf{q}\right)\propto |\sigma \left(\mathbf{q}\right){|}^2$, where $\sigma \left(\mathbf{q}\right)$ is the ground-state charge density and $\mathbf{q}={\mathbf{k}}_{\mathit{\text{s}}}-{\mathbf{k}}_{\mathit{\text{p}}}$ is the scattering momentum change between the incident ${\mathbf{k}}_{\mathit{\text{p}}}$ and scattered ${\mathbf{k}}_{\mathit{\text{s}}}$ wavevectors. An important caveat to this technique is that the phase of the $\mathbf{q}$-space charge density is lost due to the squaring. This well-known “phase problem” complicates the retrieval of the real-space charge density $\sigma \left(\mathbf{r}\right)$ by a Fourier transform of $\sigma \left(\mathbf{q}\right)$. Several methods, such as oversampling, have been developed to overcome this difficulty (2–4). Diffraction is also commonly used in noncrystalline samples to reveal, e.g., the distribution of interparticle distances in fluids. Increasingly bright X-ray free-electron laser (FEL) light sources hold the promise of producing detectable time-resolved diffraction patterns even from single molecules, revealing the complete real-space structure of the molecular charge density without the need for often time-consuming crystallization (5–8). At present, diffraction from nanocrystals have been achieved (9, 10), but not from single molecules. Recently demonstrated time-resolved spectroscopy on single molecular ions suggests the possibility for single ion time-resolved diffraction (8).

Coherent X-ray light sources capable of producing bright, ultrafast pulses have been developed [e.g., the Stanford Linear Coherent Light Source produces pulses with $10^{12}-10^{13}$ photons over an energy range of 280–20,000 eV with durations as short as $\sim 10$ fs, and a further upgrade, LCLSII, is underway (11)]. Similar hard X-ray facilities are available at the European XFEL (Hamburg), SwissFEL (Switzerland), the Korean PAL-XFEL, and the Japanese SACLA. Numerous exciting opportunities are opened up by this technology, including reconstructing real-space molecular movies via time-resolved diffraction as well as time-domain and broadband X-ray Raman experiments (8, 12–16). The development of FELs (17–20) as well as tabletop light sources, such as high-harmonic generation for soft X-rays and laser-driven plasma sources for hard X-rays (21–24), has permitted the generation of bright ultrashort X-ray pulses (25–27). This has opened up the possibility of carrying out time-dependent, pump-probe diffraction in which a system is first pumped to an excited state by a visible or UV pulse and is then probed via the diffraction of a second X-ray pulse at varying time delays, allowing the reconstruction of “molecular movies” that visualize the evolving electron density (12–15, 28, 29).

In this work, we provide a unified quantum electrodynamical (QED) description of time-resolved diffraction signals from gas-phase samples (or single molecules) and from systems that have longer-range structural order such as crystals and liquids. We show that the two types of signals are dominated by different terms and thus have a fundamentally different character. It is tempting to describe the time-resolved signals by simply replacing $\sigma \left(\mathbf{q}\right)$ in the above classical diffraction equation with the time-dependent charge density to obtain $S\left(\mathbf{q},t\right)\propto |\sigma \left(\mathbf{q},t\right){|}^2$. However, as we will show, this equation holds for diffraction from crystals but does not apply to single-molecule diffraction or to diffraction in the gas phase (Eq. 4 and refs. 30 and 31). Moreover, while picosecond diffraction (32, 33) is well established and can be interpreted by using kinetic models for the evolving charge density, femtosecond diffraction with FEL sources involves electronic coherences that must be treated with care. Although we will speak throughout of X-ray diffraction, all results are equally applicable to the diffraction of femtosecond electron pulses. This is an emerging technology that can also probe the electronic charge density of material samples (27, 34, 35). We further discuss X-ray scattering resonant with core atomic transitions, which reveals correlations of core and valence electrons, and comment on multidimensional diffraction involving photon coincidence detection where higher-order intensity correlation functions of light are detected (13, 36).

X-Ray Scattering and the Electronic Charge Density

Infrared or visible light spectroscopies may be adequately described by invoking the dipole approximation in which the field-matter interaction energy is given by the dot product of the external field and a material quantity, the transition dipole. This is the first in a series of higher-order contributions to the field-matter coupling known as the multipolar expansion (37). Retaining only the lowest (dipolar) term is well-justified as long as the radiation field amplitudes do not vary appreciably over the relevant material length scales. This condition may not hold in the hard X-ray regime, and a more general treatment is required. Rather than patching up the dipolar approximation with higher-order multipoles, it is simpler to recast the problem in the framework of the minimal-coupling Hamiltonian wherein the exact coupling of matter to the radiation field is obtained by the substitution $\widehat{\mathbf{p}}\to \widehat{\mathbf{p}}-e\widehat{\mathbf{A}}$ where $\widehat{\mathbf{p}}$ is the electronic momentum and $\widehat{\mathbf{A}}$ is the electromagnetic vector potential. The multipolar expansion is then avoided from the outset. This substitution yields the minimal coupling field-matter interaction Hamiltonian which will be used throughout the article (37)

$${\widehat{H}}_{\text{int}}=-\int \mathrm{d}\mathbf{r}\left(\widehat{\mathbf{j}}\left(\mathbf{r}\right)-\frac{1}{2}\widehat{\sigma }\left(\mathbf{r}\right)\widehat{\mathbf{A}}\left(\mathbf{r}\right)\right)\cdot \widehat{\mathbf{A}}\left(\mathbf{r}\right),$$ [1]

where we work in atomic units and $\widehat{\mathbf{j}}\left(\mathbf{r}\right)$ and $\widehat{\sigma }\left(\mathbf{r}\right)$ are the elementary field-free current operator and the charge-density operator, respectively (defined in terms of Fermionic field operators in SI Appendix, Eqs. S13 and S14). Scattering occurs when a vacuum mode of the electromagnetic field is populated due to the matter interaction with the incoming light field. Calculating the total number of photons produced in a given signal mode ${\mathbf{k}}_s$ to second order in ${\widehat{H}}_{int}$ (for derivation, see SI Appendix) gives

$$\begin{array}{ccc}\hfill S\left({\mathbf{k}}_s\right)& =\hfill & \frac{{\alpha }^3{\omega }_s}{4{\pi }^2}\int \mathrm{d}t\mathrm{d}t\prime e^{i{\omega }_s\left(t-t\prime \right)}\hfill \\ \hfill & \hfill & \times \left[{ϵ}^{\left({\lambda }_s\right)}\left({\widehat{\mathbf{k}}}_s\right)\cdot ⟨\widehat{\mathbf{J}}\left(-{\mathbf{k}}_s,t\prime \right)\widehat{\mathbf{J}}\left({\mathbf{k}}_s,t\right)⟩\cdot {ϵ}^{\left({\lambda }_s\right)*}\left({\widehat{\mathbf{k}}}_s\right)\right],\hfill \end{array}$$ [2]

where $\alpha =1/c$ is the fine-structure constant, ${\omega }_s$, ${\mathbf{k}}_s$ and ${ϵ}^{\left({\lambda }_s\right)}\left({\widehat{\mathbf{k}}}_s\right)$ are the frequency, wavevector, and polarization vector of the scattered light, and $\widehat{\mathbf{J}}\left(\mathbf{r}\right)=\widehat{\mathbf{j}}\left(\mathbf{r}\right)-\widehat{\sigma }\left(\mathbf{r}\right)\widehat{\mathbf{A}}\left(\mathbf{r}\right)$ is the gauge-invariant electromagnetic current in the presence of the vector potential (SI Appendix, Eq. S23). The expectation value $⟨\dots ⟩$ is taken over all nuclear and electronic degrees of freedom.

Hereafter, we focus on the off-resonant regime, where the X-ray photon is tuned away from core transitions while the extension to resonant scattering will be presented in Summary and Future Outlook. We thus substitute the definition of $\widehat{\mathbf{J}}$ into Eq. 2 and only retain the $\widehat{\sigma }$ terms, yielding

$$\begin{array}{ccc}\hfill S\left(\mathbf{q}\right)& =\hfill & \frac{{\alpha }^3{\omega }_s}{4{\pi }^2}{\left|{ϵ}^{\left({\lambda }_s\right)}\left({\widehat{\mathbf{k}}}_s\right)\cdot {ϵ}^{\left({\lambda }_p\right)*}\left({\widehat{\mathbf{k}}}_p\right)\right|}^2\hfill \\ \hfill & \hfill & \times \int \mathrm{d}t|A_p\left(t\right){|}^2⟨\widehat{\sigma }\left(-\mathbf{q},t\right)\widehat{\sigma }\left(\mathbf{q},t\right)⟩,\hfill \end{array}$$ [3]

where $A_p\left(t\right)$ is the temporal envelope of the vector potential of the incoming X-ray pulse; we have assumed an ultrashort pulse so that $t=t\prime$ (in Eq. 2, this can be formalized by taking the Wigner spectrogram of the X-ray $\mathbf{A}$-field to be broad and flat). Writing Eq. 3 in terms of the electric field $E_p\left({\omega }_p\right)=-i{\omega }_p{A}_p\left({\omega }_p\right)$, results in the prefactor ${\alpha }^3{\left({\omega }_s/{\omega }_p\right)}^2|{ϵ}^{\left({\lambda }_s\right)}\left({\widehat{\mathbf{k}}}_s\right)\cdot {ϵ}^{\left({\lambda }_p\right)*}\left({\widehat{\mathbf{k}}}_p\right){|}^2$, which differs from the Thomson differential scattering cross-section only (Eq. 3) in the power of the $\alpha$ and ${\omega }_s/{\omega }_p$ factors, the difference being due to the modeling of the photon absorption at the detector and the classical treatment of the incoming field (see discussion after SI Appendix, Eq. S33 in SI Appendix). We henceforth omit this prefactor for brevity.

Although formally exact when expressed in terms of the total sample electron-density operator $\widehat{\sigma }$, our final expression is more practical when recast in terms of electron densities of individual molecules ${\widehat{\sigma }}_{\alpha }$. For a sample composed of identical molecules located at positions ${\mathbf{r}}_{\alpha }$, we have ${\widehat{\sigma }}_{\text{Total}}\left(\mathbf{r}\right)={\sum }_{\alpha }\widehat{\sigma }\left(\mathbf{r}-{\mathbf{r}}_{\alpha }\right)$. The charge-density operators in Eq. 3 then generate a double sum over molecules $\alpha$ and $\beta$, which can be separated into one-molecule ($\alpha =\beta$) and two-molecule ($\alpha \ne \beta$) terms denoted $S_1$ and $S_2$, respectively:

$$S_1\left(\mathbf{q},T\right)=N\int \mathrm{d}t|E_p\left(t-T\right){|}^2⟨\widehat{\sigma }\left(-\mathbf{q},t\right)\widehat{\sigma }\left(\mathbf{q},t\right)⟩$$ [4]

$$S_2\left(\mathbf{q},T\right)=F\left(\mathbf{q}\right)\int \mathrm{d}t\left|E_p\left(t-T\right){|}^2\right|⟨\widehat{\sigma }\left(\mathbf{q},t\right)⟩{|}^2.$$ [5]

Here, $N$ is the number of active molecules, and we have explicitly indicated the dependence on the central time $T$ of the X-ray pulse envelope $E_p\left(t-T\right)$. We have further introduced the structure factor

$$F\left(\mathbf{q}\right)=\sum _{\alpha }\sum _{\beta \ne \alpha }{e}^{-i\mathbf{q}\cdot \left({\mathbf{r}}_{\alpha }-{\mathbf{r}}_{\beta }\right)},$$ [6]

which encodes the long-range, intermolecular structure of the sample. We note that, aside from the $F\left(\mathbf{q}\right)$ factor and the convolution with the X-ray temporal pulse envelope $E\left(t-T\right)$, the two-molecule signal (Eq. 5) matches the intuitive form of the classical time-resolved diffraction signal discussed in the introduction, while the single-molecule contribution (Eq. 4) does not.

In crystals, $F\left(\mathbf{q}\right)$ is sharply peaked at the Bragg points ${\mathbf{q}}_{\text{Bragg}}$ which are directly related to reciprocal lattice vectors. At these Bragg peaks, the terms in the double summation coherently add up in phase and the signal scales as $N^2$, i.e., quadratically in the molecule number. Away from the Bragg peaks, these terms have essentially a random relative phase, and the signal is negligible. The positions of these Bragg peaks can then be used to obtain the crystal structure, while the $\mathbf{q}$-space charge density can be sampled at the Bragg peaks or near the central maximum, the latter requiring that the molecules are sufficiently close compared with the probing wavelength. The effect of structural disorder in a crystal (e.g., due to phonons) is to attenuate the Bragg scattering (which originates from the average structure) and produce a diffuse scattering that, while still reaching its maximum value at the Bragg peaks, is present throughout broad regions of reciprocal space (38). Particular models of the disorder, such as the Debye–Waller (SI Appendix), can be used to interpolate between ordered and disordered samples.

In the case of liquids, $F\left(\mathbf{q}\right)$ shows rings at the nearest- and next-nearest-neighbor distances, etc., but decays to zero for larger values for the lack of long-range structure. In the completely disordered case of a gas, the molecular distribution is uniform in space and $F\left(\mathbf{q}\right)$ vanishes except at the central maximum ($\mathbf{q}=0$). This can be seen by taking the limit of large disorder (SI Appendix, Debye–Waller Factor) or by taking the continuum limit of Eq. 6 and integrating over all space, assuming a homogenous distribution of molecules to obtain a delta function $\delta \left(\mathbf{q}\right)$.

When the terms in the structure factor $F\left(\mathbf{q}\right)$ add coherently, such as at the ${\mathbf{q}}_{\text{Bragg}}$, the resulting $N^2$-scaling overwhelms the $N$-scaling of the single-molecule signal $S_1$, and the diffraction pattern is well approximated by $S_2$ (Eq. 5). In contrast, the signal between the Bragg peaks or from a sample lacking long-range order, such as a gas, is dominated by the single-molecule signal (Eq. 4) since $\left.F\left(\mathbf{q}\right)\right)$ is negligible in these regimes. Similarly, diffraction of an intense FEL pulse by a single molecule is also given by Eq. 4 (28, 31, 39).

The time dependence of the charge-density operators in Eqs. 4 and 5 can be simplified by expansion in system eigenstates. Such expansions are given in SI Appendix, but these full electronic+vibrational eigenstates are too expensive to calculate for any but the simplest systems. In the following section, we will instead expand the time-dependent wavefunction in adiabatic electronic eigenstates and keep the nuclear configuration in a real-space wave packet representation (rather than using vibronic eigenstates).

Time-Resolved Diffraction Movies of Nonadiabatic Dynamics

Conical intersections (CoIns) can be found in nearly every polyatomic molecule and dominate the outcome of many photochemical reactions (40). CoIns provide fast, sub-100-fs nonradiative decay channels that are defined by a strong coupling between nuclear and electronic degrees of freedom. Their direct spectroscopic detection has not yet been demonstrated experimentally. However, we argue that the strong mixing of the nuclear and electronic degrees of freedom creates an electronic coherence that generates clear spectroscopic signatures (41).

In the following, we will investigate the effect of electronic coherences on the diffraction pattern in ordered as well as unordered samples. In ultrafast, time-resolved optical pump/X-ray probe diffraction experiments, the system is pumped into an excited state, and the subsequent coupled electronic and nuclear dynamics is probed after a variable time-delay $T$. This is depicted diagrammatically in Figs. 1 and 2 where a preparation process by an arbitrary pulse sequence is represented by the shaded box (an example of such a preparation is shown in SI Appendix, Fig. S1), the following free-propagation period is represented by a checkered box, and arrows represent the interactions with the X-ray probe. The indices $i$, $j$, or $k$ refer to the general case representing an arbitrary number of states, and $\mathbf{R}$ refers to and arbitrary number nuclear degrees of freedom. The time-dependent wave function is then expanded as

$$\left|\mathrm{\Psi }\left(\mathbf{q},\mathbf{R},t\right)\right.⟩=\sum _i{c}_i\left(t\right)\left|{\chi }_i\left(\mathbf{R},t\right)\right.⟩\left|{\phi }_i\left(\mathbf{q},\mathbf{R}\right)\right.⟩,$$ [7]

where $c_i\left(t\right)$ is the electronic state amplitude and $\left|{\chi }_i\left(t\right)\right.⟩$ is the time-dependent normalized nuclear wave packet on the electronic state ${\phi }_i\left(\mathbf{q},\mathbf{R}\right)$ (note that we abbreviate $\left|{\varphi }_i\right.⟩$ by $|i⟩$ in the following). The time evolution of $\mathrm{\Psi }$ is governed by the molecular Hamiltonian in the basis of adiabatic electronic states:

$$H_{ij}\left(\mathbf{R}\right)={\delta }_{ij}\left(\widehat{T}+{\widehat{V}}_i\left(\mathbf{R}\right)\right)+\left(1-{\delta }_{ij}\right){\widehat{K}}_{ij}\left(\mathbf{R}\right),$$ [8]

where $\widehat{T}$ is the kinetic energy operator of the nuclei, ${\widehat{V}}_i$ is the adiabatic potential energy surface of the $i$th electronic state, and ${\widehat{K}}_{ij}$ is the nonadiabatic coupling between state $i$ and $j$.

Fig. 1.

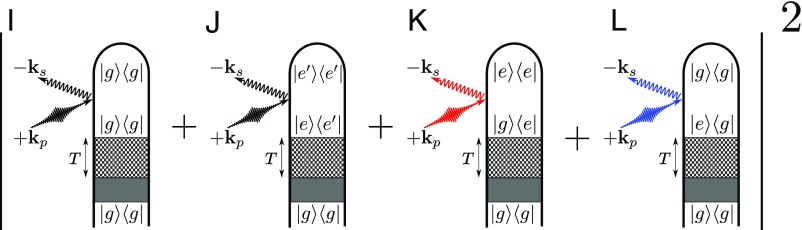
Loop diagrams for two-molecule (Eq. 5) X-ray scattering processes with the amplitude-squared form explicitly indicated. The shaded area represents an arbitrary excitation that prepares the system in a superposition state of $|g⟩$ and $|e⟩$ (further explained in SI Appendix, Fig. S1). We denote modes of the X-ray probe pulse with $p$ and $p\prime$, whereas $s$, $s\prime$ represent relevant scattering modes [${\mathbf{k}}_{p^{\left(\prime \right)}}$ has frequency ${\omega }_{p^{\left(\prime \right)}}$ and ${\mathbf{k}}_{s^{\left(\prime \right)}}$ has frequency ${\omega }_{s^{\left(\prime \right)}}$]. Elastic scattering processes come with ${\widehat{\sigma }}_{gg}$ or ${\widehat{\sigma }}_{ee}$ and are denoted by black field arrows. Inelastic processes in which the molecule gains (Stokes) or loses (anti-Stokes) energy to the field come with ${\widehat{\sigma }}_{ge}$ or ${\widehat{\sigma }}_{eg}$ depending whether the action is on the ket or bra and are denoted with red and blue field arrows to indicate the field’s spectral shift due to the particular diagram. Note: In diagram J, the energy order of states $e,e\prime$ is not set. We have depicted the elastic case for specificity. Diagrams I–L identify the corresponding terms in Eq. 11.

Fig. 2.

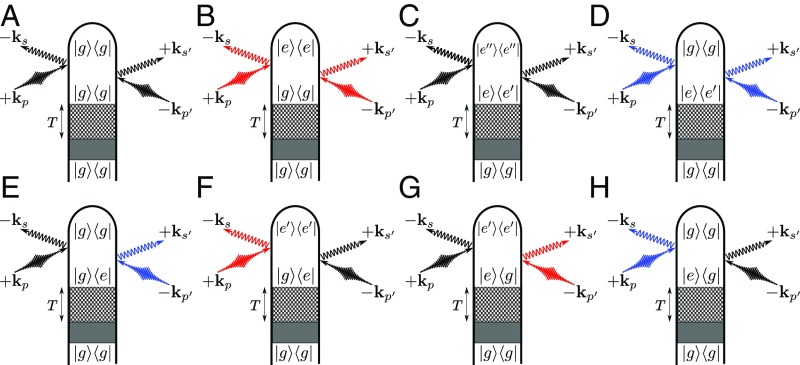
Loop diagrams for single-molecule (Eq. 4) X-ray scattering processes. The shaded area represents an arbitrary excitation that prepares the system in a superposition of $|g⟩$ and $|e⟩$ states (further explained in SI Appendix, Fig. S1). The checkered box represents a field-free propagation period $T$ that separates the state preparation from the X-ray probing process. We denote modes of the X-ray probe pulse with $p$ and $p\prime$, whereas $s$, $s\prime$ represent relevant scattering modes (${\mathbf{k}}_{p^{\left(\prime \right)}}$ has frequency ${\omega }_{p^{\left(\prime \right)}}$ and ${\mathbf{k}}_{s^{\left(\prime \right)}}$ has frequency ${\omega }_{s^{\left(\prime \right)}}$). Elastic scattering processes come with ${\widehat{\sigma }}_{gg}$ or ${\widehat{\sigma }}_{ee}$ and are denoted by black field arrows. Inelastic processes in which the molecule gains (Stokes) or loses (anti-Stokes) energy to the field come with ${\widehat{\sigma }}_{ge}$ or ${\widehat{\sigma }}_{eg}$ depending whether the action is on the ket or bra and are denoted with red and blue field arrows to indicate the field’s spectral shift due to the particular diagram. Note: In C, F, and G, the energy order of states $e,e\prime ,e^{″}$ is not set. We have depicted the elastic cases for specificity. Diagrams A–H identify the corresponding terms in Eq. 13.

Electronic operators, such as the charge density, generally depend on the nuclear configuration too, so that $\widehat{\sigma }\left(\mathbf{q}\right)=\widehat{\sigma }\left(\mathbf{q};\mathbf{R}\right)$. The charge density will therefore remain an operator due to this dependence, even after taking matrix elements in the electronic subspace. We thus denote

$$⟨i\left|\widehat{\sigma }\left(\mathbf{q},\mathbf{R}\right)\right|j⟩={\widehat{\sigma }}_{ij}\left(\mathbf{q};\mathbf{R}\right),$$ [9]

with the circumflex notating the operator-valued nature of the charge density in the nuclear $\mathbf{R}$ space. Below, we will omit the explicit $\mathbf{R}$-dependence for conciseness.

Time-Dependent Diffraction from Ordered vs. Unordered or Single-Molecule Samples.

For a sample possessing long-range order, so that the structure factor is nonvanishing, the signal is dominated by the two-molecule scattering Eq. 5, which we now recast as

$$S_2\left(\mathbf{q},T\right)=F\left(\mathbf{q}\right)\int \mathrm{d}t|E_p\left(t-T\right){|}^2{\tilde{S}}_2\left(\mathbf{q},t\right).$$ [10]

Expanding ${\tilde{S}}_2\left(\mathbf{q},t\right)$ using Eq. 7 gives the time-resolved scattering signal

$$\begin{array}{ccc}\hfill {\tilde{S}}_2\left(\mathbf{q},t\right)& =\hfill & |\sum _{e{e}^{\prime }}\underset{\left(\text{i}\right)}{\underbrace{{\rho }_{gg}\left(t\right)⟨{\chi }_g\left(t\right)\left|{\widehat{\sigma }}_{gg}\left(\mathbf{q}\right)\right|{\chi }_g\left(t\right)⟩}}\hfill \\ \hfill & \hfill & +\underset{\left(\text{j}\right)}{\underbrace{{\rho }_{e{e}^{\prime }}\left(t\right)⟨{\chi }_{e^{\prime }}\left(t\right)\left|{\widehat{\sigma }}_{e^{\prime }e}\left(\mathbf{q}\right)\right|{\chi }_e\left(t\right)⟩}}\hfill \\ \hfill & \hfill & +\underset{\left(\text{k}\right)+\left(\text{l}\right)}{\underbrace{2\mathfrak{R}\left[{\rho }_{eg}\left(t\right)⟨{\chi }_g\left(t\right)\left|{\widehat{\sigma }}_{ge}\left(\mathbf{q}\right)\right|{\chi }_e\left(t\right)⟩\right]}}{|}^2,\hfill \end{array}$$ [11]

where we have labeled the terms so as to indicate the corresponding diagrams in Fig. 2. While $F\left(\mathbf{q}\right)$ is $\sim N^2$ at the Bragg peaks and vanishes elsewhere (or broadened by the Debye–Waller factor for finite disorder), the structure of themolecular charge density is encoded in Eq. 11. Terms i and j in the amplitude are, when squared, simply the elastic ground- and excited-state scattering, respectively. Their coefficients are ${\rho }_{ii}^2$ ($i=e,g$), the square of the electronic population which is the joint probability of finding two molecules in state $|i⟩$.

Terms i and j of Eq. 11 also generate cross-terms when the amplitude is squared. These come as $\mathfrak{R}\left({\sigma }_{gg}{\sigma }_{ee}^{*}\right)$ and constitute heterodyne interference between the ground- and excited-state diffraction. For weak excitation, the ground-state signal serves as a reference local oscillator for the excited-state signal. The signal is proportional to the product of ground- and excited-state populations ${\rho }_{gg}{\rho }_{ee}$, or the joint probability of finding one molecule each in the ground and excited states. Thus, it scales favorably compared with the direct excited-state diffraction for perturbatively prepared samples (${\rho }_{ee}^2\ll 1$), a fact that has been used in crystalline and powder samples to record the excited-state charge density using the ground-state diffraction as a local oscillator to boost the excited-state signal (13, 42). Moreover, these cross-terms carry the relative phase information between ground and excited states. Thus, with knowledge of the ground-state charge density, the phase problem can be solved and ${\sigma }_{ee}\left(\mathbf{q}\right)$ can be inverted to obtain the excited-state charge distribution in real space ${\sigma }_{ee}\left(\mathbf{r}\right)$.

Finally, terms k and l in Eq. 11 arise from the combination of inelastic scattering and electronic coherences. Depending on the dynamics, the electronic coherences may rapidly decay, rendering this third term negligible so that the scattering is given only by the ground- and excited-state diffraction and their heterodyne interference. Moreover, the coherence ${\rho }_{eg}\left(t\right)$ oscillates at electronic frequencies, and thus, the inelastic scattering is also negligible when the temporal envelope of the X-ray pulse is too long to capture this oscillation. More generally, the inelastic term as well as its cross-terms with the elastic scattering can all contribute. The possibility of separating out these terms in the diffraction pattern and what could be learned by doing so is a largely unexplored territory that gradually becomes more relevant as ultrabright X-ray pulses on the time scale of electronic motion become available (43, 44).

We note that, even though our discussion has focused on electronic coherences, the same formalism applies to vibrational coherences. Indeed, vibrational wave packets are unavoidably created in the ground state via Raman processes during the pumping (illustrated in SI Appendix, Fig. S1).

In the absence of long-range intermolecular order, the vanishing structure factor $F\left(\mathbf{q}\right)$ renders the two-molecule scattering negligible, and the signal is dominated by the one-molecule scattering. We can equivalently recast the time-resolved single-molecule (or gas-phase) signal as

$$S_1\left(\mathbf{q},T\right)=N\int \mathrm{d}t|E_p\left(t-T\right){|}^2{\tilde{S}}_1\left(\mathbf{q},T\right),$$ [12]

where we similarly obtain ${\tilde{S}}_1\left(\mathbf{q},t\right)$ via Eq. 7

$$\begin{array}{ccc}\hfill {\tilde{S}}_1\left(\mathbf{q},t\right)& =\hfill & \sum _{e,e\prime ,e^{″}}\{\underset{\left(\text{a}\right)}{\underbrace{{\rho }_{gg}⟨{\chi }_g\left(t\right)\left|{\widehat{\sigma }}_{gg}^{†}{\widehat{\sigma }}_{gg}\right|{\chi }_g\left(t\right)⟩}}\hfill \\ \hfill & \hfill & +\underset{\left(\text{b}\right)}{\underbrace{{\rho }_{gg}⟨{\chi }_g\left(t\right)\left|{\widehat{\sigma }}_{ge}^{†}{\widehat{\sigma }}_{eg}\right|{\chi }_g\left(t\right)⟩}}\hfill \\ \hfill & \hfill & +\underset{\left(\text{c}\right)}{\underbrace{{\rho }_{ee\prime }⟨{\chi }_{e\prime }\left(t\right)\left|{\widehat{\sigma }}_{e\prime e^{″}}^{†}{\widehat{\sigma }}_{e^{″}e}\right|{\chi }_e\left(t\right)⟩}}\hfill \\ \hfill & \hfill & +\underset{\left(\text{d}\right)}{\underbrace{{\rho }_{ee\prime }⟨{\chi }_{e\prime }\left(t\right)\left|{\widehat{\sigma }}_{e\prime g}^{†}{\widehat{\sigma }}_{ge}\right|{\chi }_e\left(t\right)⟩}}\hfill \\ \hfill & \hfill & +2\mathfrak{R}\underset{\left(\text{f}\right)+\left(\text{g}\right)}{\underbrace{{[\rho }_{eg}\left(t\right)⟨{\chi }_e\left(t\right)\left|{\widehat{\sigma }}_{ee}^{†}{\widehat{\sigma }}_{eg}\right|{\chi }_g\left(t\right)⟩}}\hfill \\ \hfill & \hfill & +\underset{\left(\text{e}\right)+\left(\text{h}\right)}{\underbrace{{\rho }_{eg}\left(t\right)⟨{\chi }_e\left(t\right)\left|{\widehat{\sigma }}_{eg}^{†}{\widehat{\sigma }}_{gg}\right|{\chi }_g\left(t\right)⟩}\left]\right\}},\hfill \end{array}$$ [13]

where the $\mathbf{q}$-dependence is suppressed for brevity and we set ${\widehat{\sigma }}_{ij}\equiv {\widehat{\sigma }}_{ij}\left(\mathbf{q}\right)$. Each term in Eq. 13 corresponds to a particular diagram in Fig. 2. Terms a and b represent the elastic and inelastic scattering contributions (Fig. 2 A and B) from the ground state, while c and d are the equivalent terms for the excited state (Fig. 2 C and D). Terms e, f, g, and h represent mixed elastic–inelastic processes, which scatter off electronic coherences. Each of these terms originates from two diagrams, which are complex conjugates, and are grouped by the final state (Fig. 2 E–H).

X-ray diffraction is ordinarily taken to be purely elastic, and the possibility of the inelastic and mixed terms in Eq. 13 is rarely considered (28, 30, 43, 45). In most experimental circumstances, the majority of the molecular charge can be definitively assigned to particular atoms. Only few electrons participate in chemical bonds. This inspires the commonly used independent atom approximation for the molecular charge density

$$\sigma \left(q\right)=\sum _a\left|f_a\left(\mathbf{q}\right)\right|e^{i\mathbf{q}\cdot {\mathbf{R}}_a+i{\varphi }_a\left(\mathbf{q}\right)},$$ [14]

where ${\varphi }_a\left(\mathbf{q}\right)$ is the phase of $f_a$, the atomic form factor of the $a$-th atom, and $R_a$ is the position of the $a$th atom. Evaluating, e.g., $⟨{\chi }_e\left(t\right)\left|{\widehat{\sigma }}_{ee}^{†}{\widehat{\sigma }}_{ee}\right|{\chi }_e\left(t\right)⟩$ with the density from Eq. 14 yields

$$\begin{array}{ll}\hfill I_{\text{mol}}^{\left(e\right)}+I_{\text{at}}^{\left(e\right)}=\sum _a\sum _b& \left|f_a\left(\mathbf{q}\right)\right|\left|f_b\left(\mathbf{q}\right)\right|e^{i\left({\varphi }_b\left(\mathbf{q}\right)-{\varphi }_a\left(\mathbf{q}\right)\right)}\hfill \\ \hfill & \times \int \mathrm{d}\mathbf{R}\hspace{0.17em}{\mathbf{e}}^{i\mathbf{q}\cdot \left({\mathbf{R}}_b-{\mathbf{R}}_a\right)}{\chi }_e^{*}\left(\mathbf{R}\right){\chi }_e\left(\mathbf{R}\right).\hfill \end{array}$$ [15]

where we have identified the diagonal ($a=b$) and off-diagonal ($a\ne b$) terms in the double summation as the excited-state atomic ($I_{\text{at}}^{\left(e\right)}$) and molecular ($I_{\text{mol}}^{\left(e\right)}$) contributions to the scattering intensity. The former gives only $q$-dependence of the atomic form factors, while the latter reveals the interatomic distances and hence the molecular structure. Discarding the atomic contributions and taking the rotational average then gives (35, 46–48)

$$\begin{array}{ll}\hfill I_{\text{mol}}^{\left(e\right)}\left(q\right)=\sum _a\sum _{b\ne a}& \left|f_a\left(q\right)\right|\left|f_b\left(q\right)\right|\cos \left({\varphi }_a\left(q\right)-{\varphi }_b\left(q\right)\right)\hfill \\ \hfill & \times \int \mathrm{d}R\hspace{0.17em}\frac{\sin \left(q{R}_{ab}\right)}{q{R}_{ab}}{P}_{ab}^{\left(e\right)}\left(R_{ab}\right),\hfill \end{array}$$ [16]

where $P_{ab}^{\left(e\right)}\left(R\right)=|{\chi }_e\left(R\right){|}^2$ is the probability distribution of the nuclear separation $R_{ab}=|{\mathbf{R}}_a-{\mathbf{R}}_b|$ for a given electronic state. Compared with Eq. 13, this expression neglects the electronic coherences, since $P_{ab}$ only considers the nuclear wave packet in a single electronic state. The vibrational coherences are, however, included in $P_{ab}$ through the nuclear wave function. Finally, by using the atomic form factor $f_a$, contributions from valence electrons are generally neglected since the core electrons are dominant in the signal due to their much higher number.

As can be seen from Eqs. 12 and 10, the $S_1$ and $S_2$ scattering signals are fundamentally different for molecules that are not in the electronic ground state in: (i) their scaling behavior with respect to the particle number and (ii) the connection of the diffraction pattern with charge-density matrix elements. (i) The $S_2$ signal vanishes in the gas phase and only $S_1$ is observed. However, in crystalline samples, the $S_2$ signal will be the dominant one due to its $N^2$ scaling. In molecular clusters, a mixture of $S_1$ and $S_2$ can potentially be observed. (ii) The $S_1$ signal is a linear superposition of the expectation value over products of charge-density operators $⟨{\widehat{\sigma }}^{†}\sigma ⟩$. The $S_2$ signal, in contrast, is given by the square over the expectation values ${⟨\widehat{\sigma }⟩}^2$. Thus, heterodyne interference between electronic states can potentially be observed in the $S_2$ signal. However, this feature is completely absent in the gas phase. Thus, special care has to be taken when interpreting diffraction patterns of time-resolved diffraction experiments (29, 43, 49).

Monitoring the Nonadiabatic Avoided-Crossing Dynamics in NaF

We illustrate the various contributions to the diffraction signal for sodium fluoride. This molecule possesses a similar electronic structure to NaI, which was studied in the first femtochemistry experiments (50): an avoided crossing between the ionic and covalent state (potential energy curves can be found in SI Appendix). Although well known for facilitating population transport between adiabatic electronic states, the passage of nuclear wave packets through the region where electronic states are degenerate or near-degenerate also generates electronic coherences. The resulting coherent oscillations can be monitored with, e.g., photoelectron or Raman signals and reveal the time-evolving electronic energy gap as well as information on the differential topology of the electronic surfaces via the decoherence time (51, 52). Here, we explore the consequences of these dynamics for ultrafast time-resolved X-ray diffraction in gas-phase NaF (44). Iodine is a strong X-ray scatterer, and its large nuclear charge leads to a charge-density distribution heavily dominated by its core electrons. While this is still the case for molecular form factors of lighter element compounds, they have a relatively more prominent contribution of valence electrons compared with the core electrons, which is why we chose NaF.

In the following, we present simulations and analysis of the time-dependent diffraction patterns for the gas phase ($S_1\left(\mathbf{q},T\right)$) and for ordered samples ($S_2\left(\mathbf{q},T\right)$). The two states relevant for the dynamics are the ionic $X^1\mathrm{\Sigma }$ state ($\left|g\right.⟩$) and the covalent $A^1\mathrm{\Sigma }$ state ($\left|e\right.⟩$). The potential energy curves are similar to the ones of NaI (50). The $X^1\mathrm{\Sigma }$ and the $A^1\mathrm{\Sigma }$ state are coupled via a nonadiabatic coupling matrix element which induces an avoided crossing at 8 Å. The coupled nuclear+electronic dynamics is calculated by solving the time-dependent Schrödinger equation on a grid (for details, see SI Appendix).

The signal is finally obtained by evaluating Eq. 12 and inserting the time-dependent wavefunctions and density operators (${\widehat{\sigma }}_{ik}^{†}{\widehat{\sigma }}_{kj}$, as shown in SI Appendix, Fig. S4). The effective electronic coherence is obtained from the combined electronic-nuclear wavefunction as the overlap of the nuclear wave packets, which represents decoherence and the electronic density matrix elements ${\rho }_{eg}=c_e^{*}{c}_g$

$${\tilde{\rho }}_{eg}\left(t\right)={\rho }_{eg}⟨{\chi }_e\left(t\right)|{\chi }_g\left(t\right)⟩,$$ [17]

The time evolution of the excited-state wave packet reveals the decay and revival of the effective electronic coherence ${\tilde{\rho }}_{eg}$.

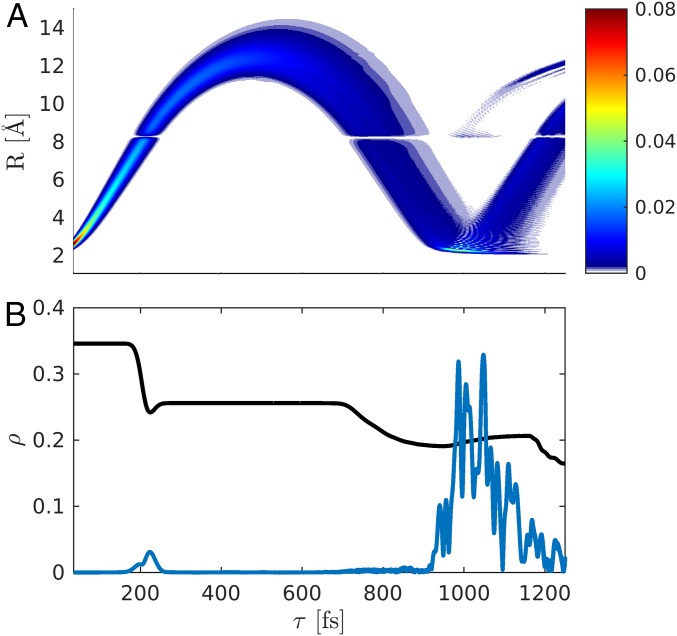
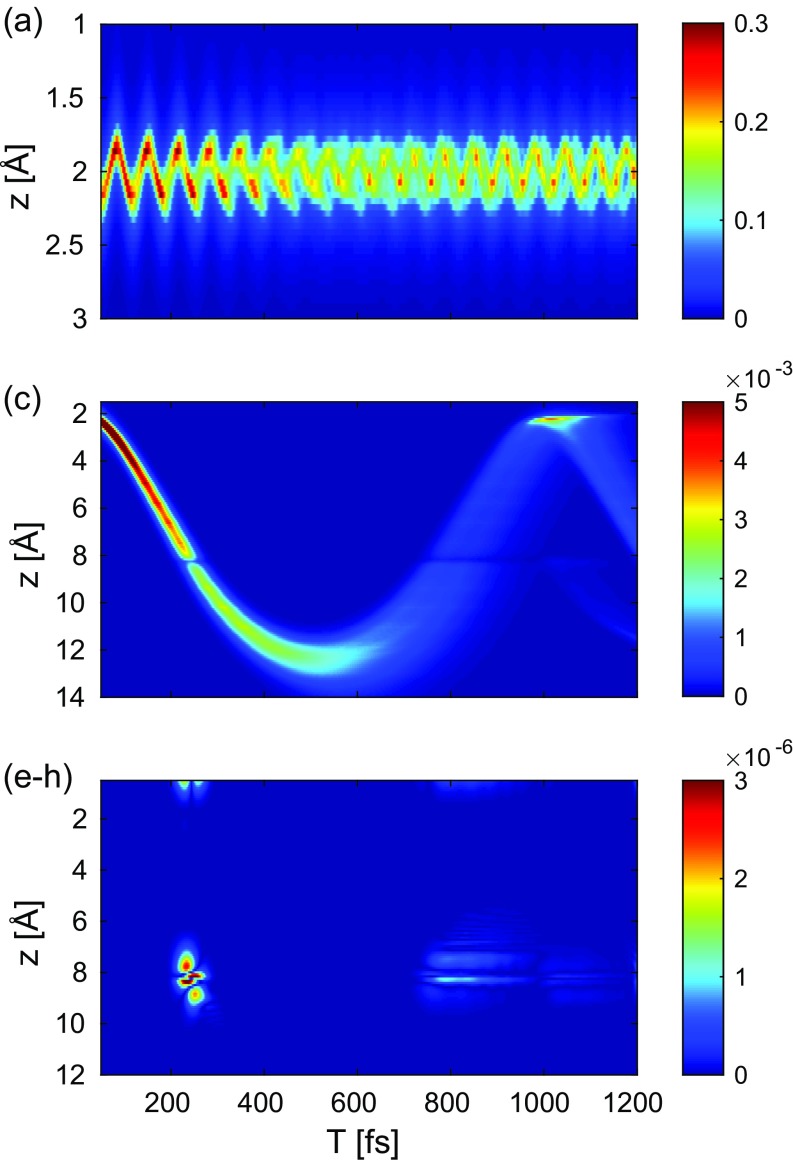
The wave packet dynamics in the excited-state potential (${\chi }_e\left(R,t\right)$) is depicted in Fig. 3A. The nuclear wave packet passes through the avoided crossing between 200 and 240 fs and reaches its outer turning point at $\sim$500 fs.

Fig. 3.

Time evolution of the nuclear wave packet in the in the covalent $A^1\mathrm{\Sigma }$ state following excitation with a 10-fs pump-pulse (FWHM). (A) Probability density. (B) Excited-state population ($A^1\mathrm{\Sigma }$, black) and the magnitude of the coherence $\left|{\tilde{\rho }}_{eg}\right|$ (blue). The initial coherence created by the pump pulse ($T<50$ fs) is not shown.

Fig. 3B shows the time-dependent excited-state population alongside the magnitude of the electronic coherence. When the wave packet passes through the avoided crossing for the first time, $\approx 10$% of the population is transferred to the ground state, and a coherence ${\rho }_{eg}$ is created. The large spike in coherence after $\approx 900$ fs stems from the wave packet returning to the Franck–Condon region and thus maximizing $⟨{\chi }_e\left(t\right)|{\chi }_g\left(t\right)⟩$ with the retained ground-state wave packet.

While we have used a fully quantum description of nuclei and electrons to calculate the molecular dynamics, this approach might not be feasible for polyatomic molecules with a large number of vibrational degrees of freedom. Semiclassical simulations methods like ab initio multiple spawning (53) or surface hopping (54, 55) can be used instead. However, special care has to be taken to correctly include electronic coherences, which are neglected in the surface-hopping protocol.

The Time-Resolved Single-Particle Diffraction Signal.

The $S_1$ diffraction pattern (Eq. 12) shown in Fig. 4 is dominated by the oscillating ground-state wave packet that was created by the 10-fs UV pump pulse (SI Appendix, Fig. S1A).

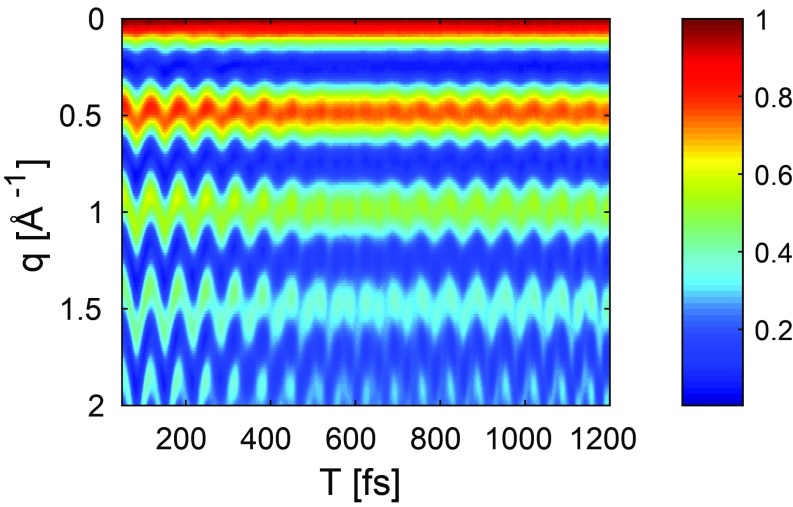
Fig. 4.

Time-dependent gas-phase diffraction pattern $S_1\left(q_z,T\right)$ (Eq. 13). The signal intensity is normalized to 1, and the probe pulse length used is 2.5 fs (FWHM of intensity).

Fig. 5 shows $S_1$ separated in its constituting terms in real space obtained via inverse Fourier transform of Eq. 13. The elastic ground-state to ground-state contribution in Fig. 5A is in close resemblance to the total $S_1$ signal in Fig. 4 and shows a wave packet that oscillates around the equilibrium bond length of NaF. A comparison of Fig. 5C (${\sigma }_{ee}^2$) with the time evolution of the nuclear wave function (Fig. 3A) makes it clear that the features of the nuclear wave-packet motion can be retrieved approximately from the elastic excited-state contribution (a detailed interpretation is given in SI Appendix). Fig. 5 E–H depicts the contribution of the electronic coherences (corresponding to diagrams in Fig. 2 E–H). At $\approx$225 fs and at $\approx$800 fs, as the wave packet enters the avoided crossing region, a coherence is created (Fig. 3B): The pattern at 8 Å is at the position of the avoided crossing. The contribution at 800 fs is caused by the returning spatially elongated wave packet passing the avoided crossing on its way back to the Franck–Condon region. The recurrence event itself in the Franck–Condon is not well resolved due to the rather large energy gap ($\approx$4 eV) and is averaged out by the 2.5-fs probe pulse. The coherence contribution is $\approx$ 3 orders of magnitude weaker than the excited-state density (Fig. 4C). The contribution stemming solely from the transition densities (${\widehat{\sigma }}_{eg}^2$, terms b and d) is $\approx 4$ orders of magnitude weaker (diagram in Fig. 2 B and D and SI Appendix, Fig. S6). It carries no information about the electronic coherence but is dominated by the shape and magnitude of the transition density ${\widehat{\sigma }}_{eg}^2$ and is closely related to the transition dipole moment (SI Appendix, Figs. S3 and S6).

Fig. 5.

Contributions to the real space signal $S_1\left(z,T\right)$ [inverse Fourier transform of $S_1\left(q_z,T\right)$]. The labeling of the figure is identical with the labeling of terms in Eq. 13.

The actinic pump pulse creates a wave motion not only in the excited-state potential but also in the ground-state potential due to a Raman process (SI Appendix, Fig. S1). A small fraction of the population is moved from the ground to the excited state, creating a “particle” excited state wave packet and a “hole” in the ground state. The respective signals in reciprocal momentum space and in real space given in Fig. 5A clearly show that the pump-pulse creates an oscillating wave packet in the ¹X state.

In conclusion, the simulated gas-phase diffraction signal of NaF undergoing nonadiabatic avoided crossing dynamics in a nonstationary state is dominated by ground- and excited-state wave packet motions and shows some weak signatures of the electronic coherence created at the avoided crossing. The interatomic distance can be extracted directly from the diffraction signal, and, as such, the shape of the nuclear wave packet can be qualitatively retrieved without further phase reconstruction. For diatomic molecules, this allows us to create a molecular movie. The coherence contributions do not merely indicate that a coherence has been created but also give a hint of where it has been created. They are significantly weaker than elastic scattering processes and appear as a rapid oscillation on top of the diffraction pattern.

The actinic pump pulse also creates a nonstationary nuclear wave packet in the electronic ground state. This must be taken into account in the interpretation of diffraction patterns since the Raman and the excited-state signals are of comparable magnitudes (SI Appendix, Fig. S1). Separating the ground- and excited-state contributions has been a long-standing open challenge in nonlinear spectroscopy (56).

Virtually all photophysical and photochemical processes in polyatomic molecules with two or more vibrational coordinates take place via CoIns (57). Observing them in diffraction experiments is an interesting open question. Once the molecule reaches a CoIn, a short-lived electronic coherence is created which can in principle be spectroscopically detected (51, 58) by soft X-rays. One example of a photochemical prototype reaction, which is mediated by a CoIn and has been studied by X-ray diffraction, is the ring-opening reaction in cyclohexadiene (59, 60). Potential signatures in time-resolved X-ray diffraction signals might also be useful to measure the Berry phase (61), which has so far eluded detection in molecules.

The Time-Resolved Two-Particle Diffraction Signal.

We now turn to diffraction signals generated from samples possessing intermolecular order such as crystals. We will display the two-molecule contribution without the structure factor $F\left(q\right)$:

$${\overline{S}}_2\left(\mathbf{q},T\right)=\int \mathrm{d}t|E_p\left(t-T\right){|}^2{\tilde{S}}_2\left(\mathbf{q},t\right),$$ [18]

where ${\tilde{S}}_2\left(\mathbf{q},t\right)$ is defined in Eq. 11. The $S_2$ signal stems from interference between pairs of molecules within an ordered sample. As a result, the signal scales quadratically with the number of molecules. The contribution from the electronic states are not simply additive any longer but are obtained from the squared magnitude of a scattering amplitude. In the following, we will analyze the full diffraction pattern as well as its components originating from the electronic states involved.

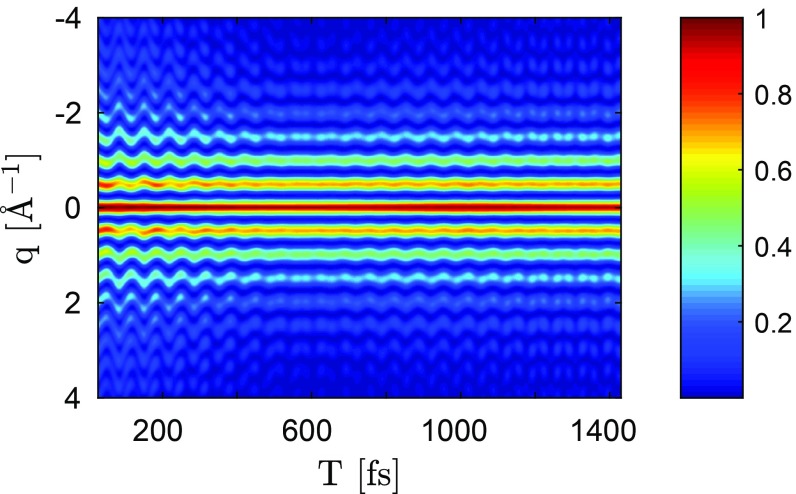
Fig. 6 shows the diffraction pattern excluding the Bragg peaks as a function of the probe delay according to Eq. 18. The diffraction pattern is dominated by the electronic ground state and the oscillating wave packet created by the Raman interaction with the pump pulse (for details, see SI Appendix, Fig. S1).

Fig. 6.

Two-molecule contribution for NaF according to Eq. 18: Momentum transfer vs. probe delay with a temporal width of the probe pulse of 2.5 fs (FWHM). The intensity of the pattern is normalized.

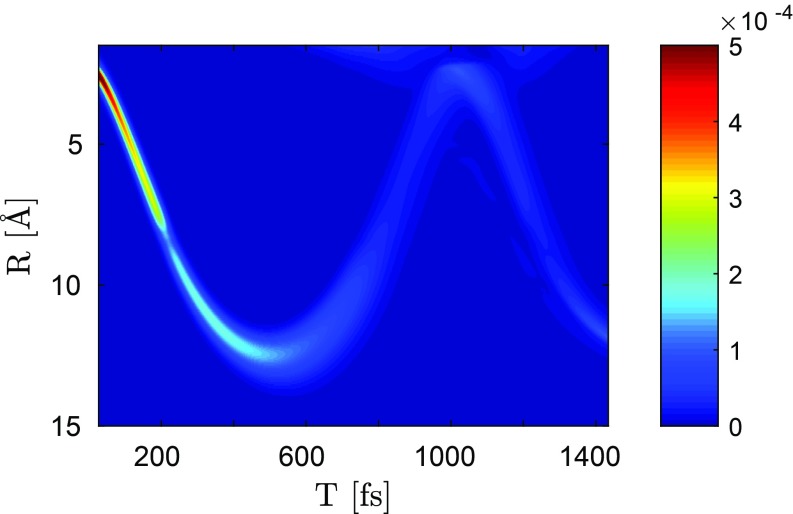
Fig. 7 depicts the time evolution of the $S_2$ diffraction pattern (in real space) under the assumption that only the electronic excited states have been populated by the pump pulse. It yields the time-resolved NaF bond distance and an approximate reconstruction of the nuclear wave packet (Fig. 7) and is in good agreement with Fig. 3A.

Fig. 7.

Real-space representation (inverse Fourier transform) of the $S_2$ signal (only the excited-state component due to $⟨{\chi }_e\left|{\sigma }_{ee}\right|{\chi }_e⟩$, inverse Fourier transform of SI Appendix, Fig. S8).

Note that the diffraction intensity not only depends on the population of the electronic state but also on the width of the nuclear wave packet. Since the spread of the wave packet increases with time, its intensity in the diffraction pattern decreases significantly.

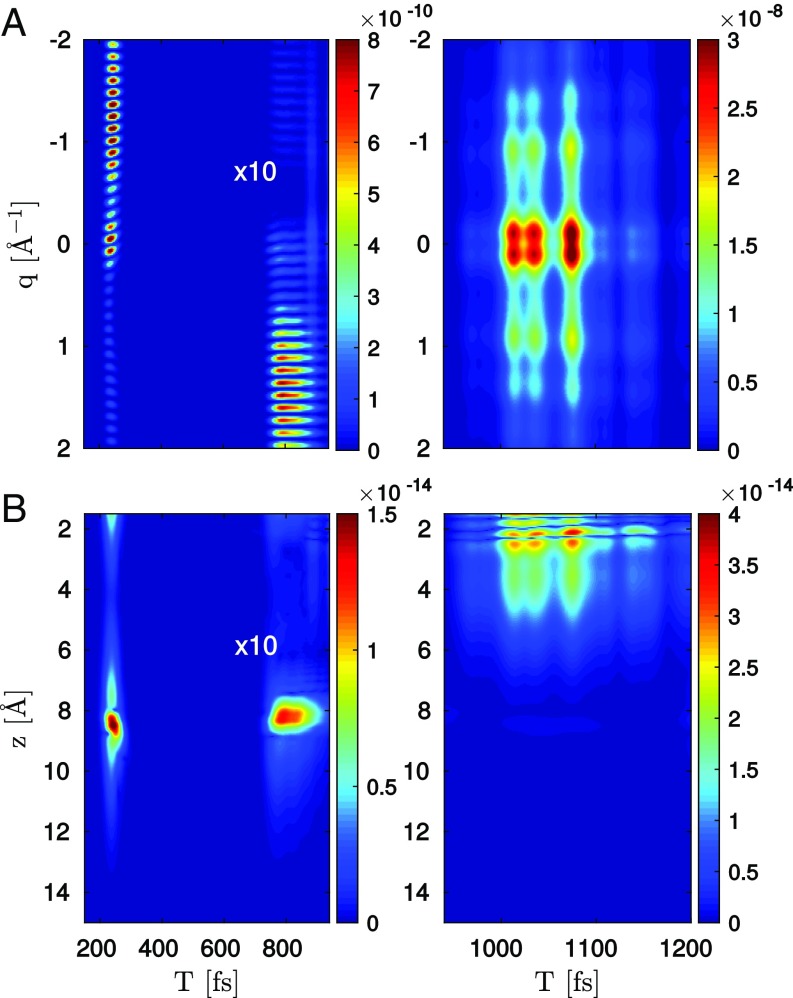
Fig. 8 depicts the evolution of the $S_2$ diffraction pattern under the assumption that only the term $2\mathfrak{R}{\rho }_{eg}\left(t\right)⟨{\chi }_g\left(t\right)\left|{\widehat{\sigma }}_{ge}\left(\mathbf{q}\right)\right|{\chi }_e\left(t\right)⟩$ (Fig. 1 K and L), including the electronic coherence and transition charge density, contributes to the signal. At 200 fs when the molecule crosses the intersection for the first time, the diffraction pattern contains a clear signature of the crossing. At $\sim$800 fs, the exited-state wave packet returns and passes the avoided crossing for a second time. The wave packet is now more spread out, resulting in a lower intensity (note that the pattern $\sim$800 fs is multiplied by a factor 10 to be visible). Between 1.0 and 1.1 ps, the wave packet returns to the Franck–Condon point. A strong coherence is created by the remaining wave packet in the electronic ground state and the returning nuclear wave packet in the excited state.

Fig. 8.

(A) Two-molecule contribution for NaF according to Eq. 18, considering only the interference term (part between 600 and 900 fs enhanced by a factor of 10). Right shows the coherence caused by the revival event, which brings the exicted-state wave packet back to the Franck–Condon region. Signal intensities are given relative to total $S_2$ signal. (B) Inverse Fourier transform of this two-molecule contribution for NaF.

The inverse Fourier transform of Fig. 8A is shown in Fig. 8B. It gives a clear indication of the interatomic separations at which the electronic coherences are created: The features at $\approx$ 8 Å can be attributed to passing through the avoided crossing. The feature at $\approx$2 Å corresponds to the aforementioned revival event where the remaining ground-state wave packet overlaps with the returning wave packet in the excited state.

The $S_1$ vs. $S_2$ Signals.

The single- and two-molecule contributions have generally different features. While only the two-molecule signal carries intermolecular information via the structure factor $F\left(\mathbf{q}\right)$, the one- and the two-molecule contributions contain similar information at the intramolecular level. Both encode the nuclear wave packet dynamics in each electronic state as well as spatial information about the electronic coherences through the transition charge densities. However, the $S_1$ signal contains no self-heterodyne interference, which is due to the different contributions to $S_1$ coming as a linear superposition of terms rather a squared magnitude. In the absence of electronic coherence, this implies that $S_1$ contributions add at the intensity level, while $S_2$ contributions add at the amplitude level. This also means that terms including the electronic coherence as a prefactor originate from a convolution of the charge density with the transition charge density ${\widehat{\sigma }}_{ii}{\widehat{\sigma }}_{ij}$ in $S_1$, rather than the transition charge density itself (${\widehat{\sigma }}_{ij}$) in $S_2$.

Finally, we note that, since $S_2$ overwhelms $S_1$ for crystalline samples and vanishes for gas-phase samples, the two signals are measured experimentally on samples in different phases. The molecular charge density need not be the same in these two cases, and our comparison has not accounted for this possible difference (i.e., we use the same molecular charge density to calculate $S_2$ and $S_1$). Moreover, intermolecular coupling in the condensed phase can lead to electron relocations (62, 63). These interesting effects go beyond the scope of this work, but can be treated with the same formalism by dropping the assumption that all molecules have identical charge densities.

Summary and Future Outlook

In this work, we have presented a unified account of time-resolved X-ray scattering starting with the minimal coupling field-matter interaction Hamiltonian. We focused our attention on pulses off-resonant from the core transitions, where the radiative coupling is proportional to the electronic charge density. In ordered samples, the scattering amplitudes of the various molecules add coherently (Eq. 5), yielding the Bragg peak pattern of the sample. Disorder causes a diffuse scattering due to fluctuations from the average structure that exists between the Bragg peaks as well, but that is also due to the coherent addition of scattering amplitudes from different molecules (Eq. 5). These two-molecule terms offer heterodyne detection in time-resolved diffraction of excited-state charge densities. In contrast, single-molecule scattering, which is all that remains in a totally unordered sample such as a gas, contains no heterodyne interference between molecular ground- and excited-state electronic charge densities in contradiction to claims made in ref. 29.

In stationary X-ray diffraction experiments, the phase of the ground-state charge density in $q$-space is often determined by oversampling (2–4). Once complete ground-state information is known, the excited-state amplitude and phase can be obtained in a heterodyne detection in samples with long-range order (13), while oversampling can again be used in gas-phase samples after subtracting off the ground-state charge density.

The present first-principles QED treatment further reveals the role of inelastic and mixed elastic–inelastic terms that are connected to the presence of electronic coherences and carry information on the spatial distribution of the electrons involved in valence molecular excitations. This includes ordinary diagonal as well as off-diagonal transition charge densities. Although weaker than elastic scattering, these terms may be observable with sufficiently bright pulses of duration comparable to electronic time scales.

We have demonstrated the various off-resonant scattering terms with the example of NaF, which possesses an avoided crossing between ionic $X^1\mathrm{\Sigma }$ and covalent $A^1\mathrm{\Sigma }$ states at an $\sim$8 Å atomic separation distance. The transition charge densities are displayed, and their contribution to the time-resolved scattering signal is shown in Fig. 5. The inelastic and mixed terms are weaker; they are appreciable only at times when the electronic coherence is present or near the avoided crossing where the transition densities peak, making them easier to separate from the purely elastic terms. Comparison of the $S_1$ and $S_2$ signals shows that $S_1$ carries signatures of electronic coherences that are orders-of-magnitude stronger than in the $S_2$ signal.

For simplicity, we have so far assumed that the X-ray pulse is tuned off-resonant from core transitions. The diffraction signal then solely monitors the ground state and valence excitations. Resonant pulses will probe core excitations as well, and such signals are dominated by the $\mathbf{j}\cdot \mathbf{A}$ coupling to the radiation field. Returning to Eq. 2 and retaining only terms proportional to $\mathbf{j}$, we obtain upon expanding to lowest order in an external probing field $A_p$:

$$\begin{array}{l}\hfill S\left(\mathbf{q},T\right)=\sum _{\alpha \beta }{e}^{i\mathbf{q}\left({\mathbf{r}}_{\alpha }-{\mathbf{r}}_{\beta }\right)}\int \mathrm{d}t\mathrm{d}t\prime e^{i{\omega }_s\left(t-t\prime \right)}{\int }_{-\infty }^t\mathrm{d}{t}_1{A}_p\left(t_1\right)\\ \hfill \times {\int }_{-\infty }^{t\prime }\mathrm{d}{t}_2{A}_p^{*}\left(t_2\right)⟨{\mathbf{j}}_{\beta }\left({\mathbf{k}}_p,t_2\right){\mathbf{j}}_{\beta }\left(-{\mathbf{k}}_s,t\prime \right){\mathbf{j}}_{\alpha }\left({\mathbf{k}}_s,t\right){\mathbf{j}}_{\alpha }\left(-{\mathbf{k}}_p,t_1\right)⟩.\\ \hfill \end{array}$$ [19]

Resonant scattering from a nonstationary state thus comes as a four-point correlation function of $\mathbf{j}$ operators and can be used to probe the time-dependent electronic currents in the system. X-ray diffraction near material transitions, known as anomalous diffraction, involves contributions from both $\sigma \left(\mathbf{r}\right){\mathbf{A}}^2\left(\mathbf{r}\right)$ and $\mathbf{j}\left(\mathbf{r}\right)\cdot \mathbf{A}\left(\mathbf{r}\right)$ couplings and has been used to aid in structure determination (64, 65). In this case, the scattering event is no longer instantaneous, and the phase induced by the time propagation (equivalently, the material transition with which the probe is resonant) means that anomalous scattering carries phase information that ordinary diffraction lacks, facilitating solution of the phase problem to allow inversion of the diffraction pattern (66, 67). Tuning the scattering wavelength can address particular anomalous scatterers, simplifying the structure-determination process (65). In SI Appendix, we give expressions for resonant scattering from a nonstationary state prepared via a four-wave-mixing process as an example of a resonant scattering technique.

We further note that we have also not explicitly specified the molecular preparation process (gray area in Fig. 2 diagrams) and kept it general. A large variety of schemes for preparing the molecule in an excited-state population or coherence are possible and have been analyzed, including nonperturbative propagation in the presence of a strong field (44, 51) as well as direct dipole coupling and resonant (64, 65) or off-resonant Raman processes (68). These latter signals involve effective polarizabilities expressed with the current densities given by:

$$\begin{array}{ll}\hfill {\mathbf{\alpha }}_{ee\prime }=\sum _{\nu \nu \prime }\sum _c& \int \mathrm{d}{\mathbf{r}}_1\mathrm{d}{\mathbf{r}}_2\hspace{0.17em}{\mathbf{j}}_{ec}^{\nu }\left({\mathbf{r}}_1\right){\mathbf{j}}_{ce\prime }^{\nu \prime }\left({\mathbf{r}}_2\right)\cdot \hfill \\ \hfill \times & \int \frac{\mathrm{d}\omega }{2\pi }\frac{{\mathbf{A}}_{\text{res}}^{\nu }\left({\mathbf{r}}_1,\omega \right){\mathbf{A}}_{\text{res}}^{\nu \prime }\left({\mathbf{r}}_2,\omega +{\omega }_{ee\prime }\right)}{\omega -{\omega }_{ee\prime }+i{\mathrm{\Gamma }}_c}.\hfill \end{array}$$ [20]

where $\nu ,\nu \prime$ are Cartesian coordinates. Such an effective polarizability can also be constructed for the final scattering event if it, too, is resonant. The dipole approximation applied to these resonant terms is the basis for the conventional treatment of X-ray Raman processes. Here, we retain the minimal coupling picture that avoids the dipole approximation and accounts for the spatial variation of the material properties over the wavelength of the X-ray field. By replacing some $\left.\sigma \left(\mathbf{q}\right)\right)$ factors by $\alpha$, we obtain a class of mixed resonant/off-resonant scattering terms that come proportional to multipoint correlation functions of the electronic charge density and effective polarizability operators.

In another exciting future development, it should be possible to carry out multiple diffraction measurements on a single molecule and detect the various diffracted photons in coincidence. Several photon-scattering events can occur and be detected, thus leading to multiple photon-counting signals (39, 69, 70) that are sensitive to multipoint correlation functions of the charge-density operator that probe spontaneous charge-density fluctuations. For example, for a two-photon counting measurement, these signals are given by ref. 68

$$\begin{array}{ll}\hfill & S_{PC-2D}\left({\mathbf{k}}_1,T_1,{\mathbf{k}}_2,T_2\right)=|{\omega }_I{\omega }_{II}{A}_1\left({\omega }_I\right)A_2\left({\omega }_{II}\right){|}^2\hfill \\ \hfill & \times ⟨{\widehat{\sigma }}^{†}\left({\mathbf{q}}_1,T_1\right){\widehat{\sigma }}^{†}\left({\mathbf{q}}_2,T_1+T_2\right)\widehat{\sigma }\left({\mathbf{q}}_2,T_1+T_2\right)\widehat{\sigma }\left({\mathbf{q}}_1,T_1\right)⟩.\hfill \end{array}$$ [21]