Genomic and environmental determinants and their interplay underlying phenotypic plasticity

Significance

Integrated analysis of genotype by environment can reveal the pattern and mechanistic interplay underlying the observed phenotype dynamics. A critical question needs to be answered to enhance our ability to conduct genomic and environmental analysis of varied phenotypic plasticity observed in natural field conditions: How to uncover patterns at different levels to facilitate complex trait dissection and performance prediction. In this study, we first uncovered the pattern of genotype response to different environments. We then uncovered the pattern generated by the combination of environmental factors and the pattern of genetic effects at the individual gene level across environments. Finally, we demonstrated that trait dissection to individual genes and genome-wide performance prediction can be conducted through a joint genomic regression analysis framework.

Abstract

Observed phenotypic variation in living organisms is shaped by genomes, environment, and their interactions. Flowering time under natural conditions can showcase the diverse outcome of the gene–environment interplay. However, identifying hidden patterns and specific factors underlying phenotypic plasticity under natural field conditions remains challenging. With a genetic population showing dynamic changes in flowering time, here we show that the integrated analyses of genomic responses to diverse environments is powerful to reveal the underlying genetic architecture. Specifically, the effect continuum of individual genes (Ma₁, Ma₆, FT, and ELF3) was found to vary in size and in direction along an environmental gradient that was quantified by photothermal time, a combination of two environmental factors (photoperiod and temperature). Gene–gene interaction was also contributing to the observed phenotypic plasticity. With the identified environmental index to quantitatively connect environments, a systematic genome-wide performance prediction framework was established through either genotype-specific reaction-norm parameters or genome-wide marker-effect continua. These parallel genome-wide approaches were demonstrated for in-season and on-target performance prediction by simultaneously exploiting genomics, environment profiling, and performance information. Improved understanding of mechanisms for phenotypic plasticity enables a concerted exploration that turns challenge into opportunity.

Differential response of genotypes to environments is common for complex traits and diseases (1). Despite existing analytic frameworks and technological advances in genomics and environmental monitoring, many longstanding biology questions could not be answered without accurately quantifying the relative contribution of genes and environment and identifying specific underlying factors. An improved understanding of genotype-by-environment interaction (G × E) would enhance our ability to predict disease risk and plant performance (2–6).

Using genetic stocks in model species under controlled and contrasting conditions, previous studies suggested that differential sensitivity of genes is the predominant genetic architecture underlying G × E (4). This mechanistic hypothesis needs to be tested for the plasticity patterns observed under natural field conditions. Studies have shown that plants can detect and assess environmental cues to anticipate future growth conditions and make developmental transitions (5). Indeed, identifying clear examples of such factors would enrich our understanding of G × E at the gene, genome, environment, and their interaction levels (4, 7).

Reaction norm describes the phenotype profile of a genotype across environments, and phenotypic plasticity measures the variation among these phenotypic values (8, 9). If a quantitative index is generated for the environments, G × E can be modeled as different performance curves of genotypes (i.e., reaction norms) along this index. However, it is challenging to identify critical environmental determinants to establish a quantitative index that is both biologically meaningful and prognostic for natural field conditions. Moreover, input values for a performance-free index need to be directly obtainable from the environmental factors before in-season forecasting can be made for a new environment.

To understand G × E, we initiated a focused study in 2010 on sorghum, a model crop species (10). Flowering time is a typical subject in G × E research (11–13) and has significant bearing on evolution and adaptation of plants to different environments (14, 15). Following our initial observation of the altered flowering times for two sorghum inbreds in summer and winter nurseries, extensive phenotyping and genetic analysis were conducted with a mapping population. Expanding the testing to two additional summer nurseries at a higher latitude site and a summer planting at the winter nursery site generated additional interesting observations. Here we show that the changing effects of individual loci (e.g., Ma₁, Ma₆, FT, and ELF3) in different environments lead to G × E interaction, which is further modified by gene-by-gene interaction. Photothermal time within a growth period is a major environmental determinant for flowering time and can be used as an environmental index. By exploiting information at the whole-genome level and across environments indexed with photothermal time values, we demonstrated that two parallel approaches can make robust performance predictions for untested individuals in untested environments.

Patterns Underlying the Apparently Complex G × E

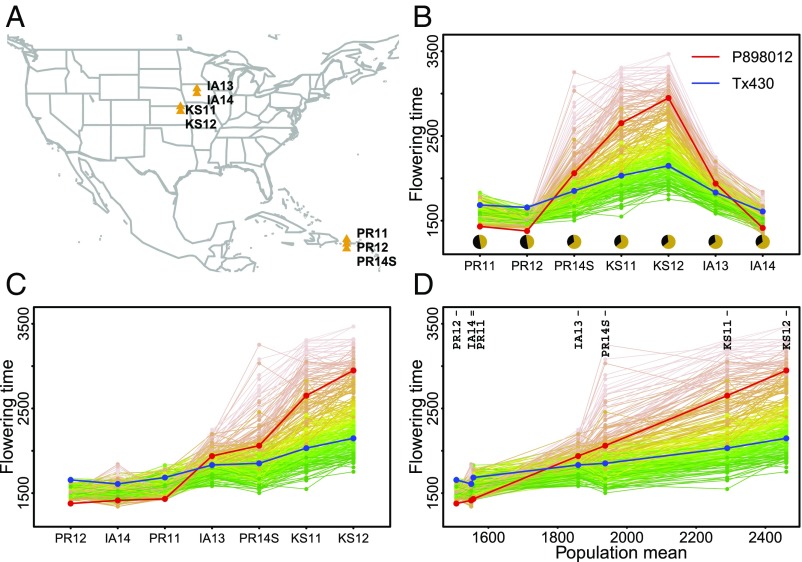
We evaluated flowering time of a genetic mapping population derived from two inbreds across seven field environments (Fig. 1A and SI Appendix, Fig. S1 and Table S1). Flowering time expressed as growing degree days (GDD) showed both rank change and scale change between two parental inbreds and among recombinant inbred lines (RILs). Without an overall modeling framework, trait correlation and prediction accuracy were low between environments with different conditions (SI Appendix, Fig. S2). Prediction accuracy was calculated as the correlation between observed values and predicted values generated from a model. Significant interaction observed in this study, however, presented an opportunity for detailed dissection of G × E because trait measurement within individual environments was highly repeatable (SI Appendix, Fig. S2 and Table S1). G × E accounted for 20% of phenotypic variance (SI Appendix, Table S2) and can be further partitioned into heterogeneity of genotypic variance (56%) and lack of genotypic correlation (44%) (SI Appendix, Tables S3 and S4).

Fig. 1.

Pattern finding in flowering time G × E of a genetic mapping population. Progression from data visualization of apparently complex G × E to pattern discovery: (A) Seven natural field environments. (B) Reaction norm based on a categorical order of photoperiod of seven environments. (C) Reaction norm based on a categorical order of population means for individual environments. (D) Reaction norm based on a numerical order of population means for individual environments. Flowering time expressed as GDD was analyzed. Each line connects the flowering time values of individual RIL across environments.

To unravel the apparently complex G × E, we first examined different ways to group environments using photoperiod, temperature, and the observed flowering time of the population (SI Appendix, Figs. S3 and S4). Observed flowering time is the outcome of different genetic and environmental factors, and it separated the seven environments into three groups. Having IA14 (with lower than usual temperature in early season) grouped with PR11 and PR12 suggested that a certain compensation between photoperiod and temperature affected plant development (4, 5, 13). The clustering of PR14S (summer planting with higher temperature and longer day length than PR11 and PR12) and IA13 also suggested this interplay. In contrast, groupings using either photoperiod or temperature profile alone did not help explain the observed performance data. When the observed flowering time was used to group genotypes, two major clusters of RILs were revealed: one with relatively high plasticity across environments and the other with low plasticity (SI Appendix, Fig. S5).

Informed by the above analyses, we updated the ordering of the seven environments (Fig. 1B) according to population mean at each environment (i.e., environmental mean) (Fig. 1C). This new ordering retained a single cross-over between the reaction norms of the two parents and much reduced cross-overs among progenies. Using the numerical values of the population means (Fig. 1D) enabled us to implement a joint regression analysis, where observed phenotypes for individuals are modeled as response curves across the environmental gradient quantified by the population means of all individuals. This well-established procedure (3, 16–18) is widely used to assess the stability (versus plasticity) of cultivars.

However, two new critical components are required before transforming this traditional approach into a broadly applicable framework to study G × E: (i) genomic models to relate individuals with and without performance data and (ii) environmental indexes, not only mathematically derivable but also biologically meaningful, to connect tested environments with new environments. Solutions to the first component already exist: Genomic prediction has been widely implemented in genetic studies (19, 20). In our specific case, genome-wide SNPs obtained through genotyping-by-sequencing are available for genomic prediction. Identifying the environmental gradient that enables quantifying a new environment without performance data, a long-standing challenge (7), must be resolved.

Environmental Index Defined by Photothermal Time

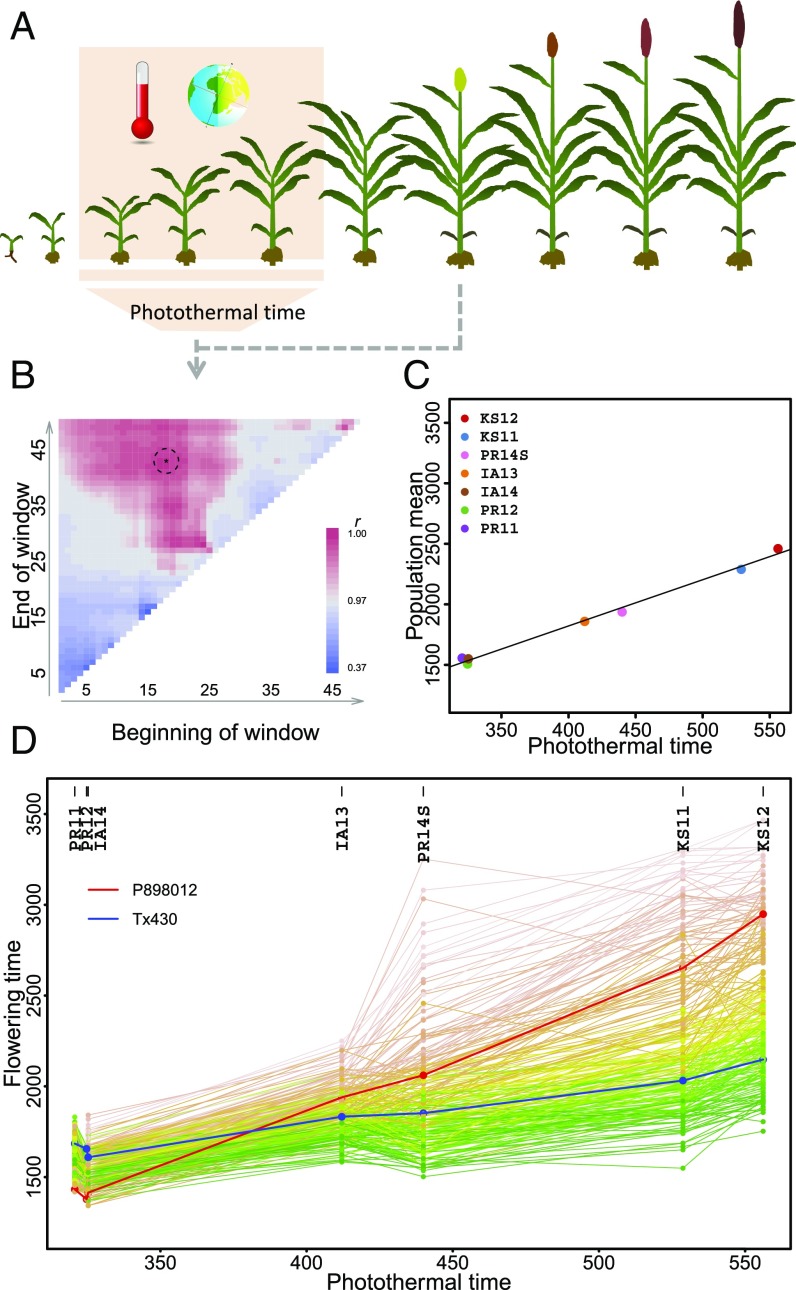
To identify an environmental index generated from external factors, we examined photothermal time, which was also indicated by our earlier analyses of clustering and ordering of the seven environments. Photothermal time is a product between GDD (temperature) and hours of daylight time (photoperiod). In previous research, photothermal time was examined for the timing of developmental stages (21–25) or modified for individual genotypes (12). Unlike earlier research, here we wanted to specifically identify a time window within which the photothermal time values can be used to replace the population means observed at different environments (Fig. 2).

Fig. 2.

Photothermal time within a critical growth window as the environmental index. (A) Schematic diagram of different growth stages including those critical to the flowering time determination. (B) Exhaustive search of the photothermal time window. (C) Correlation between population mean and photothermal time of the selected window. (D) Reaction norms of all individuals ordered numerically by the photothermal-time gradient.

We conducted the search to identify the window within which the set of average photothermal time values at these environments are best correlated with the population means of flowering time (Fig. 2). We checked different starting days and different window sizes and found that average photothermal time values from 18 to 43 days after planting had the highest correlation with flowering time means of the population in these environments (r = 0.996, P = 2 × 10⁻⁹). Photothermal time explained 99.3% of the variation in average flowering time in different environments, higher than temperature (69.4%) or photoperiod alone (30.5%) (SI Appendix, Table S5). Additional subsampling analysis supported this finding (SI Appendix, Fig. S6). As a comparison, we conducted similar window searches for photoperiod and temperature alone to confirm the advantage of using photothermal time (SI Appendix, Fig. S7). To further verify that this photothermal time parameter is biologically meaningful, we projected developmental stages for the population as a whole in individual environments. Indeed, this identified window covered the critical phase of photoperiod and temperature sensing and vegetative-to-reproductive transition (SI Appendix, Fig. S8) (26, 27). Identifying this window across diverse environments is highly desirable because the actual developmental stage measurement requires continuous and destructive sampling (i.e., examining the shoot apical meristems for floral initiation) and can be prohibitive for such a large number of genotypes. Importantly, the range of this photothermal-time index obtained from the current study covers most production environments typically encountered in major US sorghum growing areas.

We further demonstrated the general use of photothermal time as an environmental index with the field data available for a set of diverse sorghum accessions with monthly planting (SI Appendix, Fig. S9) and the growth chamber experiment data from a wide range of species, where photoperiod and temperature were the focus of the original studies (SI Appendix, Fig. S10).

With the identified photothermal-time index, three processes were enabled to conduct unified modeling and mechanistic interpretation of G × E: (i) joint genomic regression analysis (JGRA) through reaction-norm parameter estimation, (ii) JGRA through genome-wide marker effect continuum estimation, and (iii) genetic mapping and effect profiling of flowering time loci.

Genomic Predicted Reaction-Norm Parameters

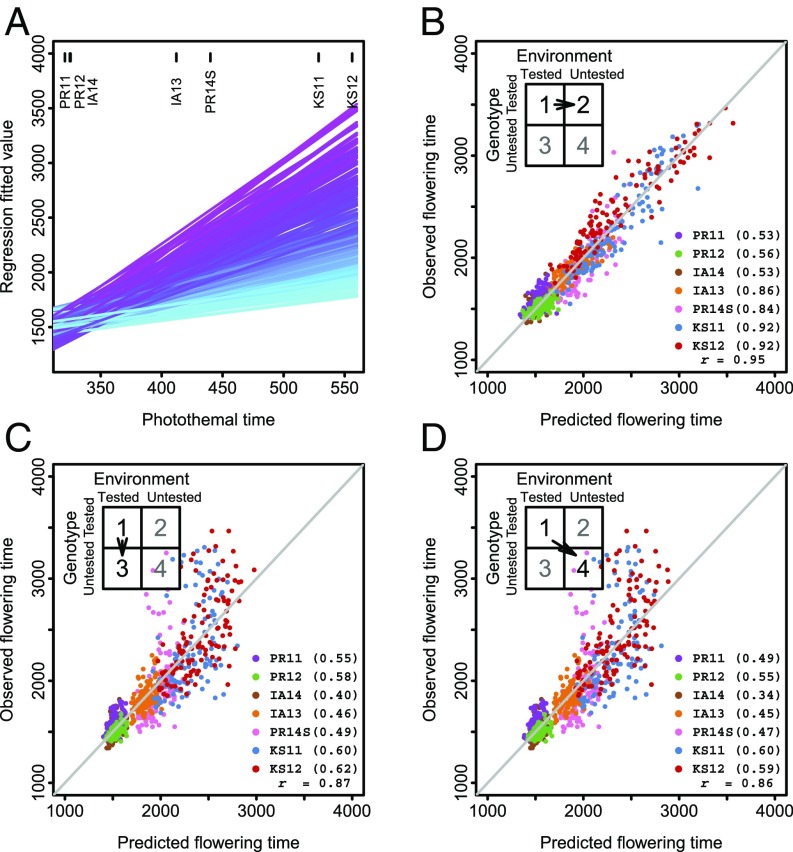
The first modeling and performance prediction approach we examined was through the reaction-norm parameters predicted using genome-wide marker information. First, the flowering time response of tested genotype across tested environments was regressed on the photothermal-time index (Fig. 3). The regression slope is an indicator of a genotype’s plasticity to different external influences (i.e., photoperiod and temperature during the transition stage), and the intercept is an indicator of a genotype’s average response to the group of environments examined. Next, the intercept and slope of untested genotypes were obtained through a genomic prediction model established with tested genotypes. Finally, the numerical input value of photothermal time determined for a specific untested environment was plugged in to obtain the predicted flowering time.

Fig. 3.

JGRA for performance prediction with reaction-norm parameters. (A) Fitted response curves of genotypes across environments. (B) Predicting tested genotypes in untested environments. (C) Predicting untested genotypes in tested environments. (D) Predicting untested genotypes in untested environments. In B–D, both prediction accuracy at each individual environment (in parentheses) and across all environments (r) are indicated; the diagonal line indicates the exact match between observed and predicted values.

Overall, we obtained accurate performance prediction for all three scenarios (overall across environments r = 0.86∼0.95, or R² = 74∼90%). Prediction accuracy for tested genotypes in untested environments was high (average individual environment r = 0.74), followed by untested genotypes in tested environments (average r = 0.53) and untested genotypes in untested environments (average r = 0.50), which is the most challenging scenario. Achieving this level of prediction accuracy is very encouraging, compared with predictions without an overall framework and relying on averages across tested environments (SI Appendix, Fig. S11). Model fitting with the complete data verified that 49% ∼95% of the variation observed for flowering time was captured with this approach (SI Appendix, Table S6).

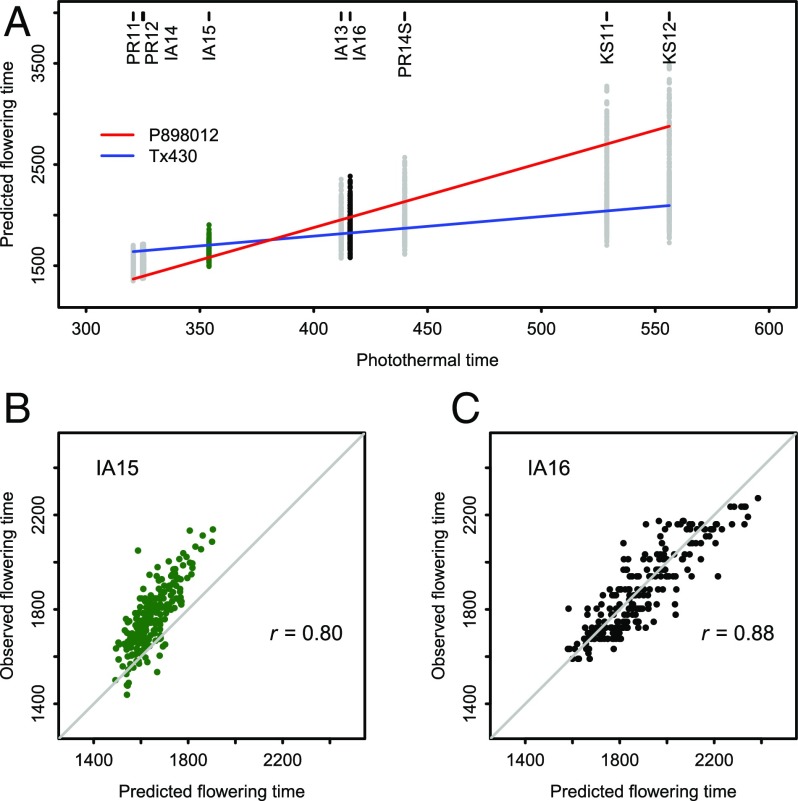
To demonstrate this strategy, we conducted experiments by growing out the population again in 2015 and 2016. With the model derived from seven environments and photothermal time values for two new environments, we obtained the predicted flowering time values. Prediction accuracy was high in both cases (Fig. 4). These predictions are “in-season” because they can be made once the environmental profile data are available to compute photothermal time as the season progresses and “on-target” because the predicted values are close to the observed values, not only having similar ranks.

Fig. 4.

Empirical validation of performance prediction through reaction-norm parameters. (A) Predicted flowering time of genotypes across environments. (B) Prediction accuracy for Iowa 2015 (IA15). (C) Prediction accuracy for Iowa 2016 (IA16). The diagonal line in B and C indicates the exact match between observed and predicted values.

Genome-Wide Marker Effect Continuum Estimation

We examined an alternative approach using the genome-wide marker effect continuum to predict flowering time (SI Appendix, Fig. S12). First, genome-wide marker effects were obtained from the individual-environment analysis using performance data from tested genotypes across tested environments. Next, these marker effects were regressed on the photothermal-time index to obtain the fitted marker effects. Finally, with these fitted marker effects, performance of untested genotypes in untested environments was obtained by factoring in the genome-wide marker profiles of the new genotypes and the specific environmental index value of the new environment. Results obtained using this approach were comparable (r = 0.86∼0.93, R² = 74∼86%) to the first approach (SI Appendix, Figs. S12 and S13).

Genetic Determinants of Flowering Time

To reveal the underlying mechanisms of G × E by focusing on specific loci (4, 5), we conducted genetic mapping for individual environments and across all environments. Several common genetic loci were detected in the combined analysis, and others were only found in certain environments (Fig. 5 and SI Appendix, Fig. S14 and Table S7). Notably, the quantitative trait locus (QTL) effect size and direction are environment-dependent. Alleles increasing flowering time in one environment can increase flowering time to a different level, decrease flowering time, or have no effect in other environments. In other words, the complex gene–environment interplay generated differential sensitivity, antagonistic pleiotropy, conditional neutrality, or no G × E for the additive effects (SI Appendix, Table S8). With the JGRA framework, genetic effect fluctuation can be seen as a dynamic manifestation of the intricate network of genetic regulators responding to different levels of environmental cues. The effect fluctuation can take different forms.

Fig. 5.

Genetic determinants underlying G × E. (A) Common and specific loci and corresponding known genes were detected from individual environment analyses. (B) Loci and corresponding known genes detected from the combined analysis of seven environments. (C) Dynamic changes of QTL additive genetic effects across environments (Q × E): differential sensitivity, antagonistic pleiotropy, or conditional neutrality. (D) Epistasis detected between two loci (Ma₁ and FT). (E) Known or potential functional polymorphisms between two alleles in four flowering time genes (Ma₁, Ma₆, FT, and ELF3). LOD, logarithm of odds; SET, single environmental trial; MET, multiple environmental trial.

We next conducted additional sequencing and bioinformatics analyses to examine genes and polymorphisms underlying these QTL. Sequence analysis revealed that the most significant QTL corresponds to the known Ma₁ gene on chromosome 6 (PRR37, Sobic.006G057866), encoding a pseudoresponse regulator protein (28). A single adenine insertion in the third exon of Tx430 allele was identified that led to a premature stop codon and nonfunctional protein (prr37^Feterrita) (29) (Fig. 5 and SI Appendix, Fig. S15). The second-most significant QTL corresponds to Ma₆ gene on chromosome 6 (Ghd7, Sobic.006G004400), a floral repressor regulated by the circadian clock and light signaling (30). The P898012 allele had a large intron insertion, leading to a potentially modified CCT domain and a weak allele (ghd7-2) (30), and the Tx430 allele had a 5-bp (GTCGA) insertion in the first exon, leading to a premature stop codon and nonfunctional protein (ghd7-1) (Fig. 5 and SI Appendix, Fig. S15). No known flowering gene was found for the QTL on chromosome 8 (qFL8.1). The candidate gene underlying the QTL on chromosome 9 (qFL9.1) is ELF3 (Sobic.009G257300). A 7.4-kb insertion of two copies of Gypsy LTR was detected in the promoter region of Tx430 allele but not in P898012 (SI Appendix, Fig. S15).

Epistatic Interaction

Complex gene regulatory networks control flowering time in plants (15), and epistatic interactions have been detected in previous research (31, 32). In sorghum, both Ma₁ and Ma₆ repress expression of the floral activator Ehd1, which activates FT to produce florigen for floral induction (28, 30). The Ma₃ gene activates Ma₁ and Ma₆, but represses Ehd1 and FT (33). In this study, a significant interaction was detected between the QTL harboring Ma₁ and the QTL harboring FT (qFL10.1, Sobic.010G045100) in the combined analysis and five individual-environment analyses (Fig. 5). Notably, the interaction was still significant in IA14 when neither marginal effect was detected. Unlike the Tx430 allele, the P898012 allele of the FT gene contained a PIF/Harbinger transposon in the promoter region, potentially altering the binding site of another regulator. This FT was one of the three most plausible florigen-encoding genes in sorghum (34).

Flowering time prediction with the identified QTL effects along the environmental index was also conducted, which serves as a benchmark to both help interpret results from two genome-wide approaches and to show the differences of these approaches (SI Appendix, Figs. S16 and S17).

Genetic Dissection of Reaction-Norm Parameters

To further demonstrate the gene–environment interplay underlying G × E, we conducted genetic mapping for the two reaction-norm parameters, intercept and slope. As expected, five QTL were detected, corresponding to the same set of genetic loci including Ma₁, Ma₆, qFL8.1, ELF3, and FT (SI Appendix, Fig. S18). Once again, a genome-wide epistasis search for both intercept and slope detected significant interaction between the two loci harboring Ma₁ and FT (SI Appendix, Fig. S18). These results showed that genetic determinants underlying the patterned differential responses of individuals to environment conditions can be uncovered using different angles of analysis.

Discussion

Integrated analysis of genes and environment can reveal the mechanistic interplay underlying the observed phenotype dynamics (4–7). By investigating the reaction norms of a genetic mapping population across a relatively diverse set of natural environments, we show that multiple concepts from different research areas can be combined to design parallel approaches that model, predict, and dissect G × E. Unifying the developmental and biometric aspects of G × E (9, 35) is enabled by genomic analyses. Examining known or candidate genes underlying the identified loci allowed us to connect the genotype-level G × E with gene × environment at the individual locus level, and together with gene × gene interaction. Different patterns of genetic effects and interaction pathways were illustrated in previous research (4, 5). Our finding of a genetic effect continuum across the environmental gradient helps interpret the underlying mechanism. Differential sensitivity, conditional neutrality, antagonistic pleiotropy, and no genetic effect × environment interaction can be viewed as emergent properties of the plant perceptron interacting with diverse environmental and developmental cues.

Improved understanding of gene × environment interaction could lead to better-informed decisions in personalized medicine and optimized breeding (2, 5, 6). A comprehensive framework for gene × environment interaction and gene × gene interaction can be established even if different sets of individuals are assessed at different environments. For plants, with a robust G × E modeling framework, observations at winter nurseries may be leveraged to enhance selection gain per unit time. Imbalanced yield trials across environments can be projected onto a series of representative environmental panels for selection, and optimized testing strategies for genotypes and environments can be designed.

We envision that this general approach of pattern search, determinant discovery, and integrated modeling may be applicable to investigating other complex traits. A single genetic mapping population derived from two contrasting parental inbreds was analyzed in the current study for flowering-time response. Future studies with diverse genetic materials in multiple species should be conducted. In this study, day length and temperature were sufficient to generate the environmental index, a critical enabling factor for integrated modeling and prediction. Other environmental factors like precipitation, radiation, and nitrogen application may emerge as critical in other scenarios and we may be able to model nonlinear relationships among them (5, 36). Comprehensive crop models (37–40) for more complex G × E may require systematic quantification or approximation of growth stages. Fortunately, this can be achieved using high-throughput phenotyping calibrated by traditional physiological measurement protocols. Advanced genomic prediction models are also being developed (41). Ultimately, viewing the complexity of G × E as an opportunity helps us build a better understanding of biology and evolution.

Materials and Methods

Population and Phenotyping.

The population with 237 RILs from a cross between Tx430 and P898012 (42) was evaluated at seven environments (SI Appendix, Table S1 and Dataset S1). A randomized complete block design with two replications was used in each environment. Flowering time was recorded as the number of days after planting when half of the plants in a plot were shedding pollen. Flowering time as GDD was then calculated with daily maximum and minimum temperature using 50 °F as the base and 100 °F as the maximum. The combined analysis across seven environments followed established procedures (7).

Environment Analysis and Search for an Environmental Index.

Temperature and day length data were retrieved from the National Oceanic and Atmospheric Administration National Centers for Environmental Information (https://www.ncdc.noaa.gov/) and the Astronomical Applications Department of the US Naval Observatory (aa.usno.navy.mil/index.php).

Physiological knowledge is essential to identify the external environmental factors to generate an environmental index (7). Photothermal time, the product of temperature and day length, was used to project the timing of developmental stages (21–25, 43). In our analysis, photothermal time was obtained as the product of GDD (t) and hours of daylight time (h). To identify a common window of days after planting to cover critical growth and photoperiod sensing stages across multiple environments, we calculated the photothermal time with different starting days (s) and different window sizes (l): $(1/l){\displaystyle \sum _s^{s+l}}(t\times h)$. Correlation coefficients were calculated between these different sets of photothermal time values and the population means in flowering time. In addition, leave-one-environment-out subsampling analysis was conducted to verify that this window is consistently detected.

Genetic Mapping.

Genotyping by sequencing generated 8,960 SNPs, and genetic map was built with 1,462 SNPs (42). Sorghum genome v1.4 was used for SNP calling and analysis. Composite interval mapping was conducted with Windows QTL Cartographer 2.5. Inclusive composite interval mapping was conducted with IciMapping 3.2 (44). QTL mapping and epistasis were conducted for individual environments (single environment trial analysis, SET) and across seven environments (multiple environmental trial analysis, MET) (45, 46). In addition, single-marker genome scan and two-dimension scan using 8,960 SNPs were conducted in R.

Functional Polymorphisms.

Known genes and candidate genes underlying the QTL were verified by checking the positions of significant SNPs, analyzing sequence polymorphisms between two inbreds, and conducting a bioinformatics search of databases. We searched potential flowering-time-related candidate genes within QTL intervals based on reference genome annotation. To identify DNA polymorphisms between two mapping parents, 15.8 Gb whole-genome Illumina paired-end reads of Tx430 (SRR2759161) and 59.8 Gb Illumina paired-end reads of P898012 (SRR4028763 and SRR4028764) were retrieved from the National Center for Biotechnology Information Sequence Read Archive and aligned to sorghum reference genome (version 3.1) by BWA through the BWA-MEM algorithm (47). Uniquely aligned reads within QTL intervals were then retrieved through Samtools (48). DNA polymorphisms between Tx430 and P898012 near candidate genes were visualized with IGV (49).

To verify the known and potential functional polymorphisms detected by short read alignment, DNA segments were amplified with oligos designed by Primer 3 (50). Amplicons of Tx430 and P898012 were further subjected for agarose gel electrophoresis for large indel variations or Sanger sequencing for SNP variations (SI Appendix, Fig. S15 and Dataset S2).

Genomic Prediction.

We adopted the common pratice for model building and validation. This process started with randomly splitting the genotypes into tested and untested groups (50%:50%) and the environments into tested and untested groups (6:1). Predictive models were built using tested genotypes in tested environments. Predictions were then made for three senarios: tested genotypes in untested envrionments, untested genotypes in tested environments, and untested genotypes in untested environments. Prediction accuracy was assessed by the correlation between observed values and predicted values. This process was repeated 50 times to obtain the average and a single run was chosen for plotting.

JGRA.

The overall modeling and prediction framework was conceived by expanding the traditional joint regression analysis (16, 17) to include two critical components: (i) a quantitative index defined by the photothermal time and (ii) a genomic component to connect individuals with performance data and those without but to be predicted.

For individuals without performance data, their predictions can be obtained by one of the two approaches: (i) JGRA through reaction-norm parameter estimation or (ii) JGRA through genome-wide marker effect continuum estimation. In all analyses, the photothermal-time index was centered at the overall mean value to obtain the intercept for each genotype or each marker, but this overall mean value was added back to the index for plotting and interpreting.

Additional information can be found in SI Appendix, SI Materials and Methods.