Significance
Fluctuating environmental conditions are thought to be important for the maintenance of species diversity, and yet our understanding of the relative contribution of different fluctuation-dependent coexistence mechanisms (the temporal storage effect and relative nonlinearity of competition) in real systems is limited. Using experiments and simulations, we show that both mechanisms consistently affect coexistence and that, contrary to long-held assumptions, the effect of relative nonlinearity can be larger in magnitude. These results may be general in that the simultaneous emergence of both mechanisms rests on two factors common to nearly all ecological systems, from the human gut to the soil microbiome: variable environmental conditions and saturating population growth rates.
Keywords: coexistence, environmental variability, storage effect, relative nonlinearity, resource competition
Abstract
Understanding the origins and maintenance of biodiversity remains one of biology’s grand challenges. From theory and observational evidence, we know that variability in environmental conditions through time is likely critical to the coexistence of competing species. Nevertheless, experimental tests of fluctuation-driven coexistence are rare and have typically focused on just one of two potential mechanisms, the temporal storage effect, to the neglect of the theoretically equally plausible mechanism known as relative nonlinearity of competition. We combined experiments and simulations in a system of nectar yeasts to quantify the relative contribution of the two mechanisms to coexistence. Resource competition models parameterized from single-species assays predicted the outcomes of mixed-culture competition experiments with 83% accuracy. Model simulations revealed that both mechanisms have measurable effects on coexistence and that relative nonlinearity can be equal or greater in magnitude to the temporal storage effect. In addition, we show that their effect on coexistence can be both antagonistic and complementary. These results falsify the common assumption that relative nonlinearity is of negligible importance, and in doing so reveal the importance of testing coexistence mechanisms in combination.
Theory suggests that the maintenance of species diversity is likely the outcome of multiple mechanisms acting in concert (1, 2), but most empirical tests of coexistence consider individual mechanisms in isolation (2). This discrepancy is particularly evident for the two broad classes of mechanisms that arise in fluctuating environments: the temporal storage effect, which formalizes the concept of temporal niche partitioning, and relative nonlinearity of competition, which can mediate coexistence through the asymmetric effects of nonlinear averaging on population growth rates (3, 4). Not only is it a challenge to partition the two mechanisms analytically (2, 5), but much work has proceeded on the tacit assumption that relative nonlinearity of competition is of minor importance (6–9). As a result, the joint contribution of the temporal storage effect and relative nonlinearity has not been quantitatively investigated in an empirical system.
The familiar concept of temporal niche partitioning was originally presented as a solution to the so-called paradox of the plankton, the seemingly inexplicable coexistence of numerous species on just a few limiting resources (10). The proposed explanation was that environmental fluctuations could afford each species a period of competitive superiority, thus avoiding any one species being excluded. Later, it was shown that for stable coexistence to arise via temporal niche partitioning, species at low density have to capitalize on low levels of competition during periods favorable to their growth, whereas the potential gains made by high-density species during favorable periods are constrained by high levels of intraspecific competition. Along with the potential to buffer losses under unfavorable conditions (e.g., via seeds or dormant cells), this density dependence in the covariance between environmental favorability and the strength of competition is the essential criterion for coexistence via the temporal storage effect (2, 3, 11). Relative nonlinearity of competition differs from the temporal storage effect in that it relies on fluctuations in the intensity of competition, rather than fluctuations in the environment itself. Due to nonlinear averaging on population growth rates, species with sharply saturating (more concave) functional responses to resource concentrations will be more harmed by variability in a limiting resource than their less concave competitors. This difference can reduce fitness inequalities between species and also benefit species at low density if the more concave species increases resource fluctuations while the more linear species dampens fluctuations (2, 11). Despite the potential for relative nonlinearity of competition to operate widely (2), logistical challenges and its perception as an esoteric and unlikely theoretical possibility have stymied its empirical study relative to the temporal storage effect.
We studied the two mechanisms together in nectar-colonizing yeasts. During dispersal from flower to flower via pollinators, fluctuating carbon (sugars) and nitrogen (amino acids) concentrations in nectar cause these yeasts to experience high variability in osmotic pressure and resource availability, respectively. Assuming trade-offs in osmotolerance, as well as saturating responses to the availability of amino acids, we expected both the temporal storage effect and relative nonlinearity of competition to operate in this system. To investigate the contribution of the two mechanisms, we simulated empirically parameterized models to first quantify mechanistic contributions and then predict the outcomes of mixed-culture experiments. To this end, we used a modified Monod competition model to mimic a sequence of nectar colonization, followed by pollinator-assisted dispersal to new flowers, with the potential for variation in osmotic pressure between flowers (Materials and Methods). We parameterized the model by running monoculture experiments in which four yeast species were inoculated into artificial microcosms across a gradient of a common sugar in nectar, sucrose (10%, 30%, and 50%, aimed at imposing increasing levels of osmotic pressure), and limiting amino acid concentrations (8–16 levels from 0 to 3.16 mM) (Materials and Methods). These treatments were chosen to reflect the range of osmotic pressure and resource availability that nectar yeasts may encounter in wild flowers (12).
Results and Discussion.
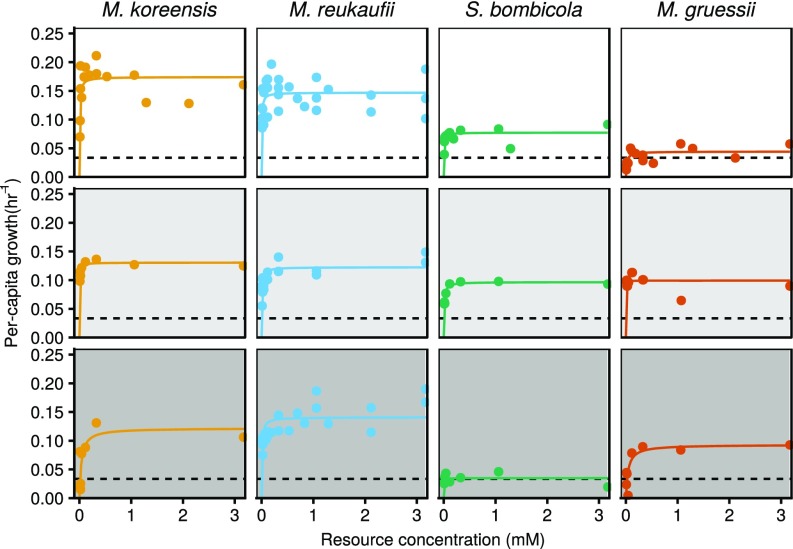
The four species varied in maximum growth rate () across the sucrose gradient (Fig. 1 and SI Appendix, Table S1). In two pairs of species (Metschnikowia reukaufii and Metschnikowia koreensis; and Metschnikowia gruessii and Starmerella bombicola), maximum growth rate () relative to each other switched between 10% and 50% sucrose. Maximum growth rates were most similar at 30% sucrose, indicating a trade-off in fitness between low and high sucrose concentrations. This trade-off is a necessary, although not sufficient, condition for a temporal storage effect. In addition, half-saturation constants () varied both between and within species at different sucrose levels (SI Appendix, Table S1). Together with fluctuations in the concentration of amino acids, this variation makes it possible that nonlinear averaging differentially affects species’ growth rates. Modeling and simulations are nevertheless required to predict competitive outcomes and quantify mechanistic contributions to coexistence.
Fig. 1.
Least-squares best fits of Monod growth functions in response to the availability of amino acids for the four focal nectar yeast species at low (Top), medium (Middle), and high (Bottom) osmotic pressure (10%, 30%, and 50% sucrose). Horizontal dashed lines represent the effective continuous mortality rate corresponding to an 80% instantaneous mortality event every 48 h, as implemented in the model simulations and competition experiments (Materials and Methods).
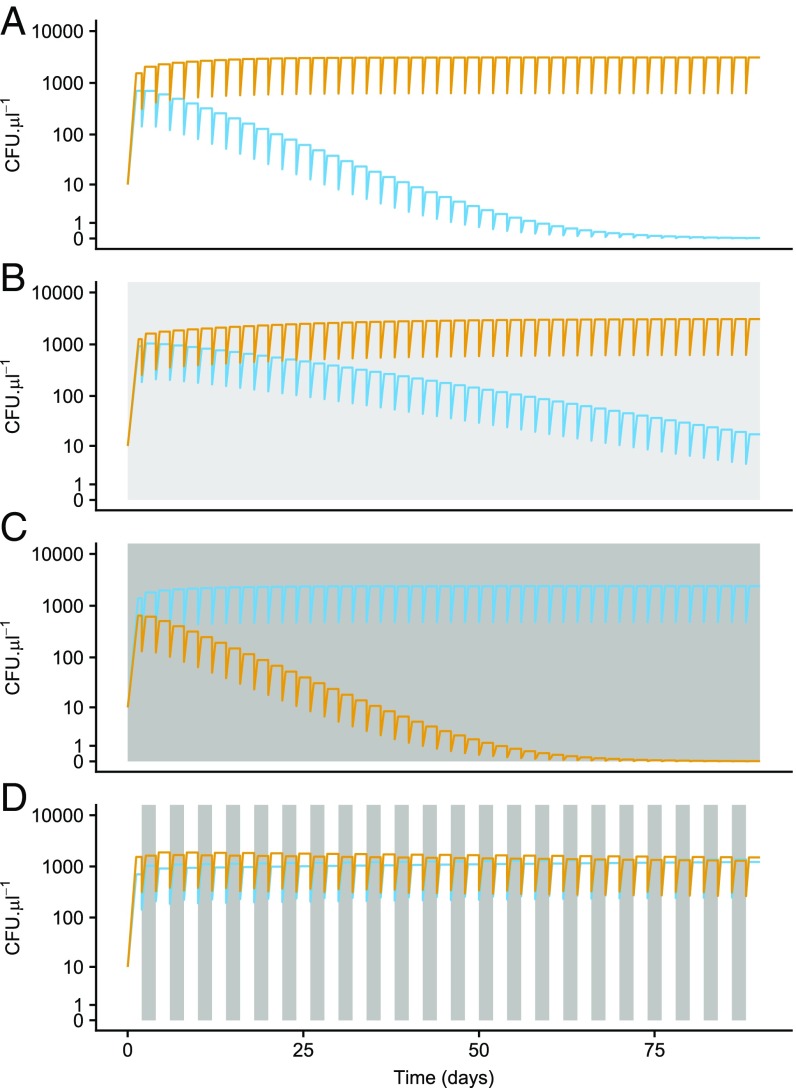
We used the estimated parameters to simulate competitive interactions between all six pairwise combinations of the four species under three constant (10%, 30%, and 50%) and one fluctuating sucrose treatment (10–50%) (Materials and Methods). These simulations were designed in concert with accompanying in vitro competition experiments, which in turn were designed to match conditions and dispersal rates observed in nature. The design included the transfer of a 20% fraction of the community to a new flower every 48 h, either at the same (constant treatment) or different (fluctuating treatment) sucrose level as donor flowers, along with a single amino acid pulse at the time of introduction to recipient flowers (SI Appendix, Fig. S1). In simulations under fluctuating conditions, species stably coexisted in two of six possible pairs: M. reukaufii and M. koreensis (Fig. 2D) and M. gruessii and S. bombicola (SI Appendix, Fig. S5D). No species pairs coexisted under constant environmental conditions (Fig. 2 A–C and SI Appendix, Figs. S2–S6).
Fig. 2.
Simulations of resource competition between M. reukaufii (blue) and M. koreensis (light orange) at constant sucrose concentrations of 10% (A), 30% (B), and 50% (C) and fluctuating every 2 d between sucrose concentrations of 10% (white bars) and 50% (gray bars) (D).
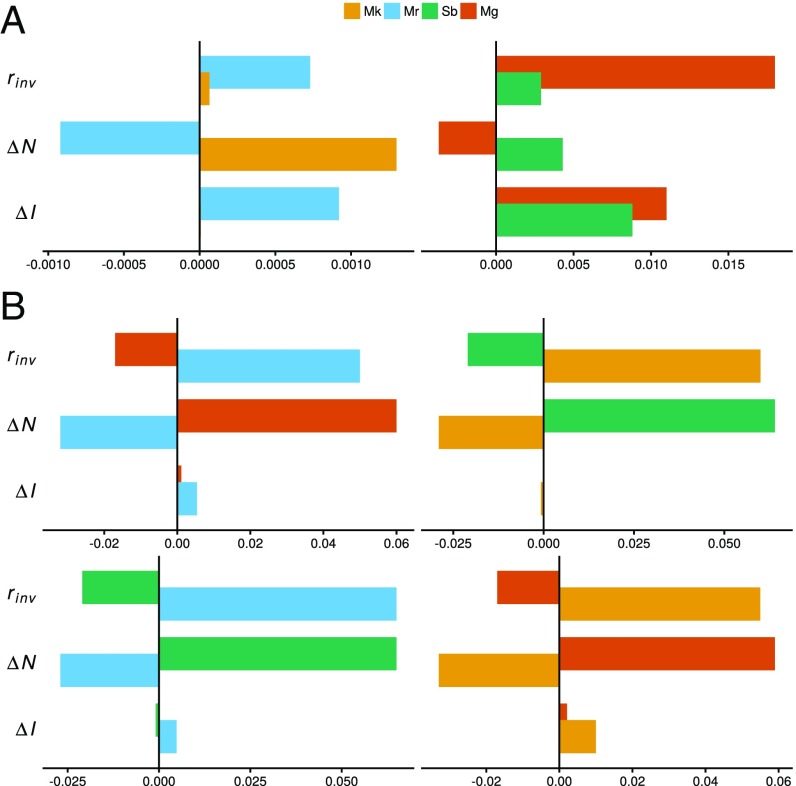
To quantify the contribution of the two mechanisms, we used additional Monte Carlo simulations to compare the growth rate of an invader with that of a resident in the presence and absence of environment-competition covariance and/or resource fluctuations (ref. 5; Materials and Methods). An advantage of this approach over previous analytic approaches (9) is that it bypasses the need to derive model-specific formulas for each mechanism, which can quickly become intractable with increasing ecological realism (5). In simulated competition between M. reukaufii and M. koreensis under fluctuating sucrose levels, we found that it was only through the joint operation of the storage effect and relative nonlinearity that the two species satisfied the mutual invasibility criterion for coexistence (Fig. 3). Despite their observed trade-off in maximum growth rate at low and high sucrose levels (Fig. 1), only M. reukaufii benefited from a temporal storage effect. Without a storage effect, M. reukaufii could not invade a resident population of M. koreensis (Fig. 3). A negligible contribution of the storage effect to M. koreensis’ growth rate was attributable to M. reukaufii being less sensitive to variation in sucrose concentrations than M. koreensis (Fig. 1), which means that as an invader, M. koreensis experienced little covariance between environmental suitability and competition when M. reukaufii was resident. In contrast, M. koreensis benefited from relative nonlinearity, such that it was able to invade a resident population of M. reukaufii. In the other coexisting pair, S. bombicola benefited from both a temporal storage effect and relative nonlinearity. Removing either mechanism would prevent it from invading a resident population of M. gruessii.
Fig. 3.
Contribution of the storage effect () and relative nonlinearity () to the growth rate () of each species as an invader () in pairwise competition, where = average fitness differences + + . (A) Pairs where coexistence is predicted because for both species. In the case of M. koreensis (Mk) and M. reukaufii (Mr), would be negative for M. koreensis without the contribution of , and negative for M. reukaufii without the contribution of . In the case of S. bombicola (Sb) and M. gruessii (Mg), M. gruessii would still have without either mechanism, while persistence of S. bombicola requires one or both mechanisms. (B) Pairs where coexistence is not predicted because one species has . In all pairs, is weak to nonexistent, while is strongly equalizing (i.e., differences in would be much larger without the contribution of ).
By canceling out the contribution that each mechanism makes to the low-density growth rate of M. reukaufii and M. koreensis (Fig. 3), it is clear that in the simultaneous absence of both mechanisms, M. reukaufii would exclude M. koreensis. It is nevertheless helpful to consider each mechanism independently to better discern how the two mechanisms interact. In an equilibrium system, where resources are supplied at a constant rate and the sucrose concentration remains at the mean level, M. reukaufii would still exclude M. koreensis because M. reukaufii has a lower mean (minimum resource level required to maintain a nonnegative growth rate). Independent of either coexistence mechanism, the pulsed delivery of resources goes some way to leveling the playing field because it shifts the time-averaged resource level higher, resulting in a reduced fitness differential between the two species. However, in the presence of a temporal storage effect alone, only M. reukaufii benefits, and M. koreensis would still be excluded. Conversely, in the presence of relative nonlinearity alone, the reverse would be true (i.e., M. koreensis would exclude M. reukaufii). By virtue of a less nonlinear functional response (averaged across sucrose variation; SI Appendix, Table S1), M. koreensis benefited from resource fluctuations, while M. reukaufii was harmed by them. Even though the amount M. reukaufii was harmed is smaller in magnitude than the amount M. koreensis benefited, a necessary condition for relative nonlinearity to act as a stabilizing mechanism, the swing in fitness was large enough for M. koreensis as the resident to prevent M. reukaufii from invading. It was then only through the additional contribution of the temporal storage effect that M. reukaufii achieved a positive growth rate as an invader. Without this mechanistic decomposition, one could have mistakenly assumed that coexistence between these two dominant species was driven exclusively by a temporal storage effect.
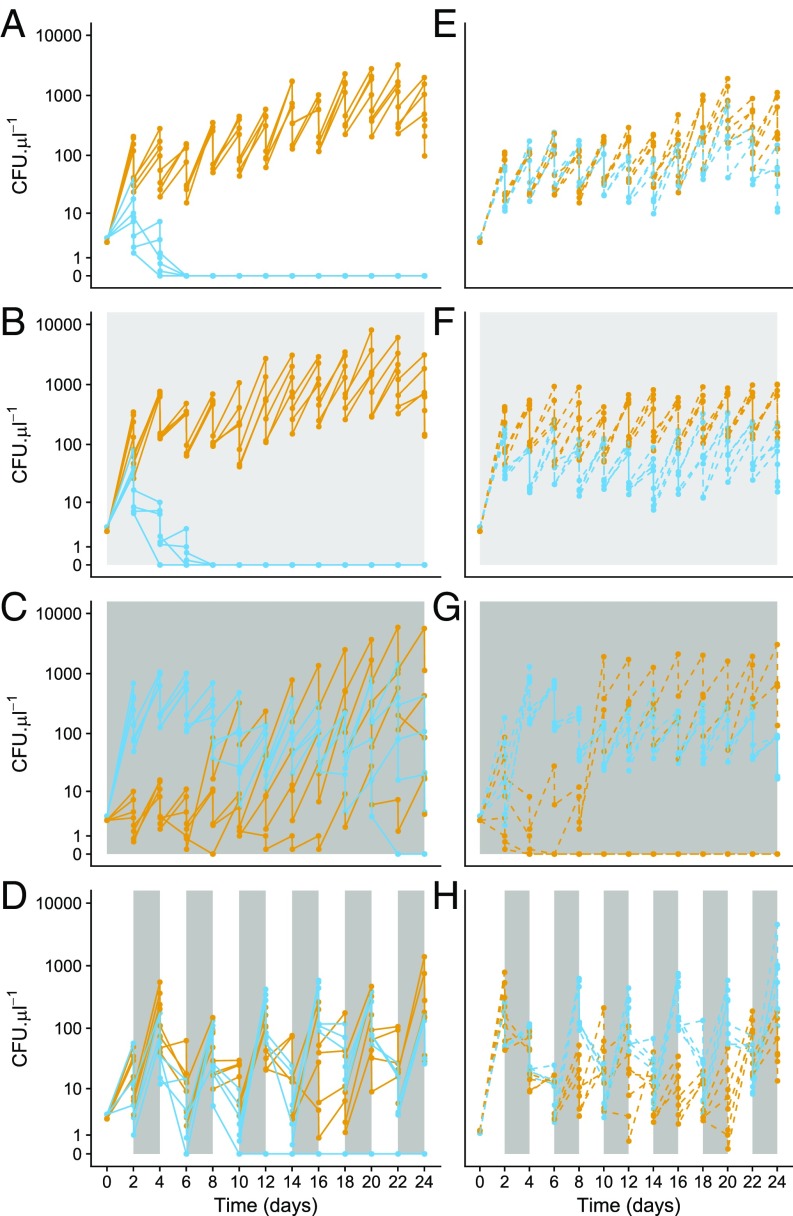
We next evaluated the simulation predictions in 24-d mixed-culture experiments. The results of these experiments matched the competitive outcomes predicted by simulations in 83% of cases. As predicted, M. reukaufii and M. koreensis often coexisted (three of four replicates) under fluctuating sucrose levels (Fig. 4D), and M. koreensis excluded M. reukaufii in all four replicates under constant conditions at both low and moderate sucrose levels (Fig. 4 A and B). Under constantly high (50%) sucrose levels, their populations initially behaved as predicted, with M. reukaufii on the brink of excluding M. koreensis, but contrary to predictions, M. koreensis recovered after 8 d and excluded M. reukaufii after 20 d in one replicate (Fig. 4C). This recovery by M. koreensis might have been caused by rapid evolution, which our model did not account for. To test the robustness of coexistence between M. reukaufii and M. koreensis, we replicated the fluctuating treatment in an additional eight microcosms. After 24 d, the pair coexisted in four of eight microcosms, with both species surviving in all eight microcosms up until day 16 (Fig. S13). The only other mixed-culture experiments that deviated from the simulation predictions were between M. gruessii and S. bombicola under low, high, and fluctuating sucrose concentrations (SI Appendix, Fig. S7). Specifically, at low and fluctuating sucrose levels, M. gruessii excluded S. bombicola, and at high sucrose, neither species persisted. Despite S. bombicola being the more efficient resource competitor in the low-sucrose treatment (Fig. 1), its exclusion by M. gruessii may suggest the presence of a non-resource-mediated interaction between these two species, which would explain the erroneous predictions.
Fig. 4.
Mixed (solid lines) and monoculture (dashed lines) times series for M. reukaufii (blue) and M. koreensis (light orange) at constant 10% (A and E), 30% (B and F), and 50% (C and G) and fluctuating 10–50% (D and H) sucrose. The fluctuating treatment was replicated in an additional eight microcosms (SI Appendix, Fig. S12).
The methodological capacity to quantify mechanistic contributions even in the absence of coexistence revealed that relative nonlinearity consistently reduced fitness difference between competing species (SI Appendix, Table S2). By design, our model and experiments were characterized by only a limited number of niche axes, but many other opportunities may exist for other stabilizing mechanisms to overcome these reduced fitness differences in real flowers. Our results, therefore, suggest that relative nonlinearity will likely still affect species coexistence in this system. Furthermore, contrary to current perceptions (7, 8, 13), the prevalence of nonlinear functional responses in many organisms points to a significant role for relative nonlinearity in other systems, including those that are more species-rich. It is generally underappreciated that the number of species that can exist via relative nonlinearity scales with the square of the number of fluctuating resources (14). Despite potentially playing a critical role in sustaining multispecies coexistence, relative nonlinearity has gone almost completely unexplored in both theoretical and empirical studies of species-rich systems (but see simulations in ref. 15). The analytical approach adopted here is equally applicable in the presence of multiple residents (5) and therefore offers untapped potential for future experimental work on multispecies coexistence.
A challenge for both analytic and simulation-based approaches to the mechanistic decomposition of coexistence is the choice of scaling factors, which weight invader and resident population growth rates to remove linear terms in the partitioning of invasion growth rates into different mechanisms (refs. 16 and 17: Materials and Methods). The scaling factors have a clear theoretical definition, but they can be difficult to estimate empirically (5). To account for this potential source of error, instead of assuming equal scaling factors, we recalculated both mechanisms using a model-specific formula for the scaling factors with parameters estimated from our data (Materials and Methods and SI Appendix, Eq. S10). These adjusted values for the temporal storage effect and relative nonlinearity were qualitatively consistent with our main findings in the majority of cases (SI Appendix, Table S3). Although the contribution of the adjusted storage effect to M. reukaufii’s growth rate was no longer critical to its coexistence with M. koreensis under fluctuating conditions, it still accounted for almost 25% of its growth rate as an invader, whereas the contribution of adjusted relative nonlinearity to M. koreensis’s invader growth rate increased by 25% (SI Appendix, Table S3). Given that scaling factors and adjusted values were sensitive to choices that should be inconsequential under the assumptions of the analytic theory (SI Appendix, Derivation of Scaling Factors), we anticipate that robust estimation of scaling factors will be an active area for research in coexistence theory.
We have demonstrated multiple fluctuation-dependent coexistence mechanisms operating in a simple microbial system. Although this study was designed to mimic a natural system as closely as possible, it remains an open question to what extent these results are reflective of this and other wild systems. An important avenue of future research will be to attempt similar partitioning exercises in more complex variable systems, such as soil, tropical rainforests, or the human gut, where both fluctuation-dependent and -independent mechanisms (e.g., resource partitioning) may often be comparable in magnitude. At the same time, to foster rapid feedback between theory and experiments, there remains significant demand for rigorously controlled laboratory studies that enable high-resolution partitioning of multiple mechanisms. We venture that a better understanding of the relative importance of simultaneously acting coexistence mechanisms will not only advance fundamental theory, but facilitate the predictability and management of ecological systems that affect environmental and human health.
Materials and Methods
Study System.
The floral nectar of animal-pollinated plants often hosts dense, but species-poor, yeast communities, making it a tractable system to investigate microbial community assembly (18). Flower-visiting animals introduce these yeasts to initially sterile nectar at low density, where they grow rapidly, thus increasing their probability of being dispersed to new flowers by subsequent visitors (19–21). Nectar chemistry can be highly variable, both within and across species, with sugar concentrations ranging from 5% to >50% (12). Although sugars are an essential resource for yeasts, sugars appear to primarily mediate nectar yeast population dynamics through osmotic stress (18, 20). Nevertheless, previous studies have shown that yeasts significantly deplete amino acids in nectar, which can lead to strong resource competition (19, 20). Some species of bacteria can withstand the high osmotic pressure of sugar-rich nectar (21–23), but experiments and observations have indicated that, owing to priority effects, bacteria are rarely abundant in flowers in which yeasts are abundant, and vice versa (24, 25).
We used four common species of nectar yeast isolated from Mimulus (Diplacus) aurantiacus nectar at Jasper Ridge Biological Preserve in the Santa Cruz Mountains of California: M. reukaufii, M. koreensis, M. gruessii, and S. bombicola (19, 21, 26). The colonies and cells of all four species are morphologically distinct on yeast malt (YM) agar and under a microscope, respectively.
Monoculture Experiments.
Monoculture assays were conducted across a factorial gradient of sucrose (10%, 30%, and 50%) and digested casein (eight concentrations from 0 to 3.16 mM) comprising a similar composition of amino acids to real nectar (27). These treatments were chosen to reflect the range of sucrose and nitrogen concentrations that nectar-dwelling microorganisms typically encounter (12, 27). Other potentially important sources of environmental variability in nectar, including temperature and pH, were held constant. Because yeast cell densities in artificial nectar are usually below the detection threshold for optical density measurements, per capita growth estimates were necessarily obtained by plating dilutions onto YM agar at set intervals.
For each “species sucrose amino acid” combination, 12 microcosms (4 replicates 3 time points) were prepared to enable destructive sampling at 12, 24, and 48 h, for a total of 1,152 monoculture assays. Inoculations were prepared immediately before the beginning of the experiment, with a single colony picked for each strain from stock solutions streaked onto YM agar 2–4 d previously. A hemocytometer was used to obtain an intended cell density of 400 cells L−1 in the inoculum. One L of the inoculum was then added to 9 L of artificial nectar for a final intended cell density in each microcosm of 40 cells L−1. However, due to stochasticity in the number of viable cells, inoculations were also plated, and the number of colony-forming units (CFUs) was enumerated to estimate the initial number of viable cells introduced. Microcosms were incubated at 27 ○C and then destructively sampled at 12-, 24-, and 48-h intervals, and dilutions (1:10 and/or 1:50) were plated onto YM agar and incubated for 2–3 d before enumerating the number of CFUs per plate.
For each species, per capita growth rate at each “amino acid sucrose” concentration was obtained from the slope of linear models fitted for the natural logarithm of CFUs (as a proxy for cell density) as a function of time. The maximum per capita growth rate was taken as the steepest significant () estimate for the slope over the first 24 or 48 h, i.e., equivalent to the largest for (we excluded densities at 12 h as an endpoint due to high variability at the within-species level). For some “species sucrose” combinations, growth rates obtained from the initial 1,152 monoculture assays were supplemented by additional growth rate data obtained from associated experiments applying the same methods.
Monod models were subsequently fit for per capita growth as a function of amino acid concentration for each species and sucrose level,
| [1] |
where is the population density (L−1), is the maximum growth rate (h−1), is the resource (amino acid) concentration (millimolar), and is the half-saturation constant (millimolar). For the purposes of model fitting, a 0.01-mM positive offset was applied to all resource values in all treatments. This was done to compensate for observed growth at 0 amino acids in some microcosms, which we speculate arises from recycling of nutrients from dead cells in the inocula and/or resource storage. The only exception was for M. gruessii at 30% where it was necessary to increase the offset to 0.02 to prevent nonsensical negative estimates for K. Nonlinear least squares was used for parameter estimation (, ) using the nls function in R (Version 3.4.0).
Model Simulations: Competitive Outcomes.
A modified Monod model, described by an impulsive nonautonomous system of ordinary differential equations (ODEs), was formulated for two species competing for a single resource. (Impulsive and nonautonomous ODEs allow for abrupt time-dependent changes to the state variables and the parameters, respectively.) The model was designed to mimic a sequence of nectar colonization followed by pollinator-assisted dispersal to new flowers. To facilitate a close replication of in silico competition assays in subsequent in vitro mixed-culture assays, the model assumes indiscriminate dispersal with respect to species identity, sterile recipient flowers at the time of colonization, and negligible mortality during growth within flowers. These assumptions are also broadly consistent with observations of yeast growth in wild and artificial flowers (19–21). Each model simulation followed the fate of a single two-species community characterized by periods of within-flower growth (Eqs. 2 and 3), punctuated by population crashing dispersal events (Eqs. 4 and 5), with zero immigration from outside the system. The model can be written as follows:
| [2] |
| [3] |
| [4] |
| [5] |
where is the resource quota (amount of resource per unit individual), is the proportion of individuals transferred to a new flower, is the magnitude of resource pulses, and is the period between dispersal events. Eqs. 4 and 5, respectively, describe the magnitude of density-independent mortality and resource supplementation that accompany a dispersal event.
The model was parameterized from the monoculture experiments, with and determined by the sucrose conditions of the different simulation treatments. was calculated once for each species as the ratio of initial resource concentration and number of cells L−1 at 48 h averaged across all sucrose and amino acid treatments (excluding the minimum and maximum amino acid levels). This approximation for is justified by the observation that all four species reach carrying capacity within 48 h under the different study treatments. The model was then simulated for all six pairwise species combinations, at three constant sucrose conditions (10%, 30%, and 50%) and one variable condition (10–50% switching every 2 d). In each simulation, the state variables (, and ) were reduced by 80% (i.e., = 0.2 in Eq. 4) every 48 h [48 h was considered a good approximation of the average time between dispersal/immigration events in this system (19)], with the remaining 20% fraction receiving a fresh resource pulse ( = 2.683 mM in Eq. 5) (SI Appendix, Fig. S1). Simulations were run by using a Runge–Kutta method (ode45) with a fixed time step of 0.1 h ( = 0.1) for 8,640 “hours,” with both competitors starting from an initial density of 10 cells L−1. In all simulations, population dynamics reached a steady state comprising one of three qualitatively different outcomes: coexistence, competitive exclusion, and extinction of one competitor (i.e., outside fundamental niche of one competitor). All simulations were run by using the deSolve package (Version 1.14) (28) in R (Version 3.4.0).
Model Simulations: Quantifying Fluctuation-Dependent Mechanisms.
To quantify the contribution of the storage effect and relative nonlinearity to coexistence outcomes, we used a Monte Carlo-based simulation approach developed by Ellner et al. (5). The approach is summarized here, but see ref. 5 for a more comprehensive explanation of the procedure.
Following ref. 5, we first explain how to quantify the temporal storage effect before outlining the additional calculations needed to quantify relative nonlinearity. For two species, the storage effect is defined as the contribution of environment-competition covariance to the difference between invader and resident long-term average growth rate (4),
| [6] |
where the population growth, , is assumed to be a positive function of the environment, , and a decreasing function of competition . In our modified Monod model, and . The denote a value for species when is effectively absent (i.e., at very low density), such that and are the competitive pressures on the resident and the invader, respectively, when the invader is at low density. The is a scaling factor that translates changes in competitive pressure experienced by a resident into those experienced by an invader.
Simulations were conducted for each species as resident and invader, where the invader’s density was held at 0 (this differed from the competitive simulations described above where the model was initiated with both species at 10 cells L−1). After removing a burn-in period, reflecting the time it takes for the resident to achieve a steady state, the long-term average invader and resident growth rates were then calculated directly from the simulation output, where
| [7] |
The parameter here is the equivalent instantaneous mortality rate, defined as (29).
Next, we recalculated using the from the simulation with new randomly shuffled values for . The effect of randomly shuffling is to break down covariance, giving rise to , which is the expected average growth rate in the absence of covariance. If we assume for now the scaling factors () are equal to 1, the storage effect () for a given invader is then the effect of removing covariance on the difference between invader and resident growth rates, i.e.,
| [8] |
We can then quantify relative nonlinearity () using a similar approach, where the “flattened” growth rate calculated at mean resource levels, , removes the effect of both the storage effect and relative nonlinearity, i.e.,
| [9] |
and therefore,
| [10] |
Note that Eq. 10 only holds when growth is linear in the environmental response, , which it is in our model. When growth is nonlinear in , the flattened simulations remove additional variance terms corresponding to the effect on of variance in and the interaction between variance in and , which require separate partitioning.
The final consideration is the scaling factors, . These measure the relative sensitivity of invader and resident to change in the competitive factor (resource depletion in our model) around the mean value of that factor when the resident is at steady state. When invader and resident differ in their sensitivity at , . Consequently, following the analytic theory, the scaling factors should be multiplied through terms 2 and 4 (, and ) in Eqs. 8–10. In the absence of significant relative nonlinearity in invader and resident functional responses, the are comparatively straightforward to quantify empirically, either analytically (model permitting) or via a regression approach (section S1.5 of ref. 5). The combined effect, however, of a pulsed resource supply and relatively nonlinear functional responses is that the can be numerically sensitive to the point at which they are approximated. To compensate for this potential source of error, we evaluated all and twice, (i) assuming all , and (ii) using a semianalytical definition (following equations S1.14 and S1.15 of ref. 5; SI Appendix, Derivation of Scaling Factors):
| [11] |
where is the mean environmental response, i.e., , and and are the mean for each species and the mean resource level (determined by the resident), respectively. Note that the time averaging of , which is necessary under the analytic approach, differs from the regression approach, where it can be left as time variant. Following the analytic theory, because the scaling factors multiply a term of they only need to be approximated to , and therefore may be suitably evaluated at mean resource values. Given mostly qualitatively consistent results between the two approaches, in the main text we report and assuming all , and include their respective values when quantified via semianalytical in SI Appendix (SI Appendix, Table S3).
Competition Experiments.
To test the predicted competitive outcomes of all model simulations, we conducted a series of 24-d serial transfer experiments (SI Appendix, Fig. S1). All four species were grown in both mixed (pairwise) and monocultures, in three constant sucrose treatments (10%, 30%, and 50%) and one variable treatment (10–50% switching every 2 d).
Strains were inoculated into 10-L nectar microcosms on day 0 at an intended density of 20 cells L−1 (as described for the monoculture experiment, the actual cell density was verified from CFUs) (SI Appendix, Fig. S1). Every 2 d, a 2-L aliquot of each microcosm was inoculated into 8 L of fresh nectar either at the same sucrose concentration (constant treatments) or a different sucrose concentration (variable treatments), for a total of 12 cycles. On the assumption that cell growth did not appreciably reduce the sucrose concentration of the nectar microcosms, the switch from 10% to 50% sucrose was achieved by introducing the 2-L aliquot at 10% to 8 L of fresh nectar at 60% (i.e., 0.2 10 + 0.8 60); the switch from 50% to 10% sucrose was achieved by introducing the 2-L aliquot at 50% to 8 L of fresh nectar at 0%. Similarly, on the assumption that all amino acids had been depleted within a microcosm after 48 h of growth, all fresh nectar comprised 2.625 mM amino acids for a final resource concentration of 2.1 mM at the beginning of each transfer cycle. At each transfer, CFUs were enumerated from dilutions of the remaining 8-L microcosm.
Three months after the original experiment, we ran an additional experiment with eight microcosms to verify the replicability of observed coexistence under fluctuating sucrose between M. reukauffi and M. koreensis. The experimental design was identical to the original experiment.
Data Availability.
The data that support the findings of this study are available on Dryad (https://doi.org/10.5061/dryad.6t161c3).
Supplementary Material
Acknowledgments
We thank Steve Ellner for valuable advice and feedback on an earlier draft and Robin Snyder and an anonymous reviewer for constructive comments. This work was supported by National Science Foundation Grants DEB 1149600 and DEB 1737758; and the Center for Computational, Evolutionary, and Human Genomics, the Department of Biology, and the Terman Fellowship of Stanford University.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
Data deposition: The data that support the findings of this study are available on Dryad (https://doi.org/10.5061/dryad.6t161c3).
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1801846115/-/DCSupplemental.
References
- 1.Amarasekare P. Trade-offs, temporal variation, and species coexistence in communities with intraguild predation. Ecology. 2007;88:2720–2728. doi: 10.1890/06-1515.1. [DOI] [PubMed] [Google Scholar]
- 2.Yuan C, Chesson P. The relative importance of relative nonlinearity and the storage effect in the lottery model. Theor Popul Biol. 2015;105:39–52. doi: 10.1016/j.tpb.2015.08.001. [DOI] [PubMed] [Google Scholar]
- 3.Chesson P, Huntly N. The roles of harsh and fluctuating conditions in the dynamics of ecological communities. Am Nat. 1997;150:519–553. doi: 10.1086/286080. [DOI] [PubMed] [Google Scholar]
- 4.Chesson P. Mechanisms of maintenance of species diversity. Annu Rev Ecol Syst. 2000;31:343–366. [Google Scholar]
- 5.Ellner SP, Snyder RE, Adler PB. How to quantify the temporal storage effect using simulations instead of math. Ecol Lett. 2016;19:1333–1342. doi: 10.1111/ele.12672. [DOI] [PubMed] [Google Scholar]
- 6.Descamps-Julien B, Gonzalez A. Stable coexistence in a fluctuating environment: An experimental demonstration. Ecology. 2005;86:2815–2824. [Google Scholar]
- 7.Adler PB, HilleRisLambers J, Kyriakidis PC, Guan Q, Levine JM. Climate variability has a stabilizing effect on the coexistence of prairie grasses. Proc Natl Acad Sci USA. 2006;103:12793–12798. doi: 10.1073/pnas.0600599103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jiang L, Morin PJ. Temperature fluctuation facilitates coexistence of competing species in experimental microbial communities. J Anim Ecol. 2007;76:660–668. doi: 10.1111/j.1365-2656.2007.01252.x. [DOI] [PubMed] [Google Scholar]
- 9.Angert AL, Huxman TE, Chesson P, Venable DL. Functional tradeoffs determine species coexistence via the storage effect. Proc Natl Acad Sci USA. 2009;106:11641–11645. doi: 10.1073/pnas.0904512106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hutchinson GE. The paradox of the plankton. Am Nat. 1961;95:137–145. [Google Scholar]
- 11.Chesson P. Quantifying and testing coexistence mechanisms arising from recruitment fluctuations. Theor Popul Biol. 2003;64:345–357. doi: 10.1016/s0040-5809(03)00095-9. [DOI] [PubMed] [Google Scholar]
- 12.Nicolson S, Fleming P. Nectar as food for birds: The physiological consequences of drinking dilute sugar solutions. Plant Syst Evol. 2003;238:139–153. [Google Scholar]
- 13.Xiao X, Fussmann GF. Armstrong–mcgehee mechanism revisited: Competitive exclusion and coexistence of nonlinear consumers. J Theor Biol. 2013;339:26–35. doi: 10.1016/j.jtbi.2013.05.025. [DOI] [PubMed] [Google Scholar]
- 14.Chesson P. Scale transition theory with special reference to species coexistence in a variable environment. J Biol Dyn. 2009;3:149–163. doi: 10.1080/17513750802585491. [DOI] [PubMed] [Google Scholar]
- 15.Huisman J, Weissing FJ. Biodiversity of plankton by species oscillations and chaos. Nature. 1999;402:407–410. [Google Scholar]
- 16.Chesson P. Multispecies competition in variable environments. Theor Popul Biol. 1994;45:227–276. [Google Scholar]
- 17.Snyder RE, Borer ET, Chesson P. Examining the relative importance of spatial and nonspatial coexistence mechanisms. Am Nat. 2005;166:E75–E94. doi: 10.1086/444441. [DOI] [PubMed] [Google Scholar]
- 18.Herrera CM, Canto A, Pozo MI, Bazaga P. Inhospitable sweetness: Nectar filtering of pollinator-borne inocula leads to impoverished, phylogenetically clustered yeast communities. Proc R Soc Biol Sci. 2010;277:747–754. doi: 10.1098/rspb.2009.1485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Peay KG, Belisle M, Fukami T. Phylogenetic relatedness predicts priority effects in nectar yeast communities. Proc R Soc Biol. 2012;279:749–758. doi: 10.1098/rspb.2011.1230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Vannette RL, Fukami T. Historical contingency in species interactions: Towards niche-based predictions. Ecol Lett. 2014;17:115–124. doi: 10.1111/ele.12204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Vannette RL, Fukami T. Dispersal enhances beta diversity in nectar microbes. Ecol Lett. 2017;20:901–910. doi: 10.1111/ele.12787. [DOI] [PubMed] [Google Scholar]
- 22.Alvarez-Perez S, Herrera CM, de Vega C. Zooming-in on floral nectar: A first exploration of nectar-associated bacteria in wild plant communities. FEMS Microbiol Ecol. 2012;80:591–602. doi: 10.1111/j.1574-6941.2012.01329.x. [DOI] [PubMed] [Google Scholar]
- 23.Fridman S, Izhaki I, Gerchman Y, Halpern M. Bacterial communities in floral nectar. Environ Microbiol Rep. 2012;4:97–104. doi: 10.1111/j.1758-2229.2011.00309.x. [DOI] [PubMed] [Google Scholar]
- 24.Tucker CM, Fukami T. Environmental variability counteracts priority effects to facilitate species coexistence: Evidence from nectar microbes. Proc R Soc Biol. 2014;281:20132637. doi: 10.1098/rspb.2013.2637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Toju H, Vannette RL, Gauthier MPL, Dhami MK, Fukami T. Priority effects can persist across floral generations in nectar microbial metacommunities. Oikos. 2018;17:345–352. [Google Scholar]
- 26.Belisle M, Peay KG, Fukami T. Flowers as islands: Spatial distribution of nectar-inhabiting microfungi among plants of Mimulus aurantiacus, a hummingbird-pollinated shrub. Microb Ecol. 2012;63:711–718. doi: 10.1007/s00248-011-9975-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Baker HG, Baker I. Amino-acids in nectar and their evolutionary significance. Nature. 1973;241:543–545. [Google Scholar]
- 28.Soetaert KER, Petzoldt T, Setzer RW. Solving differential equations in R: Package deSolve. Journal of Statistical Software. 2010;33:1–25. [Google Scholar]
- 29.Smith HL. Bacterial competition in serial transfer culture. Math Biosci. 2011;229:149–159. doi: 10.1016/j.mbs.2010.12.001. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available on Dryad (https://doi.org/10.5061/dryad.6t161c3).