Design principles for photonic crystals based on plasmonic nanoparticle superlattices

Significance

In this article, we derive a set of design principles for making photonic crystals with desired photonic stopband properties by taking advantage of spacer group, a design parameter enabled by recent advances in bottom-up assembly processes. The concept of spacer groups is experimentally realized through DNA-programmable assembly of Au nanoparticles, showing that highly reflective structures can be generated with cubic lattices and flexible spacer groups that can enable lighter and more compact 3D photonic crystals with precisely designed and even reconfigurable photonic properties. It also allows one to explore the combined effects of both photonic bandgap and the plasmonic properties of NPs, which may prove useful in fields spanning plasmonic cavity structures, optical nanocircuits, subwavelength imaging, and low-loss metamaterials.

Abstract

Photonic crystals have been widely studied due to their broad technological applications in lasers, sensors, optical telecommunications, and display devices. Typically, photonic crystals are periodic structures of touching dielectric materials with alternating high and low refractive indices, and to date, the variables of interest have focused primarily on crystal symmetry and the refractive indices of the constituent materials, primarily polymers and semiconductors. In contrast, finite difference time domain (FDTD) simulations suggest that plasmonic nanoparticle superlattices with spacer groups offer an alternative route to photonic crystals due to the controllable spacing of the nanoparticles and the high refractive index of the lattices, even far away from the plasmon frequency where losses are low. Herein, the stopband features of 13 Bravais lattices are characterized and compared, resulting in paradigm-shifting design principles for photonic crystals. Based on these design rules, a simple cubic structure with an ∼130-nm lattice parameter is predicted to have a broad photonic stopband, a property confirmed by synthesizing the structure via DNA programmable assembly and characterizing it by reflectance measurements. We show through simulation that a maximum reflectance of more than 0.99 can be achieved in these plasmonic photonic crystals by optimizing the nanoparticle composition and structural parameters.

Photonic crystals (PCs) are materials with periodically varied refractive indices, in which optical control is achieved by refractive index contrast and diffraction. When the effective wavelength of light satisfies the Bragg criterion (when the wavelength is twice the periodicity), light propagation in certain directions inside the material is “forbidden” (1). This gives rise to a photonic band gap (PBG) conceptually analogous to the electronic band gap in semiconductors. PCs have been intensively studied for use in a wide range of technologies, such as semiconductor lasers, optical integrated circuits, optical switches, and solar cells (2–5). In addition, they are commercially used for light-emitting diodes, sensors, and optical fibers.

Conventionally, PCs are structures made of dielectric materials (e.g., polymers and semiconductors) and prepared via top-down (6, 7) or bottom-up fabrication processes (8–10). In general, bottom-up techniques are attractive, because they are often simpler, less expensive, and more scalable (9, 11). PCs made with bottom-up processes are typically close packed or touching, and the techniques used to make them provide little control over crystal symmetry and lattice parameter (12).

Thus far, the primary considerations in designing PCs have been crystal symmetry and the choice of dielectric materials to increase the index contrast between the high- and low-index materials, which is crucial for achieving good photonic properties (SI Appendix, section 2) (13–16). However, there remain several intrinsic challenges, including overcoming the strain that results from interfacing materials with large lattice mismatches (17), poor crystal quality (13), and low index contrast (16, 18). Moreover, since the high-index materials are closely spaced and sometimes touching (2, 15), planes along the light propagation direction are always composed of a mixture of both high- and low-index materials—there is no well-defined separation between the high- and low-index layers, which reduces the index contrast. Hence, alternative fabrication methods that incorporate high-index materials and allow spatial separation of the high- and low-index materials may help solve challenges in PC fabrication and property tailoring.

With the advent of methods for chemically programming the formation of colloidal crystals (19, 20), additional variables can be used to tune PC properties. For example, interparticle distance, which can be finely tuned with some of the emerging techniques that incorporate spacer groups for particle assembly (21, 22), represents a yet-to-be explored parameter that could prove useful in PC design. Herein, we use finite difference time domain (FDTD) simulations and take into account the Bragg criterion to study the origin of the PBG along certain directions for 13 of 14 Bravais lattices composed of Au nanoparticles (NPs). From this analysis, general design principles are established, and based on these design rules, a simple cubic (cP) structure with an ∼130-nm lattice parameter is predicted to exhibit a broad photonic stopband, a property confirmed by synthesizing it via DNA programmable assembly (19, 22, 23) and characterizing it by reflectance measurements. Most of the data pertain to Au NPs, but the lessons learned extend to other plasmonically active materials. Importantly, we show through simulation that a maximum reflectance of >0.99 can be achieved by optimizing NP composition and crystal structural parameters, despite the concern that metallic plasmonic NPs are lossy.

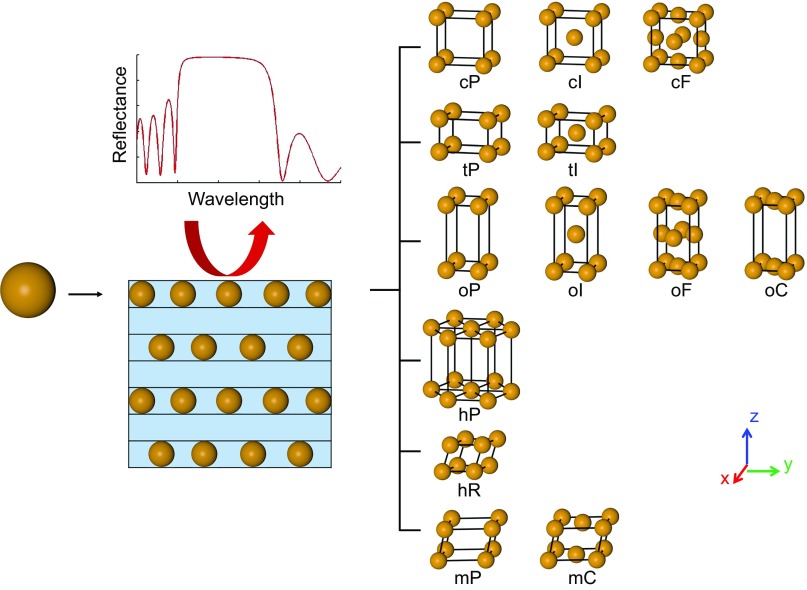
Building PCs with Plasmonic NP Superlattices

Because the NP size is smaller than the free electron mean free path, the free electrons in Au NPs are confined and interact strongly with light, giving rise to a localized surface plasmon resonance (LSPR) that can be used to focus light beyond the diffraction limit (24). The frequency of the LSPR is highly dependent on the NP’s size and shape, the dielectric environment, and the presence of neighboring plasmonic NPs (25, 26). Consequently, plasmonic NPs have been exploited for uses in many fields spanning chemical and biological sensing (27), Raman spectroscopy (28), nanoantennas (29), and therapeutics (30). Other than having local control over detailed properties at the nanoscale, the macroscopic properties of the NP ensemble, such as its effective refractive index (n_eff), can also be tuned by various structural parameters (31). Particularly, within a range of volume fraction where plasmonic coupling is not too strong, the n_eff of spherical NP ensembles can be calculated using Maxwell–Garnett effective medium theory (EMT) (32), allowing qualitative understanding of the structure dependence of their optical properties. Although metal NPs are absorptive close to the plasmon resonance frequency, EMT studies have shown that the real part of the permittivity can be enhanced well away from the plasmon frequency, where absorption is relatively small. Also, the optical response associated with plasmonic NPs is so strong that it is possible to use lattices with relatively low volume fraction (i.e., the NPs are highly separated) in constructing functional photonic lattices. Therefore, ensembles of plasmonic NPs serve as a promising candidate for the high-index material in PCs [plasmonic photonic crystals (PPCs)] (Fig. 1). Although a high effective index can be realized in plasmonic NP ensembles and there has been extensive work on plasmonic NP assemblies (20, 33, 34), large stopbands are not typically observed in such structures due to the dense-packed arrangements of NPs (35, 36). This analysis is consistent with the conclusion that plasmonic NPs must be well-separated to design effective PPCs.

Fig. 1.

Schematic representation describing the design of PPCs with Au NPs. The stopband features that are generated by light incident normal to the x–y plane are investigated. Along the z direction, the superlattice can be viewed as alternating NP and dielectric layers with high and low indices, respectively; 13 of 14 Bravais lattices are studied. In the layered structure scheme, the NPs are embedded in a homogeneous matrix. mC, base-centered monoclinic; oC, base-centered orthorhombic; oF, face-centered orthorhombic; oI, body-centered orthorhombic.

Conceptually, a periodic structure can be achieved by building a crystal where the NPs are located at each lattice site and embedded in a homogeneous dielectric medium. For a chosen direction relative to the crystal lattice, each crystalline plane contains a layer of NPs that serves as the high-index layer, and the medium between each lattice plane serves as the low-index layer. The crystal can have different lattice symmetries and lattice constants, which in turn, will affect the effective refractive index (n_eff) of the NP layer and the periodicity. To systematically investigate the effect of structural parameters on the photonic properties and provide guidelines for the construction of PPCs with large PBGs along selected directions, we have studied the optical properties of 13 of the 14 Bravais lattices to identify the roles that each lattice parameter plays (Fig. 1). In particular, FDTD simulations are carried out to investigate how the lattice parameters of PPCs—the lattice constants in all three dimensions and the angle—affect the photonic stopband features. We set up lattices with spherical Au NPs (diameter of 108 nm), all embedded in a silica matrix (as such structures can be made experimentally). Cases with different NP sizes are examined in SI Appendix, section 8. To minimize computational time and keep the simulations tractable, we found that seven layers of NPs sufficiently represented the thin PPC films (SI Appendix, Figs. S4 and S5) and were used in all simulations unless otherwise specified. Normal incidence of light (z direction) onto the (001) plane (x–y plane) of the lattice is investigated (Fig. 1); cases with different angles of incidence are discussed in SI Appendix, section 7.

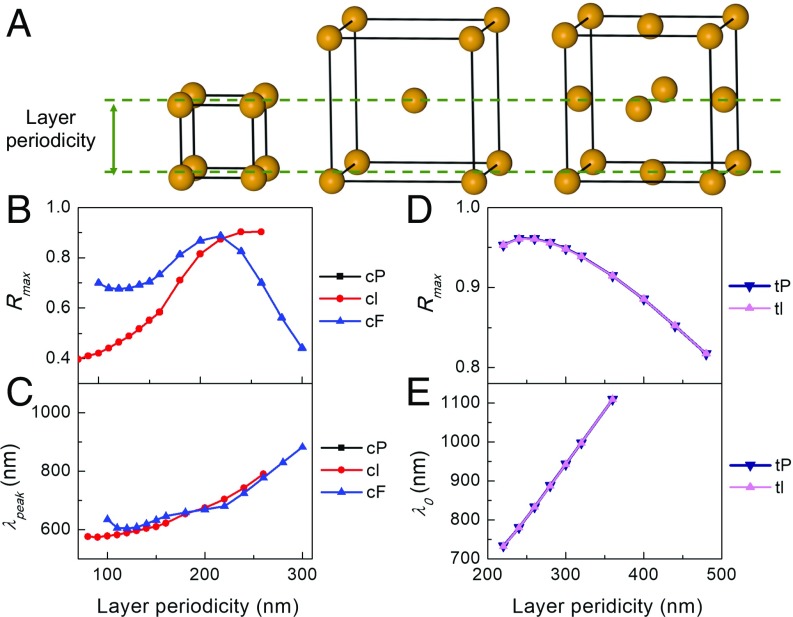
Rule 1: Layer Periodicity Compared with the Lattice Constant Along the Light Propagation Direction Dictates the Location of the Photonic Stopband

Fig. 2 summarizes the maximum reflectance (R_max) of the stopband and the peak wavelength, at which R_max is obtained, for cP, body-centered cubic (cI), and face-centered cubic (cF) lattices as a function of the periodicity of each layer along the z direction (Fig. 2A). In other words, a single cI or cF unit cell has three layers (top, middle, bottom), and the periodicity of each layer in the z direction is one-half of the lattice constant (Fig. 2A). A clear trend between the peak wavelengths and layer spacing is observed between the three lattice types (Fig. 2 B and C). It is remarkable how the peak wavelengths and maximum reflectance share similar values and trends, especially above 200-nm layer spacing. As the lattice constant increases, the peak wavelength increases, and R_max increases until it reaches a maximum value and then decreases as expected from our analysis in SI Appendix, section 2. This shows the importance of controlling the lattice constant, which is not easily achievable with conventional fabrication techniques. When the properties are plotted as a function of lattice constant (SI Appendix, Fig. S6), the correspondence between the three lattice types becomes weak. This suggests that, instead of the lattice constant in the z direction (c), the spacing between each NP layer in the light propagation direction (layer periodicity) should be considered as the periodicity of the PC (Fig. 2A).

Fig. 2.

Layer periodicity dictates the location of the photonic stopband. (A) If the superlattice is viewed as alternating layers that do and do not contain the NPs, then the layer periodicity is defined as the spacing between two adjacent layers that contain NPs. (B and C) Dependence of (B) maximum reflectance (R_max) and (C) its corresponding wavelength (λ_peak) on the layer periodicity of cP, cI, and cF superlattices. (D and E) Dependence of (D) R_max and (E) center wavelength (λ₀) on the layer periodicity for tP and tI lattices. The lattice constant within each layer is kept constant at 200 nm. Only the λ values of a reflectance larger than 0.9 are considered as the stopband, and its λ₀ is plotted as a function of layer periodicity in E.

The above point is directly shown in lattices with larger layer periodicity (>200 nm) (Fig. 2C), where the peak wavelength increases almost linearly, compared with the slow change at smaller periodicities. This complication arises, because plasmonic NPs are used as building blocks. As seen more clearly in SI Appendix, Fig. S7, where the reflection spectra of superlattices with cP crystal structure and different lattice constants are shown, the stopband overlaps with the plasmonic modes of the NP lattice at smaller lattice constants (140–200 nm). In this situation, the exact wavelength of the stopband becomes hard to predict. We simplify the discussion further by focusing on lattices where the plasmonic modes and stopband are spectrally separated. This also allows us to later test the feasibility of using EMT to estimate the n_eff and reproduce the reflectance spectra, since the EMT prediction is less accurate on the blue side of the LSPR where quadrupole modes are important in the NP response and there is more significant absorption. In addition, as the lattice constant further increases and the first-order Bragg peak red shifts, a second-order peak arises (SI Appendix, Figs. S6 and S14). For simplicity, only first-order peaks are considered.

Although the cubic lattice system can provide insight into the structure–function relationship of PPCs, the situation is limited due to the high crystal symmetry in the cubic lattice system, prompting the investigation of other lattice symmetries. Next, we move to investigate tetragonal crystal systems. Compared with the cP lattice, c is different from the lattice constant in the x–y plane (a), which allows more freedom in teasing out the structure–function relationship. Fig. 2D shows the dependence of the R_max on the layer periodicity of both tetragonal lattices (tP) while keeping a constant (200 nm). The largest R_max is reached with c ∼ 240 nm. Additional inspection shows that the periodicity at which the largest R_max is obtained involves an optimization of both layer periodicity and layer number (SI Appendix, Fig. S13). To further determine the characteristics of the stopband, we study only those with their R_max larger than 0.9 and define the bandwidth (Δλ) to be the width of the band with reflectance ≥0.9. Fig. 2E shows again that the wavelength of the center of the band (λ₀) depends linearly on the layer periodicity. Although Δλ increases, the normalized bandwidth Δλ/λ₀ decreases due to the faster increase in λ₀ (SI Appendix, Fig. S10). Interestingly, the properties of body-centered tetragonal (tI) lattices are almost identical to a tetragonal counterpart with the same layer periodicity, which we emphasize again is not c but c/2 in tI lattices. This indicates that the properties of the stopband may be independent of the relative position of the NPs between different layers as discussed below.

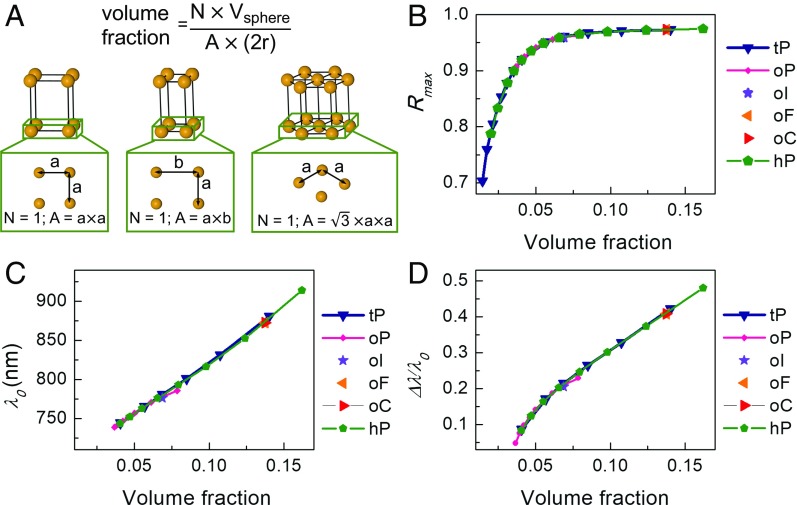
Rule 2: The Volume Fraction Rather than the Exact NP Arrangement of Each NP Layer Dictates the Bandwidth

Now that layer periodicity has been identified as a key structural parameter, we investigate the relationship between a (with fixed layer periodicity) and stopband features in SI Appendix, Fig. S15. As a increases, R_max, λ₀, and Δλ/λ₀ all decrease due to the reduced index contrast between the NP and the silica layer as the amount of Au in the NP layer is diluted by increasing a. Next, we explore the stopband features of orthorhombic lattices (oP) and hexagonal lattices (hP) and compare them with those of the tetragonal structures (Fig. 3). The layer periodicity is kept constant at 240 nm for all lattice types. From the perspective of the NP arrangement in each layer, the NPs are arranged in squares, in rectangles with the length of one side fixed (b = 250 nm), and in diamonds with 60° angle, while a is varied for tP, oP, and hP lattices, respectively (Fig. 3A). To enable comparison between different lattice symmetries, the properties are plotted against the NP volume fraction within each NP layer (Fig. 3A). A striking fact is that all of the plots for the three different lattice structures overlap. The stopband is dictated by the volume fraction rather than the exact arrangement of the NPs within each layer for fixed NP size and layer periodicity. We see in Fig. 3B that, as volume fraction increases, the R_max increases monotonically until it saturates at ∼0.97, and the 0.03 loss is due to absorption by the material (SI Appendix, Fig. S19). Interestingly, λ₀ and Δλ/λ₀ increase with increasing volume fraction (decreasing lattice constant); this is a consequence of the low-energy band edge experiencing a blue shift, while the high-energy edge remains relatively unchanged (SI Appendix, Figs. S16–S18).

Fig. 3.

The volume fraction of each NP layer dictates the R_max, λ₀, and Δλ/λ₀ of the stopband. (A) The volume fraction within each NP layer is defined in the equation, where N is the number of NPs in each unit cell, V_sphere is the volume of the NP, and A × (2r) is the volume of a unit cell: A is the area of the facet in the x–y plane of the unit cell, r is the radius of the NP. Thus, the diameter of the NP defines the thickness of the NP layer. (B) R_max, (C) λ₀, and (D) normalized bandwidth (Δλ/λ₀) of tP, oP, and hP lattices as a function of volume fraction within each NP layer. One lattice constant within the NP layer is chosen for body-centered orthorhombic (oI), face-centered orthorhombic (oF), and base-centered orthorhombic (oC), and the stopband features show good agreement with the oP lattices as predicted. The layer periodicity of all data points is 240 nm.

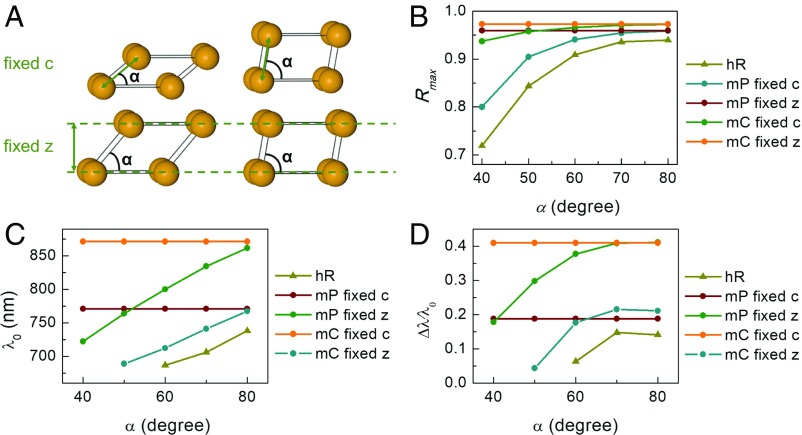
Rule 3: The Nanoparticle Registry Between Layers Does Not Affect Stopband Features

Features of the stopband of trigonal lattices (hR) are summarized in Fig. 4 B–D. Here, the lattice constant is fixed at 240 nm, while the angle is changed from 40° to 80°, and both R_max and λ₀ increase (Fig. 4 B–D and SI Appendix, Fig. S20). So far, we have shown the important roles that layer periodicity and volume fraction in each layer play, while the exact arrangement of NPs in each layer has negligible influence. However, the effect of registry between different layers has not been considered. While our observations in all of the body-centered and face-centered structures (cubic and tetragonal) indicate that registry plays a trivial role, its effect can be studied more clearly in monoclinic lattices. A monoclinic lattice (mP) allows even more degrees of freedom, where all three lattice constants (a, b, and c) and the angle (α) between layers can be independently varied. Two sets of simulations are performed where the lattice constants in each layer are fixed at a = 250 nm and b = 160 nm, while the lattice constant in the [001] direction is set, such that either the layer periodicity (fixed z) or c (fixed c) is kept constant. R_max, λ₀, and Δλ/λ₀ of the lattice with fixed c show a similar trend to that of the hR; in comparison, those of the fixed z lattices are constant, and the reflectance spectra overlap at all α (SI Appendix, Figs. S21 and S22). This proves that the registry between different layers indeed does not affect the stopband features of the lattice. This observation coincides with our expectation that the relative arrangement of NPs in each layer and between layers does not matter (when the NPs are spaced such that no strong plasmonic interaction occurs).

Fig. 4.

The registry between NP layers has a negligible effect on the stopband features. (A) Two sets of structural parameters in mP and base-centered monoclinic (mC) lattices with either fixed layer periodicity (fixed z) or fixed lattice constant c (fixed c) while changing the angle. (B) R_max, (C) λ₀, and (D) normalized bandwidth (Δλ/λ₀) of hR, mP, and mC lattices with either fixed c or z as a function of the angle α. In the fixed c (z) case, c (z) is 240 nm.

To further explore this concept, we discuss the feasibility of using EMT combined with the transfer matrix method (37) (TMM; EMT + TMM) to reproduce the spectra calculated by FDTD (SI Appendix, Fig. S26). The good qualitative agreement between the EMT + TMM and FDTD results indicates that the superlattice properties in the z direction can be treated as alternating layers of high (NP)- and low (dielectric)-index materials.

PPCs Realized Through DNA-Programmable Assembly

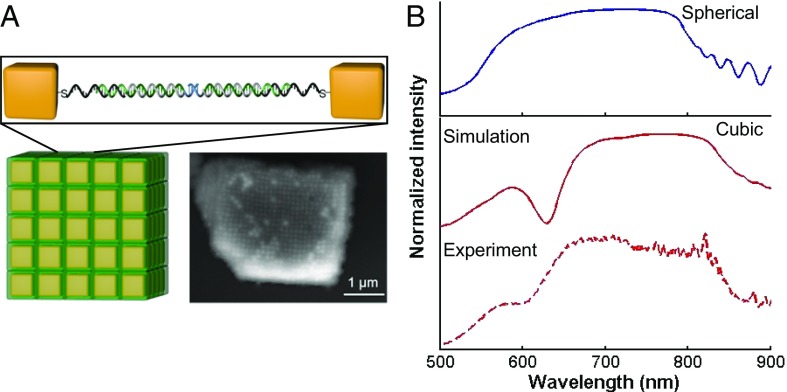
We have derived guidelines to design PPCs from analysis of the stopband features along one dimension; however, the results can be applied to any direction for a 3D PPC; 3D PPCs offer more compact design and are sought after for applications involving all-optical integrated circuits (9). Here, we explore experimental methods for realizing such 3D PPCs. DNA-programmable assembly is a promising emerging method for making PPCs, since it provides fine control and even subnanometer tunability over particle spacing (21–23). Moreover, interparticle spacing can be dynamically tuned after PC formation (21, 38), enabling dynamic tuning of the stopband location. Here, as proof of concept, we use micrometer-sized cP superlattices with well-faceted cubic crystal habits (39) made from DNA-functionalized cubic NPs to experimentally explore this concept. The cubic crystal habit facilitates the alignment of the microcrystal with its (001) facet facing up. Specifically, cubic NPs with 88 ± 4-nm edge length and 5 ± 1-nm corner rounding were used, and the lattice constant as measured by small angle X-ray scattering was 134 nm (SI Appendix, Fig. S2). The simulation results for a superlattice made of spherical NPs with the same volume and lattice constants show the existence of a broad stopband (Fig. 5B, Upper), a property that is observed both experimentally and through simulation in the cubic NP superlattice (Fig. 5B, Lower). Moreover, the experimentally observed stopband matches remarkably well with the simulation prediction, emphasizing that the design rules articulated above are not limited to spherical particles. Indeed, as in SI Appendix, Fig. S35, NPs with different shapes can be used as the building blocks for superlattices that show similar stopband properties. Although only a cP lattice is studied experimentally, other lattice structures (over 500 different crystals spanning over 30 different crystal symmetries) have been made through DNA-programmable assembly (19, 22). For lattices with symmetries that do not belong to the cubic lattice system, one can obtain different stopband properties using different crystal orientations of the same superlattice.

Fig. 5.

Experimental measurement and FDTD simulations of cubic NP superlattices. (A) Schematic representation (Lower Left) and scanning electron microscope image (Lower Right) of a superlattice made through DNA-programmable assembly of nanocubes after encasing in silica. The Au nanocube building blocks have an 88-nm edge length and a 5-nm corner rounding. The lattice constant of the superlattice is 134 nm and defined by the duplex DNA interconnects [sequences used: anchor strand: TCA ACT ATT CCT ACC TAC AAA AAA AAA A SH; linker strand: GTA GGT AGG AAT AGT TGA A TTTTTTTTTTTT ACT GAG CAG CAC TGA TTTTTTTTTTTTT A GCGC; and duplexer strand: AAAAAAAAAAAAA TCA GTG CTG CTC AGT AAAAAAAAAAAA; all strands are listed from 5′ to 3′ (SI Appendix, section 1.3 has details)]. An enlarged view of one hybridized DNA pair between nearest neighbor nanocubes in a lattice is shown in Upper. (B, Upper) Simulation result of a cP superlattice with spherical NPs that has the same lattice constant and volume fraction as the superlattice shown in A. (B, Lower) Simulation and experimental results for the superlattice shown in A.

Building PCs with Materials Other than Au

Although the aforementioned design principles have been studied for spherical Au NPs, they also extend to other plasmonic NPs and lattice structures. Indeed, by performing a set of simulations on seven-layer cubic superlattices (134-nm lattice constant) composed of 88-nm edge-length cube-shaped NPs consisting of different plasmonic materials (Ag, Au, Al, or Cu), a broad stopband can be observed for all structures (SI Appendix, Fig. S36). The superlattice made with Ag particles exhibits the highest reflectance (R_max = 0.986) and lowest absorption, a consequence of the lower losses in Ag. Indeed, R_max can be further increased on optimization of lattice constant and particle size. One simulation on a structure consisting of the same cube-shaped NPs in a tP with a = 140 and c = 300 nm shows that an R_max greater than 0.996 can be achieved (SI Appendix, Fig. S37). This large value is comparable with that of high-quality dielectric PCs and indicates the suitability of Ag NP superlattices for a wide range of applications. It is also important to note that, since the plasmonic resonance of Al NPs can be tuned into the UV region, distinct stopbands can be realized to cover the entire visible region with Al NP superlattices.

Since the advantageous properties of PPCs are attributed to the large index contrast between the NP and dielectric layers, even far away from the plasmon frequency, we also have looked into the role of plasmonic NPs by comparing results for plasmonic NP superlattices with those for superlattices composed of other metallic NPs with poor plasmonic properties (Cr, Fe, Ti) (SI Appendix, Fig. S38). While a significant stopband is present for the plasmonic NP superlattices, it is absent for lattices made from NPs with poor plasmonic properties. By varying the number of layers and the lattice constants, we show that the stopband features for superlattices made of Ti NPs are always much weaker (SI Appendix, Figs. S39 and S40) than those for superlattices made of Au NPs with similar structures over a wide range of structural parameters.

Additionally, to benchmark our technique with conventional PC fabrication methods (where dielectric materials are in general used), we investigated the stopband features of lattices made with various dielectric NPs through simulation (SI Appendix, Figs. S41‒S47). These lattices obey the same design principles derived above. However, the stopbands of lattices made with dielectric NPs saturate much more slowly, and the band widths are much narrower compared with the plasmonic NP ones with the exact same lattice parameters.

Finally, we explore the effect of dielectric medium in SI Appendix, Fig. S48. This shows that, with the same superlattice, the spectral location of the stopband can be tuned, in a similar fashion as the LSPR, by immersing or embedding it in a different dielectric medium (12).

Conclusions

Through a systematic study of the stopband features of 13 Bravais lattice structures along the z direction, we have shown that nontouching PPC superlattices can be treated as periodically alternating layers of high- and low-index materials along the light propagation direction. We have identified two key parameters that dictate the stopband features: the layer periodicity and the volume fraction of each NP layer. Interestingly, when the NPs are spaced sufficiently far away such that strong plasmonic coupling is minimized, the exact arrangement of NPs in each layer and the registry between different layers have negligible influence on the stopband properties. From a fabrication standpoint, this work conclusively shows that DNA-programmable assembly is especially and perhaps uniquely useful for making 3D PPCs, since it provides control over the spacing between NPs and lattice symmetry. The high tunability of the stopband features realized through this technique (by changing lattice parameters, NP size and composition, and the dielectric matrix) should lead to PPCs with interesting applications as cavities and filters. Compared with PCs made with purely dielectric materials, PPCs are smaller in size and lighter in weight (40). For example, with cP lattices, a saturated stopband is realized for a superlattice with a lattice constant of only 140 nm and a seven-layer thickness (the total thickness is ∼1 μm). Importantly, the volume fraction of the metal for a lattice with 200-nm particle spacing is less than 0.10. Moreover, the technique, which allows one to explore the combined effects of both the PBG and the plasmonic properties of NPs, hold promise for making and exploring PPC materials that may prove useful in plasmonic cavity structures (41, 42), optical nanocircuits (43), subwavelength imaging (44), and low-loss metamaterials (45).

Methods

FDTD Calculations.

The FDTD simulations were performed with Lumerical FDTD solutions. The structures were designed as NP lattices embedded in a homogeneous dielectric background.

EMT Approximation and TMM.

Both are performed in Matlab. Maxwell–Garnett EMT approximation is used to approximate the refractive indices of superlattices.

Superlattice Assembly.

DNA strands used in this work were designed according to the literature and synthesized on a solid support with an MM48 synthesizer (BioAutomation). Nanocubes were synthesized according to the literature. DNA functionalization and assembly were done according to the literature.

Optical Experiments.

Reflectance was performed using a Zeiss microscope (Axio Observer Z1) coupled with a spectrometer (50 g/mm grating; Princeton Instrument and charge coupled device; PyLoN). A Xenon lamp (XBO 75) with a broadband spectrum (300–1,000 nm) was used as the light source.

SI Appendix has details of experimental and theoretical methods used in this work.