Significance
We developed deconvolution of single-cell expression distribution (DESCEND), a method to recover cross-cell distribution of the true gene expression level from observed counts in single-cell RNA sequencing, allowing adjustment of known confounding cell-level factors. With the recovered distribution, DESCEND provides reliable estimates of distribution-based measurements, such as the dispersion of true gene expression and the probability that true gene expression is positive. This is important, as with better estimates of these measurements, DESCEND clarifies and improves many downstream analyses including finding differentially expressed genes, identifying cell types, and selecting differentiation markers. Another contribution is that we verified using nine public datasets a simple “Poisson-alpha” noise model for the technical noise of unique molecular identifier-based single-cell RNA-sequencing data, clarifying the current intense debate on this issue.
Keywords: single-cell transcriptomics, RNA sequencing, differential expression, Gini coefficient, highly variable genes
Abstract
Single-cell RNA sequencing (scRNA-seq) enables the quantification of each gene’s expression distribution across cells, thus allowing the assessment of the dispersion, nonzero fraction, and other aspects of its distribution beyond the mean. These statistical characterizations of the gene expression distribution are critical for understanding expression variation and for selecting marker genes for population heterogeneity. However, scRNA-seq data are noisy, with each cell typically sequenced at low coverage, thus making it difficult to infer properties of the gene expression distribution from raw counts. Based on a reexamination of nine public datasets, we propose a simple technical noise model for scRNA-seq data with unique molecular identifiers (UMI). We develop deconvolution of single-cell expression distribution (DESCEND), a method that deconvolves the true cross-cell gene expression distribution from observed scRNA-seq counts, leading to improved estimates of properties of the distribution such as dispersion and nonzero fraction. DESCEND can adjust for cell-level covariates such as cell size, cell cycle, and batch effects. DESCEND’s noise model and estimation accuracy are further evaluated through comparisons to RNA FISH data, through data splitting and simulations and through its effectiveness in removing known batch effects. We demonstrate how DESCEND can clarify and improve downstream analyses such as finding differentially expressed genes, identifying cell types, and selecting differentiation markers.
Cells are the basic biological units of multicellular organisms. Within a cell population, individual cells vary in their gene expression levels, reflecting the dynamism of transcription across cells (1–5). Traditional microarray and bulk RNA-sequencing (RNA-seq) technologies profile the average gene expression level of all cells in the population. In contrast, recent single-cell RNA-seq (scRNA-seq) methods enable the quantification of a much richer set of properties of the gene expression distribution across cells. For example, measures of dispersion such as the coefficient of variation (CV) and the Gini coefficient can be used to elucidate biological states that are not reflected in the population average (6–8). Two-state mixture models, alternatively, allow a better understanding of transcriptional regulation at the single-cell level (5, 9–11).
However, it is challenging to compute such distribution-based statistics of true gene expression due to the technical noise in scRNA-seq data (12–16). Single-cell RNA-seq protocols are complex, involving multiple steps each contributing to the substantially increased noise level of scRNA-seq relative to bulk RNA-seq. Unique molecular identifiers (UMI) (17) were introduced as a barcoding technique to reduce amplification noise, but the observed expression distribution computed from observed UMI counts is, for most genes, still a poor representation of their true expression distribution.
Recently, many computational methods for scRNA-seq analysis have been proposed, including methods for quantifying dispersion, for characterizing expression “states” using mixture models, and for finding differentially expressed genes (6, 18–26). Although some of these methods have taken technical noise into consideration, to our knowledge, there is currently no method for recovering the cross-cell gene expression distribution from scRNA-seq data, unless strong assumptions are made about this distribution. There is also a lack of methods for comparing aspects of this true biological distribution beyond the mean, especially when there is a need to adjust for confounding factors. In fact, there is still active debate on the technical noise distribution for scRNA-seq data, and a proper technical noise model is critical for studying the underlying distribution.
Here we develop deconvolution of single-cell expression distribution (DESCEND), a statistical method that deconvolves the true cross-cell gene expression distribution from observed scRNA-seq counts and quantifies how this distribution depends on cell-level covariates. Examples of common cell-level covariates are cell size, defined as the total number of RNA molecules in a cell, and cell-cycle stage. DESCEND adopts the “G-modeling” distribution deconvolution framework (27), which avoids constraining parametric assumptions. The accuracy of DESCEND is evaluated using population-matched RNA fluorescence in situ hybridization (FISH) data, in silico sample splitting, and parametric and down-sampling simulations. Our evaluations show that, under very reasonable data quality assumptions, DESCEND can accurately deconvolve the true gene expression distribution, leading to improved estimates of expression dispersion and proportion of cells with zero/nonzero expression. We benchmark against existing methods (6, 25, 28) for analyses in which comparable methods exist, but focus on demonstrating the unique applications of DESCEND in the case studies that follow.
Although the DESCEND framework can be used with any technical noise model, the datasets we use in this paper all use UMIs, for which we have decided upon a satisfactory noise model. There is a lot of debate regarding what noise model to use, even for UMI-based scRNA-seq data. Through a reanalysis of nine public datasets, we show that a Poisson distribution is sufficient to capture the technical noise in single-cell UMI counts, once the cross-cell differences in capture and sequencing efficiency have been accounted for. Thus, DESCEND adopts a “Poisson-alpha” noise model for single-cell UMI counts, which allows fast computation and stable estimation. We show using the data from Tung et al. (29) that, with this noise model, DESCEND can effectively remove artificial differences between known experimental batches.
We demonstrate the applications of DESCEND through three case studies. The first case study illustrates how to conduct differential expression analysis under a two-state model for gene expression. Here, we also conduct a transcriptome-wide examination of how gene expression distributions are associated with cell size, again using population-matched RNA FISH to validate our findings. Next, we illustrate how to use the DESCEND estimated dispersion measures, and their standard errors, for downstream inference. The second case study focuses on cell type identification, and the third case study focuses on the selection of marker genes for cell differentiation.
Results
Model Overview.
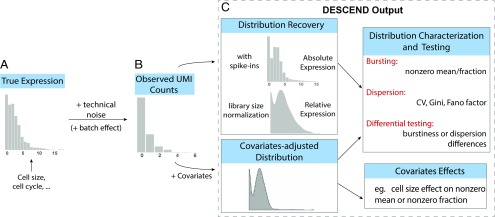
Fig. 1 gives an overview of the DESCEND framework. The observed counts in an scRNA-seq experiment are a noisy reflection of true expression levels. We model the observed count for gene in cell as a convolution of the true gene expression and technical noise,
where quantifies all aspects of the technical noise introduced in the experiment and represents the true underlying expression distribution of gene across cells. DESCEND deconvolves from the noisy observed counts , thus allowing for the estimation of any quantity related to the true underlying biological distribution. One difference between DESCEND and existing methods is that DESCEND models using a spline-based exponential family, which avoids restrictive parametric assumptions while allowing the flexible modeling of dependence on cell-level covariates.
Fig. 1.
Illustration of the framework. (A and B) The cross-cell distribution of observed counts (B) is assumed to be a convolution of the distribution of true gene expression (A) and technical noise. (C) For each gene, the output of DESCEND includes the distribution of the absolute expression levels when spike-ins are available, the distribution of relative expression with library size normalization, the distribution of covariates-adjusted expression level if covariates are presented, estimates of the bursting and dispersion parameters, differential testing results comparing the change between two cell populations, and the effects of observed covariates on gene expression.
Currently, the noise model used by DESCEND is designed for single-cell experiments that use UMIs. For extension to non-UMI read counts, see Discussion. For UMI-based single-cell RNA-seq data, DESCEND uses the default noise model , where is a cell-specific scaling constant. This model was suggested by ref. 14, and in the next section, we show through a reexamination of public data that this model is sufficient for capturing the technical noise in UMI counts when there are no batch effects. To account for batch effects, DESCEND allows a more complicated model, .
In the default noise model, DESCEND sets , by default, to the total UMI barcode count of cell ,
| [1] |
where the summation is over all biological genes (i.e., excluding spike-ins). This leads to the interpretation of being the relative expression of gene in cell . If, instead, we were interested in deconvolving the distribution of the absolute gene expression count, then we would need to rely on cell-specific spike-ins to compute the efficiency, defined as the proportion of transcripts in the cell that are sequenced,
| [2] |
where is the expected input molecule count of spike-in gene , computable from known dilution ratios. Setting to this estimated efficiency of cell leads to the interpretation of being the absolute expression of gene in the cell. Details are in Materials and Methods and SI Appendix, Mathematical Details of DESCEND.
The true gene expression distribution is expected to be complex, owing to the possibility of multiple cell subpopulations and to the transcriptional heterogeneity within each subpopulation. In particular, this distribution may have several modes and an excessive amount of zeros and cannot be assumed to abide by known parametric forms. To allow for such complexity, DESCEND adopts the technique from Efron (27) and models the gene expression distribution as a zero-inflated exponential family which has the zero-inflated Poisson, lognormal, and Gamma distributions as special cases. Natural cubic splines are used to approximate the shape of the gene expression distribution (Materials and Methods).
One meaningful aspect of is the proportion of cells where the true expression of the gene is nonzero; that is,
| [3] |
Complementary to this is the nonzero mean, defined as the average expression level among cells where the gene is expressed,
| [4] |
Note that Eqs. 3 and 4 refer to the underlying, unobserved, true gene expression distribution. The concepts of nonzero fraction and nonzero mean have appeared, under varying definitions and differing names, in single-cell studies (5, 25, 30), yet many existing approaches to estimate them (5, 18, 30–32) do not account for technical noise. If the population from which the cells are sampled can be assumed to be ergodic, then a two-state transcriptional bursting model (9, 11, 33), formulated as a periodic stochastic dynamic process, leads to a Poisson-Beta distribution for gene expression across cells. In that scenario, Eqs. 3 and 4 can be derived from the burst frequency and burst size parameters defined in the Poisson-Beta distribution. However, the strong ergodicity assumption is, in most cases, too ideal for scRNA-seq experiments, in which cell populations are unavoidably heterogeneous even when limited to a specific cell type. In DESCEND, we choose not to assume the Poisson-Beta distribution and instead focus on the more transparent quantities [3, 4].
DESCEND allows the modeling of covariate effects on both the nonzero fraction and nonzero mean. When covariates are specified, DESCEND uses a log-linear model for the covariate effect on nonzero mean and a logit model for the covariate effect on nonzero fraction. In this case, ; that is, the distribution of is cell specific, and the deconvolution result is the covariate-adjusted expression distribution (Materials and Methods).
A cell-level covariate that we study in detail is the cell size, defined as the total RNA molecule count in the cell. Cell size can be estimated by spike-in molecules added to the cell after RNA extraction: Let be the efficiency of cell obtained through Eq. 2; then
| [5] |
where is defined in Eq. 1.
DESCEND also computes standard errors and performs hypothesis tests on features of the underlying biological distribution, such as dispersion, nonzero fraction, and nonzero mean. See Materials and Methods for details.
Model Assessment and Validation
Technical noise model for UMI-based scRNA-seq experiments.
For UMI-based scRNA-seq data, Kim et al. (14) gave an analytic argument for a Poisson error model, which we discuss and clarify in SI Appendix, Mathematical Details of DESCEND. Several studies 18, 34, (35) used spike-in sets and bulk RNA splitting experiments to explore the technical noise in scRNA-seq data, finding that a Poisson distribution for UMI-based counts is plausible, but raised the issue of overdispersion. While the analyses from these studies were insightful, we believe that they failed to account for the inevitable random variations across cells/samples in the spike-in input at low concentrations. We reexamined the spike-in data from nine UMI-based scRNA-seq datasets, covering seven scRNA-seq protocols (6, 7, 29, 36–40). All of the data except for those in ref. 29 have also been analyzed in ref. 40, which showed that capture efficiency varies substantially across cells within each experiment and across experimental protocols. We show that, after accounting for the cell-to-cell variation in efficiency, the technical noise of UMI counts is simply Poisson in most cases.
For External RNA controls Consortium (ERCC) spike-in “genes,” the observed count for each gene in each cell depends on the number of input molecules and the technical noise. Due to the low spike-in concentration added to each cell, the number of input molecules for each spike-in is not fixed, but random with a certain target expectation. If we assume that the molecules in the spike-in dilution are randomly dispersed, then the number that results in each cell partition is Poisson with mean computable from the dilution ratios (see SI Appendix, SI Text, for more details). If the molecules in the spike-in dilution are not randomly dispersed, e.g., due to clumping, or if there are uncontrolled batch issues, then the input number of spike-in molecules for each cell would be overdispersed compared with the Poisson.
The key point here is that the input quantity of spike-in molecules is not fixed across cells, as assumed by current studies, but random with Poisson noise in the ideal case of perfect random dispersion with no batch variation. Such randomness in the input should not be counted as part of the technical noise of scRNA-seq experiments, as that is due to the spike-in process. Previous analyses of spike-in data have attributed this input-level variation to technical noise, thus inflating their estimates of technical noise dispersion.
To assess whether the model fits the technical noise of each dataset, we did the following: DESCEND is applied to each spike-in gene in each dataset with this error model to obtain the underlying distribution of the input molecule counts. If this model is a good approximation to the true technical noise distribution of the scRNA-seq experiment, and if the spike-ins are ideal in the sense described above, then the DESCEND-recovered input molecule () distributions of the spike-in genes should be Poisson. Conversely, if the recovered distributions show zero inflation or overdispersion compared with the Poisson, then that may be due to either a misspecified technical noise model or unaccounted experimental factors in the spike-ins. Note that the default use of DESCEND does not require spike-ins; here, the spike-ins from these nine studies are simply used to assess whether the technical noise model assumed by DESCEND is appropriate.
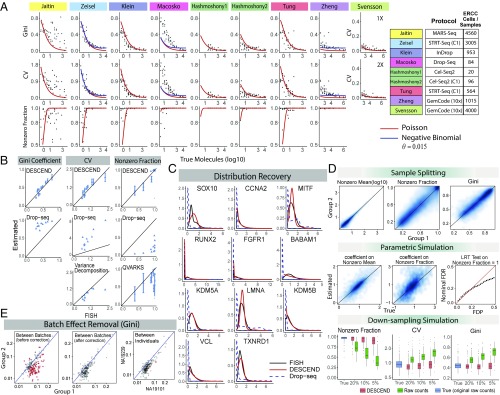
Fig. 2A shows that the DESCEND-recovered distribution in all but one (37) of the nine UMI datasets has overdispersion compared with the Poisson, where is defined in the variance-mean equation . The overdispersion is effectively zero in six of the datasets and less than 0.015 in the other two, indicating that the technical noise model used by DESCEND well approximates the technical noise in the data. As discussed above, the misfit of the Poisson to the recovered distribution for (37) data can be due to either a wrong technical noise model or clumping in the spike-ins. Note that for ref. 37, the overdispersion is high for low input values, which is the reverse of that for typical RNA-seq experiments. This pattern of overdispersion can be explained by a clumping model on the input molecules (see Materials and Methods for discussion).
Fig. 2.
Validation of DESCEND. (A) Noise model. The Poisson-alpha model is tested using nine different ERCC UMI datasets. Svensson et al. (40) include datasets at two different concentrations. The black dots are estimated quantities (Gini, CV and nonzero fraction) from the deconvolved distribution of each spike-in gene. The two solid curves show expected values of these quantities under the Poisson distribution (red) and negative binomial distribution with fixed (blue). (B) RNA FISH. Gini, CV, and nonzero fraction of 11 genes are compared between RNA FISH and the DESCEND estimates from Drop-seq counts (13). Values computed directly from observed counts and by other methods are also included. (C) FISH distribution recovery. Relative gene expression distribution is compared among RNA FISH distribution, DESCEND, and the distribution of Drop-seq observed counts. (D) Simulations. For sample splitting, estimated quantities are compared between the two split groups. For the parametric simulation, coefficients of the covariate cell are compared with the true values. The false discovery proportion (FDP) is compared with nominal FDR. For the down-sampling simulation, boxplots of estimated and “true” (original raw counts) values across genes are compared. (E) Batch effect removal in Tung et al. (29). The DESCEND-estimated Gini for each gene is compared between two replicates before (Left) and after (Center) adding batches as covariates and between two individuals (Right) after batch adjustment. The red dots are the significantly differential genes (of Gini) when FDR in controlled at level .
Evaluation of deconvolution accuracy using RNA FISH as gold standard.
Next, we evaluate the accuracy of DESCEND on the data from ref. 13, where Drop-seq and RNA FISH are both applied to the same melanoma cell line. A total of 5,763 cells and 12,241 genes were kept for analysis from the Drop-seq experiment, with median 1,473 UMIs per cell. Of these genes, 24 were profiled using RNA FISH (VCF and FOSL1 were removed from the original data; SI Appendix, SI Text). We further excluded genes with zero UMI count in more than of the cells, resulting in 12 genes. Relative gene expression distributions were recovered by DESCEND and are compared with gene expression distributions observed by RNA FISH. Since distributions recovered by DESCEND reflect relative expression levels (i.e., concentrations), for comparability the expression of each gene in FISH was normalized by GAPDH (41).
Both CV and Gini coefficients recovered using DESCEND match well with corresponding values from RNA FISH (Fig. 2B) for all 11 genes (GAPDH excluded). In comparison, Gini and CV computed on the original Drop-seq counts, standardized by library size (1), show very poor correlation and substantial positive bias; this agrees with previous observations (6, 13). For CV, a variance decomposition approach adapted from ref. 6 (SI Appendix, SI Text) shows bias toward 0 compared with values calculated from RNA FISH. This analysis also shows that the 1-SD error bars given by DESCEND reasonably quantify the uncertainty of its estimates.
DESCEND provides reasonably accurate estimates of the nonzero fraction, despite the low sequencing depth of this dataset (Fig. 2B). In contrast, the naive estimate, derived from the proportion of nonzero raw counts for each gene, is grossly inflated due to the low sequencing depth and is not a reliable estimator of nonzero fraction. DESCEND outperforms a recent method QVARKS, which estimates the nonzero fraction (called “ON fraction” in ref. 25) using a Bayesian approach.
Finally, the shape of the relative gene expression distribution (Fig. 2C) given by DESCEND matches that from FISH. In comparison, the distribution of the library-size standardized observed counts is quite different from that of their FISH counterparts, showing severe zero inflation and increased skewness.
Assessment of estimation accuracy and test validity by simulations.
We further evaluate the accuracy of DESCEND by in silico sample splitting and by parametric and down-sampling simulations. For all in silico evaluations, we start with the observed counts of the 820 oligodendrocyte cells from ref. 7, for which ERCC spike-ins are available to estimate cell-specific efficiencies. Details of each simulation are given in SI Appendix, SI Text.
First, in the sample-splitting experiment, the 820 cells are randomly split into two equal-sized groups. Since the data are split randomly, there should not be any real differences between groups. The agreement in DESCEND estimates of nonzero mean, nonzero fraction, and Gini coefficients between the two groups (Fig. 2D) indicates that the procedure has low variance and is robust to the randomness of observed counts.
The above experiment gives a model-free assessment of DESCEND estimation variance. To assess the estimation bias, we then performed a parametric simulation experiment where true gene expression counts were simulated from a lognormal distribution with cell size as covariate and where noise was simulated from our proposed noise model. True values of all involved parameters were set to be estimates from real data. We see that the estimation of covariate effects on the nonzero fraction/mean (Fig. 2D), for which there is no RNA FISH validation, is reliable. Nonzero fraction, CV, and the Gini also get accurate and unbiased estimates (SI Appendix, Fig. S1A). In addition, with the Benjamini–Hochberg procedure, DESCEND effectively controls the false discovery rate (FDR) in the test of whether the nonzero fraction is 1 (Fig. 2D).
Finally, we perform down-sampling simulations to assess how DESCEND performs under varying sequencing depth. The top 150 genes with highest total UMI count are selected and their UMI counts are treated as true expression levels. These values are then down-sampled at , and efficiency levels. The nonzero fraction, CV, and Gini coefficients estimated by DESCEND are robust to change in efficiency level while their counterparts computed directly from raw counts are severely affected by such changes (Fig. 2D and SI Appendix, Fig. S1A).
There is, of course, an endless list of parameters for which evaluations can be performed. We have merely summarized here evaluations that are relevant for the case studies discussed later in this paper.
Batch effects can be removed in differential analysis by adding batch as covariate.
Tung et al. (29) performed scRNA-seq on three human iPSC cell lines, with three technical replicates per cell line, and showed that there can be substantial variation between technical replicates. Ref. 29 further showed that simple ERCC spike-in adjustment and library size normalization cannot effectively remove this technical “batch effect.” We apply DESCEND to these data to see whether using batch as a covariate can effectively remove technical differences between replicates.
Starting from the data of ref. 29, we created two groups of cells, each containing 150 cells obtained by pooling 50 cells randomly selected from each of the three individuals. Thus, the two groups of cells should have no biological differences. However, the replicates (batches) are manually chosen to preserve the technical batch effect between the two groups: The first group contains cells sampled from one replicate for each subject: NA19098 replicate 1, NA19101 replicate 2, and NA19239 replicate 1; the second group contains cells sampled from another replicate from each subject: NA19098 replicate 3, NA19101 replicate 1, and NA19239 replicate 2. With the two groups of cells constructed in this way, any detection made during differential testing must be a false positive due to the technical differences between replicates (batch effects).
DESCEND was applied to these data to test for differences in Gini coefficient and CV between the two groups (Fig. 2E and SI Appendix, Fig. S1B). Without consideration of batch, DESCEND indeed finds many (false positive) differences in both Gini and CV. However, with batch added as covariate in the DESCEND model, the dispersion estimates from the two groups are comparable, and no significant detections are made. The fact that spike-in–based normalization cannot effectively remove this batch effect, which is effectively removed by the DESCEND model, indicates that batch effects are gene specific. We also conducted differential dispersion analysis between two biologically different samples (the three replicates from NA19101 vs. the three replicates from NA19239), with batch as covariate, and found some significant changes in Gini. The fact that significant differences are found between biologically different samples, but not between biologically identical samples, suggests that DESCEND still has the power to detect biological signals while removing batch effect.
Case Studies
Cell-size effect on expression distribution and differential testing of nonzero fraction and mean.
At the single-cell level, many genes are bursty, being inactive in some cells and active in other cells. In Eqs. 3 and 4, we defined the nonzero fraction and nonzero mean to characterize this heterogeneity in the true underlying gene expression. Using DESCEND, we analyze the scRNA-seq data of mouse hippocampal region from Zeisel et al. (7), where the 3,005 cells were classified into seven major cell types. Our goal is to characterize the dependence of nonzero fraction and nonzero mean on cell size and to find genes that are differentially expressed in these parameters between different cell types, controlling for cell size. Recall that cell size is estimated as Eq. 5.
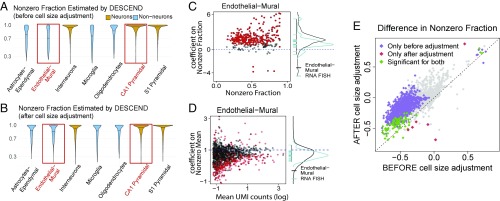
First, consider the transcriptome-wide patterns of the DESCEND deconvolved nonzero fraction and nonzero mean, without adjusting for cell size; these were estimated for each gene in each cell type separately, with no added covariates (details in SI Appendix, SI Text). As shown in Fig. 3A, the deconvolved gene expression distributions for most genes have much larger nonzero fraction in the neuron cell types (CA1 pyramidal, S1 pyramidal, and interneurons) compared with the nonneuron cell types (astrocytes–ependymal, endothelial–mural, microglia, and oligodentrocytes), thus suggesting that more genes are in the “on” state in neurons. However, neurons are known to be larger cells, and, indeed, cell-size estimates are substantially larger for neurons compared with nonneurons in this dataset (SI Appendix, Fig. S2A). Can the global increase in nonzero fraction in neurons simply be attributed to increased cell size? To answer this question we need to first quantify how cell size affects the gene expression distribution.
Fig. 3.
Differential testing on nonzero fraction/mean as in Zeisel et al. (7). Violin plots of the estimated nonzero fractions are compared across cell types (A) before and (B) after adding cell size as a covariate. (C, Left) Estimated coefficients of cell size on nonzero fraction for genes whose nonzero fraction is significantly smaller than 1 and with estimated value less than 0.9 for the endothelial–mural cell population. (C, Right) Density of all of the dots in C, Left (black curve) aligned with the density curve of the coefficients of cell size on nonzero fraction for the RNA FISH data (blue). (D) Same as C, but for coefficients on nonzero mean and all of the genes. (E) Scatter plot for the difference of the estimated nonzero fraction between the endothelial–mural and CA1 pyramidal cells before and after cell-size adjustment. Significant genes are highlighted at FDR level .
We applied DESCEND, with cell size as a covariate, to obtain the deconvolved cell-size–adjusted gene expression distribution for each gene in each of the seven cell types. The coefficients estimated by DESCEND allow us to assess, for each gene, whether its nonzero mean has superlinear, linear, or sublinear growth with cell size and whether its nonzero fraction increases, remains constant, or decreases with cell size. See statistical details in Materials and Methods. Taking the endothelial–mural cells as an example, we find that for most genes, nonzero fraction increases with cell size as the coefficients are positive (Fig. 3C). The mean trend across genes is that a doubling of cell size is associated with at least a doubling of the odds of observing at least one transcript. We also find that, globally, nonzero mean has a slightly sublinear dependence on cell size as many coefficients are below 1 (Fig. 3D). The sublinear dependence of nonzero mean on cell size is consistent with previous findings in ref. 41, which used RNA FISH to study a small set of genes and found their expression to have increased concentration in smaller cells, although the quantity measured in ref. 41 directly reflects transcription burst size. These relationships between expression distribution and cell size are consistent across all seven cell types in this study (SI Appendix, Fig. S2 E and F).
It is important to emphasize here that both cell size and true expression distribution are not directly observable quantities and that this relationship between cell size and nonzero mean/fraction is not a direct consequence of larger observed library size leading to larger change of having a nonzero count for a gene. To demonstrate further that the discovered relationships are biological, not technical, we conducted a parallel analysis of the RNA FISH data of ref. 13 (SI Appendix, SI Text). For the 23 genes (excluding GADPH) available in the RNA FISH data, we observe the same trends as above: The nonzero fraction increases with cell size, with a mean odds ratio of at least 2, and the nonzero mean increases sublinearly with cell size (Fig. 3 C and D and SI Appendix, Fig. S2C). The fact that this trend is observed using two different technologies and for eight different cell types (seven by scRNA-seq, melanoma cell line by RNA FISH) suggests that it may be a general relationship between cell size and single-cell gene expression distributions.
Fig. 3B shows the nonzero fractions across genes within each cell type, estimated by applying DESCEND with cell size as a covariate. After adjusting for differences in cell size, the transcriptome-wide patterns in nonzero fraction/mean are much more similar across cell types. This suggests that the increased nonzero fraction in neuron cells can mostly be attributed to cell-size differences. For example, compare two cell types: endothelial–mural and pyramidal CA1 cells. Before cell-size adjustment, 879 genes show significant decrease of nonzero fraction in pyramidal CA1 at FDR of (Fig. 3E and SI Appendix, Fig. S2B); the results change substantially after cell-size adjustment, with only 84 significant genes, 78 of which were in the original set of 879 genes. This highlights the importance of cell-size adjustment in differential testing.
We also test for the change on nonzero mean between endothelial–mural and pyramidal CA1 cells. Across genes, the estimated change in nonzero fraction does not seem correlated with the estimated change in nonzero mean (Fig. 3H), indicating that, after accounting for cell size, the two types of change are unrelated. Differential testing results on nonzero mean and nonzero fraction, taken together, give a more detailed characterization of differential expression (SI Appendix, Fig. S3).
DESCEND improves the accuracy of cell type identification by a better selection of highly variable genes.
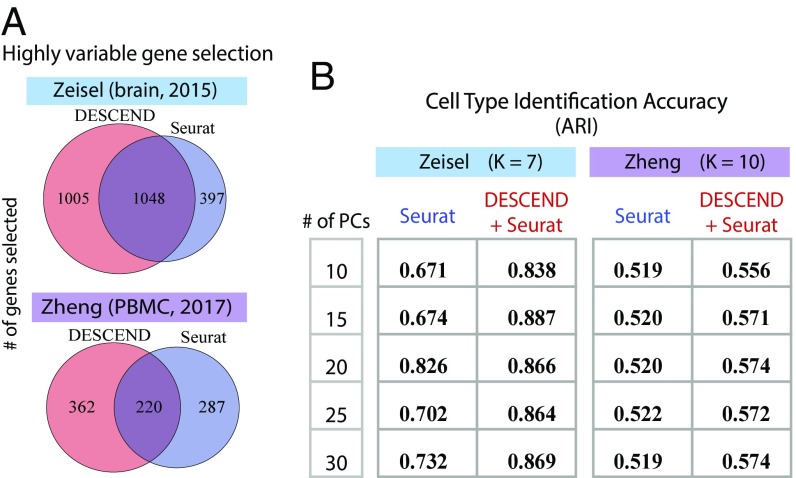
One major step in cell type identification is the selection of highly variable genes (HVG) before applying any dimension reduction and clustering algorithms (6, 34, 37, 42). Filtering out genes with low variation reduces noise while keeping the genes that are more likely to be cell subpopulation markers. Current pipelines select HVGs mainly by computing dispersion measurements, such as CV and Fano factor, directly on the raw or library-normalized counts or by variance decomposition. However, as shown in Fig. 2B, these methods are not as accurate as DESCEND in estimating the true biological dispersion of the gene expression levels. Furthermore, compared with CV and Fano factor, the Gini coefficient is a more robust indicator of dispersion (see Materials and Methods for derivation), and we have shown that DESCEND allows accurate estimate of this indicator. Here, we examine whether DESCEND-selected HVGs improve the accuracy of cell type identification when used with existing clustering algorithms.
We consider cell type identification in two datasets where somewhat reliable cell type labels are available. One consists of the 3,005 cells in ref. 7, which were classified into seven major cell types with the help of domain knowledge. The other is obtained from 10 purified cell populations derived from peripheral blood mononuclear cells (PBMC) in ref. 39, where 1,000 cells were sampled randomly from each cell type and combined to form a 10,000-cell dataset. Since the PBMC data consist mostly of immune cell subtypes (CD4+ helper T cells, CD4+/CD25+ regulatory T cells, CD4+/CD45RA+/CD24− naive T cells, CD4+/CD45RO+ memory T cells, CD8+ cytotoxic T cells, and CD8+/CD45RA+ naive cytotoxic T cells) which are well known to have similar transcriptomes, it is a more challenging test case. For both datasets, we treat the cell type labels given in their original papers as the gold standard.
There are many existing cell clustering methods for scRNA-seq. To focus on evaluating the effectiveness of the initial HVG selection step, we limit to Seurat, one of the most widely used algorithms, and compare clustering results of Seurat (Version 2.1) with a modified version of Seurat where the initial HVG selection step is replaced by DESCEND. Seurat selects HVGs by ranking the Fano factors of the normalized counts, yielding a list with only overlap with the HVGs selected by DESCEND (Fig. 4A) for both datasets. To compare cell clustering accuracy, we use the adjusted Rand index, which ranges from 0, for a level of similarity expected by chance, to 1 for identical clusters (43). The number of clusters is set to the truth for both datasets and both pipelines. Fig. 4B shows that with DESCEND, Seurat achieves consistently better results than its original version. Seurat, like most other clustering algorithms, first performs dimension reduction using principal components analysis (PCA), and the number of principal components (PCs) affects downstream clustering. As seen in Fig. 4B, the accuracy boost obtained from DESCEND-based HVG selection is consistent across the number of PCs used for dimension reduction.
Fig. 4.
Selection of HVGs and cell type identification. (A) Venn diagram of the number of selected HVGs in Seurat and using DESCEND based on the Gini coefficient. (B) Comparison of cell type identification accuracy using Adjusted Rand Index (ARI) between the original Seurat and Seurat with the HVG selection step replaced by DESCEND.
Dispersion analysis using the DESCEND-estimated Gini coefficient highlights early-stage differentiation markers for mES cells.
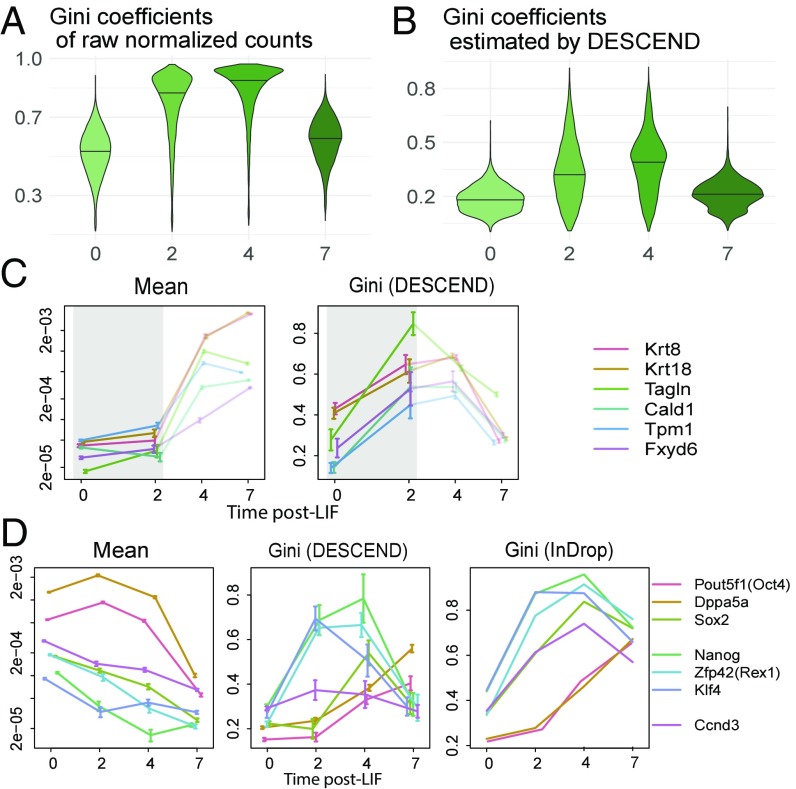
We apply DESCEND to data from Klein et al. (6), where single cells were sampled from a differentiating mESC population before and at 2 d, 4 d, and 7 d after Leukemia inhibitory factor (LIF) withdrawal. In these data, while pluripotency markers and differentiation-related genes have changes in mean expression over time, due to complete transcriptome remodeling, almost all genes have significant change in mean expression even by day 2 (SI Appendix, Fig. S4C). Thus, change in mean is not an effective measure for identifying differentiation markers. Instead, we used DESCEND to test for change in expression dispersion across the early time points, under the rationale that early differentiation markers would exhibit high heterogeneity at this initial stage.
First, consider expression dispersion as quantified by the Gini coefficients computed from the observed counts distribution, before deconvolution by DESCEND: For most genes, they are much higher at days 2 and 4, compared with days 0 and 7 (Fig. 5A). Although this pattern is consistent with our expectation that cells should exhibit higher heterogeneity during differentiation, compared with directly before or directly afterward, it is confounded by the substantially lower sequencing depth for the day 2 and 4 samples (SI Appendix, Fig. S4A). Are the higher Gini coefficients in days 2 and 4 due to the technical reason of lower sequencing depth or the biological reason of increased population heterogeneity? We applied DESCEND to compute Gini coefficients of the true expression distribution, thus removing the technical confounder of sequencing depth. DESCEND-estimated Gini coefficients confirm that Gini coefficients are indeed higher at days 2 and 4, compared with days 0 and 7 (Fig. 5B), as expected for this evolving population.
Fig. 5.
Marker genes analysis using Gini as in Klein et al. (6). (A and B) Violin plots (with solid line indicating the quantile) of Gini coefficients of raw normalized counts (A) and of the DESCEND-estimated Gini coefficients on each day (B). (C) Change of the mean relative expression and Gini coefficients for six epiblast marker genes across days. The colored error bars indicate 1 SE. (D) Change of the mean relative expression and Gini coefficients for pluripotency genes across days. For the Gini coefficients, one is estimated using DESCEND, and the other is calculated using raw normalized counts. The colored error bars indicate 1 SE.
The differentiation of mES cells upon LIF withdrawal is a poorly characterized process. Ref. 6 observed that, whereas at day 7, almost of cells have become epiblasts, at day 2 the proportion is below . Thus, the cross-cell mean expression of known epiblast markers, such as Krt8, Krt18, Tagln, Cald1, Tpm1, and Fxyd6, does not show significant increase until day 4 (Fig. 5C), when almost half of the cells show complete transcriptome reprogramming (SI Appendix, Fig. S5A). In comparison, these known marker genes belong to a much smaller set of genes that show a dramatic increase in Gini coefficient between day 0 and day 2 (Fig. 5C and SI Appendix, Fig. S4C).
DESCEND allows the computation of SEs, and from these SEs we assessed the significance of change in Gini coefficient between day 0 and day 2. At an FDR threshold of , 750 genes are significant for change in Gini coefficient. In comparison, more than 10,000 genes have significant, but very small changes, in mean between day 0 and day 2 using either DESeq2 or DESCEND, with the significance driven mostly by the much smaller SEs for mean estimation (SI Appendix, Fig. S4C). Of the 56 genes with significant change in Gini coefficient but not in mean computed by DESCEND, many are meaningful differentiation markers. For instance, the genes Tagln, Anxa2, H19, Sparc, and Ccno are listed in ref. 6 as marker genes for the cell types that appear during differentiation (SI Appendix, Fig. S4D). Jun, Anxa3, Klf6, Fos, and Dusp4 can also be marker genes for the epiblast cells as these genes show significant increase in mean expression at the later stages (day 4 or day 7) (SI Appendix, Fig. S4E).
DESCEND also allows a more detailed characterization of the activity of pluripotency factors during differentiation (44, 45). As discussed in ref. 6, the expression levels of some pluripotency genes drop gradually (Pou5f1, Dppa5a, Sox2) while those of others drop rapidly (Nanog, Zfp42, Klf4) during differentiation. This is revealed by the trend of the DESCEND-estimated Gini coefficient (Fig. 5E) across time. The rapid drop-off genes react early during differentiation, and thus their Gini coefficients increase immediately at day 2 (SI Appendix, Fig. S5). In comparison, the gradual drop-off genes react late during differentiation and thus their Gini coefficients remain unchanged at day 2, starting to increase only at day 4. In contrast, this difference in early vs. late expression drop-off is not visible by mean expression due to heterogeneity between cells with regard to their differentiation timing. As a negative control, the cell-cycle marker gene Ccnd3 has no significant change in DESCEND-estimated Gini coefficient during differentiation, agreeing with the fact that its expression heterogeneity across cells should be steady during differentiation.
Discussion
We have described DESCEND, a method for gene expression deconvolution for scRNA-seq. All results in this paper are based on a Poisson model for UMI counts. The deconvolution accuracy of DESCEND was extensively assessed through comparisons to population-matched RNA FISH data and through data splitting and simulation experiments. DESCEND’s noise model allows it to remove known batch effects, as demonstrated on data from ref. 29.
DESCEND’s formulation allows more complex noise models, which would be necessary for analysis of scRNA-seq data without UMIs where there is amplification bias and zero inflation beyond what could be captured by Poisson sampling (24, 46). But such models contain many more parameters, and the estimation of these parameters is nontrivial. Some aspects of the deconvolved distribution, such as Eqs. 3 and 4, are highly sensitive to the noise model and the estimation quality of the technical parameters. More efforts are needed to develop robust error models for non-UMI scRNA-seq data.
Even in UMI-based scRNA-seq data, technical noise may have substantial overdispersion, and a negative binomial distribution may be more appropriate. DESCEND accepts the negative binomial distribution with a known overdispersion parameter . As shown in Fig. 2A, can be estimated using the spike-in genes as the square of the CV limit when the expected number of input molecules increases. The overdispersion may also be cell or gene specific, but a more realistic model with more parameters may not always lead to better analyses if those parameters cannot be estimated reliably from data. So far, we have settled on a simple model with at most one overdispersion parameter for UMI-based data.
Without covariate adjustment, DESCEND currently requires a few seconds for deconvolution of the distribution of a single gene with hundreds of cells and 10–20 s when there are thousands of cells. Adding covariates and performing likelihood-ratio tests increase the computation cost by roughly three or four times. Computation can be easily parallelized across genes.
Accuracy of DESCEND estimation increases with number of cells and with sequencing coverage. For example, for the Drop-seq data from ref. 13, although the average UMI count per cell is only around 1,500, the large number of cells (a few thousand) allows accurate DESCEND estimation. For the data from refs. 6 and 7, there are only a few hundred cells for each condition, but the high sequencing depth and the prefiltering allow good estimates.
Code Availability
The R package DESCEND is available on the Github repository https://github.com/jingshuw/descend. All source code and intermediate analysis results that were used to generate the figures in this paper are at repository https://github.com/jingshuw/DESCEND_manuscript_source_code.
Materials and Methods
Model.
We introduce the model, estimation procedure, and inference framework here, but leave technical details and a full discussion to the accompanying mathematical supplement in SI Appendix, Mathematical Details of DESCEND.
The observed count for gene in cell is modeled as a convolution of the true gene expression and independent technical noise :
| [6] |
The default technical noise model in DESCEND is the Poisson-alpha model,
| [7] |
where is a cell-specific scaling factor. There are two ways to set , leading to two interpretations for . First, if one wishes to recover the distribution of absolute expression, one would need spike-in data for each cell to compute the proportion of transcripts sequenced (2) and set to this value. In this case, represents true absolute expression count and is the cell-specific efficiency constant. When spike-ins are not available, or when one wishes to recover the relative gene expression distribution, can be set to the total UMI count for cell in Eq. 1. In this case, represents the concentration of gene in cell . Thus, the interpretation of depends on how we set . From now on, we simply refer to as “true expression.”
DESCEND allows more complex technical noise models with gene-specific batch effects and Beta-binomial noise distribution. These extensions are described in SI Appendix, Mathematical Details of DESCEND.
Without covariates, our model assumes that true expression and our goal is to estimate . We assume that has a point mass at zero and a nonzero component belonging to an exponential family of distributions as in ref. 27. When cell-level covariates are specified, we assume that they affect expression as follows:
| [8] |
| [9] |
Thus, the covariate effect is quantified by the parameters , , and . Our goal is to conduct inference on these parameters as well as to deconvolve the “covariates-adjusted distribution.” The nonzero part of the distribution is the same as that of and the zero probability (denoted by ) of this distribution is the average of across cells . The covariates-adjusted nonzero fraction is meaningful only for differential testing, which is defined as , with centered to have mean 0 across all cell populations.
Modeling the Nonzero Component.
Let be the density of or, in the absence of covariates, the density of . We assume
| [10] |
where is a vector of parameters and is the normalization factor. When , then is the Gamma density. When , is the lognormal density. Following ref. 27, to adapt to data, we set to the 5-degree natural cubic spline basis.
As in ref. 27, we discretize to simplify estimation. That is, we assume and let
| [11] |
where is the 5-degree natural cubic spline base matrix. In DESCEND, the default setting is and is chosen as equally spaced points between 0 and the percentile of . See SI Appendix, SI Text for how is chosen.
Penalized Maximum-Likelihood Estimation.
Now we combine zero inflation and covariates adjustment with density to get the likelihood of the observed data , which we call . It is not hard to show that the likelihood has the form
where incorporates the Poisson noise and the covariate effect on nonzero mean (Eq. 8) (the formula for is in ref. 27), and is an adjustment of Eq. 11 to account for Eq. 9,
where
is the cell-specific covariate-adjusted matrix. The first element of is a rescaled and the rest of is .
Following ref. 27, we maximize a penalized log-likelihood to estimate the parameters . Suppressing in our notation, let the log-likelihood for counts of gene across cells be , and the penalized log-likelihood is , where is the penalty term. Let the Fisher information matrix of be . Based on the suggestion in ref. 27, in DESCEND the tuning parameter is adaptively chosen such that the approximated ratio of artificial to genuine information is less than to avoid overshrinkage but more than to reduce overfitting.
Statistical Inference.
Ref. 27 showed that second-order approximations provide useful inference on model parameters. By Taylor expansion of the log-likelihood around the true values of and , we have
from which one can calculate bias and SD of the estimates. For inference on functions of (such as mean, nonzero fraction, etc.), we apply the Delta method.
Now consider differential testing between two populations of cells. Let () be the value of some model parameter, which is a function of , in population . To test we compute a score,
where is the estimated mean-squared error. Permutations of the cell labels give the null distribution for P-values computation.
DESCEND uses likelihood-ratio tests with the unpenalized likelihood to conduct tests on distribution parameters in a single population; e.g., , the test on nonzero fraction in the true distribution of gene . Another example is the test of whether the cell-size covariate, in the first case study, has an effect on nonzero mean () or on nonzero fraction (). These test statistics are approximately chi-square distributed.
Finding HVGs.
We use quantile smooth regression (default quantile 0.5) to fit a smooth curve of the relationship between the mean of deconvolved distributions and Gini across genes, using the R package quantreg (47). The dispersion score of each gene is computed as the distance of the Gini from the curve, which is further normalized by its SE. We select HVGs as the genes whose normalized scores are larger than a threshold (default value is 10).
Randomness of ERCC Spike-in Counts in scRNA-seq Experiments.
Randomness of both the input counts and technical noise contributes to the randomness of ERCC spike-ins observed counts. First, the actual count of each spike-in gene in each cell deviates from its target count computed from dilution ratios and is approximately Poisson given the following three assumptions: (i) The molecules are distributed evenly in the dilution, (ii) each molecule moves independently, and (iii) the distribution of molecules in dilution does not change during the spike-in process. If any of these assumptions fail, the actual count landing in each cell would be overdispersed compared with Poisson. Such randomness is also observed empirically. For example, in ref. 7, 339 of the 3,005 cells have at least one ERCC gene (among the 38 spike-in genes with expected input count ) whose observed UMI count is even larger than its expected input count, which would not have been possible if we assume the input count is fixed.
In the ERCC data of ref. 37, the variances of the DESCEND deconvolved distributions are roughly , where is the expected input count. This overdispersion can be explained by a clumping model: If 10 molecules on average move together in the dilution before they are added to cells, and if the clumps move independently, then the variance of the observed counts would be .
Supplementary Material
Acknowledgments
J.W. is supported by NIH Grant 2 R01HG006137 and the Wharton Dean’s Fund. M.L. is supported by NIH Grants R01GM108600, R01GM125301, and R01HL113147. N.R.Z. is supported by NIH Grant R01HG006137.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1721085115/-/DCSupplemental.
References
- 1.Spencer SL, Gaudet S, Albeck JG, Burke JM, Sorger PK. Non-genetic origins of cell-to-cell variability in TRAIL-induced apoptosis. Nature. 2009;459:428–432. doi: 10.1038/nature08012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Raj A, van Oudenaarden A. Single-molecule approaches to stochastic gene expression. Annu Rev Biophys. 2009;38:255–270. doi: 10.1146/annurev.biophys.37.032807.125928. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Tay S, et al. Single-cell NF-B dynamics reveal digital activation and analog information processing in cells. Nature. 2010;466:267–271. doi: 10.1038/nature09145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Loewer A, Lahav G. We are all individuals: Causes and consequences of non-genetic heterogeneity in mammalian cells. Curr Opin Genet Dev. 2011;21:753–758. doi: 10.1016/j.gde.2011.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Shalek AK, et al. Single cell RNA Seq reveals dynamic paracrine control of cellular variation. Nature. 2014;510:363–369. doi: 10.1038/nature13437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Klein AM, et al. Droplet barcoding for single-cell transcriptomics applied to embryonic stem cells. Cell. 2015;161:1187–1201. doi: 10.1016/j.cell.2015.04.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zeisel A, et al. Cell types in the mouse cortex and hippocampus revealed by single-cell RNA-seq. Science. 2015;347:1138–1142. doi: 10.1126/science.aaa1934. [DOI] [PubMed] [Google Scholar]
- 8.Shaffer SM, et al. Rare cell variability and drug-induced reprogramming as a mode of cancer drug resistance. Nature. 2017;546:431–435. doi: 10.1038/nature22794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kaern M, Elston TC, Blake WJ, Collins JJ. Stochasticity in gene expression: From theories to phenotypes. Nat Rev Genet. 2005;6:451–464. doi: 10.1038/nrg1615. [DOI] [PubMed] [Google Scholar]
- 10.Shalek AK, et al. Single-cell transcriptomics reveals bimodality in expression and splicing in immune cells. Nature. 2013;498:236–240. doi: 10.1038/nature12172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jiang Y, Zhang NR, Li M. Scale: Modeling allele-specific gene expression by single-cell RNA sequencing. Genome Biol. 2017;18:74. doi: 10.1186/s13059-017-1200-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Eberwine J, Sul JY, Bartfai T, Kim J. The promise of single-cell sequencing. Nat Methods. 2014;11:25–27. doi: 10.1038/nmeth.2769. [DOI] [PubMed] [Google Scholar]
- 13.Torre E, et al. Rare cell detection by single-cell RNA sequencing as guided by single-molecule RNA FISH. Cell Syst. 2018;6:171–179. doi: 10.1016/j.cels.2018.01.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kim JK, Kolodziejczyk AA, Ilicic T, Teichmann SA, Marioni JC. Characterizing noise structure in single-cell RNA-seq distinguishes genuine from technical stochastic allelic expression. Nat Commun. 2015;6:8687. doi: 10.1038/ncomms9687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kolodziejczyk AA, Kim JK, Svensson V, Marioni JC, Teichmann SA. The technology and biology of single-cell RNA sequencing. Mol Cell. 2015;58:610–620. doi: 10.1016/j.molcel.2015.04.005. [DOI] [PubMed] [Google Scholar]
- 16.Stegle O, Teichmann SA, Marioni JC. Computational and analytical challenges in single-cell transcriptomics. Nat Rev Genet. 2015;16:133–145. doi: 10.1038/nrg3833. [DOI] [PubMed] [Google Scholar]
- 17.Kivioja T, et al. Counting absolute numbers of molecules using unique molecular identifiers. Nat Methods. 2012;9:72–74. doi: 10.1038/nmeth.1778. [DOI] [PubMed] [Google Scholar]
- 18.Kim JK, Marioni JC. Inferring the kinetics of stochastic gene expression from single-cell RNA-sequencing data. Genome Biol. 2013;14:R7. doi: 10.1186/gb-2013-14-1-r7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Finak G, et al. Mast: A flexible statistical framework for assessing transcriptional changes and characterizing heterogeneity in single-cell RNA sequencing data. Genome Biol. 2015;16:278. doi: 10.1186/s13059-015-0844-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gu J, Du Q, Wang X, Yu P, Lin W. 2015. Sphinx: Modeling transcriptional heterogeneity in single-cell RNA-seq. bioRxiv:027870.
- 21.Buettner F, et al. Computational analysis of cell-to-cell heterogeneity in single-cell RNA-sequencing data reveals hidden subpopulations of cells. Nat Biotechnol. 2015;33:155–160. doi: 10.1038/nbt.3102. [DOI] [PubMed] [Google Scholar]
- 22.Kharchenko PV, Silberstein L, Scadden DT. Bayesian approach to single-cell differential expression analysis. Nat Methods. 2014;11:740–742. doi: 10.1038/nmeth.2967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Prabhakaran S, Azizi E, Carr A, Pe’er D. Dirichlet process mixture model for correcting technical variation in single-cell gene expression data. In: Balcan MF, Weinberger KQ, editors. Proceedings of The 33rd International Conference on Machine Learning, PMLR. Vol 48. JMLR.org; New York: 2016. pp. 1070–1079. [PMC free article] [PubMed] [Google Scholar]
- 24.Vallejos CA, Marioni JC, Richardson S. BASiCS: Bayesian analysis of single-cell sequencing data. PLoS Comput Biol. 2015;11:e1004333. doi: 10.1371/journal.pcbi.1004333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Narayanan M, Martins AJ, Tsang JS. Robust inference of cell-to-cell expression variations from single- and k-cell profiling. PLoS Comput Biol. 2016;12:e1005016. doi: 10.1371/journal.pcbi.1005016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Korthauer KD, et al. A statistical approach for identifying differential distributions in single-cell RNA-seq experiments. Genome Biol. 2016;17:222. doi: 10.1186/s13059-016-1077-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Efron B. Empirical Bayes deconvolution estimates. Biometrika. 2016;103:1–20. [Google Scholar]
- 28.Love MI, Huber W, Anders S. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 2014;15:550. doi: 10.1186/s13059-014-0550-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tung PY, et al. Batch effects and the effective design of single-cell gene expression studies. Sci Rep. 2017;7:39921. doi: 10.1038/srep39921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.McDavid A, et al. Data exploration, quality control and testing in single-cell qPCR-based gene expression experiments. Bioinformatics. 2012;29:461–467. doi: 10.1093/bioinformatics/bts714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Delmans M, Hemberg M. Discrete distributional differential expression (D3E)–a tool for gene expression analysis of single-cell RNA-seq data. BMC Bioinformatics. 2016;17:110. doi: 10.1186/s12859-016-0944-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Vu TN, et al. Beta-Poisson model for single-cell RNA-seq data analyses. Bioinformatics. 2016;32:2128–2135. doi: 10.1093/bioinformatics/btw202. [DOI] [PubMed] [Google Scholar]
- 33.Raj A, Peskin CS, Tranchina D, Vargas DY, Tyagi S. Stochastic mRNA synthesis in mammalian cells. PLoS Biol. 2006;4:e309. doi: 10.1371/journal.pbio.0040309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Brennecke P, et al. Accounting for technical noise in single-cell RNA-seq experiments. Nat Methods. 2013;10:1093–1095. doi: 10.1038/nmeth.2645. [DOI] [PubMed] [Google Scholar]
- 35.Grün D, Kester L, Van Oudenaarden A. Validation of noise models for single-cell transcriptomics. Nat Methods. 2014;11:637–640. doi: 10.1038/nmeth.2930. [DOI] [PubMed] [Google Scholar]
- 36.Jaitin DA, et al. Massively parallel single-cell RNA-seq for marker-free decomposition of tissues into cell types. Science. 2014;343:776–779. doi: 10.1126/science.1247651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Macosko EZ, et al. Highly parallel genome-wide expression profiling of individual cells using nanoliter droplets. Cell. 2015;161:1202–1214. doi: 10.1016/j.cell.2015.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hashimshony T, et al. CEL-Seq2: Sensitive highly-multiplexed single-cell RNA-seq. Genome Biol. 2016;17:77. doi: 10.1186/s13059-016-0938-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zheng GX, et al. Massively parallel digital transcriptional profiling of single cells. Nat Commun. 2017;8:14049. doi: 10.1038/ncomms14049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Svensson V, et al. Power analysis of single-cell RNA-sequencing experiments. Nat Methods. 2017;14:381–387. doi: 10.1038/nmeth.4220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Padovan-Merhar O, et al. Single mammalian cells compensate for differences in cellular volume and DNA copy number through independent global transcriptional mechanisms. Mol Cell. 2015;58:339–352. doi: 10.1016/j.molcel.2015.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Vallejos CA, Risso D, Scialdone A, Dudoit S, Marioni JC. Normalizing single-cell RNA sequencing data: Challenges and opportunities. Nat Methods. 2017;14:565–571. doi: 10.1038/nmeth.4292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kiselev VY, et al. SC3: Consensus clustering of single-cell RNA-seq data. Nat Methods. 2017;14:483–486. doi: 10.1038/nmeth.4236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Chu LF, et al. Single-cell RNA-seq reveals novel regulators of human embryonic stem cell differentiation to definitive endoderm. Genome Biol. 2016;17:173. doi: 10.1186/s13059-016-1033-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Papatsenko D, Xu H, Ma’ayan A, Lemischka I. Stem Cells Handbook. Humana Press; New York: 2013. Quantitative approaches to model pluripotency and differentiation in stem cells; pp. 59–74. [Google Scholar]
- 46.Jia C, Kelly D, Kim J, Li M, Zhang N. 2017. Accounting for technical noise in single-cell RNA sequencing analysis. bioRxiv:116939.
- 47.Koenker R. 2017. quantreg: Quantile Regression, R package Version 5.34.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.