pStab: prediction of stable mutants, unfolding curves, stability maps and protein electrostatic frustration

Abstract

Summary

We present a web-server for rapid prediction of changes in protein stabilities over a range of temperatures and experimental conditions upon single- or multiple-point substitutions of charged residues. Potential mutants are identified by a charge-shuffling procedure while the stability changes (i.e. an unfolding curve) are predicted employing an ensemble-based statistical-mechanical model. We expect this server to be a simple yet detailed tool for engineering stabilities, identifying electrostatically frustrated residues, generating local stability maps and in constructing fitness landscapes.

Availability and implementation

The web-server is freely available at http://pbl.biotech.iitm.ac.in/pStab and supports recent versions of all major browsers.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Engineering protein and enzyme stabilities have numerous applications in biotechnological and pharmaceutical industries. In this regard, modulating charge–charge interactions has led to significant successes in engineering the stabilities of enzymes and proteins(Sanchez-Ruiz and Makhatadze, 2001; Strickler et al., 2006). We had recently developed a rapid and ensemble-based algorithm for predicting changes in protein stabilities (ΔΔG) involving charged residues using an Ising-like statistical mechanical model (the Wako-Saitô-Muñoz-Eaton, WSME model; Muñoz and Eaton, 1999; Wako and Saito, 1978) incorporating an experimentally calibrated electrostatic energy term (E_elec)(Naganathan, 2012) exhibiting a success rate of 81%, specificity of 78.5% and sensitivity of 83.6% for single-point substitutions with a maximal correlation of 0.71(Naganathan, 2013). Here, we develop a predictive web-server, pStab, for rational engineering of protein stabilities through modulation of charge–charge interactions based on the model discussed above.

2 Methods and outputs

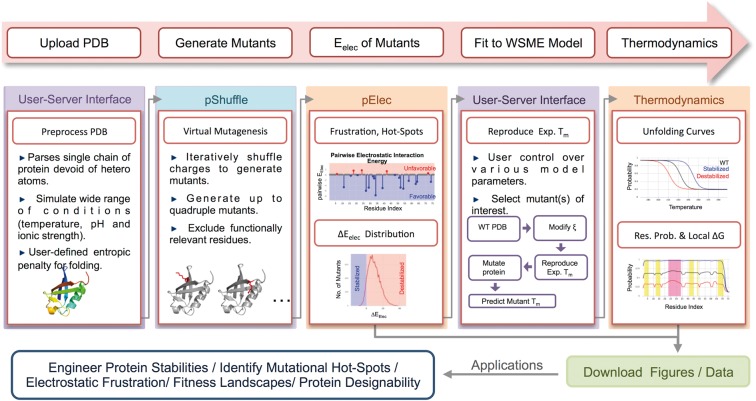
The flow chart for engineering stabilities is outlined in Figure 1. The server accepts PDB ID/file as input from the user (protein length, N ≤ 300) and generates a series of mutants by combinatorially mutating either the charged residues or charged and large polar residues (Asn/Gln; pShuffle module) (Naganathan, 2013). The user can introduce up to four single-point substitutions with an option for eliminating functionally important residues. The charge–charge interaction energy (E_elec) is calculated for each of the mutants using a modified Debye–Hückel (DH) formalism that displays a high correlation with the Tanford–Kirkwood algorithm (Tanford and Kirkwood, 1957; TK; Supplementary Fig. S1). The distribution of E_elec or ΔE_elec (i.e. referenced to the WT) for the numerous mutants is readily obtained with the total time taken dependent on the number of charged residues and the number of allowed mutations (pElec module; see Supplementary Fig. S2 for the time estimates).

Fig. 1.

Schematic diagram describing the workflow and applications of the pStab web-server

The server lists out the top 5000 stable mutants including details on electrostatically frustrated residues and mutational hot-spots; the mutant identities, distribution of E_elec and figures can then be directly downloaded. Following this step, the user is given an option for estimating the free-energy changes associated with mutation (i.e. an unfolding curve) for N ≤ 150. The specified melting temperature of the WT protein (default is 333 K) is reproduced using the WSME model from an ensemble of 2 ^N states where N is the number of residues in the protein. The unfolding curves or mean folding probabilities (estimated from the derivatives of partition functions) and residue level local stabilities (calculated by lumping together partial partition functions; see Supplementary Material) are then predicted as a function of temperature for select mutants or the top 10 stable mutants employing identical parameters to that of the WT (Thermodynamics module). While predicting the unfolding curves, the user can also choose between different options for the magnitude of entropic costs. For predicting the unfolding curves of the WT and 10 mutants, it takes ∼40 min for a 150 residue protein while taking just ∼10 min for a 100 residue protein (Supplementary Fig. S2). Note that this time period is quite short compared to the time taken for predicting even a single unfolding curve from coarse-grained (several days) and all-atom MD simulations (several months). Case studies involving mutations of ubiquitin and the residue-level stability map of a thermosensor protein are presented in Supplementary Figures S3 and S4, respectively.

3 Novelty and applications

pStab stands out from the current crop of servers (Guerois et al., 2002; Huang et al., 2007; Worth et al., 2011) in four aspects. First, it employs a simplified DH formalism that performs as well as the computationally intensive TK algorithm. It therefore provides a rapid quantitative look at the degree of electrostatic frustration together with the identity and distribution of mutational hot spots on the protein surface. Second, it does not rely on machine learning algorithms or multi-parameter energy functions. pStab resorts to a first-principles method based on equilibrium thermodynamics that is rigorously validated against different datasets and is therefore devoid of artifacts from the use of multiple correlated parameters, over-fitting or choice of feature sets. Third, the rapidity of the method allows one to construct fitness landscapes based on the distribution of electrostatic interaction energy alone for a very large number of mutants. Last, most web-servers employ a single model structure and predict the impact of mutations employing electrostatic interaction energy as a proxy and at a single temperature. In our case, we employ a large ensemble of states (up to 2 ^N microstates) and predict not only the free-energy change at one temperature but also across a range of temperatures thus simulating an entire unfolding curve.