Abstract
Single-particle tracking offers a noninvasive high-resolution probe of biomolecular reactions inside living cells. However, efficient data analysis methods that correctly account for various noise sources are needed to realize the full quantitative potential of the method. We report algorithms for hidden Markov-based analysis of single-particle tracking data, which incorporate most sources of experimental noise, including heterogeneous localization errors and missing positions. Compared to previous implementations, the algorithms offer significant speedups, support for a wider range of inference methods, and a simple user interface. This will enable more advanced and exploratory quantitative analysis of single-particle tracking data.
Introduction
Experimental techniques to track the conformational and binding states of single biomolecules can offer unique mechanistic insights into life at the molecular level but increasingly rely on statistical computing to extract quantitative and reproducible results. A simple example is super-resolved single-particle tracking (SPT) (1), in which changes in diffusion constant or between different modes of motion offer a noninvasive probe of binding and unbinding reactions in living cells (2, 3, 4).
Detecting and following single fluorophores can be challenging, and statistical methods to optimize the spot detection (5) and assembling of molecular trajectories in the presence of uncertain spot detections (6) are active research areas. Next, accurate quantitative analysis of trajectory data requires a faithful account of localization noise, which come in the form of localization errors and motion blur, sometimes referred to as “static” and “dynamic” errors, respectively (7, 8). In particular, live cell imaging often lead to heterogeneous and asymmetric localization errors, for example due to photobleaching, variability between and across cells, out-of-focus motion, or the dependence of localization errors on the diffusion constant (9, 10). Several emerging techniques for three-dimensional localization also give different precision in the axial and lateral directions (11).
A fundamental unknown in many live cell SPT studies is the number of underlying molecular states, e.g., binding states, which may differ in diffusion constant. Counting diffusive states in SPT data presents a statistical model selection problem that has so far only been solved with simplified noise models (2), which may be inappropriate in many live cell applications (10, 12).
Here, we extend our previous hidden Markov model (HMM) analysis (10) by deriving and implementing variational algorithms that increase computational speed by more than an order of magnitude, allow statistical model selection using Bayesian or information-theoretic methods, and can be generalized to a wider class of localization error models. The methods are available in a user-friendly open source software suite.
Methods
Variational diffusive HMM
The starting point for our analysis is a standard model for camera-based SPT that includes a combination of averaging (motion blur) and localization errors, in which the detected positions are related to the underlying particle trajectory through
| (1) |
Here, is the localization error (variance) in frame t, and are independent unit normal random variables. The shutter function describes how the image acquisition is distributed throughout the frame, e.g., for continuous exposure and acquisition (8).
We model the particle motion as free diffusion, with a time-dependent diffusion constant governed by a hidden Markov process with N discrete states.
For a fast variational algorithm, we seek a model in the exponential family of probability distributions (13), which yield variational algorithms of a particularly simple form that are often analytically tractable (14). This is achieved by modeling the two terms in Eq. 1 separately, i.e., keep both the true hidden path and the true exposure-averaged positions (the integral in Eq. 1) as explicit variables. In discrete time, this leads to the following model:
| (2) |
| (3) |
| (4) |
where τ and β are blur coefficients that depend on the shutter function (10). With for continuous illumination, we get and (for details, see Supporting Materials and Methods, Section S1). Position coordinates in two- or three-dimensional trajectories are treated independently, which means that we neglect possible correlations between localization errors in different directions. As detailed in Supporting Materials and Methods, this model allows variational algorithms for both maximal likelihood estimation and variational Bayes inference (VB) (13, 15). Missing positions due to, e.g., fluorophore blinking, are handled by formally setting , which eliminates contributions from Eq. 4 for those points.
Our focus in this work is the case in which the localization variances are input data estimated from the localization of single spots (10). However, one could also treat as model parameters, for example as a single average error , dependent on the hidden state , and/or varying with coordinate dimension. These modified models remain in the exponential family and thus allow similarly efficient variational algorithms that differ only in details compared to our main case.
Simulated Trajectories
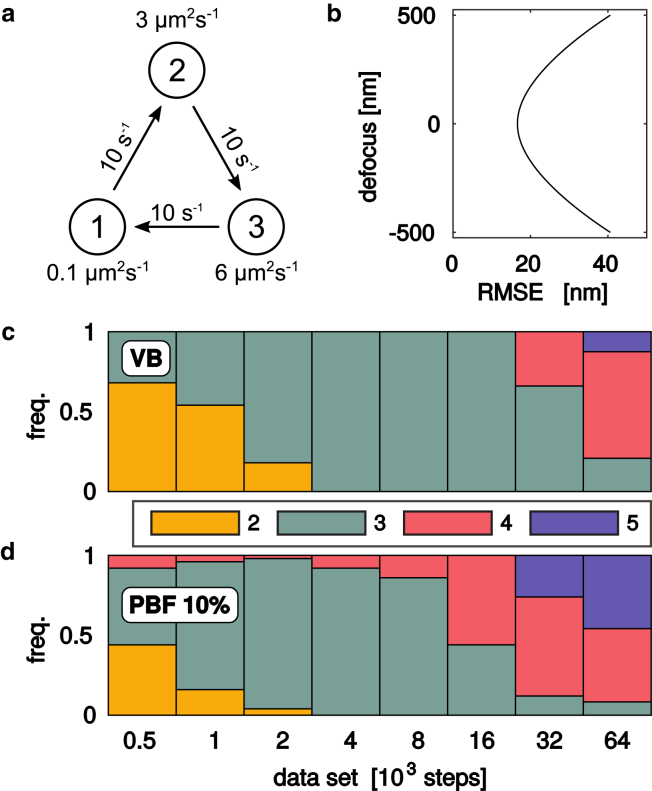
For the model selection experiments in Fig. 1 and Fig. S1, we used synthetic trajectories simulated using the analysis model, Eqs. 2, 3, and 4. We simulated a three-state model with the following parameters: diffusion constants , , and . The kinetic model is an irreversible cycle with exponentially distributed waiting times with average 100 ms (see Fig. 1 b). The positions are simulated according to Eqs. 2, 3, and 4, with time step Δt = 5 ms, and motion blur corresponding to an exposure time of (, ). Trajectories were confined to using a trajectory-wise method of images, i.e., reflecting trajectory parts outside this interval back in again ( is the z component of ).
Figure 1.
Statistical model selection. We generated a range of synthetic data sets with (a) three diffusive states and (b) defocus-dependent localization root mean-square errors, and estimated the number of states using (c) variational maximal evidence (VB), and (d) cross-validation using variational pseudo-Bayes factors using 10% of the data in the validation set (PBF 10%). For details, see Methods. To see this figure in color, go online.
For the static localization errors , we use a simple model of spot widening due to defocus (9),
| (5) |
with minimal spot width , (approximating , , in water), and . The term approximates the effect of finite pixel size (16) and the term spot-widening due to motion blur (9). We then compute for use in Eq. 4 from the approximate Cramer-Rao lower bound (16):
| (6) |
with photons per spot. This gave . Fig. 1 b shows the curve for . We analyzed the x and y components of and chose trajectory lengths to be exponentially distributed with mean length 25Δt, but discarded trajectories with length below 5Δt. For the statistical model selection study (Fig. 1; Fig. S1), we sampled data sets of various sizes (50 data sets with up to 32,000 steps, 24 data sets with 60,000 steps) from a large data set of several hundred thousand positions such that all model selection techniques used the same set of trajectories.
Simulated microscopy
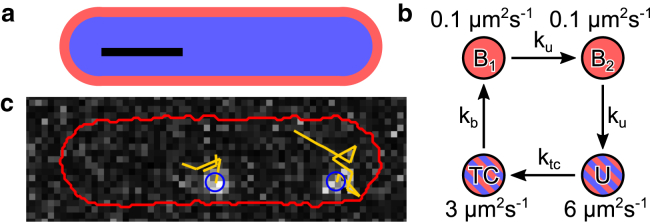
Simulated video-microscopy images for transfer-RNA (tRNA) tracking was generated using the SMeagol simulation software (12) with the spatial reaction-diffusion model illustrated in Fig. 4. We simulated uniform exposure during 1.5 of the 5 ms sampling time. Camera noise was generated using a high-gain approximation of electron-multiplying charge-coupled device noise (16) with offset 200, gain 77, and Gaussian readout noise with standard deviation 20. We used 80 nm pixels and a uniform background fluorescence that decayed from two to one photon/pixel with a decay rate of 2 . For the optics, we used a Gibson-Lanni point-spread function (PSF) model (17) generated by PSFgenerator (18) with and . This is a spherically symmetric PSF suitable for isotropic emitters or fluorophores with high rotational mobility. Fluorescent spot intensity was set to give on average of 200 photons per frame, and the average bleaching time was chosen to 20 frames. Using custom MATLAB (The MathWorks, Natick, MA) scripts, we simulated 200-frame movies with ∼30 cells spread evenly across a pixel field of view, with a few active fluorescent spots per cell. An example of one such cell is shown in Fig. 4 c.
Figure 4.
Model for simulated tracking of fluorescent tRNA molecules. (a) Shows the cross section of the simulation geometry, which consists of concentric cylinders with spherical end-caps, represents the nucleoid (blue) floating in the cytoplasm (red). Scale bars, (black) 1 μm. (b) Shows the simulated kinetic model of the tRNA cycle. Two states with low diffusion coefficients represent ribosome-bound states and are excluded from the nucleoid, whereas the unbound (U) and ternary complex (TC) states are free to roam the whole cell. (c) Shows a simulated frame with two fluorophores in a single cell, with cell outline (red) and particle tracks (yellow) added. Pixel size, 80 nm. To see this figure in color, go online.
Spot detection and localization
We use the fast radial symmetry transform (19) for spot detection and estimated spot positions and localization uncertainty using a symmetric Gaussian spot model and maximal aposteriori estimates on 9-by-9 regions of interests, as described by Lindén et al. (10). Spots with were discarded from the analysis.
Results
Model selection
The number of diffusive states is often a biological unknown of great interest, but because different numbers of diffusive states correspond to statistical models with different numbers of parameters, the counting of states is a nontrivial problem of statistical model selection.
Bayesian reasoning, including model selection, is an extension of formal logic to uncertain statements that yields unique and consistent results (20). Assuming equal prior preference for a set of candidate models with uncertain parameters and unobserved degrees of freedom (latent variables), the Bayesian approach uses marginalization to select the model with the largest (log) evidence (13, 15), which in compact notation can be written as follows:
| (7) |
Here, x denotes the observed data, M denotes the model, the latent variables (summed or integrated out as appropriate), and denotes the unknown parameters with prior distribution for the different models M.
In our case and many others, the evidence in Eq. 7 is analytically intractable, in which case a variational Bayes (VB) approximation can be an attractive approach (2, 13, 14, 15, 21, 22, 23, 24). VB yields a lower bound usable for approximate Bayesian model selection as well as approximate posterior distributions (variational distributions) of parameters and hidden states (13, 14, 15). Moreover, because it involves direct optimization of the lower bound , VB algorithms have an intrinsic parsimony that depopulates superfluous states and can be utilized for efficient greedy model search algorithms (2, 24).
However, Bayesian inference may be statistically inefficient. In particular, the common practice of using uninformative priors to minimize bias in parameter estimates means that the prior likelihood for any particular parameter value is low. This in turn can lead to overly steep penalties against models with many parameters, a phenomenon known as Lindley’s paradox, which means that an unnecessarily large amount of data is needed to resolve some feature of interest (25, 26, 27). An alternative non-Bayesian approach that avoids this difficulty is to rank competing models by their estimated predictive performance (26, 27). Next, we explore a predictive approach to model selection for SPT analysis.
The most well-known predictive performance measure is Akaike’s information criterion (AIC) (28), but this is only asymptotically valid for large data sets. For small data sets, one could instead use cross-validation, in which the data set is divided into two parts: one for estimating model parameters (“training”) and one for estimating predictive performance (“validation”). In practice, the performance is estimated from averaging over several such divisions. We implemented a variant of cross-validation with a Bayesian flavor, pseudo-Bayes factors (PBF) (27), which include prior distributions but do not suffer from Lindley’s paradox and are easy to compute with our variational algorithm (see Supporting Materials and Methods, Section S2.5).
Fig. 1 compares VB and PBF model selection on synthetic test data with three diffusive states and parameters that resemble in vivo SPT experiments in bacteria (2, 4) (see Methods). Broadly, one expects predictive model selection to avoid Lindley’s paradox and penalize complex models less severely than Bayesian methods as the amount of data increases. However, this comes at the expense of consistency, i.e., there is no guaranteed convergence to the correct model size (28, 29). These expectations are qualitatively borne out in Fig. 1, where the Bayesian VB criterion is more prone than PBF to select too few states for small data sets, but less prone to select too many states for large data sets.
There is no general rule for selecting training and validation subsets. HMMs also suffer from the additional complication that individual observations are correlated because of the hidden state dynamics, which complicates cross-validation if the data is a single trajectory (30). Here, we focus on SPT experiments that produce a large number of trajectories (2, 4) that can be used as atoms for constructing training and validation sets. Our simulated trajectories have an average length of 30, and Fig. 1 b uses randomly sampled validation sets containing ∼10% of the data. Some other choices, including AIC and the Bayesian vbSPT (VB for SPT) code (2), are explored in Fig. S1, but do not perform better.
Speedup
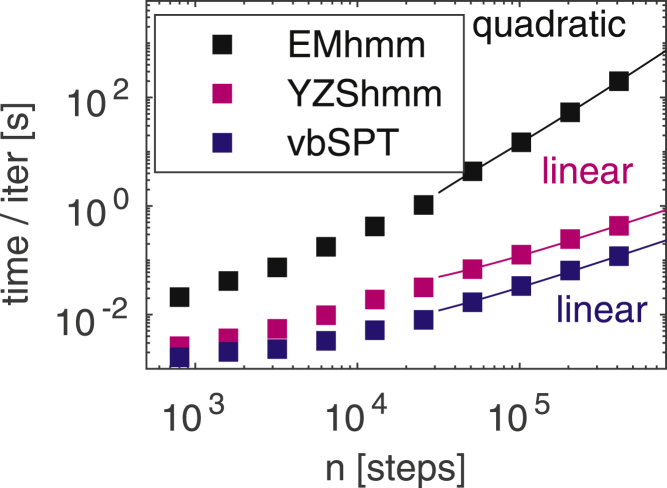
In addition to more flexibility in modeling and inference methods, the algorithms presented here are also considerably faster compared to our previous implementation (10). This is mainly because variational algorithms based on Eqs. 2, 3 and 4 are analytically tractable and hence avoid a costly numerical optimization step. However, we have also found a more efficient algorithm for partial matrix inversion (31). Fig. 2 shows the time per iteration for a three-state model on data sets of different sizes for the algorithm presented here, that of (10), and vbSPT (2). Compared to the former, we see speedups of one to two orders of magnitude for experimentally relevant data set sizes of positions as well as better scaling. However, vbSPT is faster still, which is expected because it is based on a much simpler model and thus has less to do during each iterative update.
Figure 2.
Speed of our variational algorithm (YZShmm) compared to that of Ref. (10) (EMhmm) and vbSPT (2). Time per iteration versus number of steps in the data, which has three diffusive states, was measured on a dual 6-core Intel Xeon 2.4GHz computer running MATLAB R2017a. Linear and quadratic scaling laws are guides to the eye. To see this figure in color, go online.
Finding the global optimum
Variational learning of a model and its parameters, diffusion constants, and transition rates involves finding the overall best fit to the data, but VB and other expectation-maximization-type algorithms only converge toward local optima. An additional global search is needed.
The simplest approach is to converge multiple models from different starting points. To speed things up, we use the built-in parsimony of the VB algorithms to start from complex many-state models and then systematically search for simpler ones by removing un- or low-populated states (2). However, the extra complexity of our model compared to standard HMMs (2) makes this approach more challenging to apply.
One attractive feature of our model is the ability to handle long trajectories with missing positions. However, when fitting high-dimensional models to data with missing positions, groups of superfluous states sometimes converge toward identical parameters and finite occupancy associated with the missing positions. Because this is clearly unphysical, we choose to remove such state clusters before commencing normal model pruning.
Another challenge is related to the presence of two types of latent variables for the discrete diffusive states and uncertainty in true particle positions , respectively. Although hard to quantify, it seems reasonable to expect more latent variables to yield a more complex search landscape, with more local optima for the search to get trapped in compared to ordinary HMMs in which the particle positions are not latent variables (2). More concretely, the variational treatment uses a threefold factorization ansatz (parameters, hidden states, and hidden particle trajectories), and to initialize the local optimization iterations, two of three factors need to be initialized.
We use randomly selected parameter values and explore different strategies to initialize either hidden states or hidden trajectories: uniform hidden state occupancy, hidden trajectories modeled directly on observed data (with no uncertainty or correlations between and ), and hidden trajectory models generated by a running average in which a pure diffusion model is fit to small windows of various lengths. In our testing, different methods perform best on different types of data, meaning that a wide range of initialization methods are needed to maximize the chance of finding the global optimum.
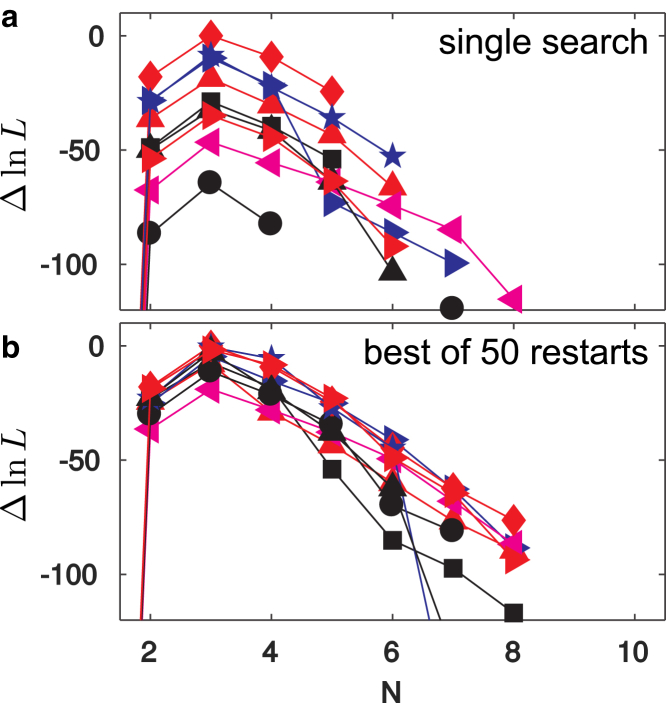
Fig. 3 shows an analysis of a data set from simulated images (see Methods) using 50 independent initializations of model parameters with 15 states and 10 different initializations of latent variables with each parameter set. Fig. 3 a shows the lower bounds of models originating from a single initial parameter set, with each line corresponding to models generated by the reductive search starting from one latent variable initialization. We see that the initialization with the largest number of nonspurious states does not lead to the best overall model, and that the search lines sometimes cross, meaning that relative ranking among the different reduction searches can change as states are removed. Looking at the best models from 50 independent parameter initializations (Fig. 3 b), we again see search lines crossing and note that the two highest-ranked model sizes originate from different initialization methods.
Figure 3.
Model search with different initialization strategies. Each color/marker combination shows the relative lower bound from the best model of each size for different initialization strategies. (a) Model search from a single parameter initialization is shown. (b) The best models from 50 independent initializations are shown. To see this figure in color, go online.
Application: simulated tRNA tracking
Quantitative live cell SPT is complex, and errors may arise during measurement, spot detection, localization, trajectory building, and trajectory analysis. Comprehensive tests of the whole analysis chain are needed to validate quantitative interpretations of the experiments under particular conditions. To evaluate the capabilities of our trajectory analysis only, we seek test data with known ground truth and sufficient realism to be experimentally relevant. We use simulated video microscopy (12) to produce realistic test data and run spot detection and localization using our standard methods (see Methods) but use our knowledge of the simulated ground truth to produce trajectories free from false positives and linking errors that may lead to bad performance that does not reflect the intrinsic quality of the trajectory analysis. We allow at most three consecutive missing positions before starting a new trajectory.
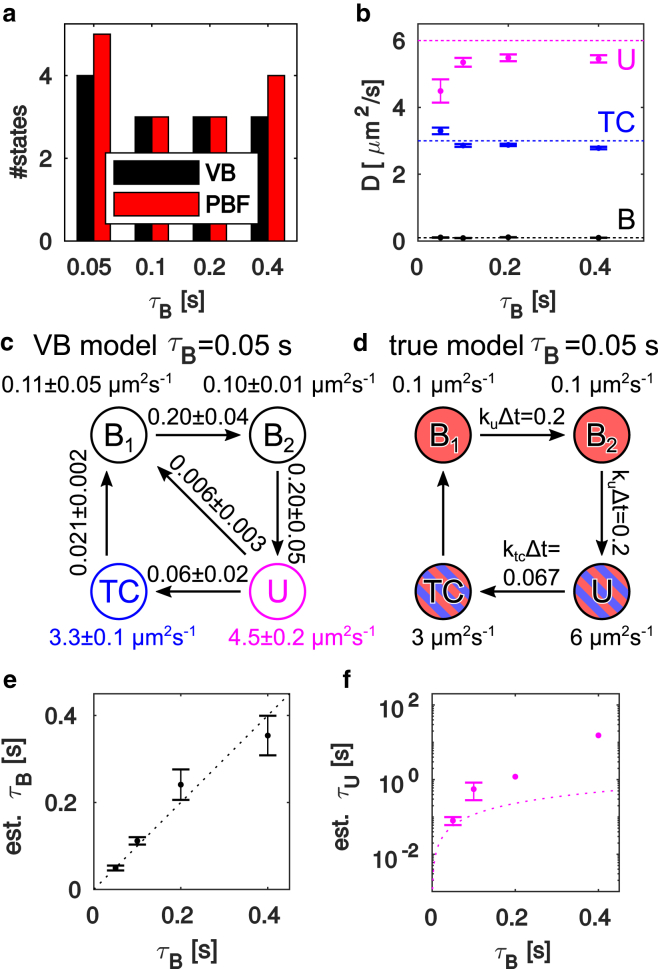
As a test problem, we consider tracking tRNA molecules in Escherichia coli cells (4, 32) (see Fig. 4), which presents several interesting difficulties. At least three discernible diffusive states may be expected: a ribosome-bound state (B, slow diffusion), an unbound state (U, fast diffusion), and a ternary complex (TC, intermediate diffusion). The ribosome-bound state further displays spatial structure in the form of nucleoid exclusion (32) as well as nonexponential waiting times (33) because tRNA goes through several reaction steps before dissociating from the ribosome (34). We constructed a simplified kinetic and spatial model incorporating these features and generated synthetic fluorescent microscopy data with a 200 Hz frame rate (12) (see Methods). We simulated a range of rate constants corresponding to a total bound state mean dwell time of between 50 and 400 ms, whereas the steady-state occupancy is kept fixed at (B/U/TC).
Not all estimated parameters have direct simulated counterparts. For example, nucleoid exclusion means that the reaction cannot take place in the nucleoid region, lowering the effective value of . Nucleoid exclusion also distorts the state occupancy of the detected spot population because defocused spots are more difficult to detect, and with our simulated focus in the cell midplane, the bound states are relatively enriched in defocused regions (4). Fig. 5 shows comparisons in which these complications are minimal, which means that we ignore overall occupancy and transitions out of the TC state.
Figure 5.
Analysis of simulated microscopy data. The different ground truth models are denoted by their total bound state dwell times: , , , and , respectively. (a) Shows the number of states selected by the VB and PBF criteria. (b) Shows diffusion coefficients for the VB-selected models. Dashed colored lines indicate the true diffusion constants of the U, TC, and states. For the model, two states near 0.1 μ are found. (c) VB-estimated parameters and (d) ground truth parameters of the four-state model are shown with transition probabilities per time step below suppressed. States are named and colored according to the obvious similarity with the true scheme in (c). (e) Bound and (f) unbound state mean dwell times, computed from the transition probability matrix. For the model, we added the dwell times of the two B states. Dashed lines indicate the true mean dwell times. Error bars indicate bootstrap SEs. In (f), missing error bars indicate where not all bootstrap replicas gave finite mean dwell times. All data sets contain ∼16,000 steps. To see this figure in color, go online.
The true model contains three diffusion constants but four kinetic states. Starting with the number of states (Fig. 5 a), we see mostly three states and note that the VB and PBF model selection agree half the time and that the PBF favors more states in cases of disagreement. Plotting the diffusion constants from VB-selected models (Fig. 5 b), we see that it finds diffusion constants close to the true values, although for the fastest kinetics , the high-D states are biased toward each other, probably because the faster dynamics produces more short events that make it more difficult for the HMM to distinguish the two fast states correctly. There is also a general downward bias in the highest diffusion constant, most likely a confinement artifact (see Fig. S2).
Regarding the kinetics, a detailed look at the four-state model for the fastest kinetics (Fig. 5 c) shows a striking resemblance to the true rate model in Fig. 5 d. The unidirectional cycle is clearly visible in the estimated parameters, and the transition probabilities corresponding to and closely resemble the underlying ground truth. The mean dwell times of this model are comparable to the average trajectory length of ∼0.12 s. For models with slower kinetics, the bound state dwell time is well captured (Fig. 5 e, black), but otherwise, the kinetics is not as well reproduced. Only one bound state is identified, the unbound dwell times (Fig. 5 f) are not close to the true values, and the transition matrices (data not shown) do not resemble the cyclic pattern of the underlying model. However, even the more limited ability to measure the mean dwell time of a slow or immobile state when that dwell time exceeds the average trajectory length could be of biological interest, for example to study the interactions of small molecules such as tRNA or proteins interacting with larger structures such as ribosomes or DNA (4).
Discussion
Together with methods to extract both positions and position uncertainty from images of single spots (10), the variational algorithm we present here makes it possible to significantly decrease analysis artifacts associated with variable localization quality due to, for example, out-of-focus motion, gradual bleaching or stage drift, or fast fluorophore blinking. We are curious to see how these tools will help researchers make more nuanced interpretations of their in vivo SPT data.
Compared to our previous implementation (10), the algorithms presented here are significantly faster and support maximal likelihood as well as VB inference. This makes exploratory analysis of large data sets practical and allows a more comprehensive statistical analysis. We compared model selection by the purely Bayesian VB approach (14, 15) to two methods based on predictive performance, the AIC (28), and a variational implementation of cross-validation using PBFs (27). Although no method avoided overfitting completely in our challenging synthetic data set, VB overfitted the least, and we recommend that for applications.
However, in light of the theoretical arguments against a purely Bayesian approach for some model selection problems (25, 26), we think the non-Bayesian methods merit further study. For example, corrections to AIC have been derived for Markov switching regression models (35) and might be generalized to our class of HMMs as well. It is also possible that the PBFs would perform better when evaluated with Monte Carlo methods (27) than with the variational approximations we used here.
There are many interesting directions to further optimize and expand these types of analysis and algorithms.
The complex statistical model used here makes it possible to tackle complex data but computationally difficult to find the globally best model. We use a brute force approach with randomly initialized greedy search for easy parallelization. This is computationally costly, and the total analysis time with our code can be 10–100 times slower than a simplified analysis with vbSPT (2) on the same trajectory set. More sophisticated global optimization schemes in which the different search processes communicate may be more efficient, for example by avoiding redundant efforts when multiple initializations converge to the same model.
Another interesting direction for further development may be to incorporate other types of heterogeneity, such as variability in the underlying diffusion constants or other model parameters (23) or explicit models of spatial structure (36).
Third, more complex motion or kinetic models could be used. Our diffusive HMM may be extended in several useful ways within the exponential family of models that enable efficient variational algorithms (14); localization errors could be treated as model parameters rather than external observations, possibly depending on the chemical state or coordinate dimension (see Supporting Materials and Methods, Section S5). There are also combinations of directed motion and confinement in harmonic potentials that still lead to Gaussian motion models (3, 37). Introducing explicit termination rates could correct bias that arises from correlations between chemical states and trajectory termination (38), for example when fast-diffusing molecules move out of focus faster than slow-diffusing ones (39).
Software
Our algorithms are freely available as open source MATLAB code from https://github.com/bmelinden/vbSPTu. The vbSPTu software suite includes a GUI to run a simple standard analysis, support for scripting large analysis tasks, and low-level tools for creating customized analysis.
Author Contributions
M.L. and J.E. planned the research and wrote the article. M.L. designed and implemented the analysis methods and generated and analyzed the data.
Acknowledgments
We are grateful to Ivan Volkov, Magnus Johansson, Elias Amselem, David Fange, and members of the Elf laboratory for sharing their insight on imaging and SPT and to Irmeli Barkefors for constructive comments on drafts of the article.
This project was funded by grants to J.E. from the Knut and Alice Wallenberg Foundation and the European Research Council (ERC-2013-CoG 616047 SMILE).
Editor: Antoine van Oijen.
Footnotes
Supporting Materials and Methods and two figures are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(18)30665-9.
Contributor Information
Martin Lindén, Email: martin.linden@icm.uu.se.
Johan Elf, Email: johan.elf@icm.uu.se.
Supporting Material
References
- 1.Manley S., Gillette J.M., Lippincott-Schwartz J. High-density mapping of single-molecule trajectories with photoactivated localization microscopy. Nat. Methods. 2008;5:155–157. doi: 10.1038/nmeth.1176. [DOI] [PubMed] [Google Scholar]
- 2.Persson F., Lindén M., Elf J. Extracting intracellular diffusive states and transition rates from single-molecule tracking data. Nat. Methods. 2013;10:265–269. doi: 10.1038/nmeth.2367. [DOI] [PubMed] [Google Scholar]
- 3.Monnier N., Barry Z., Bathe M. Inferring transient particle transport dynamics in live cells. Nat. Methods. 2015;12:838–840. doi: 10.1038/nmeth.3483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Volkov I.L., Lindén M., Johansson M. tRNA tracking for direct measurements of protein synthesis kinetics in live cells. Nat. Chem. Biol. 2018;14:618–626. doi: 10.1038/s41589-018-0063-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Smith C.S., Stallinga S., Grunwald D. Probability-based particle detection that enables threshold-free and robust in vivo single-molecule tracking. Mol. Biol. Cell. 2015;26:4057–4062. doi: 10.1091/mbc.E15-06-0448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chenouard N., Bloch I., Olivo-Marin J.C. Multiple hypothesis tracking for cluttered biological image sequences. IEEE Trans. Pattern Anal. Mach. Intell. 2013;35:2736–3750. doi: 10.1109/TPAMI.2013.97. [DOI] [PubMed] [Google Scholar]
- 7.Savin T., Doyle P.S. Static and dynamic errors in particle tracking microrheology. Biophys. J. 2005;88:623–638. doi: 10.1529/biophysj.104.042457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Berglund A.J. Statistics of camera-based single-particle tracking. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010;82:011917. doi: 10.1103/PhysRevE.82.011917. [DOI] [PubMed] [Google Scholar]
- 9.Deschout H., Neyts K., Braeckmans K. The influence of movement on the localization precision of sub-resolution particles in fluorescence microscopy. J. Biophotonics. 2012;5:97–109. doi: 10.1002/jbio.201100078. [DOI] [PubMed] [Google Scholar]
- 10.Lindén M., Ćurić V., Elf J. Pointwise error estimates in localization microscopy. Nat. Commun. 2017;8:15115. doi: 10.1038/ncomms15115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rieger B., Stallinga S. The lateral and axial localization uncertainty in super-resolution light microscopy. ChemPhysChem. 2014;15:664–670. doi: 10.1002/cphc.201300711. [DOI] [PubMed] [Google Scholar]
- 12.Lindén M., Ćurić V., Elf J. Simulated single molecule microscopy with SMeagol. Bioinformatics. 2016;32:2394–2395. doi: 10.1093/bioinformatics/btw109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bishop C. Springer; New York: 2006. Pattern Recognition and Machine Learning. [Google Scholar]
- 14.Beal M. University of Cambridge; 2003. Variational algorithms for approximate Bayesian inference. PhD thesis. [Google Scholar]
- 15.MacKay D. Cambridge University Press; Cambridge, United Kingdom: 2003. Information Theory, Inference, and Learning Algorithms. [Google Scholar]
- 16.Mortensen K.I., Churchman L.S., Flyvbjerg H. Optimized localization analysis for single-molecule tracking and super-resolution microscopy. Nat. Methods. 2010;7:377–381. doi: 10.1038/nmeth.1447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gibson S.F., Lanni F. Experimental test of an analytical model of aberration in an oil-immersion objective lens used in three-dimensional light microscopy. J. Opt. Soc. Am. A. 1992;9:154–166. doi: 10.1364/josaa.9.000154. [DOI] [PubMed] [Google Scholar]
- 18.Kirshner H., Aguet F., Unser M. 3-D PSF fitting for fluorescence microscopy: implementation and localization application. J. Microsc. 2013;249:13–25. doi: 10.1111/j.1365-2818.2012.03675.x. [DOI] [PubMed] [Google Scholar]
- 19.Loy G., Zelinsky A. Fast radial symmetry for detecting points of interest. IEEE Trans. Pattern Anal. Mach. Intell. 2003;25:959–973. [Google Scholar]
- 20.Cox R.T. Probability, frequency and reasonable expectation. Am. J. Phys. 1946;14:1–13. [Google Scholar]
- 21.Bronson J.E., Fei J., Wiggins C.H. Learning rates and states from biophysical time series: a Bayesian approach to model selection and single-molecule FRET data. Biophys. J. 2009;97:3196–3205. doi: 10.1016/j.bpj.2009.09.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Okamoto K., Sako Y. Variational Bayes analysis of a photon-based hidden Markov model for single-molecule FRET trajectories. Biophys. J. 2012;103:1315–1324. doi: 10.1016/j.bpj.2012.07.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.van de Meent J.W., Bronson J.E., Gonzalez R.L., Jr. Empirical Bayes methods enable advanced population-level analyses of single-molecule FRET experiments. Biophys. J. 2014;106:1327–1337. doi: 10.1016/j.bpj.2013.12.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Johnson S., van de Meent J.W., Lindén M. Multiple LacI-mediated loops revealed by Bayesian statistics and tethered particle motion. Nucleic Acids Res. 2014;42:10265–10277. doi: 10.1093/nar/gku563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Cousins R.D. The Jeffreys-Lindley paradox and discovery criteria in high energy physics. Synthese. 2017;194:395–432. [Google Scholar]
- 26.LaMont C.H., Wiggins P.A. The Lindley paradox: The loss of resolution in Bayesian inference. arXiv. 2016 https://arxiv.org/abs/1610.09433 arXiv:1610.09433. [Google Scholar]
- 27.Gelfand A.E., Dey D.K. Bayesian model choice: Asymptotics and exact calculations. J. Roy. Stat. Soc. B Met. 1994;56:501–514. [Google Scholar]
- 28.Burnham K.P., Anderson D.R. Springer; New York: 2013. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. [Google Scholar]
- 29.Shao J. Linear model selection by cross-validation. J. Am. Stat. Assoc. 1993;88:486–494. [Google Scholar]
- 30.Celeux G., Durand J.-B. Selecting hidden Markov model state number with cross-validated likelihood. Comput. Stat. 2008;23:541–564. [Google Scholar]
- 31.Meurant G. A review on the inverse of symmetric tridiagonal and block tridiagonal matrices. SIAM J. Matrix Anal. Appl. 1992;13:707–728. [Google Scholar]
- 32.Plochowietz A., Farrell I., Kapanidis A.N. In vivo single-RNA tracking shows that most tRNA diffuses freely in live bacteria. Nucleic Acids Res. 2017;45:926–937. doi: 10.1093/nar/gkw787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kienker P. Equivalence of aggregated Markov models of ion-channel gating. Proc. R. Soc. Lond. B Biol. Sci. 1989;236:269–309. doi: 10.1098/rspb.1989.0024. [DOI] [PubMed] [Google Scholar]
- 34.Steitz T.A. A structural understanding of the dynamic ribosome machine. Nat. Rev. Mol. Cell Biol. 2008;9:242–253. doi: 10.1038/nrm2352. [DOI] [PubMed] [Google Scholar]
- 35.Smith A., Naik P.A., Tsai C.-L. Markov-switching model selection using Kullback-Leibler divergence. J. Econom. 2006;134:553–577. [Google Scholar]
- 36.El Beheiry M., Türkcan S., Masson J.B. A primer on the Bayesian approach to high-density single-molecule trajectories analysis. Biophys. J. 2016;110:1209–1215. doi: 10.1016/j.bpj.2016.01.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Calderon C.P. Motion blur filtering: a statistical approach for extracting confinement forces and diffusivity from a single blurred trajectory. Phys. Rev. E. 2016;93:053303. doi: 10.1103/PhysRevE.93.053303. [DOI] [PubMed] [Google Scholar]
- 38.Kolomeisky A.B., Fisher M.E. Periodic sequential kinetic models with jumping, branching and deaths. Physica A. 2000;279:1–20. [Google Scholar]
- 39.Kues T., Kubitscheck U. Single molecule motion perpendicular to the focal plane of a microscope: application to splicing factor dynamics within the cell nucleus. Single Mol. 2002;3:218–224. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.