The Role of the Size and Location of the Tumors and of the Vertebral Anatomy in Determining the Structural Stability of the Metastatically Involved Spine: a Finite Element Study

Abstract

Vertebral fractures associated with the loss of structural integrity of neoplastic vertebrae are common, and determined to the deterioration of the bone quality in the lesion area. The prediction of the fracture risk in metastatically involved spines can guide in deciding if preventive solutions, such as medical prophylaxis, bracing, or surgery are indicated for the patient. In this study, finite element models of 22 thoracolumbar vertebrae were built based on CT scans of three spines, covering a wide spectrum of possible clinical scenarios in terms of age, bone quality and degenerative features, taking into account the local material properties of bone tissue. Simulations were performed in order to investigate the effect of the size and location of the tumoral lesion, the bone quality and the vertebral level in determining the structural stability of the neoplastic vertebrae. Tumors with random size and positions were added to the models, for a total of 660 simulations in which a compressive load was simulated. Results highlighted the fundamental role of the tumor size, whereas the other parameters had a lower, but non-negligible impact on the axial collapse of the vertebra, the vertebral bulge in the transverse plane and the canal narrowing under the application of the load. All the considered parameters are radiologically measurable, and can therefore be translated in a straightforward way to the clinical practice to support decisions about preventive treatment of metastatic fractures.

Introduction

Although primary spinal tumors are relatively rare [1], the spine frequently hosts metastases originating from breast, kidney, prostate and lung cancers [2], [3]. These lesions are often lytic, and preferentially located in the vertebral bodies rather than in the posterior elements. Vertebral fractures associated with the loss of structural integrity of the metastatically involved vertebrae are common, and determined to the deterioration of the bone quality in the area affected by the lesion [4], [5]. Considering the generally poor health status of these patients and the fact that factors such as cancer type and survival prognosis are often more critical than the purely orthopedic aspects, the clinical management of the increased risk of vertebral fractures can be highly problematic and is sometimes inevitably deemed as of a secondary importance [2]. It should however be noted that a vertebral fracture in a neoplastic spine, which forces the patient to bed rest and further aggravates the pain, can sometimes be the last straw and have catastrophic consequences.

The prediction of the fracture risk for each specific patient therefore gains a huge clinical relevance. Knowing that a patient may suffer from a vertebral collapse in the short term can guide the oncologist and the orthopedic specialist in deciding if preventive solutions, such as medical prophylaxis, bracing, or surgery are indicated for the patient. In the clinical practice, scoring systems such as the Spinal Instability Neoplastic Score (SINS) are used to determine the risk of fracture [6], [7], [8]. This system considers various factors, such as the size and location of the lesion in the vertebra, the region of the spine in which it is situated, the spinal alignment, and the presence of pre-existing fractures to define a score indicating the risk of vertebral fracture. These scores have been built based on previous clinical observations and descriptive studies [5] and are therefore limited in their scope to a qualitative and inherently imprecise evaluation. To improve the reliability of a scoring system, in terms of increasing its sensitivity and specificity in discriminating the high-risk cases, quantitative methods able to calculate the structural integrity of the spine in a wide scenario of neoplastic conditions should be leveraged.

The finite element (FE) method is an engineering tool of choice for the investigation of the effect of parameters related to the geometry and to the material properties, and proved to be effective for the determination of the mechanical role of tumor size and location as well as loading magnitude and speed in increasing the risk of vertebral fractures [5]. Finite element models of both thoracic [9], [10] and lumbar vertebrae [11] incorporating tumoral lesions have been developed, and were used as basis to create guideline equations for the calculation of the risk of fracture based on radiological parameters such as lesion size, bone density, involvement of pedicles and disc degeneration [12], [13]. These previous finite element studies have contributed a lot for the scientific value and clinical relevance. Nevertheless, the models used to build the equations were based on oversimplified, non-realistic anatomies and material properties, and did therefore not cover a wide spectrum of possible conditions of neoplastic spines. There is still a need for more anatomically realistic models, covering various vertebral levels and a wide range of bone material properties.

In this work, finite element models of a large number of metastatically involved vertebrae were built based on CT scans of real patients taking into account the local material properties of bone tissue, rather than simplified anatomies generated by means of parametric models. The aim of the study was to investigate the effect of several parameters such as the size and location of the tumoral lesion, the bone quality and the vertebral level in determining the structural stability of neoplastic vertebrae in the thoracolumbar spine.

Materials and Methods

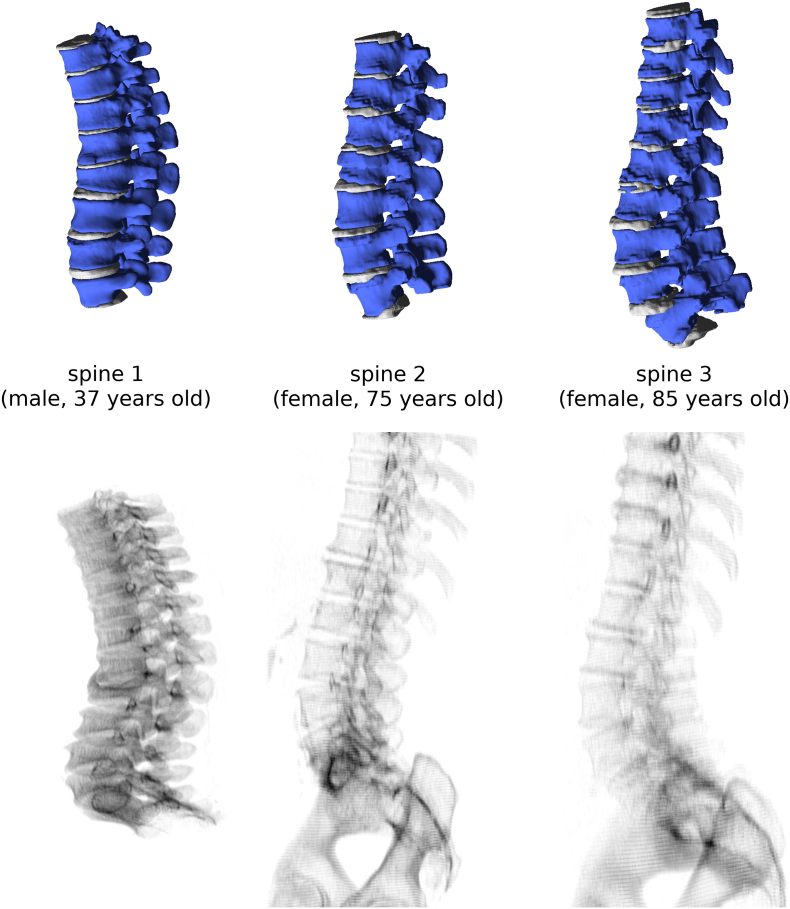
One CT scan of a thoracolumbar specimen harvested from a 37 years old male donor was used as a basis to create models of vertebrae with relatively good bone quality and no pathological anatomy (“spine 1”). Besides, two CT scans of the thoracolumbar spine of older patients have been selected from the image database of IRCCS Istituto Ortopedico Galeazzi in order to cover a wide range of age, degenerative features and bone quality. Two distinct CT scanners from the same manufacturer (SOMATOM, Siemens AG, Erlangen, Germany) were used for imaging. These two subjects were female, 75 (“spine 2”) and 85 (“spine 3”) years old respectively and had poorer bone quality. From the three scans, the regions T10-L5, T11-L4 and T9-L5 were respectively modeled, for a total of 23 vertebrae (Figure 1). Since the L1 vertebra of the third spine (“spine 3”) showed degenerative features which resulted in numerical issues and lack of convergence of the finite element models, it was not included in the subsequent data analysis, thus reducing the total number of modeled vertebrae to 22. Segmentation of vertebrae and intervertebral discs was manually performed by means of in-house C++ software implementing a threshold filter, automated removal of isolated voxels and manual editing of the selections, and then three-dimensionally reconstructed by using the marching cubes algorithm [14].

Figure 1.

Three-dimensional reconstructions (first row) and simulated planar X-rays images (second row) of the three spines used to build the finite element models.

Pre-processing of the finite element models was conducted with in-house C++ software based on the QT library (https://www.qt.io) for the graphical user interface and on the GNU Triangulated Surface (http://gts.sourceforge.net/) library for the creation and editing of the three-dimensional surfaces. In synthesis, the developed piece of software allowed for isolating each single vertebra in the reconstructed anatomy and building a series of finite element models in which tumoral lesions with random sizes were artificially added in random locations in the vertebral body (Figure 2). Only the bone and the tumoral tissue were modeled, whereas all soft tissues were neglected in the current implementation. Automated tetrahedral meshing was performed using TetGen software (http://wias-berlin.de/software/tetgen/). For each element, location-specific bone properties were assigned based on the CT number of the voxel closest to the element centroid, according to the relation [15]:

$$E=-94+6.68\mathit{CT}\#$$ (1)

where E is the elastic modulus (MPa) and CT# is the CT number in Hounsfield units. For each vertebra, the surfaces of the endplates, which were then used for the application of the boundary and loading conditions, were automatically defined as those contacting the intervertebral discs in the CT scans. A specific graphical user interface was designed to manually define the cranio-caudal direction for each vertebra, which should follow the curvature of the spine, as well as the antero-posterior and latero-lateral axes (Figure 2). The origin of the coordinate system was set in the center of the vertebral body.

Figure 2.

Exemplary finite element models of the same vertebra (L4 of “spine 1”) in which a tumoral lesion has been added (highlighted in red). For each model, the tumoral size (in mm, cm³ and in percentage of the volume of the vertebral body) as well as the coordinates of the centroid (in mm) with respect to the center of the vertebral body are reported. In the model in the top left corner, loading and boundary conditions are shown.

A distributed compressive load of 1200 N [11], which represents a worst-case scenario exceeding the physiological load in the standing posture [16], was applied to the cranial endplate surface. Nodes belonging to the caudal endplate were fixed in all directions (Figure 2). The average cranio-caudal displacement of the nodes belonging to the cranial endplate was considered as the output of the simulation and used for data analysis. Furthermore, two other outputs related to the vertebral deformation under load were calculated: (1) vertebral bulge, corresponding to the radial displacement of the vertebral body in the antero-posterior direction at the transverse midline; (2) load-induced canal narrowing (LICN), i.e. the change in canal diameter as the applied load increased by 50% from 800 to 1200 N [11], as an indicator of the risk of neurologic compromise.

For each vertebral finite element model, 30 models including tumoral lesions with random size and locations were automatically created (Figure 2). A pseudo-spherical shape was assumed for all lesions. First, a random position of the tumor centroid inside the vertebral body, therefore excluding pedicles and posterior elements, was selected by using the implementation of the random number generation in a uniform distribution included in the Boost C++ libraries (http://www.boost.org). Then, a tumor radius ranging from 2 to 20 mm was randomly generated for each of the 30 models. To represent the tumor in the finite element models, all elements the centroid of which had a distance from the tumor centroid smaller than the selected radius were reassigned to the tumor, and their material properties modified to represent a highly hydrated material with low compressibility and stiffness. Indeed, an elastic modulus of 1 MPa and a Poisson's ratio of 0.45, which result in an aggregate modulus matching the one measured in experimental compressive testing of metastatic lytic material [17], were assumed.

Considering that 30 models incorporating tumors were built of each of the 22 vertebrae, 660 simulations were run in total. ABAQUS 6.14 (Dassault Systèmes Simulia Corp., Johnston, RI, USA) in its implicit formulation was employed to conduct the simulation. Custom Python scripts were developed to run batch simulations as well as to automatically extract and plot the results of interest.

In order to determine the relevance of the various features (tumor size and position, bone quality, vertebral level) in determining axial displacement, vertebral bulge and LICN, the predictions of the finite element models were further processed to build a Gradient Boosting regression model [18], [19], by using the implementation available in Scikit-learn [20]. The importance of each feature, relative to that of the feature which resulted as the most important one, was then calculated for the three individual spines as well as for the three spines altogether, by means of the appropriate function of Scikit-learn.

Results

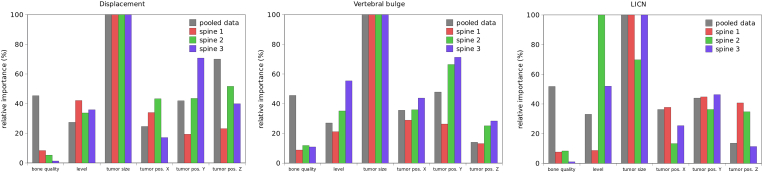
FE simulations revealed that, among the considered features, the most important predictor of the loss of structural stability was the size of the tumoral lesion (Figure 3), whereas the other features had a relatively similar importance. In general, bone quality seemed to be marginally more relevant than the tumor position and the vertebral level. The importance of bone quality emerged only when the results of all three spines were pooled, since the low variability of bone mineral density among the various vertebrae of each individual spine did not determine marked differences in the results. The cranio-caudal position of the tumor was more important than its latero-lateral and antero-posterior position in determining the average axial displacement, but was less critical for the vertebral bulge and LICN. Interestingly, the vertebral level had a relatively low importance for the axial displacement and vertebral bulge, but was determinant for LICN, especially for “spine 2” and “spine 3”.

Figure 3.

Relative importance of the various features (bone quality, vertebral level, tumor size, the coordinates of the tumor centroid (“tumor pos. X”, “tumor pos. Y” and “tumor pos. Z”) in determining average axial displacement (left), vertebral bulge (center) and LICN (right). In all charts, the importance calculated for the three individual spines as well as for the pooled data of all spines is shown.

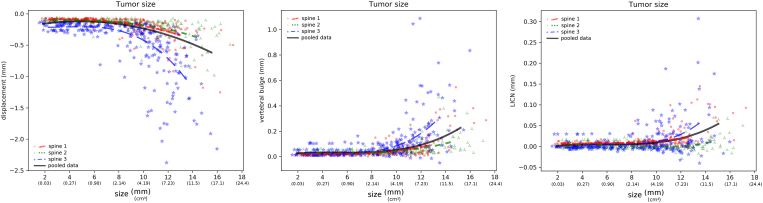
As expected, larger lesions induced higher collapse under compression load (Figure 4). In average, vertebrae with lesions greater than 12 mm yielded a compressive displacement around 0.5 mm, corresponding approximately to an 8-fold increase with respect to the displacement calculated for the same vertebrae without lesions. “Spine 1” and “spine 2” showed a similar behavior, with more than 90% of the models resulting in average compressive displacements lower than 0.5 mm. Interestingly, although “spine 2” had a generally lower bone mineral density than “spine 1”, its response resulted slightly less sensitive to the size of the lesion with respect to “spine 2”. “Spine 3” showed an abrupt increase of the compressive displacement for larger lesions, with average values for lesions with size 12 mm of 0.75 mm. Similar patterns emerged from the analysis of the vertebral bulge and LICN (Figure 3), in which “spine 3” yielded higher deformations. Interestingly, LICN predicted by “spine 1” was in general markedly higher than that of “spine 2”, with extreme values exceeding in some cases 0.05 mm.

Figure 4.

Effect of the tumor size in determining average axial displacement (left), vertebral bulge (center) and LICN (right). In all charts, the results of all simulations of the three individual spines as well as regression lines for each spine and for the pooled data of all spines are shown.

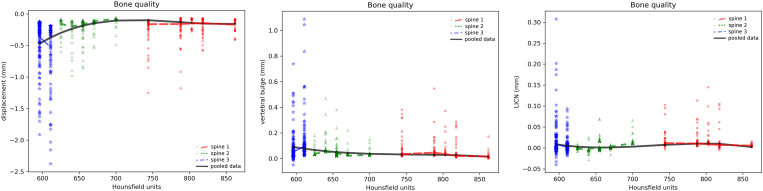
Lower bone quality, as expressed by the average Hounsfield number in the vertebral body, was associated with higher compressive displacements, vertebral bulge and LICN (Figure 5). This finding was particularly evident for “spine 3”, whereas the vertebrae from the other two spines showed again a similar response. A 6-fold difference between the compressive displacement of the models with the lowest bone mineral densities and those with good bone quality was predicted.

Figure 5.

Effect of the bone quality (in average Hounsfield units for each vertebra) in determining average axial displacement (left), vertebral bulge (center) and LICN (right). In all charts, the results of all simulations of the three individual spines as well as regression lines for each spine and for the pooled data of all spines are shown.

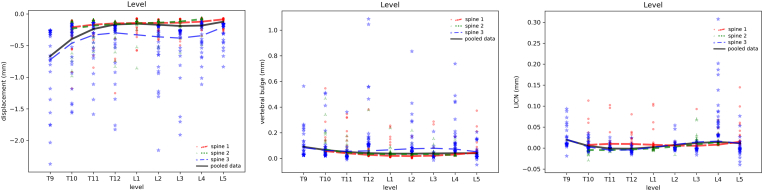
In general, the axial displacement of thoracic vertebrae resulted to be more sensitive to the presence of tumoral lesions with respect to lumbar ones, with a trend towards an increase of the compressibility for the higher levels (Figure 6). However, it should be noted that only the degenerative “spine 3” included T9, whereas “spine 1 and “spine 2″ were limited to T10, thus impacting the results in the most cranial region modeled. However, “spine 1″ showed also a tendency towards higher compressive displacements in the thoracic region, with an average 70% increase for T10 with respect to L1. All spines showed a tendency towards lower displacements proceeding from L3 to L4 and L5, likely reflecting the increase of the vertebral size in the caudal direction. Only marginal differences were predicted among the various vertebral levels in terms of vertebral bulge and LICN.

Figure 6.

Effect of the vertebral level in determining average axial displacement (left), vertebral bulge (center) and LICN (right). In all charts, the results of all simulations of the three individual spines as well as regression lines for each spine and for the pooled data of all spines are shown.

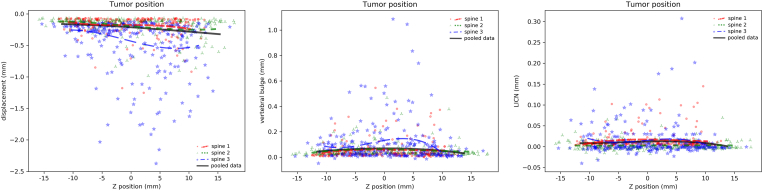
Although the tumor position resulted to be a relatively important predictor of the structural response of the vertebral, no clear trends emerged from the analysis of the results (Figure 7 and Supplementary Material). Indeed, the involvement of the anterior or posterior cortical walls did not result in a significant decrease of the structural stability of the vertebra. Vertebral bulge resulted marginally higher when the tumor was located in proximity of the center of the vertebral body. The only direction determining a marginal impact on the axial displacements was the cranio-caudal one: especially for “spine 1” and “spine 2”, a more caudal position of the lesion in the vertebral body determined a minor increase in the average collapse in compression (Figure 7).

Figure 7.

Effect of the Z coordinate of the position of the tumor centroid in determining average axial displacement (left), vertebral bulge (center) and LICN (right). In all charts, the results of all simulations of the three individual spines as well as regression lines for each spine and for the pooled data of all spines are shown.

Discussion

In this study, the effect of parameters such as the size of the tumoral lesion, its location inside the vertebral body as well as in the spine, and bone quality on the structural stability of metastatically involved vertebrae was quantified by means of finite element modeling. Results highlighted the fundamental role of the tumor size, whereas the other parameters had a lower, but non-negligible impact on the axial compression, the vertebral bulge and the canal narrowing. Noteworthy, all these parameters are radiologically measurable, and can therefore be translated in a straightforward way to the clinical practice to support decisions about preventive treatment of metastatic fractures.

In general, the predictions of the models were in good agreement with available results. Previous studies concluded that the size of the tumor has a critical importance in determining the mechanical response of the vertebrae under compression loads [11], in terms of axial collapse and deformation in the transverse plane. In a combined experimental-numerical study [11], Whyne and coworkers measured a LICN of 0.12 ± 0.088 mm under the application of an impact load of 1200 N, and of 0.0506 ± 0.0502 mm when the load increased from 800 to 1200 N, in 12 human specimens in which a tumoral lesion was artificially created. In the same study, the authors reported the experimental LICN versus bone mineral density (BMD), which resulted to vary between 0.2 mm for a low-quality bone having BMD of 0.4 g/cm², to 0.02–0.05 mm for a BMD higher than 0.6 g/cm². Even taking into account the differences in the loading conditions, the experimental measurements fall in the range of the current predictions shown in Figure 4, Figure 5. The relatively high importance predicted for bone quality and tumor size agreed with previous radiological and clinical studies [21].

With respect to the available literature, the current study introduces for the first time the simulation of patient-specific anatomies and local mechanical properties, which are critical in order to cover the wide spectrum of clinical scenarios associated with the high variability of age and clinical conditions among the affected subjects [22]. The simulation of a large number of vertebrae, and of 30 neoplastic models of each considered vertebra, further strengthened the generality and clinical applicability of the present results. Besides, since the random-generated location of the tumor could potentially cover any part of the vertebral body, a detailed investigation of the effect of the tumor location could be performed. In previous studies, the tumor had either a fixed location in the center of the vertebra [11] or in a pre-determined, limited set of possible locations in the trabecular core [10] and with involvement of the vertebral cortex [9]. It should be noted, however, that multi-tumor scenarios were neglected in the current study, whereas it resulted to have a relatively high importance in a previous computational study [9]. The present results indicated that tumor location has a definite impact on the structural response of the vertebra, but the importance of this parameter was markedly inferior to that of the tumor size.

The main outputs of this study were the average compression and the vertebral bulge, which have been assumed as indicators for the structural stability and the risk of vertebral fracture, as well as the canal narrowing, used to estimate the risk of neurological compromise. All simulations were performed under a standardized load and considered only the elastic response of the vertebra. The fracture mechanism itself, which would require introducing a yield criterion as well as a constitutive law describing the post-failure behavior of bone, was out of the scope of the present work. Therefore, a distinction between the types and extent of vertebral fractures which may result from the lesion cannot be supported by the present data. It should be noted that clinical observations showed that wedge (compression) fractures, in which the posterior cortical wall of the vertebral body remains intact, are typically rather stable and may not require any preventive treatment. On the contrary, burst fractures, in which the posterior wall is also fragmented, are commonly unstable and associated with complications related to the possible displacement of bone fragments inside the spinal canal.

All materials were modeled as elastic, and thus no time-dependent response was calculated. Other finite element studies simulated bone as well as tumoral tissues as poroelastic, i.e. as a porous solid matrix filled by a permeating fluid [9], [10], [11]. In such models, the flow of the fluid phase in a poroelastic material is governed by Darcy's law, which determines a creep/relaxation behavior matching the available experimental observations. Although the use of an elastic framework has likely a minor impact on the predictions in terms of vertebral compression for quasi-static loading, fracture mechanisms involving the pressurization of a part of the computational domain, which is typically related to fast and impact loading scenarios, could not be captured by the present models. Previous finite element and experimental studies showed that the pressurization of the fluid contained in the tumoral lesion, due to the application of fast loads, may result in high hoop stresses in the surrounding bone, leading to high risk of burst fractures [11]. Intact specimens did not show the same behavior, since the high permeability of bone tissue, several orders of magnitude higher than that of the tumor [17], hindered the formation of a high pressure under fast loading. The same research group also observed that specimens with low BMD tended to fail under quasi-static loading, whereas the mechanical failure samples with higher bone quality were more sensitive to the tumor pressurization under fast loading. Since all these clinically relevant aspects related to the time-dependent response, fluid flow and pressurization are outside of the scope of the present elastic models, further research in this direction is warranted.

In addition to the lack of time-dependent response, the developed models have several other limitations, which mostly pertain to the boundary and loading conditions employed, and may have a significant impact on the predictions. A uniformly distributed load was applied to the upper endplate surface of each vertebra, with the aim of simulating the effect of a non-degenerative intervertebral disc. Indeed, studies based on stress profilometry demonstrated that the intradiscal pressure can be assumed as almost uniform in the whole disc surface in case of healthy specimens. On the contrary, ageing and degenerative discs, likely common in patients suffering from spine tumors, showed pressure peaks, especially in proximity of the apophyseal ring [23], [24]. Furthermore, the present models simulated only the standing posture, for which a pure follower load, i.e. a compressive load following the curvature of the spine without generating any rotation of the motion segments, is considered a valid mechanical representation [25]. However, flexed postures and motions determining non-uniform pressure distributions and high bending moments have been shown to be more strongly associated to vertebral fractures [26].

In the present work, the same loading and boundary conditions have been simulated for all vertebrae. Computational studies showed that the compressive loads do not show a marked variability along the lumbar spine, but a non-negligible tendency toward an increase in the caudal direction has been reported [16], [27]. Indeed, the magnitude of the applied compressive load has been taken from the literature [11], and was aimed at replicating a worst-case scenario similar to the compressive load acting during trunk flexion [28] rather than the physiological case in the standing posture. The boundary conditions at the caudal endplate were also simplified with respect to the in vivo conditions, in which radial displacements in the transverse plane under compression should be expected, especially in case of existence of a tumoral lesion close to the endplate.

Further limitations pertain to the bone material properties, which were linear and isotropic and did not account for damage and failure. The elastic modulus of bone was directly calculated from the CT number based on a simple linear equation, whereas more sophisticated approaches have been reported [29]. Furthermore, it should be noted that CT imaging was performed on two different scanners, although from the same manufacturer. Previous studies showed that interscanner differences may be not-negligible and should be taken into account [30].

In conclusion, this computational work conducted on anatomically realistic models of a large number of vertebrae confirmed that tumor size is the most important predictor of the structural instability of metastatically involved vertebrae. Other features such as the bone quality and tumor position had a lower, but not negligible importance. Vertebral level resulted to be rather weakly associated with vertebral collapse and bulge. The relevance of the findings should be interpreted taking into account the limitations of the finite element models, which have the potential to impact on the reported results.

The following are the supplementary data related to this article.

Suppl. S1

Effect of the tumor size (in mm) in determining the average axial displacement

Suppl. S2

Effect of the tumor size (in mm) in determining the average axial displacement

Suppl. S3

Effect of the tumor size (in mm) in determining the average axial displacement

Suppl. figures.

Funding

This work was supported by the Italian Ministry of Foreign Affairs and International Cooperation and by the Ministry of Science and Technology of the People's Republic of China (grant nr. PGR00798 and 2016YFE0103700).