Redundancy in synaptic connections enables neurons to learn optimally

Significance

Humans and animals are capable of rapid learning from a small dataset, which is still difficult for artificial neural networks. Recent studies further suggest that our learning speed is nearly optimal given a stream of information, but its underlying mechanism remains elusive. Here, we hypothesized that the elaborate connection structure between presynaptic axons and postsynaptic dendrites is the key element for this near-optimal learning and derived a data-efficient rule for dendritic synaptic plasticity and rewiring from Bayesian theory. We implemented this rule in a detailed neuron model of visual perceptual learning and found that the model well reproduces various known properties of dendritic plasticity and synaptic organization in cortical neurons.

Abstract

Recent experimental studies suggest that, in cortical microcircuits of the mammalian brain, the majority of neuron-to-neuron connections are realized by multiple synapses. However, it is not known whether such redundant synaptic connections provide any functional benefit. Here, we show that redundant synaptic connections enable near-optimal learning in cooperation with synaptic rewiring. By constructing a simple dendritic neuron model, we demonstrate that with multisynaptic connections synaptic plasticity approximates a sample-based Bayesian filtering algorithm known as particle filtering, and wiring plasticity implements its resampling process. Extending the proposed framework to a detailed single-neuron model of perceptual learning in the primary visual cortex, we show that the model accounts for many experimental observations. In particular, the proposed model reproduces the dendritic position dependence of spike-timing-dependent plasticity and the functional synaptic organization on the dendritic tree based on the stimulus selectivity of presynaptic neurons. Our study provides a conceptual framework for synaptic plasticity and rewiring.

Synaptic connection between neurons is the fundamental substrate for learning and computation in neural circuits. Previous morphological studies suggest that in cortical microcircuits often several synaptic connections are found between the presynaptic axons and the postsynaptic dendrites of two connected neurons (1–3). Recent connectomics studies confirmed these observations in somatosensory (4), visual (5), and entorhinal (6) cortex, and also in hippocampus (7). In particular, in barrel cortex, the average number of synapses per connection is estimated to be around 10 (8). However, the functional importance of multisynaptic connections remains unknown. Especially, from a computational perspective, such redundancy in connection structure is potentially harmful for learning due to degeneracy (9, 10). In this work, we study how neurons perform learning with multisynaptic connections and whether redundancy provides any benefit, from a Bayesian perspective.

Bayesian framework has been established as a candidate principle of information processing in the brain (11, 12). Many results further suggest that not only computation but also learning process is also near-optimal in terms of Bayesian for a given stream of information (13–15), yet its underlying plasticity mechanism remains largely elusive. Previous theoretical studies revealed that Hebbian-type plasticity rules eventually enable neural circuits to perform optimal computation under appropriate normalization (16, 17). However, these rules are not optimal in terms of learning, so that the learning rates are typically too slow to perform learning from a limited number of observations. Recently, some learning rules have been proposed for rapid learning (18, 19), yet their biological plausibility is still debatable. Here, we propose a framework of nonparametric near-optimal learning using multisynaptic connections. We show that neurons can exploit the variability among synapses in a multisynaptic connection to accurately estimate the causal relationship between pre- and postsynaptic activity. The learning rule is first derived for a simple neuron model and then implemented in a detailed single-neuron model. The derived rule is consistent with many known properties of dendritic plasticity and synaptic organization. In particular, the model explains a potential developmental origin of stimulus-dependent dendritic synaptic organization recently observed in layer 2/3 (L2/3) pyramidal neurons of rodent visual cortex, where presynaptic neurons having a receptive field (RF) similar to that of the postsynaptic neuron tend to have synaptic contacts at proximal dendrites (20). Furthermore, the model reveals potential functional roles of anti-Hebbian synaptic plasticity observed in distal dendrites (21, 22).

Results

A Conceptual Model of Learning with Multisynaptic Connections.

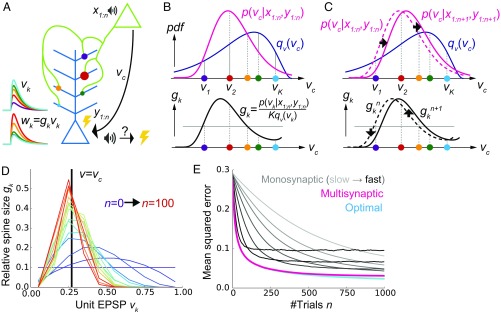
Let us first consider a model of two neurons connected with K numbers of synapses (Fig. 1A) to illustrate the concept of the proposed framework. In the model, synaptic connections from the presynaptic neuron are distributed on the dendritic tree of the postsynaptic neuron as observed in experiments (2, 3). Although a cortical neuron receives synaptic inputs from several thousands of presynaptic neurons in reality, here we consider the simplified model to illustrate the conceptual novelty of the proposed framework. More realistic models will be studied in following sections.

Fig. 1.

A conceptual model of multisynaptic learning. (A) Schematic figure of the model consisting of two neurons connected with K synapses. Curves on the left represent unit EPSP v_k (top) and the weighted EPSP w_k = g_kv_k (bottom) of each synaptic connection. Note that synapses are consistently colored throughout Figs. 1 and 2. (B) Schematics of nonparametric representation of the probability distribution by multisynaptic connections. In both graphs, x axes are unit EPSP, and the left (right) side corresponds to distal (proximal) dendrite. The mean over the true distribution p(v_c|x_1:n,y_1:n) can be approximately calculated by taking samples (i.e., synapses) from the unit EPSP distribution q_v(v) (Top) and then taking a weighted sum over the spine size factor g_k representing the ratio p(v_k|x_1:n,y_1:n)/q_v(v_k) (Bottom). (C) Illustration of synaptic weight updating. When the distribution p(v_c|x_1:n+1,y_1:n+1) comes to the right side of the original distribution p(v_c|x_1:n,y_1:n), a spine size factor g_kⁿ⁺¹ become larger (smaller) than g_kⁿ at proximal (distal) synapses. (D) An example of learning dynamics at K = 10 and q_v(v) = const. Each curve represents the distribution of relative spine sizes {g_k}, and the colors represent the growth of trial number. (E) Comparison of performance among the proposed method, the monosynaptic rule, and the exact solution (see SI Appendix, A Conceptual Model of Multisynaptic Learning for details). The monosynaptic learning rule was implemented with learning rate η = 0.01, 0.015, 0.02, 0.03, 0.05, 0.1, 0.2 (from gray to black), and the initial value was taken as $v_m^0=1/2$. Lines were calculated by taking average over 10⁴ independent simulations.

The synapses generate different amplitudes of excitatory postsynaptic potentials at the soma mainly through two mechanisms. First, the amplitude of dendritic attenuation varies from synapse to synapse, because the distances from the soma are different (23, 24). Let us denote this dendritic position dependence of synapse k as v_k, and call it the unit EPSP, because v_k corresponds to the somatic potential caused by a unit conductance change at the synapse (i.e., somatic EPSP per AMPA receptor). As depicted in Fig. 1A, unit EPSP v_k takes a small (large) value on a synapse at a distal (proximal) position on the dendrite. The second factor is the amount of AMPA receptors in the corresponding spine, which is approximately proportional to its spine size (25). If we denote this spine size factor as g_k, the somatic EPSP caused by a synaptic input through synapse k is written as w_k = g_kv_k. This means that even if the synaptic contact is made at a distal dendrite (i.e., even if v_k is small), if the spine size g_k is large, a synaptic input through synapse k has a strong impact at the soma (e.g., red synapse in Fig. 1A), or vice versa (e.g., cyan synapse in Fig. 1A).

In this model, we consider a simplified classical conditioning task as an example, although the framework is applicable for various inference tasks. Here, the presynaptic neuron activity represents the conditioned stimulus (CS), such as tone, and the postsynaptic neuron activity represents the unconditioned stimulus (US), such as shock. CS and US are represented by binary variables $x_n\in \left\{\mathrm{0,1}\right\}$ and $y_n\in \left\{\mathrm{0,1}\right\}$, where $x_n=1\left(y_n=1\right)$ denotes the presence of the CS (US) and subscript n stands for the trial number (Fig. 1A). Learning behavior of animals and humans in such conditioning can be explained by the Bayesian framework (26). In particular, to invoke an appropriate behavioral response, the brain needs to keep track of the likelihood of US given CS $v_c\equiv p\left(y_n=1|x_n=1\right)$, presumably by changing the synaptic weight between corresponding neurons. Thus, we consider supervised learning of the conditional probability v_c by multisynaptic connections, from pre- and postsynaptic activities representing CS and US, respectively. From finite trials up to n, this conditional probability is estimated as ${\overline{v}}_c^n={\displaystyle \int v_{\prime c}p\left(v_{\prime c}|x_{1:n},y_{1:n}\right)d{v}_{\prime c}}$, where x_1:n={x₁,x₂,…,x_n} and y_1:n={y₁,y₂,…,y_n} are the histories of input and output activities, and $p\left(v_c|x_{1:n},y_{1:n}\right)$ is the probability distribution of the hidden parameter v_c after n trials. Importantly, in general, it is impossible to get the optimal estimation of ${\overline{v}}_c^{n+1}$ directly from ${\overline{v}}_c^n$, because to calculate ${\overline{v}}_c^{n+1}={\displaystyle \int v_{\prime c}p\left(v_{\prime c}|x_{1:n+1},y_{1:n+1}\right)d{v}_{\prime c}}$ one first needs to calculate the distribution $p\left(v_c|x_{1:n+1},y_{1:n+1}\right)$ by integrating the previous distribution $p\left(v_c|x_{1:n},y_{1:n}\right)$ and the new observation at trial n + 1: {x_n+1, y_n+1}. This means that for near-optimal learning, synaptic connections need to learn and represent the distribution $p\left(v_c|x_{1:n},y_{1:n}\right)$ instead of the point estimation ${\overline{v}}_c^n$. However, how can synapses achieve that? The key hypothesis of this paper is that redundancy in synaptic connections is the substrate for the nonparametric representation of this probabilistic distribution. Below, we show that dendritic summation over multisynaptic connections yields the optimal estimation from the given distribution $p\left(v_c|x_{1:n},y_{1:n}\right)$, and dendritic-position-dependent Hebbian synaptic plasticity updates this distribution.

Dendritic Summation as Importance Sampling.

We first consider how dendritic summation achieves the calculation of the mean conditional probability ${\overline{v}}_c^n={\displaystyle \int v_{\prime c}p\left(v_{\prime c}|x_{1:n},y_{1:n}\right)d{v}_{\prime c}}$. It is generally difficult to evaluate this integral by directly taking samples from the distribution $p\left(v_c|x_{1:n},y_{1:n}\right)$ in a biologically plausible way, because the cumulative distribution changes its shape at every trial. Nevertheless, we can still estimate the mean value by using an alternative distribution as the proposal distribution, and taking weighted samples from it. This method is called importance sampling (27). In particular, here we can use the unit EPSP distribution q_v(v) as the proposal distribution, because unit EPSPs {v_k} of synaptic connections can be interpreted as samples depicted from the unit EPSP distribution q_v (Fig. 1B, Top). Thus, the mean ${\overline{v}}_c^n$ is approximately calculated as

$${\overline{v}}_c^n={\displaystyle \int v_{\prime c}p\left(v_{\prime c}|x_{1:n},y_{1:n}\right)d{v}_{\prime c}}\approx \frac{1}{K}{\displaystyle \sum _{k=1}^K\frac{p\left(v_c=v_k|x_{1:n},y_{1:n}\right)}{q_v\left(v_k\right)}{v}_k}={\displaystyle {\sum }_k{g}_k^n{v}_k}={\displaystyle {\sum }_k{w}_k^n},$$ [1]

where $g_k^n=p\left(v_c=v_k|x_{1:n},y_{1:n}\right)/K{q}_v\left(v_k\right)$. Therefore, if spine size g_kⁿ represents the relative weight of sample v_k, then dendritic summation over postsynaptic potentials $w_k^n\equiv g_k^n{v}_k$ naturally represents the desired value (${\overline{v}}_c^n\approx {\displaystyle {\sum }_k{w}_k^n}$). For instance, if the distribution of synapses is biased toward the proximal side (i.e., if the mean ${\overline{v}}_c^n$ is overestimated by the distribution of unit EPSPs as in Fig. 1B, Top), then synapses at distal dendrites should possess large spine sizes, while the spine sizes of proximal synapses should be smaller (Fig. 1B, Bottom).

Synaptic Plasticity as Particle Filtering.

In the previous section, we showed that redundant synaptic connections can represent probabilistic distribution p(v_c = v_k|x_1:n,y_1:n) if spine sizes {g_k} coincide with their importance $g_k^n=p\left(v_c=v_k|x_{1:n},y_{1:n}\right)/K{q}_v\left(v_k\right)$. However, how can synapses update their representation of the probabilistic distribution p(v_c = v_k|x_1:n,y_1:n) based on a new observation {x_n+1, y_n+1}? Because p(v_c = v_k|x_1:n,y_1:n) is mapped onto a set of spine sizes {g_kⁿ} as in Eq. 1, the update of the estimated distribution $p\left(v_k|x_{1:n},y_{1:n}\right)\to p\left(v_k|x_{1:n+1},y_{1:n+1}\right)$ can be performed by the update of spine sizes $\left\{g_k^n\right\}\to \left\{g_k^{n+1}\right\}$. By considering particle filtering (28) on the parameter space (see SI Appendix, The Learning Rule for Multisynaptic Connections for details), we can derive the learning rule for spine size as

$$g_k^{n+1}=\frac{1+f\left(x_{n+1},y_{n+1};v_k\right)}{1+f\left(x_{n+1},y_{n+1};w^n\right)}{g}_k^n,f\left(x,y;v\right)\equiv \left(2v-1\right)x\left(2y-1\right).$$ [2]

This rule is primary Hebbian, because the weight change depends on the product of pre- and postsynaptic activity x_n+1 and y_n+1. In addition to that, the change also depends on unit EPSP v_k. This dependence on unit EPSP reflects the dendritic position dependence of synaptic plasticity. In particular, for a distal synapse (i.e., for small v_k), the position-dependent term (2v_k − 1) takes a negative value (note that 0 ≤ v_k < 1), thus yielding an anti-Hebbian rule as observed in neocortical synapses (21, 22).

For instance, if the new data {x_n+1, y_n+1} indicate that the value of v_c is in fact larger than previously estimated, then the distribution p(v_c|x_1:n+1,y_1:n+1) shifts to the right side (Fig. 1C, Top). This means that the spine size g_kⁿ⁺¹ becomes larger then g_kⁿ at synapses on the right side (i.e., proximal side), whereas synapses get smaller on the left side (i.e., distal side; Fig. 1C, Bottom). Therefore, pre- and postsynaptic activity causes long-term potentiation at proximal synapses and induces long-term depression at distal synapses as observed in experiments (21, 22). The derived learning rule (Eq. 2) also depends on the total EPSP amplitude $w^n\equiv {\displaystyle {\sum }_k{w}_k^n}\equiv {\displaystyle {\sum }_k{g}_k^n{v}_k}$. This term reflects a normalization factor possibly modulated through redistribution of synaptic vesicles over the presynaptic axon (29). A surrogate learning rule without this normalization factor will be studied in a later section.

We performed simulations by assuming that the two neurons are connected with 10 synapses with the uniform unit EPSP distribution [i.e., q_v(v) = const.]. At an initial phase of learning, the distribution of spine size {g_kⁿ} has a broad shape (purple lines in Fig. 1D), and the mean of distribution is far away from the true value (v = v_c). However, the distribution is skewed around the true value as evidence is accumulated through stochastic pre- and postsynaptic activities (red lines in Fig. 1D). Indeed, the estimation performance of the proposed method is nearly the same as that of the exact optimal estimation, and much better than the standard monosynaptic learning rules (Fig. 1E; see SI Appendix, Monosynaptic Learning Rule for details).

Synaptogenesis as Resampling.

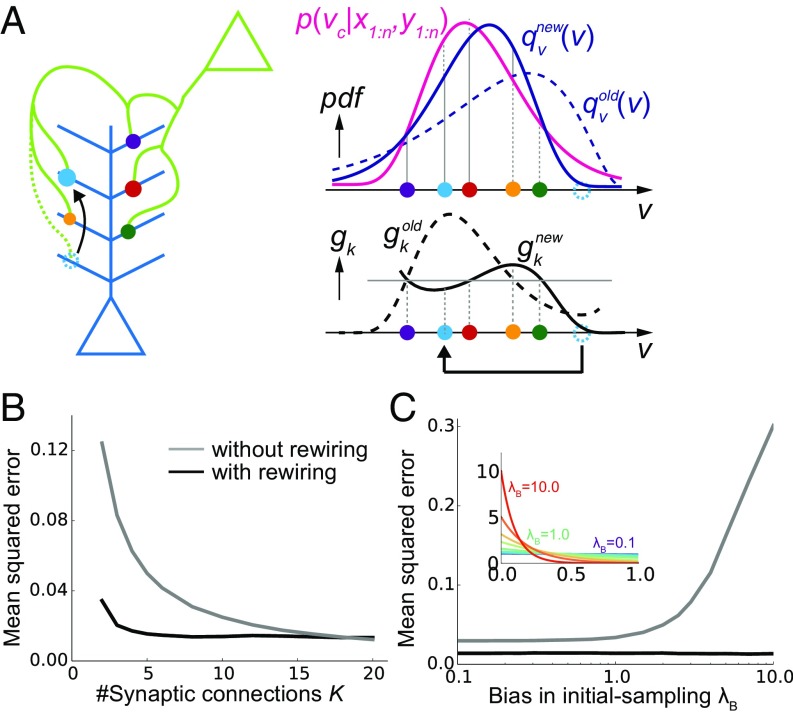
As shown above, weight modification in multisynaptic connections enables a near-optimal learning. However, to represent the distribution accurately, many synaptic connections are required (gray line in Fig. 2B), while the number of synapses between an excitatory neuron pair is typically around five in the cortical microcircuits. Moreover, even if many synapses are allocated between presynaptic and postsynaptic neurons, if the unit EPSP distribution is highly biased, the estimation is poorly performed (gray line in Fig. 2C). We next show that this problem can be avoided by introducing synaptogenesis (30) into the learning rule.

Fig. 2.

Synaptic rewiring for efficient learning. (A) Schematic illustration of resampling. Dotted cyan circles represent an eliminated synapse, and the filled cyan circles represent a newly created synapse. (B and C) Comparison of performance with/without synaptic rewiring at various synaptic multiplicity K (B), and bias in initial-sampling λ_B (C). For each bias parameter λ_B, the unit EPSP distribution {v_k} was set as $v_{k\prime }=-\log \left(1-\left[1-e^{-{\lambda }_B}\right]k\prime /K\right)$, as depicted in the inset. Lines are the means over 10⁴ simulations.

In the proposed framework, when synaptic connections are fixed (i.e., when {v_k} are fixed), some synapses quickly become useless for representing the distribution. For instance, in Fig. 2A, the (dotted) cyan synapse is too proximal to contribute for the representation of p(v_c|x,y). Therefore, by removing the cyan synapse and creating a new synapse at a random site, on average, the representation becomes more effective (Fig. 2A). Importantly, in our framework, spine size factor g_k is proportional to the informatic importance of the synapse by definition, and thus optimal rewiring is achievable simply by removing the synapse with the smallest spine size. Ideally, the new synapse should be sampled from the underlying distribution of {g_k} for an efficient rewiring (31), yet it is not clear if such a sampling is biologically plausible; hence, below we consider a uniform sampling from the parameter space. Although here we assumed simultaneous elimination and creation of synaptic contacts for simplicity, the strict balance between elimination and creation is not necessary, as will be shown later in the detailed neuron model.

By introducing this resampling process, the model is able to achieve high performance robustly. With rewiring, a small error is achieved even when the total number of synaptic connections is just around three (black line in Fig. 2B). In contrast, more than 10 synapses are required for achieving the same performance without rewiring (gray line in Fig. 2B). Similarly, even if the initial distribution of {v_k} is poorly taken, with rewiring the neuron can achieve a robust learning (black line in Fig. 2C), whereas the performance highly depends on the initial distribution of the synapses in the absence of rewiring (gray line in Fig. 2C).

Recent experimental results suggest that the creation of new synapses is clustered at active dendritic branches (32). Correspondingly, by sampling new synapses near large synapses, performance becomes better given a large number of samples (SI Appendix, Uniform and Multinomial Sampling and Fig. S1A), although this difference almost disappears under an explicit normalization (SI Appendix, Fig. S1B).

Detailed Single-Neuron Model of Learning from Many Presynaptic Neurons.

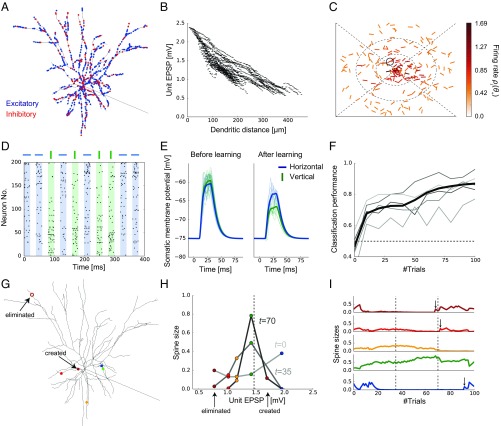
In the previous sections, we found that synaptic plasticity in multisynaptic connections can achieve nonparametric near-optimal learning in a simple model with one presynaptic neuron. To investigate its biological plausibility, we next extend the proposed framework to a detailed single-neuron model receiving inputs from many presynaptic neurons. To this end, we constructed an active dendritic model using NEURON simulator (33) based on a previous model of L2/3 pyramidal neurons of the primary visual cortex (34). We randomly distributed 1,000 excitatory synaptic inputs from 200 presynaptic neurons on the dendritic tree of the postsynaptic neuron, while fixing synaptic connections per presynaptic neuron at K = 5 (Fig. 3A; see SI Appendix, Morphology for the details of the model). We assumed that all excitatory inputs are made on spines, and each spine is projected from only one bouton for simplicity. In addition, 200 inhibitory synaptic inputs were added on the dendrite to keep the excitatory/inhibitory (E/I) balance (35). We first assigned a small constant conductance for each synapse and then measured the somatic potential change, which corresponds to the unit EPSP in the model. As observed in cortical neurons (23), input at a more distal dendrite showed larger attenuation at the soma, although variability was quite high across branches (Fig. 3B).

Fig. 3.

A detailed model of multisynaptic learning with multiple presynaptic neurons. (A) Morphology of the detailed neuron model. Blue and red points on the dendritic trees represent excitatory and inhibitory synaptic inputs, respectively. (B) Dendritic position dependence of unit EPSP. Each dot represents a synaptic contact on the dendritic tree. (C) An example of the visual selectivity patterns of presynaptic neurons. Position and angle of each bar represent the RF and the orientation selectivity of each presynaptic neuron, where the RF was defined relative to the RF of the postsynaptic neuron (the central position). Colors represent the firing rates of presynaptic neurons when a horizontal bar stimulus is presented at the RF of the postsynaptic neuron. Here, the firing rates were evaluated as the expected number of spikes within 20-ms stimulus duration (see SI Appendix, Stimulus Selectivity for details). The black circle shows the selectivity of the representative neuron depicted in G–I. (D) Examples of input spike trains generated from the horizontal (target) and vertical (nontarget) stimuli. Presynaptic neurons were sorted by their stimulus preference. Note that in the actual simulations variables were initialized after each stimulation trial. See SI Appendix, Task Configuration for details of the task. (E) Somatic responses before and after learning. Thick lines represent the average response curves over 100 trials and thin lines are trial-by-trial responses. (F) The average learning curves over 50 simulations (black line) and examples of learning curves (gray lines). (G–I) An example of learning dynamics under the multisynaptic rule (see Results for details).

Next, we consider a perceptual learning task in this neuron model. Each excitatory presynaptic neuron was assumed to be a local pyramidal neuron, modeled as a simple cell having a small RF and a preferred orientation in the visual space (Fig. 3C). Axonal projections from each presynaptic neuron were made onto five randomly selected dendritic branches of the postsynaptic neuron regardless of the stimulus selectivity, because visual cortex of mice has a rather diverse retinotopic structure (36). In this setting, the postneuron should be able to infer the orientation of the stimulus presented at its RF from the presynaptic inputs, because cells having similar RFs or orientation selectivity are often coactivated (37, 38). Thus, we consider a supervised learning task in which the postsynaptic neuron has to learn to detect a horizontal grading, not a vertical grading, from stochastic presynaptic spikes depicted in Fig. 3D. In reality, the modulation of lateral connections in L2/3 is arguably guided by the feedforward inputs from layer 4 (39, 40). However, for simplicity, we instead introduced an explicit supervised signal to the postsynaptic neuron. In this formulation, we can directly apply the rule for synaptic plasticity and rewiring introduced in the previous section (SI Appendix, The Learning Rule for the Detailed Model). In the rewiring process, a new synaptic contact was made on one of the branches on which the presynaptic neuron initially had at least one synaptic contact, to mimic the axonal spatial constraint. Here, in addition to the rewiring by the proposed multisynaptic rule, we implemented elimination of synapses from uncorrelated presynaptic neurons, to better replicate developmental synaptic dynamics.

Initially, the postsynaptic somatic membrane potential responded similarly to both horizontal and vertical stimuli, but the neuron gradually learned to show a selective response to the horizontal stimulus (Fig. 3E). After 100 trials, the two stimuli became easily distinguishable by the somatic membrane dynamics (Fig. 3 E and F; see SI Appendix, Performance Evaluation for details). Next, we examined how the proposed mechanism works in detail. To this end, we focused on a presynaptic neuron circled in Fig. 3C and tracked the changes in its synaptic projections and spine sizes (Fig. 3 G–I). Because the neuron has an RF near the postsynaptic RF, and its orientation selectivity is nearly horizontal, the total synaptic weight from this neuron should be moderately large after learning. Indeed, the Bayesian optimal weight was estimated to be around 1.5 mV in the model (vertical dotted line in Fig. 3H), under the assumption of linear dendritic integration. Overall, the unit EPSPs of the majority of synapses were initially around 1.0–1.5 mV, while smaller or larger unit EPSPs were rare due to dendritic morphology (Fig. 3B). To counterbalance this bias toward the center, we initialized the spine sizes in a U shape (light gray line in Fig. 3H). In this way, the prior distribution of the total synaptic weight becomes roughly uniform (see also Fig. 1B). After a short training, the most proximal spine (the blue one) was depotentiated, whereas spines with moderate unit EPSP sizes were potentiated (yellow and green ones on the dark gray line in Fig. 3H). This is because the expected distribution of the weight from this presynaptic neuron shifted to the left side (i.e., to a smaller EPSP) after the training, and this shift was implemented by reducing the spine size of the proximal synapse, while increasing the sizes of others (as in Fig. 1C, but here the change is to the opposite direction). Note that the most distal spine (the brown one) was also depressed here, as the expected distribution got squeezed toward the center. Finally, after a longer training, the expected distribution became more squeezed, and hence all but the green spine were depotentiated (black line in Fig. 3H). Moreover, the most distal synapse was eliminated because its spine size became too small to make any meaningful contribution to the representation, and a new synapse was created at a proximal site (open and closed brown circles in Fig. 3G, respectively) as explained in Fig. 2A. This rewiring achieves a more efficient representation of the weight distribution on average. Indeed, the new brown synapse was potentiated subsequently (top of Fig. 3I). Note that, in this example, red and blue synapses were also rewired shortly after this moment (vertical arrows above red and blue traces in Fig. 3I).

The Model Reproduces Various Properties of Synaptic Organization on the Dendrite.

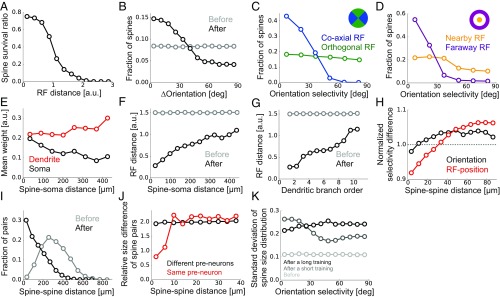
While we confirmed that the proposed learning paradigm works well in a realistic model setting, we further investigated its consistency with experimental results. We first calculated spine survival ratio for connections from different presynaptic neurons. As suggested from experimental studies (20, 39), more synapses survived if the presynaptic neuron had an RF near the postsynaptic RF after learning (Fig. 4A). Likewise, synapses having orientation selectivity similar to the postsynaptic neuron showed higher survival rates (Fig. 4B) as indicated from previous observations (5, 39). However, this orientation dependence was evident only for projections from neurons with an RF in the direction of the postsynaptic orientation selectivity (blue line in Fig. 4C), and the spines projected from neurons with orthogonal RFs remained having uniform selectivity even after learning (green line in Fig. 4C), as reported in a recent experiment (20). In contrast, both connections from neurons with nearby and faraway RFs showed clear orientation dependence, although the dependence was more evident for the latter in the model (Fig. 4D). The consistencies with the experimental results (Fig. 4 A–D) support the legitimacy of our model setting, although they were achieved by the elimination of uncorrelated spines, not by the multisynaptic learning rule per se.

Fig. 4.

Synaptic organization on the dendrite by the multisynaptic learning rule. (A) Survival ratio of spines with different RF distances from the postsynaptic neuron. (B) Fraction of spines having various orientation selectivity before and after learning. (C and D) Fraction of spines survived after learning, calculated for different orientation selectivity at coaxial/orthogonal RFs (C) and at nearby/faraway RFs (D). We defined the RF of presynaptic neuron j being orthogonal if $\pi /4\le {\phi }_j<3\pi /4/\hspace{0.17em}\text{or}\hspace{0.17em}5\pi /4\le {\phi }_j<7\pi /4$, and coaxial otherwise. The RF of neuron j was defined as nearby if r_j < 0.5 but far away if r_j > 1.0 (SI Appendix, Stimulus Selectivity). (E) Relationship between the dendritic distance and the relative weight at the dendrite g_k and the soma g_kv_k/v_max. (F) Relationship between the dendritic distance of a spine from the soma and its RF distance in the visual space. (G) The same as F, but calculated for the dendritic branch order, not the dendritic distance. (H) Dependence of normalized RF difference (red), and normalized orientation difference (black) on the between-spine distance were calculated for two synapses projected from different neurons. We used the Euclidean distance in the visual field ${\ell }_{ij}=\sqrt{{\left(r_i\cos {\phi }_i-r_j\cos {\phi }_j\right)}^2+{\left(r_i\sin {\phi }_i-r_j\sin {\phi }_j\right)}^2}$ for RF distance between presynaptic neurons i and j, and the normalization was taken over all synapse pairs. (I) Distributions of dendritic distance between synapses projected from the same presynaptic neuron before and after learning. (J) Relative spine size difference between spines projected from the same presynaptic neuron or different neurons calculated for pairs with different spine distance. The relative size difference between spine i and j was defined as |log(g_i/g_j)|. (K) SD of spine size distribution at various orientation selectivity for synapses from presynaptic neurons with nearby RFs (r_j < 0.5). The distributions for short and long training were taken after learning from 10 and 1,000 samples, respectively. All panels were calculated by taking averages over 500 independently simulated neurons, and the learning was performed from 1,000 training samples.

We next investigated changes in dendritic synaptic organization generated by the multisynaptic learning. Overall, the mean spine size was slightly larger at distal dendrites (red line in Fig. 4E), but this trend was not strong enough to compensate the dendritic attenuation (black line in Fig. 4E), being consistent with previous observations in neocortical pyramidal neurons (41). Importantly, neurons with RFs far away from the postsynaptic RF likely formed synaptic projections more on distal dendrites than on proximal ones (Fig. 4F), and at higher dendritic branch orders than at lower ones (Fig. 4G), as observed previously (20). This is because, in the proposed learning rule, if pre- and postsynaptic neurons have similar spatial selectivity, synaptic connections are preferably rewired toward proximal positions (Fig. 3G), and vice versa (Fig. 2A). Moreover, nearby spines on the dendrite showed similar RF selectivity even if multisynaptic pairs (i.e., synapse pairs projected from the same neuron) were excluded from the analysis (red line in Fig. 4H), due to the dendritic position dependence of presynaptic RFs. However, similarity between nearby spines was less significant in orientation selectivity (black line in Fig. 4H), as observed previously in rodent experiments (20, 42). These results suggest a potential importance of developmental plasticity in somatic-distance-dependent synaptic organization.

In the model, the position of a newly created synapse was limited to the branches where the presynaptic neuron initially had a projection, to roughly reproduce the spatial constraint on synaptic contacts. As a result, although there are many locations on the dendrite where the unit EPSP size is optimal for a given presynaptic neuron, only a few of them are accessible from the neuron, and hence synapses from the same presynaptic neuron may form clusters there. Indeed, by examining changes in multisynaptic connection structure, we found that the dendritic distance between two spines projected from the same presynaptic neuron became much shorter after learning (Fig. 4I), creating clusters of synapses from the same axons. This result suggests that clustering of multisynaptic connections observed in the experiments (6) is possibly caused by developmental synaptogenesis under a spatial constraint. Furthermore, as observed in hippocampal neurons (7), two synapses from the same presynaptic neuron had similar spine sizes if the connections were spatially close to each other, but the correlation in spine size disappeared if they were distant (red line in Fig. 4J). However, spine sizes of two synapses from different neurons were always uncorrelated regardless of the spine distance (black line in Fig. 4J).

Finally, we studied the spine size distribution. In the proposed framework, the mean spine size does not essentially depend on presynaptic stimulus selectivity due to normalization, but the variance may change. In particular, the spine size variance is expected to be small if the presynaptic activity is highly stochastic, because the distribution of spine sizes stays nearly uniform in this condition, while the spine size variance should increase upon accumulation of samples. Indeed, in the initial phase of learning, the variance of spine size went up for projections from neurons with horizontal orientation selectivity (gray line Fig. 4K), although the spine size variance from other presynaptic neurons caught up eventually (black line Fig. 4K). In this regard, a recent experimental study found higher variability in postsynaptic density areas for projections from neurons sharing orientation preference with the postsynaptic cell, though the data were from adult, not juvenile, mice (5).

The Multisynaptic Rule Robustly Enables Fast Learning.

The correspondence with experiment observations discussed in the previous section supports the plausibility of our framework as a candidate mechanism of synaptic plasticity on the dendrites. Hence, we further studied the robustness of learning dynamics under the proposed multisynaptic rule. Below, we turn off the spine elimination mechanism that is not compensated by creation, as this process affects the learning dynamics.

In the proposed model, if the initial synaptic distribution on the dendrite q_v(v) is close to the desired distribution p_v(v), spine size modification is in principle unnecessary. In particular, the optimal EPSPs of most presynaptic neurons are small in our L2/3 model (Fig. 3C); hence, most synaptic contacts should be placed on distal branches on average. Indeed, when the initial synaptic distribution was biased toward the distal side, improvement in classification performance became faster (black vs. blue lines in Fig. 5A). This result suggests that the synaptic distribution on the postsynaptic dendrite may work as a prior distribution.

Fig. 5.

Dynamics of the multisynaptic learning rule under various conditions. (A) Learning dynamics under various initial synaptic distributions. (Inset ) The unit EPSP distributions when synaptic connections are biased toward the distal dendrite (black), unbiased (blue), and biased toward the proximal (light blue). (B) Comparison with the monosynaptic learning. We set the learning rate as η_w = 0.03, 0.1, 0.3, 1.0, from light gray to black lines. To keep the E/I balance, the inhibitory weight was set to γ_I = 2.0 for η_w = 1.0, and γ_I = 1.25 for the rest. The magenta line is the same as the black line in A. (C) Classification performance after learning with different numbers of synapses per connection with or without rewiring. For the E/I balance, the inhibitory weights were chosen as γ_I = 2.0, 1.2, 0.75, 0.6, 0.5, 0.4, 0.3, when the number of synapses per connections were K = 2, 3, 5, 7, 9, 11, 13, respectively. (D) The performance after learning with various synaptic failure probabilities. Both in C and D, the performance was calculated after 1,000 trials. (E) Learning dynamics under the surrogate rule. Thin gray lines represent examples. All panels were calculated by taking the means over 50 simulations.

We next compared the learning performance with the standard monosynaptic learning rule in which the learning rate is a free parameter (SI Appendix, Monosynaptic Rule for the Detailed Model). If the learning rate is chosen at a small value, the neuron took a very large number of trials to learn the classification task (light gray line in Fig. 5B). However, if the learning rate was too large, the learning dynamics became unstable and the performance dropped off after a dozen trials (black line in Fig. 5B). Therefore, the learning performance was comparable to the multisynaptic rule only in a small parameter region (η_w ∼ 0.1). By contrast, in the multisynaptic rule, stable fast learning was achievable without any fine-tuning (magenta line in Fig. 5B).

As expected from Fig. 2, the proposed learning mechanism worked well even if the number of synapses per connection was small (Fig. 5C). Without rewiring, the classification task required seven synapses per connection for an 80% success rate, but three was enough with rewiring (Fig. 5C). Moreover, the learning performance was robust against synaptic failure (Fig. 5D). Although local excitatory inputs to L2/3 pyramidal cells have a relatively high release probability (43), the stochasticity of synaptic transmission at each synapse may affect learning and classification. We found that even if the half of presynaptic spikes were omitted at each synapse (see SI Appendix, Task Configuration for details), the classification performance was still significantly above the chance level (Fig. 5D). Does the presynaptic stochasticity only add up noise? This was likely the case when the release probability was kept constant because the variability in the somatic EPSP height grows with the variance of {g_k} in this scenario (SI Appendix, Fig. S2A; see SI Appendix, Presynaptic Stochasticity for details). However, if matching exists between presynaptic release probability and the postsynaptic spine size, as often observed in experiments (44, 45), the Fano factor of the somatic EPSP height decreased as the performance went up (SI Appendix, Fig. S2B), because g_k can be jointly represented by the pre- and postsynaptic factors. This result indicates that the variability in somatic EPSP may encode the uncertainty in the synaptic representation.

In the proposed model, competition was assumed among synapses projected from the same presynaptic neuron, but it is unclear if homeostatic plasticity works in such a specific manner. Thus, we next constructed a surrogate learning rule that only requires a global homeostatic plasticity. In this rule, the importance of a synapse was not compared with other synapses from the same presynaptic neuron, but was compared with a hypothesized standard synapse (SI Appendix, The Surrogate Learning Rule). When the unit EPSP size of the standard synapse was chosen appropriately, the surrogate rule indeed enabled the neuron to learn the classification task robustly and quickly (Fig. 5E). Overall, these results support the robustness and biological plausibility of the proposed multisynaptic learning rule.

Discussion

In this work, first we have used a simple conceptual model to show that (i) multisynaptic connections provide a nonparametric representation of probabilistic distribution of the hidden parameter using redundancy in synaptic connections (Fig. 1 A and B), (ii) updating of probabilistic distribution given new inputs can be performed by a Hebbian-type synaptic plasticity when the output activity is supervised (Fig. 1 C–E), and (iii) elimination and creation of spines is crucial for efficient representation and fast learning (Fig. 2). In short, synaptic plasticity and rewiring at multisynaptic connections naturally implements an efficient sample-based Bayesian filtering algorithm. Second, we have demonstrated that the proposed multisynaptic learning rule works well in a detailed single-neuron model receiving stochastic spikes from many neurons (Fig. 3). Moreover, we found that the model reproduces the somatic-distance-dependent synaptic organization observed in the L2/3 of rodent visual cortex (Fig. 4 F and G). Furthermore, the model suggests that the dendritic distribution of multisynaptic inputs provides a prior distribution of the expected synaptic weight (Fig. 5A).

Experimental Predictions.

Our study provides several experimentally testable predictions on dendritic synaptic plasticity, and the resultant synaptic distribution. First, the model suggests a crucial role of developmental synaptogenesis in the formulation of presynaptic selectivity-dependent synaptic organization on the dendritic tree (Fig. 4 F and G), observed in the primary visual cortex (20). More specifically, we have revealed that the RF dependence of synaptic organization is a natural consequence of the Bayesian optimal learning under the given implementation. Evidently, retinotopic organization of presynaptic neurons is partially responsible for this dendritic projection pattern, as a neuron tends to make a projection onto a dendritic branch near the presynaptic cell body (8, 46). However, a recent experiment reported that RF-dependent global synaptic organization on the dendrite is absent in the primary visual cortex of ferrets (47). This result indirectly supports the nonanatomical origin of the dendritic synaptic organization, as a similar organization is arguably expected in ferrets if the synaptic organization is purely anatomical.

Our study also predicts developmental convergence of synaptic connections from each presynaptic neuron (Figs. 3G and 4I). It is indeed known that in adult cortex synaptic connections from the same presynaptic neuron are often clustered (4, 6). Our model interprets synaptic clustering as a result of an experience-dependent resampling process by synaptic rewiring and predicts that synaptic connections are less clustered in immature animals. In particular, our result suggests that synaptic clustering occurs in a relatively large spatial scale (∼100 μm, as shown in Fig. 4I), not in a fine spatial scale (∼10 μm). This may explain a recent report on the lack of fine clustering structure in the rodent visual cortex (5).

Furthermore, our study provides an insight on the functional role of anti-Hebbian plasticity at distal synapses (21, 22). Even if the presynaptic activity is not tightly correlated with the postsynaptic activity, that does not mean the presynaptic input is not important. For instance, in our detailed neuron model, inputs from neurons having an RF far away from the postsynaptic RF still help the postsynaptic neuron to infer the presented stimulus (Fig. 3). More generally, long-range inputs are typically not correlated with the output spike trains, because the inputs usually carry contextual information (48), or delayed feedback signals (49), yet play important moduratory roles. Our study indicates that anti-Hebbian plasticity at distal synapses prevents these connections from being eliminated, by keeping the synaptic connection strong. This may explain why modulatory inputs are often projected to distal dendrites (48, 49), although active dendritic computation should also be crucial, especially in the case of layer 5 or CA1 pryramidal neurons (24).

Related Work.

Previous theoretical studies often explain synaptic plasticity as stochastic gradient descent on some objective functions (17, 40, 50, 51), but these models require fine-tuning of the learning rate for explaining near-optimal learning performance observed in humans (13, 14) and rats (15), unlike our model. Moreover, in this study, we proposed synaptic dynamics during learning as a sample-based inference process, in contrast to previous studies in which sample-based interpretations were applied for neural dynamics (52).

The relationship between presynaptic stochasticity and the achievement level of learning has been studied before, yet the previous models required an independent tuning of pre- and postsynaptic factors (53, 54). However, in our framework, the experimentally observed prepost matching (44, 45) is enough to approximately represent the uncertainty in learning performance by variability in the somatic membrane dynamics (SI Appendix, Fig. S2). It is known that presynaptic stochasticity can self-consistently generate a robust Poisson-like spiking activity in a recurrent network of leaky integrate-and-fire neurons (55). Hence, the uncertainty information reflected in the somatic membrane dynamics can be transmitted to downstream neurons via asynchronous spiking activity.

On the anti-Hebbian plasticity at distal synapse, previous modeling studies have revealed its potential phenomenological origins (56), but its functional benefits, especially optimality, have not been well investigated before. Particle filtering is an established method in machine learning (28), and has been applied to artificial neural networks (57), yet its biological correspondence had been elusive. A previous study proposed importance sampling as a potential implementation of Bayesian computation in the brain (58). In particular, they found that the oblique effect in orientation detection is naturally explained by sampling from a population with biased orientation selectivity. However, sampling was performed only in neural activity space, not in the synaptic parameter space unlike our model, and the underlying learning mechanism was not investigated either.

Previous computational studies on dendritic computation have emphasized the importance of active dendritic process (24), especially for performing inference from correlated inputs (59), or for computation at terminal tufts of cortical layer 5 or CA1 neurons (40). Nevertheless, experimental studies suggest the summation of excitatory inputs through dendritic tree is approximately linear (60, 61). Indeed, we have shown that a linear summation of synaptic inputs is suitable for implementing importance sampling. Moreover, we have demonstrated that even in a detailed neuron model with active dendrites a learning rule assuming a linear synaptic summation works well.

Materials and Methods

In the conceptual model, p(x_n = 1) was set at 30%, and the conditional probability v_c was randomly chosen from (0,1) at each simulation (not at each trial). Except for Fig. 2B, the number of connections was kept at K = 10. In the detailed single-neuron model, we constructed a model of L2/3 pyramidal neuron using NEURON simulator (33), based on a previous model (34). Further details are given in SI Appendix.