Adaptation of Living Systems

Abstract

Adaptation refers to the biological phenomenon where living systems change their internal states in response to changes in their environments in order to maintain certain key functions critical for their survival and fitness. Adaptation is one of the most ubiquitous and arguably one of the most fundamental properties of living systems. It occurs throughout all biological scales, from adaptation of populations of species over evolutionary time to adaptation of a single cell to different environmental stresses during its life span. In this article, we review some of the recent progress made in understanding molecular mechanisms of cellular level adaptation. We take the minimalist (or the physicist) approach and study the simplest systems that exhibit generic adaptive behaviors. We focus on understanding the basic biochemical interaction networks in living matter that are responsible for adaptation dynamics. By combining theoretical modeling with quantitative experimentation, we demonstrate universal features in adaptation as well as important differences in different cellular systems, including chemotaxis in bacterium cells (Escherichia coli) and eukaryotic cells (Dictyostelium). Future work in extending the modeling framework to study adaptation in more complex systems such as sensory neurons are discussed.

1. Introduction

Living systems, from a single cell to multi-cellular organisms and populations of interacting species, all have the amazing ability to adapt to changes in their environments. Adaptation allows living systems to adjust themselves in response to persistent changes of the environment. At the evolutionary time scale, adaptation drives species to evolve driven by changes in the environment. At the time scale of the life span of a living system, the ability to adapt is critical for the survival of the living system by maintaining its homeostasis under different environmental conditions. At the even shorter time scale of individual signaling pathways such as those for sensory signal transduction, adaptation can greatly extend the range of sensitive detection and also provides a way to compute/process environmental information.

What are the possible mechanisms for adaptation in living systems? Are there any universal principles governing interactions of the underlying living matter (biomolecules, cells, organisms) that are responsible for the vast variety of adaptive behaviors in biology? Are there any fundamental limitations to the performance of adaptation? In this paper, we review some of the recent developments in addressing these questions by combining theoretical analysis, computational modeling, and quantitative experiments for representative sensory signaling systems, including bacterium cells (Escherichia coli) and eukaryotic cells (Dictyostelium discodeum). We first provide a general mathematical framework for the two basic interaction networks that exhibit adaptation and examine their dynamics. Next, we provide a detailed description of two biological systems that employ these networks. We then study the universal properties of adaptation independent of the specific network structure. We conclude by outlining some of the remaining challenges for future investigations.

2. Adaptation as Dynamical System: a Mathematical Framework

We start with a presentation of a general mathematical framework to study adaptation. We denote X(t) as the input (stimulus strength) and Z(t) as the output of the biochemical network, where t is time. A change in X results in a change in Z with a fast response time. The output also depends on a slower internal variable Y(t), which itself depends on X, Y, and Z. The system can be described by two generic dynamical equations:

$$\frac{dZ}{dt}=G(X,Y,Z),\frac{dY}{dt}=F(X,Y,Z),$$ (1)

where F and G are the rate functions for Z and Y respectively.

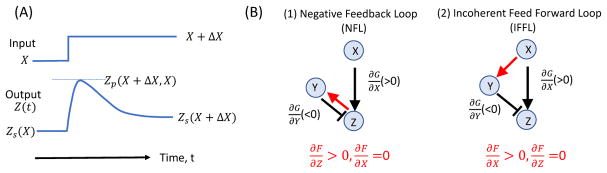
The nullclines from dZ/dt = 0 and dY/dt = 0 are given by Z = g(Y, X) and Y = f(Z, X) respectively. The steady state solution for a fixed X is determined by the intercept of the two nullclines. Here, we express the steady state solution as Y = Y_s(X) and Z = Z_s(X). A typical adaptive response is shown in Fig. 1A. Upon a sudden increase of the input from X to X + ΔX, the output of the system Z first changes from Z_s(X) to a peak value of Z_p(X + ΔX, X) before recovering (adapting) to its new steady state value Z_s(X + ΔX) at a longer time. In the following, we describe the basic requirements for adaptation.

Figure 1.

Generic adaptation behavior and responsible network motifs. A: Illustration of adaptation dynamics of the output Z(t) in response to a step function change in input from X to X + ΔX. B: The two basic network architectures (motifs) that can provide accurate adaptation. The red arrowed lines highlight the slow interactions critical for adaptation. Different placements of these slow interactions in the NFL and IFFL networks differentiate these two networks.

Separation of time scales

We can define the two time scales ${\tau }_Z\equiv -{\left(\frac{\partial G}{\partial Z}\right)}^{-1}$, and ${\tau }_Z\equiv -{\left(\frac{\partial F}{\partial Y}\right)}^{-1}$, which characterize the times scales for response and adaptation, respectively. To have a high sensitivity to a sudden change in its environment, a cell needs to first respond quickly. To maintain the high sensitivity over a wide range of backgrounds the cell needs to adapt to a constant environment over a longer time scale. Indeed, one of the key requirements for adaptation is the separation of these two time scales, i.e., τ_Z ≪ τ_Y. This means that the controller Y adjusts the system only after it has enough time to respond. Due to its slow time scale, Y can also be understood as a working memory for the signal encountered by the cell.

Response sensitivity and adaptation accuracy

There are two key characteristics for adaptation. The short time response is characterized by the response sensitivity defined as

$$S\equiv \frac{\mid Z_p(X+\mathrm{\Delta }X,X)-Z_s(X)\mid }{\mid \mathrm{\Delta }X\mid }$$ (2)

for a small ΔX. The long time recovery is characterized by the adaptation error, ε, defined as:

$$\epsilon \equiv \frac{\mid Z_s(X+\mathrm{\Delta }X)-Z_s(X)\mid }{\mid Z_p(X+\mathrm{\Delta }X,X)-Z_s(X)\mid },$$ (3)

which measures how close the output adapts back to its original value relative to the initial response. An adaptive behavior requires ε < 1, and a perfect adaptation corresponds to ε = 0 when the adapted output recovers to exactly its pre-stimulus value.

Network requirement for adaptation

Given the separation of time scales τ_Z ≪ τ_Y, the short time response Z_p can be expressed as Z_p(X + ΔX, X) ≈ g(Y_s(X), X + ΔX). For small |ΔX|, we can express the initial response as: $\mid Z_p(X+\mathrm{\Delta }X,X)-Z_s(X)\mid \approx \mid g(Y_s(X),X+\mathrm{\Delta }X)-g(Y_s(X),X)\mid =\mid \frac{\partial g}{\partial X}\mathrm{\Delta }X\mid$and the adapted response as: $\mid Z_s(X+\mathrm{\Delta }X)-Z_s(X)\mid =\mid g(Y_s(X+\mathrm{\Delta }X),X+\mathrm{\Delta }X)-g(Y_s(X),X)\mid =\mid (\frac{\partial g}{\partial X}+\frac{\partial g}{\partial Y}\times \frac{d{Y}_s}{dX})\mathrm{\Delta }X\mid$. Plugging these expressions in Eq. (3), the requirement ε < 1 results in a necessary condition for adaptation:

$$\frac{\partial g}{\partial X}\times \left[\frac{\partial g}{\partial Y}\times \frac{\partial Y_s}{dX}\right]<0.$$ (4)

The above requirement for adaptation has a simple intuitive interpretation: adaptation requires the two pathways from input to output – one direct ( $\frac{\partial g}{\partial X}$) and one indirect through $Y(\frac{\partial g}{\partial Y}\times \frac{d{Y}_s}{dX})$ – to have opposite signs, i.e., one excitatory and the other inhibitory.

Two basic network motifs for adaptation

Without losing generality, we assume that $\frac{\partial g}{\partial X}>0$, i.e., the output increases as the input increases. Furthermore, we consider the case where $\frac{\partial g}{\partial Y}<0$, i.e., the output has the opposite dependence on the control variable Y. From Eq. (4), we then have the condition for adaptation:

$$\frac{d{Y}_s}{dX}=\frac{\frac{\partial f}{\partial X}+\frac{\partial f}{\partial Z}\frac{\partial g}{\partial X}}{1-\frac{\partial f}{\partial Z}\frac{\partial g}{\partial Y}}\approx \frac{\partial f}{\partial X}+\frac{\partial f}{\partial Z}\frac{\partial g}{\partial X}>0,$$ (5)

where the last approximation was obtained by using $\frac{\partial f}{\partial Z}\frac{\partial g}{\partial Y}\propto {\tau }_Z/{\tau }_Y\ll 1$.

This adaptation condition is satisfied by two basic networks with a minimum number of non-zero interactions: (1) ∂f/∂Z > 0, ∂f/∂X = 0, and (2) ∂f/∂X > 0, ∂f/∂Z = 0. As illustrated in Fig. 1B, the first network is called the negative feedback loop (NFL) network because of the negative feedback loop Z → Y → Z. The second network is called the incoherent feed-forward loop (IFFL) network because the loop is formed by two feedforward paths, X → Z and X → Y → Z, with opposite (incoherent) signs. Indeed, an exhaustive search of all possible three-node networks found that NFL and IFFL are the only two basic network motifs that enable strong response and accurate adaptation (1).

In realistic biological systems, the dynamical variables are protein concentrations in different conformational states, and interactions are carried out by enzymatic reactions with many intermediate control elements (a vector Y⃗). However, despite their simplicity, the general dynamical system model and the basic network structures (NFL and IFFL) provide a powerful framework to understand adaptation in a wide range of different cellular systems including E. coli and Dictyostelium, which we describe below.

3. Adaptation in Bacterial Chemotaxis

Due to its relative simplicity, E. coli chemotaxis has served as an important model system to study sensory adaptation. It was first observed by Berg and Brown more than 40 years ago that upon a sudden increase in the concentration of chemo-attractant aspartate, a cell’s tumbling frequency first decreases then it recovers and eventually returns back to its prestimulus level (2). The adapted value of the tumbling frequency remains the same for a wide range of the stimulus strengths (aspartate concentrations). This accurate adaptation is remarkable given the large variations in the concentrations of the key biomolecules among individual cells (3). The quest for the molecular mechanism of adaptation motivated a large body of in-depth study into E. coli chemotaxis, which resulted in a quantitative understanding of the system.

3.1. Molecular Mechanism

Signal transduction

The bacterial chemotaxis signaling pathway has been well studied (see (4) for a review on the signaling pathway). External chemical signals are sensed by the membrane bound chemo-receptors in a bacterial cell such as E. coli. When chemoeffector molecules (ligands), such as amino acids and sugar molecules, bind with chemo-receptors, they induce subtle conformational changes of the receptor, which in turn control the kinase activity of the cytosolic protein CheA. The chemo-receptors, histidine kinase CheA, and an adaptor protein CheW form extended two dimensional cluster with up to thousands of proteins in them (5). These receptor clusters with many directly and indirectly coupled receptors are responsible for signal amplification in the system (see (6) for a recent review on modeling). The activated CheA first auto-phosphorylates and then passes the phosphate group onto the response regulator proteins CheY and CheB. The phosphorylated CheY, CheY-P, can bind with the motor switch protein FliM to control the bacterial flagellar motor’s rotational direction and thus the cell’s motility. This constitutes the “linear” part of the signal transduction in bacterial chemotaxis.

Adaptation mechanism

The linear signal transduction pathway described above allows the cell to sense and respond. However, the range of stimulus concentrations over which a cell can respond to is limited by the sensitivity range of the chemo-receptor, which is finite (less than one order of magnitude). The question arises as to how the bacterial chemosensory system functions in an environment with a wide range of chemoeffector concentrations. The answer is adaptation. We now know that at the molecular level, bacterial chemo-receptors adapt by covalent modification, i. e., methylation and demethylation catalyzed by the enzymes CheR and CheB-P, respectively. Receptor adaptation dynamically adjusts its sensitive range according to the background and allows the receptor to detect changes in the environment using the most sensitive part of its response curve.

3.2. The Standard Model of Bacterial Chemotaxis

The state of a given receptor can be represented by three variables: its activity a, its ligand occupancy status l determined by the ligand concentration [L], and its methylation level m. For a simple two-state (active and inactive) model for a receptor with 5 methylation levels and ligand binding status (ligand-bound and vacant), there are 2 × 2 × 5 = 20 states with 4 × 9 × 2 = 72 reactions among them. Mathematical models based on the transitions between these discrete states were used to study the dynamics and robustness of the system (7, 8, 9). Here, we use a simple coarse-grained model to describe the dynamics of the averaged properties of the system. Following the convention developed in the previous section, we define the output Z ≡< a > and controller Y ≡< m >, which are both continuous variables. The input is the ligand concentration X ≡ [L] (the correspondence between the different variables is summarized in Table 1). Below, we develop the simplest mathematical model for these averaged variables guided by separation of time scales and quantitative experiments.

Table 1.

Notational correspondence for bacterial and eukaryotic chemotaxis.

This review	Bacterial chemotaxis	Eukaryotic chemotaxis
Input X	Ligand concentration [L]	Ligand concentration (R)
Internal Y	Methylation level m	Activator/Inhibitor (RasGEF, RasGAP)
Output Z	Receptor activity a	Output (RasGTP)

Fast response dynamics

For bacterial chemotaxis, both the ligand binding dynamics and kinase activity dynamics are faster than the receptor methylation process. Therefore, at a time scale faster than the methylation time, we only consider the dynamics of the output Z with a constant Y:

$$\frac{dZ}{dt}=-[Z-g(Y,X)]/{\tau }_Z,$$ (6)

where τ_Z is a fast time scale that depends on both the ligand binding and kinase activation dynamics. In steady state, we have Z = g(Y, X). The functional form of g(Y, X) can be determined experimentally by measuring the input-output relationship (Z versus X) in cells with a fixed value of Y, e.g., by knocking out the methylation (CheR) and/or demethylation (CheB) enzymes (10, 11). Experimentally, this input-output relationship was found to follow a sigmoidal form with a large Hill coefficient. Theoretically, this input-output dependence can be explained by a Monod-Wyman-Changeux (MWC) model (11, 12, 13), for a large cluster of high cooperative (all-or-none) receptors or by an Ising-type model where receptors interact with its nearest neighbors in a extended lattice of receptors(14, 15, 16). The MWC model leads to a simple analytical result, which we use here:

$$g(Y,X)={[1+e^{N{f}_m(Y)}{(\frac{1+X/K_i}{1+X/K_a})}^N]}^{-1},$$ (7)

where N is the number of highly correlated receptors in the cluster, K_a(i) are the dissociation constants for the active (inactive) receptor with K_a ≫ K_i. The effects of receptor methylation are given by the free energy difference f_m(Y) between active and inactive states for a receptor that is not bound to the ligand. From experimental data, we have f_m(Y) ≈ −α(Y − m₀), and thus depends (roughly) linearly on Y with α ≈ 1.7 (17, 18).

Slow adaptation dynamics

From Eq.(7), it is clear that varying Y shifts the sensitivity of the input-output response. How does the system adjust its receptor methylation level in response to changes in the environment to enable adaptation? Details of the enzymatic reactions (methylation and demethylation) and their kinetic rates are not well known. However, significant insights into the methylation dynamics were gained by the systems level adaptation behavior. For E. coli chemotaxis, adaptation is highly accurate with an error ε ~ 1 – 4%, i.e., the adapted value of Z activity is independent of the input X, a phenomenon called perfect adaptation. A simple way to achieve perfect adaptation is to have the methylation rate function F to depend only on Z:

$$\frac{dY}{dt}=F(Z),$$ (8)

where the explicit dependence of F on Y and X are negligible. In steady state the adapted activity is determined by F(Z) = 0, which results in an adapted activity Z = Z_s independent of the input X. This perfect adaptation mechanism is related to the integral control system in engineering (19).

Given that $\frac{\partial g}{\partial Y}>0$, we need to have $\frac{dF(Z)}{dZ}<0$ (at least near Z = Z_s) to maintain stability of the adapted state. Therefore, the interactions between the output (Z) and the controller (Y) have opposite signs $\frac{dF(Z)}{dZ}\times \frac{\partial g}{\partial Y}<0$, which clearly indicates that bacterial chemotaxis adaptation is carried out by a negative feedback loop (NFL) network. Combining the fast and slow dynamical equations, Eq.(6) and Eq. (8) constitute the “standard model of bacterial chemotaxis” (20), which can be used to predict responses to arbitrary input signals (21, 18).

3.3. Comparison with Quantitative Experiments

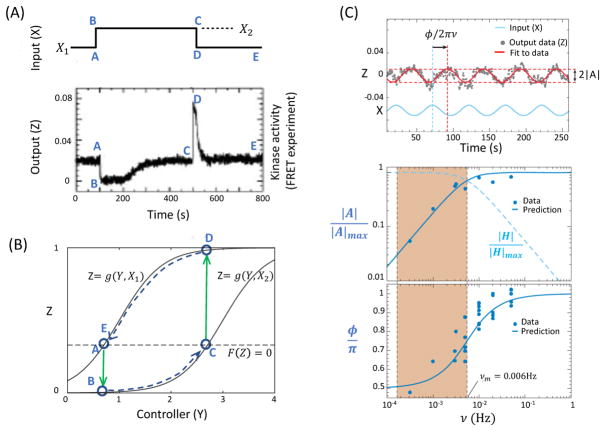
For simple step function (adding and removal) stimuli, the response of the cell have been measured in vivo by using Förster Resonance Energy Transfer (FRET) method, see Fig. 2A for a typical response to a strong stimulation (10). The standard model can be analyzed by using the nullcline analysis and exploiting the separation of time scales, as shown and explained in Fig. 2B. Furthermore, the standard model has been used to predict responses to more complex time-varying signals to compare directly with quantitative experiments.

Figure 2.

Comparison between predictions of the standard model of bacterial chemotaxis and quantitative experiments. A: Response of E. coli to step up and step down (addition and removal) of attractant MeAsp concentrations (X₁ and X₂). The response (kinase activity) is measured by using FRET (data from Sourjik and Berg(10)). B: The nullcline analysis of the dynamical equations for bacterial chemotaxis. The lettered time points (A–E) correspond to those in panel A. The solid grays lines are the Z-nullclines, Z = g(Y, X₁) and Z = g(Y, X₂), for different inputs X₁ and X₂(> X₁), respectively. The dotted line is the Y-nullcline expressed as F(Z) = 0 or Z = Z_s a constant. The solid arrowed lines (green) show the fast responses caused by changes (adding and removal) of input X between X₁ and X₂. The dotted arrowed lines (blue) show the slow adaptive dynamics along the Z–nullclines. C: The responses to oscillatory signals (top panel) are characterized by the response amplitude |A| and the phase shift ϕ. Both dependences of |A| (middle panel) and ϕ (bottom panel) on the input frequency ν agree with predictions from the standard model quantitatively. The results show that the system computes the time derivative of the signal at low frequencies (shaded region) where ν < ν_m ≈ 0.006Hz. The gradient computation can be seen directly by defining H ≡ A/(iνA_L), which remains roughly constant in the shaded region (dotted blue line in the middle panel). Part C is adapted from ref.(18).

Responses to ramps

In an environment where the attractant concentration keeps increasing in time, the receptor methylation level increases continuously to adapt. However, due to the slow adaptation, the system can only manage to adapt to an activity level Z_c that is lower than Z_s. In fact, for an exponential ramp: X = X₀e^rt with r the ramp rate, it was shown (20) from the standard model that Z_c is a constant that depends on the ramp rate r: Z_c = F⁻¹(r/α) where F⁻¹ is the inverse function of F. This remarkable connection provides a way to determine the intracellular rate function F(Z) by measuring cellular ramp responses. Indeed, a thorough in vivo study of the ramp responses using FRET (18) not only confirmed the model prediction, it also quantitatively determined the rate function F(Z). In fact, F(Z) is found to have a large linear regime around Z_s, i.e., F(Z) ≈ k_RB(Z_s − Z), where the parameter k_RB depends on the kinetic rates for the methylation and demethylation reactions catalyzed by CheR and CheB-P, respectively.

Responses to oscillatory signals

Once F(Z) is determined, the standard model can be used to predict responses to any time varying signals without any adjustable parameters. For an exponentiated sine-wave signal X(t) = X₀ exp[A_L sin(2πνt)], the standard model predicts that the response is Z(t) = Z_s + Re(A), where the complex response A = A_L exp(i(2πνt − ϕ)) with the amplitude |A| and a phase delay ϕ given by:

$$\mid A\mid =\frac{N{Z}_s(1-Z_s)}{\sqrt{1+{({\nu }_m/\nu )}^2}}{A}_L,\varphi =\pi -{tan}^{-1}({\nu }_m/\nu ),$$ (9)

where ν_m = −αNZ_s(1 − Z_s)F′(Z_s)/2π is a characteristic adaptation frequency. These predictions, Eq. (9), agree quantitatively with experiments as shown in Fig. 2C (18). Finally, by taking the Fourier transform of the signals time derivative B ≡ iνA_L and factoring this out from the response, we obtain the systems time-derivative-filtering function H ≡ A/B = NZ_s(1 − Z_s)(iν + ν_m)⁻¹, which is a constant for ν ≪ ν_m as shown in Fig. 2C. This clearly shows that E. coli computes time derivative of the signal at frequencies lower than the adaptation frequency ν_m.

Responses to realistic signals

Besides predicting responses of immobile cells to prescribed time-varying signals, the standard model has been used to understand intracellular signaling dynamics of free moving cells (22, 23). The combination of the standard model for the signaling pathway and a quantitative model for the flagellar motor response has yielded significant insights and quantitative predictions on how motile cells behave in spatial-temporally varying environments. These predictions have been tested in microfluidic experiments with stationay, stand-wave, and traveling wave gradients (24, 25, 26).

4. Adaptation in Eukaryotic Chemotaxis

Adaptation is not limited to bacterial chemotaxis but is also critically involved in eukaryotic chemotaxis. A number of eukaryotic cells respond to chemical gradients and direct their motion to higher chemoattractant concentrations (27, 28, 29). Chemotaxis plays an essential role in several biological processes, including wound healing (30), embryology (31, 32) and cancer cell migration (33). Just as in the case of bacterial chemotaxis, the external chemoattractant molecules binds to surface receptors, activating intra-cellular signaling pathways that involve a multitude of biochemical components (34). The precise molecular mechanisms for eukaryotic chemotaxis are still under debate (28, 35, 36, 34) but many of the pathway components are identified, Furthermore, these pathways are mostly conserved across different cell types, making it possible to use experimentally accessible model systems (37, 38, 39). One of the best studied model systems is Dictyostelium discoideum, a social amoeboid that uses chemotaxis to form aggregation centers following starvation (40, 41). Dictyostelium cells move fast and are relatively easy to manipulate in a laboratory setting. Furthermore, many fluorescent reporters are available which makes it possible to quantify response kinetics and amplitudes.

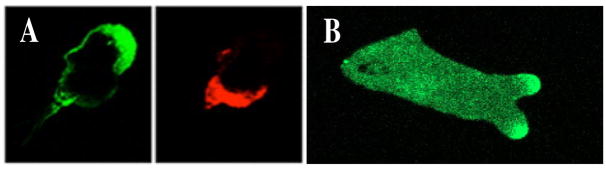
How do eukaryotic cells employ chemotaxis? Just as bacteria, eukaryotic cells are able to adapt themselves to their changing surroundings as they move up the gradient. The logic is the same as for bacteria: with an adaptive approach, cells can maintain their responsiveness over a wider range of background concentration (42, 43). Nevertheless, there are a number of important differences between bacterial chemotaxis and chemotaxis in eukaryotes. These differences are primarily due to the contrasting modes of motion between the two cell types as well as their size disparities. Instead of swimming, eukaryotic cells crawl and migrate by extending their membrane at the front of the cell while retracting the back of the cell (44, 45, 27). The resulting migration speed can range from less than 1 μm/min for macrophages and fibroblasts (46, 47) to approximately 10 μm/min for neutrophils and Dictyostelium cells (48, 49), considerably slower than the typical swimming speed of bacteria ~25 μm/s (2). Chemotaxing eukaryotic cells are, in general, also much larger than bacteria and their 2 μm size, ranging from 10 μm in diameter (neutrophils and Dictyostelium) to roughly 100 μm for elongated fibroblasts. Taken together, the much smaller speed and larger cell sizes preclude eukaryotic cells from using the time measurement mechanisms employed by swimming bacteria. Instead, these cells use spatial directional sensing mechanisms, in which the cell’s symmetry is broken, leading to a distinct back and front that can be visualized using fluorescent markers (Fig. 3) (50, 51, 52).

Figure 3.

A: Example of spatial asymmetry breaking in a neutrophil exposed to a gradient (towards the upper right). Shown are the distribution of actin (left) and phosphorylated myosin light chain (right) as revealed by fluorescent staining (From (53)) B: Spatial symmetry breaking in a Dictyostelium cell in a gradient pointing to the right. Visualized is the localization of activated Ras (RasGTP) using a Ras Binding Domain fused to Green Fluorescent Protein (RBD-GFP).

How might adaptation help eukaryotic cells during chemotaxis? Several experimental studies have shown that cells can detect very small gradients (54). For example, Dictyostelium cells can respond to concentration differences of approximately 1% across the cell body (55, 56). In addition, these cells respond to gradients with a large range of background concentrations, defined here as the spatially averaged concentration experienced by the cell. Thus, cells cannot determine their direction based on a fixed operating point as this would make them responsive only over a very small concentration range. Instead, cells must be able to compare bound receptor levels at their front and back independent of the background concentration. As suggested by several studies, this comparison will be facilitated by adaptation which ensures that the difference between front and back is independent of background levels (57, 58, 59). Importantly, experiments monitoring FRET between two subunits of the receptors have demonstrated that this adaptation occurs downstream from the chemoattractant receptors (60).

4.1. Experimental Evidence for Adaptation

Early experiments, using observations of morphological changes or using cell population assays, have suggested that cells can adapt to changing stimuli (61, 62). A more quantitative analysis of adaptation has been made possible by the recent introduction of microfluidics, coupled to improved microscopy. These experimental technique make it possible to study the dynamics of markers in single cells exposed to carefully controlled environments (63, 64, 65, 48, 56, 66, 52, 67). Recently, Takeda et al. quantified the dynamics of activated Ras, Ras-GTP, measured using the fluorescent reporter RBD-GFP (68, 69) following step stimuli of chemoattractant. This signaling component was chosen since it is immediately downstream from the G protein-coupled chemoattractant receptors, with Ras likely activating a range of downstream effectors. Thus, its response should be a more direct read-out of adaptation than components that are further downstream and which can be part of multiple feedforward and feedback loops.

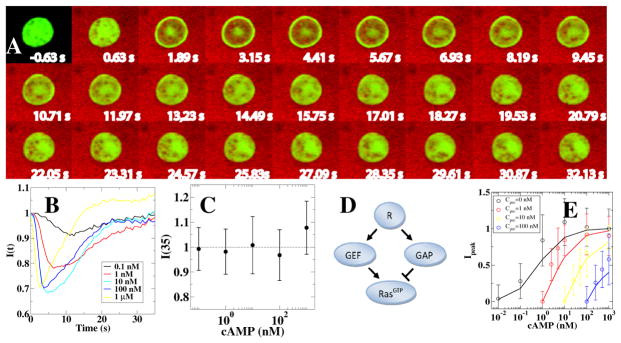
Takeda et al. found that without a change in the external cAMP concentration, RBD-GFP is found to be uniformly distributed in the cytosol (Fig. 4A). Upon a sudden increase in external cAMP concentration, however, RBD-GFP rapidly localizes to the membrane, followed by a gradual return to the cytosol (Fig. 4B). Ras dynamics was quantified following concentration increases of several orders of magnitude (0.1 nM to 1 μM) and it was found that cytosolic RBD-GFP returned to its pre-stimulus level after approximately 35s, indicating perfect adaptation (Fig. 4C). Furthermore, as can be observed from Fig. 4B, the time of the peak response decreases for increasing concentration changes. Similar qualitative behavior was found in the study by Wang et al. which examined the dynamics of PI3K (phosphoinositide 3-kinase) activation using a fluorescent phosphatidylinositol 3,4,5-trisphosphate (PIP3) specific biosensor (70) following a step change in cAMP.

Figure 4.

Adaptation measured in Dictyostelium cells (From (68)). A: Snapshots of a cell undergoing a sudden increase in chemoattractant concentration at t = 0 s (visualized in red). Activated Ras is visualized using RBD-GFP, which shows a transient translocation to the membrane. B: The RBD-GFP cytosolic fluorescence intensity, I(t), normalized by the fluorescence intensity before stimulation, as a function of time for different amounts of stimulation. Note that the time for peak response decreases when the stimulus strength increases. C: The RBD-GFP cytosolic fluorescence intensity as a function of stimulus strength shows perfect adaptation. D: Incoherent feedforward network topology consistent with experimental data: chemoattractant binds to receptors R which activate both RasGEF and RasGAP. These two enzymes then activate (GEF) and inactivate (GAP) Ras. E: Experimental results (RBD-GFP dose-response curves for different pretreatment concentrations, plotted as symbols) and the results of the incoherent feedforward network using model parameters obtained by fitting (plotted as lines).

4.2. Network Topology for Adaptation in Eukaryotic Chemotaxis

The finding that activated Ras dynamics adapts perfectly suggests that one of the two basic network motifs described above (negative feedback loop, NFL, or incoherent feed-forward loop IFFL) should be at the heart of the signaling network. Indeed, the quantitative data from the Takeda et al. experiment is able to rule out the NFL network and is consistent only with the IFFL motif. This can be most readily seen by examining the dynamics of the adaptation as a function of stimulus size. For the NFL motif, the time scales of reaching the maximum response and the subsequent return to basal levels increase significantly as the stimulus size is increased. This can be intuitively understood by realizing that the NFL motif works through a feedback loop. Consequently, a larger stimulus will result in larger deviations from equilibrium, requiring more time to return to basal levels.

For the IFFL motif, on the other hand, the response time can actually decrease upon increasing stimulus strength. This can be seen by analytically examining the dynamics of the response as a function of stimulus strength using simple zero-order forms for F and G:

$$\begin{gathered} \frac{dZ}{dt}=k_{Z}X(1-Z)-k_{-Z}YZ, \\ \frac{dY}{dt}=k_{Y}X-k_{-Y}Y. \end{gathered}$$ (10)

The steady state values are Y_s = k_Y X/k_−Y and Z_s = (k_−Y k_Z)/(k_−Y k_Z + k_Y k_−Z), illustrating that Z is independent of X, the hallmark of perfect adaptation. To approximate the dynamics of recovery, we assume that activation is much faster than inhibition so that we can use the quasi-steady approximation resulting in

$$\frac{1}{X}\frac{dZ}{dt}=k_Z(1-Z)-\frac{k_Y{k}_{-Z}}{k_{-Y}}Z$$ (11)

Thus, the recovery time scale increases with X, consistent with the experimental results.

To further determine whether the incoherent feed-forward topology is consistent with the experiments, Takeda et al. fitted the experimental data to a model containing an IFFL motif. The model is based on the biochemistry of Ras: Ras is activated by RasGEFs (guanine nucleotide exchange factors) and inactivated by RasGAPs (GTPase activating proteins). Thus, in the adaptation scheme of Fig. 1, RasGAP is the equivalent of ”Y”, activated Ras is the equivalent of ”Z”, and the chemoattractant concentration plays the role of ”X”. To account for the role of RasGEF, an additional node between the chemoattractant concentration and activated Ras (i.e., X and Z) was inserted. This correspondence between the variables is listed in Table 1. In addition, receptor kinetics was incorporated using experimentally determined values for the binding dynamics. The resulting topology, shown in Fig. 4D, has the same qualitative features as the IFFL motif of Fig. 1. The output of the model was tested using a subset of experimental data points and the value of the parameters were adjusted using a fitting procedure (68). The final model was able to reproduce all experimental results; for example, the dose-response curves of the model (lines) and of the experiments (symbols) show good agreement (Fig. 4E). The experimental curves in this figure were obtained using cells that were exposed to different and constant chemoattractant concentrations for prolonged times. Other comparisons, involving full time traces and sudden decreases of cAMP concentrations, also show satisfactory agreement between experiment and model, indicating that the IFFL motif is responsible for adaptation.

A similar conclusion was reached by Wang et al. who used a different stimulus protocol to distinguish between the two possible network motifs. Specifically, they used a linear ramp signal X = X₀ + βt where β represents the increase in concentration per unit time. It is possible to obtain an exact expression for Y as a function of time:

$$Y(t)=\frac{k_Y}{k_{-Y}}\left(X_0+\beta t+\frac{\beta }{k_{-Y}}(e^{-k_{-Y}t}-1)\right)$$ (12)

Thus, for large t, both Y and X both will increase linearly and will be proportional to the slope of the signal ramp. Therefore, the output Z will not depend on the signal and will adapt perfectly. Note, however, that in general this adaptation is slower than when a step stimulus is applied. In contrast, the NFL motif does not adapt in response to a linear ramp. The experiments of Wang et al. show that PI3K activity adapts, independent of the rate of increase of cAMP (70). Thus, combined with the study of Takeda et al., these results imply that adaptation in eukaryotic and bacterial chemotaxis operate using different mechanisms: IFFL for eukaryotes and NFL for bacteria.

4.3. Connection to Directional Sensing Models

Even though the topology of the chemotactic pathway was found to be different than the well-established bacterial chemotaxis pathway, its discovery was not a complete surprise. Eukaryotic models for chemotaxis do not only have to deal with the response to uniform concentration changes but also need to explain the spatial asymmetry observed when cells are placed in a gradient (see Fig. 3). One of the early models for directional sensing is the Local Excitation, Global Inhibition (LEGI) model, originally proposed by Parent and Devreotes (57). It contains the IFFL topology and assumes that excitation occurs locally and rapidly and that inhibition is slower and more global, modeled by including a diffusive term for the inhibitor (GAP in Fig. 3D). The main idea here is that the inhibitor will cancel out the effect of the average receptor occupancy whereas the local excitation will allow for response to local variations away from the mean (58). Adaptation will then result in a larger response at the side of the cell that is directed to the higher chemoattractant concentration than to the side pointed away from the chemoattractant source.

Even though the LEGI displays perfect adaptation and creates a spatial asymmetry in the presence of a chemoattractant gradient, it is not able to fully capture eukaryotic chemotaxis. The problem is that the generated asymmetry is always smaller than the asymmetry from the gradient. In other words, the LEGI mechanism is not able to amplify an external signal and, instead, simply reads off the external gradient. Several models have been proposed to provide the necessary amplification. For example, a variant of the LEGI model incorporates the idea of zeroth order ultrasensitivity (71). It no longer assumes that the enzymes that control the read-out component are unlimited, resulting in a reaction that is modeled by the full Michaelis-Menten kinetics. Then, for certain parameter values, the read-out component of the network can rapidly switch between a low and high state, resulting in the desired amplification (72). Another gradient sensing model uses a modular approach and postulates that the output of a LEGI module feeds into an excitable module (73, 74). Obviously, this model is still able to adapt perfectly and can generate a large response due to its excitable nature. The fact that cell responses can be described by excitable features was also noted by other studies (75, 76, 77, 78) and is motivated by the transient and stochastic protrusions and retractions of membrane extensions of cells as well as the signaling ”patches” following cAMP stimulation (79, 80). A model cell placed in a gradient will produce a LEGI response that is higher at the front than at the back of the cell. By carefully choosing the model parameters, this will result in excitations that occur more frequently at the front of the cell.

4.4. Scale Invariant Adaptive Response

In addition to perfectly adaptive, the response of the LEGI model to sudden stimulus changes can also be scale invariant. A response is said to be scale invariant if its dynamics depends solely on the ratio between the pre- and post-stimulus level. In other words, scale invariance implies that a stimulus change from X₀ to X₁ gives the same response as a stimulus change from pX₀ to pX₁. Such a “fold-change detection” has been investigated theoretically (81, 82, 83) and has been demonstrated experimentally in E. coli chemotaxis (84). In a more recent study, general necessary and sufficient rules for scale invariance were obtained for three-node network topologies (85). Furthermore, this study investigated whether the topology found in Ref. (68) (and shown in Fig. 4B) exhibits scale invariance. Examining the basic IFFL model of Eqns. 10 reveals that it is not perfectly scale invariant: changing the input X → pX in the core model will lead to Y → pY. The equation for the output, however, shows that Z depends non-trivially on both X and Y, leading to dynamics that is not scale invariant. However, in the limit where the output dynamics is very fast we can use the quasi-steady state approximation. Then, Z is given by its steady state value which can be easily verified to be invariant under a fold change in the input.

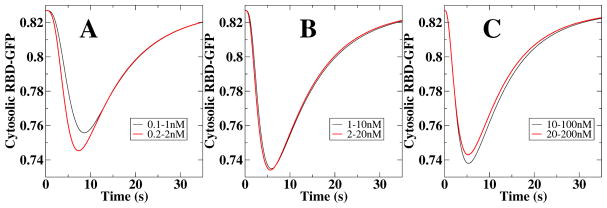
The full adaptation model, detailed in Ref.(68), only displays scale invariance for intermediate values of cAMP stimuli. This is shown in Fig. 5 where we plot the response of the full model, measured as the level of RBD-GFP, to various changes in external cAMP concentrations. For intermediate values of cAMP, the curves for 1–10nM and 2–20nM steps are nearly indistinguishable, indicating scale invariance (Fig. 4D and Fig. 6 in (85)). For smaller and for larger values of cAMP, however, the response is no longer scale invariant, as can be seen in Fig. 5A and C. The reason for the absence of scale invariance for small values of cAMP is that the steady state approximation breaks down (for an in-depth discussion of the necessary conditions for scale invariance we refer to Ref. (85)). For large values of cAMP, on the other hand, the equation of the receptor occupancy in the full model is no longer linearly dependent on the chemoattractant concentration due to receptor saturation. The resulting non-linear dependence on the cAMP concentration results in responses that are not scale invariant. These results should be testable using the microfluidics system of Takeda et al. in which the concentration is stepped systematically.

Figure 5.

Response of the adaptation model of Ref. (68) to different stimulus steps. Only the responses in B are precisely scale invariant.

5. The Effect of Adaptation: the Weber-Fechner law

Why is adaptation so essential in biology? The general answer is that adaptation allows a living system to function normally in a wide range of backgrounds. For sensory systems, this qualitative explanation is related to the well known empirical Weber-Fechner (WF) law, which states that the response (or perception) of an adaptive sensory system is proportional to the relative change in stimulus. In the following, we describe a general scaling theory for adaptive response to demonstrate the WF law.

5.1. A General Scaling Theory for Adaptive Response

As we discussed in Sec. 2, for a system adapted to an external stimulus level X, the fast response to a sudden change of stimulus to X + ΔX can be obtained by assuming that the internal variable Y remains roughly unchanged Y ≈ Y_s(X) due to its relatively slow dynamics. Based on the general observation that the primary effect of adaptation is to shift the response curve without changing its shape, we hypothesize that adaptation mainly normalizes the input by a factor K(Y_s). The peak value can then be written as:

$$Z_p(X+\mathrm{\Delta }X,X)\approx R\left(\frac{X+\mathrm{\Delta }X}{K(Y_s(X))}\right)\equiv R\left(\frac{X+\mathrm{\Delta }X}{K_s(X)}\right),$$ (13)

where R is the response function and K_s(X) is the scaling factor that depends on the background X through its direct dependence on Y_s.

The adapted output Z_s(X) at the background level X is given by Z_s(X) = R(X/K_s(X)), from which we can compute the sensitivity S:

$$S(X)\equiv \left|\frac{\mathrm{\Delta }Z}{\mathrm{\Delta }X}\right|\equiv \left|\frac{Z_p(X+\mathrm{\Delta }X,X)-Z_s(X)}{\mathrm{\Delta }X}\right|=K_s{(X)}^{-1}{R}^{\prime }(X/K_s(X)),$$ (14)

where R′ is the derivative of R.

In order to adapt over a wide range of backgrounds, the scaled stimulus strength X/K_s(X) needs to be roughly a constant for a wide range of X. To satisfy this condition, K_s needs to depend roughly linearly on X:

$$K_s(X)\approx K_0+\lambda X,$$ (15)

where K₀ and λ are constants. Perfect adaptation corresponds to K₀ = 0, where the adapted output Z_s(X) = R(λ) is independent of X. The case of no adaptation corresponds to λ = 0, where K_s = K₀ does not change with X at all.

By using Eq. (15) for K_s(X), we can compute the sensitivity from Eq. (14):

$$S(X)={(K_0+\lambda X)}^{-1}{R}^{\prime }(\frac{X}{K_0+\lambda X})\to C_0{X}^{-1}$$ (16)

for X ≫ K₀/λ with C₀ ≡ λR′(λ) a constant. From Eq. (16), we have $\mid \mathrm{\Delta }Z\mid =C_0\frac{\mid \mathrm{\Delta }X\mid }{X}$, which is exactly the Weber-Fechner (WF) law. The WF law dictates that the response only depends on the relative change of the stimulus, which is related to the fold-change detection idea that has been studied recently in both bacterial chemotaxis (86) and eukaryotic chemotaxis (85, 68) as discussed in the last Section. Here, we demonstrate the WF law regardless of details of the specific system such as its response function R as long as the general scaling hypothesis for adaptive response, Eq. (13), holds.

Next, we show the validity of the scaling hypothesis in both bacterial chemotaxis and eukaryotic chemotaxis and how the WF law can be applied to study adaptive sensory systems in general.

5.2. The Weber-Fechner Law in Different Sensory Systems

Bacterial Chemotaxis

As described in Section 3, an E. coli cell adapts to an environment with background chemical concentration X by adjusting its chemo-receptor methylation level to Y_s(X), which restores its preferred activity Z_s. When the concentration changes suddenly to a new level X + ΔX, the immediate response is given by Eq. (7). Within the range of receptor sensitivity K_i ≪ X ≪ K_a, we can simplify Eq. (7) to obtain the response in activity:

$$Z_p(X+\mathrm{\Delta }X,X)={\left[1+{\left(\frac{X+\mathrm{\Delta }X}{K_s(X)}\right)}^N\right]}^{-1},$$ (17)

which satisfies the scaling hypothesis Eq. (13). More specifically, the response function R in E. coli chemotaxis takes the form of a Hill function with a Hill coefficient N. By determining Y_s using the perfect adaptation condition Z_p(X, X) = Z_s, the scaling function is given by $K_s(X)=K_{i}exp(\alpha (Y_s-m_0))={(Z_s^{-1}-1)}^{\frac{1}{N}}X$, which depends linearly on X, confirming the scaling assumption Eq. (15) for adaptation.

We can compute the sensitivity at background X ≫ K_i:

$$S(X)\approx N{Z}_s(1-Z_s)X^{-1},$$ (18)

which is exactly the WF law. For a non-adaptive cell, the receptor methylation level does not change. For high background concentrations X ≫ K_i, the sensitivity of the non-adaptive cell $S_{na}(X)\approx N{K}_i^N{X}^{-(N+1)}$ decays much faster than S(X).

Eukaryotic Chemotaxis

For eukaryotic chemotaxis, adaptation is achieved by an IFFL network, whose dynamics are described by Eq. (10). We can compute the response by first using the quasi-equilibrium condition to determine the internal variable $Y_s\approx \frac{k_Y}{k_{-Y}}X$ at a background X. After the input changes from X to X + ΔX, the output Z starts to increase and the peak response can be found by setting dZ/dt = 0 in Eq. (10), which results in

$$Z_p(X+\mathrm{\Delta }X,X)\approx \frac{k_Z(X+\mathrm{\Delta }X)}{k_Z(X+\mathrm{\Delta }X)+k_{-Z}{Y}_s}=\frac{u}{u+1},$$ (19)

where u = (X + ΔX)/K_s(X). The scaling function $K_s(X)=k_{-Z}{k}_Z^{-1}{Y}_s=\frac{k_{-Z}{k}_Y}{k_{-Y}{k}_Z}X$ depends linearly on X in agreement with the perfect adaptation condition Eq. (15). The sensitivity at background X can be easily determined:

$$S(X)=(1-Z_s)Z_s{X}^{-1},$$ (20)

which follows the WF law. For non-adaptive mutants with a fixed Y, it is easy to show that the sensitivity decays faster as X⁻².

From Eq. (18) and Eq. (20), we show that the scaling hypothesis for adaptive response holds and the WF law is universal for adaptive systems independent of the underlying biochemical network structure (NFL or IFFL).

Sensory Neurons

The general scaling model for adaptive response can be used to describe adaptive system even in cases where the detailed adaptation mechanism is not fully understood. The functional form of the response function R can be measured by non-adaptive mutants in which K_s remains a constant independent of the background. Once R is determined, then all responses of the adaptive wild-type (WT) cells in any given backgrounds can be determined by just two parameters K₀ and λ. This approach has been used successfully to explain response sensitivities in both the rhodopsine and the olfactory neurons (87).

6. Nonequilibrium Thermodynamics of Adaptation

Inside a living cell, all biological functions, including adaptation, are carried out by biochemical reactions with a relatively small number of molecules (much smaller than Avogadro’s number). The stochastic nature of molecular reaction and diffusion give rise to significant fluctuations in biochemical reactions. Another general feature of living systems is that they are far from equilibrium. Living matter is highly dissipative. Chemical free energy harvested by metabolic processes powers interactions of living matter in different biochemical networks to achieve various biological functions. How do we describe the nonequilibrium thermodynamics of a small living system? How can a cell function accurately in the face of these noisy biochemical reactions? In the following, we will address these questions in the context of cellular sensory adaptation.

6.1. Breakdown of Detailed Balance

To understand the effect of noise in adaptation dynamics, we introduce the Langevin dynamics by including noise in the simple dynamical equations described in Section 2:

$$\frac{dZ}{dt}=G(X,Y,Z)+{\eta }_Z,,\frac{dY}{dt}=F(X,Y,Z)+{\eta }_Y,$$ (21)

$$\langle {\eta }_Z(t+t^{\prime }){\eta }_Z(t^{\prime })\rangle ={\mathrm{\Delta }}_Z\delta (t),\langle {\eta }_Y(t+t^{\prime }){\eta }_Y(t^{\prime })\rangle ={\mathrm{\Delta }}_Y\delta (t)$$ (22)

where η_Y and η_Z are noise terms due to the stochastic nature of the underlying biochemical reactions. In general, the noise strength Δ_Y and Δ_Z can depend on the variables (X, Y, Z).

For an equilibrium system with an energy functional ℰ(X, Y, Z), its dynamics is driven by the local gradient of ℰ(X, Y, Z) in addition to thermal fluctuations. For example, in its simplest form, we can have $G=-\frac{\partial \mathcal{E}}{\partial Z}$, and $F=-\frac{\partial \mathcal{E}}{\partial Y}$ with the noise strength Δ_Y = Δ_Z = 2k_BT where k_BT is the thermal energy of the heat bath the system is in equilibrium with. It is easy to show that the equilibrium Langevin equation leads to the Boltzmann distribution $exp(-\frac{\mathcal{E}}{k_{B}T})$. Independent of the specific form of ℰ(X, Y, Z), the constrain $\frac{\partial G}{\partial Y}=\frac{\partial F}{\partial Z}$ is satisfied by all equilibrium systems as a result of the detailed balance (88). However, as we discussed in Sec. 2, for adaptive systems these two cross derivative terms have different signs and thus can not be equal:

$$\frac{\partial G}{\partial Y}\ne \frac{\partial F}{\partial Z},$$ (23)

which means that detailed balance is violated in adaptation. This means that the underlying biochemical reactions are driven out of equilibrium by energy dissipation.

6.2. The Energy-Speed-Accuracy Tradeoff

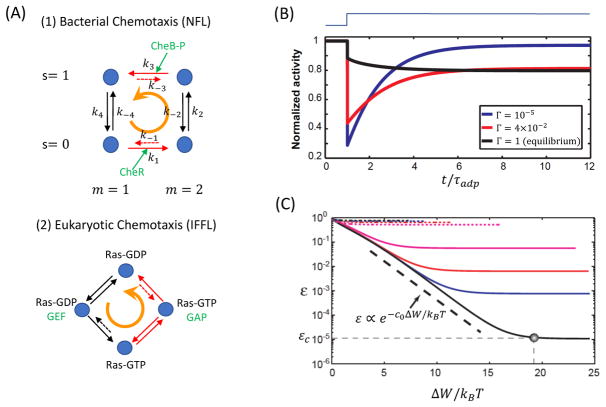
How does the system use free energy to achieve adaptation and how does the energy dissipation relate to and limit the performance of adaptation? To answer these questions we investigate the key biochemical reactions underlying the two adaptation circuit motifs – NFL and IFFL, both of which can be studied by using a simple four-state model as shown in Fig. 6A.

Figure 6.

The nonequilibrium dynamics in adaptation and the universal energy-speed-accuracy tradeoff. A: Biochemical reactions in the NFL (top) and the IFFL (bottom) networks for adaptation. Both biochemical networks break detailed balance and persistent flux cycles, as illustrated by the orange cycling arrows, exist in the adapted non-equilibrium steady state (NESS). The fast and slow reactions are distinguished by the black and red arrows, respectively. The key enzymes that facilitate the non-equilibrium reaction cycles are highlighted in green. Reactions suppressed by free energy dissipation are labeled by dotted arrows. B: No adaptation exist for the equilibrium model with Γ = 1 (black line). Adaptive dynamics occur after Γ decreases beyond certain critical value and it becomes more accurate as Γ decreases (red and blue lines). C: The energy-speed-accuracy relationship. The adaptation error ε decreases exponentially with ΔW ∝ |ln Γ| until it reaches a saturation value ε_c, which depends on specific parameters of the system as well as the background signal level. Different lines correspond to different background attractant concentrations. Part B and C are adapted from ref. (89).

For adaptation in E. coli chemotaxis, each state of the chemo-receptor is characterized by a pair of order parameters (s, m): s = 0, 1 corresponding to the active and inactive state of the receptor, and the receptor methylation level m = 1, 2 (only two adjacent levels are considered here). The biochemical transition rates between the four states are given in Fig. 6A with all the counterclockwise (CCW) and clockwise (CW) rates labeled by k_l and k_−l respectively (l = 1, 2, 3, 4).

For a fixed receptor methylation level, the transitions between the active and inactive state of the receptor is governed by the free energy levels of the two states, i.e., $\frac{k_2}{k_{-2}}=exp[E(0,2)-E(1,2)],\frac{k_4}{k_{-4}}=exp[E(1,1)-E(0,1)]$, where E(s, m) = sf_m(m) is the free energy level of state (s, m) with f_m(m) = −α(m − m₀) the methylation free energy (see Section 3). The rates for receptor methylation and demethylation, however, do not satisfy the detailed balance conditions. In particular, in order to carry out negative feedback control, the methylation rate for the inactive receptor should be enhanced relative to the demethylation rate, and the demethylation rate should be increased relative to the methylation rate for the active receptor, i.e., $\frac{k_1}{k_{-1}}>exp[E(0,1)-E(0,2)]$ and $\frac{k_3}{k_{-3}}>exp[E(1,2)-E(1,1)]$. These two non-equilibrium processes are facilitated by two enzymes – CheR for methylation and CheB-P for demthylation reactions. See Fig. 6A (upper panel).

We can define a “reversibility” parameter Γ for the whole reaction cycle:

$$\mathrm{\Gamma }\equiv \frac{{\prod }_{cw}k}{{\prod }_{\mathit{ccw}}k}=\prod _{l=1}^4\frac{k_{-l}}{k_l},$$ (24)

which determines whether the full reaction cycle is in thermal equilibrium with its environment. For Γ ≠ 1, the system is dissipative and its steady state is a non-equilibrium steady state (NESS), which needs to be maintained by a finite rate of free energy consumption.

For the adaptation network in E. coli, the negative feedback control is carried out by suppressing the “undesirable” backward reactions, which can be characterized by a small parameter γ < 1: $k_{-1}=\gamma k_{-1}^{(0)}$ and $k_{-3}=\gamma k_{-3}^{(0)}$ where the equilibrium backward rates $k_{-1}^{(0)}$ and $k_{-3}^{(0)}$ satisfy detailed balance with their corresponding forward rates, resulting in an irreversible parameter Γ = γ². For an equilibrium system with Γ = 1, the system does not adapt, see the black line in Fig. 6B. Adaptation, i.e., recovery, only occurs when Γ decreases below a critical value Γ_c(< 1). The adaptation error decreases as γ (or equivalently Γ) decreases. The adaptation error can be expressed as: ε = ε_c + ε₀γ, where ε₀ is an O(1) constant that depends on details of the system. The saturation error at γ → 0 is given by ε_c, which depends on system parameters. ε_c can be made arbitrarily small by proper design of the system (89). For those systems with ε_c ≈ 0, perfect adaptation (ε = 0) can be achieved when γ = 0.

The entropy production rate of the system can also be computed: Ṡ = Σ_l(J_l+ − J_l−) ln(J_l+/J_l−) where J_l± are the forward and backward probability fluxes for the l’th reaction. From Ṡ, we can determine a minimum free energy dissipation rate Ẇ = k_BTṠ to maintain the adapted state, where the thermal energy unit k_BT = 1 of the environment can be set to unity. It can be shown that the dissipation rate increases with the adaptation speed ${\omega }_{\mathit{adp}}\equiv {\tau }_{\mathit{adp}}^{-1}$ with τ_adp the adaptation time: Ẇ = −c₀ω_adp ln(γ), with c₀ a system dependent O(1) constant.

By varying γ, i.e., the strength of the negative feedback control, we can relate the cost of adaptation as characterized by the minimum free energy dissipation rate (Ẇ) with its performance characterized by its speed (ω_adp) and accuracy (ε):

$$\stackrel{.}{W}=c_0\times {\omega }_{\mathit{adp}}\times ln\left[\frac{{\epsilon }_0}{\epsilon -{\epsilon }_c}\right],$$ (25)

which is called the energy-speed-accuracy (ESA) tradeoff relationship as shown in Fig. 6C.

The ESA relationship seems to be general for adaptive systems. Eq. (25) was found to be valid for the IFFL network in the eukaryotic chemotaxis (90). Similar to adaptation by negative feedback control in bacterial chemotaxis, two opposing enzymes, guanine nucleotide exchange factor (GEF) and GTPase-activating protein (GAP), activate and deactivate Ras, respectively, through two different paths in eukaryotic chemotaxis as shown in Fig. 6A (lower panel). Free energy is continuously consumed in the adapted steady state to suppress the “undesirable” reverse reactions and drives a sustained cycling flux among the four states. The free energy is provided by the hydrolysis of high energy bio-molecules that are coupled with these cycles, e.g., ATP or GTP for the phosphorylation-dephosphorylation cycle in eukaryotic chemotaxis and S-adenosyl methionine (SAM) for the methylation-demethylation cycle in bacterial chemotaxis. Measurements of the adaptation dynamics in energy deprived E. coli cells are consistent with the ESA relationship (89).

The general ESA relationship provides a fundamental physical limit for an important biological function, adaptation. It also provides insights in designing biochemical circuits to achieve optimal performance with limited resources. The effect of energy dissipation on other key characteristics of adaptation has also been studied. In particular, it was found that free energy dissipation can be used to suppress fluctuation of the adapted activity without affecting the short time response of the system, a violation of the fluctuation dissipation relationship in equilibrium systems (91).

7. Adaptation in Other Biological Systems

Adaptation in cells is not limited to chemotaxis signaling. For example, it was recently found that the bacterial flagellar switch can adapt to the intracellular CheY-P level by adjusting the number of FliM molecules at the switch complex (92, 93). Adaptation also plays a key role in a variety of homeostatic processes, e.g., adaptation to hyperosmotic shocks in budding yeast Saccharomyces cerevisiae cells. In a recent study, Muzzey et al measured nuclear enrichment of the MAP kinase Hog1 and found it to perfectly adapt, meaning that the steady-state pre- and post-stimulus levels were identical (94). This study also argued for the presence of an integrator and found, through a set of carefully chosen experiments in either mutant strains or for different stimulus protocols, that a single integrating mechanism that involves Hog1 kinase activity and which regulates glycerol synthesis is responsible for the observed adaptation.

All sensory neurons show adaptive behaviors. Although the full molecular mechanism is unclear, some key steps in the adaptation pathway are known. For example, in olfactory sensing in mammalian neurons (95, 96), odorant binding induces activation of adenylyl cyclase (AC), which causes an inbound calcium (Ca⁺²) flux. The intracellular calmodulin (CaM) interacts with enriched calcium to form Ca-CaM, which activate AC phosphorylase calmodulin kinase II (CAMKII) that eventually phosphorylates and deactivates AC. For light sensing in mammalian neurons (97, 98, 99), light activates the G-protein coupled receptor (photon-sensor) that decreases the cellular level of cyclic guanosine monophosphate (cGMP) and inhibits the inbound calcium (Ca⁺²) flux, which eventually turns on the octopus rhodopsin kinase (ORK) to phosphorylate and deactivate the photon-sensor. The adaptation mechanism for the hair cells and whether it involves Ca⁺² is still controversial (100, 101). Due to the multiple time scales observed in neuron adaptation behavior, it is highly likely that a nested network consisting both NFL and IFFL motifs are employed in neuron adaptation. It is thus interesting to use the dynamical systems approach described here together with quantitative single cell measurements to determine the underlying network architecture for adaptation in more complex systems such as sensory neurons.

As a final example of adaptation we would like to point out that it does not have to be limited to single cells but can also occur at the tissue, organ, or whole body level. One example of perfect adaptation at the body level can be found in the control of calcium levels in mammals. These levels need to be well-controlled and must be within a small range of values. El-Samad et al. described how an integral control feedback mechanism is able to achieve these requirements and proposed a biologically plausible model for calcium homeostasis (102). Specifically, they showed that a previously proposed and simple feedback control mechanism is not sufficient to robustly control calcium levels and that the addition of an integrator, much like the one schematically shown in Fig. 1, is able to ensure calcium levels that are independent of the perturbation. When applied to data from cows that give birth, which represents a large calcium perturbation, the model was able to capture the perfect adaptation observed in the animals. As one can imagine, however, obtaining large amounts of quantitative data to fully capture dynamics at animal scales is a complicated and time-consuming task, illustrating why chemotaxis of single cells is a favorite system for the study of adaptation.

8. Reprise

In this paper, we reviewed the two basic molecular mechanisms, NFL and IFFL, for cellular adaptation exemplified by the bacterial and eukaryotic chemotaxis signaling pathways, respectively. Despite their different network architecture, they share many common and universal characteristics in their dynamics, energetics, and scaling behavior. To display adaptive dynamics, both pathways require a separation of time scales with a fast response and a slow recovery. Both operate out of thermal equilibrium, continuously dissipate (consume) free energy to maintain the adapted steady state. The power consumption sets a limit for the adaptation performance characterized by adaptation speed and accuracy. Adaptation maintains a high sensitivity over a wide range of background, which is directly responsible for the Weber-Fechner scaling law observed in different sensory systems. There are, however, notable differences in the dynamics of these two networks. While both the response and the recovery time scales in the IFFL network decrease with the signal strength, they increase with or are independent of the input in the NFL network. These differences can be exploited to determine the underlying molecular mechanism for adaptation from input-output measurements. Indeed, the theoretical framework we described here should be useful to understand more complicated adaptive systems in biology.

SUMMARY POINTS.

1. There are two distinct basic biochemical networks that lead to accurate adaptation – the negative feedback loop (NFL) network and the incoherent feedforward loop (IFFL) network.

2. Both NFL and IFFL networks operate with at least two separate time scales – a fast response time and a slow recovery (adaptation) time.

3. Adaptation in bacterial chemotaxis involves a NFL network motif. Adaptation in eukaryotic chemotaxis involves an IFFL network motif.

4. The time scales in IFFL decrease with the signal intensity while the NFL time scales increase with the signal or show no dependence.

5. A general scaling theory of adaptive response is developed to derive the Weber-Fechner law in both bacterial chemotaxis and eukaryotic chemotaxis systems.

6. Both bacterial chemotaxis and eukaryotic chemotaxis can show scale invariant responses or fold change detection due to adaptation.

7. Adaptation costs energy. The adapted state continuously consumes energy to maintain its stability. There is an universal tradeoff relationship among the energy dissipation rate and the adaptation speed and accuracy.

FUTURE ISSUES.

1. Probing adaptive motifs in complex signaling pathways require fast and quantifiable perturbation to intracellular components. The recently developed optogenetic methods (103), which use light to reversibly activate specific components within a pathway (104, 105, 106, 107), may be employed to decipher the pathway topology.

2. Quantitative experimental techniques, including microfluidics that generate time-varying stimuli (56, 54, 52, 108, 67) can be used together with modeling to determine key model parameters and their cell-to-cell variability.

3. The current modeling framework can be extended to study complex biochemical networks with multiple time scales and nested IFFL and NFL motifs, such as those involved in adaptation in sensory neurons.