The Effect of Strong Purifying Selection on Genetic Diversity

Negative selection is a ubiquitous evolutionary force, but its effects on diversity in large samples are poorly understood. Cvijović, Good, and Desai obtain simple analytical expressions for the whole population site frequency spectrum....

Abstract

Purifying selection reduces genetic diversity, both at sites under direct selection and at linked neutral sites. This process, known as background selection, is thought to play an important role in shaping genomic diversity in natural populations. Yet despite its importance, the effects of background selection are not fully understood. Previous theoretical analyses of this process have taken a backward-time approach based on the structured coalescent. While they provide some insight, these methods are either limited to very small samples or are computationally prohibitive. Here, we present a new forward-time analysis of the trajectories of both neutral and deleterious mutations at a nonrecombining locus. We find that strong purifying selection leads to remarkably rich dynamics: neutral mutations can exhibit sweep-like behavior, and deleterious mutations can reach substantial frequencies even when they are guaranteed to eventually go extinct. Our analysis of these dynamics allows us to calculate analytical expressions for the full site frequency spectrum. We find that whenever background selection is strong enough to lead to a reduction in genetic diversity, it also results in substantial distortions to the site frequency spectrum, which can mimic the effects of population expansions or positive selection. Because these distortions are most pronounced in the low and high frequency ends of the spectrum, they become particularly important in larger samples, but may have small effects in smaller samples. We also apply our forward-time framework to calculate other quantities, such as the ultimate fates of polymorphisms or the fitnesses of their ancestral backgrounds.

PURIFYING selection against newly arising deleterious mutations is essential to preserving biological function. It is ubiquitous across all natural populations and is responsible for genomic sequence conservation across long evolutionary timescales. In addition to preserving function at directly selected sites, negative selection also leaves signatures in patterns of diversity at linked neutral sites, which have been observed in a wide range of organisms (Begun and Aquadro 1992; Charlesworth 1996; Cutter and Payseur 2003; McVicker et al. 2009; Flowers et al. 2012; Comeron 2014; Elyashiv et al. 2016). This process is known as background selection and understanding its effects is essential for characterizing the evolutionary pressures that have shaped a population, as well as for distinguishing its effects from less ubiquitous events such as population expansions or the positive selection of new adaptive traits.

At a qualitative level, the effects of background selection are well known: it reduces linked neutral diversity by reducing the number of individuals that are able to contribute descendants in the long run. Since individuals that carry strongly deleterious mutations cannot leave descendants on long timescales, all diversity that persists in the population must have arisen in individuals that were free of deleterious mutations. Since all of these individuals are equivalent in fitness, this suggests that diversity should resemble that expected in a neutral population of a smaller size—specifically, with a size equal to the number of mutation-free individuals (Charlesworth et al. 1993).

However, an extensive body of work has shown that this intuition is not correct and that background selection against strongly deleterious mutations can lead to nonneutral distortions in diversity statistics (Charlesworth et al. 1993, 1995; Hudson and Kaplan 1994; Tachida 2000; Gordo et al. 2002; Williamson and Orive 2002; O’Fallon et al. 2010; Nicolaisen and Desai 2012; Walczak et al. 2012; Good et al. 2014). The reason for this is simple: even strong selection cannot purge deleterious alleles instantly. Instead, deleterious haplotypes persist in the population on short timescales, allowing neutral variants that arise on their backgrounds to reach modest frequencies. This is most readily apparent in statistics based on the site frequency spectrum [the number, $p\left(f\right),$ of polymorphisms which are at frequency f in the population], such as the number of singletons or Tajima’s D (Tajima 1989). As we show below, even when deleterious mutations have a strong effect on fitness, the site frequency spectrum shows an enormous excess of rare variants compared to the expectation for a neutral population of reduced effective size.

These signatures in genetic diversity are qualitatively similar to those we expect from population expansions and positive selection (Slatkin and Hudson 1991; Sawyer and Hartl 1992; Rannala 1997; Keinan and Clark 2012). A detailed quantitative understanding of background selection is therefore essential if we are to disentangle its signatures from those of other evolutionary processes.

The traditional approach to analyzing the effects of purifying selection has been to use backward-time approaches based on the structured coalescent (Hudson and Kaplan 1988, 1994). This offers an approximate framework to model how background selection affects the statistics of genealogical histories of a sample, and hence the expected patterns of genetic diversity. The approximations underlying this method are valid when selection is sufficiently strong that deleterious mutations rarely fix (Neher and Shraiman 2012), the same regime we will consider in this work. However, while these backward-time structured coalescent methods make it possible to rapidly simulate genealogies, they are essentially numerical methods and do not lead to analytical predictions. Furthermore, they give limited intuition as to the conditions under which their approximations are valid. A more technical but crucial limitation is that they rapidly become very computationally demanding in larger samples. This is becoming an increasingly important problem as advances in sequencing technology now make it possible to study sample sizes of thousands (or even hundreds of thousands) of individuals. The poor scaling of coalescent methods with sample size is of particular importance in studying background selection: since purifying selection is expected to result in an excess of rare variants, its effects increase in magnitude as sample size increases. This can reveal deviations from neutrality in large samples that are not seen in smaller samples.

Here, we use an alternative, forward-time approach to analyze how purifying selection affects patterns of genetic variation at a nonrecombining genomic segment. Our method is based on the observation that to predict single-locus statistics, such as the site frequency spectrum, it is not necessary to model the entire genealogy. Instead, we model the frequency of the lineage descended from a single mutation as it changes over time due to the combined forces of selection and genetic drift, and as it accumulates additional deleterious mutations. We then use these allele frequency trajectories to predict the site frequency spectrum, from which any other single-site statistic of interest can then be calculated (note, however, that multi-site statistics such as linkage disequilibrium or correlations between allele frequencies at different sites cannot be calculated from the site frequency spectrum).

We show that background selection creates large distortions in the frequency spectrum at linked neutral sites whenever there is significant fitness variation in the population. These distortions are concentrated in the high- and low-frequency ends of the frequency spectrum, and hence are particularly important in large samples. We provide analytical expressions for the frequencies at which these distortions occur and we can therefore predict at what sample sizes they can be seen in data.

Aside from single time-point statistics such as the site frequency spectrum, we also obtain analytical forms for the statistics of allele frequency trajectories. These trajectories have a very nonneutral character which reflects the underlying linked selection. Our approach offers an intuitive explanation for how these nonneutral behaviors arise in the presence of substantial linked fitness variation, which explains the origins of the distortions in the site frequency spectrum.

The statistics of allele frequency trajectories can also be used to calculate any time-dependent, single-site statistic. For example, we analyze how the future trajectory of a mutation can be predicted from the frequency at which we initially observe it, and we discuss the extent to which the observed frequency of a polymorphism can inform us about the fitness of the background on which it arose.

We emphasize that we focus throughout on modeling a perfectly linked genomic region. In the presence of recombination, our results offer insights about the effects of linked selection on diversity within regions that are effectively fully linked on the relevant timescales. In the Discussion, we discuss how our results can be used to provide a lower bound on the length of these segments, and therefore on the amount of linked selection relevant in sexually reproducing populations, and we comment on possible future extensions of our analysis to include recombination explicitly.

We begin in the next section by providing an intuitive explanation for the origins of the distortions in the site frequency spectrum in the presence of strong background selection, and explain why these distortions always accompany a reduction in diversity. This section summarizes the importance of correctly accounting for background selection, particularly when analyzing large samples, and should be accessible to all readers. We next define a specific model of background selection and summarize our main quantitative results.

We then present the analysis of our model. We begin by reviewing how dynamical aspects of allele frequency trajectories can be related to site frequency spectra, using the trajectories of isolated loci as an example. Readers already familiar with this intuition may choose to skip ahead, but those less interested in the technical details may find that this section provides useful intuition for the calculations in a simpler context. We then explain how this approach must be modified to account for linkage between multiple selected sites and present an intuitive description of the key features of allele frequency trajectories. These sections may be of interest to readers who wish to understand the intuitive origins of nonneutral behaviors of alleles in the presence of strong background selection. Finally, in the Analysis, we turn to a formal stochastic treatment of the trajectories of neutral and deleterious mutations. In the last section, we use these trajectories to calculate the site frequency spectrum and other statistics describing genetic diversity within the population.

Strong Background Selection Distorts the Site Frequency Spectrum

We begin by presenting a more detailed description of the effects of background selection on linked neutral alleles. We focus on analyzing the allele frequency spectrum, defined as the expected number, $p\left(f\right),$ of mutations that are present at frequency f within the population in steady state. This allele frequency spectrum contains all relevant information about single-site statistics: any such statistic of interest can be calculated by subsampling appropriately from $p\left(f\right).$

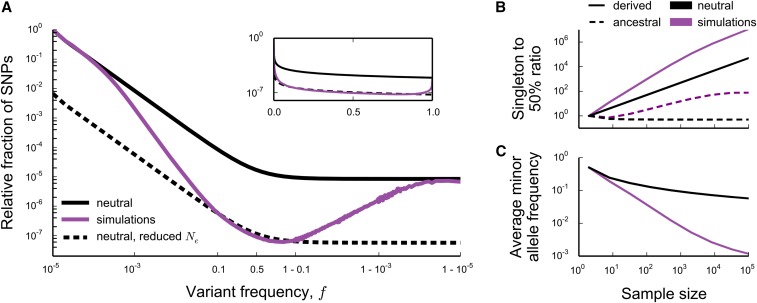
In Figure 1A, we show an example of the site frequency spectrum of neutral mutations at a locus experiencing strong background selection, generated by Wright–Fisher forward-time simulations. This example shows several key generic features of background selection. First, at intermediate frequencies the site frequency spectrum has a neutral shape, $p\left(f\right)\propto f^{-1},$ with the total number of such intermediate-frequency polymorphisms consistent with the simple reduced “effective population size” prediction (Charlesworth et al. 1993). However, at both low and high frequencies, $p\left(f\right)$ is significantly distorted. At low frequencies, we see an enormous excess of rare alleles, qualitatively similar to what we expect in expanding populations (Slatkin and Hudson 1991; Rannala 1997). We also see a large excess of very high frequency variants, leading to a nonmonotonic site frequency spectrum. This is reminiscent of the nonmonotonicity seen in the presence of positive selection (Sawyer and Hartl 1992). Notably, these distortions at both high and low frequencies arise in populations of constant size in which all variation is either neutral or deleterious.

Figure 1.

(A) The (unfolded) average site frequency spectrum of neutral alleles along a nonrecombining genomic segment experiencing strong background selection deviates strongly from the prediction of neutral theory. The purple line shows the simulated neutral site frequency spectrum in Wright–Fisher simulations of an asexual population of $N={10}^5$ individuals, where deleterious mutations occur at rate $N{U}_d=5000$ and all have the same effect on fitness $Ns=1000.$ The black lines show the neutral expectation for the site frequency spectrum of a population of N and $N_e=N{e}^{-U_d/s}$ individuals (solid and dashed line, respectively). The inset shows the same data, but with the x-axis linearly scaled to emphasize intermediate frequencies. Simulated site frequency spectra were obtained by measuring whole-population neutral site frequency spectra in 10⁵ Wright–Fisher simulations, in which neutral mutations were set to occur at rate $N{U}_n={10}^3,$ and by averaging and then smoothing the obtained curve using a box kernel smoother of width much smaller than the scale on which the site frequency spectrum varies (the kernel width was set to $<10\text{\%}$ of the minor allele frequency). (B and C) Statistics of the simulated site frequency spectrum (purple) can deviate from predictions of neutral theory (black) by many orders of magnitude in large samples, even though the effect of background selection will be small in small samples. (B) The average ratio of the number polymorphisms present as derived singletons (solid lines) or ancestral singletons (dotted lines) in the sample to the number present at 50% frequency, and (C) the average minor allele frequency of the sampled alleles.

The excess of rare derived alleles arises because selection takes a finite amount of time to purge deleterious genotypes. Thus we expect that there can be substantial neutral variation linked to deleterious alleles that, although doomed to be eventually purged from the population, can still reach modest frequencies. At the very lowest frequencies, we expect that neutral mutations arising in all individuals in the population (independent of the number of deleterious mutations they carry) can contribute. Thus, at the lowest frequencies, the site frequency spectrum should be unaffected by selection and should agree with the neutral site frequency spectrum of a population of size N. On the other hand, as argued above, the total number of common alleles must reflect the (much smaller) number of deleterious-mutation-free individuals, because only neutral mutations arising in such individuals can reach such high frequencies. Since the overall number of very rare alleles is proportional to the census population size N, and the number of common alleles reflects a much smaller deleterious-mutation-free subpopulation, there must be a transition between these two: between these extremes the site frequency spectrum must fall off more rapidly than the neutral prediction $p\left(f\right)\sim f^{-1}.$ This transition reflects the fact that as frequency increases, the effect of selection will be more strongly felt, and neutral mutations arising in genotypes of increasingly lower fitnesses will become increasingly unlikely.

As the frequency increases even further, we see from our simulations that the total number of polymorphisms increases again until, at very high frequencies, it matches the prediction for a neutral population of size equal to the census size N. Note that, at these frequencies, the total number of backgrounds contributing to the diversity is constant (i.e., all mutations reaching these frequencies must arise in the small subpopulation of mutation-free individuals). This suggests that fundamentally nonneutral behaviors must be dominating the dynamics of these high frequency neutral polymorphisms. To understand this, as well as the details of the rapid falloff at very low frequencies, we will need to develop a more detailed description of the trajectories of neutral alleles in the population; we analyze this in quantitative detail in a later section.

However, a simple argument can explain the agreement with the neutral prediction at the highest frequencies. Polymorphisms observed at these very high frequencies correspond to neutral variants that have almost reached fixation. The ancestral allele is still present in the population, but at a very low frequency. In principle, the dynamics of the derived and ancestral alleles should depend on the fitnesses of their backgrounds. However, once the frequency of the ancestral allele is sufficiently low, the effects of drift will once again dominate over the effects of selection. Thus, at extremely high frequencies of the derived allele, its dynamics must become neutral. In addition to having neutral dynamics, the overall rate at which neutral mutations enter this high-frequency regime also agrees with the rate in a neutral population at the census population size. This is because, at steady state, the total rate at which neutral mutations fix is equal to the product of the rate at which they enter the population at any point in time ($N{U}_n$) and their fixation probability, $1/N$ (Birky and Walsh 1988). Thus, since the total rate at which alleles enter this high-frequency regime is unaffected by selection, and since their dynamics within this regime are neutral, we expect that the site frequency spectrum should also agree with the neutral prediction for a population of size N.

Although these simple arguments do not provide a full quantitative explanation of the site frequency spectrum, they already offer some intuition about the presence and magnitude of the distortions due to background selection. First, these distortions arise in part as a result of the difference in the number of backgrounds on which mutations that remain at the lowest frequencies and mutations that reach substantial frequencies can arise. Thus, they will always occur when background selection is strong enough to cause a substantial reduction in the effective population size: if the pairwise diversity π is at all reduced compared to the neutral expectation ${\pi }_0$ [$\pi /{\pi }_0<1,$ or, in terms of McVicker’s B statistic, $B<1$ (McVicker et al. 2009)], these distortions exist (see Figure 1A). Second, because the distortions from the neutral shape are limited to high and low ends of the frequency spectrum, they will have limited effect on site frequency spectra of small samples, but will have dramatic consequences as the sample size increases (see Figure 1, B and C). On a practical level, this means that extrapolating conclusions from small samples about the effects of background selection can be grossly misleading.

Data availability

Code used to generate the simulated data are available at: https://github.com/icvijovic/background-selection. Supplemental material available at Figshare: https://doi.org/10.25386/genetics.6167591.

Model and Results

In the next few sections, we will analyze the dynamics of neutral mutations under background selection in detail. We focus on the simplest possible model of purifying selection at a perfectly linked genetic locus in a population of N individuals. We assume neutral mutations occur at a per-locus, per-generation rate $U_n$ and deleterious mutations occur at rate $U_d$ ($U_d\ll 1$). Throughout the bulk of the analysis, we will assume that all deleterious mutations reduce the (log) fitness of the individual by the same amount s, although we analyze the effects of relaxing this assumption in a later section. We assume that $s\ll 1$ since this is the interesting case for biologically relevant mutation rates, although we also consider the effects of more strongly deleterious (or lethal) mutations in the Discussion. We neglect epistasis throughout, so that the fitness of an individual with k deleterious mutations at this locus is $-ks.$ For simplicity we consider haploid individuals, but our analysis also applies to diploids in the case of semidominance ($h=1/2$). We assume that selection is sufficiently strong that alleles carrying deleterious mutations cannot fix in the population ($Ns{e}^{-U_d/s}\gg 1$). The opposite case, in which deleterious mutations are weak enough to routinely fix ($Ns{e}^{-U_d/s}\mathrm{\lesssim }1$), has been the subject of earlier work (Good and Desai 2013; Neher and Hallatschek 2013; Good et al. 2014). In the Discussion, we comment on the connection between these earlier weak-selection results and the strong-selection case we study here.

Our model is equivalent to the nonepistatic case of the model formulated by Kimura and Maruyama (1966) and Haigh (1978) as well as to the $h=1/2$ case of the model considered by Charlesworth et al. (1993) and Hudson and Kaplan (1994), and later studied by many other authors (Gordo et al. 2002; Seger et al. 2010; Nicolaisen and Desai 2012; Walczak et al. 2012). However, instead of modeling the genealogies of a sample of individuals from the population backwards in time, we offer a forward-time analysis of this model in which we analyze the full frequency trajectory of alleles.

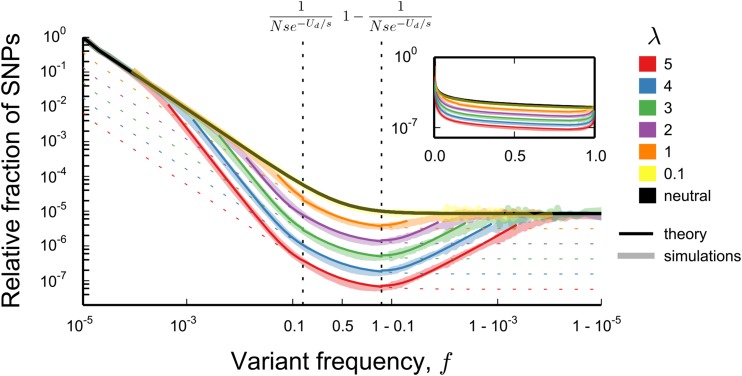
In the presence of strongly selected deleterious mutations ($Ns{e}^{-U_d/s}\gg 1$), we find that the magnitude of the effects of background selection critically depends on the ratio, λ, of the deleterious mutation rate, $U_d,$ to the selective cost of each deleterious mutation, s: $\lambda =U_d/s$ (Figure 2). This ratio controls the overall variance in the number of deleterious mutations carried by individuals in the population, which is equal to $\lambda =U_d/s$ (Kimura and Maruyama 1966). Whenever $\lambda \ll 1,$ both the overall genetic diversity and the full neutral site frequency spectrum $p\left(f\right)$ are unaffected by background selection and the site frequency spectrum $p\left(f\right)$ is to leading order equal to

$$p\left(f\right)\approx \frac{2N{U}_n}{f}\hspace{1em}\text{when }\lambda \ll 1.$$ (1)

This prediction agrees with the results of forward-time simulations (see Figure 2). The intuition behind this result is simple: in the limit that $\lambda \ll 1,$ a majority of individuals in the population are free of deleterious mutations; neutral alleles are therefore rarely linked to deleterious mutations. This results in a neutral site frequency spectrum.

Figure 2.

Comparison between the theoretical predictions for the site frequency spectrum and Wright–Fisher simulations. In all simulations, $Ns{e}^{-U_d/s}=1000\cdot e^{-5}\approx 6.73,$ while the parameter $\lambda =U_d/s$ varies from 5 to 0.1 (values shown on figure). Dashed lines show the expectations for a neutral population at reduced effective population size $N_e=N{e}^{-\lambda }.$ At frequencies smaller than $1/\left(N\sigma \right)$ (where $\sigma =\sqrt{U_{d}s}$) and larger than $1-1/(N\sigma ),$ the theoretical predictions agree with the predictions for a neutral population with census size N (black line). Within the range $1/\left(N\sigma \right)<f<1-1/(N\sigma ),$ the theoretical predictions (Equation 2) are given by colored lines. A single theory curve was constructed from Equation 2 by joining the piecewise forms using sigmoid functions (for details see Constructing a Single Curve from Piecewise Asymptotic Functions in Appendix I). Note that this involves fitting $\mathcal{O}\left(1\right)$ constants to the curve, for reasons explained in Contribution from the Peaks of Trajectories and Constructing a Single Curve from Piecewise Asymptotic Functions in Appendix I. The values of the constants used are tabulated in Table I1. In simulations in which $\lambda \ge 1,$ $N={10}^5$ whereas $N={10}^4$ for smaller λ. In all simulations, the per-individual, per-generation neutral mutation rate is $U_n=0.1$ and site frequency spectra were obtained from these simulations as described in the caption of Figure 1.

However, we will show that the site frequency spectrum of neutral mutations follows a very different form when $\lambda \gg 1:$

$$p\left(f\right)\approx \{\begin{array}{ll}\frac{2N{U}_n}{f},\hfill & \text{for}\hspace{1em}f\ll \frac{1}{N\sigma },\hfill \\ \frac{N{U}_n}{Ns{f}^2\sqrt{\lambda {\log }_{\lambda }\left(\frac{e^{\lambda }}{Nsf}\right)}},\hfill & \text{for}\hspace{1em}\frac{1}{N\sigma }\ll f\ll \frac{e^{\lambda }}{Ns},\hfill \\ \frac{2N{U}_n{e}^{-\lambda }}{f},\hfill & \text{for}\hspace{1em}\frac{e^{\lambda }}{Ns}\ll f\ll 1-\frac{e^{\lambda }}{Ns},\hfill \\ \frac{N{U}_n}{Ns\left(1-f\right){\log }_{\lambda }\left[\frac{e^{\lambda }}{Ns\left(1-f\right)}\right]},\hfill & \text{for}\hspace{1em}\frac{1}{N\sigma }\ll 1-f\ll \frac{e^{\lambda }}{Ns},\hfill \\ \frac{2N{U}_n}{f},\hfill & \text{for}\hspace{1em}1-f\ll \frac{1}{N\sigma };\hfill \end{array}$$ (2)

where $\sigma =\sqrt{U_{d}s}$ represents the standard deviation in fitness in the population, and line 2 in Equation 2 is valid up to a constant factor (see Contribution from the Peaks of Trajectories in Appendix I for details). Comparisons between Equation 2 and simulations of the model are shown in Figure 2. We note that $p\left(f\right)$ matches the site frequency spectrum of a neutral population with a smaller effective population size $N_e=N{e}^{-\lambda }$ for $1/\left(Ns{e}^{-\lambda }\right)<f<1-1/(Ns{e}^{-\lambda }),$ but deviates strongly outside this frequency range. This implies that summary statistics based on the site frequency spectrum (e.g., the average minor allele frequency) will start to deviate from the neutral expectation in samples larger than $Ns{e}^{-\lambda }=“N_{e}s”$ individuals, but not in smaller samples (Figure 1, B and C).

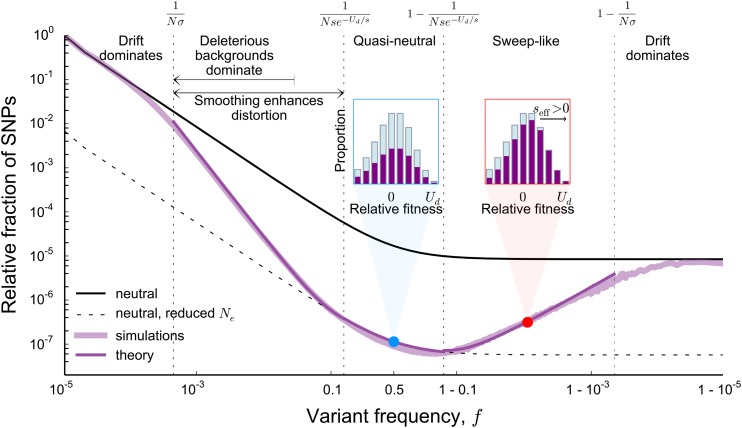
Our results also offer an intuitive interpretation of the origins of these distortions, which are summarized in Figure 3. When $U_d\gg s,$ a large majority of individuals in the population will carry some deleterious mutations at the locus, which results in substantial fitness variation within the population. However, the majority of neutral alleles are present on backgrounds that are within $\mathcal{O}\left(\sigma \right)$ of the mean of the distribution. Thus, at frequencies $f\ll 1/\left(N\sigma \right)$ and $1-f\ll 1/\left(N\sigma \right),$ the effects of genetic drift dominate over any effects of linked selection for the majority of neutral alleles. At these frequencies, the site frequency spectrum agrees with that of a neutral population of size N (see Figure 3).

Figure 3.

A summary of the dominant effects shaping the site frequency spectrum. The site frequency spectrum and theoretical predictions are reproduced from Figure 1 and Figure 2 ($\lambda =5$). At frequencies below $1/\left(N\sigma \right)$ and above $1-1/(N\sigma ),$ the allele frequency trajectories of the majority of neutral alleles are dominated by drift, resulting in neutral site frequency spectra corresponding to a population of size N. In contrast, linked selection has a crucial impact for $1/\left(N\sigma \right)<f<1-1/(N\sigma ).$ The rapid falloff of the site frequency spectrum for $1/\left(N\sigma \right)<f<1/\left(Ns{e}^{-\lambda }\right)$ is primarily a result of allele frequency trajectories having fundamentally nonneutral properties. In this regime, the number of backgrounds on which neutral alleles can arise also declines with the frequency f. As we show later, for $f\ll 1/\left(N{U}_d{e}^{-\lambda }\right),$ the site frequency spectrum is dominated by neutral mutations originating on deleterious backgrounds. In contrast to the rapid decline at lower frequencies, the site frequency spectrum has a neutral shape between $f=1/\left(Ns{e}^{-\lambda }\right)$ and $f=1-1/(Ns{e}^{-\lambda }).$ In this regime, both the neutral and wild-type allele are in approximate mutation–selection balance (see blue dot and blue inset, showing the fitness distribution of such alleles) and large fluctuations of the allele frequency mirror the neutral fluctuations of the most fit individuals. At frequencies larger than $1-1/(Ns{e}^{-\lambda }),$ the relative number of polymorphisms increases with the frequency. This pattern results from the effective positive selection of neutral alleles that fix among the fittest individuals (see red dot and red inset) and are, as a result, linked to fewer deleterious mutations than the wild type.

In contrast, the effects of linked selection have a crucial impact on allele frequency trajectories at frequencies f for which $1/\left(N\sigma \right)\ll f\ll 1-1/(N\sigma ).$ As we show in a later section, this region of the site frequency spectrum is dominated by alleles that arise on unusually fit backgrounds [with fitness with respect to the mean larger than $\mathcal{O}\left(\sigma \right)$]. For these alleles, a crucial distinction arises between their short-term and long-term behavior: although genotypes that carry any polymorphic strongly deleterious variants are guaranteed to be eventually purged from the population, those that contain fewer than average deleterious mutations are still positively selected on shorter timescales. This results in strong nonneutral features in the frequency trajectories of these alleles. Their trajectories are characterized by rapid initial expansions, followed by a peak, and eventual exponential decline (Figure 4). These deterministic aspects of allele frequency trajectories are similar to those seen by Neher and Shraiman (2011) in models of linked selection in large facultatively sexual populations. We describe them in detail in the section titled Key features of lineage trajectories. A part of the rapid falloff in the site frequency spectrum between $f=1/\left(N\sigma \right)$ and $f=1/\left(Ns{e}^{-\lambda }\right)$ results from these deterministic effects: alleles arising on backgrounds with more deleterious variants can reach more limited frequencies than alleles arising on backgrounds with fewer deleterious variants. Thus, the number of backgrounds on which neutral alleles could have arisen declines with the frequency, leading to a falloff of the site frequency spectrum.

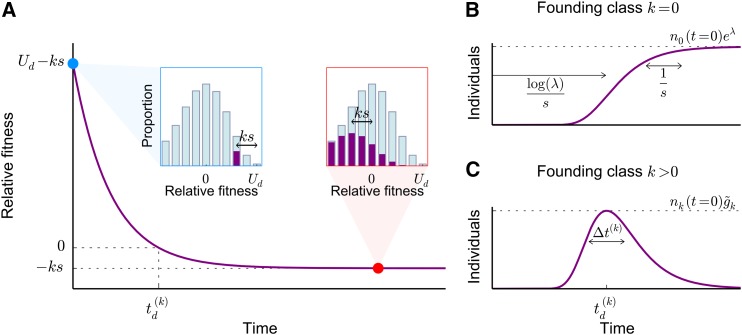
Figure 4.

(A) The average fitness of a lineage comprising individuals carrying k deleterious mutations at time $t=0$ (blue dot and blue inset). As the descendants of these individuals accumulate further deleterious mutations, the fitness of the lineage declines until the individuals accumulate an average of λ deleterious mutations (red dot) and reach their own mutation–selection balance, which is a steady-state Poisson profile with mean λ that has been shifted by the initial deleterious load, $-ks,$ (red inset). (B) In the absence of genetic drift, the size of the lineage will increase at a rate proportional to its relative fitness. Lineages arising in the class with $k=0$ deleterious mutations reach mutation–selection balance about $t_d=\log \left(\lambda \right)/s$ after arising, after which the size of the lineage asymptotes to $n_0\left(t=0\right)e^{\lambda }.$ The fitness of these lineages changes on a shorter timescale, $1/s.$ (C) In contrast, lineages arising in classes with $k>0$ deleterious mutations peak in size after a time $t_d^{\left(k\right)},$ when their average relative fitness is zero, after which they decline exponentially at rate $ks.$

However, these deterministic aspects of the allele frequency trajectory are not sufficient to produce the site frequency spectrum in Equation 2, even if stochastic effects in the early phase of the trajectory are taken into account (i.e., during “establishment”; see Desai and Fisher 2007 and Neher and Shraiman 2011). This is because fluctuations in the numbers of most-fit individuals that occur after establishment continue to drive fluctuations in the overall allele frequency. This is closely related to the fluctuations in the population fitness distribution studied by Neher and Shraiman (2012) in an analysis of Muller’s ratchet.

In the Analysis, we quantify how these fluctuations propagate to shape the statistics of allele frequency trajectories, finding that fluctuations in the number of most-fit individuals that happen on a timescale shorter than $1/s$ are smoothed out due to the finite timescale on which selection can respond. In contrast, fluctuations that happen on timescales longer than $1/s$ are faithfully reproduced in the allele frequency trajectory, which leads to quasi-neutral statistics of allele frequency trajectories at frequencies between $1/\left(Ns{e}^{-\lambda }\right)$ and $1-1/\left(Ns{e}^{-\lambda }\right)$ (see Figure 3). The smoothing of fluctuations on a finite timescale introduces an additional fundamentally nonneutral feature in the total allele frequency trajectory. This distorts the site frequency spectrum at frequencies below $1/\left(Ns{e}^{-\lambda }\right)$ above and beyond what would be predicted if we asserted a simple frequency-dependent effective population size equal to the number of backgrounds that can contribute to a given frequency.

Finally, we will demonstrate that the nonmonotonicity in the site frequency spectrum at frequencies between $1-1/(Ns{e}^{-\lambda })$ and $1-1/(N\sigma )$ arises as a result of sweep-like behaviors of neutral alleles that have fixed among the most-fit individuals in the population (see Figure 3). Because these derived alleles carry, on average, fewer deleterious mutations than the wild type, they are positively selected despite having no inherent benefit. We will show that this difference in the average number of linked deleterious mutations gives rise to an effective frequency-dependent selection coefficient $s_{\text{eff}}\left(f\right).$ This selection coefficient changes with the frequency f of the mutation as high-fitness, wild-type individuals ratchet to extinction:

$$\begin{array}{r}{s}_{\text{eff}}\left(f\right)={\log }_{\lambda }\left[\frac{1}{Ns{e}^{-\lambda }\left(1-f\right)}\right]s,\\ \text{if}\hspace{0.17em}1-f\ll \frac{1}{Ns{e}^{-\lambda }}.\end{array}$$ (3)

In the next sections, we derive the form of the site frequency spectrum in Equation 2 and explain these effects in more detail. We begin by presenting background necessary for understanding these results. We first revisit the intuition behind the shape of the site frequency spectra of isolated loci (Ewens 1963; Sawyer and Hartl 1992). We show that, in the absence of linkage between multiple selected sites, background selection does not lead to a site frequency spectrum of the form in Equation 2. Next, we explain how linkage between multiple selected sites modifies allele frequency trajectories. We revisit the key deterministic aspects of allele frequency trajectories in the presence of background selection, previously studied by Etheridge et al. (2009) and others, and extend these results to identify the key timescales important for understanding this problem. Finally, we turn to a full stochastic treatment of allele frequency trajectories in the Analysis, where we also derive the expressions for the site frequency spectra of neutral and deleterious mutations. In the Discussion, we comment on the practical implications of our results, as well as on connections to previous work and other models.

Background

Isolated loci

To gain insight into the more complicated case of linked selection, we first begin by reviewing the simplest case of a single locus isolated from any other selected loci. The probability that an allele at that locus is present at frequency f at time t, $p\left(f,t\right),$ is described by the diffusion equation:

$$\frac{\partial p}{\partial t}=-\frac{\partial }{\partial f}[sf\left(1-f\right)p]+\frac{\partial }{\partial f^2}\left[\frac{f\left(1-f\right)}{2N}p\right].$$ (4)

Ewens (1963) showed that the expected site frequency spectrum can be obtained from this forward-time description of the allele frequency trajectory: because mutations are arising uniformly in time and the time at which a mutation is observed is random, the site frequency spectrum is proportional to the average time an allele is expected to spend in a given frequency window.

In this section, we show that the low- and high-frequency ends of the site frequency spectrum of isolated loci can be obtained from a simple heuristic argument that emphasizes this connection between allele frequency trajectories and the site frequency spectrum. These calculations are not intended to be exact [resulting frequency spectra are only valid up to $\mathcal{O}\left(1\right)$ factors], but they provide intuition for the origins of key features of the site frequency spectrum that we will return to more formally below.

Consider the simplest case of isolated, purely neutral loci. Neutral mutations will arise in the population at rate $N{U}_n.$ In the absence of selection, the trajectories of these mutations are governed by genetic drift. At steady state, the number of mutations we expect to see at frequency f is simply proportional to the number of mutations that reach that frequency and the typical time each of these mutations spends at that frequency before fixing or going extinct. In the absence of selection, a new mutation that arises at initial frequency $f_0=1/N$ will reach frequency f before going extinct with probability $f_0/f=1/\left(Nf\right).$ Standard branching process calculations (Fisher 2007) show that, given that it reaches frequency f, the mutation will spend about $Nf$ generations around that frequency [defined as $\log \left(f\right)$ not changing by more than $\mathcal{O}\left(1\right)$], provided that f is small ($f\ll 1$).

By combining these results, we can calculate the expected site frequency spectrum for small f. The rate at which new mutations reach frequency f is $N{U}_n\cdot 1/\left(Nf\right).$ Those that do will remain around f (in the sense defined above) for about $Nf$ generations. Thus the total number of neutral mutations within $df$ of frequency f is $p\left(f\right)df\sim N{U}_n\cdot 1/\left(Nf\right)\cdot Nf\cdot d\left(\log f\right).$ In other words, we have

$$p\left(f\right)\sim \frac{N{U}_n}{f}.$$ (5)

This argument is valid when f is rare, but will start to break down at intermediate frequencies. However, because the wild type is rare when the mutant approaches fixation, an analogous argument can be used to describe the site frequency spectrum at high frequencies. The mutant trajectory still reaches frequency f with probability $1/\left(Nf\right).$ It will then spend roughly $N\left(1-f\right)$ generations around this frequency [i.e., within $\mathcal{O}\left(1\right)$ of $\text{log}\left(1-f\right)$]. This gives $p\left(f\right)\approx N{U}_n/f\approx N{U}_n$ in the high-frequency end of the spectrum. This simple forward-time heuristic argument reproduces a well-known result of coalescent theory (Wakeley 2009) and agrees with the more formal calculation of sojourn times in the Wright–Fisher process (Ewens 1963).

We can use a similar argument to calculate the frequency spectrum of strongly selected deleterious mutations with fitness effect $-s$ (with $Ns\gg 1$) that occur at a locus that is isolated from any other selected locus. Provided that the deleterious mutation is rare (below the “drift barrier” frequency, $f<1/\left(Ns\right)$), its trajectory is dominated by drift. Thus for $f<1/\left(Ns\right),$ the mutation trajectory will be the same as for a neutral mutation and the frequency spectrum will therefore be neutral. In contrast, at frequencies larger than $1/\left(Ns\right),$ selection is stronger than drift, which prevents the mutation from exceeding this frequency. Combining these two expressions, we find that the frequency spectrum of an isolated deleterious mutation is, to a rough approximation, given by

$$p\left(f\right)\approx \{\begin{array}{ll}\frac{N{U}_d}{f}\hfill & \text{if}\hspace{0.17em}f<\frac{1}{Ns}\hfill \\ 0\hfill & \text{otherwise.}\hfill \end{array}$$ (6)

For completeness, we also show how a similar argument can be used to obtain the frequency spectrum of beneficial mutations. Although it is not immediately obvious that this is relevant to background selection, we will later see how similar trajectories emerge in the case of strong purifying selection. Just like deleterious alleles, strongly beneficial alleles with fitness effect s (with $Ns\gg 1$) will not feel the effects of selection as long as they do not exceed the drift barrier ($f<1/\left(Ns\right)$). Their trajectory and frequency spectrum will therefore be neutral below the drift barrier. As a result, only a small fraction s of beneficial mutations will reach frequency $1/\left(Ns\right).$ However, those that do will be destined to fix since, at frequencies larger than $1/\left(Ns\right),$ selection dominates over drift. Above this threshold, selection will cause the frequency of the mutation to grow logistically at rate s [$df/dt=sf\left(1-f\right)$], spending $1/[sf\left(1-f\right)]$ generations near frequency f. This is valid as long as $f<1-1/(Ns),$ at which point the effects of drift become dominant due to the wild type being rare, and the trajectory of the mutant is once again the same as the trajectory of a neutral mutation. Combining these expressions, we obtain a rough approximation for the frequency spectrum of an isolated beneficial mutation:

$$p\left(f\right)\approx \{\begin{array}{ll}\frac{N{U}_b}{f},\hfill & \text{if}\hspace{0.17em}f<\frac{1}{Ns}\hfill \\ \frac{N{U}_b}{f\left(1-f\right)},\hfill & \text{if}\hspace{0.17em}\frac{1}{Ns}<f<1-\frac{1}{Ns}\hfill \\ N{U}_b\cdot Ns,\hfill & \text{if}\hspace{0.17em}f>1-\frac{1}{Ns}.\hfill \end{array}$$ (7)

Linked loci under background selection

We now turn to the analysis of background selection. Since we assume that all mutations have the same effect on fitness, the population can be partitioned into discrete fitness classes according to the number of deleterious mutations each individual carries at the locus. When the fitness effect of each mutation is sufficiently strong, the population assumes a steady-state fitness distribution in which the expected fraction of individuals with k deleterious mutations, $h_k,$ follows a Poisson distribution with mean $\overline{k}=\lambda$ (Kimura and Maruyama 1966; Haigh 1978):

$$h_k=e^{-\lambda }\frac{{\lambda }^k}{k!}.$$ (8)

A new allele in such a population will arise on a background with k existing mutations with probability $h_k.$

From the form of $h_k$ we see that, depending on the value of λ, the population can be in one of two regimes. In the first regime, the rate at which mutations are generated is smaller than the rate at which selection can purge them ($\lambda \ll 1$). In this case, the majority of individuals in the population carry no deleterious mutations ($h_0\approx 1$), with only a small proportion, $1-h_0\approx \lambda ,$ of backgrounds in the population carrying some deleterious variants. To leading order in λ, all new neutral mutations will arise in a mutation-free background and will remain at the same fitness as the founding genotype. Their trajectories are thus the same as the trajectories of mutants at isolated genetic loci of the same fitness as the founding genotype (see Appendix D for details). This means that the full site frequency spectrum can be calculated by summing the contributions of site frequency spectra of isolated loci that we calculated above. The neutral and deleterious site frequency spectra are, to leading order in λ, given by Equations 5 and 6, respectively (see Appendix H for details). Thus, background selection has a negligible impact on mutational trajectories and diversity when $\lambda \ll 1.$

In the opposite regime where $\lambda \gg 1,$ mutations are generated faster than selection can purge them and there will be substantial fitness variation at the locus. Consider a new allele (i.e., a new mutation at some site within the locus) that arises in this population. A short time after arising, individuals that carry this allele will accumulate newer deleterious mutations, which will lead the allele to spread through the fitness distribution. The fundamental difficulty in calculating the frequency trajectory of this allele, $f\left(t\right),$ stems from the fact that a short time after arising, individuals that carry the allele will have accumulated different numbers of newer deleterious mutations. The total strength of selection against the allele depends on the average number of deleterious mutations that the individuals that carry the allele have. This will change over time in a complicated stochastic way as the lineage purges old deleterious mutations, accumulates new ones, and changes in frequency due to drift and selection. To calculate the distribution of allele frequency trajectories in this regime, we will need to model these changes in the fitness distribution of individuals carrying the allele. Although we will formally be treating λ as a large parameter, in practice our results will also adequately describe allele frequency trajectories in the cases of moderate λ (i.e., $\lambda \mathrm{\gtrsim }2,$ see Figure 2).

To make progress, we classify individuals carrying this allele (the “labeled lineage”) according to the number of deleterious mutants they have at the locus. We denote the total frequency of the labeled individuals that have i deleterious mutations as $f_i\left(t\right),$ so that the total frequency of the lineage, $f\left(t\right),$ is given by

$$f\left(t\right)={\displaystyle \sum _i{f}_i\left(t\right)}.$$ (9)

The time evolution of the allele frequency in a Wright–Fisher process is commonly described by a diffusion equation for the probability density of the allele frequency (Ewens 2004). Instead, for our purposes, it will be more convenient to consider the equivalent Langevin equation (Van Kampen 2007):

$$\frac{d{f}_i}{dt}=\left[-is+\overline{k}\left(t\right)s\right]f_i-U_d{f}_i+U_d{f}_{i-1}+C_i\left(t\right).$$ (10)

Here, $C_i\left(t\right)$ is a noise term with a complicated correlation structure that is necessary to keep the total size of the population fixed (see Good and Desai 2013 for details), and $\overline{k}\left(t\right)$ is the mean number of mutations per individual in the entire population at time t. In the strong selection limit that we are interested in here ($Ns{e}^{-\lambda }\gg 1$), fluctuations in the mean of the fitness distribution of the population are small and $\overline{k}\left(t\right)\approx \lambda$ (Neher and Shraiman 2012).

Key features of lineage trajectories

Before turning to a detailed analysis of Equation 10, it is helpful to consider some of the key features of lineage trajectories that we will model more formally below. To begin, imagine a lineage founded by a neutral mutation in an individual with k deleterious mutations. Let the lineage comprise $n_k\left(0\right)$ individuals at some time $t=0$ shortly after arising, all of which carry k deleterious mutations (see blue inset in Figure 4A). At this time, the relative fitness of this lineage is simply $-ks-\left(-\overline{k}s\right)=U_d-ks.$ Thus, lineages founded in classes with $k>\lambda$ will tend to decline in size. In contrast, the more interesting case arises if $k<\lambda ,$ since these lineages will tend to increase in size.

However, although the overall number of individuals that carry the allele will tend to increase when $k<\lambda ,$ the part of the lineage in the founding class k (the “founding genotype”) will tend to decline in size because it loses individuals through new deleterious mutations (at per-individual rate $-U_d$). As a result, the founding genotype feels an effective selection pressure of $U_d-ks-U_d=-ks,$ which is negative for all $k>0$ and 0 for $k=0.$ This means that the lineage will increase in frequency, not through an increase in size of the founding genotype, but rather through the appearance of a large number of deleterious descendants in classes of lower fitness. The lineage must therefore decline in fitness as it increases in size.

In the absence of genetic drift, we can calculate how the size and fitness of the lineage change in time by dropping the stochastic terms in Equation 10 [subject to the initial condition $n_k\left(t=0\right)=n_k\left(0\right)$ and $n_{k+i}\left(t=0\right)=0$ for all $i\ne 0$]. These deterministic dynamics of the lineage have been analyzed previously by Etheridge et al. (2009), who showed that the number of additional mutations that an individual in the lineage carries at some later time t is Poisson distributed with mean $\lambda \left(1-e^{-st}\right).$ Thus the average number of additional deleterious mutations eventually approaches λ after $t\mathrm{\gtrsim }{t}_d=\log \left(\lambda \right)/s$ generations. At this point, the lineage has reached its own mutation–selection balance: the fitness distribution of the lineage has the same shape as the distribution of the population [i.e., $n_{i+k}\left(t\right)=h_i\cdot n_k\left(t\right)$] but is shifted by $-ks$ compared to the distribution of the population (see red inset in Figure 4A).

The average relative fitness $x\left(t\right)$ of individuals in the lineage (Figure 4A) is therefore equal to

$$x\left(t\right)=U_d{e}^{-st}-ks,$$ (11)

and the total number of individuals in the lineage is simply $n\left(t\right)=n_k\left(t=0\right)e^{{\displaystyle {\int }_0^{t}x\left(t^{\prime }\right)d{t}^{\prime }}}\equiv n_k\left(t=0\right)g_k\left(t\right),$ where we have defined

$$g_k\left(t\right)=e^{-kst+\lambda \left(1-e^{-st}\right)}.$$ (12)

Thus, we can see from Equations 11 and 12 that lineages founded in the 0-class will, on average, steadily increase in size at a declining rate until they asymptote at a total size equal to $n_k\left(t=0\right)e^{\lambda }$ roughly $t_d=\log \left(\lambda \right)/s$ generations later (see Figure 4B). In contrast, lineages founded in the k-class will increase in size for only

$$t_d^{\left(k\right)}=\frac{\log \left(\lambda /k\right)}{s}$$ (13)

generations, when they peak at a size of $n_k\left(t=0\right)\cdot {\stackrel{\sim }{g}}_k$ individuals (see Figure 4C), where we have defined

$${\stackrel{\sim }{g}}_k\equiv e^{\lambda }{\left(\frac{k}{e\lambda }\right)}^k.$$ (14)

The lineages remain near this peak size for about

$$\Delta t^{\left(k\right)}=\frac{1}{\sqrt{k}s}$$ (15)

generations (Figure 4C). At longer times, they exponentially decline at rate $-ks$ (Figure 4C).

These simple deterministic calculations capture the average behavior of an allele and show that all alleles founded in classes with $k>0$ are likely to be extinct on timescales much longer than $t_d^{\left(k\right)},$ whereas sufficiently large lineages founded in the 0-class should simply reflect the frequency in the founding class about $t_d$ generations earlier: $\langle f\left(t\right)\rangle \approx e^{\lambda }{f}_0\left(t-t_d\right).$ This is the forward-time analog of the intuition presented by Charlesworth et al. (1993).

Of course, this deterministic solution neglects the effects of genetic drift, which will be crucial, particularly because drift in each class propagates to affect the frequency of the lineage in all lower fitness classes (for a more detailed heuristic describing why drift can never be ignored, see The Importance of Genetic Drift in the Founding Class in Appendix B). Although these effects are complex, there is a hierarchy in the fluctuation terms which we can exploit to gain some intuition. From the deterministic solution above, we can see that a fluctuation of size $\delta f_i$ in class i will, on average, eventually cause a change in the total size of the lineage proportional to $\delta f_i{\stackrel{\sim }{g}}_i$ after a time delay $t_d^{\left(i\right)}.$ Thus, the fluctuations that have the largest effect on the total size of the lineage are those that occur in the class of highest fitness (i.e., the founding class k). These fluctuations will turn out to be the most important in describing the frequency trajectory of the entire allele, although fluctuations in classes of lower fitness will still matter in lineages of a small enough size.

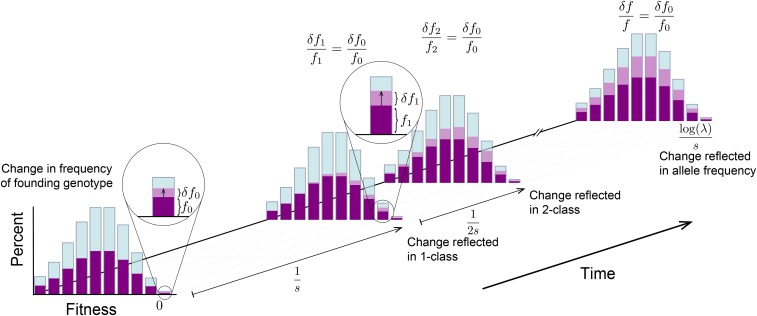
One could imagine that this result means that fluctuations in the total size of the lineage simply mirror the fluctuations in the founding class, amplified by a factor ${\stackrel{\sim }{g}}_k$ and after a time delay $t_d^{\left(k\right)}.$ If fluctuations in the founding class are sufficiently slow, this is indeed the case. However, this is not true for fluctuations that occur on shorter timescales. Consider, for example, the case where a neutral mutation is founded in the mutation-free ($k=0$) class. Imagine that the frequency of the allele in the founding class changes by a small amount from $f_0$ to $f_0+\delta f_0$ as a result of genetic drift (shown in the first panel of Figure 5). Based on the deterministic solution, this fluctuation will lead to a proportional change in the frequency of the portion of the lineage in the 1-class, and this change will take place over $\sim 1/s$ generations (see Appendix A for details). During this time, the change in the 1-class begins to lead to a shift in the frequency in the 2-class, which will mirror the change in the 0-class a further $1/\left(2s\right)$ generations later (see Figure 5). This change will then propagate, in turn, to lower classes and ultimately results in a proportional change in the total allele frequency a total of ${\displaystyle {\sum }_{i=1}^{\lambda }1/\left(is\right)}=\log \left(\lambda \right)/s$ generations later (see Figure 5).

Figure 5.

A schematic showing how a change in the frequency of the lineage in the mutation-free class propagates to affect the frequency in all classes of lower fitness. At time $t=0,$ the lineage is in mutation–selection balance at total frequency f, when the frequency of the portion of the lineage in the 0-class changes suddenly from $f_0$ to $f_0+\delta f_0.$ This change is felt in the 1-class $1/s$ generations later and propagates to the 2-class yet another $1/\left(2s\right)$ generations later. The lineage reaches a new equilibrium about $\log \left(\lambda \right)/s$ generations later, when the total allele frequency is proportional to $\left(f_0+\delta f_0\right)e^{\lambda }.$

Now consider what happens if there is another change in the frequency in the founding class. If this change occurs within the initial $1/s$ generations, it will influence the 1-class simultaneously with the first fluctuation, and thus the effect of these two fluctuations on the overall lineage frequency will be “smoothed” out. In contrast, if the changes are separated by more than $1/s$ generations, they will propagate sequentially through the fitness distribution and are ultimately mirrored in the total allele frequency. Similar arguments apply to lineages founded in other fitness classes, though the relevant timescales and scale of amplification are different.

Together, these arguments suggest that fluctuations in the founding class will have the largest impact on overall fluctuations in the lineage frequency, and these overall fluctuations will represent an amplified but smoothed-out mirror of the fluctuations in the founding class. This smoothing will be crucial: the size of the lineage in the founding class will typically fluctuate neutrally, but the smoothed-out and amplified versions will have nonneutral statistics. As we will see below, this smoothing ultimately leads to distortions in the site frequency spectrum at low frequencies ($f\ll 1/(Ns{e}^{-\lambda })$).

Analysis

Formally, we analyze all of the effects described above by computing the distribution of the frequency trajectories $f\left(t\right)$ of the allele, $p\left(f,t\right),$ from Equation 10 for an allele arising in class k. This process is complicated by the correlation structure in the $C_i\left(t\right)$ terms required to keep the population size constant. These correlations are important once the lineage reaches a high frequency and, in the presence of strong selection, they result in a complicated hierarchy of the moments of f, which do not close (Higgs and Woodcock 1995; Good and Desai 2013). However, we can simplify the problem by considering low-, high-, and intermediate-frequency lineages separately. First, at sufficiently low frequencies ($f\ll 1$), the $C_i\left(t\right)$ in Equation 10 reduce to simple uncorrelated white noise. At these low frequencies, Equation 10 thus simplifies to

$$\frac{d{f}_i}{dt}=\left(-is+\lambda s\right)f_i-U_d{f}_i+U_d{f}_{i-1}+\sqrt{\frac{f_i}{N}}{\eta }_i\left(t\right),$$ (16)

where the noise terms have $\langle {\eta }_i\left(t\right)\rangle =0$ and covariances $\langle {\eta }_i\left(t\right){\eta }_j\left(t^{\prime }\right)\rangle ={\delta }_{ij}\delta \left(t-t^{\prime }\right)$ and should be interpreted in the Itô sense. At very high frequencies ($1-f\ll 1$), a similar simplification arises. In this case, the wild-type lineage is at low frequency and we can model the wild-type frequency using an analogous coupled branching process with uncorrelated white noise terms. Finally, at intermediate frequencies, we cannot simplify the noise terms in this way. Fortunately, for the case of strong selection we consider here, we will show that for $1/\left(Ns{e}^{-\lambda }\right)\ll f\ll 1-1/(Ns{e}^{-\lambda }),$ lineage trajectories have neutral statistics on relevant timescales. As we will see below, these low-, intermediate-, and high-frequency solutions can then be asymptotically matched, giving us allele frequency trajectories and site frequency spectra at all frequencies.

In the next several subsections, we focus on the analysis of the distribution of trajectories at low and high frequencies ($f\ll 1$ or $1-f\ll 1$), where Equation 16 is valid. We then return in a later subsection to the analysis of trajectories at intermediate frequencies.

The dynamics of the lineage within each fitness class

To obtain the distribution of trajectories of the allele $p\left(f,t\right)$ at low frequencies ($f\ll 1$) from Equation 16, we will first compute the generating function of $f\left(t\right).$ This generating function is defined as

$$H_f\left(z,t\right)=\langle e^{-zf\left(t\right)}\rangle ,$$ (17)

where angle brackets denote the expectation over the probability distribution of the frequency trajectory $f\left(t\right).$ $H_f\left(z,t\right)$ is simply the Laplace transform of the probability distribution of $f\left(t\right)$ and it therefore contains all of the relevant information about the probability distribution of $f\left(t\right).$

As we have already anticipated from our discussion above, the time evolution of $f\left(t\right)$ depends on the distribution of the lineage among different fitness classes. To understand how this distribution changes under the influence of drift, mutation, and selection in these classes, we can consider the joint generating function for the $f_i\left(t\right),$

$$H\left(\left\{z_i\right\},t\right)=\langle e^{-{\displaystyle {\sum }_i{z}_i{f}_i\left(t\right)}}\rangle .$$ (18)

The generating function for the total allele frequency $H_f\left(z,t\right)$ can then be obtained from this joint generating function by setting $z_i=z.$ We will use this relationship between the two generating functions to evaluate the importance of drift, mutation, and selection within each of the fitness classes on the total allele frequency.

By taking a time derivative of Equation 18 and substituting the time derivatives $d{f}_i/dt$ from Equation 16 (where the stochastic terms should be interpreted in the Itô sense, see Appendix C), we can obtain a partial differential equation (PDE) describing the evolution of the joint generating function:

$$\frac{\partial H}{\partial t}={\displaystyle \sum _i-\left(is{z}_i-U_d{z}_{i+1}+\frac{z_i^2}{2N}\right)\frac{\partial H}{\partial z_i}}.$$ (19)

We see from Equation 19 that the joint generating function is constant along the characteristics $z_i\left(t-t^{\prime }\right)$ defined by

$$\frac{d{z}_i}{d{t}^{\prime }}=is\hspace{0.17em}{z}_i-U_d{z}_{i+1}+\frac{z_i^2}{2N}.$$ (20)

Thus, the joint generating function can be obtained by integrating along the characteristic backward in time from $t^{\prime }=0$ to $t^{\prime }=t,$ subject to the boundary condition $z_i\left(t\right)=z.$ Note that the linear terms in the characteristic equations arise from selection and mutation out of the i-class and that the nonlinear term arises from drift in class i.

In Large Lineages Arising on Unusually Fit Backgrounds in Appendix E, we show that when considering the distribution of trajectories $p\left(f,t\right)$ at frequencies $f\gg e^{\lambda }{\left[i/\left(e\lambda \right)\right]}^i/\left(2Nsi\right)={\stackrel{\sim }{g}}_i/\left(2Nsi\right)$ the nonlinear terms in Equation 20 are of negligible magnitude uniformly in time in all classes containing i or more deleterious mutations per individual, as long as $i\ll \lambda ,$ $Ns{e}^{-\lambda }\gg 1,$ and $\lambda \gg 1.$ Here, ${\stackrel{\sim }{g}}_i$ represents the peak of the expected number of individuals in a lineage founded by a single individual in class i (see Equation 14 and Figure 4C). Thus, when $f\gg {\stackrel{\sim }{g}}_i/\left(2Nsi\right),$ the effect of genetic drift is negligible in classes with i or more deleterious mutations. Conversely, when $f\ll {\stackrel{\sim }{g}}_i/\left(2Nsi\right),$ genetic drift in the class with i deleterious mutations does affect the overall allele frequency.

Since drift is negligible in classes with i or more mutations, total allele frequencies of $f\left(t\right)\gg {\stackrel{\sim }{g}}_i/\left(2Nsi\right)$ require that $f_i\left(t-t_d^{\left(i\right)}\right)\gg 1/\left(2Nsi\right).$ This threshold is reminiscent of the drift barrier, but its origin for classes below the founding class ($i>k$) is more subtle. We offer an intuitive explanation for this threshold in The Importance of Genetic Drift in Classes Below the Founding Class in Appendix B. Thus, drift in class i has an important impact on the overall frequency trajectory as long as $f_i\ll 1/\left(2Nsi\right).$ However, once $f_i$ exceeds $1/\left(2Nsi\right),$ the effect of genetic drift in that class, as well as in all classes below i, becomes negligible because the frequencies of the parts of the lineage in all classes below i are then also guaranteed to exceed the corresponding thresholds. Note that the frequency of the founding genotype $f_k$ is exponentially unlikely to substantially exceed $1/\left(2Nsk\right).$ This is because, as we explained earlier, the frequency trajectory of the founding genotype $f_k\left(t\right)$ has the same statistics as the trajectory of a mutation of fitness $-ks$ at an isolated locus (see Equation 16 and Appendix F). Thus, because $f_k$ is unlikely to exceed $1/\left(2Nsk\right),$ the overall allele frequency f of an allele founded in class k is exponentially unlikely to substantially exceed ${\stackrel{\sim }{g}}_k·1/\left(2Nsk\right)$.

In summary, by analyzing the generating function for the components of the lineage in different fitness classes, we have found that there is a clear separation between high-fitness classes in which mutation and drift are the primary forces, and classes of lower relative fitness in which mutation and selection dominate. The boundary between the stochastic and deterministic classes can be determined from the total allele frequency, allowing us to reduce a complicated problem involving a large number of coupled stochastic terms to what we will see is a small number of stochastic terms feeding an otherwise deterministic population.

Statistics of trajectories with ${\stackrel{\sim }{g}}_1/\left(2Ns\right)\ll f\ll 1$

At this point, we are in a position to calculate a piecewise form for the generating function $H_f\left(z,t\right),$ valid near any frequency f. For example, consider the allele frequency trajectory in the vicinity of some frequency ${\stackrel{\sim }{g}}_1/\left(2Ns\right)\ll f\ll 1.$ As we have explained above, at these frequencies contributions from mutations arising in class $k\ge 1$ are exponentially small, since they would require the frequency of the lineage in that class to substantially exceed $1/\left(2Ns\right),$ which happens only exponentially rarely. Thus, in this frequency range we will only see mutations arising in the mutation-free class ($k=0$). In addition to this, we have shown that at these frequencies genetic drift can be neglected in all classes but the 0-class. To obtain the generating function at these frequencies, we can therefore integrate the characteristic equations by dropping the nonlinear terms in Equation 20 for all $i>0$ [see Large Lineages Arising on Unusually Fit Backgrounds in Appendix E for details]. This yields the generating function for the frequency of the labeled lineage:

$$H_f\left(z,t\right)=\langle e^{-z\left[f_0+U_d{\displaystyle {\int }_{-\mathrm{\infty }}^{t}d\tau }{f}_0\left(\tau \right)g_1\left(t-\tau \right)\right]}\rangle ,$$ (21)

where the average is taken over all possible realizations of the trajectory in the founding class $f_0\left(t\right).$

As before, $g_1\left(t-\tau \right)$ represents the expected number of individuals descended from an individual present in the 1-class $t-\tau$ generations earlier (see Equation 12). Thus, the two terms in the exponent in Equation 21 represent the frequency of the lineage in the founding class $f_0$ and the total frequency of the deleterious descendants of that lineage. The latter are seeded into the 1-class at rate $N{U}_d{f}_0\left(\tau \right)$ and each of these deleterious descendants founds a lineage that $t-\tau$ generations later contains $g_1\left(t-\tau \right)$ individuals, so that the total frequency of the allele is simply

$$f\left(t\right)=f_0\left(t\right)+U_d{\displaystyle {\int }_{-\mathrm{\infty }}^{t}d\tau }{f}_0\left(\tau \right)g_1\left(t-\tau \right).$$ (22)

Thus, we have obtained a simple expression for the frequency of the entire allele in which all of the stochastic effects have been reduced to a single stochastic component, $f_0\left(t\right).$ Furthermore, the stochastic dynamics of $f_0\left(t\right)$ are those of a simple, isolated, neutral mutation (see schematic of such a trajectory in Figure 6B). Note, however, that the statistics of the fluctuations in $f\left(t\right)$ are not necessarily the same as the statistics of the trajectory in the founding class (see Figure 6A). This is because $f\left(t\right)$ depends on an integral of $f_0\left(t\right)$ (see Equation 22) and therefore has different stochastic properties than $f_0\left(t\right)$ itself.

Figure 6.

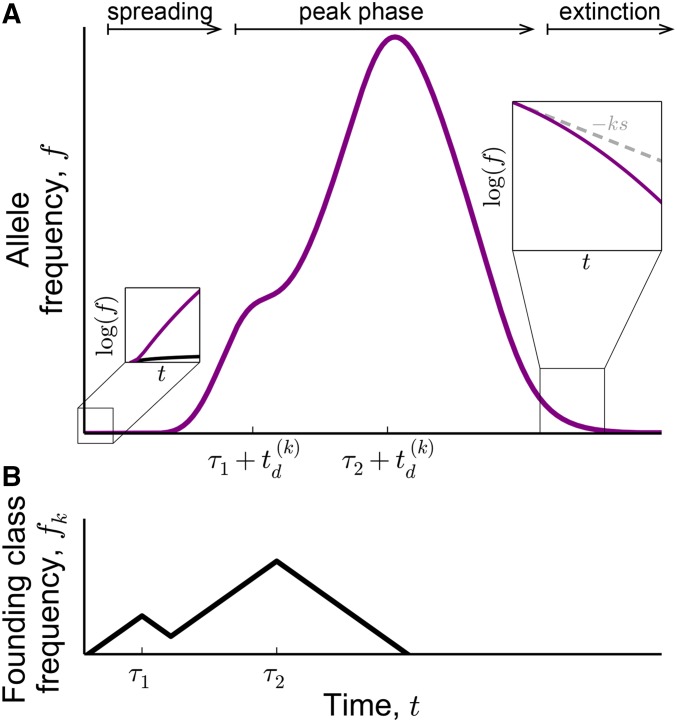
Schematic of (A) the trajectory of the total allele frequency, and (B) the trajectory of the frequency of the portion of the allele that remains in the founding class. Soon after arising in the founding class, the allele frequency rapidly increases in the spreading phase of the trajectory. Early in this phase, the total allele frequency (purple) becomes much larger than the frequency of the founding genotype [black line in left inset of (A)]. In the peak phase of the trajectory, the total allele frequency trajectory represents a smoothed-out and amplified version of the trajectory in the founding class [the relationship between the total allele frequency (purple curve) and the founding genotype frequency (black curve) is based on Equation 22]. In the extinction phase of the trajectory, the allele frequency declines at an increasing rate [right inset of (A)]. We describe the extinction phase in more detail in Appendix E and in the section of the main text titled The trajectories of high frequency alleles, $1-f\ll 1,$ where we also explain how the rate of extinction changes with the frequency.

From Equation 22, we can see that the frequency trajectory of the allele still has the same qualitative features as those we have seen in the deterministic behavior of mutations. Shortly after being founded, the lineage will become dominated by the deleterious descendants of the founding class, which are captured by the second term in Equation 22 (see left inset in Figure 6A). At early times [$t\ll t_d=\log \left(\lambda \right)/s$], the total allele frequency must rapidly grow as the lineage spreads through the fitness distribution and approaches mutation–selection balance (see Figure 6A). About $t_d$ generations after founding, the peak phase of the trajectory begins (see Figure 6A). During this phase, the average fitness of the lineage is approximately zero and the allele traces out a smoothed-out and amplified version of the trajectory in the founding class (Figure 6B). Finally, $t_d$ generations after the descendants of the last individuals present in the founding class have peaked, the average fitness of the lineage will fall significantly below zero and the extinction phase of the trajectory begins.

As we show in Appendix I, the peak phase of the trajectory is the most important for understanding the site frequency spectrum. This is also the phase during which the trajectory of the mutation spends the longest time near a given frequency. In contrast, the spreading phase (see Figure 6A) has a negligible effect on the site frequency spectrum: by this we mean that the site frequency spectrum at a given frequency will always be dominated by the peak phase of trajectories that peak around that frequency, and will not be influenced by the spreading phase of trajectories that peak at much higher frequencies. We will therefore not consider the spreading phase in the main text, but discuss it in Contribution from the Spreading Stage of Trajectories in Appendix I. The extinction phase of the trajectory can also be neglected for a similar reason, except when considering the very highest frequencies: $f\gg 1-1/(Ns{e}^{-\lambda })$ (see Contribution from the Extinction Stage of Trajectories in Appendix I). At these frequencies, the wild-type frequency is small and the mutant is in the process of fixation. To analyze the allele frequency trajectory at these frequencies, we model the wild type using the coupled branching process in Equation 16 and hence describe these trajectories by the extinction phase of the wild type.

To calculate the distribution of $f\left(t\right)$ in the peak phase, we need to calculate the distribution of the time integral of $f_0\left(t\right)$ in Equation 22. We can simplify this integral by observing that $g_1\left(t\right)$ is highly peaked in time between $t_d^{\left(1\right)}-\Delta t^{\left(1\right)}/2$ and $t_d^{\left(1\right)}+\Delta t^{\left(1\right)}/2,$ where $t_d^{\left(1\right)}$ and $\Delta t^{\left(1\right)}$ are given by Equations 13 and 15 and are annotated in Figure 4C. In other words, starting at times around $t_d^{\left(1\right)}$ generations after the lineage reaches a substantial frequency in the founding class, the labeled lineage is dominated by the deleterious descendants of individuals extant in the founding class between $t_d^{\left(1\right)}-\Delta t^{\left(1\right)}/2$ and $t_d^{\left(1\right)}+\Delta t^{\left(1\right)}/2$ generations earlier, with individuals extant in the founding class at other times having exponentially smaller contributions [see Large Lineages Arising on Unusually Fit Backgrounds in Appendix E for details]. Thus, the total size of the lineage will be proportional not to the frequency $f_0\left(t-t_d^{\left(1\right)}\right)$ in the founding class $t_d^{\left(1\right)}$ generations earlier, but to the total time-integrated frequency within some window of width $\sim \Delta t^{\left(1\right)}$ centered around that time. We call this quantity the “weight” and denote it by $W_{\Delta t^{\left(1\right)}},$ where

$$W_{\Delta t^{\left(1\right)}}\left(t\right)={\displaystyle {\int }_{t-\frac{\Delta t^{\left(1\right)}}{2}}^{t+\frac{\Delta t^{\left(1\right)}}{2}}{f}_0\left(t^{\prime }\right)d{t}^{\prime }}.$$ (23)

The total allele frequency in the peak phase is therefore equal to

$$f\left(t\right)\approx U_d{W}_{\Delta t^{\left(1\right)}}\left(t-t_d\right)g_1\left(t_d\right).$$ (24)

Thus, to calculate the distribution of the allele trajectory, we only need to calculate the distribution of the weight in the founding class over a window of specified width, $\Delta t^{\left(1\right)}.$ It is informative to consider the time-integrated form of the distribution of this weight, $p\left(W_{\Delta t^{\left(1\right)}}\right)={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}dt}p\left(W_{\Delta t^{\left(1\right)}},t\right),$ since this form is also directly relevant to the site frequency spectrum [for a discussion of the time-dependent distribution $W_{\Delta t^{\left(1\right)}}\left(t\right),$ see Appendix F]. In Appendix F we show that $p\left(W_{\Delta t^{\left(1\right)}}\right)$ is given by

$$p\left(W_{\Delta t^{\left(1\right)}}\right)\approx \{\begin{array}{ll}\frac{1}{\sqrt{2N\pi }}\frac{\Delta t^{\left(1\right)}}{W_{\Delta t^{\left(1\right)}}^{3/2}},\hfill & W_{\Delta t^{\left(1\right)}}\ll \frac{\Delta t^{{\left(1\right)}^2}}{N},\hfill \\ \frac{1}{W_{\Delta t^{\left(1\right)}}},\hfill & W_{\Delta t^{\left(1\right)}}\gg \frac{\Delta t^{{\left(1\right)}^2}}{N}.\hfill \end{array}$$ (25)

This distribution has a form that can be simply understood in terms of the trajectory in the founding class. Since genetic drift takes order $N{f}_0$ generations to change $f_0$ substantially, drift will not change $f_0$ significantly within $\Delta t^{\left(1\right)}$ generations when the frequency in the founding class exceeds $\Delta t^{\left(1\right)}/N=1/\left(Ns\right).$ As a result, the weight, $W_{\Delta t^{\left(1\right)}},$ will be approximately equal to $W_{\Delta t^{\left(1\right)}}\approx f_0\cdot \Delta t^{\left(1\right)}=f_0/s.$ Therefore, at these large frequencies, the weight simply traces the founding class frequency and the two quantities have the same distributions. At lower frequencies, $f_0\ll 1/s,$ the founding genotype will typically have arisen and gone extinct in a time of order $N{f}_{0,\max }$ generations (where $f_{0,\max }$ is the maximal frequency the lineage reaches over the course of its lifetime). By assumption, this time is much shorter than $1/s.$ Thus, the weight in a window of width $1/s$ that contains this trajectory is simply $W_{\Delta t^{\left(1\right)}}=f_{0,\max }\cdot N{f}_{0,\max }.$ This large a trajectory is obtained with probability $1/\left(N{f}_{0,\max }\right),$ from which it follows (by a change of variable) that the distribution of weights in the founding class scales as $W_{\Delta t^{\left(1\right)}}^{-3/2}.$

As we anticipated in our discussion of the propagation of fluctuations of the founding genotype through the fitness distribution (Figure 5), we have found that the trajectory of the allele in the peak phase looks like a smoothed-out, time-delayed, and amplified version of the trajectory in the founding class (Figure 6). At sufficiently high frequencies, $f\left(t\right)\gg U{\stackrel{\sim }{g}}_1\cdot 1/\left(N{s}^2\right)\sim 1/\left(Ns{e}^{-\lambda }\right),$ the timescale of the smoothing is shorter than the typical timescale of the fluctuations in the founding class. At these frequencies, the statistics of the fluctuations of the allele simply mirror the statistics of the fluctuations in the founding class, with a time delay equal to $t_d^{\left(1\right)}=\log \left(\lambda \right)/s.$

At lower frequencies, ${\stackrel{\sim }{g}}_1/\left(2Ns\right)\ll f\ll 1/\left(Ns{e}^{-\lambda }\right),$ the timescale of smoothing is much longer than the typical lifetime of the founding genotype. As a result, the deleterious descendants of the entire original genotype rise and fall simultaneously and fluctuations in the founding class are not reproduced in detail. Instead, the peak phase of the allele frequency trajectory consists of a single peak with size proportional to the total lifetime weight of the founding genotype, $W={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f\left(\tau \right)d\tau }.$ As we calculated above, the distribution of these peak sizes falls off more rapidly than neutrally. This gives us a complete description of the statistics of the peaks of allele frequency trajectories in the frequency range $f\gg {\stackrel{\sim }{g}}_1/\left(2Ns\right).$

Statistics of trajectories with $f\ll {\stackrel{\sim }{g}}_1/\left(2Ns\right)$

So far, we have only considered trajectories of lineages that reach a maximal allele frequency larger than ${\stackrel{\sim }{g}}_1/\left(2Ns\right),$ all of which must have arisen in the mutation-free class. At lower frequencies, ${\stackrel{\sim }{g}}_2/\left(4Ns\right)\ll f\ll {\stackrel{\sim }{g}}_1/\left(2Ns\right),$ the effects of genetic drift in class $i=1$ must also considered, but the behavior in classes with $i\ge 2$ is deterministic. In this case, by repeating our earlier procedure, we obtain a slightly different form for the generating function $H_f\left(z,t\right),$

$$H_f\left(z,t\right)=\langle e^{-z\left[f_0+f_1+U_d{\displaystyle {\int }_{-\mathrm{\infty }}^{t}d\tau }{f}_1\left(\tau \right)g_2\left(t-\tau \right)\right]}\rangle ,$$ (26)

so that the total allele frequency is

$$f\left(t\right)=f_0\left(t\right)+f_1\left(t\right)+U_d{\displaystyle {\int }_{-\mathrm{\infty }}^{t}d\tau }{f}_1\left(\tau \right)g_2\left(t-\tau \right).$$ (27)

The total allele frequency is once again dominated by the last term, which represents the bulk of the deleterious descendants. Thus, by an analogous argument, the peak size of the lineage is proportional to the weight in the 1-class in a window of width $\Delta t^{\left(2\right)}=1/\left(\sqrt{2}s\right):$

$$f\left(t\right)\approx U_d{W}_{\Delta t^{\left(2\right)}}\left(t-t_d^{\left(2\right)}\right){\stackrel{\sim }{g}}_2.$$ (28)

There are two types of trajectories that can reach these frequencies: trajectories that arise in the 1-class and reach a sufficiently large frequency in their founding class ($f_1\gg {\lambda }^{1/2}/\left(\sqrt{2}N{U}_d\right),$ see Appendix G); and trajectories that arise in the 0-class and reach a smaller frequency in their founding class ($f_0\ll {\lambda }^{1/2}/\left(\sqrt{2}N{U}_d\right)$), but still leave behind enough deleterious descendants in the 1-class that the overall frequency in that class exceeds $f_1\gg {\lambda }^{1/2}/\left(\sqrt{2}N{U}_d\right).$ By the argument that we outlined before, this ensures that genetic drift will negligible in classes of lower fitness (i.e., for $i\ge 2$) and is guaranteed to happen if $f_0\gg {\lambda }^{1/4}/\left(N{U}_d\right)$ (see Appendix G).

The trajectories of the former type are simple to understand since, in this case, the trajectory $f_1\left(t\right)$ is that of a simple, isolated, deleterious locus with fitness $-s$ [and $f_0\left(t\right)=0$ at all times]. By repeating the same procedure as above, we find that the time-integrated distribution of the weights in the 1-class is

$$p\left(W_{\Delta t^{\left(2\right)}}\right)\approx \frac{\Delta t^{\left(2\right)}}{\sqrt{2\pi N}{W}_{\Delta t^{\left(2\right)}}^{3/2}}{e}^{-\frac{N{s}^2{W}_{\Delta t^{\left(2\right)}}}{2}}.$$ (29)

Note that since the trajectory of a mutation in the founding 1-class is longer than $\sim 1/s$ generations only exponentially rarely, a window of length $\Delta t^{\left(2\right)}$ nearly always contains the entire founding class trajectory (see Appendix F). This is reflected in the form of the weight distribution in Equation 29, which falls as $W_{\Delta t^{\left(2\right)}}^{-3/2}$ with an exponential cutoff at $2/\left(N{s}^2\right).$ Thus, the frequency trajectory of an allele that arises in the 1-class will not mirror the fluctuations in the founding genotype. Instead, the peak phase of the allele frequency trajectory will nearly always consist of a single peak, just as we have seen in the case of alleles peaking at frequencies ${\stackrel{\sim }{g}}_1/\left(2Ns\right)\ll f\ll 1/\left(Ns{e}^{-\lambda }\right).$

We now return to the other type of trajectory that can peak in this range: alleles arising in the 0-class, but reaching a small enough frequency that the effects of genetic drift in the 1-class cannot be ignored ($f_0\ll \sqrt{\lambda }/\left(N{U}_d\right)$). Because the trajectory of these alleles in the 1-class represents the combined trajectory of multiple clonal “sublineages,” each founded by a mutational event in the 0-class, the distribution of weights in the 1-class will be different [$p\left(W_{\Delta t^{\left(2\right)}}\right)\sim W_{\Delta t^{\left(2\right)}}^{-5/4},$ see Appendix G], which leads to a different distribution of overall allele frequencies f. However, as we show in Contribution from the Peaks of Trajectories in Appendix I, these trajectories have a negligible impact on the site frequency spectrum: because the overall number of mutations arising in class 1 is substantially larger than the overall number of mutations arising in class 0, trajectories that arise in class 0 and peak in the same frequency range as mutations originating in class 1 are less frequent by a large factor (${\lambda }^{3/4},$ see Appendix G).

Similarly, at even lower frequencies in the range ${\stackrel{\sim }{g}}_{i+1}/\left[2Ns\left(i+1\right)\right]\ll f\ll {\stackrel{\sim }{g}}_i/\left(2Nsi\right)$ we will see the peaks of trajectories arising on backgrounds with i or fewer deleterious mutations. These trajectories all have a single peak of width equal to $\Delta t^{\left(i+1\right)}=1/\left(s\sqrt{i+1}\right).$ The maximal peak sizes are, once again, proportional to the total weight in the i-class, which will be distributed according to a different power law depending on the difference in the number of deleterious mutations $\Delta =k-i$ between the founding class k and the i-class (see Appendix G for details). As we show in Contribution from the Peaks of Trajectories in Appendix I, the most numerous of these mutations are those that arise in the i-class ($k=i$). The index of this most-numerous class is a quantity that we return to at multiple points and we denote it with $k_c\left(f\right).$ We can obtain an explicit form for how $k_c\left(f\right)$ depends on the frequency f by solving the implicit condition ${\stackrel{\sim }{g}}_{k_c+1}/\left[2Ns\left(k_c+1\right)\right]\ll f\ll {\stackrel{\sim }{g}}_{k_c}/\left(2Ns{k}_c\right)$ for $k_c.$ We show in Contribution from the Peaks of Trajectories in Appendix I that, to leading order,

$$k_c\left(f\right)+1\approx {\log }_{\lambda }\left(\frac{1}{Ns{e}^{-\lambda }f}\right),\text{when}\hspace{0.17em}{k}_c\left(f\right)\gg 1.$$ (30)

Finally, at the very lowest frequencies, $f\ll \sqrt{\lambda }/\left(N{U}_d\right)=1/\left(N\sigma \right),$ the site frequency spectrum is dominated by the trajectories of lineages that arise in a class that is within an standard deviation σ of the mean of the fitness distribution (i.e., lineages with $\left|\lambda -k\right|\mathrm{\lesssim }\sigma /s=\sqrt{\lambda }$). Unlike the trajectories of lineages that arise in classes of higher fitness that we discussed above, allele frequency trajectories of lineages arising within an standard deviation of the mean are typically dominated by drift throughout their lifetime [see Lineages Arising on Typical Backgrounds in Appendix E]. This is because the timescale on which these lineages remain above the mean of the fitness distribution [which is limited by $t_d\left(k\right)$] is shorter than the timescale that it takes them to drift to a frequency large enough for the effect of selection to be felt [$\sim 1/[N\left(U_d-sk\right)]\mathrm{\gtrsim }{t}_d\left(k\right)$]. Lineages arising in these classes do not reach frequencies substantially larger than $1/\left(N\sigma \right),$ and have largely neutral trajectories at frequencies that remain below this threshold.

The mirrored fluctuations of the allele at intermediate frequencies, $1/\left(Ns{e}^{-\lambda }\right)\ll f\ll 1-1/\left(Ns{e}^{-\lambda }\right)$

We have seen that the effects of genetic drift in multiple fitness classes may be important when $f\ll 1/\left(Ns{e}^{-\lambda }\right)$ but that, at frequencies larger than $1/\left(Ns{e}^{-\lambda }\right),$ genetic drift in all classes apart from the 0-class can be neglected. At these frequencies, the trajectory of the allele mirrors the fluctuations in the 0-class that occur on timescales longer than $1/s$ generations. We have also seen that overall allele frequencies larger than $1/\left(Ns{e}^{-\lambda }\right)$ correspond to 0-class frequencies of $f_0\gg 1/\left(Ns\right).$

At more substantial allele frequencies (for which the condition that $f\ll 1$ is not satisfied), the coupled branching process in Equation 16 cannot be used to adequately model the allele frequency trajectory. This is because, at these frequencies, the correlations between fluctuations in the frequencies of the mutant and of the wild type, which are imposed by the finite-size constraint of the population, become important. However, we can account for these correlations simply by making use of the fact that the effect of genetic drift in all classes but the 0-class will remain negligible as long as both the mutant and the wild type remain at sufficiently large frequencies. Thus, to model the overall allele frequency trajectory at these intermediate frequencies, we can use a simple, neutral model to describe the frequency of the mutant in the 0-class, $f_0\left(t\right),$ and the frequency of the wild type in the 0-class, $f_{\text{wt},0}\left(\text{t}\right)=h_0-f_0\left(t\right)=e^{-\lambda }-f_0\left(t\right),$ as

$$\frac{d{f}_0}{dt}=\sqrt{\frac{f_0\left(e^{-\lambda }-f_0\right)}{N}}{\eta }_0\left(t\right)$$ (31)

and treat the remainder of the population deterministically (which yields an expression for the relationship between $f_0\left(t\right)$ and $f\left(t\right)$ that is identical to Equation 22).

Furthermore, since we have assumed that $1/\left(Ns{e}^{-\lambda }\right)\ll f\ll 1-1/(Ns{e}^{-\lambda }),$ an additional simplification arises. In this frequency range, the frequency of both the mutant and of the wild-type 0-class exceed $1/\left(Ns\right).$ Thus, large fluctuations in the frequency of the mutant and of the wild type occur on timescales that are longer than $1/s$ generations. Because this timescale is longer than the timescale on which selection in lower classes responds ($1/s$), large fluctuations in the 0-class are mirrored by the overall frequency trajectory after a time delay. In other words, on timescales longer than $1/s$ generations, we can expand the exponent in the integrand in Equation 22 around its peak and approximate the total allele frequency of the mutant and the wild-type alleles as $f\left(t\right)\approx e^{\lambda }{f}_0\left(t-\log \lambda /s\right)$ and $f_{\text{wt}}\left(t\right)\approx e^{\lambda }\cdot \left\{h_0-f_0\left(t-\log \left(\lambda \right)/s\right)\right\},$ which yields a model for the total allele frequency of the mutant:

$$\frac{df}{dt}=\sqrt{\frac{f\left(1-f\right)}{N{e}^{-\lambda }}}\eta \left(t\right),$$ (32)

where $\eta \left(t\right)$ is an effective noise term with mean $\langle \eta \left(t\right)\rangle =0,$ variance $\langle \eta {\left(t\right)}^2\rangle =1,$ and auto-correlation $\langle \eta \left(t\right)\eta \left(t^{\prime }\right)\rangle$ that vanishes on timescales longer than $1/s.$ Thus, on timescales longer than $1/s,$ the allele frequency trajectory is just like that of a neutral mutation in a population of smaller size $N{e}^{-\lambda }.$ On shorter timescales, the allele frequency trajectory will be more correlated in time than the frequency trajectory of a neutral population in a population of that size and will appear smoother. However, since large frequency changes of alleles at these frequencies will only occur on a timescale of order $N{e}^{-\lambda }f,$ which is much longer than $1/s,$ this description will be sufficient for describing site frequency spectra.

We emphasize that Equation 32 relies on the overall fluctuations in the fitness distribution of the population being negligible on relevant timescales, so that the average number of deleterious mutations per individual, $\overline{k}\left(t\right),$ is approximately equal to λ (and, crucially, independent of f). We expect that this approximation is valid when $Ns{e}^{-\lambda }\gg 1,$ because the overall fluctuations in $\overline{k}\left(t\right)$ are small compared to λ in this limit (Neher and Shraiman 2012). However, it is less clear whether this approximation continues to be appropriate as $Ns{e}^{-\lambda }$ approaches more moderate $\mathcal{O}\left(1\right)$ values. A more detailed exploration of these effects would require a path-integral approach similar to that of Neher and Shraiman (2012) and is beyond the scope of this work.

The trajectories of high frequency alleles, $1-f\ll 1$

The neutral model from the previous section breaks down when the allele frequency of the mutant exceeds $1-1/(Ns{e}^{-\lambda }).$ These total allele frequencies are attained when the frequency of the founding genotype $f_0$ exceeds the frequency $h_0-1/(Ns).$ When this occurs, the frequency of the wild type in the founding class will fall below $1/\left(Ns\right)$ and fluctuations that occur on timescales shorter than $1/s$ generations will once again become important. Mutant lineages that reach such high frequencies are almost certain to fix in the 0-class. Once this happens, all individuals that carry the wild-type allele at the locus will also be linked to a deleterious variant. Thus, although the mutant carries no inherent fitness benefit, it will thereafter appear fitter than the wild type because it has fixed among the most-fit individuals in the population. The mutant will therefore proceed to perform a true selective sweep and will drive the wild-type allele to extinction.

At these high allele frequencies, $1-f\ll 1/\left(Ns{e}^{-\lambda }\right)\ll 1,$ we can once again use the coupled branching process in Equation 16 to describe the allele frequency trajectory of the wild type, $f_{\text{wt}}\left(t\right)=1-f\left(t\right).$ Seen from the point of view of the wild type, the fixation phase of the mutant corresponds to the extinction phase of the wild type (see right inset in Figure 3). To obtain a description of the allele frequency trajectory of the wild type at these times, we can expand the generating function in Equation 21 at long times, which yields

$$H_{f_{\text{wt}}}\left(z,t\right)\approx \langle e^{-z\frac{1}{Ns{e}^{-\lambda }}{e}^{-s\left(t-t_0\right)}}\rangle ,$$ (33)

for some choice of $t_0$ [see Large Lineages Arising on Unusually Fit Backgrounds in Appendix E for details]. Note that, as before, Equation 33 is valid only as long as $f_{\text{wt}}\gg {\stackrel{\sim }{g}}_1/\left(2Ns\right)$ (i.e., as long as the size of the lineage in the 1-class exceeds $1/\left(2Ns\right)$). Once the frequency of the wild type in the 1-class falls below $1/\left(2Ns\right),$ we can no longer treat this class deterministically. Once this happens, the part of the wild type that is in the 1-class will drift to extinction within about $1/s$ generations, whereas its bulk will continue to decay at a rate proportional to its average fitness, $-2s.$ This will go on for as long as the frequency in the 2-class is larger than $1/\left(4Ns\right),$ corresponding to the total frequency of the lineage being larger than ${\stackrel{\sim }{g}}_2/\left(4Ns\right).$ Once the frequency of the wild type in the 2-class also falls below $1/\left(4Ns\right),$ the bulk of the lineage will continue to decay even more rapidly, at rate $-3s,$ and so on. In general, once the frequency of the lineage in class $k_c,$ but not in class $k_c+1,$ falls below $1/\left(2Ns{k}_c\right),$ which corresponds to the total frequency of the wild type being in the range ${\stackrel{\sim }{g}}_{k_c+1}/\left[2Ns\left(k_c+1\right)\right]\ll f_{\text{wt}}\ll {\stackrel{\sim }{g}}_{k_c}/\left(2Ns{k}_c\right),$ the average fitness of the bulk of the wild type will be equal to $s_{\text{eff}}=-s\cdot \left(k_c+1\right)$ (see Figure 3).

Thus, the wild type goes extinct in a staggered fashion, dying out in classes of higher fitness first and declining in relative fitness in this process. As a result, the effective negative fitness of the wild type increases as its frequency declines, leading to an increasingly rapid exponential decay of the allele frequency (see right inset in Figure 6A). By solving the implicit condition for $k_c\left(f_{\text{wt}}\right)$ above as we did previously (see Equations E19–E21 in Appendix E), we find that average fitness of the bulk of the wild-type distribution $s_{\text{eff}}\left(f_{\text{wt}}\right)$ is to leading order equal to

$$s_{\text{eff}}\left(f_{\text{wt}}\right)=-s\left[k_c\left(f_{\text{wt}}\right)+1\right]\approx -s{\log }_{\lambda }\left(\frac{1}{Ns{e}^{-\lambda }{f}_{\text{wt}}}\right),$$ (34)

when $f_{\text{wt}}\ll 1/\left(Ns{e}^{-\lambda }\right).$ This means that the frequency trajectory of the wild type in this phase obeys

$$f_{\text{wt}}\left(t\right)\propto e^{-{\log }_{\lambda }\left(\frac{1}{N{f}_{\text{wt}}s{e}^{-\lambda }}\right)st}.$$ (35)

The Site Frequency Spectrum in the Presence of Background Selection

Having obtained a distribution of allele frequency trajectories, we are now in a position to evaluate the site frequency spectrum. Since the trajectory of any lineage depends on the fitness of the background on which it arose, we will find it convenient to divide the total site frequency spectrum, $p\left(f\right),$ into the site frequency spectra of mutations with different ancestral background fitnesses, $p\left(f,k\right).$ By definition, the total site frequency spectrum $p\left(f\right)$ is the sum over these single-class frequency spectra:

$$p\left(f\right)={\displaystyle \sum _{k}p\left(f,k\right)}.$$ (36)

We evaluate the site frequency spectrum in three overlapping regimes, $f\ll 1,$ $1/\left(Ns{e}^{-\lambda }\right)\ll f\ll 1-1/(Ns{e}^{-\lambda }),$ and $1-f\ll 1.$

The site frequency spectrum of rare alleles, $f\ll 1$

The rare end of the frequency spectrum ($f\ll 1$) consists of neutral alleles that (because they are rare) occurred on different genetic backgrounds. These alleles thus have independent allele frequency trajectories that can be described by the coupled branching process, Equation 16. As long as $f\left(t\right)\ll 1/\left(N\sigma \right),$ most lineage trajectories are dominated by genetic drift. Intuitively, this result is simple: provided that the lineage is rare enough, selection pressures in any fitness class (or more precisely, the bulk of the fitness classes where the vast majority of such alleles arise) can be neglected compared to drift. Thus, the resulting site frequency spectrum is

$$p\left(f,k\right)\approx \frac{2N{U}_n{h}_k}{f},\hspace{0.17em}\text{for}\hspace{0.17em}f\ll \frac{1}{N\sigma }.$$ (37)

At these frequencies, the total site frequency spectrum is equal to

$$p\left(f\right)={\displaystyle \sum _{k}p\left(f,k\right)}\approx \frac{2N{U}_n}{f},\text{ for}\hspace{0.17em}f\ll \frac{1}{N\sigma }.$$ (38)

This agrees with our earlier intuition that, at the lowest frequencies, the entire population contributes to the site frequency spectrum and also agrees with the results of Wright–Fisher simulations (see Figure 3). Since the effects of selection are negligible, each fitness class contributes proportionally to its size, with the largest fitness classes contributing the most (see Figure 7). The deleterious mutation-free ($k=0$) class has a negligible effect on the site frequency spectrum, contributing only a small proportion (proportional to its total frequency, $h_0=e^{-\lambda }$) of all variants seen at these frequencies.

Figure 7.

Proportions of polymorphisms at a given frequency that arose in genotypes that had a specified number of additional deleterious mutations compared to the most-fit genotype at the locus at the time they arose. The parameters in these simulations are the same as the parameters used to generate site frequency spectra in Figure 1 and Figure 3. Note that for frequencies $f>1/\left(Ns{e}^{-\lambda }\right),$ the entire site frequency spectrum comprises lineages that arose due to neutral mutations in the $k=0$ class (with only a few exceptions that arise due to rare ratchet events).

At larger frequencies, $f\gg 1/\left(N\sigma \right),$ selection plays an important role in shaping allele trajectories and the site frequency spectrum. The overall contribution of mutations originating in class k near some frequency f is determined not only by the overall rate $N{U}_n{h}_k$ at which such mutations arise, but also by the probability that these mutations reach f, which declines with the initial deleterious load k. As a result, as f increases, the site frequency spectrum will become increasingly enriched for alleles arising in unusually fit backgrounds (see Figure 7).

The contributions to the site frequency spectra $p\left(f,k\right)$ are straightforwardly obtained by integrating in time the distributions of allele frequency trajectories that we have described in the Analysis:

$$p\left(f,k\right)=N{U}_n{h}_k{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}p\left(f,k,t\right)dt}.$$ (39)

This integral is dominated by the peak phase of allele frequency trajectories, during which we have seen that the allele frequency is simply proportional to the weight in class $k_c\left(f\right)\approx \log \left[1/\left(Ns{e}^{-\lambda }f\right)\right],$ which corresponds to the class of lowest fitness in which the dynamics are not deterministic:

$$p\left(f,k,t\right)\approx \{\begin{array}{ll}p\left[f=U_d{\stackrel{\sim }{g}}_{k_c}{W}_{\Delta t^{\left(k_c\right)}}\left(t-t_d^{\left(k_c\right)}\right)\right],\hfill & k\le k_c\left(f\right),\hfill \\ 0,\hfill & \text{otherwise }.\hfill \end{array}$$ (40)

The overall site frequency spectrum is equal to the sum of these terms (Equation 36). In Contribution from the Peaks of Trajectories in Appendix I, we show that this sum is well approximated by the last term, corresponding to $k=k_c\left(f\right),$ and obtain that the site frequency spectrum in the rare end is, to leading order,

$$p\left(f\right)\approx \{\begin{array}{ll}\frac{N{U}_n}{Ns{f}^2\sqrt{\lambda {\log }_{\lambda }\left(1/\left(Nsf{e}^{-\lambda }\right)\right)}}\hfill & \text{for}\frac{\sqrt{\lambda }}{N{U}_d}\ll f\ll \frac{1}{Ns{e}^{-\lambda }},\hfill \\ \frac{2N{U}_n{e}^{-\lambda }}{f}\hfill & \text{for}\frac{1}{Ns{e}^{-\lambda }}\ll f\ll 1,\hfill \end{array}$$ (41)

where the form of the frequency spectrum for $f\ll 1/\left(Ns{e}^{-\lambda }\right)$ is valid up to a constant factor (see Contribution from the Peaks of Trajectories in Appendix I for details). A comparison between these predictions and site frequency spectra obtained in Wright–Fisher simulations of the model is shown in Figure 2.

These results reproduce much of what we may have anticipated from our analysis of allele frequency trajectories. At frequencies $f\gg 1/\left(Ns{e}^{-\lambda }\right),$ these peaks represent the mirrored and amplified trajectories in the mutation-free ($k=0$) founding class. To reach these frequencies, mutations need to arise in the mutation-free class (which happens at rate $N{U}_n{e}^{-\lambda }$) and drift to substantial frequencies ($f_0\gg 1/\left(Ns\right)$). Since fluctuations in the founding class of lineages that exceed this frequency are slow compared to the timescale on which their deleterious descendants remain at their peak ($\Delta t=1/s$), the entire allele frequency trajectory reproduces the fluctuations of the neutral founding class. Thus, neutral site frequency spectra proportional to $f^{-1}$ emerge.

At smaller frequencies, $f\ll 1/\left(Ns{e}^{-\lambda }\right),$ allele frequency trajectories reflect the smoothed-out fluctuations in the high-fitness classes. At these frequencies, the site frequency spectrum comprises a rapidly increasing number of polymorphisms as the frequency decreases for three reasons (see Figure 3 and Figure 7). First, lower frequencies correspond to smaller feeding-class weights, which are more likely simply due to the effects of drift. Note that because in this frequency range the overall allele frequency is proportional to the total weight in the founding class and not the frequency, this effect leads to the site frequency spectrum falling off at a faster rate than the baseline expectation of $f^{-1},$ which would occur in the absence of smoothing of fluctuations in the founding class due to the finite timescale of selection. Second, the number of individuals with k deleterious mutations in the locus increases with k (for $k<\lambda$), causing an increase in the overall rate at which alleles peaking at lower frequencies arise. This variation in the overall number of such alleles gives rise to the steeper power law, $f^{-2},$ that can be compared to the distribution of peaks of individual lineages, which decays at most as $f^{-3/2}.$ Finally, peaks that occur at frequencies ${\stackrel{\sim }{g}}_{k_c\left(f\right)}/\left(2Ns{k}_c\left(f\right)\right)\ll f\ll {\stackrel{\sim }{g}}_{k_c\left(f\right)-1}/\left[2Ns\left(k_c\left(f\right)-1\right)\right]$ have duration of order $\Delta t^{\left[k_c\left(f\right)\right]}\sim 1/\left(\sqrt{k_c\left(f\right)}s\right),$ which declines with the frequency f, giving rise to the root-logarithm factor.

The site frequency spectrum at intermediate and high frequencies

At frequencies much larger than $1/\left(Ns{e}^{-\lambda }\right)$ but still smaller than $1-1/(Ns{e}^{-\lambda }),$ the allele frequency trajectory is described by an effective neutral model on coarse enough timescales ($\mathrm{\gtrsim }1/s$). At these frequencies, the site frequency spectrum is

$$p\left(f\right)\approx \frac{2N{U}_n{e}^{-\lambda }}{f},$$ (42)

for

$$\frac{1}{Ns{e}^{-\lambda }}\ll f\ll 1-\frac{1}{Ns{e}^{-\lambda }}.$$

Note that this agrees with the result of the branching process calculation, which is valid in a part of this range, at frequencies corresponding to $1/\left(Ns{e}^{-\lambda }\right)\ll f\ll 1$ and $1-1/(Ns{e}^{-\lambda })\ll 1-f\ll 1.$

This breaks down at even higher frequencies $1-f\ll 1/\left(Ns{e}^{-\lambda }\right).$ These frequencies correspond to the extinction phase of the wild type, during which the allele frequency no longer mirrors the frequency in the 0-class, but instead declines exponentially at an accelerating rate (see Equation 35). Equation 35 can be straightforwardly integrated in time (see Contribution from the Extinction Stage of Trajectories in Appendix I for details), which yields the form of the site frequency spectrum at these high frequencies

$$p\left(f\right)\approx \frac{U_n}{s\left(1-f\right){\log }_{\lambda }\left(1/\left(Ns\left(1-f\right)e^{-\lambda }\right)\right)},$$ (43)

for

$$\frac{1}{N\sigma }\ll 1-f\ll \frac{1}{Ns{e}^{-\lambda }}.$$

Finally, once the wild-type frequency falls below $1/\left(N\sigma \right),$ it will be in an analogous situation as the mutant at very low frequencies: independent of how it is distributed among the fitness classes, its trajectory will be dominated by drift, since most individuals in the population have fitness that does not differ from the mean fitness by more than σ. Thus, at these frequencies, the site frequency spectrum will once again agree with the site frequency spectrum of neutral loci isolated from any selected sites in the genome:

$$p\left(f\right)\approx 2U_n,\hspace{0.17em}\text{for}\hspace{0.17em}1-f\ll \frac{1}{N\sigma }.$$ (44)

By comparing our predictions to the results of Wright–Fisher simulations, we can see that this argument correctly predicts the form of the site frequency spectrum in these regimes, as well as the frequencies at which these transitions happen (see Figure 3).

The deleterious site frequency spectrum

So far, we have focused primarily on describing the trajectories and site frequency spectra of neutral mutations. However, because the trajectory of a neutral mutation that arises in an individual with k deleterious mutations is equivalent to the trajectory of a deleterious mutation that arises in an individual with $k-1$ deleterious mutations, descriptions of trajectories of deleterious mutations follow without modification from our descriptions of trajectories of neutral mutations. The deleterious site frequency spectrum can thus be constructed from the single-class site frequency spectra of neutral mutations by a simple modification of the total rates at which new deleterious mutations arise [specifically, with the contribution to the deleterious site frequency spectrum of mutations arising in class k being equal to $p_{\text{del}}\left(f,k\right)=p_{\text{neutral}}\left(f,k+1\right)·N{U}_d{h}_k/\left(N{U}_n{h}_{k+1}\right)$]. By summing these contributions, we find that the deleterious site frequency spectrum is to leading order

$$p_{\text{del}}\left(f\right)=\{\begin{array}{ll}\frac{2N{U}_d}{f},\hfill & \text{for}\hspace{0.17em}f\ll \frac{1}{N\sigma }\hfill \\ \frac{1}{f^2\sqrt{\lambda {\log }_{\lambda }\left(1/\left(Nsf{e}^{-\lambda }\right)\right)}},\hfill & \text{if}\frac{1}{N\sigma }\ll f\ll \frac{1}{N{U}_d{e}^{-\lambda }}\hfill \\ 0\hfill & \text{otherwise, }\hfill \end{array},$$ (45)

where the form proportional to $f^{-2}{\sqrt{\log \left[1/\left(Nsf{e}^{-\lambda }\right)\right]}}^{-1}$ is once again valid up to a constant factor (for the same reason as described in Contribution from the Peaks of Trajectories in Appendix I).

Distributions of Effect Sizes

The model we have thus far considered assumes that all deleterious mutations have the same effect on fitness, s. In reality, different deleterious mutations will have different fitness effects. In Appendix J, we show that as long as the variation in the distribution of fitness effects (DFE) is small enough that $\mathrm{var}\left(s\right)/{\overline{s}}^2\ll 1/\log \left(U_d/\overline{s}\right),$ the effects of background selection are well captured by a single-s model. In practice, this means that when considering moderate values of $U_d/\overline{s}\mathrm{\lesssim }{e}^5,$ fractional differences in selection coefficients up to $1/\log \left(U_d/\overline{s}\right)\mathrm{\gtrsim }20\text{\%}$ will not substantively alter allele frequency trajectories. In this case, the combined effects of these mutations are well described by our single-s model.

However, when mutational effect sizes vary over multiple orders of magnitude, properties of the DFE will have an important impact on the quantitative details of the mutational trajectories that are not captured by our single-s model. The qualitative properties of allele frequency trajectories will remain the same (see Appendix J): alleles arising on unusually fit backgrounds will rapidly spread through the fitness distribution, peak for a finite amount of time about $t_d$ generations later, and then proceed to go extinct at a rate proportional to their average fitness cost. However, the quantitative aspects of these trajectories will be different. For instance, small differences in the fitness effects of mutations $\delta s\sim 1/t_d$ that do not affect the early stages of trajectories will be revealed on timescales of order $t_d$ and affect the size and the width of the peak of the allele frequency trajectory. We have seen that these two quantities play an important role in determining the properties of allele frequency trajectories and of the site frequency spectrum.

As a result of the fact that weaker effects and smaller differences in effect sizes play a more important role in later parts of the allele frequency trajectory, the DFE relevant during the early phases of the trajectory may be different than the DFE relevant in the later phases of the trajectory. Furthermore, since longer-lived trajectories are also those that reach higher frequencies (having originated in backgrounds of higher fitness), this can result in a different DFE that is relevant at larger frequencies compared to the DFE relevant at lower frequencies. As a result it is possible that, for certain DFEs, no single “effective” effect size can be used to describe the trajectories at all frequencies. The full analysis of a model of background selection in which mutational effect sizes have a broad distribution remains an interesting avenue for future work.

Discussion

In this work, we have analyzed how linked purifying selection changes patterns of neutral genetic diversity in a process known as background selection. We have found that whenever background selection reduces neutral genetic diversity, it also leads to significant distortions in the neutral site frequency spectrum that cannot be explained by a simple reduction in effective population size (see Figure 1). These distortions become increasingly important in larger samples and have more limited effects in smaller samples (Figure 1, B and C). In this sense, the sample size represents a crucial parameter in populations experiencing background selection.

By introducing a forward-time analysis of the trajectories of individual alleles in a fully linked genetic locus experiencing neutral and strongly selected deleterious mutations, we derived analytical formulas for the whole-population site frequency spectrum (see Equations 1 and 2). These results can be used to calculate any diversity statistic based on the site frequency spectrum in samples of arbitrary size. Our results also offer intuitive explanations of the dynamics that underlie these distortions and give simple analytical conditions that predict when such distortions occur (Figure 3). In addition to single time-point statistics such as the site frequency spectrum, our analysis also yields time-dependent trajectories of alleles. We suggest that these may be crucial for distinguishing between evolutionary models that may remain indistinguishable based on site frequency spectra alone. We explain how this intuition about the time-dependent behavior can, in principle, be used to make simple predictions about the history and future of alleles, and we explain that it suggests new statistics of time-resolved samples that can be used to distinguish between different evolutionary models. We discuss these implications in turn below.

The frequency of a mutation tells us about its history and future

In addition to describing the expected site frequency spectrum at a single time point, our analysis of allele frequency trajectories allows us to calculate time-dependent quantities such as the posterior distribution of the past frequency trajectory of polymorphisms seen at a particular frequency, their ages, and their future behavior. For example, since the maximal frequency a mutation can attain strongly depends on the fitness of the background in which it arose (with lower-fitness backgrounds constraining trajectories to lower frequencies), observing an allele at a given frequency places a lower bound on the fitness of the background on which it arose. This in turn is informative about its past frequency trajectory. For example, alleles observed at frequencies $f\gg 1/\left(N{U}_d{e}^{-\lambda }\right)$ almost certainly arose in an individual that was among the most-fit individuals in the population and experienced a rapid initial exponential expansion at rate $U_d,$ while alleles observed at frequencies $f\gg {\left[k/\left(e\lambda \right)\right]}^k/\left(2Nsk{e}^{-\lambda }\right)$ very likely arose on backgrounds with fewer than k deleterious mutations compared to the most-fit individual at the time. We emphasize that these thresholds are substantially smaller than the naive thresholds obtained by assuming that a mutation arising on a background with k mutations can only reach the drift barrier $1/\left(N_e·ks\right)$ corresponding to isolated deleterious mutations of fitness $ks$ in a population of effective size $N_e=N{e}^{-\lambda }.$

The fitness of the ancestral background on which a mutation arose is not only interesting in terms of characterizing the history of a mutation, but is also informative of its future behavior. In the strong-selection limit of background selection that we have considered here ($Ns{e}^{-\lambda }\gg 1$), deleterious mutations can fix in the population only exponentially rarely (Neher and Shraiman 2012). Thus, mutations arising on backgrounds already carrying deleterious mutations must eventually go extinct. We have shown that the site frequency spectrum at frequencies $f\ll 1/\left(Ns{e}^{-\lambda }\right)$ is dominated by mutations arising on deleterious backgrounds. Furthermore, we have shown that most polymorphisms seen at these frequencies are at the peak of their frequency trajectory. This means that we expect the frequency of such polymorphisms to decline on average. Thus, if we were to observe the population at some later time point, we expect that the polymorphisms present at such low frequencies should on average be observed at a lower frequency. In Figure 8, we show how the average change in frequency after $N{e}^{-\lambda }$ generations depends on the original frequency that a mutation was sampled at, f. Note that the expectation for a neutral population of any size is that the average allele frequency change is exactly equal to zero. In the presence of background selection, this is no longer true for neutral mutations previously observed at frequencies $f<1/\left(Ns{e}^{-\lambda }\right)$ and $f>1-1/(Ns{e}^{-\lambda })$ (see Figure 8).

Figure 8.

The average change in frequency of an allele observed at frequency f in an earlier sample. The pairs of frequencies were sampled in two consecutive sampling steps in Wright–Fisher simulations in which $N={10}^5,$ $N{U}_d=4Ns=2\cdot {10}^4.$ In the first step, the frequencies of all polymorphisms in the population and their unique identifiers were recorded. In the second sample, which was taken $\delta t=N{e}^{-U_d/s}$ generations later, the frequencies of all polymorphisms seen in the first sample were recorded [if a polymorphism had gone extinct, or fixed, a frequency $f\left(\delta t\right)=0,$ or 1, was recorded]. The average represents the average frequency change over many distinct polymorphisms and the curve has been smoothed using a Gaussian kernel with width $<5\text{\%}$ of the minor allele frequency.

In contrast, since polymorphisms observed in the range $1/\left(Ns{e}^{-\lambda }\right)\ll f\ll 1-1/(Ns{e}^{-\lambda })$ must have originated in a mutation-free background, and since their dynamics reflect neutral evolution in this 0-class, the overall dynamics of such alleles are neutral. Therefore, although drift will lead to variation in the outcomes of individual alleles in this range, the average expected frequency change is equal to zero. This expectation is confirmed by simulations (Figure 8).

Finally, we have seen that polymorphisms seen at frequencies $f\gg 1-1/\left(Ns{e}^{-\lambda }\right)$ will typically already have replaced the wild-type allele within the 0-class. Thus, the wild-type allele must eventually go extinct (except for exponentially rare ratchet events). In other words, polymorphisms seen at these frequencies are certain to fix, replacing the ancestral allele at some later point in time (see Figure 8). Together, these results show that the site frequency spectrum can be divided into three regimes in which the dynamics of individual neutral alleles are effectively negatively selected, effectively neutral, and effectively positively selected. These effective selection pressures arise indirectly as a result of the fitnesses of the variants to which a neutral mutation at a given frequency is likely to be linked. This effect is important to bear in mind when analyzing time-resolved samples where these effective selection pressures could naively be misinterpreted as evidence of direct negative selection on low frequency-derived neutral alleles, and direct positive selection on high frequency-derived neutral alleles.

The distinguishability of models based on site frequency spectra

As has long been appreciated, background selection can lead to signatures in the site frequency spectrum that are qualitatively similar to population expansions and selective sweeps (Charlesworth et al. 1993, 1995; Hudson and Kaplan 1994; Tachida 2000; Gordo et al. 2002; Williamson and Orive 2002; O’Fallon et al. 2010; Nicolaisen and Desai 2012; Walczak et al. 2012; Good et al. 2014). Here we have shown that these similarities are not only qualitative, but (up to logarithmic corrections) also quantitatively agree with the site frequency spectra produced under these very different scenarios (Yule 1924; Lea and Coulson 1949; Mandelbrot 1974). This suggests that distinguishing between these models based on site frequency spectra alone may not be possible. We emphasize that these effects of background selection that mimic population expansions are seen in neutral site frequency spectra in a model in which the population size is fixed, so using synonymous site frequency spectra to “correct” for the effects of demography may not always be justified.

The quantitative agreement between the effects of background selection and positive selection that we have seen in the high-frequency end of the frequency spectrum is not purely incidental. In the presence of substantial variation in fitness, alleles that fix among the most-fit genotypes in the population are, in a sense, truly positively selected because they are linked to fewer deleterious mutations than average. As a result, sweep-like behaviors can occur in the absence of positive selection, as long as there is substantial fitness variation, independent of the source of this variation (i.e., whether it arose as a result of beneficial or deleterious mutations). In this case, these models may be indistinguishable even using time-resolved statistics because the allele frequency trajectories themselves have similar features.

In other cases, time-resolved statistics may be able to differentiate between models that produce similar site frequency spectra. For example, under background selection the low-frequency end of the site frequency spectrum is dominated by mutations that are linked to a larger-than-average number of deleterious variants; alleles in this regime are therefore expected to decline in frequency on sufficiently long timescales [of order $\log \left(\lambda \right)/s$]. In contrast, in an exponentially expanding population, mutations present at these frequencies are very unlikely to change in frequency during the expansion. Thus we may be able to distinguish between these models using samples from the same population spaced far enough apart in time.

The effect of very strong deleterious mutations [$\mathit{s}\sim \mathcal{O}(1)$]

In our analysis of background selection, we have focused on mutations with small absolute effects on fitness ($s\ll 1$). We make this choice because although deleterious mutations with very strong effect (e.g., lethal mutations) do exist, they are unlikely to lead to a substantial reduction in genetic diversity unless they also occur at a very high rate ($U_d\sim s\sim 1$). In other words, these mutations can only have a substantial effect on reducing diversity if a large fraction of individuals in the population acquire them every generation. Thus, such mutations appear less likely to lead to strong effects on diversity in natural populations than mutations with smaller absolute effects on fitness.

Relationship to the structured coalescent

Throughout this work, we have assumed that selection against deleterious mutations is strong (i.e., $Ns{e}^{-\lambda }\gg 1$), such that they are exponentially unlikely to fix (i.e., Muller’s ratchet is rare). This is the same limit in which the structured coalescent of Hudson and Kaplan (1994) is valid. Since our forward-time analysis of mutational trajectories uses similar approximations as are implicit in that method, it therefore has the same expected range of validity and accuracy. Although this limit has occasionally been referred to as “weak selection” in some prior literature, we emphasize that an assumption that is implicit in the structured coalescent is that selection against deleterious mutations is sufficiently strong that they do not routinely fix. In Supplemental Material, Figure S1, we show that our theoretical predictions indeed produce site frequency spectra that agree with the results of forward-time simulations roughly as well as numerical predictions generated using the structured coalescent. The advantage of our method is that it provides analytical predictions and scales to arbitrary sample sizes, in contrast to the structured coalescent, which is a numerical algorithm for conducting backward-time simulations.

Relationship to results on weakly selected deleterious mutations

In the case where selection is weak enough that deleterious mutations have a substantial probability of fixation (which occurs when $Ns{e}^{-\lambda }\mathrm{\lesssim }1$), the population ratchets to lower fitness at the locus. In this limit, much like in the strong-selection case that we have studied here, the magnitude of the effects of background selection on diversity is controlled by whether or not deleterious mutations lead to substantial fitness variation at the locus. When deleterious mutation rates are weak enough that the scaled standard deviation in fitness satisfies $N\sigma \ll 1,$ site frequency spectra look largely neutral (see Figure S2 and Good et al. 2014). However, if the deleterious mutation rate is large enough that $N\sigma \gg 1,$ previous work has shown that substantial distortions can result (Neher and Shraiman 2011; Kosheleva and Desai 2013; Neher and Hallatschek 2013; Good et al. 2014). By analyzing evolutionary dynamics in this limit, Neher and Hallatschek (2013) have shown that the resulting site frequency spectrum scales as $f^{-2}$ at low frequencies and as ${\left\{\left(1-f\right)\log \left[1/\left(1-f\right)\right]\right\}}^{-1}$ at high frequencies. These forms are similar to our limiting expressions in the high- and low-frequency ends of the spectrum, but do not contain the neutral region at intermediate frequencies. This neutral region shrinks as $Ns{e}^{-\lambda }$ declines and disappears when $Ns{e}^{-\lambda }\approx 2.$ Thus, the form of the site frequency spectrum in Equation 2 approaches the limiting forms for weak selection as $Ns{e}^{-\lambda }\to 1$ (Figure S2), exactly as expected for the transition to the weakly selected regime (see also Good et al. 2014).

Earlier work has argued that genealogies in this weak-selection limit ($Ns{e}^{-\lambda }\ll 1$) approach the Bolthausen–Sznitman coalescent when fitness variance in the population is sufficiently large, $N\sigma \gg 1$ (Neher and Shraiman 2011; Kosheleva and Desai 2013; Neher and Hallatschek 2013; Good et al. 2014). Recently, Hallatschek (2017) has studied allele frequency trajectories that arise in the forward-time dual of the Bolthausen–Sznitman coalescent. Our analysis of trajectories in the presence of strong background selection reveals many of the interesting features seen in that work. For instance, we have seen that, once an allele spreads through the fitness distribution and reaches mutation–selection balance, an effective frequency-dependent selection coefficient emerges:

$$s_{\text{eff}}\left(f\right)=\{\begin{array}{ll}\log \left(Ns{e}^{-\lambda }f\right)s,\hfill & \text{if}\hspace{0.17em}f\ll \frac{1}{Ns{e}^{-\lambda }}\hfill \\ 0,\hfill & \text{if}\hspace{0.17em}\frac{1}{Ns{e}^{-\lambda }}\ll f\ll 1-\frac{1}{Ns{e}^{-\lambda }}\hfill \\ \log \left[\frac{1}{Ns{e}^{-\lambda }\left(1-f\right)}\right]s,\hfill & \text{otherwise}.\hfill \end{array}$$ (46)

This effective selection coefficient arises due to the deleterious mutations to which neutral mutations are linked and due to changes with the frequency f of the mutation as high-fitness individuals within the neutral lineage drift to extinction or fixation [see Figure 3 and Large Lineages Arising on Unusually Fit Backgrounds in Appendix E], and is equal to 0 in the quasi-neutral regime (Figure 3). This is analogous to the fictitious selection coefficient, $s_{\text{fic}}\left(f\right)=\log \left(f/(1-f)\right),$ that emerges in the model analyzed by Hallatschek (2017). The difference in the frequency dependence of the effective selection coefficient between our results and the Hallatschek (2017) model is large when $Ns{e}^{-\lambda }\gg 1,$ but becomes negligible as $Ns{e}^{-\lambda }\to 1;$ it underlies the differences between the site frequency spectra of rapidly adapting or ratcheting populations and the strong background selection limit that we have considered here.

Note, however, that there still exists a clear discrepancy between the form of the site frequency spectrum at low frequencies that arises in the Bolthausen–Sznitman coalescent, and the functional form that is obtained by analyzing evolutionary models of weak selection (Figure S3). This suggests that the correspondence between these evolutionary models and the Bolthausen–Sznitman coalescent is only approximate, even in the limit that $N\sigma \to \mathrm{\infty }.$ In particular, although the two seem to share dynamical properties which arise once the lineage spreads out through the fitness distribution (including the frequency-dependent selection coefficient), as well as similarities in some aspects of fluctuations in the numbers of high-fitness individuals as they accumulate further mutations (i.e., due to genetic draft; see, e.g., Kosheleva and Desai 2013), it is not immediately obvious that other aspects that we have described here, such as the smoothing of fluctuations due to drift, are identical in both models.

Extensions and limitations of our analysis

We have studied a simple model of a perfectly linked locus at which all mutations are either neutral or deleterious with the same effect on fitness, s. Our primary goal has been to describe the qualitative and quantitative effects of background selection on frequency trajectories and the site frequency spectrum within this simplest possible context. However, it is important to note that the assumptions of our model are likely to be violated in natural populations. In many cases, these additional complications do not change the general conclusions of our analysis. For example, the qualitative properties of the trajectories and site frequency spectra described here apply when deleterious mutations have a broader distribution of effect sizes, and we have shown here that our results are quantitatively unchanged when the distribution of effect sizes (DFE) is sufficiently narrow $\left[\mathrm{var}\left(s\right)/{\overline{s}}^2\ll 1/\log \left(U_d/\overline{s}\right)\right].$ On the other hand, when the DFE is very broad, additional work will be required to determine the quantitative properties of site frequency spectra. We anticipate different parts of the DFE may be important at different frequencies in sufficiently broad DFEs. If this is true, this would be an unusual feature of strong negative selection that does not arise in the case of strong positive selection, in which the effects of DFEs can usually be summarized by a single, predominant fitness effect (Good et al. 2012).

Finally, our assumption of perfect linkage in the genomic segment is likely to be violated in sexual populations, in which sites that are separated by shorter genomic distances are more tightly linked than distant sites. However, even in the presence of recombination, alleles will remain effectively asexual on short enough genomic distances, and are effectively freely recombining on long enough genomic distances (Franklin and Lewontin 1970; Slatkin 1972). In this case, a standard heuristic is to treat the genome as if it consists of freely recombining asexual blocks. In rapidly adapting or ratcheting populations, this heuristic has been shown to yield a rough approximation to diversity statistics when the “effective block length” is set by the condition that each block typically recombines once on the timescale of coalescence (Neher et al. 2013; Good et al. 2014; Weissman and Hallatschek 2014).

However, our analysis highlights that many of the interesting features of allele frequency trajectories in the presence of background selection occur on timescales much shorter than the timescale of coalescence. On these timescales, alleles will be fully linked on much longer genomic distances than this effective block length. This effect will be particularly important for young alleles, which are linked to long haplotypes because of the limited amount of time that recombination has had to break them up. On longer timescales, the length of the genomic segments to which these alleles are linked will become progressively shorter, but will typically not fall below the effective block length on any timescale. Given the strong dependence of allele frequency trajectories on the total mutation rate along this segment, it is less clear what effect such linkage to increasingly shorter genomic segments has on the statistics of allele frequency trajectories. A more detailed analysis of the effects of background selection in linear genomes remains an interesting direction for future work.

It is interesting to note that the effects of background selection on the site frequency spectrum in recombining genomes have been studied previously using forward-time (see, e.g., McVean and Charlesworth 2000; Kaiser and Charlesworth 2008; Zeng and Charlesworth 2010) as well as using backward-time simulations based on extensions of the structured coalescent (see, e.g., Hudson and Kaplan 1994; Zeng and Charlesworth 2011). However, much like in the asexual case, analytical predictions for the magnitude of the effects of background selection in recombining populations are usually limited to samples of two individuals (Hudson and Kaplan 1995; Nordborg et al. 1996). More recently, there has been some interest in exploring the combined effects of background selection and population subdivision (Zeng and Corcoran 2015) or partial asexuality and selfing (Agrawal and Hartfield 2016; Roze 2016). Analytical results in these cases are also often limited to very small samples and to the limit $U_d\ll s$ in which the effects of background selection are modest. We hope that our forward-time approach can be extended in future work to explore the effect of background selection in the presence of such factors more fully.

Appendix A: The Propagation of Fluctuations in the Size of the Founding Class

In this appendix, we consider in more detail how fluctuations in the size of the lineage in the founding class propagate to affect the total allele frequency. For this purpose, it will be convenient to consider a neutral mutation that arose in the $k=0$ class sufficiently long ago that it is in mutation–selection balance. Let the total frequency of the lineage be f. As in the main text, we denote the frequency of the part of the lineage that is in class i by $f_i.$ In mutation–selection balance, the $f_i$ will satisfy

$$f_i=e^{-\lambda }\frac{{\lambda }^i}{i!}f.$$ (A1)

Consider what happens if the frequency $f_0$ of the founding genotype changes suddenly to some value $f_0+\delta f_0.$ Based on the deterministic solution, after a time t, this will lead to a change in the frequency of the part of the lineage in class i, $\delta f_i\left(t\right),$ of

$$\delta f_i\left(t\right)=\delta f_0\frac{{\left[\lambda \left(1-e^{-st}\right)\right]}^i}{i!}.$$ (A2)

In other words, the relative change in the frequency of the lineage in the i-class is

$$\frac{\delta f_i\left(t\right)}{f_i}=\frac{\delta f_0}{f_0}{\left[1-e^{-st}\right]}^i.$$ (A3)

This approaches $\delta f_0/f_0$ at long times as the allele reestablishes mutation–selection balance. However, we can see from Equation A3 that this change is not felt at the same time in all classes. In the 1-class, the frequency changes gradually, at rate s (Equation A3), and results in a proportional change roughly ${\tau }_1=1/s$ generations later. In general, in the i-class, this change is felt after a total delay of roughly ${\tau }_i=\log \left(i\right)/s$ generations. Thus, the change propagates from class i to class $i+1$ over the course of

$${\tau }_{i+1}-{\tau }_i\approx \frac{1}{\left(i+1\right)s}$$ (A4)

generations.

Ultimately, ${\tau }_{\lambda }=\log \left(\lambda \right)/s=t_d$ generations later, this change will have been felt in a substantial fraction of the fitness distribution. Fitness classes near the mean of the distribution (which is λ classes below the 0-class) are those that exhibit the largest absolute change in frequency, since they contain the largest number of individuals when the lineage is in mutation–selection balance. Thus, changes in these classes account for a large proportion of the change in the total allele frequency, which explains the origin of the delay timescale, $t_d,$ that we have introduced in the main text.

Appendix B: The Large Deviations from Average Behavior Caused by Genetic Drift

In this appendix, we consider the importance of the effects of drift in each individual fitness class on the overall allele frequency. In the first subsection, we revisit a standard argument to explain why fluctuations due to genetic drift in the frequency of the founding genotype can never be neglected, framing it in terms that will be useful when considering the importance of drift in classes below the founding class. In the next subsection, we build on this argument to explain why the effects of drift become negligible in all classes i in which the frequency, $f_i,$ of the component of the lineage in that class satisfies $f_i\gg 1/\left(Nsi\right),$ but cannot be neglected in all classes in which the frequency does not exceed that threshold.

The Importance of Genetic Drift in the Founding Class

The essential reason why drift can never be neglected in the early phase of a trajectory is that deviations from the low frequency average behavior caused by drift are not small perturbations, but are extremely broadly distributed. Consider for instance a mutation that arises in class k. As we explain in the main text, the founding genotype feels an effective selection coefficient equal to $-ks.$ The “deterministic trajectory” of the founding genotype is therefore

$$\langle f_k\left(t\right)\rangle =f_k\left(0\right)e^{-kst}.$$ (B1)

In other words, the deterministic trajectory of a neutral founding genotype ($k=0$) is a flat line, whereas the deterministic trajectory of a deleterious founding genotype ($k>0$) decays exponentially at rate $ks.$

However, we know that drift leads to large deviations from the deterministic behavior in Equation B1. In fact, we have mentioned that when $f_k\ll 1/\left(Nsk\right),$ drift can lead to an x-fold increase above this expectation with probability $1/x$ (Fisher 2007). Thus, the deviations from the deterministic expectation due to drift are distributed according to an extremely broad power law. As a result, large deviations from Equation B1 are very likely. For lineages arising in the 0-class, these deviations can take the frequency of a lineage all the way to fixation. However, deleterious founding genotypes with $k>0$ are exponentially unlikely to exceed the drift barrier at $1/\left(Nsk\right).$ Thus, the distribution of deviations from the mean, deterministic behavior of these founding genotypes also follows the same power law at low frequencies ($f_k\ll 1/\left(Nsk\right)$), but is capped by selection at frequencies exceeding $1/\left(Nsk\right).$ As a result, the effects of drift on trajectories of deleterious mutations become perturbative at sufficiently large frequencies and can therefore be neglected when $f_k\gg 1/\left(Nsk\right).$

Because fluctuations in $f_k$ always propagate to classes of lower fitness, drift in the founding class has an important impact on the overall allele frequency whenever it has an important impact on $f_k.$ This means that the overall frequency trajectory of alleles founded in the 0-class will always be affected by drift in $f_k,$ which will cause large, power law-distributed deviations from the deterministic expectation of the total allele frequency trajectory. Similarly, the overall frequency trajectory of alleles founded in a class with $k>0$ deleterious mutations will be affected by drift in the founding class when the overall allele frequency satisfies $f\ll {\stackrel{\sim }{g}}_k·1/\left(Nsk\right)$ (which correspond to founding class frequencies $f_k\ll 1/\left(Nsk\right)$), but prevented by selection from exceeding frequencies larger than ${\stackrel{\sim }{g}}_k·1/\left(Nsk\right)$ (see also Appendix E).

The Importance of Genetic Drift in Classes Below the Founding Class

Given these arguments, one may wonder whether the effects of drift are also important in classes below the founding class, in which individuals carry $i>k$ deleterious mutations. Deviations from deterministic behavior in these classes (i.e., in $f_i$) are also propagated to classes of lower fitness. Such deviations in $f_i\left(t\right),$ if large, will also have a large impact on the overall frequency trajectory of the allele, $f\left(t\right).$ However, since classes below the founding class receive substantial mutational input from higher classes, it is not immediately clear whether the effects of drift on $f_i\left(t\right)$ will “average out” as a result of these mutations, or whether drift can still lead to large deviations from the deterministic expectation for $f_i\left(t\right).$ In Appendix E, we show by formally analyzing the distribution of allele frequency trajectories that drift in class i is negligible when $f_i\gg 1/\left(2Nsi\right),$ and in this appendix we give a heuristic argument explaining why this threshold arises. This heuristic argument does not reproduce $\mathcal{O}\left(1\right)$ factors that are obtained using formal methods (i.e., the factor of $1/2$ in $1/\left(2Nsi\right)$), but it offers additional intuition on the existence of this threshold and its dependence on the parameters N, s, and i.

The threshold $\sim 1/\left(Nsi\right)$ is reminiscent of the drift barrier relevant for single deleterious loci of fitness is. However its relevance in classes below the founding class is not immediately obvious. Although the individuals in class i also feel an effective selection pressure equal to $-is,$ new mutational events from class $i-1$ counter these effects of selection. Thus, it is not obvious that the combination of the opposing effects of mutation into the class and selection within the class will be stronger than the effects of drift whenever $f_i\gg 1/\left(Nsi\right)$ (as opposed to some other threshold that also depends on $U_d{f}_{i-1}$).

To gain insight into this, we consider in more detail the effects of individual mutational events into class i. Each of these mutational events can be thought of as founding a new sublineage in class i. The frequency trajectory of each sublineage is the same as that of a single locus with fitness $-is,$ and the overall trajectory $f_i\left(t\right)$ is equal to the sum of the trajectories of these sublineages. When a sublineage is small, drift will lead to large deviations from its average (deterministic) frequency trajectory, which is also given by Equation B1. However, as in the founding class, at frequencies larger than $1/\left(Nsi\right)$ these deviations are capped by the effects of selection. Thus, the drift barrier $1/\left(Nsi\right)$ represents the frequency above which fluctuations cannot lead to large deviations of individual sublineages from the average behavior.

To understand when drift has an important impact on the overall i-class trajectory $f_i\left(t\right),$ we can consider how these deviations in the trajectories of the sublineages add. At sufficiently small frequencies, $f_i\ll 1/\left(Nsi\right),$ the overall trajectory $f_i$ will be equal to the sum of random trajectories that have an extremely broad distribution. In this case, the sum will be dominated by the trajectory of the largest sublineage, which will be very different than the average trajectory. Thus, even when the total number of mutational events into class i is large, the effects of genetic drift in class i may not be negligible if each of these mutational events results in a relatively small trajectory. In other words, fluctuations due to drift in the frequency trajectories do not average out, but are rather dominated by the largest deviation from the mean. Conversely, when the total number of sublineages is large enough that many of them reach the frequency $1/\left(Nsi\right)$ (which is guaranteed to happen if the total number of mutational events into the i-class is much larger than $1/\left(si\right)$), the overall frequency of the lineage will be much larger than $1/\left(Nsi\right).$ In this case, the largest event is no longer very different than the average event; the effects of genetic drift are therefore negligible compared to the effects of selection. The transition between these two behaviors happens when $f_i\sim 1/\left(Nsi\right),$ which roughly corresponds to exactly one sublineage exceeding $1/\left(Nsi\right).$ We discuss these effects using a more formal approach in Appendix G. Note that, by extending this argument to classes $i+1$ and lower, we can verify that once the frequency trajectory in class i exceeds $1/\left(Nsi\right)$ and becomes predominantly shaped by mutation and selection, the frequency of the allele in all lower-fitness classes is also guaranteed to exceed the corresponding frequency thresholds. This is why we can also neglect the effects of drift in all classes below a class in which the frequency exceeds $1/\left(Nsi\right).$

Appendix C: The Generating Function for the Total Size of the Labeled Lineage

In this appendix, we consider the generating function for the total frequency of the lineage,

$$H_f\left(z,t\right)=\langle e^{-zf\left(t\right)}\rangle ,$$ (C1)

and derive a partial differential equation describing how it changes in time. As described in the main text, when the size of the lineage is small [$f\left(t\right)\ll 1$], its dynamics are described by the coupled system of Langevin equations for the components $f_i\left(t\right)$ of the total frequency f that denote the frequency of the part of the lineage that carry i deleterious mutations,

$$\frac{d{f}_i\left(t\right)}{dt}=-i{s}_i{f}_i+U_d{f}_{i+1}+\sqrt{\frac{f_i}{N}}{\eta }_i\left(t\right).$$ (C2)

In Equation C2, the ${\eta }_i$ are independent, uncorrelated Gaussian noise terms. The total allele frequency is equal to the sum of these components, $f\left(t\right)={\displaystyle {\sum }_i{f}_i\left(t\right)}.$

Note that the total allele frequency $f\left(t\right)$ is not a Markov random variable since its evolution depends on the details of the distribution of the individuals within the lineage among the fitness classes. However, the frequencies of the components $f_i\left(t\right)$ are jointly Markov, with their joint distribution described by the joint generating function

$$H\left(\left\{z_i\right\},t\right)=\langle \exp \left[-{\displaystyle \sum _i{z}_i{f}_i\left(t\right)}\right]\rangle .$$ (C3)

The generating function for $f\left(t\right)$ can be obtained from the joint generating function by setting $z_i=z$ for all i. We can obtain a PDE for the joint generating function by Taylor expanding $H\left(\left\{z_i\right\},t+dt\right)$ and substituting in the differentials $d{f}_i\left(t\right)=-is{f}_{i}dt+U_d{f}_{i-1}dt+\sqrt{f_i/N}\sqrt{dt}{\eta }_i\left(t\right)$ from Equation C2, which yields

$$\frac{\partial H}{\partial t}={\displaystyle \sum _i-\left(is{z}_i+\frac{z_i^2}{2N}-U_d{z}_{i+1}\right)\frac{\partial H}{\partial z_i}}.$$ (C4)

We can solve this PDE for the joint generating function by using the method of characteristics. The characteristic curves $z_i\left(t-t^{\prime }\right)$ are defined by

$$\frac{d{z}_i}{d{t}^{\prime }}=is{z}_i-U_d{z}_{i+1}+\frac{z_i^2}{2N},$$ (C5)

and satisfy the boundary condition $z_i\left(t\right)=z.$ The linear terms in the characteristic equation arise from selection and mutation out of the i-class, and the nonlinear term arises from drift. Along these curves, the generating function is constant and so $H\left(\left\{z_i\right\},t\right)=H\left(\left\{z_i\left(0\right)\right\},0\right)=e^{-{\displaystyle {\sum }_i{f}_i\left(0\right)z_i\left(0\right)}},$ where the initial condition $f_i\left(0\right)={\delta }_{ik}/N$ corresponds to a single individual present in class k at $t=0.$ Thus, to obtain a solution for the joint generating function, we need to integrate along the characteristics in Equation C5 backwards in time from $t^{\prime }=0$ to $t^{\prime }=t.$ In the next few appendices, we obtain these solutions in the limits of weak ($U_d\ll s$) and strong mutation ($U_d\gg s$).

Appendix D: Trajectories in the Presence of Weak Mutation ($U_d\ll s$)

When deleterious mutations arise more slowly than selection removes them ($U_d/s\equiv \lambda \ll 1$), deleterious descendants of a lineage are much less numerous than the founding genotype. To see this, we can expand the characteristics $z_i\left(t-t^{\prime }\right)$ in powers of the small parameter λ. At leading order, the characteristics are uncoupled and can be straightforwardly integrated to obtain

$$z_i^0\left(0\right)=\frac{z{e}^{-ist}}{1+\frac{z}{2Nsi}\left(1-e^{-ist}\right)}.$$ (D1)

By substituting this zeroth-order solution into Equation C5, we find that corrections due to deleterious descendants are $\mathcal{O}\left(\lambda \right)$ and are therefore small uniformly in z. Thus, the generating function for the total f of the labeled lineage t generations after arising in class k is

$$H_f\left(z,t\right)=\exp \left[-\frac{\frac{1}{N}z{e}^{-kst}}{1+\frac{z}{2Nsk}\left(1-e^{-kst}\right)}\right]+\mathcal{O}\left(\lambda \right),$$ (D2)

which agrees with classic results by Kendall (1948) for the generating function of independently segregating loci of fitness $-ks.$

Equation D2 can be inverted to obtain the probability distribution, $p\left(f,t\right),$ by an inverse Laplace transform:

$$p\left(f,t\right)={\displaystyle {\int }_{-i\mathrm{\infty }}^{i\mathrm{\infty }}\frac{dz}{2\pi i}}{e}^{fz}{H}_f\left(z,t\right).$$ (D3)

This distribution is well known, and can be obtained by standard methods. Noting that $H_f\left(t,z\right)$ has a single essential singularity at $z=-2Nsk/\left(1-e^{-kst}\right),$ we can perform the integral above either exactly by contour integration (by closing the contour using a large semicircle in the left half-plane and a straightforward application of the residue theorem, which gives a solution in terms of Bessel functions) or approximately by the method of steepest descents (taking care to deform the contour to pass through the saddle point on the right of the essential singularity). By carrying out this inverse Laplace transform, we obtain that the extinction probability by time t is

$$p\left(f=0,t\right)=\exp \left[-\frac{2sk}{1-e^{-skt}}{e}^{-skt}\right],$$ (D4)

which becomes of order one when $t\mathrm{\gtrsim }1/\left(sk\right),$ in agreement with our intuition that a lineage of fitness $ks$ can only survive for order $1/\left(ks\right)$ generations. For nonextinct lineages, the probability distribution of the frequency is

$$p\left(f,f>0,t\right)\approx \sqrt{\frac{\frac{2Nks}{1-e^{-kst}}\sqrt{\frac{e^{-kst}}{N}}}{4\pi }}{f}^{-3/4}\exp \left[-\frac{2Nks}{1-e^{-kst}}f{\left(1-\sqrt{\frac{e^{-kst}}{Nf}}\right)}^2\right].$$ (D5)

The site frequency spectrum can be obtained from this distribution of frequencies by integrating Equation D5 in time, or by an alternative method that we present in Appendix F.

Appendix E: Trajectories in the Presence of Strong Mutation ($U_d\gg s$)

When deleterious mutations arise faster than selection can remove them, mutation will play an important role in shaping the trajectory. The relative strength of mutation and selection compared to drift will depend on the frequency of the lineage. Drift will remain the dominant force at frequencies $f\ll 1/\left(N{U}_d\right).$ However, at larger frequencies, the mutation and selection terms will become important and we will see that the effects of drift in classes of low enough fitness become negligible.

Small Lineages ($f\ll 1/\left(N{U}_d\right)$)

The dominant term in the characteristic equation in this regime (which corresponds to $z\gg N{U}_d$ in the generating function) is the drift term

$$\frac{d{z}_i}{d{t}^{\prime }}\approx \frac{z_i^2}{2N},$$ (E1)

which has the solution

$$z_i\left(0\right)\approx \frac{z}{1+\frac{zt}{2N}}.$$ (E2)

We can verify that mutation and selection are negligible compared to drift on timescales of order $t\sim 1/U_d$ as long as $i\mathrm{\lesssim }2\lambda .$ Note that this condition ($i\mathrm{\lesssim }2\lambda$) is satisfied for essentially all of the individuals in the population since ${\displaystyle {\sum }_{i=0}^{2\lambda }{h}_i}\approx 1-\sqrt{2\pi /\lambda }{e}^{\left(-2\lambda +1\right)\log \left(2+1/\lambda \right)+\lambda }\approx 1.$ By summing the $z_i\left(0\right)$ terms, we find that on these timescales the generating function for the frequency of the mutation is

$$H_f\left(z,t\right)\approx \exp \left]-\frac{\frac{z}{N}}{1+\frac{zt}{2N}}\right],$$ (E3)

which is just the generating function for the frequency of a neutral lineage (cf. Equation D2). On longer timescales ($t\gg 1/\left(N{U}_d\right)$), this approximation breaks down and mutation and selection cannot be neglected for lineages arising in fitness classes far above the mean of the fitness distribution (with $k\ll \lambda -\sqrt{\lambda }$). This is because the probability that a portion of the lineage in a class with fewer than $\lambda -\sqrt{\lambda }$ mutations has drifted to a high enough frequency to feel the effects of mutation and selection becomes substantial on longer timescales, which can also be seen from the probability distribution of nonextinct lineages (Equation D5). We consider the generating function of these unusually fit mutations at these higher frequencies in the next subsection. In contrast, mutations that arise on more typical backgrounds with $k>\lambda -\sqrt{\lambda }$ mutations can drift to higher frequencies, of order $\sqrt{\lambda }/\left(N{U}_d\right),$ before feeling the effects of selection, but cannot substantially exceed a total frequency $\sqrt{\lambda }/\left(N{U}_d\right).$ We analyze their trajectories in the following subsection.

Large Lineages ($f\gg 1/\left(N{U}_d\right)$) Arising on Unusually Fit Backgrounds ($k\ll \lambda -\sqrt{\lambda }$)

In lineages that reach higher frequencies, a large number of deleterious descendants arise every generation. This leads to strong couplings between the sizes of the components of the lineage in different fitness classes, and diminishes the importance of genetic drift in classes of lower fitness, which receive large numbers of deleterious descendants from classes of higher fitness. We find that, in classes of low enough fitness, the effects of genetic drift are negligible and the dominant balance is between the linear mutation and selection terms.

The solution to the linear (deterministic) problem has been obtained by Etheridge et al. (2009), but we reproduce the derivation briefly for completeness. In the absence of drift, the characteristics evolve according to

$$\frac{d{z}_i}{d{t}^{\prime }}=is{z}_i-U_d{z}_{i+1}\equiv {\displaystyle \sum _i{\mathrm{ℒ}}_{ij}{z}_j},$$ (E4)

which defines the linear operator ${\mathrm{ℒ}}_{ij}.$ $\mathrm{ℒ}$ has right eigenvectors ${\mathit{\phi }}^{\left(\mathit{j}\right)}$ with eigenvalues $-js$ given by

$${\phi }_i^{\left(j\right)}=\{\begin{array}{ll}\frac{{\left(-\lambda \right)}^{j-i}}{\left(j-i\right)!},\hfill & 0\le i\le j\hfill \\ 0,\hfill & \text{otherwise},\hfill \end{array}$$ (E5)

and corresponding left eigenvectors

$${\psi }_i^{\left(j\right)}=\{\begin{array}{ll}\frac{{\lambda }^{i-j}}{\left(i-j\right)!},\hfill & i>j\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}$$ (E6)

We can verify that the left and right eigenvectors are orthonormal [${\mathit{\psi }}^{\left(\mathit{i}\right)}\cdot {\mathit{\phi }}^{\left(\mathit{j}\right)}={\displaystyle {\sum }_l{\psi }_l^{\left(i\right)}{\phi }_l^{\left(j\right)}}={\delta }_{ij}$]. By eigenvalue decomposing $z_i\left(t\right)$ and integrating backward in time from $t^{\prime }=0$ to $t^{\prime }=t,$ we obtain $z_i\left(t-t^{\prime }\right)={\displaystyle {\sum }_j{e}^{-js{t}^{\prime }}{b}_j{\phi }_i^{\left(j\right)}},$ where the amplitudes $b_j$ are set by the boundary condition at $t^{\prime }=0,$ $b_j={\mathit{\psi }}^{\left(\mathit{j}\right)}\cdot \mathit{z}\left(t\right)={\mathit{\psi }}^{\left(\mathit{j}\right)}\cdot \mathit{z}={\displaystyle \sum _{i=j}^{\infty }{z}_j{\lambda }^{i-j}/\left(i-j\right)!}.$ Finally, a summation yields

$$z_i\left(t-t^{\prime }\right)=e^{-is{t}^{\prime }}{\displaystyle \sum _{j=0}^{\mathrm{\infty }}\frac{{\left[\lambda \left(1-e^{-s{t}^{\prime }}\right)\right]}^j}{j!}{z}_{i+j}}.$$ (E7)

Setting the boundary condition at $t=0$ to $f_i\left(0\right)={\delta }_{ki}/N$ and evaluating $z_k\left(0\right),$ we reproduce the result by Etheridge et al. (2009): in the absence of genetic drift, the descendants of the labeled lineage follow a Poisson distribution that starts in class k and has mean $\lambda \left(1-e^{-st}\right)$ and amplitude $e^{-kst}{e}^{-\lambda \left(1-e^{-st}\right)}/N.$

To evaluate the effect of genetic drift on the total size of the lineage at some later time point we set $z_i=z.$ A sufficient (but not necessary) condition for genetic drift in class i being negligible in determining the total size of the lineage at some later time point t is that the nonlinear term $z_i{\left(t-t^{\prime }\right)}^2/\left(2Ns\right)\ll i{z}_i\left(t-t^{\prime }\right)$ uniformly in $t^{\prime }.$ In the vicinity of some frequency $f\left(t\right)\sim f,$ corresponding to $z\left(t\right)=z\sim 1/f,$ we find that the nonlinear term is negligible uniformly in $t^{\prime }$ as long as

$$e^{-is{t}^{\prime }}{e}^{\lambda \left(1-e^{-s{t}^{\prime }}\right)}\ll 2Nsif\text{\hspace{1em}for}\hspace{0.17em}\text{all}\hspace{0.17em}{t}^{\prime },0<t^{\prime }<t.$$ (E8)

Note that the condition in Equation E8 is obtained by plugging in the relationship between $z_i\left(t-t^{\prime }\right)$ and $z\left(t\right)=z\sim 1/f$ (from Equation E7) into the condition that $z_i{\left(t-t^{\prime }\right)}^2/\left(2Ns\right)\ll i{z}_i\left(t-t^{\prime }\right).$ Since the left-hand side in Equation E8 is bounded by $e^{-is{t}^{\prime }}{e}^{\lambda \left(1-e^{-s{t}^{\prime }}\right)}\le e^{\lambda }{\left(i/\left(\lambda e\right)\right)}^i={\stackrel{\sim }{g}}_i,$ the inequality is guaranteed to be satisfied uniformly in t as long as

$$f\gg \frac{1}{2Nsi}{\stackrel{\sim }{g}}_i.$$ (E9)

Defining $k_c\left(f\right)$ to be the smallest integer for which $f\gg {\stackrel{\sim }{g}}_{k_c+1}/\left[2Ns\left(k_c+1\right)\right]$ we can verify that genetic drift is negligible in all classes with $i>k_c\left(f\right)$ but not in class $k_c\left(f\right).$

Note that self-consistency of the deterministic solution for $k_c<\lambda$ implies that when $f\gg {\stackrel{\sim }{g}}_{k_c+1}/\left[2Ns\left(k_c+1\right)\right]$ the frequency of the part of the allele in class i satisfies $f_i\gg 1/\left(2Nsi\right)$ for all $i>k_c,$ but not for $i\le k_c.$ Also note that this inequality can only be satisfied for some $k_c<\lambda$ if the founding class is sufficiently far above the fitness distribution ($\lambda -k\gg \sqrt{\lambda },$ where ${\stackrel{\sim }{g}}_k\gg 1$). We return to lineages founded in classes with $k>\lambda -\sqrt{\lambda }$ mutations in the next subsection.

Thus, since genetic drift has a negligible effect in classes containing more than $k_c$ deleterious mutations, the characteristics $z_i\left(t^{\prime }\right)$ are given by the deterministic solution above, which we have already integrated. The frequency of the part of the lineage in classes with $i>k_c$ is therefore a deterministic function of the frequency trajectory in class $k_c,$ $f_{k_c}\left(t\right).$ We can solve for this deterministic function straightforwardly by explicitly including $f_{k_c}\left(t\right)$ as a variable mutational source term for classes of lower fitness. This yields an expression for the generating function of the entire lineage

$$H_f\left(z,t\right)=\langle e^{-z{\displaystyle {\sum }_{i=k}^{k_c}{f}_i\left(t\right)}-z{U}_d{\displaystyle {\int }_{-\mathrm{\infty }}^{t}d\tau }{f}_{k_c}\left(\tau \right)g_{k_c+1}\left(t-\tau \right)}\rangle ,$$ (E10)

when

$$z\ll \frac{2Ns\left(k_c+1\right)}{{\stackrel{\sim }{g}}_{k_c+1}},$$ (E11)

where we have used the notation from the main text: $g_i\left(t\right)=e^{-ist+\lambda \left(1-e^{-st}\right)}.$

The relationship between the feeding class trajectory $f_{k_c}\left(t\right)$ and the allele frequency trajectory f(t)

Equivalently, this result can be rewritten in terms of the relationship between the allele frequency trajectory $f\left(t\right)$ and the trajectory of the portions of the alleles in classes with $k\le k_c:$

$$f\left(t\right)={\displaystyle \sum _{i=k}^{k_c}{f}_i\left(t\right)}+U_d{\displaystyle {\int }_{-\mathrm{\infty }}^{t}d\tau }{f}_{k_c}\left(\tau \right)g_{k_c+1}\left(t-\tau \right),$$ (E12)

which is valid as long as $f\gg {\stackrel{\sim }{g}}_{k_c+1}/\left[2Ns\left(k_c+1\right)\right].$ Because the expression on the right-hand side of Equation E12 is dominated by the last term, the full allele frequency trajectory reduces to a single stochastic term $f_{k_c}.$ Therefore, we can calculate the distribution of $p\left(f,t\right)$ near any given frequency f by: (1) determining the feeding class $k_c\left(f\right),$ which corresponds to the class of lowest fitness in which genetic drift is not negligible; and (2) calculating the distribution of this time integral of the trajectory in that class, $f_{k_c}\left(t\right),$ subject to the boundary condition that $f_k\left(0\right)=1/N.$

In principle, this is still challenging if $k_c>k$ because the trajectory in class $k_c$ still depends on the trajectories in higher-fitness classes, all of which are stochastic. In addition, calculating the distribution of the convolution of $f_{k_c}\left(t\right)$ and $g_{k_c+1}\left(t\right)$ is still difficult, even when $k_c=k.$ Fortunately, a simplification arises from the highly peaked nature of $g_{k_c+1}\left(t-\tau \right).$ Because the exponent in $g_{k_c+1}\left(t-\tau \right)$ is peaked in time, the integral in Equation E12 is, up to exponentially small terms, dominated by the region in which $g_{k_c+1}\left(t-\tau \right)f_{k_c}\left(\tau \right)$ is largest. Since the variation in the magnitude of $g_{k_c+1}\left(t-\tau \right)$ is much larger than the variation in the magnitude of $f_{k_c}\left(\tau \right),$ the integral will be dominated by the window during which $g_{k_c+1}\left(t-\tau \right)$ is at its peak, as long as $f_{k_c}\left(\tau \right)\ne 0$ in that window. In that case, we can make a Laplace-like approximation in Equation E12, in which we expand $g_{k_c+1}\left(t-\tau \right)$ around its peak, and neglect contributions that are far away from this peak, since these are exponentially small. Near $\tau =t-t_d^{\left(k_c+1\right)}=t-\log \left[\lambda /\left(k_c+1\right)\right]/s$

$$g_{k_c+1}\left(t-\tau \right)\approx {\stackrel{\sim }{g}}_{k_c+1}{e}^{-\left(k_c+1\right)s^2{\left[t-\tau -t_d^{\left(k_c+1\right)}\right]}^2},$$ (E13)

which yields

$$\begin{array}{c}f\left(t\right)\approx U_d{\stackrel{\sim }{g}}_{k_c+1}{\displaystyle {\int }_{-\mathrm{\infty }}^{t}d\tau }{f}_{k_c}\left(\tau \right)e^{-\left(k_c+1\right)s^2{\left(t-\tau -t_d^{\left(k_c+1\right)}\right)}^2}\\ \approx U_d{\stackrel{\sim }{g}}_{k_c+1}{\displaystyle {\int }_{t-t_d^{\left(k_c+1\right)}-\frac{\Delta t^{\left(k_c+1\right)}}{2}}^{t-t_d^{\left(k_c+1\right)}+\frac{\Delta t^{\left(k_c+1\right)}}{2}}{f}_{k_c}\left(\tau \right)d\tau }\equiv U_d{\stackrel{\sim }{g}}_{k_c+1}{W}_{\Delta t^{\left(k_c+1\right)}}\left(t-t_d^{\left(k_c+1\right)}\right).\end{array}$$ (E14)

As a result of this simplification, the allele frequency does not depend on the full frequency trajectory in the feeding class $f_{k_c}\left(t\right),$ but only on its time integral (weight) in a window of width $\Delta t^{\left(k_c+1\right)}=1/\left(\sqrt{k_c+1}s\right)$ around $t-t_d^{\left(k_c+1\right)},$ which we denote by $W_{\Delta t^{\left(k_c+1\right)}}\left(t-t_d^{\left(k_c+1\right)}\right).$ Note that Equation E14 implies a simple condition in terms of the allele frequency trajectory in this feeding class $k_c$ that specifies when drift is negligible in downstream classes. We have shown above that as long as the total allele frequency $f\gg {\stackrel{\sim }{g}}_{k_c+1}/\left[2Ns\left(k_c+1\right)\right]$ drift is negligible in classes with more than $k_c$ deleterious mutations per individual. From Equation E14, we can see that this condition can be restated in terms of the weight in the feeding class as

$$W_{\Delta t^{\left(k_c+1\right)}}\left(t-t_d^{\left(k_c+1\right)}\right)\gg \frac{1}{2N{U}_{d}s\left(k_c+1\right)}.$$ (E15)

Thus, $k_c$ can also be thought of as corresponding to the class of highest fitness in which the weight exceeds $1/\left(2N{U}_{d}s\left(k_c+1\right)\right).$

The approximation we have used in Equation E14 breaks down at very early times [$t\ll t_d^{\left(k\right)}$] and very late times, during which $f_{k_c}\left(\tau \right)=0$ in the relevant window. These correspond to the spreading and extinction phases of the trajectory. We show in Appendix I that the former has a negligible impact on the site frequency spectrum. The latter phase however has an important effect at very high frequencies of the mutant, i.e., when the wild type is rare and in its own extinction phase. During this extinction phase,

$$g_{k_c+1}\left(t-\tau \right)\approx e^{\lambda -\left(k_c+1\right)s\left(t-\tau \right)}$$ (E16)

uniformly in t and the frequency trajectory is well approximated as

$$f\left(t\right)\approx U_d{e}^{\lambda -\left(k_c+1\right)st}{\displaystyle {\int }_{-\mathrm{\infty }}^{t}d\tau }{f}_{k_c}\left(\tau \right)e^{\left(k_c+1\right)s\tau }.$$ (E17)

Applying the Laplace approximation once again, we conclude that the integral in Equation E17 is dominated by the window of width $1/\left[\left(k_c+1\right)s\right]$ prior to extinction in the k_c-class and therefore only weakly depends on time. Thus, during this extinction phase, the allele frequency decays exponentially at rate $\left(k_c+1\right)s$ and can be written as

$$f\left(t\right)=f_{\text{peak}}{e}^{-\left(k_c+1\right)s\left(t-t_{\text{peak}}\right)},$$ (E18)

for some choice of $t_{\text{peak}},$ where $f_{\text{peak}}$ reflects the maximal frequency the trajectory reached before the onset of the extinction phase.

Thus, we can see that in the extinction phase of the trajectory, the effective fitness of the lineage changes with the frequency according to

$$s_{\text{eff}}\left(f\right)=-\left[k_c\left(f\right)+1\right]s.$$ (E19)

To obtain an explicit expression for how the feeding class $k_c\left(f\right)$ and therefore $s_{\text{eff}}\left(f\right)$ depend on the frequency f, we can solve the condition that ${\stackrel{\sim }{g}}_{k_c+1}/\left[2Ns\left(k_c+1\right)\right]\ll f\ll {\stackrel{\sim }{g}}_{k_c}/\left(2Ns{k}_c\right)$ for $k_c$ by setting $f=C\left(f\right)·{\stackrel{\sim }{g}}_{k_c+1}/\left[2Ns\left(k_c+1\right)\right]$ for some $C\left(f\right)$ that satisfies $1\ll C\left(f\right)\ll \lambda .$ We find that, to leading order,

$$k_c\left(f\right)+1\approx {\log }_{\lambda }\left(\frac{1}{Ns{e}^{-\lambda }f}\right)\hspace{1em}\text{when}\hspace{0.17em}{k}_c\left(f\right)\gg 1.$$ (E20)

By plugging this back into the expression for $s_{\text{eff}}\left(f\right),$ we find that, in the extinction phase of the trajectory, the effective selection coefficient changes with the frequency of the lineage according to

$$s_{\text{eff}}\left(f\right)=-{\log }_{\lambda }\left(\frac{1}{Ns{e}^{-\lambda }f}\right)s,\hspace{1em}\text{if}\hspace{0.17em}f\ll \frac{1}{Ns{e}^{-\lambda }}.$$ (E21)

In summary, we have shown in this appendix that the allele frequency trajectory in the peak phase of the allele only depends on the time integral of the frequency in class $k_c$ over a window of specified width $\Delta t^{\left(k_c+1\right)}$ and that, outside this peak phase, the trajectory has an even simpler time-dependent form that we described above.

As we will see in Appendix F, the generating function for this relevant weight in class $k_c$ is straightforward to calculate when $k_c$ is the founding class (i.e., for $k_c=k$). This case is relevant for trajectories that arise in class k and exceed frequencies $f_k\gg 1/\left(N\sqrt{U_{d}s\left(k+1\right)}\right),$ which means that the feeding-class weight will exceed $1/\left(2N{U}_{d}s\left(k+1\right)\right)$ for a certain period of time.

However, not all trajectories that arise in class k will reach such large frequencies. We have seen in an earlier section that trajectories that do not ever exceed frequencies much larger than $1/\left(N{U}_d\right)$ will have a trajectory that is dominated by drift throughout its lifetime. However, even those that do exceed $f_k\gg 1/\left(N{U}_d\right)$ and therefore leave behind a large number of deleterious descendants will often not reach the much larger frequency $f_k\gg 1/\left(N\sqrt{U_{d}s\left(k+1\right)}\right).$ In this case, we will have to treat multiple fitness classes stochastically and the weight relevant for the peak of the trajectory will be that in class $k_c>k.$ For $k_c>k\left(\ge 0\right),$ a further simplification results from the fact that the width of the window $\Delta t^{\left(k_c+1\right)}\left(t\right)$ is longer than the lifetime of the mutation in class $k_c$ (see Appendix F and Appendix G for details). We use this simplification to calculate the resulting weight distribution in Appendix G. Finally, in Appendix I we use these results to obtain expressions for the average site frequency spectrum both in the case of strong and weak mutation.

Lineages Arising on Typical Backgrounds ($k-\lambda >-\sqrt{\lambda }$)

Lineages founded in classes with $k>\lambda -\sqrt{\lambda }$ mutations will not enter the semideterministic regime described above. This is because selection in each individual class i in which they can be present prevents $f_i$ from exceeding $1/\left(Nsi\right)<1/\left(Nsk\right)\approx 1/\left(N{U}_d\right),$ where the latter ($1/\left(N{U}_d\right)$) is the necessary threshold for a large enough number of deleterious descendants to be generated that their dynamics become dominated by selection in some class below the i-class. This threshold equal to $1/N{U}_d$ emerges from our analysis of the coupled branching process in the previous subsection and is further clarified and discussed in Appendix G.

In contrast to lineages arising far above the mean of the fitness distribution, the frequency trajectories of lineages that arise near the mean of the fitness distribution are dominated by drift and are eventually capped by negative selection at large enough frequencies. Selection becomes an important force about $1/\sqrt{U_{d}s}=1/\sigma$ generations after the lineage was founded. At this time, the accumulated deleterious load since arising becomes large enough to affect the trajectory of the mutation. This deleterious load will affect the trajectory substantially when the frequency of the lineage $f\left(t\right)$ becomes comparable to the drift barrier set by its current relative fitness $x\left(t\right),$ $1/\left(Nx\left(t\right)\right).$ The expected fitness of a lineage founded near the mean of the distribution [with $\left|x\left(0\right)\right|\mathrm{\lesssim }\sigma$] is $\langle x\left(t\right)\rangle =x\left(0\right)-U_d\left(1-e^{-st}\right).$ Provided that the lineage has not drifted to extinction by t, its expected frequency at t is $f\left(t\right)\sim t/N.$ Thus, when $f\left(t\right)\approx 1/\left(Nx\left(t\right)\right),$ the effect of selection will dominate over drift. This occurs when $t\sim 1/\sqrt{U_{d}s}=1/\sigma .$ Thus, lineages that arise near the mean of the fitness distribution have a trajectory that has neutral statistics for the majority of its lifetime, but does not exceed $1/N\sigma .$ Finally, lineages arising in classes far below the mean of the fitness distribution ($k-\lambda \gg \sqrt{\lambda }$), will also be dominated by drift, but limited to even lower frequencies. However, these lineages are also comparatively rare and only have a small relative impact on the lowest-frequency part of the site frequency spectrum ($f\ll 1/\left(N\sigma \right)$).

Appendix F: The Distribution of Allele Frequencies and of the Weight in the Founding Class

In this appendix, we calculate the distribution of frequencies $f_k\left(t\right)$ and weights $W_{\Delta t}\left(t\right)={\displaystyle {\int }_{t-\Delta t/2}^{t+\Delta t/2}{f}_k\left(t^{\prime }\right)d{t}^{\prime }}$ for the stochastic process defined by

$$\frac{d{f}_k}{dt}=-ks{f}_k+\sqrt{\frac{f_k}{N}}\eta \left(t\right),$$ (F1)

with $f_k\left(0\right)=1/N$ and $f_k\left(t\right)=0$ for $t<0.$ This process describes the trajectory of the component of the lineage that remains in the founding class (the founding genotype). To calculate these distributions, we begin by defining the joint generating function for the frequency $f_k\left(t\right)$ and the total time-integrated weight up to time t:

$$W\left(t\right)={\displaystyle {\int }_0^t{f}_k\left(t^{\prime }\right)d{t}^{\prime }}.$$ (F2)

The joint generating function for these two quantities is defined as

$$G\left(z,\zeta ,t\right)=\langle e^{-z{f}_k\left(t\right)-\zeta W\left(t\right)}\rangle ,$$ (F3)

and satisfies the PDE

$$\frac{\partial G\left(z,\zeta ,t\right)}{\partial t}=-\left(-\zeta +ksz+\frac{z^2}{2N}\right)\frac{\partial G\left(z,\zeta ,t\right)}{\partial z}.$$ (F4)

Once again, we solve this PDE using the method of characteristics. The characteristics $z\left(t-t^{\prime }\right)$ are defined by

$$\frac{dz}{d{t}^{\prime }}=-\zeta +ksz+\frac{z^2}{2N},\frac{d\zeta }{d{t}^{\prime }}=0,$$ (F5)

and are subject to the boundary condition $z\left(t\right)=z,$ $\zeta \left(t\right)=\zeta .$ The generating function is constant along the characteristics ($dG/d{t}^{\prime }=0$), and therefore satisfies

$$G\left(z,\zeta ,t\right)=G\left(z\left(0\right),\zeta \left(0\right),0\right).$$ (F6)

After integrating the ordinary differential equations in Equation F5, we find that the characteristics follow

$$z\left(t-t^{\prime }\right)=a_{+}+\left(a_{+}-a_{-}\right)\frac{\left(z-a_{+}\right)\exp \left[\frac{-\left(a_{+}-a_{-}\right)t^{\prime }}{2N}\right]}{z-a_{-}-\left(z-a_{+}\right)\exp \left[\frac{-\left(a_{+}-a_{-}\right)t^{\prime }}{2N}\right]},$$ (F7)

with $a_{\pm }=Nsk\left[-1\pm \sqrt{1+2\zeta /\left(N{\left(sk\right)}^2\right)}\right].$

We can verify that the correct marginal generating function for the frequency of the lineage emerges from this result by setting $\zeta =0$ and imposing the boundary condition $G\left(z,0,t\right)=G\left(z\left(0\right),0,0\right)=e^{-z\left(0\right)/N},$ which corresponds to the initial frequency at $t=0$ being $1/N.$

To obtain the marginal generating function for the weight in the window between $t-\Delta t/2$ and $t+\Delta t/2,$ we set $z=0,$ $t=\Delta t,$ and choose a boundary condition that reflects the distribution of frequencies $f_k\left(t-\Delta t/2\right)$ generations after the lineage was founded (see Equation D2):

$$G_W\left(z=0,\zeta ,t=\Delta t\right)=\exp \left\{-\frac{\frac{1}{N}z\left(0\right)e^{-ks\left(t-\frac{\Delta t}{2}\right)}}{1+\frac{z\left(0\right)}{2Nsk}\left[1-e^{-ks\left(t-\frac{\Delta t}{2}\right)}\right]}\right\},$$ (F8)

where

$$z\left(0\right)=\frac{2\zeta }{sk\left\{\sqrt{1+\frac{2\zeta }{N{\left(sk\right)}^2}}\coth \left[\frac{ks\Delta t}{2}\sqrt{1+\frac{2\zeta }{N{\left(ks\right)}^2}}\right]+1\right\}}.$$ (F9)

The generating function in Equation F8 captures the full time-dependent behavior of the weight in the founding class in a window of width $\Delta t$ and can be inverted by standard methods. However, it is in practice unnecessary to invert Equation F8 to calculate the site frequency spectrum. For our purposes here, we will be mostly concerned with two special cases: the total weight in the founding class from founding to extinction, $W={\displaystyle {\int }_0^{\mathrm{\infty }}f\left(t^{\prime }\right)d{t}^{\prime }},$ and the time integral of the distributions of frequencies $p\left[f\left(t\right)\right]$ and weights $p\left[W_{\Delta t}\left(t\right)\right]$ in a window of specified width $\Delta t.$ The former case has been calculated previously by Weissman et al. (2009). We quote and discuss this result for completeness in the section below. We then analyze the latter case in the following section.

The Distribution of the Total Lifetime Weight in the Founding Class, $W={\displaystyle {\int }_0^{\mathrm{\infty }}f\left(t^{\prime }\right)d{t}^{\prime }}$

The first special case that will be relevant to our analysis of trajectories and allele frequency spectra is the total integrated weight in the founding class from founding ($t=0$) to extinction. By setting $\Delta t=t/2$ in Equations F8 and F9, we find that the generating function for the total weight from founding to some later time t is

$$G_W\left(\zeta ,t\right)=\exp \left[-\frac{2\zeta }{Nsk\left\{\sqrt{1+\frac{2\zeta }{N{\left(sk\right)}^2}}\coth \left[\frac{kst}{2}\sqrt{1+\frac{2\zeta }{N{\left(ks\right)}^2}}\right]+1\right\}}\right].$$ (F10)

Note that Equation F10 becomes independent of time when $t\mathrm{\gtrsim }2/\left(ks\right)$ (uniformly in ζ), which agrees with our heuristic intuition that the lifetime of a mutation in class k is not longer than $\sim 2/\left(ks\right)$ generations. Since we have shown in Large Lineages Arising on Unusually Fit Backgrounds in Appendix E that the allele frequency trajectory $f\left(t\right)$ depends on the weight in a window of width $\Delta t\ge \Delta t^{\left(k+1\right)}=1/\left(\sqrt{k+1}s\right)$ (where the $\ge$ sign follows because $k_c\ge k$) that is longer than $\sim 1/\left(ks\right)$ for $k>1$ (with $k=1$ being the marginal case), the distribution of $W_{\Delta t^{\left(k+1\right)}}\left(t\right)$ will be either equal to the total lifetime weight of the allele [for $t\mathrm{\lesssim }\Delta t^{\left(k+1\right)}$] or negligible for $t\mathrm{\gtrsim }\Delta t^{\left(k+1\right)}.$

By taking the limit $t\to \mathrm{\infty }$ in Equation F10, we obtain that the generating function for the distribution of the lifetime weight in the founding class is

$$G_W\left(\zeta \right)=\exp \left[-\frac{2\zeta }{\sqrt{{\left(Nsk\right)}^2+2\zeta N}}\right].$$ (F11)

The inverse Laplace transform of Equation F11 can be evaluated by standard methods, which yields the distribution of the lifetime weight in the founding class:

$$p\left(W\right)=\sqrt{\frac{1}{2N\pi }}\frac{1}{W^{3/2}}{e}^{\frac{-N{\left(ks\right)}^{2}W}{2}-\frac{1}{2NW}}.$$ (F12)

The Time Integrals of $p\left(f,t\right)$ and $p\left(W_{\Delta t},t\right)$

To calculate the average site frequency spectrum, we need to calculate the time integral of the distributions of frequencies and weights over time. In principle, this can be done by inverting Equation F8 and then integrating the distribution of $W_{\Delta t}\left(t\right)$ over time. However, since this is a somewhat laborious calculation, we will use a convenient mathematical shortcut in which we first solve for the distribution of weights in a different stochastic process and then relate this back to the original process in Equation F1.

Specifically, we consider the stationary limit of the stochastic process defined by the Langevin equation:

$$\frac{df}{dt}=\theta -ksf+\sqrt{\frac{f}{N}}\eta \left(t\right).$$ (F13)

This describes the time evolution of the frequency of a lineage with fitness $-ks$ in which individuals are continuously generated by mutation at some rate $N\theta$ (and have frequency $1/N$ at the time when they are generated). This process is relevant because the distribution of frequencies and weights in the stationary process are related to the time integrals of the distributions of $f\left(t\right)$ and $W_{\Delta t}\left(t\right).$ More precisely, in the limit that $\theta \to 0$ (keeping N constant), the distributions of f (and its time integrals) in the stationary process are the same as the time-integrated distributions of the nonstationary process, provided that we also divide by the total rate at which new individuals are generated, $N\theta ,$ to ensure proper normalization. That is,

$${\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}p\left[f_k\left(t\right)\right]dt}=\underset{\theta \to 0}{\lim }\frac{1}{N\theta }\cdot p\left(f,f>0,\theta \right).$$ (F14)

We denote the joint generating function for the frequency, f, and weight in this process, $W\left(t,\theta \right)={\displaystyle {\int }_0^{t}W\left(t^{\prime },\theta \right)d{t}^{\prime }},$ by

$$G_{\theta }\left(z,\zeta ,t\right)=\langle e^{-zf\left(t,\theta \right)-\zeta W\left(t,\theta \right)}\rangle .$$ (F15)

$G_{\theta }\left(z,\zeta ,t\right)$ satisfies the PDE

$$\frac{\partial G_{\theta }\left(z,\zeta ,t\right)}{\partial t}=-\left(-\zeta +ksz+\frac{z^2}{2N}\right)\frac{\partial G_{\theta }\left(z,\zeta ,t\right)}{\partial z}-\theta z{G}_{\theta }\left(z,\zeta ,t\right).$$ (F16)

Note that the generating functions for the two processes are related and that, by setting $\theta =0$ in Equation F16, we obtain the generating function for the nonstationary process (see Equation F4). In particular, the characteristics for Equation F16 are the same as the characteristics for Equation F4 and they follow the form we calculated previously and quoted in Equation F7. Along these characteristics, the generating function satisfies

$$\frac{d{G}_{\theta }}{d{t}^{\prime }}=\theta z\left(t-t^{\prime }\right)G_{\theta },$$ (F17)

or equivalently, after integrating,

$$G_{\theta }\left(z,\zeta ,t\right)=G_{\theta }\left(z\left(0\right),\zeta \left(0\right),0\right)\exp \left[-\theta {\displaystyle {\int }_0^{t}z\left(t-t^{\prime }\right)d{t}^{\prime }}\right].$$ (F18)

However, the boundary conditions for the two processes are different. The nonstationary process is subject to the boundary condition that there is a single individual present in the lineage at $t=0,$ $G\left(z\left(0\right),\zeta \left(0\right),0\right)=e^{-z\left(0\right)/N},$ whereas the stationary process is subject to the boundary condition that the process is stationary at the initial time point, $t^{\prime }=t.$ The stationary property of the frequency distribution is guaranteed by the boundary condition $G_{\theta }\left(z\left(0\right),\zeta \left(0\right),0\right)={\left[1+z\left(0\right)/\left(2Nsk\right)\right]}^{-2Ns\theta }.$ This can be obtained either by inspection or by substituting an arbitrary boundary condition and finding the limiting form for the generating function for the frequency as $t\to \mathrm{\infty },$ and noting that $z\left(0\right)$ becomes independent of z as $t\to \mathrm{\infty },$ so the initial condition has no impact on the frequency distribution.

Plugging in the expression for $z\left(t-t^{\prime }\right)$ from Equation F7 into Equation F18 and performing the integral over $t^{\prime },$ we arrive at the solution to the joint generating function for $f\left(\theta \right)$ and $W\left(\theta \right),$

$$G_{\theta }\left(z,\zeta ,t\right)=G_{\theta }\left(z\left(0\right),\zeta \left(0\right),0\right)\exp \left[-\theta a_{+}t\right]{\left\{1+\left(z-a_{+}\right)\frac{1-\exp \left[-\frac{\left(a_{+}-a_{-}\right)t}{2N}\right]}{a_{+}-a_{-}}\right\}}^{-2N\theta }.$$ (F19)

To obtain the marginal generating function for $f\left(\theta \right),$ we set $\zeta =0,$ giving $a_{+}=0,a_{-}=-2Nsk,$ and

$$G_{\theta ,f}\left(z\right)={\left(1+\frac{z}{2Nsk}\right)}^{-2N\theta }.$$ (F20)

Conversely, to get the generating function for $W\left(t,\theta \right)$ we set $z=0,$ which after some rearranging yields

$$z\left(0\right)=\frac{2\zeta }{sk\left\{\sqrt{1+\frac{2\zeta }{N{\left(sk\right)}^2}}\coth \left[\frac{kst}{2}\sqrt{1+\frac{2\zeta }{N{\left(ks\right)}^2}}\right]+1\right\}}$$ (F21)

and

$$G_{\theta ,W}\left(\zeta \right)=e^{Nsk\theta t}{\left\{\frac{1+\frac{\zeta }{N{\left(sk\right)}^2}}{\sqrt{1+\frac{2\zeta }{N{\left(sk\right)}^2}}}\sinh \left[\frac{kst}{2}\sqrt{1+\frac{2\zeta }{N{\left(ks\right)}^2}}\right]+\cosh \left[\frac{kst}{2}\sqrt{1+\frac{2\zeta }{N{\left(ks\right)}^2}}\right]\right\}}^{-2N\theta }.$$ (F22)

We invert Equations F20 and F22 below.

Inversion of the generating functions in Equations F20 and F22

Since only the nonextinct portion of the process contributes to the site frequency spectrum, when inverting the generating functions for the weight and frequency, we will use the following relationship between the probability distribution $p\left(g\right)$ and the moment-generating function $G_g\left(z\right)$ of a random variable g:

$$p\left(g\right)={\displaystyle {\int }_{-i\mathrm{\infty }}^{i\mathrm{\infty }}\frac{dz}{2\pi i}}{e}^{zg}{G}_g\left(z\right)=\underset{x\to \mathrm{\infty }}{\lim }\left[\frac{e^{ixg}{G}_g\left(ix\right)-e^{-ixg}{G}_g\left(-ix\right)}{2\pi ig}\right]+{\displaystyle {\int }_{-i\mathrm{\infty }}^{i\mathrm{\infty }}\frac{dz}{2\pi i}}\frac{e^{zg}}{g}\left[-\frac{\partial G_g}{\partial z}\right].$$ (F23)

From the definition of the moment-generating function and the sine limit definition of the Dirac δ function [${\lim }_{x\to \mathrm{\infty }}\sin \left(xg\right)/\left(\pi g\right)=\delta \left(g\right)$], it follows that the boundary terms amount to the probability mass at $g=0$ and that the distribution of the nonzero portion of the process is

$$p\left(g,g>0\right)={\displaystyle {\int }_{-i\mathrm{\infty }}^{i\mathrm{\infty }}\frac{dz}{2\pi i}}\frac{e^{zg}}{g}\left[-\frac{\partial G_g}{\partial z}\right].$$ (F24)

After plugging this expression and the generating function for the frequency Equation F20 into Equation F14 and taking the $\theta \to 0$ limit, we find that the time-integrated distribution of frequencies in the founding class is

$${\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}p\left[f_k\left(t\right)\right]dt}=\frac{2}{f_k}{e}^{-2Nsk{f}_k}.$$ (F25)

The time-integrated distribution of weights in the feeding class can be obtained in an entirely analogous fashion. In this case, it will be convenient to treat the cases $k=0$ and $k>0$ separately. When $k=0,$ a lengthy but straightforward substitution of Equation F22 into Equation F24 gives

$$\underset{\theta \to 0}{\lim }\frac{p\left(W,W>0,\theta \right)}{N\theta }=\frac{1}{W}{\displaystyle {\int }_{-i\mathrm{\infty }}^{i\mathrm{\infty }}\frac{d\zeta }{2\pi i}}{e}^{\zeta W}\left[\frac{1}{\zeta }+\frac{t}{\sqrt{2N\zeta }\tanh \left(\sqrt{\frac{\zeta }{2N}}t\right)}\right].$$ (F26)

The simplest way to carry out this integral is by contour integration. To do this, we close the contour using a large semicircle in the left half-plane. The contribution from this circle vanishes as the radius of the semicircle approaches infinity, and so the integral considered above is equal to the sum of the residues within the left half-plane. The integrand has simple poles at $\sqrt{\zeta /\left(2N\right)}=n\pi i/t$ for $n\ge 0$ with residues $2e^{-n^2{\pi }^{2}2NW/t^2},$ which yields

$$\underset{\theta \to 0}{\lim }\frac{p\left(W,W>0,\theta \right)}{N\theta }=\frac{1}{W}\left[2+2{\displaystyle \sum _{n=1}^{\mathrm{\infty }}{e}^{-\frac{n^2{\pi }^{2}2NW}{t^2}}}\right]=\frac{1}{W}\left\{1+{\vartheta }_3\left[0,\exp \left(-\frac{2{\pi }^{2}NW}{t^2}\right)\right]\right\},$$ (F27)

where ${\vartheta }_3$ is the elliptic theta function. Asymptotic expansions for small and large arguments give

$$\underset{\theta \to 0}{\lim }\frac{p\left(W,W>0,\theta \right)}{N\theta }=\{\begin{array}{ll}\frac{1}{\sqrt{2N\pi }}\frac{t}{W^{3/2}},\hfill & W\ll \frac{t^2}{2N{\pi }^2},\hfill \\ \frac{2}{W},\hfill & W\gg \frac{t^2}{2N{\pi }^2}.\hfill \end{array}$$ (F28)

The case $k>0$ is slightly more straightforward to evaluate since the length of the intervals we are interested in is longer than the typical timescale of selection, $t=\Delta t^{\left(k+1\right)}=1/\left(\sqrt{k+1}s\right)\mathrm{\gtrsim }1/\left(ks\right).$ As a result, the arguments in the hyperbolic functions in Equation F22 satisfy $kst·\sqrt{1+2\zeta /\left(N{\left(ks\right)}^2\right)}\mathrm{\gtrsim }1$ (for $k>1,$ with $k=1$ being the marginal case), which yields a simple form for the distribution of nonzero weights:

$$\begin{array}{c}\underset{\theta \to 0}{\lim }\frac{p\left(W,W>0,\theta \right)}{N\theta }=\frac{1}{W}{\displaystyle {\int }_{-i\mathrm{\infty }}^{i\mathrm{\infty }}\frac{d\zeta }{2\pi i}}{e}^{-\zeta W}\underset{\theta \to 0}{\lim }\left[-\frac{1}{N\theta }\frac{\partial G\left(\zeta ,t\right)}{\partial \zeta }\right]\\ \approx \frac{1}{W}{\displaystyle {\int }_{-i\mathrm{\infty }}^{i\mathrm{\infty }}\frac{d\zeta }{2\pi i}}{e}^{-\zeta W}\frac{t}{Nsk}\cdot \frac{1}{\sqrt{1+\frac{2\zeta }{N{\left(sk\right)}^2}}}.\end{array}$$ (F29)

Note that the expression in Equation F29 reduces to a standard Gaussian integral. By carrying out this integral, we obtain for the time integral of the distribution of weights in the founding class:

$${\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}p\left[W\left(t^{\prime }\right)\right]d{t}^{\prime }}=\underset{\theta \to 0}{\lim }\frac{p\left(W,W>0,\theta \right)}{N\theta }\approx e^{-N{\left(sk\right)}^{2}W/2}\frac{t}{\sqrt{2N\pi }{W}^{3/2}}.$$ (F30)

Appendix G: The Distribution of Weights in Classes Below the Founding Class

We have seen in Appendix E that, when the allele frequency trajectory in the founding class $f_k\left(t\right)$ is small enough, the effects of genetic drift cannot be ignored in multiple fitness classes. In this section, we consider how the trajectories (and their weights) in these stochastic classes are coupled and derive the distribution of lifetime weights in class $k+\Delta ,$ in which individuals carry $\Delta$ more mutations compared to individuals in the founding class.

The Relationship Between the Trajectory in the Founding Class k, and the Weight in Class $k+1$

We begin by considering the total lifetime weight in the class right below the founding class ($i=k+1$), which we will denote $W_{k+1}.$ $W_{k+1}$ clearly depends on the weight in the founding class, $W_k,$ since the total number of mutational events from the k-class into the ($k+1$)-class is equal to $N{U}_d{W}_k.$ As we describe in The Importance of Genetic Drift in Classes Below the Founding Class in Appendix B, each one of these mutational events founds a sublineage, and the stochastic trajectory of each sublineage is described by Equation F1. The total weight of the lineage in class $k+1$ is simply the sum of the weights of each of these sublineages. The generating function of the lifetime weight in the $k+1$ class, $W_{k+1},$ is related to the lifetime weight in the founding class $W_k$ according to

$$G_{W_{k+1}}\left(\zeta \right)=\langle \exp \left[-\zeta {\displaystyle \sum _{j=0}^{N{U}_d{W}_k}{W}_{k+1}^{\left(j\right)}}\right]\rangle ,$$ (G1)

where $W_{k+1}^{\left(j\right)}$ denotes the weight of the sublineage founded by the $j^{\text{th}}$ mutational event. Since the $W_{k+1}^{\left(j\right)}$ are independent and identically distributed, the generating function of their sum is equal to the product of their generating functions and

$$G_{W_{k+1}}\left(\zeta \right)=\langle G_{W_{k+1}^{\left(1\right)}}^{N{U}_d{W}_k}\left(\zeta \right)\rangle ,$$ (G2)

where the final average is taken over the distribution of the weight, $W_k,$ in the k-class. The generating functions of $W_k$ and $W_{k+1}^{\left(1\right)}$ are both given by Equation F11.

Using the same methods that we used to invert Equation F11, we obtain that the distribution of the total weights in class $k+1,$ conditioned on the weight in class k being equal to $W_k,$ is

$$p\left(W_{k+1}|W_k\right)=\frac{N{U}_d{W}_k}{\sqrt{2\pi N}}\frac{1}{W_{k+1}^{3/2}}{e}^{-\frac{N{\left[s\left(k+1\right)\right]}^2{W}_{k+1}}{2}-\frac{{\left(N{U}_d{W}_k\right)}^2}{2N{W}_{k+1}}}.$$ (G3)

We can see from this equation that the neutral decay of the distribution of weights in class $k+1,$ which results from drift and is proportional to $1/W^{3/2},$ is exponentially cut off for $W_{k+1}\ll {\left(N{U}_d{W}_k\right)}^2/(2N)$ and for $W_{k+1}\gg 2/\left\{N{\left[s\left(k+1\right)\right]}^2\right\}.$. The latter, high-weight cutoff is familiar from before and results from selection within the $k+1$ class. The low-weight cutoff results from the pressure of incoming mutational events.

A simple heuristic can explain the dependence of the low-weight cutoff on the weight in the founding class, $W_k.$ The weight $W_{k+1}$ is at least as large as the weight of the largest sublineage. Because each of the $N{U}_d{W}_k$ mutational events generates a sublineage that survives for T generations with probability $1/T$ and leaves a weight of order $T^2/N,$ at least one of these sublineages will survive for T generations with probability equal to $1-{\left(1-1/T\right)}^{N{U}_d{W}_k}\approx 1-e^{-N{U}_d{W}_k/T}.$ This probability is of order 1 for $T\sim N{U}_d{W}_k,$ which means that with probability order 1 at least one of the sublineages will have weight $T^2/N\sim {\left(N{U}_d{W}_k\right)}^2/N.$ Note that this also means that when $W_k>1/\left(N{U}_d^2\right)$ (consistent with the lineage exceeding frequency $1/\left(N{U}_d\right)$ in the founding class), the weight in the next class is guaranteed to be larger than the weight in the founding class. This means that lineages that exceed the frequency $1/\left(N{U}_d\right)$ in the founding class are almost guaranteed to generate an even larger number of individuals in the next class, which generates an even larger number of individuals in the following class, and so on.

We have implicitly assumed that the trajectory of each of the sublineages is dominated by drift. This will be true as long as $T<1/[\left(k+1\right)s]$ [i.e., as long as $W_k<1/[N\sqrt{U_{d}s\left(k+1\right)}]$]. In contrast, when $W_k\gg 1/[N\sqrt{U_{d}s\left(k+1\right)}],$ a large number the lineages will exceed the frequency $1/\left[Ns\left(k+1\right)\right]$ in the next class, and the trajectory in that class will become dominated by selection. We have shown in Appendix E that once this happens, drift in class $k+1$ and all classes below it will become negligible. Note that this heuristic argument also explains the self-consistency condition that emerged in Appendix E (see Equation E15) and explains why genetic drift becomes negligible in the ($k_c+1$)-class whenever the weight in the $k_c$-class is larger than $1/\left[N\sqrt{U_{d}s\left(k_c+1\right)}\right].$.

In the section below, we will use the insights above to evaluate the weight distribution in class $k+\Delta ,$ conditioned on the lineage arising in class k and selection being negligible in all classes beneath it, $W_i\ll 1/\left[N{\left(si\right)}^2\right]$ for $i\le k+\Delta .$ Because the lifetime of the longest-lived sublineage in each of these classes is at most $1/\left(is\right)$ in this limit and because the sublineages are seeded into the i-class over a time that is, by assumption, shorter than $1/\sqrt{U_{d}is},$ the total lifetime of the lineage in all of these classes is strictly shorter than $\Delta t^{\left(i\right)},$ which is why we do not need to be concerned with the full, time-dependent properties of the distribution of weights in this class. Instead, the calculation of the distribution of lifetime weights will suffice for calculating the site frequency spectrum.

The Distribution of the Weight in Class $k+\Delta$

Having obtained the distribution of the weight in class $k+1,$ conditioned on the weight in class k being equal to $W_k$ (see Equation G3), we can calculate the marginal distribution of weights $W_{k+1}$ by averaging over $W_k.$ In the limit that $1/\left(N{U}_d^2\right)\ll W_k\ll 1/\left[N\sqrt{U_{d}s\left(k+1\right)}\right]$ and $W_{k+1}\ll 1/\left[N{\left(sk\right)}^2\right]$ that we are interested in here, this distribution is

$$p\left(W_{k+1}\right)={\displaystyle {\int }_0^{\mathrm{\infty }}d{W}_k}p\left(W_k\right)p\left(W_{k+1}|W_k\right)=\frac{2^{1/4}\mathrm{\Gamma }\left(\frac{5}{4}\right)}{\pi }{N}^{-1/4}{U}_d^{1/2}{W}_{k+1}^{-5/4}.$$ (G4)

Note that the distribution in the ($k+1$)-class decays less rapidly than in the k-class. In particular, the probability that the weight in the ($k+1$)-class exceeds $1/\left[N{U}_{d}s\left(k+2\right)\right]$ (and leads to the deterministic propagation of individuals in classes with $k+2$ or more deleterious mutations) is

$$P\left[W_{k+1}\ge \frac{1}{N{U}_{d}s\left(k+2\right)}\right]=\frac{2^{1/4}\Gamma \left(\frac{1}{4}\right)}{\pi }{U}_d{\left(\frac{k+2}{\lambda }\right)}^{1/4},$$ (G5)

which is larger than the probability that the weight in the k-class exceeds the corresponding value by a large factor $\sim {\lambda }^{1/4},$ consistent with our intuition that the weight in the class below the founding class is guaranteed to exceed the weight in the founding class if $N{U}_d^2{W}_k>1.$

In general, we can calculate the distribution of the weight in class $k+\Delta$ by iterating this procedure. Specifically, the distribution of the weight in class $W_{k+2}$ conditioned on the weight in class $k+1$ being equal to $W_{k+1}$ also follows Equation G3 (but with k changed to $k+1$). By repeating the above procedure $\Delta$ times, we find that the distribution of lifetime weights in class $k+\Delta$ is

$$\begin{array}{c}p\left(W_{k+\Delta }\right)=\frac{1}{\sqrt{2\pi N}}\frac{1}{W_{k+\Delta }^{1+2^{-\left(\Delta +1\right)}}}\cdot {\displaystyle \prod _{j=1}^{\Delta }\frac{\mathrm{\Gamma }\left[\frac{1}{2}\left(1-2^{-j}\right)\right]}{2\sqrt{\pi }}{\left(\frac{N{U}_d^2}{2}\right)}^{2^{-\left(j+1\right)}}}\\ =U_d\frac{{\displaystyle {\prod }_{j=1}^{\Delta }\Gamma \left[\frac{1}{2}\left(1-2^{-j}\right)\right]}}{{\left(2\sqrt{\pi }\right)}^{\Delta +1}}{\left(\frac{N{U}_d^2{W}_{k+\Delta }}{2}\right)}^{-2^{-\left(\Delta +1\right)}}\frac{1}{W_{k+\Delta }}.\end{array}$$ (G6)

Appendix H: The Site Frequency Spectrum in the Presence of Weak Mutation ($U_d\ll s$)

In the following two appendices, we use the results obtained in previous sections to calculate the site frequency spectrum of the labeled lineage in the limits that $f\ll 1$ and $1-f\ll 1,$ by evaluating and inverting the generating function $H_f\left(z,t\right)$ for the total frequency of the labeled lineage.

We have seen in Appendix D that trajectories of mutations in the presence of weak background selection ($U_d\ll s$) are, to leading order in the small parameter λ, the same as those of isolated loci with fitness $-ks.$ In Appendix F, we have shown that the time-integrated distribution of allele frequencies of a single, isolated locus of fitness $-ks$ is

$$p\left(f,f>0\right)=\frac{2}{f}{e}^{-2Nskf},$$ (H1)

which agrees with classical results by Ewens (1963) and Sawyer and Hartl (1992). Thus, the contribution to the site frequency spectrum of neutral mutations arising in class k is

$$p\left(f,k\right)=N{U}_n{h}_{k}p\left(f,f>0\right)=\frac{2N{U}_n{h}_k}{f}{e}^{-2Nskf}+\mathcal{O}\left(\lambda \right).$$ (H2)

Summing the contributions of all the classes, we find that the full neutral site frequency spectrum is

$$p\left(f\right)={\displaystyle \sum _{k}p\left(f,k\right)}=\frac{2N{U}_n}{f}+\mathcal{O}\left(\lambda \right).$$ (H3)

The site frequency spectrum of deleterious mutations follows from the same argument, since the trajectory of a deleterious mutation arising on the background of an individual with k deleterious mutations is the same as the frequency trajectory of a neutral mutation arising in an individual with $k+1$ deleterious mutations. Thus, the site frequency spectrum of deleterious mutations is

$$p_{\text{del}}\left(f\right)={\displaystyle \sum _{k}N{U}_d{h}_k}\cdot \frac{2}{f}{e}^{-2Ns\left(k+1\right)f}=\frac{2N{U}_d}{f}{e}^{-2Nsf}+\mathcal{O}\left(\lambda \right),$$ (H4)

which once again agrees to leading order with the site frequency spectrum that we would have obtained assuming that all selected sites at the locus were isolated.

Appendix I: The Site Frequency Spectrum in the Presence of Strong Mutation ($U_d\gg s$)

In this appendix, we calculate the site frequency spectrum of the labeled lineage in the limits that $f\ll 1,$ $1-f\ll 1,$ and that $\lambda \gg 1$ by evaluating and inverting the generating function $H_f\left(z,t\right)$ for the total frequency of the labeled lineage.

In the presence of strong mutation, we have seen that trajectories of mutations are dominated by drift at the lowest frequencies, where the generating function reduces to the generating function of a neutral mutation and is simply equal to the $k=0$ limit of the single locus-generating function in Equation D2. We have already calculated the site frequency spectrum that results from these trajectories in the previous section. Plugging in these results, we find that

$$p\left(f\right)={\displaystyle \sum _{k}N{U}_n{h}_k}\cdot \frac{2}{f}\approx \frac{2N{U}_n}{f}\hspace{1em}\text{for }f\ll \frac{1}{N\sigma }.$$ (I1)

The site frequency spectrum at these frequencies is dominated by the contributions of lineages arising in average backgrounds, with $\left|k-\lambda \right|\mathrm{\lesssim }\sqrt{\lambda }=\sigma /s.$ By the same argument, the frequency spectrum of deleterious mutations at the same frequencies is also

$$p_{\text{del}}\left(f\right)={\displaystyle \sum _{k}N{U}_d{h}_k}\cdot \frac{2}{f}\approx \frac{2N{U}_d}{f}\hspace{1em}\text{for }f\ll \frac{1}{N\sigma }.$$ (I2)

At larger frequencies, the site frequency spectrum becomes dominated by lineages arising in unusually fit backgrounds, with $k-\lambda \ll -\sqrt{\lambda }.$ Their trajectories are instead described by Equation E10. We have seen that the integral in the exponent of Equation E10 has a different dependence on t for $t\ll t_d^{\left(k\right)},$ $t\sim t_d^{\left(k\right)},$ and $t\gg t_d^{\left(k\right)},$ which we have labeled the “spreading,” “peak,” and “extinction” phases of the trajectory. In evaluating the site frequency spectrum $p\left(f\right),$ it will be convenient to calculate the contributions from each of these phases separately. We denote these contributions as $p_{\text{spread}}\left(f\right),$ $p_{\text{peak}}\left(f\right),$ and $p_{\text{ext}}\left(f\right),$ and the full site frequency spectrum is obtained by summing:

$$p\left(f\right)=p_{\text{spread}}\left(f\right)+p_{\text{peak}}\left(f\right)+p_{\text{ext}}\left(f\right).$$ (I3)

We evaluate $p_{\text{peak}}\left(f\right)$ and $p_{\text{ext}}\left(f\right)$ in the next two subsections of this appendix. We then show in the last subsection of this appendix that the contribution from $p_{\text{spread}}\left(f\right)$ is subdominant to that of $p_{\text{ext}}\left(f\right).$

Contribution from the Peaks of Trajectories

In Large Lineages Arising on Unusually Fit Backgrounds in Appendix E, we have shown that, in the peak phase of the trajectory, the total allele frequency is

$$f\left(t\right)\approx U_d{\stackrel{\sim }{g}}_{k_c+1}{W}_{\Delta t^{\left(k_c+1\right)}}\left(t-t_d^{\left(k_c+1\right)}\right),$$ (I4)

where $k_c$ is the class with the smallest number of mutations for which $f\gg {\stackrel{\sim }{g}}_{k_c+1}/\left[2Ns\left(k_c+1\right)\right]$ or equivalently, the class with the smallest number of mutations in which the weight exceeds $1/\left[N{U}_{d}s\left(k_c+1\right)\right].$

We have seen above in Appendix G that, to achieve such a large weight in class $k_c,$ a mutation could have arisen in class $k=k_c$ and traced an unusually large trajectory, or arisen in class $k_c-1$ and traced a smaller trajectory in that class, which led to the creation of a large number of deleterious descendants in class $k_c,$ at least one of which had weight exceeding $1/\left[N{U}_{d}s\left(k_c+1\right)\right].$ Alternatively, it could have also arisen in class $k_c-2$ and traced an even smaller trajectory in that class that led to a larger weight in class $k_c-1,$ and a sufficiently large weight in class $k_c$ for genetic drift to be negligible in classes $i>k_c+1.$ In other words, in the range of frequencies

$$\frac{1}{2Ns\left(k_c+1\right)}{\stackrel{\sim }{g}}_{k_c+1}\ll f\ll \frac{1}{2Ns{k}_c}{\stackrel{\sim }{g}}_{k_c},$$ (I5)

we see the peaks of trajectories originating in classes $k<k_c,$ as long their weight in class $k_c$ is large enough that genetic drift in classes of lower fitness can be ignored. All of these peaks contribute to the site frequency spectrum and, by integrating Equation I4 in time, we find that

$$\begin{array}{c}{p}_{\text{peak}}\left(f\right)={\displaystyle \sum _{k=0}^{k_c\left(f\right)}N{U}_n{h}_k}\cdot p\left[f=U_d{\stackrel{\sim }{g}}_{k_c+1}{W}_{\Delta t^{\left(k_c+1\right)}}|\text{arose}\hspace{0.17em}\text{in}\hspace{0.17em}k\right]\\ ={\displaystyle \sum _{k=0}^{k_c\left(f\right)}N{U}_n{h}_k}\cdot \frac{1}{U_d{\stackrel{\sim }{g}}_{k_c+1}}\cdot p\left[W_{\Delta t^{\left(k_c+1\right)}}=\frac{f}{U_d{\stackrel{\sim }{g}}_{k_c+1}}|\text{arose}\hspace{0.17em}\text{in}\hspace{0.17em}k\right],\end{array}$$ (I6)

where the last term represents the time-integrated distribution of weights in a window of width $\Delta t^{\left(k_c+1\right)}$ in class $k_c$ of a lineage that arose in class k. This distribution is given by Equation F28 for $k_c=0.$ Otherwise, when $k_c>1,$ the time-integrated distribution in Equation I6 is equal to the product of the window width, $\Delta t^{\left(k_c+1\right)},$ and the distribution of lifetime weights in the founding class, given in Equation G6.

Since we have previously calculated all of these quantities, we can now turn to evaluating the sum in Equation I6. When $f\gg {\stackrel{\sim }{g}}_1/\left(2Ns\right),$ then $k_c=0,$ and the sum in Equation I6 has only one term ($k=0$). By substituting in the expression for the time-integrated distribution of weights in Equation F28, we find that

$$p_{\text{peak}}\left(f\right)=\{\begin{array}{ll}\frac{2N{U}_n{e}^{-\lambda }}{f},\hfill & \text{if}\hspace{0.17em}f\gg \frac{1}{Ns{e}^{-\lambda }}\hfill \\ \frac{N{U}_n}{f^{3/2}}{\left[\frac{2e^{-\lambda }}{\pi eNs}\right]}^{1/2},\hfill & \frac{1}{N{U}_d{e}^{-\lambda }}\ll f\ll \frac{1}{Ns{e}^{-\lambda }}\hfill \end{array}.$$ (I7)

At lower frequencies $\left(1/\left(N\sqrt{U_{d}s}\right)\ll f\ll {\stackrel{\sim }{g}}_1/\left(2Ns\right)\right),$ lineages originating in multiple different fitness classes will be able to contribute to the site frequency spectrum. At these frequencies,

$$p_{\text{peak}}\left(f\right)={\displaystyle \sum _{k=0}^{k_c\left(f\right)}N{U}_n{h}_k}\frac{\Delta t^{\left(k_c+1\right)}}{U_d{\stackrel{\sim }{g}}_{k_c+1}}p\left(W_{k+\Delta }=\frac{f}{U_d{\stackrel{\sim }{g}}_{k_c+1}}|k+\Delta =k_c\right).$$ (I8)

Plugging in the expression for $p\left(W_{k+\Delta }\right)$ from Equation G6, we find

$$p_{\text{peak}}\left(f\right)=\frac{N{U}_n\lambda }{\sqrt{\pi }f}\frac{1}{\sqrt{k_c\left(f\right)+1}}{\displaystyle \sum _{k=0}^{k_c}{h}_k\frac{{\displaystyle {\prod }_{j=1}^{k_c-k}\mathrm{\Gamma }\left[\frac{1}{2}\left(1-2^{-j}\right)\right]}}{{\left(2\sqrt{\pi }\right)}^{k_c-k+1}}{\left(\frac{N{U}_{d}f}{{\stackrel{\sim }{g}}_{k_c+1}}\right)}^{-2^{-\left(k_c-k+1\right)}}}.$$ (I9)

Because $\lambda \gg 1,$ this sum is dominated by the $k=k_c$ term, since $h_k$ decays much more rapidly with decreasing k than any of the other terms increase. To evaluate the f-dependence of this term for $f\ll {\stackrel{\sim }{g}}_1/\left(2Ns\right)$ and $k_c\left(f\right)\gg 1,$ we repeat the same procedure as in Large Lineages Arising on Unusually Fit Backgrounds in Appendix E to obtain an explicit form for $k_c\left(f\right).$ Briefly, to solve the self-consistency condition for $k_c\left(f\right),$ ${\stackrel{\sim }{g}}_{k_c+1}/\left[2Ns\left(k_c+1\right)\right]\ll f\ll {\stackrel{\sim }{g}}_{k_c}/\left(2Ns{k}_c\right),$ we set $f={\stackrel{\sim }{g}}_{k_c+1}·C\left(f\right)/\left[2Ns\left(k_c+1\right)\right]$ for some $C\left(f\right)$ that satisfies $1\ll C\left(f\right)\ll \lambda$ and find that to leading order

$$k_c\left(f\right)+1\approx {\log }_{\lambda }\left(\frac{1}{Ns{e}^{-\lambda }f}\right)\hspace{1em}\text{when}\hspace{0.17em}{k}_c\left(f\right)\gg 1.$$ (I10)

Plugging in, we obtain that the leading-order term in the distribution of peak sizes is

$$p_{\text{peak}}\left(f\right)\approx \frac{N{U}_{n}C{\left(f\right)}^{1/2}}{2\sqrt{2}\pi \sqrt{\lambda }Ns{f}^2}\frac{1}{\sqrt{{\log }_{\lambda }\left(\frac{1}{Ns{e}^{-\lambda }f}\right)}},\hspace{1em}\text{for}{\log }_{\lambda }\left(\frac{1}{Ns{e}^{-\lambda }f}\right)\gg 1.$$ (I11)

The term $C\left(f\right)$ depends on f weaker than logarithmically and on frequency scales on which $p_{\text{peak}}\left(f\right)$ changes substantially it will be approximately constant, $C\left(f\right)\approx C.$

Because the crossover between the $f^{-3/2}$ scaling of $p_{\text{peak}}\left(f\right),$ which occurs at high frequencies ${\stackrel{\sim }{g}}_1/\left(2Ns\right)\ll f\ll 1/\left(Ns{e}^{-\lambda }\right)$ [where $k_c\left(f\right)+1=1$], and the $f^{-2}\log {\left[1/\left(Ns{e}^{-\lambda }f\right)\right]}^{-1/2}$ behavior, which is valid at substantially lower frequencies [where $k_c\left(f\right)\gg 1$], is in principle broad, this constant factor C is difficult to determine: asymptotic matching does not typically work well in the presence of such broad transitions and crude “patching” methods do not, in general, offer satisfactory results (Hinch 1991). Thus, Equation I11 is undetermined up to the constant factor $C^{1/2},$ which is between 1 and $\sqrt{\lambda }.$ For our purposes here, this level of precision is sufficient—$\mathcal{O}\left(1\right)$ precision in the form of the spectrum was, after all, expected in the Laplace-like approximation that we used in Large Lineages Arising on Unusually Fit Backgrounds in Appendix E to calculate the stochastic integral over the trajectory of the feeding class. Thus, by absorbing the $2\sqrt{2}\pi$ term into this constant factor and relabeling $C^{1/2}$ as C, we find that the peak contribution to the site frequency spectrum is

$$p_{\text{peak}}\left(f\right)\approx \frac{N{U}_n}{\sqrt{\lambda }Ns{f}^2}\frac{C}{\sqrt{{\log }_{\lambda }\left(\frac{1}{Ns{e}^{-\lambda }f}\right)}},\hspace{1em}\text{for}{\log }_{\lambda }\left(\frac{1}{Ns{e}^{-\lambda }f}\right)\gg 1,$$ (I12)

with C in the range $1\ll C\ll \sqrt{\lambda }.$

Contribution from the Extinction Stage of Trajectories

Once the trajectory is beyond its peak, the total allele frequency decays as

$$f\left(t\right)=f_{\text{peak}}{e}^{-\left[k_c\left(f\right)+1\right]s\left(t-t_{\text{peak}}\right)},$$ (I13)

where $f_{\text{peak}}$ denotes the maximal frequency that the trajectory reaches and Equation I13 is valid for $t\gg t_d^{\left(k\right)}.$ Note that this stage only exists for frequencies $f\ll 1/\left(Ns{e}^{-\lambda }\right).$ At higher frequencies, $f\gg 1/\left(Ns{e}^{-\lambda }\right),$ the total allele frequency simply mirrors smoothed fluctuations in the founding class. Equation I13 can be straightforwardly integrated in time to obtain the contribution of this trajectory to the site frequency spectrum

$$p\left(f|f_{\text{peak}}\right)=\{\begin{array}{ll}\frac{1}{\left[k_c\left(f\right)+1\right]sf},\hfill & \text{if}\hspace{0.17em}{f}_{\text{peak}}\gg f,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}$$ (I14)

Averaging Equation I14 over all possible trajectories, we find that

$$p_{\text{ext}}\left(f\right)=N{U}_n\frac{1}{f}\frac{1}{\left[k_c\left(f\right)+1\right]s}\text{Prob}\left(f_{\text{peak}}>Df\right),$$ (I15)

where $D>1$ is a constant that we have introduced to correctly account for the fact that the peak phase occurs at frequencies that are at least $\mathcal{O}\left(1\right)$ higher than the frequencies in the extinction stage.

For peak frequencies $f_{\text{peak}}\ll 1/(Ns{e}^{-\lambda }),$ we have already calculated the overall time-integrated distribution of peak sizes of lineages arising in classes of all fitness and we can use this result to calculate the total probability that a trajectory passes through f in its extinction stage,

$$\text{Prob}\left(f_{\text{peak}}>Df\right)=\frac{{\displaystyle {\int }_{Df}^{\mathrm{\infty }}{p}_{\text{peak}}\left(f^{\prime }\right)d{f}^{\prime }}}{N{U}_n\Delta t^{\left(k_c+1\right)}}=\frac{C}{\sqrt{\lambda }NfD}.$$ (I16)

This means that the contribution to the site frequency spectrum from the extinction phase of trajectories is equal to

$$p_{\text{ext}}\left(f\right)=\frac{N{U}_n}{D\sqrt{\lambda }Ns{f}^2}\frac{C}{{\log }_{\lambda }\left(\frac{1}{Ns{e}^{-\lambda }f}\right)}<\frac{N{U}_n}{\sqrt{\lambda }Ns{f}^2}\frac{C}{{\log }_{\lambda }\left(\frac{1}{Ns{e}^{-\lambda }f}\right)}.$$ (I17)

Therefore, $p_{\text{ext}}\left(f\right)$ is strictly smaller than $p_{\text{peak}}\left(f\right)$ by a factor ${\left[{\log }_{\lambda }\left[1/\left(Ns{e}^{-\lambda }f\right)\right]\right]}^{1/2},$ which is large when $f\ll 1/\left(Ns{e}^{-\lambda }\right).$ Thus, this phase of the trajectory has a small effect on the low-frequency end of the spectrum.

However, in the high-frequency end of the spectrum, when $1-f\ll 1/\left(Ns{e}^{-\lambda }\right),$ the only contribution comes from this extinction phase of the wild type, which starts once the mutant approaches the frequency $f\gg 1-1/\left(Ns\right)$ in the 0-class. These events happen at rate equal to $N{U}_n{e}^{-\lambda }\cdot 1/\left(N{e}^{-\lambda }\right)=U_n$ and each contributes $\sim 1/\{s\left[k_c\left(1-f\right)+1\right]\left(1-f\right)\}$ to the site frequency spectrum. Multiplying these two terms, we find that the site frequency spectrum is proportional to

$$p_{\text{dec}}\left(f\right)=\frac{U_n}{s}\frac{1}{\left(1-f\right){\log }_{\lambda }\left[\frac{1}{Ns\left(1-f\right)e^{-\lambda }}\right]},\hspace{1em}\text{if}\hspace{0.17em}\frac{1}{N\sigma }\ll 1-f\ll \frac{1}{Nsf{e}^{-\lambda }}.$$ (I18)

Contribution from the Spreading Stage of Trajectories

At frequencies $f\ll 1/\left(Ns{e}^{-\lambda }\right),$ the site frequency spectrum also receives contributions from the spreading stage of trajectories, in which the allele frequency rapidly increases as the allele spreads through the fitness distribution. In this stage, the rate at which the frequency increases is strictly larger than what it would be if we ignored any contributions from the founding class after the mutation exceeds frequency $1/\left(N{U}_d\right)$ [i.e., assuming $f\left(t\right)=e^{-kst+\lambda (1-e^{-st})}/\left(N{U}_d\right)$]:

$$\frac{df\left(t\right)}{dt}\ge fs\left(\lambda e^{-st}-k\right).$$ (I19)

Far below the peak of the trajectory, where $\lambda e^{-st}\gg k,$ the contribution from this stage of a single trajectory to the frequency spectrum that passes through f is thus simply bounded by

$$p_{\text{single}}\left(f\right)=\langle \frac{1}{\left|\frac{df}{dt}\right|}\rangle \le \frac{1}{fs\lambda e^{-st}}\approx \frac{1}{sf\log \left(\frac{1}{Ns{e}^{-\lambda }f}\right)}=\frac{1}{sf\log \left(\lambda \right){\log }_{\lambda }\left(\frac{1}{Ns{e}^{-\lambda }f}\right)}\ll \frac{1}{sf\left[k_c\left(f\right)+1\right]}.$$ (I20)

Since the number of trajectories that pass through frequency f in the spreading phase is the same number that pass through f in the extinction phase, the contribution from the spreading phase to the site frequency is strictly smaller than that of the extinction phase throughout the region where both contributions exist, $f\ll 1/\left(Ns{e}^{-\lambda }\right).$

Constructing a Single Curve from Piecewise Asymptotic Functions

In the previous sections of this appendix, we have shown that the site frequency spectrum is given by

$$p\left(f\right)\approx \{\begin{array}{ll}\frac{2N{U}_n}{f},\hfill & \text{for}\hspace{1em}f\ll \frac{1}{N\sigma },\hfill \\ \frac{N{U}_n}{Ns{f}^2\sqrt{\lambda {\log }_{\lambda }\left(\frac{e^{\lambda }}{Nsf}\right)}},\hfill & \text{for}\hspace{1em}\frac{1}{N\sigma }\ll f\ll \frac{e^{\lambda }}{Ns},\hfill \\ \frac{2N{U}_n{e}^{-\lambda }}{f},\hfill & \text{for}\hspace{1em}\frac{e^{\lambda }}{Ns}\ll f\ll 1-\frac{e^{\lambda }}{Ns},\hfill \\ \frac{N{U}_n}{Ns\left(1-f\right){\log }_{\lambda }\left[\frac{e^{\lambda }}{Ns\left(1-f\right)}\right]},\hfill & \text{for}\hspace{1em}\frac{1}{N\sigma }\ll 1-f\ll \frac{e^{\lambda }}{Ns},\hfill \\ \frac{2N{U}_n}{f},\hfill & \text{for}\hspace{1em}1-f\ll \frac{1}{N\sigma }.\hfill \end{array}$$ (I21)

As we have explained, line 2 of Equation I21 is valid up to a constant factor $C_1\left(\lambda \right)$ that is bounded by $1\ll C_1\left(\lambda \right)\ll \sqrt{\lambda }.$ These piecewise functions represent the leading-order behaviors far away from the transitions between the different regimes, which occur at $f=1/\left(N\sigma \right),$ $1/\left(Ns{e}^{-\lambda }\right),$ $1-1/(Ns{e}^{-\lambda }),$ and $1-1/(N\sigma ).$ For practical purposes, it is often convenient to construct a single theoretical curve that joins these curves at these transition points, while maintaining the correct form far away from the transition points. This procedure is not intended to extend the validity of the results outside of the regimes where asymptotic forms are available and is certainly not guaranteed to produce the correct functional forms at the transitions. However, it often yields satisfactory results, especially when the transitions are narrow in practice and when the two asymptotic forms are expected to lie on opposite sides of the behavior at the transition (i.e., one is expected to overestimate, and the other to underestimate). In the present case, the latter condition is true at the transitions at $1/\left(Ns{e}^{-\lambda }\right)$ and $1-1/(Ns{e}^{-\lambda }).$

Here, we have used a sigmoid function,

$$g\left(f\right)=\frac{1}{1+e^{+Ns{e}^{-\lambda }f}}$$ (I22)

to join the functional forms at the transitions, which has the convenient property

$$g\left(f\right)\approx \{\begin{array}{cc}1,& \text{for}\hspace{0.17em}f\ll \frac{1}{Ns{e}^{-\lambda }}\\ 0,& \text{for}\hspace{0.17em}f\gg \frac{1}{Ns{e}^{-\lambda }}\end{array}.$$ (I23)

In addition to this, because the forms are valid when $1/\left(N\sigma \right)\ll f\ll 1/\left(Ns{e}^{-\lambda }\right)$ and $1/\left(N\sigma \right)\ll 1-f\ll 1/\left(Ns{e}^{-\lambda }\right)$ have logarithmic divergences near the transitions (i.e., for $f,1-f=1/\left(Ns{e}^{-\lambda }\right)$), we also add small additive factors to these logarithms to avoid nonsensical results. Specifically, to compare our theoretical predictions with simulations, we plot

$$p_{\text{joined}}\left(f\right)=2N{U}_n\left[\frac{C_{1}g\left(f\right)}{Ns{f}^2\sqrt{\lambda \cdot \left[\log \left(\frac{1}{Ns{e}^{-\lambda }f}\right)+C_2\right]}}+\frac{\left[1-g\left(f\right)\right]\left[1-g\left(1-f\right)\right]e^{-\lambda }}{f}+\frac{C_{3}g\left(1-f\right)}{Ns\left(1-f\right)\left\{\log \left[\frac{e^{\lambda }}{Ns\left(1-f\right)}\right]+C_4\right\}}\right],\hspace{1em}\text{for}\frac{1}{N\sigma }\ll f\ll 1-\frac{1}{N\sigma }.$$ (I24)

$C_1,$ $C_2,$ $C_3,$ and $C_4$ were chosen to ensure visual smoothness of the curve. Note that the constant $C_3$ is only necessary to ensure visual smoothness of the curve at limited λ (adding $C_4$ to the denominator to control the logarithmic divergence causes the curve to be shifted downward, and $C_3$ helps to correct for this). We tabulate the values used in Table I1.

TABLE I1.

Values of small constants defined in Eq. (I24) that were used in this paper.

λ	C1	C2	C3	C4
≥3	1.5	0.5	1.4	1
≤2	1.0	0.5	1.4	1

In principle, we could also use a similar procedure to join the asymptotic forms at the transitions at $1/\left(N\sigma \right)$ and $1-1/(N\sigma ).$ However, since both asymptotic forms overestimate the site frequency spectrum near these transitions, this works no better than simply setting

$$p\left(f\right)=\{\begin{array}{ll}\frac{2N{U}_n}{f},\hfill & \text{for}\hspace{0.17em}f\le \frac{1}{N\sigma }\hfill \\ p_{\text{joined}}\left(f\right),\hfill & \text{for}\frac{1}{N\sigma }<f<1-\frac{1}{N\sigma }\hfill \\ \frac{2N{U}_n}{f}\hfill & \text{for}\hspace{0.17em}1-\frac{1}{N\sigma }\le f.\hfill \end{array}$$ (I25)

This is the choice we have made when calculating theoretical predictions for site frequency spectra of smaller samples, which were necessary for comparisons with the structured coalescent.

Appendix J: Distributions of Effect Sizes

When the effects of deleterious mutations are not all identical but instead have a distribution with finite width, $\rho \left(s\right),$ the deterministic dynamics that arise through the combined action of mutation and selection will be modified. In this appendix, we consider these deterministic dynamics. For concreteness, we assume that the fitness effects of new mutations come from a gamma distribution with mean $\overline{s}$ and shape parameter α,

$$\rho \left(s\right)=\frac{{\alpha }^{\alpha }}{\mathrm{\Gamma }\left(\alpha \right){\overline{s}}^{\alpha }}{e}^{-s\alpha /\overline{s}},$$ (J1)

and that these deleterious mutations occur at an overall rate $U_d.$

Under the assumption that all mutations have strong enough effects on fitness that the fitness of the population at the locus does not experience Muller’s ratchet on timescales of coalescence, the mean fitness of an allele at the locus will be equal to $-U_d,$ with the most-fit individuals being those with no deleterious mutations and an absolute fitness equal to zero. Consider now the deterministic dynamics of a lineage founded in an individual at absolute fitness $-x.$ The fitness of the lineage founded by this lineage will change as it accumulates new deleterious mutations according to

$$x\left(t\right)=-x+U_d{\displaystyle {\int }_0^{\mathrm{\infty }}ds}\rho \left(s\right)e^{-st}.$$ (J2)

Evaluating this integral, we find

$$x\left(t\right)=-x+U_d{\left(1+\frac{\overline{s}t}{\alpha }\right)}^{-\alpha }.$$ (J3)

When α is sufficiently large, corresponding to a sufficiently narrow fitness distribution, the resulting trajectory is well approximated by assuming that all fitness effects are the same and equal to the average fitness $\overline{s}$ [or, more precisely, the harmonic mean of $\rho \left(s\right),$ $\overline{s}·\left(\alpha -1\right)/\alpha \approx \overline{s}$]. To calculate how large α needs to be for this approximation to be valid, we can calculate the deterministic expectation for the average number of individuals in the lineage at time t after founding. This quantity is equal to

$$g\left(x,t\right)=\exp \left[{\displaystyle {\int }_0^{t}x\left(t^{\prime }\right)d{t}^{\prime }}\right]=\exp \left\{-xt+\frac{U_d\alpha }{\overline{s}\left(\alpha -1\right)}\left[1-{\left(1+\overline{s}t/\alpha \right)}^{-\left(\alpha -1\right)}\right]\right\}.$$ (J4)

We see that this differs from the single-s expression only in the last term, proportional to ${\left(1+\overline{s}t/\alpha \right)}^{-\left(\alpha -1\right)}.$ At sufficiently short times, $t\mathrm{\lesssim }\alpha /\overline{s},$ this is well approximated by $e^{-\overline{s}t\left(\alpha -1\right)/\alpha }.$ On sufficiently long timescales, this will not be the case. However, because the overall magnitude of this term becomes negligible at times long after the peak of $g\left(x,t\right),$ $t\gg t_d,$ we only need it to remain well approximated by an exponential on timescales $t\mathrm{\lesssim }{t}_d,$ which requires that $\alpha \gg \log \left(U_d/\overline{s}\right)\gg 1.$ When this is the case, $g\left(x,t\right)$ is, up to perturbative corrections, given by

$$g\left(x,t\right)\approx \exp \left[-xt+\frac{U_d\alpha }{\left(\alpha -1\right)\overline{s}}\left(1-e^{-\frac{\alpha \overline{s}}{\alpha -1}t}\right)\right],$$ (J5)

and the effects of selection are well described by a single-s model on all timescales.