Estimating the impact of changes to occupational standards for silica exposure on lung cancer mortality

Abstract

Background

Respiratory exposure to silica is associated with the risk of death due to malignant and non-malignant disease. 2.3 million U.S. workers are exposed to silica. Occupational exposure limits for silica are derived from a number of lines of evidence, including observational studies. Observational studies may be subject to healthy worker survivor bias, which could result in underestimates of silica’s impact on worker mortality and, in turn, bias risk estimates for occupational exposure limits.

Methods

Using data on 65,999 workers pooled across multiple industries, we estimate the impacts of several hypothetical occupational exposure limits on silica exposure on lung cancer and all-cause mortality. We use the parametric g-formula, which can account for healthy worker survivor bias.

Results

Assuming we could eliminate occupational exposure, we estimate that there would be 20.7 fewer deaths per 1,000 workers in our pooled study by age 80 (95% confidence interval: 14.5, 26.8), including 3.91 fewer deaths due to lung cancer (95%CI: 1.53, 6.30). Less restrictive interventions demonstrated smaller, but still substantial risk reductions.

Conclusions

Our results suggest that occupational exposure limits for silica can be further strengthened to reduce silica-associated mortality and illustrate how current risk analysis for occupational limits can be improved.

INTRODUCTION

Respiratory exposure to crystalline silica, a basic component of soils and rocks, is an occupational hazard associated with multiple causes of death including non-malignant respiratory diseases ^1,2, lung cancer ³, renal disease ⁴ and heart disease ⁵, as well as all-cause mortality ⁶. The United States Occupational Safety and Health Administration (OSHA) estimates that 2.3 million U.S. workers are exposed across multiple trades (https://www.osha.gov/Publications/OSHA3683.pdf). In 1997, the International Agency for Research on Cancer classified crystalline silica (hereafter “silica”) as a human carcinogen, based on evidence for the association between silica exposure and lung cancer.⁷ Analysis of a pooled cohort study of nearly 66,000 workers in 2001 suggested that lung cancer rates increased with cumulative exposure.⁸ At the time of the pooled study, the OSHA permissible exposure limit (hereafter “limit”) for silica exposure was 100 μg/m^3, a standard set in 1971. The authors of the pooled study estimated that the excess, lifetime, lung-cancer mortality risk for a 45-year exposure at the OSHA limit would be 1.1%–1.7% higher than the background risk of 3%–6%. In 2016 OSHA revised the limit to 50 μg/m³, estimating that the lifetime excess risk would be cut in half relative to the previous limit. Such estimates of long-term or lifetime risk are essential to establish workplace standards for silica exposure.

Crucially, OSHA’s estimates of lifetime lung cancer risk may be subject to healthy worker survivor bias, possibly resulting in underestimates of the mortality due to lung cancer caused by occupational silica exposure.^9,10 In general, when the effect of cumulative exposure over time is the metric of interest, healthy worker survivor bias results when healthier workers stay employed longer and accumulate more exposure. Those who leave work cease their exposure. Further, leaving work is often a risk factor for subsequent disease and death. Thus, cumulative exposure is lower among those who would otherwise be at higher risk, an example of confounding. In addition, if exposure causes people to leave work, leaving work is then also an intermediate variable on the pathway between cumulative exposure and disease (Figure 1a); adjustment for such variables in regression models or via stratification results in selection bias.¹¹ Hence traditional methods of adjusting for a confounder cannot work because unadjusted estimates are confounded but adjusted estimates are also biased (an accessible discussion is given by Buckley et al.¹⁰).^10,12 Several recent studies of occupational cohorts have demonstrated or suggested that healthy worker survivor bias results in underestimates of the effects of occupational exposures such as radon,¹³ arsenic,¹⁴ diesel,¹⁵ and metalworking fluids.¹⁶ In the case of silica-exposed workers, healthy worker survivor bias may be particularly impactful because silica-induced disease (typically silicosis, a consequence of high exposure) may induce workers to leave work (Figure 1b). Leaving work, due to silica-induced disease, may be a particularly strong risk factor for subsequent mortality, and thus a potential mechanism underlying healthy worker survivor bias.

Figure 1.

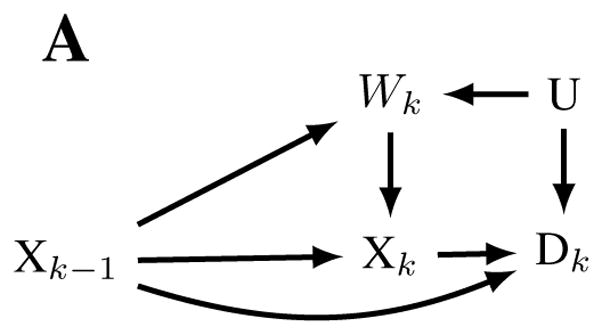
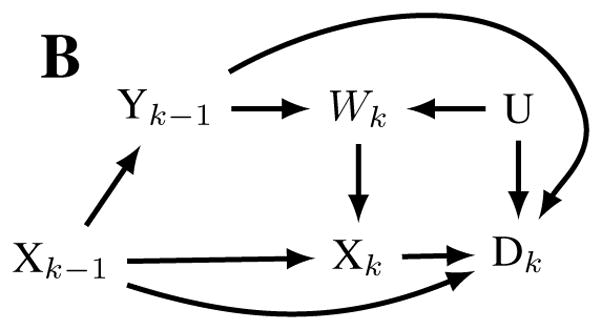
Causal diagrams representing hypothesized relationships that may result in healthy worker survivor bias in a general setting (panel A) and in the setting of occupational exposure to silica. Nodes represent time (k) specific measurements of silica exposure (X), active employment (W), Mortality (D), unmeasured risk factors for disease and employment (U), and silicosis (Y). Healthy worker survivor bias can be conceptualized as confounding of the X_k → D_k relationship by W_k (due to the pathways X_k ← W_k ← U → D_k,X_k ← W_k ← Y_k−1 → D_k ), which is not amenable to standard analytic approaches because the confounder is affected by prior exposure X_k−1. Under a standard analytic approach, adjusting for measured confounder W_k introduces collider bias by opening up the non-causal backdoor path X_k−1 → W_k ← U → D_k.

In the current manuscript, we estimate the cumulative incidence of mortality (hereafter, “risk”¹⁷) from lung cancer and other causes of death using the parametric g-formula, which can be used to correct for healthy worker survivor bias. ^18,19 Using a pooled study of 10 occupational cohorts described previously by Steenland et al.,⁸ we estimate the risk of lung-cancer-specific and all-cause mortality at age 80. We also assess the possible presence and magnitude of healthy worker survivor bias in risk estimates, and whether silicosis might explain some of that bias.

METHODS

Study population

Data from the current analysis come from a pooled study of 10 occupational cohorts of workers exposed to silica dust. The pooled cohort was described previously in detail in a detailed exposure–response analysis by Steenland et al.⁸ and Mannetje et al.²⁰ The 10 cohorts include 65,999 workers from the United States (granite workers,²¹ industrial sand workers,²² diatomaceous earth workers,²³ and gold miners²⁴), China (tungsten miners, tin miners, and pottery workers²⁵) South Africa (gold miners²⁶), Australia (gold miners²⁷), and Finland (granite workers²⁸). Cohorts were chosen in the original pooled analysis based on a Medline search to identify all occupational cohorts exposed to crystalline silica. The group of 10 cohorts was selected from all eligible studies based on the absence of concomitant exposures and the presence of quantitative exposure measurements. The start and end of follow-up varied by study, but started as early as October 1919 and ended as late as June 1998. This analysis was approved by the institutional review board of the International Agency for Research on Cancer.

Mortality

The sources outlining the collection of mortality data, including dates and causes of death, for each cohort are given by Steenland et al.⁸ Underlying cause of death was coded according to the International Classification of Diseases (ICD) revision in use at the time of death. We defined two categories of cause of death: death due to lung cancer (ICD versions 6 and 7 codes = 162 and 163, and ICD versions 8 and 9 code = 162); and death due to all other causes (all other ICD codes, or missing ICD code). Workers were censored at age 90 if they were not noted to have died by that age.

Silicosis incidence

Silicosis incidence was available for the cohorts of Chinese tungsten miners, tin miners, and pottery workers.²⁵ Dust-exposed workers from these cohorts were screened annually via roentgenograms from 1963 onwards, and stage and date at first diagnosis was recorded for each case. Incident silicosis was defined as radiographic silicosis with Chinese stage 1 silicosis or above diagnosed during follow-up (1972 or later), and those diagnosed before 1972 were considered prevalent cases.²⁵ Workers received annual chest x-rays to screen for silicosis while working, and every 2–3 years after leaving work. Chinese silicosis stage 1 or above agreed 89% of the time with International Labor Organization (ILO) defined silicosis, based on a side by side comparison of 150 chest x-rays by a panel of 12 Chinese radiologists and 3 US clinicians (B-readers).^29,30

Exposure

Estimates of exposure to silica, expressed in terms of mass in air (μg/m^3) were derived for each cohort by Mannetje et al.²⁰ Exposure data included area and personal measures as well as expert assessment and measurements abstracted from previously summarized data. Occupational history was obtained from each plant. For the three Chinese cohorts, only the ‘usual-job’ was available, while complete occupational history was available for the other cohorts. Final exposure estimates were job- and time-specific, and these were used to assign exposures to each person-year based on occupational history. We calculated cumulative exposure, measured in μg/m³-years, as the sum of the exposure intensity multiplied by the number of years exposed.

Statistical analysis

Assessing components of healthy worker survivor bias

Following our prior analyses of other occupational populations,^13,14 and an approach described in Naimi et al.,³¹ we quantitatively assessed potential for healthy worker survivor bias in regression analyses our study population. This approach is roughly equivalent to testing for the existence (but not direction) of arrows on Figures 1a, given that the figure is otherwise correct. This implies, for example, that the arrows represent causal relationships between two variables. Briefly, this assessment involves estimating (a) the magnitude of the association between employment status (active vs. inactive) and mortality as well as (b) the magnitude of the association between cumulative silica exposure and the rate of leaving employment. The effect of employment on exposure (which, with (a), is a sufficient condition for confounding) is implied by the fact that exposure occurs only at work. The presence of component (a) indicates the employment status is potentially a confounder, while presence of (b) indicates that it may also be an intermediate variable (or a collider³²). If both are true then special analytic methods (such as the g-formula) are needed to adjust for time-varying confounding.

For component (a), we estimated the hazard ratio contrasting active employment versus unemployment using a Cox model for all-cause mortality. For component (b), we followed Neophytou et al.¹⁵ by quantifying the association between the time-to-leave-work and cumulative exposure (log exposure, 15-year lag) using an accelerated failure time model which allows time-varying covariates. In this model, time starts at date of first employment and the terminal event is leaving work, subject to censoring by death, loss to follow-up or the end of follow-up. Based on a directed acyclic graph we adjusted for sex, race, date of birth (linear), calendar time (cubic spline), and study (stratification) in both models. The choice between the Cox model and the accelerated failure time model was made for consistency with the literature.

To supplement our assessment of (a) and (b), we also quantified the association between the time-to-leave work and silicosis in the three Chinese cohorts. For this analysis, we also utilized accelerated failure time models for time-varying-covariates. The exposure was ever-silicosis (lagged 1–5 years), which was assigned a value of 1 if the worker had been previously diagnosed with silicosis, and 0 otherwise. We adjusted for log-cumulative exposure (lagged 1 year more than silicosis), sex, race, date of birth (linear), calendar time (linear), and study (stratification). To aid interpretation of model results, we estimated the standardized median time-to-event at fixed values of the exposures. This is association estimate is made by averaging accelerated failure time model predictions (at fixed values of exposure) across all observations in the data.

Parametric g-formula

We used the parametric g-formula to estimate cause-specific risks among workers. The parametric g-formula is an approach used to quantify the expected distribution of outcomes under changes to the distribution of some exposure of interest. Specifically, we are interested in quantifying the effects (on mortality) of hypothetical changes in occupational silica exposure limits implemented at the start of follow-up. The parametric g-formula allows us to estimate the effects of such interventions, provided that identification assumptions (described later) are met.^19,33

Our general approach in the parametric g-formula^14,34–37 is that we fit models to the observed data to predict for each worker, for each year of follow-up 1) whether they are exposed if employed (in the Chinese cohorts not all employed workers were exposed), 2) their level of exposure at that time, 3) whether they left employment that year, and 4) whether they died of lung cancer or of another cause. These models include fixed covariates such as date of birth and sex, as well as time-specific predictors such as age in a given year, cumulative years of employment, and cumulative exposure level in the previous year. Next, based on these models, we use Monte Carlo sampling to create a pseudo-cohort which simulates the observed cohort’s experience with respect to exposure, time employed, and risk (called the ‘natural course’). The natural course is a g-formula estimate of cause-specific mortality under no intervention. Assuming the natural course accurately represents the observed data (an assumption that we evaluate), we can then ‘intervene’ in this pseudo-cohort to fix a new level of maximum exposure (e.g. a given current standard). This procedure avoids the problem posed by healthy worker survivor bias in typical regression models, namely adjusting for a time-varying confounder (leaving work) which may also be affected by exposure. Under each intervention, the rate of leaving work is allowed to vary according to exposure, and no further adjustment for leaving work is needed to estimate risk. Further details of our algorithm and models are given in the eAppendix and eTable 1.

Hypothetical interventions

In addition to the natural course, we estimate cause-specific risks under five hypothetical policy interventions to change personal exposure limits. These interventions are 100 μg/m³ (the OSHA standard from 1989 to 2016), 50 μg/m³ (the OSHA standard set in 2016), 25 μg/m³ (the limit proposed by the Association Advancing Occupational and Environmental Health in 2006), 10 μg/m³, and complete elimination of occupational silica exposure. We operationalized these limits in the model as follows: among all those participants with a predicted exposure above the limit, we set the value of exposure to the limit; among participants with a predicted exposure below the limit, we did not modify their exposure. In all cases we assumed full compliance with the limits. Causal effects estimated under these changes to exposure distribution can be thought of as population attributable effects.³⁸

For each intervention, we estimate the risk difference at age 80 by subtracting the risk under the intervention from the risk in the natural course. We use the risk difference to estimate the change in the number of cause-specific deaths by age 80 per 1000 workers expected under each hypothetical intervention. Age 80 was selected as a salient age for which most cohorts had adequate data, and at which cumulative risk for all-cause mortality would not be 100% but most exposure effects would have occurred. Participants were retained in the data until age 90 to leverage the data at older ages. We also estimated the years of life saved for each intervention using the expected person time in the pooled cohort under each intervention, subject to censoring by the end of follow-up. We used a non-parametric bootstrap with 200 iterations to estimate Wald-type 95% confidence intervals (CI) for g-formula estimates by using the estimate from the data +/− 1.96 times the bootstrap standard error. Illustrative SAS code for the current analysis is available on the author’s GitHub page (https://github.com/alexpkeil1/SilicaStudy)

Quantifying healthy worker survivor bias

We used a novel approach to quantify the strength of healthy worker survivor bias with the g-formula. Based on the assumption that healthy worker survivor bias results from confounding by employment status, we re-fit the models used in the g-formula after removing employment status from the models for mortality (i.e. we assume no path W_k ← U → D_k in Figure 1a) and removing exposure from the model for leaving employment (i.e. we assume no path X_k−1 → W_k in Figure 1a). These models reflect the assumptions underlying current OSHA risk estimates and reflect one way of expressing the null hypothesis that healthy worker survivor bias does not affect our results. We refer to this as the null model, which includes adjustment for all other measured confounders. Thus, assuming we have correctly specified all models, we can assess the magnitude of healthy worker survivor bias by comparing intervention-specific risk differences from our primary results, denoted by RD_A, with the null-model risk differences denoted by RD_N. We calculate the magnitude of healthy worker survivor bias as the relative change in the risk difference, given by (RD_A − RD_N)/RD_A. We also perform a sensitivity analysis in which we only remove employment status from the mortality models.

RESULTS

Across the 10 cohorts in the study, there were 65,999 workers who accrued over 1.4 million person–years at risk. Over follow-up there were 15,188 deaths, including 1,077 attributed to lung cancer (Table 1). Among the Chinese cohorts, 13% of workers developed incident silicosis by the end of follow-up in 1994; of these 84% were diagnosed during employment, and the remainder after employment.

Table 1.

Number of workers, annual exposure, exposure duration and mortality among 10 pooled cohort studies of workers occupationally exposed to silica, 1919–1998, United States, South Africa, Australia, Finland, China.

Industry	Workers	Person-years	Follow-up	Exposure period	Silica exposurea	Exposure durationc	Deaths
					Median (IQR)b	Median (IQR)b	All	Lung cancer
US diatomaceous	2,342	66,057	1942–94	1942–94	127 (17,204)	2.8 (0.7, 12.9)	749	77
South Africa gold	2,260	31,477	1967–86	1967–72	154 (139,217)	0.18 (0.1, 0.3)	1009	77
US gold	3,345	114,345	1919–96	1919–78	27 (19,52)	2.0 (1.0, 7.5)	1925	156
Australia gold	2,209	43,636	1961–93	1961–93	214 (132,482)	8.6 (4.2, 13.7)	1342	135
US granite	5,408	121,019	1950–82	1950–82	40 (10,70)	10.5 (3.0, 19.0)	1762	125
Finnish granite	1,026	28,686	1940–93	1940–86	600 (390,1724)	5.9 (1.4, 15.3)	418	39
US industrial sand	4,064	93,766	1940–98	1940–89	52 (17,90)	3.5 (0.9, 12.0)	886	87
China tungsten	28,478	611,699	1972–94	1972–94	112 (22,303)	14.5 (8.4, 21.8)	4549	174
China pottery	9,011	194,098	1972–94	1972–94	36 (0,219)	13.7 (7.6, 22.2)	1592	85
China tin	7,856	170,404	1972–94	1972–94	69 (1,218)	18.9 (10.8, 22.9)	956	122
Overall	65,999	1,475,188			75 (2,236)	14.7 (7.7, 22.1)	15,188	1,077

Note that figures may differ from those reported in Steenland et al. (2001) due to averaging over different time-frames

^aMeasured in μg/m³, average person–time at work

^bIQR indicates interquartile range

^cMeasured in years, averaged over individuals

Components of healthy worker survivor bias

Regarding component (a), being actively employed was associated with a nearly 60% lower hazard versus not being actively employed in any of the study cohorts (eTable 2). Regarding component (b), higher cumulative exposure was associated with a shorter time to leave work, a result which was similar for across exposure lags (eTable 3). We estimate a standardized median difference of −0.2 working years (out of a median 15 working years per individual) comparing the 25^th percentile of cumulative exposure (referent; 28 μg/m³-years) to the 75^th (6717 μg/m³-years). Ever-silicosis was also associated with a shorter time to leave work, yielding a standardized median difference of −2.3 working years comparing non-silicotics (referent) with ever-silicotics (eTable 4). Thus, cumulative silica exposure is associated with leaving employment, and silicosis is a plausible factor to explain part of this association. Further, leaving employment is strongly related to mortality. We considered silicosis a potential additional time-varying confounder in a sensitivity analysis, which resulted in slightly higher effect estimates for lung cancer mortality, and slightly lower estimates for other causes of death in the three Chinese cohorts (eTable 5).

Parametric g-formula

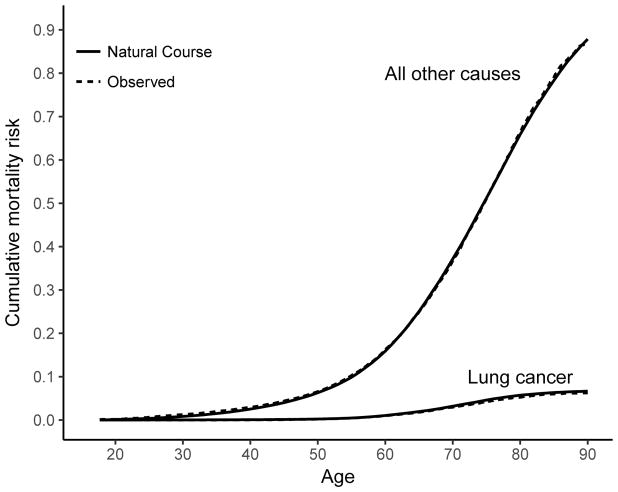
Under the natural course, the mean cumulative exposure and person–time exposed were similar to the observed data (eTable 6). Crude mortality rates for lung cancer in the natural course pseudo-population were similar to the observed data, as were mortality rates for all other causes (eTable 7). There was good overall agreement in the risk curves between the natural course and the observed data (Figure 2).

Figure 2.

Cumulative mortality of lung cancer and other causes of death among 10 pooled cohort studies of workers occupationally exposed to silica, 1919–1998, United States, South Africa, Australia, Finland, China. The age-specific risk was calculated using a modification of the Kaplan–Meier method for the observed data and the natural course intervention estimated using the parametric g-formula.

Under no intervention on exposure (the natural course), the expected number of deaths per 1000 (95% CI) at age 80 was 55.2 (53.6, 56.8) for lung cancer and 702 (698, 707) for all causes (Table 2). Given complete elimination of exposure during follow-up, per 1000 workers we would expect 3.91 fewer lung cancer deaths by age 80 (95% CI: 1.53, 6.30), and 16.8 fewer deaths from other causes (95% CI: 1.4, 23.1; Table 2). At age 80, there was an expected monotonic increase in the number of deaths delayed or prevented at increasingly restrictive hypothetical exposure limits. In a sensitivity analysis, we modeled exposure in mortality models with cubic splines (rather than quadratic polynomials as in the main analysis), which yielded similar results to our primary analysis (eTable 8). We estimate that 5,158 or 7,857 years of life among the cohort could have been gained under the 2016 standard or complete elimination, respectively, relative to the natural course.

Table 2.

Deaths per 1000 under no intervention (“natural course”) and deaths delayed or prevented by age 80 per 1000 workers for a series of hypothetical occupational exposure limits, 65,999 silica exposed workers across 10 pooled cohorts from the United States, South Africa, Australia, Finland, and China, 1919–1998.

	Deaths delayed or prevented per 1000 workers			Years of life saved (all causes)
	Lung cancer	Other causes	All causes
Natural coursea	0 (ref)	0 (ref)	0 (ref)	0 (ref)
100 ug/m3	1.71 (−0.814, 4.24)	8.77 (2.65, 14.9)	10.5 (4.40, 16.6)	3859 (2122, 5598)
50 ug/m3	2.47 (0.216, 4.72)	11.7 (5.58, 17.7)	14.1 (8.34, 19.9)	5158 (3409, 6906)
25 ug/m3	3.03 (0.927, 5.14)	13.3 (6.57, 20.0)	16.3 (9.99, 22.7)	6337 (4614, 8060)
10 ug/m3	3.41 (1.30, 5.52)	15.2 (9.02, 21.3)	18.6 (12.6, 24.5)	7067 (5195, 8940)
Eliminate exposure	3.91 (1.53, 6.30)	16.8 (10.4, 23.1)	20.7 (14.5, 26.8)	7857 (5891, 9823)

^aUnder the natural course, deaths per 1,000 workers by age 80 (95% CI) were 30.3 (29.3, 31.3) for lung cancer and 359 (356, 362) for all other causes.

In the null-model approach, the estimated impact of each hypothetical intervention was reduced relative to adjusted analyses (eTable 9). We estimate that healthy worker survivor bias results in a 28% underestimate of the risk for lung cancer and a 50% underestimate for other causes of death. In a sensitivity analysis, we fit a second null-model in which we removed only the terms for employment in the mortality models, which yielded similar but slightly attenuated estimates relative to our first null model (eTable 10).

DISCUSSION

Using data from nearly 66,000 workers from seven industries in five countries, we estimated that implementation of an occupational silica exposure limit of 50 μg/m³ over the period of follow-up would have prevented nearly 924 deaths by age 80 in a cohort this size (i.e., 14 deaths by age 80 per 1,000 workers). Approximately 165 of these deaths would be due to lung cancer (i.e., 2.5 per 1000 workers). More stringent limits would have further reduced silica-associated deaths. Complete elimination of silica exposure would result in the additional reduction of nearly seven deaths per 1,000 workers by age 80 (with 1.5 of these from lung cancer). Premature deaths due to silica exposure result in a substantial loss of years of life, reflected by our estimate of nearly 7,900 years of life lost in the cohort due to silica exposure during follow-up.

We also estimated that healthy worker survivor bias results in a 30%–50% underestimate of the excess risk comparing the natural course with complete elimination of exposure. While these results are subject to, in particular, assumptions about correct model form, our analysis suggests that current OSHA standards are based on estimates that are subject to healthy worker survivor bias. Thus, the recently implemented OSHA standard may be less effective at protecting worker health than OSHA’s risk assessments would suggest.

Consistent with much of the prior literature on silica, we found that much of the apparent benefit of reducing silica exposure would be experienced via reductions in non-lung-cancer mortality. OSHA recently estimated that 20% of the deaths prevented or delayed (by age 85) would be from lung cancer; in our analysis, lung cancer deaths constituted approximately 21% of the lives extended beyond age 80 from reducing the limit from 100 to 50 μg/m³. Our estimates of excess deaths at each exposure limit are not directly comparable to OSHA’s estimates, however. OSHA estimates are based on continuous exposure at the occupational exposure limit for 45 years. Our estimates, on the other hand, presume that many workers will continue to be exposed below the limit, and many will leave employment before 45 years, and thus represent a more probable estimate of the true benefit of changing occupational standards.

Our null model represents our estimated impact of interventions if we had ruled out healthy worker survivor bias, a priori. Current OSHA regulations also encode the assumptions that exposure does not affect employment and employment is not independently associated with mortality. Thus, our null model quantifies the extent to which key assumptions underlying current occupational limits may lead to biased impact estimates. For the target parameter of risk under some hypothetical occupational limit, we refer to this bias as healthy worker survivor bias. Critically, our estimate of the mortality reduction under complete elimination of exposure demonstrates that current standards can greatly improve with respect to worker health. Notably, we fit an additional null-model but allowed exposure to impact employment, and results did not change substantially, suggesting that simply adding a function of work history into a standard regression model may not lead to substantial selection bias of conditional hazard or rate ratios.

The Chinese cohorts represent one of the largest available sources of data on incident silicosis in a working population. Our findings suggested that onset of silicosis may be contributing factor in healthy worker survivor bias. We estimated that workers with silicosis left work earlier than non-silicotics, controlling for duration and cumulative exposure, and silicosis is one of the primary sources of excess morbidity and mortality among silica exposed workers. Further, the only cause of silicosis is silica exposure, indicating that silicosis may represent a time-varying confounder that is affected by prior exposure. Consequently, special approaches that can handle such variables, such as the g-formula, are required for analysis. Based on hypothesized relationships in Figure 1, an approach that can appropriately adjust for confounding by employment status is sufficient to control possible confounding by silicosis. In our analysis, we used appropriate methods to adjust for active employment status, which may be sufficient to control healthy worker survivor bias.¹⁰

To estimate lifetime excess risk under occupational limits, OSHA and prior published studies have relied on baseline mortality rates from the general population.^8,39 In contrast, our estimates of mortality in the absence of exposure are based on estimates of baseline risk made within the pooled data. Thus, our estimates are not subject to healthy hire bias, an empirical phenomenon in which working populations often experience lower sex- and age-specific mortality rates than general populations. Our use of an internal referent is possible because the parametric g-formula relies on models which can be utilized to extrapolate mortality rates from very low exposures to zero exposure. Thus, the validity of our estimates rely on the assumption that we have specified the models correctly in that this extrapolation reflects what we would observe in the population, had exposure truly been zero. In addition to the statistical assumption of correct model specification, making causal inference with the parametric g-formula relies on other identification assumptions.⁴⁰ We rely on the assumptions of treatment-variation irrelevance,^41,42 no measurement error bias,⁴³ positivity,⁴⁴ and no interference.⁴⁵ We note that the validity of any estimate of population risk, including OSHA’s estimates using life-table methods, also requires that these assumptions hold. Thus, the parametric g-formula represents an attractive alternative to life-table methods for predicting the effects of occupational exposure limits, especially when healthy worker survivor and healthy hire bias may be present.

Modeling assumptions are stronger for the g-formula than for alternative approaches based on fewer models. Notably, these we can identify gross violations of these assumptions via the natural course. Our results showed good correspondence between the natural course and the observed data. Computational considerations preclude exhaustive sensitivity analyses of g-formula results; for example, bootstrapping to get standard errors took nearly 250 computing hours for the primary analysis. However, one sensitivity analysis using cubic splines for exposure agreed well with our primary results, supporting our chosen model form. Nonetheless, apparently good fitting models may still encode statistical assumptions that do not accurately reflect associations within the data. To address this concern, we opted for model flexibility over parsimony, which relaxes model specification assumptions at the cost of decreased precision. Importantly, even if we assume that our primary analysis is based on correctly specified models with a minimally sufficient set of confounders, the null model will still be misspecified if it makes incorrect statistical assumptions.

The parametric g-formula is one of several approaches that have been proposed to address healthy worker survivor bias. Other approaches include structural nested models,^13,16,46,47 marginal structural models⁴⁸ and doubly-robust methods.⁴⁹ The parametric g-formula was attractive for the current analysis in that it allowed flexible exposure response models while still yielding highly interpretable estimates that are not subject to healthy worker survivor bias or problems with non-positivity.^44,50 Such an approach is especially attractive in light of previous findings of an apparently non-linear exposure response between silica and lung cancer,⁸ which may bias excess risk estimates based on a linear exposure-response model, such as those from OSHA.

The data used for this study were selected for the low expected influence of confounding from other occupational exposures, such as radon or arsenic. While the lack of co-exposures helps to reduce problems of internal validity, our results may not generalize well to other settings in which co-exposures modify the effect of silica. One potential shortcoming of the pooled study data with respect to studying mortality is the lack of smoking data. Smoking could be a source of unmeasured confounding if it is associated with exposure intensity (e.g. annual exposure) in strata of prior exposure, age, calendar time, sex, race, and study. Steenland et al.⁸ concluded that smoking was unlikely to account for the association between cumulative silica exposure and lung cancer based on the apparent lack of confounding by smoking in several cohort specific analyses in which smoking was measured.^2,27,28,51 If smoking modifies the effect of exposure on some scale, however, the lack of smoking data may introduce model misspecification because we would likely need to include interaction terms between smoking and exposure in the model. Brown (2009) noted that limited evidence suggests that effect-measure modification between smoking and linear terms for exposure is multiplicative for lung cancer but evidence is unclear for other outcomes.⁵² It is difficult to intuit whether this result would hold for our more flexible functions of exposure, so this remains a point for future work.

Given the demonstrated benefits of the parametric g-formula with respect to bias in longitudinal studies and quantification of hypothetical intervention effects, we believe our approach demonstrates an important way to leverage epidemiologic data for informing policy choices using occupational data.