Sensitivity Analyses for Misclassification of Cause of Death in the Parametric G-Formula

Abstract

Cause-specific mortality is an important outcome in studies of interventions to improve survival, yet causes of death can be misclassified. Here, we present an approach to performing sensitivity analyses for misclassification of cause of death in the parametric g-formula. The g-formula is a useful method to estimate effects of interventions in epidemiologic research because it appropriately accounts for time-varying confounding affected by prior treatment and can estimate risk under dynamic treatment plans. We illustrate our approach using an example comparing acquired immune deficiency syndrome (AIDS)-related mortality under immediate and delayed treatment strategies in a cohort of therapy-naive adults entering care for human immunodeficiency virus infection in the United States. In the standard g-formula approach, 10-year risk of AIDS-related mortality under delayed treatment was 1.73 (95% CI: 1.17, 2.54) times the risk under immediate treatment. In a sensitivity analysis assuming that AIDS-related death was measured with sensitivity of 95% and specificity of 90%, the 10-year risk ratio comparing AIDS-related mortality between treatment plans was 1.89 (95% CI: 1.13, 3.14). When sensitivity and specificity are unknown, this approach can be used to estimate the effects of dynamic treatment plans under a range of plausible values of sensitivity and specificity of the recorded event type.

Cause-specific mortality is an important outcome in studies of interventions to improve survival, yet causes of death can be misclassified. Understanding the effects of interventions on specific causes of death is important to optimizing strategies to improve life expectancy. In many settings, cause-of-death information from death certificates is available through state vital statistics offices and processed nationally in centralized databases, such as the National Death Index in the United States. This information can be combined with data on clinical care or lifestyle factors to estimate the effects of treatment strategies or interventions on cause-specific mortality.

The parametric g-formula is one method that provides consistent estimates of the effects of interventions, exposures, or treatment strategies in a given target population under a set of identifying assumptions (1). The parametric g-formula offers advantages over standard regression models in some settings because it appropriately accounts for time-varying confounding affected by prior treatment (1), and it can be used to estimate the effects of dynamic treatment plans (2) or treatment plans that depend on the natural value of treatment (3). Like standard regression models, the g-formula assumes that the outcome, treatment plans, and covariates are measured without error.

The g-formula can be used to answer questions related to cause-specific mortality. However, some cause-of-death information abstracted from death certificates may be misclassified, leading to bias in estimates of the effects of treatment plans of interest. Here, we describe how existing methods to perform sensitivity analyses for outcome misclassification can be integrated into the parametric g-formula to account for error in the cause-of-death designations from death certificates, using as motivation a leading example of an evaluation of antiretroviral treatment timing on risk of acquired immune deficiency syndrome (AIDS)-related death.

METHODS

Existing observational studies (2, 4, 5) and trials (6, 7) indicate that early therapy improves survival among patients with human immunodeficiency virus (HIV). Here we assessed the extent to which delayed therapy initiation separately increased the risk of both AIDS- and non–AIDS-related mortality and performed a sensitivity analysis to produce estimates under various assumptions about sensitivity and specificity of the cause-of-death designation.

Specifically, we implemented this sensitivity analysis to examine the possible impacts of outcome misclassification on the estimated difference in the 10-year cumulative incidence of AIDS- and non–AIDS-related mortality among patients with CD4 cell counts over 500 cells/mm³ between 2 HIV treatment strategies: 1) immediate therapy, “initiate antiretroviral therapy immediately upon entry into care”; and 2) delayed therapy, “initiate antiretroviral therapy when CD4 cell count first drops below 350 cells/mm³ or the patient is diagnosed with AIDS.”

Study population

The Centers for AIDS Research Network of Integrated Clinical Systems (CNICS) was developed to support population-based HIV research in the United States (8). The CNICS cohort includes HIV-positive adults engaged in clinical care from January 1, 1998, to the present at 8 Centers for AIDS Research sites (Case Western Reserve University; Fenway Community Health Center of Harvard University; Johns Hopkins University; University of Alabama at Birmingham; University of California, San Diego; University of California, San Francisco; University of North Carolina; and University of Washington). All patients attending 2 primary HIV medical-care visits at a study site are eligible for CNICS and followed for clinical events, lab measurements, and medications while they remain in care at study sites. Institutional review boards at each site approved study protocols. Patients provided written informed consent to be included in the CNICS cohort or contributed administrative and/or clinical data with a waiver of written informed consent where approved by local institutional review boards.

Patients who entered HIV clinical care at a CNICS site between January 1, 1998, and December 31, 2014, and had not previously initiated combination antiretroviral therapy (ART), which was defined as treatment with 3 or more antiretroviral drugs, were eligible for inclusion in this analysis (n = 20,931). We included only patients with a CD4 cell count over 500 cells/mm³ and a detectable viral load (over 400 copies/mL) at CNICS enrollment (n = 4,123). Patients were excluded if they were missing information on transmission risk factor, race, or sex (n = 241), leaving 3,882 patients in the cohort for analysis.

Patients were followed from entry into care at a CNICS site until death, loss to follow-up, or administrative censoring at 10 years after CNICS enrollment or December 31, 2014. Patients were considered to be lost to follow-up after 12 months without a documented clinic visit, CD4 cell count, or viral load measurement. Therapy initiation was defined as initiation of 3 or more antiretroviral drugs within a 1-week period.

Outcome ascertainment

The outcomes of interest were AIDS-related and non–AIDS-related mortality. Each CNICS site maintains a registry of deaths among patients at that site and semiannually queries the United States Social Security Death Index and/or National Death Index to confirm reported deaths and record deaths not captured by the CNICS sites. Information on cause of death was available from the National Death Index or state vital statistics registries for 110 of 178 deaths. We classified deaths as “AIDS-related” if the underlying cause of death on the death certificate was coded with International Classification of Diseases, Tenth Revision (ICD-10), codes B20–B24.9. All other deaths were classified as not AIDS-related, although interpretation of the results for non–AIDS-related mortality is complicated by the inclusion of deaths that are not likely to be affected by treatment, such as injuries. We assumed that cause-of-death information was missing at random given measured covariates (9).

Causes of death in the National Death Index may be misclassified for at least 2 reasons. First, identifying a single cause of death is difficult in many settings, and the level of consideration in assigning the underlying cause of death varies based on where the death occurs and who fills out the death certificate. Second, algorithms used for postprocessing of death certificates may reclassify deaths among people with HIV due to non HIV-related causes to one of the ICD-10 codes used for HIV-related mortality. Due to the possibility of error in recording cause of death on death certificates for HIV-positive decedents, and an acknowledged unreliability of reported AIDS-related deaths on death certificates (10), we used a sensitivity analysis to explore how results might change if the sensitivity and specificity of a report of AIDS-related death on a death certificate were set to each of several plausible values. We report results under the assumption of perfect measurement (i.e., sensitivity = specificity = 1) and under sensitivity analyses allowing sensitivity to range from 1 to 0.9 and specificity to range from 0.95 to 0.9.

Statistical methods

The parametric g-formula

The quantities of interest are the counterfactual risks of death due to each cause, or cumulative incidence functions, under immediate therapy initiation and under delayed therapy initiation (11). Formally, the risks are defined as $F_g\left(t,j\right)=P\left(T^g\le t,J^g=j\right)$, where $T^g$ is the time from CNICS enrollment to death from any cause under treatment plan $g$, and $J^g$ is the cause of death under treatment plan $g$. $T^g$ and $J^g$ are potential outcomes because they are the outcomes that would have occurred under treatment plan $g$.

The true potential outcomes are unobserved (12, 13). However, under a set of assumptions, the g-formula provides consistent estimates of the counterfactual risk functions under each treatment plan based only on observed data. These assumptions include 1) no measurement error of treatment plan, outcome, or covariates (12); 2) exchangeability between participants in the study sample observed to follow plan $g$ and participants not following plan $g$, perhaps conditional on a set of covariates $Z$; 3) treatment plan positivity, or that all participants have nonzero probability of following treatment plan $g$ conditional on covariates $Z$ (14); 4) exchangeability between participants under complete observation and participants lost to follow-up or missing key data at time $t$, perhaps conditional on covariates $Z$ (15, 16); and 5) observation positivity, or that all participants have nonzero probability of being observed at time $t$, conditional on $Z$. Here, we relax assumption 1 to allow uncertainty in the cause-of-death designations.

Details on implementation of the parametric g-formula in general and to compare ART strategies are described elsewhere (2, 5, 17). Briefly, our implementation of the g-formula to estimate the effects of a treatment plan on cause-specific mortality involved modeling the conditional probability of death due to any cause during each month and the probability that a predicted death was due to the cause of interest, given that the person was predicted to die during that month. The g-formula accounts for time-fixed and time-varying confounders through a generalization of standardization in which we estimate the density of all possible covariate histories and sum the risk of mortality over these histories (17, 18). Let $Y_i(t)$, $C_i(t)$, and $A_i(t)$ be indicators of death from any cause, censoring (due to drop-out or reaching the end of the study in calendar time), and treatment in month $t$ for participant $i$, respectively. ${\mathit{Z}}_{\mathit{i}}\left(\mathit{t}\right)$ represents a vector of covariates for participant $i$ at time $t$, and $J_i$ is an indicator that participant $i$ died from AIDS. The participant subscript $i$ will be suppressed where possible below, and overbars will represent history.

If censoring is uninformative, the risk of dying due to cause $j$ by time $t$ under no intervention on treatment plan can be written as equation 1:

$$\begin{array}{ll}F\left(t,j\right)\hfill & =\sum _{{\overline{a}}_t}\sum _{\overline{z_t}}\sum _{k=0}^{t}P[J=j|Y\left(k\right)=1,\overline{A}\left(k\right)=\overline{a}\left(k\right),\overline{Z}\left(k\right)=\overline{z}\left(k\right),Y\left(k-1\right)=C\left(k\right)=0]\hfill \\ \hfill & \times P[Y(k)=1|\overline{A}(k)=\overline{a}(k),\overline{Z}(k)=\overline{z}(k),Y(k-1)=C\left(k\right)=0]\hfill \\ \times \prod _{s=0}^k\hfill & \left(\begin{array}{l}P[A\left(s\right)=a(s)|\overline{Z}\left(s\right)=\overline{z}\left(s\right),\overline{a}(s-1),Y(s-1)=C(s)=0]\hfill \\ \times f[z\left(s\right)|z(s-1),\overline{a}(s-1),Y(s-1)=C(s)=0]\hfill \\ \times \mathit{P}[Y(s-1)=0|\overline{A}\left(s-1\right)=\overline{a}\left(s-1\right),\overline{Z}(s-1)=\overline{z}(s-1),Y(s-2)=C(s-1)=0]\hfill \end{array}\right)\hfill \end{array}$$ (1)

Under assumptions 1–4 above, the counterfactual risk at time $t$ under treatment plan $g$ can be consistently estimated (2, 5, 17, 19) as equation 2 below:

$$\begin{array}{ll}{F}_g\left(t,j\right)\hfill & =\sum _{{\overline{a}}_t}\sum _{\overline{z_t}}\sum _{k=0}^{t}P[J=j|Y\left(k\right)=1,\overline{A}\left(k\right)=\overline{a}\left(k\right),\overline{Z}\left(k\right)=\overline{z}\left(k\right),Y\left(k-1\right)=C\left(k\right)=0]\hfill \\ \hfill & \times P[Y(k)=1|\overline{A}(k)=\overline{a}(k),\overline{Z}(k)=\overline{z}(k),Y(k-1)=C\left(k\right)=0]\hfill \\ \times \prod _{s=0}^k\hfill & \left(\begin{array}{l}{P}^g[A\left(s\right)=a(s)|\overline{Z}\left(s\right)=\overline{z}\left(s\right),\overline{a}(s-1),Y(s-1)=C(s)=0]\hfill \\ \times f[z\left(s\right)|z(s-1),\overline{a}(s-1),Y(s-1)=C(s)=0]\hfill \\ \times P[Y\left(s-1\right)=0|\overline{A}\left(s-1\right)=\overline{a}\left(s-1\right),\overline{Z}\left(s-1\right)=\overline{z}\left(s-1\right),Y\left(s-2\right)=C\left(s-1\right)=0]\hfill \end{array}\right)\hfill \end{array}$$ (2)

where, at time $t=0$, $Z(t-1)$ is defined as the values of the covariates at CNICS enrollment, $A\left(t-1\right)=0$, and $Y\left(t-1\right)=0$.

In equation 2, we replace the estimated probability of receiving exposure $a$ at time $s$ in the observed data, $P[A\left(s\right)=a(s)|\overline{Z}\left(s\right)=\overline{z}\left(s\right),\overline{a}(s-1),Y(s-1)=C(s)=0]$, with the probability of receiving treatment $a$ at time $s$ under treatment plan $g$, $P^g[A\left(s\right)=a(s)|\overline{Z}\left(s\right)=\overline{z}\left(s\right),\overline{a}(s-1),Y(s-1)=C(s)=0]$. Note that this probability is set by the investigator. Under “immediate treatment” $(g=0)$, $P^{g=0}[A\left(s\right)=1|\overline{Z}\left(s\right)=\overline{z}\left(s\right),\overline{a}(s-1),Y(s-1)=C(s)=0]=1$ for all time points. Under delayed treatment $(g=1)$, $P^{g=1}[A\left(s\right)=1|\overline{Z}\left(s\right)=\overline{z}\left(s\right),\overline{a}(s-1),Y(s-1)=C(s)=0]=1$ if CD4 cell count was (or had ever been observed) below 350 cells/mm³, and 0 otherwise. $Z$ included time-fixed covariates, including sex, race, ethnicity, HIV–transmission risk factor (history of injection-drug use or male-to-male sexual contact), and age, year, CD4 cell count, and viral load at CNICS enrollment. $Z$ also contained time-varying covariates including CD4 cell count, viral load, and AIDS status at each clinic visit. Continuous variables were modeled flexibly using restricted quadratic splines. In the results presented, we allowed a 6-month grace period (20) for participants in the delayed treatment arm to initiate treatment after their CD4 cell counts dropped below 350 cells/mm³. Details on this implementation of the parametric g-formula, including implementation of the grace period, are provided in Web Appendix 1 (available at https://academic.oup.com/aje).

Briefly, to implement an analysis using the parametric g-formula, one first estimates each of the conditional probabilities for the cause of death among those who died, the probability of death due to any cause, and the density of time-varying covariates at each time point in the observed data (step 1). In low-dimensional settings, such as when few binary covariates must be considered, these conditional probabilities may be estimated nonparametrically. However, when $Z$ is high-dimensional, parametric models are used to estimate one or more components of the above equation. In step 2, a large Monte Carlo sample of participants at CNICS enrollment is drawn (with replacement) from the study population. The distribution of covariates at CNICS enrollment is estimated nonparametrically using the empirical distribution in the Monte Carlo sample. In step 3, the investigator sets $P^g[A\left(s\right)=a\left(s\right)|\overline{Z}\left(s\right)=\overline{z}\left(s\right),\overline{a}(s-1),Y(s-1)=C(s)=0]$ according to the treatment plan of interest and, in step 4, uses the conditional probabilities (or regression coefficients) estimated in step 1 to simulate the follow-up experience for the participants in the Monte Carlo sample under each treatment plan. In this setting, some decedents were missing information on cause of death. We imputed the causes of death for these individuals using the g-formula under the assumption that cause-of-death data was missing at random (details are given in Web Appendix 2 including Web Tables 1 and 2). Details on using penalized maximum likelihood to estimate the cause-of-death model in settings with few deaths due to a specific cause are provided in Web Appendix 3.

Sensitivity analysis for outcome misclassification

The conditional probabilities in step 1 are typically estimated using pooled linear-logistic regression fit by maximum likelihood. Logistic regression provides consistent estimates of the conditional probabilities if models are correctly specified and treatment plans, covariates, and outcomes are measured without error in the observed data.

We confined our attention to accounting for error in the cause-of-death designation. If causes of death are misclassified, the conditional probabilities or regression coefficients estimated in the model for cause of death in step 1 are likely to be incorrect. To illustrate this point, consider the pooled logistic regression model we wish to fit in step 1 among participants known to die at time $k$:

$$\begin{array}{ll}\tau \hfill & =P[J=1|Y\left(k\right)=1,\overline{A}\left(k\right)=\overline{a}\left(k\right),\overline{Z}\left(k\right)=\overline{z}\left(k\right),Y\left(k-1\right)=C\left(k\right)=0]\hfill \\ & =\mathrm{expit}\{{\mathrm{\beta }}_0+{\mathrm{\beta }}_1\overline{A}\left(k\right)+{\mathrm{\beta }}_{2}h\left\{\overline{Z}\left(k\right)\right\}+{\mathrm{\beta }}_{3}h\left(k\right)\},\end{array}$$ (3)

where $h\left\{x\right\}$ represents an arbitrary function of the given variable and $\mathrm{expit}\left(x\right)=1/\{1+\exp \left(-x\right)\}$. To estimate the counterfactual risk functions, consistent estimation of $\mathrm{\beta }=\{{\mathrm{\beta }}_0,{\mathrm{\beta }}_1,{\mathrm{\beta }}_2,{\mathrm{\beta }}_3\}$ is necessary.

However, we observe error-prone cause of death $J\prime$ in place of $J$. A standard g-formula analysis (ignoring error in cause of death), might fit a pooled logistic model for $J\prime$:

$$\begin{array}{ll}\mathrm{\tau }\prime \hfill & =P[J\prime =1|Y\left(k\right)=1,\overline{A}\left(k\right)=\overline{a}\left(k\right),\overline{Z}\left(k\right)=\overline{z}\left(k\right),Y\left(k-1\right)=C\left(k\right)=0]\hfill \\ \hfill & =\mathrm{expit}\{{\mathrm{\gamma }}_0+{\mathrm{\gamma }}_{1}h\left\{\overline{A}\left(k\right)\right\}+{\mathrm{\gamma }}_{2}h\left\{\overline{Z}\left(k\right)\right\}+{\mathrm{\gamma }}_{3}h\left(k\right)\}.\hfill \end{array}$$ (4)

If the sensitivity or specificity of $J\prime$ as a measure for $J$ is less than 1, then $\mathrm{\gamma }\ne \mathrm{\beta }$, and the g-formula will no longer provide a consistent estimate of the counterfactual risk function $F_g\left(t,j\right)$.

However, we can estimate the parameters of $\mathrm{\tau }$ in step 1 under a range of plausible values for sensitivity and specificity by modifying the likelihood function for the cause-of-death model. Details on this procedure have been described previously for sensitivity analyses and to account for misclassification in standard regression models in settings with validation data (21–24). Below, we describe how to estimate the conditional probabilities in step 1 under a range of plausible values for the misclassification parameters (i.e., sensitivity and specificity), as in a sensitivity analysis.

We begin by specifying the logistic likelihood for the cause-of-death model in the true data:

$$L\left(\mathrm{\beta }\right)=\prod _{i=1}^N{\mathrm{\tau }}_i^{j_i}{\left(1-{\mathrm{\tau }}_i\right)}^{\left(1-j_i\right)}$$ (5)

Because the true cause-of-death indicator $J$ is not available, we rewrite the likelihood using the error-prone cause-of-death indicator $J\prime$ and investigator-assigned misclassification probabilities (i.e., sensitivity $(se)$ and specificity $(sp)$) as follows:

$$\begin{array}{ll}L\left(\mathrm{\beta }\right)\hfill & =\prod _{i=1}^N{\left\{{\mathrm{\tau }}_i\times se+\left(1-{\mathrm{\tau }}_i\right)\times \left(1-sp\right)\right\}}^{{j\prime }_i}\hfill \\ \hfill & {\times \left\{\left(1-{\mathrm{\tau }}_i\right)\times sp+{\mathrm{\tau }}_i\times \left(1-se\right)\right\}}^{(1-{j\prime }_i)}\hfill \end{array}$$ (6)

where $se=P\left(J\prime =1|J=1\right)$ and $sp=P(J\prime =0|J=0)$. We assume that misclassification is nondifferential with respect to covariates, although in settings with rich validation data or prior knowledge, sensitivity and specificity can be estimated conditional on covariates (23).

If the values of sensitivity and specificity are correct, the modified likelihood function given by equation 6 will provide consistent estimates for $\mathrm{\beta }$ that match the estimates that would be obtained by applying the likelihood function shown in equation 5 to the true data. However, estimates obtained using the modified likelihood function will be less precise than estimates from the true data as sensitivity and specificity move away from 1.

We evaluated the finite sample performance of the proposed approach using simulation experiments. Specifically, we compared bias (i.e., the difference between the true value and the estimated value), the standard deviation of the bias, and mean squared error (i.e., the sum of the bias squared and the variance of the bias) between the standard g-formula and the g-formula modified to account for outcome misclassification under several levels of misclassification severity. Details on the design of the simulation studies can be found in Web Appendix 4.

RESULTS

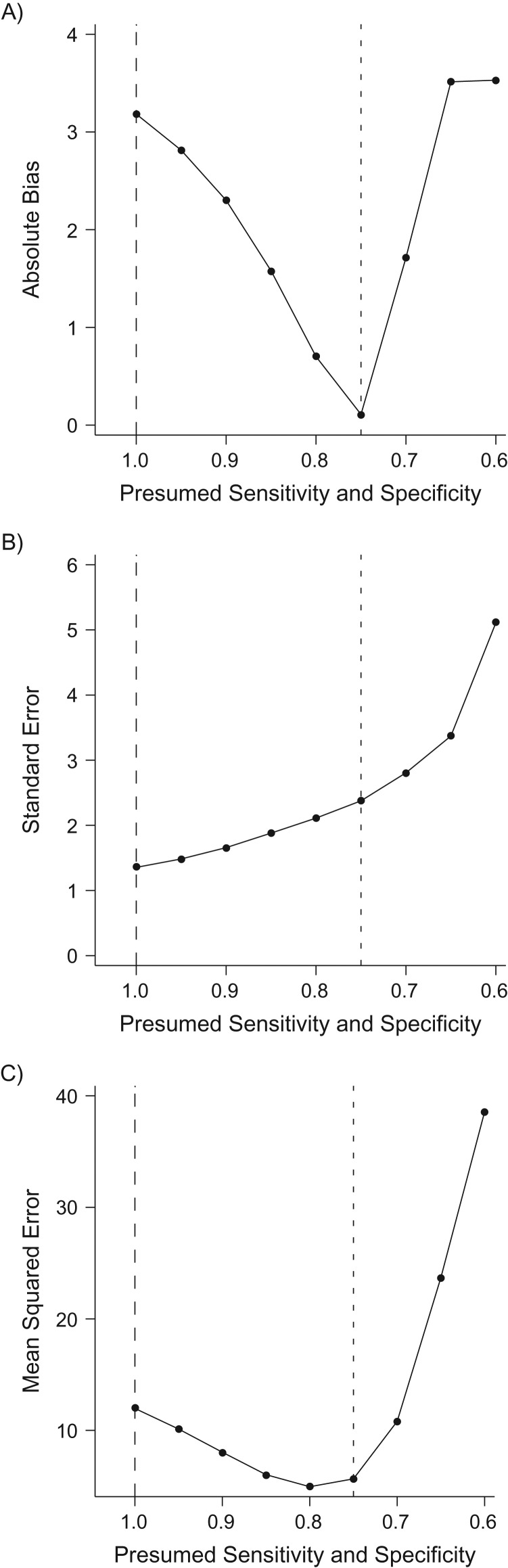
In simulation experiments, the bias in the standard g-formula increased as sensitivity and specificity decreased (Table 1). The modified g-formula approach had little bias in all scenarios examined if presumed values of sensitivity and specificity were correct. However, estimates obtained using the modified approach also became less precise as the quality of the outcome measurement deteriorated, resulting in increasing mean squared error, although mean squared error was smaller for the modified g-formula approach than for the standard g-formula approach in all scenarios. If the presumed values of sensitivity and specificity were incorrect, the modified g-formula approach yielded estimates with residual bias due to misclassification, although bias was not as severe as under the standard g-formula approach in which sensitivity and specificity were assumed to be 1 (Figure 1).

Table 1.

Results from 1,000 Simulated Cohorts Illustrating the Performance of the Parametric G-Formula to Estimate the Risk Difference When Sensitivity and Specificity are Known

Scenario	Specificity	Sensitivity	Standard G-Formula				Modified G-Formula
			Risk Difference	Biasa	Standard Errorb	MSEc	Risk Difference	Bias	Standard Error	MSE
1	1.0	1.0	10.45	0.15	1.09	1.22	10.45	0.15	1.09	1.22
2	0.9	0.9	9.04	−1.25	1.22	3.04	10.49	0.20	1.44	2.11
3	0.9	0.7	6.99	−3.30	1.24	12.44	10.39	0.10	1.98	3.93
4	0.7	0.9	8.92	−1.37	1.33	3.67	10.76	0.47	1.84	3.61
5	0.7	0.7	6.99	−3.31	1.40	12.91	10.77	0.47	2.97	9.05

Abbreviation: MSE, mean squared error.

^a Bias was defined as the difference between the true risk difference and the estimated risk difference.

^b Standard error was estimated as the standard deviation of the bias.

^c MSE was the sum of the squared bias and the variance.

Figure 1.

Simulation results illustrating the bias (A), standard error (B), and mean squared error (C) under the proposed approach to estimate the risk difference in a cohort of 3,000 patients when true sensitivity = specificity = 0.75 under various presumed values of (equal) sensitivity and specificity in 1,000 simulation experiments. Dashed lines refer to the value one would see under a standard analysis (assuming perfect sensitivity and specificity) and dotted lines refer to the value one would see under an analysis that correctly assumed sensitivity and specificity to be 0.75.

Table 2 presents the characteristics of the study population at CNICS enrollment. Of the 3,882 patients who entered care at a CNICS site between 1998 and 2014 with a CD4 cell count over 500 cells/mm³, 82% were male (n = 3,193), 34% were black (n = 1,338), and 68% were men who have sex with men (n = 2,635). At CNICS enrollment, the median calendar year was 2006 (interquartile range, 2002–2010), the median age was 36 (interquartile range, 28–43) years, the median CD4 cell count was 648 (interquartile range, 567–783) cells/mm³, and the median viral load was 11,253 (interquartile range, 3,072–42,777) copies/mL.

Table 2.

Demographic and Clinical Characteristics at Enrollment of 3,882 Eligible^a Patients at 8 Clinical Sites, Who Entered Treatment Between January 1, 1998, and December 31, 2014, and Were Followed for Mortality for up to 10 Years, Centers for AIDS Research Network of Integrated Clinical Systems, United States

Characteristic	At CNICS Enrollment (n = 3,882)
	No. of Patients	%
Male sex	3,193	82
Black race	1,338	34
Hispanic ethnicity	334	9
Injection-drug user	500	13
MSM	2,635	68
AIDS	215	6
Age group, years
18–30	1,272	33
31–50	2,277	59
>50	333	9
CD4 cell count at entry
500–600	1,411	36
601–750	1,293	33
751–1,000	881	23
>1,000	297	8
CD4 cell count at ART
0–200	100	3
201–350	287	7
351–500	393	10
>500	1,309	34
Did not initiate ART while in the study	1,793	46
Year of CNICS enrollment
1998–2002	1,062	27
2003–2007	1,179	30
2008–2014	1,641	42

Abbreviations: AIDS, acquired immune deficiency syndrome; ART, antiretroviral therapy; CNICS, Centers for AIDS Research Network of Integrated Clinical Systems; MSM, men who have sex with men.

^a Eligible patients were ART-naive, virally unsuppressed patients who were linked to care at a CNICS site with an initial CD4 cell count above 500 cells/mm³.

Of the 3,882 patients included in the analysis, 2,089 initiated ART during the study period, 1,450 patients were lost to CNICS follow-up while ART-naive, and 721 patients were lost to CNICS follow-up after starting ART. During the 10 years of follow-up, 178 deaths occurred, including 36 AIDS-related deaths, 74 non–AIDS-related deaths, and 68 deaths with unknown cause. Because the number of deaths observed to be AIDS-related was small, we estimated the parameters in the cause-of-death model using penalized maximum likelihood as described in Web Appendix 3.

Under no intervention on treatment, the 10-year risk of all-cause mortality was 12%. The risk ratio comparing all-cause mortality under immediate treatment to delayed treatment was 1.19 (95% confidence interval (CI): 0.98, 1.56), and the risk difference was 1.91% (95% CI: 0.72, 2.60).

Table 3.

Standardized 10-Year Risk of Mortality According to Whether Death Was Related to Acquired Immune Deficiency Syndrome^a, Among 3,882 Eligible^b Patients Who Entered Treatment at 8 Clinical Sites Between January 1, 1998, and December 31, 2014, Centers for AIDS Research Network of Integrated Clinical Systems, United States

Analysis Type and Treatment Arm	Sensitivity	Specificity	AIDS-Related Mortality					Non–AIDS-Related Mortality
			10-Year Risk (%)	Risk Ratio	95% CI	Risk Difference	95% CI	10-year Risk (%)	Risk Ratio	95% CI	Risk Difference	95% CI
Standard analysis
No intervention	1.00	1.00	3.67					8.47
Immediate ART	1.00	1.00	2.11	1.00	Referent	0	Referent	8.05	1.00	Referent	0	Referent
Delayed ART	1.00	1.00	3.64	1.73	1.17, 2.54	1.53	0.62, 2.45	8.43	1.05	0.86, 1.27	0.38	−1.19, 1.95
Sensitivity analyses
Scenario 1
No intervention	1.00	0.95	3.32					8.74
Immediate ART	1.00	0.95	1.85	1.00	Referent	0	Referent	8.30	1.00	Referent	0	Referent
Delayed ART	1.00	0.95	3.27	1.76	1.12, 2.77	1.41	0.43, 2.40	8.75	1.06	0.88, 1.28	0.50	−1.08, 2.07
Scenario 2
No intervention	1.00	0.90	3.13					9.13
Immediate ART	1.00	0.90	1.59	1.00	Referent	0	Referent	8.57	1.00	Referent	0	Referent
Delayed ART	1.00	0.90	3.05	1.91	1.04, 3.51	1.46	0.34, 2.57	9.19	1.05	0.87, 1.27	0.45	−1.14, 2.05
Scenario 3
No intervention	0.95	0.90	3.25					8.96
Immediate ART	0.95	0.90	1.65	1.00	Referent	0	Referent	8.49	1.00	Referent	0	Referent
Delayed ART	0.95	0.90	3.12	1.89	1.13, 3.14	1.47	0.45, 2.48	9.08	1.05	0.86, 1.29	0.44	−1.10, 1.99
Scenario 4
No intervention	0.90	0.95	3.60					8.55
Immediate ART	0.90	0.95	1.93	1.00	Referent	0	Referent	8.27	1.00	Referent	0	Referent
Delayed ART	0.90	0.95	3.59	1.86	1.19, 2.91	1.66	0.64, 2.68	8.44	1.03	0.85, 1.26	0.25	−1.32, 1.81
Scenario 5
No intervention	0.90	0.90	3.31					8.85
Immediate ART	0.90	0.90	1.70	1.00	Referent	0	Referent	8.50	1.00	Referent	0	Referent
Delayed ART	0.90	0.90	3.27	1.93	1.18, 3.14	1.57	0.58, 2.57	9.04	1.04	0.85, 1.27	0.34	−1.19, 1.86

Abbreviations: AIDS, acquired immune deficiency syndrome; ART, antiretroviral therapy; CI, confidence interval.

^a Participants could have received no intervention, immediate ART, or delayed ART. In the delayed group, patients initiated ART at their first visit at which CD4 cell count was <350 cells/mm³ or the patient was diagnosed with AIDS.

^b Patients who entered care with a CD4 cell count over 500 cells/mm³ were eligible and were followed for death for up to 10 years.

Using the standard g-formula approach assuming no misclassification, the estimated 10-year risk of AIDS-related mortality increased from 2.11% under immediate treatment to 3.64% under delayed treatment, for a risk ratio of 1.73 (95% CI: 1.17, 2.54) and a risk difference of 1.53% (95% CI: 0.62, 2.45) (Table 3). The 10-year risk of non–AIDS-related mortality increased from 8.05% under immediate treatment to 8.43% under delayed treatment, for a risk ratio of 1.05 (95% CI: 0.86, 1.27) and a risk difference of 0.38% (95% CI: −1.19, 1.95).

Lower rows of Table 3 present results allowing for varying degrees of misclassification of cause of death. Under all treatment plans, as specificity moved away from 1, the estimated 10-year cumulative incidence of mortality due to AIDS decreased, while mortality due to non-AIDS causes increased. As sensitivity also moved away from 1, the cumulative incidence estimates depended on the relative values of sensitivity and specificity. For all scenarios assuming imperfect cause-of-death ascertainment, the risk ratio comparing AIDS-related mortality between immediate and delayed treatment was further from the null than the risk ratio under perfect cause-of-death ascertainment, although estimates were less precise. Risk ratios comparing non–AIDS-related mortality between treatment plans were mostly unchanged as sensitivity and specificity moved away from 1 but were also less precise.

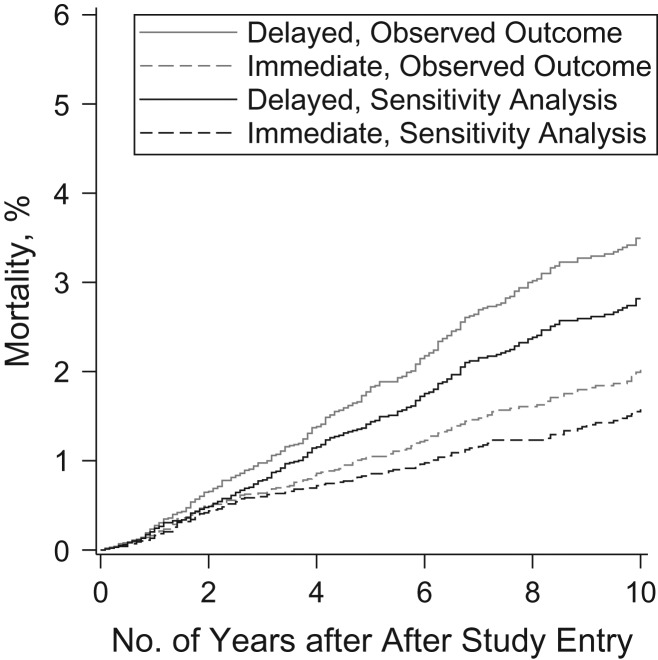
Figure 2 presents graphical results under the assumption that sensitivity was 95% and specificity was 90%. Figures illustrating the cumulative incidence for AIDS-related mortality under each of the other scenarios examined in the sensitivity analyses are presented in Web Figure 1.

Figure 2.

Standardized cumulative incidence functions for mortality related to acquired immune deficiency syndrome, under immediate and delayed treatment conditions, using standard analysis and sensitivity analysis (setting sensitivity to 95% and specificity to 90%), among 3,882 patients who entered care with a CD4 cell count over 500 cells/mm³ between January 1, 1998, and December 31, 2014, at 8 clinical sites, and who were followed for death for up to 10 years, Centers for AIDS Research Network of Integrated Clinical Systems, United States.

DISCUSSION

Here, we have described and demonstrated a method to estimate effects of dynamic treatment plans on cause-specific mortality under various assumptions about misclassification of cause of death. Results from simulation experiments indicate that accounting for outcome misclassification using the proposed approach reduces both bias and mean squared error in estimates of the risk ratio, provided that sensitivity and specificity are known.

Error in cause-of-death designations is sometimes addressed using an adjudication process. For example, the CoDe protocol (10) is a standardized adjudication process for determining the cause of death among HIV-positive decedents through medical record review. However, adjudication is a resource-intensive process that may be prohibitively expensive. In addition, adjudication procedures are subject to error themselves and are limited by missing data, given that many deaths occur outside medical care settings. The proposed approach provides a framework for incorporating previously developed approaches to account for outcome misclassification into the parametric g-formula in settings where adjudication is infeasible or where one wishes to account for possible error in an adjudication process.

Magder and Hughes (25), Lyles et al. (23), Edwards et al. (24, 26), and others (27) have described approaches to account for outcome misclassification in regression models using maximum likelihood–based approaches. Here, we show how to modify the likelihood of one of the regression models used in the parametric g-formula to reduce bias in counterfactual risk functions for cause-specific mortality. As in the maximum likelihood–based approaches to account for measurement error in regression models described elsewhere, our approach to this sensitivity analysis could be extended to allow sensitivity and specificity to differ according to treatment history or values of other covariates. For example, with additional information on the performance of the cause-of-death designation on death certificates in the presence of specific comorbidities, this approach could be extended to allow sensitivity and specificity to vary as a function of comorbid conditions or to cluster within hospitals.

In each scenario explored in the sensitivity analysis, we assumed the values of sensitivity and specificity were known without error. This approach could be extended to incorporate internal or external validation data as in Lyles et al. (23) or to place prior distributions on sensitivity and specificity (28–30). One could place prior distributions on sensitivity and specificity using the data priors described by Greenland (31, 32) or within the context of a Bayesian implementation of the parametric g-formula (33, 34). For both the sensitivity-analysis approach presented here and the Bayesian approach, the investigator must incorporate external knowledge about the likely values of sensitivity and specificity. Because the observed data offer some constraints on the joint distribution of possible values of sensitivity and specificity (35, 36), only a portion of the possible combinations of sensitivity and specificity must be explored. For example, because only 36 AIDS-related deaths were reported out of 178 total deaths, the lower bound on specificity was around 80% (i.e., there could have been no more than 36/178 = 20% false positives).

Sensitivity and specificity estimated from validation data or from prior knowledge are subject to uncertainty. With validation data, one could allow this uncertainty to propagate through the analysis to the final point estimate by resampling both the validation data and the main study data in each bootstrap sample. With prior knowledge, one could accomplish this by drawing values of sensitivity and specificity from their prior distributions in each bootstrap sample. In each case, the resulting 95% confidence interval would incorporate both random error in the main study data and uncertainty in the values of sensitivity and specificity (32). In contrast, 95% confidence intervals from the sensitivity-analysis approach presented here incorporated only random error in the main study, representing the amount of uncertainty we would have in each scenario if the proposed values of sensitivity and specificity were known to be correct.

We also assumed that the month of death was known. In countries with established death registries, this assumption is likely realistic. However, in resource-limited settings with no national death registry, the vital status in a given month may also be subject to error. In these cases, the proposed approach may not yield consistent estimates of the counterfactual cause-specific mortality functions without further modification to the likelihood to account for error in vital status in each month as well as the cause of death. Similarly, extensions to the proposed method will be required to account for outcome misclassification for other endpoints (e.g., disease incidence) in which the timing and event type are subject to error.

In conclusion, we have shown how the parametric g-formula can be used to estimate counterfactual cumulative incidence functions for cause-specific mortality when event types are misclassified if the sensitivity and specificity of the cause-of-death designation are known. When sensitivity and specificity are not known, this approach can be used to estimate the effects of dynamic treatment plans under a range of plausible values of sensitivity and specificity of the recorded event type.

Abbreviations

AIDS

acquired immune deficiency syndrome

ART

antiretroviral therapy

CI

confidence interval

CNICS

Centers for AIDS Research Network of Integrated Clinical Systems

HIV

human immunodeficiency virus