Molecular Time Sharing through Dynamic Pulsing in Single Cells

SUMMARY

In cells, specific regulators often compete for limited amounts of a core enzymatic resource. It is typically assumed that competition leads to partitioning of core enzyme molecules among regulators at constant levels. Alternatively, however, different regulatory species could time share, or take turns utilizing, the core resource. Using quantitative time-lapse microscopy, we analyzed sigma factor activity dynamics, and their competition for RNA polymerase, in individual Bacillus subtilis cells under energy stress. Multiple alternative sigma factors were activated in ~1-hr pulses in stochastic and repetitive fashion. Pairwise analysis revealed that two sigma factors rarely pulse simultaneously and that some pairs are anti-correlated, indicating that RNAP utilization alternates among different sigma factors. Mathematical modeling revealed how stochastic time-sharing dynamics can emerge from pulse-generating sigma factor regulatory circuits actively competing for RNAP. Time sharing provides a mechanism for cells to dynamically control the distribution of cell states within a population. Since core molecular components are limiting in many other systems, time sharing may represent a general mode of regulation.

In Brief

Cellular regulatory factors often compete for limited amounts of core enzymes. Sharing is typically assumed to involve statically partitioning core enzyme molecules. In contrast, using time-lapse movies, we find that Bacillus subtilis alternative sigma factors, which compete for core RNA polymerase, activate dynamically in stochastic, repetitive, hour-long pulses. Using mathematical modeling, we show how such pulsatile competitive circuits can effectively time share, or take turns using, core polymerase under similar conditions. Time-sharing represents an alternative mode of resource sharing in cells.

INTRODUCTION

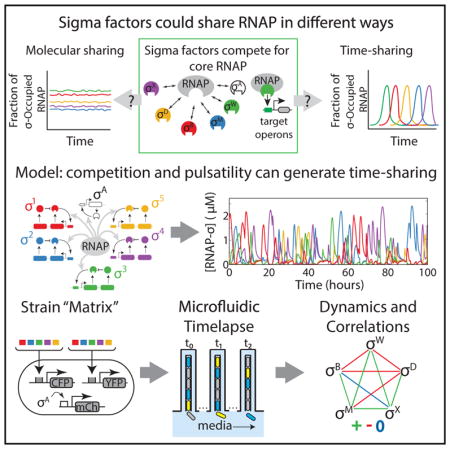
Many core cellular components are shared among distinct regulatory factors or substrates in the cell. For example, the proteasome is shared by multiple substrate proteins, the ribosome by multiple mRNA species, and core RNA polymerase (RNAP) by multiple sigma factors in bacteria (Figures 1A and 1B). When the shared core component is present in limited supply, sharing gives rise to competition between regulatory factors. At steady state, it is generally assumed that each substrate or factor utilizes an approximately constant fraction of core component molecules. However, certain regulatory systems may operate more dynamically, and far from a steady state. This opens up the possibility that sharing could occur in time. In such a time-sharing system, the core component would effectively take turns, interacting predominantly with only one or a few of its many potential partner species at any given time (Figure 1C). Despite the familiarity of time-sharing strategies in engineered systems such as computers and communication networks, it is unknown whether, or how, time sharing could occur in cells.

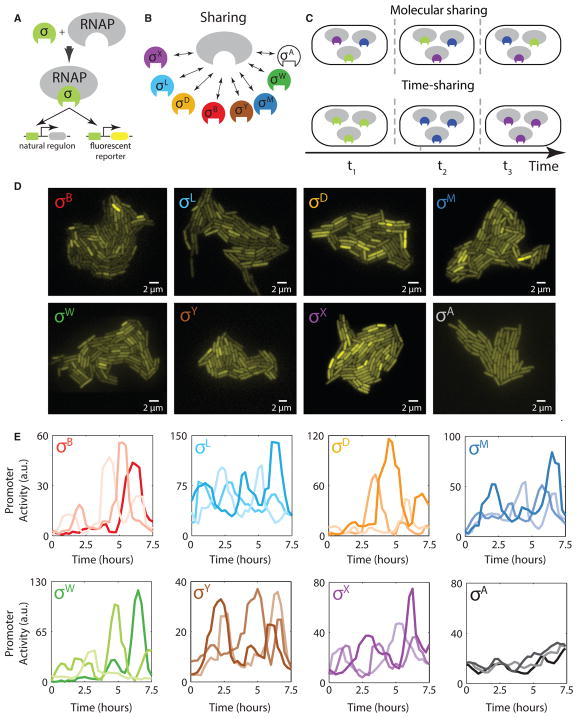
Figure 1. Multiple Alternative Sigma Factors Pulse under Energy Stress.

(A) Alternative sigma factors bind core RNAP to activate target genes, including endogenous targets (left target) and the engineered fluorescent reporters used here (right target).

(B) Multiple distinct alternative sigma factor species (colored shapes) share core RNAP (gray). The “housekeeping” sigma factor σ^A (white) also utilizes core RNAP.

(C) In principle, sigma factor species could share core RNAP by partitioning, with each sigma factor species utilizing some constant fraction of total RNAP (molecular sharing, top). Alternatively, they could share RNAP in time, with one or more sigma factors occupying a large fraction of RNAP for some period, followed by a different sigma factor or factors for another period of time, and so on (time sharing, bottom). Only three distinct species are shown here for simplicity.

(D) Fluorescent reporter expression in growing microcolonies shows heterogeneous activation of seven alternative sigma factors, as indicated, and homogeneous activation of σ^A (bottom right) under energy stress conditions.

(E) Time-lapse analysis reveals stochastic pulsing of alternative sigma factors in individual cell lineages. Here, each plot shows sigma factor activity time traces derived from analysis of corresponding fluorescent reporter genes in three different cell lineages (different line shades). For each plot, the y axis shows rate of fluorescent protein production, approximating instantaneous sigma factor activity. Note that the housekeeping sigma factor σ^A shows much less variability over time. See also Figures S1 and S2.

In bacteria, alternative sigma factors function as subunits of the RNAP holoenzyme, directing it to specific sets of target promoters (Boylan et al., 1993; Helmann, 2002, 2016; Paget, 2015; Price et al., 2001) (Figure 1A). In many contexts, alternative sigma factors actively compete for limiting amounts of RNAP (Ganguly and Chatterji, 2012; Grigorova et al., 2006; Hicks and Grossman, 1996; Maeda et al., 2000). In addition to competition, alternative sigma factors are typically controlled through a multi-stage regulatory system with feedback. In these systems, sigma factors are negatively regulated through cognate anti-sigma factors, which can (Cao et al., 2003; Estacio et al., 1998) prevent their association with core RNAP. These anti-sigma factors can in turn be inhibited by specific inputs or stresses to enable sigma factor activation (Gruber and Gross, 2003). Finally, sigma factors typically activate their own operons, which often contain the genes for both the sigma factor and its anti-sigma factor, creating interlocking positive and negative feedback loops (Cao et al., 2002, 2003; Estacio et al., 1998; Huang et al., 1999; Kalman et al., 1990; Yoshimura et al., 2004).

As a result of this regulatory structure, sigma factors can exhibit complex dynamics, even under constant environmental conditions. For example, the alternative sigma factor σ^B in Bacillus subtilis is activated in a sustained series of stochastic pulses in response to energy stress (Locke et al., 2011; Narula et al., 2016). These pulses represent events in which many σ^B molecules simultaneously become active, associate with core RNAP to initiate transcription of target genes, and then deactivate. However, σ^B is only 1 of 17 alternative sigma factors in B. subtilis (Gruber and Gross, 2003) (Table S1). It has remained unclear whether pulsing is specific to σ^B or occurs across the broader set of alternative sigma factors, whether multiple sigma factors pulse under the same conditions, and how pulsing relates to competition for core RNAP. Given that the concentration of each sigma factor species may change with time and that they compete with varying affinities for limiting amounts of core RNAP, describing and understanding the dynamics that may arise in a system expressing multiple sigma factors is non-trivial.

Here, we analyze the dynamics of multiple alternative sigma factors in B. subtilis cells under energy stress conditions at the level of individual cells. In addition to σ^B, we find that multiple other alternative sigma factors, including σ^D, σ^M, σ^W, and σ^X, also activate in repetitive pulses. Based on these observations, we explore the idea that RNAP could be shared more dynamically in time. We illustrate the principles of pure biochemical time sharing using mathematical models, and then ask which aspects of the alternative sigma factor dynamics observed in vivo may be explained by dynamic competition for RNAP, of which pure time sharing is a special case. Finally, we discuss how time sharing can, in principle, provide a mechanism for dynamically controlling the distribution of cell states or phenotypes within a population.

RESULTS

Understanding the dynamics of multiple sigma factors interacting with one another through competition for core RNAP requires the ability to visualize their activity over time in individual cells. To achieve this, we constructed a set of reporter strains, each containing a yellow fluorescent protein gene specifically activated by one of the B. subtilis alternative sigma factors not involved in sporulation (Figure 1A; Table S1). Fluorescent reporters were chromosomally integrated at the sacA locus (see STAR Methods), and specifically responded to their corresponding sigma factors (Figure S1A). We analyzed these strains in a minimal medium containing 40 μg/mL mycophenolic acid (MPA), a drug that reduces cellular ATP levels and stimulates a broad energy stress response (Zhang and Haldenwang, 2005) (Figure S1B). Visualizing fluorescent protein levels in single cells revealed markedly heterogeneous activation of seven alternative sigma factors in these conditions (Figure 1D). In contrast, the housekeeping sigma factor σ^A, which has higher affinity for core RNAP and lacks an anti-sigma factor (Rollenhagen et al., 2003), was activated in a more homogeneous manner, suggesting that this type of heterogeneous activation was not general to all sigma factors (Figures 1D, S1C, and S1D).

While the distributions of total fluorescent protein expressed from alternative sigma factor promoters exhibited skewed distributions with extended tails (Figure S1C), similar to those previously observed under conditions of pulsatile activation of σ^B (Locke et al., 2011), this cumulative readout can obscure dynamics on timescales faster than the cell cycle. Therefore, we computed for each cell the approximate instantaneous rate of fluorescent protein production from its corresponding target promoter, and corrected for photobleaching and dilution due to cell growth (Dunlop, 2014; Young et al., 2011) (see STAR Methods). This instantaneous activity should reflect the rate at which free sigma factor (not sequestered by its cognate anti-sigma factor) can associate with available core RNAP and initiate transcription at target promoters (Locke and Elowitz, 2009). It therefore depends on sigma factor protein levels, anti-sigma factor levels, and the availability of core RNAP.

For these experiments, we seeded cells on pads of low-melt agarose in minimal media with 40 μg/mL MPA, and used quantitative time-lapse fluorescence imaging to analyze individual cells within growing microcolonies. This analysis revealed that the seven alternative sigma factors mentioned above were activated in a pulsatile fashion (Figures 1E and S1D; Movie S1). Pulses appeared to be generated stochastically, as no significant correlations were observed in sister cell pairs (Figure S2A), or between a parent cell and its two daughters (Figure S2B). Widespread stochastic pulsing of this type was not specific to MPA-induced stress, as stationary phase conditioned media also caused pulsing of many sigma factors (Figure S3A). Also, this pulsing did not require σ^B, a factor previously shown to pulse (Figure S3B) (Locke et al., 2011).

We next sought to characterize the pulse dynamics more precisely. Because pulses occur much less than once per cell cycle, this required analysis over many generations. Exponential accumulation of cells on agarose pads limits the number of generations that can be analyzed, and leads to non-stationary environmental conditions. To circumvent these issues, we turned to the mother machine, a microfluidic device that enables analysis of a single cell over tens or hundreds of cell division events (Taheri-Araghi et al., 2015; Wang et al., 2010) (Figure 2A; Movie S2). More specifically, we used a mother machine variant optimized for B. subtilis that features a shallow side channel beside the main growth trenches to enhance diffusion of media over long distance to reach cells at the end of each trench (Norman et al., 2013). In the mother machine, we grew each reporter strain in minimal media containing 40 μg/mL MPA. Analysis of reporter dynamics revealed qualitatively similar dynamics as those observed on agarose pads, with five alternative sigma factors exhibiting pulsatile behavior (Figure 2B), with similar distributions of pulse shapes (Figures 2C and 2D), with typical durations on the order of 1 hr (Figure 2E), and varying frequencies (Figure 2F). The mean pulse showed an increase in activity relative to baseline activity of at least 5-fold for each sigma factor. σ^Y and σ^L were not active under these conditions, possibly due to the more chemostatic conditions in the device and the consequent prevention of buildup of secreted components. Therefore, they were not considered further in these experiments.

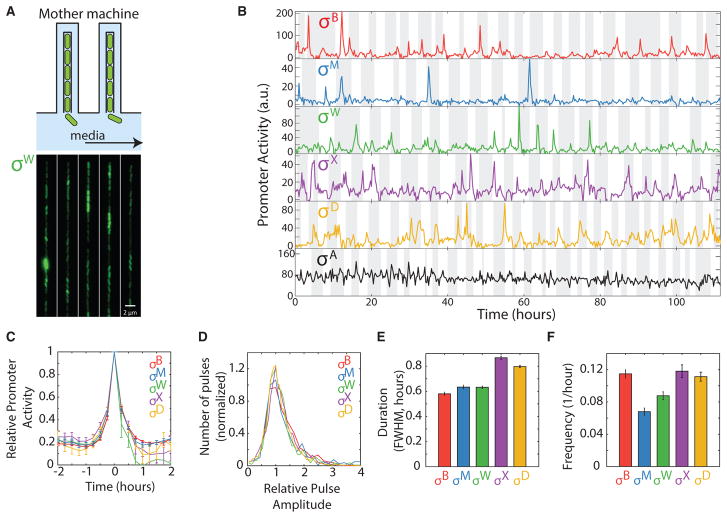
Figure 2. Five Alternative Sigma Factors Exhibit Pulsatile Dynamics over Extended Timescales in the Mother Machine.

(A) The mother machine microfluidic device enables long-term analysis of a single cell maintained at the end of a channel for multiple cell generations (schematic, top, and image of cells in device, bottom).

(B) Analysis of individual cell lineages show pulsatile dynamics of five alternative sigma factors as well as the constitutively active sigma factor σ^A for over 100 hr. Traces represent rates of fluorescent protein expression from target promoters for each sigma factor (promoter activity). Cell cycles are indicated by alternating gray and white vertical bands. Note that activity values in these conditions are not directly comparable with those in Figure 1E.

(C) Mean pulse dynamics for each alternative sigma factor species. For each sigma factor, n ≥ 320 pulses were detected, aligned around their peaks, and averaged. Error bars are SEM.

(D) Distribution of normalized pulse amplitudes for the indicated sigma factors.

(E) Mean pulse durations, quantified as full-width at half maximum (FWHM) for each of the alternative sigma factors. Error bars are SEM.

(F) Pulse frequencies for the indicated sigma factors. Error bars are SEM.

See also Figure S3.

To understand how pulsing affects the mode of sharing core RNAP, we constructed a mathematical model where sigma factor pulsing is driven by key regulatory features common to many alternative sigma factor systems (see STAR Methods). These features include two feedback loops, based on transcriptional autoregulation and inhibition by a co-expressed anti-sigma factor, as well as activation by an input. For simplicity, we represent this activation process as a molecular ligand that inactivates the anti-sigma factor (Figures 3A and S4A), although, in principle, it can be any process with double-negative logic that inactivates the anti-sigma in a concentration-dependent manner. This feedback structure occurs in all five alternative sigma factors examined in the mother machine, but has only been characterized in the context of σ^B (Locke et al., 2011). As such, the model is not intended to be a precise representation of any specific sigma factor system, but rather to explore the behaviors that such systems could generate when they are coupled through competition for RNAP. In particular, anti-sigma factors utilize diverse mechanisms for activation, and the ligand does not directly represent a specific molecular component. In contrast to other work modeling the control of sigma factor activities at steady state (Grigorova et al., 2006; Mauri and Klumpp, 2014; Narula et al., 2016), we focused on dynamic pulsatile behaviors.

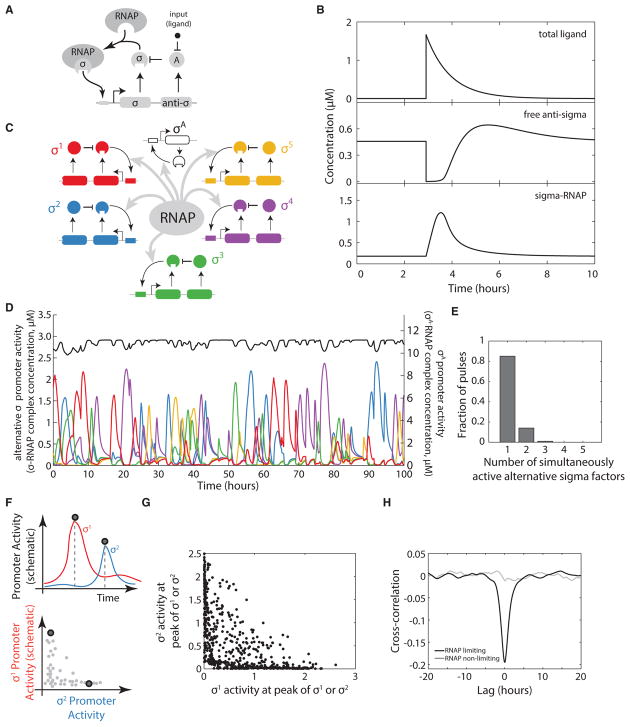
Figure 3. A Mathematical Model Shows Time Sharing in Alternative Sigma Factor Dynamics.

(A) Schematic of model of a single pulsatile alternative sigma factor species. The sigma factor autoregulates its own operon, which contains genes for the sigma factor and its cognate anti-sigma factor. An input, taken to be a small-molecule ligand (black dot), induces pulses by reducing the inhibitory activity of the anti-sigma factor.

(B) The simple sigma factor model can generate a pulsatile response to a sudden increase in ligand. Model parameters are in given in the STAR Methods (set A).

(C) Multiple alternative sigma factor circuits identical to the one in (A), along with a constitutive sigma factor representing σ^A, operating in the same cell, are coupled through sharing of core RNA polymerase (gray arrows).

(D) The multi-sigma factor model produces pulsatile dynamics of each alternative sigma factor (colored traces, left y axis), but more constant dynamics for σ^A (black, right y axis).

(E) Histogram showing the mean fraction of sigma factors active during pulses in the dynamics shown in (D). Most of the time, only one or two alternative sigma factors are active (exceeding a threshold value of 0.2 μM) simultaneously.

(F) Quantifying the co-occurrence of pulses of distinct sigma factors (schematic). A pulse detection algorithm recognizes pulses in either of two sigma factors (vertical dashed lines, upper panel). Sigma factor activities at each of these points can then be plotted relative to one another, as illustrated in the lower panel.

(G) Pulse amplitudes for all detected simulated pulses, plotted as in the lower panel of (F). The constraint of total RNAP limits the sum of the two sigma factor activities.

(H) Cross-correlation functions between the activities of two alternative sigma factors show anti-correlation between when RNA polymerase is limiting (black) but not when it is in excess (gray). See also Figures S4 and S5.

We identified physiologically reasonable parameters (STAR Methods) that lead to pulsatile dynamics similar to those observed experimentally for an individual sigma factor (Figure 3B). In this regime, pulses are initiated through a stochastic burst of ligand production. These bursts are assumed to be cell intrinsic based on the lack of correlation in pulsing between sister cells (Figure S2A; STAR Methods). The ligand pulse can suddenly reduce the activity of its cognate anti-sigma factor and thereby de-inhibit the corresponding sigma factor. Autoregulation of the sigma factor operon initially amplifies the pulse by upregulating expression of the sigma factor itself. Finally, the pulse eventually terminates itself through increased expression of the anti-sigma factor, which is part of the sigma operon (Figures 3B and S4B). These results show that the simple sigma/anti-sigma operon architecture is capable of generating pulsatile dynamics under physiologically reasonable conditions.

To explore how multiple pulsatile sigma factor species interact dynamically under conditions of limiting RNAP, we expanded the model to include five identical, but orthogonal, pulsatile sigma factor systems (Figure 3C). In addition, to represent the constitutive, non-pulsatile σ^A (Figure 1E), we incorporated an additional sigma factor species with no anti-sigma factor. All sigma factors were coupled to one another exclusively through competition for limiting amounts of shared core RNAP (STAR Methods). Such competition has been established in previous work (Ganguly and Chatterji, 2012; Grigorova et al., 2006; Hicks and Grossman, 1996; Maeda et al., 2000), and is further supported by experiments in which ectopic expression of σ^B repressed σ^W and σ^D activity under these conditions (Figures S5A, S5B, and S5C).

The model generated pulsatile dynamics for each of the alternative sigma factors, and an approximately constant activity for σ^A, consistent with experiments (Figures 3D and S5D). In this regime, more than 80% of core RNAP not bound to σ^A was occupied by one alternative sigma (Figure 3E). Furthermore, the sigma factors actively excluded one another, suppressing simultaneous pulses of multiple sigma factors (Figures 3F and 3G), and generating an overall anti-correlation in their activity when RNAP was limiting, but not when it was in excess (Figure 3H). We suggest that the regime, which does not depend on the use of symmetric parameter sets for the alternative sigma factors (Figure S8C), represents perfect time sharing.

The anti-correlations, characteristic of perfect time sharing, arise because each sigma factor pulse reduces the amount of core RNAP available for other sigma factors over a typical pulse duration (~1 hr). Subsequent termination of the pulse causes the sigma factor to relinquish core RNAP, allowing other sigma factors to initiate pulses (Figures S4B and S5D). While the overall rate of pulsing in this parameter regime is controlled by the rate of underlying stochastic inputs, represented in the model by ligand species, these ligands are uncorrelated with one another. The exclusion of simultaneous pulsing results from coupling between sigma factor species, which can arise only from competition for core RNAP. These modeling results show that time sharing dynamics can emerge from the combination of pulsatile activation dynamics from individual sigma factor operons and coupling through competition for core RNAP.

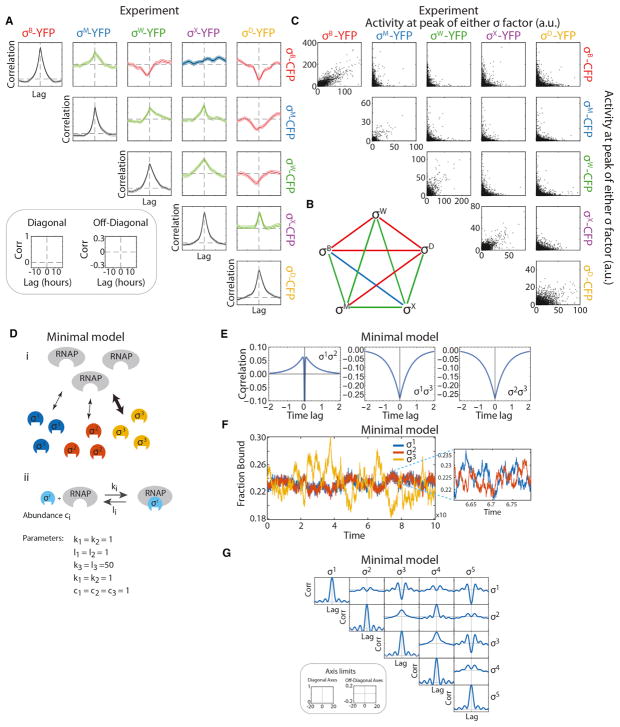
These simulations provoke the experimental question of what dynamic relationships occur among the pulsatile sigma factors within the same cell. To address this issue, we constructed a 5×5 “matrix” of strains (15 strains in total, i.e., the upper half matrix plus the diagonal), each containing a cyan fluorescent protein (CFP) reporter for one sigma factor, and a yellow fluorescent protein (YFP) reporter for a second sigma factor (Figure 4A). The matrix also included “diagonal” strains containing two distinguishable fluorescent reporters for the same sigma factor to establish the upper limit of possible correlation (Elowitz et al., 2002). Finally, all strains contained a third fluorescent protein (mCherry) reporter for σ^A activity (see STAR Methods). Using the mother machine, we recorded movies of individual cells from each of these 15 strains (Figure 4B; Movie S3), flowing minimal media containing 40 μg/mL MPA at a constant rate into the microfluidic device. We then quantified instantaneous promoter activities for all reporter pairs over time in each individual cell lineage (Figure 4C).

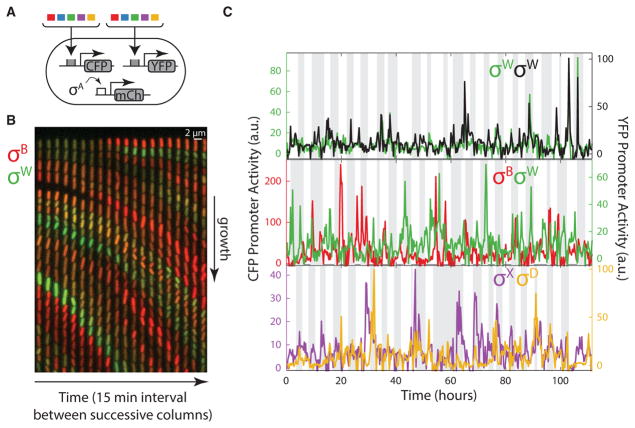
Figure 4. A Matrix of Multi-reporter Strains Enables Analysis of Dynamic Correlations between Different Alternative Sigma Factors.

(A) A matrix of strains was constructed, each of which contains a chromosomally integrated CFP reporter for one sigma factor (colored boxes) and a chromosomally integrated YFP reporter for another (second set of colored boxes), along with mCherry under the control of σ^A (schematic).

(B) Filmstrip from a mother machine movie, showing a single lane at 15 min intervals. P_B-CFP is shown in red, overlaid with P_W-YFP in the green channel (see Movie S3). Anti-correlations between the sigma factors are apparent from the lack of cells showing similar intensities in green and red channels (i.e., the lack of yellow cells).

(C) Example traces showing the activity dynamics of different pairs of alternative sigma factors, including strains with two reporters for the same sigma factor (top), and other pairs (lower two panels). See also Figure S6.

To understand the dynamic relationships between each pair of sigma factors, we computed the cross-correlation function of each pair of CFP and YFP fluorescence traces. As expected, strains with two reporters for the same alternative sigma factor showed strong positive correlations (Figure 5A). By contrast, four of the ten off-diagonal strains showed negative correlation between two different sigma factors, as predicted by the model (Figures 5A and 5B). These negative correlations occur despite the many factors expected to positively correlate the signals, including extrinsic fluctuations in cell growth rate and global gene expression parameters (e.g., transcription and translation efficiencies) (Bar-Even et al., 2006; Elowitz et al., 2002; Newman et al., 2006; Paulsson, 2004; Volfson et al., 2006), and the co-activation of multiple sigma factors by overlapping stresses, including MPA (Locke et al., 2011; Zhang and Haldenwang, 2005). The same negative correlations also appeared when using a “pulse-triggered averaging” analysis approach that specifically focuses on pulses within these time traces (Lin et al., 2015) (Figure S6). Of the remaining six pairs, five showed positive correlations that were significant, although substantially weaker than those observed for diagonal strains (Figure 5A). These will be discussed in detail below. Finally, one sigma factor pair showed no strong correlation in either direction. It is interesting that, while the positively correlated pairs exhibited more simultaneous pulses than expected if the two sigma factors were independent, simultaneous pulses were still rare even for the positively correlated pairs. This can be seen by plotting co-occurrences of pulses for all sigma factor pairs (Figure 5C).

Figure 5. Dynamic Correlations between Sigma Factors in the Same Cell.

(A) Fifteen double-reporter strains for pairs of alternative sigma factors (including “diagonal” strains with two reporters for the same sigma factor) were monitored in the mother machine. The corresponding time traces were analyzed by cross-correlation analysis. The resulting matrix of cross-correlations shows both positive (green), negative (red), and one approximately neutral correlation (blue). Each plot displays the mean cross-correlation (solid line) and the SE of the mean (shading). The diagonal strains do not show perfect correlation due to noise, and provide an upper limit on the possible strength of positive correlations.

(B) Diagram compactly summarizing the pattern of correlations revealed in (A), also using green, red, and blue to represent positive, negative, and neutral correlations, respectively.

(C) Scatterplots of pulse amplitudes for the sigma factor pairs shown in (A) (cf. Figure 3F). Each dot represents an event in which one or both sigma factors pulse (STAR Methods).

(D) Positive correlations can arise from competitive interactions in a minimal model of sigma factor-RNAP interactions. (Di) A minimal model of three sigma factors competing for binding to a limited pool of core RNAP. (Dii) The model assumes equilibrium binding/unbinding and uses three parameters for each sigma factor: its abundance (c_i), and its binding (k_i) and unbinding (l_i) rates to core RNAP.

(E) Cross-correlation functions of the bound fractions of all pairs of sigma factors calculated directly from the spectral densities. Bound fractions of sigma factors 1 and 2 exhibit positive correlations over sufficiently large timescales (or, equivalently, sufficiently low frequencies in the spectral densities).

(F) Simulated traces of binding fluctuations of the three sigma factors for the same parameter values. The bound fraction of sigma factor 3 fluctuates on a longer timescale than sigma factors 1 and 2. Over these timescales, the other two sigma factors are anti-correlated with sigma factor 3 but positively correlated with each other. In contrast, over shorter timescales (inset) the bound fraction of sigma factors 1 and 2 are negatively correlated as expected from competitive binding.

(G) Next, we extended the analytical model to six sigma factors (five observed and one unobserved) and searched for parameters that resulted in a 5 × 5 correlation matrix (among the five observed sigma factors) that exhibited a complex mixture of positive and negative correlations. The resulting correlation matrix is shown here (see Figure S7D for the optimal choice of parameters). Despite its simplicity, competitive interactions are sufficient to generate a complex pattern of positive and negative correlations. See also Figures S6 and S7.

Perfect time sharing, as demonstrated by the model (Figure 3H), is predicated on exclusively negative pairwise correlations between sigma factors and results in pulses where one alternative sigma factor is exclusively active (Figure 3E). In vivo, however, the appearance of positive and negative pairwise correlations between sigma factors is consistent with partial time sharing under these conditions, but also indicates a more complex and asymmetrical dynamical structure. This can be seen in the correlation graph (Figure 5B), where no two sigma factors share the same pattern of correlations with other sigma factors (Segrè et al., 2005). Even σ^B and σ^D, which show similar (although not identical) interactions with the other sigma factors, are anti-correlated with one another. We next asked whether the complex dynamical correlations observed here could be explained by competition for RNAP, or whether they require more specific regulatory interactions.

To address this question, we constructed a minimal, analytically solvable model of sigma factors competing for a common pool of core RNAP, dispensing with the regulatory features incorporated in the computational model discussed above (Figure 5D). We solved this model for an arbitrary number of sigma factors under the simplifying assumption of small equilibrium fluctuations (see STAR Methods)We obtained analytical expressions for the cross-correlation functions between all sigma factor pairs in terms of the binding/unbinding rates of the sigma factors to core RNAP and their abundances.

These results show that competitive binding interactions alone are sufficient to generate complex correlation graphs with mixtures of positive and negative correlations (see STAR Methods). For example, in the case of three sigma factors, it is possible for two of the sigma factors, σ¹ and σ², to exhibit positive correlations with each other, and negative correlations with σ³ (Figures 5E and S7A). This occurs when σ³ has slower binding and unbinding rates to core RNAP compared with those of the other two. In this regime, the fraction of core RNAP bound by σ³ fluctuates at a timescale longer than that of the other two sigma factors. At shorter timescales, σ¹ and σ² are both more likely to be found bound to core RNAP when the fraction of bound σ³ is lower than its steady-state value, resulting in a positive correlation between σ¹ and σ² (Figure 5F).

Similarly, it was possible to generate complex patterns of dynamical correlations among five sigma factors under certain parameter regimes in the simple model (Figure 5G). The analytical minimal model thus demonstrates that complex correlation patterns, including positive correlations between certain pairs of sigma factors, can arise from competitive interactions alone, even without more specific regulatory interactions (although these could also exist in the biological system). Most critically, these results show that complex correlation patterns can arise from asymmetries in the parameters governing sigma factors’ interaction with core RNAP.

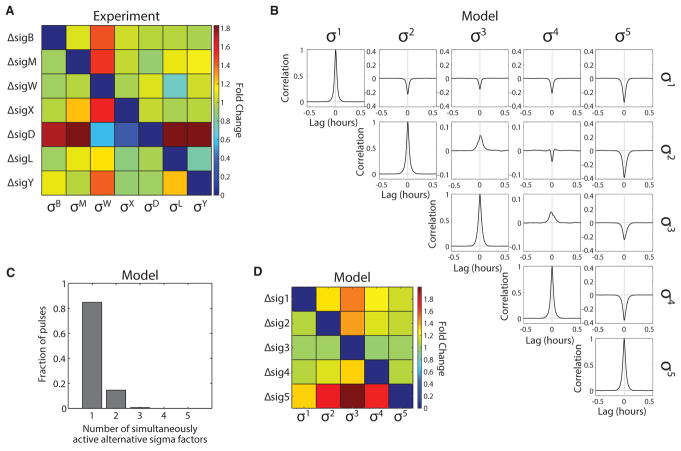
To determine whether sigma factors exhibit such asymmetric relationships with core RNAP in vivo, we constructed a 7 × 7 deletion “matrix” of strains. Sigma factor deletions enable analysis of competitive interactions without potential overexpression artifacts. Each strain in the matrix was deleted for one sigma factor and contained a YFP fluorescent reporter for another sigma factor. This matrix contained all five pulsatile strains whose correlations were analyzed in the mother machine, as well as σ^Y and σ^L. All strains also contained a constitutive fluorescent protein (mCherry) to assist in cell segmentation. For each strain in the matrix, we grew cells in liquid minimal media containing 40 μg/mL MPA, and quantified sigma factor activity by acquiring static fluorescence microscopy snapshots and quantitatively analyzing single-cell expression levels (see “Sample Preparation for Liquid Culture Snapshots and Agarose Pad Movies,” STAR Methods).

If most interactions between sigma factors result from competition for core RNAP, then regardless of which sigma factor is deleted, removing one sigma factor should cause similar relative effects on the remaining sigma factors. By contrast, if interactions are dominated by more specific regulatory interactions, the deletion matrix would be expected to show very different effects for each sigma factor deletion. Analysis of the deletion matrix revealed that deletion of six of the seven sigma factors predominantly increased σ^W activity, with smaller effects on other sigma factors (Figures 6A, S8A, and S8B). This result suggests that competition plays a major role in determining sigma factor activity. There was one exception to this pattern: deletion of sigD increased activity of all sigma factors except σ^W and σ^X. In addition, the sigD deletion, unlike the others, strongly affected cell size, suggesting additional pleiotropic effects (Figure S8A). Together, these results suggest that competition is asymmetric, with σ^W and σ^D being more and less susceptible, respectively, to competition than other sigma factors. Deletion of σ^D also appeared to cause a broader set of effects on cell physiology compared with other sigma factors.

Figure 6. Diversity in Sigma Factor Competition and Correlation.

(A) To systematically analyze competition between sigma factors, we constructed a deletion matrix. Each strain in the matrix is genetically deleted for one sigma factor (rows), and contains a chromosomally integrated fluorescent reporter for another sigma factor (columns). Cells were grown in minimal media with 40 μg/mL MPA. Mean reporter expression was measured by fluorescence microscopy. Each element in the matrix shows the fold change in sigma factor activity upon deletion of another sigma factor relative to wild-type. For instance, the ΔsigB, P_W-yfp strain (row 1, column 3) exhibited ~1.4-fold more fluorescent signal relative to the P_W-yfp reporter strain without deletion. The elements along the “diagonal” of the deletion matrix reflect negative controls on the sigma factors reporter strains’ specificity. Asymmetric interactions are evident from the increased fold change along the ΔsigD row and the σ^W column.

(B) Simulated cross-correlations for asymmetric parameters inspired by the results in (A); see (D), and parameter set B in STAR Methods. A mixture of positive and negative cross-correlations can arise from asymmetric competition for core RNAP. Each trace is the average of 81 cross-correlation functions, calculated from 28,000 simulated cell cycles.

(C) Histogram showing the distribution of the number of sigma factors simultaneously active during pulses in the dynamics displayed in Figure S8C (parameter set B in STAR Methods). Pulse detection threshold was as in Figure 3E, except for σ³, which used a threshold of 0.1 μM.

(D) The asymmetric sigma factor model recapitulates the broad features of the experimental deletion matrix. The deletion matrix was simulated in the model (parameter set B in STAR Methods) by removing each alternative sigma factor one at a time, and then simulating the rest of the sigma factors. Each simulation was run for 28,000 cell cycles. Deletion of σ⁵ increases the activity of all other sigma factors. σ³ is most sensitive to deletion of any other sigma factor. See also Figure S8.

We next asked whether the asymmetric competition observed in the deletion matrix could explain the complex mixture of experimental pairwise correlations between sigma factors. To answer this question, we used insights from the deletion matrix (Figure 6A), and the simplified model of competitive interactions (Figures 5D–5G and S7), to create a hierarchy of sigma factor “strengths” in the model. First, we increased the upregulated production rate of one sigma factor (labeled σ⁵) by a factor of 1.4, making it more dominant in competitive interactions, analogous to σ^D. Second, we reduced the affinity of a different sigma factor (σ³) for core RNAP, making it more susceptible to competition, like σ^W. Third, for the remaining sigma factors, we used two intermediate strengths, with one sigma factor possessing a higher affinity to core RNAP than the other two (see model parameters, set B, in STAR Methods). As in the simpler case described in Figure 3, time sharing dominates, with prevalent negative correlations between alternative sigmas (Figure 6B) and ~85% of pulses occurring in isolation; in only 15% of the pulses, two (or more) sigma factors were active simultaneously (Figure 6C).

In this model, the hierarchy of sigma factor strengths qualitatively recapitulated most of the experimentally observed asymmetric interactions. “Deletion” of most sigma factors in the model predominantly increased activity of σ³, the σ^W-like sigma factor, while deletion of σ⁵, the σ^D-like sigma factor, increased all other sigma factor activities (Figure 6D). Furthermore, the resulting pattern of positive and negative pairwise correlations in the model (Figure 6B) also resembled that observed experimentally (Figure 5A). σ⁵ exhibited negative correlations with all other sigma factors. This result matched most experimental observations.

The exception was the σ^D -σ^X pair, which exhibited positive correlations in the experiments. σ^D and σ^X also deviated from expectation in the experimental deletion matrix, where sigD deletion caused a decrease, rather than an increase, in σ^X activity (Figure 6A). These results suggest that there could be a more complex and specific regulatory interaction between these two sigma factors. In the model, σ³ generally behaved like σ^W with respect to its correlations with other sigma factors. It correlated negatively with σ⁵, and positively with the weaker sigma factors σ² and σ⁴, which we identify with σ^X and σ^M. These simple parameters did not capture all dynamic interactions. For instance, σ^B showed positive and neutral, rather than negative, interactions with σ^M and σ^X, respectively. Nevertheless, taken together, our results demonstrate that sigma factor competition, in the absence of additional regulation, can generate patterns of mixed pairwise correlations, broadly similar to those observed experimentally. Moreover, this work suggests that, although it is not perfect, many alternative sigmas may operate in regimes where time sharing contributes to the promoter activity dynamics observed.

DISCUSSION

Here we have analyzed the dynamics of sigma factor activity and competition in B. subtilis under energy stress. Despite the steady-state nature of the environmental conditions, we find that many sigma factors activate not at constant levels, but rather through repetitive pulsing (Figures 1 and 2). These dynamics expand previously published observations of σ^B pulsing (Locke et al., 2011) to a much broader set of sigma factors, and suggest that pulsing is a general mode of sigma factor activation. Based on analogy with σ^B regulation, pulsatile activity likely results from the interaction of a positive feedback loop on sigma factor expression and a negative feedback loop mediated by the corresponding anti-sigma factor. A model based on this generic architecture, in which sigma factors compete for limiting RNAP, demonstrates that competition can distribute pulsatile sigma factor activities in time, reducing their temporal overlap and resulting in negative correlations between their activities, among more complex dynamics.

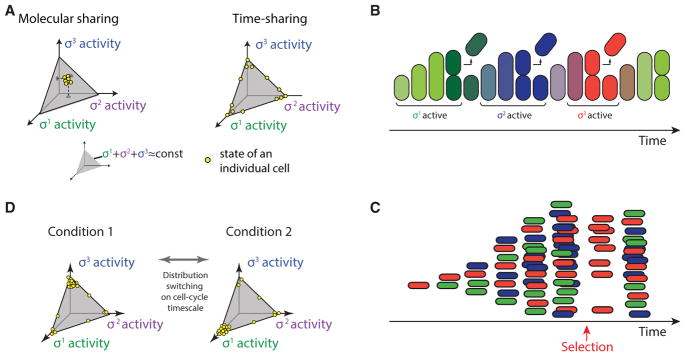
An ideal time-sharing system allows cells to focus the limited resource of core RNAP on a few alternative sigma factor regulons at a time, rather than spreading it across all sigma factor regulons at lower, constant levels (Figure 1C). These dynamics have a strong effect on the distribution of sigma factor activity states within a population. For example, consider three hypothetical alternative sigma factors. Without pulsatile dynamics (molecular sharing), all cells would exhibit relatively similar phenotypic states, with intermediate activities of each sigma factor, constrained by the total amount of core RNAP (Figure 7A, left simplex). By contrast, time sharing causes sigma factor activities to mainly occupy the edges and vertices of the allowed state-space (Figure 7A, right simplex), and to dynamically transition from one such state to another in a stochastic fashion. In the time-sharing regime, inputs to the system could effectively regulate the fraction of time that cells spend in various sigma factor activation states by controlling the relative frequency of pulses of different sigma factors. In addition, because the pulse durations observed here, of ~1 hr, are comparable with the duration of the cell cycle in these conditions, time sharing could cause successive cell cycles to be dominated by different sigma factor programs and corresponding phenotypes (Figure 7B). In this way, cells could control the distribution of activity states in the population, and regenerate the entire distribution of states after a perturbation (Figures 7C and 7D).

Figure 7. Time Sharing Could Control the Distribution of Cell States in a Population.

(A) Two distinct modes of sigma factor sharing (schematic). Competition for core polymerase restricts mean sigma factor activities to a subspace indicated by gray triangle, on which the sum of sigma factor activities is constant. In molecular sharing, each sigma factor would be active at a constant, intermediate level, with all cells (yellow dots) in similar states. In time sharing, cells predominantly occupy the vertices and edges of the allowed subspace (yellow dots, right triangle), and switch dynamically among these states through pulsing. They are therefore distributed over a broader variety of expression states at any given time. We consider a hypothetical symmetric three sigma factor system for conceptual illustration.

(B) Because the duration of pulses is comparable with the cell-cycle duration, cells tend to switch states from one cell cycle to the next (schematic). Here, colors indicate activity levels of each of three sigmas, following the scheme in (A).

(C) A schematic population of time-sharing cells. As in (B), colors indicate activities of three sigma factors. Due to stochasticity of sigma factor pulses, under these assumptions, the distribution of cell states can recover within one cell cycle from a perturbation to the cell state distribution (e.g., selection for the red state, arrow).

(D) In the time-sharing system, dynamic switching among states enables changes to the environment to rapidly shift the population from one distribution to another (left and right spaces, schematic).

The question remains whether the pulsatile dynamics observed at the level of alternative sigma promoters have phenotypic consequences. For phenotypic time sharing to occur, two conditions must be satisfied. First, anti-correlations observed with fluorescent protein reporters should reflect corresponding anti-correlations between phenotypes. Because the fluorescent reporter proteins used here are stable, their concentrations should be proportional to those of stable endogenous sigma factor target proteins, and thus the dynamic reporter correlations measured here likely reflect correlations among endogenous genes. Unstable target proteins could increase the magnitude of correlations by reducing time averaging. Second, individual sigma factor pulses must generate sufficient amounts of target gene products to affect cellular functions. Future work should address the propagation of pulses to specific phenotypes.

The dynamics observed here deviate from perfect time sharing in several ways. First, sigma factor activities are not exclusively pulsatile, as some basal activity is observed between pulses (Figure 2B). Second, competition appears to be asymmetric (Figure 6A). Third, the sigma factors exhibit a complex mixture of positive and negative correlations, rather than uniform negative correlations (Figure 5A). Modeling revealed how such mixed correlations can arise from asymmetric competition, particularly when sigma factors differ in the relative timescales of their interactions with RNAP (Figure S7). Higher-dimensional measurements of more than two alternative sigma factors at a time will be necessary to fully understand these complex dynamics.

While pulses are a strong feature here, sigma factor dynamics in general vary between systems and contexts. For example, the transition from exponential phase to stationary phase in Escherichia coli (Gruber and Gross, 2003), and the developmental program of sporulation in B. subtilis (Fimlaid and Shen, 2015), both involve, in different ways, sequentially ordered replacement of one sigma factor by another. In addition, the same sigma factor can activate with repetitive pulsing or adaptive dynamics in different contexts, as has been shown for σ^B (Cabeen et al., 2017; Young et al., 2013). Our observations are not incompatible with previously analyzed modes of activation, but rather enlarge the spectrum of dynamical modes implemented by sigma factor systems.

STAR★METHODS

KEY RESOURCES TABLE

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Bacterial and Virus Strains
PY79	BGSC 1A747	PY79
PY79; ppsB::PtrpE-mCherry PhleoR	(Locke et al., 2011)	JP1
JP1;ytvA::NeoR	This paper	JP2
JP2;sacA::PB-yfp CmR	This paper	JP3
JP2;sacA::PM-yfp CmR	This paper	JP4
JP2;sacA::PW-yfp CmR	This paper	JP5
JP2;sacA::PX-yfp CmR	This paper	JP6
JP2;sacA::PD-yfp CmR	This paper	JP7
JP2;sacA::PL-yfp CmR	This paper	JP8
JP2;sacA::PY-yfp CmR	This paper	JP9
JP2;sacA::PA-yfp CmR	This paper	JP10
JP3;rsbU-rsbX::TetR	This paper, (Locke et al., 2011)	JP11
JP4; sigM::TetR	This paper, (Luo and Helmann, 2009)	JP12
JP4; sigW::ErmR	This paper, (Luo and Helmann, 2009)	JP13
JP6;sigX::SpectR	This paper, (Cao and Helmann, 2002)	JP14
sigD::TetR	(Helmann et al., 1988; Steinmetz and Richter, 1994)	JP15
JP7; sigD::TetR	This paper, (Helmann et al.,1988; Steinmetz and Richter, 1994)	JP16
JP1; sacA::PL-yfp CmR	This paper, (Wiegeshoff et al., 2006)	JP17
JP17;sigL::KanR	This paper	JP18
JP1; sacA::PY-yfp CmR	This paper	JP19
JP19;sigY::KanR	This paper, (Cao et al., 2003)	JP20
JP3;amyE::PB-3Xcfp SpectR	This paper	JP21
JP3;amyE::PM-3Xcfp SpectR	This paper	JP22
JP3;amyE::PW-3Xcfp SpectR	This paper	JP23
JP3;amyE::PX-3Xcfp SpectR	This paper	JP24
JP3;amyE::PD-3Xcfp SpectR	This paper	JP25
JP4;amyE::PB-3Xcfp SpectR	This paper	JP26
JP4;amyE::PM-3Xcfp SpectR	This paper	JP27
JP4;amyE::PW-3Xcfp SpectR	This paper	JP28
JP4;amyE::PX-3Xcfp SpectR	This paper	JP29
JP4;amyE::PD-3Xcfp SpectR	This paper	JP30
JP5;amyE::PB-3Xcfp SpectR	This paper	JP31
JP5;amyE::PM-3Xcfp SpectR	This paper	JP32
JP5;amyE::PW-3Xcfp SpectR	This paper	JP33
JP5;amyE::PX-3Xcfp SpectR	This paper	JP34
JP5;amyE::PD-3Xcfp SpectR	This paper	JP35
JP6;amyE::PB-3Xcfp SpectR	This paper	JP36
JP6;amyE::PM-3Xcfp SpectR	This paper	JP37
JP6;amyE::PW-3Xcfp SpectR	This paper	JP38
JP6;amyE::PX-3Xcfp SpectR	This paper	JP39
JP6;amyE::PD-3Xcfp SpectR	This paper	JP40
JP7;amyE::PB-3Xcfp SpectR	This paper	JP41
JP7;amyE::PM-3Xcfp SpectR	This paper	JP42
JP7;amyE::PW-3Xcfp SpectR	This paper	JP43
JP7;amyE::PX-3Xcfp SpectR	This paper	JP44
JP7;amyE::PD-3Xcfp SpectR	This paper	JP45
JJB213; rsbU-rsbX::TetR	This paper	JP46
JP1 ; rsbU-rsbX::TetR	This paper	JP47
JP47; amyE::Phyperspank-sigB SpectR	This paper	JP48
JP48; pyrD::PB-cfp KanR	This paper	JP49
JP49; sacA::PW-yfp CmR	This paper	JP50
JP49; sacA::PD-yfp CmR	This paper	JP51
JP50; hag::ErmR	This paper, (Koo et al., 2017)	JP52
JP51; hag::ErmR	This paper, (Koo et al., 2017)	JP53
JP21;hag::ErmR	This paper, (Koo et al., 2017)	JP54
JP26;hag::ErmR	This paper, (Koo et al., 2017)	JP55
JP31;hag::ErmR	This paper, (Koo et al., 2017)	JP56
JP36;hag::ErmR	This paper, (Koo et al., 2017)	JP57
JP41;hag::ErmR	This paper, (Koo et al., 2017)	JP58
JP27;hag::ErmR	This paper, (Koo et al., 2017)	JP59
JP32;hag::ErmR	This paper, (Koo et al., 2017)	JP60
JP37;hag::ErmR	This paper, (Koo et al., 2017)	JP61
JP42;hag::ErmR	This paper, (Koo et al., 2017)	JP62
JP33;hag::ErmR	This paper, (Koo et al., 2017)	JP63
JP38;hag::ErmR	This paper, (Koo et al., 2017)	JP64
JP43;hag::ErmR	This paper, (Koo et al., 2017)	JP65
JP39;hag::ErmR	This paper, (Koo et al., 2017)	JP66
JP44;hag::ErmR	This paper, (Koo et al., 2017)	JP67
JP45;hag::ErmR	This paper, (Koo et al., 2017)	JP68
JP2; amyE::Phyperspank-yfp SpectR	This paper	JP69
JP69; hag::ErmR	This paper, (Koo et al., 2017)	JP70
JP3; rsbU-rsbX::TetR	This paper, (Locke et al., 2011)	JP71
JP4; rsbU-rsbX::TetR	This paper, (Locke et al., 2011)	JP72
JP5; rsbU-rsbX::TetR	This paper, (Locke et al., 2011)	JP73
JP6; rsbU-rsbX::TetR	This paper, (Locke et al., 2011)	JP74
JP7; rsbU-rsbX::TetR	This paper, (Locke et al., 2011)	JP75
JP8; rsbU-rsbX::TetR	This paper, (Locke et al., 2011)	JP76
JP9; rsbU-rsbX::TetR	This paper, (Locke et al., 2011)	JP77
JP3; sigD::TetR	This paper, (Helmann et al.,1988; Steinmetz and Richter, 1994)	JP78
JP4; sigD::TetR	This paper, (Helmann et al.,1988; Steinmetz and Richter, 1994)	JP79
JP5; sigD::TetR	This paper, (Helmann et al.,1988; Steinmetz and Richter, 1994)	JP80
JP6; sigD::TetR	This paper, (Helmann et al.,1988; Steinmetz and Richter, 1994)	JP81
JP7; sigD::TetR	This paper, (Helmann et al.,1988; Steinmetz and Richter, 1994)	JP82
JP8; sigD::TetR	This paper, (Helmann et al.,1988; Steinmetz and Richter, 1994)	JP83
JP9; sigD::TetR	This paper, (Helmann et al.,1988; Steinmetz and Richter, 1994)	JP84
JP3; sigL::KanR	This paper, (Wiegeshoff et al., 2006)	JP85
JP4; sigL::KanR	This paper, (Wiegeshoff et al., 2006)	JP86
JP5;sigL::KanR	This paper, (Wiegeshoff et al., 2006)	JP87
JP6;sigL::KanR	This paper, (Wiegeshoff et al., 2006)	JP88
JP7;sigL::KanR	This paper, (Wiegeshoff et al., 2006)	JP89
JP8;sigL::KanR	This paper, (Wiegeshoff et al., 2006)	JP90
JP9;sigL::KanR	This paper, (Wiegeshoff et al., 2006)	JP91
JP3;sigM::TetR	This paper, (Luo and Helmann, 2009)	JP92
JP4;sigM::TetR	This paper, (Luo and Helmann, 2009)	JP93
JP5;sigM::TetR	This paper, (Luo and Helmann, 2009)	JP94
JP6;sigM::TetR	This paper, (Luo and Helmann, 2009)	JP95
JP7;sigM::TetR	This paper, (Luo and Helmann, 2009)	JP96
JP8;sigM::TetR	This paper, (Luo and Helmann, 2009)	JP97
JP9;sigM::TetR	This paper, (Luo and Helmann, 2009)	JP98
JP4; sigW::ErmR	This paper, (Luo and Helmann, 2009)	JP99
JP4; sigW::ErmR	This paper, (Luo and Helmann, 2009)	JP100
JP5; sigW::ErmR	This paper, (Luo and Helmann, 2009)	JP101
JP6; sigW::ErmR	This paper, (Luo and Helmann, 2009)	JP102
JP7; sigW::ErmR	This paper, (Luo and Helmann, 2009)	JP103
JP8; sigW::ErmR	This paper, (Luo and Helmann, 2009)	JP104
JP9; sigW::ErmR	This paper, (Luo and Helmann, 2009)	JP105
JP3;sigX::SpectR	This paper, (Cao and Helmann, 2002)	JP106
JP4;sigX::SpectR	This paper, (Cao and Helmann, 2002)	JP107
JP5;sigX::SpectR	This paper, (Cao and Helmann, 2002)	JP108
JP6;sigX::SpectR	This paper, (Cao and Helmann, 2002)	JP109
JP7;sigX::SpectR	This paper, (Cao and Helmann, 2002)	JP110
JP8;sigX::SpectR	This paper, (Cao and Helmann, 2002)	JP111
JP9;sigX::SpectR	This paper, (Cao and Helmann, 2002)	JP112
JP3;sigY::KanR	This paper, (Cao et al., 2003)	JP113
JP4;sigY::KanR	This paper, (Cao et al., 2003)	JP114
JP5;sigY::KanR	This paper, (Cao et al., 2003)	JP115
JP6;sigY::KanR	This paper, (Cao et al., 2003)	JP116
JP7;sigY::KanR	This paper, (Cao et al., 2003)	JP117
JP8;sigY::KanR	This paper, (Cao et al., 2003)	JP118
JP9;sigY::KanR	This paper, (Cao et al., 2003)	JP119
JP7; hag::ErmR	This paper, (Koo et al., 2017)	JP120
Chemicals, Peptides, and Recombinant Proteins
Mycophenolic Acid	MP Biomedicals	Cat #194172
Recombinant DNA
Plasmid ECE174, sacA::P?-yfp CmR, where ? can be SigB,D,L,M,W,X,Y target site	This paper, (Locke et al., 2011)	Plasmid #1 (see STAR Methods)
Plasmid pDL30, amyE::P?-3Xcfp SpectR, where ? can be sigB,D,M,W,X, target site	This paper	Plasmid #2 (see STAR Methods)
Plasmid pDR-111, amyE::Phyperspank-sigB SpectR	This paper	Plasmid #3 (see STAR Methods)
Plasmid ECE171, pyrD::PB-cfp kanR	This paper	Plasmid #4 (see STAR Methods)
Plasmid pDR-111, amyE::Phyperspank-yfp SpectR	This paper	Plasmid #5 (see STAR Methods)
Software and Algorithms
Custom MATLAB Algorithms for Image Analysis	This paper, (Locke et al., 2011)

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Michael B. Elowitz, at melowitz@caltech.edu.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

This section details the sample preparation for experiments as well as the mathematical model, as well as a reference table for which strains werve to generate specific figures.

Table of Figures and Associated Strains

Figure	Strains
1	JP3…JP10
2	JP54, JP59, JP63, JP66, JP68, JP70
3	n/a
4	JP56, JP63, JP67
5	JP54…JP68
6	JP71…JP119
7	n/a
S1	JP3…JP10, JP71, JP82, JP90, JP93, JP101, JP109, JP119
S2 A,B,C	JP3…JP9
S2 D	JP73
S3A,B	JP54, JP59, JP63, JP66, JP68, JP70
S3C	JP7, JP120
S4	JP52, JP53
S5	n/a
S6	JP54…JP68
S7	n/a
S8	JP3, JP71, JP78, JP85, JP92, JP99, JP106, JP113

Bacillus subtilis Strains

All strains were constructed in the PY79 genetic background, and the list of strains used is given in the Key Resources Table. Many strains and genomic DNA were kind gifts of C.W. Price (see references), and many sigma factor deletion strains were kind gifts from John Helmann. Several strains were obtained from the Bacillus Genetic Stock Center (BGSC), and their strain codes are noted in the Key Resources Table.

In this table, in the column labeled “Source,” the term “This paper” indicates that this strain was constructed by the authors. Additional citations in the “Source” column reflect genetic material (or information) that was utilized to construct the strain. Genetic deletions were made by replacing genes of interest with a selection marker, typically by transforming genomic DNA alreading containing such marker into the relevant strain, and then selecting with the appropriate antibiotic.

Antibiotic resistance was switched using a previously described antibiotic switching vector system(Steinmetz and Richter, 1994). Deletions were made by replacing genes of interest with a selection marker via a linear DNA fragment homologous to the region of interest.

METHOD DETAILS

Plasmid Construction

All plasmids were cloned using E. coli strain DH5α and a combination of standard molecular cloning techniques and non-ligase dependent cloning using Clontech In-Fusion Advantage PCR Cloning kits. Plasmid constructs were integrated into B. subtilis chromosomal regions via double crossover using standard techniques. The following list provides a description of each plasmid constructed, with details on integration position/cassette and selection marker given at the beginning. Note that all plasmids below replicate in E. coli but not in B. subtilis.

Plasmid list:

1. ppsB::P_trpE-mCherry Erm^R -This plasmid was used to provide uniform expression of mCherry from a σ^A-dependent promoter, enabling automatic image segmentation (cell identification) in time-lapse movie analysis. A minimal σ^A promoter from the trpE gene was cloned into a vector with ppsB homology regions (Locke et al., 2011). The original integration vector was a gift from A. Eldar (Eldar et al., 2009). For some strains, the selection marker was subsequently changed, in B. subtilis, to either Kan^R or Phleo^R.

2. sacA::P_?-yfp Cm^R -Target promoters of each alternative sigma factor, (B, D, L, M, W, X, Y, A) were cloned into the EcoRI/BamHI sites of AEC127 (Eldar et al., 2009). For σ^A, a minimal σ^A promoter was used from the trpE gene(Locke et al., 2011). Target promoter sequences for alternative sigmas are described below.

3. amyE::P_?-3Xcfp Spect^R. Target promoters of each alternative sigma factor (B, D, L, M, W, X, Y), were cloned into the EcoRI/Nhe1 sites of plasmid amyE::3XCFP Spect^R (Locke et al., 2011). This plasmid, based on pDL30, contains 3 tandem copies of cfp, each with its own RBS. Target promoter sequences are described below.

4. amyE::P_hyperspank-sigB Spect^R - The coding region of sigB, along with a 5′ transcriptional terminator, was cloned downstream of the P_hyperspank IPTG-inducible promoter in plasmid pDR-111 (gift of D. Rudner, Harvard).

5. pyrD::P_B-cfp kan^R. Target promoter of σ^B, followed by the CFP fluorescent protein gene, was cloned into the EcoRI/BseRI site of the ECE171 plasmid (Middleton and Hofmeister, 2004).

Target Promoters for Sigma Factors

Below is a list of the target promoters used to report on each sigma factor’s activity. Each sequence below contains a binding site for the corresponding sigma factor. These sequences were cloned upstream of a standard cassette containing an RBS followed by the yfp reporter gene. Note restriction enzyme sites are not included in the displayed sequences.

1. σ^B : Sequence was chosen from the σ^B binding site upstream of the rsbV gene (Boylan et al., 1993; Kalman et al., 1990).5′-GTT TCTTGGAGCGTCCTGATCTGCAGAAGCTCATTGAGGAACATATGTGTTCCTCTGCGCAGGAAATGGTCAAAAACATTTATGA CAGCCTCCTCAAATTGCAGGATTTTCAGCTTCACGATGATTTTACGTTAATTGTTTTGCGGAGAAAGGTTTAACGTCTGTCAG ACGAGGGTATAAAGCAACTAGTGATTTGAAGGAAAATTTG-3′

2. σ^D: Sequence was chosen from the σ^D binding site upstream of the flgB gene (Estacio et al., 1998).5′ – TTTTGCATTTTTCTTCA AAAAGTTTCAAAAATGCCGAAAAGAAAGGAGAAAAAACAGAAATTCTG –3′

3. σ^L: Sequence was chosen from the σ^L binding site upstream of the ptb gene (Debarbouille et al., 1999).5′-AATATGGCCTTGCA AATGAAGGCATGCAATAATTTGCAGAATAAACGCAAACATCTGCACGAATGTTTCGGTATACCTGGTATGACAGCACCCTTA AGAGCTGGCATGGAACTTGCATAATAAAAGGCGGAG – 3′

4. σ^M: Sequence was chosen from the σ^M binding site upstream of the sigM gene (Horsburgh and Moir, 1999).5′ – TTTGCATGTA ATGTGCAACTTTAAACCTTTCTTATGCGTGTATAACATAGAGG-3′

5. σ^W: Sequence was chosen from the σ^W binding site upstream of the ydbS gene (Cao et al., 2002).5′ – TTAAGAATGAAACC TTTCTGTAAAAGAGACGTATAAATAACGACGAAAAAAAG – 3′

6. σ^X: Sequence was chosen from the σ^X binding site upstream of the sigX gene (Huang et al., 1997).5′ – TTGTAATGTAACTTTTC AAGCTATTCATACGACAAAAAAGTGAACGGAGGG – 3′

7. σ^Y: Sequence was chosen from the σ^Y binding site upstream of the sigY gene (Cao et al., 2003).5′ – GAATTGTAAAAAAGATGA ACGCTTTTGAATCCGGTGTCGTCTCATAAGGCAGAAAAACA – 3′

These promoters were first cloned into the appropriate plasmid (see section Plasmid Construction), and next, these plasmids were transformed into appropriate B. subtilis strains (see Key Resources Table). This transformation step resulted in an expression chromosomally integrated at a target locus.

Microscopy

All data were acquired using a CoolSnap HQ2 camera attached to a Nikon inverted TI-E microscope, equipped with the Nikon Perfect Focus System (PFS) hardware autofocus module. Molecular Devices commercial software (Metamorph 7.5.6.0) controlled microscope, camera, motorized stage (ASI instruments), and epifluorescent and brightfield shutters (Sutter Instruments). For experiments in liquid culture and agarose pads, epi-illumination was provided by a 300 W Xenon light source (LamdbaLS, Sutter instruments) connected via a liquid light guide into the illuminator of the scope. Between days, relative lamp intensity levels were monitored by taking an image of fluorescent beads and measuring their mean intensity. Exposure times were then adjusted to keep per exposure light levels constant between experiments. For experiments in the mother machine, epi-illumination was provided by a solid state white light source (Lumencor SOLA, Lumencor SOLA). Phase contrast illumination was provided by a halogen bulb to allow verification of cell focus and cell shape. Temperature control was achieved using an enclosed microscope chamber(Nikon) attached to a temperature sensitive heat exchanger set to 37 °C. All experiments used a Phase 100× Plan Apo (NA 1.4) objective. Chroma filter sets used were as follows: #41027 (mCherry), #41028 (YFP), and #31044v2 (CFP). The interval between consecutive imaging was 15 minutes.

Sample Preparation for Liquid Culture Snapshots and Agarose Pad Movies

Unless otherwise noted, cells were grown in Spizizen’s minimal media, or SMM (Spizizen, 1958), which uses 0.5% glucose as the carbon source. Mycophenolic acid (MPA) was dissolved in DMSO and diluted 1,000 fold into working concentrations in liquid and pad conditions. IPTG was dissolved in H₂O and diluted 1,000 fold into working concentrations. Concentrations of 0.1% DMSO were not found to affect cell growth or σ^B activity.

Samples were prepared following a time-lapse microscopy protocol described previously (Young et al., 2011). A stab from a glycerol stock was inoculated into SMM, placed into a 30 °C shaking incubator, and grown overnight. Cells were then diluted back to a final concentration of 0.01 OD₆₀₀ in a total volume of 2 ml of SMM. Cells were then grown in a 37 °C shaker for 3 hours.

For liquid culture experiments, MPA (MP Biomedicals cat #194172) was then added to the culture to a final concentration for 40 μg/ml. Cells were returned the 37 °C shaker for 3 hours, after which 2 μl of culture was spotted onto an agarose pad. Agarose pads were constructed of 1.5% low melt agarose solution in PBS, and then imaged, as described in the ‘Microscopy’ section.

For time-lapse movies, cells were spotted on solidified 1.5% low melt agarose in SMM pads. MPA was also added to the pads to final concentration of 40 μg/ml. These prepared pads were then enclosed in coverglass bottom dishes (Wilco #HBSt-5040), sealed with parafilm or grease to prevent evaporation, and then imaged.

Sample Preparation for Stationary-Phase (Conditioned Medium) Experiments

Conditioned medium was prepared growing PY79 wild-type B. subtilis strain in 2 ml of LB at 37 °C for 4.5h. Then, this culture was diluted in 23 ml of fresh LB and was grown at 37 °C for 17.5h. After this, cells were removed by centrifugation (at 5,000 rpm for 10 min) and the supernatant was sterilized by filtration (using 0.2 μm pore-size filters) and stored at −80 °C. This conditioned media protocol was defined previously (Espinar et al., 2013).

Cells were grown from glycerol stocks in LB until OD₆₀₀ 1.5–3.5, then diluted back into LB (1:10) in PBS to an OD₆₀₀ of 0.05. This culture was grown at 37 °C for a minimum of 4 hours and a maximum of 7, when cells were diluted to an OD₆₀₀ of 0.8–0.1 with conditioned medium (1:45) in PBS for imaging. 1.5% low melting agarose pads were prepared with conditioned medium (1:45) in PBS. Cells were allowed to equilibrate for 2–3 hours before initiating time-lapse imaging.

Sample Preparation for Mother Machine Experiments

Wafer Construction

Silicon wafers were constructed using photolithography by Shivakumar Bhaskaran at the Searle CleanRoom Manager at the University of Chicago. The CAD file for the design was a kind gift from Richard Losick and Johan Paulsson (Norman et al., 2013).

Chip Construction

Mother machine chips were constructed by first mixing Sylgard 184 (Dow Corning) Parts A and B in ratios of 10 to 1 by weight, respectively. Both parts were thoroughly mixed together, and then degassed in a vacuum chamber (Welch 256413-01) for 1 hr or until there was no visual sign of bubbles. The PDMS mixture was poured onto a wafer that had been placed into a ‘boat’ of aluminum foil, then baked at 65 °C overnight. The solidified PDMS was then carefully peeled off the wafer, cut with a scalpel to isolate the device, and fluidic inlets and outlets were created with with a 0.5 mm diameter hole punch (World Precision Instruments).

Chip Bonding to Coverslip

Glass coverslips (#1.5 Gold Seal 3416) were cleaned by sonicating in an Isopropanol Bath for 30 minutes, then sonicating in deionized water 3 times for 30 min. The microfluidic chips were cleaned simply by applying and removing Scotch tape multiple times. Chips were bonded using a plasma cleaner (Autoglow) with an attached O₂ tank, at 50 W for 6 seconds, and was performed at the Micro Nano Fabrication Laboratory at Caltech. The chip-coverslip complex was then baked at 85 °C overnight. Importantly, we found using O₂ with the plasma cleaner strengthened the bond between the glass coverslip and PDMS chip.

Cell Preparation and Cell Loading onto Chip

Cells were grown from glycerol stocks in SMM at 30 °C overnight. Cells were diluted to 0.01 OD₆₀₀ in the morning, and then grown for 3 hours at 37 °C. MPA was then added to a final concentration of 40 μg/ml, and then the culture was grown at 37 °C for another 6 hours. Cells were then pipetted into the chip inlet by utilizing gel loading tips (Molecular BioProducts 2155). To ensure cell entry into the narrow side channels of the chip, the entire coverslip and chip assembly was placed into a custom adapter (Norman et al., 2013), and then spun in a tabletop microcentrifuge (Eppendorf 5424R) for 10 min at 3,000 rcf.

Fluidic Inlet and Outlet

Fluid flow was driven by a syringe pump (NE-1600, syringepumps.com), which can drive up to six 10-ml syringes (BD 309604) in parallel. Unless otherwise noted, we used a flow rate of 1.5 μl/min. We used Tygon tubing (Saint Gobain AAD04103) for all tubing purposes. A blunt end needle (McMaster-Carr 75165A681) interfaced between the syringe and the tubing, and the same blunt end needle (with luer lock tip removed) interfaced between the tubing and the chip.

Media Driven by the Syringe

Unless noted otherwise, the media used in the mother machine was SMM, supplemented with 40 μg/ml MPA and 100 μg/ml BSA (Sigma A7906).

The exception was the competition assay in the mother machine. Syringes were initially loaded with the media as described above, namely SMM + 40 μg/ml MPA + 100 μg/ml BSA. But in the middle of acquisition, the syringes were switched to new syringes that contained the same media, excepted supplemented with additional 1 mM IPTG.

Mother Machine Microscopy

The coverslip/chip apparatus with attached fluidic inputs and outputs was fixed to the microscope stage insert (I-3014, ASI Imaging) using lab tape, and then imaged as described in the Microscopy section.

Competition Assay in the Mother Machine

Cells were loaded into the mother machine as described above.

Mathematical Model of σ Factor Pulsing and Competition

We constructed a model to simulate the activity of five identical, alternative sigma factor pathways, plus a housekeeping sigma factor, all interacting only through their association with shared RNA polymerase core (R). The main features of the model are:

• Transcriptional autoregulation. Each sigma factor comprises an operon containing the σ factor (S_i, where i = 1, 2, …5) and its cognate anti-σ factor (A_i). This operon is activated by its own σ factor. A sixth σ factor with no anti-σ is considered, representing the housekeeping factor σ^A.

• Inhibition by a co-expressed anti-σ factor. The σ factor binding to its cognate anti-σ prevents it from associating with RNAP.

• Limiting levels of RNAP resulting in competitive binding between σ factors.

• A ligand that sequesters its cognate anti-σ. A common feature among extra-cytoplasmic (ECF) sigma factors is that in most cases the anti-σ is a transmembrane protein that only releases its cognate sigma factor when it receives a certain input from the extracellular environment (Helmann, 2002). Hence, we implemented in the model a ligand (L_i) responsible for sequestration of its cognate anti-σ, to allow for the release of the corresponding σ factor. As shown below, we assume Poisson distributed steps in L_i, which trigger sigma factor activation pulses.

This minimal structure is sufficient to generate pulses in the σ·RNAP complex concentration in response to pulsatile ligand fluctuations. Even though the ligand fluctuations are uncorrelated among sigmas, RNAP competition leads to anticorrelations in σ·RNAP complex concentration that enable the alternative sigma factors to time-share core RNAP (Figure 3H).

An additional equation (Equation S2, below) simulates σ^A, the main - or housekeeping - σ factor. Its structure resembles that of the alternative σ factors, but without an anti-σ factor or corresponding ligand. The removal of the anti-σ factor results in a non-pulsatile and constitutive σ^A·RNAP concentration.

The transcription terms for σ factors and anti-σ factors are assumed to be linear, as are all degradation terms. The positive transcriptional regulation is modeled with Michaelis-Menten kinetics. σ^A is assumed to be expressed at higher levels than the alternative σ factors. Negative regulation occurs through sequestration, with linear rates for complex association and dissociation. Importantly, the sigma-RNAP complex produces more anti-sigma factor than sigma factor, a feature consistent with experimental measurements (Li et al., 2014). This relative advantage in anti-sigma production allows anti-sigma levels to overcome sigma factor activation and terminate the pulse. The ligand pulses were uncorrelated in time and exponentially distributed in magnitude. This was motivated by previous observations (Friedman et al., 2006; Raj et al., 2006; Taniguchi et al., 2010) that cellular protein concentrations follow a gamma distributed Ornstein-Uhlenbeck (GOU) process (Locke et al., 2011). This implementation allows for independent manipulation of mean ligand pulse size and pulse frequency. To optimize computational efficiency, ordinary (not stochastic) differential equations were solved between the stochastic ligand bursts in the discretized stochastic GOU process.

The following ODEs describing the dynamics for each species and their complexes were solved numerically in MATLAB using a variable step BDF method (http://www.mathworks.co.uk/help/matlab/ref/ode15s.html). Parameters can be found in the table below. The MATLAB codes for the model simulation and analysis are available upon request.

Alternative σ Factors (S_i)

$$\begin{gathered} \mathit{transcription}+\mathit{positive}\mathit{auto}-\mathit{regulation}+\mathit{complex}\mathit{dissociation}+\mathit{complex}\mathit{association}+\mathit{degradation} \\ \frac{d{[S]}_i}{dt}={\alpha }_s+{\beta }_s{[RS]}_i+k_{rs-}{[RS]}_i+k_{sa-}{[SA]}_i-k_{rs+}[R]{[S]}_i-k_{sa+}{[S]}_i{[A]}_i-{\delta }_s{[S]}_i \end{gathered}$$ (Equation S1)

Housekeeping σ Factor (S_A)

$$\begin{gathered} \mathit{transcription}+\mathit{positive}\mathit{auto}-\mathit{regulation}+\mathit{degradation} \\ \frac{d{[S]}_A}{dt}={\alpha }_{sA}+{\beta }_{sA}{[RS]}_A+k_{\mathit{rsA}-}{[RS]}_A-k_{\mathit{rSA}+}[R]{[S]}_A-{\delta }_{sA}{[S]}_A \end{gathered}$$ (Equation S2)

Anti-σ Factors (A_i)

$$\begin{gathered} \mathit{transcription}+up-\mathit{regulation}+\mathit{complex}\mathit{dissociation}-\mathit{complex}\mathit{association}-\mathit{degradation} \\ \frac{d{[A]}_i}{dt}={\alpha }_a+{\beta }_a{[RS]}_i+k_{sa-}{[SA]}_i+k_{al-}{[AL]}_i-k_{sa+}{[S]}_i{[A]}_i-k_{al+}{[A]}_i{[L]}_i-{\delta }_a{[A]}_i \end{gathered}$$ (Equation S3)

RNA Polymerase·σ Factor Complex (RS)

$$\begin{gathered} \mathit{complex}\mathit{association}-\mathit{complex}\mathit{dissociation}-\mathit{degradation} \\ \frac{d{[RS]}_i}{dt}=k_{rs+}[R]{[S]}_i-k_{rs-}{[RS]}_i-{\delta }_{rs}{[RS]}_i \end{gathered}$$ (Equation S4)

RNA Polymerase·σ^A Complex (RS_A)

$$\begin{gathered} \mathit{complex}\mathit{association}-\mathit{complex}\mathit{dissociation}-\mathit{degradation} \\ \frac{d{[RS]}_A}{dt}=k_{\mathit{rsA}+}[R]{[S]}_A-k_{\mathit{rsA}-}{[RS]}_A-{\delta }_{\mathit{rsA}}{[RS]}_A \end{gathered}$$ (Equation S5)

Anti-σ Factor·σ Factor Complex (SA)

$$\begin{gathered} \mathit{complex}\mathit{association}-\mathit{complex}\mathit{dissociation}-\mathit{degradation} \\ \frac{d{[SA]}_i}{dt}=k_{sa+}{[S]}_i{[A]}_i-k_{sa-}{[SA]}_i-{\delta }_{sa}{[SA]}_i \end{gathered}$$ (Equation S6)

Ligand (L)

$$\begin{gathered} \mathit{complex}\mathit{dissociation}-\mathit{complex}\mathit{association}-\mathit{degradation} \\ \frac{d{[L]}_i}{dt}=k_{al-}{[AL]}_i-k_{al+}{[A]}_i{[L]}_i-{\delta }_l{[L]}_i \end{gathered}$$ (Equation S7)

Anti-σ Factor·Ligand Complex (AL)

$$\begin{gathered} \mathit{complex}\mathit{association}-\mathit{complex}\mathit{dissociation}-\mathit{degradation} \\ \frac{d{[AL]}_i}{dt}=k_{al+}{[A]}_i{[L]}_i-k_{al-}{[AL]}_i-{\delta }_{al}{[AL]}_i \end{gathered}$$ (Equation S8)

The free amount of RNAP is given by the conservation law

$$[R]=R_{\mathit{tot}}-\sum _i{[RS]}_i$$ (Equation S9)

where the sum runs over all sigma factors, including the housekeeping sigma factor.

Finally, in order to randomly trigger pulses of sigma factor activation, the dynamics of the ligands are modified by adding the random quantity ε₀ (exponentially distributed and uncorrelated between sigma factor species) at random times T₀ (uniformly distributed) throughout the simulation.

$$L(t)\to L(t)+{\epsilon }_{0}L(t)$$ (Equation S10)

The ligand bursts triggering the sigma factor pulses could in principle have an origin external or internal to the cells. An external perturbation would result in adjacent cells pulsing together. The fact that we did not observe sister cells pulsing together on agarose pads (Figure S2A) argues against an external origin for pulsing. Similarly, a cell experiencing a large enough internal ligand perturbation would pulse, but its daughter cells would also inherit this pulse-inducing molecule, meaning they would pulse as well. Thus, under these conditions a pulse in the parent cell increases the probability of pulsing in the daughter cells, something not observed experimentally (Figure S2B).

Based on these considerations, we implemented a different type of internal perturbation, in which it is the sharp change in the concentration of the ligand that is critical for pulse generation. Here, a sharp rise in ligand concentration sequesters the anti-sigma factor, which in turn frees up its cognate sigma factor to bind RNAP (Figure S4B). The sigma-RNAP complex creates more sigma factors via positive autoregulation, which sustains the pulse even when the ligand is no longer present. In other words, the ligand itself is not strictly necessary once the chain of events is initiated. In this scenario, we do not expect a parent cell’s pulse to increase the chances of its daughters pulsing, consistent with observations.

Model Parameters

Given the current limitations in what is known about the regulation of alternative sigma factors, we lack sufficient information to construct a biochemically detailed model without introducing many unverified assumptions and unknown parameters. Therefore, the goal of the model is not to represent the complete complexity of the system, but rather to show that under a minimal set of assumptions that incorporate features common to many sigma factors, dynamics like those observed experimentally could occur. We selected biologically reasonable values for model parameters, shown in the table below. In particular, the decay rate of all species is assumed to correspond to the cell division time, here considered to be 1 hour (that is, we assume dilution dominates degradation for protein removal). The ligand burst sizes and total RNAP concentration are chosen to correspond to abundances on the order of 10⁴ molecules per cell. The relative expression rates (both basal and regulated) of the anti-sigma factors with respect to their corresponding cognate sigma are chosen on the order of 1.5, based on previous work (Li et al., 2014) showing that anti-sigma factors can be produced at higher rates than sigma factors. Finally, the sigma factor-RNAP dissociation constant is assumed to be 10-fold lower for the housekeeping sigma factor than for the alternative sigma factors, following existing literature (Sharma and Chatterji, 2010).

Reaction	Parameter	Description	Reactant(s)	Value	Value
				Set A	Set B
Basal transcription	αs	Basal rate	alternative σ factor	1.5 nM/min	1.5 nM/min
	αsA	Basal rate	housekeeping σ factor σA	180 nM/min	180 nM/min
	αa	Basal rate	anti-σ factor	2.3 nM/min	2.25 nM/min
Up-regulation	βs	Transcription rate	alternative σ factor	0.06 min−1	0.06, 0.06, 0.06, 0.06, 0.084 min−1
	βsA	Transcription rate	σA	6×10−4 min−1	6×10−4 min−1
	βa	Transcription rate	anti-σ factor	0.09 min−1	0.09 min−1
Association	krs+	Binding rate	RNAP, σ factor	0.03 nM−1 min−1	0.03, 0.0091, 0.003, 0.0091, 0.03 nM−1 min−1
	krsA+	Binding rate	RNAP, σA	0.3 nM−1 min−1	0.3 nM−1 min−1
	ksa+	Binding rate	σ factor, anti-σ factor	0.024 nM−1 min−1	0.024, 0.001716, 0.024, 0.0024, 0.024 nM−1 min−1
	kal+	Binding rate	anti-σ factor, ligand	0.018 nM−1 min−1	0.018 nM−1 min−1
Dissociation	krs−	Unbinding rate	RNAP·σ factor complex	0.3 min−1	0.3, 0.99, 3, 0.99, 0.3 min−1
	krsA−	Unbinding rate	RNAP·σA factor complex	0.3 min−1	0.3 min−1
	ksa−	Unbinding rate	σ factor·anti-σ factor complex	0.06 min−1	0.06 min−1
	kal−	Unbinding rate	anti-σ factor·ligand complex	0.03 min−1	0.03 min−1
Degradation	δs	Degradation rate	alternative σ factor	0.0167 min−1	0.0167 min−1
	δsA	Degradation rate	housekeeping σA factor	0.0167 min−1	0.0167 min−1
	δa	Degradation rate	anti-σ factor	0.0167 min−1	0.0167 min−1
	δrs	Degradation rate	RNAP·σ factor complex	0.0167 min−1	0.0167 min−1
	δrsA	Degradation rate	RNAP·σA complex	0.0167 min−1	0.0167 min−1
	δsa	Degradation rate	σ factor·anti-σ factor complex	0.0167 min−1	0.0167 min−1
	δal	Degradation rate	anti-σ factor·ligand complex	0.0167 min−1	0.0167 min−1
	δl	Degradation rate	ligand	0.0167 min−1	0.0167 min−1
Total RNAP	Rtot	Concentration	RNAP	12.6 μM	12.6 μM
Burst size	ε0	Concentration	ligand	10 μM	10 μM
Burst frequency	T0	Rate	ligand	3.33×10−3min−1	3.33×10−3min−1

Analytical Minimal Model of Competing Sigma Factors

Here we introduce a minimal model of an arbitrary number sigma factors competing for binding to a common pool of core RNAP, dispensing with the regulatory features of the sigma factors captured in the more detailed computational model (main text). We derive the analytical form of the cross-correlation function of the steady-state fluctuations in the bound fractions of the sigma factors, in terms of the microscopic parameters of the model (abundances of the molecular species and their binding/unbinding rates). For the case of three or more sigma factors we show that, counter-intuitively, under some parameter regimes it is possible for certain pairs of sigma factors to exhibit positive correlations in their fluctuations.

First, we write down the rate equations for the dynamics of binding and unbinding of two species with a common factor (the core RNAP). The following notation will be used:

• σ₁: total concentration of sigma factor 1 (bound or unbound).

• σ₂: total concentration of sigma factor 2 (bound or unbound).

• p: total concentration of the core RNAP (bound or unbound).

• n₁: fraction of core RNAP molecules that are bound by sigma factor 1. Note that the concentration of bound sigma 1 is simply n₁p.

• n₂: fraction of core RNAP molecules that are bound by sigma factor 2.

We also define:

• c₁: ratio of abundance of total core RNAP to total sigma factor 1, p/σ₁.

• c₂: ratio of abundance of total core RNAP to total sigma factor 2, p/σ₂.

The key attribute of the binding and unbinding equations is the competition between the two sigma factors. Namely, if a core RNAP molecule is bound by sigma factor 1 then it is not available for binding with sigma factor 2, and vice-versa.

The equation takes the form,

$$p\frac{d{n}_1}{dt}=f_1({\sigma }_1-p{n}_1)p(1-n_1-n_2)-l_{1}p{n}_1$$ (Equation S11)

This equation can be simplified by dividing both sides by p and redefining the forward rate constant as k₁ = f₁σ₁.

$$\frac{d{n}_1}{dt}=k_1(1-c_1{n}_1)(1-n_1-n_2)-l_1{n}_1$$ (Equation S12)

The binding/unbinding dynamics of sigma factor 2 can be described by a similar equation. Taken together, we have a coupled set of ODEs for the fraction of core RNAP bound by each type of sigma factor:

$$\begin{gathered} \frac{d{n}_1}{dt}=k_1(1-c_1{n}_1)(1-n_1-n_2)-l_1{n}_1 \\ \frac{d{n}_2}{dt}=k_2(1-c_2{n}_2)(1-n_1-n_2)-l_2{n}_2 \end{gathered}$$ (Equation S13)

To find the steady-state values of the fractional occupation of core RNAP by each sigma factor, we set the left-hand side of the above equations to zero and solve for n₁ and n₂:

$$\begin{gathered} k_1(1-c_1{\overline{n}}_1)(1-{\overline{n}}_1-{\overline{n}}_2)-l_1{\overline{n}}_1=0 \\ {k}_2(1-c_2{\overline{n}}_2)(1-{\overline{n}}_1-{\overline{n}}_2)-l_2{\overline{n}}_2=0 \end{gathered}$$ (Equation S14)

n̄₁ and n̄₂ depend on the values of the parameters k_i, l_i and c_i, with i = 1,2.

To introduce fluctuations in the above equations, we consider small thermal fluctuations that result in changes in the rate constants k_i→k_i + δk and l_i→l_i + δl_i. We then compute the resulting fluctuations in the occupation fractions around the steady-state values n_i→n_i + δn_i. Assuming that the fluctuations are small, we can expand the above equations to first order in δk_i, δl_i and δn_i, which leads to

$$\frac{d\delta n_1}{dt}=[-k_1{c}_1(1-{\overline{n}}_1-{\overline{n}}_2)-k_1(1-c_1{\overline{n}}_1)-l_1]\delta n_1+[-k_1(1-c_1{\overline{n}}_1)]\delta n_2+[(1-c_1{\overline{n}}_1)(1-{\overline{n}}_1-{\overline{n}}_2)]\delta k_1-{\overline{n}}_1\delta l_1$$ (Equation S15)

A similar equation can be written for the fluctuations in the core RNAP occupation fraction of sigma factor 2, δn₂. For brevity, only equations for sigma factor 1 are shown.

Assuming that binding and unbinding fluctuations occur at equilibrium, the forward and reverse rates are related through the free energy change of the reaction,

$$\frac{k_1}{l_1}=\mathit{exp}\left(\frac{F_1}{k_{B}T}\right),$$ (Equation S16)

where k_BT is the Boltzmann constant multiplied by the temperature of the system. The change in free energy of binding can also fluctuate from thermal kicks F₁→F₁ + δF₁. Assuming small fluctuations, linearizing the above equation gives the relationship between fluctuations of the rate constants and fluctuations in the change in free energy of the reaction.

$$\frac{\delta k_1}{k_1}-\frac{\delta l_1}{l_1}=\frac{\delta F_1}{k_{B}T}$$ (Equation S17)

Inserting Equation S17 into Equation S15 and simplifying gives

$$\frac{d\delta n_1}{dt}=[-k_1{c}_1(1-2{\overline{n}}_1-{\overline{n}}_2)-k_1-l_1]\delta n_1+[-k_1(1-c_1{\overline{n}}_1)]\delta n_2+{\overline{n}}_1{l}_1\frac{\delta F_1}{k_{B}T}$$ (Equation S18)

Finally, to get rid of the time-derivative on the left-hand side, we consider the fluctuations in the frequency domain, defining $\delta {\stackrel{\sim }{n}}_1(\omega )={\int }_0^{\infty }\delta n_1(t)e^{i\omega t}dt$. Taking the Fourier transfer of both sides of the above equation gives,

$$-i\omega \delta {\stackrel{\sim }{n}}_1(\omega )=[-k_1{c}_1(1-2{\overline{n}}_1-{\overline{n}}_2)-k_1-l_1]\delta {\stackrel{\sim }{n}}_1(\omega )+[-k_1(1-c_1{\overline{n}}_1)]\delta {\stackrel{\sim }{n}}_2(\omega )+{\overline{n}}_1{l}_1\frac{\delta F_1}{k_{B}T}$$ (Equation S19)

The two coupled equations for fluctuations in the bound fractions of sigma factors 1 and 2 can be succinctly represented in matrix form.

$$\left[\begin{array}{c}\delta {\stackrel{\sim }{F}}_1\\ \delta {\stackrel{\sim }{F}}_2\end{array}\right]=k_{B}T\left[\begin{array}{cc}\frac{-i\omega +k_1{c}_1(1-2{\overline{n}}_1-{\overline{n}}_2)+k_1+l_1}{{\overline{n}}_1{l}_1}& \frac{1}{1-{\overline{n}}_1-{\overline{n}}_2}\\ \frac{1}{1-{\overline{n}}_1-{\overline{n}}_2}& \frac{-i\omega +k_2{c}_2(1-{\overline{n}}_1-2{\overline{n}}_2)+k_2+l_2}{{\overline{n}}_2{l}_2}\end{array}\right]\left[\begin{array}{c}\delta {\stackrel{\sim }{n}}_1\\ \delta {\stackrel{\sim }{n}}_2\end{array}\right]$$ (Equation S20)

We can present the above equation in a more compact form by introducing the matrix Λ.

$$\delta \stackrel{\sim }{\mathbf{F}}=\mathrm{\Lambda }\delta \stackrel{\sim }{\mathbf{n}}$$ (Equation S21)

Equation S21 relates fluctuations in core RNAP occupation fraction δn to fluctuations in the free energy δF. This is a linear response relation, with the free energy playing the role of the driving force (Bialek and Setayeshgar, 2005; Hormoz, 2013). From this relationship, we can calculate the power-spectrum of fluctuations in n by using the fluctuation dissipation theorem, which relates the rate of decay of correlations to the response function (Bialek and Setayeshgar, 2005; Hormoz, 2013; Kubo, 1966)

$$S(\omega )=\frac{2k_{B}T}{\omega }\mathfrak{J}\left({\mathrm{\Lambda }}^{-1}\right)$$ (Equation S22)

𝔍 denotes the imaginary part of the inverse of matrix Λ. From S we can compute the covariance matrix,

$$\langle \delta n_i(t)\delta n_j(t+\tau )\rangle ={\int }_{-\infty }^{\infty }\frac{d\omega }{2\pi }{S}_{ij}(\omega )e^{-i\omega \tau }.$$ (Equation S23)

The left-hand side of the above equation is the quantity measured in the experiments, namely, the cross-correlation of fluctuations in the fraction of bound sigma factors. The right-hand side is an analytical expression in terms of the parameters of the model (Equation S13) and the abundance (c_i) and binding and unbinding rate constants (k_i and l_i) of each sigma factor.

Extension to an Arbitrary Number of Sigma Factors

We now extend the above results for two sigma factors to an arbitrary number N of sigma factors simultaneously competing for binding to the same pool of core RNAP. As before, the dynamics of sigma factor i is described by three relevant parameters: its abundance c_i (with respect to total core RNAP concentration), and its binding and unbinding rate constants to core RNAP, k_i and l_i respectively.

In analogy with Equation S13, the rate of change of the fraction of core RNAP bound by sigma factor i is given by,

$$\frac{d{n}_i}{dt}=k_i(1-c_i{n}_i)\left(1-\sum _{j=1}^N{n}_j\right)-l_i{n}_i$$ (Equation S24)

where $1-{\sum }_{j=1}^N{n}_j$ is the total fraction of unbound core RNAP.

Similarly, Equation S18 can also be easily generalized to the case of N sigma factors.

$$\frac{d\delta n_i}{dt}=\left[-k_i{c}_i\left(1-{\overline{n}}_i-\sum _{j=1}^N{\overline{n}}_j\right)-k_1-l_1\right]\delta n_i+[-k_i(1-c_i{\overline{n}}_i)]\left(\sum _{k\ne i}^N\delta n_k\right)+{\overline{n}}_i{l}_i\frac{\delta F_i}{k_{B}T}$$ (Equation S25)

where the ${\displaystyle \sum _{k\ne i}}$–denotes summation of k for all values of 1 to N except for i. n_i is the steady-state of the bound fraction of sigma factor i, and satisfies the equation

$$k_i(1-c_i{\overline{n}}_i)\left(1-\sum _{j=1}^N{\overline{n}}_j\right)-l_i{\overline{n}}_i=0$$ (Equation S26)

Equation S21, which relates the fluctuations in bound fraction of core RNAP to fluctuations of the binding energy of each sigma factor, still holds in matrix form. For N sigma factors, the matrix Λ takes the form,

$$\left[\begin{array}{cccc}\frac{-i\omega +k_1{c}_1\left(1-{\overline{n}}_1-{\sum }_{j=1}^N{\overline{n}}_j\right)+k_1+l_1}{{\overline{n}}_1{l}_1}& \dots & \frac{1}{1-{\sum }_{j=1}^N{n}_j}& \dots \\ ⋮& & & \\ \frac{1}{1-{\sum }_{j=1}^N{n}_j}& \ddots & & \\ & & \frac{-i\omega +k_i{c}_i\left(1-{\overline{n}}_i-{\sum }_{j=1}^N{\overline{n}}_j\right)+k_i+l_i}{{\overline{n}}_i{l}_i}& \\ ⋮& & & \ddots \end{array}\right]$$ (Equation S27)

Note that all the off-diagonal entries of the matrix are equal to $1/(1-{\sum }_{j=1}^N{n}_j)$.

Finally, the spectral density of the fluctuations can be calculated as before using the fluctuation-dissipation theorem.

$$S(\omega )=\frac{2k_{B}T}{\omega }\mathfrak{J}\left({\mathrm{\Lambda }}^{-1}\right)$$ (Equation S28)

Cross-correlation functions can be obtained by taking the Fourier transform of S,

$$\langle \delta n_i(t)\delta n_j(t+\tau )\rangle ={\int }_{-\infty }^{\infty }\frac{d\omega }{2\pi }{S}_{ij}(\omega )e^{-i\omega \tau }$$ (Equation S29)

Nothing in the above derivation precludes the possibility of a mixture of positive and negative correlations for certain parameter regimes. Next, we demonstrate how positive correlations between certain pairs of sigma factors can emerge in the case of three sigma factors.

Example: Three Sigma Factors

Consider three sigma factors competing for binding to the same pool of core RNAP (Figure 5D), with the following parameter values: k_i = l_i = 50 for i = 1,2, k₃ = l₃ = 1, c₁ = c₂ = c₃ = 1. These parameters imply that the abundances of the three sigma factors are equal. However, the binding and unbinding rates of the first two sigma factors to RNAP are faster than that of sigma factor 3. Therefore, the fraction of core RNAP bound by sigma factor 3 fluctuates at a time scale longer than that of the other two sigma factors.

To obtain analytical expressions for the correlation functions, we used Equation S22 to calculate S₁₂(ω), S₁₃(ω), and S₂₃(ω) for the above parameters (Figure S7A). As expected, S₁₃(ω) is the same as S₂₃(ω), and both functions are negative, indicating that fluctuations of the bound fraction of sigma factor 3 are negatively correlated with those of the other two sigma factors. This is not surprising, since competition for binding implies that if a larger fraction of core RNAP is bound by sigma factor 3, then a smaller fraction ought to be bound by sigma factors 1 and 2, resulting in negative correlations. However, the power spectrum of the correlation function between sigma factors 1 and 2 is positive for low frequencies. This implies that fluctuations of bound fractions of sigma factors 1 and 2 can be positively correlated over sufficiently long time scales.

To better understand the resulting correlations, we used Equation S23 to convert the calculated spectral densities to cross-correlation functions, C_ij(τ) = 〈δn_i(t)δn_j(t+τ)〉, by taking their inverse Fourier transforms (Figure 5E). As expected, for all lag times τ the cross-correlation function between sigma factor 3 and the other two sigma factors is negative. However, fluctuations between sigma factors 1 and 2 are positively correlated for sufficiently large lag times τ.

We now ask what is the physical origin of the positive correlations between sigma factors 1 and 2. These two sigma factors 1 and 2 follow the dynamics of the slower sigma factor 3. For example, if the fraction of bound sigma factor 3 fluctuates below its steady state value then sigma factors 1 and 2 are both more likely to be found bound to core RNAP. Hence, fluctuations in the bound fraction of sigma factors 1 and 2 are expected to be positively correlated over the time scales set by the binding/unbinding rates of sigma factor 3. Conversely, in the shorter time scale set by the binding/unbinding rates of sigma factors 1 and 2, the fraction of core RNAP bound to sigma factor 3 can be considered a constant. Over these times scales, sigma factors 1 and 2 compete for the remaining available core RNAP through exclusionary binding, and are therefore anti-correlated.

Finally, to validate the finding of positive and negative correlations at different time-scales, we directly simulated the equations of the simple model for N sigma factors, Equation S24, as stochastic differential equations (implemented in Matlab). An example trace is shown in Figure 5F. The bound fraction of sigma factors 1 and 2 are anti-correlated with that of sigma factor 3 but positively correlated with each other. For instance, an increase in the bound fraction of sigma factor 3 results in a decrease in the bound fractions of both sigma factors 1 and 2, resulting in positive correlations. Over shorter time scales, however, fluctuations in the bound fraction of sigma factors 1 and 2 are anti-correlated (inset in Figure 5F) as expected from competitive interactions. Critically, any readout of the bound fractions of the sigma factors that integrates over the shorter time scales (for example a fluorescent reporter) will only reveal the positive correlations at the longer time scales. Taken together, these results show that positive correlations between some pairs of sigma factors can arise from competitive binding interactions alone in some parameter regimes.

QUANTIFICATION AND STATISTICAL ANALYSIS

Image Analysis for Liquid Culture Snapshots

Quantitative image analysis of microscopy images was performed in MATLAB as described previously (Rosenfeld et al., 2005). Briefly, constitutive mCherry fluorescence was used as a segmentation channel, and cell edges were detected using a Laplacian of Gaussian filter. The segmentation masks identified with mCherry were then used to extract cell fluorescence values from other channels.

Image Analysis for Agarose Pad Movies

Quantitative movie analysis used custom image analysis code, the Schnitzcells software written in MATLAB, as described in previous work (Young et al., 2011). Briefly, cells were segmented on the constitutive mCherry using edge detection with a Laplacian of Gaussian filter. Cell masks were then manually corrected, tracked, and then the cell tracks were further manually corrected, all using Schnitzcells.

Image Analysis for Mother Machine Movies

Each microscope image contained multiple subchannels (lanes in the mother machine). We used custom MATLAB code to automatically identify subchannels, and crop them out into new image files. This was important not only to follow cells in individual subchannels, but to reduce the computational load of segmentation (described below).

Cell segmentation was accomplished using the Trainable Weka Segmentation plugin in Fiji, and was automated using a custom Beanshell script inside Fiji. We were careful to train the plugin to accurately separate adjacent cells. Cell tracking of the mother cell was done in MATLAB, where for every frame we took the mother cell at the ‘end’ of the channel. This tracking method produced accurate tracks except in cases of cell death or flickering segmentation, where a cell very dim in mCherry could be segmented in one frame but not the next, leading to a tracking error. To correct tracking errors, we used a custom MATLAB interactive system, based on one used previously (Lin et al., 2015). By manually searching for errors in cell length, we manually marked problematic tracks to be excluded from further analysis. Finally, extraction of cell fluorescence and other cell properties such as cell length were done in MATLAB.

Promoter Activity Calculation

Single-cell promoter activity was computed using previously reported methods (Locke et al., 2011), for both agarose pad and mother machine movies. Briefly, we are interested in finding the instantaneous rate of fluorescent protein production in individual cells. We calculate this quantity from timelapse microscopy by taking a time derivative of the fluorescent protein level in the cell. Consider a timelapse movie of a single growing B. subtilis cell expressing yfp. For the moment, let us ignore cell division, so we are simply considering the cell as it elongates along its major axis. We denote the total fluorescence of the cell T(t), the yfp promoter activity (i.e. production rate) P(t), and the combined rate of YFP photobleaching and degradation, γ. T(t) and P(t) are functions of time. The rate of YFP degradation rate is typically negligible. These variables are related to each other as follows:

$$T^{\prime }(t)=P(t)-\gamma T(t)$$ (Equation S30)

Here, the prime notation indicates a time derivative, and computing P(t) evidently requires measurement of the time derivative T’(t). Although we could try to differentiate T(t) from microscopy data, this can be sensitive to cell segmentation errors. As an alternative, we can replace T(t) with T(t) = M(t)V(t), where M(t) is the mean fluorescence of the cell, and V(t) is the cell volume. In addition, since B. subtilis grows lengthwise, we replace V(t) with V(t) = cL(t), where c is a constant and L(t) is the measured cell length at time t. The value c should be approximately equivalent to the cell’s cross-sectional area, but we will omit c in further calculations, since it will only change the final values by a constant factor, and fluorescence units are arbitrary to begin with. After substituting these 2 relationships into the above equation for T’(t), we can solve for P(t):

$$\begin{gathered} T^{\prime }(t)=P(t)-\gamma T(t) \\ {(M(t)V(t))}^{\prime }=P(t)-\gamma M(t)V(t) \\ {M}^{\prime }(t)V(t)+M(t)V^{\prime }(t)=P(t)-\gamma M(t)V(t) \\ {M}^{\prime }(t)L(t)+M(t)L^{\prime }(t)=P(t)-\gamma M(t)L(t) \\ P(t)=M^{\prime }(t)L(t)+M(t)L^{\prime }(t)+\gamma M(t)L(t) \\ \text{Promoter}\text{activity}\equiv \frac{P(t)}{L(t)}=M^{\prime }(t)+M(t)\frac{L^{\prime }(t)}{L(t)}+\gamma M(t) \end{gathered}$$ (Equation S31)

This final equation enables us to calculate the promoter activity, or sigma activity, defined as $\frac{P(t)}{L(t)}$, or the production rate per unit length of the cell. Sigma activity can be interpreted as the approximate protein production rate per chromosomal equivalent, allowing comparison of protein production through all points in the cell cycle. To compute time derivatives, the measured values of M(t) and L(t) were first smoothed to reduce noise (MATLAB smooth function with Lowess algorithm). For γ, we used a value of 0.05 as described previously (Locke et al., 2011).

Pulse Identification for Agarose Pad Movies

To automatically identify pulses from the promoter activity traces, we used custom MATLAB software (Locke et al., 2011). The code first identified local maxima (peaks) in the traces of promoter activity vs. time. A point in the trace was deemed a peak if its height was the largest within a window of 7 frames (frames were separated by time intervals of 10–15 min depending on the movie). In other words, a peak at time t_k must have height greater than all heights at times t_k−3 through t_k+3. For peaks near the start or end of the trace, the window size was decreased as necessary, e.g. a peak at timepoint t₃ was compared against t₀–t₆.

To suppress peaks arising from random fluctuations, the code utilized 2 additional parameters: 1) amplitude and 2) amplitude relative to baseline. The amplitude was defined as the height of the peak minus the average height of the 2 flanking minima surrounding the peak. The amplitude relative to baseline was defined as the height of the peak divided by the average height of the 2 flanking minima. The code rejected potential peaks whose amplitude is below the defined threshold of 7.5 arbitrary units (a.u.). The code also rejected peaks whose amplitude relative to baseline was less than 0.5 a.u. These two thresholds were chosen to avoid peak detection in timelapse data from a non-pulsatile P_hyperspank-yfp strain induced with IPTG, where the IPTG level was such that the average activity of the P_hyperspank-yfp was equal to that of the P_B-yfp strain at 40 μg/ml MPA. Note the P_hyperspank-yfp strain in movies shows only small fluctuations that are qualitatively distinct from the large pulses from the alternative sigma factor reporter strains. The results of automatic pulse detection were checked against raw data and the promoter activity traces and showed good agreement with manual identification of pulses.

Pulse Identification for Mother Machine Movies and Pulse Characteristic Calculations

Pulses were identified from promoter activity traces using MATLAB’s findpeaks function, where the minpeakdistance option was set to 5 to prevent double-counting peaks, and the minpeakheight option was set to 1.7 standard deviations above the mean activity to suppress detection of small fluctuations. Pulse identification showed good agreement with manual inspection of pulses.

Pulse characteristics were also found with MATLAB’s findpeaks function, which outputs the peak widths and peak amplitudes. The average pulse shape (Figure 2C) was found by taking each pulse, subtracting its baseline, and then dividing by the amplitude. The baseline was calculated by subtracting the pulse’s maximum value from the amplitude output by findpeaks. Data was pooled across multiple matrix strains carrying the same fluorescent reporter for any given sigma factor, resulting in at least 320 pulses per sigma factor. The normalized pulse amplitude distributions (Figure 2D) were normalized by the distribution mode.

Cross Correlation Functions, Pulse Triggered Averaging, and Pulse Amplitude Scatter Plots

All figure panels for the cross correlation functions (Figure 5A), pulse triggered averages (Figure S6) and amplitude scatter plots (Figure 5C) were calculated from the same underlying dataset, namely from the matrix strains grown in the mother machine. For each matrix strain, we obtained at least 73 single cell traces, each of which was > ~30 cell cycles in length.

Cross correlation functions (ccf) were calculated using MATLAB’s xcov function, with the ‘unbiased’ option, and were performed on mean fluorescence (not on promoter activity traces). To correct for long-term changes in sigma factor activity, the mean time trace was first subtracted from each trace. The cross-correlation function (ccf) for each trace was calculated separately, and the resulting set of ccf’s was averaged for Figure 5A. Each average ccf was calculated from at least 73 single cell traces.

The pulse triggered average plots (Figure S6) were also calculated from mean fluorescence traces. Each mean fluorescence time trace was first standardized by subtracting the mean trace and then dividing by the standard deviation. Peaks were computationally identified for one sigma factor (the ‘trigger’), and for each peak a time window in the other sigma factor (the ‘plotted’ sigma factor) was extracted. The time window was centered at the peak in the ‘triggered’ sigma. All such extracted time windows were averaged and then plotted. Thus, the same data set was used to generate multiple plots. For example, row 1, column 5 and row 5, column 1 were generated from the same underlying dataset: the P_B-cfp, P_D-yfp strain. Each trace is the average of at least 75 peaks, and the shaded error bars are s.e.m..

The scatter plots in Figure 5C were based on promoter activity traces from the matrix of reporter strains, analyzed in the mother machine (Figure 4). Pulses were identified using MATLAB’s findpeaks function, retaining only peaks above the mean promoter activity. Each point in the scatter represents a timepoint in which findpeaks identified a peak in either the CFP or YFP promoter activity traces (or both).

Deletion Matrix Experiments

Deletion matrix strains were inoculated into Spizizen’s minimal media, and grown overnight in 30 °C shaker. In the morning, strains were diluted back to OD₆₀₀ of 0.01, and grown for 2 hours at 37 °C. This cycle was repeated two more times. After the final back-dilution to OD₆₀₀ of 0.01, strains were grown until the OD₆₀₀ reached ~0.1, which took about 3 hours. MPA was then added to the media to a final concentration of 40 μg/ml. Strains were then grown for an additional 3 hours at 37 °C. Next, cells were transferred to 1.5% Agarose Pads, and imaged with fluorescence microscopy. Details of agarose pad preparation and microscopy were as described in section ‘Sample Preparation for Liquid Culture Snapshots and Agarose Pad Movies’ and section ‘Image Analysis for Liquid Culture Snapshots’.

DATA AND SOFTWARE AVAILABILITY

All data and software used in this manuscript are available upon request, for contact information see section ‘Contact for Reagent and Resource Sharing’.

ADDITIONAL RESOURCES

All relevant information, software, and data are provided in previous sections.

Highlights.

• Alternative sigma factors activate in repetitive pulses under constant conditions

• Time-lapse movies reveal positive and negative dynamic correlations

• Sigma factors appear to compete with different strengths for core RNAP

• Modeling shows competing pulsatile sigma factors can dynamically “time share” RNAP