Structure and topology of band structures in the 1651 magnetic space groups

Topological properties of band structures in magnetic materials are systematically studied using symmetry representations.

Abstract

The properties of electrons in magnetically ordered crystals are of interest both from the viewpoint of realizing novel topological phases, such as magnetic Weyl semimetals, and from the application perspective of creating energy-efficient memories. A systematic study of symmetry and topology in magnetic materials has been challenging given that there are 1651 magnetic space groups (MSGs). By using an efficient representation of allowed band structures, we obtain a systematic description of several basic properties of free electrons in all MSGs in three dimensions, as well as in the 528 magnetic layer groups relevant to two-dimensional magnetic materials. We compute constraints on electron fillings and band connectivity compatible with insulating behavior. In addition, by contrasting with atomic insulators, we identify band topology entailed by the symmetry transformation of bands, as determined by the MSG alone. We provide an application of our results to identifying topological semimetals arising in periodic arrangements of hedgehog-like magnetic textures.

INTRODUCTION

The recent discovery of topological insulators and other topological phases (1) has revitalized the venerable subject of band theory. In addition to the explosion of understanding of different forms of band topology and how symmetries protect or prevent them, researchers are making rapid progress on several other fronts. For example, fundamental questions, such as the connection between electron count and insulating behavior (2–10), as well as the constraints imposed by crystal symmetries on the connectivity of bands (3–5, 10–17), have been resolved. New information has also been gleaned by contrasting real-space and momentum-space descriptions in all 230 crystal space groups (SGs) of nonmagnetic materials (3–5, 8–10, 15, 16, 18).

Increasingly, attention is turning to electronic systems that combine magnetism with band topology. Here, a further panoply of novel topological phenomena is anticipated. Examples that scientists have already realized, to name just a few, include the quantized anomalous Hall effect in magnetic topological insulators (19, 20) and the topological Hall effect in skyrmion crystals (21–25). Researchers are also now studying magnetic Weyl semimetal candidates intensively (26–28). In addition to the fundamental physics interest of these novel phases, current-driven magnetic textures, such as domain walls or skyrmions, could be harnessed in technological applications, for example, in the development of energy-efficient memory devices (29).

Despite these strong motivations, the pace of discovery of magnetic topological materials has been relatively slow compared to their nonmagnetic counterparts. There are at least two reasons for this: First, magnetic materials are necessarily correlated, making the prediction of the magnetic structure and properties more challenging. Consequently, the set of well-characterized magnetic materials is relatively small. Second, the sheer complexity of combining magnetic structures with SGs makes an exhaustive study of the theoretical possibilities daunting. There are a total of 1651 different magnetic SGs (MSGs), which were only tabulated in the 1950s. In addition, unlike for the 230 nonmagnetic SGs (2, 30), relevant group-representation information is not always readily available.

Here, we will tackle the second problem by providing a systematic understanding of electronic band structures (BSs) in the 1651 MSGs. Inspired by the recent synthesis of atomically thin magnets (31, 32), we also discuss the 528 magnetic layer groups (MLGs), relevant to two-dimensional (2D) magnetic materials. We report the results for three key properties, which are tabulated in section S1 and described below.

First, we determine electron fillings that can be compatible with insulating behavior in all MSGs. The electron count is a fundamental characteristic of an electronic crystal. The presence of nonsymmorphic symmetries, such as glides and screws, enforces connectivity of bands that raises the required fillings for realizing band insulators (3–5, 12). These conditions may be useful in the search for magnetic Weyl semimetals, as one can target fillings that, while forbidding band insulators, are nonetheless consistent with nodal-point Fermi surfaces (13, 33, 34).

Next, it has long been known that representations of energy levels at high-symmetry points must connect in specific ways in obtaining a set of isolated bands (11). We can view this as a refinement of the filling condition, which imposes additional constraints on BSs (14–17). The solutions to these constraints are most conveniently represented as a vector space (but with integer coefficients, so more accurately a “lattice” in mathematical terminology) (14, 15, 35) and are described using only a handful of basis vectors whose precise number d_BS depends on the MSG.

Last, we contrast the general BSs defined in the momentum space with the subset of those obtained from “atomic insulators” (AIs), in which electrons are tightly bound to sites in the lattice furnishing orbitals with different symmetries. Significantly, we find that this produces a vector space of the same dimension, which in mathematical terms, is summarized by the equality d_AI = d_BS. However, the bases for BSs and AIs do not generally coincide, and we determine the classes of BSs that cannot be reduced to any atomic limit. This leads to an obstruction to finding symmetric localized Wannier states (36, 37) and corresponds to a band topology that one can diagnose without detailed information about the electronic wave functions. We give an example of how this can be used to diagnose topological semimetals and also an example of a nodal-line semimetal diagnosed through its filling. The latter consists of hedgehog-antihedgehog magnetic order with a lone electron at the core of these defects, leading to a gapless behavior.

We note that scientists have recently made a great deal of progress on related problems for nonmagnetic SGs (9, 10, 15, 16, 18). However, in the case of MSGs, these problems have only been attacked in certain restricted settings, for example, in generalizing the parity criterion (38) in order to identify Weyl semimetals, Chern insulators, and axion insulators (35, 39–42). In this study, we carry out a systematic study of all MSGs. In particular, it is important to emphasize that, although our approach has several features in common with K-theory–based classifications (14, 43–45), we do not seek to fully classify crystalline electronic phases here. As discussed in a recent insightful work (14) for 2D wallpaper groups, part of such a general classification includes band structure connectivities, a problem that has been posed since the early days of band theory (11). Using a result we proved below, we construct a framework that greatly simplifies these computations, which enables an extension of previous results (9, 10, 15) to the physically important case of MSGs.

In addition, topological distinctions revealed using our symmetry-based indicators fit naturally into well-established frameworks (14, 15, 43, 45) and remain stable upon the addition of trivial degrees of freedom. Yet, our approach is inherently symmetry-based, and so for crystals with low symmetry, that is, with only lattice translations, one cannot diagnose topological insulators without further knowledge of the wave functions. A similar caveat pertains to the complementary quantum chemistry approach of (16), which elaborates on the theory developed by (3), and takes a specific set of orbitals at fixed locations in the crystal as an input. While convenient for representing quantum chemistry information, it is less suited to capture stable topological distinctions that survive the inclusion of additional trivial bands. In addition, one forgoes the simplification arising from the vector space such as representation of energy bands that allowed us to generate results for all MSGs, while the work of Bradlyn et al. (16) is currently confined to just the 230 SGs.

MATERIALS AND METHODS

Magnetic BSs

Let us begin by reviewing some background materials concerning electronic BSs arising from a magnetic material. There are a total of 1651 MSGs and 528 MLGs (2, 30, 46–48). Among the 1651 MSGs, 230 of them were identical to SGs, in which only unitary spatial symmetries were considered (type I MSGs). All other MSGs had an equal number of unitary and antiunitary elements: $\mathcal{M}=\mathcal{G}+\mathcal{A}$. The unitary part $\mathcal{G}$ was identical to 1 of the 230 SGs, and the antiunitary part $\mathcal{A}$ could be generally written in the form $\tilde{\mathcal{T}}\mathcal{G}$, where $\tilde{\mathcal{T}}\equiv \mathcal{T}{\mathit{g}}_0$ is the product of a spatial operation g₀ and time reversal (TR) $\mathcal{T}$. When g₀ belongs to $\mathcal{G}$, the MSG is simply the direct product of an SG $\mathcal{G}$ and ${\mathbb{Z}}_2^{\mathcal{T}}$. This led to another 230 MSGs, one for each SG, that are called type II. When g₀ is not an element of $\mathcal{G}$, there are two types further differentiated by whether g₀ is a pure translation (type IV) or not (type III). For type II to IV MSGs, the little group of k and the site-symmetry group of x may also have an antiunitary part, in addition to the usual unitary part. Note that in the literature [for example, (49)], our definition of type III and IV MSGs are sometimes called type IIIa and IIIb, respectively. In addition, there are two common labeling schemes for MSGs: Opechowski-Guccione and Belov-Neronova-Smirnova (BNS). In this study, we followed the BNS notation, where an MSG was labeled by a pair of integers written as S. L, with S corresponding to 1 of the 230 SG and L corresponding to an extra label to differentiate between different magnetic descendants. [Refer to, for example, (50) for the precise meaning of these numbers.]

Next, we introduced a general formalism for the efficient analysis of BS properties based on representations of the little group (14, 15, 35). Our main focus here was to address how the formalism developed for SGs could be readily applied to MSGs. We defined a BS as a set of bands isolated from others by band gaps above and below at all high-symmetry momenta, where by a high-symmetry momentum, we referred to a k in the Brillouin zone at which the unitary part of the little group, ${\mathcal{G}}_{\mathit{k}}$, is necessarily larger than the translation subgroup T. In 3D, they can be high-symmetry points, lines, or planes. A BS can be characterized by the set of nonnegative integers $\mathit{n}=\{{\mathit{n}}_{\mathit{k}}^{\mathrm{\alpha }}\}$ that count the number of times an irreducible representation (irrep) ${\mathit{u}}_{\mathit{k}}^{\mathrm{\alpha }}$ of ${\mathcal{G}}_{\mathit{k}}$ appears. As we are interested in systems of spinful electrons, the irreps ${\mathit{u}}_{\mathit{k}}^{\mathrm{\alpha }}$ here are generally projective because of the spin-¹/₂ nature of electrons (also called “double-valued”). Since $\{{\mathit{n}}_{\mathit{k}}^{\mathrm{\alpha }}\}$ cannot be changed smoothly without gap closing or symmetry breaking, $\mathit{n}=\{{\mathit{n}}_{\mathit{k}}^{\mathrm{\alpha }}\}$ serves as “topological invariants” defined for each BS.

The integers $\mathit{n}=\{{\mathit{n}}_{\mathit{k}}^{\mathrm{\alpha }}\}$ cannot be chosen freely, since symmetries demand that they satisfy a collection of compatibility relations (2, 11). Since $\mathcal{G}$ is a subgroup of $\mathcal{M}=\mathcal{G}+\mathcal{A}$, the full list of compatibility relation $\mathcal{C}$ imposed on an $\mathcal{M}$-symmetric BS can be split into two sets, ${\mathcal{C}}_{\mathcal{G}}$ arising from $\mathcal{G}$ and ${\tilde{\mathcal{C}}}_{\mathcal{A}}$ from $\mathcal{A}$. Let us denote by ${\{\text{BS}\}}_{\text{phys}}^{\mathcal{G}}$ and {BS}_phys the set of all n’s satisfying ${\mathcal{C}}_{\mathcal{G}}$ and $\mathcal{C}$, respectively. Here, the subscript “phys” indicates that all ${\mathit{n}}_{\mathit{k}}^{\mathrm{\alpha }}$’s in $\mathit{n}=\{{\mathit{n}}_{\mathit{k}}^{\mathrm{\alpha }}\}$ are non-negative, which is required for interpreting them as the multiplicities of irreps in a physical BS. We will introduce another set ${\{\text{BS}\}}^{(\mathcal{G})}$ that relaxes this nonnegative condition later. Note that ${\{\text{BS}\}}_{\text{phys}}^{\mathcal{G}}$ and {BS}_phys differed only in the imposition of ${\tilde{\mathcal{C}}}_{\mathcal{A}}$. In general, the antiunitary part $\mathcal{A}$ requires a pairing of $\mathit{b}\in {\{\text{BS}\}}_{\text{phys}}^{\mathcal{G}}$ with another $\mathit{b}\prime \in {\{\text{BS}\}}_{\text{phys}}^{\mathcal{G}}$, unless b itself is already symmetric under $\tilde{\mathcal{T}}$. The pairing type can be easily determined using the Herring rule (2). (In section S4, we provided a more elaborated review on the compatibility relations and the Herring rule.)

Band topology

Having described some generalities about BSs, we now review how knowledge about the real space can inform band topology (9, 15). We defined the trivial class of BSs by the AIs, which were band insulators that were smoothly connected to a limit of vanishing hopping and hence were deformable to product states in real space. Equivalently, an AI admits symmetric, exponentially localized Wannier functions.

To specify an AI, one should choose a position x in real space at which electrons were localized and the type of the orbital put on that site. All inequivalent choices of the position x were classified by Wyckoff positions (51). The orbital can be chosen from the (co-)irreps of the site-symmetry group of x (section S5). Given these choices, an $\mathcal{M}$-invariant AI can be constructed by placing a symmetry-related orbital on each site of the $\mathcal{M}$-symmetric lattice and filling them by electrons. The AI has a specific combination of irreps in the momentum space, which automatically satisfies $\mathcal{C}={\mathcal{C}}_{\mathcal{G}}+{\tilde{\mathcal{C}}}_{\mathcal{A}}$. We listed up all distinct n’s corresponding to an AI by varying x and the orbital type. We listed up all distinct n’s corresponding to an AI by varying the position x and the orbital type, and we obtained {AI}_phys, a subset of {BS}_phys. If one replaces $\mathcal{M}$ above with $\mathcal{G}$, one gets the set of $\mathcal{G}$-symmetric AIs, ${\{\text{AI}\}}_{\text{phys}}^{\mathcal{G}}$.

Now, we are ready to tell which elements of {BS}_phys must be topologically nontrivial and which elements can be trivial. This can be judged by contrasting the elements of {BS}_phys with those in {AI}_phys. Namely, any b ∈ {BS}_phys not belonging to {AI}_phys necessarily features nontrivial band topology because, by definition, there does not exist any atomic limit of the BS with the same combinations of irreps. This is a sufficient (but not necessary) condition to be topologically nontrivial: Here, we exclusively focused on the band topology that can be diagnosed by the set of irreps at high-symmetry momenta.

The simplest way of exploring the nontrivial elements of {BS}_phys is thus to consider the complement of {AI}_phys in {BS}_phys, as in (15) and (52). However, this set has a complicated mathematical structure. To simplify the analysis, we allowed for the formal subtraction of bands and extended the values of ${\mathit{n}}_{\mathit{k}}^{\mathrm{\alpha }}$ to any integer, including the negative ones, à la a K-theory analysis. {BS}_phys then becomes an abelian group $\{\text{BS}\}={\mathbb{Z}}^{{\mathit{d}}_{\text{BS}}}$ (known as a “lattice” in the mathematical nomenclature) (14, 15, 35). In other words, there are d_BS basis “vectors” ${\{{\mathit{b}}_{\mathit{i}}\}}_{\mathit{i}=1}^{{\mathit{d}}_{\text{BS}}}$, and {BS} can be expressed as $\{{\sum }_{\mathit{i}=1}^{{\mathit{d}}_{\text{BS}}}{\mathit{m}}_{\mathit{i}}{\mathit{b}}_{\mathit{i}}|{\mathit{m}}_{\mathit{i}}\in \mathbb{Z}\}$. Similarly, by allowing negative integers when taking superposition of AIs, we got another abelian group $\{\text{AI}\}={\mathbb{Z}}^{{\mathit{d}}_{\text{AI}}}$, which is a subgroup of {BS}. The band topology we are interested in is now encoded in the quotient group

$${\mathit{X}}_{\text{BS}}\equiv \{\text{BS}\}/\{\text{AI}\}$$ (1)

dubbed the symmetry-based indicator of band topology (15). As we will see shortly, the quotient group is always a finite abelian group and hence must be a product of the form ${\prod }_{\mathit{i}}{\mathbb{Z}}_{{\mathit{n}}_{\mathit{i}}}$.

Constructing BSs from AIs

To compute X_BS, the natural first step was to identify ${\tilde{\mathcal{C}}}_{\mathcal{A}}$, the extra compatibility relations enforced by the antiunitary symmetries. Contrary to this expectation, we now show that, on the basis of our previous results on SGs, one can directly compute {BS} and X_BS for any MSG $\mathcal{M}$ without deriving ${\tilde{\mathcal{C}}}_{\mathcal{A}}$. This served to demonstrate the power of the present approach: Symmetry content and connectivity of BSs could be readily extracted without the large overheads mandated by the conventional approach.

To this end, we first revisited the relevant aspects of the theory for an SG $\mathcal{G}$. By definition, ${\{\text{AI}\}}^{\mathcal{G}}$ is a subgroup of ${\{\text{BS}\}}^{\mathcal{G}}$, and therefore, a priori, it could be the case that ${\mathit{d}}_{\text{AI}}^{\mathcal{G}}<{\mathit{d}}_{\text{BS}}^{\mathcal{G}}$ strictly. However, by an explicit computation for all the 230 SGs, Po et al. (15) found that ${\mathit{d}}_{\text{BS}}^{\mathcal{G}}={\mathit{d}}_{\text{AI}}^{\mathcal{G}}$ always holds. This statement has an important implication: Every $\mathit{b}\in {\{\text{BS}\}}^{\mathcal{G}}$ can be expanded as b = ∑_iq_ia_i with rational coefficients ${\mathit{q}}_{\mathit{i}}\in \mathbb{Q}$ using a basis ${\{{\mathit{a}}_{\mathit{i}}\}}_{\mathit{i}=1}^{{\mathit{d}}_{\text{AI}}^{\mathcal{G}}}$ of ${\{\text{AI}\}}^{\mathcal{G}}$. In other words, full knowledge of the group ${\{\text{BS}\}}^{\mathcal{G}}$ can be obtained from that of ${\{\text{AI}\}}^{\mathcal{G}}$.

On the basis of this result for SGs, we will now prove the same statement, namely, d_BS = d_AI, for any MSG $\mathcal{M}$. This result enabled us to efficiently compute {BS} and X_BS for all MSGs and MLGs using only information contained in {AI}, which could be readily extracted from the tabulated Wyckoff positions (46–48).

Our proof was centered on the following observation: Recall $\mathcal{M}=\mathcal{G}+\mathcal{A}$, where $\mathcal{G}$ is unitary and $\mathcal{A}=\tilde{\mathcal{T}}\mathcal{G}$ is the antiunitary part generated by $\tilde{\mathcal{T}}=\mathcal{T}{\mathit{g}}_0$ for some spatial symmetry g₀. Note that, for type II MSGs, ${\mathit{g}}_0\in \mathcal{G}$ and can be chosen to be the identity, whereas for types III and IV, ${\mathit{g}}_0\stackrel{/}{\in }\mathcal{G}$. Now, consider a $\mathcal{G}$-symmetric collection of fully filled local orbitals in real space, which defines an AI $\mathit{a}\in {\{\text{AI}\}}_{\text{phys}}^{\mathcal{G}}$. This AI is not generally symmetric under $\mathcal{M}$,; that is, it may not be invariant under the action of $\tilde{\mathcal{T}}$. However, if we stack it together with its $\tilde{\mathcal{T}}$-transformed copy, we will arrive at an $\mathcal{M}$-symmetric AI. Algebraically, this means $\mathit{a}+\tilde{\mathcal{T}}\mathit{a}\in {\{\text{AI}\}}_{\text{phys}}$.

In the momentum space, a similar symmetrization procedure could be performed on the representation content. Suppose that {|k, i〉} is a basis of an irrep ${\mathit{u}}_{\mathit{k}}^{\mathrm{\alpha }}$ of ${\mathcal{G}}_{\mathit{k}}$. Then, the $\tilde{\mathcal{T}}$-transformed copy, $\{\tilde{\mathcal{T}}|\mathit{k}\mathit{i}\rangle \}$, forms a basis of an irrep ${\mathit{u}}_{\mathit{k}\prime }^{\mathit{\alpha }\prime }$ of ${\mathcal{G}}_{\mathit{k}\prime }$ (section S4). When b represents a BS that contains ${\mathit{u}}_{\mathit{k}}^{\mathrm{\alpha }}{\mathit{n}}_{\mathit{k}}^{\mathrm{\alpha }}$-times, we denote by $\tilde{\mathcal{T}}\mathit{b}$ a BS that contains ${\mathit{u}}_{\mathit{k}\prime }^{\mathit{\alpha }\prime }$ the same number of times. For any $\mathit{b}\in {\{\text{BS}\}}^{\mathcal{G}}$, $\mathit{b}+\tilde{\mathcal{T}}\mathit{b}$ satisfies the compatibility conditions ${\tilde{\mathcal{C}}}_{\mathcal{A}}$ and hence belongs to {BS}. We presented the explicit form of $\tilde{\mathcal{T}}\mathit{b}$ in section S6.

We are now ready to prove the statement. Observe that any B ∈ {BS} also belongs to ${\{\text{BS}\}}^{\mathcal{G}}$, and as ${\mathit{d}}_{\text{BS}}^{\mathcal{G}}={\mathit{d}}_{\text{AI}}^{\mathcal{G}}$, it can be expanded on the basis of ${\{\text{AI}\}}^{\mathcal{G}}$

$$\mathit{B}={\displaystyle {\sum }_{\mathit{i}}}{\mathit{q}}_{\mathit{i}}{\mathit{a}}_{\mathit{i}},{\mathit{q}}_{\mathit{i}}\in \mathrm{\mathbb{Q}}$$ (2)

Now, we symmetrize both sides of Eq. 2 by $\tilde{\mathcal{T}}$. Since B is $\mathcal{M}$-invariant, $\mathit{B}+\tilde{\mathcal{T}}\mathit{B}=2\mathit{B}$, so

$$\mathit{B}=\frac{1}{2}(\mathit{B}+\tilde{\mathcal{T}}\mathit{B})={\displaystyle {\sum }_{\mathit{i}}}\frac{1}{2}{\mathit{q}}_{\mathit{i}}({\mathit{a}}_{\mathit{i}}+\tilde{\mathcal{T}}{\mathit{a}}_{\mathit{i}})$$ (3)

As argued, ${\mathit{a}}_{\mathit{i}}+\tilde{\mathcal{T}}{\mathit{a}}_{\mathit{i}}\in \{\text{AI}\}$ (note that linearity was invoked when we extended the argument form ${\{\text{AI}\}}_{\text{phys}}^{\mathcal{G}}$ to a general element of ${\{\text{AI}\}}^{\mathcal{G}}$). This proves that any B ∈ {BS} can be expanded in terms of {AI} (using rational coefficients), an equivalent statement of d_AI = d_BS. Furthermore, it implies that the quotient group X_BS = {BS}/{AI} does not contain any $\mathbb{Z}$-factor and hence is a finite abelian group of the form ${\prod }_{\mathit{i}}{\mathbb{Z}}_{{\mathit{n}}_{\mathit{i}}}$.

To summarize, we showed that the set of AIs and BSs was identical as far as their dimensionality goes. This is a powerful statement, since it means that we could simply focus on AIs, study their symmetry representations in momentum space, and then take rational combinations to generate all BSs. However, we caution that one has to properly rescale the entries of n when an irrep is paired with another copy of itself according to the Herring rule. For full details of the treatment, we refer interested readers to (15).

Following this strategy, we performed the first calculation of d_BS, X_BS, and ν_BS for all of the 1651 MSGs and 528 MLGs. The full list of the computation results are tabulated in tables S1 to S7. For readers’ convenience, we reproduced a few examples from these tables in Tables 1 and 2.

Table 1. Characterization of BSs in a MSG (excerpt from tables S1 to S6).

MSG*		d†	XBS‡	νBS§
2.4	I	9	(2, 2, 2, 4)	1
2.7	IV	5	(2)	2
3.4	IV	3	(2)	2
209.51	IV	3	(1)	2a

*MSG number in the BNS notation, followed by a Roman numeral I, …, IV indicating its type.

†Number of linearly independent BSs.

‡Symmetry-based indicator of band topology, which takes the form ${\prod }_{\mathit{i}}{\mathbb{Z}}_{{\mathit{n}}_{\mathit{i}}}$, denoted by the collection of positive integers (n₁, n₂, ⋯).

^§For most of the MSGs, the set of physical BS fillings {ν}_BS and the set of AI fillings {ν}_AI agree with each other, and they take the form ${\{\mathrm{\nu }\}}_{\text{BS}}={\{\mathrm{\nu }\}}_{\text{AI}}={\mathrm{\nu }}_{\text{BS}}\mathbb{N}$. The superscript letter a indicates violation to this rule, as detailed in table S8.

Table 2. Characterization of MLGs through the corresponding MSG (excerpt from table S7).

MSG*		d†	XBS†	vBS†
2.5 (1)	II	5	(2)	2
2.5 (2)	II	5	(2)	2
2.5 (3)	II	5	(2)	2
3.4 (1)	IV	3	(2)	2
3.4 (2)	IV	2	(1)	2

*The numbers in parentheses label the different ways to project the MSG down to 2D planes (section S7).

†Defined as in Table 1.

RESULTS

Representation-enforced semimetals

As an application of our results, here, we introduce new classes of representation-enforced semimetals (reSMs). A BS is said to be a reSM when (i) there are gap closings at some generic (that is, not high symmetry) momenta in the Brillouin zone and (ii) the gaplessness is mandated by the combination of irreps at high-symmetry momenta. Note that only unitary symmetries are incorporated in defining a high-symmetry momentum, and the notion of a BS only requires a continuous gap at all high-symmetry points, lines, and planes. reSMs arise when the topological band gap closings are buried in the low-symmetry regions of the Brillouin zone, rendering them hard to diagnose in conventional electronic structure calculations, but are nonetheless readily detectable and are robust against numerical uncertainty because of their representation-enforced nature. All previously known examples of reSMs concern TR-broken systems in 3D with either the inversion (35, 41) or $\overline{4}$ rotation symmetry (42). The new classes we propose here are realized in spin-orbit–coupled systems in 2D or 3D and are associated with type III or IV MSGs.

Our example is the type IV MSG 3.4 (P_a112) that is generated by C_2z (the π rotation about z axis) and $\tilde{\mathcal{T}}\equiv \mathcal{T}{\mathit{T}}_{\frac{1}{2}{\mathit{a}}_1}$ (half translation by $\frac{1}{2}{\mathit{a}}_1$, followed by TR) apart from lattice translations. (The type III MSG 13.69 can also host a Dirac semimetal by means of a nearly identical mechanism; see section S8.) According to Table 1, this MSG has two classes of combinations of C_2z eigenvalues, as indicated by ${\mathit{X}}_{\text{BS}}={\mathbb{Z}}_2$. As we shall see now, the 3D BS belonging to this nontrivial class hosts at least four Weyl points, where the Weyl points with opposite charities are maximally separated in the k₃ direction.

To understand this band topology step by step, let us first remove the lattice translation in z and take a single layer parallel to the xy plane. The MSG then reduces to the MLG p_a112, which corresponds to the entry 3.4 (1) in Table 2 with ${\mathit{X}}_{\text{BS}}={\mathbb{Z}}_2$. The rotation C_2z is a symmetry at the four TR-invariant momenta (TRIMs) of the 2D BZ, whose eigenvalues are either ± i for spinful electrons. When k₁ = 0, the antiunitary symmetry $\tilde{\mathcal{T}}$ with ${\tilde{\mathcal{T}}}^2={(-1)}^{\widehat{\mathit{F}}}{\widehat{\mathit{T}}}_{{\mathit{a}}_1}=-1$ demands the pairing of the two eigenvalues of C_2z. In contrast, when k₁ = π, ${\tilde{\mathcal{T}}}^2=+1$, and no pairing is required. For this MLG, ${\mathit{X}}_{\text{BS}}={\mathbb{Z}}_2$, and the topological index distinguishing the two classes is given by

$$\mathrm{\eta }={\displaystyle \prod _{\mathit{n}:\text{occupied}}}{\displaystyle \prod _{\mathit{k}=(\mathrm{\pi },0),(\mathrm{\pi },\mathrm{\pi })}}{\mathrm{\eta }}_{\mathit{n},\mathit{k}}$$ (4)

where η_n,k is the C_2z eigenvalue of the n-th band. η = +1 for any AI, while η = −1 for nontrivial BSs. Note that this invariant is similar to those identified in some previous works (35, 38, 41, 42, 53).

Next, we show that the nontrivial BS with η = −1 corresponds to 2D magnetic Dirac reSMs (twofold degeneracy at the gapless point) enabled by a strong spin-rotation symmetry breaking, as illustrated in Fig. 1. Denoting the standard Pauli matrices by σ_0,…,3, the combined symmetry $\tilde{\mathcal{T}}{\mathit{C}}_{2\mathit{z}}$ dictates that the local 2-by-2 Hamiltonian h(k) near a gapless point takes the form

$$\mathit{h}(\mathit{k})={\displaystyle \sum _{\mathit{i}=0}^2}{\mathit{g}}_{\mathit{i}}(\mathit{k}){\mathrm{\sigma }}_{\mathit{i}}$$ (5)

that is, the σ₃ term is missing. Since the number of tunable parameters k₁ and k₂ is the same as the number of relevant coefficients [g₁(k) and g₂(k)], the gaplessness is stable against perturbations respecting the symmetries (54). To see this more explicitly, we note that the symmetry $\tilde{\mathcal{T}}{\mathit{C}}_{2\mathit{z}}$ quantizes the Berry phase $\mathit{B}({\mathit{k}}_1)={\int }_{-\mathrm{\pi }}^{\mathrm{\pi }}\mathit{d}{\mathit{k}}_2{\mathit{A}}_2({\mathit{k}}_1)$ to be 0 or π at any k₁. The topological index η = −1 dictates that B(0) ≠ B(π), implying the presence of a gap closing somewhere in 0 < k₁ < π. Using a k ⋅ p analysis, one can confirm that the bands disperse linearly, leading to a Dirac node. We note that, compared to the protection of Dirac node by an eigenvalue exchange of nonsymmorphic symmetries (34, 55–57), the present Dirac node has a more topological character.

Fig. 1. Magnetic reSM.

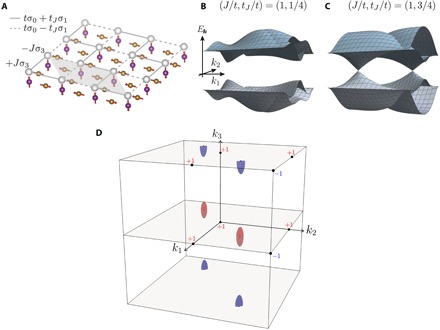
(A) Example tight-binding model for reSM. There are two sublattices per unit cell (shaded) due to an antiferromagnetic order m_x, producing a total of four bands. On-site potential J stands for the exchange coupling $-\mathit{J}{\mathit{m}}_{\mathit{x}}\cdot {\mathit{c}}_{\mathit{x}}^{†}\mathrm{\sigma }{\mathit{c}}_{\mathit{x}}$. In addition to the standard nearest-neighbor hopping t, a spin-dependent hopping ± t_Jσ_x is included, which can be viewed as originating from an exchange coupling to a magnetic moment in the middle of the nearest-neighbor bonds (section S8). (B) Dispersion relation at J/t = 1 and t_J/t = 1/4. In this case, η in Eq. 4 is +1, and the dispersion is gapped between the second and the third bands. (C) Dispersion relation at J/t = 1 and t_J/t = 3/4. Now, η = −1, and a pair of Dirac nodes exist as predicted. (D) Fermi surface of the 3D version of the reSM. The two Weyl points on the k₃ = 0 (k₃ = π) plane have the chirality +1 (–1), indicating a huge Fermi arc on some 2D surfaces. The signs on the TRIMs indicate the product of the C_2z rotation eigenvalues of occupied bands in this model.

Given this understanding of the 2D layer with MLG 3.4, let us now recover the third dimension by stacking the copies of 2D layers with generic interlayer couplings. The resulting BS, fully symmetric under MSG 3.4, host a total of four Weyl points: two on the k₃ = 0 plane and the other two on the k₃ = π plane, as depicted in Fig. 1D. Note that the two Weyl points on the k₃ = 0 plane are related by C_2z rotation (or equivalently in this setup, $\tilde{\mathcal{T}}$) symmetry and so must have the same chirality. Consequently, the two Weyl points on the k₃ = π plane have the opposite chirality. This large separation of the Weyl points with opposite chiralities dictates the presence of long Fermi arcs on the surface. Let us stress again that this nontrivial BS is indicated by the rotation eigenvalues at TRIMs via the formula in Eq. 4 applied to the k₃ = 0 plane of the 3D BS. This illustrates how the ideas described in the present work can guide the search for ideal magnetic Weyl semimetals. We leave a full analysis of magnetic reSMs to future works.

Filling-enforced semimetals

As another application of our theory, we attack the following problem: Given an MSG $\mathcal{M}$, what are the electron fillings ν at which band insulators are allowed? One of the primary interests in solving this problem lies in the search of topological semimetals: If a material has an electron filling incompatible with any band insulator, it must have symmetry-protected gaplessness near the Fermi energy, provided that a band theory description is applicable. We refer to these systems as filling-enforced (semi)metals. Once the MSG describing the magnetic order is identified, one can readily predict these systems using our results on ν_BS. For stoichiometric compounds with perfect crystalline order and commensurate magnetism, one can further show that spatial symmetries quantize the physically allowed fillings, which in turn, allows one to further diagnose the fermiology of the filling-enforced (semi)metals. We relegate a detailed discussion to section S2 and summarize the results on the predicted fermiology in tables S9 to S12.

While one can perform a systematic analysis of filling-enforced semimetals (feSMs) using the tables mentioned above, it is instructive to discuss a physical picture linking a real-space description of the magnetic ordering to the momentum-space obstruction to realizing any band insulator. To this end, we first contrast the effect of topologically trivial and nontrivial magnetic orders on local electronic energy levels. When the surrounding magnetic moments order ferromagnetically, as in Fig. 2A, the electronic levels are Zeeman-split and nondegenerate. In contrast, when the moments are arranged into the hedgehog defect shown in Fig. 2B, the magnetic point group symmetries at the defect core demand that all single-particle local energy levels exhibit even degeneracies; that is, such a magnetic order forbids a gapped state when a lone electron is localized to the defect core.

Fig. 2. Magnetic feSMs.

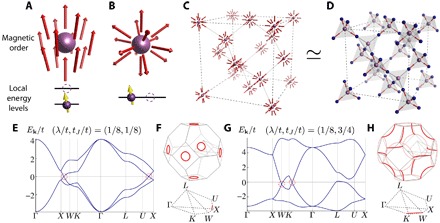
(A and B) Symmetries of a magnetic order can prohibit AIs at odd-site fillings. (A) The magnetic point group symmetries of a ferromagnetic arrangement are compatible with nondegenerate local energy levels. (B) However, those of the depicted hedgehog defect force all the energy levels to exhibit even degeneracies, which forbids AIs when a lone electron is localized to the purple site. (C) When hedgehog and antihedgehog defects are arranged into a diamond lattice, the previous argument suggests that no AI is allowed whenever the site fillings at the defect cores are odd. (D) The hypothetical magnetic structure in (C) could be realizable in spinel structures if the diamond sites are occupied by atoms with odd atomic numbers (purple) and the magnetic atoms (blue) at the pyrochlore sites exhibit an all-in-all-out magnetic order. (E to H) feSMs arising from the magnetically ordered Fu-Kane-Mele model (Eq. 6). (E) When the magnetically modulated hopping t_J is weak compared to the spin-orbit coupling λ, the fermiology is governed by rings of gap closing (circled in red), growing out from the original Dirac points at X when t_J = 0. (F) The positions of the rings in the Brillouin zone are shown in red. (G and H) For ${\mathit{t}}_{\mathit{J}}\ge 2\sqrt{2}\mathrm{\lambda }$, the nodal rings become connected at the momentum W. Thin lines indicate copies of the gapless momenta in the repeated zone scheme, included to illustrate the connectivity of the rings.

To be compatible with lattice translations, however, there must be a balance between defects and antidefects in each unit cell. An interesting situation arises when the positions of the defects and antidefects are further related by symmetries prohibiting them from annihilation. As an example, consider the diamond lattice with one sublattice occupied by hedgehog defects, and the other sublattice, symmetry-related to the first by a glide mirror, occupied by antihedgehogs (Fig. 2C). The symmetries of this system are described by MSG 227.131 (type III). Suppose the defect core (that is, the diamond sites) corresponds to an atom with an odd atomic number, which leads to an electron filling of ν = 2 mod 4 per primitive unit cell. According to the previous argument, it should be impossible to obtain an AI by localizing all the electrons. This suggests that the electron filling might lead to an obstruction to forming a band insulator and hence enforcing a (semi)metallic behavior. Our result of ν_BS = 4 for this MSG (table S6) implies that all band insulators are ruled out at the specified filling of ν = 2 mod 4. In table S10, we further see that this corresponds to a feSM with movable nodal features.

Curiously, the hypothetical structure depicted in Fig. 2C could be relevant for materials with the chemical formula AB₂O₄ taking the spinel structure, where the A atoms, occupying the diamond sites, are surrounded by the B atoms sitting at the pyrochlore positions. If the B atoms are magnetically ordered into the all-in-all-out configuration (Fig. 2D), it can be viewed as a lattice realization of the described hedgehog-antihedgehog lattice in MSG 227.131. This suggests the following tight-binding model as an example of the feSM described

$$\widehat{\mathit{H}}={\displaystyle \sum _{\langle \mathit{i}\mathit{j}\rangle }}{\widehat{\mathit{c}}}_{\mathit{i}}^{†}(\mathit{t}{\mathrm{\sigma }}_0+4{\mathit{t}}_{\mathit{J}}{\mathit{d}}_{\mathit{i}\mathit{j}}\cdot \mathrm{\sigma }){\widehat{\mathit{c}}}_{\mathit{j}}+\mathit{i}8\mathrm{\lambda }{\displaystyle \sum _{\langle \langle \mathit{i}\mathit{j}\rangle \rangle }}{\widehat{\mathit{c}}}_{\mathit{i}}^{†}({\mathit{d}}_{\mathit{l}\mathit{i}}\times {\mathit{d}}_{\mathit{l}\mathit{j}})\cdot \mathrm{\sigma }{\widehat{\mathit{c}}}_{\mathit{j}}$$ (6)

where ${\widehat{\mathit{c}}}_{\mathit{i}}$ and ${\widehat{\mathit{c}}}_{\mathit{i}}^{†}$ represent the fermion operators corresponding to an s-orbital localized to the diamond site i (spin indices are suppressed), 〈ij〉 and 〈〈ij〉〉, respectively, denote first- and second-nearest-neighbor bonds, and d_ij is the vector connecting the site j to i (the lattice constant of the conventional cell is set to 1). In the term ∝ λ, we let l denote the common nearest neighbor of i and j. Note that one can physically interpret t_J as a modulation of the nearest-neighbor hopping by exchange coupling with the magnetic moment at pyrochlore sites, and λ parameterizes the symmetry-allowed spin-orbit coupling between the second-nearest-neighbor sites.

When t_J = 0, Eq. 6 is TR-symmetric (corresponding to the type II MSG 227.129) and reduces to the undistorted Fu-Kane-Mele model defined on the diamond lattice hosting three symmetry-related Dirac points (table S9) (58). Unlike lattice distortions, which lead to topological insulators (58), TR-symmetry breaking described by t_J ≠ 0 leads to a feSM. The Dirac points in the original Fu-Kane-Mele model are unstable toward this perturbation, and our results indicate that the semimetallic behavior is enforced by a more delicate band connectivity (table S10). This is explicitly verified in the example BSs plotted in Fig. 2 (E to H), showing how the Dirac points split into (doubly degenerate) nodal rings as t_J increases from 0.

This example serves only as a particular instance of the 421 MSGs we identified to be compatible with feSMs (section S2). A full list of these MSGs is presented in tables S9 and S10. Armed with this list, we studied the magnetic structures listed on the Bilbao Crystallographic Server (50) and found that the experimentally characterized magnetic materials YFe₄Ge₂ and LuFe₄Ge₂ (and related compounds) in the type III MSG 58.399 are realistic magnetic feSM candidates (59, 60). For these compounds, a nonmagnetic atom with an odd atomic number (Lu or Y) sits at a maximal symmetry site of multiplicity 2, whereas their surrounding magnetic moments (Fe) ordered into a pattern symmetric under the combined symmetry of spatial inversion and TR. Such a magnetic ordering falls into our broad description of nontrivial defect lattices, and these compounds are expected to feature Dirac points, pinned to high-symmetry momenta, near the Fermi energy (table S9).

We remark that the method described here can be readily applied to any other commensurate magnetic crystals where both the chemical formula and the MSG describing the magnetic order have been identified. In particular, a local-moment description is inessential: The filling criterion established on the basis of our computation of ν_BS applies equally well to systems exhibiting itinerant magnetism, as long as a band theory description remains applicable.

Indicator for antiferromagnetic topological insulator

As the last application of our results, let us make a connection of symmetry-based indicators of MSGs, fully computed in this work, to some previously studied topological insulators in TR-broken settings. As a canonical example, we discuss the type IV MSG 2.7 generated by the inversion symmetry I and the half translation, followed by TR, $\tilde{\mathcal{T}}\equiv \mathcal{T}{\mathit{T}}_{\frac{1}{2}{\mathit{a}}_{\mathit{z}}}$. This MSG has two classes of the combination of inversion parities, as indicated by ${\mathit{X}}_{\text{BS}}={\mathbb{Z}}_2$ in Table 1. The topological index distinguishing the two classes is given by

$$\mathrm{\xi }={(-1)}^{\frac{1}{4}{\displaystyle {\sum }_{\mathit{n}:\text{occupied}}}{\displaystyle {\sum }_{\text{TRIMs}}}{\mathrm{\xi }}_{\mathit{n},\mathit{k}}}=\pm 1$$ (7)

Here, ξ_n,k is the parity of the n-th occupied band. To understand this formula, note first that even- and odd-parity bands form a Kramers pair at the TRIMs with k_z = π. This is because I and $\tilde{\mathcal{T}}$ anticommute when k_z = π. Thus, the four TRIMs with k_z = π never contribute to the index. On the other hand, when k_z = 0, I and $\tilde{\mathcal{T}}$ commute, and ${\tilde{\mathcal{T}}}^2=-1$. This means that the same parity eigenvalue appears twice at TRIMs with k_z = 0. In Fig. 3A, we illustrated an example of the parity combination with ξ = −1.

Fig. 3. Symmetry indicators for antiferromagnetic topological insulators.

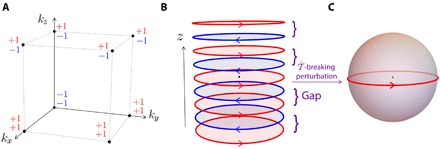
(A) Example of the inversion parity combination of valence bands in the ${\mathbb{Z}}_2$ nontrivial phase of MSG 2.7. (B) Realization of the ${\mathbb{Z}}_2$ nontrivial phase by staggered stacking of Chern insulators. The red (blue) disks represent a Chern insulator with C = +1 (C = −1). (C) Breaking the $\tilde{\mathit{T}}$ symmetry (the half translation in z, followed by the TR) leads to a “higher-order” state with a 1D equatorial chiral mode on the surface (62–71).

As demonstrated in (61), the index ξ = −1 implies a nontrivial band topology, the so-called “antiferromagnetic topological insulator” that supports gapless surface Dirac modes. The antiferromagnetic topological insulator can be understood as a staggered stacking of Chern insulators, in which a Chern insulator with C = +1 (described by red disks in Fig. 3B) is on every z = n ($\mathit{n}\in \mathbb{Z}$) plane and the one with C = −1 (blue disks) is on $\mathit{z}=\mathit{n}+\frac{1}{2}$($\mathit{n}\in \mathbb{Z}$) plane. All these Chern insulators are related by the $\tilde{\mathcal{T}}$ symmetry.

If we introduce a perturbation that breaks the $\tilde{\mathcal{T}}$ symmetry, the C = +1 Chern insulator at z = n (n ≠ 0) and the C = −1 Chern insulator at $\mathit{z}=\mathit{n}\mp \text{sign}(\mathit{n})\frac{1}{2}$ can pair-annihilate with each other in an inversion symmetric manner, leaving only the C = +1 Chern insulator on the z = 0 plane, as shown in Fig. 3C. This 1D chiral edge state on the surface of 3D topological insulators has been studied by Sitte et al. (62) and Zhang et al. (63) and its counterparts in many other symmetry settings have been found recently (64–71). Assuming that the inversion symmetry is unbroken, we see that one can diagnose this phase by another symmetry-based indicator for the type I MSG 2.4, which is simply the SG with only the inversion I apart from the lattice translation. According to Table 1, this MSG has ${\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_4$ classification, and the insulator hosting the 1D chiral edge mode constructed here belongs to the class (0, 0, 0, 2) in this classification.

CONCLUSION

Here, we revisit the old problem of assigning a global irrep label to each connected branch of a BS (11), generalizing our recent results on TR-symmetric systems (15) to all 1651 MSGs. Our central results are the computation of three fundamental quantities associated with magnetic BSs, which are tabulated in section S1: (i) d_BS, which characterizes the number of independent building blocks of energy bands; (ii) X_BS, which, akin to the Fu-Kane parity criterion (38), serves as a symmetry-based indicator of band topology; and (iii) ν_BS, which dictates the electron fillings at which band insulators are possible. We further demonstrate the utility of these results by applying them to the study of topological semimetals, focusing on cases where the absence of a band gap is either diagnosed through the symmetry representations at isolated high-symmetry points or mandated by the electron filling. In particular, we identify the exhaustive list of MSGs capable of hosting feSMs (section S2).

Although a full database on our computation of the basis vectors of the groups {BS} and {AI} is not included, we note that one can readily generate such a database (15): Our proof of d_BS = d_AI for all MSGs implies that full knowledge on {BS} is encoded in that of {AI}, and the latter can be computed by analyzing, for instance, hypothetical structures constructed by combining irreps of the site-symmetry groups to each of the Wyckoff positions. As long as all high-symmetry momenta are included in the analysis and the doubling of any irrep (according to the Herring rule) is incorporated, {BS} can be recovered by forming linear superpositions of the entries in {AI} using rational coefficients, subjected only to the constraint that the resultant irrep multiplicities must all be integer-valued. One can perform these calculations without deriving the compatibility relations, and this circumvents the careful convention-fixing required in both tabulating and using these results. In view of this, we refrain from providing a database on them.

We close by highlighting several interesting open questions that we leave for future studies: (i) performing a comprehensive study on the identification and characterization of reSMs in all 2D and 3D MSGs; (ii) developing a theory of quantized physical responses, or a proof of the absence thereof, for each nontrivial class in the exhaustive list of X_BS we computed; and (iii) finding realistic topological materials based on systematic searches using the diagnostics our theory provides. Finally, we remark that some aspects of our filling criterion generalize to the interacting setting (72), similar to the corresponding relation between the results for TR symmetric crystals (8, 10).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/8/eaat8685/DC1

Section S1. Tables for spinful electrons

Section S2. feSMs in stoichiometric compounds

Section S3. Notations

Section S4. Compatibility relations

Section S5. Details of AIs

Section S6. Details of $\tilde{\mathcal{T}}$b

Section S7. Magnetic layer groups

Section S8. Tight-binding model for reSM

Section S9. Tables for spinless electrons

Table S1. Characterization of MSGs in the triclinic family for spinful electrons.

Table S2. Characterization of MSGs in the monoclinic family for spinful electrons.

Table S3. Characterization of MSGs in the orthorhombic family for spinful electrons.

Table S4. Characterization of MSGs in the tetragonal family for spinful electrons.

Table S5. Characterization of MSGs in the hexagonal family for spinful electrons.

Table S6. Characterization of MSGs in the cubic family for spinful electrons.

Table S7. Characterization of the projections of MSGs that correspond to MLG, assuming spinful electrons.

Table S8. MSGs for which spinful electrons exhibit exceptional filling patterns.

Table S9. MSGs that can host feSMs with nodal-point Fermi surfaces pinned at high-symmetry momenta.

Table S10. MSGs that can host feSMs with movable nodal Fermi surfaces.

Table S11. MSGs that can host filling-enforced metals.

Table S12. Effect of turning on spin-orbit coupling on the fermiology of TR-symmetric filling-enforced (semi)metals.

Table S13. Characterization of MSGs in the triclinic family for spinless electrons.

Table S14. Characterization of MSGs in the monoclinic family for spinless electrons.

Table S15. Characterization of MSGs in the orthorhombic family for spinless electrons.

Table S16. Characterization of MSGs in the tetragonal family for spinless electrons.

Table S17. Characterization of MSGs in the hexagonal family for spinless electrons.

Table S18. Characterization of MSGs in the cubic family for spinless electrons.

Table S19. MSGs for which spinless electrons exhibit exceptional filling patterns.