Abstract
Kinesin‐1 is a homodimeric motor protein that can move along microtubule filaments by hydrolyzing ATP with a high processivity. How the two motor domains are coordinated to achieve such high processivity is not clear. To address this issue, we computationally studied the run length of the dimer with our proposed model. The computational data quantitatively reproduced the puzzling experimental data, including the dramatically asymmetric character of the run length with respect to the direction of external load acting on the coiled‐coil stalk, the enhancement of the run length by addition of phosphate, and the contrary features of the run length for different types of kinesin‐1 with extensions of their neck linkers compared with those without extension of the neck linker. The computational data on other aspects of the movement dynamics such as velocity and durations of one‐head‐bound and two‐head‐bound states in a mechanochemical coupling cycle were also in quantitative agreement with the available experimental data. Moreover, predicted results are provided on dependence of the run length upon external load acting on one head of the dimer, which can be easily tested in the future using single‐molecule optical trapping assays.
Keywords: coordination, kinesin, mechanochemical coupling, molecular motor, run length
Abbreviations
- [ATP]
ATP concentration
- 1HB
one‐head‐bound
- 2HB
two‐head‐bound
- ADP
adenosine diphosphate
- AMP‐PNP
adenylyl‐imidodiphosphate
- ATP
adenosine triphosphate
- ATPase
adenosine triphosphatase
- ATPγS
adenosine 5′‐O‐(3‐thiotriphosphate)
- CL
cysteine‐light
- DmK‐6AA
Drosophila kinesin‐1 with six additional amino acid residues inserted into the C‐terminal portion of the linker region of each head
- DmK‐WT
wild‐type Drosophila kinesin‐1
- HsK‐CL
cysteine‐light human kinesin‐1
- HsK‐CL‐6AA
cysteine‐light human kinesin‐1 with six additional amino acid residues inserted into the C‐terminal portion of the linker region of each head
- MD
molecular dynamics
- MT
microtubule
- NL
neck linker
- Pi
phosphate
Conventional kinesin (kinesin‐1) is a homodimeric motor protein that can move processively along microtubule (MT) filaments to transport cargo within cells by hydrolyzing ATP 1. It is a model system for studying biological molecular motors that can move processively on linear tracks. To understand the molecular mechanism of kinesin‐1's processive movement, besides structural studies 2, 3, 4, various experimental methods have been employed to study its movement dynamics 5, 6, 7, 8, 9, 10. In particular, using single‐molecule optical trapping, many aspects of its dynamics, such as the velocity, stall force, and mechanochemical coupling ratio, have been studied elaborately 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21. The processivity, which is characterized by the run length (i.e. the distance traveled by an individual motor on its liner track before dissociating), is another important factor that characterizes the dynamics of a molecular motor.
Recently, using high‐resolution single‐molecule optical trapping techniques, Milic et al. 22 measured systematically the run length of Drosophila kinesin‐1 dimer under both hindering (backward) and assisting (forward) loads. Interestingly, they found that the addition of phosphate in the solution enhanced the run length. Even more interestingly, the experimental data showed a dramatic asymmetry of the run length with respect to the direction of the external load acting on the coiled‐coil stalk 22, 23. Under a moderate forward load, the run length was an order of magnitude shorter than under the corresponding backward load 22, 23. Furthermore, the sensitivity of the run length to load, as characterized by a distance parameter, was dramatically lower in the forward‐load regime than in the backward‐load regime 22, 23. These results are very puzzling. According to Kramers theory, the dependence of a motor's unbinding rate, ε, on the external force, F, is calculated by ε = ε0exp(|F|/|F d), where ε0 is the unbinding rate under no force and F d is the unbinding force. On the other hand, the experimental data showed that the movement velocity, v, decreases with the increase in the magnitude of the backward force but is nearly independent of the magnitude of the forward force 23. Thus, it would be expected that a backward force causes a larger decrease in the run length (L = v/ε) than a forward force of the same magnitude, which is contrary to the experimental data 22, 23. Additionally, Andreasson et al. 23 found that by extending the neck linkers (NLs) of Drosophila kinesin‐1 dimer, the run length under no load was reduced greatly compared with the wild‐type case, whereas the NL extension only causes a small reduction in the velocity. On the contrary, for a cysteine‐light (CL) human kinesin‐1 construct, where a residue cysteine in the NL domain was mutated, the extension of the NLs has an insensitive effect on the run length or even increases the run length under no load, while the extension causes a large reduction in the velocity 24, 25. However, even qualitative explanations of the above puzzling experimental data have not been presented up to now. How does Drosophila kinesin‐1 dimer show the dramatically asymmetric character of the run length with respect to the direction of the external load? By extension of their NLs, why do different types of kinesin‐1 dimer behave rather differently or contrarily in their run length and velocity compared with those with no extension of the NLs? As is known, the dissociation of the kinesin dimer from MT, which determines the run length, involves the coordination of the two heads of the dimer during the processive stepping, and the coordination involves the mechanochemical coupling of the dimer. Thus, quantitative explanations of these experimental data on the run length and, in particular, the dramatic asymmetry of the run length with respect to the direction of the external load and the rather different characters of the run length for different types of dimers with extensions of the NLs have important implications for the mechanochemical coupling mechanism of the dimer.
Theoretically and computationally, the mechanism and dynamics of the processive movement of kinesin‐1 dimers have also been studied extensively 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36. More recently, a model for the processive movement of the dimeric kinesin was presented 37. With the model, diverse experimental data on the movement dynamics of the dimeric kinesin‐1 were explained quantitatively, such as the effects of varying solution viscosity, varying the external loads acting on the bead attached to the coiled‐coil stalk and on the bead attached to one head of the dimer, nullifying the NL docking, and extending the NLs on the velocity, mechanochemical coupling ratio, stall force, and randomness parameter 37. Moreover, the experimentally observed asymmetric or limping stepping dynamics of the homodimer and different features on the velocity versus the external load between different types of the kinesin‐1 dimer were also explained quantitatively 38.
In this work, we improved the model presented previously 37, 38. With the improved model, we studied computationally the processivity of the kinesin‐1 dimer, to understand the detailed mechanochemical coupling mechanism. The computational data reproduce well diverse experimental data on the run length and the corresponding velocity, providing a consistent and quantitative explanation of the above‐mentioned puzzling experimental data, as well as other experimental data such as the durations of one‐head‐bound (1HB) and two‐head‐bound (2HB) states in one step of the processive movement of the dimer, and the effect of additional phosphate on run length. Furthermore, to further test the model, some predicted results are provided.
Materials and methods
The model
The model of processive movement of dimeric kinesin is described as follows, which is an improvement on that proposed before 37. It is built up based mainly on three pieces of experimental and computational evidence and/or arguments.
-
(a)The experimental data showed that the kinesin head in the nucleotide‐free, ATP, or ADP.Pi state has a strong interaction with MT, whereas in the ADP state, it has a weak interaction 39, 40, 41, 42, 43, 44. The structural data showed that the strong interaction of MT tubulin heterodimer with the kinesin head in the strong MT‐binding state induces large conformational changes in the tubulin heterodimer 45. The recent all‐atom molecular dynamics (MD) simulations showed that the MT tubulin heterodimer with such conformational changes has a much weaker binding energy to the ADP–head than unperturbed MT tubulin heterodimers (X‐X. Shi, Y‐B. Fu, S‐K. Guo, P‐Y. Wang, H. Chen, P. Xie, under review). Thus, it is argued that immediately after the Pi release, the binding energy of the ADP–head with the local MT‐binding site (denoted by E w1), where the head in the strong MT‐binding state has just bound, is temporarily weaker than that with other unperturbed MT‐binding sites (denoted by E w2 > E w1) 35, 36, 37, 38. In a time t r, the local tubulin relaxes to its normally unperturbed conformation, with the interaction energy of the ADP–head with the local tubulin becoming the same as that with other tubulins. As a result, the interaction potential between the head and MT along a MT protofilament in an ATPase cycle is approximately shown in the inset of Fig. 1. (See Section S1 in Supporting information for a mathematical description of the interaction potential.)
Figure 1.
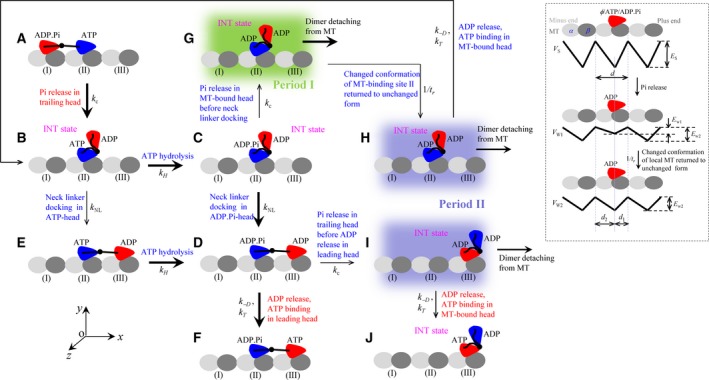 Schematic illustrations of the model of a typical forward stepping of the dimer at saturating ATP. Inset shows interaction potentials between the single kinesin head and MT along a MT protofilament during an ATPase cycle, with the top panel showing the strong interaction potential, VS, in nucleotide‐free (φ), ATP, or ADP.Pi states; the middle panel showing the weak interaction potential, VW 1, in ADP state immediately after Pi release; and the bottom panel showing the weak interaction potential, VW 2, in ADP state in a period of time t r after Pi release. (A) The trailing head in ADP.Pi state binds strongly to the rear MT‐binding site (I) while the leading head in ATP state binds strongly to the forward MT‐binding site (II). The trailing head with its NL pointing forward has a larger Pi release rate than the leading head with its NL not pointing forward. (B) Upon Pi release in the trailing head, due to the very weak affinity (E w1) between the ADP–head and the local MT‐binding site (I), driven by the thermal noise, the trailing ADP–head diffuses rapidly to the intermediate position relative to the other MT‐bound head, where the two heads have strong affinity. (C) ATP is hydrolyzed to ADP.Pi in the MT‐bound head. (D) In the intermediate state with the MT‐bound head in ADP.Pi state, the NL docking takes place, weakening the interaction between the two heads. Then, the thermal noise drives the tethered head to diffuse rapidly to the forward MT‐binding site (III). (E) In the intermediate state of (B), before ATP is hydrolyzed to ADP.Pi in the MT‐bound head, NL docking can also take place with a very low probability due to the very slow rate of NL docking in ATP state, weakening the interaction between the two heads. The tethered head then diffuses rapidly to the forward MT‐binding site (III). (F) Stimulated by MT ADP is released rapidly, followed by ATP binding. (G) From (C), Pi release can also occur occasionally in the MT‐bound head before its NL docking. Before the affinity of the MT‐bound ADP–head for the local MT‐binding site (II) changes from E w1 to E w2, the dimer can easily detach from MT by overcoming the very weak affinity E w1. (H) From (G) the affinity of the MT‐bound ADP–head for the local MT‐binding site (II) changes from E w1 to E w2 in time t r. The dimer also has a large probability to detach from MT before ADP release from the MT‐bound head by overcoming weak affinity E w2. If the dimer has not detached until ADP release, which is followed by ATP binding, the system returns to (B). (I) From (D), Pi release can also occur occasionally in the trailing head before ADP release in the leading head. The dimer has a large probability to detach from MT before ADP release from the MT‐bound head by overcoming weak affinity E w2. (J) From (I), the dimer has not detached until ADP release, which is followed by ATP binding. The thickness of the arrow represents the magnitude of the transition probability under no load. The states (shaded in green and blue) where the dimer can detach from MT are indicated.
Schematic illustrations of the model of a typical forward stepping of the dimer at saturating ATP. Inset shows interaction potentials between the single kinesin head and MT along a MT protofilament during an ATPase cycle, with the top panel showing the strong interaction potential, VS, in nucleotide‐free (φ), ATP, or ADP.Pi states; the middle panel showing the weak interaction potential, VW 1, in ADP state immediately after Pi release; and the bottom panel showing the weak interaction potential, VW 2, in ADP state in a period of time t r after Pi release. (A) The trailing head in ADP.Pi state binds strongly to the rear MT‐binding site (I) while the leading head in ATP state binds strongly to the forward MT‐binding site (II). The trailing head with its NL pointing forward has a larger Pi release rate than the leading head with its NL not pointing forward. (B) Upon Pi release in the trailing head, due to the very weak affinity (E w1) between the ADP–head and the local MT‐binding site (I), driven by the thermal noise, the trailing ADP–head diffuses rapidly to the intermediate position relative to the other MT‐bound head, where the two heads have strong affinity. (C) ATP is hydrolyzed to ADP.Pi in the MT‐bound head. (D) In the intermediate state with the MT‐bound head in ADP.Pi state, the NL docking takes place, weakening the interaction between the two heads. Then, the thermal noise drives the tethered head to diffuse rapidly to the forward MT‐binding site (III). (E) In the intermediate state of (B), before ATP is hydrolyzed to ADP.Pi in the MT‐bound head, NL docking can also take place with a very low probability due to the very slow rate of NL docking in ATP state, weakening the interaction between the two heads. The tethered head then diffuses rapidly to the forward MT‐binding site (III). (F) Stimulated by MT ADP is released rapidly, followed by ATP binding. (G) From (C), Pi release can also occur occasionally in the MT‐bound head before its NL docking. Before the affinity of the MT‐bound ADP–head for the local MT‐binding site (II) changes from E w1 to E w2, the dimer can easily detach from MT by overcoming the very weak affinity E w1. (H) From (G) the affinity of the MT‐bound ADP–head for the local MT‐binding site (II) changes from E w1 to E w2 in time t r. The dimer also has a large probability to detach from MT before ADP release from the MT‐bound head by overcoming weak affinity E w2. If the dimer has not detached until ADP release, which is followed by ATP binding, the system returns to (B). (I) From (D), Pi release can also occur occasionally in the trailing head before ADP release in the leading head. The dimer has a large probability to detach from MT before ADP release from the MT‐bound head by overcoming weak affinity E w2. (J) From (I), the dimer has not detached until ADP release, which is followed by ATP binding. The thickness of the arrow represents the magnitude of the transition probability under no load. The states (shaded in green and blue) where the dimer can detach from MT are indicated. -
(b)
The available experimental data showed that the NL can be docked into its motor domain in a nucleotide‐dependent manner 46. Based on the experimental data 46, 47, we make the following argument on this nucleotide‐dependent NL docking. When an MT‐bound kinesin head is in the nucleotide‐free and ADP states, the NL is unable to dock. When the head is in the ADP.Pi state, there is a small free energy (denoted by E NL) to facilitate efficiently its NL docking. The docking involves N‐terminal strand β0 of the motor domain forming a cover–neck bundle with strand β9 of the NL 48, which occurs when the two strands are in proximity. (See Section S2 for a mathematical description of the potential of the effect of NL docking into the MT‐bound head on the movement of the other tethered ADP–head.) In the ATP state, the NL has a lower efficiency or rate of docking than in the ADP.Pi state, as fluorescence polarization microscopy data showed 47. In the Discussion, we will further discuss the nucleotide‐dependent NL docking.
-
(c)
We argue that there exists an interaction between the two heads. When the NLs of both heads are undocked, the two heads have a high binding energy (denoted by E I1), and the NL docking in one head weakens the interaction between the two heads, with the binding energy denoted by E I2 < E I1. (See Section S3 for a mathematical description of the potential of the interaction between the two kinesin heads.) Note that with this argument together with argument (b), the biochemical data of Hackney 49, showing that upon the dimer with both heads bound by ADP mixing with MT only one‐half of the ADP molecules are released and addition of ATP molecules leads to release of other half of the ADP molecules, can be explained well.
Based on the three pieces of experimental evidence and/or arguments, a typical forward stepping of the dimer at saturating ATP is schematically shown in Fig. 1. Before stepping, the trailing head in the ADP.Pi state binds strongly to the rear MT‐binding site (I), while the leading head in the ATP state binds strongly to the forward MT‐binding site (II) (the available single‐molecule data indicating that ATP can bind to the leading head when the trailing head is bound strongly to MT 25) (Fig. 1A). The trailing head with its NL pointing forward has a larger Pi release rate than the leading head with its NL not pointing forward (the biochemical evidence for this characteristic is discussed in the section ‘The choice of parameter values’). Upon Pi release in the trailing head (with a rate constant k c), due to the very weak affinity (E w1) between the ADP–head and the local MT‐binding site (I), driven by the thermal noise, the trailing ADP–head detaches from site (I) and then diffuses rapidly to the intermediate position relative to the other MT‐bound head, where the two heads bind together strongly (Fig. 1B) (the state of the dimer with one head bound to MT and the other ADP–head bound to the MT‐bound head is called the intermediate state or 1HB state). ATP is hydrolyzed to ADP.Pi in the MT‐bound head (with a rate constant k H) (Fig. 1C). In the intermediate state (Fig. 1C), with the MT‐bound head in ADP.Pi state and strand β9 of the NL being close to strand β0 of the motor domain, NL docking takes place efficiently by forming the cover–neck bundle (with a high rate constant k NL). The docking weakens the interaction between the two heads. Then, the thermal noise drives the tethered ADP–head to diffuse rapidly to the nearest forward MT‐binding site (III) (Fig. 1D). Note here that the NL docking in the MT‐bound head provides an energy barrier E NL to prevent the tethered ADP–head from moving backward to the rear MT‐binding site (I). In the intermediate state (Fig. 1B), before ATP is hydrolyzed to ADP.Pi in the MT‐bound head, NL docking can also take place with a very low probability due to the slow rate of NL docking in the ATP state, weakening the interaction between the two heads. The thermal noise then drives the tethered ADP–head to diffuse rapidly to the nearest forward MT‐binding site (III) (Fig. 1E), which is followed by ATP hydrolysis to ADP.Pi in the trailing head (with the rate constant k H) (Fig. 1D). After the ADP–head binds to the forward MT‐binding site (III) (Fig. 1D), stimulated by MT, ADP is released rapidly (with a rate constant k –D) and ATP of saturating concentration then binds immediately to the nucleotide‐free head (with a rate constant k T) (Fig. 1F).
It can be noted that in the intermediate state of Fig. 1C, Pi release can also occur occasionally in the MT‐bound head before its NL docking takes place (Fig. 1G). In Fig. 1G, before the affinity of the MT‐bound ADP–head for the local MT‐binding site (II) changes from E w1 to E w2, the dimer can easily detach from MT by overcoming the very weak affinity E w1. If the dimer has not detached from MT until the affinity of the MT‐bound ADP–head for the local MT‐binding site (II) changed from E w1 to E w2 in time t r (Fig. 1H), the dimer also has a large probability to detach from MT before ADP release from the MT‐bound head by overcoming weak affinity E w2 (Fig. 1H). If the dimer has not detached until ADP release, the system returns to that of Fig. 1B. Note also that in Fig. 1D, Pi release can also occur occasionally in the trailing head before ADP release in the leading head (Fig. 1I). In the intermediate state of Fig. 1I, the dimer also has a large probability to detach from MT before ADP release from the MT‐bound head by overcoming weak affinity E w2. If the dimer has not detached until ADP release, the system transits to that of Fig. 1J, which is the same as that of Fig. 1B except that the dimer has moved a step forward.
Equations to describe the movement of tethered ADP–head relative to nucleotide‐free head, ATP–head, or ADP.Pi–head bound fixedly to MT
In this work, for simplicity of analysis, we do not consider the dissociation of the nucleotide‐free head, ATP–head, or ADP.Pi–head from MT, because in nucleotide‐free, ATP, and ADP.Pi states, the kinesin head binds to MT strongly. In this section, we present equations for the movement of the ADP–head relative to the nucleotide‐free head, ATP–head, or ADP.Pi–head bound fixedly to MT. We define the coordinate oxyz as shown in Fig. 1, where the origin of the coordinate (0,0,0) is at the center‐of‐mass position of the MT‐bound head. We consider the translation motion of the ADP–head in three dimensions (denoted by coordinates x, y, and z) and rotation in three directions. The rotation is described by nutation motion (characterized by angle α), rotation motion (characterized by angle θ), and precession motion (characterized by angle ϕ). When the kinesin head is in the MT‐binding site, α, θ, and ϕ correspond to the angles of rotation in the xoz, xoy, and yoz planes, respectively.
As done in the single‐molecule optical trapping experiments 22, we consider a micrometer‐sized bead with diameter of 2R bead attached to the coiled‐coil stalk of the dimer and an external force acting on the bead. With one kinesin head binding fixedly to MT at position (0,0,0), the translation and rotation of the other ADP–head relative to the MT‐bound head in viscous solution can be described by Langevin equations 37, 38
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
where , and x bead and y bead denote, respectively, the x‐coordinate and y‐coordinate of the center of mass of the bead (for simplicity but without loss of generality, the motion of the bead in the z‐coordinate is not considered). V W (x, y, z, α, θ, ϕ) is the potential of the ADP–head interacting with the MT‐binding site during the period after Pi release and before ADP release with the other nucleotide‐free head, ATP–head, or ADP.Pi–head bound fixedly to MT (see Section S1), V NL(x) is the potential characterizing the effect of the NL docking to the MT‐bound head on the motion of the tethered ADP–head (see Section S2), V I (x, y, z, α, θ, ϕ) is the potential of interaction between the two kinesin heads (see Section S3), and F NL is the force acting on the ADP–head that results from the stretching of the NLs (see Section S4).
In Equations ((1), (2), (3), (4), (5), (6), (7), (8), (9), (10), (11), (12)), we take the followings into consideration. Due to the steric restriction of MT and considering the size of the kinesin head with radius r head = 2.5 nm, it is required that y ≥ y 0 = 0 and r ≥ 2r head = 5 nm. Due to the steric restriction of MT and considering the size of the bead with radius R bead, it is required that y bead ≥ R bead. For the longitudinal or x component of the external force, F x, the vertical or y component is calculated by F y = |F x|tanΘ0 and sinΘ0 = R bead/(R bead + l kinesin), where l kinesin = 54 nm is the length of the coiled‐coil stalk of the kinesin dimer 38 and 2R bead = 0.44 μm as used in the experiments 22. F x is defined as negative when it points backward (i.e. the –x direction) and positive when it points forward (i.e. the +x direction), while F y is defined as positive when it points upward (i.e. the +y direction). It is considered that the x component of the interaction force between the bead and kinesin dimer acts only on the NL of the head that has a larger distance to the bead along the x direction. Thus, when the distance between a kinesin head and bead along the x direction is smaller than d/2, no x component of the internally elastic force exists between them, with d = 8.2 nm being the distance between two successive binding sites along a MT protofilament. Function sgn(x) is the sign function, and function H(x) is defined as follows: H(x) = 1 if x > 0 and H(x) = 0 if x ≤ 0. It is noted that when the two heads are bound simultaneously to MT, each head experiences a vertical force because the two heads have the same distance to the bead along the y direction. When only one head is bound to MT and the other head is detached from MT, only the MT‐bound head experiences a vertical force, because the distance of the bead to the MT‐bound kinesin head along the vertical y direction is larger than that to the detached kinesin head. For approximation, we consider here that when the ADP–head is in the range of 0 ≤ y < 1 nm (noting that when bound to MT, the head is in the position of y = 0), the ADP–head experiences the vertical force, and when in other ranges (y ≥ 1 nm), the ADP–head experiences no vertical force. The drag coefficients on the kinesin head are calculated by Γx = Γy = Γz = 6πη0 r head and Γα = Γθ = Γφ = 8πη0 , where η0 is the solution viscosity in the vicinity of MT. Since the viscosity in the vicinity of MT is larger than that far away from MT, we take η0 = 0.02 g·cm−1·s−1, which is about twofold larger than that in water. The term ξi(t) (i = x, y, z, α, θ, ϕ) is the fluctuating Langevin force on the kinesin head, with (i j) and , where k B is the Boltzmann constant and T is absolute temperature. The drag coefficients on the bead are calculated by = 6πη0Rbead. The terms and are the fluctuating Langevin forces on the bead along the x and y directions, respectively, with (j = x, y), and . The connection between the bead and C‐terminal ends of the NLs is characterized by an elastic linear spring with a spring constant C. In the calculation, we take C = 0.1 pN·nm−1 (we have checked that varying the value of C has little effect on the calculated results). The initial conditions for Equations ((1), (2), (3), (4), (5), (6), (7), (8), (9), (10), (11), (12)) are: (x 0, y 0, z 0, α0, θ0, ϕ 0) = (−d, 0, 0, 0, 0, 0), x bead0 = −d/2 + F x/C, and y bead0 = F y/(2C).
Equations to describe the movement of kinesin when two heads are in the ADP state
When both ADP–heads are bound simultaneously to MT, the movement of one head relative to the other can still be described by Equations ((1), (2), (3), (4), (5), (6), (7), (8), (9), (10), (11), (12)). If one head is detached from MT with an affinity of E w1 (see Fig. 1), it would most probably bind immediately to the other MT‐bound ADP–head due to the high binding energy E I1 between them because the NL of the MT‐bound ADP–head is undocked. If one head is detached from MT with an affinity of E w2 (see Fig. 1), it would either rebind immediately to MT or bind immediately to the other MT‐bound ADP–head. When the two ADP–heads are bound together strongly, the movement of the MT‐bound ADP–head relative to MT can be described by the following equations:
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
where F NL is the force acting on the MT‐bound ADP–head that results from the stretching of the NLs (see Section S4). Here, for simplicity of treatment, the bead and C‐terminal end of the NL of MT‐bound ADP–head are implicitly considered to be connected rigidly. The initial conditions for Equations ((13), (14), (15), (16), (17), (18), (19), (20)) are as follows: (x 0, y 0, z 0, α0; θ0, ϕ 0) = (0, 0, 0, 0, 0, 0), x bead0 = (x bead0 = 0 when F x = 0), and y bead0 = (y bead0 = R bead + l kinesin when F x = F y = 0), where l NL is the length of the NL under a pulling force of magnitude .
Monte Carlo simulations of processive movement and dissociation of dimeric kinesin
Using Equations ((1), (2), (3), (4), (5), (6), (7), (8), (9), (10), (11), (12), (13), (14), (15), (16), (17), (18), (19), (20)), we can simulate the mechanical step of the movement of a kinesin head following Pi release relative to the other MT‐bound kinesin head and the dissociation of the dimer from MT using a stochastic Runge–Kutta algorithm, as done before 35, 37, 38, 50. Then, we can simulate processive movement of the dimer by also considering continuous ATPase activities, which can be simulated using a Monte Carlo algorithm, as used before 37, 38, 51. In the Monte Carlo simulations, during each time step Δt (Δt = 10−4 s in our simulation), a random number ran is generated with uniform probability between 0 and 1. The state transition with rate constant k i (where i represents T, H, c, NL, –D) takes place if ran ≤ P i, and the transition does not take place if ran > P i. Here, P i = k iΔt is the probability of state transition in each time step Δt, k T = [ATP] represents ATP binding rate to the nucleotide‐free head, with being the second‐order rate constant for ATP binding and [ATP] being the ATP concentration, k H represents the rate constant of ATP hydrolysis, k c represents the rate constant of Pi release, k NL represents the rate constant of NL docking into the motor domain of MT‐bound head in the ATP or ADP.Pi state when the detached ADP–head is in the intermediate position, and k –D represents the rate constant of ADP releasing from ADP–head. In our simulations, the rate constant k i (where i represents T, H, c, NL, –D) is independent of the strain on the NL (see next section).
As mentioned above, we take the following into consideration to study the dissociation of the dimer from MT. When one head of the dimer in the nucleotide‐free, ATP, or ADP.Pi state binds strongly to MT, the binding affinity of the head to the MT is very large so that the dissociation of the dimer from the MT is negligibly small. This implies that only when both heads are simultaneously in the ADP state is the dissociation of the dimer taken into account. In the calculations, when both heads move to positions of y > 10 nm, the dimer is considered to dissociate from MT.
From 1000 simulated traces of the displacement of the center of mass of the dimer versus time, the total displacement in each trace can be obtained and the velocity in each trace can be calculated from the total displacement divided by the total time before dissociation. The run length and mean velocity are computed from all of individual displacements and velocities, respectively.
The choice of parameter values
In this work, we focus on two types of kinesin‐1: Drosophila kinesin‐1 and CL human kinesin‐1. Values of the parameters related to the NL docking, the interaction between the kinesin head and MT, and the interaction between the two kinesin heads are taken as follows. We take the NL‐docking energy E NL = 6k B T for Drosophila kinesin‐1 and E NL = 4.5k B T for CL human kinesin‐1 (Table 1), as done before 38. Note that the residue mutation in the NL domain of CL human kinesin‐1 reduces E NL. We take E w1 = 19.8k B T and E w2 = 40k B T for Drosophila kinesin‐1, and E w1 = 25.3k B T and E w2 = 43k B T for CL human kinesin‐1 (Table 1). These values of E w1 = 19.8k B T or 25.3k B T and E w2 = 40k B T or 43k B T are close to those obtained by all‐atom MD simulations (X‐X. Shi, Y‐B. Fu, S‐K. Guo, P‐Y. Wang, H. Chen, P. Xie, under review), and different types could have slightly different values of the binding affinity of the head to MT. For both types of the kinesin, we take t r = 10 μs (Table 1), as done before 37, 38. Values of the rate constant of NL docking, k NL, in different nucleotide states for both types of the kinesin are taken as follows. As discussed in detail in the Discussion section, the available experimental data indicated that the rate constant of the NL docking in the ADP.Pi state is much higher than that in the ATP state 47, 52, 53, 54. Thus, in the intermediate state, when the MT‐bound head is in the ADP.Pi state, we take k NL = 800 s−1, which is consistent with the available biochemical data 55, while when the MT‐bound head is in ATP state, we take the rate constant of the NL docking to be very small, for example, k NL = 1 s−1 in the calculation (Table 1). When the MT‐bound head is in the nucleotide‐free or ADP state, since its NL is unable to dock, we take k NL = 0. Provided that E I1 > 40k B T and E I2 < 20k B T, varying the values of E I1 and E I2 has little effect on our results presented in this work.
Table 1.
Values of parameters for WT Drosophila kinesin‐1 (DmK) and CL human kinesin‐1 (HsK)
| Parameter | Value | |
|---|---|---|
| DmK | HsK | |
| E NL | 6k B T | 4.5k B T |
| E w1 | 19.8k B T | 25.3k B T |
| E w2 | 40k B T | 43k B T |
| t r (μs) | 10 | 10 |
| k NL (s−1) (ADP.Pi state) | 800 | 800 |
| k NL (s−1) (ATP state) | 1 | 1 |
| k c (s−1) (NL pointing forward) | 185 | 185 |
| (s−1) (NL not pointing forward) | k c/40 | k c/40 |
| (μm −1·s−1) | 4 | 4 |
| k H (s−1) | 350 | 350 |
| k –D (s−1) | 370 | 370 |
The parameters related to ATPase activity are described as follows. The experimental data of Yildiz et al. 24 showed that extending the NLs by any length (implying that the tension on the NL is varied) has an insensitive effect on the ATPase rate of the dimer. On the other hand, the biochemical data showed that during the processive movement under saturating ATP, the rate‐limiting step of the ATPase activity is Pi release 56. Moreover, during a forward step, the Pi release in the trailing head can occur simultaneously with the ADP release, ATP binding, and then ATP hydrolysis in the leading head. Thus, we consider that the tension on the NL has no effect on the rate constant of Pi release; that is, the rate constant of Pi release is independent of the external load acting on the bead attached to the coiled‐coil stalk of the dimer, which is also consistent with the recent single‐molecule data 57. However, we consider that the rate constant of Pi release is dependent on the pointing direction of its NL. When the NL points in the forward direction, the head has a much larger rate constant of Pi release than when the NL points in the backward direction, which can be understood by considering that when pointing forward, the NL can interact with the head and the interaction enhances Pi release rate. This is consistent with the experimental data showing that by deleting the NL (implying that the interaction of the NL with the head is removed), the ATPase rate is reduced greatly, while the ADP release rate is unaffected 58. Thus, in the state with two heads bound simultaneously to MT, for the leading head, its rate constant of Pi release, , is much smaller than that, , for the trailing head. In the intermediate state, when the NL of the MT‐bound head is stretched forward by a length of l NL > 2.8 nm, it is considered to point forwards, and thus, the rate constant of Pi release is equal to k c, while in other cases, the rate constant of Pi release is equal to . In the calculation, we take = k c/40 (Table 1), as done before 37, 38, and take k c = 185 s−1 for both types of the kinesin (Table 1). This value of k c is close to the biochemical data 5.
The second‐order rate constant, , for ATP binding always has a constant value independent of the tension on and pointing direction of the NL, and we take = 4 μm −1·s−1 for both types of the kinesin (Table 1), which is close to the biochemical data 5. The rate constant of ATP hydrolysis also always has a constant value independent of the tension on and pointing direction of the NL, and we take k H = 350 s−1 for both types of the kinesin (Table 1), which is also consistent with the biochemical data 5.
Based on the available single‐molecule optical trapping data showing that the external force affects the affinity of ADP for kinesin, with the affinity under a backward force being smaller than under a forward force 59, we consider that the tension on the NL affects the rate constant of ADP release. Thus, we take the rate constant of MT‐stimulated ADP release from the trailing head, , where σ is a constant larger than 1. In the intermediate state with MT‐bound head in the ADP state, the rate constant of MT‐stimulated ADP release is also taken to be . To be consistent with the biochemical data 5, 56, we take k –D = 370 s−1 for both types of the kinesin (Table 1). In addition, we take σ = 3.1 for Drosophila kinesin‐1 and σ = 1.8 for CL human kinesin‐1. When ADP–head is detached from the MT, without MT stimulation, the ADP‐release rate is taken to be 0.
Results
Run length for wild‐type Drosophila kinesin‐1
In this section, we study the effect of the external force on the run length of wild‐type Drosophila kinesin‐1 (called DmK‐WT), with the force–extension relation of the NL of one head obtained by all‐atom MD simulations being shown in Fig. S1. In Fig. 2A, we show our calculated results (open circles) of the run length versus the external force and compare with the experimental data (filled circles) of Milic et al. 22 and Andreasson et al. 23. The corresponding results for the velocity are shown in Fig. 2B. Here, the external force is defined as being positive and negative when it assists and resists the forward movement, respectively. It is seen that our calculated data for both the run length and velocity are in quantitative agreement with the experimental data. The data in Fig. 2A show a dramatic asymmetry of the run length with respect to the direction of the external force, with the run length under a moderate forward load being much shorter than that under no or a moderate backward load. These results can be understood as follows.
Figure 2.
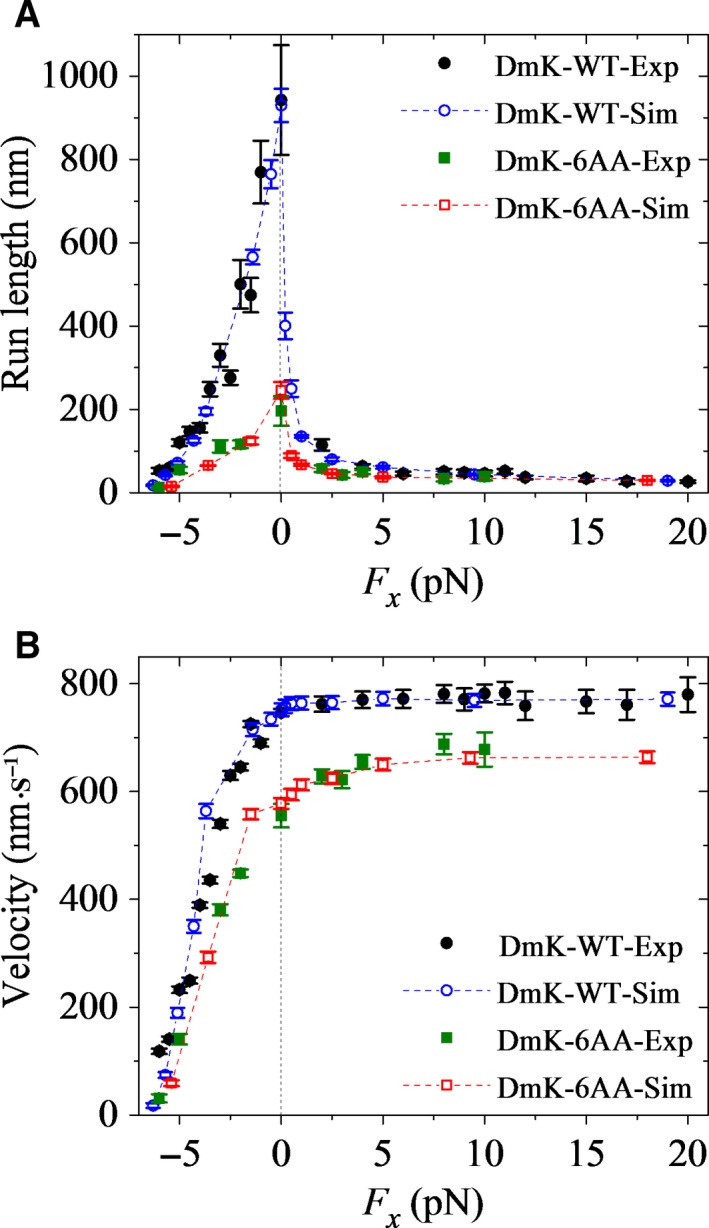
Dependence of run length and velocity of Drosophila kinesin‐1 upon the external force acting on the coiled‐coil stalk at saturating ATP. Open symbols are calculated data and filled symbols are experimental data taken from Milic et al. 22 and Andreasson et al. 23. Error bars represent SEM (n = 1000). (A) Run length versus longitudinal component (F x) of the external force for DmK‐WT (circles) and DmK‐6AA (squares). (B) Velocity versus longitudinal component (F x) of the external force for DmK‐WT (circles) and DmK‐6AA (squares).
Since upon Pi release, the trailing head moves rapidly to the intermediate position, and after the NL docking of the MT‐bound head, the tethered ADP–head moves rapidly to the next forward MT‐binding site or to the previous backward MT‐binding site, the detaching of the dimer from MT occurs mainly in the intermediate state, where one head is bound to MT, with its NL being undocked, and the other ADP–head is bound strongly to the MT‐bound head. Furthermore, since in nucleotide‐free, ATP, or ADP.Pi state, the MT‐bound head binds strongly to MT, its dissociation from MT is negligible. Thus, the detaching of the dimer from MT occurs mainly during two periods in the intermediate state. One period (called Period I) is after Pi release occurs in the MT‐bound head and before the affinity of the MT‐bound ADP–head for the local MT changes from E w1 to E w2 (Fig. 1G). The other period (called Period II) is when the MT‐bound head is in the ADP state with its affinity for MT being E w2 (Fig. 1H and I). In Period I, upon Pi release, the binding affinity of the MT‐bound head to the local MT becomes very weak, with a small affinity E w1; the head has a very large probability to detach from MT within time t r. In Period II, since ADP–head binds to MT weakly, with an affinity E w2, the head also has a large probability to detach from MT before ADP release within a time (1/k –D) that is much longer than t r.
That the run length under a moderate forward load is much shorter than that under no or a moderate backward load arises from the detaching of dimer from MT that occurs in Period I. In the intermediate state, before the NL of the MT‐bound head is docked, the NL is driven to point in the forward direction under the forward load, and by contrast, it is not pointed in the forward direction under no or the backward load. Thus, in the intermediate state, before the NL docking, the rate constant of Pi release from the MT‐bound head under the forward load is much larger than that under no or the backward load (see the section ‘The choice of parameter values’ in Materials and methods). The result is that in the intermediate state, before the NL docking, the probability of Pi release occurring in the MT‐bound head, that is, the occurrence probability of Period I, under the forward load is significantly larger than that under no or the backward load. Consequently, the dimer at the intermediate state has a much larger probability to detach from MT under the forward load than under no or the moderate backward load.
In the above (Fig. 2), we focus on the case at saturating ATP. Now, we consider the case at low ATP concentrations. In Fig. 3A, we show the calculated results of the run length versus [ATP] at a given longitudinal component of the external force, F x = +4 pN (filled circles). The corresponding results of velocity versus [ATP] are also shown in Fig. 3A (filled squares). It is seen that although the velocity increases sensitively with the increase of [ATP], the run length is nearly independent of [ATP], which can be explained as follows. Before ATP binding, the dimer is most of the time in the state with the nucleotide‐free head bound strongly to MT and the detached ADP–head in the intermediate position bound strongly to the nucleotide‐free head, which is consistent with the experimental and structural observations 60, 61. Since the nucleotide‐free head binds strongly to MT, it is considered not to dissociate from MT. After ATP binding, since ATP hydrolysis is rapid and the NL docking is very slow, the NL is almost unable to dock before ATP hydrolysis to ADP.Pi. Hence, it is expected that the dissociation probability of the dimer would be nearly the same as that for the case at saturating [ATP], giving the run length at a very low [ATP] to be nearly the same as that at saturating [ATP]. In our calculations, for simplicity, we have neglected the dissociation during the period when the kinesin head in the nucleotide‐free state binds strongly to MT. Considering the small dissociation probability during the long period in the nucleotide‐free state of the MT‐bound head, the run length at low [ATP] would become slightly smaller than that at saturating [ATP], which is in good agreement with the single‐molecule data of Milic et al. 22 and Andreasson et al. 23.
Figure 3.
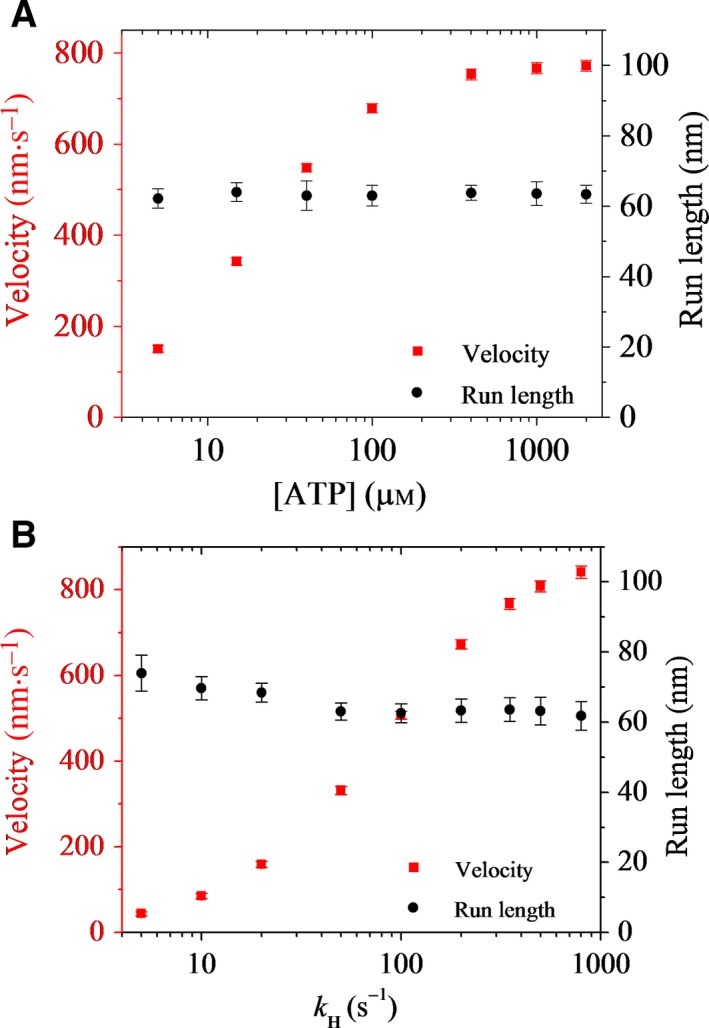
Effects of ATP concentration and replacing ATP with a slowly hydrolyzable ATP analog, ATPγS, on run length and velocity of Drosophila kinesin‐1. Error bars represent SEM (n = 1000). (A) Run length (circles) and velocity (squares) versus ATP concentration under a given longitudinal component of the external force acting on the coiled‐coil stalk, F x = +4 pN. (B) Run length (circles) and velocity (squares) versus rate constant of ATPγS hydrolysis, kH, under F x = +4 pN and saturating ATPγS.
We next consider the case at saturating ATPγS, a slowly hydrolyzable ATP analog 22. For this case, the dimer is most of the time in the state with two heads in the ATPγS or ADP.γSPi state binding strongly to MT, with no dissociation. After γSPi is released in the trailing head, the tethered ADP–head moves rapidly to the intermediate position. Since in the intermediate state the MT‐bound head is most probably in the ADP.γSPi or ATPγS state, and in the ATPγS state the NL docking is very slow, it is expected that the dissociation probability of the dimer would be similar to that for the case with ATP, giving a similar run length for the two cases. For example, in Fig. 3B, we show the calculated results of run length versus the rate constant of ATPγS hydrolysis, k H, under F x = +4 pN (filled circles), with values of other parameters being unchanged. The corresponding results for the velocity are also shown in Fig. 3B (filled squares). It is seen that although the velocity increases sensitively with the increase in k H, the run length decreases only slightly with the increase in k H. In our calculations, for simplicity, we have neglected the dissociation during the period when the kinesin head in ATPγS or ADP.γSPi state binds strongly to MT. Considering the small dissociation probability during the long period in the ATPγS state, the run length at low k H would become closer to that for the case with ATP (with k H = 350 s−1), implying that the run length for the case with ATPγS is close to that for the case with ATP. These are in good agreement with the single‐molecule data of Milic et al. 22 and Andreasson et al. 23.
Run length for Drosophila kinesin‐1 with extended neck linkers
In this section, we study the effect of the external force on the run length of Drosophila kinesin‐1 with extended NLs. As calculated in our previous work 38, for kinesin‐1 dimers with one, two, three, four, five, and six additional amino acid residues inserted into the C‐terminal portion of the linker region of each head, their velocities across all negative loads only have small changes but have large drops relative to those with no extension of the NLs, which is consistent with the experimental data 23. Here, we only focus on the kinesin with six additional amino acid residues (with sequence LQASQT) inserted into the C‐terminal portion of the linker region of each head (called DmK‐6AA), as done in Andreasson et al. 23. Since the amino acid residues inserted into the NL are far away from the motor domain, the insertions should have no effect on the interaction of the head with MT, the interaction between the two heads and the NL docking. As the available experimental data indicated 24, the insertions have no effect on the rate constants of ATP hydrolysis and Pi release. However, since the single‐molecule data indicated that the tension on the NL affects the rate constant of ADP release 59, the insertions should affect the rate constant of MT‐stimulated ADP release. Consequently, we take the same values for all parameters for DmK‐6AA as those for DmK‐WT except k –D and the force–extension relation of the NL. Using all‐atom MD simulations, the calculated results of the force–extension relation of the NL of one head for DmK‐6AA are shown in Fig. S2. From Figs S1 and S2, it is seen that when the two heads are bound to MT simultaneously, with one NL being stretched to a length of d/2 = 4.1 nm, the internally stretched force between the two heads is nearly zero for DmK‐6AA, whereas it is about 30 pN for DmK‐WT. Thus, in the calculations, we take the rate constant of ADP release from both the leading and trailing heads for DmK‐6AA to be (σ = 3.1) (see section ‘The choice of parameter values’ in Materials and methods). In Fig. 2A, we also show our calculated results (open squares) of the run length for DmK‐6AA versus the external force and compare with the experimental data (filled squares) of Andreasson et al. 23. The corresponding results for the velocity are shown in Fig. 2B. It is seen that the calculated data for both run length and velocity are also in good agreement with the experimental data. That the origin of the run length of DmK‐6AA under no or a backward load is greatly smaller than that of DmK‐WT is explained as follows.
For Drosophila kinesin‐1, the value of E w2 = 40k B T (see Table 1) gives a larger probability of the dimer detaching from MT during Period II than during Period I under no or a backward load. On the other hand, for DmK‐6AA, the rate constant of ADP release from the leading head is slower than that for DmK‐WT, leading to the occurrence probability of Period II for DmK‐6AA being larger than that for DmK‐WT. Consequently, the probability of the dimer detaching from MT for DmK‐6AA is larger than that for DmK‐WT, leading to the run length of the former being smaller than that of the latter. By contrast, under a forward load, the run length of DmK‐6AA is close to that for DmK‐WT (Fig. 2A). This is because under the forward load, the run length is mainly determined by the detaching of dimer from MT that occurs in Period I (see above), and for both DmK‐6AA and DmK‐WT, the occurrence probabilities of Period I are comparable.
Durations of one‐head‐bound and two‐head‐bound states
Recently, using high‐resolution single‐molecule microscopy, Mickolajczyk and Hancock 62 observed that for Drosophila kinesin‐1, extending the NLs increases the mean duration of the 1HB state, while it has little effect on the mean duration of the 2HB state in one step of processive movement of the dimer. To explain these data, we calculate the mean duration of 1HB state to be about 3.2 ms for DmK‐WT and to be about 6.1 ms for DmK‐6AA under no load and saturating ATP (2 mm), with the latter being evidently larger than the former, and the mean duration of the 2HB state to be about 7.8 ms for DmK‐WT and about 8.1 ms for DmK‐6AA, with the two values being close to each other. These are in agreement with the single‐molecule data 62. The origin of the above feature is explained as follows. Since the rate constant of ADP release in the leading head for DmK‐6AA is slower than that for DmK‐WT, there is a larger probability for DmK‐6AA to be in the 1HB state with MT‐bound head bound by ADP than for DmK‐WT. On the other hand, the duration of the 1HB state is equal to the total time of ADP release, ATP binding, ATP hydrolysis, and then NL docking in the MT‐bound head, with the rate constants of ATP binding (k b), ATP hydrolysis (k H), and NL docking (k NL) being the same for both DmK‐6AA and DmK‐WT. Thus, it is expected that the mean duration of the 1HB state for DmK‐6AA is larger than for DmK‐WT. By contrast, based on our model, the duration of the 2HB state is mainly determined by the time of Pi release in the trailing head. Since Pi release rate is independent of the NL length, it is expected that the mean duration of the 2HB state for DmK‐6AA is close to that for DmK‐WT.
In addition, the biochemical data of Mickolajczyk and Hancock 62 showed that extending the NLs of Drosophila kinesin‐1 increases the time of half‐site ADP release at saturating ATP. In our model, the time of half‐site ADP release at saturating ATP is approximately calculated by τhalf = 1/k H + 1/k c + 1/k NL + 1/k –D. Since terms k H, k c, and k NL are the same for both DmK‐6AA and DmK‐WT, whereas k –D (the rate constant of ADP release in the leading head) for DmK‐6AA is smaller than that for DmK‐WT, it is expected that τhalf for DmK‐6AA is larger than that for DmK‐WT. The calculated value of τhalf is about 17.89 ms for DmK‐6AA and is about 12.22 ms for DmK‐WT, with the difference Δτhalf = 5.67 ms, in good agreement with the biochemical data 62.
Moreover, we studied the mean durations of the 1HB and 2HB states versus [ATP] for CL human kinesin‐1, with the calculated results being shown in Fig. 4A, where the single‐molecule data of Isojima et al. 60 on CL human kinesin‐1 are also shown for comparison. It is seen that the mean duration of the 1HB state increases significantly with the decrease in [ATP], whereas the mean duration of the 2HB state increases only slightly with the decrease in [ATP]. These results are in quantitative agreement with the experimental data. The inverse of the mean duration of the 1HB state versus [ATP] satisfies the Michaelis–Menten relation (Fig. 4B), which is also in agreement with the single‐molecule data of Isojima et al. 60.
Figure 4.
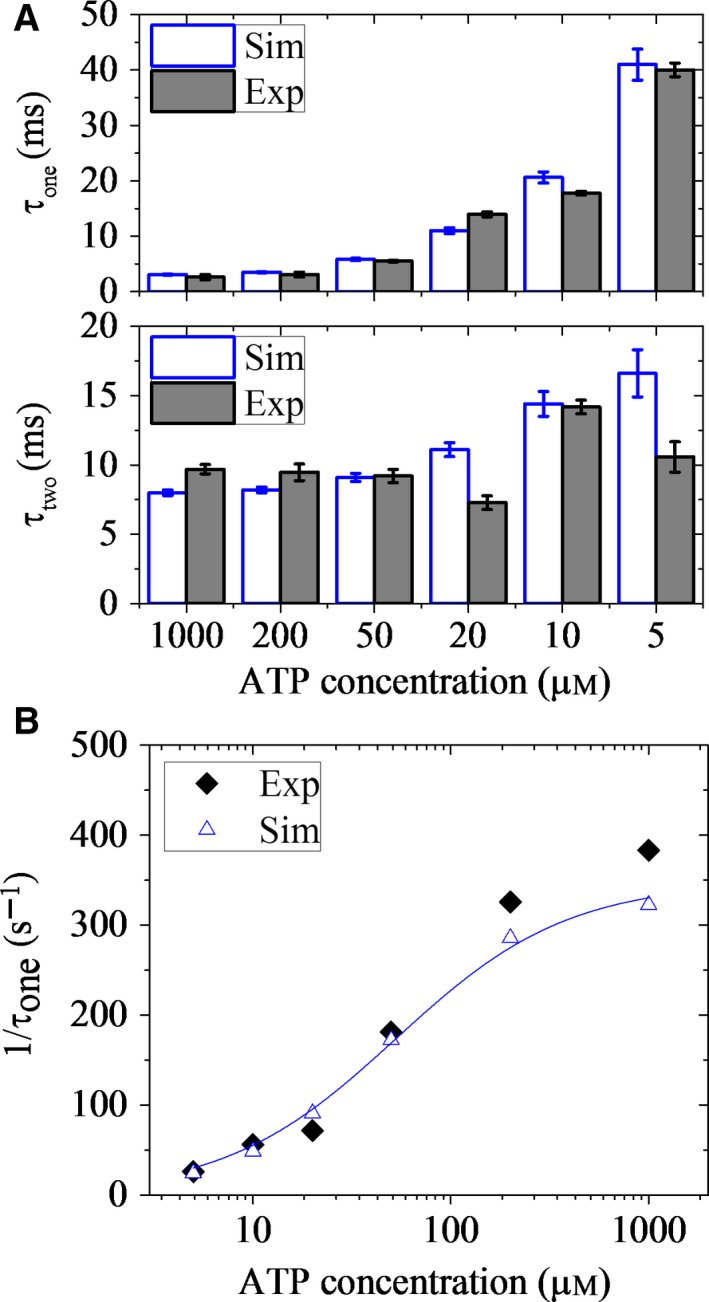
Durations of one‐head‐bound (1HB) and two‐head‐bound (2HB) states during processive movement of cysteine‐light (CL) human kinesin‐1 under no load. (A) Mean durations of 1HB state (upper) and 2HB state (lower) versus ATP concentration. Open columns are calculated data, and filled columns are experimental data taken from Isojima et al. 60. Error bars represent SEM (n = 1000). (B) Inverse of the mean duration of 1HB state as a function of ATP concentration. Open symbols are calculated data, and filled symbols are experimental data taken from Isojima et al. 60. Line is the fit with the Michaelis–Menten equation, 1/τ1 = k cat [ATP]/KM + [ATP]). The fit parameters are k cat = 348 s−1 and KM = 53 μm.
Run length for cysteine‐light human kinesin‐1
As seen above (Fig. 2A), for Drosophila kinesin‐1, under no load, the run length of DmK‐6AA is reduced greatly compared with that of DmK‐WT. By contrast, for CL human kinesin‐1, the available single‐molecule data showed that the extension of NLs has an insensitive effect on or even increases slightly the run length under no load although it has a sensitive effect on or decreases largely the velocity 24, 25. Here, we give quantitative explanations of these contrary results.
First, we studied the effect of the external force on the run length of CL human kinesin‐1 without extension of the NLs (called HsK‐CL), with the force–extension relation of the NL of one head obtained by all‐atom MD simulations being shown in Fig. S3. The calculated results of the run length versus the external force are shown in Fig. 5A (open circles), where for comparison, the available experimental value of the run length under no load (filled circle) 24 is also shown. The corresponding results for the velocity are shown in Fig. 5B. It is seen that the calculated data for both the run length and velocity are in quantitative agreement with the experimental data. As expected, the curve of the run length versus the external load for HsK‐CL (Fig. 5A) resembles that for DmK‐WT (Fig. 2A), both showing the dramatic asymmetry with respect to the direction of the load.
Figure 5.
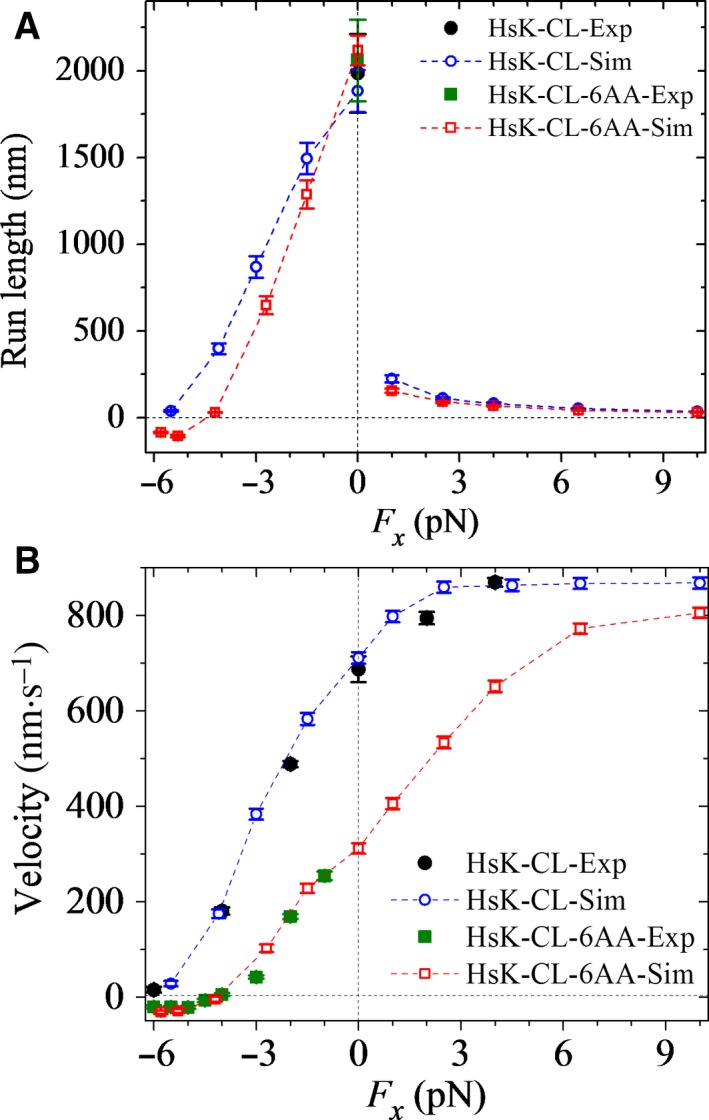
Dependence of run length and velocity of cysteine‐light (CL) human kinesin‐1 upon the external force acting on the coiled‐coil stalk at saturating ATP. Open symbols are calculated data. Error bars represent SEM (n = 1000). (A) Run length versus longitudinal component (F x) of the external force for HsK‐CL (circles) and HsK‐CL‐6AA (squares). Filled symbols are experimental data taken from Yildiz et al. 24. (B) Velocity versus longitudinal component (F x) of the external force for HsK‐CL (circles) and HsK‐CL‐6AA (squares). Filled symbols are experimental data taken from Andreasson et al. 23 and Clancy et al. 25.
Then, we studied the effect of the external force on the run length of CL human kinesin‐1 with extended NLs. Here, we focus on the CL human kinesin‐1 with six additional amino acid residues (e.g. with sequence AEQKLT) inserted into the C‐terminal portion of the linker region of each head (called HsK‐CL‐6AA). Our calculated data of both the run length and velocity are insensitive to the sequences of the inserted amino acids. As mentioned above for DmK‐6AA, we take the same values for all parameters for HsK‐CL‐6AA as those for HsK‐CL except k –D and the force–extension relation of the NL. As mentioned above for DmK‐6AA, we take the rate constant of ADP release from both the leading and trailing heads for HsK‐CL‐6AA to be k –D/σ (σ = 1.8) (see ‘The choice of parameter values’ in Materials and methods). The results of the force–extension relation of the NL of one head for HsK‐CL‐6AA calculated using all‐atom MD simulations are shown in Fig. S4. In Fig. 5A, we also show the calculated results of the run length versus the external force for HsK‐CL‐6AA (open squares), where for comparison, the available experimental value of the run length under no load (filled square) 24 is also shown. The corresponding results for the velocity are shown in Fig. 5B. It is seen that the calculated data for both the run length and velocity are in quantitative agreement with the experimental data. More puzzling, it is noted that the run length of HsK‐CL‐6AA under no load is slightly larger than that of HsK‐CL (Fig. 5A), and by contrast, the run length of DmK‐6AA under no load is much smaller than that of DmK‐WT (Fig. 2A). The contrary features between HsK‐CL‐6AA and DmK‐6AA compared with those with no extension of the NLs are explained as follows.
As mentioned in the above section, the value of E w2 = 40k B T for Drosophila kinesin‐1 gives the detaching of the dimer from MT arising mainly from that occurring during Period II under no load, resulting in the probability of the dimer detaching from MT for DmK‐6AA being larger than that for DmK‐WT. By contrast, the value of E w2 = 43k B T (see Table 1) for CL human kinesin‐1 gives the detaching of the dimer from MT as arising mainly from that occurring during Period I and to a minor extent from that occurring during Period II under no load. Since for HsK‐CL‐6AA, the rate constant of ADP release from the leading head is smaller than that for HsK‐CL, the ensuing ATP binding, ATP hydrolysis, and then Pi release in the leading or MT‐bound head are delayed for HsK‐CL‐6AA relative to those for HsK‐CL. As a result, under no load, the probability for Pi release to occur before NL docking at the intermediate state for HsK‐CL‐6AA is smaller than for HsK‐CL; that is, the probability for Period I to occur for HsK‐CL‐6AA is smaller than for HsK‐CL. Thus, although the probability for Period II to occur for HsK‐CL‐6AA is larger than for HsK‐CL, considering that the detaching during Period II makes a minor contribution it is understandable that the total probability of the dimer detaching from MT in one step for HsK‐CL‐6AA is slightly smaller than that for HsK‐CL. As a result, the run length of the former is slightly larger than that of the latter.
Furthermore, it is interesting to see from Figs 2B and 5B that compared to the case with no extension of the NLs, the velocity of HsK‐CL‐6AA under no load has a larger reduction than DmK‐6AA. By contrast, as shown in Figs 2A and 5A, the run length of HsK‐CL‐6AA under no load is slightly larger than that with no extension of the NLs, whereas the run length of DmK‐6AA is reduced greatly. More interestingly, it is seen from Figs 2B and 5B that even under a large forward load (20 pN), the velocity of DmK‐6AA is evidently smaller than DmK‐WT, and by contrast, only under a moderate forward load (e.g. 9 pN), the velocity of HsK‐CL‐6AA approaches nearly to that of HsK‐CL, which is in agreement with the single‐molecule data of Yildiz et al. 24. Additionally, it is seen from Fig. 5 that HsK‐CL‐6AA is capable of undertaking many rearward steps when –6 pN ≤ F x ≤ –5 pN, with negative velocity and run length, whereas no such processive backstepping is observed for HsK‐CL when F x ≥ –6 pN, with the velocity and run length having positive values. By contrast, from Fig. 2B, it is seen that both DmK‐6AA and DmK‐WT show no such processive backstepping when F x ≥ –6 pN, with positive velocity and run length.
Effect of the presence of additional Pi in solution on run length
For simplicity of analysis, we consider that the presence of additional Pi in solution increases the lifetime of the post‐hydrolysis ADP.Pi state, as done in Milic et al. 22, which can be interpreted as inhibition of Pi release. In the calculation, this consideration is equivalent to the reduction in rate constant of Pi release, k c. Thus, we calculate the run length and velocity for DmK‐WT by taking the value of k c to be decreased by γ‐fold (γ > 1) compared to that used in Fig. 2 and values of other parameters to be the same as those used in Fig. 2. In Fig. 6A,B, we show the calculated results of the run length and velocity, respectively, versus external force with γ = 2.3. For comparisons, the calculated data of Fig. 2 without additional Pi in solution are also reshown in Fig. 6. In insets of Fig. 6, we show the ratios of the calculated run length and velocity in the presence of additional Pi to the corresponding ones without the additional Pi, where for comparison the ratios of available single‐molecule data with 100 mm Pi in solution to the corresponding ones without additional Pi in solution at F x = 4 pN 22 are also shown. The ratios of the calculated run length and velocity in the presence of additional Pi to the corresponding ones without the additional Pi at F x = 4 pN with varying γ are shown in Fig. S5. From Figs 6 and S5, it is seen that with γ = 2.3, the calculated data are in agreement with the single‐molecule data. Moreover, from Figs 6 and S5, we see that the presence of additional Pi increases the run length, which is in agreement with the single‐molecule data 22, and by contrast, the presence of additional Pi decreases the velocity, which is also consistent with the single‐molecule data 22. These are easily understandable because decreasing k c reduces the occurrence probabilities of both Period I and Period II, which results in the reduction in the dissociation probability of the dimer, and decreasing k c reduces evidently the velocity.
Figure 6.
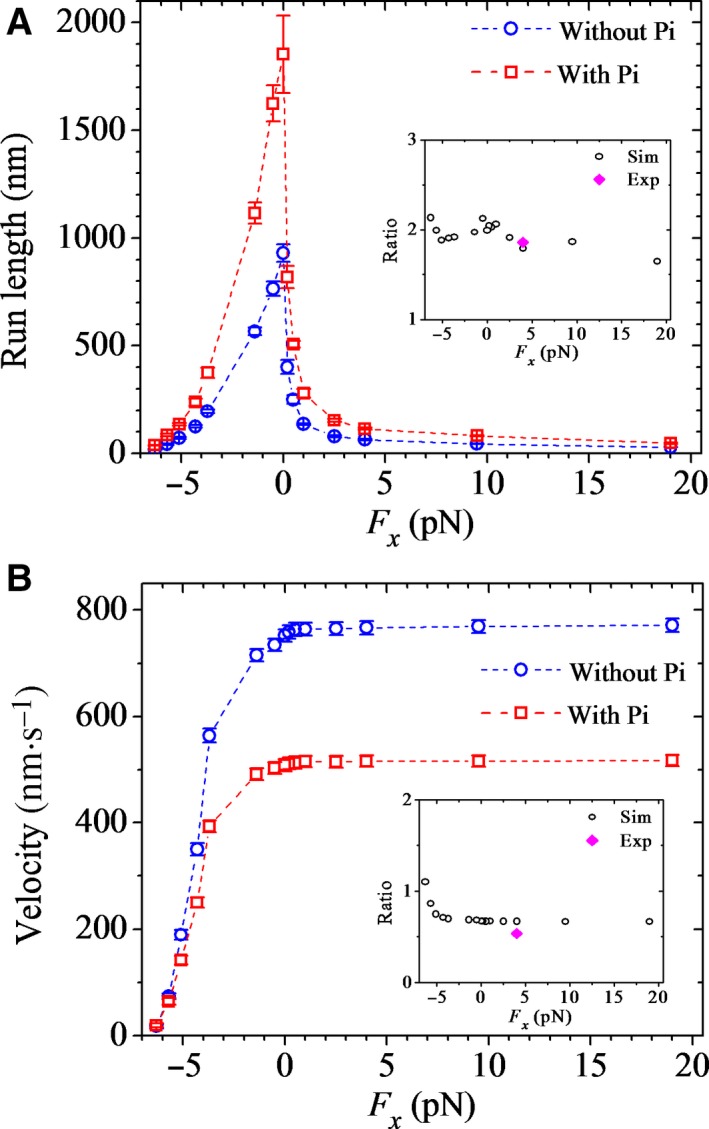
Effects of the presence of additional Pi in solution on run length and velocity of Drosophila kinesin‐1 at saturating ATP. The results are calculated with γ = 2.3. Error bars represent SEM (n = 1000). (A) Run length versus longitudinal component (F x) of the external force acting on the coiled‐coil stalk for DmK‐WT. Inset shows ratios of the run length in the presence of additional Pi in solution to the corresponding one in the absence of additional Pi (open symbols), and the ratio of the experimental data at [Pi] = 100 mm to that at [Pi] = 0 under the forward external force of 4 pN (filled symbol) is also shown 22. (B) Velocity versus longitudinal component (F x) of the external force for DmK‐WT. Inset shows ratios of the velocity in the presence of additional Pi in solution to the corresponding one in the absence of additional Pi (open symbols), and the ratio of the experimental data at [Pi] = 100 mm to that at [Pi] = 0 under the forward external force of 4 pN (filled symbol) is also shown 22.
Dependence of run length on external force acting on one head
In this section, we study the run length and velocity of wild‐type Drosophila kinesin‐1 with one head being attached to a micrometer‐sized bead and an external load acting on the bead, as done in the single‐molecule optical trapping assays of Guydosh and Block 63, explaining the experimental data on the velocity 63 and providing predicted results on the run length. For this case, the equations for the mechanical stepping of the dimers are given in Section S6. By comparing the experimental data of Guydosh and Block 63 with those of Andreasson et al. 23, it is seen that the velocity under no load for the former is slightly smaller than that for the latter. Thus, to be consistent with the experimental data of Guydosh and Block 63, we take k c = 120 s−1, which is smaller than the value given in Table 1, with other parameters having the same values as those given in Table 1.
Figure 7A,B shows our calculated results (open squares) of the load dependences of run length and velocity, respectively, where the corresponding available experimental data on the velocity (filled squares) of Guydosh and Block 63 are also shown. For comparisons, in Fig. 7, we also show the calculated results (open circles) for the case under the external load acting on the bead attached to the coiled‐coil stalk and the corresponding experimental data on the velocity (filled circles) of Guydosh and Block 63. From Fig. 7B, we see that the calculated data on the velocity for both the case with the bead attached to one head and the case with the bead attached to the coiled‐coil stalk are in agreement with the experimental data. Additionally, it is seen that under the forward load, the velocity for the case with the bead attached to one head is slightly larger than that for the case with the bead attached to the coiled‐coil stalk. This is explained as follows. Under the forward load acting on the detached head, after it moves in front of the MT‐bound head, it is still acted on by the forward load, enhancing the probability for the detached head to move directly to the next forward MT‐binding site without staying at the intermediate position for a short time of 1/k NL and thus bringing forward the time of ADP release. By contrast, under the forward load acting on the stalk, after the detached head moves in front of the MT‐bound head, the load acts on the MT‐bound head rather than on the detached head. Thus, the forward load has little effect on the probability for the detached head to move directly to the next forward MT‐binding site.
Figure 7.
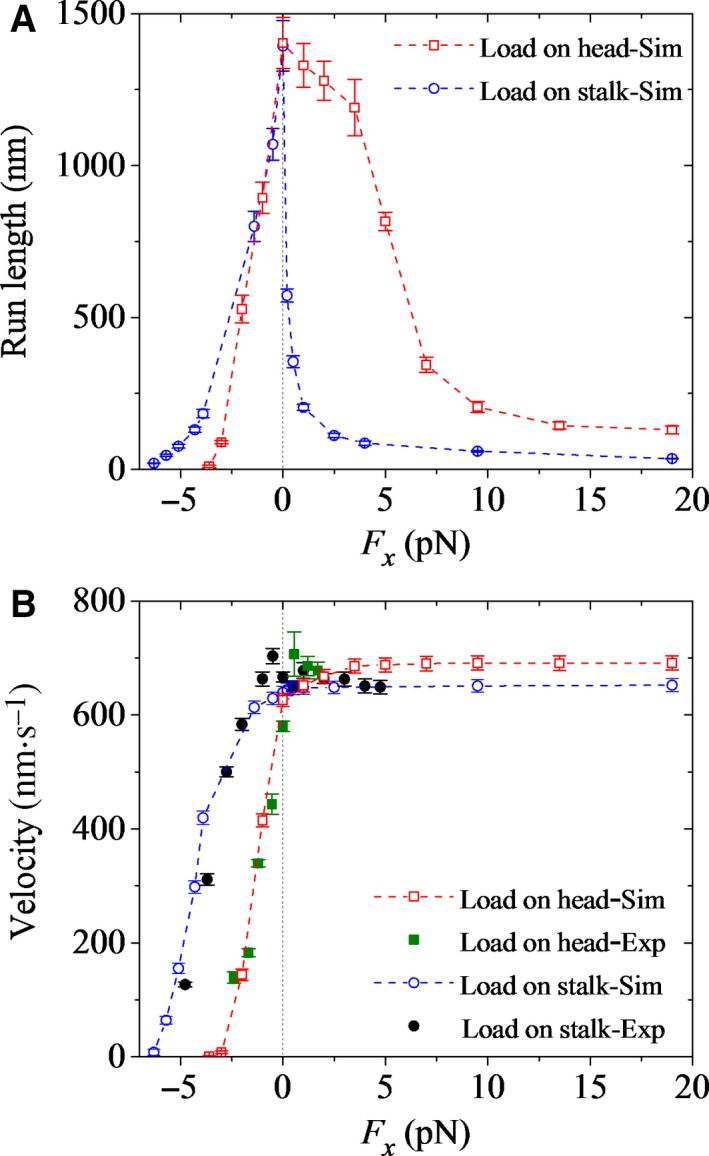
Dependence of run length and velocity of Drosophila kinesin‐1 upon the external force at saturating ATP. Error bars represent SEM (n = 1000). (A) Run length versus longitudinal component (F x) of the external force acting on one head (open squares). For comparisons, the calculated data for the case of the external force acting on the coiled‐coil stalk (open circles) are also shown. (B) Velocity versus longitudinal component (F x) of the external force acting on one head (open squares). For comparisons, the calculated data for the case of the external force acting on the coiled‐coil stalk (open circles) are also shown. Open symbols are calculated data, and filled symbols are experimental data taken from Guydosh and Block 63.
From Fig. 7A, we see that for the case with the bead attached to one head, the run length decreases sensitively with the increase in the magnitude of the backward load, which is similar to the case with the bead attached to the coiled‐coil stalk. This is easily understandable, because for both the cases, the decrease in the run length arises from both the decrease in the velocity and the increase in the rate constant of dissociation of the motor from MT that occurs during Period II. Interestingly, from Fig. 7A, we see that for the case with the bead attached to one head, the run length decreases mildly with the increase in the forward load, which is in contrast to the case with the bead attached to the coiled‐coil stalk, where the run length drops sharply under even a small forward load. In other words, for the former case, the dependence of run length on load is consistent with the expectation from Kramers theory, whereas for the latter case, the dependence of run length on load is contrary to the expectation from Kramers theory. This is because for the former case, the forward load has no effect on the pointing direction of the NL of the MT‐bound head in the intermediate state, whereas for the latter case, the forward load drives the NL of the MT‐bound head to point forward, greatly accelerating its Pi release and thus greatly increasing the occurrence probability of Period I. For the former case, the mild decrease in the run length with the increase in the forward load arises from the mild increase of the rate constant of dissociation of the motor from MT that occurs during Period II. By contrast, for the latter case, the sharp decrease in the run length under even a small forward load arises from the large probability of dissociation that occurs during Period I.
Discussion
In the model presented previously 37, 38, it was assumed that when the MT‐bound head is in the ATP or ADP.Pi state, once the detached head is near the intermediate position, the NL of the MT‐bound head is docked into its motor domain immediately, implying that the NL docking occurs with a rate of k NL → . With this model, diverse experimental data on the dynamics of kinesin‐1 except the processivity were explained quantitatively 37, 38. In this work, to be consistent with the available fluorescence polarization microscopy data 47, we improve the model by assuming that in the intermediate state, k NL has a small value when the MT‐bound head is in the ATP state and has a finite and large value when the MT‐bound head is in the ADP.Pi state to study the processivity of kinesin‐1. This implies that even at saturating ATP, there is a time period in which the detached head is in the intermediate position relative to the MT‐bound head before diffusing to the next MT‐binding site. This is consistent with the recent single‐molecule data of Isojima et al. 60 and Mickolajczyk et al. 52. In the intermediate state with the detached ADP–head bound strongly to the MT‐bound head, the N‐terminal strand β0 of the motor domain of the MT‐bound head and the strand β9 of the NL are in proximity so that the cover–neck bundle is able to form; that is, the NL is able to dock 48, 64. On the other hand, it takes time for the NL docking to complete. As a consequence, it is inferred that the existence of the intermediate state could function biologically to make the NL docking take place efficiently. The NL docking then prevents the tethered ADP–head from moving backward under the backward load after it moves to the position in front of the MT‐bound head, thus increasing the stall force 37 rather than acting as the driving force to make the ADP–head detach from the previous MT‐binding site and then move forward.
Nucleotide‐dependent neck‐linker‐docking efficiency
Based on the fluorescence polarization microscopy data showing that in the ATP state, the NL has a lower docking efficiency than in the ADP.Pi state 47 and the single‐molecule optical trapping and microscopy data 22, 52, it has been proposed that in the ATP state, the NL is only partially docked, while in the ADP.Pi state, the NL docking is complete 22, 52. If this is true, it would imply that with the non‐hydrolyzable ATP analog AMP‐PNP, the dimer cannot transit from the 1HB state into the 2HB state, and only in the ADP.Pi state can the dimer enter into the 2HB state. However, many studies with AMP‐PNP have shown that hydrolysis is not required for the dimer to enter the 2HB state 43, 53, 65, 66, 67. Moreover, the experimental data showed that AMP‐PNP and ATPγS can also trigger release of ADP from a tethered intermediate, but with a much smaller rate than ADP.Pi 52, 53, 54. Thus, to be consistent with all of the experimental data, we propose here that in the ATP state the NL docking is less efficient, with a very slow rate, while in the ADP.Pi state, the NL docking is efficient, with a high rate.
The model can explain diverse aspects of movement dynamics
Since the change of the binding affinity of ADP–head to the previous MT‐binding site from E w1 to E w2 takes a very short time, t r = 10 μs, it is evident that the finite value of k NL (with 1/k NL = 1.25 ms in the ADP.Pi state) has little effect on all of the theoretical data for kinesin‐1 presented in the previous work 37, 38. For example, some typical data are shown in Figs 2B, 5B and 7B showing the effects of the external force and extension of NLs on the velocity, in Fig. S6 showing the effect of NL docking on the velocity, and in Fig. S7 showing the effect of solution viscosity on the velocity. Thus, the modified model presented in this work can not only quantitatively explain diverse experimental data on kinesin‐1 dynamics such as the velocity, mechanochemical coupling ratio, and limping effects, as done in the previous work 37, 38, but also explain quantitatively experimental data on the processivity 22, 23, 24.
The sensitivity of the calculated results to the relevant parameters
As it is time consuming, in this work, we only made detailed calculations with parameter values (see Table 1) that can give good agreement with the available experimental data. It is instructive to see the sensitivity of the calculated results to the relevant parameters. For example, some results for DmK‐WT are given in Fig. S8, where we change one of its parameter values while keeping other parameter values unchanged.
From Fig. S8A, it is seen that changing E NL by 0.6k B T has only a slight (< 1%) effect on the velocity and run length under the forward and low backward loads. Under the large backward load (e.g. F x = –4.3 pN), increasing and decreasing E NL by 0.6k B T increases and decreases the run length by about 1% and 13%, respectively, and increases and decreases the velocity by about 28% and 34%, respectively. This can be understood as follows. The energy barrier E NL prevents the tethered ADP–head in the intermediate position from moving backward to the trailing position. Under the forward and low backward loads, this backward movement probability is very low, and thus changing E NL by a small value has only a slight effect on the motility. Under the large backward load, this backward movement probability is high, and thus changing E NL has a larger effect on the motility.
From Fig. S8B, it is seen that changing E w1 by 1k B T has nearly no effect on both the run length and the velocity. This can be understood as follows. Under the internally stretched force of the NLs for DmK‐WT with both heads bound to MT, after Pi release occurs in the trailing head the head has a nearly 100% probability to escape the potential well of depth E w1 ≤ 20.8k B T within time t r 37. Thus, provided E w1 ≤ 20.8k B T, the change of E w1 has nearly no effect on the motility of DmK‐WT. However, for DmK‐6AA with longer NL length, after Pi release occurs in the trailing head, the head does not have a 100% probability to escape the potential well of depth E w1 = 19.8 k B T within time t r. Thus, the change of E w1 can affect the velocity of DmK‐6AA.
From Fig. S8C, it is seen that increasing and decreasing E w2 by 1k B T increases and decreases the run length, respectively, by about 20–60% under no and backward loads, whereas changing E w2 by 1k B T has a smaller effect (<20%) on the run length under forward load. This can be understood as follows. Under no and backward loads, the run length is determined largely by the dissociation occurring during Period II, with the dissociation rate depending approximately exponentially on E w2. Under the forward load, the run length is determined mainly by the dissociation occurring during Period I, which is independent of E w2, and the dissociation occurring during Period II has a small contribution to the overall dissociation. As expected, under forward and low backward loads, changing E w2 by 1k B T has nearly no effect on the velocity, because the dissociation has nearly no effect on the velocity. However, under a large backward load (e.g. F x = –4.3 pN), increasing and decreasing E w2 by 1k B T increases and decreases the velocity by about 4% and 25%, respectively. This is because decreasing E w2 increases the probability of the leading ADP–head detaching from MT before ADP release, thus increasing the probability of backward stepping under the large backward load.
From Fig. S8D, it is seen that changing k NL by 10% has only a slight effect on the velocity, but increasing and decreasing k NL results in an evident but small (< 6%) increase and decrease in the run length, respectively. This can be understood as follows. Since k NL is large and non‐rate limiting, changing its value by 10% has only a slight effect on the ATPase rate and thus has only a slight effect on the velocity. The occurrence probability of Period I increases with the increase in ratio of k c to k NL. Thus, increasing k NL decreases the occurrence probability of Period I, decreasing the dissociation probability and increasing the run length.
From Fig. S8E, it is seen that increasing and decreasing k c by 10% results in a small (< 3%) increase and decrease in the velocity, respectively. This is easily understandable, because increasing k c increases the ATP rate and thus increases the velocity. On the contrary, increasing and decreasing k c by 10% decreases and increases the run length, respectively, by about 10%. This can be understood as follows. The occurrence probability of Period I increases with the increase in ratio of k c to k NL, and the occurrence probability of Period II increases with the increase in ratio of k c to k –D. Thus, increasing k c increases the occurrence probabilities of both Period I and Period II, increasing the dissociation probability and decreasing the run length.
Concluding remarks
We present an improved model for the processive movement of the dimeric kinesin‐1 molecular motor, with which we study the movement dynamics of the motor, particularly for the run length and velocity, to understand the detailed molecular mechanism of mechanochemical coupling and coordination of the two heads of the dimer during its highly processive movement on MT. The dissociation of the motor from MT occurs during two periods—Period I and Period II—when the motor is in the intermediate or 1HB state. Period I is after Pi release occurs in the MT‐bound head prior to its NL docking and before the affinity of the MT‐bound ADP–head for the local MT changes from much weaker E w1 to weak E w2 (see inset of Fig. 1), while Period II is when the MT‐bound head is in the ADP state with its weak affinity for the local MT being E w2. During other periods when there is at least one head in the nucleotide‐free, ATP, or ADP.Pi state bound strongly to MT, the dissociation of the motor is negligible. In a mechanochemical coupling, both Period I and Period II occur rarely, resulting in a very low probability of dissociation and thus a high processivity.
We provide a quantitative explanation of the puzzling single‐molecule data on the run length versus external load acting on the coiled‐coil stalk, revealing the origin of the dramatically asymmetric character of the run length with respect to the direction of the load and the run length dropping sharply under even a small forward load. The origin is due to the asymmetric occurrence probability of Period I, which is in turn due to the fact that the Pi release rate in the MT‐bound head is much larger when its NL is driven in the forward direction under the forward load than when the NL is not in the forward direction under the backward load. The contrary features of the run length for different types of kinesin‐1 (Drosophila and human kinesins) with extensions of their NLs compared with those without extension of the NLs are explained quantitatively. The origin of the contrary features is as follows. For Drosophila kinesin with E w2 = 40k B T, the dissociation during Period II makes the main contribution to the overall dissociation under no or backward load. By contrast, for human kinesin with E w2 = 43k B T, the dissociation during Period II makes a smaller contribution than Period I to the overall dissociation under no load. The extension of the NLs decreases the ADP‐release rate from the leading head. This increases the occurrence probability of Period II but decreases the occurrence probability of Period I, thus resulting in the decrease in the processivity for Drosophila kinesin but a slight increase of the processivity for human kinesin. In addition, the single‐molecule data on durations of the 1HB and 2HB states during processive movement are explained quantitatively. The single‐molecule data showing the enhancement of the run length by the addition of phosphate in solution are explained well. The computational data on other aspects of the movement dynamics such as the force dependence of velocity are also in quantitative agreement with the available experimental data. In a word, the above diverse, puzzling, and contrary experimental data are explained quantitatively and consistently with the same set of parameter values (Table 1).
Moreover, we predict that in sharp contrast to the case under the forward load acting on the coiled‐coil stalk, the run length only decreases mildly with the forward load acting on one head of the dimer, with the latter case giving an opposite asymmetry of the run length with respect to the direction of the load compared to the former case (Fig. 7A). These predictions can be tested easily by future single‐molecule optical trapping assays.
Author contributions
SG wrote programs, performed simulations, analyzed the data, and reviewed the manuscript. XS and PW analyzed the data and reviewed the manuscript. PX proposed the model, organized the research, analyzed the data, and wrote the manuscript.
Supporting information
Appendix S1. Extended Materials and Methods.
Fig. S1. Force–extension relation of the neck linker of DmK‐WT head.
Fig. S2. Force–extension relation of the neck linker of DmK‐6AA head.
Fig. S3. Force–extension relation of the neck linker of HsK‐CL head.
Fig. S4. Force–extension relation of the neck linker of HsK‐CL‐6AA head.
Fig. S5. Effects of the presence of additional Pi in solution on run length and velocity of DmK‐WT at saturating ATP.
Fig. S6. Effect of the neck linker docking on the velocity of kinesin‐1.
Fig. S7. Effect of the solution viscosity η on the velocity of kinesin‐1.
Fig. S8. The sensitivity of the calculated run length and velocity to the relevant parameters for DmK‐WT.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 11775301) and National Key R&D Program of China (2016YFA0301500).
References
- 1. Vale RD, Reese TS and Sheetz MP (1985) Identification of a novel force‐generating protein, kinesin, involved in microtubule‐based motility. Cell 42, 39–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Kozielski F, Sack S, Marx A, Thormählen M, Schönbrunn E, Biou V, Thompson A, Mandelkow EM and Mandelkow E (1997) The crystal structure of dimeric kinesin and implications for microtubule‐dependent motility. Cell 91, 985–994. [DOI] [PubMed] [Google Scholar]
- 3. Kikkawa M (2008) The role of microtubules in processive kinesin movement. Trends Cell Biol 18, 128–135. [DOI] [PubMed] [Google Scholar]
- 4. Gigant B, Wang W, Dreier B, Jiang Q, Pecqueur L, Plückthun A, Wang C and Knossow M (2013) Structure of a kinesin–tubulin complex and implications for kinesin motility. Nat Struct Mol Biol 20, 1001. [DOI] [PubMed] [Google Scholar]
- 5. Cross RA (2004) The kinetic mechanism of kinesin. Trends Biochem Sci 29, 301–309. [DOI] [PubMed] [Google Scholar]
- 6. Asbury CL (2005) Kinesin: World's tiniest biped. Curr Opin Cell Biol 17, 89–97. [DOI] [PubMed] [Google Scholar]
- 7. Block SM (1998) Leading the procession: new insights into kinesin motors. J Cell Biol 140, 1281–1284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Vale RD and Milligan RA (2000) The way things move: looking under the hood of molecular motor proteins. Science 288, 88–95. [DOI] [PubMed] [Google Scholar]
- 9. Cross RA (2004) Molecular motors: kinesin's interesting limp. Curr Biol 14, R158–R159. [PubMed] [Google Scholar]
- 10. Yildiz A and Selvin PR (2005) Kinesin: walking, crawling or sliding along? Trends Cell Biol 15, 112–120. [DOI] [PubMed] [Google Scholar]
- 11. Svoboda K, Schmidt CF, Schnapp BJ and Block SM (1993) Direct observation of kinesin stepping by optical trapping interferometry. Nature 365, 721–727. [DOI] [PubMed] [Google Scholar]
- 12. Coppin CM, Pierce DW, Hsu L and Vale RD (1997) The load dependence of kinesin's mechanical cycle. Proc Natl Acad Sci USA 94, 8539–8544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Schnitzer MJ and Block SM (1997) Kinesin hydrolyses one ATP per 8‐nm step. Nature 388, 386–390. [DOI] [PubMed] [Google Scholar]
- 14. Kojima H, Muto E, Higuchi H and Yanagida T (1997) Mechanics of single kinesin molecules measured by optical trapping nanometry. Biophys J 73, 2012–2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Visscher K, Schnitzer MJ and Block SM (1999) Single kinesin molecules studied with a molecular force clamp. Nature 400, 184–189. [DOI] [PubMed] [Google Scholar]
- 16. Schnitzer MJ, Visscher K and Block SM (2000) Force production by single kinesin motors. Nat Cell Biol 2, 718–723. [DOI] [PubMed] [Google Scholar]
- 17. Nishiyama M, Higuchi H and Yanagida T (2002) Chemomechanical coupling of the forward and backward steps of single kinesin molecules. Nat Cell Biol 4, 790–797. [DOI] [PubMed] [Google Scholar]
- 18. Asbury CL, Fehr AN and Block SM (2003) Kinesin moves by an asymmetric hand‐over‐hand mechanism. Science 302, 2130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Kaseda K, Higuchi H and Hirose K (2003) Alternate fast and slow stepping of a heterodimeric kinesin molecule. Nat Cell Biol 5, 1079–1082. [DOI] [PubMed] [Google Scholar]
- 20. Carter NJ and Cross RA (2005) Mechanics of the kinesin step. Nature 435, 308–312. [DOI] [PubMed] [Google Scholar]
- 21. Taniguchi Y, Nishiyama M, Ishii Y and Yanagida T (2005) Entropy rectifies the Brownian steps of kinesin. Nat Chem Biol 1, 342–347. [DOI] [PubMed] [Google Scholar]
- 22. Milic B, Andreasson JOL, Hancock WO and Block SM (2014) Kinesin processivity is gated by phosphate release. Proc Natl Acad Sci USA 111, 14136–14140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Andreasson JOL, Milic B, Chen G‐Y, Guydosh NR, Hancock WO & Block SM (2015) Examining kinesin processivity within a general gating framework. eLife 4, e07403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Yildiz A, Tomishige M, Gennerich A and Vale RD (2008) Intramolecular strain coordinates kinesin stepping behavior along microtubules. Cell 134, 1030–1041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Clancy BE, Behnke‐Parks WM, Andreasson JOL, Rosenfeld SS and Block SM (2011) A universal pathway for kinesin stepping. Nat Struct Mol Biol 18, 1020–1027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Fisher ME and Kolomeisky AB (2001) Simple mechanochemistry describes the dynamics of kinesin molecules. Proc Natl Acad Sci USA 98, 7748–7753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Hyeon C and Onuchic JN (2007) Mechanical control of the directional stepping dynamics of the kinesin motor. Proc Natl Acad Sci USA 104, 17382–17387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Wang Z, Feng M, Zheng W and Fan D (2007) Kinesin is an evolutionarily fine‐tuned molecular ratchet‐and‐pawl device of decisively locked direction. Biophys J 93, 3363–3372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Shao Q and Gao YQ (2006) On the hand‐over‐hand mechanism of kinesin. Proc Natl Acad Sci USA 103, 8072–8077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Liepelt S and Lipowsky R (2007) Kinesin's network of chemomechanical motor cycles. Phys Rev Lett 98, 258102. [DOI] [PubMed] [Google Scholar]
- 31. Chowdhury D (2013) Stochastic mechano‐chemical kinetics of molecular motors: a multidisciplinary enterprise from a physicist's perspective. Phys Rep 529, 1–197. [Google Scholar]
- 32. Zhang Z and Thirumalai D (2012) Dissecting the kinematics of the kinesin step. Structure 20, 628–640. [DOI] [PubMed] [Google Scholar]
- 33. Goldtzvik Y, Zhang Z and Thirumalai D (2016) Importance of hydrodynamic interactions in the stepping kinetics of kinesin. J Phys Chem B 120, 2071–2075. [DOI] [PubMed] [Google Scholar]
- 34. Wagoner JA and Dill KA (2016) Molecular motors: power strokes outperform Brownian ratchets. J Phys Chem B 120, 6327–6336. [DOI] [PubMed] [Google Scholar]
- 35. Xie P (2008) Stepping behavior of two‐headed kinesin motors. Biochim Biophys Acta 1777, 1195–1202. [DOI] [PubMed] [Google Scholar]
- 36. Xie P (2010) Mechanism of processive movement of monomeric and dimeric kinesin molecules. Int J Biol Sci 6, 665–674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Guo S‐K, Wang P‐Y and Xie P (2017) A model of processive movement of dimeric kinesin. J Theor Biol 414, 62–75. [DOI] [PubMed] [Google Scholar]
- 38. Guo S‐K, Wang P‐Y and Xie P (2017) Dynamics of dimeric kinesins: limping, effect of longitudinal force, effects of neck linker extension and mutation, and comparison between kinesin‐1 and kinesin‐2. Int J Biol Macromol 105, 1126–1137. [DOI] [PubMed] [Google Scholar]
- 39. Crevel IMTC, Lockhart A and Cross RA (1996) Weak and strong states of kinesin and ncd. J Mol Biol 257, 66–76. [DOI] [PubMed] [Google Scholar]
- 40. Hancock WO and Howard J (1999) Kinesin's processivity results from mechanical and chemical coordination between the ATP hydrolysis cycles of the two motor domains. Proc Natl Acad Sci USA 96, 13147–13152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Sosa H, Peterman EJG, Moerner WE and Goldstein LSB (2001) ADP‐induced rocking of the kinesin motor domain revealed by single‐molecule fluorescence polarization microscopy. Nat Struct Biol 8, 540–544. [DOI] [PubMed] [Google Scholar]
- 42. Quinlan ME, Forkey JN and Goldman YE (2001) Kinesin‐ADP: whole lotta shakin’ goin’ on. Nat Struct Biol 8, 478–480. [DOI] [PubMed] [Google Scholar]
- 43. Uemura S, Kawaguchi K, Yajima J, Edamatsu M, Toyoshima YY and Si Ishiwata (2002) Kinesin–microtubule binding depends on both nucleotide state and loading direction. Proc Natl Acad Sci USA 99, 5977–5981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Cross RA (2016) Mechanochemistry of the kinesin‐1 ATPase. Biopolymers 105, 476–482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Morikawa M, Yajima H, Nitta R, Inoue S, Ogura T, Sato C and Hirokawa N (2015) X‐ray and Cryo‐EM structures reveal mutual conformational changes of Kinesin and GTP‐state microtubules upon binding. EMBO J 34, 1270–1286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Rice S, Lin AW, Safer D, Hart CL, Naber N, Carragher BO, Cain SM, Pechatnikova E, Wilson‐Kubalek EM, Whittaker M et al (1999) A structural change in the kinesin motor protein that drives motility. Nature 402, 778–784. [DOI] [PubMed] [Google Scholar]
- 47. Asenjo AB, Weinberg Y and Sosa H (2006) Nucleotide binding and hydrolysis induces a disorder‐order transition in the kinesin neck‐linker region. Nat Struct Mol Biol 13, 648–654. [DOI] [PubMed] [Google Scholar]
- 48. Khalil AS, Appleyard DC, Labno AK, Georges A, Karplus M, Belcher AM, Hwang W and Lang MJ (2008) Kinesin's cover‐neck bundle folds forward to generate force. Proc Natl Acad Sci USA 105, 19247–19252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Hackney DD (1994) Evidence for alternating head catalysis by kinesin during microtubule‐stimulated ATP hydrolysis. Proc Natl Acad Sci USA 91, 6865–6869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Xie P, Dou S‐X and Wang P‐Y (2007) Processivity of single‐headed kinesin motors. Biochim Biophys Acta 1767, 1418–1427. [DOI] [PubMed] [Google Scholar]
- 51. Xie P (2016) Dynamic relationships between ribosomal conformational and RNA positional changes during ribosomal translocation. Heliyon 2, e00214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Mickolajczyk KJ, Deffenbaugh NC, Ortega Arroyo J, Andrecka J, Kukura P and Hancock WO (2015) Kinetics of nucleotide‐dependent structural transitions in the kinesin‐1 hydrolysis cycle. Proc Natl Acad Sci USA 112, E7186–E7193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Ma Y‐Z and Taylor EW (1997) Interacting head mechanism of microtubule‐kinesin ATPase. J Biol Chem 272, 724–730. [DOI] [PubMed] [Google Scholar]
- 54. Farrell CM, Mackey AT, Klumpp LM and Gilbert SP (2002) The role of ATP hydrolysis for kinesin processivity. J Biol Chem 277, 17079–17087. [DOI] [PubMed] [Google Scholar]
- 55. Rosenfeld SS, Jefferson GM and King PH (2001) ATP reorients the neck linker of kinesin in two sequential steps. J Biol Chem 276, 40167–40174. [DOI] [PubMed] [Google Scholar]
- 56. Gilbert SP, Moyer ML and Johnson KA (1998) Alternating site mechanism of the kinesin ATPase. Biochemistry 37, 792–799. [DOI] [PubMed] [Google Scholar]
- 57. Dogan MY, Can S, Cleary FB, Purde V and Yildiz A (2015) Kinesin's front head is gated by the backward orientation of its neck linker. Cell Rep 10, 1967–1973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Cao L, Wang W, Jiang Q, Wang C, Knossow M and Gigant B (2014) The structure of apo‐kinesin bound to tubulin links the nucleotide cycle to movement. Nat Commun 5, 5364. [DOI] [PubMed] [Google Scholar]
- 59. Uemura S and Si Ishiwata (2003) Loading direction regulates the affinity of ADP for kinesin. Nat Struct Mol Biol 10, 308–311. [DOI] [PubMed] [Google Scholar]
- 60. Isojima H, Iino R, Niitani Y, Noji H and Tomishige M (2016) Direct observation of intermediate states during the stepping motion of kinesin‐1. Nat Chem Biol 12, 290–297. [DOI] [PubMed] [Google Scholar]
- 61. Alonso MC, Drummond DR, Kain S, Hoeng J, Amos L and Cross RA (2007) An ATP gate controls tubulin binding by the tethered head of kinesin‐1. Science 316, 120–123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62. Mickolajczyk KJ and Hancock WO (2017) Kinesin processivity is determined by a kinetic race from a vulnerable one‐head‐bound state. Biophys J 112, 2615–2623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Guydosh NR and Block SM (2009) Direct observation of the binding state of the kinesin head to the microtubule. Nature 461, 125–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64. Hwang W, Lang MJ and Karplus M (2008) Force generation in kinesin hinges on cover‐neck bundle formation. Structure 16, 62–71. [DOI] [PubMed] [Google Scholar]
- 65. Mori T, Vale RD and Tomishige M (2007) How kinesin waits between steps. Nature 450, 750–754. [DOI] [PubMed] [Google Scholar]
- 66. Asenjo AB and Sosa H (2009) A mobile kinesin‐head intermediate during the ATP‐waiting state. Proc Natl Acad Sci USA 106, 5657–5662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Asenjo AB, Krohn N and Sosa H (2003) Configuration of the two kinesin motor domains during ATP hydrolysis. Nat Struct Biol 10, 836–842. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1. Extended Materials and Methods.
Fig. S1. Force–extension relation of the neck linker of DmK‐WT head.
Fig. S2. Force–extension relation of the neck linker of DmK‐6AA head.
Fig. S3. Force–extension relation of the neck linker of HsK‐CL head.
Fig. S4. Force–extension relation of the neck linker of HsK‐CL‐6AA head.
Fig. S5. Effects of the presence of additional Pi in solution on run length and velocity of DmK‐WT at saturating ATP.
Fig. S6. Effect of the neck linker docking on the velocity of kinesin‐1.
Fig. S7. Effect of the solution viscosity η on the velocity of kinesin‐1.
Fig. S8. The sensitivity of the calculated run length and velocity to the relevant parameters for DmK‐WT.


