Designing Well-Structured Cyclic Pentapeptides Based on Sequence–Structure Relationships

Abstract

Cyclic peptides are a promising class of molecules for unique applications. Unfortunately, cyclic peptide design is severely limited by the difficulty in predicting the conformations they will adopt in solution. In this work, we use explicit-solvent molecular dynamics simulations to design well-structured cyclic peptides by studying their sequence–structure relationships. Critical to our approach is an enhanced sampling method that exploits the essential transitional motions of cyclic peptides to efficiently sample their conformational space. We simulated a range of cyclic pentapeptides from all-glycine to a library of cyclo-(X₁X₂AAA) peptides to map their conformational space and determine cooperative effects of neighboring residues. By combining the results from all cyclo-(X₁X₂AAA) peptides, we developed a scoring function to predict the structural preferences for X₁-X₂ residues within cyclic pentapeptides. Using this scoring function, we designed a cyclic pentapeptide, cyclo-(GNSRV), predicted to be well structured in aqueous solution. Subsequent CD and NMR spectroscopy revealed that this cyclic pentapeptide is indeed well structured in water, with NOE and J-coupling values consistent with the predicted structure.

Graphical Abstract

INTRODUCTION

Cyclic peptides (CPs) have promising applications in nanotechnology,^1–3 as well as potential therapeutics, targeting a variety of protein–protein interactions (PPIs).^4–12 PPIs play critical roles in important and disease-relevant biological processes.^13,14 Modulating PPIs thus provides a means to control diverse cellular functions for both fundamental research and disease intervention.^15,16 Despite the promise of CPs for these applications, de novo design of well-structured CPs in aqueous solution remains challenging. CPs tend to form multiple conformations in solution,^17–28 making them difficult to design or even characterize. Furthermore, the limited availability of solution structural information makes it difficult to develop sequence–structure relationships for CPs. Currently, there is no tractable experimental method to synthesize and characterize the structural ensembles of hundreds of CPs to determine which CPs are well structured, and ultimately to understand how CP sequences control structures.^29–32

While experimental determination of structural ensembles is difficult, there have been many promising contributions from computational simulations.^33–51 Recently, we developed a novel, highly efficient enhanced sampling method custom-tailored to CPs by identifying their essential transitional motions (coupled two-dihedral angle movements).⁴⁹ This enhanced sampling method has made it possible for us to quickly and efficiently sample a CP’s structural ensemble, with the inclusion of explicit water.^49–51 This platform produces more rapidly converged results, allowing us to simulate more systems than was previously possible. This advance has made it much more feasible to gather the broad simulation data needed to study sequence–structure relationships for CPs. In this work, we used this method to systematically simulate over 70 head-to-tail cyclized pentapeptides, uncovered their sequence–structure relationships and ultimately designed a well-structured CP.

MATERIALS AND METHODS

Model peptides

The following model peptides were used in this study: cyclo-(GGGGG); cyclo-(X₁AAAA), where X₁ was any of the 20 natural amino acids; cyclo-(X₁X₂AAA), where X₁/X₂ was G, A, V, F, R, D, N or S; cyclo-(GFSEV); cyclo-(GNSRV) and cyclo-(GFNDV). Two different initial structures of each CP, S1 and S2 (structure 1 and structure 2, respectively), were prepared using the Chimera molecular modeling package.⁵² To construct each CP, the linear peptide was first built, followed by linkage of the N- and C- terminal residues and subsequent energy minimization.

Bias-exchange metadynamics simulations

Following preparation in Chimera, each initial structure was solvated using a pre-equilibrated box of water molecules. Minimal number of ions were added to neutralize the charge of the whole system. Each structure was then energy minimized using the steepest descent algorithm, followed by a four-step equilibration process. First, to allow the solvent molecules to equilibrate, a 50 ps isochoric–isothermal (NVT) simulation followed by a 50 ps isobaric–isothermal (NPT) simulation were performed. In both simulations, a harmonic constraint was placed on the peptide heavy atoms, with a force constant of 1,000 kJ/mol·nm². Subsequently, a 100 ps NVT simulation followed by a 100 ps NPT simulation were performed without any restraints, to equilibrate the entire system. A thermostat of 300 K and a barostat of 1 bar were used for all equilibrations.

The NPT ensemble was used for all BE-META production simulations. The temperature was maintained at 300 K using the V-rescale thermostat,⁵³ with a time coupling constant of 0.1 ps. The CP and the solvent were coupled to two separate thermostats, in order to mitigate the “hot solvent–cold solute” problem.^54,55 The pressure was maintained at 1 bar using the Berendsen barostat⁵⁶ was used to maintain the pressure at 1 bar, with a time coupling constant of 2.0 ps and an isothermal compressibility of 4.5×10⁻⁵ bar⁻¹. All bonds involving hydrogen were constrained using the LINCS algorithm.⁵⁷ Dynamics of the system were evolved using the leapfrog algorithm,⁵⁸ with a time step of 2 fs. Both short-range Lennard-Jones and electrostatic nonbonded interactions were truncated at 1.0 nm. Beyond the cutoff distance, Particle Mesh Ewald (PME)⁵⁹ was used for the electrostatic interactions, with a Fourier spacing of 0.12 nm and an interpolation order of 4. A long-range dispersion correction⁶⁰ for the energy and pressure was used for the Lennard-Jones interaction beyond the cutoff. All trajectories were saved every 1 ps for subsequent analysis.

All simulations were performed using the RSFF2 force field⁶¹ with TIP3P water⁶² in Gromacs 4.6.7⁶³ with the PLUMED 2 plugin.⁶⁴ The RSFF2 force field was found to accurately recapitulate several CP crystal structures⁴⁸ and therefore will be used throughout this work. Conformational sampling of all CPs was enhanced using BE-META simulations. The collective variables (CVs) in the BE-META simulations consist of two types of 2D biases. The first 2D bias is along ϕ_i×ψ_i, where ϕ/ψ are the backbone dihedral angles of the same residue. The second type of 2D bias is along ψ of one residue and ϕ of the next residue, ψ_i×ϕ_i+1. These 2D biases were previously found to enhance the conformational sampling of CPs efficiently.⁴⁹ Both types of the 2D biases are performed on each residue, giving a total of 10 biased replicas for a cyclic pentapeptide. Gaussian hills were deposited every 4 ps, with a height of 0.1 kJ/mol and a width of 0.314 rad. Exchanges were attempted every 5 ps between different replicas. For analysis of an unbiased structural ensemble, five neutral replicas were added, giving a total of 15 replicas per CP.

Principal component and cluster analysis

To characterize the structural ensemble of each CP, the last 50 ns of the unbiased replicas were analyzed using dihedral principal component analysis (dPCA) with the ϕ and ψ angles of all residues.^65,66 However, if the peptide sequence is homogeneous (i.e. cyclo-(AAAAA)) an additional step needs to be performed prior to dPCA. To take degeneracy into account, the previously developed root-mean-square deviation (RMSD) scheme was applied.⁴⁹ In brief, first the ϕ/ψ dihedral angles of the neutral replicas were calculated. For a cyclic pentapeptide with a homogeneous sequence there are five ways of reordering each frame. The RMSD to a reference structure was calculated for each of the five permutations, and the structure with the lowest RMSD to the reference structure was used to reorder the CP.

Following dPCA, the population of each cluster was calculated using a density peak-based cluster analysis.⁶⁷ For cluster analysis, the principal subspace along the first three principal components (PC1, PC2 and PC3) was divided into 50×50×50 grids. Only grids with a population greater than 0.1 were used in cluster analysis. The population of each cluster was determined by summing the population of every grid the cluster contained. dPCA and cluster analysis was used to analyze the structural ensembles of cyclo-(X₁AAAA), cyclo-(X₁X₂AAA), cyclo-(GFSEV), cyclo-(GNSRV) and cyclo-(GFDNV).

Simulation convergence was monitored using the normalized integrated product (NIP)³⁸ of the density profiles along PC1, PC2 and PC3 of the S1 and S2 simulations. Convergence was achieved when the density profiles were similar. Final simulation lengths ranged from 100 ns to 300 ns. All further analysis was performed on the S1 simulations.

Cut-off turn analysis

Due to their highly constrained nature, cyclic pentapeptides typically form structures containing a β-turn plus a tight turn on the opposite side of the CP. The four commonly observed β-turns and tight turns give a total of 16 turn combinations (Figure 1A). However, for cyclo-(GGGGG), dPCA and cluster analysis did not identify all 16 turn combinations. To determine whether all turn combinations were present in cyclo-(GGGGG), turns were identified if the ϕ/ψ dihedral angles were within 35° of the ideal values for a specific type of turn (Figure 1A). Similarly, this cut-off based turn type analysis was used to compare all 16 types of turn combinations in the cyclo-(X₁AAAA) and cyclo-(X₁X₂AAA) pentapeptides (Figures 3A and S1), as the dPCA–cluster analysis was unable to pick up combinations with very low populations.

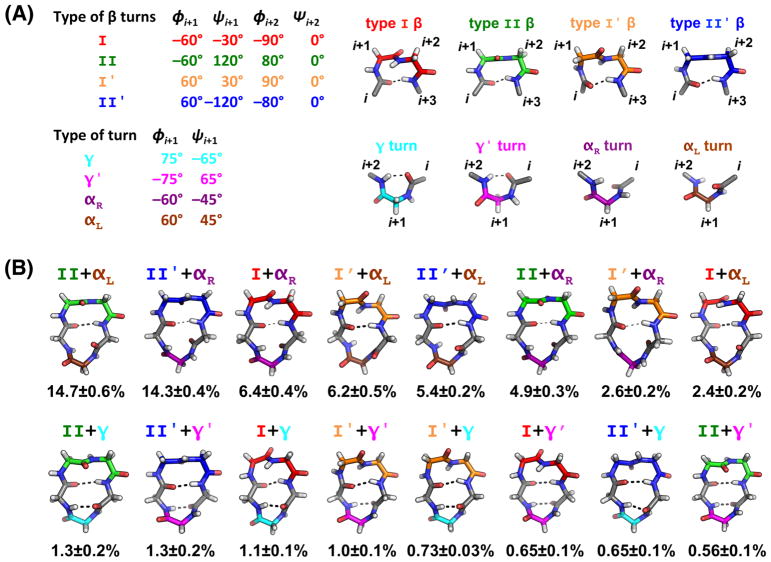
Figure 1.

Cyclic pentapeptides typically form a β-turn plus a tight γ/γ′ or α_R/α_L turn opposite the β-turn. (A) Ideal dihedral angles, representative structures and hydrogen bond patterns for the four types of β-turns and four types of tight turns. (B) Populations and representative structures for the 16 turn types from our BE-META simulations of cyclo-(GGGGG). Type I, I′, II and II′ β-turns are shown in red, orange, green and blue, respectively. Tight turns γ, γ′, α_R and α_L are shown in cyan, magenta, purple and brown, respectively. Populations and standard deviation were calculated from the five neutral replicas of the S1 simulations.

Figure 3.

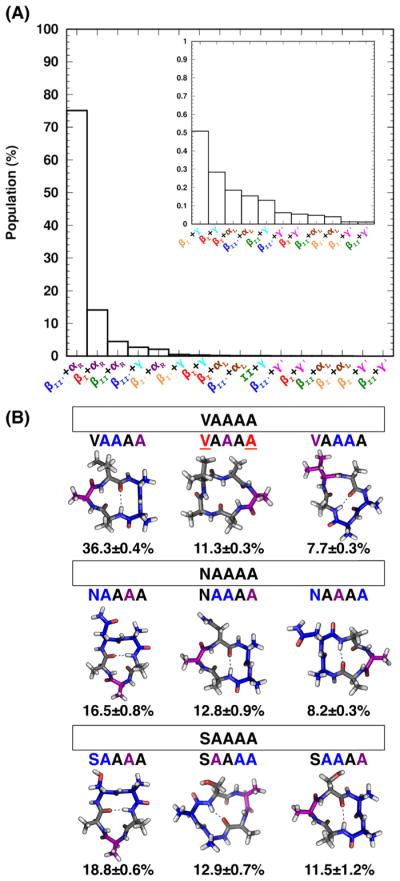
(A) Populations of 16 turn combinations from simulations of cyclo-(X₁AAAA). Results use the cut-off turn analysis (see Materials and Methods for analysis details). (B) Populations and representative structures of the three most populated clusters of cyclo-(VAAAA), cyclo-(NAAAA) and cyclo-(SAAAA). Type II′ β-turn and α_R turn are shown and their locations in the sequences highlighted in blue and purple, respectively. The location of distorted type I β-turn in the sequence is highlighted in red and underlined. Populations and standard deviation were calculated from the five neutral replicas of the S1 simulations.

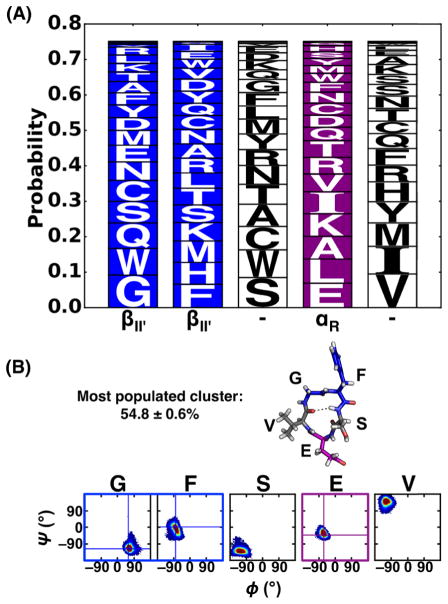
Logo plot for individual amino acids from cyclo-(X₁AAAA) simulations

To determine the most probable amino acid for each position of a given turn combination, we weighted X₁ in cyclo-(X₁AAAA) using the following scheme. The preference of the amino acid X₁, when X₁ ≠ A, for each of the five locations within a given turn combination was determined by its population from cut-off turn analysis. In the case of cyclo-(AAAAA), there are five degenerate amino acids, and the population was divided by five for the associated position in the logo plot. The logo plot for cyclo-(X₁AAAA) for the β_II′+α_Rturn combination is shown in Figure 4A.

Figure 4.

(A) Logo plot for cyclo-(X₁AAAA) with the β_II′+α_R turn combination. Results use cut- off turn analysis of the S1 simulations (see Materials and Methods for analysis details). Type II′ β-turn and α_R turn are shown and their locations in the sequences highlighted in blue and purple, respectively. (B) Population, representative structure and Ramachandran plot for the most populated cluster of cyclo-(GFSEV). Type II′ β-turn and α_R turn are shown in blue and purple boxes, respectively. Population and standard deviation was calculated from the five neutral replicas of the S1 simulation.

Neighbor analysis for X₁X₂ from cyclo-(X₁X₂AAA) simulations

To help design well-structured cyclic peptides, a scoring function based on neighboring residues was developed using the simulation results of cyclo-(X₁X₂AAA), where X₁/X₂ is G, V, F, R, D, N and S. To evaluate the preference score for a sequence cyclo-(X₁X₂X₃X₄X₅) to adopt a specific β-turn at X₁X₂ and a specific tight turn at X₄, the sequence was broken down into five sets of nearest neighbor pairs – X₁X₂, X₂X₃, X₃X₄, X₄X₅ and X₅X₁, and the total preference score was the sum of the five populations for each pair to adopt the desired structure in the simulations of cyclo-(X₁X₂AAA), cyclo-(X₂X₃AAA), etc. For example, the score for sequence cyclo-(X₁X₂X₃X₄X₅) adopting a type II′ β-turn at X₁X₂ and an α_R turn at X₄ was calculated as follows. We analyzed the structural ensemble of cyclo-(X₁X₂AAA) using the cut-off based turn analysis to evaluate the population of cyclo-(X₁X₂AAA) that adopts a type II′ β-turn at X₁X₂ and an α_R turn at A⁴, the population of cyclo-(AX₂X₃AA) that adopts a type II′ β-turn at ¹AX² and an α_R turn at A⁴, the population of cyclo-(AAX₃X₄A) that adopts a type II′ β-turn at ¹AA² and an α_R turn at X⁴, etc. The score was then calculated as the sum of these five populations, when each pair is located at the desired location of the target turn combination (example for cyclo-(GNSRV) shown in Figure 5A).

Figure 5.

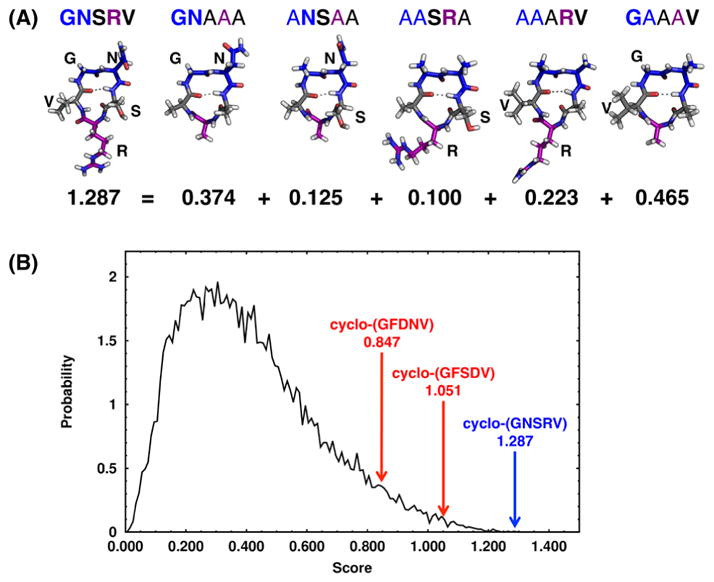
Cyclo-(GNSRV) was predicted to have high preference to adopt a β_II′+α_R turn combination based on neighbor pair scoring. (A) (Top) β_II′+α_R turn combination for cyclo-(GNSRV) and its five parent sequences: cyclo-(GNAAA), cyclo-(ANSAA), cyclo-(AASRA), cyclo-(AAARV) and cyclo-(GAAAV). Neighbor pairs are bolded, and type II′ β-turn and tight turn α_R are shown in blue and purple, respectively. (Bottom) Neighbor scores, which were calculated from using cut-off analysis for the corresponding β_II′+α_R turn combination. (B) Distribution of scores for the β_II′+α_R turn combination for the 16,807 sequences of cyclo-(X₁X₂X₃X₄X₅), where X₁/X₂/X₃/X₄/X₅ were G, V, F, R, D, N or S. Well-structured CP cyclo-(GNSRV) and its score is highlighted in blue. Cyclo-(GFSDV), the proxy of cyclo-(GFSEV), from simulations of cyclo-(X₁AAAA), and cyclo-(GFDNV) and their associated scores are highlighted in red.

Thermodynamics decomposition

To further understand the structural ensemble of a CP, we performed thermodynamics decomposition of the S1 simulation. ΔG between clusters was calculated using the Boltzmann equation, using the ratios of cluster populations and the most populated cluster as a reference. ΔG was then further separated into ΔH and ΔS, where ΔH was estimated from the difference in potential energy between clusters. ΔH was then further decomposed into peptide in vacuum ( $\mathrm{\Delta }{H}_{\mathrm{P}}^{\text{vac}}$) and the rest (ΔH_rest). To perform this decomposition, the potential energy of two groups was calculated: peptide and solvent/ions (note that ions may not be present in all systems). The peptide enthalpy ( $\mathrm{\Delta }{H}_{\mathrm{P}}^{\text{vac}}$) consisted of peptide Lennard-Jones ( $\mathrm{\Delta }{H}_{\mathrm{P}}^{\text{LJ}}$), short-range and 1,4 electrostatics ( $\mathrm{\Delta }{H}_{\mathrm{P}}^{\text{EE}(\text{SR}+1,4)}$), bonds ( $\mathrm{\Delta }{H}_{\mathrm{P}}^{\text{bond}}$), angles ( $\mathrm{\Delta }{H}_{\mathrm{P}}^{\text{angle}}$), proper dihedrals ( $\mathrm{\Delta }{H}_{\mathrm{P}}^{\text{dih.}}$) and improper dihedrals ( $\mathrm{\Delta }{H}_{\mathrm{P}}^{\text{imp.}}$). ΔS was further decomposed into configurational entropy of the peptide ( $\mathrm{\Delta }{S}_{\mathrm{P}}^{\text{conf}}$) and solvation entropy (ΔS_w). $\mathrm{\Delta }{S}_{\mathrm{P}}^{\text{conf}}$ was calculated using the maximum information spanning tree (MIST)^68–70 method and ΔS_w was calculated using $\mathrm{\Delta }{S}_{\mathrm{w}}=\mathrm{\Delta }S-\mathrm{\Delta }{S}_{\mathrm{P}}^{\text{conf}}$.

Linear peptide synthesis

The linear peptide was synthesized at 0.04 mmol scale on HMPB-ChemMatrix resin (PCAS BioMatrix Inc., loading = 0.5 mmol/g). The linear peptides was prepared with C-terminal glycine to facilitate head-to-tail cyclization. The HMPB resin was firstly functionalized with glycine: 5 mmol Fmoc-glycine-OH and 2.5 mmol N,N′-diisopropylcarbodiimide (DIC) were dissolved in 15 mL dimethylformamide (DMF). After 10 minutes at room temperature, the mixture was added to 0.75 g HMPB resin in a 20-mL Torviq fritted syringe. After another 1 minute, 0.05 mmol 4-dimethylaminopyridine (DMAP) was added and reacted at room temperature for 16 hours, followed by 3 times wash with DMF, twice 5 min deprotection with 20% (v/v) piperidine in DMF and 4 times wash with DMF. The resin was washed thoroughly with dichloromethane (DCM) and dried under vacuum. Following solid-phase peptide synthesis (SPPS) was carried out on a synthesizer for automated flow peptide synthesis (AFPS).⁷¹ After completion of the SPPS, the resin was washed thoroughly with DCM and dried under vacuum. The resins were transferred to a 50-mL plastic tube and the peptide was simultaneously cleaved from the resin and side-chain deprotected by treatment with 2.5% (v/v) water, 2.5% (v/v) 1,2-ethanedithiol (EDT), and 1% (v/v) triisoproprylsilane in neat trifluoroacetic acid (TFA) for 2 hours at room temperature. The resulting solution containing peptide was triturated and washed with cold diethyl ether (pre-chilled in –80° C freezer) two times. The obtained gummy-like solid was dissolved in 50% H₂O: 50% acetonitrile containing 0.1% TFA and lyophilized.

Peptide cyclization and purification

The lyophilized crude peptide was directly used for cyclization. Cyclization condition: 0.5 mM peptide, 1.5 mM 1-[bis(dimethylamino)methylene]-1H-1,2,3-triazolo[4,5-b]pyridinium 3-oxid hexafluorophosphate (HATU), 3 mM N,N-diisopropylethylamine (DIEA), DMF as solvent, room temperature for 1 hour. The cyclization reaction was quenched by adding TFA. After removing solvents by rotary evaporator, the reaction mixture was re-dissolved in water containing 10% dimethyl sulfoxide (DMSO) and purified on Agilent 1260 Infinity Automated LC/MS Purification System, with a semi- preparative Reverse Phase-HPLC column (Agilent Zorbax 300SB C₃ column: 21.2 × 250 mm, 7 μm, linear gradient: 1–41% B over 80 min, flow rate: 4 mL/min). The purity of fractions was confirmed by LC-MS analysis. The fractions containing pure cyclized peptide were combined and lyophilized to yield cyclized peptide powder.

NMR characterization

The peptide was dissolved in H₂O:D₂O (90:10) at a concentration of roughly 3.5 mM. 1D and 2D ¹H NMR spectra were recorded on a Bruker 600 MHz spectrometer with CryoProbe at 288 K. Complete resonance assignments were made using homonuclear ¹H–¹H TOCSY and ROESY experiments. Standard pulse programs available from the Bruker library were used, with mixing times of 60 ms for the TOCSY and 250 ms for the ROESY. ¹H chemical shifts were referenced to DSS (δ 0.00 ppm) in water. ³J_NH, C_Hα coupling constants were measured from 1D ¹H NMR.

CD characterization

Compounds were dissolved in water to concentrations of 87.5 μM as measured by peptide weight. Equal concentrations of the peptides were verified prior to CD analysis by subjecting peptides to analytical HPLC and normalizing based on peak volumes. CD spectra were obtained on a Jasco J-815 CD Spectrometer at 20° C using the following measurement parameters: wavelength range 190–260 nm; step resolution, 0.5 nm; speed, 20 nm/min; accumulations, 3; response, 1 sec; bandwidth, 1 nm; path length, 0.1 cm.

RESULTS AND DISCUSSION

Structural ensembles of cyclo-(GGGGG) and cyclo-(AAAAA) map out the available conformational space for simple cyclic pentapeptides

Cyclic pentapeptides typically form a β-turn plus a tight turn opposite the β-turn.^72–79 There are four types of β-turns (β_I, β_II, β_I′, and β_II′) and four types of tight turns (γ, γ′, α_R and α_L) that are commonly observed (Figure 1A), leading to 16 possible turn combinations for cyclic pentapeptides. A cyclic pentapeptide with a β-turn and a tight turn of γ or inverse-γ (γ′) tend to form two intra-peptide hydrogen bonds (Figure 1B, bottom row), while a cyclic pentapeptide having a β-turn and a tight turn with a dihedral angle of a right-handed or left-handed α-helix (α_R and α_L, respectively) will form only one intra-peptide hydrogen bond (at the β-turn site; Figure 1B, top row). All these 16 turn combinations were seen in our bias-exchange metadynamics (BE-META) simulations of cyclo-(GGGGG) and are shown in Figure 1B. The most populated conformation was a β_II+α_L, with a population of 14.7 ± 0.6%. We observed that the mirror-image turn combination, β_II′+α_R, has a similar population (14.3 ± 0.4%) as β_II+α_L. Since glycine is achiral, theoretically, conformations that are mirror images of each other should have exactly the same population. In our simulations of cyclo-(GGGGG), each conformation and its mirror image indeed had similar populations (Figure 1B), further supporting convergence of our simulation results.

Among the 16 turn combinations observed in cyclo-(GGGGG), all clusters with an α_R/α_L turn (top row of Figure 1B) were more populated than clusters with a γ/γ′ turn (bottom row of Figure 1B). To further understand this structural preference of cyclo-(GGGGG), we performed thermodynamics decomposition on the 16 clusters (Table S1). The thermodynamics of clusters 1 and 2 were almost identical, which is consistent with the fact that they are mirror images of each other (β_II+α_L vs. β_II′+α_R). The third and fourth most populated clusters, β_I+α_R and β_I′+α_L, had more favorable solvation enthalpy compared to the most populated clusters. However, they both had an unfavorable peptide enthalpy relative to the top clusters (most populated clusters; β_II+α_L and β_II′+α_R), arising from unfavorable electrostatics, angles and dihedrals. Clusters 5 and 6 formed the β_II′+α_L and β_II+α_R turn combinations, respectively, and were less stable than the most populated clusters due to peptide electrostatics and dihedrals. The least populated turn combinations involving α_L and α_R, β_I′+α_R and β_I+α_L (clusters 7 and 8) had unfavorable peptide angles and dihedrals compared to the most populated cluster.

In contrast to clusters 1–8, clusters 9–16 formed a γ/γ′ turn instead of adopting an α_R/α_L conformation. Since clusters with a γ/γ′ turn form two intra-peptide hydrogen bonds, their peptide electrostatics were more favorable than the most populated cluster (Table S1). However, clusters with a γ/γ′ turn all had unfavorable angles and dihedrals as well as unfavorable solvation enthalpy, relative to the top cluster. A combination of these factors makes clusters with γ/γ′ turns have lower populations than their α_R/α_Lcounterparts.

Moving from achiral glycine to the simplest all L-amino acid peptide, cyclo-(AAAAA), we expected turn combinations involving an α_R turn to be preferred over an α_L turn, based on the ϕ angle preferences for an L-amino acid. The four most populated clusters of cyclo-(AAAAA) from our BE-META simulation are shown in Figure 2, and indeed all these turn combinations had a tight α_R turn rather than a tight α_L turn, corresponding to clusters 2, 3, 6, and 7 in Figure 1B for cyclo-(GGGGG). Similar to cyclo-(GGGGG), β_II′+α_R was the most favorable turn combination, with a population of 52.9 ± 0.7%. The second most populated cluster formed a distorted type β_I+α_R, where the distorted type I β-turn had nearly ideal dihedral angles for a type I β-turn, but deviation in the ψ angle of the i+2 residue results in a turn that does not frequently hydrogen bond.

Figure 2.

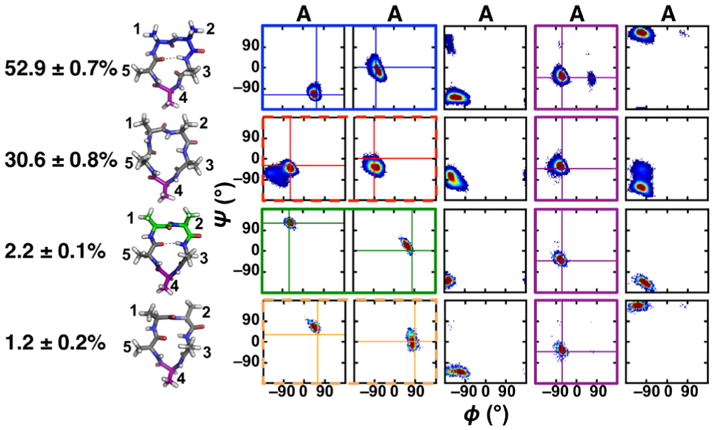
Populations, representative structures and Ramachandran plots for the top four clusters of cyclo-(AAAAA). Type II β, type II′ β and α_Rturns are shown and boxed in the Ramachandran plots in green, blue and purple, respectively. Distorted type I and I ′ β-turns are boxed in the Ramachandran plots by red and orange dashed lines, respectively. Populations and standard deviation were calculated from the five neutral replicas of the S1 simulation.

Breaking down the thermodynamics of cyclo-(AAAAA), the distorted β_I+α_R cluster had less favorable electrostatics and dihedrals compared to the most populated β_II′+α_R turn combination (Table S2). The third and fourth most populated clusters formed a β_II+α_R and a distorted type β_I′+α_R, and compared to cyclo-(GGGGG), the preferred order of all the α_R-containing clusters remained the same. Both clusters 3 and 4 were less favorable than the most populated cluster due to entropy, specifically peptide configurational entropy. Looking at the peptide contribution to the thermodynamics, clusters 3 and 4 have poor electrostatics and cluster 4 (distorted β_I′+α_R) also had unfavorable angles compared to the most populated β_II′+α_R( Table S2).

Overall, for the thermodynamics of cyclo-(GGGGG), we found that the most populated conformation, and its mirror-image counterpart, are stabilized over the other clusters via either peptide or solvation enthalpy. The most populated conformation of cyclo-(AAAAA), on the other hand, is entropically more favorable than the other clusters due to either configurational or solvation entropy. The complex balance between peptide enthalpy, solvation enthalpy and entropy for these two simple cyclic pentapeptide systems reaffirms the necessity of using explicit water in CP simulations to accurately describe each thermodynamic factor.

Structural ensembles of cyclo-(XAAAA) show structural preferences of each amino acid

To understand how different amino acids affect structural preferences of a cyclic pentapeptide, we performed BE-META simulations of cyclo-(X₁AAAA), where X₁ was any of the 20 basic amino acids. The population and turn combination of the three most populated clusters for each of these 20 sequences are given in Table S3. We found that the turn combination β_II′+α_R was by far the most prevalent, accounting for ~75% of all the turn combinations that form for these 20 CPs (Figure 3A). The second most populated turn combination was a distorted β_I+α_R (~14%). Although β_II′+α_R predominated among the turn combinations observed for these 20 CPs, the locations of the type II′ β-turn and the α_R residue varied within the X₁AAAA sequence (Figure 3B and Table S3).

By combining the results from all 20 cyclo-(X₁AAAA) CPs, we constructed a logo plot showing the probability of each amino acid for each location in the β_II′+α_R turn combination (Figure 4A). We hypothesized that combining the most probable amino acid at every position of the β_II′+α_R-structured cyclic pentapeptide would produce a sequence that adopts a well-structured conformation. Based on the results shown in Figure 4A, the sequence, cyclo-(GFSEV), was predicted to be the most structured for a β_II′+α_R turn combination, with the β_II′ turn located at ¹GF² and α_R turn located at E⁴. To verify this prediction, this designed sequence was simulated using BE-META simulations to characterize its structural ensemble. The most populated cluster (55%) of cyclo-(GFSEV) was indeed the β_II′+α_R turn combination, with the type II′ β-turn at ¹GF² and a tight α_R turn at E⁴ (Figure 4B). However, this population (~55%) was not significantly higher than the most populated cluster of simple cyclo-(AAAAA) (~53%). This result suggests that the structural preferences for each of the 20 amino acids within cyclo-(X₁AAAA) are not necessarily additive, implying that neighboring residues might affect each other’s structural preferences. This would explain why merely using results from cyclo-(X₁AAAA) studies was unable to design a particularly well-structured cyclic pentapeptide.

Structural ensembles of cyclo-(X₁X₂AAA) reveal cooperative effects between neighboring amino acids

To understand the effects of neighboring amino acids on the structural ensemble of a cyclic pentapeptide, we performed BE-META simulations of cyclo-(X₁X₂AAA), where X₁/X₂ was G, A, V, F, R, D, N or S. These eight amino acids were chosen as a representative subsection of the 20 basic amino acids. The populations and turn combinations of the three most populated clusters for each of these 56 sequences is given in Table S4. Similar to cyclo- (X₁AAAA), most of the top clusters formed a tight α_R turn, which is consistent with the ϕ angle preferences for an L-amino acid. However, there were a few instances where a γ turn occurs in the top three clusters. Nonetheless, we observed that β_II′+α_R remains the most prevalent in all 56 cyclo-(X₁X₂AAA) CPs, similar to cyclo-(X₁AAAA) (Figure S1 compared to Figure 3A). In fact, β_II′+α_R was the most populated cluster for 49 out of the 56 sequences. However, turn locations varied in the top clusters forming β_II′+α_R, depending on their sequences.

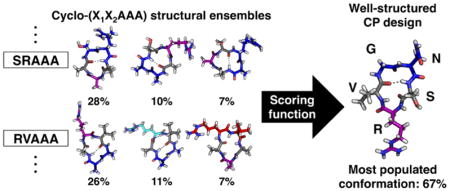
Rational design of well-structured CPs

To help design a well-structured cyclic pentapeptide, we used the structural ensemble results of cyclo-(X₁X₂AAA) CPs to develop a scoring function based on the observed populations for the desired conformation. The scoring function combined the structural preferences of each neighboring pair (X₁X₂, X₂X₃, etc.) in a cyclic pentapeptide cyclo-(X₁X₂X₃X₄X₅) for a specific conformation (see “Neighbor analysis for X₁X₂ in cyclo-(X₁X₂AAA)” in Materials and Methods in the SI). Since alanine was a common filler amino acid in the cyclo-(X₁X₂AAA) data set, we first ignored A and only analyzed structural preferences and developed scoring functions for X₁X₂ pairs, where X₁/X₂ was G, V, F, R, D, N or S. The sequences and scores for the 20 highest-scoring cyclo-(X₁X₂X₃X₄X₅) sequences for the β_II′+α_R turn combination, with a type II′ β-turn at X₁X₂ and an α_R turn at X₄, are given in Table S5. Of all 16,807 sequences, cyclo-(GNSRV) received the highest score (1.287) for the β_II′+α_R turn combination (Figure 5A and highlighted in blue in Figure 5B). To verify this prediction, BE-META simulations of cyclo-(GNSRV) were performed. The simulation results revealed a well-structured conformational ensemble, with the most populated cluster forming a type II′ β-turn at ¹GN² and a tight α_R turn at R⁴, as predicted by the scoring function, with a population of 67% (Figure 6A).

Figure 6.

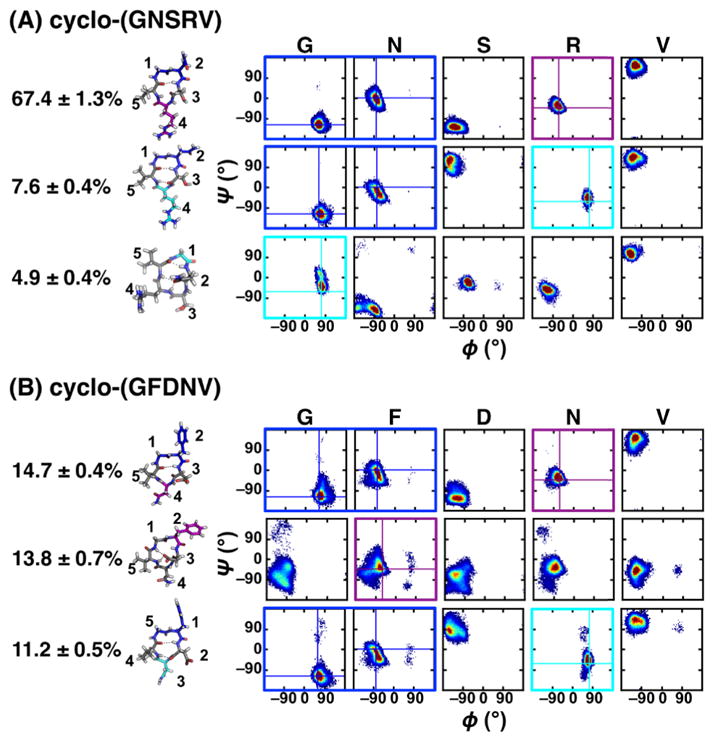
Populations, representative structures and Ramachandran plots for the top three clusters of (A) cyclo-(GNSRV) and (B) cyclo-(GFDNV). Type II′ β-turns are shown in blue boxes. Tight turns γ and α_R are shown in cyan and purple boxes, respectively. Populations and standard deviation were calculated from the five neutral replicas of the S1 simulation.

To further understand why cyclo-(GNSRV) is well-structured, we performed thermodynamics decomposition on this peptide and on the five parent cyclo-(X₁X₂AAA) peptides that contain the five relevant neighbor pairs (Table S6). Comparing the location of the turns in cyclo-(GNSRV) to the locations of the turns in the five parent sequences, cyclo-(GNAAA), cyclo-(AAARV) and cyclo-(GAAAV) all had the β_II′+α_R turns at the same location as cyclo-(GNSRV) in the most populated cluster. However, in cyclo-(ANSAA) and cyclo-(AASRA), the β_II′+α_R turn combination corresponding to cyclo-(GNSRV) occurred as the third and second most populated clusters, respectively. The comparison of the thermodynamics of cyclo-(GNSRV) and the five parent sequences shows that a variety of factors stabilized the most populated clusters, and that these factors are generally consistent among the five neighbor-pair peptides and cyclo-(GNSRV). For example, the most populated cluster of cyclo-(GNSRV), cyclo-(AAARV) and cyclo-(GAAAV) formed a β_II′+α_R, while the second most populated cluster formed a β_II′+γ with the γ turn is at the same residues as the α_R turn. In all three simulations, the top clusters were stabilized over the second clusters due to enthalpy. Specifically, even though the β_II′+γ clusters have more favorable intra-peptide electrostatics, they have more unfavorable dihedrals and much more unfavorable solvation enthalpy as compared to the most populated cluster. Interestingly, the most populated conformation of cyclo-(GNSRV) is both enthalpically and entropically stabilized over clusters 2 and 3. This is unlike any of the other five parent sequences, whose most populated cluster is stabilized by either enthalpy or entropy alone.

Previously, using the simulation results of cyclo-(X₁AAAA), where X₁ was any of the 20 basic amino acids, cyclo-(GFSEV) was predicted to have the highest preference for the β_II′+α_R turn combination. However, BE-META simulations of cyclo-(GFSEV) showed that the population of the desired structure (β_II′+α_R) was only 55%, a modest improvement from the 53% in cyclo- (AAAAA). Indeed, when using the scoring functions derived from the cyclo-(X₁X₂AAA) simulations results, the score for the β_II′+α_R conformation for cyclo-(GFSDV), the proxy of cyclo-(GFSEV) since in the cyclo-(X₁X₂AAA) data set X₁/X₂ could only be G, V, F, R, D, N or S, ranked poorly at number 277, with a score of 1.051 (highlighted in red in Figure 5B). This observation verified the importance of incorporating the neighboring effects in scoring the cyclic peptide’s structural preference.

The predicted II′+α_R structure of cyclo-(GNSRV) is supported by NMR

To corroborate our simulation predictions, we synthesized cyclo-(GNSRV) and characterized its structure in aqueous solution. NMR spectroscopy provided high-resolution data describing the structural ensemble of cyclo-(GNSRV) in water. The 1D spectrum and 2D spectra from ROESY and TOCSY experiments provided ample evidence that cyclo-(GNSRV) was well structured in water (Figures S2–S5), and these data were wholly consistent with the predicted type II′ β-turn at ¹GN² and α_R turn at R⁴ (Table S7–S8). Overall, protons had unique, well-resolved and well-dispersed chemical shifts, consistent with a single predominant structure. We observed several NOEs that support the predicted β_II′+α_R structure. For example, for types I and I′ β-turns, the distance between the H_N protons of the i+1 and i+2 residues and the distance between the H_N protons of the i+2 and i+3 residues are both small (< 3 Å); on the other hand, in types II and II′ β-turns, only the distance between the H_N protons of the i+2 and i+3 residues is small (< 3 Å) (Figure 1A). In the ROESY spectra of cyclo-(GNSRV) we observed a strong NOE between Asn²(H_N) and Ser³(H_N), but no NOE was observed between Gly1(H_N) and Asn2(H_N) (Figure 7A; Figure S6; Table S7). The presence of this specific H_N–H_N NOE and the lack of the other provides strong support for a type II or II′ β-turn at residues ¹GN², rather than a type I or I′ β-turn. Similarly, the distance between the H_N protons of the i+1 and i+2 residues is only small in a α_R or α_L turn, but not in a γ or γ′ turn (Figure 1A). We observed a strong NOE between Arg⁴(H_N) and Val5(H_N) (Figure S6; Table S7), which supports a α_R turn centered at Arg4. J-values allowed estimation of the ϕ angle for Arg⁴ at –60 ± 30° (Figure S6; Table S8), which is consistent with an α_R turn rather than an α_L turn. Similarly, the ϕ angles for Ser³ and Val⁵ were estimated at –120 ± 30° based on the J-values, which are also in agreement with the predicted structure (Figure 6A; Figure S6 and Table S8).

Figure 7.

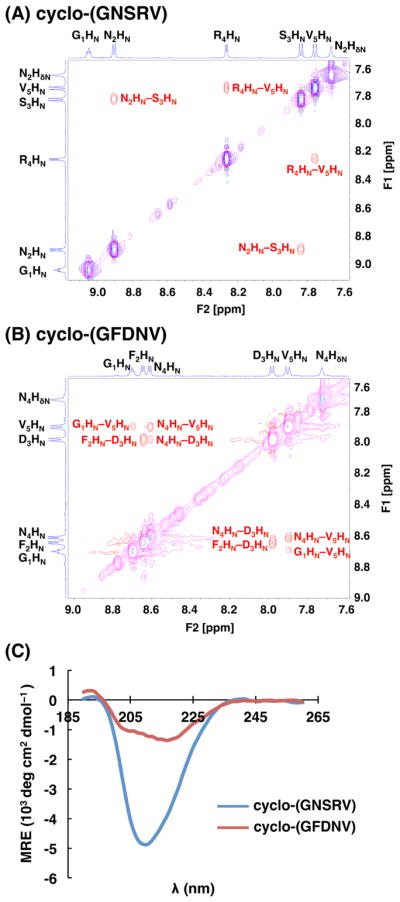
Structural characterization of cyclo-(GNSRV) and cyclo-(GFDNV). (A) H_N region of ROESY spectrum (red, magenta) for cyclo-(GNSRV). TOCSY spectrum (blue, cyan) is overlaid to highlight separate spin systems. Two ROESY cross-peaks were observed in this region, between N₂H_N and S₃H_N and between R₄H_N and V₅H_N. (B) H_N region of ROESY and TOCSY spectra for cyclo-(GFDNV). Four different ROESY N_H-N_H cross-peaks were observed. (C) Circular dichroism spectra for both cyclic peptides at 87.5 μM in aqueous solution at 20 °C, plotted as mean residue ellipticity (MRE).

Design of an unstructured control for cyclo-(GNSRV)

We observed that one of the parent sequences of the well-structured cyclo-(GNSRV), cyclo-(VGAAA), adopted a relatively structured β_II′+α_R configuration (58%; Table S4), suggesting that it might be possible that any cyclic pentapeptide containing the VG motif would have a rather strong preference for the β_II′+α_R configuration regardless of the rest of the sequence. To test this hypothesis, based on our scoring function, we designed a negative control, cyclo-(GFDNV) (highlighted in red in Figure 5B), which contained the VG motif but had a low score for the β_II′+α_R configuration. BE-META simulations showed that although the most populated cluster of cyclo-(GFDNV) still adopted a type II′ β-turn at residues ¹GF² and an α_R turn at N⁴, its population was, however, a mere 14.7% (Figure 6B).

To corroborate the simulation results of our negative control, we synthesized and characterized cyclo-(GFDNV) using NMR spectroscopy (Figures S7–S10; Tables S9–S10). Overall, specific NOEs and J-values consistent with a single predominant structure, as observed for cyclo-(GNSRV), were not observed for cyclo-(GFDNV). For instance, instead of a distinct, selective pattern of H_N–H_N NOEs, we observed four out of the five possible H_N–H_N NOEs (Figure 7B; Table S9). This indicates that no one single structure predominates in solution, but that multiple different structures with various underlying turn combinations are present. Also, J-values allowed estimation of ϕ angles for Asp³ and Val⁵. Both of these values were estimated at –120 ± 30°, which was not consistent with an α-turn at either residue (Table S10). Finally, we observed an additional set of peaks within the NMR spectrum of cyclo-(GFDNV) that integrated to roughly 33% of the total peak volume (Figure S11). These are consistent with the presence of two or more conformations within the ensemble that are stable on the NMR timescale. This is another clear indicator that this peptide does not have a single predominant structure in aqueous solution.

CD spectroscopy is complementary to NMR and provides a low-resolution but informative measurement of the extent of peptide structure in solution. As shown in Figure 7C, the CD spectra of cyclo-(GNSRV) and cyclo-(GFDNV) show broad minima between 208 and 218 nm, consistent with mixed α-helical and β-sheet structures. The negative ellipticity from cyclo-(GNSRV) is roughly fourfold more intense than that of cyclo-(GFDNV). Though it is difficult to calculate the degree of structure accurately from CD data for cyclic peptides this small, these data do indicate a much higher degree of structure for cyclo-(GNSRV) compared to cyclo-(GFDNV).

CONCLUSIONS

In summary, using an efficient enhanced sampling method tailored for CPs, we characterized the structural ensembles of more than 70 head-to-tail cyclized pentapeptides. We demonstrated the value of these data by using them to rationally design a CP with a high degree of structure in water. We note that although this designed CP sequence is well structured despite a lack of proline residues. Inclusion of proline is a common strategy to stabilize turn structures but limits the design space for CP development.⁸⁰

While the scoring function derived from cyclo-(X₁X₂AAA) enabled us to design well-structured CPs that adopt the β_II′+α_R turn combination, the distribution of the scores shows that most sequences are likely not well-structured (Figure 5B). Furthermore, the scores for the other turn combinations (such as β_I+α_R) are all minimal, suggesting that it would be extremely unlikely to favor these conformations using simple sequence substitutions. For example, cyclo-(AFDAG) has the highest score to adopt β_I+α_R, with the type I β-turn at ¹AF² and the tight α_R turn at A⁴. However, this score is only 0.208. BE-META simulation of cyclo-(AFDAG) shows that indeed the top cluster of this CP was β_I+α_R, however, with a population of < 30%. Therefore, to design well-structured cyclic pentapeptides that adopt conformations other than the β_II′+α_R turn combination demonstrated here, non-natural amino acids are likely needed. D-amino acids are a logical choice, though incorporating other non-natural amino acids, such as N-methylated amino acids, β-amino acids and proline analogs may also prove to be useful tools for CP design. The effects of incorporating these non-natural amino acids are currently being investigated.

Having a simulation method which exploits the essential transitional motions of CPs has allowed us to efficiently simulate more than 70 head-to-tail cyclized pentapeptides and thereby better understand their sequence–structure relationships. We demonstrated the value of these data by using them to rationally design a CP with a high degree of structure in water. This method is not limited to cyclic pentapeptides or head-to-tail cyclized peptides, and can be readily extended to larger systems or macrocycles cyclized by other linking chemistries. This work is a clear demonstration of how rigorous, explicit-solvent simulation methods are opening new opportunities to rationally design CPs with desired structures, providing a platform to rationally design novel CPs.