Dynamic modulation of external conditions can transform chemistry into logic gates

Abstract

We introduce a new method for transforming chemical systems into desired logical operators (e.g. NAND gates) or similar signal-manipulation components. The method is based upon open-loop dynamic regulation, where external conditions such as feed-rate, lighting conditions, etc., are modulated according to a prescribed temporal sequence that is independent of the input to the network. The method is first introduced using a simple didactic model. We then show its application in transforming a well-stirred cubic autocatalytic reaction (often referred to as the Selkov–Gray–Scott model) into a logical NAND gate. We also comment on the applicability of the method to biological and other systems.

1. Introduction

Natural computing is a broad field of research at the intersection of computer science, physics, chemistry and biology. Its two main areas are the study of biology-inspired computing (e.g. neural networks and genetic algorithms), and information processing in organisms, including, for example, the computational aspects of self-assembly and biochemical reactions—see Rozenberg et al. [1] for a review. These research areas are largely inspired by the impressive adaptivity demonstrated by living systems. Even the simplest single-celled organisms are capable of adaptation, and whether one sees this as a computational process (e.g. [2,3]), or one focuses upon sensorimotor feedback dynamics [4,5], it is interesting to consider how these organisms, which lack nervous tissues, can use chemical processes to ‘process information’, i.e. to transform sensory input into functional motor output.

A recurring goal in this area is to implement chemistry-based ‘information processing units’ such as logic gates. Efforts to build logic gates and other signal-processing devices out of chemistry date back at least as far as 1974 [6], and a range of approaches, both theoretical and experimental, have been taken. These involve diverse chemical media, including biochemical systems (e.g. enzyme reaction networks [7,8], gene-regulatory networks [9–11], peptide-based computing [12] and DNA-computing [13]); abiotic chemistry (e.g. Belousov–Zhabotinsky oscillators [14], the bistable iodate–arsenous acid reaction [15] or other molecules [16]); and mathematical idealizations or abstractions of chemistry (sometimes referred to as ‘artificial chemistry’ [17]), where networks are designed to satisfy various desiderata and the constraints of actual chemistry are, for the moment, ignored. One example of this last class of study can be found in the work of Hjemfelt et al. [18–20], who proposed a reaction motif that recreates McCulloch–Pitts neuron dynamics and that can be assembled into networks that accomplish Boolean operations. This work was then used to implement a chemistry based pattern-generator neural network using the bistable iodate–arsenous acid reaction run in a continuous flow stirred-tank reactor (CSTR) [15].

The target behaviours in these studies include switching and rectification [7], mimicking the behaviour of neurons [18–20], and other functions, but perhaps the most popular goal has been to recreate the Boolean operations of logic gates such as AND, XOR, NAND, etc. Part of the appeal of logic gates is that they are sufficient for implementing flip-flop memory units, half-adders and the other networks from which modern computers are made.

Often, the first step for implementing chemistry-based logic gates is to decide how the Boolean values (true and false) will be represented. The most intuitive way to do so is to equate certain reactant concentrations with Boolean values (e.g. high acidity = true; low acidity = false) and to identify or develop chemical reactions that transform those concentrations in ways that correspond to the desired Boolean operations. Other representations are also possible. For instance in excitable media [21], the presence or the absence of chemical waves can be used to play the role of binary logic values, chemical wave propagation in narrow capillary tubes play the role of information transmission between inputs and outputs, and the specific geometric configuration of capillary tubes dictates the computation to be done. A similar idea is explored in [22], where the network of capillary tubes is replaced by a ‘printed circuit’ of catalyst. This idea of using excitable media is pushed further by Adamatzky and co-workers [23,24] (see also [25–27] for reviews). In their approach, localized excitations (wave fragments) are sent on ballistic trajectories in an architecture less excitable medium. Computation is the result of the interactions between the localized excitations, and complicated logic circuits can be implemented in this collision-based computing paradigm.

In general, chemistry does not naturally perform these kinds of operations. In other words, substantial human intervention is required to produce chemical-logic gates, and it is interesting to consider for a moment the forms of these interventions. In a few rare cases, such as template-molecule-based DNA-computing or gene-regulatory networks, researchers can select the reactants so as to design reaction networks. This is only possible for rather small reaction networks, with relatively recent work [28] reporting that ‘the largest and most complex program constructed so far’ consists of three gates, built using 11 regulatory proteins. This pales in comparison to silicon-based logic gates (modern CPUs have hundreds of millions of gates), but evolution works under different constraints and to accomplish different goals from human engineered computers. It will be interesting to see how this area advances.

When it is not possible to arbitrarily design reaction networks (and this is the more typical scenario), the alternative is to construct an environment (i.e. ‘external’ or ‘boundary’ conditions) in which the chemistry operates, so as to cause it to perform the desired operation. This is most easily seen in Adamatzky's and others' work in excitable media, where the shape of the spatial boundaries causes the propagating waves to interact as desired, but the same idea underlies the development of logic gates based upon bistable reactions in CSTRs [29], or light modulated Belousov–Zhabotinsky micro-droplets [14], etc. In these latter cases, the external conditions are not (only) the shape or properties of the containers, but also include feed-rates, lighting conditions or other phenomena that influence the chemical reactions in various ways.

It is well established that varying the external conditions of chemical systems can change their dynamical regimes. This change can be quantitative, such as when light is used to influence decay or reaction rates [30–34], or qualitative, when a parameter crosses a bifurcation point, such as the use of light to suppress oscillations in the chlorine dioxide–iodine–malonic acid reaction [35].

In all cases that we are aware of, the developers of chemical logic gates have employed static external conditions, i.e. conditions that do not change during the evaluation of logical operation(s)¹. In this paper, we show that in some cases a sequence of external conditions is sufficient to transform a well-stirred chemical system (sometimes referred to as the Selkov–Gray–Scott model [36,37]) into one capable of logical operations. Note that the method presented here is conceptually very different from other approaches in the field. Instead of designing a (sometimes extremely) fine-tuned chemical system with fixed external conditions to perform a logical operation, we subject an existing chemical system to a prescribed temporal sequence of changes in its external conditions. We argue that this type of reasoning is more likely to be applicable to biological systems.

The rest of this paper is organized as follows. Because the method we are presenting is new, we first provide in §2 a didactic example, where our ‘dynamic external condition’ method is applied to a minimal mathematical toy example. We then show that the method can transform a well-known cubic autocatalytic chemical model into a logic gate in §3. We finally discuss the applicability of the method to biological and other systems in §4.

2. Dynamic external conditions in a simple toy example

For illustrative purposes, we now show how modulation of a dynamical system's parameters can transform it into a logical NOT gate, which transforms true input into false and false input into true (the action of a NOT gate is shown in table 1). For our base dynamical system, we will consider a bead on a saddle-shaped wire (figure 1). Depending on where the bead is placed, it will slide into one of the two ‘troughs’. To identify such a dynamical system with a logic gate, it is necessary to specify what is meant by inputs and outputs for that gate. In this toy example, we decide that inputs are determined by which half-side of the wire the bead is initially placed and outputs are determined by which trough the bead ends up in. For both input and output, we consider the right (left) half to correspond with a true (false) value. The motion of the bead represents the operation of the gate.

Table 1.

NOT logic table.

input	output
TRUE	FALSE
FALSE	TRUE

Figure 1.

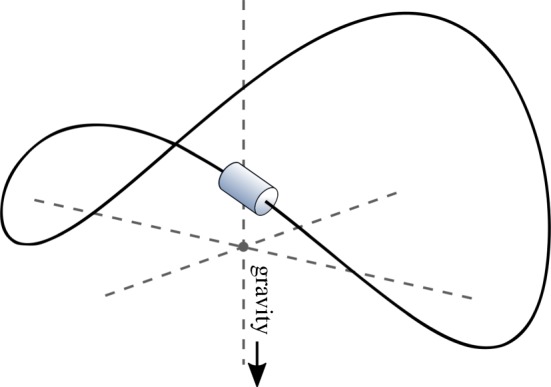
Bead moving on a saddle-shaped wire used as a toy model to implement a NOT gate. Note that the projection of the saddle-shaped wire on the horizontal plane gives a circle (as depicted in figure 2) and that gravity is pointing down. (Online version in colour.)

As it stands, this system does not represent a NOT gate. The bead ends in the same trough in which it starts and so the system can be considered an IDENTITY gate, where true input produces true output and false input produces false output. Indeed no matter the shape of the wire, no static configuration of the wire would be able to accomplish a NOT operation. To cause the bead to switch sides and thus the system to act as a NOT gate, we can subject the saddle-shaped wire to a predetermined sequence of rotations² that take place after the bead is placed in a way that is entirely independent of the bead's location. The rotations are comparable to changes in the external conditions of the bead.

We make these ideas mathematically precise by considering the following one-dimensional periodic dynamical system:

2.1

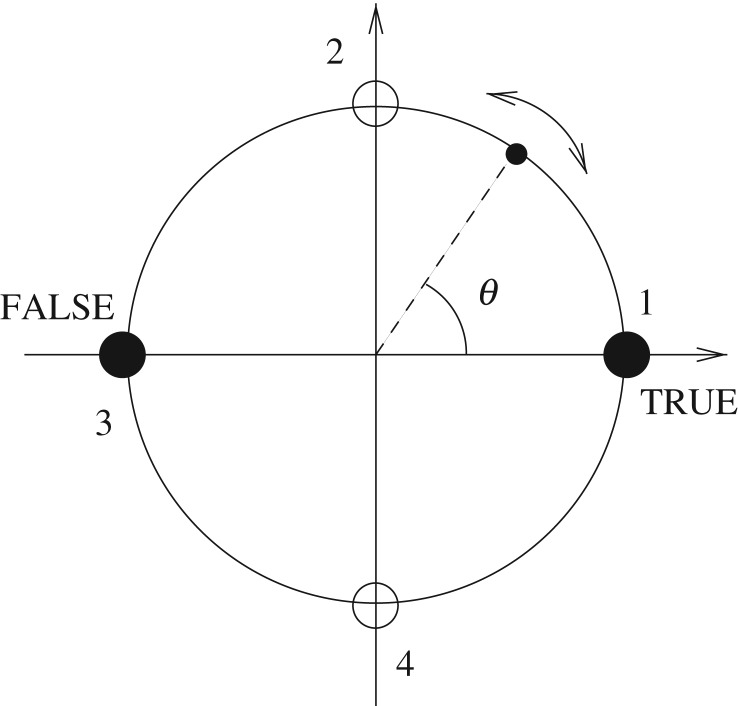
where θ(t) denotes the angular position of a bead moving on a circle and ϕ is a phase parameter. The angular velocity of the bead depends on its position and can be either positive (counterclockwise) or negative (clockwise), depending on the sign of the sine function in equation (2.1). The fixed points of the system are θ^*₁ = ϕ/2, θ^*₂ = π/2 + ϕ/2, θ^*₃ = π + ϕ/2 and θ^*₄ = 3π/2 + ϕ/2. θ^*₁ and θ^*₃ are attractive fixed points, while θ^*₂ and θ^*₄ are repulsive. The phase, ϕ, implements rotations of the saddle-shaped wire around the vertical axis of figure 1, as discussed below. When ϕ = 0, for any initial condition in the right (left) half-circle θ_RHC (θ_LHC), the bead asymptotically goes to the fixed point θ^*₁ (θ^*₃). The system thus has two basins of attraction, and the separatrix, i.e. the manifold separating those basins, is the points θ^*₂ and θ^*₄. As described above, we associate the attractor of each of these basins with Boolean values, such that θ^*₁ ≡ true and θ^*₃ ≡ false. Figure 2 illustrates this dynamical system for ϕ = 0, showing the saddle-shaped wire of figure 1 viewed from above, with the repulsive fixed points of the crests and attractive fixed points of the troughs indicated as open and closed circles, respectively.

Figure 2.

Dynamical system where a bead (small black circle) moves on a circle according to equation (2.1) (with ϕ = 0). Large numbered black and white circles represent attractive (θ^*₁, θ^*₃) and repulsive (θ^*₂, θ^*₄) fixed points, respectively. In our toy example, we assign θ^*₁ to mean true and θ^*₃ to mean false.

As already described informally, for ϕ = 0, this dynamical system operates as an IDENTITY gate, transforming initial conditions associated with a true input θ(t = 0)∈θ_RHC into a true output state and initial conditions associated with a false input θ(t = 0)∈θ_LHC, into a false output state. We now show how by judiciously modifying the external conditions, it is possible to transform this dynamical system into a logical NOT gate. More explicitly, for initial conditions in or near the true state (i.e. θ(t = 0)∈θ_RHC) we want the system to approach (at asymptotically large times) the false state and inversely, for initial conditions in or near the false state (i.e. θ(t = 0)∈θ_LHC), the system should approach the true state. To accomplish this goal, we first identify a ‘handle’, i.e. an ‘external condition’—a parameter that we can modulate. Examples of such parameters in chemical systems include flow rates, temperature, stirring rates, etc. For this exercise, we use the phase parameter, ϕ, as an externally adjustable parameter. We also assume (both here and in the subsequent chemical model) that changes to external conditions are fast compared with the other dynamics so that changes in parameter regimes can be approximated as discrete jumps. When this assumption does not hold, additional equations describing this parametric dynamics can be coupled to the main dynamics.

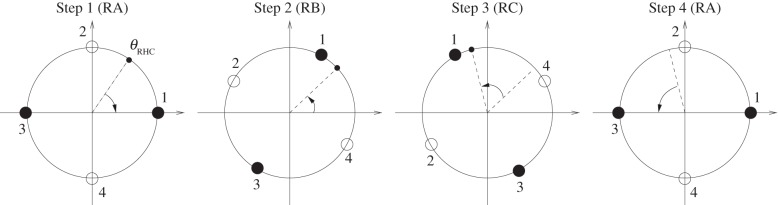
It is now possible to identify a temporal sequence of external conditions that produces the desired behaviour One such sequence is shown in figure 3. In Step 1, the system is placed in Regime-A (RA), where ϕ = ϕ_RA = 0. The system evolves in this regime for the duration τ_RA, which is chosen to be sufficiently long for the bead to approach close to the fixed point centred within the basin in which it started, i.e. 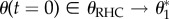and 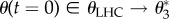. In Step 2, the system's dynamics are changed to Regime-B (RB) by setting the external condition ϕ = ϕ_RB = 2π/3 for a duration τ_RB. This rotates all fixed points counterclockwise by 60°, and for the duration τ_B the bead will be attracted to the new position of the fixed points whether it started this step in θ^*₁ or θ^*₃. In Step 3, we enter Regime-C (RC) by setting ϕ = ϕ_RC = 4π/3 for a time τ_RC. In this parameter regime, the fixed points are rotated counterclockwise by a further 60°, and again the bead follows. Finally, in Step 4, the system is returned to its original configuration, Regime-A (ϕ = ϕ_RA = 0) for a time τ₄. Since the bead is now on the opposite side of the separatrix from which it started, it moves to the fixed point that is on the opposite side of where it began. To summarize, initial conditions associated with a true input now result in a false output state , and initial conditions associated with a false input result in a true output state 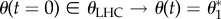. We have thus transformed the system into a NOT gate.

Figure 3.

Example of dynamic external conditions necessary to turn the toy dynamical system (2.1) into a NOT gate. See text for explanations of the steps. The labels ‘RA’, ‘RB’ and ‘RC’ correspond to the three regimes discussed in the main text.

Before we introduce our chemistry-based example, a few further comments are in order. First, we note that everything about the sequence of the external conditions is independent of the initial condition of the state of the system. Put another way, there are no rules that say, for instance, to change to Regime-X if the system is in a particular state or if the input is true, etc. We emphasize this so as to make clear that the logical operation is performed within the modulated system—not outside of it, i.e. not by the modulation itself.

Second, we observe that the dynamic sequence of external conditions shown in figure 3 is not unique. The values of ϕ_i and τ_i for each step are constrained, but substantial freedom is allowed in their choice. For instance, the duration of Step 2 (τ_RB) must be long enough for the bead to move at least 30° counterclockwise, but apart from that is not constrained. Similarly, the duration τ_RC must be sufficiently long for the bead to cross the separatrix that is present in the Regime-A state, but is otherwise unconstrained. Also, other regimes could have been used, for instance, replacing all 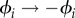would accomplish the same final operation by moving the fixed points clockwise instead of counterclockwise.

Finally, we observe that this example has treated the simple case of a NOT gate, which has only one input (associated with the initial condition of the dynamical system). Other important gates (AND, OR, NAND, etc.) have two inputs. To be able to implement those gates using dynamic external conditions, the two inputs must be combined into one initial condition for the dynamical system. For instance, a linear combination of the two inputs could be used. An explicit example of this in a chemical context is presented in the next section.

It is important to emphasize that in our method, external conditions are regulated by an ‘open-loop’ controller, where external conditions are regulated according to a pre-determined sequence that is entirely independent of both the current state of the chemistry and the input given to the system. The logical operation is thus performed by the chemical medium and not by the process regulating it.

3. Dynamic external conditions in a chemical model

We now show how a cubic-autocatalytic chemical reaction can be turned into a NAND gate by dynamic modification of its external conditions. The action of a NAND gate is shown in table 2. The NAND logic gate was selected for its universality, i.e. the fact that all logical operations can be constructed out of networks of this gate [38]. The chemical model (sometimes referred to as the Selkov–Gray–Scott model) was selected as it is a well-studied system that is known to be capable of interesting and complicated dynamics [37]. It is given by

3.1

and

3.2

where U = U(t) and V = V(t) are chemical concentrations. These equations can be thought of as describing a continuous well-stirred flow reaction system, where autocatalyst V reacts with substrate U, transforming it into more V according to the reaction 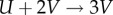. The reactants are fed into the reactor at rates described by parameters F_u and F_v, and they are removed at rates described by terms r_uU and r_vV . Without loss of generality, we choose the values r_u = 1.5, r_v = 3 and λ = 1 in the following; other values would change the details of our results, but not the overall reasoning.

Table 2.

NAND logic table.

input A	input B	output
FALSE	FALSE	TRUE
FALSE	TRUE	TRUE
TRUE	FALSE	TRUE
TRUE	TRUE	FALSE

As was the case for the toy model, a first step is to find parameters that can be adjusted externally. We pick the ‘feed-rate’ parameters, F_u and F_v, as our tunable external conditions. In other situations, it may make sense to pick other parameters. For example, if the reaction rate (λ) were influenced by the presence of light, λ could be used instead of (or in addition to) the feed-rate parameters.

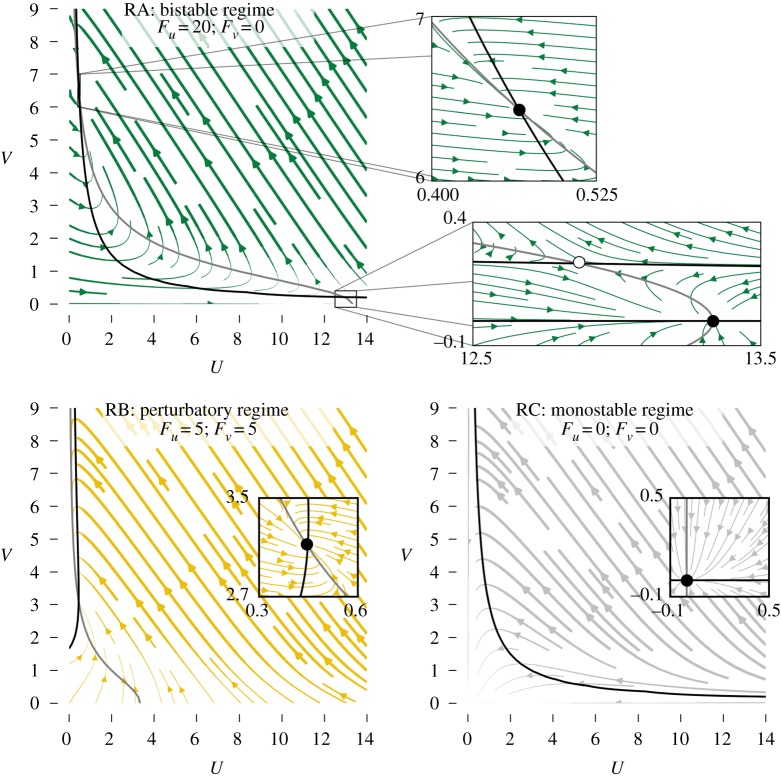
Once again, there is more than one way to modulate the parameters to cause the system to operate as a logic gate. It is useful (but not necessary, see Discussion) to have two fixed points that we can associate with the two Boolean values. We thus start by identifying a configuration of the adjustable parameters for which the system is bistable (see appendix A for an analysis of the fixed points of the model). These values are indicated in the row labelled RA (for Regime-A) in table 3 and plots in figure 4 show the dynamics of the system when the system is in this configuration. We associate a Boolean value with each of the two fixed points, arbitrarily selecting (U, V)_false ≈ (13.33, 0) to represent false and (U, V)_true ≈ (0.5, 6.5) to represent true (figure 4).

Table 3.

Parameter regimes.

regime	Fu	Fv
RA (bistable)	20	0
RB (perturbatory)	5	5
RC (monostable)	0	0

Figure 4.

Dynamics for three different parameter regimes of the cubic-autocatalytic chemical reaction represented by equations (3.1) and (3.2). V and U nullclines are indicated by black and grey curves, respectively. Filled and open circles represent stable and unstable fixed points, respectively. Note that in some insets, non-sensical negative values of U and V are shown to provide insight into the stability of the fixed points. (Online version in colour.)

We assume that the mechanism through which the system receives inputs from upstream gates is by way of diffusion or some other process, such that the input is the average of two of the Boolean states, attenuated by some constant, k. For example, if the chemical NAND gate were to be implemented with the use of a CSTR, the two inputs might correspond to samples taken from upstream CSTR-based gates. The net effect on the concentration of the reference chemical in the CSTR would thus depend on the average of the two input concentrations, diluted in the whole reaction volume. In this example, k represents the effect of dilution. For the Selkov–Gray–Scott model, the possible inputs (initial conditions) are thus I_FF = k(U, V)_false, I_TT = k(U, V)_true and I_TF = I_FT = k((U, V)_true + (U, V)_false)/2 = k(6.6, 3.25), where k is set to 0.15. Similar to system parameters r_u, r_v and λ, the exact value of k is not important for our method to work, but is important in the modelling of realistic physical/chemical situations. A different value of k might affect the specifics of each regime (timing, values of the parameters), but not the overall recipe. For instance, in the present case the value of k was chosen such that of the four possible input values, only I_TT lies above Regime-A's separatrix (see figure 5a). We confirmed in numerical simulations that small changes to k (we checked k∈[0.11, ..0.18]) would have no effect upon the logical operation performed. Larger changes to k can change the type of logical operation accomplished. For instance, a k value of 0.25 places both I_TF and I_FT above the separatrix, which causes the regime sequence to accomplish a NOR operation instead of NAND (confirmed in numerical simulation, results not shown). Changing regime parameters, or the sequence or duration of regimes used would allow further flexibility in selecting a value for k. For instance, the parameter F_u influences the position of the separatrix in Regime-A.

Figure 5.

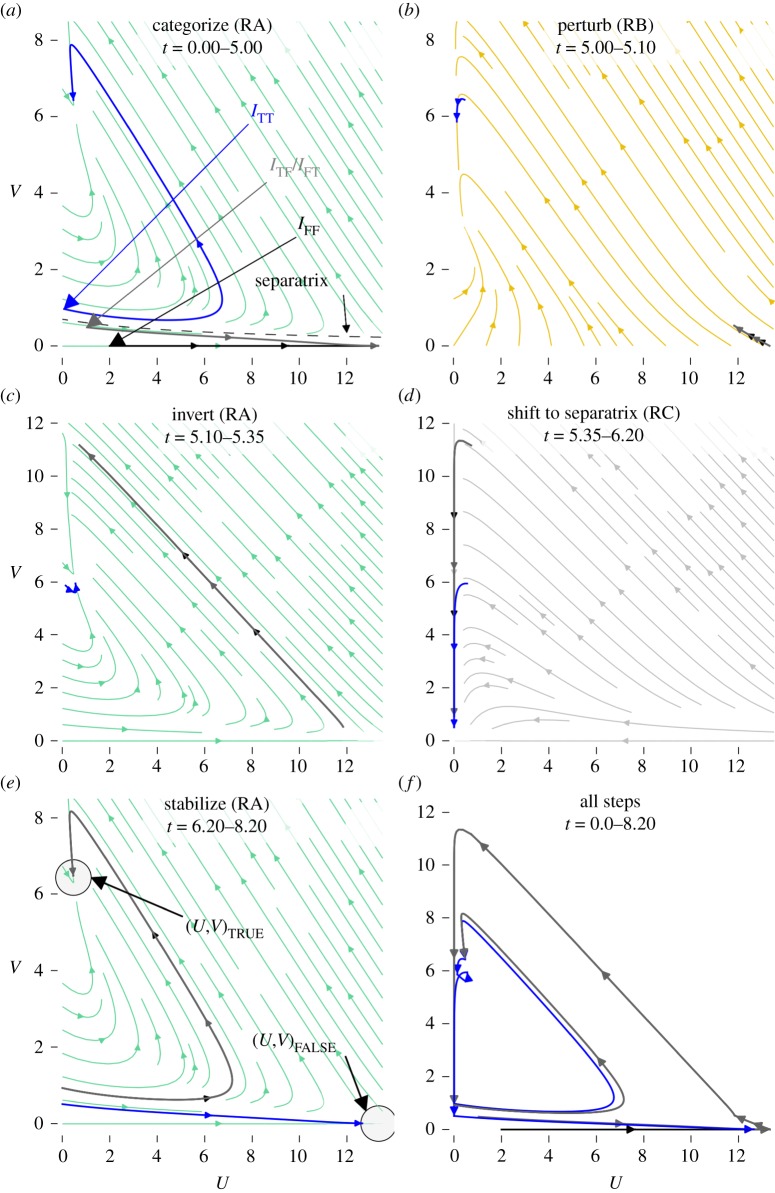
Phase portraits of the cubic-autocatalytic reaction represented by equations (3.1) and (3.2) performing a NAND operation. Frames (a–e) each indicate a different phase of the computation where the system is placed in one of three parameter regimes (RA, RB or RC). The duration of each phase is indicated in table 4 and at the top of each frame. Trajectories from initial conditions corresponding to each of the possible inputs are colour coded such that the blue trajectory corresponds to an input of (true,true), the black trajectory corresponds to an input of (false,false) and the grey trajectory corresponds to an input of (true,false) or (false,true). Frame (f) shows the entire sequence. In frame (a), the separatrix between the two basins of attraction in this regime is indicated by a dashed line. Note that frames (c), (d) and (f) have a different vertical scale. (Online version in colour.)

To operate as a NAND gate, trajectories that start at initial conditions I_FF, I_TF and I_FT must end at (U, V)_true and initial condition I_TT must end at (U, V)_false. There is no single fixed parametric regime of the system that accomplishes this behaviour. But we now explain how this behaviour can be achieved when the system is placed in the temporal sequence of external conditions specified in table 4.

Table 4.

NAND regime sequence.

step name	regime	duration
categorize	RA (bistable)	5.00
perturb	RB (perturbatory)	0.10
invert	RA (bistable)	0.25
shift to separatrix	RC (monostable)	0.85
stabilize	RA (bistable)	2.00

We start with the system in the bistable regime (regime RA in table 3). This categorizes the trajectories such that those initial conditions that are associated with an output of true are at one of the fixed points, while the other initial condition falls into the other fixed point (figure 5a). If we were implementing an AND gate rather than a NAND gate, we could stop here, as inputs I_FF, I_TF and I_FT are at (U, V)_false and I_TT is at (U, V)_true. However, AND gates are not universal, and to accomplish our goal of creating a NAND gate, we must ‘invert’ the system such that those trajectories at (U, V)_false are moved to (U, V)_true and vice versa.

We briefly place the system in the perturbatory regime (regime RB in table 3), which causes a small increase in V for all of the trajectories (Step 2, figure 5b). This small increase in V means that when the system is returned to the bistable regime in Step 3 (figure 5c), the I_FF, I_TF and I_FT trajectories are no longer in the (U, V)_false basin of attraction, and they move on a transient that takes them higher than the I_TT trajectory. If we were to stay in the bistable regime for a long time, all of the trajectories would approach (U, V)_true. This would be bad as it would no longer be possible to distinguish between the four inputs. To prevent this from happening, we move to the monostable regime (Step 4, figure 5d) before the system comes to equilibrium. In this regime, the feed rates F_u and F_v are both 0, causing all of the trajectories to decrease in both U and V . We again make use of the transient dynamics by moving the system into the bistable regime before the system comes to equilibrium. With the correct timing, at the start of the final bistable regime (Step 5, figure 5e) the I_FF, I_TF and I_FT are on one side of the separatrix, within the basin of attraction of (U, V)_true and I_TT is on the other side, within the basin of attraction of (U, V)_false. Left in this final regime of the sequence, the I_FF, I_TF and I_FT trajectories approach (U, V)_true and the I_TT approaches (U, V)_false, and we have successfully completed a NAND operation.

This process involves the sequential use of three different parameter regimes, the bistable regime (RA), the perturbatory regime (RB) and the monostable regime (RC). Although the timing of the duration of each regime must be somewhat precise, in our experience the values of the parameters for the regime do not need to be precisely tuned, provided they perform the desired qualitative dynamics (e.g. bistability, or desired transient dynamics). The values of the parameters for each regime can be found in table 3 and the order and duration of regimes for performing a NAND operation in a non-spatial system can be seen both in figure 5 and table 4.

4. Discussion

The toy and chemical models presented above are two simple examples of dynamical systems that can be turned into logic gates using dynamic external conditions. The method presented here is general and could in principle be applied to other dynamical systems, including chemical systems.

The NAND gate that we have implemented includes two properties that are necessary if the gates are to be assembled into networks of gates that are capable of useful computation above and beyond a simple NAND operation. The first property is error correction. Both of the presented systems employ a bistable regime, where two distinct stable fixed points are used to correct for noise or small perturbations in the initial conditions, and steering the trajectory to a well-defined, time-invariant state that is a function of the input. This error-correcting ‘categorization’ step limits the influence of initial conditions upon subsequent steps. Without this error correction, noise can accumulate within sequences of gates, making them ineffective when combined into larger computational circuits thus limiting the possibility of composing them into useful computational networks. Magnasco [39] discusses this idea in the context of chemical neurons.

The second property concerns the transmission of the output of one logic gate into the input of a subsequent ‘downstream’ gate. If chemical logic gates are to be composed into networks capable of more complex computation, it must be possible to use the output of certain gates as the input of others. Not all previous research on chemistry-based logic gates has fully addressed this demanding requirement. For example, in Wang et al. [14], input to a chemical logic gate is defined by the presence or the absence of oxidation spikes in the Belousov–Zhabotinsky reaction of two ‘input’ droplets, whereas the output in this system is defined by a delay in the autonomous oscillations of a third ‘output’ droplet. Without further work, it is unclear how this output could be used as the input for a subsequent downstream gate. The idea here that we want to emphasize is that for chemical logic gates to be composable into networks, the ‘format’ or ‘representation’ of output Boolean values must be the same as (or compatible with) that of the input. Our method allowed us to produce a chemical logic gate where the output of the gate, once diffused and diluted, could be used as input for another gate.

In general, the process of designing of a specific gate using dynamic external conditions depends strongly on the underlying system and on the number and effect(s) of the externally adjustable parameters. In some cases, there will be no solution; no sequence of external conditions will cause the base system to perform the desired behaviour. In general, it is difficult to establish whether or not a solution exists but occasionally, when certain fundamental properties are absent from the base system or when the effects of external conditions are limited, the absence of a solution can be quickly established. For instance, if a system always has a single basin of attraction, regardless of any external parameter shifts, it seems that it would be impossible to create a NAND gate with error correction. Our example systems employ two stable fixed points to accomplish error correction, but it is interesting to speculate that one could replace one or more fixed points with limit cycles or chaotic attractors—provided those attractors are sufficiently separated in phase space, then they could be used as Boolean value representations. Multistability could in principle be used to implement n-valued logic gates and that other forms of signal processing, such as amplification, dynamic range compression, etc., could be accomplished with monostable or other systems.

For the presented method to work, the tunable external conditions must have sufficient influence upon the system's dynamics. Typical external conditions for chemistry include flow rate, temperature, stirring rate and light-sensitive reaction rate, but in many specific cases these parameters may not sufficiently influence the chemical dynamics, making it impossible to use the presented method. Additionally, we have assumed that the parametric shifts can occur quickly compared to the other dynamics. In some systems, it may be possible to relax this assumption, but in others it may be impossible to regulate the external conditions quickly enough to avoid undesired transients. Ultimately, the properties of the chemical medium (reaction rates, diffusion rate, etc.) in which the computation is taking place impose a number of unavoidable constraints that might limit the experimental applicability of the method. For instance, the shift to the separatrix (table 4) might be hard to achieve experimentally if reactions are too fast.

The necessary or desired characteristics for a base system to be amenable to this method are difficult to describe at this stage. The method requires a case by case study of its dynamics in different regimes and trial and error and experimentation. From a practical point of view, it means that a mathematical model of the dynamics is very helpful (perhaps even necessary) to find out all the regimes and timings for the method to work. Since models of chemical dynamics are often approximate, this can add a layer of difficulty when applying this method to complex chemical systems.

With regards to the chemical processing of information in biological systems, our approach to chemical logic gates is conceptually different from previous studies on the subject. For instance, the chemical logic gates of [18–20] require building a precise network of chemical neurons (each made of many chemicals) in order to perform a certain logical operation. The networks are built specifically for the task they are designed for, and the absence of one or more chemicals could disrupt its proper functioning. This high level of fine tuning seems to be generic of other chemical gate designs. This may be hard to achieve naturally in a biological setting.

It is interesting to return for a moment to one of the motivations of natural computing: understanding how organisms process information. The approach presented here is different from previous approaches to chemical logic in that it uses existing ‘chemical hardware’ (already designed for certain tasks) to process information. By playing on the external conditions of some pre-existing chemical dynamics, cells may be able to perform a logical operation by re-purposing some of its internal chemical components by dynamically regulating the external conditions of that chemistry (e.g. transport of reactants through the cell membrane). In addition, our two examples explicitly show that there is no unique temporal sequence of external conditions and also substantial freedom in the choice of parameters in our method. So it is not unreasonable to think that evolution could tweak relatively easily the external conditions of biological processes in order for them to perform logical operations or other forms of signal manipulation. This makes the above method a potentially useful way of processing information in biological systems. We are not aware of any example of natural or synthetic biological systems that uses such a method, but it would be interesting to pursue research in that direction.

5. Conclusion

We have shown that a well-known cubic autocatalytic chemical model can be transformed into a logic gate by changing its external conditions according to a prescribed time-dependent sequence that is independent of the state of the system and of the input to the system. The method is general and could in principle be applied to other dynamical systems. In a parallel publication, we present our application of the method to a spatial model (where diffusion effects are important), showing how the method can be used to take advantage of spatial symmetries and produce a network of logic gates out of a uniform chemical medium.

Appendix A. Fixed points of the Selkov–Gray–Scott model

The fixed points of the Selkov–Gray–Scott model in the case where F_v = 0 are obtained by setting equations (3.1) and (3.2) to zero. There are three fixed points in total:

A 1

and

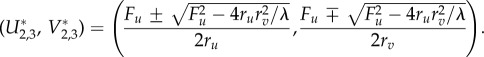A 2

The stability of the system can be obtained by linearizing equations (3.1) and (3.2) around each fixed point [40]. The linearized system is

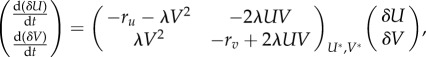A 3

where δU, δV represent small deviations in concentrations around the fixed point (U^*, V^*). For the parameter values specified below equations (3.1) and (3.2) and in table 3, we get that Regime-A has two stable fixed points at (13.33, 0) and (0.46, 6.43) and one unstable fixed point at (12.87, 0.23), while Regime-C has only one stable fixed point at (0, 0). The analysis of Regime-B is more complicated, since the expressions for the fixed points (A 1) and (A 2) are obtained under the assumption that F_v = 0. Analytical expressions for the fixed points in Regime-B exist, but they are not particularly illuminating and we do not include them here. Nonetheless, it is possible to show that for the parameter values specified in table 3, there is a single stable fixed point at (0.45, 3.11).

Data accessibility

This article has no additional data.

Authors' contributions

M.E. conceived of the study, carried out the numerical simulations and participated in the writing of the manuscript; J.S.G. conceived of the study, contributed in the more theoretical aspects of the study and participated in the writing of the manuscript; J.P.M. coordinated the study, participated in its design and helped draft the manuscript. All authors gave final approval for publication.

Competing interests

The authors have no competing interests.

Funding

This research is supported by Repsol S.A.