Skip to main content
PMC home page
Journal of Computational Biology logoLink to Journal of Computational Biology
. 2018 Jul 1;25(7):726–739. doi: 10.1089/cmb.2017.0267

BBK* (Branch and Bound Over K*): A Provable and Efficient Ensemble-Based Protein Design Algorithm to Optimize Stability and Binding Affinity Over Large Sequence Spaces

Adegoke A Ojewole 1,,2,,†, Jonathan D Jou 1,,†, Vance G Fowler 3, Bruce R Donald 1,,4,,*
PMCID: PMC6074059  PMID: 29641249

Abstract

Computational protein design (CPD) algorithms that compute binding affinity, Ka, search for sequences with an energetically favorable free energy of binding. Recent work shows that three principles improve the biological accuracy of CPD: ensemble-based design, continuous flexibility of backbone and side-chain conformations, and provable guarantees of accuracy with respect to the input. However, previous methods that use all three design principles are single-sequence (SS) algorithms, which are very costly: linear in the number of sequences and thus exponential in the number of simultaneously mutable residues. To address this computational challenge, we introduce BBK*, a new CPD algorithm whose key innovation is the multisequence (MS) bound: BBK* efficiently computes a single provable upper bound to approximate Ka for a combinatorial number of sequences, and avoids SS computation for all provably suboptimal sequences. Thus, to our knowledge, BBK* is the first provable, ensemble-based CPD algorithm to run in time sublinear in the number of sequences. Computational experiments on 204 protein design problems show that BBK* finds the tightest binding sequences while approximating Ka for up to 105-fold fewer sequences than the previous state-of-the-art algorithms, which require exhaustive enumeration of sequences. Furthermore, for 51 protein–ligand design problems, BBK* provably approximates Ka up to 1982-fold faster than the previous state-of-the-art iMinDEE/Inline graphic/Inline graphic algorithm. Therefore, BBK* not only accelerates protein designs that are possible with previous provable algorithms, but also efficiently performs designs that are too large for previous methods.

Keywords: : molecular ensembles, OSPREY, predicting binding affinity, protein design, structural biology, sublinear algorithms

1. Introduction

Protein design is the prediction of protein sequences with desired biochemical functions, which often involve binding to a target ligand. Computational protein design (CPD) casts functional design into a structural optimization problem whose goal is to find amino acid sequences that fold into specified three-dimensional structures. Protein design algorithms search a space defined by a biophysical input model, which defines the sequence and structural search space (i.e., the input structure, allowed amino acid mutations, and allowed protein flexibility); the optimization objective (e.g., design for binding affinity); and the energy function (Boas and Harbury, 2007). Protein design algorithms (Donald, 2011; Gainza et al., 2016) have successfully predicted protein sequences that fold and bind desired targets in vitro and in vivo. For example, these algorithms have been used, with experimental validation, to predict drug resistance (Frey et al., 2010; Reeve et al., 2015; Ojewole et al., 2017a) and to design enzymes (Lilien et al., 2005; Stevens et al., 2006; Georgiev and Donald, 2007; Chen et al., 2009), new drugs (Gorczynski et al., 2007), inhibitors of protein–protein interactions (Georgiev et al., 2008; Roberts et al., 2012), epitope-specific antibody probes (Georgiev et al., 2012), and even neutralizing antibodies (Georgiev et al., 2014; Rudicell et al., 2014).

Computational methods can potentially search a large number of sequences to predict the proteins that bind most tightly to a target ligand in less time and with fewer resources than in vitro methods such as phage display (Carmen and Jermutus, 2002; Pál et al., 2006). However, four computational challenges have prevented protein design algorithms from realizing this potential. First, for each binding interface, an exponentially large number of conformations in each binding partner's ensemble must be pruned or considered to accurately predict binding affinity (Gilson et al., 1997; Lilien et al., 2005; Georgiev et al., 2008; Donald, 2011). Second, for each sequence, finding the lowest energy conformations that most influence binding affinity is NP-hard (Pierce and Winfree, 2002; Kingsford et al., 2005; Xu, 2005; Xu and Berger, 2006; Peng et al., 2015), making algorithms that guarantee optimality expensive for larger designs. Third, mutating a protein sequence induces conformational changes in the protein structure. Since such conformational changes occur over many continuous degrees of freedom, algorithms that model continuous flexibility must search over a large continuous conformation space. Fourth, the number of protein sequences (i.e., the sequence space) grows exponentially with the number of simultaneously mutable residues in the design. Therefore, previous algorithms either focus on accurately modeling smaller designs or attempt larger designs by making simplifications that (1) ignore the ensemble nature of proteins, (2) disregard continuous conformational flexibility, or (3) return heuristic solutions with no guarantees. A discussion of these simplifications and their ramifications for protein design follows [see also Supplementary Information (SI) section 2 (Ojewole et al., 2017b)].

Global Minimum Energy Conformation (GMEC)-based algorithms (Desmet et al., 1992; Gainza et al., 2012; Roberts and Donald, 2015; Hallen and Donald, 2016; Viricel et al., 2016) assume that the lowest energy conformation accurately predicts binding affinity. However, GMEC-based designs cannot accurately model entropic change due to binding (Fleishman et al., 2011) and can disproportionately favor sequences with energetically favorable GMECs over sequences with tight binding affinity (Lilien et al., 2005; Georgiev et al., 2008; Chen et al., 2009; Sciretti et al., 2009; Roberts et al., 2012; Silver et al., 2013). Many protein design algorithms (Leaver-Fay et al., 2011; Traoré et al., 2013, 2016; Simoncini et al., 2015; Viricel et al., 2016) rely on a simplified, discrete model of side-chain flexibility. However, discrete rotamers model a small subset of protein energetics, which are sensitive to small atomic movements not permitted by the discrete model. To overcome this limitation, researchers have developed provable algorithms (Georgiev et al., 2008; Gainza et al., 2012; Roberts et al., 2012; Hallen et al., 2015, 2016; Roberts and Donald, 2015) that incorporate continuous side-chain flexibility (Georgiev et al., 2008; Gainza et al., 2012). Another important aspect of design algorithms is the quality of the computed results. Whereas GMEC-based design is NP-hard (Pierce and Winfree, 2002; Kingsford et al., 2005; Xu, 2005; Xu and Berger, 2006), computation of thermodynamic ensembles and associated partition functions is #P-hard (Valiant, 1979; Nisonoff, 2015; Viricel et al., 2016). Provable protein design algorithms return either the optimal sequences or conformations (Desmet et al., 1992; Leach and Lemon, 1998; Gainza et al., 2012; Hallen et al., 2013; Traoré et al., 2013, 2016; Roberts and Donald, 2015; Simoncini et al., 2015; Viricel et al., 2016) with respect to the input model or return provably good approximate solutions (Lilien et al., 2005; Georgiev et al., 2008; Roberts et al., 2012; Hallen et al., 2015, 2016). Nonprovable algorithms such as Metropolis Monte Carlo methods (Lee and Levitt, 1991; Kuhlman and Baker, 2000; Leaver-Fay et al., 2011) instead use stochastic methods to rapidly sample the space described by the input model. These algorithms return solutions without any guarantees. Thus, ensemble-based design, a realistic model of structural flexibility, and provable optimality of the computed sequences with respect to the input model improve the predictive power of protein design algorithms. However, each of these design principles also increases the cost of protein design (as a function of the number of sequences).

Single-sequence (SS) algorithms, which explicitly evaluate each possible sequence, are powerful and versatile. Molecular dynamics (Leech et al., 1996; Zheng et al., 2008), for instance, is frequently applied to design for binding affinity. The approach models ensembles and continuous flexibility. Provable algorithms have also been developed to model these two phenomena. The K* algorithm (Lilien et al., 2005; Georgiev et al., 2008; Roberts et al., 2012) in osprey (Lilien et al., 2005; Georgiev et al., 2006, 2008; Georgiev and Donald, 2007; Gainza et al., 2012, 2013; Roberts et al., 2012; Hallen et al., 2013, 2015, 2016; Roberts and Donald, 2015; Hallen and Donald, 2016; Jou et al., 2016) uses a combination of dead-end elimination pruning (Georgiev et al., 2008; Gainza et al., 2012) and A* (Hart et al., 1968; Leach and Lemon, 1998; Roberts et al., 2015) gap-free conformation enumeration to provably and efficiently approximate Ka. K* and all previous provable ensemble-based algorithms that model continuous side-chain flexibility (Hallen et al., 2015, 2016) are SS algorithms. The empirical and asymptotic runtime complexity of SS algorithms is linear in the number of possible sequences, and, therefore, exponential in the number of mutable residues. Thus, designs with many mutable residues rapidly become intractable when using SS algorithms. The comets algorithm (Hallen and Donald, 2016) in osprey is the only provable multistate design algorithm that is more efficient than SS algorithms. However, its binding predictions are GMEC based rather than ensemble based. Additional background and references are located in SI section 2 (Ojewole et al., 2017b).

To efficiently search large sequence spaces while retaining all the benefits of provable guarantees, ensemble-based design, and continuous side-chain flexibility, we present a new, provable algorithm: Branch and Bound over K* (BBK*). The key innovation of BBK* is the multisequence (MS) bound: BBK* efficiently computes upper and lower bounds on the binding affinities of partial sequences, which are shared by a combinatorial number of full sequences. By avoiding costly SS computation, BBK* runs in time sublinear in the number of sequences. To our knowledge, BBK* is the first provable, ensemble-based algorithm to do so. BBK* not only avoids explicitly computing all possible sequences, but also provably and efficiently enumerates sequences in a gap-free decreasing order of binding affinity. Therefore, BBK* provides a vast performance improvement over the previous state-of-the-art, by not only accelerating protein designs that were possible with previous provable algorithms but also efficiently handling large designs that previous algorithms could not compute in a reasonable amount of time.

By presenting BBK*, our article makes the following contributions:

  • (1) A novel, ensemble-based algorithm that provably computes the same results as the previous state of the art (exhaustive search over sequences) but is empirically combinatorially faster, returns a gap-free list of sequences in decreasing order of binding affinity, and runs in time sublinear in the number of sequences.

  • (2) Proofs of correctness for MS bounds, a key innovation in BBK*.

  • (3) A new two-pass bound that more efficiently computes a provable 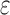Inline graphic-approximation to the desired partition functions.

  • (4) Totally 255 protein designs showing that BBK* approximates binding affinity for full sequences up to 1982-fold faster than the best previous algorithm and that BBK* computes the best binding sequences in a large sequence space up to 105-fold more efficiently than exhaustive search.

  • (5) Support for both continuous side-chain and backbone flexibility, demonstrating the ability of BBK* to handle multiple modes of protein flexibility in addition to large conformation and sequence spaces.

  • (6) An implementation of BBK* in our laboratory's open-source osprey (Lilien et al., 2005; Georgiev et al., 2006, 2008; Georgiev and Donald, 2007; Gainza et al., 2012, 2013; Roberts et al., 2012; Hallen et al., 2013, 2015, 2016; Roberts and Donald, 2015; Hallen and Donald, 2016; Jou et al., 2016) protein design software package, available for download as free software.

2. Computing the Partition Function

To successfully design for improved binding affinity Ka, design algorithms must consider the energy of more than just the GMEC. In particular, all algorithms that design for improved Ka optimize the ratio of partition function Z for the bound and unbound states of the protein and ligand [Eq. (2)]. Protein design can thus be cast as an optimization problem. For an n-residue protein design problem with at most a amino acids per mutable residue, let P, L, and PL denote the unbound protein, unbound ligand, and bound protein–ligand complex, respectively. For each sequence s, let 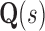Inline graphic be the set of discrete rigid rotamer conformations defined by the allowed amino acids for each mutable residue of s. For a rigid rotamer conformation c, let 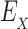Inline graphic be a pairwise energy function with respect to input structure X, which may be one of P, L, or PL. In particular, we consider the case of design with continuous rotamers (Georgiev et al., 2008; Gainza et al., 2012). We define 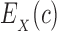Inline graphic to be the energy of c for structure X after energy minimizing the side chains of mutable residues.

2.1. K*

We define the Boltzmann-weighted partition function 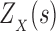Inline graphic as

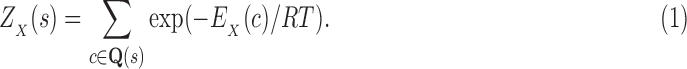graphic file with name eq8.gif

We define the K* score, a partition function ratio that approximates binding affinity, 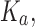Inline graphic as

graphic file with name eq10.gif

As stated in Section 1, the K* approximation and, by extension, the full partition function are #P-hard to compute (Valiant, 1979; Nisonoff, 2015; Viricel et al., 2016). Therefore, researchers have not only developed heuristic algorithms that rapidly compute loose partition function bounds, but also developed efficient, provable algorithms that compute Inline graphic-approximations to the partition function. Probabilistic algorithms bound the partition function either provably (Wainwright et al., 2013) or nonprovably (Fromer and Yanover, 2008). An efficient Inline graphic-approximation to 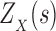Inline graphic is computed in Lilien et al. (2005), Georgiev et al. (2008), and Roberts et al. (2012). However, these methods are designed to compute partition functions for SSs. For an n-residue design with at most t possible amino acids at each residue and q rotamers per amino acid, provable SS methods must compute or bound the partition functions of all tn sequences, each with qn conformations. Thus, previous SS algorithms for protein design for binding affinity take time exponential in n (Inline graphic(tn)) when computing the sequence with the best predicted binding affinity.

Therefore, to provably find the best binding sequences, new efficient provable algorithms are needed to search over an exponentially large sequence space, in which each sequence represents an exponentially large conformation space. BBK* addresses this need. BBK* compares partial sequences (for which some mutable residues have not been assigned an amino acid identity) without computing the partition functions for all full sequences (which assign a specific amino acid to each mutable residue). BBK* computes bounds on the free energies of partial sequences, and avoids enumerating conformations from sequences with poor binding affinity by pruning sequences during search. As we describe in Section 3, pruning these sequences circumvents prohibitive computational costs required to compute many SS K* scores.

3. A* Search Over Sequences, with Multisequence Bounds

It may at first seem counter-intuitive to compute the sequence with optimal binding affinity, along with its predicted K* score, without explicitly computing the K* scores of all possible sequences. Indeed, all previous ensemble-based provable methods, as well as many heuristic methods, are SS methods: they must individually evaluate and compare each sequence to provably return the optimal sequence. In contrast, BBK* bounds the K* ratios of a combinatorial number of sequences efficiently and can prune these sequences without computing any SS bounds. The key to this improvement is the observation that a partial sequence 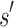Inline graphic with poor predicted binding affinity adversely affects the K* score of the combinatorial set of sequences that contain 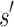Inline graphic. 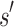That is, the best possible K* score consistent with Inline graphic limits the K* ratio of all sequences consistent with Inline graphic. Henceforth, we refer to a bound on the binding affinity for a sequence as a bound on the sequence. To compute a bound on all sequences consistent with 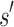Inline graphic, BBK* computes the partition function for an ensemble that contains conformations from multi-sequence. Figure 1 shows the difference between SS and MS ensembles. The K* ratio of a MS ensemble is a provable upper bound on the best possible K* ratio of all sequences that contain 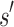Inline graphic. We show this MS bound is not only cheaper to compute, but it also allows BBK* to compare a combinatorial number of sequences without computing any SS bounds. By bounding every possible sequence consistent with a partial sequence, BBK* can provably eliminate those sequences, and prune a combinatorial number of sequences without performing any SS computation. Figure 2 illustrates the combinatorial speedup provided by MS bound pruning, whereby pruning the partial sequence obviates computation of all SSs containing the partial sequence. MS bounds are not limited to pruning based on binding affinity, however. They are also useful for pruning combinations of sequences whose favorable K* scores are due to energetically unfavorable unbound states that cannot fold into ligand-binding poses. SS methods compute binding affinity for each of these sequences. In contrast, BBK* prunes these partial sequences using MS bounds, thereby avoiding many costly SS computations. Details are provided in section A.7 of the SI (Ojewole et al., 2017b).

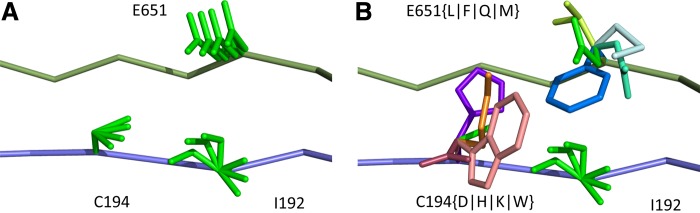
FIG. 1.

FIG. 1.

Open in a new tab

A toy protein design problem in which conformational ensembles (A) and optimal mutations (B) must be computed at three residues. Residues of the fibronectin F1 module (Fn, blue ribbon) and of a fragment of Staphylococcus aureus fibronectin binding protein A (FNBPA-5, green ribbon) are shown (PDB id: 2RL0). Side-chain conformations, labeled with amino acid identity, are also shown per residue. (A) Previous provable methods require a fully defined sequence to compute an SS 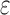Inline graphic-approximation bound on binding affinity [i.e., a 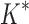Inline graphic score, Eq. (2)]. (B) A key innovation in this article is the MS bound for binding affinity in protein design. An MS bound is a provable bound on the binding affinity of a partial sequence. Unassigned residues, whose amino acid identities are not defined by the partial sequence, adopt side-chain conformations from multiple amino acids, shown as the blue, purple, pink, and light blue ensembles. Thus, an MS bound is a provable upper bound on the binding affinity of all sequences containing that partial sequence, and is obtained without computing any SS bounds. (The full analysis of the Fn:FNBPA-5 design problem is described in Section 4.3). MS, multi-sequence; SS, single sequence.

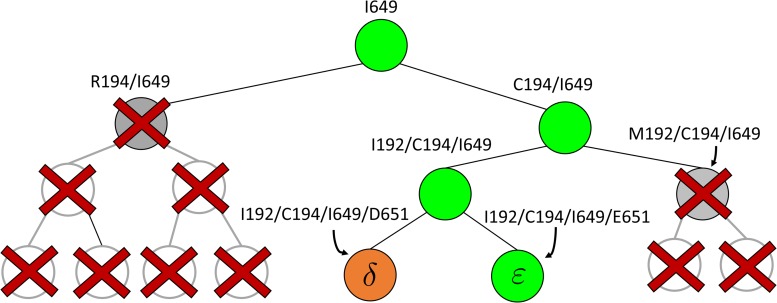
FIG. 2.

FIG. 2.

Open in a new tab

BBK* pruning efficiently explores the sequence space. An example design of residues 192 and 194 of the fourth fibronectin F1 module and residues 649 and 651 of a fragment Staphylococcus aureus fibronectin binding protein a-5 is shown (Fig. 1, PDB id: 2RL0). As BBK* searches the sequence space (tree above) its MS bounds provably prunes subtrees from the sequence space. All sequences containing R194/I649 are pruned (red crosses) after computing exactly one MS bound: the bound on the partial sequence R194/I649, which is an upper bound for all sequences containing R194/I649. Sequences containing M192/C194/I649 are pruned (red crosses) after computing only the MS bound for the partial sequence M192/C194/I649. All pruned sequences and partial sequences, shown as empty gray circles, have no additional computation performed. Even though SS bounds are initiated for both I192/C194/I649/E651 and I192/C194/I649/D651, the latter is pruned after computing a mer e 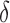Inline graphic-approximation bound (orange leaf node), which is cheaper, and not as tight as a 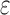Inline graphic-approximate bound. A provable 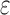Inline graphic-approximation bound (green leaf node) is computed for only the optimal sequence, I192/C194/I649/E651. In contrast, SS methods compute separate 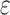Inline graphic-approximate bounds (which are expensive) for all eight possible sequences, shown as leaf nodes in the tree.

The improvement of BBK* over SS methods can be measured using cost per sequence. We show the improvement is threefold: BBK* (a) reduces the cost to compute a bound on a combinatorial number of sequences, (b) eliminates all computational costs once a sequence is pruned, and (c) when it must compute a bound for an SS, computes a bound that is in many cases cheaper than the bounds computed by previous SS algorithms. To guarantee that the first sequence returned is optimal, an algorithm must either compute or bound the partition function for all possible sequences. Previous provable algorithms compute a provable SS bound of the partition function, called an 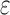Inline graphic-approximation (SS-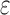Inline graphic bound), for each sequence (Lilien et al., 2005; Georgiev et al., 2008; Roberts et al., 2012). These SS-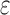Inline graphic bounds are guaranteed to be within a user-specified 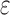Inline graphic of the K* score for a sequence. BBK* also provably returns the optimal sequences, but does so without enumerating all possible sequences. Instead of SS-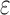Inline graphic bounds, BBK* computes an MS bound, which is an upper bound on the best possible K* score of multiple sequences that share a common partial sequence.

We will now compare the cost of bounding sequences with SS algorithms with the cost with BBK*. Consider an n-residue protein design: we are given an initial partial sequence 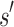Inline graphic, which fixes amino acid identity (but not the rotamer) for a residues, and u residues do not have a fixed amino acid identity 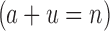Inline graphic. If the design problem allows at most t amino acids per unassigned 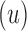Inline graphic residue and at most q rotamers for any amino acid, there are tu sequences containing 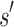Inline graphic and qa partial conformations defined by 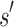Inline graphic. A complete sequence would still have qn conformations, and computing the energy of a conformation takes 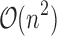Inline graphic time using a pairwise energy function. Thus, an SS algorithm would spend 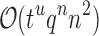Inline graphic worst-case time individually computing the K* scores of all tu sequences. In contrast, the cost of an MS bound is 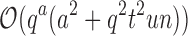Inline graphic, which includes 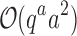Inline graphic time to compute the pairwise energy of the a assigned residues of all qa partial conformations, and 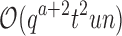Inline graphic time to compute a bound on the energy of each partial conformation. By reducing two exponentials from tu to t2, and from qn to 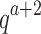Inline graphic, BBK* computes an MS bound in time sublinear in the number 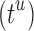Inline graphic of sequences. The cost to compute a single provable MS bound (that holds for all tu sequences) is, therefore, significantly smaller than the cost to compute tu SS bounds. Furthermore, these MS bounds are used to prune partial sequences containing combinations of mutations: for a pruned partial sequence 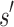Inline graphic, all tu sequences containing 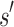Inline graphic are provably eliminated from search without any additional computation. That is, BBK* provably, combinatorially prunes the search space. Since this pruning occurs during search, rather than as a preprocessing step, the pruning performed by BBK* is distinct from previous pruning techniques such as dead-end elimination (Desmet et al., 1992; Dahiyat and Mayo, 1996). BBK* pruning is used after dead-end elimination pruning to further improve empirical performance. Finally, MS bounds are in many cases inexpensive to compute when compared with the 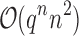Inline graphic complexity of computing an SS-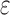Inline graphic bound for an SS. Since there are qa partial conformation energy bounds to compute, the cost of an MS bound increases exponentially as a increases. Obviously, when 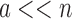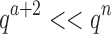Inline graphic, Inline graphic. This is very advantageous for A* search, because a is initially very small: when BBK* begins search, 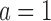Inline graphic, and increases one at a time. Furthermore, 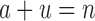Inline graphic, and a never exceeds n. Thus in many cases 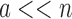Inline graphic, and MS bound costs of 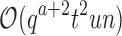Inline graphic are significantly smaller than the SS-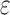Inline graphic costs of 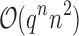Inline graphic for an SS. Use of MS bounds enables BBK* to efficiently bound and prune sequences that would otherwise require 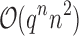Inline graphic time each to evaluate.

The algorithmic advances that make MS bounds possible are new bounds on partial and full sequences. We denote the design states unbound protein, unbound ligand, and bound complex as P, L, and PL, respectively. The following definitions of these new bounds are sufficient for the theorems provided in the main article—the precise definitions involve some subtleties, which are deferred to section A of the SI (Ojewole et al., 2017b). Given a sequence s and a state 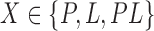Inline graphic, the function 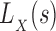Inline graphic is a provable lower bound of the partition function for s in state X, and 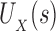Inline graphic is a provable upper bound on the partition function for s in state X. 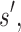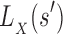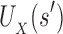For a partial sequence Inline graphic Inline graphic and Inline graphic are, respectively, partition function lower and upper bounds for the combinatorial number of sequences containing 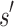Inline graphic. 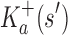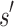These lower- and upper-bounding functions are combined into an upper-bounding function Inline graphic on the partition function ratio of Inline graphic.

Definition 1. Let s be a sequence. 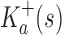Inline graphic is defined as follows:

graphic file with name eq67.gif

The following theorem establishes the relationship between the partition function ratio of a partial sequence and the partition function ratio of any sequence containing the partial sequence:

Theorem 1. Let s be a partial or complete sequence. For any partial sequence 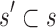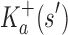Inline graphic, Inline graphic bounds 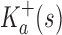Inline graphic from above:

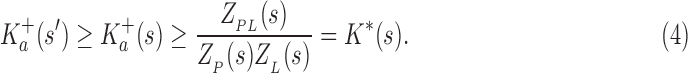graphic file with name eq71.gif

A proof of this theorem is provided in section A.3 of the SI (Ojewole et al., 2017b). Theorem 1 shows that the bounds used by BBK* are admissible. That is, they never underestimate the K* ratio of any partial sequence. Thus, BBK* uses 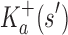Inline graphic as the optimistic bounding function for A* search. Previously, A* search has been used to provably enumerate conformations within some energy window Ew of the GMEC (Leach and Lemon, 1998) and to provably approximate the partition function of single sequences (Lilien et al., 2005; Georgiev et al., 2008; Donald, 2011; Roberts et al., 2012). Since Equation (4) defines an admissible bound over sequences, all of the provable guarantees of A* apply to BBK*. With these guarantees, BBK* provably searches over sequences rather than conformations, and is guaranteed to return a gap-free list of sequences in order of decreasing binding affinity.

3.1. Algorithm overview

BBK* bounds all possible sequences either with the MS bounds described in Section 3, or by computing an SS bound as described in Lilien et al. (2005), Georgiev and Donald (2007), and Roberts et al. (2012). In brief, to bound an SS, BBK* computes a gap-free list of conformations whose statistical mechanical energies [Eq. (1)] are used to bound the K* ratio. The algorithm reports an error bound 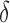Inline graphic such that the computed bound is guaranteed to be no more than a 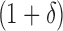Inline graphic factor greater than the true K* ratio. We refer to these SS, 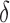Inline graphic-approximate bounds (Georgiev et al., 2008; Georgiev, 2009) as SS-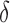Inline graphic bounds. As the gap-free list of conformations used for an SS-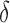Inline graphic bound grows in size, the computed SS bound becomes tighter (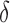Inline graphic decreases). Eventually, 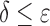Inline graphic, and the SS bound becomes a provable 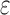Inline graphic-approximation, which we refer to as an SS-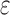Inline graphic bound. We refer to an SS-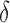Inline graphic bound constructed this way as a running bound, which BBK* incrementally tightens as it enumerates additional conformations (Georgiev et al., 2008).

BBK* maintains a max heap whose node values correspond to either full or partial sequences and whose node keys are an upper bound on all K* scores [Eq. (2)] in the sequence space represented by the node. The heap is initialized with a node representing the entire sequence space. BBK* then repeatedly removes the max node x of the heap and performs one of the following operations:

  • (1) Branch. If x contains a partial sequence 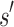Inline graphic, then 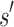Inline graphic is expanded. Expansion creates t new child nodes by selecting an unassigned residue r in 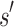Inline graphic, and creating a new child node for each allowed amino acid a at r. Each child node contains 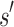Inline graphic plus the additional mutation of a assigned at r. These nodes are bounded with MS bounds or SS-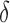Inline graphic bounds and reinserted into the heap.

  • (2) Update. If x contains a complete sequence s, whose bound is an SS-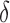Inline graphic bound, then BBK* enumerates m additional conformations (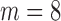Inline graphic in our study), tightening the SS-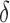Inline graphic bound. x is reinserted into the heap, with the updated SS-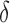Inline graphic bound as its key. Computing this tighter SS-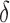Inline graphic bound is important for pruning sequences, as shown by our computational experiments in Section 4.2.

  • (3) Return. If node x contains a full sequence, whose bound is an SS-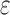Inline graphic bound, then the sequence in x has the best K* score of all unenumerated sequences (as with A*, all better sequences are guaranteed to have already been enumerated). The sequence of x is returned.

BBK* terminates when it has enumerated the top k sequences (by SS-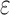Inline graphic bound), where k is a user-specified number. A detailed description of the algorithm is provided in section A.8 of the SI (Ojewole et al., 2017b).

4. Computational Experiments

We implemented BBK* in our laboratory's open source osprey (Gainza et al., 2013) protein design package and compared our algorithm with the previous state-of-the-art SS iMinDEE/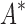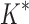Inline graphic/Inline graphic algorithm (Lilien et al., 2005; Georgiev et al., 2008; Roberts et al., 2012). We computed the five best binding sequences using both BBK* and iMinDEE/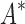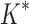Inline graphic/Inline graphic for 204 different protein design problems from 51 different protein–ligand complexes. For each protein–ligand interface, we created four design problems spanning the wild-type sequence and all sets of single, double, triple, and quadruple mutants, respectively. In each design problem, we modeled either eight or nine residues at the protein–ligand interface as mutable and flexible. Each mutable residue was allowed to assume its wild-type identity or mutate to 13–19 other amino acids. 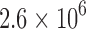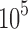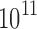The size of the resulting design problems ranged from 10 to Inline graphic sequences and Inline graphic to Inline graphic conformations (over all sequences). In all cases, we modeled continuous side-chain flexibility using continuous rotamers (Gainza et al., 2012; Roberts and Donald, 2015). As in Georgiev et al. (2008) and Gainza et al. (2012), rotamers from the Penultimate Rotamer Library (Lovell et al., 2000) were allowed to minimize to any conformation within 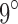Inline graphic of their modal 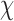Inline graphic-angles. For all design problems, we performed minimized dead-end elimination pruning (minDEE) (Georgiev et al., 2008), followed by either iMinDEE/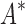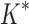Inline graphic/Inline graphic or BBK*. The initial pruning window (Gainza et al., 2012) was 0.1 kcal/mol, and the SS-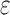Inline graphic bound accuracy was 0.683 [details are provided in section A.9 of the SI (Ojewole et al., 2017b)]. Each design either provably returned the optimal sequences or was terminated after 30 days. A detailed description of the 51 protein–ligand systems in our experiments, the 204 protein design problems based on these systems, and our experimental protocol is provided in section C.1 of the SI (Ojewole et al., 2017b).

4.1. Performance comparison

As the size of the sequence space increases, so does the efficiency of BBK* over iMinDEE/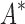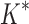Inline graphic/Inline graphic (Fig. 3), demonstrating that the complexity of BBK* is in practice sublinear in the number of sequences. Because iMinDEE/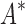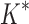Inline graphic/Inline graphic computes individual sequence binding energies as SS-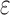Inline graphic bounds, we first measured the efficiency of BBK* using the number of SS-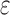Inline graphic bounds computed. Since 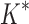Inline graphic scores in iMinDEE/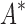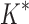Inline graphic/Inline graphic are based on minimized conformation energies (Lilien et al., 2005; Georgiev et al., 2008; Gainza et al., 2012), whose computation represents a major computational bottleneck, we also measured efficiency using the number of conformation energy minimizations performed. 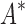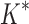Last, we compared the running times of BBK* with those of iMinDEE/Inline graphic/Inline graphic.

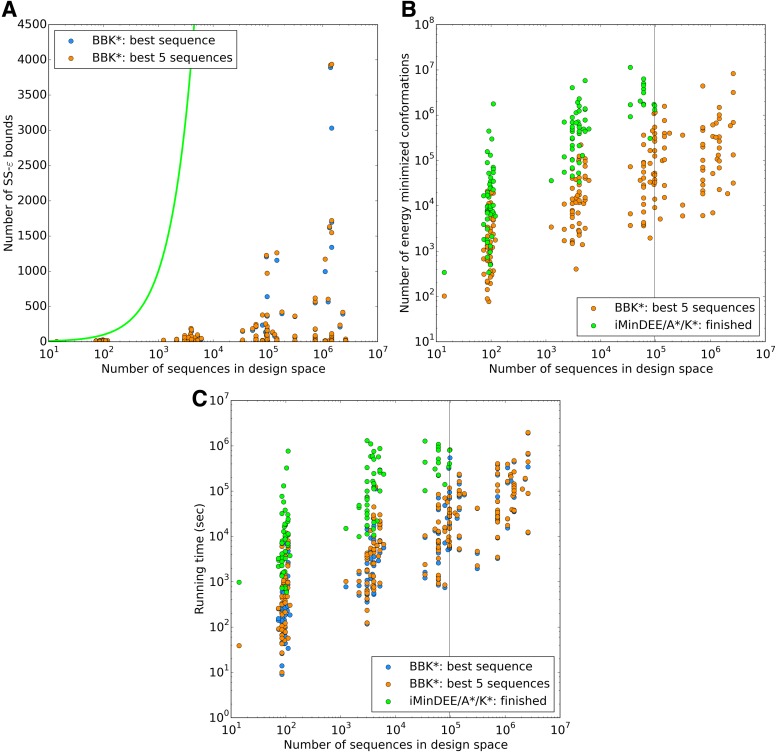
FIG. 3.

FIG. 3.

Open in a new tab

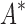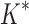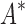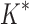BBK* is up to five orders of magnitude more efficient than iMinDEE/Inline graphic/Inline graphic. BBK* completed all 204 designs within a 30-day limit, whereas iMinDEE/Inline graphic/Inline graphic completed only 107. (A) The number of SS-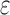Inline graphic bounds performed versus the number of sequences in the design space. Results are shown for computing only the best sequence (blue) and computing the best five sequences (orange). SS algorithms, including the best previous algorithm iMinDEE/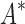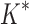Inline graphic/Inline graphic, must compute binding affinity for all possible sequences (green curve). BBK* required up to 6 × 105-fold fewer SS-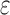Inline graphic bounds to find the best sequences. (B) The number of energy-minimized conformations by BBK* and iMinDEE/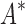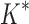Inline graphic/Inline graphic versus the number of sequences in the design space. 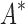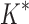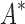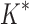iMinDEE/Inline graphic/Inline graphic completed only 107 of 204 designs (left of the vertical line) before the 30-day timeout. For these designs, BBK* was up to 1700-fold more efficient. (C) BBK* and iMinDEE/Inline graphic/Inline graphic running times versus the number of sequences in the design space. 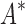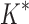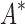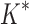For the 107 designs completed by iMinDEE/Inline graphic/Inline graphic within 30 days (left of the vertical line), BBK* was up to 800-fold more efficient than iMinDEE/Inline graphic/Inline graphic.

We divide the design problem sizes into three categories: the smallest problems have between 10 and 102 sequences, medium-sized problems contain between 102 and 104 sequences, and the largest problems contain between 104 and 107 sequences. After 30 days, BBK* completed all 204 designs, but iMinDEE/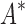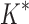Inline graphic/Inline graphic completed only 107 of 204 designs: all 39 of the smallest designs, 54 of 63 medium-sized designs, and only 14 of the 111 largest designs. We now discuss results for the 107 designs completed by iMinDEE/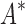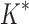Inline graphic/Inline graphic. Because iMinDEE/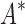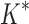Inline graphic/Inline graphic computes individual sequence binding energies as SS-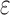Inline graphic bounds, we first measured the efficiency of BBK* using the number of SS-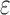Inline graphic bounds computed (Fig. 3A). For small, medium, and large designs, respectively, BBK* was on average 17-fold, 162-fold, and 2568-fold more efficient than iMinDEE/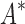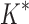Inline graphic/Inline graphic. Next, we measured efficiency using the number of conformation energy minimizations performed (Fig. 3B). Here, BBK* minimized, on average, 10-, 43-, and 113-fold fewer conformations for small, medium, and large-sized designs, respectively, compared with iMinDEE/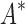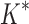Inline graphic/Inline graphic. Last, we compared empirical running times for both methods (Fig. 3C). On average, BBK* was 36-, 67-, and 97-fold faster than iMinDEE/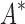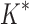Inline graphic/Inline graphic for small, medium, and large-sized designs, respectively.

Based on the data from the 107 designs that iMinDEE/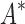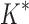Inline graphic/Inline graphic was able to complete within 30 days, we conclude that BBK* provides a combinatorial speedup over iMinDEE/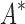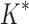Inline graphic/Inline graphic. Crucially, BBK* is not only more efficient but also retains the provability guarantees and biophysical modeling improvements (i.e., ensemble-based design and continuous flexibility) employed by SS iMinDEE/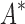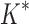Inline graphic/Inline graphic. In one large design (2.6 × 106 sequences), involving a camelid single-domain V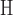Inline graphicH antibody fragment in complex with RNase A (PDB id: 2P49), BBK* pruned >99.9% of sequences to provably find the best five sequences. Therefore, BBK* can design over similarly sized sequence spaces to high-throughput experimental screening methods such as phage display (Carmen and Jermutus, 2002; Pál et al., 2006).

4.2. Sequence space pruning

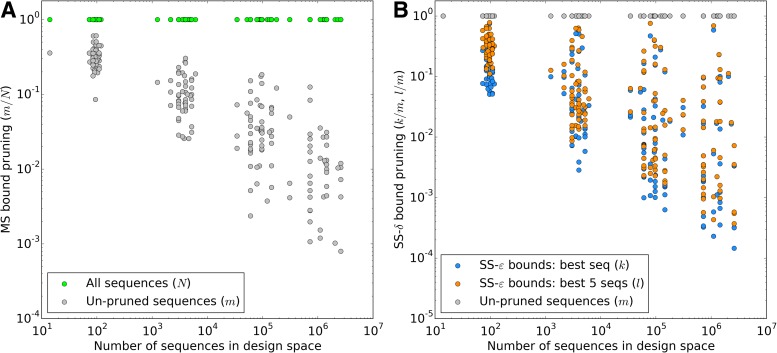
BBK* owes its efficiency to two complementary modes of sequence pruning: MS bound pruning and SS-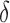Inline graphic bound pruning. Figure 4A shows the efficiency gains in BBK* due to MS bound pruning. In small, medium, and large design problems, respectively, BBK* pruned up to 90%, 99%, and 99.9% of the sequence design space using MS bound pruning. These data show that the amount of MS pruning increased significantly with the size of the design space. Figure 4B illustrates the efficiency gains in BBK* due to SS-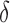Inline graphic bound pruning. In small, medium, and large design problems, respectively, SS-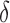Inline graphic pruning eliminates up to 98%, 99.9%, and 99.99% of the sequences not pruned by MS pruning. These data show that the amount of SS-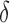Inline graphic pruning increased with the size of the design problem. Further details are provided in sections A.10 and B.1 of the SI (Ojewole et al., 2017b).

FIG. 4.

FIG. 4.

Open in a new tab

BBK* used MS and SS-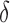Inline graphic bounds to prune up to 99.99999% of the sequence space. (A) Sequence space reduction due to MS pruning. The fraction of unpruned sequences (gray) normalized to the total number of sequences (green). BBK* used MS bounds to provably prune up to 99.9% of the sequence space. BBK* does not compute SS-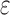Inline graphic bounds for pruned sequences. (B) The fraction of BBK* SS-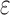Inline graphic bounds (blue for the best sequence and orange for the best five sequences) normalized to the number of sequences not pruned by MS bound pruning (gray). To compute the best sequences, BBK* calculated SS-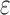Inline graphic bounds for as few as 0.01% of the unpruned sequences. The remaining 99.99% of these sequences were pruned at mere SS-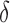Inline graphic accuracy.

Importantly, MS bound pruning and SS-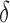Inline graphic bound pruning have multiplicative synergy, producing a combined pruning effect of up to 99.99999% of the original sequence space while provably finding the five best binding sequences. In one example, we redesigned the protein–protein interface (PPI) of a camelid affinity-matured single-domain VHH antibody fragment (PDB id: 2P4A). The sequence space, 2.6 × 106 sequences, consisted of all quadruple mutants in the 9-residue PPI. BBK* pruned all but 2078 sequences using MS pruning and then pruned 2071 sequences from these remaining 2078 sequences using SS-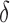Inline graphic bound pruning. These data show how BBK* prunes a combinatorial number of sequences from the design space, producing dramatic efficiency gains over SS methods. See SI section 5.2 for details (Ojewole et al., 2017b).

4.3. Design with coupled continuous side-chain and backbone flexibility

To determine whether design with a fixed backbone and continuous rotamers predicts tight binding in the same sequences as does a model with both local backbone flexibility and continuous rotamers, we used BBK* to redesign the human fibronectin F1:Staphylococcus aureus FNBPA-5 interface (Lower et al., 2011) (PDB id: 2RL0) for binding affinity. As we discuss below, the flexible backbone model favors binding in different sequences than the fixed backbone model does. Details of our experimental protocol are provided in section C.3 of the SI (Ojewole et al., 2017b).

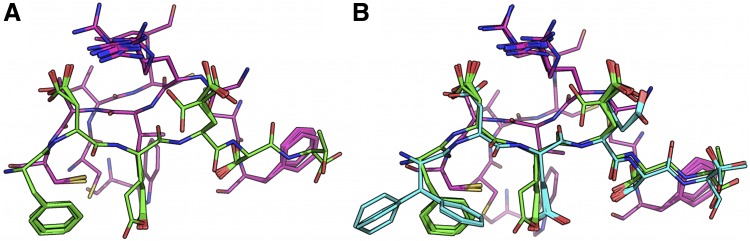
In the first experiment, we redesigned the fibronectin F1:FNBPA-5 interface for binding affinity over the wild-type sequence and 15 single amino acid polymorphisms. Our results showed that using the flexible backbone model versus the fixed backbone model increased the size of the design conformation space by 1417-fold but only increased the running time by 4-fold in BBK*. By comparison, iMinDEE/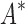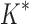Inline graphic/Inline graphic required 48-fold more time than BBK* to complete the flexible backbone design. Our results also showed that the BBK* sequence rankings between the two input models had a Spearman correlation coefficient of only 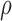Inline graphic = 0.53. Thus, the flexible backbone model favors binding in different sequences than the fixed backbone model does. For instance, the FNBPA-5 D650E mutant is predicted to bind less tightly than the wild-type in the fixed backbone model (Fig. 5A) but more tightly than WT in the flexible model (Fig. 5B). In our second experiment, the sequence design space consisted of the wild-type sequence and 25 single amino acid polymorphisms. The BBK* sequence rankings produced by the two input models had a Spearman correlation coefficient of 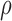Inline graphic = 0.82 [additional details are provided in section B.2 of the SI (Ojewole et al., 2017b)]. Relative to the fixed backbone model, the flexible backbone model increased the size of the design conformation space by 8447-fold but only increased the running time by only 1.7-fold in BBK*. iMinDEE/Inline graphic/Inline graphic required 89-fold more time than BBK* to complete the design using the flexible backbone model.

FIG. 5.

FIG. 5.

Open in a new tab

BBK* efficiently handles coupled continuous side-chain and local backbone flexibility. Selected residues from ensembles, computed by BBK*, of human fibronectin F1 modules 4–5 (magenta) in complex with a fragment of Staphylococcus aureus fibronectin binding protein A 5 [FNBPA-5, PDB id: 2RL0, (Lower et al., 2011)]. The design space consisted of the wild-type sequence and either 15 or 25 single amino acid mutants. (A) Ensemble of the wild-type sequence based on the original crystal structure. The design used a fixed FNBPA-5 backbone (green) and continuous side-chain flexibility. (B) Ensemble of the wild-type sequence using two backbones: the original FNBPA-5 backbone (green) and a second backbone (PDB id: 2RKY, cyan) with RMSD 1.3 Å from the original [found using the MASTER program (Zhou and Grigoryan, 2015)]. The sequence rankings [by 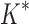Inline graphic score, Eq. (2)] from the fixed and flexible backbone models had Spearman correlation coefficients of 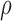Inline graphic = 0.53 and 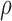Inline graphic = 0.82 in the 15 and 25 mutant designs, respectively. This shows that the flexible backbone model favors binding in very different sequences than the fixed backbone model does.

It is important to note that these experiments are only possible with provable algorithms. Without the provable guarantees of BBK*, it would be difficult and perhaps unsound to compare the results of CPD with and without coupled continuous side-chain and backbone flexibility, since differences induced by the fixed backbone and rotamer model cannot be deconvolved from differences stemming from undersampling or inadequate stochastic optimization. Thus, BBK* provides provable methods to analyze the difference in predicted sequences between different models of side-chain and backbone flexibility.

5. Conclusion

BBK* fills an important lacuna in protein design: we presented a novel algorithm that can search efficiently not over the energies of single conformations, but over the binding affinity of sequences. BBK* is, to our knowledge, the first provable, ensemble-based algorithm to search in order of binding affinity and run in time sublinear in the number of sequences. Previously, protein designers either employed heuristic algorithms to compute locally optimal sequences, or computed provably accurate approximations of binding affinity for each sequence individually. BBK* not only computes the globally optimal sequences, but it also does so while combinatorially pruning the search space. Our experiments show that BBK* can search over sequence spaces of up to 2.6 × 106 sequences, a capacity comparable with high-throughput experimental screening methods such as phage display. Thus, BBK* liberates binding affinity-based protein design from the efficiency barrier imposed by exhaustive search. Ensemble-based design for affinity over large sequence spaces was previously possible only with heuristic algorithms (with no guarantees), or using high-throughput wet-bench experiments. BBK* enables CPD by providing new Ka algorithms, with provable guarantees, for these large-scale protein designs.

Acknowledgments

We would like to thank Drs. Mark Hallen and Pablo Gainza for helpful discussions and for providing useful protein–ligand binding problems; Dr. Jeffrey Martin for assisting with software optimizations; Jack Holland, Dr. Gevorg Grigoryan, Hunter Nisonoff, Anna Lowegard, and all members of the Donald laboratory for helpful discussions; and the NSF (GRFP DGF 1106401 to A.A.O.) and NIH (R01-GM78031 and R01-GM118543 to BRD, R01-HL119648 to V.G.F.) for funding.

Author Disclosure Statement

No competing financial interests exist.

References

  1. Boas F.E., and Harbury P.B. 2007. Potential energy functions for protein design. Curr. Opin. Struct. Biol. 17, 199–204 [DOI] [PubMed] [Google Scholar]
  2. Carmen S., and Jermutus L. 2002. Concepts in antibody phage display. Brief Funct. Genomic Proteomic. 1, 189–203 [DOI] [PubMed] [Google Scholar]
  3. Chen C.-Y., Georgiev I., Anderson A.C., et al. 2009. Computational structure-based redesign of enzyme activity. Proc. Natl Acad. Sci. U. S. A. 106, 3764–3769 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Dahiyat B.I., and Mayo S.L. 1996. Protein design automation. Protein Sci. 5, 895–903 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Desmet J., De Maeyer M., Hazes B., et al. 1992. The dead-end elimination theorem and its use in protein side-chain positioning. Nature 356, 539–542 [DOI] [PubMed] [Google Scholar]
  6. Donald B.R. 2011. Algorithms in Structural Molecular Biology. MIT Press, Cambridge, MA [Google Scholar]
  7. Fleishman S.J., Khare S.D., Koga N., et al. 2011. Restricted sidechain plasticity in the structures of native proteins and complexes. Protein Sci. 20, 753–757 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Frey K.M., Georgiev I., Donald B.R., et al. 2010. Predicting resistance mutations using protein design algorithms. Proc. Natl Acad. Sci. U. S. A. 107, 13707–13712 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Fromer M., and Yanover C. 2008. A computational framework to empower probabilistic protein design. Bioinformatics 24, i214–i222 [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Gainza P., Nisonoff H.M., and Donald B.R. 2016. Algorithms for protein design. Curr. Opin. Struct. Biol. 39, 16–26 [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Gainza P., Roberts K.E., and Donald B.R. 2012. Protein design using continuous rotamers. PLoS Comput. Biol. 8, e1002335. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Gainza P., Roberts K.E., Georgiev I., et al. 2013. Program, user manual, and source code are available at www.cs.duke.edu/donaldlab/software.php. OSPREY: Protein design with ensembles, flexibility, and provable algorithms. Methods Enzymol. 523, 87–107 [DOI] [PMC free article] [PubMed]
  13. Georgiev I., and Donald B.R. 2007. Dead-end elimination with backbone flexibility. Bioinformatics 23, i185–i194 [DOI] [PubMed] [Google Scholar]
  14. Georgiev I., Lilien R.H., and Donald B.R. 2006. Improved pruning algorithms and divide-and-conquer strategies for dead-end elimination, with application to protein design. Bioinformatics 22, e174–e183 [DOI] [PubMed] [Google Scholar]
  15. Georgiev I., Lilien R.H., and Donald B.R. 2008. The minimized dead-end elimination criterion and its application to protein redesign in a hybrid scoring and search algorithm for computing partition functions over molecular ensembles. J. Comput. Chem. 29, 1527–1542 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Georgiev I., Schmidt S., Li Y., et al. 2012. Design of epitope-specific probes for sera analysis and antibody isolation. Retrovirology 9, P50 [Google Scholar]
  17. Georgiev I.S. 2009. Novel algorithms for computational protein design, with applications to enzyme redesign and small-molecule inhibitor design [Ph.D. thesis]. Duke University, Durham, NC: Retrieved from http://hdl.handle.net/10161/1113 [Google Scholar]
  18. Georgiev I.S., Rudicell R.S., Saunders K.O., et al. 2014. Antibodies VRC01 and 10E8 neutralize HIV-1 with high breadth and potency even with IG-framework regions substantially reverted to germline. J. Immunol. 192, 1100–1106 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Gilson M.K., Given J.A., Bush B.L., et al. 1997. The statistical-thermodynamic basis for computation of binding affinities: A critical review. Biophys. J. 72, 1047–1069 [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Gorczynski M.J., Grembecka J., Zhou Y., et al. 2007. Allosteric inhibition of the protein-protein interaction between the leukemia-associated proteins Runx1 and CBFbeta. Chem. Biol. 14, 1186–1197 [DOI] [PubMed] [Google Scholar]
  21. Hallen M.A., and Donald B.R. 2016. Comets (Constrained optimization of multistate energies by tree search): A provable and efficient protein design algorithm to optimize binding affinity and specificity with respect to sequence. J. Comput. Biol. 23, 311–321 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Hallen M.A., Gainza P., and Donald B.R. 2015. Compact representation of continuous energy surfaces for more efficient protein design. J. Chem. Theory Comput. 11, 2292–2306 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hallen M.A., Jou J.D., and Donald B.R. 2017. LUTE (Local unpruned tuple expansion): Accurate continuously flexible protein design with general energy functions and rigid Rotamer-Like efficiency. J. Comput. Biol. 24(6), 536–546 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Hallen M.A., Keedy D.A., and Donald B.R. 2013. Dead-end elimination with perturbations (DEEPer): A provable protein design algorithm with continuous sidechain and backbone flexibility. Proteins 81, 18–39 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Hart P., N.J., N., and Raphael B. 1968. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. SSC. 4, 100–114 [Google Scholar]
  26. Jou J.D., Jain S., Georgiev I.S., et al. 2016. BWM*: A novel, provable, ensemble-based dynamic programming algorithm for sparse approximations of computational protein design. J. Comput. Biol. 23, 413–424 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kingsford C.L., Chazelle B., and Singh M. 2005. Solving and analyzing side-chain positioning problems using linear and integer programming. Bioinformatics 21, 1028–1039 [DOI] [PubMed] [Google Scholar]
  28. Kuhlman B., and Baker D. 2000. Native protein sequences are close to optimal for their structures. Proc. Natl Acad. Sci. U. S. A. 97, 10383–10388 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Leach A.R., and Lemon A.P. 1998. Exploring the conformational space of protein side chains using dead-end elimination and the a* algorithm. Proteins 33, 227–239 [DOI] [PubMed] [Google Scholar]
  30. Leaver-Fay A., Tyka M., Lewis S.M., et al. 2011. Rosetta3: An object-oriented software suite for the simulation and design of macromolecules. Methods Enzymol. 487, 545–574 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Lee C., and Levitt M. 1991. Accurate prediction of the stability and activity effects of site-directed mutagenesis on a protein core. Nature 352, 448–451 [DOI] [PubMed] [Google Scholar]
  32. Leech J., Prins J.F., and Hermans J. 1996. Smd: Visual steering of molecular dynamics for protein design. Comput. Sci. Eng. 3, 38–45 [Google Scholar]
  33. Lilien R.H., Stevens B.W., Anderson A.C., et al. 2005. A novel ensemble-based scoring and search algorithm for protein redesign and its application to modify the substrate specificity of the gramicidin synthetase a phenylalanine adenylation enzyme. J. Comput. Biol. 12, 740–761 [DOI] [PubMed] [Google Scholar]
  34. Lovell S.C., Word J.M., Richardson J.S., et al. 2000. The penultimate rotamer library. Proteins 40, 389–408 [PubMed] [Google Scholar]
  35. Lower S.K., Lamlertthon S., Casillas-Ituarte N.N., et al. 2011. Polymorphisms in fibronectin binding protein A of Staphylococcus aureus are associated with infection of cardiovascular devices. Proc. Natl. Acad. Sci. U. S. A. 108, 18372–18377 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Nisonoff H. 2015. Efficient partition function estimation in computational protein design: Probabalistic guarantees and characterization of a novel algorithm [B.S. Thesis]. Department of Mathematics, Duke University [Google Scholar]
  37. Ojewole A., Lowegard A., Gainza P., et al. 2017a. OSPREY predicts resistance mutations using positive and negative computational protein design. Methods Mol. Biol. 1529, 291–306 [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Ojewole A.A., Jou J.D., Fowler V.G., et al. 2017b. Supplementary information: BBK* (Branch and Bound over K*): A provable and efficient ensemble-based protein design algorithm to optimize stability and binding affinity over large sequence spaces for sparse approximations of computational protein design. Available at: www.cs.duke.edu/donaldlab/Supplementary/jcb17/bbkstar Last accessed on February23, 2018 [DOI] [PMC free article] [PubMed]
  39. Pál G., Kouadio J.-L.K., Artis D.R., et al. 2006. Comprehensive and quantitative mapping of energy landscapes for protein-protein interactions by rapid combinatorial scanning. J. Biol. Chem. 281, 22378–22385 [DOI] [PubMed] [Google Scholar]
  40. Peng J., Hosur R., Berger B., et al. 2015. iTreePack: Protein complex Side-Chain packing by dual decomposition. arXiv:1504.05467 [q-bio.BM] [Google Scholar]
  41. Pierce N.A., and Winfree E. 2002. Protein design is NP-hard. Protein Eng. 15, 779–782 [DOI] [PubMed] [Google Scholar]
  42. Reeve S.M., Gainza P., Frey K.M., et al. 2015. Protein design algorithms predict viable resistance to an experimental antifolate. Proc. Natl Acad. Sci. U. S. A. 112, 749–754 [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Roberts K.E., Cushing P.R., Boisguerin P., et al. 2012. Computational design of a PDZ domain peptide inhibitor that rescues CFTR activity. PLoS Comput. Biol. 8, e1002477. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Roberts K.E., and Donald B. R. 2015. Improved energy bound accuracy enhances the efficiency of continuous protein design. Proteins 83, 1151–1164 [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Roberts K.E., Gainza P., Hallen M.A., et al. 2015. Fast gap-free enumeration of conformations and sequences for protein design. Proteins 83, 1859–1877 [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Rudicell R.S., Kwon Y.D., Ko S.-Y., et al. 2014. Enhanced potency of a broadly neutralizing HIV-1 antibody in vitro improves protection against lentiviral infection in vivo. J Virol 88, 12669–12682 [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Sciretti D., Bruscolini P., Pelizzola A., et al. 2009. Computational protein design with side-chain conformational entropy. Proteins 74, 176–191 [DOI] [PubMed] [Google Scholar]
  48. Silver N.W., King B.M., Nalam M.N.L., et al. 2013. Efficient computation of small-molecule configurational binding entropy and free energy changes by ensemble enumeration. J. Chem. Theory Comput. 9, 5098–5115 [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Simoncini D., Allouche D., de Givry S., et al. 2015. Guaranteed discrete energy optimization on large protein design problems. J. Chem. Theory Comput. 11, 5980–5989 [DOI] [PubMed] [Google Scholar]
  50. Stevens B.W., Lilien R.H., Georgiev I., et al. 2006. Redesigning the PheA domain of gramicidin synthetase leads to a new understanding of the enzyme's mechanism and selectivity. Biochemistry 45, 15495–15504 [DOI] [PubMed] [Google Scholar]
  51. Traoré S., Allouche D., André I., et al. 2013. A new framework for computational protein design through cost function network optimization. Bioinformatics 29, 2129–2136 [DOI] [PubMed] [Google Scholar]
  52. Traoré S., Roberts K.E., Allouche D., et al. 2016. Fast search algorithms for computational protein design. J. Comput. Chem. 37, 1048–1058 [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Valiant L.G. 1979. The complexity of computing the permanent. Theor. Comput. Sci. 8, 189–201 [Google Scholar]
  54. Viricel C., Simoncini D., Barbe S., Schiex T. 2016. Guaranteed Weighted Counting for Affinity Computation: Beyond Determinism and Structure. In: Rueher M. (eds) Principles and Practice of Constraint Programming. CP 2016. Lecture Notes in Computer Science, vol 9892 Springer, Cham: DOI 10.1007/978-3-319-44953-1_46 [DOI] [Google Scholar]
  55. Wainwright M.J., Jaakkola T.S., and Willsky A.S. 2013. A new class of upper bounds on the log partition function. CoRR abs/1301.0610 [Google Scholar]
  56. Xu J. 2005. Rapid protein side-chain packing via tree decomposition. 9th Annual International Conference, RECOMB 3500, 423–439 [Google Scholar]
  57. Xu J., and Berger B. 2006. Fast and accurate algorithms for protein side-chain packing. J. ACM 53, 533–557 [Google Scholar]
  58. Zheng F., Yang W., Ko M.-C., et al. 2008. Most efficient cocaine hydrolase designed by virtual screening of transition states. J. Am. Chem. Soc. 130, 12148–12155 [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Zhou J., and Grigoryan G. 2015. Rapid search for tertiary fragments reveals protein sequence-structure relationships. Protein Sci. 24, 508–524 [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Journal of Computational Biology are provided here courtesy of Mary Ann Liebert, Inc.

RESOURCES