Covariate adjusted classification trees

SUMMARY

In studies that compare several diagnostic groups, subjects can be measured on certain features and classification trees can be used to identify which of them best characterize the differences among groups. However, subjects may also be measured on additional covariates whose ability to characterize group differences is not meaningful or of interest, but may still have an impact on the examined features. Therefore, it is important to adjust for the effects of covariates on these features. We present a new semi-parametric approach to adjust for covariate effects when constructing classification trees based on the features of interest that is readily implementable. An application is given for postmortem brain tissue data to compare the neurobiological characteristics of subjects with schizophrenia to those of normal controls. We also evaluate the performance of our approach using a simulation study.

1. Introduction

One may want to examine a set of characteristics or features measured on subjects belonging to one of multiple groups and attempt to determine a subset of these features that is superior in characterizing the differences among the examined groups. However, the ability of these features to do so may be obscured by the effects of covariates that are also measured, but are not of interest with respect to characterizing the group differences. In this case, this subset of features may be more accurately identified if the confounding effects of these covariates can be somehow adjusted for or, in other words, removed (Tu and others, 1997).

We were motivated to explore approaches for adjusting for covariate effects in the context of discrimination techniques due to our analyses of human postmortem brain tissue studies conducted in the Conte Center for the Neuroscience of Mental Disorders (CCNMD) in the Department of Psychiatry at the University of Pittsburgh. This center focuses on understanding the neurobiology of schizophrenia. In a typical CCNMD study, schizophrenia subjects and normal controls are measured not only on different brain biomarkers of scientific interest but also on covariates including subject’s age at death, gender, brain tissue storage time (the amount of time brain tissue has been held in storage), and postmortem interval (PMI), that is, elapsed time between time of death and time of tissue collection. The primary aim in these studies is to identify those brain biomarkers that best characterize the differences between the schizophrenia and control diagnostic groups, without the effects of covariates not intrinsically meaningful to our CCNMD collaborators in understanding schizophrenia. In this setting, removing the confounding effects of these covariates on the examined brain biomarkers creates a clearer picture of which biomarkers truly characterize the differences between schizophrenia subjects and controls.

There is an extensive literature dealing with discrimination methodology. Parametric approaches include logistic discriminant analysis (Tu and others, 1997), as well as linear discriminant analysis (LDA), which is based on the assumption of joint normality among features. More recently, Li and others (2003) formulated extensions of LDA to nonlinear discriminant analysis using kernel function operators. One nonparametric discrimination approach is that of constructing classification trees, which was initially developed by various authors including Breiman, Friedman, Olshen, and Stone (Breiman and others, 1984) (hereafter denoted as BFOS). Recent extensions of classification trees include the approach developed by Kim and Loh (2003) which incorporates LDA and statistical testing methods, and the tree ensemble approach of Random Forests developed by Breiman (2001a). Other nonparametric discrimination approaches include support vector machines (Cortes and Vapnik, 1995).

There are currently several approaches to adjust for covariate effects when assessing the association between a set of feature variables and a response variable, for example, a classification variable. Crainiceanu and others (2008), Wang and others (2012), and Wilson and Reich (2014) developed methods for identifying optimal sets of covariates to adjust for. Friston and others (1995) developed an adjustment approach for statistical parametric maps of neuroimaging data that consists of fitting a linear model to each outcome while controlling for covariate effects. Based on the model, residuals are computed and the brain map is based on these residuals. Nonyane and Foulkes (2008) used a similar approach for Random Forests. Yet, the available literature that clearly develops the theoretical framework of adjusting for covariate effects on feature variables in the context of discrimination approaches appears to be limited to discriminant analysis. Specifically, early methods to adjust for covariate effects on feature data were developed for LDA by Cochran and Bliss (1948), with further developments by Lachenbruch (1977) and Tu and others (1997) (hereafter, denoted as L&T), as well as Asafu-Adjei (2011); Asafu-Adjei and others (2013). The core of these methodologies is to adjust for covariate effects using the conditional distributions of the feature data for a given covariate value in a population setting. The computational implementation of these adjustment methodologies is equivalent to fitting a linear or nonlinear model to the training feature data controlling for group and covariate effects, computing the resulting residual feature values in each group, and then basing the discriminant analysis on these residuals. Tu and others (1997) and Dukart and others (2011) also implemented this covariate adjustment approach for logistic discriminant analysis and support vector machines, respectively, but neither of these approaches provide details for their theoretical basis.

Therefore, there does not appear to be any such covariate adjustment method that is available and theoretically justified for classification trees, whose advantages over other discrimination methods include its simplicity and ease of interpretation. As a result, one finds papers such as Knable and others (2002) that use classification trees to identify post-mortem brain tissue biomarkers that best characterize the differences among three mental disorder diagnostic groups and controls, but fail to account for the effect that these measured covariates can have on the biomarker measurements. To lay the groundwork for our proposed modification to classification trees, we first summarize the BFOS construction method from a more general, population-based perspective, amplifying the initial approaches taken by Shang and Breiman (1996) in their development of distribution based trees. We do this primarily to provide a theoretical basis for incorporating the covariates into the BFOS construction approach using the conditional distributions of the feature data.

There are intricacies, as well as computational issues, in this implementation that soon become apparent. One such intricacy is whether or not to allow the subset of features identified as best characterizing the group differences to depend on the covariates. Later in our discussion, we show that this can happen when covariates have differential effects on the examined features in the different groups. For example, in pre-processing the data in a post-mortem tissue study, there may be situations where subject’s age at death affects the biomarkers differentially by diagnostic group, so that it makes sense for the biomarkers identified as best characterizing the diagnostic group differences to depend on the subject’s age at their time of death. However, in the neurobiological studies we have collaborated on, interest has mainly been expressed in identifying a set of such biomarkers that remains the same regardless of subject’s age at death or any other covariate value.

Therefore, we focus on developing a model for the conditional distribution of the feature data that allows us to adjust for covariate effects when constructing a tree based on the feature data, while yielding a subset of features that best characterizes the differences among groups and does not depend on covariate values. Specifically, in the spirit of L&T, we formulate a semiparametric model that allows us to fit a linear or nonlinear model to the training feature data that controls for group and covariate effects. Based on this model, we compute the residual (or covariate adjusted) feature values in each group, and construct a covariate adjusted classification tree (COVACT) by analyzing these residual values using standard classification tree software. Although this approach may make sense intuitively, incorporating the conditional distribution of the feature data ensures that considering these residual values in COVACT is theoretically valid and not simply an ad-hoc approach.

In Section 2, we begin by briefly discussing the motivation behind examining the conditional distribution of the feature data in our proposed approach and by giving some of the notation used throughout our discussion. We then provide our population-based formulation of the BFOS construction approach in Section 3, where we also develop a tree construction approach for the case where the feature data come from one of 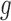known distributions conditional on a given covariate value. In Section 4, we detail our proposed COVACT construction approach. We apply COVACT to postmortem brain tissue data in Section 5, and use a simulation study to evaluate its performance in Section 6. In Section 7, we conclude with a final discussion.

2. Motivation and notation

2.1. The effects of covariates in discrimination

Our primary goal is to accurately identify which features best characterize the differences among groups, without the masking effects of covariates that are not of interest with respect to distinguishing among groups. Examining the conditional distribution of the feature data for a given covariate value allows for the estimation and adjustment of these covariate effects. Demonstrations of this are depicted in Figure 1a of Tu and others (1997) and in supplementary material available at Biostatistics online, which illustrate that the true ability of a feature to distinguish among groups is much more apparent if one examines that feature’s values adjusted to a common covariate value.

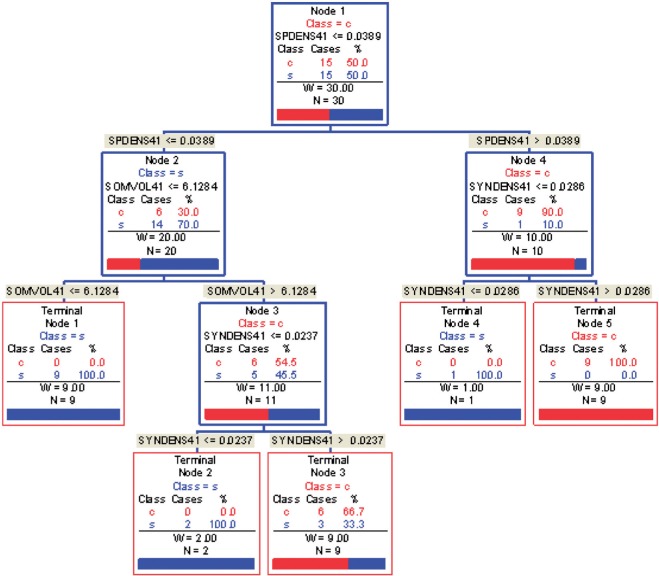
Fig. 1.

COVACT for sweet data. SpDens41, SomVol41, and SynDens41 correspond to SP-IR puncta density, somal volume, and SY-IR puncta density for BA 41, adjusted for the effects of age at death, gender, PMI, and storage time. In each terminal node, a label of “classs” corresponds to subjects classified as having schizophrenia, while that of “classc” corresponds to subjects classified as controls.

2.2. Notation

Let 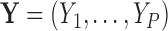denote a random real-valued feature vector corresponding to a set of possible measurement values for an observed subject whose group membership is unknown. We then define 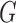as a random variable denoting group membership (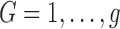) for this subject and 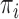as the prior probability of membership in group 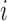(i.e. 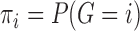). In addition, we let 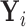denote 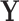given membership in group 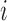, so that 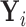has a distinct population cumulative distribution function (CDF) 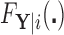in the 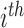group. In the context of decision trees, the entire feature space, which contains all possible values for 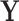, is defined as the root node 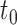of a particular tree and all distinct subsets of this feature space 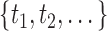as descendant nodes.

For a particular node 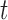, that is, subset of the feature space, let 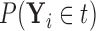denote 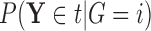, which we can compute using 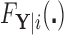. We then have that

$$P(G=i|\mathbf{Y}\in t)={\pi }_{i}P({\mathbf{Y}}_i\in t)/P(\mathbf{Y}\in t)$$ (2.1)

and

$$P(\mathbf{Y}\in t)=\sum _{i=1}^g{\pi }_{i}P({\mathbf{Y}}_i\in t).$$ (2.2)

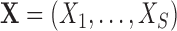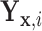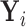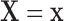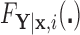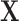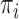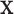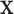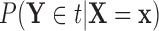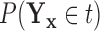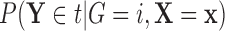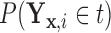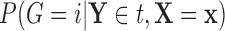Suppose we consider a set of random covariates that is related to the examined features. Let denote conditional on , with population CDF . In this context, we assume that has no relevance in characterizing differences among groups and, thus, specify the group priors to be independent of . For a given , we denote as , as , and as 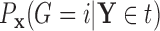, so that

$$P_{\mathbf{x}}(G=i|\mathbf{Y}\in t)=\frac{P_{\mathbf{x}}(G=i,\mathbf{Y}\in t)}{P({\mathbf{Y}}_{\mathbf{x}}\in t)}=\frac{{\pi }_{i}P({\mathbf{Y}}_{\mathbf{x},i}\in t)}{P({\mathbf{Y}}_{\mathbf{x}}\in t)}$$ (2.3)

and

$$P({\mathbf{Y}}_{\mathbf{x}}\in t)=\sum _{i=1}^g{P}_{\mathbf{x}}(G=i,\mathbf{Y}\in t)=\sum _{i=1}^g{\pi }_{i}P({\mathbf{Y}}_{\mathbf{x},i}\in t).$$ (2.4)

3. Classification trees: A population-based formulation

Most presentations of classification trees in the literature do not treat it from a population-based viewpoint, with the exception of a few approaches such as those taken by Shang and Breiman (1996). For instance, BFOS focus on empirical approaches towards tree construction and do not present the underlying population distribution framework. In Section 3.1, we provide a brief unified summary of the BFOS approach to classification tree construction purely from a population perspective. This presentation allows us to incorporate covariate effects into our tree construction in Section 3.2 by working with the conditional distributions of the feature data.

3.1. Traditional procedure

For convenience, we assume unit misclassification costs throughout. To initiate construction of a classification tree, a feature element 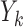and a cut point 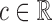are chosen to split the feature space into two complementary descendant nodes 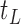and 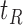, such that a goodness of split (GOS) criterion defined by the split 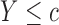is maximized over all feature elements and values of 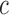. This splitting procedure is then applied recursively to 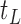, , 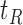and all subsequent descendant nodes until further splitting ceases to substantially increase group purity, as defined by some user-defined criterion. Once splitting stops, let 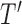denote the resulting tree consisting of nodes split using the chosen GOS criterion and nodes that are not split, which are termed as terminal nodes. For instance, if the root node 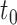is split while its descendant nodes 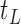and 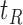are not, the final tree 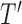would consist of the root node 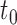and the terminal nodes 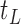and . 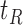If 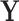for a particular subject falls into terminal node 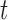, then that subject is assigned to group 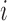if 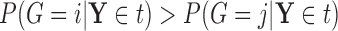or equivalently, if ().

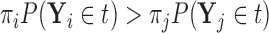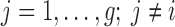In choosing the optimal split for each node, one GOS criterion that has been used is the twoing criterion (defined for empirical data by BFOS and easily extendable for the population case). Another GOS criterion is based on a measure of impurity for node 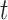, denoted 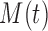, where 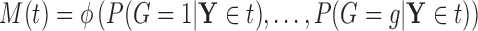for a specified impurity function 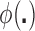, which is typically chosen to be strictly concave on the unit simplex (see BFOS; Asafu-Adjei, 2011, for more details). In the case of population distributions, we rephrase this latter GOS criterion as

$$M(t)-\left\{P(\mathbf{Y}\in t_L|\mathbf{Y}\in t)M(t_L)+P(\mathbf{Y}\in t_R|\mathbf{Y}\in t)M(t_R)\right\}$$ (3.1)

(see BFOS). Intuitively, the bracketed quantity in (3.1) measures the within group heterogeneity of the left and right descendant nodes of node 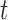. We want this quantity to be no larger than the measure 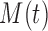of within group heterogeneity of node 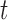. This way, the descendant nodes of 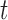become more internally homogeneous, or at least no more heterogeneous, with respect to group compared with node 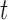. Examples of impurity measures 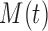include the Gini and Deviance indices, two functions of 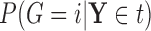that are strictly concave (see BFOS), which ensures that the impurity of node 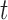is always decreased when it is split for continuous 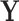(proof provided in supplementary material available at Biostatistics online).

It is worth noting that the formulation of the BFOS approach from a population-based perspective allows for a parametric alternative to the standard non-parametric BFOS approach. One can assume that 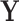comes from some parametric, for example, normal, distribution and use the training data to estimate any unknown parameters (see Asafu-Adjei, 2011, for an illustration). Population classification trees also have a very useful monotone invariance property (see supplementary material available at Biostatistics online for more details). This property states that transforming each feature using separate strictly monotone functions does not affect the tree structure, that is, the order of splitting features and direction of splits for a particular tree.

With available data, the probabilities required for this construction procedure can be estimated nonparametrically by computing the corresponding empirical CDFs. This is actually the standard approach to the BFOS tree construction method and can be readily implemented using various software packages. To account for the fact that trees initially constructed using this non-parametric approach may substantially overfit the training data, BFOS developed a minimal cost complexity pruning approach to remove specific nodes, resulting in trees with minimized misclassification rates (see BFOS for more details). In other words, the use of minimal cost complexity pruning, which we note does not involve any formal statistical testing, results in trees with features (and their corresponding splits) that are most useful in predicting group membership and, thus, characterizing group differences.

3.2. Conditional classification tree

Based on our formulation in Section 3.1, we construct a tree that conditions on 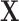in a straightforward manner. To obtain a conditional tree 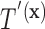for covariate value 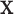, we replace the marginal probabilities 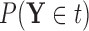and 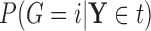with their conditional counterparts 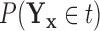and 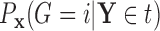defined in Section 2.2. Note that the relations in (2.3) and (2.4) are identical to those in (2.1) and (2.2), respectively, where 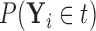is replaced with 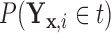. Thus, assuming that 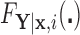and 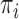are known for a given 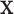, we can construct 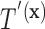in the same manner used to construct 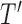in Section 3.1 by simply replacing 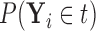with .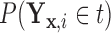

3.3. Conditional procedure issues

Although this construction approach accounts for the relationship between the examined features and covariates that are assumed to have no importance in characterizing group differences (i.e., 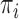not depending on 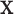), it is still possible that the resulting tree structure can depend on 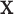. As noted in Section 1, there may be settings where one expects the tree structure to depend on covariate values, e.g., where the covariate effect on the examined features is differentially expressed across groups. However, in our noted neurobiological settings, we do not want the neurobiological features identified as best characterizing the differences among groups to depend on any particular covariate value 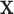(even though the cut points may). In Section 4, we introduce a specific population model that accounts for covariate effects on the examined features and allows for the development of a tree structure that is independent of .

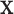4. Covact

4.1. Linear invariance property

The following invariance property is crucial in our model development (proof provided in supplementary material available at Biostatistics online).

Result 1: Let 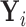and 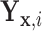have CDFs 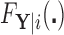and 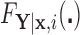, respectively, in the 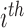group. Suppose that 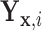is equal in distribution to 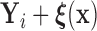(i.e., 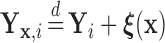), where 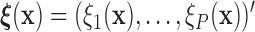is a known function of that does not depend on group. For a chosen GOS criterion, let be the classification tree based on 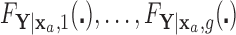for covariate value 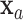and 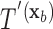be the classification tree based on 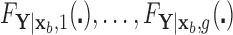for covariate value 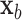. Then, 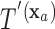and 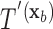have the same set of splitting variables and the set of cut points for 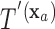, , 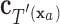are related to those of 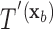, , 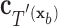by = .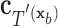

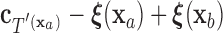Therefore, if the conditional distribution of 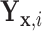is a location shift of the distribution of 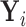by the known value 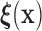, then the set of splitting variables for the conditional tree 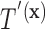does not depend on 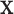. One may also think of the linear invariance property as stating that if the effects of covariates on the feature data do not depend on group, then there is no interaction between features and covariates for predicting group membership based on our tree. Verifying the assumption that the effects of covariates on the examined features are not group dependent can be done by verifying that there are no significant group by covariate interactions for any of the features.

4.2. Population case

For the remainder, we assume that 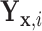has CDF 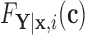= 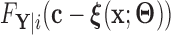for a given 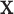, where the function 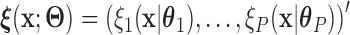is a known smooth function of 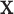and parameter vectors 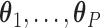that is independent of group. In the spirit of L&T, we assume that 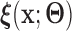is a parametric function of 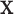so that we can use 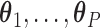to estimate the magnitude of each covariate effect on the feature data. Based on our model for 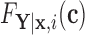, we have that if 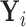has CDF 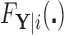, then 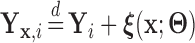. As in Section 3.1, we also assume unit misclassification costs.

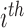Alternatively, we may examine the distribution of the covariate adjusted feature vector in the group, so that 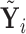has CDF 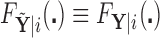. Clearly, the conditional probabilities 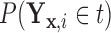obtained from 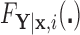can equivalently be expressed as 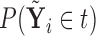obtained from 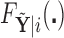. Once we compute these probabilities, we can construct the covariate adjusted tree 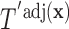using the traditional approach in Section 3.1 by simply replacing 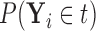with 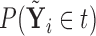. Therefore, by assuming that the feature variables are shifted by the function 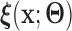, we can apply our population-based formulation of the BFOS approach to the covariate adjusted feature data in order to construct a tree 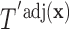that suitably adjusts for covariate effects.

Based on Result 1, the following facts regarding 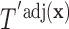hold:

• 1. Let 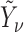and 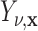correspond to any of the 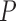features in 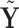and 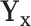(the group membership of which is unknown). We then have that the split 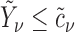in 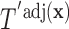is equivalent to the split 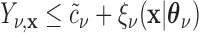in the tree based on 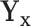. For example, if a feature that has been adjusted for some covariate effect is greater than a constant value for a specific split in 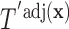, then this feature will be greater than a value that depends on that covariate when expressed on the original scale.

• 2. Regardless of the value of 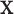, 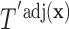allows for the identification of a covariate independent subset of features that best characterizes the differences among the 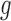groups while accounting for all relevant covariate effects.

4.3. COVACT estimation using training data

The first step in estimating the CDFs 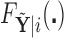needed to construct our covariate adjusted tree is to estimate the parameter vectors 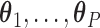from the available training data 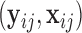(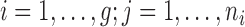). Based on Tu and others (1997), a simple approach to do so is to assume that the conditional mean of the random feature vector 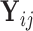= 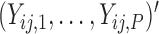is given by 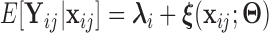= 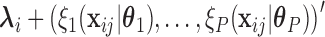, where 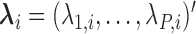denotes the effect of belonging to the 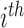group. We then use least squares (LS) estimation to obtain the estimates 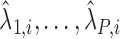, 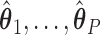that minimize the criteria 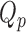= 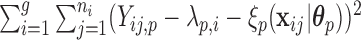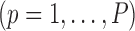. We note that there may be instances where 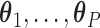are not identifiable, in which case 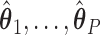are not unique. However, regardless of these estimates, the trees obtained from our construction approach produce the same results (details provided in supplementary material available at Biostatistics online). As noted below, the estimates of 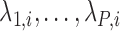are not used in our construction approach, so whether or not these parameters are identifiable does not affect our resulting tree.

Once we obtain the estimates 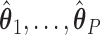, we can compute the covariate adjusted feature data 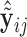= = 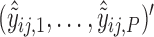= 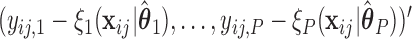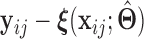. Holding , 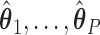fixed, we then view 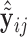as a random sample of 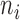observations from 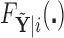, so that we can compute the empirical CDFs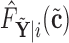 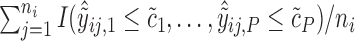. Based on the estimates 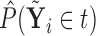obtained from 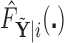, we can construct our covariate adjusted tree by applying the standard non-parametric BFOS approach to the covariate adjusted feature data. Thus, it is important to observe that our COVACT construction approach can be easily implemented using standard classification tree software and its variations.

In this manner, we can view our tree construction approach as a semi-parametric generalization of the approach developed by L&T. Specifically, we first use a parametric model to estimate the parameter vectors 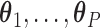that we use to compute our covariate adjusted feature data. The CDFs for these adjusted feature data are then estimated non-parametrically in order to yield our final covariate adjusted tree.

5. Application to postmortem tissue data

Our COVACT methodology is now illustrated in the context of four post-mortem brain tissue studies conducted by Sweet and others (2003, 2004, 2007, 2008) at the CCNMD. Across these studies, six biomarkers are examined, consisting of three measures taken from the primary auditory cortex: synaptophysin-immunoreactive (SY-IR) puncta density for Brodmann’s areas (BA) 41 and for BA 42; pyramidal cell somal volume for BA 41 and for BA 42 (natural logarithm scale), and spinophilin-immunoreactive (SP-IR) puncta density for BA 41 and for BA 42. In each study, age at death, gender, PMI, and brain tissue storage time are included as covariates for both schizophrenia subjects and normal controls. Although there are slight differences in the numbers of subjects used in each study, there are 30 subjects common to all four studies that we use in our application. Our objective here is to illustrate how COVACT and the traditional BFOS approach perform in identifying which subsets of biomarkers best characterize the differences between schizophrenia and control subjects. Performance is measured by estimating the misclassification rates from the resulting trees. The manner in which we applied COVACT, as well as the traditional BFOS approach and covariate adjusted LDA (for comparative purposes), is detailed in supplementary material available at Biostatistics online.

Figures 1 and 2 display, respectively, the trees produced from the biomarker data adjusted for the effects of the included covariates using COVACT, and the unadjusted biomarker data. In each terminal node of each tree, a label of “classs” or “classc” means that subjects with measurements falling into that node are classified into the schizophrenia or control groups, respectively. Adjusting for the effects of age at death, gender, PMI, and tissue storage time, COVACT identifies SY-IR puncta density, somal volume, and SP-IR puncta density for BA 41 as best characterizing the differences between schizophrenia subjects and normal controls, where the resulting tree is observed to misclassify only 10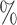 of all subjects (see Table 1). On the other hand, when these covariate effects are ignored, the traditional BFOS approach only identifies SP-IR puncta density for BA 41 and is observed to misclassify 20 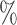of all subjects. The increased classification accuracy under COVACT, compared with the traditional BFOS approach, makes sense intuitively. COVACT removes the masking effects of covariates from the examined features, which would help to more accurately identify subsets of features that best characterize the group differences. In addition, when we apply LDA to the six biomarkers adjusted for the examined covariate effects, the resulting discriminant function misclassifies 23.3 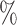of all subjects. Therefore, COVACT also outperforms covariate adjusted LDA with respect to classification accuracy. Compared with LDA, classification trees allow for a finer and more flexible partitioning of the feature space. Therefore, it is easier for classification trees to uncover the structure of the feature data that truly defines the differences among groups.

Fig. 2.

Traditional classification tree for sweet data. In each terminal node, a label of “classs” corresponds to subjects classified as having schizophrenia, while that of “classc” corresponds to subjects classified as controls. SpDens41 corresponds to SP-IR puncta density for BA 41.

Table 1.

Classification results for sweet data C—control, S—schizophrenia

Approach	True Group	Classified as C	Classified as S	Total	Observed error rate
COVACT	C	15	0	15	0.1
	S	3	12	15
	Total	18	12	30
Covariate	C	10	5	15	0.233
adjusted LDA	S	2	13	15
	Total	12	18	30
Unadjusted	C	11	4	15	0.2
	S	2	13	15
	Total	13	17	30

Due to the small sample size, however, this difference in classification accuracy needs to be viewed with caution.

6. Simulation study

6.1. Motivation

To more extensively compare the classification performances of COVACT and the traditional BFOS approach, we conduct a simulation study based on data settings that mimic those examined by the four Sweet and others studies discussed in Section 5. Specifically, we generate feature values using the six biomarkers measured across these studies and covariate values using the values for subject’s age at death, PMI, and brain tissue storage time (averaged across all four studies). In conducting our study, we are interested in evaluating how the degree of correlation between features and covariates impacts classification accuracy for COVACT relative to traditional classification trees and, thus, only consider the continuous covariates of subject’s age at death, PMI, and brain tissue storage time. We compare the classification accuracy of both approaches in seven scenarios where in each, we consider the cases of 2, 3, 4, and 6 features with 30, 60, and 240 observations are considered and the generated data satisfy the main assumption of COVACT described in Section 4.2. The manner in which this study was conducted is detailed in supplementary material available at Biostatistics online.

6.2. Conclusions

The classification results from our simulation study are detailed in supplementary material available at Biostatistics online. In short, both COVACT and the traditional BFOS approach have lower misclassification rates, on average, as the number of features increases. However, COVACT yields generally lower misclassification rates relative to the traditional BFOS approach, regardless of the number of features, observations, and covariates that are adjusted for. This also holds in each group we consider, which indicates that COVACT is generally less conservative than the traditional BFOS approach. In addition, the decrease in misclassification rates for COVACT relative to the traditional BFOS approach becomes more pronounced as the number of covariates increases. Therefore, these results, in conjunction with those from Section 5, these results provide support for the improved classification performance of COVACT.

7. Discussion

We develop our proposed COVACT methodology by first approaching the traditional BFOS tree construction method, which is primarily meant to be used with training data, from a population-based standpoint. In doing so, we not only provide a parametric alternative to the standard non-parametric BFOS approach but we also establish a basis to integrate the conditional distribution of the feature data for a fixed covariate value into the BFOS approach, in order to account for the relationship that may exist between the features and covariates of interest. Considering that our proposed modification for the BFOS method may produce trees that vary depending on covariate value, we formulate our COVACT construction approach, which has two desirable properties. First, and perhaps most importantly, it allows us to use the traditional BFOS approach to construct a tree using feature data that have been adjusted for covariate effects, so that available software packages can be used. Also, COVACT produces a tree that can be used to identify a unique subset of features, independent of covariate value, that best characterizes the differences among the groups of interest while adjusting for the effects of all relevant covariates. Through simulation studies and a practical application, we have shown that when covariate effects are evident, COVACT can yield more accurate results than traditional classification trees that ignore these effects.

With COVACT, we have developed a tree-based approach that accounts for covariate effects when identifying which subset of features best characterizes the differences among groups, a subset that does not change depending on covariate value. However, as was pointed out in Sections 1 and 3.3, there may be situations where it is meaningful to have this subset of features vary depending on a particular covariate value(s), for example, subject’s age at death in the context of post-mortem tissue studies. There may also be situations in which covariate effects on the examined features are differentially expressed across groups, a case in which the main assumption of the linear invariance property on which COVACT is based is violated. In these instances, one will need to consider approaches for constructing covariate-dependent conditional classification trees with available training data, which are discussed in Asafu-Adjei (2011).

We are familiar with studies in the literature, for example, Breiman (2001b), that discuss classification methods with higher classification accuracy than classification trees, including the ensemble learning approach of Random Forests. However, these same studies demonstrate the great decrease in simplicity and interpretability for these classification methods relative to classification trees. Although we place a high premium on accuracy, we also place a high premium on the interpretability of our results. Therefore, we believe that the high level of interpretability for classification trees goes a long way in compensating for the relatively small decrease in accuracy, which is why we develop our adjustment approach in the context of classification trees.

One variation to our setting that is of interest is unequal misclassification costs, which we can easily incorporate into our COVACT methodology. In addition, there may be studies where subjects are not only measured on covariates, but are also matched across different groups on several demographic factors. Along with covariates, group matching may also have a significant impact on the features of interest, in which case a subtle modification to our COVACT approach is required (see Asafu-Adjei, 2011, for a detailed discussion).

Supplementary Material

Supplementary material is available at http://biostatistics.oxfordjournals.org.

Funding

This work was supported by the National Institutes of Health (T32NS048005, F32NS081904, and MH084053) which supported J.K.A.; (MH084053 and MH103204) which supported A.R.S. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH.