Efficient Estimation for Semiparametric Structural Equation Models With Censored Data

Abstract

Structural equation modeling is commonly used to capture complex structures of relationships among multiple variables, both latent and observed. We propose a general class of structural equation models with a semiparametric component for potentially censored survival times. We consider nonparametric maximum likelihood estimation and devise a combined Expectation-Maximization and Newton-Raphson algorithm for its implementation. We establish conditions for model identifiability and prove the consistency, asymptotic normality, and semiparametric efficiency of the estimators. Finally, we demonstrate the satisfactory performance of the proposed methods through simulation studies and provide an application to a motivating cancer study that contains a variety of genomic variables. Supplementary materials for this article are available online.

1. INTRODUCTION

Structural equation modeling (SEM) is a very general and powerful approach to capture complex relationships among multiple factors, both observed and latent (Bollen 1989). A typical SEM framework consists of a structural model that connects latent variables and a measurement model that relates latent variables to observed variables. SEM is extremely popular in the social sciences and psychology, where unmeasured quantities and psychological constructs, such as human intelligence and creativity, can be related to and investigated through observed data. The text of Bollen (1989) has been cited more than 20,000 times. Recently, SEM has gained popularity in medical and public health research (Dahly et al. 2009; Naliboff et al. 2012).

Our interest in SEM was motivated by its potential application to integrative analysis in genomic studies. Recent technological advances have made it possible to collect different types of genomic data, including DNA copy number, SNP genotype, DNA methylation level, and expression levels of mRNA, microRNA, and protein, on a large number of subjects. There is a growing interest in integrating these genomic platforms so as to understand their biological relationships and predict disease progression and death, which are considered potentially censored survival times (The Cancer Genome Atlas (TCGA); https://tcga-data.nci.nih.gov/tcga/).

SEM with discrete survival times has been studied by Rabe-Hesketh et al. (2001; 2004), Muthén and Masyn (2005), and Moustaki and Steele (2005). For continuous survival time, Larsen (2004; 2005) adopted the proportional hazards model (Cox 1972) with a single latent variable to capture the association between the survival time and other observed variables; Asparouhov et al. (2006) considered a more general formulation of the association among the latent and observed variables. SEM with the Cox proportional hazards model for the survival component has been adopted for more complex settings, such as multivariate survival times (Stoolmiller and Snyder 2006) and competing risks (Stoolmiller and Snyder 2013). A popular software program, Mplus (Muthén and Muthén 1998–2015), has implemented SEM with survival data under the proportional hazards model. The estimation of the nonparametric baseline hazard function is based on piecewise-constant splines, and no theoretical justification is available. In fact, the standard error estimator for the baseline hazard function is incorrect.

In this article, we propose a general SEM framework that includes a semiparametric component of the measurement model for potentially censored survival times. Specifically, we formulate the effects of latent and observed covariates on survival times through a broad class of semiparametric transformation models that includes the proportional hazards model as a special case. The observed covariates may include manifest variables that depend on latent variables. We study nonparametric maximum likelihood estimation (NPMLE), under which the cumulative hazard functions are estimated by step functions with jumps at observed survival times.

The proposed SEM is reminiscent of joint modeling for survival and longitudinal data (Henderson et al. 2000; Tsiatis and Davidian 2004). With the latter, the observed longitudinal variables are considered error-prone measurements of some underlying latent variables, but the measurements themselves are not causal determinants of the survival time. By contrast, our SEM framework allows latent variables to have direct effects on survival times, as well as indirect effects through other manifest variables. In addition, our framework accommodates much more complex relationships among latent variables.

A major challenge in our theoretical development is model identifiability. Even for an SEM with normally distributed variables, no single set of conditions exists that is both necessary and sufficient for model identifiability. Methods that deal with special cases of the normal SEM were proposed by Bollen (1989), Reilly and O’Brien (1996), Vicard (2000), and Bollen and Davis (2009), among others. Most of the methods are based on the fact that identifiability can be established by solving the equations relating the first two model-implied moments to the sample moments. This approach is not directly applicable to models with nonparametric components, as infinite-dimensional parameters cannot be identified through a finite number of equations. Because the proportional hazards structure results in a likelihood function that takes the form of a Laplace transform, however, we are able to develop sufficient conditions under which the identifiability of a semiparametric SEM can be established by inspecting simpler parametric models.

Another theoretical challenge is the invertibility of the information operator. For the information operator to be invertible, we require that the score statistic along any nontrivial submodel is non-zero. As in the case of model identifiability, general conditions for the invertibility of the information operator for semiparametric models do not exist. In the existing work involving latent variables for survival times (Kosorok et al. 2004; Zeng and Lin 2010), verifying the invertibility of the information operator involves inspecting the local behavior of the score statistic around the zero survival time. This approach does not make full use of the variability of the score statistic contributed by the survival times and cannot deal with the proposed general modeling framework. We show that the invertibility of the information operator can be verified by inspecting the parametric components of the SEM under some mild conditions in the survival model.

The rest of this article is structured as follows. In Section 2, we formulate the model and describe our approach to establish model identifiability. In Section 3, we discuss the numerical implementation of the NPMLE. In Section 4, we present theoretical results for model identifiability and describe the asymptotic properties of the estimators. In Section 5, we report the results from simulation studies. In Section 6, we provide an application to the TCGA data, which motivated this work. We make some concluding remarks in Section 7 and relegate theoretical proofs to the Appendix.

2. BASIC FRAMEWORK

2.1 Model and Likelihood

Let η denote a q-vector of latent variables, Y denote an r-vector of uncensored manifest variables, (T₁, …, T_K) denote K potentially censored survival times, and W and Z denote two vectors of observed covariates. Without loss of generality, assume that the support of the covariates includes zero. We specify the conditional distributions of η given Z, Y given Z and η, and T_k given W, Z, Y, and η as follows:

$$\mathit{\eta }\mid \mathit{Z}~F_{\eta }(·\mid \mathit{Z};\mathit{\nu }),$$ (1)

$$\mathit{Y}\mid (\mathit{Z},\mathit{\eta })~F_Y(·\mid \mathit{Z},\mathit{\eta };\mathit{\psi }),$$ (2)

$${\mathrm{\Lambda }}_{T_k}(t\mid \mathit{W},\mathit{Z},\mathit{Y},\mathit{\eta })=G_k\{{\mathrm{\Lambda }}_k(t)e^{{\mathit{W}}^{\mathrm{T}}{\mathit{\vartheta }}_k+{\mathit{Z}}^{\mathrm{T}}{\mathit{\beta }}_k+{\mathit{Y}}^{\mathrm{T}}{\mathit{\alpha }}_k+{\mathit{\eta }}^{\mathrm{T}}{\mathit{\varphi }}_k}\},k=1,\dots ,K,$$ (3)

where F_η (· | Z, ν) denotes a q-variate normal distribution function indexed by a parameter vector ν, F_Y (· | Z, η; ψ) denotes an r-variate parametric distribution function indexed by a parameter vector ψ, Λ_Tk is the cumulative hazard function of T_k given (W,Z,Y, η), G_k is a known increasing function, Λ_k is an unspecified positive increasing function with Λ_k(0) = 0, and (ϑ_k, β_k, α_k,ϕ_k) are unknown regression parameters.

Model (1) is the structural model of the latent variables. Model (2) is the measurement model of Y. We assume that Y and η are independent of W given Z. Models (1) and (2) represent the existing SEM framework with Y not restricted to be normally distributed. Equation (3) includes the proportional hazards and proportional odds models as special cases with the choices of G_k (x) = x and G_k (x) = log (1 + x), respectively. The proportional hazards model has been considered in the literature.

The survival time T_k is subject to right censoring by C_k. It is assumed that (C₁, …, C_K) are independent of (T₁, …, T_K) and η conditional on Y, Z, and W. Define T̃_k = min(T_k,C_k) and Δ_k = I(T_k ≤ C_k), where I(·) is the indicator function. For a sample of size n, the observed data consist of 𝒪_i ≡ (T̃_1i, … T̃_Ki,Δ_1i, …, Δ_Ki,Y_i,Z_i,W_i) (i = 1, …, n).

Let θ denote the collection of all Euclidean parameters, and write 𝒜 = (Λ₁, …, Λ_K). The likelihood function for θ and 𝒜 is proportional to

$$\begin{array}{l}{L}_n(\mathit{\theta },\mathcal{A})=\prod _{i=1}^n\int \prod _{k=1}^K{\left[{\lambda }_k\left({\stackrel{\sim }{T}}_{ki}\right)e^{{\mathit{W}}_i^{\mathrm{T}}{\mathit{\vartheta }}_k+{\mathit{Z}}_i^{\mathrm{T}}{\mathit{\beta }}_k+{\mathit{Y}}_i^{\mathrm{T}}{\mathit{\alpha }}_k+{\mathit{\eta }}^{\mathrm{T}}{\mathit{\varphi }}_k}\times G_k^{\prime }\left\{{\mathrm{\Lambda }}_k\left({\stackrel{\sim }{T}}_{ki}\right)e^{{\mathit{W}}_i^{\mathrm{T}}{\mathit{\vartheta }}_k+{\mathit{Z}}_i^{\mathrm{T}}{\mathit{\beta }}_k+{\mathit{Y}}_i^{\mathrm{T}}{\mathit{\alpha }}_k+{\mathit{\eta }}^{\mathrm{T}}{\mathit{\varphi }}_k}\right\}\right]}^{{\mathrm{\Delta }}_{ki}}\\ \times exp\left[-G_k\left\{{\mathrm{\Lambda }}_k\left({\stackrel{\sim }{T}}_{ki}\right)e^{{\mathit{W}}_i^{\mathrm{T}}{\mathit{\vartheta }}_k+{\mathit{Z}}_i^{\mathrm{T}}{\mathit{\beta }}_k+{\mathit{Y}}_i^{\mathrm{T}}{\mathit{\alpha }}_k+{\mathit{\eta }}^{\mathrm{T}}{\mathit{\varphi }}_k}\right\}\right]\\ \times f_Y({\mathit{Y}}_i\mid {\mathit{Z}}_i,\mathit{\eta };\mathit{\psi })f_{\eta }(\mathit{\eta }\mid {\mathit{Z}}_i;\mathit{\nu })\mathrm{d}\mathit{\eta },\end{array}$$ (4)

where f′(x) = df(x)/dx for any function f, ${\lambda }_k={\mathrm{\Lambda }}_k^{\prime },f_Y=F_Y^{\prime }$, and $f_{\eta }=F_{\eta }^{\prime }$. The NPMLE is defined to be the maximizer of L_n(θ,𝒜), in which Λ_k is treated as a step function with jumps at T̃_ki with Δ_ki = 1 (i = 1, …, n).

2.2 Model Identifiability

We describe our approach to establish model identifiability in this section and defer the technical details to Section 4. The identifiability results can be summarized by two simple rules. Suppose that we have arranged the survival times such that for some 0 ≤ K₁ ≤ min(q,K), each of (T₁, …, T_K1) regresses on and only on one latent variable and a set of covariates that are independent of the latent variables. (We allow K₁ = 0 if no survival time satisfies the given conditions, in which case Rule 1 below is vacuous.) We call an observed variable X an indicator of a latent variable η if X follows a generalized linear model with η as a covariate and is independent of all other manifest variables and survival times conditional on η. We have the following rules:

• Rule 1. The latent variables attached to (T₁, …, T_K1) can be treated as observed if each of (T₁, …, T_K1) depends on at least one observed covariate.

• Rule 2. If each latent variable has a separate continuous indicator and the distributions of the latent variables and the indicators are identifiable, then the whole model is identifiable.

To illustrate the usefulness of the two identifiability rules, we present two examples.

Example 1

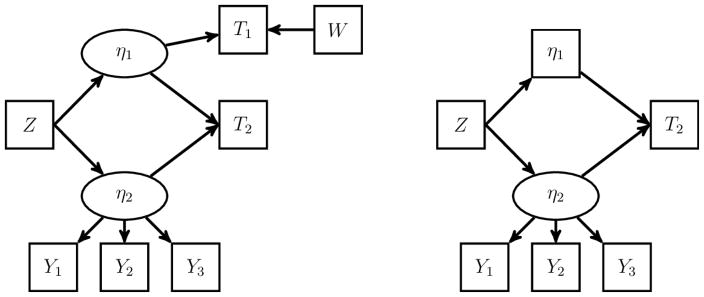
Consider the model depicted in Figure 1. In the model, Y₁, Y₂, and Y₃ are conditionally independent normal manifest variables of η, and T is a survival time that follows the proportional hazards model with covariate η. Assume that the regression parameter of Y₁ on η is fixed to be one, E(η) = 0, and the regression parameters of η in the models of Y₂ and Y₃ are non-zero.

Figure 1.

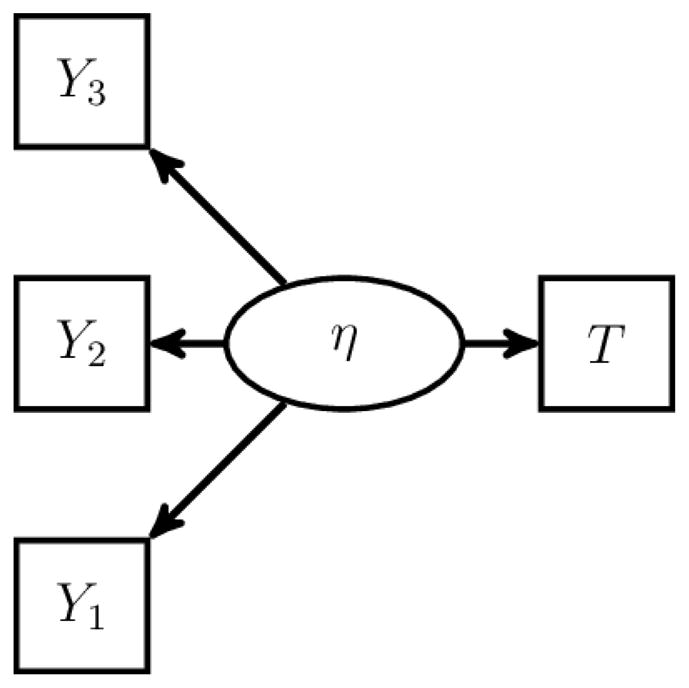
The First Example of SEM to Illustrate the Identifiability Rules. The SEM con- sists of one latent variable, one survival time, and three conditionally independent normal manifest variables.

The above model is similar to the joint model for survival and longitudinal variables. By Bollen (1989)’s three-indicator rule, the model of (Y₁, Y₂, Y₃, η) is identifiable. With Y₁ serving as an indicator of η, Rule 2 implies that the remaining parameters are identifiable. Note that Rule 1 is not applicable in this case because T does not depend on an independent covariate. In fact, the model is not identifiable without (Y₁, Y₂, Y₃) because the scale of the baseline hazard function and the variance of η cannot be separated.

Example 2

Consider the model depicted on the left-hand side of Figure 2. In the model, Y₁, Y₂, and Y₃ are conditionally independent normal manifest variables of η₂, T₁ is a survival time that follows the proportional hazards model with covariates W and η₁, and T₂ is a survival time that follows the proportional hazards model with covariates η₁ and η₂. Assume that W and Z are non-constant and linearly independent, the regression parameters for the latent variables in the models of T₁ and Y₁ are fixed to be one, E(η₁) = E(η₂) = 0, and the regression parameters of W in the model of T₁ and η₂ in the models of Y₂ and Y₃ are non-zero.

Figure 2.

The Second Example of SEM to Illustrate the Identifiability Rules. The left panel is an SEM that consists of two latent variables, two observed covariates, two survival times, and three conditionally independent normal manifest variables. The right panel is an intermediate step in identifying the SEM on the left.

First, we use T₁ to help identify the latent variable distributions. By Rule 1, η₁ can be treated as observed when identifying the model. The problem thus reduces to identifying the model shown on the right-hand side of Figure 2. The model can then be shown identifiable by the arguments used in Example 1.

3. COMPUTATION OF THE NPMLE

In this section, we use Z to denote both W and Z with β_k (k = 1, …,K) as the corresponding vector of regression parameters. Application of a transformation G_k can be viewed as inclusion of an extra latent variable log s_k in the regression equation, where s_k is a random variable with density g_k such that $G_k(x)=-log{\int }_0^{\infty }{e}^{-xt}{g}_k(t)\mathrm{d}t$. We adopt the Expectation-Maximization (EM) algorithm (Dempster et al. 1977) by treating the latent variables, including those introduced by the transformations, as missing data. We perform occasional Newton-Raphson steps to speed up the convergence.

In the combined algorithm, either an EM step or a Newton-Raphson step is performed at each iteration. To avoid confusion, we call the latter an outer Newton-Raphson step. For an EM step, note that the conditional expectation for any function φ of (η_i, s_i) ≡ (η_i, s_1i, …, s_Ki) given the observed data is

$$\begin{array}{l}\mathrm{E}\{\phi ({\mathit{\eta }}_i,{\mathit{s}}_i)\mid {\mathcal{O}}_i\}={\mathcal{C}}^{-1}\int \int \phi (\mathit{\eta },\mathit{s})\prod _{k=1}^K({\left[{\mathrm{\Lambda }}_k\{{\stackrel{\sim }{T}}_{ki}\}{s}_k{e}^{{\mathit{Z}}_i^{\mathrm{T}}{\mathit{\beta }}_k+{\mathit{Y}}_i^{\mathrm{T}}{\mathit{\alpha }}_k+{\mathit{\eta }}^{\mathrm{T}}{\mathit{\varphi }}_k}\right]}^{{\mathrm{\Delta }}_{ki}}\\ \times exp(-{\int }_0^{{\stackrel{\sim }{T}}_{ki}}{s}_k{e}^{{\mathit{Z}}_i^{\mathrm{T}}{\mathit{\beta }}_k+{\mathit{Y}}_i^{\mathrm{T}}{\mathit{\alpha }}_k+{\mathit{\eta }}^{\mathrm{T}}{\mathit{\varphi }}_k}\mathrm{d}{\mathrm{\Lambda }}_k(t)))\\ \times f_Y\left({\mathit{Y}}_i\mid {\mathit{Z}}_i,\mathit{\eta };\mathit{\psi }\right)f_{\eta }\left(\mathit{\eta }\mid {\mathit{Z}}_i;\mathit{\nu }\right)g(\mathit{s})\mathrm{d}\mathit{\eta }\mathrm{d}{s}_1\cdots \mathrm{d}{s}_K,\end{array}$$

where Λ_k {t} is the jump size of the step function Λ_k at t, s = (s₁, …, s_K), $g(\mathit{s})={\prod }_{k=1}^K{g}_k(s_k)$, and 𝒞 equals the above integral evaluated at φ(·, ·) = 1. We use the Gauss-Hermite quadrature to approximate the integrals. To reduce the number of abscissas, we adopt an adaptive quadrature approach (Liu and Pierce 1994). Denote the approximation of the conditional expectation as Ê(·). After taking expectation on the functions involved, we update (β_k, α_k,ϕ_k) by the one-step Newton-Raphson algorithm on

$$\sum _{i=1}^{n}log{\left[\frac{\widehat{\mathrm{E}}\{s_{ki}exp({\mathit{Z}}_i^{\mathrm{T}}{\mathit{\beta }}_k+{\mathit{Y}}_i^{\mathrm{T}}{\mathit{\alpha }}_k+{\mathit{\eta }}_i^{\mathrm{T}}{\mathit{\varphi }}_k)\}}{{\sum }_{j=1}^{n}I({\stackrel{\sim }{T}}_{kj}\ge {\stackrel{\sim }{T}}_{ki})\widehat{\mathrm{E}}\{s_{kj}exp({\mathit{Z}}_j^{\mathrm{T}}{\mathit{\beta }}_k+{\mathit{Y}}_j^{\mathrm{T}}{\mathit{\alpha }}_k+{\mathit{\eta }}_j^{\mathrm{T}}{\mathit{\varphi }}_k)\}}\right]}^{{\mathrm{\Delta }}_{ki}}.$$

Then, we update the cumulative baseline hazard function by

$${\widehat{\mathrm{\Lambda }}}_k\{T_{ki}\}=\frac{{\mathrm{\Delta }}_{ki}}{{\sum }_{j=1}^{n}I({\stackrel{\sim }{T}}_{kj}\ge {\stackrel{\sim }{T}}_{ki})\widehat{\mathrm{E}}\{s_{kj}exp({\mathit{Z}}_j^{\mathrm{T}}{\mathit{\beta }}_k+{\mathit{Y}}_j^{\mathrm{T}}{\mathit{\alpha }}_k+{\mathit{\eta }}_j^{\mathrm{T}}{\mathit{\varphi }}_k)\}},$$

where (β_k, α_k,ϕ_k) are evaluated at the current estimates. In addition, we update the remaining parameters at the maximum of

$$\sum _{i=1}^n\widehat{\mathrm{E}}[log\{f_Y({\mathit{Y}}_i\mid {\mathit{Z}}_i,{\mathit{\eta }}_i;\mathit{\psi })f_{\eta }({\mathit{\eta }}_i\mid {\mathit{Z}}_i;\mathit{\nu })\}].$$

If a closed-form solution is not available, then we apply the one-step Newton-Raphson algorithm to the above expression instead. The above algorithm can be generalized to the case where components of Y_i that do not appear in the model of the survival times are missing at random for some subjects. In this case, we simply drop the corresponding f_Y terms in the evaluation of Ê and the complete-data log-likelihood.

For an outer Newton-Raphson step, we apply the one-step Newton-Raphson algorithm directly to the logarithm of L_n(θ,𝒜) given in (4) using a similar adaptive quadrature approximation. At the current estimates, the first derivative of log L_n(θ,𝒜), i.e., the score statistic, is the same as the first derivative of the expected complete-data log-likelihood. The Hessian matrix used in the Newton-Raphson algorithm can be obtained by Louis (1982)’s formula.

To determine whether an EM step or an outer Newton-Raphson step is to be performed, we keep track of the difference in the log-likelihood at the previous iteration, either an EM or an outer Newton-Raphson step, and the difference at the previous outer Newton-Raphson step. For each iteration, if the log-likelihood difference at the previous step is too small relative to that at the previous outer Newton-Raphson step, then an outer Newton-Raphson step is performed; otherwise, an EM step is performed. Upon convergence, Louis (1982)’s formula is used to obtain the information matrix for the estimation of the standard errors.

The reason that we use a combination of the EM and Newton-Raphson algorithms instead of the Newton-Raphson algorithm alone is two-fold. First, EM steps are more stable, which is important, especially in early iterations. Second, in the estimation of the survival model under the EM algorithm, the regression parameters can be obtained by maximizing the partial-likelihood-type function, and the estimators of the baseline hazard functions take the form of the Breslow estimator. Unlike the Newton-Raphson algorithm, the EM algorithm does not involve the inversion of a high-dimensional matrix.

4. THEORETICAL PROPERTIES

4.1 Identifiability Conditions

As discussed in Section 2, we set aside K₁ survival times, T₁, …, T_K1, that are used to identify the distribution of the underlying latent variables. We assume that span(ϕ₁, …, ϕ_K1) = ℝ^K₁. We can choose the K₁ survival times such that each is associated with a few, preferably only one, latent variables. (K₁ is allowed to be 0, in which case we rely solely on the manifest variable Y to identity the latent variable distribution.) Without loss of generality, we assume that ϕ_k = e_k (k = 1, …, K₁), where e_k is a q-vector with 1 at the kth position and 0 elsewhere. This assumption can be satisfied by applying a linear transformation to the latent variables. Effectively, we fix the scale of the first K₁ latent variables, as is common when establishing model identifiability for SEM. We partition η into (η₁, η₂), where η₁ ≡ (η₁₁, …, η_1K1) consists of the first K₁ components of η.

We consider the following identifiability conditions. For the “baseline” hazard functions (Λ₁, …, Λ_K), we only require identifiability on [0, τ], where τ denotes the study duration.

• (C1)If (1,W^T,Z^T,Y^T)^Tc = 0 almost surely for some vector c of appropriate dimension, then c = 0. For k = 1, …,K, λ_k is continuous and strictly positive on [0, τ], and there exists a positive and measurable function g_k such that $exp\{-G_k(t)\}={\int }_0^{\infty }{e}^{-ts}{g}_k(s)\mathrm{d}{m}_k(s)$, where m_k is the Lebesgue measure or the counting measure at 1.
• (C2)For k = 1, …,K₁, E(Y^Tα_k | Z = 0) = 0, and E(η | Z = 0) = 0. Also, for any vectors c₁ and c₂ of appropriate dimensions, E(e^{YTc₁+ηTc₂} | Z) is finite almost surely.
• (C3)For k = 1, …,K₁, ϑ_k is non-zero, and α_k and β_k are zero.
• (C4)Consider two sets of parameters (ψ, ν) and (ψ̃, ν̃). Let f_Y,η1 be the density of (Y, η₁) given Z. Then, f_Y,η1 (Y, η₁ | Z; ψ, ν) = f_Y,η1 (Y, η₁ | Z; ψ̃, ν̃) for all Z, Y, and η₁ implies that ψ = ψ̃ and ν = ν̃.
• (C5)Let (Y⁺, ${\mathit{\eta }}_1^{+}$) be the components of (Y, η₁) that appear in the regression of T_k for some k = K₁ + 1, …,K, and let (Y⁻, ${\mathit{\eta }}_1^{-}$) be the remaining components. Let F_η2|Y,η1 be the distribution function of η₂ given (Z,Y, η₁) with (Y⁻, ${\mathit{\eta }}_1^{-}$) treated as a parameter vector. Then, η₂ is complete sufficient in {F_η2|Y,η1 (· | Z,Y, η₁): Z = z₀,Y⁺ = y₀, ${\mathit{\eta }}_1^{+}={\mathit{\eta }}_{10}$ for any fixed z₀, y₀, and η₁₀.

Remark 1

Condition (C1) pertains to basic requirements on the covariates, the baseline hazard functions, and the transformation functions such that the survival model with observed covariates is identifiable. If m_k is a point mass at 1, then G_k is simply the identity function. Condition (C2) fixes the location parameters of the latent variables and the manifest variables that appear in the regression models of the first K₁ survival times. Condition (C3) requires that the first K₁ survival times depend only on their corresponding latent variable and W. The presence of a covariate besides the latent variable is necessary for distinguishing the contributions of the baseline hazard function and the latent variable to the distribution of a survival time that follows a mixture distribution. Condition (C4) requires that the model with observed (Y, η₁) is identifiable. Condition (C5) requires that η₂ is complete sufficient conditional on (Y, η₁), where components of (Y, η₁) that do not appear in the regression of T_k (k = K₁ + 1, …, K) are treated as parameters, and the rest are held fixed. Conditions (C2) and (C3) are vacuous if K₁ = 0, and condition (C5) is vacuous if K₁ = K.

We have the following identifiability result.

Theorem 1

Under conditions (C1)–(C5), the model specified by (1)–(3) is identifiable.

Remark 2

The condition that α_k and β_k are zero for k = 1, …, K₁ separates the first K₁ survival times from the remaining observed variables that are associated with the latent variables. This condition is used to simplify the presentation of the identifiability conditions. In the proof of Theorem 1, we consider generalized versions of conditions (C3)–(C5), where α_k and β_k are allowed to be non-zero.

Remark 3

Theorem 1 implies that the distribution of the latent variable underlying a given survival time can be completely identified if the survival time only regresses on the latent variable and a set of independent covariates. Thus, the survival times make it easy to identify the model, as only a single survival time is enough to identify an underlying latent variable. By contrast, this property does not hold for normal random variables.

Remark 4

The derivation of model identifiability from condition (C5) utilizes the property of complete sufficient statistics. The derivation is applicable to general latent variable models; the general result is given by Lemma 1 in the Appendix. Lemma 1 allows for the establishment of model identifiability by inspecting just a part of the model. It includes Reilly and O’Brien (1996)’s side-by-side rule, which states that the loadings of an observed variable on any number of latent variables are identifiable if each of the latent variables is attached to a separate independent observed variable whose distribution is identifiable, as a special case.

4.2 Asymptotic Properties

Let d be the dimension of θ, θ₀ denote the true value of θ, and Λ_0k denote the true value of Λ_k (k = 1, …, K). We impose the following conditions.

• (D1)The parameter θ₀ lies in the interior of a compact set Θ ⊂ ℝ^d, and the function Λ_0k is continuously differentiable with ${\lambda }_{0k}(t)\equiv {\mathrm{\Lambda }}_{0k}^{\prime }(t)>0$ on [0, τ] for each k = 1, …,K.
• (D2)With probability one, P(T̃_ki = τ | W,Z) > δ₀ (k = 1, …,K) for some fixed δ₀ > 0.
• (D3)
  Consider any fixed Z and (ψ, ν) ∈ Θ_ψν, where Θ_ψν consists of the (ψ, ν)-component of every θ ∈ Θ. For any constant a₁ > 0 and δ = 0, 1,

  $$\mathrm{E}\left\{\int e^{a_1(1+\mid \mathit{Y}\mid +\mid \mathit{\eta }\mid )}{f}_Y{(\mathit{Y}\mid \mathit{Z},\mathit{\eta };\mathit{\psi })}^{\delta }{f}_{\eta }(\mathit{\eta }\mid \mathit{Z};\mathit{\nu })\mathrm{d}\mathit{\eta }\right\}<\infty .$$
  Also, for j = 1, 2, 3, there exists a constant a₂ > 0 such that

  $$\left|\frac{\frac{{\partial }^j}{\partial {\mathit{\psi }}^j}{f}_Y(\mathit{Y}\mid \mathit{Z},\mathit{\eta };\mathit{\psi })}{f_Y(\mathit{Y}\mid \mathit{Z},\mathit{\eta };\mathit{\psi })}\right|+\left|\frac{\frac{{\partial }^j}{\partial {\mathit{\nu }}^j}{f}_{\eta }(\mathit{\eta }\mid \mathit{Z};\mathit{\nu })}{f_{\eta }(\mathit{\eta }\mid \mathit{Z};\mathit{\nu })}\right|\le e^{a_2(1+\mid \mathit{Y}\mid +\mid \mathit{\eta }\mid )}.$$
  In addition, for some positive constants M_j and c_j, N_j ∈ ℝ^r, and φ₁ ∈ ℓ^∞(ℝ^r),

  $$e^{{\sum }_{j=1}^q-M_j\mid b_j\mid }\le e^{{\sum }_{j=1}^q({\mathit{N}}_j^{\mathrm{T}}\mathit{Y}{b}_j+c_j{b}_j^2)}{\phi }_1(\mathit{Y})f_Y(\mathit{Y}\mid \mathit{Z},\mathit{\eta };\mathit{\psi })f_{\eta }(\mathit{\eta }\mid \mathit{Z};\mathit{\nu })\le e^{{\sum }_{j=1}^q{M}_j\mid b_j\mid },$$

  where b = S (η) for some one-to-one linear transformation S.

• (D4)
  The function G_k is four-times differentiable, G_k (0) = 0, and $K_{1k}{(1+x)}^{-{\kappa }_{1k}}\le G_k^{\prime }(x)\le K_{2k}{(1+x)}^{{\kappa }_{2k}}$ for some positive constants κ_1k, κ_2k, K_1k, and K_2k. Also, G_k(x)/x^ρk → M_k or G_k(x)/log(x) → M_k as x → ∞ for some positive constants M_k and ρ_k. In addition, exp {−G_k(x)} ≤ μ_k (1 + x)^−κ_3k for some μ_k and κ_3k > κ_2k + 1. Furthermore, for some r_k,

  $$\underset{x\ge 0}{sup}\frac{|G_k^{″}(x)|+|G_k^{(3)}(x)|+|G_k^{(4)}(x)|}{G_k^{\prime }(x){(1+x)}^{r_k}}<\infty ,$$

  where $G_k^{″}$ and $G_k^{(j)}$ denote the second and jth derivatives of G_k, respectively.

• (D5)
  Let (Z^(k),Y^(k)) be the components of (Z,Y) that appear in the regression of T_k (k = 1, …,K₁). For any vectors h₁, h_2k, and h_3k of appropriate dimensions, if

  $$\frac{\partial }{\partial (\mathit{\psi },\mathit{\nu })}{f}_{Y,{\eta }_1}{\left(\mathit{Y},{\mathit{\eta }}_1\mid \mathit{Z};\mathit{\psi },\mathit{\nu }\right)}^{\mathrm{T}}{\mathit{h}}_1-\sum _{k=1}^{K_1}\left({\mathit{Z}}^{(k)\mathrm{T}}{\mathit{h}}_{2k}+{\mathit{Y}}^{(k)\mathrm{T}}{\mathit{h}}_{3k}\right)\frac{\partial }{\partial {\eta }_{1k}}{f}_{Y,{\eta }_1}\left(\mathit{Y},{\mathit{\eta }}_1\mid \mathit{Z};\mathit{\psi },\mathit{\nu }\right)$$

  is equal to 0 for all Z, Y, and η₁, then h₁ = 0, h_2k = 0, and h_3k = 0 for k = 1, …,K₁, where f_Y,η1 is defined in condition (C4).

Remark 5

Conditions (D1)–(D4) are similar to the conditions of Zeng and Lin (2010) for joint modeling of longitudinal and survival data. Extra conditions are imposed on the transformations and the distributions of Y and η to accommodate the presence of unbounded covariate Y in the survival model. Condition (D5) is for the invertibility of the information operator. If α_k = 0 and β_k = 0 for k = 1, …, K₁, then condition (D5) simply requires that the information matrix of the model for (Y, η₁) is invertible. This is parallel to condition (C4) for identifiability.

Remark 6

The conditions for identifiability and the invertibility of the information operator (C1)–(C5), and (D5) differ significantly from the corresponding conditions (C5) and (C7) of Zeng and Lin (2010). The latter are stated under very general settings, but they are hard to verify for specific models, especially under our SEM framework. By contrast, our conditions are easier to verify and have intuitive interpretations. For the model in Example 1, (D5) simply requires that the model of (Y₁, Y₂, Y₃, η₁) given Z has a non-zero score statistic, which clearly holds.

Let 𝒜₀ = (Λ₀₁, …,Λ_0K) and (θ̂, 𝒜̂) be the NPMLE of (θ, 𝒜). Also, let 𝒱 = {v ∈ ℝ^d, |v| ≤ 1} and 𝒬 = {h (t): ||h (t)||_{V [0,τ]} ≤ 1} with ||·||_{V [0,τ]} being the total variation norm on [0, τ]. We consider (θ̂ − θ₀, 𝒜̂ − 𝒜₀) as a random element in l^∞(𝒱 × 𝒬^K) with

$$\left(\widehat{\mathit{\theta }}-{\mathit{\theta }}_0,\widehat{\mathcal{A}}-{\mathcal{A}}_0\right)(\mathit{v},h_1,\dots ,h_K)={\left(\widehat{\mathit{\theta }}-{\mathit{\theta }}_0\right)}^{\mathrm{T}}\mathit{v}+\sum _{k=1}^K{\int }_0^{\tau }{h}_k(s)\mathrm{d}\left({\widehat{\mathrm{\Lambda }}}_k-{\mathrm{\Lambda }}_{0k}\right)(s).$$

We have the following results.

Theorem 2

Under conditions (C1)–(C5) and (D1)–(D5),

1. $\mid \widehat{\mathit{\theta }}-{\mathit{\theta }}_0\mid +{\sum }_{k=1}^K{sup}_{t\in [0,\tau ]}\mid {\widehat{\mathrm{\Lambda }}}_k(t)-{\mathrm{\Lambda }}_{0k}(t)\mid {\to }_{a.s.}0$; and

2. n^1/2(θ̂ − θ₀, 𝒜̂ − 𝒜₀) →_d 𝒢 in l^∞(𝒱 × 𝒬^K), where 𝒢 is a continuous zero-mean Gaussian process. Furthermore, the limiting covariance matrix of n^1/2(θ̂ − θ₀) attains the semiparametric efficiency bound.

Remark 7

The proof of Theorem 2 relies on the Donsker properties of certain classes of functions. It is more challenging to establish the Donsker results in our setting than in previous settings (e.g., Kosorok et al. (2004) and Zeng and Lin (2010)) because the likelihood function of the proposed model may contain the unbounded variable Y.

Remark 8

A key step in proving the asymptotic normality of the NPMLE is to show that the information operator is invertible. The result is given by Lemma 2 in the Appendix, which states that condition (D5), together with conditions (C1)–(C3), and (C5), implies that the information operator of the model is invertible. With this result, we can verify the invertibility of the information operator of the semiparametric model by inspecting the parametric part of the model that contains the observed and latent variables. For the frailty models in Kosorok et al. (2004), verification of the invertibility of the information operator involves inspection of the local behavior of the score around T = 0. However, that approach is limited to frailty distributions that are indexed by a one-dimensional parameter and is not directly applicable to cases with more complex latent variable distributions such as those in our setting.

5. SIMULATION STUDIES

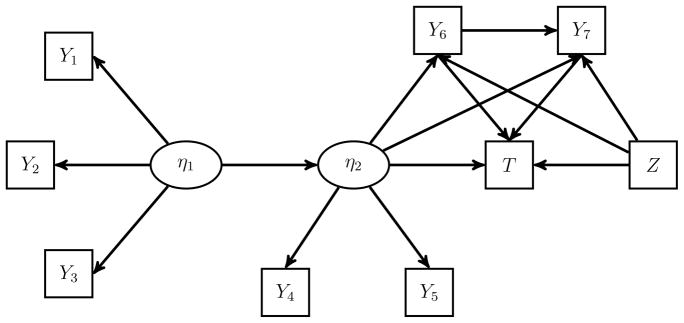
We considered a model with covariates Z = (Z₁,Z₂)^T, two latent variables (η₁, η₂), observed continuous variables (Y₁, …, Y₅), observed binary variables (Y₆, Y₇), and a survival time T. Their distributions are given by

$$\begin{array}{lll}\hfill {\mathrm{\Lambda }}_T(t\mid \mathit{Z},Y_6,Y_7,{\eta }_2)& =\hfill & G\{{\mathrm{\Lambda }}_0(t)exp({\mathit{X}}_T^{\mathrm{T}}{\mathit{\beta }}_T+{\varphi }_T{\eta }_2)\},{\mathit{X}}_T={(Z_1,Z_2,Y_6,Y_7)}^{\mathrm{T}},\hfill \\ \hfill \text{logit}\{\mathrm{P}(Y_6=1\mid \mathit{Z},{\eta }_2)\}& =\hfill & {\mathit{X}}_{Y_6}^{\mathrm{T}}{\mathit{\beta }}_{Y_6}+{\varphi }_{Y_6}{\eta }_2,{\mathit{X}}_{Y_6}={(1,Z_1,Z_2)}^{\mathrm{T}},\hfill \\ \hfill \text{logit}\{\mathrm{P}(Y_7=1\mid \mathit{Z},Y_6,{\eta }_2)\}& =\hfill & {\mathit{X}}_{Y_7}^{\mathrm{T}}{\mathit{\beta }}_{{\mathit{Y}}_7}+{\varphi }_{Y_7}{\eta }_2,{\mathit{X}}_{Y_7}={(1,Z_1,Z_2,Y_6)}^{\mathrm{T}},\hfill \\ \hfill Y_j\mid {\eta }_1& ~\hfill & \mathrm{N}({\beta }_{Y_j}+{\varphi }_{Y_j}{\eta }_1,{\sigma }_{Y_j}^2),j=1,2,3,\hfill \\ \hfill Y_j\mid {\eta }_2& ~\hfill & \mathrm{N}({\beta }_{Y_j}+{\varphi }_{Y_j}{\eta }_2,{\sigma }_{Y_j}^2),j=4,5,\hfill \\ \hfill {\eta }_2& ~\hfill & \mathrm{N}({\beta }_{\eta }{\eta }_1,{\sigma }_{{\eta }_2}^2),\hfill \\ \hfill {\eta }_1& ~\hfill & \mathrm{N}(0,{\sigma }_{{\eta }_1}^2).\hfill \end{array}$$

The parameters ϕ_Y1 and ϕ_Y4 are fixed to be one. The model is depicted in Figure 3.

Figure 3.

Model Used in Simulation Studies. The SEM consists of two latent variables, an observed covariate, seven binary or normal manifest variables, and a survival time that regresses on the latent variable, some manifest variables, and the observed covariates.

We set Z₁ and Z₂ to independent standard normal and Bernoulli(0.5), respectively, and Λ₀(t) = t². We considered the class of logarithmic transformations G(x) = r⁻¹ log(1 + rx) with r = 0 or 1, which correspond to the proportional hazards and proportional odds models, respectively. We generated the censoring times from Exp(c), where c was chosen to yield approximately 30% censored observations. We set (Y₁, …, Y₅) to be missing completely at random for 30% of the subjects. We set the sample size to 400 and set the number of abscissa points to 20 for each Gauss-Hermite quadrature. We simulated 1,000 datasets for each setting. The results are summarized in Table 1.

Table 1.

Simulation Results for the SEM with Two Latent Variables.

Dep	Ind	Proportional Hazards Model					Proportional Odds Model
		Param	Bias	SE	SEE	CP	Param	Bias	SE	SEE	CP
T	Z1	0.100	0.004	0.075	0.073	0.95	0.100	0.004	0.109	0.107	0.94
	Z2	−0.200	−0.004	0.180	0.182	0.95	−0.200	0.008	0.264	0.270	0.95
	Y6	0.100	0.001	0.145	0.143	0.95	0.100	0.000	0.214	0.208	0.95
	Y7	0.200	−0.007	0.167	0.163	0.95	0.200	−0.007	0.233	0.236	0.95
	η2	0.500	0.020	0.167	0.166	0.96	0.500	0.024	0.225	0.223	0.96
	Λ0(t1)	0.202	0.003	0.050	0.049	0.95	0.212	0.004	0.073	0.071	0.95
	Λ0(t2)	0.518	0.010	0.121	0.118	0.95	0.608	0.019	0.204	0.201	0.94
	Λ0(t3)	1.103	0.042	0.258	0.251	0.95	1.588	0.088	0.550	0.542	0.95
Y1	Int	0.000	0.000	0.074	0.073	0.94	0.000	0.001	0.074	0.073	0.94
	Var	1.000	−0.015	0.132	0.128	0.96	1.000	−0.016	0.132	0.128	0.97
Y2	Int	0.000	0.002	0.076	0.073	0.94	0.000	0.002	0.076	0.073	0.94
	η1	1.000	0.022	0.220	0.204	0.94	1.000	0.021	0.218	0.204	0.94
	Var	1.000	−0.013	0.130	0.129	0.96	1.000	−0.012	0.129	0.129	0.96
Y3	Int	0.000	0.001	0.076	0.073	0.95	0.000	0.002	0.076	0.073	0.95
	η1	1.000	0.021	0.214	0.203	0.95	1.000	0.021	0.215	0.204	0.96
	Var	1.000	−0.010	0.132	0.128	0.96	1.000	−0.010	0.133	0.129	0.96
Y4	Int	0.000	−0.001	0.077	0.075	0.95	0.000	−0.001	0.077	0.076	0.95
	Var	1.000	−0.026	0.193	0.184	0.96	1.000	−0.032	0.215	0.210	0.96
Y5	Int	0.000	−0.002	0.078	0.076	0.94	0.000	−0.001	0.079	0.076	0.94
	η2	1.000	0.048	0.296	0.276	0.94	1.000	0.057	0.339	0.323	0.95
	Var	1.000	−0.031	0.195	0.187	0.96	1.000	−0.036	0.219	0.214	0.96
Y6	Int	0.000	−0.005	0.286	0.273	0.94	0.000	−0.006	0.286	0.273	0.94
	Z1	−0.500	0.001	0.112	0.113	0.95	−0.500	0.001	0.112	0.113	0.95
	Z2	0.500	0.021	0.307	0.297	0.95	0.500	0.021	0.307	0.297	0.95
	η2	0.000	0.008	0.226	0.220	0.96	0.000	0.007	0.228	0.221	0.97
Y7	Int	1.000	0.032	0.338	0.345	0.96	1.000	0.030	0.337	0.345	0.96
	Z1	1.000	0.028	0.148	0.148	0.96	1.000	0.028	0.148	0.148	0.96
	Z2	0.200	0.002	0.333	0.342	0.96	0.200	0.002	0.333	0.342	0.96
	Y6	−0.200	−0.011	0.264	0.264	0.95	−0.200	−0.009	0.264	0.264	0.95
	η2	0.000	0.006	0.262	0.253	0.97	0.000	0.008	0.266	0.255	0.97
η1	Var	0.500	0.009	0.139	0.134	0.95	0.500	0.009	0.138	0.134	0.95
η2	η1	0.500	0.008	0.156	0.147	0.93	0.500	0.008	0.160	0.151	0.94
	Var	0.500	0.007	0.175	0.168	0.96	0.500	0.013	0.194	0.191	0.97

NOTE: Each row corresponds to the regression parameter of the dependent variable “Dep” on the independent variable “Ind” or some other parameter in the model of “Dep”. “Int” and “Var” stand for the intercept and error variance, respectively. The parameters Λ₀(t₁), Λ₀(t₂), and Λ₀(t₃) correspond to the cumulative baseline hazard function values at the 25%, 50%, and 75% quantiles of the survival time. The true value of a parameter is given under “Param”. “Bias” is the empirical bias; “SE” is the empirical standard error; “SEE” is the empirical mean of the standard error estimator; and “CP” is the empirical coverage probability of the 95% confidence interval.

The estimators of all parameters are virtually unbiased for both the proportional hazards and proportional odds models. The standard error estimators accurately reflect the true variations, and the coverage probabilities of the confidence intervals are close to the nominal level. Standard error estimators for the parameters in the survival model are larger under the proportional odds model than under the proportional hazards model. As a result, the standard error estimators for the parameters associated with η₂ are larger. The standard error estimators for the remaining parameters are very similar between the two models.

We also evaluated Mplus (Muthén and Muthén 1998–2015) under the proportional hazards model, and the results are presented in Table S.1 of the Supplementary Materials. The results for the Euclidean parameters are similar to those presented in Table 1. Mplus provides estimator for the baseline hazard function instead of the cumulative baseline hazard function. Its standard error estimator does not reflect the true variation, and the coverages of the confidence intervals are far below the nominal level.

6. REAL DATA ANALYSIS

We analyzed a dataset on patients with serous ovarian cancer from the TCGA project (The Cancer Genome Atlas Research Network 2011). Genomic variables include DNA copy number, SNP genotype, DNA methylation level, and levels of expression of mRNA, microRNA, total protein, and phosphorylated protein. Demographic and clinical variables include age at diagnosis, race, tumor stage, tumor grade, time to tumor progression, and time to death. There are a total of 586 patients. The median follow-up time was about 2.5 years, and roughly 30% of the patients were lost to follow-up before tumor progression or death. The data are available from http://gdac.broadinstitute.org/.

We focused on the integrative analysis of clinical outcomes and expression levels of mRNA, total protein, and phosphorylated protein. We considered mRNA expression as a latent variable that can only be observed with error through three microarray platforms, namely Agilent 244K Whole Genome Expression Array, Affymetrix HT-HG-U133A, and Affymetrix Exon 1.0. We assumed that the effects of a gene on clinical outcomes are mediated through unobserved protein activity. The latent protein activity is modified by mRNA expression and is manifest through the observed protein expression measurements, which were obtained from the reverse-phase protein arrays platform. Figure 4 depicts the SEM fit for each gene. We assumed that the observed variables follow the distributions described in Section 5, with (Y₁, Y₂, Y₃) being the three microarray measurements, (Y₄, Y₅) = (Total protein expression, Phosphorylated protein expression), (Y₆, Y₇) = (Tumor stage, Tumor grade), (Z₁, Z₂) = (Age, Race), and T being progression-free survival time.

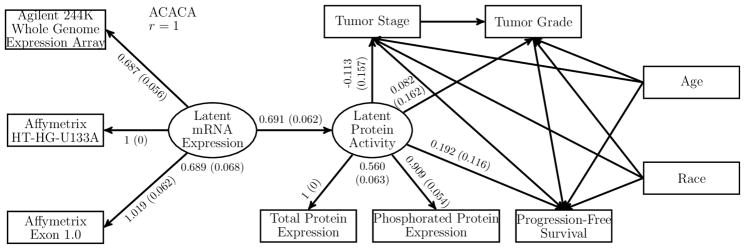
Figure 4.

Results from the SEM Analysis of the Gene ACACA. Analysis results are from 542 patients with ovarian cancer in the TCGA project. The numbers besides an arrow correspond to the point estimate and standard error estimate (in parentheses) of the regression parameter. The numbers below the latent variables correspond to the point estimate and standard error estimate (in parentheses) of the error variance.

We dichotomized tumor stage into stage II/III versus stage IV and tumor grade into grade 2 versus grade 3/4. Race was dichotomized into white and non-white. We allowed mRNA expression and protein expression data to be missing for some subjects. We excluded patients with tumor stage I or grade 1, as those patients may have a disease that is biologically different from that of patients with tumors of other stages or grades. For each gene, we fit the class of transformation models with G(x) = r⁻¹ log(1 + rx) over a grid of r = (0, 0.1, …, 2). We selected the model with the smallest AIC or, equivalently, the largest log-likelihood value.

We present the results for the gene ACACA. The sample size is 542. About 30% of the subjects do not have protein expression data, and over 10% of the subjects miss at least one mRNA expression measurement. The best-fitting model is obtained at r = 1, which corresponds to the proportional odds model. The point estimates and standard error estimates of the parameters associated with the latent variables are shown in Figure 4. The remaining results are shown in Table S.2 of the Supplementary Materials. The latent variables have strong positive association with the measurement platforms. As expected, latent protein activity and latent mRNA expression are highly correlated. Latent protein activity is positively associated with progression-free survival time, with a p-value of 0.100. Specifically, higher latent protein activity is associated with shorter progression-free survival time, which agrees with the findings of the literature (Menendez and Lupu 2007). The association of ACACA with tumor stage or tumor grade is weak.

The results for the parameters in the non-survival models are similar between r = 0 and 1. The parameters in the survival model have different interpretations between r = 0 and 1. With r = 0, a unit increase in latent protein activity would have a multiplicative effect of exp(0.068) on the hazard function. With r = 1, a unit increase in the latent protein activity would have a multiplicative effect of exp(−0.192) on the survival odds. For this dataset, the proportional odds model provides much stronger evidence for the effect of protein activity on progression-free survival than the proportional hazards model.

For the Cox proportional hazards model, we also present the results from Mplus in Table S.2. The results from NPMLE and Mplus are similar for most parameters. There are considerable differences between the cumulative baseline hazard function estimates. The standard error estimates for the cumulative baseline hazard function are not available from Mplus.

For comparisons, we also fit a proportional odds model without latent variables for progression-free survival on the covariates and the two protein expression variables, where the subjects with missing protein expression data were discarded. The p-value of the Wald test for the joint effect of protein expression is 0.157. With r = 0, the Wald test p-value is 0.578. Therefore, analyses based on standard models fail to conclude a strong association between the protein expression and progression-free survival. The power of the proposed SEM framework stems from the appropriate handling of missing data, the dimension reduction of the observed covariates, and the flexibility of the survival model.

7. DISCUSSION

In this article, we consider semiparametric SEM for potentially right-censored survival time data. We prove the consistency, asymptotic normality, and semiparametric efficiency of the NPMLE. We propose new rules for establishing model identifiability and invertibility of the information operator. We construct an EM algorithm to compute the NPMLE and introduce occasional Newton-Raphson steps to accelerate the convergence.

One contribution of Theorem 1 is that it reduces a semiparametric identifiability problem to a parametric one; it shows that the inclusion of the semiparametric component does not make the model less identifiable but, in some sense, makes the model more easily identifiable. With that being said, the result hinges on correct specification of the model and does not guarantee empirical identifiability in a finite sample. Therefore, care should be taken when fitting a model that is nearly non-identifiable. Another main result of ours is given by Lemma 1. This lemma is applicable to a wide range of latent variable models and allows one to deduce the identifiability of a model by inspecting just part of it.

Invertibility of the information operator has received much less attention in the literature than model identifiability. In this article, we prove a general result for invertibility of the information operator. It is evident from the proof that the invertibility of the information operator can be established using techniques similar to those used to establish model identifiability. Specifically, the key to the proof of the identifiability of the mixture Cox model is that with the presence of a covariate that is independent of the latent variable, the contributions to the likelihood from the latent variable and the baseline hazard function can be separated by considering different values of the covariate. (In a normal mixture model, however, we lack such identifiability results precisely because the random effect and error term are combined linearly and their distributions cannot be distinguished.) As a result, if two sets of parameters give rise to the same marginal survival function, then they must do so by giving rise to the same random-effect distribution. Based on the proportional hazards structure, we prove a parallel result for the invertibility of the information operator: the existence of a submodel with zero score implies that the random-effect distribution has zero score along that submodel as well. Therefore, to ensure the invertibility of the information operator of the mixture Cox model, one only has to ensure that the information matrix of the random-effect distribution is invertible.

Our work can be extended in several directions. First, one may be interested in expanding the model by inclusion of more latent and observed variables. As the number of variables increases, the number of parameters to be estimated increases as well. Then, it may be desirable to perform variable selection. Because a single variable may be associated with multiple parameters, one may prefer not to treat parameters as the basic unit of selection, as in traditional lasso methods (Tibshirani 1996). Instead, methods like group lasso (Yuan and Lin 2006) that penalize parameters associated with a variable as a group may be considered.

In our model, the distribution of the manifest variable Y is fully parametric. One can allow a nonparametric transformation on Y. A major challenge arises in extending the asymptotic results to unbounded nonparametric transformation, as the estimator of the transformation function can be unbounded (Zeng and Lin 2010).

Finally, it would be of interest to consider interval-censored data. Interval censoring results in a different likelihood function, which makes the computation of the NPMLE and the derivation of its asymptotic properties challenging, even for univariate survival time data. The asymptotic theory for interval-censored data is only available in a few simple cases; see Huang and Wellner (1997) for a review.

APPENDIX: TECHNICAL DETAILS

We present the following conditions, which are clearly implied by conditions (C3)–(C5):

• (C3′)For k = 1, …, K₁, ϑ_k is a non-zero vector.
• (C4′)Consider two sets of parameters (α_k, β_k, ψ, ν) and (α̃_k, β̃_k, ψ̃, ν̃) for k = 1, …, K₁, and let η̃₁ = (η̃₁₁, …, η̃_1K1), where η̃_1k = Y^T(α_k−α̃_k)+Z^T(β_k−β̃_k)+η_1k. Let f_{Y, η1} be the density of (Y, η₁) given Z. Then, f_{Y, η1} (Y, η₁ | Z; ψ, ν) = f_{Y, η1} (Y, η̃₁ | Z; ψ̃, ν̃) for all Z, Y, and η₁ implies that α_k = α̃_k, β_k = β̃_k, ψ = ψ̃, and ν = ν̃.
• (C5′)For k = K₁ + 1, …, K, let (Y^(k), ${\mathit{\eta }}_1^{(k)},{\mathit{\eta }}_2^{(k)}$) be the components of (Y, η₁, η₂) that appear in the regression of T_k, and let (Y^−(k), ${\mathit{\eta }}_1^{-(k)},{\mathit{\eta }}_2^{-(k)}$) be the remaining components. If ${\mathit{\eta }}_2^{(k)}$ is non-empty, then (Y^−(k), ${\mathit{\eta }}_1^{-(k)}$) is non-empty, and ${\mathit{\eta }}_2^{(k)}$ is complete sufficient in { $F_{{\eta }_2^{(k)}\mid Y,{\eta }_1}(·\mid \mathit{Z},\mathit{Y},{\mathit{\eta }}_1):\mathit{Z}={\mathit{z}}_0,{\mathit{Y}}^{(k)}={\mathit{y}}_0,{\mathit{\eta }}_1^{(k)}={\mathit{\eta }}_{10}$} for any fixed z₀, y₀, and η₁₀, where $F_{{\eta }_2^{(k)}\mid Y,{\eta }_1}$ is the distribution function of ${\mathit{\eta }}_2^{(k)}$ given (Z,Y, η₁) with (Y^−(k), ${\mathit{\eta }}_1^{-(k)}$) treated as a parameter vector.

We prove Theorem 1 under the generalized conditions (C1), (C2), and (C3′)-(C5′). The proof makes use of two lemmas given at the end of this appendix. We first provide an overview of the proof. For any two sets of parameters (ϑ_k, α_k, β_k, ϕ_k, Λ_k, ψ, ν) and (ϑ̃_k, α̃_k, β̃_k, ϕ̃_k, Λ̃_k, ψ̃, ν̃), assume that the likelihood values at the two sets of parameters are identical almost surely. By definition, the model is identifiable if the equality of the likelihood values implies the equality of the two sets of parameters. We derive the equality of the two sets of parameters in the following steps:

1. By conditions (C1), (C2), and (C3′) and the identifiability of the mixture Cox model (Kortram et al. 1995), ϑ_k = ϑ̃_k and Λ_k = Λ̃_k for k = 1, …, K₁.

2. With some algebraic manipulation, the likelihood function can be expressed in the form of the Laplace transform of the distribution of a function of (Y, η₁). The uniqueness of the Laplace transform, together with condition (C4′), implies that (α_k, β_k, ψ, ν) = (α̃_k, β̃_k, ψ̃, ν̃) for k = 1, …, K₁.

3. By the uniqueness of the Laplace transform and the complete sufficiency of η₂ imposed by condition (C5′), the equality of the likelihood functions of (T_K1+1, …, T_K, Y) implies the equality of the likelihood functions of (T_K1+1, …, T_K, Y, η). By the identifiability of the Cox model, we conclude that (ϑ_k, α_k, β_k, ϕ_k) = (ϑ̃_k, α̃_k, β̃_k, ϕ̃_k) for k = K₁ + 1, …, K.

Proof of Theorem 1

The likelihood is given in (4). Here, we consider a single observation and drop the subscript i. Using the arguments in Section 10.1 of Zeng and Lin (2010), we can set each survival time to be right censored at any time point within [0, τ] when establishing identifiability. Consider two sets of parameters (ϑ_k, α_k, β_k, ϕ_k, Λ_k, ψ, ν) and (ϑ̃_k, α̃_k, β̃_k, ϕ̃_k, Λ̃_k, ψ̃, ν̃) such that the likelihood values for an observation with the K survival times being right censored are equal almost surely, i.e.,

$$\begin{array}{l}\int \prod _{k=1}^K\left[\int exp\left\{-{\mathrm{\Lambda }}_k(t_k)s_k{e}^{{\mathit{W}}^{\mathrm{T}}{\mathit{\vartheta }}_k+{\mathit{Z}}^{\mathrm{T}}{\mathit{\beta }}_k+{\mathit{Y}}^{\mathrm{T}}{\mathit{\alpha }}_k+{\mathit{\eta }}^{\mathrm{T}}{\mathit{\varphi }}_k}\right\}{g}_k(s_k)\mathrm{d}{m}_k(s_k)\right]\times f_{Y,\eta }\left(\mathit{Y},\mathit{\eta }\mid \mathit{Z};\mathit{\psi },\mathit{\nu }\right)\mathrm{d}\mathit{\eta }\\ =\int \prod _{k=1}^K\left[\int exp\left\{-{\stackrel{\sim }{\mathrm{\Lambda }}}_k(t_k)s_k{e}^{{\mathit{W}}^{\mathrm{T}}{\stackrel{\sim }{\mathit{\vartheta }}}_k+{\mathit{Z}}^{\mathrm{T}}{\stackrel{\sim }{\mathit{\beta }}}_k+{\mathit{Y}}^{\mathrm{T}}{\stackrel{\sim }{\mathit{\alpha }}}_k+{\mathit{\eta }}^{\mathrm{T}}{\stackrel{\sim }{\mathit{\varphi }}}_k}\right\}{g}_k(s_k)\mathrm{d}{m}_k(s_k)\right]\times f_{Y,\eta }\left(\mathit{Y},\mathit{\eta }\mid \mathit{Z};\stackrel{\sim }{\mathit{\psi }},\stackrel{\sim }{\mathit{\nu }}\right)\mathrm{d}\mathit{\eta }\end{array}$$ (A.1)

for all t₁, …, t_K ∈ [0, τ], W, Z, and Y, where f_Y,η is the density of (Y, η) given Z. If m_k is a point mass at one, then s_k is fixed at one, g_k = 1, and the integration with respect to m_k(s_k) can be omitted. For simplicity of description, assume that m_k is the Lebesgue measure. Note that

$$\int s{g}_k(s)\mathrm{d}s=-\underset{t\to 0^{+}}{lim}\frac{\mathrm{d}}{\mathrm{d}t}{\int }_0^{\infty }{e}^{-ts}{g}_k(s)\mathrm{d}s=-\underset{t\to 0^{+}}{lim}\frac{\mathrm{d}}{\mathrm{d}t}exp\{-G_k(t)\}=G_k^{\prime }(0)<\infty .$$

Thus, a transformation model can be written as a random-effect proportional hazards model with known distributions (g₁, …, g_K) for random effects (s₁, …, s_K) with finite means.

First, we show that the baseline hazard functions of the first K₁ survival times are identifiable. For each k = 1, …, K₁, set t_l → 0 for l ≠ k on both sides of (A.1). On each side of the resulting equation, integration with respect to Y results in the likelihood of a mixture Cox model with s_ke^YTα_k+η_1k or s_ke^{YTα̃_k+η_1k} as a latent variable. Let E(· | Z) and Ẽ(· | Z) be the expectations under f_Y,η(· | Z; ψ, ν) and f_Y,η(· | Z; ψ̃, ν̃), respectively. Theorem 3 of Kortram et al. (1995) implies that E(s_ke^YTα_k+η_1k | Z = 0)Λ_k = Ẽ(s_ke^{YTα̃_k+η_1k} | Z = 0)Λ̃_k on [0, τ], ϑ_k = ϑ̃_k, and the distribution of E(s_ke^YT_αk+η_1k | Z = 0)⁻¹s_ke^YTα_k+η_1k under f_Y,η(· | Z;ψ, ν) is equal to that of Ẽ(s_ke^{YTα̃_k+η_1k} | Z = 0)⁻¹s_ke^{YTα̃_k+η_1k} under f_Y,η(· |Z; ψ̃, ν̃). Because E(Y^Tα_k + η_1k | Z = 0) = Ẽ(Y^T α̃_k + η_1k| Z = 0) = 0 by condition (C2), we see that Λ_k = Λ̃_k on [0, τ].

Second, we show that the likelihood function takes the form of a Laplace transform and use the uniqueness of the Laplace transform to prove the identifiability of (α_k, β_k, ψ, ν) (k = 1, …, K₁). Setting t_k → 0 for k = K₁ + 1, …, K and W = 0 on both sides of (A.1), we have

$$\begin{array}{l}\int \prod _{k=1}^{K_1}\left[\int exp\left\{-{\mathrm{\Lambda }}_k(t_k)s_k{e}^{{\mathit{Z}}^{\mathrm{T}}{\mathit{\beta }}_k+{\mathit{Y}}^{\mathrm{T}}{\mathit{\alpha }}_k+{\eta }_{1k}}\right\}{g}_k(s_k)\mathrm{d}{s}_k\right]f_{Y,\eta }(\mathit{Y},\mathit{\eta }\mid \mathit{Z};\mathit{\psi },\mathit{\nu })\mathrm{d}\mathit{\eta }\\ =\int \prod _{k=1}^{K_1}\left[\int exp\left\{-{\mathrm{\Lambda }}_k(t_k)s_k{e}^{{\mathit{Z}}^{\mathrm{T}}{\stackrel{\sim }{\mathit{\beta }}}_k+{\mathit{Y}}^{\mathrm{T}}{\stackrel{\sim }{\mathit{\alpha }}}_k+{\eta }_{1k}}\right\}{g}_k(s_k)\mathrm{d}{s}_k\right]f_{Y,\eta }\left(\mathit{Y},\mathit{\eta }\mid \mathit{Z};\stackrel{\sim }{\mathit{\psi }},\stackrel{\sim }{\mathit{\nu }}\right)\mathrm{d}\mathit{\eta }.\end{array}$$ (A.2)

Let U = (U₁, …, U_K1), U_k = s_ke^η_1k, and f_U|Y be the density function of U given Z and Y. By the uniqueness of the Laplace transform, for any continuous functions f and f̃, any open set 𝒮, and any positive real numbers c and c̃,

$${\int }_0^{\infty }{e}^{-\mathit{cst}}f(t)\mathrm{d}t={\int }_0^{\infty }{e}^{-\stackrel{\sim }{c}st}\stackrel{\sim }{f}(t)\mathrm{d}t\forall s\in \mathcal{S}$$

implies that f(t) = (c/c̃)f̃(ct/c̃) for all t > 0. Therefore, the equality of (A.2) for all t₁, …, t_K1, Z, and Y implies that

$$f_{U\mid Y}\left(\mathit{U}\mid \mathit{Z},\mathit{Y};\mathit{\psi },\mathit{\nu }\right)=e^{{\sum }_{k=1}^{K_1}{\mathit{Z}}^{\mathrm{T}}({\mathit{\beta }}_k-{\stackrel{\sim }{\mathit{\beta }}}_k)+{\mathit{Y}}^{\mathrm{T}}({\mathit{\alpha }}_k-{\stackrel{\sim }{\mathit{\alpha }}}_k)}{f}_{U\mid Y}\left(\stackrel{\sim }{\mathit{U}}\mid \mathit{Z},\mathit{Y};\stackrel{\sim }{\mathit{\psi }},\stackrel{\sim }{\mathit{\nu }}\right)$$ (A.3)

for all U, Z, and Y, where Ũ = (Ũ₁, …, Ũ_K1), and Ũ_k = e^{ZT(β_k−β̃_k)+YT(α_k−α̃_k)}U_k. Let f_η1|Y be the density of η₁ given Z and Y. By the definition of U,

$$\begin{array}{l}{f}_{U\mid Y}(\mathit{U}\mid \mathit{Z},\mathit{Y};\mathit{\psi },\mathit{\nu }){\int }_{s_k>0}{f}_{{\eta }_1\mid Y}(log{U}_1-log{s}_1,\dots ,log{U}_{K_1}-log{s}_{K_1}\mid \mathit{Z},\mathit{Y};\mathit{\psi },\mathit{\nu })\prod _{k=1}^{K_1}{U}_k^{-1}{g}_k(s_k)\mathrm{d}(s_1,\dots ,s_{K_1})\\ {\int }_{{ℝ}^{K_1}}{f}_{{\eta }_1\mid Y}(log{U}_1-v_1,\dots ,log{U}_{K_1}-v_{K_1}\mid \mathit{Z},\mathit{Y};\mathit{\psi },\mathit{\nu })\prod _{k=1}^{K_1}{U}_k^{-1}{\overline{g}}_k(v_k)e^{v_k}\mathrm{d}(v_1,\dots ,v_{K_1}),\end{array}$$

where ḡ_k(v) = g_k(e^v). Thus, (A.3) implies that

$${\int }_{{ℝ}^{K_1}}\{f_{{\eta }_1\mid Y}(log{U}_1-v_1,\dots ,log{U}_{K_1}-v_{K_1}\mid \mathit{Z},\mathit{Y};\mathit{\psi },\mathit{\nu })-f_{{\eta }_1\mid Y}(log{\stackrel{\sim }{U}}_1-v_1,\dots ,log{\stackrel{\sim }{U}}_{K_1}-v_{K_1}\mid \mathit{Z},\mathit{Y};\stackrel{\sim }{\mathit{\psi }},\stackrel{\sim }{\mathit{\nu }})\}\prod _{k=1}^{K_1}{\overline{g}}_k(v_k)e^{v_k}\mathrm{d}(v_1,\dots ,v_{K_1})=0.$$ (A.4)

Consider two arbitrary continuous functions f, g: ℝ → ℝ. Note that

$${\int }_{-\infty }^{\infty }{e}^{-st}(f\ast g)(t)\mathrm{d}t={\int }_{-\infty }^{\infty }{e}^{-st}f(t)\mathrm{d}t{\int }_{-\infty }^{\infty }{e}^{-st}g(t)\mathrm{d}t$$

for any s such that the integrals are defined, where $(f\ast g)(t)\equiv {\int }_{-\infty }^{\infty }f(t-s)g(s)\mathrm{d}s$ is the convolution of f and g. Therefore, (f * g)(·) = 0 implies that

$${\int }_{-\infty }^{\infty }{e}^{-st}f(t)\mathrm{d}t{\int }_{-\infty }^{\infty }{e}^{-st}g(t)\mathrm{d}t=0,$$

which, if g is positive, implies that f(·) = 0 by the uniqueness of the bilateral Laplace 27 transform (Chareka 2007). Because ḡ_k(·)e^(·) is positive, (A.4) implies that f_η1|Y (η₁ | Z,Y; ψ, ν) = f_η1|Y (η̃₁ | Z,Y; ψ̃, ν̃), where η̃₁ is defined in condition (C4′). By condition (C4′), (α_k, β_k, ψ, ν) = (α̃_k, β̃_k, ψ̃, ν̃) for k = 1, …, K₁.

It remains to identify the parameters associated with (T_K1+1, …, T_K). By the uniqueness of the Laplace transform, (A.1) implies that

$$\begin{array}{l}\int \prod _{k=K_1+1}^K\left\{\int e^{-{\mathrm{\Lambda }}_k(t_k)s_k{e}^{{\mathit{W}}^{\mathrm{T}}{\mathit{\vartheta }}_k+{\mathit{Z}}^{\mathrm{T}}{\mathit{\beta }}_k+{\mathit{Y}}^{\mathrm{T}}{\mathit{\alpha }}_k+{\mathit{\eta }}^{\mathrm{T}}{\mathit{\varphi }}_k}}{g}_k(s_k)\mathrm{d}{s}_k\right\}{f}_{Y,\eta }(\mathit{Y},\mathit{\eta }\mid \mathit{Z};\mathit{\psi },\mathit{\nu })\mathrm{d}{\mathit{\eta }}_2\\ =\int \prod _{k=K_1+1}^K\left\{\int e^{-{\stackrel{\sim }{\mathrm{\Lambda }}}_k(t_k)s_k{e}^{{\mathit{W}}^{\mathrm{T}}{\stackrel{\sim }{\mathit{\vartheta }}}_k+{\mathit{Z}}^{\mathrm{T}}{\stackrel{\sim }{\mathit{\beta }}}_k+{\mathit{Y}}^{\mathrm{T}}{\stackrel{\sim }{\mathit{\alpha }}}_k+{\mathit{\eta }}^{\mathrm{T}}{\stackrel{\sim }{\mathit{\varphi }}}_k}}{g}_k(s_k)\mathrm{d}{s}_k\right\}{f}_{Y,\eta }(\mathit{Y},\mathit{\eta }\mid \mathit{Z};\mathit{\psi },\mathit{\nu })\mathrm{d}{\mathit{\eta }}_2\end{array}$$

for all t_K1+1, …, t_K, W, Z, Y, and η₁, i.e., η₁ can be treated as observed for identifying the remaining parameters. Under condition (C5′), we can use the arguments in the proof of Lemma 1 to show that the integrands in the above equality are equal at each value of η₂. We conclude that (ϑ_k, α_k, β_k, ϕ_k, Λ_k) = (ϑ̃_k, α̃_k, β̃_k, ϕ̃_k, Λ̃_k) for k = K₁+1, …, K.

We provide an overview for the proof of Theorem 2. The consistency of the NPMLE is proved in the following steps:

1. By conditions (D2)–(D4), the NPMLE exists, i.e., Λ̂_k(τ) < ∞.

2. By conditions (D3) and (D4), Λ̂_k(τ) is uniformly bounded. Helly’s selection theorem then implies that every subsequence of Λ̂_k has a further converging subsequence.

3. By the Glivenko-Cantelli properties of the log-likelihood and related functions given by Lemma S2 in the Supplementary Materials, the identifiability of the model, and the non-negativity of the Kullback-Leibler divergence, we conclude the consistency of the NPMLE.

The asymptotic normality of the NPMLE follows mainly from the arguments of van der Vaart (1998, pp. 419–424). Donsker properties of the score and related functions are given by Lemma S2 in the Supplementary Materials, and the invertibility of the information operator is given by Lemma 2.

Proof of Theorem 2

We use Z to denote both W and Z with β_k (k = 1, …, K) being the corresponding vector of regression parameters. Let

$$\begin{array}{l}\mathrm{\Psi }\left({\mathcal{O}}_i;\mathit{\theta },\mathcal{A}\right)=\prod _{k=1}^K\int {\left[e^{{\mathit{Z}}_i^{\mathrm{T}}{\mathit{\beta }}_k+{\mathit{Y}}_i^{\mathrm{T}}{\mathit{\alpha }}_k+{\mathit{\eta }}^{\mathrm{T}}{\mathit{\varphi }}_k}{G}_k^{\prime }\left\{e^{{\mathit{Z}}_i^{\mathrm{T}}{\mathit{\beta }}_k+{\mathit{Y}}_i^{\mathrm{T}}{\mathit{\alpha }}_k+{\mathit{\eta }}^{\mathrm{T}}{\mathit{\varphi }}_k}{\mathrm{\Lambda }}_k\left({\stackrel{\sim }{T}}_{ki}\right)\right\}\right]}^{{\mathrm{\Delta }}_{ki}}\\ \times exp\left[-G_k\left\{e^{{\mathit{Z}}_i^{\mathrm{T}}{\mathit{\beta }}_k+{\mathit{Y}}_i^{\mathrm{T}}{\mathit{\alpha }}_k+{\mathit{\eta }}^{\mathrm{T}}{\mathit{\varphi }}_k}{\mathrm{\Lambda }}_k\left({\stackrel{\sim }{T}}_{ki}\right)\right\}\right]f_Y\left({\mathit{Y}}_i\mid {\mathit{Z}}_i,\mathit{\eta };\mathit{\psi }\right)f_{\eta }\left(\mathit{\eta }\mid {\mathit{Z}}_i;\mathit{\nu }\right)\mathrm{d}\mathit{\eta },\end{array}$$

Ψ̇_θ(𝒪_i; θ, 𝒜) be the derivative of Ψ(𝒪_i; θ, 𝒜) with respect to θ, and Ψ̇_k(𝒪_i; θ, 𝒜)[H_k] be the derivative of Ψ(𝒪_i; θ, 𝒜) along the path (Λ_k + εH_k).

First, we prove the consistency. By condition (D4),

$$\begin{array}{l}{\left[e^{{\mathit{Z}}_i^{\mathrm{T}}{\mathit{\beta }}_k+{\mathit{Y}}_i^{\mathrm{T}}{\mathit{\alpha }}_k+{\mathit{\eta }}^{\mathrm{T}}{\mathit{\varphi }}_k}{G}_k^{\prime }\left\{e^{{\mathit{Z}}_i^{\mathrm{T}}{\mathit{\beta }}_k+{\mathit{Y}}_i^{\mathrm{T}}{\mathit{\alpha }}_k+{\mathit{\eta }}^{\mathrm{T}}{\mathit{\varphi }}_k}{\mathrm{\Lambda }}_k\left({\stackrel{\sim }{T}}_{ki}\right)\right\}\right]}^{{\mathrm{\Delta }}_{ki}}{e}^{-G_k\left\{e^{{\mathit{Z}}_i^{\mathrm{T}}{\mathit{\beta }}_k+{\mathit{Y}}_i^{\mathrm{T}}{\mathit{\alpha }}_k+{\mathit{\eta }}^{\mathrm{T}}{\mathit{\varphi }}_k}{\mathrm{\Lambda }}_k({\stackrel{\sim }{T}}_{ki})\right\}}\\ \le e^{O(1+\mid \mathit{Y}\mid +\mid \mathit{\eta }\mid )}{\left\{1+{\mathrm{\Lambda }}_k\left({\stackrel{\sim }{T}}_{ki}\right)\right\}}^{-{\mathrm{\Delta }}_{ki}-{\kappa }_{3k}+{\kappa }_{2k}+1}.\end{array}$$

Thus, condition (D3) implies that

$$\mathrm{\Psi }({\mathcal{O}}_i;\mathit{\theta },\mathcal{A})\le \prod _{i=1}^n\mathcal{F}({\mathcal{O}}_i;\mathit{\theta })\prod _{k=1}^K{\left\{1+{\mathrm{\Lambda }}_k({\stackrel{\sim }{T}}_{ki})\right\}}^{-{\mathrm{\Delta }}_{ki}-{\kappa }_{3k}+{\kappa }_{2k}+1},$$ (A.5)

where ℱ(𝒪_i; θ) is a random variable with |E{log ℱ(𝒪_i; θ)}| < ∞ for any θ. By condition (D2), P(T̃_ki = τ) is positive. Therefore, if Λ_k (τ) = ∞, then the right-hand side of (A.5) is zero for large n. We conclude that Λ̂_k (τ) < ∞, such that the NPMLE exists.

We then show that lim sup_nΛ̂_k (τ) < ∞ almost surely. From (A.5),

$$\begin{array}{l}\frac{1}{n}log{L}_n\left(\widehat{\mathit{\theta }},\widehat{\mathcal{A}}\right)=\frac{1}{n}\sum _{i=1}^n\sum _{k=1}^K{\mathrm{\Delta }}_{ki}log{\widehat{\mathrm{\Lambda }}}_k\{{\stackrel{\sim }{T}}_{ki}\}+\frac{1}{n}\sum _{i=1}^{n}log\mathrm{\Psi }({\mathcal{O}}_i;\widehat{\mathit{\theta }},\widehat{\mathcal{A}})\\ \le \frac{1}{n}\sum _{i=1}^{n}log\mathcal{F}({\mathcal{O}}_i;\widehat{\mathit{\theta }})+\frac{1}{n}\sum _{i=1}^n\sum _{k=1}^K{\mathrm{\Delta }}_{ki}log{\widehat{\mathrm{\Lambda }}}_k\{{\stackrel{\sim }{T}}_{ki}\}-\frac{1}{n}\sum _{i=1}^n\sum _{k=1}^K({\mathrm{\Delta }}_{ki}+{\kappa }_{3k}-{\kappa }_{2k}-1)log\left\{1+{\widehat{\mathrm{\Lambda }}}_k({\stackrel{\sim }{T}}_{ki})\right\}.\end{array}$$

Let $\stackrel{\sim }{N}=n^{-1}{\sum }_{i=1}^n({\mathrm{\Delta }}_{1i}I({\stackrel{\sim }{T}}_{1i}\le ·),\dots ,{\mathrm{\Delta }}_{Ki}I({\stackrel{\sim }{T}}_{Ki}\le ·))$. Clearly,

$$\frac{1}{n}log{L}_n({\mathit{\theta }}_0,\stackrel{\sim }{N})=-\frac{1}{n}\sum _{i=1}^n\sum _{k=1}^K{\mathrm{\Delta }}_{ki}logn+\frac{1}{n}\sum _{i=1}^{n}log\mathrm{\Psi }({\mathcal{O}}_i;{\mathit{\theta }}_0,\stackrel{\sim }{N}).$$

The second term on the right-hand side of the above equation is O_p (1). Thus,

$$\begin{array}{l}\frac{1}{n}log{L}_n\left(\widehat{\mathit{\theta }},\widehat{\mathcal{A}}\right)-\frac{1}{n}log{L}_n\left({\mathit{\theta }}_0,\stackrel{\sim }{N}\right)+O_p(1)\\ \le \frac{1}{n}\sum _{i=1}^n\sum _{k=1}^K{\mathrm{\Delta }}_{ki}log[n{\widehat{\mathrm{\Lambda }}}_k\{{\stackrel{\sim }{T}}_{ki}\}]-\frac{1}{n}\sum _{i=1}^n\sum _{k=1}^K({\mathrm{\Delta }}_{ki}+{\kappa }_{3k}-{\kappa }_{2k}-1)log\left\{1+{\widehat{\mathrm{\Lambda }}}_k({\stackrel{\sim }{T}}_{ki})\right\}.\end{array}$$

Note that (κ_3k − κ_2k − 1) is positive by condition (D4). Using the partitioning argument similar to those of Murphy (1994) and Parner (1998), we can show that the right-hand side of the above inequality tends to −∞ if lim sup_n Λ̂_k (τ) = ∞. By definition of (θ̂, 𝒜̂), the left-hand side of the inequality is bounded below by an O_p(1) term. Therefore, Λ̂_k (τ) is uniformly bounded.

Given the boundedness of Λ̂_k (τ), Helly’s selection theorem implies that, for any subsequence of n, we can always choose a further subsequence such that Λ̂_k converges pointwise to some monotone function ${\mathrm{\Lambda }}_k^{\ast }$ and θ̂ converges to θ^*. The desired consistency result follows if we can show that ${\mathrm{\Lambda }}_k^{\ast }={\mathrm{\Lambda }}_{0k}$ and θ^* = θ₀ almost surely. With an abuse of notation, let {n}_{1,2, …} be the subsequence. Define

$${\stackrel{\sim }{\mathrm{\Lambda }}}_k(t)=-\sum _{i=1}^n{\mathrm{\Delta }}_{ki}I\left({\stackrel{\sim }{T}}_{ki}\le t\right){\left\{\sum _{j=1}^n\frac{{\stackrel{.}{\mathrm{\Psi }}}_k({\mathcal{O}}_j;{\mathit{\theta }}_0,{\mathcal{A}}_0)\left[I\left({\stackrel{\sim }{T}}_{ki}\le ·\right)\right]}{\mathrm{\Psi }({\mathcal{O}}_j;{\mathit{\theta }}_0,{\mathcal{A}}_0)}\right\}}^{-1}.$$

By Lemma S2 in the Supplementary Materials and the properties of Donsker (and therefore, Glivenko-Cantelli) classes,

$$\frac{1}{n}\sum _{j=1}^n\frac{{\stackrel{.}{\mathrm{\Psi }}}_k({\mathcal{O}}_j;{\mathit{\theta }}_0,{\mathcal{A}}_0)\left[I(s\le ·)\right]}{\mathrm{\Psi }({\mathcal{O}}_j;{\mathit{\theta }}_0,{\mathcal{A}}_0)}\to \mathrm{E}\left(\frac{{\stackrel{.}{\mathrm{\Psi }}}_k({\mathcal{O}}_i;{\mathit{\theta }}_0,{\mathcal{A}}_0)\left[I(s\le ·)\right]}{\mathrm{\Psi }({\mathcal{O}}_i;{\mathit{\theta }}_0,{\mathcal{A}}_0)}\right)$$

uniformly on [0, τ]. Because the score function along the path Λ_k = Λ_0k + εI (· ≥ s) with other parameters fixed at their true values has zero expectation,

$$-\mathrm{E}\left\{\frac{{\stackrel{.}{\mathrm{\Psi }}}_k({\mathcal{O}}_i;{\mathit{\theta }}_0,{\mathcal{A}}_0)\left[I(s\le ·)\right]}{\mathrm{\Psi }({\mathcal{O}}_i;{\mathit{\theta }}_0,{\mathcal{A}}_0)}\right\}=\frac{\mathrm{d}P\left({\stackrel{\sim }{T}}_{ki}{\mathrm{\Delta }}_{ki}<s\right)/\mathrm{d}s}{{\lambda }_{0k}(s)}.$$

Algebraic manipulation yields that the uniform limit of Λ̃_k on [0, τ] is Λ_0k. Note that

$${\widehat{\mathrm{\Lambda }}}_k(t)={\int }_0^t\frac{\left|n^{-1}{\sum }_{j=1}^n{\stackrel{.}{\mathrm{\Psi }}}_k({\mathcal{O}}_j;{\mathit{\theta }}_0,{\mathcal{A}}_0)\left[I(s\le ·)\right]/\mathrm{\Psi }({\mathcal{O}}_j;{\mathit{\theta }}_0,{\mathcal{A}}_0)\right|}{\left|n^{-1}{\sum }_{j=1}^n{\stackrel{.}{\mathrm{\Psi }}}_k({\mathcal{O}}_j;\widehat{\mathit{\theta }},\widehat{\mathcal{A}})\left[I(s\le ·)\right]/\mathrm{\Psi }({\mathcal{O}}_j;\widehat{\mathit{\theta }},\widehat{\mathcal{A}})\right|}\mathrm{d}{\stackrel{\sim }{\mathrm{\Lambda }}}_k(s).$$

We have shown that the numerator of the integrand in the above equation converges uniformly. Similarly, we can show that the denominator of the integrand in the above equation converges uniformly to |E{Ψ̇_k(𝒪_i; θ^*,𝒜^*)[I (s ≤ ·)]/Ψ(𝒪_i; θ^*,𝒜^*)}| and that the limit is bounded away from 0. Because Λ̃_k converges uniformly to Λ_0k, which is differentiable with respect to t, ${\mathrm{\Lambda }}_k^{\ast }$ is also differentiable with respect to t. It follows that dΛ̂_k/dΛ̃_k converges uniformly to ${\lambda }_k^{\ast }/{\lambda }_{0k}$ on [0, τ], where ${\lambda }_k^{\ast }={\left({\mathrm{\Lambda }}_k^{\ast }\right)}^{\prime }$. As n⁻¹ log L_n(θ̂, 𝒜̂) − n⁻¹ log L_n(θ₀, 𝒜̃) is non-negative,

$$\frac{1}{n}\sum _{i=1}^n\sum _{k=1}^K{\mathrm{\Delta }}_{ki}log\frac{\mathrm{d}{\widehat{\mathrm{\Lambda }}}_k\left({\stackrel{\sim }{T}}_{ki}\right)}{\mathrm{d}{\widehat{\mathrm{\Lambda }}}_k\left({\stackrel{\sim }{T}}_{ki}\right)}+\frac{1}{n}\sum _{i=1}^{n}log\frac{\mathrm{\Psi }({\mathcal{O}}_i;\widehat{\mathit{\theta }},\widehat{\mathcal{A}})}{\mathrm{\Psi }({\mathcal{O}}_i;{\mathit{\theta }}_0,\widehat{\mathcal{A}})}\ge 0.$$

By the Glivenko-Cantelli properties of the class of functions of log Ψ(𝒪_i; θ, 𝒜) given by Lemma S2 and the uniform convergence of dΛ̂_k/dΛ̃_k, setting n → ∞ on both sides of the above inequality yields

$$\mathrm{E}\{log\frac{{\prod }_{k=1}^K{\lambda }_k^{\ast }{({\stackrel{\sim }{T}}_{ki})}^{{\mathrm{\Delta }}_{ki}}\mathrm{\Psi }({\mathcal{O}}_i;{\mathit{\theta }}^{\ast },{\mathcal{A}}^{\ast })}{{\prod }_{k=1}^K{\lambda }_{0k}{({\stackrel{\sim }{T}}_{ki})}^{{\mathrm{\Delta }}_{ki}}\mathrm{\Psi }({\mathcal{O}}_i;{\mathit{\theta }}_0,{\mathcal{A}}_0)}\}\ge 0.$$

The left-hand side of the above inequality is the negative Kullback-Leibler distance of the density indexed by (θ^*,𝒜^*). From the identifiability of the model implied by Theorem 1, we conclude that θ^* = θ₀ and ${\mathrm{\Lambda }}_k^{\ast }={\mathrm{\Lambda }}_{k0}$. The desired consistency result follows.

To prove the asymptotic normality of the NPMLE, we adopt the arguments of van der Vaart (1998, pp. 419–424). Let ℘_n be the empirical measure determined by n i.i.d. observations, and let ℘ be the true probability measure. Let ℓ̇_θ(θ, 𝒜) be the derivative of log L_n(θ, 𝒜) with respect to θ, and let ℓ̇_k(θ, 𝒜)[H_k] be the derivative of log L_n(θ, 𝒜) along the path (Λ_k + εH_k). For any v ∈ ℝ^d and 𝒲 = (h₁, …, h_K) with h_k ∈ BV [0, τ], where BV [0, τ] is the space of functions of bounded variation on [0, τ], we have

$${\mathcal{P}}_n\left({\mathit{v}}^{\mathrm{T}}{\stackrel{.}{\ell }}_{\theta }(\widehat{\mathit{\theta }},\widehat{\mathcal{A}})+\sum _{k=1}^K{\widehat{\ell }}_k(\widehat{\mathit{\theta }},\widehat{\mathcal{A}})[\int h_k\mathrm{d}{\widehat{\mathrm{\Lambda }}}_k]\right)=0.$$

In addition,

$$\mathcal{P}\left({\mathit{v}}^{\mathrm{T}}{\stackrel{.}{\ell }}_{\theta }({\mathit{\theta }}_0,{\mathcal{A}}_0)+\sum _{k=1}^K{\stackrel{.}{\ell }}_k({\mathit{\theta }}_0,{\mathcal{A}}_0)[\int h_k\mathrm{d}{\mathrm{\Lambda }}_{0k}]\right)=0.$$

Therefore,

$$\begin{array}{l}\sqrt{n}\left({\mathcal{P}}_n-\mathcal{P}\right)\left({\mathit{v}}^{\mathrm{T}}{\stackrel{.}{\ell }}_{\theta }(\widehat{\mathit{\theta }},\widehat{\mathcal{A}})+\sum _{k=1}^K{\stackrel{.}{\ell }}_k(\widehat{\mathit{\theta }},\widehat{\mathcal{A}})[\int h_k\mathrm{d}{\widehat{\mathrm{\Lambda }}}_k]\right)\\ =-\sqrt{n}\mathcal{P}\{\left({\mathit{v}}^{\mathrm{T}}{\stackrel{.}{\ell }}_{\theta }(\widehat{\mathit{\theta }},\widehat{\mathcal{A}})+\sum _{k=1}^K{\stackrel{.}{\ell }}_k(\widehat{\mathit{\theta }},\widehat{\mathcal{A}})[\int h_k\mathrm{d}{\widehat{\mathrm{\Lambda }}}_k]\right)\\ -\left({\mathit{v}}^{\mathrm{T}}{\stackrel{.}{\ell }}_{\theta }({\mathit{\theta }}_0,{\mathcal{A}}_0)+\sum _{k=1}^K{\stackrel{.}{\ell }}_k({\mathit{\theta }}_0,{\mathcal{A}}_0)[\int h_k\mathrm{d}{\mathrm{\Lambda }}_{0k}]\right)\}.\end{array}$$ (A.6)

From the Donsker properties of the classes of functions of ℓ̇_θ and ℓ̇_k implied by Lemma S2 and the consistency of θ̂ and 𝒜̂, we conclude that the left-hand side of (A.6) equals

$$\sqrt{n}\left({\mathcal{P}}_n-\mathcal{P}\right)\left({\mathit{v}}^{\mathrm{T}}{\stackrel{.}{\ell }}_{\theta }({\mathit{\theta }}_0,{\mathcal{A}}_0)+\sum _{k=1}^K{\stackrel{.}{\ell }}_k({\mathit{\theta }}_0,{\mathcal{A}}_0)[\int h_k\mathrm{d}{\mathrm{\Lambda }}_{0k}]\right)+o_p(1).$$

This term converges to a Gaussian process in l^∞(𝒱 ×𝒬^K). By the Taylor series expansion, the right-hand side of (A.6) is of the form

$$\begin{array}{l}-\sqrt{n}\left\{B_1{[\mathit{v},\mathcal{W}]}^{\mathrm{T}}(\widehat{\mathit{\theta }}-{\mathit{\theta }}_0)+\sum _{k=1}^K\int B_{2k}[\mathit{v},\mathcal{W}]\mathrm{d}({\widehat{\mathrm{\Lambda }}}_k-{\mathrm{\Lambda }}_{0k})\right\}\\ +o_p\left(\sqrt{n}\left|\widehat{\mathit{\theta }}-{\mathit{\theta }}_0\right|+\sqrt{n}\sum _{k=1}^K{\Vert {\widehat{\mathrm{\Lambda }}}_k-{\mathrm{\Lambda }}_{0k}\Vert }_{V[0,\tau ]}\right),\end{array}$$

where ℬ ≡ (B₁,B₂₁, …,B_2K) is the information operator and is linear in ℝ^d ×BV [0, τ]^K. By Lemma 2, ℬ is invertible. The rest of the proof then follows the arguments of van der Vaart (1998, pp. 419–424). Finally, because v^Tθ̂ is an asymptotically linear estimator of v^Tθ₀ with the influence function lying in the space spanned by the score functions, θ̂ is an efficient estimator for θ₀.

The following two lemmas are used in the proofs of Theorem 1 and Theorem 2 and are proved in Section S2 of the Supplementary Materials.

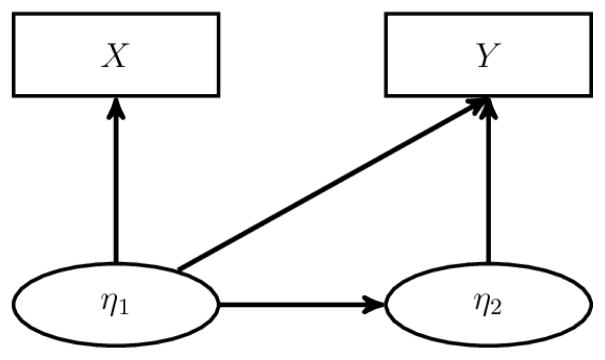
Lemma 1

Let Model A be

$$\begin{array}{lll}\hfill \mathit{X}\mid ({\mathit{\eta }}_1,{\mathit{\eta }}_2)\stackrel{d}{=}\mathit{X}\mid {\mathit{\eta }}_1& ~\hfill & F_{X\mid {\eta }_1}(·\mid {\mathit{\eta }}_1),\hfill \\ \hfill \mathit{Y}\mid ({\mathit{\eta }}_1,{\mathit{\eta }}_2)& ~\hfill & F_{Y\mid \eta }(·\mid {\mathit{\eta }}_1,{\mathit{\eta }}_2),\hfill \\ \hfill {\mathit{\eta }}_2\mid {\mathit{\eta }}_1& ~\hfill & F_{{\eta }_2\mid {\eta }_1}(·\mid {\mathit{\eta }}_1),\hfill \\ \hfill {\mathit{\eta }}_1& ~\hfill & F_{{\eta }_1},\hfill \end{array}$$

where (X,Y) are observed, and (η₁, η₂) are latent. Model A is depicted in Figure A.1. Let $f_{X\mid {\eta }_1}=F_{X\mid {\eta }_1}^{\prime },f_{Y\mid \eta }=F_{Y\mid \eta }^{\prime },f_{{\eta }_2\mid {\eta }_1}=F_{{\eta }_2\mid {\eta }_1}^{\prime }$, and $f_{{\eta }_1}=F_{{\eta }_1}^{\prime }$. Assume that: (a) for any density functions f̃_{Y |η} and f̃_η2|η1,

$$\int f_{Y\mid \eta }(\mathit{Y}\mid {\mathit{\eta }}_1,{\mathit{\eta }}_2)f_{{\eta }_2\mid {\eta }_1}({\mathit{\eta }}_2\mid {\mathit{\eta }}_1)\mathrm{d}{\mathit{\eta }}_2=\int {\stackrel{\sim }{f}}_{Y\mid \eta }(\mathit{Y}\mid {\mathit{\eta }}_1,{\mathit{\eta }}_2){\stackrel{\sim }{f}}_{{\eta }_2\mid {\eta }_1}({\mathit{\eta }}_2\mid {\mathit{\eta }}_1)\mathrm{d}{\mathit{\eta }}_2\forall \mathit{Y},{\mathit{\eta }}_1$$

implies that (f_{Y |η}, f_η2|η1) = (f̃_{Y |η}, f̃_η2|η1), i.e., the model for Y is identifiable if η₁ is observed, (b) F_X|η1 and F_η1 are identifiable based on (X,Y), and (c) η₁ is a complete sufficient statistic in {F_η1|X(· | X) : X ∈ 𝒳}, where F_η1|X is the conditional distribution function of η₁ given X, and 𝒳 is the range of X. Then, Model A is identifiable. A sufficient condition for η₁ to be complete sufficient is that the density of X is of the form

$$f_{X\mid {\eta }_1}(\mathit{X}\mid {\mathit{\eta }}_1)\propto \prod _{j=1}^{q}exp\{X_j{s}_j({\mathit{\eta }}_1)-a_j({\mathit{\eta }}_1)\}{b}_j(X_j),$$

where X = (X₁, …,X_q), η₁ ↦ (s₁(η₁), …, s_q(η₁)) is one-to-one, and b_j is non-zero on some open set.

Figure A.1.

SEM Considered in Lemma 1. The SEM consists of two sets of latent variables and two sets of observed variables that may all be multivariate. The observed variable X depends only on the latent variable η₁, but the observed variable Y depends on both sets of latent variables.

Lemma 2

Under conditions (C1), (C2), (C3′), (C5′), and (D5), the model given by (1)–(3) has an invertible information operator.