Estimation and Inference of Quantile Regression for Survival Data Under Biased Sampling

Abstract

Biased sampling occurs frequently in economics, epidemiology, and medical studies either by design or due to data collecting mechanism. Failing to take into account the sampling bias usually leads to incorrect inference. We propose a unified estimation procedure and a computationally fast resampling method to make statistical inference for quantile regression with survival data under general biased sampling schemes, including but not limited to the length-biased sampling, the case-cohort design, and variants thereof. We establish the uniform consistency and weak convergence of the proposed estimator as a process of the quantile level. We also investigate more efficient estimation using the generalized method of moments and derive the asymptotic normality. We further propose a new resampling method for inference, which differs from alternative procedures in that it does not require to repeatedly solve estimating equations. It is proved that the resampling method consistently estimates the asymptotic covariance matrix. The unified framework proposed in this article provides researchers and practitioners a convenient tool for analyzing data collected from various designs. Simulation studies and applications to real datasets are presented for illustration. Supplementary materials for this article are available online.

1. Introduction

Biased sampling occurs frequently, either naturally or by design, in many observational studies. For example, the cross-sectional prevalent cohort sampling scheme is commonly employed to study a rare disease. It is well known that the prevalent sampling scheme favors individuals who survive longer, because diseased individuals who died before the recruitment would not be sampled. As a result, prevalent cases do not comprise a representative sample of the target population. Problems of this sort can also be found in cross-sectional studies in ecology (McFadden 1962; Muttlak and McDonald 1990; Chen 2010), industrial quality control (Cox 1969), and economics (Kiefer 1988; Helsen and Schmittlein 1993; de Uña Álvarez 2004). Another commonly encountered biased sampling method is the case-cohort design (Prentice 1986; Chen 2001). The case-cohort design provides an economical approach to conducting epidemiological studies that involve rare diseases and/or expensive exposures, where covariate information is collected from all failures but only from a representative subsample of censored observations. Various extensions of the case-cohort design can be found in Borgan et al. (2000), Kulich and Lin (2004), and Samuelsen et al. (2007).

Ignoring sampling bias may lead to substantial estimation bias and fallacious inference. This issue has drawn considerable attentions recently; however, most existing literature focuses on either the proportional/additive hazards or the accelerated failure time models. For the Cox proportional hazards (PH) model, estimation procedures under length-biased sampling have been studied in Luo and Tsai (2009), Qin and Shen (2010), and Huang and Qin (2012); large sample properties for case-cohort sampling have been developed in Self and Prentice (1988), Lin and Ying (1993), and Chen and Lo (1999); see also Lu and Tsiatis (2006), Shen et al. (2009), and Kim et al. (2013) for corresponding treatments under the linear transformation model, a generalization of the Cox model. For the accelerated failure time (AFT) model, estimation procedures under various biased samplings have been discussed in Shen et al. (2009), Kong and Cai (2009), Chen (2010), among others.

In this article, we propose a general approach for analyzing biased sampling data using quantile regression. The most prominent feature of quantile regression is its ability to accommodate heterogenous effects of the covariates, which can influence not only the location but also the shape of the survival time distribution. It is known that the heterogeneity in covariate effects cannot be easily incorporated in either the Cox PH model or the AFT model. Furthermore, the conditional quantile of the survival time is easier to interpret than the hazard function and is often of direct interest. Existing work on censored quantile regression without biased sampling includes Ying et al. (1995), Portnoy (2003), McKeague et al. (2001), Peng and Huang (2008), Wang and Wang (2009), and many others. For a general introduction to quantile regression, we refer to Koenker (2005).

Recently, several authors have considered quantile regression under biased sampling. Chen and Zhou (2012) and Wang and Wang (2014) investigated length-biased data. Both procedures require estimating the censoring time distribution. Chen and Zhou (2012) assumed a Cox PH model for the censoring distribution; however, their estimation procedure can lead to biased estimation under a misspecified censoring time distribution. On the other hand, Wang and Wang (2014) relied on a nonparametric kernel smoothing estimator of the censoring distribution that can suffer from the curse of dimensionality in practice. For the classical case-cohort sampling scheme, Zheng et al. (2013) developed an estimation procedure for quantile regression. These existing formulations, however, can neither be applied to other biased sampling schemes nor yield efficient inference on the regression parameters.

The main contribution of this article is twofold. First, our formulation offers the first unified approach for estimating the conditional quantile of the survival time under a variety of biased sampling schemes, including, in particular, length-biased sampling, case-cohort, and stratified case-cohort designs. We prove that the proposed estimators are consistent and asymptotically normal. We establish the theory of the regression coefficient estimate as a process of the quantile index while the majority of the literature discusses inference for a fixed (set of) quantiles. Resampling methods are also proposed to construct confidence intervals and the consistency of the bootstrapping procedure is justified. Second, we show that the efficiency of the proposed estimation procedure can be improved by incorporating additional knowledge about the bias sampling mechanism. Using length-biased sampling as an example, we demonstrate that an efficient estimate can be obtained by combining estimating equations via the generalized method of moments (GMM; Hansen 1982). Compared with Chen and Zhou (2012) and Wang and Wang (2014), the new approach avoids estimating the nuisance censoring time distribution, which can be challenging in the case of covariate-dependent censoring.

From the application perspective, the unified solution is expected to benefit a wide range of applications with different types of biased samples. The codes for simulations and numerical studies, composed in MATLAB, are available upon request.

The rest of the article is organized as follows. In Section 2.1, we motivate the procedure using complete data without censoring. In Section 2.2, we present a unified framework for the censored data under biased sampling; in Section 3 we discuss in detail length-biased and right-censored data and demonstrate how to improve the estimation efficiency by GMM. Theoretical properties are studied in Section 4. Sections 5 and 6 present the simulation results and real datasets analysis, respectively. Section 7 concludes the article. All the technical proofs are presented in the supplementary material.

2. Quantile Regression Under Biased Sampling

2.1 Complete Data Without Censoring

We first consider the ideal case where the survival time is observed for all subjects. Not only does this serve to motivate the more technically involved censoring case in Section 2.2 but also is of independent interest, see, for example, the applications in Robbins and Zhang (1988), Sun and Woodroofe (1991), Gilbert (2000), and Efromovich (2004).

Let T^* and Z^* denote the survival time and the p-dimensional vector of covariates of the target population. For τ ∈ (0, 1), the conditional quantile function of T^* given Z^* = z is defined as Q(τ | z) = inf{t: P(T^* ≤ t | Z^* = z) ≥ τ }. We consider the following quantile regression model

$$Q(\tau \mid \mathbf{z})=exp\{{\mathbf{z}}^{\top }{\mathit{\beta }}_0(\tau )\},\text{for}\tau \in (0,1),$$ (1)

where β₀(τ) is the vector of unknown quantile regression coefficients describing the effects of covariates Z^* on the τ th quantile of log T^*. Compared with the AFT model and the Cox model, the quantile regression model (1) is more flexible in the sense that the covariate effect is not restricted to be constant across different τ ‘s.

Denote the conditional density, hazard, and cumulative hazard functions of T^* given Z^* = z by f (t | z), λ(t | z), and Λ(t | z), respectively. We use A^*, whenever applicable, to denote the time from the initiation event, such as the onset of a disease, to sampling. Note that A^* is often referred to as the truncation time. Let T, A, and Z be the observed survival time, truncation time, and covariate vector under a biased sampling scheme, and let f_T (t | Z) denote the conditional density of T given the covariate Z.

The observed data consist of n iid replicates of (T, Z, A), denoted by (T_i, Z_i, A_i), for i = 1, …, n. We consider a general biased sampling scheme (e.g., Kim et al. 2013) where the density ratio f_T (t | Z)/f (t | Z) is well-defined on the support of T^* and there exists a function w(t) such that

$$f_T(t\mid \mathbf{Z})=\frac{w(t)f(t\mid \mathbf{Z})}{\int w(s)f(s\mid \mathbf{Z})ds}.$$ (2)

Here the weight function w(t) is known for a given study design; moreover, it describes the sampling bias of an observation, that is, it specifies the relationship between the distribution of the survival time T^* in the target population and that of the observed survival time T.

For random variables (T^*, Z^*) of the target population, it is straightforward to show that the stochastic process $I(T^{\ast }\le t)-{\int }_0^{t}I(T^{\ast }\ge t)d\mathrm{\Lambda }(t\mid {\mathbf{Z}}^{\ast })$ is a martingale with respect to the σ-filtration ℱ_t containing information up to time t. Hence, we have

$$E\{dI(T^{\ast }\le t)-I(T^{\ast }\ge t)d\mathrm{\Lambda }(t\mid {\mathbf{Z}}^{\ast })\mid {\mathbf{Z}}^{\ast }\}=0,$$ (3)

where the expectation is taken with respect to the conditional distribution of T^* given Z^*. As a result, in the absence of sampling bias, we can construct consistent estimation procedures based on Andersen et al. (1993). Under biased sampling, however, replacing T^* with T yields biased estimation. As suggested by the following lemma, unbiased estimating equations can be constructed by weighing the observations inversely proportional to the sampling weight.

Lemma 1

Under the biased sampling scheme specified in (2), we have

$$E_{\mathbf{Z}}\{dI(T\le t)-v(t)I(T\ge t)d\mathrm{\Lambda }(t\mid \mathbf{Z})\}=0,$$ (4)

where v(·), the weight function, is

$$v(t)=\frac{w(t)}{w(T)},$$ (5)

and, for ease of notation, the conditional expectation E_Z is taken with respect to biased sampling distribution f_T (· | Z) given covariates Z.

Equation (4) serves as a basis for constructing unbiased estimating equations for a general family of biased sampling schemes. In particular, setting v_i(t) = w(t)/w(T_i), we have the estimating equations

$$n^{-1/2}\sum _{i=1}^n{\mathbf{Z}}_i\left\{I(T_i\le t)-{\int }_0^t{v}_i(s)I(T_i\ge s)d\mathrm{\Lambda }(s\mid {\mathbf{Z}}_i)\right\}=0.$$

Under the quantile regression model (1), we have $\mathrm{\Lambda }(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(\tau )}\mid {\mathbf{Z}}_i)=-log(1-\tau )$ for τ ∈ (0, 1). As in Peng and Huang (2008), replacing t with $e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(\tau )}$ in the foregoing estimating equation yields

$$S_n(\mathit{\beta },\tau )=n^{-1/2}\sum _{i=1}^n{\mathbf{Z}}_i\left\{I(T_i\le e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(\tau )})-{\int }_0^{\tau }{v}_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(s)})I(T_i\ge e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(s)})dH(s)\right\}=0,$$ (6)

with H(s) = −log(1 − s) for 0 ≤ s < 1.

If additional knowledge is available about the biased sampling mechanism, other choices of the weight function based on (5) may be used to derive a more efficient estimator (Section 3). We consider the following example for an illustration.

Example 1 (Left truncation)

Left truncation occurs when individuals come under observation only when they are event free before the truncation time A^*, that is, T^* ≥ A^*. Here A^* is usually assumed to be conditionally independent of T^* given Z^* (Kalbfleisch and Prentice 2002, p. 14). Under left-truncation, we have

$$f_T(t\mid \mathbf{Z},A)=\frac{I(t\ge A)f(t\mid \mathbf{Z})}{\int I(s\ge A)f(s\mid \mathbf{Z})ds}.$$ (7)

Thus the weight function is given by w(t) = I(t ≥ A) and, by noting that w(T_i) = I(T_i ≥ A_i) = 1 in the observed data, we have v_i(t) = I(t ≥ A_i).

In the special case of length-biased sampling, where the truncation time A^* is uniformly distributed, the residual lifetime T_i − A_i and the truncation time A_i have an exchangeable joint distribution (Vardi 1989). By exploiting this special structure, we can show that

$$\begin{gathered} E_{\mathbf{Z}}\{dI(T_i\le t)\}=E_{\mathbf{Z}}\{I(t\ge A_i)I(T_i\ge t)d\mathrm{\Lambda }(t\mid {\mathbf{Z}}_i)\} \\ =E_{\mathbf{Z}}\{I(t\ge T_i-A_i)I(T_i\ge t)d\mathrm{\Lambda }(t\mid {\mathbf{Z}}_i)\}. \end{gathered}$$

It follows that, for any π ∈ [0, 1], setting v_i(t) = πI(t ≥ A_i) + (1 − π)I(t ≥ T_i − A_i) in (6) yields unbiased estimating equations. Further discussion of this example under right censoring is given in Section 3.1.

2.2 Proposed Method for Censored Data Under Biased Sampling

We now consider the more challenging case where the survival time is subject to right censoring. Similar to Section 2.1, we denote by T^* the survival time in the target population and by C^* the censoring time, where T^* and C^* are assumed to be conditionally independent given the covariates Z^* and the possible truncation time A^*. For left-truncated and right censored data, one can conceptually define C^* to be the sum of the underlying truncation time A^* and the independent censoring time that terminates the observation of the residual lifetime beyond A^* (see Section 3.1 for more details). Let T̃^* = min(T^*, C^*) and Δ^* = I(T^* ≤ C^*). The conditional density function of (T̃^*,Δ^*), given the corresponding covariates Z^*, is denoted as f_T̃^*,Δ^* (t, δ | Z^*) for t ≥ 0 and δ ∈ {0, 1}.

Under a biased sampling scheme, let T and C be the corresponding survival and censoring times, respectively. Note that (T, C) has a different distribution from that of (T^*, C^*) due to the sampling bias.

We define T̃ = min(T, C) and Δ = I(T ≤ C). We assume that the conditional “mixed” joint density of (T̃,Δ) given Z (and possible truncation time A), f_T̃,Δ(t, δ | Z), satisfies

$$f_{\stackrel{\sim }{T},\mathrm{\Delta }}(t,\delta \mid \mathbf{Z})=\frac{w(t,\delta )f_{{\stackrel{\sim }{T}}^{\ast },{\mathrm{\Delta }}^{\ast }}(t,\delta \mid \mathbf{Z})}{{\sum }_{d\in \{0,1\}}\int w(s,d)f_{{\stackrel{\sim }{T}}^{\ast },{\mathrm{\Delta }}^{\ast }}(s,d\mid \mathbf{Z})ds},$$ (8)

where w(s, δ) is the bias function for sampling. This generalizes the setup in Section 2.1 to incorporate right censoring. Many common forms of biased sampling settings fall under the proposed framework, which includes left-truncation, case-cohort sampling, stratified case-cohort sampling, and others; see Examples 2–4 below. Formulation (8) resembles the setting of Kim et al. (2013), which, however, did not consider the length-biased sampling studied in Wang (1991), Asgharian et al. (2002), Shen et al. (2009), and many others. We consider the length-biased sampling, an important special case under our framework, in Section 3. More importantly, based on the proposed framework, we will further study efficient estimation of the model parameters.

As a generalization of (3), (T̃^*, Δ^*, Z^*) in the target population satisfies

$$E\{d{\mathrm{\Delta }}^{\ast }I({\stackrel{\sim }{T}}^{\ast }\le t)-I({\stackrel{\sim }{T}}^{\ast }\ge t)d\mathrm{\Lambda }(t\mid {\mathbf{Z}}^{\ast })\mid {\mathbf{Z}}^{\ast }\}=0,$$

where the expectation is taken with respect to (T^*,Δ^*) given Z^* and, as defined in Section 2.1, Λ(t | Z^*) denotes the cumulative hazard function of T^* given Z^* (Andersen et al. 1993). We aim at constructing the weight function v_i(t) such that the above equation still holds with (T^*,Δ^*) replaced by (T, Δ). Let Y_i(t) = I(T̃_i ≥ t) and N_i(t) = Δ_iI(T̃_i ≤ t), i = 1, …, n.

Lemma 2

Under the biased sampling scheme in (8), we have

$$E_{\mathbf{Z}}\{dN(t)\}=E_{\mathbf{Z}}\{v(t)Y(t)d\mathrm{\Lambda }(t\mid \mathbf{Z})\},$$

where v(·), the weight function, is given by

$$v(t)=\frac{w(t,1)}{w(\stackrel{\sim }{T},\mathrm{\Delta })}=\frac{f_{{\stackrel{\sim }{T}}^{\ast },{\mathrm{\Delta }}^{\ast }}(\stackrel{\sim }{T},\mathrm{\Delta }\mid \mathbf{Z})}{f_{\stackrel{\sim }{T},\mathrm{\Delta }}(\stackrel{\sim }{T},\mathrm{\Delta }\mid \mathbf{Z})}\times \frac{f_{\stackrel{\sim }{T},\mathrm{\Delta }}(t,1,\mathbf{Z})}{f_{{\stackrel{\sim }{T}}^{\ast },{\mathrm{\Delta }}^{\ast }}(t,1\mid \mathbf{Z})},$$ (9)

and E_Z is the expectation with respect to biased sampling distribution f_T̃,Δ conditional on Z.

In the absence of censoring, that is, C = ∞, we have (T̃,Δ) ≡ (T, 1) and therefore v(·) reduces to the form in Lemma 1. When v_i(t) = w(t, 1)/w(T̃_i, Δ_i) for i = 1, …, n, we can write

$$E_{\mathbf{Z}}\left[n^{-1/2}\sum _{i=1}^n{\mathbf{Z}}_i\left\{N_i(e^{{\mathbf{Z}}_i^{\top }{\mathit{\beta }}_0(\tau )})-{\int }_0^{e^{{\mathbf{Z}}_i^{\top }{\mathit{\beta }}_0(\tau )}}{v}_i(t)Y_i(t)d\mathrm{\Lambda }(t\mid {\mathbf{Z}}_i)\right\}\right]=0.$$

A change of variable gives

$$E_{\mathbf{Z}}\left[n^{-1/2}\sum _{i=1}^n{\mathbf{Z}}_i\left\{N_i(e^{{\mathbf{Z}}_i^{\top }{\mathit{\beta }}_0(\tau )}){\int }_0^{\tau }{v}_i(e^{{\mathbf{Z}}_i^{\top }{\mathit{\beta }}_0(s)})Y_i(e^{{\mathbf{Z}}_i^{\top }{\mathit{\beta }}_0(s)})dH(s)\right\}\right]=0.$$

This leads to the following unbiased estimating equations

$$S_n(\mathit{\beta },\tau )=n^{-1/2}\sum _{i=1}^n{\mathbf{Z}}_i\left\{N_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(\tau )})-{\int }_0^{\tau }{v}_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(s)})Y_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(s)})dH(s)\right\}=0.$$ (10)

The weight function (9) provides a systematic way to construct the estimating equations for many biased sampling schemes. We consider some examples below for illustration.

Example 2 (Left truncation and right censoring)

Consider the left truncation setting in Example 1. Conditional on the truncation time A, we have

$$f_{\stackrel{\sim }{T},\mathrm{\Delta }}(t,\delta \mid \mathbf{Z})=\frac{I(A\le t)f_{{\stackrel{\sim }{T}}^{\ast },{\mathrm{\Delta }}^{\ast }}(t,\delta \mid \mathbf{Z})}{{\sum }_{d\in \{0,1\}}\int I(A\le s)f_{{\stackrel{\sim }{T}}^{\ast },{\mathrm{\Delta }}^{\ast }}(s,d\mid \mathbf{Z})ds}.$$

Following (9), this implies v_i(t) = I(A_i ≤ t). Thus, (10) can be reexpressed as

$$S_n(\mathit{\beta },\tau )=n^{-1/2}\sum _{i=1}^n{\mathbf{Z}}_i\left\{N_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(\tau )})-{\int }_0^{\tau }I\left(A_i\le e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(s)}\right)Y_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(s)})dH(s)\right\}=0.$$

Further discussion on this example is provided in Section 3 on efficient estimation.

Example 3 (Case-cohort design)

Under the case-cohort design (Prentice 1986), complete information on covariates is collected only for uncensored observations. For censored observations, suppose that the probability of selecting a censored individual into the sub-cohort is p, p ∈ (0, 1). Under this biased sampling, the distribution of (T̃,Δ) satisfies

$$f_{\stackrel{\sim }{T},\mathrm{\Delta }}(t,\delta \mid \mathbf{Z})=\frac{\{\delta +(1-\delta )p\}{f}_{{\stackrel{\sim }{T}}^{\ast },{\mathrm{\Delta }}^{\ast }}(t,\delta \mid \mathbf{Z})}{{\sum }_{d\in \{0,1\}}\int \{d+(1-d)p\}{f}_{{\stackrel{\sim }{T}}^{\ast },{\mathrm{\Delta }}^{\ast }}(s,d\mid \mathbf{Z})ds}.$$

Following (9), v_i(t) = 1/{Δ_i + (1 −Δ_i)p}, and this gives

$$S_n(\mathit{\beta },\tau )=n^{-1/2}\sum _{i=1}^n{\mathbf{Z}}_i\left\{N_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(\tau )})-{\int }_0^{\tau }\frac{1}{{\mathrm{\Delta }}_i+(1-{\mathrm{\Delta }}_i)p}{Y}_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(s)})dH(s)\right\}=0.$$

Note that the estimating equation has the form in Zheng et al. (2013).

Example 4 (Stratified case-cohort design)

The stratified case-cohort design was proposed to improve the efficiency of the traditional case-cohort design (Borgan et al. 2000; Kulich and Lin 2004), where the probability of selecting a censored observation into the subcohort, p(X), is allowed to depend on X, a vector of covariates that may or may not overlap with Z. As in Example 3, we have

$$f_{\stackrel{\sim }{T},\mathrm{\Delta }}(t,\delta \mid \mathbf{Z})=\frac{\{\delta +(1-\delta )p(\mathbf{X})\}{f}_{{\stackrel{\sim }{T}}^{\ast },{\mathrm{\Delta }}^{\ast }}(t,\delta \mid \mathbf{Z})}{{\sum }_{d=\{0,1\}}\{d+(1-d)p(\mathbf{X})\}{f}_{{\stackrel{\sim }{T}}^{\ast },{\mathrm{\Delta }}^{\ast }}(s,d\mid \mathbf{Z})ds},$$

which implies that (10) can be constructed with v_i(t) = 1/{Δ_i + (1 − Δ_i)p(X_i)}.

2.3 Computation of β̂(τ)

The proposed estimating equations under different biased sampling schemes share the same generic form as in (10).

Motivated by Peng and Huang (2008), we adopt a grid-based algorithm. The estimator of β(τ), denoted by β̂(τ), is defined as a right-continuous piecewise-constant function that jumps only on a grid 𝒮_L(n) = {0 = τ₀ < τ₁ < ··· < τ_L(n) = τ_u < 1}, where τ_u is some constant subject to certain identifiability constraint due to censoring; see condition C4 in the supplementary materials. Note that when τ = 0, from the model assumption (1), we have 0 = Q(0 | z) = exp{z^⊤β₀(0)}. Therefore, we choose β̂(0) such that exp{z^⊤ β̂(0)} = 0. Let ||𝒮_L(n)|| = sup_1≤k≤L(n) |τ_k − τ_k⁻¹|. The estimate β̂(τ_k) is obtained by sequentially solving the following estimating equation:

$$n^{-1/2}\sum _{i=1}^n{\mathbf{Z}}_i\left\{N_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }({\tau }_k)})-\sum _{j=0}^{k-1}{v}_i(e^{{\mathbf{Z}}_i^{\top }\widehat{\mathit{\beta }}({\tau }_j)})Y_i(e^{{\mathbf{Z}}_i^{\top }\widehat{\mathit{\beta }}({\tau }_j)})\times (H({\tau }_{j+1})-H({\tau }_j))\right\}=0.$$

Following Peng and Huang (2008), the above equation can be transformed into an L₁ optimization problem that can be solved using the Barrodale–Roberts algorithm (Barroda and Roberts 1974). Alternatively, the corresponding optimization subroutine can be implemented easily in MATLAB via the function fminsearch. One practical concern is the choice of the grid size in the sequential procedure. Theoretically, as shown in the proof of Theorem 1, a grid with size of order o(n^−1/2) ensures weak convergence. In the simulation study, we adopt an equally spaced grid with size 0.01 and find it works satisfactorily for a variety of settings. Alternatively, we may adopt the estimation procedure based on estimating integral equations proposed in Huang (2010).

3. Efficiency Improvement With GMM

In this section, we show that the efficiency of the unified estimation procedure described in Section 2 can be further improved by applying the GMM method (Hansen 1982). To our best knowledge, this is the first attempt in the literature to study the efficient estimation for quantile regression under biased sampling. In Section 3.1, we consider the case where external information about the sampling mechanism is available. We use length-biased sampling as an example to illustrate how the external knowledge about the distribution of the underlying truncation time can be incorporated in the estimation of regression parameters. In Section 3.2, we focus on general biased sampling scheme and demonstrate that significant efficiency gain can be achieved by properly introducing a class of weight functions in the estimating procedure.

3.1 Efficiency Improvement Using Additional Sampling Information

When additional knowledge about the biased sampling mechanism is available, it is possible to incorporate the additional information to improve the estimation efficiency through the generalized method of moments. Here, we focus on the length-biased sampling example and demonstrate how an optimal weight function can be determined.

We write V as the residual lifetime measured from the truncation time A to failure. Suppose V is censored by C̃, where C̃ is independent of (A, V) conditional on Z, then the observed survival and censoring times, T and C, can be expressed as

$$T=A+V\text{and}C=A+\stackrel{\sim }{C}.$$

Conditional on Z, the density of T, f_T (t | Z), can be related to the conditional density of T^*, f (t | Z), under the stationarity assumption (Lancaster 1990, chap. 3)

$$f_T(t\mid \mathbf{Z})=\frac{1}{\mu (\mathbf{Z})}tf(t\mid \mathbf{Z}),$$

where μ(Z) = ∫ tf (t | Z)dt is a normalizing term. In addition, the joint distribution of A and V is (Vardi 1989)

$$f_{A,V}(a,v\mid \mathbf{Z})=\frac{1}{\mu (\mathbf{Z})}f(a+v\mid \mathbf{Z})I(a>0,v>0).$$

Denote the conditional density and survival functions of C̃ as g_c(t | Z) and S_c(t | Z):= P(C̃ > t | Z). Recall that T̃_i = min(T_i,C_i), Δ_i = I(T_i ≤ C_i), N_i(t) = Δ_iI(T̃_i ≤ t) and Y_i(t) = I(T̃_i ≥ t). As shown in Example 2, conditional on the truncation time A, we can take the weight function following (9) as

$$v_i(t)=\frac{f_{{\stackrel{\sim }{T}}^{\ast },{\mathrm{\Delta }}^{\ast }}({\stackrel{\sim }{T}}_i,{\mathrm{\Delta }}_i\mid {\mathbf{Z}}_i)}{f_{\stackrel{\sim }{T},\mathrm{\Delta }}({\stackrel{\sim }{T}}_i,{\mathrm{\Delta }}_i\mid {\mathbf{Z}}_i)}\times \frac{f_{\stackrel{\sim }{T},\mathrm{\Delta }}(t,1\mid {\mathbf{Z}}_i)}{f_{{\stackrel{\sim }{T}}^{\ast },{\mathrm{\Delta }}^{\ast }}(t,1\mid {\mathbf{Z}}_i)}=I(A_i\le t).$$ (11)

Here, we defer the derivation of (11) to the supplementary material. It follows that

$$E_{\mathbf{Z}}\{d{N}_i(t)-I(A_i\le t)Y_i(t)\mathrm{\Lambda }(t\mid {\mathbf{Z}}_i)\}=0.$$ (12)

We can also construct other weight functions under the stationarity assumption. In particular, as shown in Huang and Qin (2012),

$$E_{\mathbf{Z}}\{d{N}_i(t)-{\mathrm{\Delta }}_{i}I({\stackrel{\sim }{T}}_i-A_i\le t)Y_i(t)\mathrm{\Lambda }(t\mid {\mathbf{Z}}_i)\}=0.$$ (13)

We can, therefore, define a family of subject-specific weight functions by combining the results in (12) and (13):

$$v_i(t;\pi )=\pi I(A_i\le t)+(1-\pi ){\mathrm{\Delta }}_{i}I({\stackrel{\sim }{T}}_i-A_i\le t),$$ (14)

where π ∈ [0, 1]. It follows directly from (12) and (13) that

$$E_{\mathbf{Z}}\left[n^{-1/2}\sum _{i=1}^n{\mathbf{Z}}_i\left\{N_i(e^{{\mathbf{Z}}_i^{\top }{\mathit{\beta }}_0(\tau )})-{\int }_0^{exp\{{\mathbf{Z}}_i^{\top }{\mathit{\beta }}_0(\tau )\}}{v}_i(t;\pi )Y_i(t)d\mathrm{\Lambda }(t\mid {\mathbf{Z}}_i)\right\}\right]=0,$$ (15)

and a change of variable gives

$$E_{\mathbf{Z}}\left[n^{-1/2}\sum _{i=1}^n{\mathbf{Z}}_i\left\{N_i(e^{{\mathbf{Z}}_i^{\top }{\mathit{\beta }}_0(\tau )})-{\int }_0^{\tau }{v}_i(e^{{\mathbf{Z}}_i^{\top }{\mathit{\beta }}_0(s)};\pi )Y_i(e^{{\mathbf{Z}}_i^{\top }{\mathit{\beta }}_0(s)})dH(s)\right\}\right]=0.$$

This motivates the following estimating equations:

$$S_n(\mathit{\beta },\tau ;\pi )=n^{-1/2}\sum _{i=1}^n{\mathbf{Z}}_i\left\{N_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(\tau )})-{\int }_0^{\tau }{v}_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(s)};\pi )Y_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(s)})dH(s)\right\}=0.$$ (16)

The unbiasedness of the above estimating equation holds under covariate-dependent censoring. Moreover, the proposed method does not need a consistent estimate of the conditional censoring distribution function S_c(t|Z). This relaxation substantially reduces the computational complexity, especially when the number of covariates is not small; see the simulation studies in Section 5.

Efficiency improvement using GMM

We now apply the GMM method (Hansen 1982) to improve the estimation results. Our goal is to determine a best combination of (12) and (13) in the sense that the resulting standard error of the estimator β̂ is minimized. Let

$$\eta (\mathit{\beta },\tau )=\left(\begin{array}{c}{S}_n(\mathit{\beta },\tau ;\pi =0)\\ S_n(\mathit{\beta },\tau ;\pi =1)\end{array}\right),$$

where S_n(β, τ; π = 0) and S_n(β, τ; π = 1) are simply (16) with v_i(t; π = 0) = I(T̃_i − A_i ≤ t) and v_i(t; π = 1) = I(A_i ≤ t), respectively. The GMM estimator of β minimizes

$$\eta {(\mathit{\beta },\tau )}^{\top }W{({\widehat{\mathit{\beta }}}_{int},\tau )}^{-1}\eta (\mathit{\beta },\tau ),$$

where W is a 2p × 2p positive definite working covariance matrix, depending on the true parameter β₀(·), which is usually evaluated at some preliminary consistent estimator β̂_int(·). A simple way to get the initial estimate β̂_int(·) is to solve (16) with π = 0.5.

The asymptotically efficient estimator β̂_eff(τ) is obtained when W(β̂_int, τ) = var[η(β̂_int, τ)], that is,

$${\widehat{\mathit{\beta }}}_{\text{eff}}(\tau )=arg\underset{\mathit{\beta }}{min}\eta {(\mathit{\beta },\tau )}^{\top }var{\{\eta ({\widehat{\mathit{\beta }}}_{int},\tau )\}}^{-1}\eta (\mathit{\beta },\tau ).$$

We can estimate var{η(β̂_int, τ)} by the sample covariance matrix η(β̂_int, τ)η(β̂_int, τ)′. This data-driven approach provides a way to construct the optimal linear combination of estimating equations in η(β̂_int, τ). In Section 5, we demonstrate via simulations the improvement in efficiency by using this GMM approach.

3.2 Efficiency Improvement Using Additional Weight Functions

In this section, we show how the efficiency of the estimates can be improved for a general biased sampling scheme. It follows from Lemma 2 that

$$E_{\mathbf{Z}}\{\psi (t)dN(t)\}=E_{\mathbf{Z}}\{\psi (t)v(t)Y(t)d\mathrm{\Lambda }(t\mid \mathbf{Z})\},$$

where ψ(t) is a weight function that may depend on Z. As a result, estimating Equation (10) can be generalized as

$$n^{-1/2}\sum _{i=1}^n{\mathbf{Z}}_i\left\{\psi ({\stackrel{\sim }{T}}_i)N_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(\tau )})-{\int }_0^{\tau }\psi (e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(s)})v_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(s)})\times Y_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(s)})dH(s)\right\}=0.$$ (17)

Thus, we can construct a family of weighted estimating equations by considering different choices of ψ. The possibly data-dependent weight function ψ plays a similar role as the weight function in the rank-based estimating equations in the AFT model (Tsiatis 1990; Ying 1993; Jin et al. 2003).

Intuitively, one would consider the optimal choice of ψ that minimizes the asymptotic variance of the estimates. However, direct estimation of the optimal ψ for the quantile regression under biased sampling is very challenging. This is mainly due to two reasons. First, the optimal ψ involves the derivative of the unknown density function of the failure time. Although estimation of the derivative in the absence of biased sampling has been studied under the AFT model (e.g., Lin and Chen 2013), a special case of the model (1), the heterogeneity effects of the covariates under the quantile regression make the problem much more complicated and challenging. Kernel smoothing techniques may be applied, but their performance can be poor when there are more than a few covariates and/or there is a large number of quantiles that need to be estimated. Second, the optimal ψ also depends on the sampling weight function v. This makes ψ a study-specific function for different biased sampling schemes and further complicates the derivation of the optimal ψ. Even for the special case of the AFT model, the optimal weight has not yet been established in the literature.

To this end, we propose a computationally efficient and robust method to improve the estimation efficiency. Equation (17) provides different estimating equations for β and, as before, we can apply the GMM method to improve the estimation from (10).

In particular, consider K weight functions and denote ψ(t) = {ψ₁(t), …, ψ_K (t)}^⊤. Let η(β, τ) be the estimating equations for the given sets of weights, that is,

$$\eta (\mathit{\beta },\tau )=n^{-1/2}\sum _{i=1}^n{\mathbf{Z}}_i\otimes \left\{\mathit{\psi }({\stackrel{\sim }{T}}_i)N_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(\tau )})-{\int }_0^{\tau }\mathit{\psi }(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(s)})v_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(s)})Y_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(s)})dH(s)\right\},$$ (18)

where ⊗ is the Kronecker product. The GMM estimator of β(τ) minimizes

$$\eta {(\mathit{\beta },\tau )}^{\top }W{({\widehat{\mathit{\beta }}}_{int},\tau )}^{-1}\eta (\mathit{\beta },\tau ),$$

where W is a positive definite working covariance matrix, depending on some initial estimator β̂_int(·). A simple way to get β̂_int(·) is to use the estimator from the unweighted estimating equation. Then the asymptotically efficient estimator of β(τ), denoted by β̂_eff(τ), is obtained as

$${\widehat{\mathit{\beta }}}_{\text{eff}}(\tau )=arg\underset{\mathit{\beta }}{min}\eta {(\mathit{\beta },\tau )}^{\top }var{\{\eta ({\widehat{\mathit{\beta }}}_{int},\tau )\}}^{-1}\eta (\mathit{\beta },\tau ).$$ (19)

We again adopt a grid-based algorithm to solve β̂_eff(τ). Specifically, consider the efficient estimator β̂_eff(τ) at a fixed τ. In the grid 𝒮_L(n) = {0 = τ₀ < τ₁ < ··· < τ_L(n) = τ_u < 1} used to solve the unweighted estimating equation, there is τ_L^*∈ 𝒮_L(n) such that τ_L^*≤ τ < τ_L^*+1. For 0 = τ₀ < τ₁ < ··· < τ_L^*, we define

$${\eta }^{\ast }(\mathit{\beta },{\tau }_k)=n^{-1/2}\sum _{i=1}^n{\mathbf{Z}}_i\otimes \left\{\mathit{\psi }({\stackrel{\sim }{T}}_i)N_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }({\tau }_k)})-\sum _{j=0}^{k-1}\mathit{\psi }(e^{{\mathbf{Z}}_i^{\top }\widehat{\mathit{\beta }}({\tau }_j)})\times v_i(e^{{\mathbf{Z}}_i^{\top }\widehat{\mathit{\beta }}({\tau }_j)})Y_i(e^{{\mathbf{Z}}_i^{\top }\widehat{\mathit{\beta }}({\tau }_j)})\{H({\tau }_{j+1}-H({\tau }_j)\}\right\}.$$ (20)

To estimate β̂_eff(τ), we choose β̂_eff(0) such that exp{z^⊤ β̂_eff(0)} = 0 and then sequentially estimate β̂_eff(τ_k), 1 ≤ k ≤ L^*, by minimizing

$${\eta }^{\ast }{(\mathit{\beta },{\tau }_k)}^{\top }W{({\widehat{\mathit{\beta }}}_{int},\tau )}^{-1}{\eta }^{\ast }(\mathit{\beta },{\tau }_k).$$

Finally, we have efficient estimator for β̂_eff(τ) as β̂_eff(τ_L^*).

Remark 1

The proposed approach uses a combination of K weight functions {ψ₁(t), …, ψ_K (t)} to approximate the optimal weight function ψ^*. In practice, we may take simple polynomial functions of t for ψ’s. As K increases, the method is expected to provide a better approximation for ψ^* while introducing additional estimation variation and higher computational cost. In Section 5, we illustrate through simulations the efficiency improvement.

Remark 2

For the length biased sampling, under the stationarity assumption, we can also construct estimating equations using an unconditional approach, which takes the expectation with respect to V and A.

We consider an unconditional version of the weight function v_i. Note that setting the weight function ${\int }_0^t{S}_c(s\mid {\mathbf{Z}}_i)ds$ in estimating Equation (17) yields

$$\begin{gathered} E_{\mathbf{Z}}\left[\frac{N_i(e^{{\mathbf{Z}}_i^{\top }{\mathit{\beta }}_0(\tau )})}{{\int }_0^{{\stackrel{\sim }{T}}_i}{S}_c(s\mid {\mathbf{Z}}_i)ds}\right]=E_{\mathbf{Z}}\left\{{\int }_0^{exp({\mathbf{Z}}_i^{\top }{\mathit{\beta }}_0(\tau ))}\frac{1}{{\int }_0^t{S}_c(s\mid {\mathbf{Z}}_i)ds}{v}_i(t)Y_i(t)d\mathrm{\Lambda }(t\mid {\mathbf{Z}}_i)\right\} \\ =\frac{\tau }{\mu ({\mathbf{Z}}_i)}=E_{\mathbf{Z}}\left\{\frac{{\mathrm{\Delta }}_i\tau }{{\int }_0^{{\stackrel{\sim }{T}}_i}{S}_c(s\mid {\mathbf{Z}}_i)ds}\right\}. \end{gathered}$$

This leads to the estimating equation

$$\sum _{i=1}^n\frac{{\mathbf{Z}}_i{\mathrm{\Delta }}_i}{{\int }_0^{{\stackrel{\sim }{T}}_i}{S}_c(s\mid {\mathbf{Z}}_i)ds}\left\{N_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(\tau )})-\tau \right\}=0,$$

which is the estimation procedure proposed in Wang and Wang (2014). Similarly, for π = 1, it follows from

$$E_{\mathbf{Z}}\left[\frac{1}{t{S}_c(t-A_i\mid {\mathbf{Z}}_i)}\{d{N}_i(t)-v_i(t)Y_i(t)d\mathrm{\Lambda }(t\mid {\mathbf{Z}}_i)\}\right]=0$$

and

$$\begin{gathered} E_{\mathbf{Z}}\left\{{\int }_0^{exp({\mathbf{Z}}_i^{\top }{\mathit{\beta }}_0(\tau ))}\frac{v_i(t)Y_i(t)}{t{S}_c(t-A_i\mid {\mathbf{Z}}_i)}d\mathrm{\Lambda }(t\mid {\mathbf{Z}}_i)\right\}=\frac{\tau }{\mu ({\mathbf{Z}}_i)} \\ =E_{\mathbf{Z}}\left\{\frac{{\mathrm{\Delta }}_i\tau }{{\stackrel{\sim }{T}}_i{S}_c({\stackrel{\sim }{T}}_i-A_i\mid {\mathbf{Z}}_i)}\right\} \end{gathered}$$

that

$$\sum _{i=1}^n\frac{{\mathbf{Z}}_i{\mathrm{\Delta }}_i}{{\stackrel{\sim }{T}}_i{S}_c({\stackrel{\sim }{T}}_i-A_i\mid {\mathbf{Z}}_i)}\{N_i(e^{{\mathbf{Z}}_i^{\top }\mathit{\beta }(\tau )})-\tau \}=0.$$

We can combine the above unconditional estimating equation with that proposed in the previous section by applying the GMM method. However, a consistent estimator for the censoring distribution S_c(· | Z) is required for this unconditional estimation procedure. This introduces additional complexity of the estimation procedure. Hence, we do not further pursue the unconditional approach in this article.

4. Large-Sample Properties and Statistical Inference

4.1 Asymptotic Properties

We first establish the uniform consistency and weak convergence of the estimator β̂(τ) given in (10) of Section 2.2 for the general biased sampling scheme. Applying empirical processes techniques, we investigate the large-sample behavior of β̂(τ) as a process of τ. The results are summarized in Theorem 1.

Theorem1

Assume that Conditions C1–C5 (stated in the online supplemental material) hold. If lim_n→∞ ||𝒮_L(n)|| = 0, for any τ_l ∈ (0, τ_u), then sup_{τ∈[τℓ,τu]} ||β̂(τ) − β₀(τ)|| → 0 in probability. In addition, if lim_n→∞ n^1/2 ||𝒮_L(n)|| = 0, then n^1/2{β̂(τ) − β₀(τ)} converges weakly to a Gaussian process for τ ∈ [τ_ℓ, τ_u].

The covariance structure of the aforementioned Gaussian process and the proof of Theorem 1 are given in the online supplemental materials. Next, we state in Theorem 2 the large-sample property of the proposed efficient estimator described in Section 3.2.

Theorem 2

Consider the GMM efficient estimator given in (19) at τ ∈ [τ_ℓ, τ_u]. Under Conditions C1–C6, n^1/2{β̂_eff(τ) − β₀(τ)} converges weakly to a multivariate normal distribution.

Remark 3

Although a sequential procedure (Sections 2.3 and 3.2) is used to estimate the quantile regression coefficients, similarly to Peng and Huang (2008), the numerical instability of β(τ) at small τ has little impact on the estimation at larger τ ‘s; see, for example, Lai and Ying (1988) for a study of tail instability.

4.2 A New Resampling Procedure for Inference

In this section, we propose a new resampling approach that provides a consistent estimator of the asymptotic covariance matrix (Theorem 3). The resampling method avoids the difficulty of estimating the unknown density functions of both the survival time and the censoring times in the asymptotic covariance matrix. It has the flavor of the perturbation approach of Jin et al. (2003) and Peng and Huang (2008), but enjoys the novel feature that it does not require to repeatedly solve estimating equations. In particular, it is considerably faster than a more straightforward resampling method (described in online supplementary materials) that directly extends the perturbation idea and needs to calculate the estimation path β̂^*(·) many times.

To describe the new resampling procedure, we first introduce some notation. For b ∈ ℝ^p, define

$$\begin{gathered} m(\mathbf{b})=E\{\mathbf{Z}N(e^{{\mathbf{Z}}^{\top }\mathbf{b}})\},m_n(\mathbf{b})=\frac{1}{n}\sum _{i=1}^n\left\{{\mathbf{Z}}_i{N}_i(e^{{\mathbf{Z}}_i^{\top }\mathbf{b}})\right\}, \\ \stackrel{\sim }{m}(\mathbf{b})=E\left\{\mathbf{Z}v(e^{{\mathbf{Z}}^{\top }\mathbf{b}})Y(e^{{\mathbf{Z}}^{\top }\mathbf{b}})\right\}, \\ {\stackrel{\sim }{m}}_n(\mathbf{b})=\frac{1}{n}\sum _{i=1}^n\left\{{\mathbf{Z}}_i{v}_i(e^{{\mathbf{Z}}_i^{\top }\mathbf{b}})Y_i(e^{{\mathbf{Z}}_i^{\top }\mathbf{b}})\right\}, \\ \mathbf{B}(\mathbf{b})=E\{{\mathbf{Z}}^{\otimes 2}{f}_{\stackrel{\sim }{T},\mathrm{\Delta }}(e^{{\mathbf{Z}}^{\top }\mathbf{b}},1\mid \mathbf{Z})exp({\mathbf{Z}}^{\top }\mathbf{b})\}, \\ \mathbf{J}(\mathbf{b})=-E\{{\mathbf{Z}}^{\otimes 2}v(e^{{\mathbf{Z}}^{\top }\mathbf{b}})f_{\stackrel{\sim }{T}}(e^{{\mathbf{Z}}^{\top }\mathbf{b}}\mid \mathbf{Z})exp({\mathbf{Z}}^{\top }\mathbf{b})\}. \end{gathered}$$

The new method is motivated by the theoretical property of the estimating equation. From Equation (S5) in the online supplemental materials, we can write

$$n^{1/2}[m\{\widehat{\mathit{\beta }}(\tau )\}-m\{{\mathit{\beta }}_0(\tau )\}]=\varphi \{-S_n({\mathit{\beta }}_0,\tau )\}+o_p(1).$$

where ϕ(g)(τ) is defined in (S6) in the online supplement. Theorem 1 shows that $\sqrt{n}\{\widehat{\mathit{\beta }}(\tau )-{\mathit{\beta }}_0(\tau )\}$ converges weakly to a Gaussian process with covariance matrix B{β₀(τ)}⁻¹ Σ^*[B{β₀(τ)}⁻¹]^⊤, where Σ^*(τ) denotes the limiting covariance matrix of n^1/2[m{β̂(τ)} − m{β₀(τ)}]. To evaluate the limiting distribution of $\sqrt{n}[\widehat{\mathit{\beta }}(\tau )-{\mathit{\beta }}_0(\tau )]$, one can estimate B{β₀(τ)} and the distribution of n^1/2[m{β̂(τ)} − m{β₀(τ)}] as follows.

1. Estimation of B{β₀(τ)}. Motivated by Zeng and Lin (2008), we use a perturbation method to estimate B{β₀(τ)}, which is the slope of m_n(·) with respect to β(τ). Specifically, M independent multivariate standard normal variables {γ_i}_i=1,...,M are generated to serve as the perturbations on the estimated β̂(τ). These perturbed values n^1/2m_n{β̂(τ) + n^−1/2γ_i} will then be regressed on γ_i. The resulting slope matrix B̂{β̂(τ)}, whose jth row is the jth least square slope estimate, is a consistent estimator of B{β₀(τ)}.

2. Estimation of the distribution of n^1/2[m{β̂(τ)} − m{β₀(τ)}]. We derive the following approximation result for ϕ{−S_n(β₀, τ)} (see (S4) in the online supplementary materials)

   $$\begin{gathered} n^{1/2}[m\{\widehat{\mathit{\beta }}(\tau )\}-m\{{\mathit{\beta }}_0(\tau )\}]=-\{S_n({\mathit{\beta }}_0,{\tau }_k)-S_n({\mathit{\beta }}_0,{\tau }_{k-1})\}-\sum _{\ell =2}^k\prod _{h=\ell }^k[\mathbf{I}+\mathbf{J}\{{\mathit{\beta }}_0({\tau }_{h-1}){\mathbf{B}}^{-1}\{{\mathit{\beta }}_0({\tau }_{h-1})\}\}\{H({\tau }_h)-H({\tau }_{h-1})\}]\{S_n({\mathit{\beta }}_0,{\tau }_{h-1})-S_n({\mathit{\beta }}_0,{\tau }_{h-2})\}+o_p(1) \\ \triangleq {\varphi }_n\{-S_n({\mathit{\beta }}_0,\tau )\}+o_p(1). \end{gathered}$$ (21)

   The approximation holds uniformly in τ. As a result, we can use the distribution of ϕ_n{−S_n(β₀, τ)} to estimate that of n^1/2[m{β̂ (τ)} − m{β₀(τ)}]. The expression (21) of ϕ_n{−S_n(β₀, τ)} involves the unknown matrices B and J. As in Step (i), we can get estimates for B(β₀(τ_h)) and J(β₀(τ_h)), h = 1, . . . , k, by applying the perturbation method for m_n(·) and m̃_n(·), respectively. With the estimates of B and J, we use the perturbed estimating functions S̃_n(β̂, τ) to construct an estimator of the distribution of ϕ_n{−S_n(β₀, τ)}. Specifically, we show in the proof of Theorem 3 that ϕ_n{−S̃_n(β̂, τ)} has the same limiting distribution as ϕ_n{−S_n(β₀, τ)}. Then we generate M_b (some large number) replicates of S̃_n(β̂, τ) and use the corresponding empirical distribution of ϕ_n{−S̃_n(β̂, τ)} to estimate that of ϕ_n{−S_n(β₀, τ)}.

Combining (i) and (ii), we can use the distribution of B̂{β̂(τ)}⁻¹ ϕ_n{−S̃_n(β̂, τ)} as an estimator of that of $\sqrt{n}\{\widehat{\mathit{\beta }}(\tau )-{\mathit{\beta }}_0(\tau )\}$. We present the following result that validates inference based on such resampling procedure.

Theorem 3

Assume Conditions C1–C5 are satisfied. Conditional on the observed data, B̂ {β̂ (τ)}⁻¹ ϕ_n{−S̃_n(β̂, τ)} converges weakly to the same limiting process of n^1/2{β̂(τ) − β₀(τ)} for τ ∈ [τ_ℓ, τ_u], where τ_ℓ ∈ (0, τ_u).

Remark 4

Unlike existing resampling approaches, such as Jin et al. (2003) and Peng and Huang (2008), our new method does not require to repeatedly solve the estimating equations, which is quite time consuming in the sequential optimization of the estimating equations; thus our method is computationally fast. The consistency of the proposed resampling method is established in Theorem 3 and we can use the resampling percentiles to construct confidence intervals for β₀. It is worth mentioning that in general, the weak convergence of the resampling estimates may not directly imply the convergence the bootstrapped moments, such as the covariance matrix, and additional regularity conditions may be needed to establish such convergence (see, e.g., Kato 2011; Cheng 2015).

Remark 5

At the beginning with small τ values, the estimates for B̂ and Ĵ matrices may not be stable due to the small sample size. In this case, for small τ values, we may apply the perturbed resampling method (described in online supplementary materials) while for larger values, we adopt the introduced new estimation procedure.

5. Simulation Studies

Length-biased Sampling

In the first set of simulations, we consider length-biased sampling. We generate the survival time from the following log-linear model

$$log{T}^{\ast }=Z_1{\beta }_1+Z_2{\beta }_2+(1+\gamma Z_1)\epsilon ,$$

where ε follows a normal distribution and γ controls the level of heteroscedasticity. In particular, if γ is 0, the above model reduces to the classical accelerated failure time model. The corresponding conditional quantile function is

$$Q_{log(T^{\ast })}(\tau \mid \mathbf{Z})={\beta }_{(0)}(\tau )+Z_1{\beta }_{(1)}(\tau )+Z_2{\beta }_{(2)}(\tau ),$$

where Z = (Z₁, Z₂)′, β₍₀₎(τ) = Q(τ), β₍₁₎(τ) = β₁ + γQ(τ) = 1 + γQ(τ), β₍₂₎(τ) = β₂ = −1, and Q(τ) denotes the τth quantile of ε. We generate Z₁ from a Bernoulli distribution with P(Z₁ = 1) = 0.5 and Z₂ from a uniform distribution, Unif(−0.5, 0.5). The initiation time A is generated from the Unif(0, u_A) distribution, where u_A > 0 is a constant that exceeds the upper bound of T^* such that P(T^* ∈ (t ± δ) | A < T^*) = 0 for t > u_A and a small δ > 0. We only retain the pairs with T^* > A, which results in the length-biased sample T_i = A_i +V_i for i = 1, . . . , n. Due to the conditionally independent censoring, only T̃_i = min(T_i,C_i) = A_i + min(V_i,C̃_i) can be observed, for i = 1, . . . , n.

In our study, γ is set as 1; ε is generated from a normal distribution N(0, 0.5²); u_A is set to be 50; and C̃_i is generated from an exponential distribution with rate [1 − 0.9I(Z₂ > 0)]λ. The value of λ is chosen according to the prespecified censoring proportions, 20% and 40%. We consider the weight function specified in (14) and summarize in Table 1 the results for different values of π’s (with π_eff corresponding to the GMM estimator) when the censoring rate is 20%.

Table 1.

Simulation results for length-biased data (20% censoring rate) for different values of π(π_eff corresponds to the GMM estimator). Bias: average bias of the estimate; SE: average variance of the estimate; MSE: mean squared error of the estimate.

π	τ	Estimators	n = 200			n = 400
			Bias	SE	MSE	Bias	SE	MSE
0.00	0.25	β̂(0)(τ)	−0.033	0.297	0.089	−0.047	0.184	0.036
		β̂(1)(τ)	−0.087	0.511	0.269	0.032	0.346	0.121
		β̂(2)(τ)	0.022	0.308	0.095	0.002	0.176	0.031
	0.50	β̂(0)(τ)	−0.026	0.226	0.052	−0.020	0.108	0.012
		β̂(1)(τ)	−0.054	0.356	0.129	0.009	0.234	0.055
		β̂(2)(τ)	0.021	0.243	0.059	−0.001	0.125	0.016
0.50	0.25	β̂(0)(τ)	−0.023	0.254	0.065	−0.030	0.174	0.031
		β̂(1)(τ)	−0.062	0.481	0.236	0.011	0.334	0.112
		β̂(2)(τ)	0.005	0.260	0.068	−0.008	0.169	0.029
	0.50	β̂(0)(τ)	−0.014	0.142	0.020	−0.012	0.115	0.013
		β̂(1)(τ)	−0.034	0.319	0.103	0.000	0.231	0.053
		β̂(2)(τ)	0.008	0.167	0.028	−0.009	0.123	0.015
1.00	0.25	β̂(0)(τ)	−0.048	0.287	0.084	−0.035	0.191	0.038
		β̂(1)(τ)	−0.046	0.582	0.341	−0.019	0.365	0.133
		β̂(2)(τ)	0.016	0.286	0.082	0.010	0.191	0.036
	0.50	β̂(0)(τ)	−0.027	0.168	0.029	−0.014	0.123	0.015
		β̂(1)(τ)	−0.028	0.353	0.125	−0.009	0.253	0.064
		β̂(2)(τ)	0.014	0.203	0.041	0.001	0.128	0.016
πeff	0.25	β̂(0)(τ)	−0.044	0.198	0.041	−0.045	0.154	0.026
		β̂(1)(τ)	0.039	0.389	0.153	−0.090	0.304	0.100
		β̂(2)(τ)	−0.036	0.176	0.032	0.078	0.130	0.023
	0.50	β̂(0)(τ)	0.010	0.136	0.019	−0.009	0.091	0.008
		β̂(1)(τ)	0.067	0.263	0.073	−0.085	0.210	0.051
		β̂(2)(τ)	−0.076	0.124	0.021	0.041	0.100	0.012

We observe that the choice of π does not affect the biases of the estimators significantly. However, the standard error associated with the GMM estimator is lower than that of their counterparts evaluated at other values of π, say at π = 0.00, 0.50, or 1.00. In other words, the GMM procedure improves the efficiency of the proposed estimator. We observe that the performance of the estimator with π = 0.5 is similar to that of the GMM estimator. In the remaining numerical study, for computational simplicity with length-biased data, we adopt π = 0.5 and find it works well in various scenarios. Note that π = 0.5 has an interpretation of striking a good balance between the two estimating equations (12) and (13), which are set for adjusting biases due to left-truncation and right censoring, respectively. We also observe that the perturbation approach provides a satisfactory estimate of the standard error of the proposed estimator.

In addition to bias, standard error, and mean squared error, Table 2 also summarizes the estimated standard error (SEE) based on the perturbation approach illustrated in Section 4 as well as the empirical coverage of the 95% Wald-type confidence intervals. For the resampling scheme, M_b is set to be 500 to estimate the asymptotic variance of the proposed quantile estimator. We ran M = 2500 perturbed estimated values for evaluating B̂ and Ĵ. For the choice of perturbation number M, we have tried different values of M ranging from500 to 10,000, and we observed that the values of M do not significantly affect the numerical results. On average, the proposed new method is four times faster than the traditional resampling procedure for cases where the sample size is 400. For comparison, we also report the estimate that ignores the biases that exist in the sample and carries out the method in Peng and Huang (2008) without any modification. We denote this naive estimator as β̂ (τ)_Naive and it is evident that this naive estimator has substantial bias.

Table 2.

Simulation results for length-biased data (20% and 40% censoring rates); Bias: estimated bias of the estimates; SE: estimated variances of the estimates; SEE: averages of the resampled variance estimates; ECP: empirical coverage probabilities of the 95% Wald-type confidence intervals; MSE: mean squared error of the estimates.

Censoring	τ	Estimators	n = 200					n = 400
			Bias	SE	SEE	ECP	MSE	Bias	SE	SEE	ECP	MSE
20%	0.25	β̂(0)(τ)	−0.042	0.248	0.283	0.972	0.063	−0.005	0.130	0.128	0.956	0.035
		β̂(1)(τ)	−0.014	0.486	0.503	0.952	0.256	−0.043	0.304	0.331	0.970	0.122
		β̂(2)(τ)	−0.004	0.255	0.244	0.944	0.065	0.001	0.129	0.114	0.928	0.031
		β̂(0)(τ)Naive	0.307	0.117	0.095	0.212	0.108	0.166	0.048	0.085	0.400	0.030
		β̂(1)(τ)Naive	0.854	0.230	0.160	0.148	0.756	0.814	0.085	0.120	0.000	0.670
		β̂(2)(τ)Naive	0.270	0.349	0.337	0.820	0.199	0.054	0.274	0.236	0.878	0.078
	0.50	β̂(0)(τ)	−0.016	0.145	0.185	0.966	0.021	−0.014	0.111	0.130	0.966	0.012
		β̂(1)(τ)	0.020	0.323	0.363	0.962	0.105	−0.001	0.229	0.283	0.982	0.052
		β̂(2)(τ)	−0.013	0.168	0.150	0.926	0.028	0.007	0.114	0.104	0.924	0.013
		β̂(0)(τ)Naive	0.302	0.039	0.049	0.890	0.002	0.000	0.004	0.049	0.900	0.000
		β̂(1)(τ)Naive	0.277	0.172	0.170	0.652	0.121	−0.555	0.042	0.085	0.000	0.309
		β̂(2)(τ)Naive	0.141	0.322	0.295	0.856	0.123	0.002	0.263	0.253	0.978	0.069
40%	0.25	β̂(0)(τ)	−0.033	0.238	0.263	0.966	0.063	−0.008	0.132	0.125	0.950	0.036
		β̂(1)(τ)	0.022	0.511	0.505	0.936	0.256	−0.031	0.312	0.291	0.936	0.112
		β̂(2)(τ)	−0.007	0.244	0.215	0.920	0.065	0.003	0.126	0.118	0.958	0.031
		β̂(0)(τ)Naive	0.261	0.114	0.130	0.472	0.081	0.248	0.087	0.088	0.248	0.069
		β̂(1)(τ)Naive	0.890	0.177	0.194	0.004	0.823	0.891	0.128	0.132	0.000	0.811
		β̂(2)(τ)Naive	0.262	0.347	0.364	0.886	0.189	0.283	0.236	0.251	0.806	0.136
	0.50	β̂(0)(τ)	−0.011	0.142	0.188	0.964	0.020	−0.012	0.117	0.129	0.952	0.013
		β̂(1)(τ)	0.041	0.315	0.362	0.968	0.101	0.006	0.237	0.280	0.968	0.054
		β̂(2)(τ)	−0.025	0.166	0.155	0.938	0.028	0.001	0.111	0.105	0.922	0.013
		β̂(0)(τ)Naive	0.250	0.124	0.127	0.466	0.078	0.248	0.080	0.088	0.206	0.068
		β̂(1)(τ)Naive	1.017	0.200	0.202	0.000	1.074	1.020	0.134	0.140	0.000	1.059
		β̂(2)(τ)Naive	0.522	0.360	0.380	0.724	0.402	0.549	0.249	0.263	0.452	0.363

The performance of the proposed method is comparable with that of Wang and Wang (2014) when the number of covariates is small. However, due to the use of kernel smoothing for estimating the censoring probability, Wang and Wang (2014) is not practical when the censoring distribution depends on more than two covariates. In the following example, we examine the performance of the new method in a setting where the censoring distribution depends on four covariates. We generate random data from

$$log{T}^{\ast }=Z_1{\beta }_1+Z_2{\beta }_2+Z_3{\beta }_3+Z_4{\beta }_4+(1+\gamma Z_1)\epsilon ,$$

where β₀ = (1, −1, 0.5, −0.5)^⊤, Z₃’s and Z₄’s are generated from N(1, 0.5) and N(−1, 0.5), respectively; Z₁ and Z₂ are generated in the same fashion as we discussed earlier. The censoring times are assumed to follow a Cox proportional hazard models with covariates Z_ℓ (ℓ = 1, . . . , 4) and model parameters (0.5, 1.0, −0.5, 1.0) and the baseline cumulative hazard function Λ₀(c) = −15 to achieve the target censoring rate. We consider sample sizes 500 and 1000, and 500 iterations for each case. The estimated standard errors and coverage probabilities are obtained based on 500 perturbed resamplings. It is noteworthy that a larger sample size is needed to ensure more accurate coverage probabilities when the number of covariates is larger. Table 3 confirms that the proposed procedure yields unbiased estimates of β and consistent estimates of the corresponding variances.

Table 3.

Simulation results for length-biased data with censoring times generated from a Cox proportional hazard model with four covariates; Bias: simulated bias of the estimates; SE: simulated variances of the estimates; SEE: averages of the resampled variance estimates; ECP: empirical coverage probabilities of the 95% Wald-type confidence intervals; MSE: mean squared errors of the estimates.

τ	Estimators	n = 500					n = 1000
		Bias	SE	SEE	ECP	MSE	Bias	SE	SEE	ECP	MSE
0.25	β̂(0)(τ)	0.008	0.269	0.224	0.936	0.072	−0.026	0.203	0.184	0.956	0.042
	β̂(1)(τ)	−0.026	0.189	0.174	0.940	0.036	−0.033	0.115	0.127	0.960	0.014
	β̂(2)(τ)	0.003	0.311	0.319	0.952	0.097	0.011	0.221	0.222	0.956	0.049
	β̂(3)(τ)	−0.023	0.165	0.158	0.932	0.028	0.000	0.121	0.119	0.928	0.015
	β̂(4)(τ)	0.012	0.178	0.157	0.926	0.032	0.000	0.123	0.119	0.928	0.015
	β̂(0)(τ)Naive	0.369	0.171	0.167	0.396	0.165	0.357	0.108	0.121	0.152	0.139
	β̂(1)(τ)Naive	0.693	0.096	0.101	0.000	0.489	0.693	0.064	0.070	0.000	0.484
	β̂(2)(τ)Naive	0.094	0.177	0.189	0.912	0.040	0.084	0.119	0.129	0.896	0.021
	β̂(3)(τ)Naive	−0.047	0.098	0.104	0.936	0.012	−0.039	0.070	0.072	0.920	0.006
	β̂(4)(τ)Naive	0.049	0.105	0.104	0.928	0.013	0.050	0.068	0.073	0.896	0.007
0.50	β̂(0)(τ)	−0.001	0.163	0.180	0.964	0.027	0.011	0.107	0.114	0.982	0.012
	β̂(1)(τ)	−0.038	0.127	0.125	0.948	0.018	−0.048	0.087	0.076	0.946	0.008
	β̂(2)(τ)	0.021	0.213	0.226	0.964	0.046	0.010	0.139	0.152	0.954	0.019
	β̂(3)(τ)	−0.011	0.116	0.108	0.932	0.014	−0.011	0.072	0.079	0.964	0.005
	β̂(4)(τ)	0.005	0.122	0.108	0.928	0.015	0.006	0.080	0.080	0.962	0.006
	β̂(0)(τ)Naive	0.404	0.229	0.209	0.504	0.215	0.006	0.212	0.114	0.676	0.045
	β̂(1)(τ)Naive	0.674	0.096	0.098	0.000	0.463	0.238	0.079	0.101	0.284	0.063
	β̂(2)(τ)Naive	0.157	0.165	0.177	0.868	0.052	0.060	0.155	0.161	0.956	0.028
	β̂(3)(τ)Naive	−0.056	0.110	0.107	0.908	0.015	−0.059	0.103	0.082	0.880	0.014
	β̂(4)(τ)Naive	0.071	0.109	0.111	0.912	0.017	0.064	0.101	0.082	0.860	0.014

Classical case-cohort sampling

We generate the survival time from the following log-linear model

$$logT=Z_1{\beta }_1+Z_2{\beta }_2+\epsilon ,$$

where ε follows a normal distribution N(0, 0.5²), Z₁ follows a Bernoulli distribution with success probability 0.5 and Z₂ follows a uniform distribution Unif (−1, 1). The true parameter values are (1.0, −1.0). The censoring time C_i is generated from an exponential distribution with rate [1 − 0.9I(Z₂ > 0)]λ, where λ is chosen to achieve a roughly 80% censoring rate. Such a high level of censoring rate corresponds to cases more natural to apply case-cohort designs (e.g., rare-disease studies). Cohort sizes of 100 and 200 are drawn by simple random sampling with one-third of these samples being observed failures. For the resampling scheme, B is set to be 500 to estimate the asymptotic variance of the proposed estimator. Same as the procedure in length-biased simulations, an equally spaced grid with 𝒮_L(n) = 0.01 is selected. These settings are comparable with those discussed in Zheng et al. (2013) in the sense that the estimates are all but unbiased with mean squared errors very close to 0.

We illustrate through simulations the improvement in efficiency by using additional weight functions as introduced in Section 3.2. Our numerical study shows that the weight functions, ψ(t) = (ψ₁(t),ψ₂(t),ψ₃(t)) = (1, t, 1/t), generally give stable and improved estimates. Note that the first weight function ψ₁ gives the original estimating Equation (10), ψ₂ assigns more weights on survival times around the tail regions, and ψ₃ puts more weight on shorter survival times. Table 4 summarizes the simulation results. We observe that the GMM-type estimator β̂(τ)_eff improves the efficiency of the estimators significantly, particularly when the subcohort size is smaller. Moreover, the corresponding SEE’s computed via the proposed resampling method are with good empirical coverage probabilities.

Table 4.

Simulation results for case-cohort designs; Bias: average bias of the estimates; SE: average variances of the estimates; SEE: averages of the resampled variance estimates; ECP: empirical coverage probabilities of the 95% Wald-type confidence intervals; MSE: mean squared error of the estimates.

τ	Estimators	Subcohort size: 100					Subcohort size: 200
		Bias	SE	SEE	ECP	MSE	Bias	SE	SEE	ECP	MSE
0.25	β̂(0)(τ)	0.023	0.120	0.117	0.944	0.015	0.021	0.085	0.090	0.944	0.008
	β̂(1)(τ)	0.036	0.225	0.220	0.960	0.052	0.024	0.161	0.157	0.948	0.027
	β̂(2)(τ)	0.027	0.203	0.203	0.944	0.042	0.031	0.140	0.142	0.940	0.021
	β̂(0)(τ)eff	0.016	0.099	0.102	0.948	0.010	0.020	0.071	0.083	0.970	0.005
	β̂(1)(τ)eff	−0.039	0.191	0.218	0.972	0.038	0.035	0.147	0.140	0.932	0.023
	β̂(2)(τ)eff	0.010	0.173	0.195	0.972	0.030	0.010	0.122	0.144	0.976	0.015
	β̂(0)(τ)Naive	−0.170	0.121	0.288	0.998	0.044	−0.163	0.088	0.243	1.000	0.034
	β̂(1)(τ)Naive	−0.076	0.211	1.445	0.992	0.050	−0.081	0.168	0.287	0.992	0.035
	β̂(2)(τ)Naive	−0.026	0.206	0.400	0.998	0.043	−0.026	0.143	0.307	1.000	0.021
0.50	β̂(0)(τ)	0.000	0.125	0.140	0.972	0.016	0.013	0.099	0.097	0.936	0.010
	β̂(1)(τ)	0.002	0.305	0.315	0.980	0.093	0.002	0.192	0.190	0.928	0.037
	β̂(2)(τ)	−0.001	0.224	0.236	0.958	0.050	0.002	0.153	0.168	0.940	0.023
	β̂(0)(τ)eff	0.002	0.102	0.126	0.976	0.010	0.011	0.079	0.086	0.944	0.006
	β̂(1)(τ)eff	−0.015	0.192	0.201	0.952	0.037	0.006	0.168	0.153	0.926	0.028
	β̂(2)(τ)eff	0.000	0.184	0.215	0.980	0.034	−0.002	0.138	0.161	0.968	0.019
	β̂(0)(τ)Naive	−0.080	0.121	0.172	1.000	0.021	−0.129	0.117	0.139	0.960	0.030
	β̂(1)(τ)Naive	−0.095	0.984	1.879	0.952	0.976	−0.132	0.175	0.294	0.900	0.048
	β̂(2)(τ)Naive	0.098	0.249	0.282	0.968	0.071	0.031	0.176	0.207	0.972	0.032

Stratified case-cohort sampling

We generate the survival and censoring times similarly as in the classical case-cohort sampling example except that the probability of subjects being selected varies according to their covariates Z’s. Selection probabilities for cases (p₁) and censored samples (p₂) are specified as follows: p₁(Z) = 1 − {1 + exp(2.5 + 0.25Z₂)}⁻¹ and p₂(Z) = 1 − {−1.5 + 0.5 exp(2Z₂)}⁻¹. Under this setup, about one third of the samples selected are cases while the mean overall censoring rate is maintained at a level of 75%. We also examined the performance of the efficient estimator under the stratified case-cohort sampling. The results are summarized in Table 5. Biases are negligible in all cases and the ECPs are close to their nominal values. For the efficient estimator, reductions in standard errors of β̂(τ) are also observed.

Table 5.

Simulation results for stratified case-cohort designs; Bias: average bias of the estimates; Var: average variances of the estimates; Est Var: averages of the resampled variance estimates; ECP: empirical coverage probabilities of the 95% Wald-type confidence intervals; MSE: mean squared error of the estimates.

τ	Estimators	Subcohort size: 200					Subcohort size: 400
		Bias	SE	SEE	ECP	MSE	Bias	SE	SEE	ECP	MSE
0.25	β̂(0)(τ)	0.071	0.131	0.137	0.940	0.031	0.047	0.096	0.122	0.980	0.011
	β̂(1)(τ)	0.058	0.103	0.096	0.950	0.014	0.057	0.070	0.082	0.949	0.008
	β̂(2)(τ)	−0.058	0.142	0.140	0.940	0.024	−0.063	0.090	0.108	0.934	0.012
	β̂(0)(τ)eff	0.014	0.030	0.042	0.980	0.001	0.018	0.034	0.036	0.938	0.001
	β̂(1)(τ)eff	−0.027	0.095	0.084	0.940	0.010	0.003	0.082	0.064	0.934	0.007
	β̂(2)(τ)eff	−0.003	0.128	0.102	0.944	0.016	−0.008	0.072	0.105	0.970	0.005
	β̂(0)(τ)Naive	−0.193	0.069	0.180	0.980	0.042	−0.202	0.054	0.133	0.794	0.044
	β̂(1)(τ)Naive	−0.073	0.060	0.125	0.986	0.009	−0.080	0.047	0.094	0.932	0.009
	β̂(2)(τ)Naive	0.086	0.094	0.133	0.974	0.016	0.087	0.074	0.100	0.932	0.013
0.50	β̂(0)(τ)	0.027	0.115	0.115	0.964	0.014	0.053	0.107	0.127	0.948	0.014
	β̂(1)(τ)	0.006	0.082	0.088	0.984	0.007	0.018	0.068	0.077	0.974	0.005
	β̂(2)(τ)	0.000	0.154	0.148	0.960	0.024	−0.013	0.105	0.117	0.970	0.011
	β̂(0)(τ)eff	0.004	0.030	0.044	0.964	0.001	0.011	0.031	0.035	0.950	0.001
	β̂(1)(τ)eff	−0.004	0.098	0.081	0.972	0.010	0.018	0.080	0.063	0.924	0.007
	β̂(2)(τ)eff	−0.014	0.085	0.103	0.964	0.007	0.001	0.077	0.103	0.976	0.006
	β̂(0)(τ)Naive	−0.194	0.102	0.120	0.696	0.048	−0.220	0.072	0.095	0.222	0.054
	β̂(1)(τ)Naive	−0.071	0.078	0.083	0.930	0.011	−0.087	0.055	0.067	0.772	0.011
	β̂(2)(τ)Naive	0.082	0.100	0.105	0.888	0.017	0.092	0.077	0.082	0.792	0.015

6. Real Data Analysis

6.1 Analysis of the CSHA Dataset

We first apply the procedure discussed in Section 2.2 to the Canadian Study of Health and Aging (CSHA) study, which is a multi-center study of the epidemiology of dementia in Canada. It followed 10,263 senior Canadians over a period from 1991 to 2001 and collected a wide range of information on their changing health status over time. Among these over 10,000 elderly who were 65 years or older, 1132 people were identified as having dementia. Excluding subjects with missing dates of disease onset, we analyze 818 senior individuals that can be classified into three groups, namely, (i) probable Alzheimer’s disease (393 patients), (ii) possible Alzheimer’s disease (252 patients), and (iii) vascular dementia (252 patients). A total of 180 study subjects among 818 are censored, resulting in a censoring rate about 22%.

Following Wang and Wang (2014), we apply the proposed method to the following model:

$$\begin{gathered} Q_{\tau }(log{T}_i\mid {\mathbf{z}}_i)={\beta }_{(0)}(\tau )+{\beta }_{(1)}(\tau )z_{1i}+{\beta }_{(2)}(\tau )z_{2i}, \\ i=1,\dots ,818, \end{gathered}$$

where z_1i and z_2i are dummy variables indicating if the ith subject is classified into probably Alzheimer’s disease or possible Alzheimer’s disease, respectively. The vascular dementia group is used as the reference group.

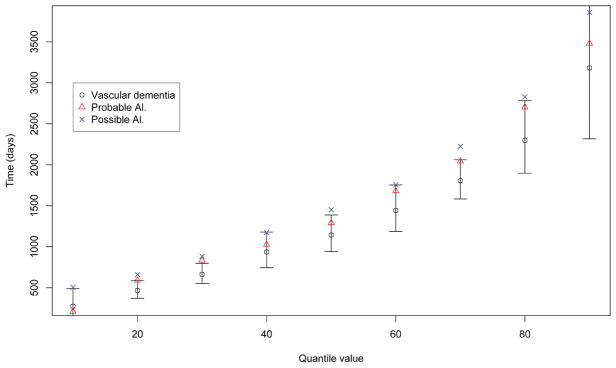
Table 6 summarizes the estimates of the proposed method with π = 0.5. Again, we obtain very similar point estimates for different values of π. A total of 500 perturbation resampling procedures are carried out to estimate the standard errors of the estimators, which are presented in parentheses in the table. Figure 1 demonstrates the estimated quantiles of the three dementia subtypes, where the vertical lines correspond to the 95% pointwise confidence intervals of the estimated quantiles of the patients in the baseline group (vascular dementia). Ning et al. (2011) found no significant difference in survival times among the three types of dementia when considering the mean survival time with the AFT model. In our analysis, however, we observe that seniors with possible Alzheimer’s disease tend to have longer survival time than those who suffered from vascular dementia. Such an observation is evident in Figure 1 where the estimated quantiles corresponding to possible Alzheimer’s disease are not fully covered by the confidence intervals constructed with respect to the baseline vascular dementia patients. Our results agree with the findings presented in Wang and Wang (2014).

Table 6.

Dementia example—Regression coefficient estimates and standard errors.

τ	0.10	0.20	0.30	0.40	0.50	0.60	0.70	0.80	0.90
β̂(0)(τ)	5.616 (0.297)	6.146 (0.118)	6.497 (0.095)	6.842 (0.118)	7.041 (0.099)	7.275 (0.100)	7.499 (0.067)	7.740 (0.098)	8.065 (0.162)
β̂(1)(τ)	−0.274 (0.384)	0.236 (0.160)	0.230 (0.105)	0.092 (0.135)	0.122 (0.117)	0.153 (0.105)	0.123 (0.083)	0.162 (0.112)	0.089 (0.182)
β̂(2)(τ)	0.608 (0.4166)	0.344 (0.155)	0.285 (0.128)	0.225 (0.141)	0.239 (0.129)	0.197 (0.118)	0.209 (0.097)	0.208 (0.128)	0.193 (0.201)

NOTE: Bold formatting indicates Type 1 error is 5%.

Figure 1.

Estimated quantiles of population survival times for the three categories of dementia for the Canadian Study of Health and Aging (CSHA) dataset. The vertical lines correspond to the pointwise 95% confidence interval constructed for the baseline group population quantile survival time.

6.2 Application to Case-Cohort Designs—Welsh Nickel Refiners Study

We now analyze a dataset collected in the South Welsh nickel refiners study (Appendix VIII of Breslow and Day 1987). The data consist of 679 subjects employed in a nickel refinery. The goal of the study is to investigate the association between the development of nasal sinuses and the exposure to nickel. The follow-up through 1981 uncovered 56 deaths from cancer of the nasal sinus; hence the censoring rate is higher than 90%. Breslow and Day (1987), followed by Lin and Ying (1993), analyzed the mortality data on the nasal sinus cancer using the Cox model with (modified) case-cohort design. Previous studies found that AFE (age at first employment), YFE (year at first employment), and EXP (exposure level) are significant factors. Lin and Ying (1993) considered the following regression covariates: log(AFE-10), log of the age of the first employment minus 10 years, (YFE-1915)/10, (YFE-1915)² /100, two transformed versions of number of years working in the refinery since 1915 and log(EXP+1), the log exposure level; some of the subjects had zero exposure and hence EXP+1 is considered so that its logged value is nonnegative and well-defined.

The identifiability of the quantile estimates is only valid up to the 15th quantile because the Kaplan–Meier estimate, based on the full cohort, does not drop further after it reaches 0.85. We will compare the results obtained from a (i) full cohort, (ii) a subcohort collected under the traditional setting, and (iii) a subcohort collected under stratified case-cohort procedure as described in Section 2.2. In particular, we use p₁ = 1 − {1 + exp(−1 + LOGAFE)}⁻¹ and p₂ = 1 − {1 + exp(−3 + LOGAFE)}⁻¹ for selecting cases and censored subjects into the sample. This leads to, on average a sample size of 310. The spaced grid was selected to be of size 0.001 for these numerical studies. 500 resamplings were carried for evaluation of the standard errors of the proposed estimates. We also applied the methodology introduced in Section 3.2 to obtain a more efficient set of estimates. Similar to our simulation setting, the weight function of ψ(t) = (ψ₁(t),ψ₂(t),ψ₃(t)) = (1, t, 1/t) was applied. It can be observed that, based on the results presented in Table 7, both the original and the improved estimates obtained from subcohorts due to classical/stratified case-cohort samplings are similar to their counterparts based on the full cohort data. The standard errors of these estimates are also similar.

Table 7.

SouthWales nickel refinery example—Regression coefficient estimates and standard errors.

τ	Full cohort (n = 679)			Classical case-cohort (n = 350)			Stratified case-cohort (n = 310)
	0.05	0.10	0.15	0.05	0.10	0.15	0.05	0.10	0.15
β̂LOGAFE(τ)	−0.708 (0.199)	−0.708 (0.202)	−0.530 (0.106)	−0.728 (0.202)	−0.611 (0.202)	minus;0.642 (0.108)	−0.682 (0.162)	−0.502 (0.178)	−0.494 (0.226)
β̂YFE/10(τ)	0.043 (0.110)	0.001 (0.007)	−0.024 (0.103)	0.049 (0.070)	0.042 (0.070)	0.220 (0.217)	0.054 (0.042)	0.017 (0.096)	0.268 (0.809)
β̂YFE2/100(τ)	0.325 (0.184)	0.293 (0.223)	0.209 (0.153)	0.335 (0.223)	0.260 (0.223)	0.383 (0.250)	0.276 (0.193)	0.250 (0.233)	0.392 (1.042)
β̂LOGEXP(τ)	−0.161 (0.073)	−0.160 (0.036)	−0.269 (0.046)	−0.161 (0.036)	−0.222 (0.036)	−0.174 (0.046)	−0.169 (0.067)	−0.281 (0.076)	−0.303 (0.080)
β̂LOGAFE(τ)eff	−0.653 (0.084)	−0.6091 (0.078)	−0.500 (0.062)	−0.655 (0.068)	−0.634 (0.064)	−0.654 (0.117)	−0.580 (0.154)	−0.600 (0.173)	−0.499 (0.141)
β̂YFE/10(τ)eff	−0.001 (0.001)	−0.002 (0.001)	0.027 (0.001)	0.001 (0.001)	0.001 (0.040)	0.001 (0.001)	−0.001 (0.001)	0.004 (0.002)	0.001 (0.001)
β̂YFE2/100(τ)eff	0.310 (0.160)	0.246 (0.140)	0.2677 (0.121)	0.256 (0.196)	0.139 (0.106)	0.166 (0.122)	0.237 (0.142)	0.114 (0.065)	0.253 (0.157)
β̂LOGEXP(τ)eff	−0.166 (0.024)	−0.154 (0.030)	−0.301 (0.042)	−0.208 (0.034)	−0.136 (0.020)	−0.194 (0.045)	−0.125 (0.019)	−0.129 (0.019)	−0.225 (0.030)

NOTE: Bold formatting indicates Type 1 error is 5%.

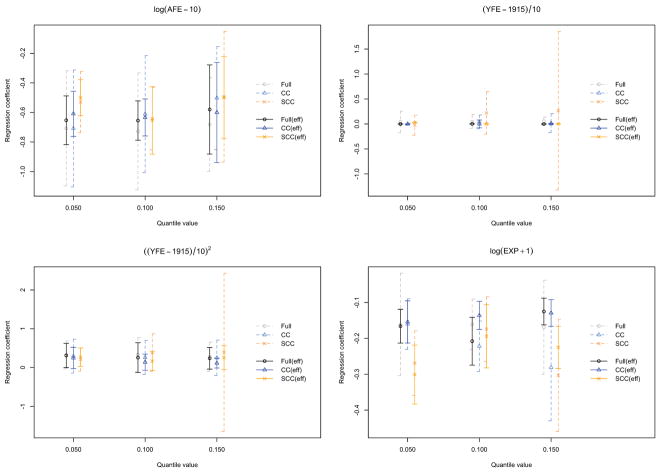
Figure 2 is included for the purpose of presenting an overall performance of the proposed method on this nickel refinery dataset. It displays the average point estimates and the corresponding pointwise standard errors of the four covariates for the 5th, the 10th, and the 15th quantiles. It is noteworthy that the covariate log(AFE-10) is significant for all the quantiles. This is consistent with the findings discussed in Lin and Ying (1993) and Kim et al. (2013). Another covariate that was found to be statistically significant in the two aforementioned literature, log(EXP+1), is also significant in our study.

Figure 2.

Estimated quantiles of population survival times for the South Wales nickel refinery dataset. The black, blue, and orange solid lines correspond to the point estimates based on the samples obtained from the full cohort, classical case-cohort sampling scheme, and stratified case-cohort sampling scheme, respectively. Their associated pointwise 95% confidence intervals are presented by (dotted) lines of the same colors.

7. Conclusion and Discussions

Biased sampling arises frequently in many observational studies. Conventional approaches without accounting for the sampling bias can lead to substantial estimation bias and fallacious inference. In this article, we introduce a general quantile regression approach to deal with data collected from various biased sampling schemes. While our method can handle some specific types of biased sampling schemes that have been studied in the literature, it also covers more general case-cohort designs including stratified case-cohort and case-cohort sampling on a length-biased dataset, length-biased sampling that is proportional to the follow-up time (see Kim et al. 2013), all of which have not yet been previously investigated. Moreover, the one-size-fit-all formulation provides practitioners with a convenient tool for quantile regression modeling on their datasets collected under various sampling schemes. Because construction of the estimating equations does not require an estimate of the censoring time distribution, the proposed method can handle more complex problems with higher dimensional covariates than the existing methods.

Another major contribution of our work concerns with the efficiency improvement for the quantile regression. When there is additional sampling information, we show that the GMM approach can be applied to obtain an efficient estimate for length-biased survival data under cross-sectional sampling. In a more general setting, one can construct a set of weighted estimating equations so as to seek additional information by combining them via GMM. Numerical results show the proposed efficient estimates out perform the existing methods. It is worth-while to point out that the proposed method is generic and can be easily extended to other models where the theoretically optimal weight function is hard to obtain. In particular, it would be interesting to explore the efficiency improvement in the quantile regression without biased sampling.

The choice of the weight function v(t) is usually informed by study design and prior knowledge about the disease incidence process, as seen in many research works on case–control studies and prevalent cohort studies (see, e.g., Shen et al. 2009; Kong and Cai 2009; Luo and Tsai 2009; Chen 2010; Qin and Shen 2010; Huang and Qin 2012; Kimet al. 2013; Zheng et al. 2013). When the knowledge about biased sampling scheme is not available, a data-driven weight function may be developed by applying a similar technique considered by Qin et al. (2002); however, the method requires a multiple-sampling setting, where a unbiased sample must be obtained to ensure identifiability of the model parameters. Therefore, in the one-sampling setting of the current article, neither identifiability nor estimation of v(t) is available due to the lack of unbiased sample.

There are several other directions that are worth pursuing. One issue of the proposed method, as discussed in Peng and Huang (2008), is identifiability of upper quantiles due to the abundance of censored observations toward the tail. This feature is particularly prominent for biased-sampling cases due to potentially high censoring rates as we have seen in case-cohort designs for instance. It is of interest to incorporate the method of Portnoy (2014) in the current setup and investigate the benefits of jackknife under various biased-sampling settings.