Summary
This article is motivated by the increasing need to model risk for large hospital and health care systems that provide services to diverse and complex patients. Often, heterogeneity across a population is determined by a set of factors such as chronic conditions. When these stratifying factors result in overlapping subpopulations, it is likely that the covariate effects for the overlapping groups have some similarity. We exploit this similarity by imposing structural constraints on the importance of variables in predicting outcomes such as hospital admission. Our basic assumption is that if a variable is important for a subpopulation with one of the chronic conditions, then it should be important for the subpopulation with both conditions. However, a variable can be important for the subpopulation with two particular chronic conditions but not for the subpopulations of people with just one of those two conditions. This assumption and its generalization to more conditions are reasonable and aid greatly in borrowing strength across the subpopulations. We prove an oracle property for our estimation method and show that even when the structural assumptions are misspecified, our method will still include all of the truly nonzero variables in large samples. We demonstrate impressive performance of our method in extensive numerical studies and on an application in hospital admission prediction and validation for the Medicare population of a large health care provider.
Keywords: Heterogeneity, Hierarchical penalization, Risk prediction, Variable selection
1. Introduction
According to recent studies (Pfuntner, Wier, and Steiner, 2013; Moore, Levit, and Elixhauser, 2014), inpatient hospital services account for 7% of health care utilization but constitute the largest share of total health care spending, 29%, in the United States in 2009. As health care costs continue to rise and the population ages, policymakers are increasingly concerned about the growing burden of hospital-based medical care expenses on the government, insurers, patients, and employers. As a result, there is an urgent need to build predictive models for hospital admissions and readmissions so that hospitals and health care systems can intervene to improve care and reduce costly admissions. In particular, the primary motivation of this article is risk modeling for a Medicare Accountable Care Organization (ACO). One goal of ACOs is to provide a system of coordinated and targeted care for Medicare beneficiaries to improve health outcomes. Accurate assessment of the hospitalization risk of patients with different co-morbidities can help inform an ACO’s care coordination and management programs.
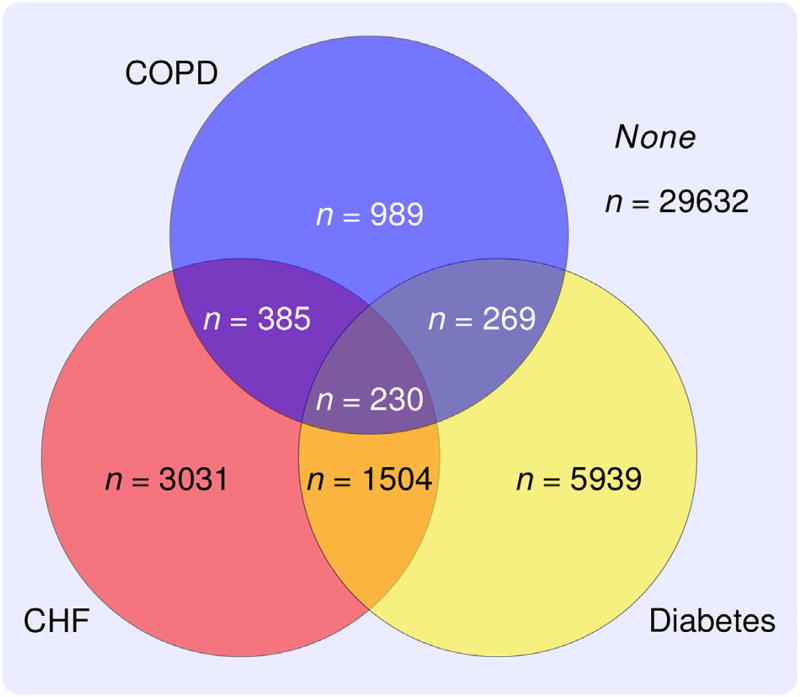
However, there are many challenges in building predictive models for the risk of hospitalization among the Medicare ACO patients with different co-morbidities. First, there is a large number of variables available from both electronic health records (EHR) and Medicare claims. Furthermore, some of these variables are disease specific. For example, the Glycated Hemoglobin (A1c) test is usually only measured for patients with diabetes. In addition, a particularly challenging issue researchers face in hospital-wide risk modeling is the heterogeneity of the study population. Many patients, especially the elderly, have multiple chronic conditions, further complicating modeling efforts. For example, in our motivating study, we are faced with the subpopulations shown in Figure 1. In particular, three prevalent chronic conditions, congestive heart failure (CHF), diabetes, and chronic obstructive pulmonary disease (COPD), increase health care costs substantially through repeated hospital admission. Hence, it is important to build reliable risk prediction models for the subpopulations with these conditions. A major complication in constructing reliable models for these populations is the inherent differences among the subpopulations with different chronic conditions. For example, the effect of hypertension among patients with CHF may increase the risk of hospitalization. However, it is known that hypotension can be a hospitalization risk for patients with diabetes (Lipska et al., 2014) and as such, the effect of blood pressure may be different for these two different populations. Furthermore, the effect of blood pressure for patients with both CHF and diabetes may be altogether different from patients with only CHF or only diabetes.
Figure 1.
The above illustration depicts the sample sizes for each of the strata in the UW Health population included into the study.
To account for such heterogeneity, risk models should be flexible, allowing for covariate effects to vary across different subpopulations. One direct way is to build models for every subpopulation. Another approach would be to construct a single model which accounts for heterogeneity by including all possible interactions between the indicators of CHF and diabetes and all covariates. However, this approach leads to a complex model and can be hard to present or summarize the results. Furthermore, these approaches do not make efficient use of the data as there may be intrinsic structure underlying the subpopulations. Specifically, we may expect certain variables to contribute to hospital admission for all patients. On the other hand, we also can expect a variable related to diabetes (e.g., A1c level) to be important for subjects with diabetes whether they have other co-morbidities or not. Ignoring this structural information may result in a loss of efficiency, especially in the subpopulations with smaller sample sizes (i.e., those with more conditions).
In the approach of this article, we incorporate the above discussed structural assumptions in variable selection to borrow strength across subpopulations. We assume that the effects of each covariate can differ for different subpopulations, but their importance respects the hierarchical structure of the stratifying factors. We assume that if a particular variable is predictive for patients with only one condition (e.g., CHF), it should be predictive for patients with that condition and additional conditions (e.g., CHF and diabetes). However, a variable can be predictive for patients with both conditions but not for those with single conditions. For example, pioglitazone and other similar medications for diabetes may cause or worsen CHF (Tannen et al., 2013). Therefore, such medication information can be predictive of hospitalization risk for patients with both diabetes and CHF, but may not be predictive for diabetic patients without CHF. In smaller subpopulations, such as those with three or more chronic conditions, this hierarchical constraint can especially aid in the selection of important covariates and can thus help in borrowing strength across the various subpopulations. The smaller subpopulations usually are of more importance as they are high utilizers of the health care services.
The above assumption is materialized in this article through a penalty which induces hierarchical variable selection for heterogeneous populations with overlapping patterns. The penalty is based on the overlapping group lasso, an extension of the group lasso penalty of Yuan and Lin (2006) which allows for some of the groups of covariates to overlap. In essence, our approach addresses variable selection of interactions to capture heterogeneity. Therefore, existing variable selection approaches for interactions can potentially be applied in our setting (Zhao, Rocha, and Yu, 2009; Bien, Taylor, and Tibshirani, 2013). However, these approaches do not allow the interaction term to be selected unless the main effect is selected. Framing our setup in terms of interactions, we could think of the coefficients for the, say, the diabetes only and CHF only subpopulations to be the main effects and the interaction to be the coefficients for the subpopulation with both diabetes and CHF. Using existing approaches would not allow for the coefficients for the subpopulation with both diabetes and CHF to be included without the coefficients for the diabetes only and CHF only subpopulations. This does not seem to be plausible scientifically-speaking. For example, many diabetic drugs are known to have cardiac side effects. Therefore, consumption of these drugs can be innocuous for diabetic patients with healthy hearts but problematic for patients with both diabetes and CHF.
A key methodological contribution of this article is in leveraging the overlapping group lasso to explicitly handle data-generating scenarios with multiple subpopulations. Our formulation relaxes the requirement of independence between subpopulations. Furthermore, while there are theoretical results for the latent group lasso (Percival, 2012), to our knowledge, there are no theoretical results for the adaptive overlapping group lasso or such extensions to generalized linear models.
We prove consistency of variable selection and asymptotic normality when our hierarchical selection assumption holds. We show that even when our structural assumption does not hold, our selection will still consistently include all of the truly nonzero coefficients. Some truly zero coefficients may be selected in this case, but asymptotic normality still holds and thus the truly zero coefficients will converge in probability to zero. We show that the above asymptotic results hold under the generalized linear models and semiparametric linear models. Through extensive numeric studies and analysis of the ACO data, we demonstrate that our approach outperforms various ad hoc approaches of addressing population heterogeneity.
2. Methodology
Consider a model with covariate effects that differ based on C stratifying factors. For example, suppose, we have three stratifying factors H, P, and D (congestive Heart failure, chronic obstructive Pulmonary disease, and Diabetes, respectively) on which we would like to stratify the main effects of our model. The form of the population stratified on these factors is depicted in Figure 1. Then all of the possible subpopulations are HPD, the subpopulation with all three factors, HP, HD, PD, H, P, D, and none, the subpopulation with none of the three factors. More generally, when a model is stratified on C binary factors, this results in K = 2C subpopulations. Here, we focus on binary stratifying factors instead of factors with multiple levels such as age categories. In such a model, each covariate has 2C different effects, one for each subpopulation. For k = 1,…, K, let Xk denote the covariate information for subpopulation k. For simplicity of presentation, we will assume that all subpopulations have the same set of covariates available. Therefore Xk is of dimension nk × p. Let Yk be the response vector of length nk for subpopulation k. Our methodology can naturally handle cases where there are covariates (e.g., A1c) specific to certain subpopulations. In such cases, the number of parameters can differ for different subpopulations.
To describe the structure of coefficients of covariates across the given subpopulations, we introduce a double-subscript notation for the coefficients and the relevant variables to which they correspond. We denote βk, j as the coefficient of jth covariate for subpopulation k. In this notation, all coefficients for subpopulation k are represented by the vector βk,· = (βk,1,…, βk, p) and all coefficients for jth covariate are represented by the vector β·,j= (β1, j,…, βK, j). Naturally, we use β to represent all coefficients corresponding to all covariates across all subpopulations.
The density of a generalized linear model with canonical link given a single observation (yk, xk) for subpopulation k can be written as:
| (1) |
where , xk = (xk,1,…, xk, p), and are the true coefficients.
We assume that ϕ(θk) is a convex function for each k = 1,…, K. This is true for most generalized linear models. For example, in the Gaussian linear model, ϕ(θk) is a strictly convex quadratic form. In logistic regression, ϕ(θk) = log(1 + eθk) is a strictly convex function. In the log-linear regression model, ϕ(θk) = exp(θk) is also a strictly convex function.
A widely used framework for the selection of variables in generalized linear models is the penalized log-likelihood method. In order to borrow strength across the overlapping subpopulations, we propose to perform variable selection in a hierarchical fashion by maximizing the following penalized likelihood
| (2) |
where P is an overlapping group lasso penalty with special structure to induce hierarchical selection patterns and the likelihood ℓk is the likelihood corresponding to subpopulation k. In particular, we choose
| (3) |
where βG, j = (β·, j)G as the subvector of β·, j defined by the index set G ⊆ {1,…, K}, λG, j represents group-specific weights, 𝒢 is a set of groups of covariates, and ‖η‖2 denotes for a vector η ∈ Rd. Specifically, each element in 𝒢 is a set of indices corresponding to covariates in β. We will discuss how 𝒢 is constructed later in this section. A sensible choice of λG, j is |G|1/2, where |G| denotes the cardinality of the indices in G, however this may not guarantee consistent selection. In particular, if a condition similar to the irrepresentable condition (specified in Jenatton et al. (2011)) does not hold, then selection consistency is not guaranteed. Furthermore, this choice of weights may not guarantee an oracle property, which would guarantee consistent estimation in spite of misspecification of our hierarchical assumption. To address this issue, we adopt adaptive weights analogous to the adaptive lasso weights of Zou (2006). Specifically, we set for some γ > 0, where is the maximum likelihood estimate of the jth coefficient from an unpenalized GLM for subpopulation k. When all groups contain single coefficient, our optimization problem reduces to the adaptive lasso.
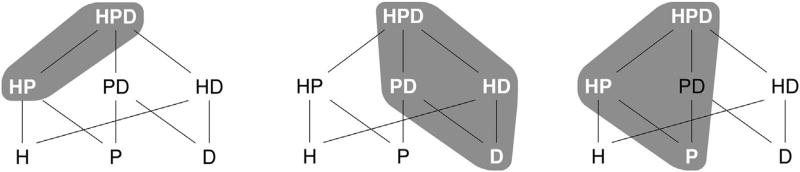
The key for our proposed approach is the specific choice of 𝒢 in (3). The groups in 𝒢 are chosen to have overlapping elements in a way that enables variable selection of the covariate effects in a hierarchical fashion. Examples of the selection patterns of interest are illustrated in Figure 2. We will formally define the elements in 𝒢 which induce these selection patterns later in this section. In order to construct 𝒢 appropriately, we must work with either the zero patterns or the non-zero patterns induced by a specific choice of 𝒢. A zero pattern is a subset of the covariate effects which have been set to zero and a non-zero pattern is a subset of the covariate effects which are non-zero. The zero pattern for variable selection from the overlapping group lasso is the union of groups. Specifically, for the set 𝒢 of all groups, by the results in Jenatton, Audibert, and Bach (2011) the possible zero-patterns can be represented as
The non-zero patterns, denoted as 𝒵C ≡ {ZC: Z ∈ 𝒵}, can be represented as the intersection of complements of elements in 𝒢 and is thus more difficult to work with directly than 𝒵. To see how 𝒢 might be constructed, consider a scenario with just two stratifying factors H and P. If we choose 𝒢 to be {{H}, {P}, {H, P, HP}}, then we can see that the corresponding set 𝒵 only allows covariates to be selected for the H or P subpopulations if they are also selected in the HP subpopulation. Additional covariates can, however, be selected only for the HP subpopulation.
Figure 2.
The left and center diagrams illustrate two examples of the desired variable selection patterns for overlapping strata. The two gray-highlighted groups in the leftmost diagrams represent the types of selection patterns of interest. Specifically, the two highlighted patterns on the left are elements in 𝒵C, where the corresponding group structure 𝒢 is defined in equation (4). The diagram on the right illustrates the selection properties when the group structure is misspecified. The groups with white text (HPD, HP, and P) form a true nonzero pattern which violates the structure imposed by our proposed penalty. The gray highlighted color indicates the nonzero pattern which will be selected asymptotically by our estimator with the incorrect group structure.
Before the most general case is constructed, we will develop some notation. Let the contained sets (the sets below the denoted set in the hierarchy, where HPD is defined as the top of the hierarchy) be . Then for each covariate,
| (4) |
Checking 𝒵 for this choice of 𝒢 verifies that this group structure imposes the desired hierarchical selection constraints. Note that there is no structural pattern imposed on the coefficients corresponding to the none subpopulation. It is often unreasonable to assume that effects of variables for the subpopulation with none of the stratifying factors should be affected by subpopulations with any of the stratifying factors. For concreteness, if the stratifying factors are chronic conditions, the none group would correspond to the population with no chronic conditions.
More generally, for any given set of stratifying factors, S1,…, Sc, the set of groups which induces the desired selection pattern is the union of all possible contained sets generated by S1,…, Sc in addition to the set {none}. Specifically, the set of groups is
The hierarchical penalty can still be applied for scenarios with disease-specific covariates. For example, blood A1c may only be available for diabetic patients. In this case, if we have stratifying factors H, P, and D, we would impose hierarchical selection for blood A1c only within subpopulations of patients with diabetes. We can simply remove all terms corresponding to non-diabetic populations in the formulation of the penalty. For A1c, the group structure would be .
3. Computation and Asymptotic Properties
Computation for the group lasso with overlapping groups is non-trivial. A general computational algorithm for minimizing , with overlapping groups is described in the online Supplementary Material. The algorithm is straightforward to implement, is computationally efficient, and can accommodate any convex ℓk.
In the rest of this section, we present theoretical results regarding selection consistency for the adaptive group lasso penalties with potentially overlapping groups. Suppose that the group structure described above is true in the sense that the hierarchical structure imposed by the groups accurately reflects the structure of important covariates in the data. The following theorems give us the model selection consistency and oracle properties when p is fixed. The model selection consistency guarantees that with probability tending to 1, the estimated nonzero coefficients will be nonzero in truth and the estimated zero coefficients to be zero. The oracle property guarantees that our estimation for the nonzero coefficients is as asymptotically efficient as if we had known in advance which coefficients are zero. The following results hold for any overlapping group lasso penalty, not just the specific choice of groups we propose.
We prove similar results in two classes of widely-used models. The first result pertains to scenarios where ℓk is the log-likelihood for any generalized linear model. The second result pertains to the linear model under milder assumptions than are required for the results for generalized linear models and is presented in the online Supplementary Material. The proofs are available in the online Supplementary Materials as well. The conditions required for both cases are similar to the conditions required for the asymptotic properties of the maximum likelihood and least squares estimates, respectively.
3.1. Assumptions
In this subsection, we lay out the assumptions required for asymptotic results for the overlapping group lasso for generalized linear models. We prove that using an adaptively weighted sparsity-inducing penalty, we can obtain oracle properties with overlapping group structure. Again, our sparsity-inducing estimator is defined by the following problem
| (5) |
where , ϕ(Xkβk,·) represents a nk-dimensional vector with transformation ϕ(·) on each entry of Xkβk,·, ek is a nk-dimensional vector with all ones, and is the total sample size. We set , where is the maximum likelihood estimate of the jth coefficient from an unpenalized GLM for subpopulation k and γ > 0. When all groups contain a single coefficient, our optimization problem reduces to the adaptive lasso. Thus, the theoretical result below can be seen as a natural extension of the adaptive lasso for generalized linear models.
We assume the following regularity conditions:
-
(C.1)
is finite and positive definite, where Ek[·] is the expectation w.r.t xk under the measure of subpopulation k.
-
(C.2)For subpopulation k, there is a sufficiently large enough open set 𝒪k that contains such that ∀βk,· ∈ 𝒪k,
and
for all 1 ≤ j, l, m ≤ p. -
(C.3)
0 < infk =1,…,K .
3.2. Asymptotic Results
The following results are applicable to settings more general than the specific group structure presented in Section 2. In particular, we show an oracle property for the selection of nonzero patterns which arise from any specified group structure. As a result, asymptotic results for our hierarchical penalty are obtained immediately. We first present the asymptotic results for cases where the possible zero patterns induced by the specified group structure includes the true zero pattern. Under this case, the group structure has been correctly specified.
The sets J·, j ⊂ {1,…, K} and Ĵ·, j ⊂ {1,…, K} are the index sets corresponding to the nonzero coefficients in and β̂·, j, respectively, and Jk,· ⊂ {1,…, p} is the index set for nonzero coefficients in . For a m × m matrix A, and H1, H2 ⊆ {1,…, m}, let the matrix AH1H2 in R|H1|×|H2| be the submatrix of A with rows of A indexed by H1 and columns of A indexed by H2.
Theorem 1
Assume the data are generated under the model represented by equation (1) and that our estimator is given by equation (5). Furthermore, assume that the non-zero patterns 𝒵 induced by the specified group structure 𝒢 contain the true zero pattern. Assume conditions (C.1)–(C.3) and let for some γ > 0 such that N(γ+1)/2 λ → ∞. If , then we have the following:
| (6) |
and
| (7) |
where and .
An important aspect of Theorem 1 and following theorems is that they do not require independence between subpopulations. It is expected that subpopulations with shared chronic conditions are similar to each other, and hence we would not expect them to be independent from each other.
We now present results that pertain to cases where the group structure has been misspecified in the sense that the set 𝒵C induced by a particular choice of 𝒢 does not contain the true non-zero pattern of β0. In such cases, we prove that although the true non-zero pattern will not be recovered exactly, at least all of the truly non-zero coefficients will be estimated to be non-zero in an asymptotic sense. To clarify the specific non-zero pattern that is recovered under group misspecification, we introduce notation similar to that in Jenatton et al. (2011).
For any subset I ⊆ {1,…, K} and a given set of groups 𝒢, the hull is defined as the complement of the union of all groups not overlapping with I:
Our results show that the adaptive overlapping group lasso is consistent in selecting the hull of the true nonzero coefficients in addition to providing optimal estimation of the hull. This implies that if the group structure 𝒢 is misspecified, the hull of J·, j, the true nonzero pattern of , can be consistently selected and estimated and if the group structure is indeed correctly specified, the true nonzero pattern will be consistently estimated. Essentially, the hull of the true nonzero pattern induced by a group structure 𝒢 (and corresponding 𝒵C) is the smallest element in 𝒵C that covers, or contains, the true non-zero pattern. An example of the hull of a nonzero pattern which will be selected is illustrated in the right-most diagram in Figure 2.
Note that Hull(Ĵ·, j) = Ĵ·, j. Denote H·, j = Hull(J·, j). Similar to Jk,· = {j ∈ {1,…, p} : k ∈ J·, j}, we can define Hk,· = {j ∈ {1,…, p} : k ∈ H·, j}, which corresponds to the hull of the nonzero pattern for the covariates corresponding to population k.
Theorem 2
Assume the data are generated under the model represented by equation (1) and that our estimator is given by equation (5). Here, we do not necessarily assume that the group structure is correctly specified. Assume conditions (C.1)–(C.3) and let for some γ > 0 such that N(γ+1)/2 λ → ∞. If , then we have the following:
| (8) |
and
| (9) |
where and .
We emphasize that Theorem 2 does not require that the group structure 𝒢 is correctly specified. However, if the group structure is indeed correctly specified, the classical oracle property holds, with our estimator obtaining the same asymptotic efficiency as if we knew the non-zero coefficients in advance and in addition obtaining variable selection consistency. If the group structure is misspecified, our estimator has the oracle property for selection of the hull of the true nonzero pattern, in which case our estimator obtains the same asymptotic efficiency as if we knew the true hull in advance. Because, we can correctly identify the asymptotic distribution under group structure misspecification, the resulting inclusion of some extra covariates which are truly zero may not be a serious issue, as their estimates will converge in probability to zero. Scenarios where our structural assumption may hold for many variables yet not for some should pose less of an issue. Thus, Theorem 1 can be considered a corollary of Theorem 2.
3.3. Standard Error and Degrees of Freedom
Tibshirani (1996) and Fan and Li (2001) proposed estimating standard errors of shrinkage estimates by utilizing a ridge regression approximation of the penalized likelihood solution. We follow this type of approach for standard error and degrees of freedom estimation. Note that when is not too close to 0, the penalty applied to βk, j can be locally approximated by a quadratic function
Then assuming that the log-likelihood is smooth with respect to β with first two partial derivatives continuous, then equation (2) can be locally approximated with a quadratic function. Minimizing with respect to the local approximation yields
where
Hence by standard techniques, a sandwich estimator of the covariance of β̂k,· is
Furthermore, the number of effective parameters in the adaptive overlapping group lasso estimator can be approximated by .
4. Simulation
Simulation studies were carried out to evaluate and compare the finite-sample performance of various models. In the simulation, we considered the number of stratifying factors C = 2, 3, 4, corresponding to a total number of subpopulations K = 22, 23, 24. The sample size per condition combination nk was chosen to be the same and varied from 25 to 500, yielding corresponding total sample sizes of N = nk · 2C. The number of covariates p was set to 100, resulting in a total number of parameters to be estimated of 100 · 2C.
The data were generated according to a logistic model where the coefficients βk,· were generated with a hierarchical zero-structure and the error terms are independent and identically distributed. Among the p = 100 coefficients, the number m which can be nonzero was varied from 25, 50, 100. Each βk, j for j = 1,…, m was set to 0 with a probability to achieve an overall sparsity level of 0.875. For each βk, j set to 0, all βk*, j with k* < k in the hierarchy are also set to 0. Each βk, j for j = m + 1,…, 100 was set to 0, thus resulting in overall zero proportions of 0.875, 0.75, and 0.50 for m = 25, 50, and 100, respectively. The nonzero coefficients were generated from a uniform random variable on (−c, −0.5c) ∪ (0. 5c, c), where c > 0. The strength of signal was varied by varying c from 0.25, 0.5, 1.
We evaluate our method in addition to several other approaches of handling population heterogeneity. The “Separate Lasso” approach maximizes K penalized likelihoods, ℓk(βk,·) − λk‖βk,·‖1, separately for each subpopulation. Another similar approach to address heterogeneity of main effects is provided by maximizing the following likelihood:
The primary difference between this, which we call the “Expanded Lasso” and the “Separate Lasso” is that there is one intercept in the Expanded Lasso and one tuning parameter instead of K tuning parameters. We also fit models with interactions of the stratifying variables with all of the covariates, which we call the “Interaction Lasso” and “Interaction HierLasso.” The former uses a lasso penalty on all coefficients whereas the latter utilizes an overlapping group lasso penalty which enforces the hierarchy as specified in Zhao et al. (2009). Note that our method with the adaptive weights cannot be fit when nk < p. Therefore, we also fit alternatively a model that uses λG, j = |G|1/2. We denote this method in the simulation as “vennLasso.” Our method is denoted as “vennLasso Adaptive.” Our simulation covers the p > n paradigm and as such our theoretical results for the vennLasso Adaptive method do not apply. Motivated by the work of Huang et al. (2008), we use marginal regression estimates to construct λG, j for the adaptive version of the vennLasso when p > n.
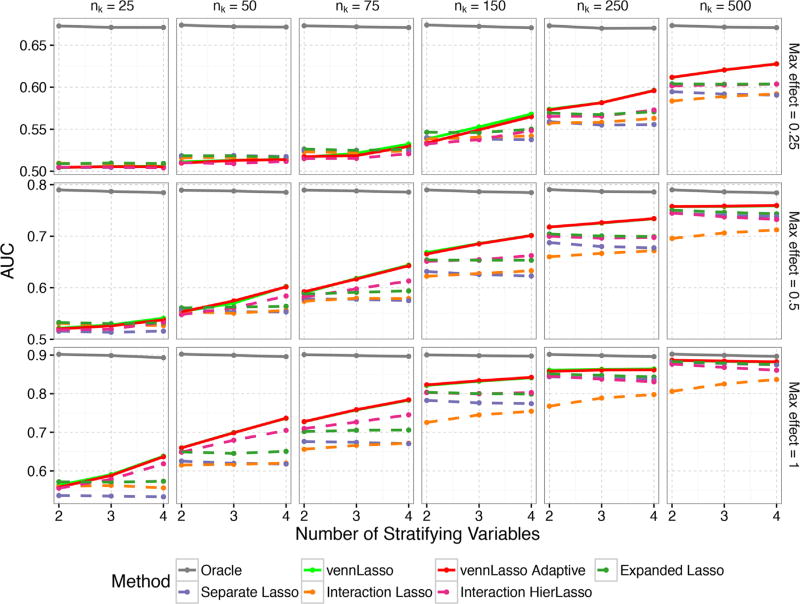
The models are compared in terms of predictive performance as measured by area under the receiver operating characteristic curve (AUC) on an independent data set of 10,000 observations. The AUC results are shown in Figure 3 for the setting with p = 100 and the average sparsity of the coefficients is 0.875, meaning on average 87.5% of coefficients are zero. When the information contained in simulated data sets is relatively weak, that is when the sample size per stratum nk, or the max effect size, or the number of stratifying variables C are small, the advantage of our method is not obvious as all methods performed quite inadequately. The advantage of our method is more noticeable when nk becomes bigger (e.g., 75) or C becomes bigger (e.g., 4) or the signal strength is stronger (e.g., max effect size of 1). The average AUCs from our methods are larger than 0.7 whereas the AUC from the second best method (“Interaction HierLasso”) is just about 0.66 when nk = 150, C = 4, and the max effect size is 0.5. In the extreme case when the information contained in simulated data sets is very strong, that is when nk is as large as 500 and C = 4, all methods (except “Interaction Lasso”) perform well. The improvement of our method over the comparison methods also seems to be more noticeable with larger C. Results for other settings with higher and lower sparsity are very similar and thus the figures corresponding to these simulations are in the online Supplemental Materials.
Figure 3.
The number of covariates is set to 100 and the average sparsity of the coefficients is 0.875 for this simulation. The number of observations listed is the number of observations per subpopulation. Hence, the number of coefficients to be estimated and the number of total observations increase together, but their ratio is consistent.
While prediction is the primary interest of this article, we also investigate the variable selection properties of vennLasso and vennLasso Adaptive. We investigate the average number of false positives and false negatives. With some compromise of false positives, our methods tend to have much better false negative controls than other approaches when C is larger. These results are presented in the online Supplementary Materials. Furthermore, average coverage levels for adaptive version of our proposed estimator are also given in the online Supplementary Materials for some selected settings. The coverage levels are close to 95% overall, but slight over-coverage can also happen in some settings.
Computation time for the vennLasso and vennLasso adaptive scale well when the number of observations increases, however, the computation time increases exponentially with the number of stratifying factors C, as C increases the number of parameters exponentially. In no setting is the computation time longer than approximately 4000 seconds on average. Computation times for the vennLasso and vennLasso Adaptive are given in the online Supplementary Materials.
5. Modeling Hospital Admission with Validation
The ACO data to be modeled contains information on hospital admissions for 41,979 patients. The data for each patient are collected on a monthly basis. Of interest for the ACO each month is the predicted risk of hospitalization for the following 3 month period. 12 months of baseline data are utilized for each patient for modeling hospitalization within the subsequent 3 month period. Covariates include lab values such as A1c level, health care payment information, demographic information, Hierarchical Condition Categories (HCC) variables (Pope et al., 2004), primary care and specialty care visits, baseline hospital admission information, medications, and other various medical information. The response is an indicator of whether any given patient was hospitalized during the 3 month follow-up period.
We compare all the methods that were used in the simulation section on a validation approach. The data were split randomly into training and validation datasets of sizes 20,989 and 20,990, respectively. The three modeling approaches were estimated using the training sample based on logistic regression models. The tuning parameter for each of the models was chosen via 10-fold cross validation using area under to ROC curve (AUC). The models were then validated by evaluating the AUC on the validation data. A breakdown of the validation and selection results for each of the approaches by subpopulations is presented in Table 1. The performance of vennLasso Adaptive is nearly the same as the other methods on the subpopulation with no conditions (with the vennLasso Adaptive having an AUC of 0.767 and others ranging from 0.701 to 0.770), however for all of the other subpopulations vennLasso Adaptive and the vennLasso perform markedly better, especially for most of the smallest subpopulations. For example, for the subpopulation with all three chronic conditions the vennLasso adaptive and vennLasso have an AUC of 0.629 and 0.619, respectively, whereas others have an AUC ranging from 0.501 to 0.568. As the focus of risk modeling is often the populations of complex patients with many chronic conditions and higher disease burden, it is crucial to construct effective risk models for them in particular. Often, these subpopulations are of greatest interest to hospital administrators, who often target complex patients with more chronic conditions with tailored interventions to help improve their outcomes. We also compare our approach with the others in terms of oveall AUC for the entire validation set population. From these results displayed in Table 2, we can see that our approach performs better overall as well. On this dataset, the Interaction Lasso was computed in 678 seconds, the Separate Lasso was computed in 44 seconds, the Expanded Lasso was computed in 517 seconds, the Interaction HierLasso was computed in 4395 seconds, the vennLasso was computed in 3874 seconds, and the vennLasso adaptive was computed in 4119 seconds. Full computation details for all methods including computation times are given in the online Supplementary Materials.
Table 1.
This table investigates the performance in terms of AUC of the different modeling approaches on the various subpopulations as defined by the chronic conditions CHF, COPD, and diabetes. Each row represents a separate subpopulation (with ‘N’ indicating the absence of the condition and ‘Y’ the presence). The best AUC for each subpopulation is printed in bold.
| AUC | Number of variables selected | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|||||||||||
| (CHF, COPD, Diabetes) |
Sample size train |
Sample size validation |
VennLasso | VennLasso adaptive |
Interaction lasso |
Interaction hierLasso |
Separate lasso |
Expanded lasso |
VennLasso | vennLasso adaptive |
Separate lasso |
Expanded lasso |
| (N, N, N) | 14, 939 | 14, 693 | 0.760 | 0.767 | 0.769 | 0.766 | 0.770 | 0.701 | 119 | 85 | 47 | 17 |
| (Y, N, N) | 1, 488 | 1, 543 | 0.692 | 0.692 | 0.687 | 0.690 | 0.683 | 0.665 | 35 | 34 | 15 | 17 |
| (N, Y, N) | 471 | 518 | 0.727 | 0.721 | 0.667 | 0.701 | 0.604 | 0.687 | 20 | 17 | 97 | 4 |
| (N, N, Y) | 2, 917 | 3, 022 | 0.699 | 0.693 | 0.690 | 0.695 | 0.679 | 0.649 | 36 | 35 | 15 | 19 |
| (Y, Y, N) | 196 | 189 | 0.587 | 0.593 | 0.609 | 0.519 | 0.583 | 0.512 | 33 | 31 | 2 | 12 |
| (Y, N, Y) | 720 | 784 | 0.752 | 0.750 | 0.760 | 0.740 | 0.706 | 0.722 | 54 | 54 | 34 | 18 |
| (N, Y, Y) | 138 | 131 | 0.727 | 0.726 | 0.688 | 0.725 | 0.569 | 0.510 | 43 | 42 | 2 | 2 |
| (Y, Y, Y) | 120 | 110 | 0.619 | 0.629 | 0.567 | 0.568 | 0.501 | 0.533 | 55 | 60 | 33 | 14 |
Table 2.
This table investigates the performance of each method in terms of overall AUC on the entire population in the validation data.
| Method | Validation AUC |
|---|---|
| vennLasso | 0.784 |
| vennLasso Adaptive | 0.782 |
| Separate Lasso | 0.765 |
| Expanded Lasso | 0.706 |
| Interaction Lasso | 0.782 |
| Interaction HierLasso | 0.779 |
6. Discussion
The proposed penalty aids in unifying analyses involving heterogeneous populations by borrowing strength in variable selection across subpopulations. Our variable selection assumptions are biologically plausible and as such result in more meaningful and interpretable models. We have demonstrated the superiority of our approach over ad hoc approaches in numerical examples and in a large scale application to health system risk modeling. In particular, it can dramatically improve predictive performance for smaller subpopulations while maintaining good predictive performance for larger subpopulations. This property is especially useful, as the smaller subpopulations are of great interest as they represent those with many chronic conditions and are at higher risk of poor outcomes.
Throughout this article, we have modeled the outcome of hospital admission as a binary indicator. While this measure is the primary interest of the ACO, it does not reflect the true nature of the outcome. Specifically, hospital admission is a time-to-event outcome and furthermore patients often experience hospital admissions many times. As such, it is a worthwhile effort to extend our framework to a semicompeting risks model.
In practice, one can also imagine scenarios where some covariates have similar magnitude of effects regardless of the subpopulations. For example, the effect of blood pressure could feasibly be the same for all subpopulations without CHF. In this case, estimation efficiency can be improved if such effects are encouraged to be more similar. An extension of our method to incorporate this idea is to add a fused lasso penalty to subpopulations which are “adjacent” in the hierarchy shown in Figure 2. Specifically, with two conditions, H and D, for each the jth covariate, we would have the two following fused lasso penalties: and λD,HD|βD, j − βHD, j| but not λH,D|βH, j − βD, j|. The weight is chosen to be the adaptive weight . This penalty can provide a safeguard against subpopulation misspecification and could allow for the data to determine which effects should be constant across all subpopulations.
Supplementary Material
Acknowledgments
We would like to thank the Associate Editor and anonymous referees for their helpful comments and suggestions. Research reported in this article was partially funded through two Patient-Centered Outcomes Research Institute (PCORI) Awards (ME-1409-21219 and HSD-1603-35039). The views in this publication are solely the responsibility of the authors and do not necessarily represent the views of the PCORI, its Board of Governors or Methodology Committee.
Footnotes
Additional theoretical results, proofs, details on our ADMM algorithm, and additional numerical results referenced in Sections 3 and 4 are available with this article at the Biometrics website on Wiley Online Library. Our code is available for use as an R package, downloadable at the following location: https://github.com/jaredhuling/vennLasso.
References
- Bien J, Taylor J, Tibshirani R. A lasso for hierarchical interactions. The Annals of Statistics. 2013;41:1111–1141. doi: 10.1214/13-AOS1096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J, Li R. Variable selection via nonconcave penalized likelihood and its oracle properties. Journal of the American Statistical Association. 2001;96:1348–1360. [Google Scholar]
- Huang J, Ma S, Zhang C-H. Adaptive lasso for sparse high-dimensional regression models. Statistica Sinica. 2008:1603–1618. [Google Scholar]
- Jenatton R, Audibert J-Y, Bach F. Structured variable selection with sparsity-inducing norms. The Journal of Machine Learning Research. 2011;12:2777–2824. [Google Scholar]
- Lipska K, Ross J, Wang Y, Inzucchi S, Minges K, Karter A, et al. National trends in us hospital admissions for hyperglycemia and hypoglycemia among medicare beneficiaries, 1999 to 2011. Journal of the American Medical Association Internal Medicine. 2014;174:1116–1124. doi: 10.1001/jamainternmed.2014.1824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore B, Levit K, Elixhauser A. Costs for hospital stays in the united states, 2012: Statistical brief #181. Healthcare Cost and Utilization Project (HCUP) Statistical Briefs. 2014:1–12. [Google Scholar]
- Percival D. Theoretical properties of the overlapping groups lasso. Electronic Journal of Statistics. 2012;6:269–288. [Google Scholar]
- Pfuntner A, Wier L, Steiner C. Costs for hospital stays in the united states, 2010: Statistical brief #146. Healthcare Cost and Utilization Project (HCUP) Statistical Briefs. 2013:1–11. [Google Scholar]
- Pope GC, Kautter J, Ellis RP, Ash AS, Ayanian JZ, Ingber MJ, et al. Risk adjustment of Medicare capitation payments using the CMS-HCC model. Health Care Financing Review. 2004;25:119–141. [PMC free article] [PubMed] [Google Scholar]
- Tannen R, Xie D, Wang X, Yu M, Weiner MG. A new comparative effectiveness assessment strategy using the thin database: Comparison of the cardiac complications of pioglitazone and rosiglitazone. Pharmacoepidemiology and Drug Safety. 2013;22:86–97. doi: 10.1002/pds.3360. [DOI] [PubMed] [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society, Series B (Methodological) 1996;58:267–288. [Google Scholar]
- Yuan M, Lin Y. Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society, Series B (Statistical Methodology) 2006;68:49–67. [Google Scholar]
- Zhao P, Rocha G, Yu B. The composite absolute penalties family for grouped and hierarchical variable selection. The Annals of Statistics. 2009;37:3468–3497. [Google Scholar]
- Zou H. The Adaptive Lasso and Its Oracle Properties. Journal of the American Statistical Association. 2006;101:1418–1429. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.