Consumer product chemical weight fractions from ingredient lists

Abstract

Assessing human exposures to chemicals in consumer products requires composition information. However, comprehensive composition data for products in commerce are not generally available. Many consumer products have reported ingredient lists that are constructed using specific guidelines. A probabilistic model was developed to estimate quantitative weight fraction (WF) values that are consistent with the rank of an ingredient in the list, the number of reported ingredients, and labeling rules. The model provides the mean, median, and 95% upper and lower confidence limit WFs for ingredients of any rank in lists of any length. WFs predicted by the model compared favorably with those reported on Material Safety Data Sheets. Predictions for chemicals known to provide specific functions in products were also found to reasonably agree with reported WFs. The model was applied to a selection of publicly available ingredient lists, thereby estimating WFs for 1293 unique ingredients in 1123 products in 81 product categories. Predicted WFs, although less precise than reported values, can be estimated for large numbers of product–chemical combinations and thus provide a useful source of data for high-throughput or screening-level exposure assessments.

Introduction

Performing any assessment of human exposure to chemicals in consumer products requires both a knowledge of the types of products in which chemicals are found and quantitative estimates of their concentrations (i.e., weight fractions, WFs). Such data are needed to inform aggregate (e.g., multi-pathway, multi-route, and multi-source) assessments^1,2,3,4,5,6. Chemical ingredient information is also required to characterize likely mixtures of chemicals in support of estimation of cumulative exposures to substances having a common endpoint^7,8. Finally, quantitative composition information is critical for characterizing the variability and uncertainty in human exposure estimates used in risk evaluations. The recent National Academies of Sciences report ‘Using 21st Century Science to Improve Risk-Related Evaluations’ notes that uncertainty in chemical source information such as product composition is a major obstacle to exposure estimation⁶ and paucity of concentration data has been identified as a significant data gap in exposure assessments of consumer product chemicals.^9,10,11 However, manufacturers in the U.S. are not required to disclose the WFs of specific ingredients in consumer products except in the case of active ingredients in certain products¹² or in the case of chemicals with known health hazards covered by the Occupational Safety and Health Administration’s Hazard Communication Standard.¹³

Researchers have attempted to fill gaps in product ingredient data. The U.S. Environmental Protection Agency (EPA) developed an extensive database of information on the use of chemicals (including use in products) curated from multiple online secondary data sources.¹⁴Goldsmith et al.¹⁵ collected product composition data from publicly available Material Safety Data Sheets (MSDS). Chevillotte et al.¹¹developed methods for predicting chemical composition of products using generic ingredient information and patent-based quantitative information. In this paper, we expand on these efforts and develop a model for predicting quantitative ranges of WFs for intentionally-added chemicals, based on information provided in ingredient lists on product labels. The approach is based on the fact that lists which follow labeling guidelines provide sufficient information to constrain the range of possible WF values for the ingredients.

Consumer products regulated by the U.S. Food and Drug Administration (FDA), including cosmetics and personal care products, must have labels that include ingredient lists established using the following requirements:12

1. All intentionally added ingredients must be listed unless they are claimed to be a trade secret. The name of an ingredient accepted by FDA as a trade secret need not be disclosed on the label. In lieu of declaring the name of that ingredient, the phrase “and other ingredients” is used at the end of the ingredient declaration.

2. Ingredients are listed in descending WF order, with the following exceptions:

   1. If the product is considered to be a drug, then the active ingredients must be listed first and the WFs must be reported.

   2. Ingredients with WFs below 0.01 can be listed in any order.

   3. Color additives can be listed separately at the end of the list of ingredients and in any order.

3. Fragrance and flavor compounds may be declared individually by their appropriate label names or as “fragrance” and “flavor.” If a fragrance compound also serves as a flavor, it must be declared as “flavor and fragrance.”

Some manufacturers voluntarily provide ingredient data to the public for certain other product types. For example, the American Cleaning Institute (ACI) and the Canadian Consumer Specialty Products Association have organized their member companies to provide ingredient lists for cleaning, air care, floor maintenance, and automotive products. These lists are reported in a manner similar to FDA. Specifically, all ingredients are reported in descending order of WF and ingredients with WFs <0.01 may be reported in any order.¹⁶ Consumer product manufacturers may also provide online product disclosure sheets that list all ingredients in descending WF order.

We propose that the relationship between these labeling rules and possible values of ingredient WFs can be modeled using Monte Carlo techniques, and we present an algebraic model for predicting WF ranges for intentionally-added substances from ingredient lists. We use composition data previously collected by the US EPA ^15,17 to select key model parameters. We apply the model to estimate WFs for 1293 unique ingredients in 1123 real products. The predictions are summarized by ingredient, product categories, and previously developed harmonized chemical function categories.^17,18 The estimates were evaluated by comparing them to WFs reported on MSDS for similar products and functions. These methods can be applied to thousands of additional lists to fill gaps in existing information for high-throughput aggregate exposure assessments for chemical screening or prioritization.

Methods

All analyses were performed in R version 3.3.2 (ref. ¹⁹) or SAS version 9.4.²⁰ We first developed a Monte Carlo model for lists in which all ingredients were reported and ranked according to decreasing WF. This method was then modified to address lists in which ingredients with WF <0.01 were randomly ordered. The two versions of the model (called Case 1 and Case 2) were required since both approaches are used by manufacturers to create ingredient lists that appear on product labeling. Finally, approaches were developed for addressing special cases wherein color additives, trade secret ingredients, or active ingredients were not reported in WF order. Simulation results were compared to an existing dataset of reported WF values. Optimal model assumptions were determined and predictions made for lists having various lengths.

Model for Ingredient Lists Ranked by Descending WF (Case 1)

The equations below describe WF values for ingredients in terms of an upper and lower bound. These bounds are a function of the number of reported ingredients in the product, the ingredient rank (position in the list), a minimum WF for intentionally added ingredients, and the total WF associated with unlisted components (e.g., contaminants or unreported substances).

We assume that intentionally added ingredients have a minimum plausible WF (WF_m), based on the reasoning that performing an intended function requires some minimum concentration. We denote the ingredient rank in a list as i, where i=1 for the first ingredient and Nfor the last ingredient. For the first ingredient (i=1), the upper bound on WF (WF_1,upper) is calculated by subtracting from the total product WF (WF_total=1) the sum of: (1) the WF associated with all unreported substances (WF_u) and (2) the WF associated with all other reported ingredients (i.e., those with rank >1). WF_1,upper is determined when the total WF of the remaining ingredients is minimized (i.e., all of the remaining ingredients have WF=WF_m). Thus:

$$\mathrm{W}{\mathrm{F}}_{1\cdot \mathrm{U}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{r}}=1-\left(\mathrm{W}{\mathrm{F}}_{\mathrm{u}}+\mathrm{W}{\mathrm{F}}_{\mathrm{m}}\left(N-1\right)\right)$$ (1)

The upper bounds for the remaining ingredients (WF_i,upper, i ≠ 1) have two constraints. First, WF_i,upper must be less than WF_total minus the sum of: (1) WF_u, (2) the WF associated with all remaining reported ingredients (as in Eq. (1)), and (3) the combined WF of all ingredients with rank < i (i.e., those before it in the list). Second, the value must be less than the WF value of the ingredient immediately before it on the list (i−1). Therefore:

$$\mathrm{W}{\mathrm{F}}_{i\cdot \mathrm{U}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{r}}=\min \left[1-\left(\mathrm{W}{\mathrm{F}}_{\mathrm{u}}+\mathrm{W}{\mathrm{F}}_{\mathrm{m}}\left(N-i\right)+{\displaystyle \sum _{j=1}^{i-1}\mathrm{W}{\mathrm{F}}_j}\right),\mathrm{W}{\mathrm{F}}_{i-1}\right]\left(i\ne 1\right)$$ (2)

The lower limit on the WF for any ingredient i (WF_{i, lower}) occurs when the sum of the WF for ingredients with rank >i is at a maximum value, which occurs when they are all equal to WF_i, (as they cannot exceed WF_i when the list is rank ordered based on WF). Thus WF_{i, lower} can be estimated by dividing the remaining fraction of the product (once WF_uand the sum of the WFs with higher rank are subtracted) by the number of remaining ingredients (N-i+1).

$$\mathrm{W}{\mathrm{F}}_{i\cdot \mathrm{l}\mathrm{o}\mathrm{w}\mathrm{e}\mathrm{r}}=\frac{1-\left(\mathrm{W}{\mathrm{F}}_{\mathrm{u}}+{\displaystyle {\sum }_{j=1}^{i-1}\mathrm{W}{\mathrm{F}}_j}\right)}{N-i+1}$$ (3)

The distribution of WF_i within its upper and lower bounds is

$$\mathrm{W}{\mathrm{F}}_i=\mathrm{W}{\mathrm{F}}_{i\cdot \mathrm{l}\mathrm{o}\mathrm{w}\mathrm{e}\mathrm{r}}+X\left[\mathrm{W}{\mathrm{F}}_{i\cdot \mathrm{U}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{r}}-\mathrm{W}{\mathrm{F}}_{i\cdot \mathrm{l}\mathrm{o}\mathrm{w}\mathrm{e}\mathrm{r}}\right]$$ (4)

where X is a continuous random variable between 0 and 1, sampled from a distribution of a given shape (e.g., for a uniform distribution X∼U([0,1]). Valid combinations of WF_u and WF_m are constrained by the number of ingredients, N:

$$1-\mathrm{W}{\mathrm{F}}_u\ge \mathrm{W}{\mathrm{F}}_m\times N$$ (5)

In applying the model, a value WF₁ is randomly selected from its range WF_1,upper-WF_1,lower (calculated with Eqs. (1) and (3)). The sampled WF₁value is used to calculate the upper and lower bounds for WF₂. The value of WF₂ is determined by randomly sampling between its upper and lower bounds and then used to calculate bounds for WF₃, and so on for all i. This entire process is repeated in a Monte Carlo manner, sampling many initial WF₁ values. The result is a WF distribution for each ingredient in the product list, which can be characterized using metrics such as the mean, 50th percentile (median), lower 95% confidence limit (LCL), and upper 95% confidence limit (UCL).

As predicted WFs are a function of the total number of ingredients, separate runs of the model are required to assess ingredient lists of various lengths. The approach also requires that the user make assumptions for the values of WF_m and WF_u and shape of the distribution X. An example result for a generic product with three ingredients is illustrated in Figure 1. The impacts of various assumptions for model inputs are explored below; however, it is useful to note that WFs for ingredients are particularly sensitive to WF₁. The shape of the distribution X for WF₁ has a dramatic effect on the WF distributions for the remaining ingredients. If WF₁ is close to its upper bound, then the WFs of remaining ingredients must occur at very low levels. There are products where this occurs. For example, a liniment may contain an active ingredient at a small WF (e.g., 0.015 menthol) dissolved in a large amount of acetone (along with small amounts of fragrances, colorants, etc.). At the other extreme, if WF₁ is at or near its lower bound, then the remaining compounds will occur at similar concentrations. The example of this phenomena is illustrated for a product with five ingredients in Figure 2.

Figure 1:

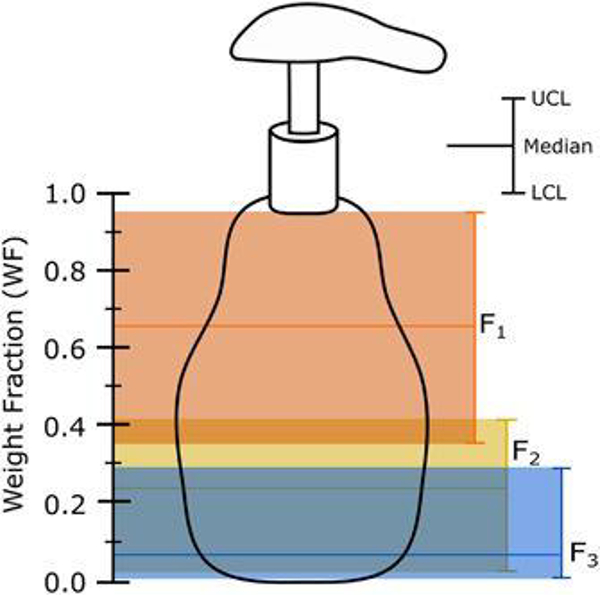
Predicted median, 95% lower confidence limit (LCL) and 95% upper confidence limit (UCL) for each ingredient of a product formulation with N=3 ingredients. The assumed values of the minimum plausible weight fraction for intentionally-added ingredients (WF_m) and the unreported weight fraction (WF_u) were 10⁻⁹ and 0.05, respectively. The distribution of the weight fraction was assumed to be uniformly distributed between the calculated bounds (Eqs. (1)–(4)) for each ingredient.

Figure 2:

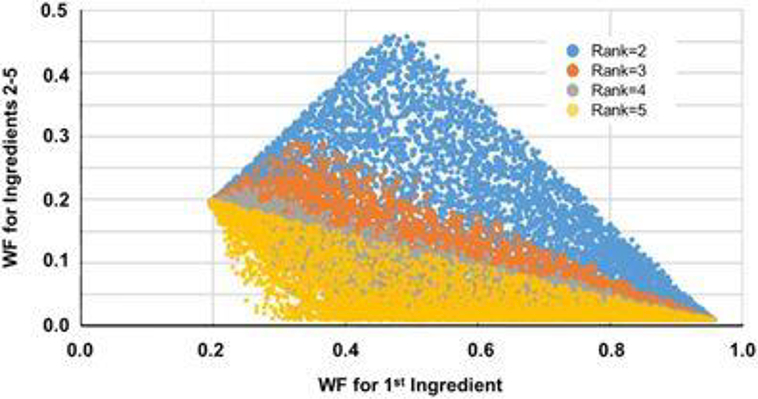
Simulated weight fractions (WF) for ingredients with ranks 2–5 as a function of the WF of the first ingredient (5000 Monte Carlo simulations) for a product with 5 ingredients. When the sampled WF for the first ingredient is close its lower bound (Eq. (3)), all the remaining ingredients have similar predicted WFs. As the sampled WF of the first ingredient increases towards its upper bound (Eq. (1)), predicted WFs for other ingredients become more variable. Finally, as the first WF reaches its upper bound, all the other ingredients approach the minimum plausible weight fraction for intentionally added ingredients (WF_m).

Alterations to the WF Model for Case 2

The Monte Carlo model described above can be adjusted to account for labeling rules allowing ingredients below a given WF to be reported in a random order, for example, the 0.01 WF threshold in the FDA guidelines and the ACI initiative (Case 2). To address this rule in each iteration of the Monte Carlo analysis, WFs for all ingredients are first calculated using Eqs. (1)–(5). The order of ingredients having a predicted WF less than the threshold is then randomly shuffled.

Addressing Special Types of Ingredients

Under the FDA rules, WFs for active ingredients are reported at the beginning of a list. In this case the value of WF_u is increased to account for the WFs of the active ingredients (as it represents the fraction not accounted for by the ordered part of the list). The total number of ingredients is also reduced to N_new=N−N_active where N_active is the number of active ingredients. The model is then applied to generate predictions for the remaining ingredients, resulting in point estimates for each of the active ingredients and distributions for the remaining ingredients.

As stated above, when ingredients meet the FDA criteria for a trade secret they are reported as “other ingredients” at the end of the list. In addition, color additives may be reported at the end of the list. In these cases, the assumed value of WF_u can be revised to account for these additional ingredients (e.g., based on a priori knowledge of likely WFs).

Sensitivity Analyses and Selection of Model Parameters

The inputs to the model (WF_m, WF_u, and the shape X of the WF distribution between the upper and lower bounds) were selected here based on review of available data and sensitivity analyses. WF data curated by EPA from MSDS^{15, 17} were used to identify reasonable values for WF_m and X. No empirical data were identified for selecting a value for WF_u. A sensitivity analysis was performed to determine the impact of alternative assumptions for the three inputs. The WF model was used to generate distributions for “generic” ingredient lists of different lengths using the different assumptions; lists having 2–20 ingredients were modeled. Model predictions for both Case 1 and Case 2 were repeated assuming WF_u=0, 0.01, 0.05, 0.10, 0.25, and 0.50 for WF_massumptions of 10⁻⁹ and 10⁻³. WF_u values were selected based on the assumption that chemicals in ingredient lists will reflect at least half of the weight; the two WF_m values were the minimum and 5th percentile of midrange WF reported in the MSDS data. Ten thousand (10,000) Monte Carlo repetitions were performed for each simulation in order to resolve WF percentiles for all ingredients. Mean, median, LCL, and UCL statistics were calculated for each ingredient rank in each list. Reasonable values of WF_m, WF_u were selected based on these analyses.

The sensitivity analyses were repeated using uniform, symmetric triangular (mode=0.5), and high-weighted triangular (mode=1.0) random distributions for X (Supplementary Figure S1). These shapes were selected as they are the simplest examples of bounded distributions. Predictions from the WF model using each of the three shapes for Xwere compared against midrange ingredient WFs reported in the MSDS data for lists of different lengths. The MSDS WF data for individual products were somewhat incomplete since many sheets omit common substances with low toxicity (e.g., water). As result, the values of N and the rankings of individual ingredients for some products were uncertain. To minimize the impact of this uncertainty, only products with a sum reported midrange WF >0.6 were used to assess the selection of X. A total of 330 MSDS met these criteria; lists with 2–7 ingredients contained enough products (N_products > 4) to allow for comparison. Based on these comparisons, a recommended shape X was selected for the final model.

Application of the WF Model to Case Study Ingredient Lists

The WF model was applied in a case study using real ingredient lists obtained from online sources (e.g., from product ingredient disclosure sheets). Sources of data included: Arm and Hammer (www.armandhammer.com), n=35 products; Palmolive (www.palmolive.com), n=16; Procter and Gamble (www.pandg.com), n=226; and Unilever (www.unilever.com), n=846. The products in these lists were categorized via a set of product use categories (PUCs) (e.g., toothpaste and shampoo) developed for exposure modeling.^{1, 17} Where possible, chemicals were categorized according to their function in products (as in Isaacs et al.¹⁷ and Phillips et al.¹⁸) Details of the collection and curation of the lists and categorization of products and chemicals are given in the SI. In total, 1123 lists (containing 24,228 individual ingredient observations and 1293 unique ingredient names) were collected.

Using selected values (see Results) for WF_m, WF_u, and X, the model was applied (10,000 repetitions) to generate WFs for generic lists having 2–55 ingredients (the minimum and maximum N in the lists) using both Case 1 and 2 labeling rules. Each of the real products was then assigned a set of ingredient WF predictions matching its list length. Based on information provided on its ingredient disclosure sheets, lists obtained from Unilever were assigned Case 1 predictions (all ingredients were reported in descending order); all other lists were assumed to follow the ACI communication guidelines, and assigned Case 2 predictions, as the sources were identified via the ACI communication initiative webpage.¹⁶

Lists having color additives noted at the end (14 products) were treated uniquely. The mean average WF associated with known colorants in personal care and household cleaning products in the MSDS database was 0.012 (N=1544); the median was 0.001, and the 95th percentile only 0.05. As changes in WF_u below 0.1 were shown to have little effect on model predictions (see Results), unique model runs were not performed for these products. However, the value of N was reduced to correct for the colorants not included in the rank-ordered list.

The ultimate result was that each ingredient in each product was assigned median, LCL, and UCL WF predictions. These metrics were summarized by ingredient/chemical, by function (e.g., solvents), and by function within different PUCs (e.g., solvents in shampoo). These results were also compared with the MSDS data.

Results

Determination of WF Model Inputs

The impact of assuming different values of WF_u for products having 2–20 ingredients is shown in Figure 3. In this case, X was assumed uniform and WF_m was assumed to be 10⁻⁹. There was little impact of changing WF_u at values of WF_u < 0.1, as this value is small compared with the estimated WFs for ingredients with near the top of the list. As WF_uincreases, WFs decrease, as the upper bound on WF₁ becomes significantly decreased by WF_u. These results imply that when WF_uvalues are assumed to be quite low, estimates for most ingredients should be valid (i.e., only the most highly-ranked ingredients would be impacted by an incorrect assumption). Similar results were obtained for the other shapes of X (results not shown). Therefore, for further application of the model we chose a relatively small WF_u (0.01).

Figure 3:

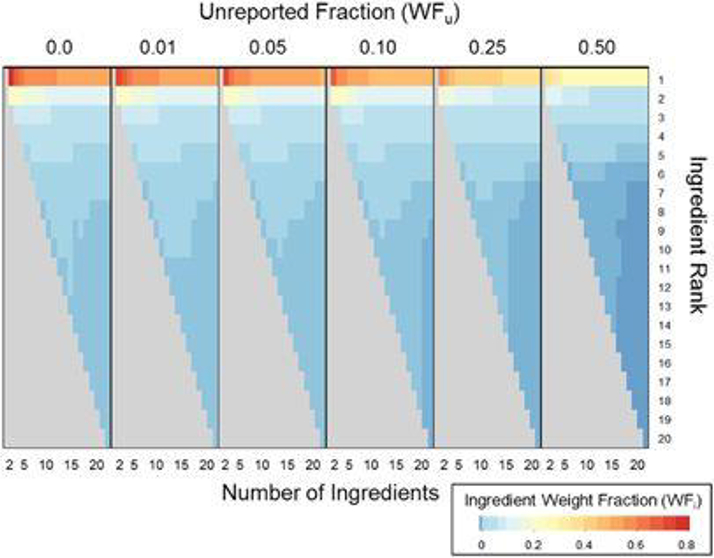
Impact of unreported product fraction (WF_u) on predicted weight fractions (WF). The minimum plausible WF for intentionally-added ingredients (WF_m) was 10⁻⁹ and X was assumed to be uniform. Case 1 labeling ruls (eall ingredients reported in descending WF order) were assumed.

The five runs illustrated in Figure 3 were repeated assuming WF_m=0.001 (results not shown). Increasing WF_m decreased predicted WF for ingredients at the top of the list slightly, as increasing WF_m increases the lower bounds for ingredients. However, the differences in the predictions between the two tested WF_m values were small. The maximum decrease in median WF for any ingredient was 0.015; the largest differences all occurred for i=1. The largest decrease associated with any other ingredient was 0.0042. Therefore, due to the relative insensitivity of the model to WF_m in this range of reasonable values, we chose to use our initial assumption of 10⁻⁹ (the MSDS minimum).

Predictions using WF_u=0.01 and WF_m=10⁻⁹ for different shapes of the probability distribution X were examined and compared with the EPA MSDS data (Figure 4). The differences in WF when using a uniform versus a symmetric triangle distribution for X were small. Using a high-weighted triangle distribution for X gave higher WF for ingredients at the beginning of the list and much lower WFs for ingredients later in the list (Figure 4a). Comparisons of the model with midrange MSDS values for products having five ingredients (N_products=45) are given in Figure 4b; comparisons for products with three (N_products=89) and seven (N_products=4) ingredients are given in Supplementary Figure S2. Predicted median (symbols) and UCL/LCL (whiskers) are compared against median, 5th percentile, and 95^th percentile MSDS WFs. The predicted WFs were reasonably close to the MSDS values, generally with the median WF of each ingredient falling within an order of magnitude of the median value from MSDS. Across products with different numbers of ingredients, MSDS medians compared best to WF predictions made assuming either a uniform or symmetric triangle for X. The comparisons were best for products with more reported ingredients, which could indicate that some MSDS products with only 3 reported components were missing data.

Figure 4:

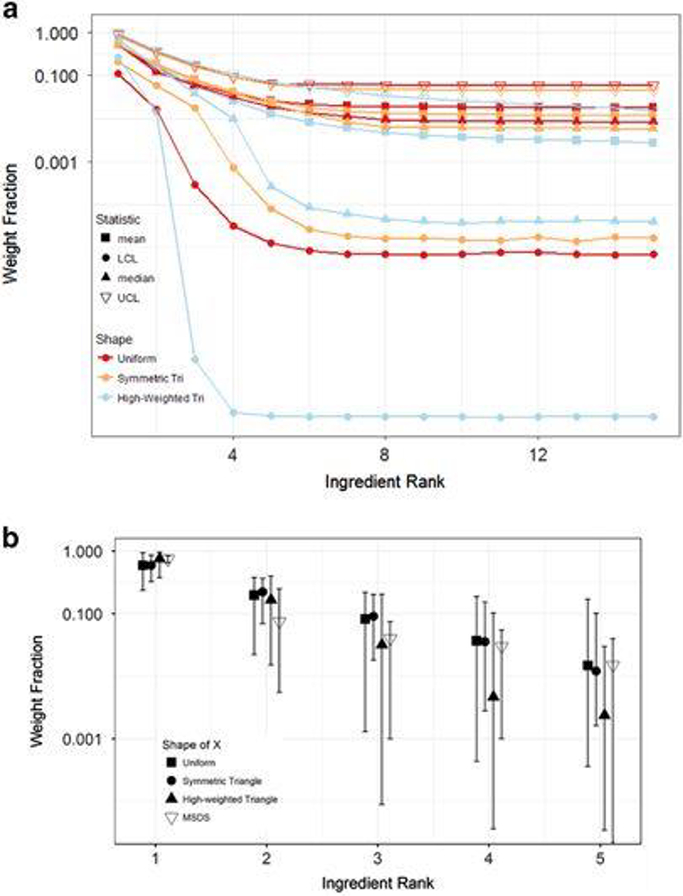
Impact of three different assumptions for the shape of random variable X (WF_m=10⁻⁹ and WF_u=0.01). (a) Impact of shape Xon predicted WFs for a generic product with 15 ingredients (Case 2 labeling rules). (b) Comparison of predicted weight fractions from ingredient lists with WF values reported on Material Safety Data Sheets (MSDS) for products having 5 (N_products=45) reported ingredients. Plotted points are means; bars extend to the 5th (LCL) and 95th (UCL) percentiles.

Empirical distributions of WF₁ from MSDS were examined (Supplementary Figure S3); these distributions were not broken out by number of ingredients due to the relatively small product sample sizes. The distributions for WF₁ were slightly different for products having water as a first ingredient versus other products, but these differences were not significant (two-sample Kolmogorov-Smirnov test, P=0.8). These distributions were best approximated as a uniform distribution, despite the fact that there were spikes in WF₁ around “nominal” reporting values of WF (e.g., 0.8). These results support the assumption of a uniform distribution for X.

Model Predictions for Lists of Various Lengths

Final model predictions using WF_m=10⁻⁹, WF_u=0.01, and a uniform distribution for X were generated for Case 1 and Case 2 rules for generic ingredient lists having 2–55 ingredients. Median and upper 95% UCL WF for products with 1–15 ingredients for Case 1 are given in Table 1; full results are given in Supplementary Table S2. The mean and UCL WF decrease as expected for each ingredient as the number of ingredients increases. The median WF of the first ingredient was most sensitive (in terms of absolute fraction) to the increasing number of ingredients (ranging from 0.746 for a single-ingredient product to 0.532 for a product having 15 ingredients). Ingredients with ranks of 2 and above become less sensitive to changes in the number of ingredients. For products with a large number of ingredients the median values of WF associated with each ingredient rank decreases most rapidly for ranks of eight or less. Similar patterns are seen in the UCL.

Table 1:

Results of the WF model for WF_m=10⁻⁹ and WF_u=0.01 for formulations with 2–15 ingredients.

Number of Ingredients
	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Rank	Median predicted WF for ingredient
1	0.746	0.655	0.613	0.586	0.578	0.570	0.556	0.550	0.542	0.545	0.546	0.525	0.530	0.532
2	0.244	0.242	0.222	0.197	0.175	0.160	0.149	0.141	0.137	0.132	0.128	0.128	0.124	0.119
3		0.074	0.085	0.083	0.081	0.079	0.076	0.073	0.070	0.067	0.063	0.063	0.060	0.058
4			0.029	0.036	0.039	0.039	0.039	0.037	0.036	0.034	0.033	0.034	0.033	0.030
5				0.015	0.020	0.023	0.024	0.022	0.023	0.021	0.020	0.021	0.020	0.019
6					0.009	0.014	0.016	0.016	0.016	0.014	0.015	0.015	0.014	0.014
7						0.008	0.011	0.012	0.013	0.011	0.012	0.012	0.011	0.011
8							0.008	0.010	0.011	0.010	0.010	0.011	0.010	0.010
9								0.007	0.009	0.009	0.009	0.010	0.009	0.009
10									0.008	0.008	0.009	0.009	0.008	0.008
11										0.007	0.008	0.009	0.008	0.008
12											0.008	0.009	0.008	0.008
13												0.008	0.008	0.008
14													0.007	0.008
15														0.008
	95% UCL for ingredient
1	0.967	0.954	0.953	0.948	0.948	0.951	0.945	0.944	0.947	0.947	0.948	0.944	0.944	0.944
2	0.471	0.412	0.390	0.381	0.377	0.371	0.364	0.365	0.363	0.364	0.357	0.360	0.361	0.356
3		0.294	0.248	0.217	0.202	0.192	0.184	0.180	0.173	0.174	0.171	0.172	0.168	0.167
4			0.216	0.189	0.161	0.140	0.124	0.115	0.110	0.105	0.100	0.098	0.093	0.091
5				0.172	0.150	0.132	0.116	0.105	0.095	0.087	0.080	0.075	0.070	0.066
6					0.143	0.126	0.113	0.101	0.091	0.083	0.077	0.072	0.066	0.062
7						0.122	0.111	0.099	0.089	0.082	0.075	0.070	0.065	0.060
8							0.109	0.099	0.089	0.081	0.074	0.069	0.064	0.060
9								0.097	0.088	0.081	0.074	0.069	0.064	0.059
10									0.088	0.081	0.074	0.069	0.063	0.059
11										0.080	0.074	0.069	0.063	0.059
12											0.073	0.069	0.063	0.059
13												0.069	0.063	0.059
14													0.063	0.059
15														0.059

1. Abbreviation: WF, weight factor.

2. A uniform distribution shape between ingredient upper and lower bounds was used. All ingredients were reported in descending order (Case 1). Full results for both labeling cases are given in the Supplementary Information.

The impact of assuming a WF threshold for ingredient ordering (Case 1 versus Case 2) was found to be modest. A comparison of predicted WFs for Case 1 versus Case 2 for a product with 15 ingredients assuming WF_u=0.01 and a uniform distribution for X is shown in Supplementary Figure S4. There was little impact of labeling case assumption on mean, median, or UCL WF (especially for ingredients near the top of the lists). However, the LCL for Case 2 flattens out more quickly as a function of ingredient rank compared to Case 1.

Predicted WFs for Collected Ingredient Lists

WFs were assigned for all ingredients in the 1123 collected public lists (SI Supplementary Table S3) using WFs predicted using Case 1 or 2 labeling rules and WF_m=10⁻⁹, WF_u=0.01, and X=U[0,1]. As described in the Methods, Case 1 predictions were applied to lists obtained from Unilever and Case 2 predictions applied to all other lists, and model inputs were adjusted for lists where color additives were reported at the end.

Predicted WF metrics (median, UCL, and LCL WF) for the list ingredients were averaged across chemical functions and ingredient names. The predictions for functions (Supplementary Table S4) were consistent with general knowledge of consumer product formulations; for example, “Solvents” had the highest predicted average median WF (0.21), whereas preservatives had the lowest (0.005). Ingredients with at least 20 occurrences in products are summarized in Supplementary Table S5 (ranked by average median estimated WF across products); chemicals with highest average median WF included ubiquitous ingredients such as ethyl alcohol, butane (a propellant), and water, which had the highest predicted median WF (0.41). A comparison between the predicted WFs and midrange MSDS-reported values, by function in PUC (e.g., solvents in hairsprays), is shown in Figure 5. There was reasonable agreement between the MSDS values and the model predictions WFs, given that MSDS sheets often report a WF range for an ingredient (e.g., 0.3–1).

Figure 5:

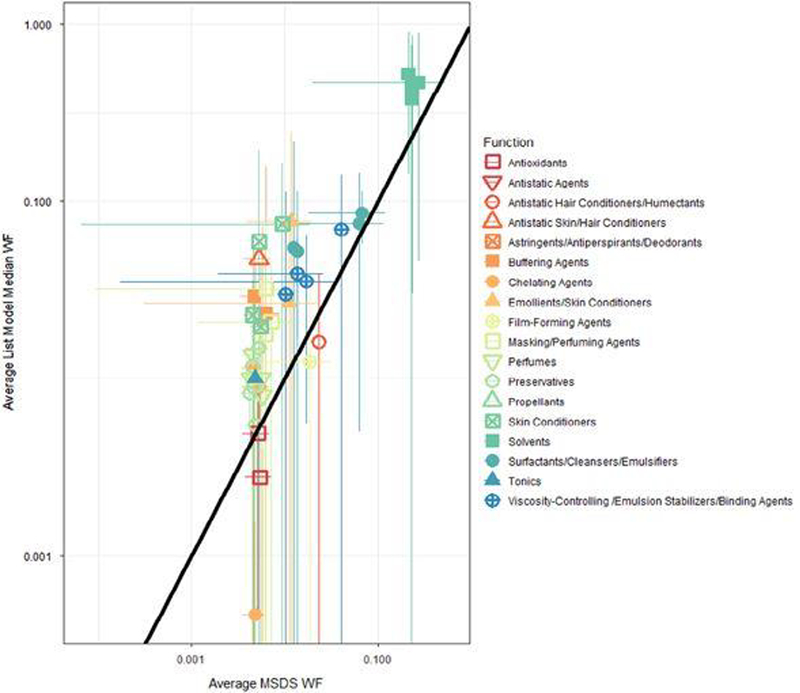
Evaluation of WFs predictions by product use category (PUC) and function: WFs reported on MSDS sheets are plotted versus list model predictions for 96 PUC function combinations. List model predictions are average median WFs across products in PUCs for all ingredients having a known function (e.g., solvents in hairsprays). Error bars indicate SD in the median WF across products within PUC.

Discussion

We present here a methodology to estimate plausible WF ranges for consumer product ingredients based on product labels. The approach is based on algebraic reasoning and is not dependent on the nature of the products. Thus, it should be applicable to any product where the ingredient list is known to follow the FDA or similar rules. The methodology used does require assumptions concerning WF_u, WF_m, and the shape of the WF distribution between calculated bounds. As shown above, the predictions are relatively insensitive to uncertainties in WF_mand values of WF_u that are less than 0.1. However, the approach is dependent on an assumption of the WF of the first ingredient, and the shape of the distribution of WF values between the minimum and maximum values of each ingredient.

In this study we recommend using a uniform distribution of WFs between predicted bounds for each ingredient. Assuming a uniform distribution is consistent with empirical MSDS data for the first ingredient (largest WF) and produces estimates for ingredients of different ranks that approximate MSDS-reported values. The methodology also produces plausible predictions for certain classes of ingredients. Chemicals providing certain functions (e.g., solvents, propellants, and emulsifiers) are predicted to have larger WFs, consistent with typical product formulations that include these types of ingredients. The finding that assuming a uniform distribution produces plausible results suggests that consumer products generally include products that are dominated by a single ingredient and products that contain multiple ingredients at similar concentrations (e.g., as illustrated in Figure 2).

The model is also able to account for chemicals that are not listed in order of WF. We were able to produce WF predictions for products that placed colorants at the end of the ingredient list by using known information about colorant WFs. In the case of products that include trade secret ingredients, the model estimates should be interpreted more carefully, as one does not know the true WF_u value that these ingredients represent. In the ingredient lists presented here, there were no products with trade secret ingredients. Application of this model to lists curated from other sources should take this into account. In the future, the method could be adjusted for the case in which some particular ingredients have additional information (e.g., some known or estimated bounds) based on a priori knowledge, such as a regulatory limit or a known function.

The WF predictions developed here are best-suited to screening-level evaluations of individual chemicals or substances, rather than any higher-tier evaluation of an entire formulation. Although the predicted chemical WF of the product is conserved (adds to 1) for any individual Monte Carlo run of the model and for the mean values of the ranges, the same is not true for the percentiles (e.g., medians or UCLs), which would be important if one were performing a quantitative assessment of the mixture comprising the formulation. However, the median predicted WFs could certainly inform mixture analyses wherein binning concentrations (e.g., as high/low) was appropriate.

The predictions of WF produced from this approach are uncertain. The range between the LCL and UCL can exceed an order of magnitude for ingredients with higher ranks (close to the top of the list) on longer lists. This indicates that although the rules used to create the lists constrain the values of WF they do not precisely define the values. Despite this inherent uncertainty, there are a number of reasons why the results are useful. There are large numbers of products with ingredient lists that have no MSDS sheets or sheets with minimal composition data. Larger numbers of ingredients per product were found here (median=21) compared to the MSDS data (median=6). The larger number may reflect the fact that many MSDS sheets omit components viewed as being nontoxic (e.g., water, starch, etc.) and as a result do not reflect all ingredients. In these cases, predictions based on ingredients lists are an effective way of characterizing composition. Finally, even given the size of the uncertainty the model allows assessors to set useful upper bounds on the WF of a chemical in a product. For example, if a product has eight listed ingredients the assessor can conclude that it is very likely that the one ranked first will have a WF no higher than 0.956 and that the one ranked eighth will be no higher than 0.11. Finally, MSDS data are also reported in terms of ranges, and may also be subject to uncertainty. Where actual WFs are reported, however, these values should be given preference over the predictions made using this approach.

An additional challenge in the use of this approach is chemical synonomy. As mentioned above, ingredient lists use multiple names for ingredients. As a result, the same chemical may be listed in multiple ways (vinegar, acetic acid, ethanoic acid, etc.). Other efforts have curated ingredients lists for limited numbers of chemicals of interest, for example, Gabb and Blake²¹ examined 55 chemicals and endocrine disruptors associated with asthma. In that study, over 38,000 product lists were examined after a significant curation effort to harmonize ingredient names. Ongoing development and curation of chemical databases such as EPA’s Distributed Structure-Searchable Toxicity Database²² and dissemination and integration tools such as the CompTox dashboard²³ will expand our ability to efficiently resolve synonyms for thousands of chemicals at a time, allowing us to leverage additional sources for online lists (e.g., online retailers) and generate predictions for chemicals using data reported under various names.

Finally, it is important to note that reported ingredients do not fully characterize chemicals in consumer products. Ingredients or chemicals may be missing (e.g., due to being a trade secret) or characterized by a generic term (e.g., “fragrance”, “color”) that cannot be mapped to a unique chemical. As discussed above, products also include unintended ingredients. Although this modeling approach does not address these contaminants, it expands the chemicals and products for which quantitative information can be developed. Under the Exposure Forecasting (ExpoCast) project²⁴, EPA is using new non-targeted or “suspect-screening” mass-spectrometry methods to identify thousands of chemicals in environmental media, including consumer products^25,26. Future efforts should focus on ground-truthing our ingredient-based information with measured data, and exploring the extent of the gaps that occur when only reported ingredient data are used.

In summary, we have developed a quantitative WF model that provides a rapid and straightforward way to develop estimates of the magnitude and variability in WF for thousands of products in commerce for which composition data are unavailable. We provide chemical-specific WF predictions for 1293 ingredients in 1123 real products, and present guidelines for applying these models to other lists. These methods can conservatively fill data gaps hindering screening-level exposure assessments, risk evaluations, and quantitative chemical mixture analyses for consumer product chemicals.