Abstract
The brain is a complex system that integrates and processes information across multiple time scales by dynamically coordinating activities over brain regions and circuits. Correlations in resting-state functional magnetic resonance imaging (rsfMRI) signals have been widely used to infer functional connectivity of the brain, providing a metric of functional associations that reflects a temporal average over an entire scan (typically several minutes or longer). Not until recently was the study of dynamic brain interactions at much shorter time scales (seconds to minutes) considered for inference of functional connectivity. One method proposed for this objective seeks to identify and extract recurring co-activation patterns (CAPs) that represent instantaneous brain configurations at single time points. Here, we review the development and recent advancement of CAP methodology and other closely related approaches, as well as their applications and associated findings. We also discuss the potential neural origins and behavioral relevance of CAPs, along with methodological issues and future research directions in the analysis of fMRI co-activation patterns.
Keywords: Resting-state fMRI, Dynamic Brain Connectivity, Co-activation Brain Patterns
Introduction
The advent of resting-state functional magnetic resonance imaging (rsfMRI) has significantly improved our understanding of the organization of large-scale brain networks in health and disease (Biswal et al., 1995; Fox and Raichle, 2007; Zhang and Raichle, 2010). The rapid growth of resting-state research stemmed from the observation that temporal correlations between spontaneous fMRI signals of different brain regions correspond well with known functional connections and networks. Resting-state connectivity is conventionally assessed by computing temporal correlations over an entire scan, which is typically several (and possibly tens of) minutes long. While this “static” connectivity analysis reveals core functional systems and shows similar information as structural brain connectivity (Greicius et al., 2009; Honey et al., 2009), it neglects time-varying information in resting-state fMRI signals that may provide further information about brain function (Hutchison et al., 2013).
Efforts to extract and quantify time-varying information in resting-state fMRI data have opened up a new area of research on “dynamic” resting-state functional connectivity (DFC) and accompanying methodology. Among the existing set of DFC methods, one approach deviates from conventional time-domain approaches by regarding single fMRI volumes at individual time points, instead of fMRI time courses, as basic units of analysis, and focusing on recurring co-activation patterns (CAPs) of the brain and their variability over time. Whereas several excellent reviews describe DFC methods and their applications more generally (Hutchison et al., 2013; Preti et al., 2017), a dedicated survey of CAP analysis is absent to date. Here, we aim to fill this gap by 1) elucidating the basic rationale behind the CAP analysis and its relation to rsfMRI connectivity, 2) surveying variants of CAP analysis methods and their applications, focusing particularly on the aim of understanding global signal variations, 3) examining similarities and dissimilarities between the CAP method and other related DFC approaches, 4) discussing potential neuronal correlates of transient CAP events, 5) identifying issues and limitations of the CAP method that researchers should be cautious about, and 6) proposing potential directions for future research in this area. These topics will be organized into separate sections below.
Temporal decomposition of resting-state data into co-activation patterns
Early explorations of the time-varying nature of rsfMRI connectivity applied sliding-window and time-frequency coherence analyses (Chang and Glover, 2010; Hutchison et al., 2012; Sakoğlu et al., 2010). These and related approaches examine rsfMRI correlation/coherence within time windows (often 1–2 minutes) much shorter than a typical scanning session, aiming at uncovering more transient interactions between brain areas. However, most approaches for such “dynamic” connectivity analyses are still based on pairwise relationships between fMRI time series. Though very straightforward, these time-domain methods have limitations for quantifying fMRI data, which typically has orders of magnitude more voxels (N) than time points (T). If pairwise correlations were calculated for all possible voxel pairs, the resulting cross-correlation matrix would have orders of magnitude more elements (N×(N−1)/2, considering its symmetry) than actual measurements N×T, with a maximal rank T−1 much lower than its size N. This rank-deficit matrix would represent a very redundant quantification of data covariance. Likewise, resting-state networks (RSNs) typically comprise thousands of brain voxels but are derived from correlations computed over [often] only hundreds of time points. The discordance between spatial and temporal dimensions simply suggests that the pairwise correlations between two voxels is actually accompanied by co-variation of a much larger number of brain voxels. The presence of covariation across large sets of voxels is the rationale behind the practice of using much larger brain parcels from atlases (Finn et al., 2015) or networks identified with spatial independent component analysis (ICA) (Allen et al., 2012) rather than voxels, for functional connectivity analyses, although this would to some degree undermine the spatial resolution of fMRI. However, in addition to motivating dimensionality reduction, the widespread dependence across voxels also strongly motivates the use of methods that capture joint dependencies in the activity across more than two brain areas.
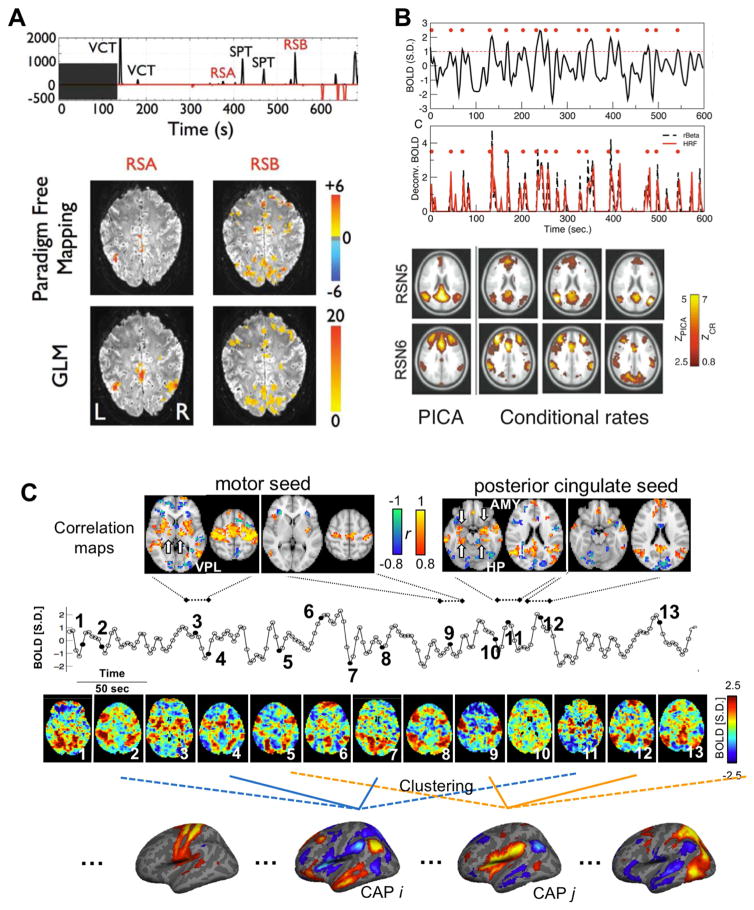
A similar rationale is also behind the observation that RSNs can be derived from subsets of acquired time points. Using either a paradigm free mapping (PFM) (Gaudes et al., 2011; Petridou et al., 2013) (Figure 1A) or point process analysis (PPA) (Tagliazucchi et al., 2012a, 2011) (Figure 1B), studies have demonstrated that many brain voxels co-activate in apparently meaningful patterns as brief, temporally sparse events. For example, based on spikes in activation time series (ACT) derived with the PFM method, not only were task events and associated fMRI co-activation patterns detected, but the task-unrelated events (RSA and RSB in Figure 1A) were also identified with clear spatial patterns of co-activations. Simply averaging the co-activation events at subsets of acquired time points generated RSN patterns similar to those obtained with all data using conventional approaches such as seed-based correlation and spatial ICA (Figure 1B) (Tagliazucchi et al., 2012a, 2011). These findings are not entirely surprising given that extreme points in a time series dominate pairwise correlations (Cifre et al., 2017). Moreover, from the network perspective, these time points are likely those for which RSNs have their peak activity (Laumann et al., 2016). However, a really intriguing question is whether a subset of individual time points, whose average gives a specific RSN pattern, merely show instantaneous spatial patterns that are noisy fluctuations around the average pattern, or whether they truly differ from each other and indicate functionally distinct configurations of activity.
Figure 1.
Three major methods that focus on co-activation events in resting-state fMRI. (A) Two task-unrelated activation events detected by the parameter free mapping (PFM) and their spatial patterns. The activation and deactivation events are detected from fMRI signals of a representative subject as spikes in activation time series (ACT) derived using the PFM (black and red traces in the top panel). In addition to those evoked by visually cued tapping (VCT) and self-paced tapping (SPT) tasks, there were also two task-unrelated activation events (RSA and RSB) were detected in the positive ACT. The spatial activation patterns of the RSA and RSB are derived using the PFM and general linear modal (GLM) and shown in the bottom panel. All panels in (A) are adapted from (Gaudes et al., 2011). (B) Point process analysis (PPA) identifies supra-threshold events in fMRI signals. The point process events (red dots in the top panel) were defined as time points where the normalized fMRI signals cross a threshold of 1 (red dashed line in the first row) from below. These events coincide well with the peaks of de-convolved fMRI signals derived using either the hemodynamic response function (HRF) or the rBeta function (the second row of the top panel). Conditional rate maps of these events (the right three columns of the bottom panel), which indicate the probability of seeing such events at different brain regions conditional on seeing one at a given seed, show very similar network patterns as those derived by probabilistic ICA (the left column of the bottom row). All panels in (B) are adapted from (Tagliazucchi et al., 2012a). (C) Co-activation patterns (CAPs) and dynamic resting-state fMRI connectivity. Thirteen examples of single fMRI volumes show clear instantaneous patterns of brain co-activations that even include thalamic nuclei and hippocampus (the third row). They are corresponding to black solid circles shown in the normalized fMRI signal from the posterior cingulate cortex (PCC) region (the second row with a unit of standard deviation (S.D.)). Seed-based correlation maps (the top row) within four short time windows (16.1 seconds, 7 fMRI volumes) are largely determined by instantaneous brain co-activation patterns of included time points. For example, the presence of ventral posterolateral nucleus (VPL) in one of the sensorimotor maps is attributed to the co-activation at the time point 3, and the presence of the amygdala (AMY) and hippocampus (HP) in one of the PCC maps can be explained by the instantaneous pattern at time point 11. CAPs were derived by grouping all time points into subgroups using clustering and then taking the means (centroids) of these subgroups (the bottom row).
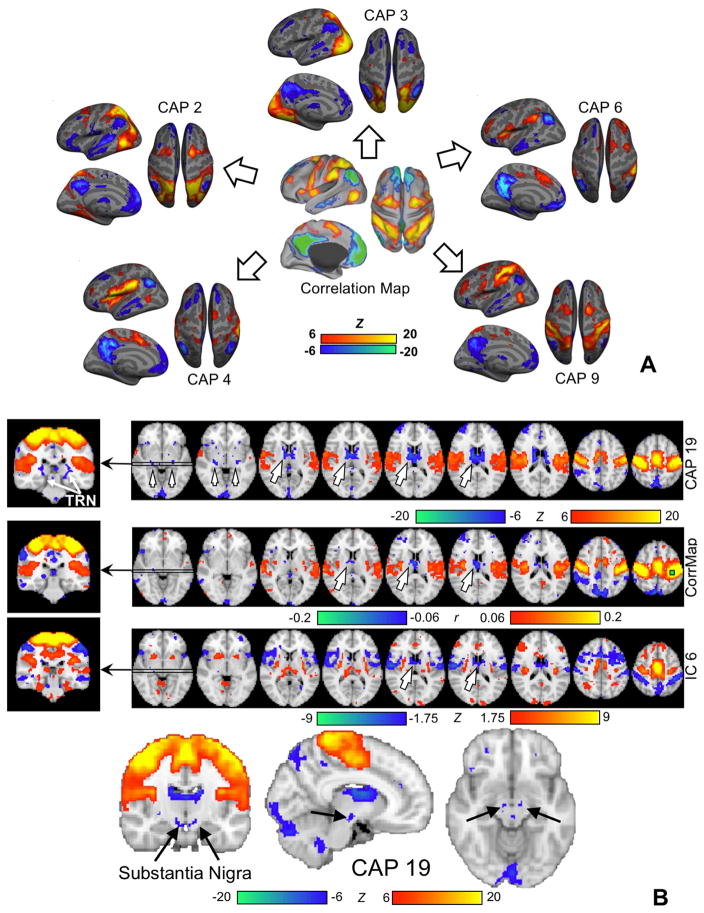
Much evidence points to the latter. Inspecting fMRI volumes at individual time points revealed clear but distinct spatial patterns (Liu et al., 2013; Liu and Duyn, 2013a) (Figure 1C). As discussed above, simply averaging a subset of suprathreshold time points at a seed region would generate a RSN pattern similar to the correlation map with respect to this seed. However, even this subset of time points, which supposedly belong to the same RSN, actually showed distinct spatial patterns. A specific region, e.g., the posterior cingulate cortex, can dynamically co-activate with different sets of brain regions at different times (Liu and Duyn, 2013a). With this knowledge, we applied a clustering algorithm to further divide a subset of time points that show high activity at a specified seed region into multiple subgroups based on their spatial similarity, and then averaged the volumes within each subgroup to generate CAPs (Liu and Duyn, 2013a). Taking this approach, the default mode network (DMN) was temporally decomposed into multiple DMN CAPs with spatial features that suggest their distinct neural and functional relevance – showing, for example, co-activations at small but specific brain structures such as the hippocampus and the caudate nucleus. The clustering algorithm was also directly applied to all, instead of a subset of, time points to extract CAPs corresponding to different RSNs in a completely data-driven way (Liu et al., 2013) (Figure 1C, bottom section). A group of resulting CAPs show strong co-activations in different sets of the task-positive network while the DMN is de-activated, suggesting that these two major brain networks, i.e., the DMN and task-positive network, may have a many-to-one correspondence rather than the one-to-one relationship suggested by stationary correlation analysis (Fox et al., 2005) (Figure 2A). In addition, very specific thalamocortical co-(de)activations were observed in CAPs, e.g., among the thalamic reticular nuclei (TRN), substantia nigra (SN), and sensorimotor cortex, but not in outcomes of seed-based correlation analyses and spatial ICA (Figure 2B). From the above, the implementation of the CAP method can be summarized into three simple steps: (1) standardizing each voxel’s time course to Z scores (i.e., zero mean and unit standard deviation), (2) applying clustering to classify time points (including either all time points or a subset of points showing high signal at a pre-defined seed region) into multiple groups based on spatial correlations of their instantaneous co-activation pattern, and (3) averaging the spatial pattern of time points that were classified into the same group to generate the CAPs.
Figure 2.
Co-activation patterns can temporally decompose stationary correlations and reveal fine-scale thalamocortical synchronization. (A) Negative correlations between the default mode network (DMN) and task-positive networks that was found previously with seed-based correlation analysis (Fox et al., 2005) may actually reflect anti-phase co-(de)activations between the DMN and different sets of task-positive network at different time points, as shown by a set of CAPs derived using the whole-brain CAP approach (Liu et al., 2013). (B) Sensorimotor co-activation is accompanied by specific deactivations in subcortical regions, including the anterior and medial dorsal nuclei (AN/MDN) of the thalamus (big arrows), a shell-shape structure around the thalamus that we tentatively regard as the thalamic reticular nucleus (TRN) (the top row), and the substantia nigra (SN) sitting right above the pons (the bottom row). These subcortical structures are either much less clear or completely absent in outcomes of the seed-based correlation analysis (the second row) and spatial ICA (the third row).
The CAP concept opens up a new perspective on DFC. Specifically, we can consider the rsfMRI connectivity within a short window to be largely determined by 1) whether the window includes fMRI volumes with clear patterns of instantaneous co-activations and 2) what types of patterns it includes (Figure 1C, top section) (Figure S8 in Liu et al., 2013; Petridou et al., 2013). Therefore, the temporal variability of rsfMRI connectivity over short sliding windows can be regarded from the perspective of CAPs. More importantly, the apparent neurophysiological relevance of CAPs, as indicated by their specific spatial patterns, suggests that temporal variability of rsfMRI connectivity is, at least partly, attributed to dynamic organization of the brain, rather than merely noise or physiological artifacts. It also suggests a possibility that the CAPs, and thus rsfMRI connectivity and RSNs, are in part induced by transient neuronal events that occur only sporadically in very brief periods of time.
Variants and applications of the CAP method
A few variants of the CAP method have been proposed and applied to fMRI data acquired from different species to extract and quantify brain dynamics under different brain conditions. Among them, an innovation-driven CAP (iCAP) approach was proposed to separate temporally overlapping CAPs (Karahanoğlu and Van De Ville, 2015). Clear patterns of instantaneous co-activations at single rsfMRI volumes suggest that they could be induced by transient neuronal events; however, if time intervals between such events are shorter than the hemodynamic delay of fMRI signals, CAPs induced by distinct temporal events would be mixed together within a single rsfMRI volume. The rationale behind the iCAP approach is to include an additional deconvolution step, akin to those included in the early studies employing PPA and PFM methods (Gaudes et al., 2011; Petridou et al., 2013; Tagliazucchi et al., 2012a, 2011), before the application of clustering analysis. Although the basic idea of this approach is interesting, a further assessment of additional gains compared with the original CAP method is needed.
A novel method was also proposed to derive an “overall dominant CAP-set”, which can potentially mitigate the sensitivity of the original CAP method to the choice of cluster numbers and increase its robustness when applied to a relatively smaller dataset (Chen et al., 2015). This method includes an algorithm for automatically sorting and retaining a subgroup of CAPs that contribute significantly to overall network patterns. In this study, the temporal fraction (TF) and the frequency of state alternations (FA), which are similar to metrics proposed in other DFC studies (Allen et al., 2012; Karahanoğlu and Van De Ville, 2015; Taghia et al., 2017), were derived to quantify CAP-related brain dynamics. The TF was defined as the fraction of time that each CAP occupies, and the FA was calculated as the number of switches between different CAPs. Applying the proposed algorithm and metrics to fMRI signals acquired during continuous working memory task performance and resting state revealed a reduced number of dominant CAPs, increased spatial consistency across CAPs, and increased fractional contributions of a few dominant CAPs during the working memory condition compared to resting state.
In parallel with the significant progress of CAP research in humans, the CAP method has also been applied in an animal study and revealed interesting brain dynamics in rats (Liang et al., 2015). This study systematically examined the spatiotemporal dynamics of infralimbic cortex-related (IL) and primary somatosensory cortex-related (S1) networks when rats were in an awake or anesthetized condition. In both conditions, both IL and S1 networks could be decomposed into several spatially reproducible and temporally alternating CAPs, suggesting that dynamic rsfMRI connectivity was a characteristic feature in rodents even in widely dissimilar physiological conditions. More importantly, this study showed that anesthesia can profoundly impact the dynamic rsfMRI connectivity of neural circuits subserving cognitive and emotional functions, but might have less of an effect on sensorimotor-related systems. The finding is in general consistent with an investigation of connectivity states in monkeys under awake and anesthetized conditions using other DFC approaches (Barttfeld et al., 2014).
The concept of CAPs has also been applied to task fMRI. The term “co-activation” has actually long been used in the area of task fMRI meta-analyses, where it is commonly referred to as task-evoked co-activation across a large number of fMRI experiments (Toro et al., 2008). Clustering of transient spatial patterns, the essential idea behind the CAP methodology, was recently introduced into the analysis of task fMRI to identify “brain modes” (bModes) that represent transient network configuration during task performance (Bordier and Macaluso, 2015). The bModes method was applied to fMRI data from an experiment with multiple tasks and conditions and successfully identified multiple brain modes representing distinct evoked patterns in response to complicated combinations of stimuli.
The CAP method was also directly applied to fMRI data acquired when subjects were engaged in a continuous visual attention task or at rest (Bray et al., 2015). It was found that brain “hub” regions, which show flexible connectivity with other brain regions and high community density in graph analyses, are dynamically involved in different CAPs. More importantly, such dynamic involvement is significantly modulated by the task, as the occurrence rates of CAPs differed significantly between the rest and attentive state. The findings provide a novel interpretation, from the perspective of network dynamics, for brain hubs identified by graph analyses.
Global rsfMRI signal and brain-wide co-activations
In addition to RSN-specific correlations, the concept of brain co-activation also provides a novel perspective for understanding the global rsfMRI signal, i.e., the mean signal averaged over the whole brain or the gray matter regions, and spatially non-specific correlations with which it is linked. The global signal is a prevalent phenomenon in rsfMRI research and much effort is being paid in order to understand its origin and functional role. It shows large variation across experimental scans and/or subjects and appears sensitive to brain state changes induced by hypnotic drugs (Kiviniemi et al., 2005; Licata et al., 2013), caffeine (Wong et al., 2013), natural sleep (Fukunaga et al., 2006), and diseases (Yang et al., 2014), and can introduce spatially non-specific correlations that may confound rsfMRI connectivity quantification (Fox et al., 2013). Similar to the discussion above regarding RSN-specific correlations, an important question regarding this global signal is whether it predominantly reflects heightened correlations between regions that are uniformly distributed over time, or whether it instead reflects transient covariation of brain activity that occurs in brief epochs. Taking a novel geometric view of fMRI correlations, He and Liu first demonstrated that the global rsfMRI signal actually represents an additive component to the mean rsfMRI signal and can lead to, rather than result from, a general increase of spatially non-specific rsfMRI correlations (He and Liu, 2012). A recent study from the same group further demonstrated that effects of the global signal on rsfMRI connectivity are condensed into a subset of time points (Nalci et al., 2017), supporting the latter view.
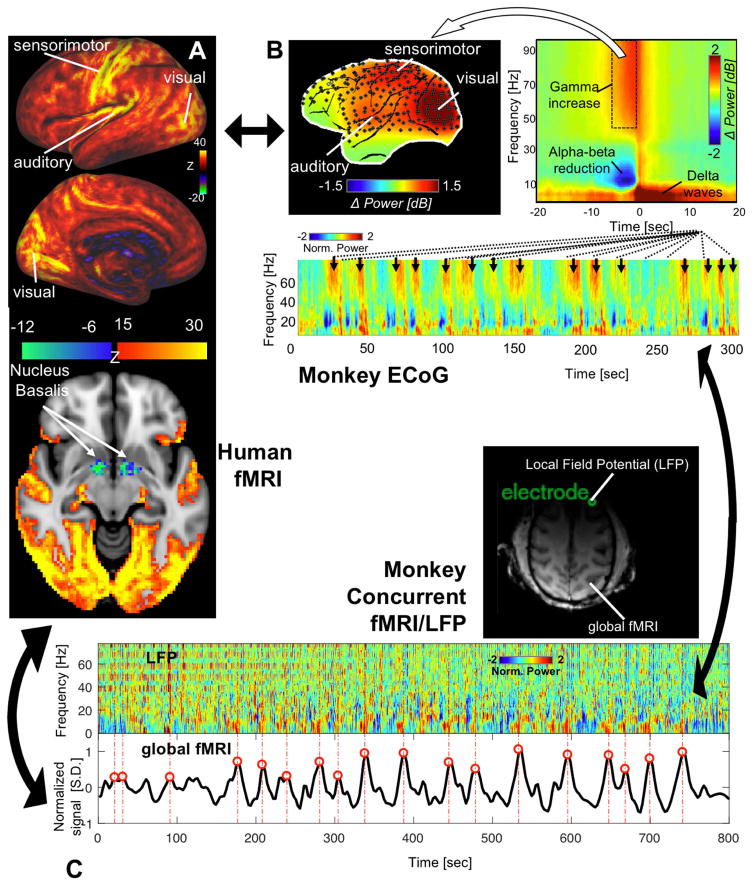
Consistent with these findings is a series of studies applying CAP methodology. To address a major controversy regarding whether anti-correlations between the DMN and task-positive network (Fox et al., 2005) resulted artifactually (K. Murphy et al., 2009; Saad et al., 2012) from a global signal regression (GSR) procedure designed to remove the global rsfMRI signal (Fox et al., 2013), the CAP decomposition was applied to rsfMRI data pre-processed with and without GSR (Liu and Duyn, 2013b). Distinct GSR effects were found in two types of CAPs. GSR had little effects on the DMN CAPs, wherein DMN co-activation was accompanied by strong de-activation of the task-positive network regardless of whether GSR is applied. In contrast, sensory CAPs, including sensorimotor and visual CAPs, were dramatically affected by GSR and show strong brain-wide co-activation if GSR was not used (Liu and Duyn, 2013b). In other words, the global rsfMRI signal may be driven by brain-wide but sensory-dominant co-activations that occur non-uniformly in time. These findings from fMRI provide important clues for the search of neural correlates of the global rsfMRI signal, and significant progress has been made recently by a group of studies (Liu et al., 2018, 2015), which will be discussed in detail in the section “Possible neural origins of CAPs”. Most recently, the pattern of such brain-wide co-activation was further investigated in greater detail by applying a modified CAP method to high resolution rsfMRI data from the Human Connectome Project (HCP) (Van Essen et al., 2013). In addition to confirming its sensory dominance, this study showed that widespread co-activation in the cortex is associated with spatially specific de-activation in subcortical wake-promoting regions, including the Nucleus Basalis in the basal forebrain and the dorsal midline thalamus of the ascending arousal system (Liu et al., 2018) (Figure 3A). This finding explains empirical observations of a close relationship between the global rsfMRI signal and brain arousal states (Fukunaga et al., 2006; Kiviniemi et al., 2005; Licata et al., 2013; Wong et al., 2013).
Figure 3.
Global rsfMRI co-activation pattern (CAP) and sequential spectral transition (SST) electrophysiological events observed in three independent datasets. (A) The global CAP, derived from the Human Connectome Project (HCP) data by averaging the spatial pattern of time points showing the highest 16.6% global signals, shows widespread but sensory-dominant co-activations (top). Interestingly, this nearly whole-brain co-activation is associated with opposite de-activations in subcortical arousal-promoting regions, including the Nucleus Basalis (NB) at the basal forebrain (bottom), adapted from (Liu et al., 2018). (B) The global mean spectrogram of 128-channel electrocorticography (ECoG) recordings from monkeys during light sleep shows a characteristic SST event that occurs repeatedly (black arrows in the bottom panel). The averaged time-frequency pattern of SST (top right) indicates sequential power changes in three distinct frequency bands, among which the gamma-band (42–87 Hz) power increase at the SST is widespread but show highest amplitude at sensory regions (top left). (C) Local field potential (LFP) recorded by a single electrode in a macaque’s frontal cortex shows recurring SST events (top), each of which is followed by a peak in the global fMRI signal (red lines and circles, bottom) measured concurrently.
Comparison between the CAP method and other dynamic FC approaches
Given that the CAP method naturally focuses on temporally heterogeneous information in rsfMRI data and is closely related to DFC, it is important to identify its similarities and differences with other DFC approaches, particularly those spatial-domain methods that treat fMRI volumes as the basic unit of analysis.
As the most popular data-driven method for rsfMRI data analysis, spatial ICA (Beckmann et al., 2005; Kiviniemi et al., 2003) can be regarded as a spatial domain approach, since it models each rsfMRI volume as a mixture of a group of spatial independent components (ICs) to be recovered. Though not conventionally regarded as a DFC method, spatial ICA does provide a time course for each resulting IC showing the changes in its contribution to the observed data over time. Nevertheless, the resulting ICs often show minimal spatial overlap, that appears helpful for generating a functional parcellation of the brain. For this reason, it has become common to apply spatial ICA (Allen et al., 2012; Smith et al., 2012), particularly with a high model order, as a preprocessing step for spatial dimensionality reduction, similar to using parcels derived from brain atlases. In comparison with the CAPs, significant temporal correlations would remain among the spatial ICs, and subsequent analyses are often applied to further investigate interactions between networks represented by these ICs.
To overcome the aforementioned limitation of spatial ICA, temporal ICA has been proposed to extract “temporal function modes” (TFMs) of the brain (Smith et al., 2012). The temporal independence assumption of TFMs might be, to some extent, close to the exclusive presence of a CAP at a given time point. However, a comparison between these two approaches did not suggest a strong correspondence (Liu et al., 2013). This may be explained by very different implementations of the two methods. For example, to achieve a stable temporal ICA on fMRI, which typically has much more voxels than time points, spatial ICA was first applied to reduce the spatial dimensionality, which might be partly responsible for the differences in their outputs.
An iterative algorithm has been proposed to extract quasi-periodic patterns (QPP) of the brain, which are spatiotemporal rsfMRI patterns of propagating activity (Majeed et al., 2011; Thompson et al., 2014). Similar to the CAP method, the QPP algorithm also seeks to identify and then combine rsfMRI volumes with similar patterns. However, it focuses on spatiotemporal pattern of chunks of consecutive volumes, rather than the spatial pattern of single volumes, in order to reveal propagating activity over a short period of time. In addition, an iterative procedure, instead of clustering, was used to obtain a QPP by updating a template chunk of rsfMRI volumes with significantly correlated chunks at different times. Compared with the CAP approach, the QPP method’s focus on identifying propagating activity may lead to a somewhat lower sensitivity to identify brief co-activation patterns.
Clustering has been combined with sliding-window correlation analysis to identify functional connectivity states of the brain (Allen et al., 2012). Similar to the CAP method, clustering was applied temporally to extract and then combine recurring patterns of rsfMRI. However, unlike the CAP method, it was applied to correlation matrices of RSNs within sliding windows of 44 seconds, instead of single fMRI volumes, and the resulting connectivity states thus represent drain dynamics at a much coarser time scale. Moreover, the connectivity states represent a set of relationships between brain regions, which are distinct from the spatial patterns of brain co-activations.
Hidden Markov models (HMM) were recently introduced to study temporal dynamics of rsfMRI signals by linking distinct co-activation patterns to a dynamic sequence of discrete brain states (Chen et al., 2016; Taghia et al., 2017; Vidaurre et al., 2017a, 2017b). The HMM method is similar to the CAP approach in that individual rsfMRI volumes are classified into multiple groups in an unsupervised way. Unlike CAP analysis, the individual volumes are modeled in the HMM as a mixture of the brain states and thus linked to each state with a given probability. Moreover, the temporal transitions between these states are assumed to follow a Markov process. Despite this additional constraint, the state transition probabilities are derived automatically with HMM whereas with CAP analysis, these need to be derived separately.
Possible neural origins of CAPs
As is clear from the preceding discussion, various analysis methods can be used to extract functional network patterns from fMRI data. The advantages and appropriateness of choosing a specific method, as well as the interpretation of the extracted information, depend on the type and nature of neuronal activity that underlies the rsfMRI signal. It is likely that, under general conditions, many types of neural activity can contribute to spontaneous fMRI signals and that these types of activities may have distinct functional significance and each favors a specific analysis method. Despite the rapidly growing use of rsfMRI for the investigation of brain function in health and disease, this area remains relatively unexplored, and no clear picture of the neuronal contributions to rsfMRI has yet emerged. In the following we will review the current understanding, and offer some speculative discussion of the neural origin of CAPs.
CAP analysis is motivated by the possibility that spontaneous fMRI signal results from brief and temporally isolated (on the fMRI times scale) instances of neural activity. This is a departure from approaches such as correlation analysis and ICA that were motivated by the notion of ongoing interactions between regions, with the resulting network patterns and correlation values to a large extent stationary and independent of the temporal segment analyzed. Early interpretations of the rsfMRI signal considered repetitive temporal patterns such as those originating from continuous modulating sources, including neuro-modulation originating from the brainstem (Biswal et al., 1995; Golanov et al., 1994), as well as vasomotor modulations (Hudetz et al., 1998). Subsequent studies have emphasized that different brain regions may contribute to the rsfMRI signal at different frequencies (see e.g.(Liao et al., 2013; Salvador et al., 2008; Thompson and Fransson, 2015; Xue et al., 2014)). The notion that spontaneous brain activity has contributions from oscillatory neuronal sources is widely accepted in electrophysiology, where data is often analyzed in frequency bands such as delta, theta, alpha, beta, mu, and gamma. In fact, a number of studies have suggested that the relative proportion of electrophysiological power in these frequency bands may be specific for the brain’s different functional regions (Brookes et al., 2011; de Pasquale et al., 2010; Logothetis et al., 2012). Similarly, functional specificity has been found for the fMRI correlates of these electrophysiological signals (Jann et al., 2010; Mantini et al., 2007; Tagliazucchi et al., 2012a). Nevertheless, these electrophysiological findings should not be seen as evidence for an oscillatory nature of the fMRI signal because they are too fast and are often too transient to appear as oscillations at the corresponding frequencies in the (slow) fMRI signal.
With the introduction of CAP analysis, the notion that rsfMRI signal may (at least in part) originate from brief, event-like activity rather than ongoing, possibly oscillatory, interactions have become more widespread. This possibility is supported by a number of observations in the electrophysiological literature of both cortical and subcortical origin. Phenomena such as K-complexes and slow waves (Luczak et al., 2007; Massimini et al., 2004; M. Murphy et al., 2009; Steriade et al., 1993) are though to initiate locally and spread (“travel”) over the cortex within time frames of 100s of milliseconds. Their cortical spreading may be facilitated by lateral connectivity between neurons and their local networks of excitation and inhibition (for review see e.g. (Cabral et al., 2017)), with a potential subcortical (e.g. thalamic) contribution. Such lateral connectivity therefore may be reflected in spontaneous cortical activity patterns (Arieli et al., 1995; O’Hashi et al., 2017). A similar mechanism may underlie the phenomenon of “microstates” observed with EEG (Britz et al., 2010; Musso et al., 2010; Van de Ville et al., 2010; Yuan et al., 2012) and MEG (Baker et al., 2014); nevertheless it is unclear whether the relatively rapid (100s of ms) alternation between states would lead to the apparently much slower incidence rates of CAPs.
Global CAPs, on the other hand, may have contributions from widespread cortical changes associated with changes in brain state. For example, the interplay between arousal and sleep promoting regions in the brainstem and basal forebrain may lead to sudden changes in arousal state that is reflected in widespread changes in cortical activity (Saper et al., 2005). Among the many subcortical regions that have been shown to effectuate widespread cortical changes are the rostral ventrolateral medulla (Golanov et al., 1994), and the pedunculo-pontine nucleus (Mena-Segovia et al., 2008). During sleep, contributions to the global fMRI signal may come from cortical involvement in sleep spindles (Muller et al., 2016) and hippocampal ripples (Logothetis et al., 2012).
Recent evidence for the potential influence of arousal state changes on the global fMRI signal has come from studies employing simultaneous fMRI-electrophysiology (Chang et al., 2016; Liu et al., 2018). Specifically, a sequential spectral transition (SST) event was identified in global electrophysiological signals at arousal transitions and showed similar brain-state dependency as the global fMRI signal (Figure 3B). Moreover, it is indeed associated with profound, widespread changes in fMRI signal recorded simultaneously, and thus could be a candidate electrophysiological signature for the global fMRI signal (Liu et al., 2018, 2015) (Figure 3C).
Notably, the success of CAP analysis in extracting time-varying functional networks, or of identifying the SST event for the global CAP, should not be seen as evidence the neuronal activity underlying network patterns is in the form of discrete, neural events that are temporally sparse, as compared to a more continuous ongoing interaction between brain regions that are part of a network. Barring a comprehensive understanding of the underlying activity, interpretation that the spontaneous fMRI signal results from “critical brain dynamics” and avalanches (Tagliazucchi et al., 2012b) may be premature. At the same time, the interpretation of CAPs (and ICA/correlation analysis for that matter) could depend on the type of underlying neuronal activity. For example, two temporally independent processes A and B occurring in regions 1 and 2 may be interpreted variably depending on the type of neuronal activity. If both A and B are temporally sparse (on the fMRI time scale), CAP analysis will extract them correctly. However, if there is substantial temporal overlap of processes A and B, a non-meaningful CAP pattern with both regions 1 and 2 might be extracted in addition to those for A and B.
Other Issues and limitations
As discussed above, the CAP analysis has many unique features compared with other dynamic FC approaches. For instance, it provides single-volume temporal resolution, has a minimal set of assumptions, constraints, and transformations of rsfMRI data, and has the flexibility of choosing seed-based or whole-brain implementations. One the other hand, this uniqueness also comes with challenges and limitations.
The greatest challenge for CAP analysis, and likely also for other dynamic rsfMRI connectivity approaches, is the limited amount of information contained within a typical 5–10 min rsfMRI scan. Even though robust RSN structures can be derived from such short scanning sessions, these correlational patterns originate largely from brain co-activations at a subset of time points. If they are further decomposed temporally into multiple CAPs, there will be even less information for a specific CAP, which may not be sufficient for any meaningful quantifications and statistics of CAP dynamics. This issue can be partially mitigated by combining data from a relatively large number of scans and/or subjects. However, it is unclear how inter-subject variation in structural connectivity would affect the group level CAP analysis. One may also consider increasing the length of resting-state fMRI sessions, but it would be very hard to keep subjects in a constant state of vigilance over an extended period of time (Tagliazucchi and Laufs, 2014). On the other hand, the CAP analysis is unlikely to benefit significantly from a high, sub-second sampling rate given the intrinsic slowness of fMRI signals, as well as the observation that consecutive time points tend to show similar instantaneous rsfMRI co-activation patterns.
Data quality could be more important for CAP analysis than for stationary correlation analysis. The clustering step for CAP analysis is completely based on the spatial similarity of individual rsfMRI volumes. Therefore, the signal-to-noise ratio (SNR) at single volumes, which will determine whether clear patterns can be seen in instantaneous co-activations, is essential for a successful CAP analysis. A strategy that could be helpful to enhance the signal-to-noise ratio of a single volume is to apply a spatial mask that covers only extreme voxels (e.g., top 10% and bottom 5%) clustered together when computing spatial similarity between them. This step appears to significantly increase statistical scores of CAP maps without changing their general patterns (Liu and Duyn, 2013a). However, the use of this step could involve additional effort for the selection of an optimal threshold. An alternative could be to exclude time points that do not show unrealistic (e.g. artifactual) patterns and focus the analysis on remaining ones.
Caution should be exercised when using the seed-based CAP decomposition (Liu and Duyn, 2013a). First, the method involves selecting a subset of time points showing the highest signals at a specified seed region for subsequent clustering analysis, but what percentage of time points one should select is still an open question. Secondly, since all selected time points have a high signal at the seed region, so will all resulting CAPs, which are averages of these points. Therefore, some CAPs may just represent chance-level co-occurrence of the seed region and other brain networks rather than have any physiological meaning. To differentiate this type of CAPs, an appropriate control, e.g., the same number of time points randomly selected, is needed to estimate chance-level occurrence frequency of other networks without considering the seed. This issue should be minimal for the whole-brain CAP approach in which no seed region is specified upfront (Liu et al., 2013).
The target number of CAPs to be classified is hard to determine. In fact, there is probably not a ‘magic number’ that can truly define the number of versatile configurations of functional networks. Although it is parsimonious to consider instantaneous brain co-activations classified into the same CAP group to be induced by the same neuronal process that appears repeatedly, this may not be true. Instead of well separated clusters, the instantaneous co-activations at individual time points could have a hierarchical relationship. The rsfMRI volumes classified into a coarsely defined cluster, e.g., for a visual CAP, could potentially be further divided into smaller groups that represent CAPs with finer differences, given sufficient data and spatial resolution.
Correlations have been found between the rsfMRI signal and noise sources, such as head motion (Power et al., 2015), respiratory volume (Birn et al., 2006), and heart rate (Chang et al., 2009), and the findings have raised concerns about the potential influence of noise on the outcomes of rsfMRI data analysis. In comparison to time-domain correlation analysis, CAP analysis is less sensitive to noise sources that are transient in nature. A major limitation of temporal domain approaches is that transient events could have substantial effects on final quantifications. For examples, a short deep breath or a head movement will introduce synchronized fMRI signal changes and increase temporal correlations over the entire scan (Power et al., 2015, 2012). The issue is particularly serious for dynamic connectivity analyses combining temporal correlation/coherence metrics with sliding-window approach, because temporal variability in connectivity could be actually induced by transient noise of non-neuronal origin (also discussed in Hutchison et al. 2013). In contrast, individual rsfMRI volumes are basic elements for the CAP analysis. If transient noise events induce a systematic pattern in corresponding rsfMRI volumes, they are expected to be classified as a separate CAP reflecting this pattern and thus generally separable from CAPs of neural origin. Otherwise, the random effects of different noise events could be cancelled out through averaging given enough data of sufficient quality and are expected to have minimal impact on final CAP outputs. Practical validation will be required to confirm these theoretical predictions based on the mechanistic principles of the CAP method.
Future directions
New CAP metrics are needed for the quantification of various aspects of brain dynamics. The CAP method suggests a new framework for investigating dynamic rsfMRI connectivity, and potentially provides an extra dimension of information about brain dynamics. However, only a few metrics have been developed so far to quantify the occurrence rate and transition frequency of CAPs. There are potentially other aspects of brain dynamics that can be characterized by metrics developed based on CAPs, such as the dwell time of CAPs and the temporal dependency of consecutive CAPs. The new metrics are expected to provide valuable information about the brain network dynamics that is not available with conventional metrics.
Combining rsfMRI with other neuroimaging modalities, such as the electroencephalogram (EEG), may provide further insight into neuronal correlates of CAPs and additional information about brain network dynamics. Electrophysiological recordings have already helped identify a neuronal event, i.e., the SST, that underlies the non-specific co-activation of widespread brain regions (Liu et al., 2018). However, the neural correlates of network-specific CAPs remain unknown. Future studies combining multimodal neuroimaging techniques will be promising for unraveling the neuronal processes underlying network-specific CAPs. Moreover, different neuroimaging modalities may also provide complementary information about brain dynamics. For example, electrophysiological recordings directly sample brain activity at a very fast rate and enable a frequency-specific decomposition of neuronal activity. Such complementary information could be critical for separating brain processes indistinguishable with the fMRI signal alone. For example, the DMN co-activations under anesthetized condition and those evoked by a cognitive task that are indistinguishable in fMRI may have distinct electrophysiological signatures in EEG.
The relationship between physiological signals and spatially non-specific CAPs is also an interesting topic for future research. Both cardiac and respiratory signals are significantly correlated with rsfMRI signals from widespread brains regions (Birn et al., 2006; Shmueli et al., 2007). Although these correlations were largely interpreted as evidence of non-neuronal contributions to rsfMRI connectivity, it is worth noting that these physiological functions are regulated by the autonomic system and could be linked to brain activity as well. It has been shown that a simple behavioral difference in the status of eye closure can lead to distinct correlations between physiological data and rsfMRI signals, indicating the important role of brain states in modulating this physio-rsfMRI relationship (Yuan et al., 2013). Transient arousal changes may mediate this physio-rsfMRI correlation by eliciting non-specific brain co-activations and concurrent changes in physiological signals. A similar rationale can also be applied to the relationship observed between the rsfMRI signal and head motion, because transient arousal events, e.g., micro-sleep or micro-arousal, are expected to be accompanied by a certain amount of motion and also because the widely used motion index DVARS (Power et al., 2012) is equally sensitive to global fMRI signal changes that are not caused by motion. Understanding the relationships between the brain-wide CAP and these noise sources may provide critical information about whether these relationships are causal and informative of a neural process.
Conclusion
The CAP method and other similar approaches, which regard single fMRI volumes as the basic element of analysis, constitute a major departure from conventional time-domain methods that infer functional connectivity based on temporal correlations of rsfMRI time series. They describe time-varying information of rsfMRI signals at temporal resolutions closer to a single fMRI time point, and provide a novel perspective for understanding DFC. This method also raises the possibility that rsfMRI connectivity may originate from transient neuronal events occurring at brief epochs in time. The concept of co-activation helps to reframe current notions about the global resting-state fMRI signal and elucidate its underlying electrophysiological correlate. Nevertheless, an appropriate use of CAP approaches requires a clear understanding of their similarities and differences with other DFC methods, the complementary information they may offer, and their potential issues and limitations. Future research is needed to further improve these techniques and the understanding of associated findings.
Highlights.
RsfMRI dynamics may provide critical information about brain function and dysfunction
RsfMRI dynamics can be understood and quantified via distinct brain co-activations
We review a unique co-activation pattern (CAP) method for dynamics rsfMRI analyses
Acknowledgments
This research was supported (in part) by the NIH Intramural Research, and the NIH Pathway to Independence Award (K99/R00) 4R00NS092996-02.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Allen EA, Damaraju E, Plis SM, Erhardt EB, Eichele T, Calhoun VD. Tracking Whole-Brain Connectivity Dynamics in the Resting State. Cereb cortex. 2012;24:663–676. doi: 10.1093/cercor/bhs352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arieli a, Shoham D, Hildesheim R, Grinvald a. Coherent spatiotemporal patterns of ongoing activity revealed by real-time optical imaging coupled with single-unit recording in the cat visual cortex. J Neurophysiol. 1995;73:2072–2093. doi: 10.1152/jn.1995.73.5.2072. [DOI] [PubMed] [Google Scholar]
- Baker AP, Brookes MJ, Rezek IA, Smith SM, Behrens T, Smith PJP, Woolrich M. Fast transient networks in spontaneous human brain activity. Elife. 2014;2014:1–18. doi: 10.7554/eLife.01867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barttfeld P, Uhrig L, Sitt JD, Sigman M, Jarraya B, Dehaene S. Signature of consciousness in the dynamics of resting-state brain activity. Proc Natl Acad Sci. 2014;112:201418031. doi: 10.1073/pnas.1418031112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckmann CF, Deluca M, Devlin JT, Smith SM. Investigations into Resting-state Connectivity using Independent Component Analysis. Philos Trans R Soc L B Biol Sci. 2005;360:1001–13. doi: 10.1098/rstb.2005.1634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birn RM, Diamond JB, Smith MA, Bandettini PA. Separating respiratory-variation-related fluctuations from neuronal-activity-related fluctuations in fMRI. Neuroimage. 2006;31:1536–1548. doi: 10.1016/j.neuroimage.2006.02.048. S1053-8119(06)00124-8 [pii] [DOI] [PubMed] [Google Scholar]
- Biswal B, Yetkin FZ, Haughton VM, Hyde JS. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn Reson Med. 1995;34:537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- Bordier C, Macaluso E. Time-resolved detection of stimulus/task-related networks, via clustering of transient intersubject synchronization. Hum Brain Mapp. 2015;36:3404–3425. doi: 10.1002/hbm.22852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bray S, Arnold AEGF, Levy RM, Iaria G. Spatial and temporal functional connectivity changes between resting and attentive states. Hum Brain Mapp. 2015;36:549–565. doi: 10.1002/hbm.22646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Britz J, Van De Ville D, Michel CM. BOLD correlates of EEG topography reveal rapid resting-state network dynamics. Neuroimage. 2010;52:1162–1170. doi: 10.1016/j.neuroimage.2010.02.052. [DOI] [PubMed] [Google Scholar]
- Brookes MJ, Woolrich M, Luckhoo H, Price D, Hale JR, Stephenson MC, Barnes GR, Smith SM, Morris PG. Investigating the electrophysiological basis of resting state networks using magnetoencephalography. Proc Natl Acad Sci U S A. 2011;108:16783–16788. doi: 10.1073/pnas.1112685108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cabral J, Kringelbach ML, Deco G. Functional connectivity dynamically evolves on multiple time-scales over a static structural connectome: Models and mechanisms. Neuroimage. 2017 doi: 10.1016/j.neuroimage.2017.03.045. [DOI] [PubMed] [Google Scholar]
- Chang C, Cunningham JP, Glover GH. Influence of heart rate on the BOLD signal: The cardiac response function. Neuroimage. 2009;44:857–869. doi: 10.1016/j.neuroimage.2008.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C, Glover GH. Time-frequency dynamics of resting-state brain connectivity measured with fMRI. Neuroimage. 2010;50:81–98. doi: 10.1016/j.neuroimage.2009.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang C, Leopold DA, Scholvinck ML, Mandelkow H, Picchioni D, Liu X, Ye FQ, Turchi JN, Duyn JH. Tracking brain arousal fluctuations with fMRI. Proc Natl Acad Sci U S A. 2016;113:4518–4523. doi: 10.1073/pnas.1520613113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen JE, Chang C, Greicius MD, Glover GH. Introducing co-activation pattern metrics to quantify spontaneous brain network dynamics. Neuroimage. 2015;111:476–488. doi: 10.1016/j.neuroimage.2015.01.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen S, Langley J, Chen X, Hu X. Spatiotemporal Modeling of Brain Dynamics Using Resting-State Functional Magnetic Resonance Imaging with Gaussian Hidden Markov Model. Brain Connect. 2016;6:326–334. doi: 10.1089/brain.2015.0398. [DOI] [PubMed] [Google Scholar]
- Cifre I, Zarepour M, Horovitz SG, Cannas S, Chialvo DR. On why a few points suffice to describe spatiotemporal large-scale brain dynamics 2017 [Google Scholar]
- de Pasquale F, Della Penna S, Snyder AZ, Lewis C, Mantini D, Marzetti L, Belardinelli P, Ciancetta L, Pizzella V, Romani GL, Corbetta M. Temporal dynamics of spontaneous MEG activity in brain networks. Proc Natl Acad Sci U S A. 2010;107:6040–6045. doi: 10.1073/pnas.0913863107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finn ES, Shen X, Scheinost D, Rosenberg MD, Huang J, Chun MM, Papademetris X, Todd Constable R. Functional connectome fingerprinting: identifying individuals using patterns of brain connectivity. Nat Neurosci. 2015;18:1–11. doi: 10.1038/nn.4135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Raichle ME. Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nat Rev Neurosci. 2007;8:700–711. doi: 10.1038/nrn2201. nrn2201 [pii]\n. [DOI] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc Natl Acad Sci U S A. 2005;102:9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Zhang D, Snyder AZ, Raichle ME. The Global Signal and Observed Anticorrelated Resting State Brain Networks The Global Signal and Observed Anticorrelated Resting State Brain Networks. J Neurophysiol. 2013;101:3270–3283. doi: 10.1152/jn.90777.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukunaga M, Horovitz SG, van Gelderen P, de Zwart JA, Jansma JM, Ikonomidou VN, Chu R, Deckers RHR, Leopold DA, Duyn JH. Large-amplitude, spatially correlated fluctuations in BOLD fMRI signals during extended rest and early sleep stages. Magn Reson Imaging. 2006;24:979–992. doi: 10.1016/j.mri.2006.04.018. [DOI] [PubMed] [Google Scholar]
- Gaudes CC, Petridou N, Dryden IL, Bai L, Francis ST, Gowland PA. Detection and characterization of single-trial fMRI bold responses: Paradigm free mapping. Hum Brain Mapp. 2011;32:1400–1418. doi: 10.1002/hbm.21116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golanov EV, Yamamoto S, Reis DJ. Spontaneous waves of cerebral blood flow associated with a pattern of electrocortical activity. Am J Physiol. 1994;266:R204–14. doi: 10.1152/ajpregu.1994.266.1.R204. [DOI] [PubMed] [Google Scholar]
- Greicius MD, Supekar K, Menon V, Dougherty RF. Resting-state functional connectivity reflects structural connectivity in the default mode network. Cereb Cortex. 2009;19:72–78. doi: 10.1093/cercor/bhn059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He H, Liu TT. A geometric view of global signal confounds in resting-state functional MRI. Neuroimage. 2012;59:2339–2348. doi: 10.1016/j.neuroimage.2011.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honey CJ, Sporns O, Cammoun L, Gigandet X, Thiran JP, Meuli R, Hagmann P. Predicting human resting-state functional connectivity from structural connectivity. Proc Natl Acad Sci U S A. 2009;106:2035–2040. doi: 10.1073/pnas.0811168106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudetz AG, Biswal BB, Shen H, Lauer KK, Kampine JP. Spontaneous fluctuations in cerebral oxygen supply. An introduction. Adv Exp Med Biol. 1998;454:551–559. doi: 10.1007/978-1-4615-4863-8_66. [DOI] [PubMed] [Google Scholar]
- Hutchison RM, Womelsdorf T, Allen EA, Bandettini PA, Calhoun VD, Corbetta M, Della Penna S, Duyn JH, Glover GH, Gonzalez-Castillo J, Handwerker DA, Keilholz S, Kiviniemi V, Leopold DA, de Pasquale F, Sporns O, Walter M, Chang C. Dynamic functional connectivity: Promise, issues, and interpretations. Neuroimage. 2013;80:360–378. doi: 10.1016/j.neuroimage.2013.05.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchison RM, Womelsdorf T, Gati JS, Everling S, Menon RS. Resting-state networks show dynamic functional connectivity in awake humans and anesthetized macaques. Hum Brain Mapp. 2012;34:2154–2177. doi: 10.1002/hbm.22058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jann K, Kottlow M, Dierks T, Boesch C, Koenig T. Topographic electrophysiological signatures of fMRI resting state networks. PLoS One. 2010;5:1–10. doi: 10.1371/journal.pone.0012945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karahanoğlu FI, Van De Ville D. Transient brain activity disentangles fMRI resting-state dynamics in terms of spatially and temporally overlapping networks. Nat Commun. 2015;6:7751. doi: 10.1038/ncomms8751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiviniemi V, Kantola JH, Jauhiainen J, Hyvarinen A, Tervonen O. Independent component analysis of nondeterministic fMRI signal sources. Neuroimage. 2003;19:253–260. doi: 10.1016/s1053-8119(03)00097-1. S1053811903000971 [pii] [DOI] [PubMed] [Google Scholar]
- Kiviniemi VJ, Haanpää H, Kantola JH, Jauhiainen J, Vainionpää V, Alahuhta S, Tervonen O, Haanpaa H, Kantola JH, Jauhiainen J, Vainionpaa V, Alahuhta S, Tervonen O. Midazolam sedation increases fluctuation and synchrony of the resting brain BOLD signal. Magn Reson Imaging. 2005;23:531–537. doi: 10.1016/j.mri.2005.02.009. [DOI] [PubMed] [Google Scholar]
- Laumann TO, Snyder AZ, Mitra A, Gordon EM, Gratton C, Adeyemo B, Gilmore AW, Nelson SM, Berg JJ, Greene DJ, McCarthy JE, Tagliazucchi E, Laufs H, Schlaggar BL, Dosenbach NUF, Petersen SE. On the Stability of BOLD fMRI Correlations. Cereb Cortex. 2016:1–14. doi: 10.1093/cercor/bhw265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang Z, Liu X, Zhang N. Dynamic resting state functional connectivity in awake and anesthetized rodents. Neuroimage. 2015;104:89–99. doi: 10.1016/j.neuroimage.2014.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao XH, Xia MR, Xu T, Dai ZJ, Cao XY, Niu HJ, Zuo XN, Zang YF, He Y. Functional brain hubs and their test–retest reliability: A multiband resting-state functional MRI study. Neuroimage. 2013;83:969–982. doi: 10.1016/j.neuroimage.2013.07.058. [DOI] [PubMed] [Google Scholar]
- Licata SC, Nickerson LD, Lowen SB, Trksak GH, MacLean RR, Lukas SE. The hypnotic zolpidem increases the synchrony of BOLD signal fluctuations in widespread brain networks during a resting paradigm. Neuroimage. 2013;70:211–222. doi: 10.1016/j.neuroimage.2012.12.055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Chang C, Duyn JH. Decomposition of spontaneous brain activity into distinct fMRI co-activation patterns. Front Syst Neurosci. 2013;7:101. doi: 10.3389/fnsys.2013.00101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, De Zwart JA, Scholvinck ML, Chang C, Ye FQ, Leopold DA, Duyn JH. Subcortical evidence for a contribution of arousal to fMRI studies of brain activity. Nat Commun. 2018 doi: 10.1038/s41467-017-02815-3. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Duyn JH. Time-Varying Functional Network Information Extracted from Brief Instances of Spontaneous Brain Activity. Proc Natl Acad Sci U S A. 2013a;110:4392–4397. doi: 10.1073/pnas.1216856110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Duyn JH. Resting-State fMRI Signal Anti-Correlation Exists in Absence of Global Signal Regression. Proc. 21st ISMRM Annu. Meet; Salt Lake City, Utah, USA 2251. 2013b. [Google Scholar]
- Liu X, Yanagawa T, Leopold DA, Chang C, Ishida H, Fujii N, Duyn JH. Arousal transitions in sleep, wakefulness, and anesthesia are characterized by an orderly sequence of cortical events. Neuroimage. 2015;116:222–231. doi: 10.1016/j.neuroimage.2015.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logothetis NK, Eschenko O, Murayama Y, Augath M, Steudel T, Evrard HC, Besserve M, Oeltermann A. Hippocampal-cortical interaction during periods of subcortical silence. Nature. 2012;491:547–553. doi: 10.1038/nature11618. [DOI] [PubMed] [Google Scholar]
- Luczak A, Bartho P, Marguet SL, Buzsaki G, Harris KD, Barthó P, Marguet SL, Buzsáki G, Harris KD. Sequential structure of neocortical spontaneous activity in vivo. Proc Natl Acad Sci U S A. 2007;104:347–352. doi: 10.1073/pnas.0605643104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Majeed W, Magnuson M, Hasenkamp W, Schwarb H, Schumacher EH, Barsalou L, Keilholz SD. Spatiotemporal dynamics of low frequency BOLD fluctuations in rats and humans. Neuroimage. 2011;54:1140–1150. doi: 10.1016/j.neuroimage.2010.08.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mantini D, Perrucci MG, Del Gratta C, Romani GL, Corbetta M, Gratta DCR, Gl, Corbetta M, Del Gratta C, Romani GL, Corbetta M, Gratta DCR, Gl, Corbetta M, Del Gratta C, Romani GL. Electrophysiological signatures of resting state networks in the human brain. Proc Natl Acad Sci U S A. 2007;104:13170–13175. doi: 10.1073/pnas.0700668104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Massimini M, Huber R, Ferrarelli F, Hill S, Tononi G. The sleep slow oscillation as a traveling wave. J Neurosci. 2004;24:6862–6870. doi: 10.1523/JNEUROSCI.1318-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mena-Segovia J, Sims HM, Magill PJ, Bolam JP. Cholinergic brainstem neurons modulate cortical gamma activity during slow oscillations. J Physiol. 2008;586:2947–2960. doi: 10.1113/jphysiol.2008.153874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller L, Piantoni G, Koller D, Cash SS, Halgren E, Sejnowski TJ. Rotating waves during human sleep spindles organize global patterns of activity that repeat precisely through the night. Elife. 2016;5 doi: 10.7554/eLife.17267.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy K, Birn RM, Handwerker DA, Jones TB, Bandettini PA. The impact of global signal regression on resting state correlations: are anti-correlated networks introduced? Neuroimage. 2009;44:893–905. doi: 10.1016/j.neuroimage.2008.09.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy M, Riedner BA, Huber R, Massimini M, Ferrarelli F, Tononi G. Source modeling sleep slow waves. Proc Natl Acad Sci U S A. 2009;106:1608–1613. doi: 10.1073/pnas.0807933106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Musso F, Brinkmeyer J, Mobascher A, Warbrick T, Winterer G. Spontaneous brain activity and EEG microstates. A novel EEG/fMRI analysis approach to explore resting-state networks. Neuroimage. 2010;52:1149–1161. doi: 10.1016/j.neuroimage.2010.01.093. [DOI] [PubMed] [Google Scholar]
- Nalci A, Rao BD, Liu TT. Global signal regression acts as a temporal downweighting process in resting-state fMRI. Neuroimage. 2017;152:602–618. doi: 10.1016/j.neuroimage.2017.01.015. [DOI] [PubMed] [Google Scholar]
- O’Hashi K, Fekete T, Deneux T, Hildesheim R, van Leeuwen C, Grinvald A. Interhemispheric Synchrony of Spontaneous Cortical States at the Cortical Column Level. Cereb Cortex. 2017;36:1–14. doi: 10.1093/cercor/bhx090. [DOI] [PubMed] [Google Scholar]
- Petridou N, Gaudes CC, Dryden IL, Francis ST, Gowland PA. Periods of rest in fMRI contain individual spontaneous events which are related to slowly fluctuating spontaneous activity. Hum Brain Mapp. 2013;34:1319–1329. doi: 10.1002/hbm.21513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Barnes KA, Snyder AZ, Schlaggar BL, Petersen SE. Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. Neuroimage. 2012;59:2142–2154. doi: 10.1016/j.neuroimage.2011.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power JD, Schlaggar BL, Petersen SE. Recent progress and outstanding issues in motion correction in resting state fMRI. Neuroimage. 2015;105:536–551. doi: 10.1016/j.neuroimage.2014.10.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preti MG, Bolton TAW, Van De Ville D. The dynamic functional connectome: State-of-the-art and perspectives. Neuroimage. 2017 doi: 10.1016/j.neuroimage.2016.12.061. [DOI] [PubMed] [Google Scholar]
- Saad ZS, Gotts SJ, Murphy K, Chen G, Jo HJ, Martin A, Cox RW. Trouble at rest: how correlation patterns and group differences become distorted after global signal regression. Brain Connect. 2012;2:25–32. doi: 10.1089/brain.2012.0080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakoğlu Ü, Pearlson GD, Kiehl KA, Wang YM, Michael AM, Calhoun VD. A method for evaluating dynamic functional network connectivity and task-modulation: Application to schizophrenia. Magn Reson Mater Physics, Biol Med. 2010;23:351–366. doi: 10.1007/s10334-010-0197-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salvador R, Martínez A, Pomarol-Clotet E, Gomar J, Vila F, Sarró S, Capdevila A, Bullmore E. A simple view of the brain through a frequency-specific functional connectivity measure. Neuroimage. 2008;39:279–289. doi: 10.1016/j.neuroimage.2007.08.018. [DOI] [PubMed] [Google Scholar]
- Saper CB, Scammell TE, Lu J. Hypothalamic regulation of sleep and circadian rhythms. Nature. 2005;437:1257–1263. doi: 10.1038/nature04284. [DOI] [PubMed] [Google Scholar]
- Shmueli K, van Gelderen P, de Zwart JA, Horovitz SG, Fukunaga M, Jansma JM, Duyn JH. Low-frequency fluctuations in the cardiac rate as a source of variance in the resting-state fMRI BOLD signal. Neuroimage. 2007;38:306–320. doi: 10.1016/j.neuroimage.2007.07.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, Miller KL, Moeller S, Xu J, Auerbach EJ, Woolrich MW, Beckmann CF, Jenkinson M, Andersson JLR, Glasser MF, Van Essen DC, Feinberg DA, Yacoub ES, Ugurbil K. Temporally-independent functional modes of spontaneous brain activity. Proc Natl Acad Sci U S A. 2012;109:3131–3136. doi: 10.1073/pnas.1121329109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steriade M, Nunez a, Amzica F. Intracellular analysis of relations between the slow (< 1 Hz) neocortical oscillation and other sleep rhythms of the electroencephalogram. J Neurosci. 1993;13:3266–3283. doi: 10.1073/pnas.90.5.2078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taghia J, Ryali S, Chen T, Supekar K, Cai W, Menon V. Bayesian switching factor analysis for estimating time-varying functional connectivity in fMRI. Neuroimage. 2017;155:271–290. doi: 10.1016/j.neuroimage.2017.02.083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tagliazucchi E, Balenzuela P, Fraiman D, Chialvo DR. Criticality in large-scale brain fmri dynamics unveiled by a novel point process analysis. Front Physiol. 2012a Feb;3:1–12. doi: 10.3389/fphys.2012.00015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tagliazucchi E, Balenzuela P, Fraiman D, Montoya P, Chialvo DR. Spontaneous BOLD event triggered averages for estimating functional connectivity at resting state. Neurosci Lett. 2011;488:158–163. doi: 10.1016/j.neulet.2010.11.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tagliazucchi E, Laufs H. Decoding Wakefulness Levels from Typical fMRI Resting-State Data Reveals Reliable Drifts between Wakefulness and Sleep. Neuron. 2014;82:695–708. doi: 10.1016/j.neuron.2014.03.020. [DOI] [PubMed] [Google Scholar]
- Tagliazucchi E, von Wegner F, Morzelewski A, Brodbeck V, Laufs H. Dynamic BOLD functional connectivity in humans and its electrophysiological correlates. Front Hum Neurosci. 2012b:6. doi: 10.3389/fnhum.2012.00339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson GJ, Pan WJ, Magnuson ME, Jaeger D, Keilholz SD. Quasi-periodic patterns (QPP): Large-scale dynamics in resting state fMRI that correlate with local infraslow electrical activity. Neuroimage. 2014;84:1018–1031. doi: 10.1016/j.neuroimage.2013.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson WH, Fransson P. The frequency dimension of fMRI dynamic connectivity: Network connectivity, functional hubs and integration in the resting brain. Neuroimage. 2015;121:227–242. doi: 10.1016/j.neuroimage.2015.07.022. [DOI] [PubMed] [Google Scholar]
- Toro R, Fox PT, Paus T. Functional coactivation map of the human brain. Cereb Cortex. 2008;18:2553–2559. doi: 10.1093/cercor/bhn014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van de Ville D, Britz J, Michel CM. EEG microstate sequences in healthy humans at rest reveal scale-free dynamics. Proc Natl Acad Sci U S A. 2010;107:18179–84. doi: 10.1073/pnas.1007841107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K. The WU-Minn Human Connectome Project: an overview. Neuroimage. 2013;80:62–79. doi: 10.1016/j.neuroimage.2013.05.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vidaurre D, Abeysuriya R, Becker R, Quinn AJ, Alfaro-Almagro F, Smith SM, Woolrich MW. Discovering dynamic brain networks from big data in rest and task. Neuroimage. 2017a doi: 10.1016/j.neuroimage.2017.06.077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vidaurre D, Smith SM, Woolrich MW. Brain network dynamics are hierarchically organized in time. Proc Natl Acad Sci. 2017b:201705120. doi: 10.1073/pnas.1705120114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong CW, Olafsson V, Tal O, Liu TT. The amplitude of the resting-state fMRI global signal is related to EEG vigilance measures. Neuroimage. 2013;83:983–990. doi: 10.1016/j.neuroimage.2013.07.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xue S-W, Li D, Weng X-C, Northoff G, Li D-W. Different Neural Manifestations of Two Slow Frequency Bands in Resting Functional Magnetic Resonance Imaging: A Systemic Survey at Regional, Interregional, and Network Levels. Brain Connect. 2014;4:242–255. doi: 10.1089/brain.2013.0182. [DOI] [PubMed] [Google Scholar]
- Yang GJ, Murray JD, Repovs G, Cole MW, Savic A, Glasser MF, Pittenger C, Krystal JH, Wang X-J, Pearlson GD, Glahn DC, Anticevic A. Altered global brain signal in schizophrenia. Proc Natl Acad Sci U S A. 2014;111:7438–43. doi: 10.1073/pnas.1405289111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan H, Zotev V, Phillips R, Bodurka J. Correlated slow fluctuations in respiration, EEG, and BOLD fMRI. Neuroimage. 2013;79:81–93. doi: 10.1016/j.neuroimage.2013.04.068. [DOI] [PubMed] [Google Scholar]
- Yuan H, Zotev V, Phillips R, Drevets WC, Bodurka J. Spatiotemporal dynamics of the brain at rest - Exploring EEG microstates as electrophysiological signatures of BOLD resting state networks. Neuroimage. 2012;60:2062–2072. doi: 10.1016/j.neuroimage.2012.02.031. [DOI] [PubMed] [Google Scholar]
- Zhang D, Raichle ME. Disease and the brain’s dark energy. Nat Rev Neurol. 2010;6:15–28. doi: 10.1038/nrneurol.2009.198. nrneurol.2009.198 [pii] [DOI] [PubMed] [Google Scholar]