Membrane Elastic Deformations Modulate Gramicidin A Transbilayer Dimerization and Lateral Clustering

Abstract

Gramicidin A (gA) is a short β-helical peptide known to form conducting channels in lipid membranes because of transbilayer dimerization. The gA conducting dimer, being shorter than the lipid bilayer thickness, deforms the membrane in its vicinity, and the bilayer elastic energy contributes to the gA dimer formation energy. Likewise, membrane incorporation of a gA monomer, which is shorter than the lipid monolayer thickness, creates a void, thereby forcing surrounding lipid molecules to tilt to fill it. The energy of membrane deformation was calculated in the framework of the continuum elasticity theory, taking into account splay, tilt, lateral stretching/compression, Gaussian splay deformations, and external membrane tension. We obtained the interaction energy profiles for two gA monomers located either in the same or in the opposite monolayers. The profiles demonstrated the long-range attraction and short-range repulsion behavior of the monomers resulting from the membrane deformation. Analysis of the profile features revealed conditions under which clusters of gA monomers would not dissipate because of diffusion. The calculated dependence of the dimer formation and decay energy barriers on the membrane elastic properties was in good agreement with the available experimental data and suggested an explanation for a hitherto contentious phenomenon.

Introduction

Gramicidin A (gA) is a peptide antibiotic produced by Bacillus brevis. The peptide consists of 15 alternating L- and D-amino acid residues. gA is majorly hydrophobic and, being applied exogenously, easily incorporates into a lipid membrane with a water/membrane distribution coefficient of ∼10⁻⁴ (1). In the membrane, gA can adopt the form of a transmembrane dimer composed of head-to-head linked β^6.3-helical monomers that results in the opening of an ion channel (2, 3, 4, 5, 6, 7, 8). At the same time, being dissolved in organic solvents, it can adopt several other conformations (9, 10, 11, 12). As demonstrated by electron spin resonance spectroscopy (13), in lipid membranes there is equilibrium among conducting dimers, free monomers, and a small fraction of other nonchannel forms, such as gA double helices. According to electrophysiological measurements (14), the equilibrium of conducting dimers and nonchannel forms (mainly presented by gA monomers) in a “usual” membrane is strongly shifted toward monomers (∼1:100). In these experiments, the channel-forming activity can be seen as a series of stepwise changes in membrane conductance. gA channels can be characterized by the conductance “step” amplitude, probability of channel formation (probability of transmembrane dimerization), and average lifetime of the conductive state (2, 14).

Being associated with monomer/dimer equilibrium, the formation of gA channels should depend on the concentration of membrane-incorporated monomers and the rate of their lateral diffusion. Once the conductive state is lost (the transmembrane dimer dissociated), the released monomers are expected to be free to diffuse and form conductive channels with other dimerization partners. Busath and colleagues (15) described an experimental investigation of the evolution of the electric conductivity of a large membrane after fusion with vesicles containing gA at high concentrations. Immediately after the fusion, the total conductivity of the membrane increased in a stepwise manner because of the incorporation of transmembrane dimers of gA molecules initially confined to a small area. The lateral diffusion of gA in the large membrane was expected to result in a monotonous reduction of its local surface concentration and hence a decrease in the likelihood of dimerization. The average conductivity of the membrane was thus expected to decay with time. However, it proved practically invariable on the scale of tens of minutes, with multiple events of formation and disappearance of conductive dimers occurring within this period. The authors hypothesized that closure of the gA channels is associated with a reversible conformational transition in the dimer (internal gating) rather than dissociation of the dimer into freely diffusing monomers (15). The assumption, however, directly contradicted the results accumulated over decades of investigation by other laboratories, which were in good agreement with the notion that the conductive channels are formed by means of dimerization (and that the dimers dissociate back into monomers). In particular, the dimerization explained well the impact of a voltage jump applied to the membrane (14) or a flash of light in the presence of a photosensitizer (16). Besides, the experimental evidence that the lifetime of the channels formed by laterally linked dimers of gramicidin is much longer than the lifetime of ordinary gA channels (17, 18, 19) is also against the internal gating mechanism. Recently, the long-lasting conductivity of the membranes received a plausible explanation, alternative to the internal gating of gA channels (20). It was explicitly demonstrated that the vesicles and the membrane of large area can exchange gA molecules without complete fusion. However, Lum and colleagues (20) could not explain the extremely low probability of formation of gA and gramicidin M (gM) heterodimers delivered to the membrane in different vesicles, which was observed by Busath and colleagues (15).

The length of the gA monomer along the axis of the helix is ∼1 nm (21), whereas the thickness of the hydrophobic zone of the monolayer in the membrane formed from a “common” lipid (e.g., dioleoylphosphatidylcholine (DOPC), diC18:1) is ∼1.5 nm (22, 23, 24). Therefore, the transmembrane gA dimer is ∼1 nm shorter than the usual width of the bilayer membrane hydrophobic core. This means that the membrane has to be deformed in the vicinity of a monomer or a conductive dimer. The average thickness of the membrane with incorporated gA was experimentally shown to differ from that of a pure bilayer (25). The thickness of the relatively “thin” dilauroylphosphatidylcholine (diC12:0) bilayer increased upon incorporation, whereas that of the thicker dimyristoylphosphatidylcholine (diC14:0) bilayer decreased in both cases toward approximately the same average thickness of ∼3.2 nm between the planes of phosphorus atoms of lipids from the two opposite monolayers. The observed decrease in the average thickness of the dimyristoylphosphatidylcholine membrane in the presence of gA does not necessarily imply the transbilayer dimerization of gA. Indeed, shallow incorporation of the monomer into the lipid bilayer creates a void immediately under the peptide in the corresponding monolayer. This void has to be filled with acyl tails of the neighboring lipid molecules, which should cause a reduction of the average thickness of the affected monolayer in the immediate neighborhood of the peptide. However, transbilayer dimerization of the peptide appears to be the only viable option for the increase of the average membrane thickness upon incorporation of gA into the dilauroylphosphatidylcholine bilayer. Any deviation of the membrane thickness from its equilibrium value means the emergence of elastic deformations, which require mechanical work to be performed. Thus, both too “thick” and too “thin” membranes are expected to hinder gA channel activity. Some optimal thickness of the bilayer should exist, in which gA conducting dimer formation is accompanied by only minimal membrane distortion. The parameters of the conductive channel (the probability of formation and the lifetime) were shown to depend on the elastic properties of the lipid bilayer, including the lateral tension (26), the membrane thickness (21, 27), and the monolayer spontaneous curvature (28).

Except for several studies on molecular dynamics modeling (29, 30), it was usually assumed that the membranes are not deformed near the gramicidin monomers so that only the dependence of deformations in the vicinity of a conductive dimer (or partly dissociated dimer (27)) upon the parameters of the membrane in elastic models of different levels of discretization was analyzed. The strong influence of the membrane mechanical parameters on the formation probability and lifetime of the conductive dimer considerably complicates the task of formulating a consistent hypothesis about the internal channel gating, as suggested by Busath and colleagues (15).

In this work, we consider a continuous trajectory of formation of a conductive dimer from two initially separated monomers. Elastic deformations are also assumed to occur near the individual monomers because the length of their helices is smaller than the thickness of the hydrophobic zone of a lipid monolayer. As monomers approach each other, deformations induced by them start to overlap, causing considerable lateral interaction. We use the elasticity theory of liquid crystals adapted to lipid membranes to calculate the interaction energy profile as a function of the distance between the monomers, the change of the elastic energy upon formation of the conductive dimer, and the conductive channel lifetime and the probability of their formation. The results of the analysis are compared with the available experimental data. We demonstrate that the characteristics of the interaction energy profile of a pair of monomers explain the preservation of conductivity in a large-area membrane observed in (15) without the assumption about the internal gating of the gA channel.

Materials and Methods

We consider the deformations of a lipid bilayer occurring in the presence of peptides in one or two monolayers using gA as an example. As discussed above, a gA monomer deforms the membrane around it, and several peptides in close proximity interact through overlapping of the induced deformations. When a pair of gA monomers dimerizes to form a conductive channel, the field of induced membrane deformations around the pair changes, and the energy associated with the deformation affects the channel lifetime and monomer/dimer equilibrium. The goal of this work is to evaluate the energy of peptide interaction mediated by lipid bilayer deformations.

The membrane deformations are considered in the continuous approximation. The assumption is justified by the characteristic lengths of deformations being significantly greater than the characteristic lateral dimensions of lipid molecules. The elastic energy is calculated in the framework of the Hamm-Kozlov model (31), in which the state of the lipid bilayer is determined by the field of unit director vectors n characterizing the time-averaged orientation of the acyl chains of lipid molecules. The field of directors is defined on an arbitrary surface lying inside a monolayer referred to as the dividing surface. The surface is characterized by a field of unit vectors normal to it, N, and the field of specific change of the dividing surface area relative to its area in the initial, nondeformed state, $\alpha =\frac{\mathit{\Delta }a}{a}$. Besides that, the state of the monolayer is determined by the local thickness field. The normal and the director are considered to be directed into the monolayer. In this analysis, we consider four types of deformations: 1) splay, characterized by the splay modulus B and quantitatively described by the divergence of the director along the neutral surface div(n); 2) tilt, characterized by the tilt modulus K_t and described by the tilt vector field t = n/(nN) − n ≈ n − N, where (nN) stays for the scalar product of the director and the normal vectors and where, for small deformations, (nN) = |n||N|cos(θ) = cos(θ) ≈ 1 − θ²/2 ≈ 1 (θ is a small angle between n and N); 3) lateral stretch/compression, characterized by the stretch/compression modulus K_a and described by the surface area change field α; and 4) the contribution of Gaussian curvature K characterized by the modulus k_G. External lateral tension, σ, of the membrane is also taken into account. We utilize the specific dividing surface inside the lipid monolayer, where the energy contributions from splay and lateral stretch/compression deformations are independent of each other. This surface is known as the neutral surface and is located at a distance of ∼0.7 nm from the outer surface of the monolayer in the area of junction between the polar head groups and the acyl tails of lipid molecules (32). Besides, we introduce some (arbitrary) reference plane parallel to the surface of the undeformed membrane to describe the shapes of neutral surfaces of deformed monolayers.

In the quadratic approximation, the energy of monolayer deformation can be expressed as follows (31):

$$W=\int dS\left(\frac{B}{2}{\left(\text{div}\mathbf{n}+J_0\right)}^2-\frac{B}{2}{J}_0^2+\frac{K_t}{2}{\mathbf{t}}^2+\frac{K_a}{2}{\left(\alpha -{\alpha }_0\right)}^2+\frac{\sigma }{2}{\left(\mathbf{g}\mathbf{r}\mathbf{a}\mathbf{d}H\right)}^2+k_{G}K\right),$$ (1)

where J₀ is the spontaneous curvature of the lipid monolayer, H is the distance from the reference plane to the neutral surface of the monolayer measured along the normal to the reference plane, and α₀ = σ/K_a is the equilibrium stretching of the monolayer caused by the lateral tension. In a certain Cartesian system of coordinates with Oxy plane parallel to the average membrane plane, the contribution of the Gaussian curvature can be written as $K=\frac{\partial n_x}{\partial x}\frac{\partial n_y}{\partial y}-\frac{\partial n_x}{\partial y}\frac{\partial n_y}{\partial x}$, where n_x, n_y are projections of the director onto Ox, Oy axes, respectively. Integration in Eq. 1 is performed over the neutral surface of the monolayer. We choose the reference state of a monolayer as the planar monolayer (zero geometric curvature), which is not subject to lateral tension. The energy necessary to bring the monolayer from its spontaneous state (zero lateral tension, the geometric curvature equal to the spontaneous curvature J₀) to the reference state equals the following:

$$W_0=\int dS\left(\frac{B}{2}{\left(0-J_0\right)}^2+\sigma \right)=\int dS\left(\frac{B}{2}{J}_0^2+\sigma \right).$$ (2)

This energy is subtracted from the energy of a monolayer obtained with respect to its energy in the spontaneous state in Eq. 1 to relate the elastic energy to the reference state.

A “usual” lipid monolayer at room temperature is similar to a layer of smectic A liquid crystal with unstructured (laterally liquid) layers (33). For such liquid crystals, the vector field of directors is conservative, i.e., curl(n) = 0, under the assumptions of the linear theory of elasticity (34), which we utilize in this work. Thus, neither twist nor bend deformations are applicable to lipid membranes, as their energies are proportional to (n⋅curl(n))² and [n × curl(n)]², respectively. These deformations are generally common for nematic rather than smectic A liquid crystals. Physically, this means that the corresponding elastic moduli in smectic A are very high and that the energy stored in twist and bend deformations is thus negligibly small (34).

It was recently demonstrated in (35) that the elastic energy functional Eq. 1 should be augmented by a second-order term proportional to the product div(n)div(t). Despite the apparent importance of this work and its high impact on the field of membrane elasticity, the question on this additional term is still open. As the authors indicate, this term leads to inevitable instability of the membrane, making the energy functional not positively determined. That makes practical use of this additive impossible; further investigations should be carried out to bring the modified model to more physically meaningful results with the flat lipid bilayer being stable. We thus opted not to include the term ∼div(n)div(t) into the energy functional.

The hydrophobic part of the membrane is assumed to be locally volumetrically incompressible, as is justified by the large value of its volumetric compressibility modulus ∼10¹⁰ J/m³ (36). The volumetric incompressibility imposes a constraint on the mechanical deformation fields. With the adopted accuracy, the local volumetric incompressibility condition can be written as follows (31):

$$h_c=h-\frac{h^2}{2}\text{div}\mathbf{n}-h\alpha ,$$ (3)

where h_c is the current local monolayer thickness, and h is the thickness of the undeformed monolayer.

The gramicidin monomer is represented as an infinitely rigid nondeformable cylinder with a radius of r₀ and a hydrophobic part length of h_p. Our model assumes that gramicidin imposes boundary conditions upon deformations, i.e., on the functional Eq. 1. Based on the geometric meaning of the director (Fig. S1), the director at the boundary of gA can be evaluated as follows:

$$\begin{array}{l}{n}_n\left(r=r_0\right)\equiv n_0=-\left(h-h_p\right){\left({\left(h-h_p\right)}^2+h_p^2\right)}^{-\frac{1}{2}},\\ n_{\tau }\left(r=r_0\right)=0,\end{array}$$ (4)

where n_n and n_τ are the normal and the tangential component of the director at the gA boundary on the neutral surface of the corresponding monolayer, respectively, and r₀ is the radius of the gA molecule (we assume that r₀ = 1 nm). It must be also taken into account that all the deformations tend toward zero at a sufficiently large distance from the peptide:

$$n_{\tau }\left(\mathrm{\infty }\right)=0,n_n\left(\mathrm{\infty }\right)=0,\mathrm{div}\left(\mathbf{n}\left(\mathrm{\infty }\right)\right)=0,\mathbf{t}\left(\mathrm{\infty }\right)=\mathbf{0},\mathbf{grad}\left(H\left(\infty \right)\right)=\mathbf{0},\alpha \left(\mathrm{\infty }\right)=0.$$ (5)

Thus, the problem of evaluating the interaction energy of gA monomers is reduced to the problem of minimization of the elastic energy functional, Eq. 1, with the Dirichlet boundary conditions Eqs. 4 and 5. In the framework of our model, any membrane inclusion is modeled by the boundary conditions imposed on the membrane shape and deformations. Because the energy functional (Eq. 1) could be minimized for different peptide configurations (boundary conditions), the developed formalism is applicable for the description of a large variety of membrane proteins, including amphipathic peptides (37, 38, 39, 40) and channels.

Special cases

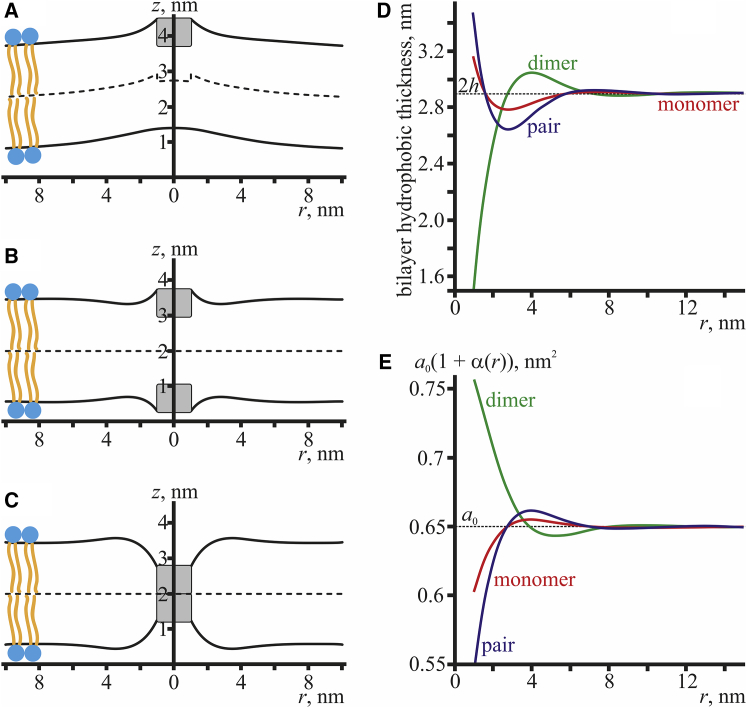
Although the elastic energy functional Eq. 1 is of the second order in deformations and the corresponding Euler-Lagrange equations are linear equations in partial derivatives, the boundary conditions Eqs. 4 and 5 do not allow for solving the problem analytically even in the case of two gA molecules at a finite distance. An analytical solution is only possible in several special cases in which the system has an additional symmetry and the problem becomes effectively unidimensional. In these cases, the Euler-Lagrange equations become ordinary differential equations. Three configurations of peptides can be considered under the assumption of the cylindrical symmetry of the system: 1) a single peptide (Fig. 1 A), 2) a pair of peptides one under the other in the opposite monolayers of the membrane (Fig. 1 B), and 3) a conductive dimer formed by two peptides located in the opposite monolayers (Fig. 1 C). Details of the analytical minimization of the energy functional, Eq. 1, and the obtaining of the spatial distribution of deformations under conditions of the rotational symmetry for these three special cases (Fig. 1) are presented in the Eqs. S1–S14.

Figure 1.

Cylindrically symmetrical configuration of peptides. (A) An isolated gramicidin monomer, (B) a pair of monomers coaxially located in two opposite monolayers, and (C) a conductive dimer are shown. The red dotted lines illustrate the channel pore lumen. The black dotted line designates the rotational symmetry axis of the configurations. To see this figure in color, go online.

General case

Generally, configurations of peptides lack any symmetry. The gA monomers deform the membrane. If the distance between the peptides is large enough, the deformations are independent as they do not overlap, and the total elastic energy of the membrane is a sum of the energies of deformation induced by each peptide. As the peptides come closer to each other, the deformations start to overlap, leading to effective lateral interaction. In this case, the total energy is not equal to the doubled energy of deformations induced by a single peptide. The difference between the elastic energy at the finite peptide-to-peptide distance and the deformation energy of two infinitely separated peptides is referred to as the interaction energy. Thus, considering peptide pairwise interaction, we account only for the membrane deformations induced by the peptides.

Due to the analytical difficulty of minimizing the elastic energy functional, Eq. 1, under the boundary conditions Eqs. 4 and 5 in the absence of the additional symmetry, we resorted to numeric minimization of the functional using a finite difference scheme. Details of the numerical minimization of the energy functional, Eq. 1, in the most general case of absence of any symmetry in the system are presented in Eqs. S1–S3 and S15–S18.

Collective phenomena

Below, we consider a system of N_u particles in the upper monolayer and N_d particles in the lower monolayer of lipid membrane of an area S, corresponding to particle surface concentrations C_u = N_u/S and C_d = N_d/S, respectively. We assume that the particles are independent in the sense that the interaction energy can achieve its minimum for each couple regardless of the state of other particles. Then, the energy of a couple can be expressed as follows:

$$U_{couple}=\frac{\underset{S}{\int }{W}_{\mathrm{int}}{e}^{-\frac{W_{\mathrm{int}}}{k_{B}T}}d\mathbf{r}}{\underset{S}{\int }{e}^{-\frac{W_{\mathrm{int}}}{k_{B}T}}d\mathbf{r}}\approx \frac{\underset{S}{\int }{W}_{\mathrm{int}}{e}^{-\frac{W_{\mathrm{int}}}{k_{B}T}}d\mathbf{r}}{S},$$ (6)

where W_int = W(2L) − W(∞) is the energy of interaction of two particles. The integral in the second denominator of Eq. 6 was taken under the assumption that the membrane surface area S is much greater than the region in which the interaction energy W_int(r) is substantially nonzero. The total energy of the system is given by the following:

$$U=\frac{N_u^2}{2}\frac{\underset{S}{\int }{W}_{uu}{e}^{-\frac{W_{uu}}{k_{B}T}}d\mathbf{r}}{S}+N_u{N}_d\frac{\underset{S}{\int }{W}_{ud}{e}^{-\frac{W_{ud}}{k_{B}T}}d\mathbf{r}}{S}+\frac{N_d^2}{2}\frac{\underset{S}{\int }{W}_{dd}{e}^{-\frac{W_{dd}}{k_{B}T}}d\mathbf{r}}{S},$$ (7)

where W_uu, W_dd, and W_ud are the interaction energies between monomers in the upper, bottom, and opposite monolayers, respectively; obviously, W_uu = W_dd. The interaction energy profiles, W_uu and W_ud (appended by the energy of two isolated monomers), are presented in Fig. 5, B and C, in the paragraph titled “Gramicidin A monomer/monomer and dimer/dimer interactions” of Results. This total energy corresponds to the chemical potential μ_u,d = μ^id_u,d + μ^int_u,d, where μ^id_u,d is the chemical potential of the ideal two-dimensional gas of the particles, and μ^int_u,d is the derivative of the total energy U with respect to N_u or N_d, respectively. The diffusive flow J is known to be generally determined by the chemical potential according to the following relation:

$$\mathbf{J}\mathbf{\sim }C\mathrm{\times }\mathbf{grad}\mu .$$ (8)

Figure 5.

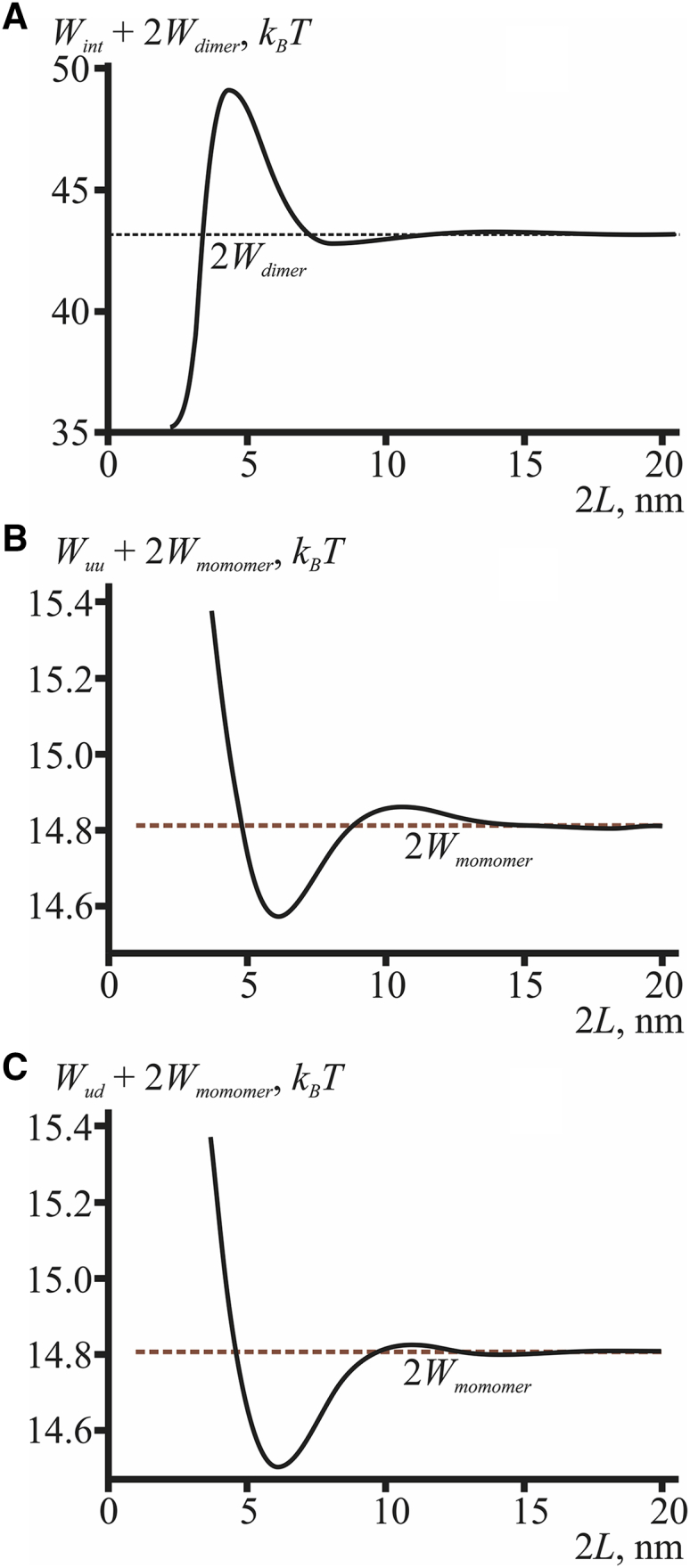
The energy of membrane deformation in the vicinity of two gramicidin dimers (A) and monomers (B and C) as a function of the distance between the monomers. (B) The monomers here are in the same monolayer, whereas in (C) the monomers are in the opposite monolayers. The black horizontal dashed line corresponds to the energy 2W_dimer of two infinitely distant gramicidin dimers; the brown horizontal dashed lines correspond to the energy 2W_monomer of two infinitely distant isolated gramicidin molecules. To see this figure in color, go online.

We consider the case of a high local concentration of gA in the form of a spot on the membrane, assuming the characteristic length of a change in concentration to be much greater than the characteristic distance of interaction between individual particles. We also assume local thermodynamic equilibrium to exist so that we can use the above-mentioned chemical potential in the case of variable concentrations. Taking into account the extra term U in the chemical potential, the flow in the case of symmetrically distributed gA is given by the following:

$$\mathbf{J}\mathbf{\sim }{k}_{B}T\cdot \mathbf{grad}C\mathrm{+}C\cdot \mathbf{grad}C\cdot I\left(T\right)\mathrm{,}$$ (9)

where

$$I\left(T\right)=\underset{S}{\int }{W}_{uu}{e}^{-\frac{W_{uu}}{k_{B}T}}d\mathbf{r}+\underset{S}{\int }{W}_{ud}{e}^{-\frac{W_{ud}}{k_{B}T}}d\mathbf{r}.$$ (10)

As can be seen from Eq. 9, the flow tends to zero at a certain critical concentration of ${С}_{crit}=-k_{B}T/I\left(T\right)$, which corresponds to a stable, nondiffusing cluster of gA in the membrane.

Results

System parameters

We are going to use the following parameters for graphical representation of the obtained results: monolayer splay modulus B = 10 k_BT (k_BT ≈ 4 × 10⁻²¹ J) (22), tilt modulus (per monolayer) K_t = 40 mN/m (31, 41), monolayer lateral stretch/compression modulus K_a = 120 mN/m (22), area per lipid molecule a₀ = 0.65 nm² (29), thickness of the hydrophobic part of the monolayer h = 1.45 nm (typical for DOPC (22, 23, 24)) unless specified otherwise, Gaussian curvature modulus (per monolayer) K_G = −3 k_BT, and lateral tension (per monolayer) σ = 0.1 mN/m unless specified otherwise. The depth of insertion of a gA molecule measured from the neutral surface inward the monolayer was assumed at h_p = 0.75 nm. The value of the boundary director n₀ = −0.68 is obtained from Eq. 4 at a given hydrophobic length of gramicidin h_p and monolayer thickness h.

Special cases: cylindrically symmetrical configurations of peptides

The membrane shapes calculated for the cylindrically symmetrical configurations of the peptides are shown in Fig. 2 for an isolated monomer (Fig. 2 A), a pair of juxtaposed monomers (Fig. 2 B), and a conductive dimer (Fig. 2 C). The radial distributions of the bilayer hydrophobic thickness, H_u(r) − H_d(r) (see Eq. S1), around an isolated monomer, a pair of monomers, and a dimer are shown in Fig. 2 D. The radial distributions of the area per lipid molecule are presented in Fig. 2 E; the area is the same in both monolayers, even for the gA monomer, because of the specific symmetry of the deformations (see Eq. S7). As illustrated by Fig. 2, the membrane deformations occur in all three cases. Except for several works on molecular dynamics (e.g., (29, 30)), earlier it was assumed in a number of publications that only the conductive dimers cause membrane deformations, whereas a single monomer or a juxtaposed pair leave the membrane unperturbed (27, 28, 42, 43). The deformations in these cases are caused by a mismatch between the length of the gA molecule and the thickness of the monolayer. Under the condition of local volumetric incompressibility, nonzero director values occur at the peptide boundary both in the case of an isolated monomer and in the case of a juxtaposed pair (see Eqs. 4, S12, and S13). This yields nontrivial (nonzero) solutions of the Euler-Lagrange system of equations, Eq. S5, for spatial distribution of deformations. In the case of a conductive dimer, nontrivial solutions arise because of the constraints imposed on the bilayer thickness at the boundary of the dimer, Eq. S14. The deformations occurring in all three cylindrically symmetrical configurations are to be taken into account in the analysis of the dependence of energy barriers for the formation and disappearance of the conductive state upon the membrane elastic parameters, in particular upon the monolayer thickness and lateral tension (26, 27). In some previous works (26, 27, 43, 44), the barrier-to-dimer formation was simply assumed to be equal to the energy of the membrane deformation in the vicinity of the dimer calculated with respect to the energy of a planar unperturbed bilayer. However, the conductive dimer is formed from a pair of juxtaposed monomers; this configuration is formed from two initially isolated monomers. Accordingly, the energy barrier to formation of a conductive state should be calculated from the nonzero energy of the membrane deformation in the vicinity of the pair of isolated monomers. Because both energies—that of a dimer and that of a pair of monomers—depend on the elastic parameters of the membrane, their difference might depend on these parameters in a rather nontrivial manner, which needs to be taken into account during interpretation of the experimental results.

Figure 2.

Calculated membrane shapes for the cylindrically symmetrical configurations of peptides: (A) an isolated monomer, (B) a pair of juxtaposed monomers, and (C) a conductive dimer. The dashed curves illustrate the shape of the intermonolayer surfaces, and the solid curves illustrate the shapes of the neutral surfaces of the monolayers. Gramicidin molecules are shown as gray rectangles. (D) The radial distribution of the bilayer hydrophobic thickness, H_u(r) − H_d(r) (see Eq. S1), is shown around an isolated monomer (red curve), a pair of juxtaposed monomers (blue curve), and a dimer (green curve). (E) The radial distribution of the area per lipid molecule, a(r) = a₀(1 + α(r)), is shown around an isolated monomer (red curve), a pair of juxtaposed monomers (blue curve), and a dimer (green curve). The elastic properties of the membrane correspond to these of DOPC (diC18:1), except for the spontaneous curvature: it was assumed to be zero. To see this figure in color, go online.

Dependence of the probability of dimer dissociation on the lateral tension

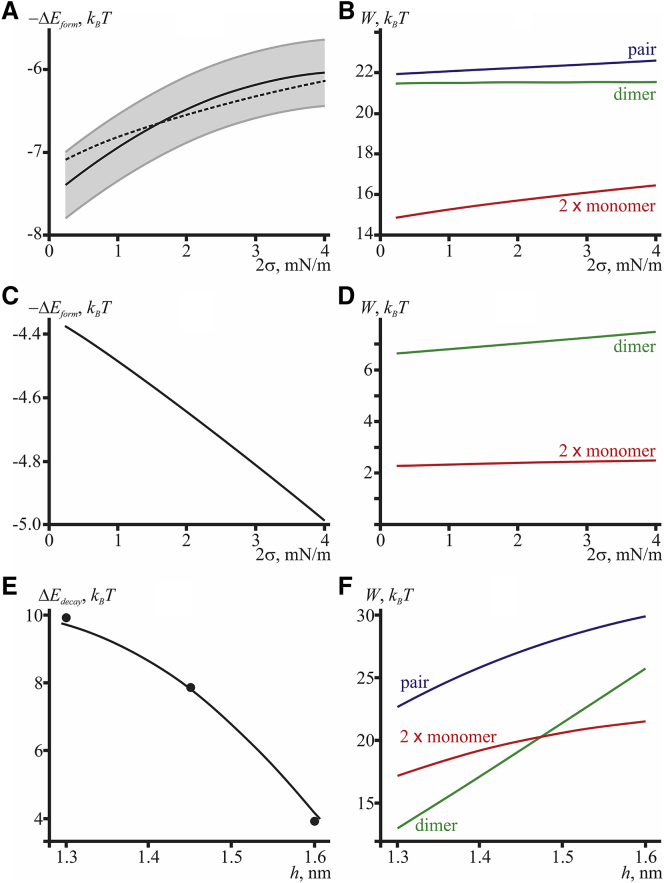
To compare the results of analysis with the experimental data, we used the works in which the dependence of the probability of disappearance of the conductive state upon lateral tension (26) and the dependence of probability of formation of the conductive state on the lipid bilayer thickness (27) were investigated. According to the study by Goulian and colleagues (26), to achieve the conductive state corresponding to the dimer configuration, two isolated monomers have to be brought into juxtaposition and then dimerized. Bringing the monomers into juxtaposition requires mechanical work against the elastic forces. The amount of work depends on the membrane tension and other mechanical parameters. The dimerization process also requires mechanical work to be performed against elastic forces, which is achieved by the formation of six hydrogen bonds between the N-termini of two monomers (13). The hydrogen bonding energy is independent of the elastic parameters of the membrane. Thus, the energy barrier of ΔE_form = W_pair − 2W_monomer needs to be crossed to achieve the conductive state, and the energy barrier of ΔE_decay = W_pair − W_dimer needs to be crossed to destroy the conductive state.

As it was shown in the work by Goulian and colleagues (26), the logarithm of probability of formation of the conductive state, which was measured by the authors as a function of the membrane lateral tension, equals $\left(-\mathit{\Delta }{E}_{form}/k_{B}T\right)$ to within an additive constant. Fig. 3 A illustrates the dependence of the energy difference ΔE_form = W_pair − 2W_monomer on the membrane lateral tension calculated on the basis of our model (dashed curve) and the result of approximation of the experimental data from (26) (solid curve). Within the statistical uncertainty, our model adequately describes the experimental data.

Figure 3.

(A) Dependence of the sign-inversed energy barrier, −ΔE_form = 2W_monomer − W_pair, upon lateral tension, 2σ, of the DOPC membrane (dashed curve). The solid curve shows the result of a quadratic approximation of the experimental data from (26). The gray curves delineate the statistical spread of the experimental data (shaded as light gray). (B) The dependence of the energies of deformations induced by two isolated monomers, 2W_monomer (red curve), a pair of juxtaposed monomers, W_pair (blue curve), and the energy of conductive dimer, W_dimer (green curve), upon the lateral tension of the DOPC lipid membrane, 2σ. (C) The dependence of the sign-inversed energy barrier, −ΔE_form = 2W_monomer − W_dimer, is shown upon lateral tension, 2σ, of the thin membrane, where hydrophobic thickness is smaller than that of the dimer (2h = 1.1 nm). (D) The dependence of the energies of deformation induced by two isolated monomers, 2W_monomer (red curve), and the energy of conductive dimer W_dimer (green curve) upon the lateral tension of the thin membrane, 2σ. (E) The dependence of the energy barrier ΔE_decay = W_pair − W_dimer upon the lipid monolayer thickness (solid curve) is shown. Black circles — experimental points from (27) vertically shifted by a certain constant value. (F) The dependence of the membrane elastic energy induced by two monomers, 2W_monomer (red curve), a pair of juxtaposed monomers, W_pair (blue curve), and a dimer, W_dimer (green curve), upon the monolayer thickness is shown. For (C) and (D), the spontaneous curvature was assumed to linearly decrease with the increasing monolayer thickness: J_C16:1 = 0.08 nm⁻¹, J_C18:1 = 0.06 nm⁻¹, and J_C20:1 = 0.04 nm⁻¹. To see this figure in color, go online.

Fig. 3 B illustrates the dependence of the energies of the cylindrically symmetrical configurations of the peptides on lateral tension for the cases of two isolated monomers 2W_monomer (red curve), a pair of juxtaposed monomers W_pair (blue curve), and conductive dimer W_dimer (green curve). All three energies depend on lateral tension in a different manner, creating the opportunity for nontrivial dependence of the energy difference −ΔE_form = 2W_monomer − W_pair (Fig. 3 A) upon the lateral tension. We should note that when calculating the energy of different states (in particular, the configurations denoted in Special Cases), we take into account only the energy of elastic deformations of the membrane induced by the peptides and neglect any direct peptide-peptide and lipid-peptide interactions. Besides, we assume that the state of the peptide is independent of the deformations it induces, as the peptide is considered as an infinitely rigid undeformable cylinder.

For the chosen set of the elastic parameters, our model predicts stimulation of gA channel activity upon application of the lateral tension. Martinac and Hamill have experimentally demonstrated that the lateral tension may either activate or inactivate the channel activity depending on the thickness of the lipid bilayer (45). In diC20:1 and thicker lipid membranes, the tension activates gramicidin channels, whereas in diC18:1 and thinner lipid membranes, it inactivates them. The authors conclude that the lateral tension activates channels in bilayers whose thickness exceeds the gramicidin dimer length and inactivates channels in thinner bilayers. For the thicknesses utilized in (45) of diC18:1 and diC20:1 bilayers of 2.7 and 3.0 nm, respectively, and the length of the gA dimer of 2.6 nm, the explanation quantitatively agrees with the experimental observations (45). However, for the more realistic hydrophobic thickness of the diC18:1 bilayer of 2.8 nm (29) and the length of the gA dimer of 2.2 nm (21, 46), this explanation does not work. However, qualitatively the effect of switching the response of gA channels to applied lateral tension upon variation of the hydrophobic thickness of the membrane can also be predicted in the framework of our model. For bilayers whose thicknesses exceed the length of the gA dimer, the activation by the lateral tension directly follows from the plot Fig. 3 B: the membrane elastic energy in the case of two isolated monomers grows faster than the elastic energy in the cases of the dimer and a pair of juxtaposed monomers upon application of the lateral tension. Thus, the barrier of the channel formation decreases as the tension grows. In the membrane, whose thickness is smaller than the gA dimer length, the configuration of a pair of juxtaposed monomers does not exist; the conducting dimer can only be formed directly from the two isolated monomers, with negative hydrophobic mismatch, i.e., increased bilayer thickness, at the dimer boundary. Upon application of the lateral tension, the membrane elastic energy in this case grows faster than in the case of the two isolated monomers (Fig. 3 D), thus resulting in an increase of the energy barrier of channel formation (Fig. 3 C).

Thus, as predicted by our continuum elastic model, the lateral tension of the membrane may either activate or inactivate the channel activity of gA depending on the relation of the hydrophobic thickness of the bilayer and the length of the gA dimer. The theoretical results are in qualitative agreement with the available experimental data (26, 45).

Dependence of the probability of dimer formation on the lipid membrane thickness

According to the experimental work of Lundbaek and Andersen (27), the logarithm of the conductive state lifetime ln(τ_life) = ΔE_decay to within an additive constant. The ln(τ_life) was measured as a function of the thickness of the hydrophobic part of the lipid bilayer. The lipid bilayer was formed from monopalmitolein (C16:1), monoolein (C18:1), and monoeicosenoin (C20:1) dissolved in squalene rather than from “common” lipids. For comparison with the experimental dependence of the barrier ΔE_decay upon the membrane thickness, we estimated the corresponding values for the membranes consisting of the lipids С_16:1 (h = 1.3 nm), С_18:1 (h = 1.45 nm), and С_20:1 (h = 1.6 nm), assuming that the elasticity moduli change insignificantly upon the change of the acyl chain length from 16 to 20 carbon atoms and that the spontaneous curvature depends linearly on the acyl chain length. Thus, the respective spontaneous curvatures are J_C16:1 = 0.08 nm⁻¹, J_C18:1 = 0.06 nm⁻¹, and J_C20:1 = 0.04 nm⁻¹. The following energy barriers were obtained: ΔE_decay(h = 1.3 nm) = 9.7 k_BT, ΔE_decay(h = 1.45 nm) = 7.8 k_BT, and ΔE_decay(h = 1.6 nm) = 4.2 k_BT. It is generally believed that head-to-head dimerization of gramicidin is provided by the formation of six hydrogen bonds between monomers located in opposite monolayers (13). The energy of these bonds does not depend on the elastic properties of the lipid bilayer, in particular on its thickness or lateral tension, and can be considered as a certain constant (negative) addition to the energy of the elastic deformations of the membrane arising near the conducting dimer. Thus, the total energy of the dimer is determined to within an unknown constant: the energy of the hydrogen bonds formed during dimerization. Thus, the energy barrier, ΔE_decay = W_pair − W_dimer, can also be determined to within the unknown constant, although this constant should be the same for different monolayer thicknesses. We only calculated the contribution of the elastic energy into the total energy barrier, not taking into account the energy of hydrogen bonds formed during dimerization. The experimentally obtained energy barrier values are ΔE_decay(h = 1.3 nm) = 5.64 k_BT, ΔE_decay(h = 1.45 nm) = 3.58 k_BT, and ΔE_decay(h = 1.6 nm) = −0.35 k_BT. In Fig. 3 E, these values, shown as black circles, were shifted upward by the same constant to fit the calculated dependence ΔE_decay(h) (solid line). The slope of the straight line approximating the dependence of the energy barrier on the bilayer thickness calculated with the aid of our model amounts to −18 k_BT/nm, whereas the experimental results yield the value of −20 k_BT/nm (Fig. 3 E).

Fig. 3 F illustrates the dependence of the energies of three cylindrically symmetrical configurations of peptides upon the monolayer thickness. All three energies depend differently on the thickness, yielding a nontrivial dependence of the energy barrier ΔE_decay = W_pair − W_dimer upon h. Of note, the energy of the conductive dimer is smaller than the energy of a pair of juxtaposed monomers only in the case of positive spontaneous curvature of the monolayer consisting of the lipids used in the membrane-forming solution (27). The spontaneous curvature of “regular” lipids, such as DOPC, is usually negative (47, 48). In this case, the energy of a pair of monomers proves considerably smaller than the energy of a conductive dimer (Fig. 4 B).

Figure 4.

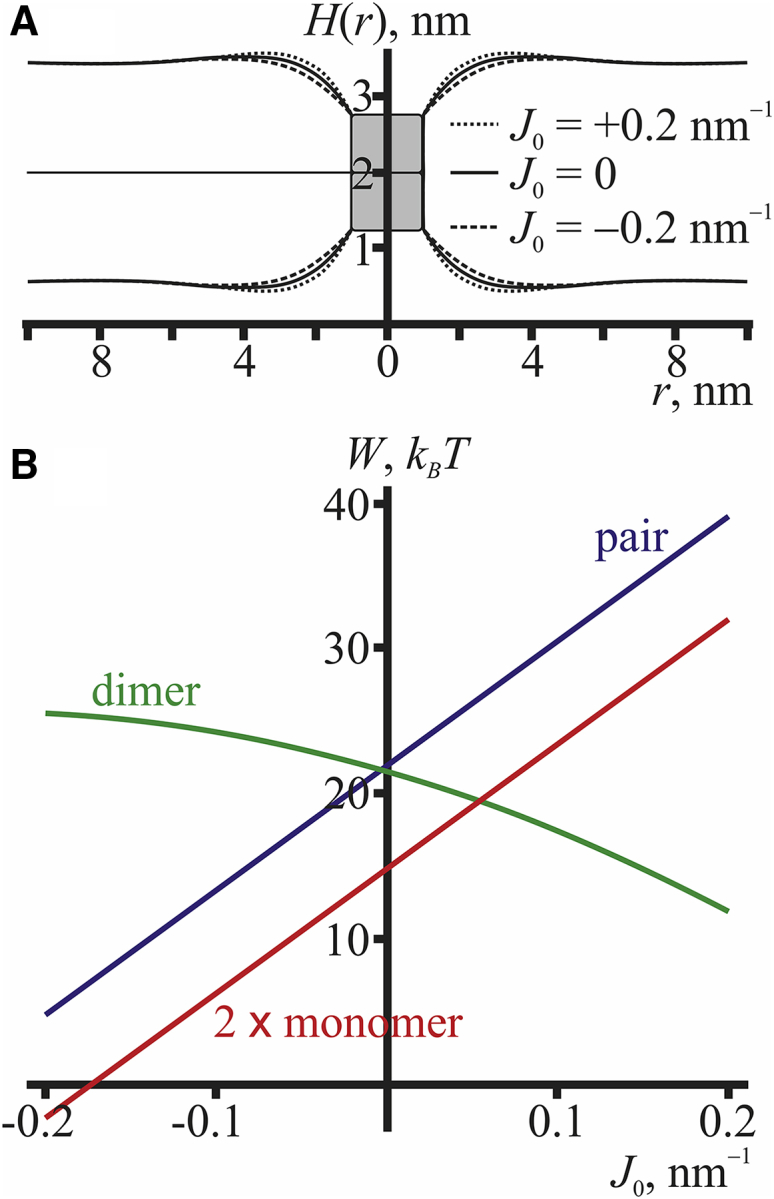
(A) Shapes of the membrane in the vicinity of the conducting dimer for different spontaneous curvatures of the monolayer: solid curve, J₀ = 0; dashed curve, J₀ = −0.2 nm⁻¹; and dotted curve, J₀ = +0.2 nm⁻¹. (B) The dependence of the energy of elastic deformations induced by two monomers, 2W_monomer (red curve), pair of juxtaposed monomers, W_pair (blue curve), and dimer, W_dimer (green curve), upon the monolayer spontaneous curvature is shown. To see this figure in color, go online.

Thus, our continuum elastic model predicts the decrease of gA channel lifetime in membranes of successively increasing thickness (accompanied by decreased spontaneous curvature of the monolayers (48)). Good agreement of the calculated values with the experimental results for the dependence of ΔE_decay on the membrane thickness (27) and of ΔE_form on the lateral tension (26) suggests that our model adequately describes the “gramicidin-lipid bilayer” system.

Dependence of the energy of the symmetric configurations upon the spontaneous curvature of monolayers

The deformations induced by peptides in their vicinity include, but are not limited to, the splay deformation. The energy of splay deformations depends on the spontaneous curvature of monolayers. The spontaneous curvature does not enter the Euler-Lagrange equations or their solutions directly (see Eqs. S5–S8). However, as this parameter stands in the energy (Eq. 1), the spontaneous curvature affects the membrane shape and distribution of deformations by influencing the integration constants of the solutions (Eq. S7). The only term containing the spontaneous curvature in the energy functional is the following:

$$W_{spont}=\int J_0\text{div}\mathbf{n}dS=J_0\int \mathbf{n}\left(\mathit{\Gamma }\right)\mathbf{d}\mathit{\Gamma }.$$ (11)

Here, we utilized the divergence theorem to proceed from the integral over the neutral surface (S) to the integral over the peptide boundary (Γ). Thus, for rotationally symmetric configurations, the spontaneous curvature in the elastic energy stands multiplied by the boundary director and the boundary perimeter. If the boundary director is fixed, as in the cases of isolated monomers and a pair of juxtaposed monomers, the corresponding term is just an additive constant to the elastic energy, which does not affect the membrane shape. In the case of the conductive dimer, we do not fix the boundary director; the director is obtained by minimization of the elastic energy, and thus, the spontaneous curvature influences the membrane shape. The effect of the spontaneous curvature on the shape of the membrane in the vicinity of the conducting dimer is illustrated in Fig. 4 A. From the figure, it is seen that in the case of the positive spontaneous curvature, the contact angle of the neutral surface at the dimer boundary increases compared to the case of negative spontaneous curvature, so that the lipid polar heads “overhang” the channel pore at J₀ > 0.

Fig. 4 B illustrates the dependence of the energies of the cylindrically symmetrical configurations of peptides, 2W_monomer, W_pair, and W_dimer upon the spontaneous curvature of the monolayer. The spontaneous curvatures of the two monolayers of the membrane were assumed to be equal. Only the energy of elastic deformations was taken into account in the calculations; hence, the curve corresponding to the dimer energy can be vertically shifted by a certain constant value corresponding to the energy of hydrogen bonds, which is independent of the spontaneous curvature. The energies of a monomer and a pair of monomers depend linearly on the spontaneous curvature, both of them decreasing with the decrease of the spontaneous curvature. The corresponding straight lines are parallel, because as discussed above, the contribution of the spontaneous curvature into the energy is linear: W_S = −πr₀BJ₀(n_d(r₀) + n_u(r₀)), whereas the fixed director at the boundary of the gA molecule is the same for an isolated monomer and a pair of monomers, n₀ < 0. Thus, in the case of a pair of monomers, the spontaneous curvature contribution to the energy is W_S^pair = −πr₀BJ₀(n_d(r₀) + n_u(r₀)) = −πr₀BJ₀(n₀ + n₀) = 2πr₀BJ₀|n₀|. In the case of two isolated monomers, the corresponding contribution is 2W_S^monomer = −2πr₀BJ₀(n_d(r₀) + n_u(r₀)) = −2πr₀BJ₀(n₀ + 0) = 2πr₀BJ₀|n₀| = W_S^pair. In the configuration of a conductive dimer, the director at the peptide boundary is not fixed, but the bilayer thickness is; the energy dependence on the spontaneous curvature in this case becomes nonlinear. As can be seen from Fig. 4 B, the dimer energy W_dimer increases with decreasing spontaneous curvature, and the energy barrier for the decay of the conductive state ΔE_decay = W_pair − W_dimer, defined to within a fixed energy of hydrogen bonding, decreases. Accordingly, the lifetime of the conductive channel is also expected to decrease with decreasing spontaneous curvature.

It has been experimentally shown that the lifetime of the conductive state indeed decreases with decreasing spontaneous curvature (28) and increases with increasing spontaneous curvature (49). In (28), the spontaneous curvature was varied by means of adding cations (H⁺, Ca²⁺, Mg²⁺) to the solution bathing the membranes formed of a negatively charged lipid (dioleoylphosphatidylserine, diC18:1). It was assumed that neutralization of the lipid charge by the added counterions would mitigate the electrostatic repulsion of the lipid head groups, resulting in a spontaneous curvature decrease. In (49), a spontaneous curvature increase was achieved by replacing a lipid with weakly negative spontaneous curvature (diphytanoylphosphatidylcholine) with the one having a positive spontaneous curvature value (lysophosphatidylcholine). In both experimental systems, the possibility of inhomogeneous lateral distribution of components in the deformation field in the vicinity of peptides complicated the interpretation of the results.

Our continuum elastic model thus predicts the lifetime of the conductive channel to decrease with decreasing spontaneous curvature of the membrane. The prediction qualitatively agrees with the available experimental data (28, 49). The energy barrier of the channel formation, ΔE_form = W_pair − 2W_monomer, is predicted to be independent of the spontaneous curvature.

gA monomer/monomer and dimer/dimer interactions

Using the approach outlined in General Case, we calculated the dependence of the membrane elastic energy in the vicinity of two gramicidin dimers upon the distance between them (Fig. 5 A). At large separations, the energy of elastic deformations induced by each dimer is additive, and the total elastic energy equals 2W_dimer. As the dimers approach each other, the deformations induced by them overlap, leading to effective interaction characterized by the energy W_int. At distances of 2L ∼4–8 nm, the interaction is repulsive, whereas at shorter distances of 2L < 4 nm, it switches to strong attraction. On average, such an energy profile considerably favors the aggregation of gramicidin dimers, as the elastic energy at the minimal dimer separation is ∼8 k_BT lower than the energy of deformations induced by two infinitely separated dimers, 2W_dimer (Fig. 5 A).

We used the same generic approach to obtain the dependence of the membrane elastic energy in the vicinity of two monomers upon the distance between them in the case when the molecules are situated in the same monolayer (Fig. 5 B) and when they are in the opposite monolayers (Fig. 5 C). As can be seen in Fig. 5, B and C, for any mutual arrangement of gA molecules, the interaction force between them is repulsive at short distances (2L < 6 nm) and attractive at longer distances (6 nm < 2L < 10 nm). At a distance of 2L ≈ 6 nm, the elastic energy is minimal, which corresponds to a stable state of the system. At distances above ∼10 nm, the deformations induced by the monomers no longer overlap, and there is practically no interaction between the molecules.

The energy profiles in the cases of monomers located in the same monolayer (Fig. 5 B) and in the opposite monolayers (Fig. 5 C) look very similar. The similarity arises because the characteristic lengths of deformations (decay and oscillations) depend only on the elastic properties of lipid monolayers (Eq. S8) and not on the position of the peptides. Characteristic lengths determine the structure of the energy profiles, in particular the locations of minima and maxima. Besides, the monolayers are coupled to each other through the intermonolayer surface. In equilibrium, all forces and torques generated by the opposite monolayers at the intermonolayer surface should be exactly balanced. This requirement imposes a certain symmetry on the spatial distribution of deformations in the opposing monolayers (see Eq. S7). This symmetry additionally contributes to the similarity of the energy profiles of interaction of the gA monomers located in the same monolayer (Fig. 5 B) and in opposing monolayers (Fig. 5 C). The main difference between the profiles is their behavior at small distances: in the case of monomers in the same monolayer, the peptides should not overlap (the energy is infinite for L < r₀), whereas in the case of monomers located in the opposite monolayers, the configurations with L < r₀ are not prohibited, although they cost a substantial amount of energy, of the order of 20 k_BT (comparable with the energy of a pair of monomers, Figs. 3, B and F and 4).

Taking into account the membrane perturbation induced by isolated gA molecules, the energy of attraction between the molecules amounts to about W_uu(∞) − W_uu(6 nm) ≈ W_ud(∞) − W_ud(6 nm) ≈ 0.2 k_BT₀. Unfortunately, the integrals in Eq. 10 do not generally yield analytical integration in the case of numerically calculated interaction energy. The main issue is the integrand multiplier dr ∼ (2πr), due to which a small uncertainty of numeric determination of the energy of two monomers transforms into a large uncertainty of the integrals in Eq. 10 at large values of $r$. We applied the following algorithm for numeric quantification of these integrals. First, we found the average energy of two (infinitely) distant isolated gA molecules (Fig. 5, B and C, brown horizontal dashed lines). Then, we determined the distance between the monomers R_max, at which the same energy value is achieved at 2L > 6 nm. Thereafter, the integrals were only calculated in the region πR²_max, which physically corresponds to the assumption of predominant contribution of short-range forces to the interaction of monomers. This process allows us to find from Eqs. 9 and 10 the critical concentration ${С}_{crit}=-k_{B}T/I$, at which the gA cluster is stable. Substituting the numerically obtained energies W_uu(2L) and W_ud(2L) (Fig. 5, B and C) and assuming short-range interaction, we determined the value of I(T). For room temperature T₀ ≈ 300 К, the critical concentration is C_crit = 0.025 nm⁻². It should be pointed out that the developed theory predicts the stable mode only qualitatively because the correlations between particles and interactions between three or more particles were disregarded in the calculations. These effects become significant at higher concentrations. However, the qualitative predictions suggest the possible existence of an ordered phase with a high surface concentration of gA at room temperature.

Thus, the elastic energy profile obtained for two approaching conducting dimers allows the prediction of a strong aggregation of the channels even at a low dimer:lipid ratio. For gA monomers, a weak aggregation is expected upon exceeding the critical surface concentration of the monomers.

Discussion

In this work, we analyzed deformations occurring in the vicinity of gA peptides incorporated into lipid membranes for cylindrically symmetrical configurations: an isolated monomer, a pair of juxtaposed monomers in the opposite monolayers, and a conductive dimer (Fig. 1). Membrane deformations proved to occur in all three configurations (Fig. 2).

The neutral surface profile of the upper monolayer goes up (increase in z coordinate) at the peptide boundary for the isolated monomer (Fig. 2 A). At the peptide boundary, the fixed projection of the director onto the Or axis is negative (n(r₀) = n₀ = −0.68) and tends toward zero far from the peptide (n(r → ∞) = 0). Such director distribution corresponds to a concave neutral surface, in accordance with the volumetric incompressibility condition, Eq. 3. It becomes obvious if tilt deformation is prohibited. In this case, the director coincides with the normal to the neutral surface. The negative projection of the normal onto the Or axis at r = r₀ and zero projection at r → ∞ leads to that on the average div(n) = div(N) = −J_av ≈ (N(∞)−N(r₀))/l_decay = −n₀/l_decay > 0, where J_av is the average geometric curvature of the neutral surface and l_decay is the characteristic length of the decay of deformations. Thus, J_av ≈ n₀/l_decay < 0, which corresponds to the concave neutral surface. As the neutral surface is horizontal at r → ∞, it has to go up (on average) in the vicinity of the single peptide boundary. In the case of a pair of monomers, the fixed negative director projections at peptide boundary r = r₀ lead to concave surfaces of both monolayers. However, there is no significant change in the z-coordinate of the surfaces at r = r₀, as the neutral surface of the upper monolayer tends to go up, and the neutral surface of the lower monolayer tends to go down. Because the peptides in the upper and lower monolayers are identical, they induce identical (but opposite in sign) bending torques in the monolayers, compensating each other without significant displacement of the neutral surfaces along the z-coordinate. For the conductive dimer, we do not set the value of the director at the boundary; only membrane thickness is fixed. The boundary director value in this case is obtained from the total elastic energy minimization; this value appears to be positive, leading to a convex (on average) monolayer neutral surface (Fig. 2 C).

Our radial profiles of bilayer hydrophobic thickness (Fig. 2 D) and area per lipid molecule (Fig. 2 E) calculated for the case of a juxtaposed pair of monomers are qualitatively similar to the profiles obtained by molecular dynamics (MD) for the conductive dimer (29, 30). In terms of the theory of elasticity, this means that in MD, the director projection to the radial axis at the dimer boundary is fixed at some negative value despite thinning of the membrane around the dimer. The negative director projection value may be achieved if the effective shape of the dimer is more similar to an hourglass rather than to a cylinder that indeed may take place because of bulky tryptophan side chains located in the vicinity of a monolayer neutral surface (13, 46). However, the fixed negative value of the director projection at the dimer boundary should lead to an abrupt increase of the membrane elastic energy upon the approaching of two dimers, analogously to the case of the membrane-mediated interaction of two monomers with a fixed boundary director (Fig. 5, B and C). As the dimers approach each other, the reorientation of the director from its value at the boundary of the left dimer to its value at the boundary of the right dimer takes place on successively decreasing distance, which is equivalent to the growth of |div(n)|, i.e., to the growth of the splay energy (see Eq. 1). However, according to our calculations, the membrane elastic energy abruptly decreases as the distance between the dimers reaches ∼4 nm (Fig. 5 A). It points to the capability of reorientation of the boundary director to relax the total elastic energy. Our profile of the dimer interaction energy is in qualitative agreement with the profiles obtained in (50) by MD modeling. The MD profile predicts repulsion of the dimers at distances exceeding 2L ∼4 nm and strong attraction as the distance becomes shorter than ∼4 nm, with the interaction energy thus having a local maximum at 2L ∼4 nm (compare with the profile in Fig. 5 A). For dipalmitoylphosphatidylcholine (diC16:0), MD evaluates the energy drop between the local maximum (2L ∼4 nm) and the energy minimum at a small distance between the dimers (2L ∼2 nm) as ∼7.5 kcal/mol ≈ 12 k_BT (50), which is in good agreement with our calculated value of ∼14 k_BT (Fig. 5 A), although our model predicts stronger repulsion at L > 4 nm. The barriers for the dimer approaching are ∼3.5 and ∼6 k_BT in MD modeling (50) and our calculations, respectively.

The results of the MD modeling in works (29, 46, 50) implies that deformations induced by a dimer spread to ∼2–4 nm around it. Our calculations predict substantially larger extension of dimer-induced membrane distortions, ∼6 nm (Fig. 2, D and E). To match the MD results with continuum elastic modeling, the radial dependence of the stretch/compression modulus K_a with the hardening factor of 4.27 is introduced in (46). This elastic model neglects some substantial membrane properties. First of all, the deformation of tilt is not taken into account, although its elastic modulus (K_t ∼40 mN/m) is several times smaller than the stretch/compression modulus (K_a ∼120 mN/m). Besides, the membrane was not subjected to the condition of local volumetric incompressibility. This condition is generally responsible for the oscillation of deformations. For the upper monolayer, the substitution n = t + N = t + grad(H) into the condition of the local volumetric incompressibility, Eq. 3, yields the following:

$$h_c=H-M=h-\frac{h^2}{2}\text{div}\mathbf{n}-h\alpha =h-\frac{h^2}{2}\text{div}\left(\mathbf{t}+\mathbf{g}\mathbf{r}\mathbf{a}\mathbf{d}\left(H\right)\right)-h\alpha ,$$ (12)

where M is the distance between the reference plane and intermonolayer surface measured along the normal to the reference plane. Eq. 12 can be transformed into the equation of harmonic oscillator:

$$\mathit{\Delta }H+\frac{2}{h^2}H=\frac{2}{h^2}M+\frac{2}{h}-\text{div}\left(\mathbf{t}\right)-\frac{2}{h}\alpha ,$$ (13)

where Δ = div(grad) is the Laplace operator. The left-hand side of the equation determines the oscillation of deformations, generated mainly by the splay, div(n). The right-hand side of the equation is responsible for the decay of oscillations of the neutral surface. The decay is provided by the tilt (div(t)) and the lateral stretch/compression ((2/h)α) deformational modes. Thus, a decrease rather than an increase of the stretch/compression modulus K_a is expected to reduce the membrane area affected by deformations. According to (46), the elastic energy of deformations induced by the gA dimer is divided between the deformational modes as follows: stretch/compression (with variable modulus), 49%; splay, 33%; Gaussian curvature, 17%; and surface tension, less than 1%. In the framework of our model, the elastic energy distribution between the deformational modes is somewhat different, mainly due to accounting for the tilt deformation. For constant modulus K_a = 120 mN/m, the data are as follows: stretch/compression, 28.9%; splay, 31.6%; Gaussian curvature, 6.4%; surface tension, 0.4%; and tilt, 32.7%, i.e., the splay and tilt store the major part of the elastic energy (∼65%). For constant K_a = 4.27⋅120 mN/m = 512.4 mN/m, the data are as follows: stretch/compression, 10.9%; splay, 41.9%; Gaussian curvature, 3.4%; surface tension, 0.3%; and tilt, 43.5%, i.e., again the most energy (∼85%) is stored in splay and tilt deformations. This is also expected to be the case for K_a varying from 512.4 mN/m at the dimer boundary to 120 mN/m far from the dimer.

In the calculations, we tacitly assumed that gA monomers incorporate into the membrane in such a manner that the axis of the helix is approximately perpendicular to the membrane surface, and the end face of the helix containing several tryptophan residues is situated in the acyl chain-polar head interface area. To the best of our knowledge, the structure and orientation of a gA monomer in the membrane have not been experimentally determined to date. The effective spontaneous curvature of gA in the inverted H_II phase, measured in (51), is found to be highly negative, which corresponds to deeper penetration of the peptide into the lipid monolayer. However, these results were obtained in a strongly curved monolayer lipid phase rather than in a lamellar bilayer membrane and can be inconsistent with the position and orientation of gA molecules in regular membranes. In (29, 30), molecular modeling techniques were used to demonstrate that the axis of a gA molecule is indeed oriented almost normally to the membrane surface (tilt angle ∼10°), and the tryptophan residues are preferentially located in the vicinity of the lipid monolayer neutral surface. From the standpoint of the linear elasticity theory, the depth of incorporation of the monomer is of no consequence. In the case of shallow insertion, the director at the gramicidin boundary must be negative, whereas in the case of deep insertion, it has to be positive. However, according to Hooke’s law, the deformation energy is independent of the boundary director sign, being a function of n₀². In the case of very deep insertion of the gA monomer or in the very thin membrane, the configurations of a pair of juxtaposed monomers and a dimer coincide; as in the thin membrane, it is impossible to place one monomer on the top of the other monomer without setting the membrane thickness equal to the doubled monomer length at the peptide boundary. Generally, the presence and positions of maxima and minima in the dependence of the deformation energy on the distance between gA monomers (Fig. 5, B and C) are determined by the characteristic lengths of deformation, i.e., by the physical properties of the membrane rather than by the boundary conditions imposed by gramicidin. Changes in the depth of insertion and orientation of monomers would change the boundary director value and the interaction energy profile (Fig. 5, B and C) scaling as n₀² without any change in the minima and maxima positions. At small separation distances, it becomes substantial whether the boundary director is fixed, as in the case of two interacting monomers (Fig. 5, B and C), or the boundary director may reorient to relax the total elastic energy, as in the case of two interacting dimers (Fig. 5 A). The fixed boundary director leads to growth of the elastic energy of approaching peptides, whereas the free boundary director allows for relaxing the elastic energy at small separation distances, thus favoring aggregation (compare Fig. 5, A–C).

Earlier, membrane deformations induced by gA and conversely the influence of the elastic properties of the lipid bilayer on the parameters of gA channels were considered by a number of authors (26, 27, 28, 30, 43). The rapid and quantitatively measurable responses of the channels (conductivity, lifetime, and likelihood of dimerization) to changes in the membrane elastic properties allow using gA as a molecular sensor of elastic forces (44). Previously, only deformations induced by conductive gA dimers were taken into account in the analysis of the influence of the elastic properties of the lipid bilayer on the parameters of the channels in the framework of different continuum theories (26, 27, 28, 42); in any other configuration, the membrane was deemed undeformed. The following expression was used to calculate the energy of deformations induced by the conductive dimer (44):

$$\mathit{\Delta }{G}_{def}=H_B{\left(l_p–d_0\right)}^2+H_X\left(l_p–d_0\right)c_0–H_C{c}_0^2,$$ (14)

where H_B, H_X, and H_C are certain coefficients depending on the elastic properties of the lipid bilayer; d₀ is the bilayer thickness; l_p is the length of the dimer; and c₀ is the monolayer spontaneous curvature. Generally, the quadratic form of the expression Eq. 14 is a direct consequence of the linear elasticity theory, i.e., of Hooke’s law. As demonstrated in (43), the term quadratic in the spontaneous curvature occurs only under specific conditions imposed on the shape of the monolayer surface at the gA boundary. In the framework of our model, the quadratic dependence on spontaneous curvature occurs when the boundary director is not fixed, as is the case with conductive dimer configuration (Fig. 4, green curve). In the configurations of an isolated monomer and a pair of monomers, the director at the gA boundary had a fixed value of n₀, and the energies of these configurations linearly depended on the spontaneous curvature (Fig. 4, red and blue curves). In general, our model is more inclusive because we take into account the membrane deformations induced not only by the conductive dimer but also by individual monomers and pairs of juxtaposed monomers, and these deformations are factored into the calculated energy barriers. However, because the elasticity theory we use is also linear, the general quadratic form of the membrane deformation energy, Eq. 14, is maintained for all the cylindrically symmetric configurations of the peptides. The energy barriers are determined by the differences of the energies of the states, and hence, their values are also quadratic, similar to Eq. 14.

Eq. 14 does not include the membrane lateral tension. According to the results of (26), application of the lateral tension to a membrane increases both the probability of formation of conductive dimers and their lifetime, which was explained by a decrease in the membrane thickness, according to the following equation (in our notation):

$$\frac{\mathit{\Delta }h}{h}=-\frac{\sigma }{K_a},$$ (15)

where Δh is the change of the monolayer thickness caused by the applied lateral tension. Within the framework of our model, this contribution is reflected by the term α₀ of spontaneous stretching of the monolayer subjected to the lateral tension (see Eq. 1). The lateral tension was shown to activate gA channels in relatively thick membranes, e.g., made from diC20:1 lipid (45). This effect was attributed to the thinning of the membrane in accordance with Eq. 15, leading to better matching of the dimer length and the bilayer thickness. Moreover, in this work, it is demonstrated that the application of the lateral tension to relatively thin membranes (e.g., made from diC18:1 lipid) leads to inactivation of the channels, as the membrane becomes too thin, and the dimer formation again requires overcoming of substantial elastic stress as the membrane has to stretch at the dimer boundary (45). The experimental setup utilized in this work does not allow for control of the lateral tension, so the change of the membrane thickness cannot be determined quantitatively. However, the effect of switching of the tension-induced activation and inactivation of gA channels depending on the membrane thickness is physically reasonable. Our continuum elastic model qualitatively predicts the activation of the channels in the membrane, whose hydrophobic thickness exceeds the length of the dimer (2h > 2h_p) (Fig. 3, A and B), and inactivation of the channels in thin membranes (2h < 2h_p) (Fig. 3, C and D) upon application of the lateral tension.

However, usually K_a ≫ σ, and the main effects of the lateral tension on the membrane are associated with the fact that membrane deformations always increase the area of the neutral surface of the monolayer in comparison with its area in the planar nondeformed state. The additional area has to be pulled out of a lipid reservoir, which requires mechanical work to be performed against the lateral tension. Thus, under identical boundary conditions, the larger the lateral tension that is applied to the membrane, the more elastic energy of the membrane will be achieved. Earlier, we have demonstrated that the application of lateral tension leads to an increase in the line tension of an edge of transmembrane pore (23, 24, 52) as well as the line tension of the boundary of ordered membrane domains (rafts) due to the mismatch of the thickness of the raft and the bulk membrane (53, 54, 55). This effect is equally applicable to the formally inextensible membrane (K_a → ∞) because in this case, it is associated with an increase in the monolayer surface area by drawing additional lipid from a reservoir rather than due to the expansion of the membrane. According to Eq. 15, the change in the monolayer thickness caused by lateral tension tends toward zero at K_a → ∞. An increase in the probability of formation of conductive dimers due to a change in monolayer thickness was vividly shown by investigations of gA behavior in the membranes under electrostriction (14). If the membrane is considered as a capacitor with a finite compressibility module, the application of transmembrane potential should cause the attraction of the capacitor “plates” and hence a decrease in the membrane thickness. It was demonstrated in (14) that the application of transmembrane potential indeed increased the probability of conductive dimer formation. For the membranes formed without organic solvent or with the use of “heavy” solvents such as squalene, the change in the bilayer thickness caused by transmembrane voltage is described by Eq. 15 with the substitution 2σ = 2σ₀ + C_mU²/2, where U is the applied transmembrane voltage, σ₀ is the lateral tension of the membrane monolayer at zero transmembrane voltage, and C_m is the membrane-specific capacity (56, 57). If the membranes are formed with the use of “light” solvents such as decane in addition to the replacement 2σ = 2σ₀ + C_mU²/2, an effective modulus characterizing the compression of the bilayer containing inclusions of organic solvent has to be substituted into Eq. 15 instead of the lateral compression/stretch modulus K_a.

Besides the cylindrically symmetric configurations of peptides, we also considered a general case of arbitrary relative positions of two dimers (Fig. 5 A) and two monomers (Fig. 5, B and C) in the membrane and calculated the dependence of the membrane deformation energy on the distance between the gA molecules. The energy profile for two approaching dimers allows prediction of strong aggregation, as the elastic energy in the case of contacting dimers is ∼8 k_BT lower than the energy of deformation induced by two infinitely separated dimers (Fig. 5 A). Our calculated profile qualitatively agrees with the profile of approaching gA dimers in the membrane made from diC16:0 lipid obtained by MD (50). In this work, the clustering of gA dimers is indeed observed even at the relatively low dimer/lipid ratio of 1:72.

For monomers, the energy interaction profile allows prediction of gA clustering when the surface density exceeds C_crit = 0.025 nm⁻². From the energy profiles in Fig. 5, B and C, it is clear that the distance between the particles in equilibrium should be ∼6 nm. This rough estimation gives approximately one particle per 36 nm² corresponding to the critical concentration of ∼0.028 nm⁻², which is very close to the value C_crit = 0.025 nm⁻² obtained from integration in Eq. 10. The only advantage of using Eq. 10 is taking into account the depth of the energy well under the condition of the finite temperature T.

Earlier, based on the analysis of dipalmytoylphosphatidylcholine (diC16:0) monolayer compression isotherms (58), the conclusion was made that gA clustering occurs at a gA molar ratio of several mole percent, with the clustering-associated energy gain being maximal at a ratio of about ∼5 mol %. Assuming the average area per lipid molecule to be ∼0.7 nm², it can be estimated that the critical concentration C_crit = 0.025 nm⁻² corresponds to the mole ratio of ∼2 mol %, which is in good agreement with the published results (58). In a recent publication, Chistyulin and colleagues (59) observed clustering of a gA derivative having the first valine residue replaced by glutamine. Lateral clustering of gA detected with the aid of x-ray scattering was also described by Harroun and colleagues (25). However, in (25), the experiments were performed on lipid membranes with gA incorporated at a molar ratio of 1:10, which corresponds to gA monomers surrounded by a single layer of lipids or gA dimers surrounded by ∼1.5–2 layers of lipid. Our model should not be applied to such high gA concentrations because triple interactions become highly probable. Nevertheless, the model predicts the formation of clusters in a certain range of concentrations and demonstrates that at relatively high surface densities of the peptide, the diffusion flow effectively vanishes, i.e., the clusters cease to dissolve. Thus, our model allows for explanation of the results presented in (15), where gA-mediated ionic conductivity of the membrane was shown not to decay on the timescale of tens of minutes after fusion of small (∼100 nm) gA-containing vesicles with a planar lipid bilayer of a large area. If gA clusters were dissolving, the probability of formation of the transmembrane conductive dimer would have been decreasing with time, resulting in rapid decay of membrane conductivity. Jones and colleagues (15) also performed experiments with the fusion of gA-containing vesicles with a bilayer containing gM, differing from gA in the channel properties. The gA-gM heterodimers formed extremely rarely in these experiments, i.e., only in 4 ± 3% of cases, whereas in the case of simultaneous incorporation of gA and gM into vesicles at a ratio of 1:1, heterodimers were observed in 38 ± 22% cases after fusion with a lipid bilayer. Based on these data, Jones and colleagues (15) concluded that the conductive dimers almost never exchange dimerization partners, i.e., the dimers never fully dissociate. Our model offers an alternative explanation for these results. We suggest that in the case of preliminary incorporation of gM into the lipid bilayer, it forms clusters with high surface density of gM and large areas of practically pure lipid bilayer. Upon subsequent fusion of gA-containing vesicles with the bilayer, gA also forms clusters. According to our calculations, the diffusion flux from the clusters with high concentration of the peptides is almost equal to zero, and hence, gA and gM can almost never meet to form heterodimers. It was reported recently in (20) that vesicles could exchange gA with the bilayer without complete fusion, and therefore, the long-term persistence of conductivity after fusion of several gA-containing vesicles with the bilayer could be explained by continuous inflow of new gA molecules from free vesicles. However, the results presented in (20) do not explain the extremely low probability of gA-gM heterodimerization after the fusion of gA-containing vesicles with the gM-containing bilayer (15), whereas our model explains it by a specific profile of interaction energy of gramicidin molecules caused by membrane deformations.

To conclude, in this work, we developed a continuum elastic model based on the theory of elasticity of liquid crystals adapted to lipid membranes (31). In the framework of the model, the energy of membrane deformations induced by gA monomers and dimers was considered. The analysis allowed us to obtain the dependence of the energy barrier of the conducting dimer formation and its lifetime on the membrane lateral tension, hydrophobic thickness, and spontaneous curvature. The dependence is in qualitative agreement with the available experimental data. The elastic energy profile obtained for two approaching conducting dimers allows us to predict a strong aggregation of the channels even at low dimer:lipid ratios, in agreement with MD modeling (50). For gA monomers, a weak aggregation is expected upon exceeding the critical surface concentration of the monomers. This allows us to explain the results of (15) without assumption of the internal gating of gA channels.

Author Contributions

O.V.K. performed the numerical calculations. T.R.G. developed the analytical formalism. K.V.P. generalized and improved the theoretical model. E.A.K. and Y.N.A. designed the research and performed comparisons with the experimental data. S.A.A. designed the research, analyzed the results, and served as the scientific coordinator. All authors wrote and corrected the article.

Editor: Ana-Suncana Smith.

Supporting Citations

References (60, 61) appear in the Supporting Material.