A Fluorescence Correlation Spectrometer for Measurements in Cuvettes

Abstract

We have developed a fluorescence correlation spectroscopy (FCS) setup for performing single-molecule measurements on samples inside regular cuvettes. The cuvette FCS uses a horizontally mounted extra-long working distance, 0.7 NA, air objective with a working distance of >1.8 mm instead of a high NA water or oil immersion objective. The performance of the cuvette FCS is found to be highly sensitive to the quality and alignment of the cuvette. The radial resolution and effective observation volume obtained using the optimized setup are ∼340 nm and 1.8 fL, respectively. The highest molecular brightness and the signal/noise ratio in the autocorrelation data achieved using an aqueous solution of rhodamine B are greater than 44 kHz and 110, respectively. Here, we demonstrate two major advantages of cuvette FCS. For example, the cuvette FCS can be used for measurements over a wide range of temperatures that is beyond the range permitted in the microscope-based FCS. Furthermore, cuvette FCS can be coupled to automatic titrators to study urea-dependent unfolding of proteins with unprecedented accuracy. The ease of use and compatibility with various accessories will enable applications of cuvette FCS in the experiments that are regularly performed in spectrofluorometers but are generally avoided in microscope-based FCS.

Introduction

Fluorescence correlation spectroscopy (FCS) is a powerful single-molecule technique with widespread applications in biophysics. FCS is widely used in measurements of molecular size, chemical kinetics, conformational dynamics of biomolecules, protein-ligand interactions, and protein aggregation (1, 2, 3, 4). There have been extensive developments over the past two decades to extend the applications of FCS in live cells and tissue samples. For example, several flavors of imaging FCS techniques have been developed for measurements of membrane dynamics, cellular and nuclear localization, and transport of biomolecules in live cells (5, 6, 7, 8). Furthermore, development of two-photon FCS has extended applications of FCS in tissues and other thick samples (9).

Conventionally, FCS modules are attached to confocal microscopes for the high spatial resolution and the signal/noise ratio (S/N) achieved in confocal microscopy. Consequently, applications of FCS have several limitations in many of the biophysical experiments. For example, the folding and unfolding of proteins using chemical or thermal denaturation are rarely studied using FCS (10, 11, 12). Kinetic experiments that require stirring of the samples cannot be performed using microscope-based FCS setups. Furthermore, experiments that require nonaqueous or corrosive solvents are seldom performed using FCS (13). However, these experiments are performed regularly in most biophysics and biochemistry laboratories using spectrofluorometers. Therefore, an FCS setup capable of performing measurements inside a cuvette with high S/N can enable applications of FCS in a large number of biophysical experiments.

A major obstacle for performing FCS in a cuvette is that the thickness of the optical windows of commercially available cuvettes is ∼1.25 mm. Conventional FCS setups employ high numerical aperture (NA ≥ 1.2) objective lenses, which are carefully corrected for both spherical and chromatic aberrations. However, these objectives have working distances of less than 0.31 mm and hence cannot be used for measurements inside cuvettes. Although the high NA objectives are required to achieve high S/N, FCS measurements using low NA optics have been reported earlier on a few occasions. For example, Garai et al. performed FCS measurements using a single-mode optical fiber with NA = 0.13 for detection of amyloid aggregates inside a centrifuge tube (14). Altamore et al. used a low NA (NA = 0.4), long working distance objective to perform scanning FCS measurements inside glass test tubes for single-particle detection and characterization of bacteria (15). However, these experiments are applicable only for characterization of highly bright and large particles because of the poor S/N of the FCS data. More recently, Banachowicz et al. have shown that with careful adjustment of the correction collar, extra-long working distance (ELWD) objectives with NA ≥ 0.4 can be used with thick cover slides to obtain reasonable-quality FCS data from aqueous solutions of Alexa488 (16). However, the S/Ns obtained in these measurements were shown to be low, requiring averaging of the autocorrelation data for ∼30 min.

In this article, we have investigated whether ELWD objectives can be used for FCS experiments inside regular cuvettes. We envision that for cuvette FCS to become a popular single-molecule technique, it must be highly sensitive for fast and accurate measurements of the autocorrelation function (ACF). Furthermore, it must be easy to use, and the measurements must be robust. Here, we report building a highly sensitive setup suitable for performing FCS measurements inside regular cuvettes. We have characterized the factors that critically affect the performance of the cuvette FCS setup. Our setup can yield a molecular brightness of >44 kHz, S/N > 110, and a diffusion time (τ_D) of ∼63 μs for rhodamine B in phosphate-buffered saline (PBS) at pH 7.4. The effective observation volume obtained in this setup is ∼1.8 fL.

Theory

The performance of an FCS setup is characterized by two important parameters, viz the spatial resolution and the S/N of the ACF. Because we are using an air objective but the samples are in aqueous media, the effects of the optical aberrations due to refractive index mismatch also need to be considered carefully. These aspects have been studied extensively both theoretically and experimentally by several groups (17, 18, 19, 20, 21). A brief overview of the theory relevant to the characterization of the cuvette FCS setup is presented here.

Resolution in FCS

Like all the microscope-based FCS setups, the cuvette FCS is also built using a confocal detection scheme (see Fig. 1). The point-spread function (PSF) of a confocal observation volume is generally approximated by a three-dimensional (3D) Gaussian (22) as follows:

$$PSF\left(r,z\right)=I\left(\mathrm{0,0}\right)\text{exp}\left(-\frac{2r^2}{{\sigma }_r^2}-\frac{2z^2}{{\sigma }_z^2}\right)\text{.}$$ (1)

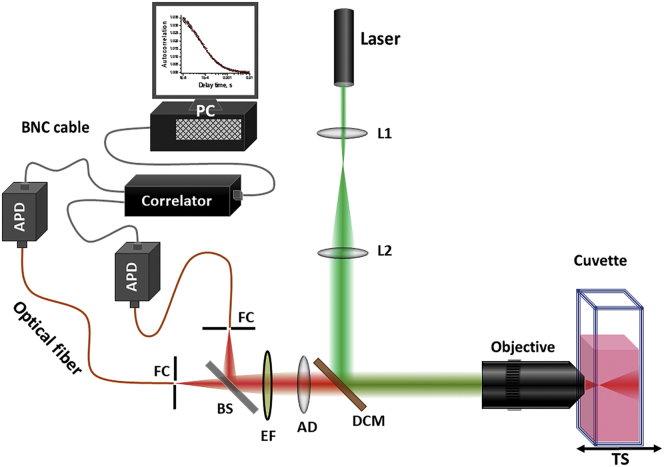
Figure 1.

Schematic of the cuvette FCS setup. Laser (543 nm, CW), L1, L2: lenses, L1 is aspheric lens; DCM, dichroic mirror; AD, achromatic doublet lens; EF, emission filter; BS, 50/50 beam splitter; FC, fiber coupler; TS, micrometer translation stage; Objective, ELWD, air objective, 0.7 NA, WD = 2.6–1.8 mm. To see this figure in color, go online.

I(0,0) is the peak intensity, and σ_r and σ_z are the radial and the axial dimensions of the PSF, respectively. The resolution of confocal detection is critically dependent on the NA of the objective and the size of the pinhole. Both the radial and the axial resolution improve with an increase of NA; hence, high NA objectives are preferred in FCS (23). Although smaller pinholes increase the resolution, they also reduce the collection efficiency of fluorescence, leading to poor S/N. Hence, the size of the pinhole is decided by considering both resolution and S/N. Typically, the recommended size of the pinhole is about the size of the Airy disc unit (AU) (23). Considering a 0.7 NA, 60× air objective, and λ = 580 nm, 1 AU at the image plane is

$$1AU=\frac{1.22\lambda }{NA}\times magnification\cong \frac{1.22\times 0.580\times 60}{0.7}=61\mu m\text{.}$$ (2)

The ACF of a freely diffusing species in a perfectly 3D Gaussian PSF can be expressed analytically by the following expression (24):

$$G\left(\tau \right)=\frac{1}{\langle N\rangle }\left(\frac{1}{1+\frac{\tau }{{\tau }_D}}\right){\left(\frac{1}{1+\frac{\tau }{{\omega }^2{\tau }_D}}\right)}^{\frac{1}{2}}\text{,}$$ (3)

where <N> is the average number of fluorophore molecules in the effective confocal observation volume (V_eff), ω is the structure parameter (i.e., ω = σ_z/σ_r), and τ_D is the diffusion time of the particle in the solution. Experimentally, V_eff can be estimated from <N> if the concentration (C) of the sample is known, as follows:

$$V_{eff}=\frac{\langle N\rangle }{C\times N_{Av}}\text{,}$$ (4a)

where N_av is the Avogadro number and C is the molar concentration. It may be noted here that the volume of the PSF (V_PSF) is proportional to the V_eff. The proportionality constant, commonly known as the γ-factor, is equal to 1/(2√2) for a 3D Gaussian PSF (25). Because the FCS observation volume is an ellipsoid, V_eff is dependent on the σ_r and σ_z by the following relation:

$$V_{eff}={\pi }^{\frac{3}{2}}{\sigma }_r^2{\sigma }_z\text{.}$$ (4b)

The radial resolution of the FCS observation volume can be estimated from the measured value of the τ_D, as follows:

$${\tau }_D=\frac{{\sigma }_r^2}{4D}\text{,}$$ (4c)

where D is the diffusion coefficient of the molecule in the solution. It is clear in Eqs. 3 and (4a), (4b), (4c), a–c that the measured ACF of a fluorophore with known C and D can be analyzed to obtain V_eff, σ_r, σ_z, and hence, the dimensions of the confocal volume. The ω can be obtained from fitting the ACF with Eq. 3, or it can be calculated from the ratio of σ_z and σ_r using (4a), (4b), (4c), a–c. The values of ω determined using the two independent approaches would be the same if the 3D Gaussian approximation of the PSF holds truly (26).

Optical aberrations in FCS

Although the PSF in the confocal setup is approximated by a 3D Gaussian, it can deviate significantly in presence of mismatch of refractive indices (RIs) between the immersion and the sample media. Because we are using an air objective (RI = 1.0) but the samples used are in aqueous buffer (RI = 1.33), the optical aberrations in cuvette FCS need to be investigated carefully. Optical aberrations in the above-mentioned case have not been characterized earlier, but the aberrations in the case of high NA (NA = 1.3) oil immersion (RI = 1.54) objective being used in confocal imaging of samples in aqueous media have been characterized extensively both theoretically and experimentally (17, 27). Because the PSFs were calculated numerically, below we summarize the important observations of these studies qualitatively. 1) The spherical aberrations increase with increasing depth of focal spot inside the sample, 2) the peak intensity of the PSF drops rapidly, 3) the σ_r remains almost unaffected, but 4) the σ_z increases almost linearly with the ratio of the RIs of the two media. However, the aberrations are small when a low NA (NA = 0.8) objective is used (17). Whereas most of the earlier reports have used imaging to characterize the aberrations in the confocal PSF, here we have used FCS measurements to do that (see Eqs. 3 and (4a), (4b), (4c)). Furthermore, Hess and Webb have shown that the assumption of a perfectly Gaussian PSF is not valid in FCS setups, particularly when high NA objectives are used. They proposed that this can be tested by measuring the photon count rate per molecule (CPM) as a function of the size of the pinhole (26). The CPM can be easily calculated in FCS experiments from the total count rate (CR) and the <N> (e.g., CPM = CR/<N>).

S/N in FCS

Detailed theoretical and experimental investigations of the S/N in the ACF have been presented earlier in several pioneering articles (20, 21, 28). Qualitatively, if the τ × CPM ≪ 1, then the S/N in the ACF at any correlation time, τ, depends primarily on two parameters: the average number of photons detected within τ and the total time of acquisition (T), giving rise to the following relationship (25):

$$\frac{S}{N}\approx CPM\times T^{0.5}\text{.}$$ (5)

Therefore, the S/N in FCS can be improved by using a longer acquisition time (T) or by maximizing the CPM.

Materials and Methods

Building the cuvette FCS setup

Fig. 1 shows the schematic of the cuvette FCS setup. All the optics and the optomechanical components, unless mentioned otherwise, are purchased from Thorlabs (Newton, NJ). The FCS setup is built using a 30 mm cage system. The cage rods define the geometry of the setup, and the cage plates are used for mounting the optics. The excitation laser used here is a green (λ = 543 nm) He-Ne laser (Melles Griot, Carlsbad, CA). The laser beam is expanded to 12 mm by using a pair of lenses, viz, L1 and L2, with focal lengths of 25 and 200 mm, respectively. L1 is an aspheric lens. The objective used is an ELWD, 60×, 0.7 NA air objective (CFI S Plan Fluor ELWD 60×) from Nikon Instruments (Melville, NY). The dichroic mirror is an ultraflat dual bandpass (part number ZT488/543rpc) from Chroma Technology (Bellows Falls, VT). The cuvette holder is made at the machine shop at Tata Institute of Fundamental Research, Hyderabad, India. It is custom designed such that it is compatible with the 30 mm cage system (Fig. S1). A home-built temperature controller was used to maintain the temperature of the cuvette holder. The cuvette holder is mounted on a micrometer translation stage (TS) for adjusting the distance between the objective and cuvette. The fluorescence collected by the objective is focused at a pinhole using an achromatic doublet lens (f = 200 mm). The fluorescence is split into two channels using a 50/50 beam splitter. A multimode optical fiber (diameter = 50 μm) is used as a pinhole in each confocal detection channel. The optical fibers are mounted on X-Y-Z micrometer stages for precision positioning of the pinhole. The detectors used are avalanche photodiodes from Excelitas Technologies (Covina, CA). The emission filter is a bandpass filter (607 ± 35 nm) from Semrock (Rochester, NY). The correlator card is from http://correlator.com.

Fluorescence labeling of proteins

An N-terminal fragment of apoE4 (Nt-apoE4) and α-synuclein are expressed and purified, as described elsewhere (29, 30). The T4-lysozyme is a kind gift from Subhendu Pandit and Dr. Pramodh Vallurupalli at the Tata Institute of Fundamental Research, Hyderabad. Bovine serum albumin (BSA) is purchased from Sigma Aldrich (St. Louis, MO). The cysteine residues in NT-apoE4 (A102C) and α-synuclein (A69C) are labeled using tetramethylrhodamine (TMR) maleimide. T4-lysozyme and BSA are labeled at the N-terminal amine using 5/6-carboxy-TMR succinimidyl ester. The unreacted dye is removed by size-exclusion chromatography using a Superdex 200 column (GE Healthcare, Little Chalfont, UK) in PBS buffer. Amylin is synthesized by solid-phase peptide synthesis using standard fmoc chemistry. TMR is attached to the N-terminal amine of amylin using 5 (6)-carboxytetramethylrhodamine on the resin. The TMR amylin is purified by size-exclusion chromatography using a Superdex peptide column (GE Healthcare) and PBS as the running buffer. The purity of the proteins and the peptide are verified by mass spectrometry. TMR-5-maleimide and 5/6-carboxytetramethylrhodamine succinimidyl ester are purchased from Thermo Fisher Scientific (Waltham, MA). All other chemicals are purchased from Sigma. The cuvette used for most of the cuvette FCS measurements is from Hellma (catalog number 101-10-40; Hellma, Plainview, NY).

Analysis of the FCS data

The ACF data are fitted by assuming a single diffusing species using Eq. 3. The values of <N> and τ_D obtained from the fitting are used to calculate the V_eff, σ_r, and σ_z of the FCS observation volume using (4a), (4b), (4c), a–c. The CPM is estimated from the CR and the <N>.

FCS measurements as a function of the depth of the focal spot inside the cuvette

The depth of the FCS observation volume inside the sample is changed by moving the cuvette holder with a micrometer stage (TS in Fig. 1). In Fig. 2 A, the distances shown are measured from the inner surface of the wall of the cuvette. The surface is located by observing the bright reflection of the focused excitation laser from this surface.

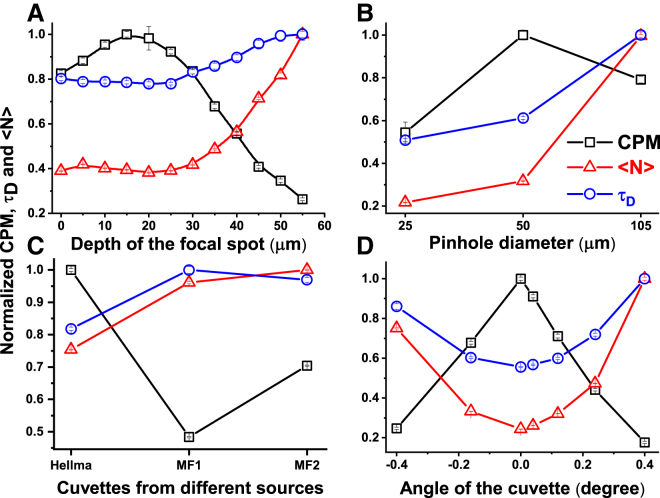
Figure 2.

Optimization of the performance of the cuvette FCS. The effects of focal depth (A), pinhole size (B), cuvette quality (C), and angular alignment of the cuvette (D) are shown. G(τ) and CR data obtained from aqueous solution of rhodamine B are analyzed to estimate <N>, τ_D, and CPM. The squares, triangles, and circles represent normalized CPM, N, and τ_D respectively. Clearly, <N> and τ_D remain almost unchanged if the focal depth is <25 μm. The smallest <N> and τ_D are obtained with a 25 μm pinhole, but the highest CPM is obtained with a 50 μm pinhole. To see this figure in color, go online.

Measurement of angular misalignment of the cuvette

Although the cuvette holder is designed to ensure compatibility with the cage system of the FCS setup, a small amount of angular displacement of the cuvette holder is still possible. This is due to the slightly larger internal diameter of the holes in the cuvette holder than the outer diameter of the cage rods. The angular position of the cuvette holder can be adjusted using two Teflon screws that are used also for mounting the cuvette holder to the cage plate in the cage system. Because the overall angular displacement (θ) is very small, it is measured using the deflection of a laser beam that is reflected from the optical window of the cuvette on a screen (Fig. S2).

The FCS measurements at different excitation powers and different concentrations of rhodamine B

The power of excitation light reaching the sample was measured by measuring the power of the incident laser light right after the objective using a power meter (Newport, Irvine, CA). The intensity of the excitation beam was modulated by using neutral density filters. The optical densities of the filters used in our experiments are 0, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.3, and 1.6. To calculate the S/N, the SD and the mean of G(τ) at each τ are calculated from 10 identical measurements of G(τ) using 114, 56, 28, and 14 μW of excitation laser power. The S/N is calculated using the following relationship: S/N = < G(τ)>/SD.

For the concentration-dependence experiments, a stock solution of 10 μM rhodamine B was prepared in water. The stock was diluted to the final concentrations of 3, 4, 5, 7, 10, 21, 31, 42, 52, 62, 83, 104, 124, 145, 165, 205, and 245 nM in PBS (pH 7.4) buffer.

Measurements in commercial microscope-based FCS

We have used a PicoQuant FCS module integrated with an Olympus confocal microscope (Olympus Fluoview FV3000; Olympus, Tokyo, Japan) installed recently at the Tata Institute of Fundamental Research. For our experiments, in this setup, we have used a solid-state laser at 561 nm (Coherent, Santa Clara, CA), a water immersion objective with NA = 1.2, and a pinhole size of 1 AU. It may be noted here that the wavelength of the lasers used in cuvette FCS and the PicoQuant FCS are somewhat different. However, the extinction coefficient of rhodamine B at 543 and 561 nm are quite similar.

FCS measurements at different temperatures

The design of the homebuilt cuvette holder is shown in Fig. S1. In our setup, the temperature of the holder and the sample is found to be equal within a range of 15–60°C, and it can be controlled within ±0.4°C. Therefore, here FCS measurements were performed in this range of temperature. At each temperature, a total of 10 autocorrelation traces of a duration of 30 s are recorded. The z-position of the cuvette is optimized for the best CPM at each temperature. The viscosity of water as a function of temperature is reported elsewhere (31).

FCS measurements at different concentrations of urea

Urea denaturation experiments were carried out with the help of an autotitrator coupled to the cuvette FCS setup. The autotitrator (ATS-530; Jasco, Easton, MD) is operated by the software of a Jasco spectrofluorometer. The autotitrator uses two syringes: one for injecting a defined μL volume of 10 M urea solution into the sample and the other for withdrawing an equal amount of solution from the cuvette. We have used a total of 24 injections/withdrawals of 100 μL each for the data presented in Fig. 6 and a total of 77 injections/withdrawals of 32 μL each for the data presented in Fig. 7 to vary the concentration of urea in the sample from 0 to 7 M. The sample is mixed for 90 s immediately after injection using a teflon-coated magnetic bead with the help of a magnetic stirrer. The magnetic stirrer is then stopped for 10 min for performing the FCS measurements. The start and stop of stirring is controlled by a timer (Selec, Navi Mumbai, Maharashtra, India). Hence, the entire experiment is performed in an automatic manner. At each concentration of urea, 20 recordings of 30 s each were collected. However, the first six autocorrelations were not used for analysis to avoid artifacts that may arise because of residual flow in the sample after stopping the stirrer. The viscosity of urea used in the analysis is reported elsewhere (32). The data presented in Figs. 6 and 7 are the averages of three independent experiments. The R_h of TMR-labeled Nt-apoE4 was calculated using the following expression:

$$R_{h,Nt-apoE4}=\frac{R_{h,rhodamineB\times }{\tau }_{D,Nt-apoE4}}{{\tau }_{D,rhodamineB}}\text{.}$$ (6)

Figure 6.

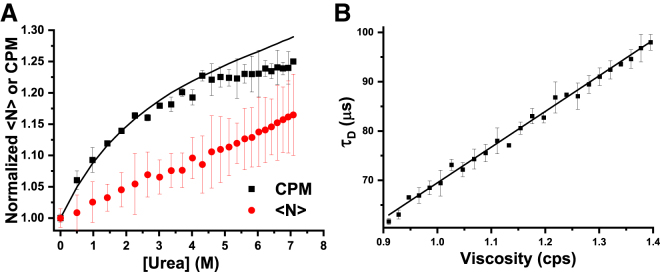
Cuvette FCS measurements in urea. (A) Normalized plots of CPM (squares) and <N> (circles) are obtained from FCS measurements, and quantum yield (solid line) is obtained from spectrofluorometer measurements on 100 nM rhodamine B in 0–7 M urea. The increase of CPM (squares) is consistent with the urea-dependent increase of quantum yield of rhodamine B fluorescence (solid line). The small (∼15%) increase of <N> may arise because of desorption of the fluorophore from the cuvette windows due to serial dilution of the sample. (B) Plot of τ_D versus viscosity of urea is shown. Linear increase of τ_D with viscosity is consistent with the SE relationship. Titration and mixing of urea have been performed using an autotitrator and a magnetic stirrer, respectively. To see this figure in color, go online.

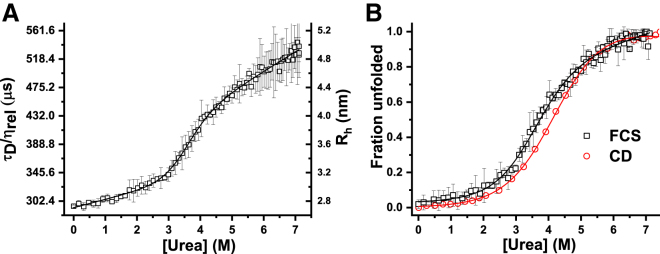
Figure 7.

Unfolding of TMR-Nt-apoE4 monitored by cuvette FCS. (A) The squares represent experimental data (τ_D or R_h) measured by FCS. The R_h values of the folded and the unfolded states are 2.8 and 4.8 nm, respectively. (B) Fraction of unfolded Nt-apoE4 is measured by FCS (squares) and by CD (circles). The solid lines are fits using a two-state model (36). The values of ΔG, m, and denaturation midpoints are summarized in Table S1. Titration and mixing of urea have been performed using an autotitrator and a magnetic stirrer, respectively. To see this figure in color, go online.

The R_h of rhodamine B is known to be 0.57 nm (33). We note here that the fluorophore is diluted during each injection/withdrawal cycle. The plot of <N> in Fig. 6 A is corrected by the dilution factor.

To calculate the unfolded fraction (F_u) of the protein as a function of the concentration of urea, the G(τ) data are fitted using the two-component diffusion model:

$$G\left(\tau \right)=g_f\left(\frac{1}{1+\frac{\tau }{{\tau }_{Df}}}\right){\left(\frac{1}{1+\frac{\tau }{{\omega }^2{\tau }_{Df}}}\right)}^{\frac{1}{2}}+g_u\left(\frac{1}{1+\frac{\tau }{{\tau }_{Du}}}\right){\left(\frac{1}{1+\frac{\tau }{{\omega }^2{\tau }_{Du}}}\right)}^{\frac{1}{2}}\text{.}$$ (7a)

The suffixes f and u correspond to folded and unfolded proteins, respectively. Assuming that the molecular brightness of the folded and the unfolded proteins are the same, ɡ_f (or ɡ_u) can be expressed in terms of <N_f> and <N_u> by the following relation (34):

$$g_{f,u}=\frac{\langle N_{f,u}\rangle }{{\left(\langle N_f\rangle +\langle N_u\rangle \right)}^2}\text{.}$$ (7b)

It may be seen from Fig. 7 A that τ_Du/τ_Df = 520/300 ∼1.7 for Nt-apoE4. Hence, it is difficult to resolve the folded and the unfolded species using the two-component model, particularly when the ratio of <N_f> and <N_u> is significantly less or greater than 1.0 (35). Therefore, fitting of G(τ) with (7a), (7b) a leads to redundancies in the determination of the values of both <N> and τ_D. To circumvent this problem, we fix the values of both τ_Du and τ_Df while fitting the G(τ) data with (7a), (7b) a. Here, we have used τ_Df/η_rel = 300 μs and τ_Du/η_rel = 520 μs (see Fig. 7 A). Because τ_D increases linearly with viscosity (η), the values of τ_Df and τ_Du are scaled with relative viscosity (η_rel = η_urea/η_water) of the urea solution. The fraction of unfolded proteins (F_u) at any concentration of urea is estimated as follows: F_u = ɡ_u/(ɡ_u+ɡ_f). The F_u values as a function of urea are fitted using a two-state model (36) to evaluate the free energy (ΔG) and the “m” value of folding of the protein.

Ensemble measurement of fluorescence of rhodamine B

Dependence of quantum yield (QY) of rhodamine B on temperature and urea has been measured using a spectrofluorometer (Jasco) equipped with a temperature-controlled cell holder and coupled to an autotitrator. The excitation was set at 543 nm, and the emission was set at 580 nm. In the case of the experiment with urea, the total fluorescence is corrected appropriately with the dilution factor arising from dilution of the sample due to injection of urea and withdrawal of the sample by the autotitrator.

Unfolding of Nt-apoE4 by circular dichroism

Urea dependent unfolding of 1 μM Nt-apoE4 prepared in PBS buffer is performed at 25°C in a spectropolarimeter (Jasco) coupled with an autotitrator (Jasco). The concentrations of urea in the protein solution is increased by withdrawal of a fixed μL volume of the solution followed by injection of the same volume of 10 M urea. Because the protein is diluted during each withdrawal/injection cycle, the measured circular dichroism (CD) signal is finally corrected for the dilution. Because Nt-apoE4 is a helical protein, the CD is monitored at 225 nm.

Results

The cuvette FCS setup

Fig. 1 shows the schematic of the cuvette FCS setup. This setup is similar to the conventional FCS setup, with two major differences. First, the objective is mounted horizontally. Such geometry is required for FCS measurements inside a cuvette. Second, we have used a commercially available ELWD plan fluor air objective with an NA equal to 0.7. These objectives are corrected for both spherical and chromatic aberrations, but the corrections are less extensive than the plan apochromat objectives. However, the advantage of using the ELWD objective is that its working distance is >1.8 mm and that the correction collar can be adjusted for cover glasses of thicknesses up to 1.3 mm. The ELWD objectives have been used earlier to perform FCS measurements on thick cover glass (16). However, the reported S/Ns of the ACF were poor.

Optimization of the performance of the setup

We then investigate the factors that affect the performance of the cuvette FCS most critically. The resolution of the cuvette FCS is characterized by σ_r and V_eff of the observation volume and the sensitivity by S/N of the ACF (G(τ)). To evaluate these factors, we have performed FCS measurements on a solution of rhodamine B in PBS at 25°C. The G(τ) data are analyzed to determine <N>, τ_D, ω, and the CPM of the fluorophore in the FCS observation volume using Eq. 3. All the G(τ) data along with the fits are presented in Fig. S3. V_eff and σ_r are then estimated from <N> and τ_D, as discussed in (4a), (4b), (4c), a–c. We use CPM as a qualitative measure of S/N (see Eq. 5). In all of our experiments, the correction collar of the objective is fixed according to thickness of the wall of the cuvette, i.e., for thicknesses equal to 1.25 mm.

First, we characterize how the performance of cuvette FCS depends on the depth of the focal spot inside the cuvette. Fig. 2 A shows that <N> and τ_D are nearly constant when the depth is less than 25 μm but increase rapidly thereafter. Because <N> and τ_D are proportional to V_eff and σ_r², respectively, both the axial and the radial resolution remain nearly unchanged if the depth of the focus is less than 25 μm, but it worsens rapidly beyond this distance. The same figure shows that the CPM is the highest at a depth of 15 μm, but it decreases on either side of 15 μm. The results presented above are consistent with the observations reported by Hell et al., which found that the effects of focal depth on the axial and the radial resolutions are small even in the presence of mismatch of RIs in the case of low NA (NA = 0.8) objectives (17). Furthermore, Hell et al. showed that the peak intensity of the PSF falls sharply with the depth of the focal spot (17). It is unclear why the CPM shows a peak at a depth of 15 μm instead of at a depth equal to zero. We think that for distances very close to the cuvette, aberrations may be introduced because of partial focusing of the excitation inside the wall of the cuvette. Taken together, the data presented in Fig. 2 A indicate that the confocal PSF in cuvette FCS remains nearly unchanged if the focal spot is kept within 25 μm. Therefore, we keep the depth of focus at nearly 15 μm in all of our FCS experiments.

We then examine the effects of the size of the confocal pinhole on the FCS data using multimode optical fibers of different diameters. Diameters of the fibers used are 25, 50, and 105 μm. Fig. 2 B shows that both <N> and τ_D increase with increasing size of the pinholes. This is expected, as larger pinholes are expected to increase both σ_r and σ_z (23, 26). Although <N> and τ_D, which are obtained using the 25 μm fiber, are the smallest, the corresponding values obtained using the 50 μm fiber are only slightly (∼10%) larger. However, the CPM obtained using the 25 μm fiber is ∼50% lower than that obtained with the 50 μm fiber. Because in our setup 1 AU is ∼61 μm, decreasing the size of the pinhole below 50 μm leads to significant loss of CPM without much improvement of the resolution (23). Therefore, we have chosen the 50 μm multimode optical fiber as the pinhole in our cuvette FCS setup. Furthermore, in Fig. 2 B, it may be seen that the CPM obtained with the 100 μm fiber is ∼20% less than that obtained with the 50 μm fiber. Hess and Webb have argued that CPM as a function of pinhole diameter should not exhibit any peak in the case of a perfectly 3D Gaussian PSF (26). Therefore, the small peak of the CPM observed at a pinhole size of 50 μm in Fig. 2 B indicates deviations from a perfectly Gaussian PSF.

We then examine whether and how the quality and the alignment of the cuvette affect the performance of the cuvette FCS. Fig. 2 C shows the comparison of the CPM, <N>, and τ_D obtained using quartz cuvettes procured from three different manufacturers, referred to here as Hellma, MF1, and MF2. The dimensions of all the three cuvettes are the same, e.g., the thickness of the optical window = 1.25 mm and the pathlength = 10 mm. It may be seen that the CPM, <N>, and τ_D obtained using different cuvettes differ by 2.0-, 1.4-, and 1.2-fold, respectively. Therefore, the quality of the optical windows of the cuvettes is extremely important for the S/N of the FCS data. In fact, the CPM obtained using the MF1 and MF2 cuvettes is also dependent on the particular side of the cuvette facing the path of the excitation (data not shown). We then test how the angular alignment of the cuvette influences cuvette FCS. Fig. 2 D shows how the CPM, <N>, and τ_D depend on the angle between the face of the objective and the optical window of the cuvette. It may be seen that CPM decreases by ∼4-fold, <N> increases by ∼4-fold, and τ_D increases by ∼2-fold for an angular misalignment of 0.40°. Hence, the best sensitivity and resolution in the cuvette FCS is achieved when the cuvette surface is parallel to the face of the objective. The reasons behind the striking effects of quality and angular alignment of the cuvette are not clear, but we think that it may arise because of the following reasons discussed below. Enderlein et al. have shown that FCS measurements can be affected in the presence of even small deviations (∼5 μm) in the thickness of the cover glasses (37). Hence, uniformity of the thickness of optical windows of the cuvettes can play crucial roles in the performance of cuvette FCS. Dross et al. have found that the FCS observation volume may be distorted if the focus is moved in the lateral direction from the optical axis of the objective (38). Therefore, tilt of the cuvette can cause similar optical aberrations. This problem can be severe, particularly in the case of cuvette FCS, because of the relatively high thickness of the optical windows of cuvettes. Furthermore, we have examined the birefringence of the cuvettes by CD (Fig. S4). Clearly, the cuvettes from MF1 and MF2 show nonzero CD, suggesting significant birefringence of the walls of these cuvettes. Hence, birefringence of the walls of the cuvette may, at least partly, affect the resolution of the confocal PSF. We note here that another contributing factor to the angular dependence may arise if the ELWD objectives are not optimally corrected for the flatness of the field of view. Because the best performance is achieved using Hellma cuvette, all the FCS measurements reported in the rest of the article are performed using this cuvette.

Calibration of the observation volume and the S/N of G(τ)

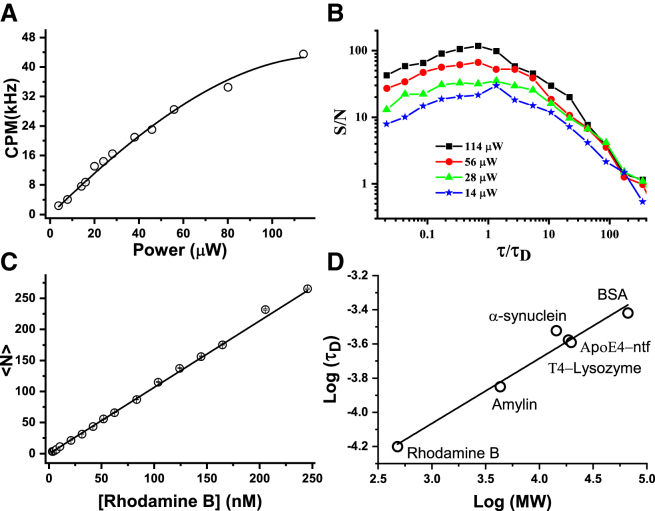
We then calibrate the cuvette FCS setup by performing measurements in aqueous solution of rhodamine B at 25°C to estimate the CPM, S/N, V_eff, σ_r, σ_z, and ω. Fig. 3 A shows that the CPM of rhodamine B increases monotonically with the incident laser power. The increase of CPM deviates from linearity above 50 μW of incident power, but it does not reach complete saturation even at the highest intensity (114 μW) used here. It may be seen that the maximal CPM obtained here using rhodamine B is 44 kHz. We note here that this is the total CPM; hence, the CPM recorded in each detection channel is ∼22 kHz. The average τ_D obtained from the analysis of the G(τ) data is 64 ± 2 μs (Fig. S5, A and B). Fig. 3 B shows the plots of the S/N (= <G(τ)>/SD) as a function of τ/τ_D. Expectedly, S/N increases with an increase of CPM due to increase of excitation intensity (20, 21, 25). Document S1. Supporting Materials and Methods, Figs. S1–S11, and Table S1, Document S2. Article plus Supporting Material D shows that the S/N at τ = τ_D increases linearly with CPM, as expected from Eq. 5. The highest S/N obtained in cuvette FCS is ∼110 at the highest CPM of 22 kHz per detection channel. Fig. 3 C shows the plot of <N> as a function of concentration (C) of rhodamine B. Expectedly, <N> varies linearly with C over the entire range of concentration. Linear fit of the data yields slope = 1.1 molecule/nM. Hence, the estimated value of V_eff in cuvette FCS is 1.8 ± 0.1 fL (see Eq. 4 a). Fig. S6, A and B show that mean τ_D of rhodamine B obtained from the analysis of the G(τ) data is 63 ± 2 μs. Using the known diffusion coefficient (D = 4.5 × 10⁻⁶ cm²/s) of rhodamine B in water, the σ_r is found to be ∼337 nm (Eq. 4 c). Using Eq. 4 b, σ_z and structure parameter (ω) are estimated to be 2.85 μm and 8.5, respectively. Figs. S5 C and S6 C show that the value of ω obtained from the fitting of the G(τ) using Eq. 3 is ∼10 ± 1. Therefore, the values of ω obtained using the two independent approaches agree quite well. This indicates that 3D Gaussian approximation of the PSF of the observation volume in cuvette FCS holds quite well.

Figure 3.

Calibration of the sensitivity and the observation volume of the cuvette FCS. (A) CPM (kHz) is shown as a function of incident laser power obtained using aqueous solution of rhodamine B. Symbols represent data, and the solid line is the fit using a parabola. The CPM deviates from linearity for incident power >50 μW. (B) The S/N of the G(τ) data is measured at 114, 56, 28, and 14 μW excitation power. Expectedly, the S/N increases with the CPM. (C) The average number of molecules (<N>) in the effective observation volume (V_eff) is shown as a function of concentration of rhodamine B. Symbols represent data. The slope of the fitted line is 1.1 molecules/nM, indicating V_eff = 1.8 fL. (D) The log-log plot of τ_D versus molecular weight (MW) of free dye and several TMR-labeled-proteins is shown. Symbols represent data, and the solid line is linear fit. The slope obtained is 0.36 ± 0.01. The expected slope for globular proteins is 0.33 (39). To see this figure in color, go online.

We then examine if cuvette FCS is suitable for measurements using proteins of different sizes. We performed FCS measurements on amylin, α-synuclein, T4-lysozyme, an N-terminal fragment of apolipoprotein E4 (Nt-apoE4), and BSA fluorescently labeled with TMR. The G(τ) data along with the fits are shown in Fig. S7. All the proteins are fluorescently labeled with TMR. Fig. 3 D shows that log(τ_D) varies linearly with log(molecular weight). The slope of the line is equal to 0.36 ± 0.01. The expected scaling exponent is 0.33 for globular proteins (12, 39). Hence, the measured τ_D values are consistent with the scaling law for globular proteins. The τ_D of α-synuclein is found to be somewhat higher, which is consistent with the extended conformation of α-synuclein in native conditions (40).

Comparison of cuvette FCS with a commercial microscope-based FCS

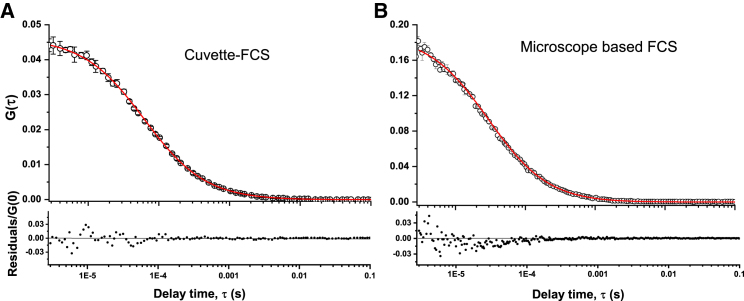
We then compare the sensitivity of the cuvette FCS measurements with that of a microscope-based commercial FCS setup. The commercial setup used here is a PicoQuant FCS module attached to an Olympus confocal microscope. The objective used in the commercial FCS is a water objective with NA = 1.2. Fig. 4, A and B show the autocorrelation data with the fits (and the residuals) obtained from 20 nM rhodamine B in PBS at 25°C using cuvette FCS and the PicoQuant FCS, respectively. The power of the excitation laser used is 28 μW in both of the setups. It may be seen that the G(0) obtained in cuvette FCS is ∼1/4 of that obtained using the PicoQuant FCS, indicating a four-times-larger V_eff in the cuvette FCS. Fig. S8 shows that the S/N of the G(τ) obtained using the two setups are similar. Comparison of the CPM, S/N, V_eff, σ_r, σ_z, and ω obtained using these two setups is summarized in Table 1. It may be seen that the σ_r, σ_z, and V_eff values achieved in cuvette FCS are, respectively, 1.4-, 2.5-, and 3.9-times-larger than those obtained using the conventional FCS setup. Because the NA of the objective used in cuvette FCS is 1.7-times-smaller than that used in the commercial FCS, the expected increases of σ_r, σ_z, and V_eff in cuvette FCS are 1.7-, 2.5-, and 7.2-times, respectively (23). Furthermore, the CPM and the S/N in cuvette FCS are quite similar to those of the commercial FCS. Taken together, the data presented above indicate that the cuvette FCS performs significantly better than expected in comparison to the commercial FCS.

Figure 4.

Comparison of cuvette FCS (A) and a commercial microscope-based FCS (B). Upper panels show the G(τ) data with the fits. Lower panels show the residuals normalized by G(0). The objective in microscope-based FCS is water immersion with NA = 1.2 (B). The same concentration (20 nM) of rhodamine B and the same incident laser power (28 μW) has been used in both of the setups. G(0) is four-times smaller in cuvette FCS (A) than in the microscope-based FCS (B). However, residuals normalized by G(0) are quite similar between the two setups. Comparison of <N>, τ_D, and CPM is presented in Table 1, and the S/N are shown in Fig. S8. To see this figure in color, go online.

Table 1.

Comparison of Cuvette FCS and a Commercial Conventional FCS

	Obtained from Fitting G(τ)a Using Eq. 3					Calculated Using (4a), (4b), (4c), a–c
	<N>	τD (μs)	σz/σr	CPM (kHz)	S/Nb	Veff (fL)	σr (nm)	σz (μm)	σz/σr
Cuvette FCS	21.7 ± 0.3	63 ± 2	10 ± 1	16.4	50	1.8 ± 0.1	337 ± 3	2.84 ± 0.2	8.4 ± 0.1
Commercial FCS	5.3 ± 0.2	33 ± 1	6 ± 0.5	17.7	51	0.43 ± 0.04	245 ± 4	1.29 ± 0.1	5.3 ± 0.1

^aFCS measurements have been performed on a 20 nM rhodamine B solution in PBS at RT using 28 μW excitation laser power.

^bS/N calculated at τ/τ_D =1 using five identical measurements of G(τ) acquired for 30 s each.

Applications of cuvette FCS in temperature- and denaturant-dependent experiments

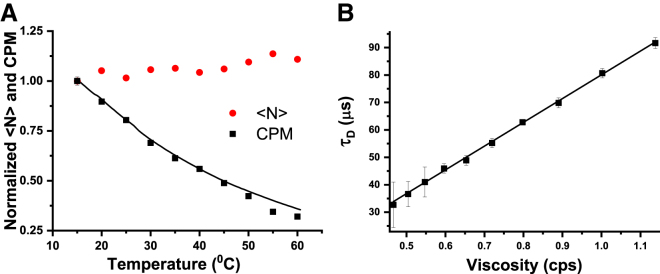
We then examine the suitability of the cuvette FCS setup for measurements in conditions that are generally avoided in microscope-based FCS. In confocal microscopes, the range of experimental temperature is generally restricted to 25–37°C because of incompatibility of the objectives at higher or lower temperatures. Because we are using an air objective, the temperature of the sample does not affect the objective. Here, we perform FCS measurements on rhodamine B in PBS buffer over a range of temperatures, starting from 15 to 60°C. Fig. 5 A shows how <N> and CPM change with temperature. It may be seen that <N> remains almost constant, indicating the robustness of V_eff over the entire range of temperature used here. This is also evident from the G(τ) data presented in Fig. S9, which shows that G(0) is nearly the same at all the temperatures. The CPM is found to decrease by ∼3-fold between 15 and 60°C. The solid line in the same figure indicates that the loss of CPM is consistent with the loss of fluorescence QY of rhodamine B with the increase of temperature measured in a spectrofluorometer. Because the viscosity of water changes with temperature, we have plotted the τ_D as a function of the viscosity of the solution. Fig. 5 B shows that τ_D of rhodamine B increases linearly with the viscosity of water, as may be expected from the Stokes-Einstein (SE) relationship (41). Taken together, measurements of <N>, CPM, and τ_D suggest that cuvette FCS is suitable for measurements over a wide range of temperatures. Although here we have used a limited range of temperatures, with an appropriately designed cuvette holder, even larger ranges of temperatures can be used for measurements using cuvette FCS. For example, using a specially designed cell and an ELWD objective lens, Połatyńska et al. have shown that FCS measurements can be performed in a much larger range of temperatures (from 15 to 200°C) (42). However, in their setup, they have used a microscope-based setup and a thin glass coverslip as the optical window instead of the thick cuvette used here.

Figure 5.

Performance of cuvette FCS over an extended range of temperatures. (A) Normalized <N> (circles) and CPM (squares) are shown as a function of temperature. The solid line represents temperature-dependent normalized quantum yield of rhodamine B, measured using a spectrofluorometer. (B) τ_D versus viscosity is shown. Here, the viscosity of the solution changes because of changes in temperature. The linear increase of τ_D with viscosity is consistent with the SE relationship. To see this figure in color, go online.

We then examine if the cuvette FCS can be used for measurements in urea. Here, we have coupled an automatic titrator with the cuvette for addition of urea into the buffer. Additionally, a magnetic stirrer is used for intermittent mixing of the solution (see Materials and Methods for the details). Therefore, the entire experiment is performed in an automatic manner. The temperature is maintained at 25°C. Fig. 6 A shows the plots of <N> and CPM as a function of the concentration of urea. In this plot, both <N> and <CPM> are normalized by its values measured in 0 M urea. It may be seen that <N> increases by ∼15% between 0 and 7 M urea. The increase of <N> may indicate an increase of V_eff due to gradual worsening of the σ_z at higher concentrations of urea. Because the RI of the urea solution increases by ∼5%, the confocal PSF may be expected to be elongated by the same extent (19, 43). Hence, the expected increase of V_eff is ∼5%. However, Fig. S10 B shows that the structure parameter of the FCS observation volume remains almost constant between 0 and 7 M urea, indicating no major or systematic increase of optical aberrations in urea. Because the error bars on the determination of the structure parameter are large, a change of 5% may not be noticeable. Another possible cause of increase of <N> could be due to adsorption of the fluorophore on the cuvette walls at higher concentrations, followed by desorption of the fluorophore during dilutions (34). We used BSA in the solution to minimize adsorption, but it may not be possible to eliminate adsorption fully. The same figure shows that CPM increases by ∼25% between 0 and 7 M urea. This is counterintuitive because optical aberrations at higher concentrations of urea would decrease the CPM (17, 19). To examine if the QY increases in urea, we measured the fluorescence of rhodamine B in varying concentrations of urea in a spectrofluorometer. The solid line in Fig. 6 A shows that ensemble fluorescence of rhodamine B increases by ∼30% between 0 and 7 M urea, indicating an increase of its QY in urea. Furthermore, a urea-dependent increase of QY is in good agreement with the increase of CPM measured by cuvette FCS, although there are small differences at higher urea concentrations. Finally, we examine how the τ_D of rhodamine B varies with urea. Because viscosity of the solution changes with the concentration of urea, here we have plotted the τ_D as a function of viscosity. Fig. 6 B shows that the τ_D of rhodamine B increases linearly with an increase of viscosity of the urea solution, as expected from the SE relationship as shown earlier by Sherman et al. (11). The G(τ) data with the fits at various concentrations of urea are shown in Fig. S10 A. We note here that although some authors have used repeated adjustments of correction collar of the objective to minimize aberrations due to mismatch of the RIs, we find that this step can be eliminated if the observation volume is kept fixed within a depth of ∼15 μm inside the cuvette (Fig. 2 A). Taken together, the data presented above indicate that cuvette FCS provides robust measurements of CPM and τ_D in urea. Furthermore, measurements in urea using cuvette FCS are highly convenient compared to those using conventional FCS setups.

Study of urea-dependent unfolding of Nt-apoE4 by cuvette FCS

Finally, we examine if cuvette FCS can be successfully employed to study the unfolding of proteins induced by urea. Here, we have performed the unfolding of TMR-labeled Nt-apoE4 at 25°C. The Nt-apoE4 is a four-helix bundle (Protein Data Bank (PDB): 1gs9). The hydrodynamic radius (R_h) of Nt-apoE4 calculated using hydropro10 is 2.67 nm (44). Fig. 7 A shows that R_h of Nt-apoE4 in the native buffer is equal to 2.7 ± 0.1 nm, indicating good agreement with the calculated R_h. Furthermore, the viscosity normalized diffusion time (τ_D/η_rel) of Nt-apoE4 increases monotonically from ∼300 to 520 μs, corresponding to an increase of R_h from ∼2.7 to 4.8 nm between 0 and 7 M urea. Additionally, the increase of τ_D/η_rel (or R_h) shows a sigmoidal transition consistent with the cooperative unfolding of the Nt-apoE4 in urea. To plot the fraction of unfolded proteins as a function of concentration of urea, we then analyze the G(τ) using a two-component diffusion model ((7a), (7b) a). Because the two-component model introduces two additional fitting parameters, this leads to redundancy in the determination of both <N> and τ_D. Hence, we fix the values of the τ_D/η_rel of both the folded and the unfolded proteins using the values obtained from Fig. 7 A to fit G(τ) with (7a), (7b) a (see Materials and Methods for details). We note here that the unfolded states of several proteins have been shown to undergo gradual expansion with increasing concentrations of the chemical denaturants (12, 45). Therefore, fixing the value of τ_D/η_rel of the unfolded state ignores such effects. Fig. 7 B shows that the fractions of unfolded Nt-apoE4 as a function of urea measured by cuvette FCS and CD agree well with each other. The stability parameters obtained from the analysis of the fraction unfolded data using a two-state model (36) are summarized in Table S1. The values of ΔG obtained from the FCS and CD data are 3.3 ± 0.4 and 3.3 ± 0.2 kCal/mol, respectively. Thus, ΔG measured by cuvette FCS and CD agree with each other, and this is also consistent with the published results (46). However, the midpoint of denaturation obtained from the FCS data is somewhat smaller than that obtained from the CD data. Consequently, the “m” values obtained using the two different techniques are also different. This may indicate mechanistic differences between the expansion of tertiary structure and the loss of secondary structure of the protein (11, 12, 47). G(τ) data with the fits at different concentrations of urea are shown in Fig. S11.

Discussion

Here, we have demonstrated that FCS measurements can be performed inside regular cuvettes with high sensitivity. Sensitivity of the cuvette FCS is critically dependent on several factors, such as the focal depth and the quality and angular alignment of the cuvette. Therefore, these factors need to be taken into account while building the cuvette FCS setup and performing the measurements. A major advantage of the cuvette FCS setup is that the resolution and the sensitivity that can be achieved are comparable to the commercial microscope-based FCS. In Table 1, we have shown that the V_eff and the σ_r obtained in cuvette FCS are only moderately larger than that generally observed in a commercial microscope-based FCS that uses high NA objectives. To our surprise, we find that the CPM and the S/N obtained (using the same laser power) in the commercial FCS and our cuvette FCS are almost identical (Table 1). The highest CPM obtained from an aqueous solution of rhodamine B in the cuvette FCS is ∼44 kHz. This is comparable to the reported maximal CPM of 30–50 kHz obtained from Alexa488 in aqueous buffer using a commercial PicoQuant FCS (48). We note here that the CPM and S/N obtained using a high NA objective is expected to be much higher than that obtained using a low NA objective due to higher collection efficiency and excitation power density. For example, Połatyńska et al. used a microscope-based FCS setup and reported that the CPM obtained using a 0.6 NA ELWD air objective in the same setup is ∼35-times smaller compared to that obtained using a 1.2 NA water immersion objective. This led to the poor S/N in G(τ) in the case of the low NA objective (42). Comparable values of the S/N obtained using our cuvette FCS and a commercial FCS indicate that the commercial FCS setup is not optimized to the maximal achievable sensitivity. One reason behind this less-than-optimal sensitivity of the PicoQuant FCS could be due to the use of hybrid photomultiplier tube detectors instead of the avalanche photodiodes. The other possibilities include use of solid-state lasers, which generally exhibit imperfections in the wave front. Additionally, commercial FCS setups generally use more optical elements than the home-built ones. Extra optical elements in the fluorescence detection path can cause significant loss of CPM.

Cuvette FCS offers several advantages over microscope-based FCS instruments. Two major advantages have been demonstrated here. For example, cuvette FCS allows measurements over a large range of temperatures. Our data presented in Fig. 5 suggest that cuvette FCS measurements are highly robust over a range of temperatures from 15 to 60°C. Furthermore, cuvette FCS can be integrated with automatic titrators and magnetic stirrers for fully automated titration experiments. Use of automatic titrators and temperature-controlled cell holders are particularly advantageous in acquiring a large number of highly accurate data points, as may be seen in Figs. 6 and 7. Furthermore, cuvette FCS can be used for studies of unfolding of proteins induced by chemical denaturants such as urea. Although FCS yields single-molecule-level information, denaturant-induced unfolding of biomolecules is seldom performed in FCS. There are major difficulties in measurements of diffusion time or molecular size in urea in conventional FCS setups. The difficulties arise due to mismatch of RI between the solution and the immersion media, leading to optical aberrations (10, 49). In microscope-based FCS measurements, samples containing different concentrations of urea are measured individually. To minimize the aberrations, some authors adjust the correction collar of the objective at each concentration of the denaturant (10). Alternatively, the correction collar is kept fixed, but the distance between the objective and the coverslip is adjusted carefully for each sample to keep the depth of the focal point very close to the coverslip (11). In cuvette FCS, the correction collar is fixed according to the thickness of the wall of the cuvette. The distance between the objective and the cuvette is fixed such that the observation volume is at ∼15 μm from the inner surface of the cuvette wall. Because we are using a low NA objective, the optical aberrations are minimal within a focal depth of 0–25 μm (Fig. 2 A) (17). Therefore, low NA objectives may be preferable when aberrations due to mismatch of the RIs need to be avoided. In our setup, the concentration of urea can be changed by manual pipetting or by using autotitrators. Therefore, titration experiments in the cuvette FCS can be fully automated. Such automation has not been demonstrated in microscope-based FCS.

Single-molecule studies of denaturant-dependent folding and unfolding of proteins is an important area of research in biophysics. For example, Sherman and Haran have used single-molecule Förster resonance energy transfer and FCS to measure GdnCl-induced expansion of protein L to determine the coil-globule transition point and calculated the per-residue average solvation energy (41). Furthermore, Schuler and co-workers have demonstrated that single-molecule studies of protein unfolding can be used to estimate net interaction energy of the unfolded form of a protein in a solvent (12). However, there are only a few studies of protein unfolding using FCS reported in the literature, most likely due to the inherent difficulties in performing these experiments (10, 11, 41). Here, we have demonstrated that cuvette FCS can be used conveniently to study urea-dependent unfolding of proteins using Nt-apoE4 (Fig. 7). We find that the free energy of folding of Nt-apoE4 measured by FCS is the same as that obtained from CD experiments. However, an increase of hydrodynamic size due to unfolding is found to be less cooperative than the loss of secondary structure. This may indicate that the expansion of the tertiary structure precedes the disruption of the secondary structure. Similar observations were reported in case of protein L by Sherman et al. (11).

We speculate that cuvette FCS can be useful in addressing several other problems. For example, FCS has been used to monitor formation of oligomers and protofibrils in the early stages of protein aggregation (50). However, nucleation-dependent aggregation kinetics is generally slow, occurring over several hours, days, or weeks. Therefore, in vitro, these processes are accelerated by agitations such as stirring and/or by raising the temperature of incubation (51). Cuvette FCS would be suitable to monitor such processes. Cuvette FCS can also be used for measurements in nonaqueous solvents, including corrosive solvents such as those experiments involving solvent-dependent dynamics of colloids, polymers, or biopolymers such as intrinsically disordered proteins. Furthermore, cuvette FCS can offer significant advantages in measurements at very low concentrations of biomolecules because of the low surface-to-volume ratio of cuvettes and because of the compatibility of its surfaces to passivation by covalent linkage of polyethylene glycol to minimize adsorption (52). We propose that cuvette FCS may be adapted to perform experiments such as scanning FCS on samples held inside regular glass or quartz test tubes. Scanning FCS has been used to detect fluorescently dim but large objects such as bacteria (15). We think that the high sensitivity of the cuvette FCS would enable detection and characterization of much smaller hazardous pathogens such as viruses. Cuvette FCS is potentially compatible with the rapid mixing flow cells commonly used in stopped-flow kinetic experiments. However, the time resolution in FCS experiments is limited by the acquisition time of the autocorrelation data. Because the acquisition time in FCS is typically >1 s, the cuvette FCS coupled to a stopped-flow setup can be used to monitor the kinetics of the processes with a characteristic timescale of ∼1 s. Furthermore, with an appropriately designed cell holder, cuvette FCS can also be adapted for measurements at high pressures (53).

We would like to note here that the limited range of the commercially available ELWD objectives limits the design of the cuvette FCS at present. Currently, the commercially available ELWD objectives with correction collars for cover glass thicknesses are dry objectives. Because most of the experiments involving biomolecules are performed in aqueous buffers, a water immersion objective would be preferred. If such objectives become available commercially in the near future, this can circumvent the optical aberrations suffered by the dry objectives and improve the performance of the cuvette FCS further.

Finally, we propose that our setup can be integrated with spectrofluorometers. Spectrofluorometers are highly popular for applications in a wide range of experiments in biochemistry and biophysics laboratories. However, these measurements provide only ensemble-level information. Therefore, cuvette FCS can be extremely useful in performing single-molecule measurements in most of the experiments that are performed regularly in spectrofluorometers but not performed in microscope-based FCS instruments.

Author Contributions

K.G. conceptualized the experiments. B.S., T.B.S., B.K., and K.G. designed and performed the research. B.S. and K.G. analyzed the data and wrote the article.

Editor: Jochen Mueller.