Iterative Subspace Screening for Rapid Sparse Estimation of Brain Tissue Microstructural Properties

Abstract

Diffusion magnetic resonance imaging (DMRI) is a powerful imaging modality due to its unique ability to extract microstructural information by utilizing restricted diffusion to probe compartments that are much smaller than the voxel size. Quite commonly, a mixture of models is fitted to the data to infer microstructural properties based on the estimated parameters. The fitting process is often non-linear and computationally very intensive. Recent work by Daducci et al. has shown that speed improvement of several orders of magnitude can be achieved by linearizing and recasting the fitting problem as a linear system, involving the estimation of the volume fractions associated with a set of diffusion basis functions that span the signal space. However, to ensure coverage of the signal space, sufficiently dense sampling of the parameter space is needed. This can be problematic because the number of basis functions increases exponentially with the number of parameters, causing computational intractability. We propose in this paper a method called iterative subspace screening (ISS) for tackling this ultrahigh dimensional problem. ISS requires only solving the problem in a medium-size subspace with a dimension that is much smaller than the original space spanned by all diffusion basis functions but is larger than the expected cardinality of the support of the solution. The solution obtained for this subspace is used to screen the basis functions to identify a new subspace that is pertinent to the target problem. These steps are performed iteratively to seek both the solution subspace and the solution itself. We apply ISS to the estimation of the fiber orientation distribution function (ODF) and demonstrate that it improves estimation robustness and accuracy.

1 Introduction

Microstructural tissue properties can be inferred with the help of diffusion MRI (DMRI) thanks to its sensitivity to the restricted motion of water molecules owing to barriers such as cellular membranes. Microstructural information is typically obtained from diffusion parameters estimated via fitting to the acquired data some biophysical models. Fitting models such as the tensor model [1] is relatively simple and straightforward. But fitting models that are more sophisticated, such as the multi-compartmental models used in AxCaliber [2] and NODDI [3], is much more involved with significantly greater computational load. Computational complexity is further increased when certain structure is imposed on the solution, such as sparsity [4,5].

In a recent work called AMICO [6], the authors show that it is possible to speed up AxCaliber and NODDI estimation several orders of magnitude by re-formulating the fitting problem as a linear system that can be efficiently solved using very fast algorithms. However, this work is limited to a sparse sampling of the parameter space (30 basis functions for AxCaliber and 145 basis functions for NODDI) and is also limited to voxels containing only a single principal diffusion direction. When extending AM-ICO for the more realistic case of multiple white matter (WM) directions per voxel [7], the number of the basis functions would need to be significantly increased, causing the optimization problem to be very high dimensional and computationally very expensive. A similar situation occurs in the estimation of the fiber orientation distribution function (ODF), as in [5], when one needs to increase the number of angular directions of the basis functions for improving accuracy.

In this paper, we propose a method called iterative subspace screening (ISS) to solve this kind of ultrahigh dimension problem more efficiently. ISS requires only solving the target problem in a medium-size subspace with a dimension that is much smaller than the original space spanned by all the basis functions, but is larger than the expected cardinality of the support of the solution. ISS is a subspace pursuit algorithm [8] involving the following iterative steps:

1. Subspace Selection: Select a potential solution subspace by screening out irrelevant basis functions. This is done by element-wise regression of the fitting residual similar to iterative sure independence screening (ISIS) [9] and subspace pursuit (SP) [8].

2. Subspace Solution: Solve for the solution, assumed sparse, in the selected subspace and compute the fitting residual. The fitting residual is then used in the subspace selection step above to refine the subspace so that irrelevant basis functions can be discarded and relevant ones can be included.

Such subspace selection approach allows us to remove from consideration many basis functions that might never be active and contribute to the solution. This is motivated by the fact that, in our case, the solution is sparse and hence resides in a small subspace. Since the dimension of the ISS subspace is typically much smaller, the solution can be obtained much faster with potentially lesser local minima that may result from the high dimensionality. We demonstrate the effectiveness of ISS on the problem of fiber ODF estimation and show that significant speed up can be achieved. Extension of ISS for AxCaliber and NODDI, similar to AMICO, should be straightforward.

2 Approach

2.1 Problem Description

The problem we are interested in solving has the following form:

$$\underset{f\ge 0}{\text{min}}\left\{\varphi \left(f\right)=l\left(f\right)+r\left(f\right)\right\},$$ (1)

where in our case $l\left(\mathbf{f}\right)={\Vert \mathbf{A}\mathbf{f}-\mathbf{s}\Vert }_2^2$ is a smooth and convex data fidelity term with respect to observation vector $\mathbf{s}\in {\mathrm{ℝ}}^N$ and .(f) is a sparsity-inducing regularization term that is not necessarily smooth or convex. In diffusion MRI, one would typically fill the columns of basis matrix $\mathbf{A}\in {\mathrm{ℝ}}^{N\times P}$ with the set of basis functions derived from diffusion models with varying parameters, such as orientation and diffusivity. The vector $\mathbf{f}\in {\mathrm{ℝ}}^P$ consists of the corresponding volume fractions associated with the basis functions. For example, for estimating the fiber ODF as in [5], one would fill the columns of A with the signal vectors sampled from tensor models oriented uniformly in all directions. For fast AxCaliber [2] and NODDI [3] estimation using a linear system as described in AMICO [6], one would fill the columns of A with signal vectors from compartment models orientated in a direction estimated via fitting a diffusion tensor. If the parameter space is sampled densely, the above estimation would be computationally very expensive and can be susceptible to local minima due to the high dimensionality and high correlation between the basis functions.

Algorithm 1.

Iterative Subspace Screening

Input : A, s, .

Initialization:

1. ${\mathcal{J}}^{\left(0\right)}$ = {. indices of the entries with the largest magnitudes in vector ATs} 2. r(0) = residual $\left(\text{s,}{\mathbf{A}}_{{\mathcal{J}}^{\left(0\right)}}\right)$ 3. f(0) = 0

Iteration : At iterations . = 1, 2, …, go through the following steps:

1. ${\mathcal{J}}^{\left(k\right)}$ = {. indices of the non-zeros entries of f(.−1) and the entries with the largest magnitudes in vector ATr(.−1)} 2. Set f(.) = solve $\left(\text{s,}{\mathbf{A}}_{{\mathcal{J}}^{\left(k\right)}}\right)$ 3. r(.) = residual $\left(\text{s,}{\mathbf{A}}_{{\mathcal{J}}^{\left(k\right)}}\right)$ 4. If ‖r(.)‖>‖r(.−1)‖, quit the iteration.

Output : The solution f = f(.−1).

2.2 Iterative Subspace Screening (ISS)

We propose a method called iterative subspace screening (ISS) to tackle this kind of ultrahigh dimension problem more efficiently. ISS requires only solving the target problem (1) in a medium-size subspace with a dimension that is much smaller than the original space spanned by all the basis functions, but is larger than the expected cardinality of the support of the solution. This is based on the observation that the problem (1) can be rewritten as

$$\underset{f_{\mathcal{J}}\ge \mathbf{0},{\mathbf{f}}_{\overline{\mathcal{J}}}=\mathbf{0},\left|\mathcal{J}\right|=D}{\text{min}}\left\{\varphi \left(\mathrm{f}\right)=l_{\mathcal{J}}\left(\mathrm{f}\right)+r_{\mathcal{J}}\left(\mathrm{f}\right)\right\},$$ (2)

subject to . ≤ . is larger than the expected cardinality of the support of the solution. Here, $l_{\mathcal{J}}\left(\mathrm{f}\right)={\Vert {\mathbf{A}}_{\mathcal{J}}{\mathrm{f}}_{\mathcal{J}}-s\Vert }_2^2$ with ${\mathrm{f}}_{\mathcal{J}}$ being the subvector formed by the elements of f indexed by set $\mathcal{J}\subseteq \left\{1,2,\dots ,P\right\},\overline{\mathcal{J}}=\left\{1,2,\dots ,P\right\}\backslash \mathcal{J}$ and ${\mathbf{A}}_{\mathcal{J}}$ being the sub-matrix formed the columns of A indexed by $\mathcal{J}$. The regularization term $r_{\mathcal{J}}\left(\mathrm{f}\right)$ now penalizes only the elements in f that are indexed by $\mathcal{J}$. We can think of problem (2) as concurrently solving for the solution subspace and the solution itself. This problem is clearly non-convex, non-smooth, and discontinuous; but decoupling subspace identification from the problem allows us to devise an algorithm that focuses on determining the solution in a subspace that actually contains the solution and not in the original subspace, especially when the original problem (1) is very high dimensional (i.e., . is large). As we shall see later, this subspace can be progressively refined by including basis functions that will contribute to the solution and by discarding those that will not. Since the solution is sparse, most basis functions are irrelevant to the solution and can be removed from consideration, reducing significantly the computation cost. Note that if the solution to (1) resides in the identified subspace, solving for (2) will give the same solution as (1).

Proposed Solution

We propose to solve (2) by alternating between solving for $\mathcal{J}$ and solving for f. At each iteration, one only needs to solve for f in a medium-size subspace with dimension . ≤ .. To select the subspace, we perform an element-wise regression of the fitting residual with the basis functions. That is, at the .-th iteration, we first compute the fitting residual r^(.−1) = residual $\left(\mathbf{s},{\mathbf{A}}_{\mathcal{J}}{ }_{{ }^{\left(k-1\right)}}\right)=\mathbf{s}-{\mathbf{A}}_{\mathcal{J}}{ }_{{ }^{\left(k-1\right)}}{\mathbf{f}}_{\mathcal{J}}{ }_{{ }^{\left(k-1\right)}}$ and then use it to determine a subspace of dimension .. This subspace is spanned by the basis functions corresponding to the non-zero elements of f^(.−1) and, in addition, the basis functions corresponding to the largest entries of A^Tr^k−1. Based on this new subspace, with the constituent basis functions indexed by ${\mathcal{J}}^{\left(k\right)}$, we solve for f^(.), i.e., f^(.) = solve $\left(\mathbf{s},{\mathbf{A}}_{\mathcal{J}\left(k\right)}\right)$, via (2) with ${\mathcal{J}}^{\left(k\right)}$ fixed. This solution can then be used to recompute the residual and refine the subspace. Since at each iteration, the residual vector will be used to screen out a significant number of basis functions, thus removing a big portion of the original subspace, we call our method iterative subspace screening (ISS). See Algorithm 1 for a step-by-step summary of ISS. In addition to reducing significantly the computation time by not having to solve the problem in the original high-dimensional space, ISS can also deal with collinearity between basis functions. By performing subspace screening using the residual vector, some unimportant basis functions that are highly correlated with the important basis functions can be discarded, as observed in [9].

Grouped Variant

We can take advantage of the relationships between basis functions by grouping them [9]. We can divide the pool of . basis functions into disjoint groups, each with a number of basis functions. ISS can then be applied to the selection of basis function groups instead of the individual basis functions. This will reduce the chance of missing important basis functions by taking advantage of the joint information among them, making the estimation more reliable. This can be achieved by modifying Step 1 in the .-loop of Algorithm 1 to select the top . groups of basis functions with the greatest ℓ₂-norm of inner products with the residual vector. We shall show how grouping can be used in ISS to help solve sparse-group approximation problem similar to the one described in [10].

A Specific Case

To demonstrate the utility of ISS, we select to use the general sparse-group regularization $r\left(\mathbf{f}\right)=\gamma \left[\alpha {\Vert \mathbf{f}\Vert }_0+\left(1-\alpha \right) {\displaystyle {\sum }_{g\in G}\mathcal{I}}\left({\Vert {\mathbf{f}}_g\Vert }_2\right)\right]$, where $\mathcal{I}\left(z\right)$ is an indicator function returning 1 if z ≠ 0 or 0 if otherwise. The ℓ₀-“norm” gives the cardinality of the support, i.e., ${\Vert \mathbf{f}\Vert }_0=\left|\text{supp}\left(\mathbf{f}\right)\right|=\left|\left\{k:f_k\ne 0\right\}\right|$. Parameters α ∈ [0,1] and γ> 0 are for penalty tuning, analogous to those used in the sparse-group LASSO [10]. Note that α = 1 gives the ℓ₀ fit, whereas α = 0 gives the group ℓ₀ fit. Note that in contrast to the more commonly used ℓ₁-norm penalization, we have chosen here to use ℓ₀-“norm” cardinality-based penalization. As reported in [11], ℓ₁-norm penalization [5] conflicts with the unit sum requirement of the volume fractions and hence results in suboptimal solutions.

3 Experiments

3.1 Data

Synthetic Data

For quantitative evaluation, we generated a synthetic dataset for evaluation of ISS. The dataset was generated using a mixture of four tensor models. Two of which are anisotropic and represent two white matter (WM) compartments that are at an angle of 60° with each other. The other two are isotropic and represent the gray matter (GM) and cerebrospinal fluid (CSF) compartments. The generated diffusion-attenuated signals therefore simulate the partial volume effects resulting from these compartments. The volume fractions and the diffusivities of the compartments were allowed to vary in ranges that mimic closely the real data discussed in the next section. Various levels of noise (SNR=10, 20, 30, with respect to the signal value at . = 0 s/mm²) was added.

Real Data

Diffusion weighted (DW) data from the Human Connectome Project (HCP) [12] were used. The 1.25 × 1.25 1.25 mm³ data were acquired with diffusion weightings . = 1000, 2000, and 3000 s/mm² each applied in 90 directions. 18 baseline images with low diffusion weighting . = 5 s/mm² were also acquired. All images were acquired with reversed phase encoding for correction of EPI distortion.

3.2 Methods of Evaluation

For the synthetic data, our aim is to estimate the fiber ODFs [13] and evaluate their accuracy by comparing their peaks (local maxima) with respect to the ground truth. The orientational discrepancy (OD) measure defined in [14] was used as a metric for evaluating the accuracy of peak estimation. For the real data, we want to evaluate whether consistent results are given by ISS compared with the original problem (1).

The fiber ODF was estimated by fitting to the data the compartment models for WM, GM, and CSF. Similar to [15], the WM is represented by a large number of anisotropic single-tensor models with orientations distributed evenly on a unit sphere. Dissimilar to [15], however, we allow the axial and radial diffusivities to vary. The GM and CSF are represented using isotropic tensor models with GM having a lower range of diffusivities compared with CSF. Mathematically, this is realized by filling the columns of A with the above models with different parameters, i.e., orientations and diffusivities, and then solving problem (1) (or (2)) for the corresponding volume fractions f. Structure is imposed on the problem by grouping the WM models for each direction as well as the GM models and the CSF models. The tuning parameters were set as follows: γ = 1 × 10⁻⁴ and α = 0.05. . was set to about 15% of ..

3.3 Results

Synthetic Data

To show that ISS improves the speed of estimation, we evaluated the computation time of ISS in comparison with solving the original problem (1). We perform this for different numbers of subdivisions of the icosahedron, giving different numbers of directions for the WM models and hence different numbers of columns. for A. 3, 4, 5, and 6 subdivisions of the icosahedron give respectively 321, 1281, 5121, and 20481 directions on a hemisphere. Figure 1 shows that ISS improves the speed of convergence remarkably.

Fig. 1.

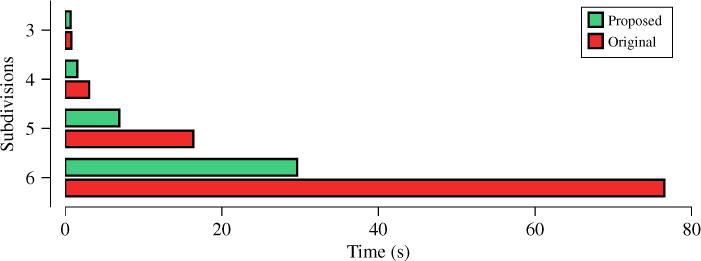
Computation times.

Next, we proceeded to evaluate whether such increase in speed implies a decrease in ODF estimation accuracy. Figure 2, perhaps surprisingly, indicate that ISS actually improves ODF estimation accuracy. This can be explained from the fact that solving the problem in a lower-dimensional subspace can help alleviate the problem of local minima, especially when the problem is non-convex as in our case.

Fig. 2.

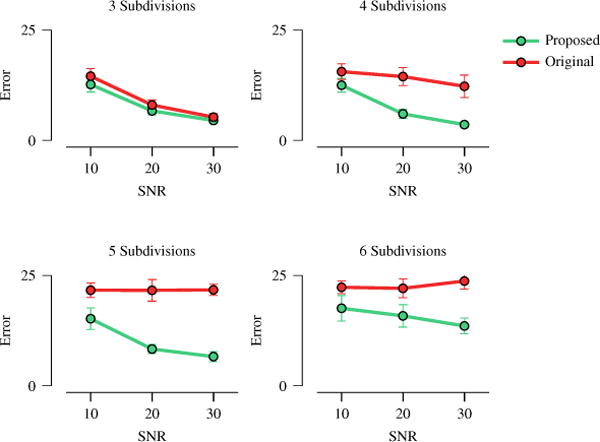
ODF estimation error measured via orientational discrepancy (OD). The error bars indicate the standard deviations.

Real Data

Figure 3 shows the WM ODF glyphs at a portion of the centrum semiovale. The images show that the centrum semiovale contains elements of the corticospinal tract (blue), corpus callosum (red), and superior longitudinal fasciculus (green), including voxels with two- and three-way intersections of these elements. The images indicate that ISS gives consistent results comparable to the original problem. However, we could observe that ISS in fact improves ODF estimation in some voxels (marked by white boxes) and gives ODF estimates that are more coherent and match better with the underlying anatomy.

Fig. 3.

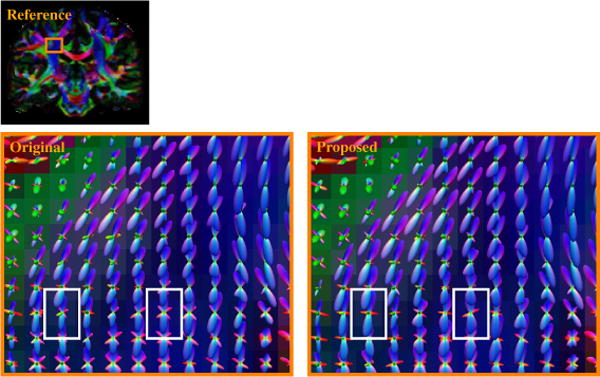
WM ODF glyphs at the centrum semiovale. White boxes mark examples of improvements given by ISS.

4 Conclusion

We have proposed a method for improving the speed and robustness of solving least-squares problems that are regularized by sparse inducing norms. We applied our method called iterative subspace screening (ISS) to ODF estimation and showed that better and faster estimates of the fiber orientations can be obtained. In the future, ISS will be applied to improve the speed and accuracy of estimation techniques for microstructure, such as AxCaliber and NODDI.