Current-induced dynamics of skyrmion strings

Nonlinear Hall effect related to current-driven skyrmion string motion is observed experimentally and analyzed theoretically.

Abstract

Dynamics of string-like objects is an important issue in a broad range of physical systems, including vortex lines in superconductors, viscoelastic polymers, and superstrings in elementary particle physics. In noncentrosymmetric magnets, string forms of magnetic skyrmions are present as topological spin objects, and their current-induced dynamics has recently attracted intense interest. We show in the chiral magnet MnSi that the current-induced deformation dynamics of skyrmion strings results in transport response associated with the real-space Berry phase. Prominent nonlinear Hall signals emerge above the threshold current only in the skyrmion phase. We clarify the mechanism for these nonlinear Hall signals by adopting spin density wave picture to describe the moving skyrmion lattice; deformation of skyrmion strings occurs in an asymmetric manner due to the Dzyaloshinskii-Moriya interaction, which leads to the nonreciprocal nonlinear Hall response originating from an emergent electromagnetic field. This finding reveals the dynamical nature of string-like objects and consequent transport outcomes in noncentrosymmetric systems.

INTRODUCTION

Topologically stable defects cannot be unwound by continuous transformation or weak perturbations (1). As for string-like topological defects, topological stability determines the degree of freedom of bends; for example, when part of a string is pulled, the string does not break but flexibly deforms. Because of this nature, the string-like topological defects exhibit rich forms and dynamical properties. One of the most prototypical examples is vortex lines in type II superconductors (SCs); aggregates of vortex lines form various states, such as the glass state and the liquid state, depending mainly on the relative strength of the pinning force, thermal fluctuations, and the energy cost of bending vortex lines (2). Moreover, deformations are also dynamically induced by external forces such as electrical current (3).

Recently, a string-like topological defect has been found in spin systems, that is, skyrmion strings (4–8). A skyrmion string is a vortex-like topological spin structure 5 to 200 nm in diameter and 10 to 10,000 μm in length along the external magnetic field direction, emerging in noncentrosymmetric magnets because of competition between ferromagnetic exchange interaction and the Dzyaloshinskii-Moriya (DM) interaction. The topological nature of skyrmions, characterized by a topological number of −1, not only guarantees their stability against weak perturbations but also produces unique transport phenomena related to the real-space Berry phase, which acts as an emergent electromagnetic field to conduction electrons (7, 8), such as the topological Hall effect (9), low current drive (10), and the consequent emergent electric field analogous to electromagnetic induction (11). In particular, the latter has inspired research studies on skyrmion-based memory device applications (12). However, in previous research studies on current-induced translational motion, skyrmion strings were treated as two-dimensional objects or straight cylinders, and the degree of freedom of the deformation of skyrmion strings (that is, flexibility) was ignored. In reality, a skyrmion string has a flexible nature as in the case of the vortex line. Hence, especially under translational motion in the presence of random impurities, skyrmion strings should dynamically deform to avoid impurities (Fig. 1A). This assumption is based on simulations in a two-dimensional system (13), according to which a translationally moving skyrmion is deformed to avoid impurities; it is natural to extend the concept of the deformation to a skyrmion string in a three-dimensional system. We note that current-induced dynamics of skyrmion strings in a three-dimensional system has also been simulated to find flexible deformation of the strings (14). In this study, we investigate current-induced deformation dynamics of skyrmion strings arising from this flexibility. To this end, we focus on the nonlinear Hall effect, which is empirically known as a sensitive probe for current-induced spin dynamics in noncentrosymmetric systems (15). In the following, we demonstrate that skyrmion strings asymmetrically deformed because of their flexible nature and the DM interaction, consequently giving rise to a nonreciprocal nonlinear Hall response originating from an emergent electromagnetic field.

Fig. 1. Experimental configurations and the second-harmonic Hall effect in MnSi.

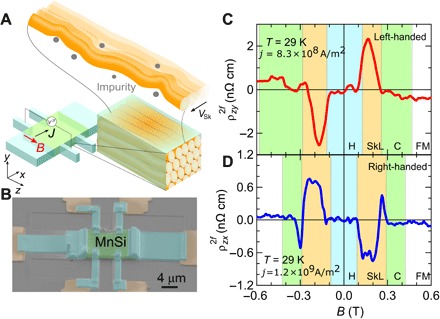
(A) Schematic picture of translationally moving skyrmion strings and the experimental setup for second-harmonic Hall measurement. (B) Scanning electron microscope image of a MnSi thin-plate sample: MnSi crystal (green), gold electrodes (yellow), tungsten (light blue) to fix the MnSi and to connect the gold electrodes to MnSi, and a silicon stage (gray). (C and D) Magnetic field dependence of second-harmonic Hall resistivity (${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$) in right-handed (C) and left-handed (D) MnSi crystals. The blue, orange, green, and white shadows represent helical (H), SkL, conical (C), and ferromagnetic (FM) phases, respectively.

RESULTS AND DISCUSSION

B20-type MnSi has a noncentrosymmetric lattice structure, which can exist in two enantiomeric forms: right- and left-handed structures. From the viewpoint of symmetry, the nonreciprocal nonlinear Hall electric field (E_z) in MnSi can be described as follows

$${\mathit{E}}_{\mathit{z}}=\mathrm{\alpha }({\mathit{j}}_{\mathit{x}},{\mathit{B}}_{\mathit{z}}){\mathit{j}}_{\mathit{x}}$$ (1)

Here, j_x and B_z are the x component of current density and the z component of magnetic field, respectively, and the nonreciprocal nonlinear Hall coefficient α(j_x, B_z) is pseudoscalar, which is an odd function of j_x and B_z (Fig. 1A). The nonreciprocal response in the nonlinear transport phenomenon is defined as different responses to positive and negative currents (±j) when viewed from the current direction. A direction of the nonlinear Hall electric field is parallel or antiparallel to B_z, depending on crystal chirality (see also the Supplementary Materials). We fabricated microscale MnSi thin plates by using a focused ion beam (FIB) (Fig. 1B) to increase current density under the limitations of external high-precision current sources. The crystal chirality was determined by using convergent beam electron diffraction (CBED) (16, 17). To detect nonlinear Hall signals, we performed second-harmonic measurement; we input low-frequency sine-wave AC and measured the real and imaginary parts of second-harmonic complex resistivity (Re ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ and Im ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$), which are directly linked to the nonreciprocal nonlinear Hall coefficient (see the Supplementary Materials). First, we show typical profiles of the second-harmonic Hall effect. As shown in Fig. 1 (C and D), the B dependence of Re ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ of both right- and left-handed crystals exhibits prominent enhancement in the skyrmion lattice (SkL) phase, in which the skyrmion strings form a triangular lattice (see Fig. 1A for the schematic). The signs of Re ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ are reversed between right- and left-handed crystals, in accordance with the expected contributions from the nonreciprocal nonlinear Hall effect. Figure 2A shows the B dependence of Re ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ in the left-handed MnSi crystal with current densities j = 2.1 × 10⁸ A/m² (blue lines) and j = 8.3 × 10⁸ A/m² (red lines) at various temperatures. The magnitude of Re ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ measured with j = 2.1 × 10⁸ A/m² is small enough below noise levels. In contrast, in the case of Re ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ measured with j = 8.3 × 10⁸ A/m², the prominent signals of Re ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ are observed in the skyrmion phase. The clear correspondence between the SkL phase and the conspicuous Re ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ signals is further confirmed in the contour map of Re ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ with j = 8.3 × 10⁸ A/m² in the T-B phase diagram (Fig. 2B; see the Supplementary Materials for the determination of the magnetic phase diagram).

Fig. 2. The second-harmonic Hall effect near the transition temperature.

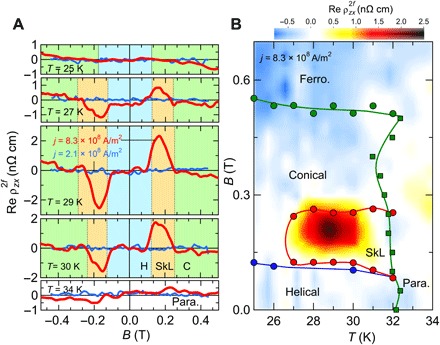
(A) Magnetic field dependence of the real part of second-harmonic Hall resistivity (Re ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$) measured with current densities j = 2.1 × 10⁸ A/m² (blue lines) and j = 8.3 × 10⁸ A/m² (red lines). The blue, orange, green, and white shadows represent helical, SkL, conical, and ferromagnetic phases, respectively. (B) Contour mapping of Re ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ in the temperature–magnetic field plane. The blue, green, and red circles denote helical-to-conical, conical-to-ferromagnetic, and SkL-to-conical phase transitions, respectively, determined from kinks in the magnetic field dependence of planar linear Hall resistivity. The green squares represent helical, conical, and SKL-to-paramagnetic phase transitions determined from inflection points of the temperature dependence of longitudinal resistivity (see also the Supplementary Materials).

To gain more insight, we measured the detailed current-density dependence of ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$. Taking into account the increase in sample temperature owing to Joule heating, we derived the temperature from the longitudinal resistivity of the thin-plate sample itself and adjusted the temperature of the heat bath so that the sample temperature remained constant. Figure 3A shows the current-density dependence of the temperature of the sample, demonstrating that the temperature (T) of the sample remained nearly constant within the 29.0 ± 0.08 K range. The current-density dependence of $\mathrm{R}\mathrm{e} {\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ at T = 29 K measured by using sine-wave AC with f = 13 Hz exhibits a nonmonotonous profile (Fig. 3B). Here, we note that the current-density dependence measured by using sine-wave AC and square-wave current is almost identical. This result rules out the possibility that the nonmonotonous current dependence results from a temporal temperature change, which would possibly occur in the case of sine-wave AC but not in the case of square-wave current (see also the Supplementary Materials). The profile of the current-density dependence of Re ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ is divided into three distinct regimes: (i) almost zero below j_th = 3.2 × 10⁸ A/m², (ii) monotonic increase between j_th and j_CO = 8.9 × 10⁸ A/m², and (iii) monotonic decrease above j_CO. This indicates that the nature of the SkL state changes with increasing current density. These changes are widely observed in charge density wave (CDW) (18, 19) and SC vortices (20, 21): (i) pinned lattice state at low current densities, (ii) disordered flow of lattice affected by the pinning potential in intermediate current densities, and (iii) recovery of crystallinity due to motional narrowing, that is, relative reduction of the pinning force, at large current densities, termed dynamical reordering. Such a dynamical phase diagram is also theoretically predicted for SkL in the presence of a strong random pinning potential (22). On the basis of this theoretical prediction and the analogousness to dynamical phase diagrams of CDW and SC vortices, we assign j_th and j_CO to the onset of disordered translational motion and dynamical reordering of skyrmion strings, respectively. Note that j_th corresponds to the dynamical phase transition point, while j_CO characterizes the crossover (CO). The temperature dependences of j_th and j_CO (Fig. 3C) are also consistent with the above assignment; j_th and j_CO decrease with increasing temperature because thermal activation effectively weakens the pinning force. Therefore, a plausible scenario accounting for the nonmonotonous current dependence of ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ is that the translational motion of deformed skyrmion strings occurs at current densities between j_th and j_CO, leading to the second-harmonic Hall signal along the B direction. We note that the critical current density required for the translational motion of SkL, j_th = 3.2 × 10⁸ A/m², is two orders of magnitude larger than that reported for bulk MnSi (10, 11). This is perhaps due to the chemical disorder/strain on the wide top and bottom surfaces of the sample plate (see Fig. 1A) caused by the device fabrication procedure, which involved focused ion (Ga ion) beams, which act as additional pinning sites for skyrmion strings.

Fig. 3. Current density and frequency dependence of the second-harmonic Hall effect.

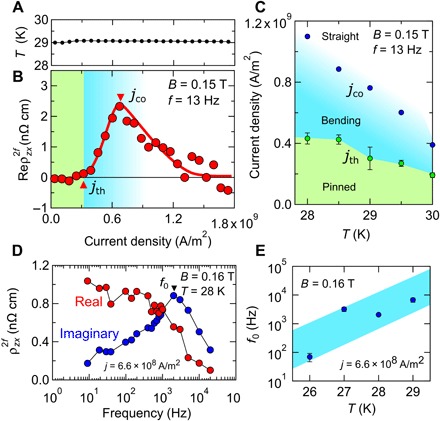
(A and B) Current density (j) dependence of the temperature of the MnSi thin-plate sample estimated from longitudinal resistivity (A) and the real part of second-harmonic Hall resistivity (Re ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$) at B = 0.15 T measured with the frequency f = 13 Hz (B). The red solid curve is a guide to the eyes. (C) Temperature dependence of threshold current densities j_th and the crossover point j_CO at B = 0.15 T. The values of j_th and j_CO at T = 29.0 K are represented as triangles in (B). (D) Dependence of the real part (line with red dots) and the imaginary part (line with blue dots) of ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ on the input current frequency at T = 28 K and B = 0.16 T. (E) Temperature dependence of frequency (f₀), where the imaginary part of ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ peaks. The f₀ values at T = 28 K are represented by the inverse triangle in (D). The thick light blue band is a guide to the eyes.

The close relationship between the second-harmonic Hall effect and the translational motion of skyrmion strings is further confirmed by the dependence of ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ on the input-current frequency. In Fig. 3D, we show the frequency dependence of Re ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ and Im ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ measured with j = 7.0 × 10⁸ A/m² at T = 28 K. At around f = 3 kHz, Re ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ shows a rapid decrease together with the Im ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ peak, and both Re ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ and Im ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ are almost zero above f = 6 kHz. This nonmonotonous frequency dependence in the present frequency range (f < 10 kHz) could not be explained by conventional mechanisms of the second-harmonic Hall effect, such as spin-orbit torque (15) or asymmetric electron-magnon scattering (23), with typical frequencies of several gigahertz. Because the characteristic frequency in motion of nanoscale spin structures such as ferromagnetic domain walls is below several megahertz (24), the observed frequency dependence can be interpreted as representing the relationship between ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ and the translational motion of skyrmion strings; skyrmion strings cannot follow the AC with a frequency (f) above 6 kHz. The profile of the observed frequency dependence of ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ resembles that of the skyrmion velocity (v_sk) derived from Thiele’s equation (see the Supplementary Materials). Additionally, as shown in Fig. 3E, the frequency (f₀) at which Im ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ peaks increases with increasing temperature. Because skyrmion strings can be driven faster at higher temperatures owing to the assistance of thermal activation, the temperature dependence of f₀ also reasonably supports the relationship between ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{2\mathit{f}}$ and the translational motion of SkL.

To clarify the dominant mechanism of the nonlinear Hall signal along the B direction, we calculate the current-induced dynamics of skyrmion strings and the consequent emergent electromagnetic field in the presence of impurity potentials. The model corresponds to experimental situations in which skyrmion strings flow while accompanying distortions (that is, j_th < j < j_CO). In the following, we demonstrate that the experimental observation is well explained in terms of the current-driven asymmetric deformation dynamics of skyrmion strings and the consequent generation of the emergent electromagnetic field. On the basis of the spin density wave picture, the spin texture for SkL is given by the triple-helix state with the modulated phase in space-time (4, 7, 25). This deformation corresponds to the low-lying spin-wave excitation modes of SkL, namely, phasons (25). The response function for phasons is calculated from the energy cost of the deformation based on the DM ferromagnetic Hamiltonian in the presence of impurities (26)

$$\mathit{H}={\displaystyle \int }\frac{\mathit{d}\mathbf{r}}{{\mathit{a}}^3}[\frac{1}{2}\mathit{J}{\mathit{a}}^2{(\nabla \mathbf{n})}^2+\mathit{D}\mathit{a}\mathbf{n}\cdot (\nabla \times \mathbf{n})-\mathit{g}{\mathrm{\mu }}_{\mathrm{B}}\mathbf{B}\cdot \mathbf{n}]+{\displaystyle \int }\frac{\mathit{d}\mathbf{r}}{{\mathrm{\ell }}^3}\mathit{V}(\mathbf{r}){({\mathit{n}}^{\mathit{z}})}^2$$ (2)

where the first, second, third, and fourth terms are Heisenberg interaction, DM interaction, Zeeman term, and impurity potential, respectively. The length $\mathrm{\ell }(>$ lattice constant a) is the average distance between impurities, and the inverse of skyrmion radii is given by Q = |D|/(Ja) in this model. Combining the above Hamiltonian with the Berry phase term in the action, we derive a dynamical response function (see Materials and Methods). The excitation energy ϵ(q) of SkL, which is determined from the pole of the response function, has the following form (27): ϵ(q) = αq² + βq⁴ + γq⁴q_z + O(q⁶) (Fig. 4A). The third term with q_z shows nonreciprocity of skyrmion string dynamics along the z direction, which is crucial to the nonlinear Hall effect, as shown in the following.

Fig. 4. Emergent electromagnetic fields for dynamically generated deformed skyrmion strings.

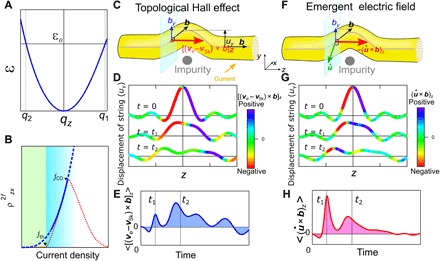
(A) Dispersion relation of the low-energy excitation (ε) of SkL with a propagating vector along the external magnetic field direction (q_z). (B) Schematic for the current dependence of nonreciprocal nonlinear (second-harmonic) Hall resistivity. The solid blue line represents the theoretical calculation, which is valid for the current density between j_th and j_CO, and the broken blue line denotes the square of the current density and is simply a guide to the eyes. The red line indicates the experimentally observed current profile (see also Fig. 3B). (C and F) Schematics of emergent electromagnetic fields for the deformation of a skyrmion string when it collides with point-like impurity. u represents the displacement vector of a skyrmion string. The red arrows denote the z components of the topological Hall electric field [(v_e − v_Sk) × b]_z (C) and the emergent electric field ${\mathit{e}}_{\mathit{z}}=-{[\widehat{\mathbf{u}}\times \mathbf{b}]}_{\mathit{z}}$ (F). (D and G) Position (z) dependence of the displacement of skyrmion strings shown together with the color map of the z components of both (v_e − v_Sk) × b (D) and $\mathit{e}=-\widehat{\mathbf{u}}\times \mathbf{b}$ (G) at several time points. (E and H) Time dependence of the average z components of both (v_e − v_Sk) × b (E) and $\mathbf{e}=-\widehat{\mathbf{u}}\times \mathbf{b}$ (H) over the skyrmion string.

First, to provide an intuitive picture of the current-induced string dynamics in the presence of impurities and consequent emergent electromagnetic fields, we focus on a flowing single skyrmion string bent to avoid an impurity as a representative example of deformed skyrmion strings. Bending of the skyrmion string is described by the displacement vector u = (u_x, u_y, 0) (Fig. 4C), and the Hall electric field originating from emergent magnetic and electric fields is given by e + (v_e − v_Sk) × b, where ${\mathbf{v}}_{\mathit{e}}={\mathit{v}}_{\mathit{e}}\widehat{\mathbf{x}}$ and ${\mathbf{v}}_{\text{Sk}}={\mathit{v}}_{\text{Sk}}\widehat{\mathbf{x}}$ are the velocity of electrons and skyrmions (v_Sk ≲ v_e) and $\mathbf{e}=-\widehat{\mathbf{u}}\times \mathbf{b}$ and (v_e − v_Sk) × b are the emergent electric field and the topological Hall electric field in the moving frame of skyrmions, respectively (see also the Supplementary Materials). As shown in Fig. 4 (C and F), the electric field E_z along the magnetic field direction is nonzero only when a skyrmion string bends. For a detailed investigation of electric fields along the B direction arising from current-induced dynamical bending, we calculate the time evolution of the bending skyrmion string by using ϵ(q) and its eigenmode and the concomitant magnitude of [(v_e − v_Sk) × b]_z and $-{[\widehat{\mathbf{u}}\times \mathbf{b}]}_{\mathit{z}}$ (see the Supplementary Materials for detailed calculations). Figure 4 (D and G) shows the time evolution of a bending skyrmion string shown together with the color map of the magnitude of [(v_e − v_Sk) × b]_z and $-{[\widehat{\mathbf{u}}\times \mathbf{b}]}_{\mathit{z}}$, respectively, and Fig. 4 (E and H) shows the time dependence of their averages over the skyrmion string. At the initial state (t = 0), because deformation is symmetric, both [(v_e − v_Sk) × b]_z and $-{[\widehat{\mathbf{u}}\times \mathbf{b}]}_{\mathit{z}}$ cancel out. With increasing time, however, the skyrmion string asymmetrically deforms because of the nonreciprocity of the dispersion ϵ(q), which leads to the nonzero average of E_z. The above intuitive picture thus indicates asymmetric deformation of skyrmion strings; therefore, the emergent electromagnetic fields play a crucial role in the nonreciprocal nonlinear Hall signal along the B direction.

Next, to gain more insight, we calculate the nonreciprocal response in SkL. Here, we note that the deformations of skyrmion strings are described as collective excitations, which include other types of deformations in addition to the bending deformation. The dynamical spin texture generates emergent electromagnetic fields that are given in the laboratory frame by (28, 29)

$${\mathit{b}}_{\mathrm{\mu }}=\frac{\mathrm{\hslash }}{2\mathit{e}}{\displaystyle \sum _{\mathrm{\nu }\mathrm{\lambda }}}{\mathrm{ϵ}}_{\mathrm{\mu }\mathrm{\nu }\mathrm{\lambda }}\mathbf{n}\cdot ({\partial }_{\mathrm{\nu }}\mathbf{n}\times {\partial }_{\mathrm{\lambda }}\mathbf{n})$$ (3)

$${\mathit{e}}_{\mathrm{\mu }}=\frac{\mathrm{\hslash }}{\mathit{e}}\mathbf{n}\cdot ({\partial }_{\mathrm{\mu }}\mathbf{n}\times {\partial }_{\mathit{t}}\mathbf{n})$$ (4)

The Hall electric field in the DC limit is

$${\mathbf{E}}^{\text{DC}}=\underset{\mathit{T}\to \infty }{\text{lim}}{\displaystyle {\int }_{-\mathit{T}}^{\mathit{T}}}\frac{\mathit{d}\mathit{t}}{2\mathit{T}}{\displaystyle \int }\frac{\mathit{d}\mathbf{r}}{\mathrm{\Omega }}\mathit{P}\langle \mathbf{e}(\mathbf{r},\mathit{t})+{\mathbf{v}}_{\mathit{e}}\times \mathbf{b}(\mathbf{r},\mathit{t})\rangle$$ (5)

where Ω is the volume of the system, P is the spin polarization of the conduction electron at the Fermi level, and the angle bracket denotes the impurity average. We expand the expression with respect to the impurity potentials (see Materials and Methods). After some calculations, we obtain the leading-order contribution to the nonlinear Hall resistivity defined by ${\mathit{E}}_{\mathit{z}}^{\text{DC}}={\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{\text{DC}}{\mathit{j}}_{\mathit{x}}$

$${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{\text{DC}}~\frac{{\mathit{P}}^2\mathrm{\hslash }\mathit{a}}{{\mathit{e}}^2}\cdot \frac{{\left(\frac{\mathrm{\hslash }{\mathit{a}}^2}{\mathit{e}}{\mathit{j}}_{\mathrm{c}}\right)}^3}{{\mathit{J}}^2\mathit{D}}{\left(\frac{\mathit{j}}{{\mathit{j}}_{\mathrm{c}}}\right)}^2$$ (6)

where the electrical current is given by j = en_ev_e, with n_e ~ a⁻³ denoting electron density. Here, critical current density (j_c) can be described by the impurity potential in Eq. 2 (see Materials and Methods). From Eq. 6, the sign of D, which depends on crystal chirality, corresponds to the sign of nonreciprocal nonlinear Hall resistivity, which is consistent with experimental observations (Fig. 1, C and D). We take the following parameters for MnSi (30): a ≃ 2. 9 Å; J = J₀S², with J₀ ≃ 150 K being the Heisenberg exchange at T = 0 and with the helical spin moment S = 0.02 taken near the transition temperature; D = 0. 1J; and P ≃ 0.1. We have roughly estimated the typical value at j = 2j_c by using Eq. 6 as ${\mathrm{\rho }}_{\mathit{z}\mathit{x}}^{\text{DC}}\simeq 0.4 \text{n}\mathrm{\Omega } \text{cm}$, which is comparable to the experimental values.

Although Eq. 6 is valid in the disordered skyrmion flowing regime at the current density with j_th < j < j_CO (see also the broken line in Fig. 4B), where the spin-transfer torque dominates over the collective pinning of SkL, the above microscopic mechanism also qualitatively explains the experimental observation of the decrease of the nonlinear Hall signal above j_CO, which we assign to the onset of dynamical reordering (that is, onset of reduction of the effective pinning force). Because a stronger disorder potential yields a larger deformation of SkL, the nonlinear Hall signal is an increasing function of the strength of the pinning potential. Therefore, the effective reduction of the pinning force reduces the deformation of skyrmion strings, leading to the decrease of nonlinear Hall signals.

Finally, we discuss the nonreciprocal nonlinear Hall resistivity under DC density below j_c and in single-helix states (that is, helical and conical phases). In the former case, because the q_z-linear term in the response function, which is the source of nonreciprocity, enters only together with the dynamical term, the pinned skyrmions do not have the nonreciprocal term. Hence, the Hall electric field ${\mathit{E}}_{\mathit{z}}^{\text{DC}}$ does not arise in the pinned regime below j_c, which is also consistent with experimental observations. In the single-helix state, because both e_z and b_y involve the derivative ∂_z along the magnetic field direction as seen from Eqs. 3 and 4, the nonreciprocal nature along the z direction is necessary. This effect is characteristic of SkL with a multiple-Q nature but is absent in the single-helix state. Hence, the Hall electric field ${\mathit{E}}_{\mathit{z}}^{\text{DC}}$ is observed only for SkL.

We have demonstrated that the current-induced asymmetric deformation of skyrmion strings arising from both their flexible nature and the DM interaction results in a nonreciprocal transport response related to the real-space Berry phase of skyrmion strings. The asymmetric dynamics and the consequent nonreciprocal transport response are some of the generic properties of the dynamics of string-like objects in noncentrosymmetric systems, including vortex lines in noncentrosymmetric SCs as well as skyrmion strings in chiral magnets investigated here.

MATERIALS AND METHODS

Sample preparation

Single crystals of MnSi were synthesized by using the Czochralski method. Their crystalline chirality was confirmed by using the CBED method. Using the FIB technique (NB-5000, Hitachi), we cut the thin plates out of those single crystals. The dimensions of the thin plates were typically ~10 μm × 10 μm × 500 nm. The thin plates were mounted on a silicon stage and fixed by FIB-assisted tungsten deposition. The gold electrodes were patterned by combining photolithography and electron beam deposition techniques. We prepared several thin plates with left-handed and right-handed chirality in order to confirm reproducibility.

Transport measurement

Linear longitudinal resistivity and planar Hall resistivity were measured by using the DC transport option of the Physical Property Measurement System. Second-harmonic resistivity was measured by using a lock-in technique (SR-830, Stanford Research Systems); we input low-frequency sine-wave AC and measured second-harmonic resistivity. To confirm the negligible effect of Joule heating, we simultaneously monitored the temperature by measuring longitudinal resistivity.

Calculation of the nonreciprocal nonlinear Hall effect in SkL

We begin with the spin texture of the disordered SkL, which is given by superposing the three deformed helix states as (4, 7, 25)

$$\begin{array}{cc}\hfill \mathbf{n}(\mathbf{r},\mathit{t})=& {\displaystyle \sum _{\mathit{i}=1}^3}[{\mathrm{\beta }}_{\mathit{i}}(\mathbf{r},\mathit{t}){\widehat{\mathbf{Q}}}_{\mathit{i}}+\sqrt{1-{\mathrm{\beta }}_{\mathit{i}}{(\mathbf{r},\mathit{t})}^2}{\mathbf{n}}_{\mathit{i}}(\mathbf{r},\mathit{t})]\hfill \\ \hfill {\mathbf{n}}_{\mathit{i}}(\mathbf{r},\mathit{t})=& \widehat{\mathbf{z}}\text{cos}[{\mathbf{Q}}_{\mathit{i}}\cdot (\mathbf{r}-\mathbf{R}(\mathit{t}))+{\mathrm{\varphi }}_{\mathit{i}}(\mathbf{r},\mathit{t})]+\hfill \\ & {\widehat{\mathbf{Q}}}_{\mathit{i}}\times \widehat{\mathit{z}} \text{sin}[{\mathbf{Q}}_{\mathit{i}}\cdot (\mathbf{r}-\mathbf{R}(\mathit{t}))+{\mathrm{\varphi }}_{\mathit{i}}(\mathbf{r},\mathit{t})]\hfill \end{array}$$

where Q_{i = 1,2,3} are modulation wave vectors of the helices perpendicular to the external magnetic field along the z direction. The low-energy dynamics of SkL can be effectively described by the above dynamical phason field variables. The hat symbol represents a unit vector, and ${\widehat{\mathbf{Q}}}_1=(-\frac{\sqrt{3}}{2},-\frac{1}{2},0),{\widehat{\mathbf{Q}}}_2=(\frac{\sqrt{3}}{2},-\frac{1}{2},0), \text{and} {\widehat{\mathbf{Q}}}_3=(0,1,0)$. The dynamical field variables ϕ_i and β_i describe the deformation from the perfect lattice induced by the collision of spins with impurities. The phason field ϕ_i shows the modulation of the phase of the helix, which is relevant to the low-energy dynamics of SkL, and its canonical conjugate variable β_i represents a tilt of spin moment from the plane perpendicular to Q_i. The vector R(t) is a uniform displacement driven by the external electrical current and has the form R(t) = v_Skt in the DC limit.

Next, we consider the action for deformation field variables. The Berry phase term has the form (25, 30)

$${\mathit{S}}_{\mathrm{B}}=\mathit{i}\mathrm{\hslash }{\displaystyle \int }\mathit{d}\mathit{t}{\displaystyle \int }\frac{\mathit{d}\mathbf{r}}{{\mathit{a}}^3}{\displaystyle \sum _{\mathit{i}\mathit{j}}}(\frac{9}{8}{\mathit{E}}_{\mathit{i}\mathit{j}}{\mathrm{\varphi }}_{\mathit{i}}{\stackrel{.}{\mathrm{\varphi }}}_{\mathit{j}}-\frac{3}{2}{\mathit{P}}_{\mathit{i}\mathit{j}}{\mathrm{\beta }}_{\mathit{i}}{\stackrel{.}{\mathrm{\varphi }}}_{\mathit{j}})$$

which describes the dynamics of spin texture. Here, we have introduced the symmetric and antisymmetric matrices by ${\mathit{P}}_{\mathit{i}\mathit{j}}=\frac{2}{3}{\widehat{\mathbf{Q}}}_{\mathit{i}}\cdot {\widehat{\mathbf{Q}}}_{\mathit{j}}$ and ${\mathit{E}}_{\mathit{i}\mathit{j}}=\frac{2}{3}\widehat{\mathbf{z}}\cdot ({\widehat{\mathbf{Q}}}_{\mathit{i}}\times {\widehat{\mathbf{Q}}}_{\mathit{j}})$, respectively. We can consider the new phason field variables by ${\mathrm{\varphi }}_{\mathit{x}}=\frac{1}{\sqrt{2}}(-{\mathrm{\varphi }}_1+{\mathrm{\varphi }}_2)$, ${\mathrm{\varphi }}_{\mathit{y}}=\frac{1}{\sqrt{6}}(-{\mathrm{\varphi }}_1-{\mathrm{\varphi }}_2+2{\mathrm{\varphi }}_3)$, and ${\mathrm{\varphi }}_{\mathit{s}}=\frac{1}{\sqrt{3}}({\mathrm{\varphi }}_1+{\mathrm{\varphi }}_2+{\mathrm{\varphi }}_3)$, which correspond to two (x, y) translational modes and a massive breathing mode, respectively (25, 27). Similar quantities for β are also considered. We have neglected the massive breathing mode because the low-lying energy mode gives a dominant contribution. The above action is written only by translational modes, which is confirmed by rewriting the action in terms of ϕ_x,y,s and β_x,y,s.

The action is then given by S = S_B − ∫dtH, which determines the equation of motion and the response functions. The explicit form is written as

$$\begin{array}{c}{\mathrm{\varphi }}_{\mathit{i}}(\mathbf{r},\mathit{t})={\displaystyle \sum _{\mathit{j}}}{\displaystyle \int }\mathit{d}\mathbf{r}\mathrm{\prime }\mathit{d}\mathit{t}\mathrm{\prime }{\mathit{G}}_{\mathit{i}\mathit{j}}(\mathbf{r}-\mathbf{r}\mathrm{\prime },\mathit{t}-\mathit{t}\mathrm{\prime }){\mathit{F}}_{\mathit{j}}(\mathbf{r}\mathrm{\prime },\mathit{t}\mathrm{\prime })\\ {\mathit{F}}_{\mathit{i}}(\mathbf{r},\mathit{t})=\frac{2\mathit{V}(\mathbf{r})}{{\mathrm{\ell }}^3}{\mathit{n}}^{\mathit{z}}(\mathbf{r},\mathit{t})\text{sin}[{\mathbf{Q}}_{\mathit{i}}\cdot (\mathbf{r}-\mathbf{R}(\mathit{t}))+{\mathrm{\varphi }}_{\mathit{i}}(\mathbf{r},\mathit{t})]\\ {\mathrm{\beta }}_{\mathit{i}}(\mathbf{r},\mathit{t})=\frac{3\mathit{J}\mathrm{\hslash }}{2{\mathit{D}}^2}{\displaystyle \sum _{\mathit{j}}}({\mathit{P}}_{\mathit{i}\mathit{j}}+\frac{3}{\mathit{Q}}{\mathit{E}}_{\mathit{i}\mathit{j}}{\partial }_{\mathit{z}}){\stackrel{.}{\mathrm{\varphi }}}_{\mathit{j}}(\mathbf{r},\mathit{t})\end{array}$$

Namely, the deformations ϕ_i and β_i are generated from the impurity pinning force F_i through the response function G_ij. The term with the z derivative in the equation for the β field is responsible for the nonreciprocal nature of skyrmion strings. The Fourier-transformed Green function is given by

$${\mathit{G}}_{\mathit{i}\mathit{j}}^{-1}(\mathbf{q},\mathrm{\omega })=(\mathit{J}{\mathit{a}}^2{\mathbf{q}}^2-\frac{9\mathit{J}{\mathrm{\hslash }}^2}{4{\mathit{D}}^2}{\mathrm{\omega }}^2-\mathit{i}\mathrm{\lambda }\mathrm{\hslash }\mathrm{\omega }){\mathit{P}}_{\mathit{i}\mathit{j}}+(\frac{9\mathit{i}\mathrm{\hslash }}{4}\mathrm{\omega }+\frac{27\mathit{i}{\mathit{J}}^2{\mathrm{\hslash }}^2\mathit{a}}{4{\mathit{D}}^3}{\mathrm{\omega }}^2{\mathit{q}}_{\mathit{z}}){\mathit{E}}_{\mathit{i}\mathit{j}}$$

Here, we have introduced the damping term with the dimensionless coefficient λ. Because the low-energy dynamics is important at a small current density, we can neglect the high-order term with ω² and obtain the excitation energy as

$$\mathrm{ϵ}(\mathbf{q})=\frac{4\mathit{J}{\mathit{a}}^2}{9}{\mathbf{q}}^2-\frac{16{\mathit{J}}^3{\mathit{a}}^4}{81{\mathit{D}}^2}{\mathbf{q}}^4-\frac{16{\mathit{J}}^4{\mathit{a}}^5}{27{\mathit{D}}^3}{\mathbf{q}}^4{\mathit{q}}_{\mathit{z}}+\mathit{O}({\mathit{q}}^6)$$

The quadratic dispersion at small q originates from a topological property of SkL (30). The third term on the right-hand side with q_z shows nonreciprocal excitation. We note that the frequency ω here corresponds to the excitation energy of SkL and is not related to the frequency f of the external current, which is used to measure second-harmonic resistivity, because we considered the DC limit (see also the Supplementary Materials for the relationship between the DC limit of the nonreciprocal nonlinear Hall effect, which we discussed theoretically, and second-harmonic resistivity).

We assume the spatially uncorrelated impurity potential with $\langle \mathit{V}(\mathbf{r})\mathit{V}(\mathbf{r}\prime )\rangle ={\mathit{V}}_{\text{imp}}^2{\mathrm{\ell }}^3\mathrm{\delta }(\mathbf{r}-\mathbf{r}\prime )$, where the angle bracket denotes the impurity average. V_imp can be written in terms of the critical current density (j_c), and the final expression contains only j_c, as will be discussed later. We now consider the Hall electric field in the DC limit (see also Eqs. 3 to 5). Because β_i ∝ ωϕ_i from canonical conjugate relations, the terms that directly involve the phason field variables ϕ_i are dominant at low frequencies, compared to contributions from β_i field variables. By expanding the expression with respect to deformation field variables, the leading-order contribution is given by

$${\mathit{E}}_{\mathit{z}}^{\text{DC}}=\underset{\mathit{T}\to \infty }{\text{lim}}{\displaystyle {\int }_{-\mathit{T}}^{\mathit{T}}}\frac{\mathit{d}\mathit{t}}{2\mathit{T}}{\displaystyle \int }\frac{\mathit{d}\mathbf{r}}{\mathrm{\Omega }}\mathit{P}\langle {({\mathbf{v}}_{\mathit{e}}-{\mathbf{v}}_{\text{Sk}})}_{\mathit{x}}{\mathit{b}}_{\mathit{y}}+{\mathit{e}}_{\mathit{z}}^{\mathrm{\prime }}\rangle$$

$$\simeq \frac{\mathit{P}{\mathit{b}}_{\mathit{z}}}{3{\mathit{Q}}^2}{\displaystyle \sum _{\mathit{i}\mathit{j}\mathit{k}}}{\mathit{E}}_{\mathit{i}\mathit{j}}\underset{\mathit{T}\to \infty }{\text{lim}}{\displaystyle {\int }_{-\mathit{T}}^{\mathit{T}}}\frac{\mathit{d}\mathit{t}}{2\mathit{T}}{\displaystyle \int }\frac{\mathit{d}\mathbf{r}}{\mathrm{\Omega }}[{\mathbf{Q}}_{\mathit{i}}\cdot ({\mathbf{v}}_{\mathit{e}}-{\mathbf{v}}_{\text{Sk}})+{\partial }_{\mathit{t}}{\mathrm{\varphi }}_{\mathit{i}}]{\partial }_{\mathit{z}}{\mathrm{\varphi }}_{\mathit{j}}{\mathrm{\beta }}_{\mathit{k}}^2$$

In this equation, the emergent magnetic field b_y is of third-order with respect to the deformation field variables, and the emergent electric field e_z associated with dynamical internal deformation is the fourth-order term. We note that the second-order and first-order terms for e_z and b_y exist without integrating over space-time but vanish in the DC and uniform limit with negligible boundary contributions. A similar conclusion can be obtained if we consider the single skyrmion string (see the Supplementary Materials). Expanding the phason field with respect to the impurity potentials as ϕ = ϕ⁽¹⁾ + ϕ⁽²⁾ + O(V³), we now write the leading-order contribution for the Hall electric field in terms of the Fourier transposed variables as

$${\mathit{E}}_{\mathit{z}}^{\text{DC}}=(\frac{{\mathit{v}}_{\mathit{e}}}{{\mathit{v}}_{\text{Sk}}}-1){\mathit{E}}_1+{\mathit{E}}_2$$

$$\begin{array}{c}{\mathit{E}}_1=\\ -\frac{9\mathrm{i}\mathit{P}\mathrm{\hslash }\mathrm{\omega }*}{16\mathit{e}}{\left(\frac{3\mathit{J}{\mathrm{\hslash }}^2}{2{\mathit{D}}^2}\right)}^2{\displaystyle \sum _{\mathit{i}\mathit{j}\mathit{k}\mathit{l}}}{\mathit{E}}_{\mathit{i}\mathit{j}}{\mathrm{\alpha }}_{\mathit{i}}{\displaystyle \int }\frac{\mathit{d}{\mathbf{q}}_1\mathit{d}{\mathbf{q}}_2\mathit{d}{\mathbf{q}}_3\mathit{d}{\mathrm{\omega }}_1\mathit{d}{\mathrm{\omega }}_2\mathit{d}{\mathrm{\omega }}_3}{{(2\mathrm{\pi })}^{12}}{\mathit{q}}_{1\mathit{z}}{\mathrm{\omega }}_2{\mathrm{\omega }}_3\times \\ ({\mathit{P}}_{\mathit{k}\mathit{l}}+\frac{6\mathrm{i}}{\mathit{Q}}{\mathit{E}}_{\mathit{k}\mathit{l}}{\mathit{q}}_{3\mathit{z}})\times [\langle {\mathrm{\varphi }}_{\mathit{j}}^{(2)}({\mathbf{q}}_1,{\mathrm{\omega }}_1){\mathrm{\varphi }}_{\mathit{k}}^{(1)}({\mathbf{q}}_2,{\mathrm{\omega }}_2){\mathrm{\varphi }}_{\mathit{l}}^{(1)}({\mathbf{q}}_3,{\mathrm{\omega }}_3)\rangle +\\ \langle {\mathrm{\varphi }}_{\mathit{j}}^{(1)}({\mathbf{q}}_1,{\mathrm{\omega }}_1){\mathrm{\varphi }}_{\mathit{k}}^{(2)}({\mathbf{q}}_2,{\mathrm{\omega }}_2){\mathrm{\varphi }}_{\mathit{l}}^{(1)}({\mathbf{q}}_3,{\mathrm{\omega }}_3)\rangle +\\ \langle {\mathrm{\varphi }}_{\mathit{j}}^{(1)}({\mathbf{q}}_1,{\mathrm{\omega }}_1){\mathrm{\varphi }}_{\mathit{k}}^{(1)}({\mathbf{q}}_2,{\mathrm{\omega }}_2){\mathrm{\varphi }}_{\mathit{l}}^{(2)}({\mathbf{q}}_3,{\mathrm{\omega }}_3)\rangle ]\\ {\mathit{E}}_2=\\ -\frac{9\mathit{P}\mathrm{\hslash }}{16\mathit{e}}{\left(\frac{3\mathit{J}{\mathrm{\hslash }}^2}{2{\mathit{D}}^2}\right)}^2{\displaystyle \sum _{\mathit{i}\mathit{j}\mathit{k}\mathit{l}}}{\mathit{E}}_{\mathit{i}\mathit{j}}{\displaystyle \int }\frac{\mathit{d}{\mathbf{q}}_1\mathit{d}{\mathbf{q}}_2\mathit{d}{\mathbf{q}}_3\mathit{d}{\mathbf{q}}_4\mathit{d}{\mathrm{\omega }}_1\mathit{d}{\mathrm{\omega }}_2\mathit{d}{\mathrm{\omega }}_3\mathit{d}{\mathrm{\omega }}_4}{{(2\mathrm{\pi })}^{16}}{\mathrm{\omega }}_1{\mathit{q}}_{2\mathit{z}}{\mathrm{\omega }}_3{\mathrm{\omega }}_4\times \\ ({\mathit{P}}_{\mathit{k}\mathit{l}}+\frac{6\mathrm{i}}{\mathit{Q}}{\mathit{E}}_{\mathit{k}\mathit{l}}{\mathit{q}}_{4\mathit{z}})\langle {\mathrm{\varphi }}_{\mathit{i}}^{(1)}({\mathbf{q}}_1,{\mathrm{\omega }}_1){\mathrm{\varphi }}_{\mathit{j}}^{(1)}({\mathbf{q}}_2,{\mathrm{\omega }}_2){\mathrm{\varphi }}_{\mathit{k}}^{(1)}({\mathbf{q}}_3,{\mathrm{\omega }}_3){\mathrm{\varphi }}_{\mathit{l}}^{(1)}({\mathbf{q}}_4,{\mathrm{\omega }}_4)\rangle \end{array}$$

where ${\mathrm{\alpha }}_{\mathit{i}}={\widehat{\mathbf{v}}}_{\text{Sk}}\cdot {\widehat{\mathbf{Q}}}_{\mathit{i}}$. We have defined ω* = Qv_Sk, which is the characteristic frequency for moving skyrmions corresponding to the periodic passage of the “washboard potential” of SkL. These are evaluated with the conservation laws of momentum and energy which naturally enter through Fourier transformation. The contributions E₁ and E₂ are those from emergent fields b_y and e_z in the moving frame, respectively. The contributions from both e_z and b_y are of fourth-order with respect to V_imp and have the same parameter dependence. Hence, these can be of the same orders of magnitude, which are numerically shown later. Keeping the q_z-linear term in the lowest order, we obtain the leading-order contribution for the Hall electric field as

$${\mathit{E}}_{\mathit{z}}^{\text{DC}}\simeq \frac{243\mathit{P}\mathit{D}}{512\mathit{e}\mathit{a}}{\left(\frac{\mathit{a}}{\mathrm{\ell }}\right)}^6{\left(\frac{{\mathit{V}}_{\text{imp}}}{\mathit{J}}\right)}^4\frac{{(\mathrm{\hslash }{\mathrm{\omega }}_0^{*})}^3}{{|\mathit{D}|}^3}\left[\right(\frac{{\mathit{v}}_{\mathit{e}}}{{\mathit{v}}_{\text{Sk}}}-1){\mathit{f}}_{\mathit{b}}(\mathrm{\lambda })+{\mathit{f}}_{\mathit{e}}(\mathrm{\lambda })]$$

We have defined ${\mathrm{\omega }}_{\mathrm{*}}^0=\frac{\mathit{J}}{|\mathit{D}|}\mathrm{\omega }*={\mathit{v}}_{\text{Sk}}/\mathit{a}$. The dimensionless functions f_b(λ) and f_e(λ) represent contributions from emergent magnetic and electric fields in the moving frame, respectively, and can be evaluated by performing the q-integrals of products of four Green functions. Figure S1 shows the damping coefficient λ dependences of f_b(λ) and f_e(λ). For weak impurities, assuming that the damping coefficient λ for the moving regime near j_c has a characteristic similar to the one in the pinned regime with j < j_c, we can use the relation λ ~ 1 derived for pinned SkL, and then the function f_e,b(λ) ~ f_e,b(1) can be regarded as a constant on the order of unity. We have thus confirmed that these functions can be of the same orders of magnitude. Because the signs are not unique, the Hall electric field can be either negative or positive depending on the form of disorder potentials.

For comparison, we have also checked another form of the impurity potential. Namely, we choose the random Ising field ${\mathit{H}}_{\text{imp}}=\int \frac{\mathit{d}\mathbf{r}}{{\mathrm{\ell }}^3}\mathit{V}(\mathbf{r}){\mathit{n}}^{\mathit{z}}$ instead of random anisotropy. While the parameter dependences (such as ω*, V_imp, J, and D) of the Hall electric field are the same, the values of dimensionless functions f_b(λ) and f_e(λ) are nearly 10³ times smaller than those for random anisotropy. Hence, the value of the Hall signal is sensitively dependent on the types of the impurity potentials.

Let us relate the pinning potential to the critical current density. The energy supplied to the spin texture through spin transfer torque is given by H_ext = Pb_z∫dr j_xu_y, where u_y = (−ϕ₁ −ϕ₂ + 2ϕ₃)/Q is a displacement along the y direction (30). This energy is set as equal to the pinning energy at the critical current density (31). For the weak pinning case, the SkL is collectively pinned by impurities in the range over the pinning length ${\mathrm{\xi }}_{\mathrm{p}}~\mathit{a}{\left(\frac{\mathit{J}}{{\mathit{V}}_{\text{imp}}}\right)}^2{\left(\frac{\mathrm{\ell }}{\mathit{a}}\right)}^3$. The relation for the energy density balance is

$$\frac{\mathit{P}{\mathit{b}}_{\mathit{z}}{\mathit{j}}_{\mathrm{c}}}{\mathit{Q}}~\frac{\sqrt{{\mathit{V}}_{\text{imp}}^2{({\mathrm{\xi }}_{\mathrm{p}}/\mathrm{\ell })}^3}}{{{\mathrm{\xi }}_{\mathrm{p}}}^3}$$

which shows ${\mathit{j}}_{\mathrm{c}}\propto {\mathit{V}}_{\text{imp}}^4$. Rewriting the impurity pinning potential at the critical current density and noting the magnitude relation v_Sk ≲ v_e, we obtained Eq. 6.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/8/eaat1115/DC1

Section S1. Determination of the magnetic phase diagram for MnSi thin plates

Section S2. Relationship between the nonreciprocal nonlinear Hall effect and second-harmonic resistivity

Section S3. Current dependence of the nonlinear Hall effect measured by using square-wave current

Section S4. Frequency dependence of skyrmion velocity

Section S5. Calculation of nonreciprocal nonlinear Hall responses to AC

Section S6. Calculation of current-induced dynamics of a single skyrmion string

Fig. S1. Functional forms of the dimensionless functions f_b(λ) and f_e(λ).

Fig. S2. Temperature dependence of longitudinal resistivity and magnetic field dependence of planar Hall resistivity.

Fig. S3. Current dependence of the nonreciprocal nonlinear Hall effect measured by using square-wave current.

Fig. S4. Frequency dependence of skyrmion velocity.

References (32–34)