Arrhythmic hazard map for a 3D whole‐ventricle model under multiple ion channel block

Abstract

Background and Purpose

To date, proposed in silico models for preclinical cardiac safety testing are limited in their predictability and usability. We previously reported a multi‐scale heart simulation that accurately predicts arrhythmogenic risk for benchmark drugs.

Experimental Approach

We created a comprehensive hazard map of drug‐induced arrhythmia based on the electrocardiogram (ECG) waveforms simulated under wide range of drug effects using the multi‐scale heart simulator described here, implemented with cell models of human cardiac electrophysiology.

Key Results

A total of 9075 electrocardiograms constitute the five‐dimensional hazard map, with coordinates representing the extent of the block of each of the five ionic currents (rapid delayed rectifier potassium current (I _Kr), fast (I _Na) and late (I _Na,L) components of the sodium current, L‐type calcium current (I _Ca,L) and slow delayed rectifier current (I _Ks)), involved in arrhythmogenesis. Results of the evaluation of arrhythmogenic risk based on this hazard map agreed well with the risk assessments reported in the literature. ECG databases also suggested that the interval between the J‐point and the T‐wave peak is a superior index of arrhythmogenicity when compared to the QT interval due to its ability to characterize the multi‐channel effects compared with QT interval.

Conclusion and Implications

Because concentration‐dependent effects on electrocardiograms of any drug can be traced on this map based on in vitro current assay data, its arrhythmogenic risk can be evaluated without performing costly and potentially risky human electrophysiological assays. Hence, the map serves as a novel tool for use in pharmaceutical research and development.

Abbreviations

AMED

Japan Agency for Medical Research and Development

APD

action potential duration

CiPA

Comprehensive Proarrhythmia Assay

ETPC_unbound

effective therapeutic plasma concentration

FEM

finite element method

HERG

human ether‐a‐go‐go related gene

MEXT

Ministry of Education, Culture, Sports, Science and Technology – Japan

TdP

torsade de pointes

UT‐Heart

the heart simulator developed by the University of Tokyo‐based team

Introduction

The growing cost and time required for drug research and development (R&D) necessitates the introduction of a novel approach to cardiotoxicity testing (Hamburg, 2011; Chi, 2013b). In particular, the drug‐induced arrhythmia, torsade de pointes (TdP), is a rare but sometimes fatal adverse effect of commonly used drugs and this had made screening for arrhythmia propensity mandatory for all drug candidates. Because the approaches mandated by current regulations, namely, a single potassium human ether‐a‐go‐go related gene (http://www.guidetopharmacology.org/GRAC/ObjectDisplayForward?objectId=572) current assay and in vivo ECG testing, are costly and sometimes lead to false‐positive results; regulatory agencies have announced the implementation of a new paradigm incorporating a computational integration of a multiple ionic current assay into a cardiomyocyte model (Chi, 2013a; Chi, 2013b; Gintant et al., 2016).

Although the use of a cellular model is expected to greatly facilitate the screening process, accurate predictions of arrhythmia resulting from complex interactions among the different types of cells in heart tissue require organ‐level simulation, which remains a technical challenge. With advancements in computational science bolstered by high‐performance computing technology, it is now possible to reproduce the heartbeat in a realistic three‐dimensional simulation model of the human heart implemented with mathematical models of functional molecules (Noble, 2002; Washio et al., 2010; Okada et al., 2011; Sugiura et al., 2012; Washio et al., 2013; Okada et al., 2013a). Applying such technologies, researchers have attempted in silico cardiotoxicity screening for human subjects, but to date, most have shown only changes in ECG wave forms induced by drugs or current activities, that is, surrogate markers. Thus, these screening tests are unable to predict arrhythmogenicity (Zemzemi et al., 2013; Sadrieh et al., 2014).

We have recently succeeded in accurately predicting the arrhythmogenicity of 12 drugs with known TdP risk, through the in vitro measurement of blocking actions on multiple ionic currents by reproducing a realistic human 12‐lead ECG in silico (Okada et al., 2015). This method can be applied to any drug candidate, but the requirement of a high‐performance computer is an obstacle to its widespread use. Alternatively, if an open access ECG database covering the wide range of drug effects were available, expensive computers would no longer be needed for each user. However, the high computational burden has made this project impractical. In a previous study, the computational time for a single beat with our heart simulator (degrees of freedom = 285 294 896, number of cell models = 22 750 008) was 3 h with 254 cores (Intel Xenon E5‐2670, 2.6 GHz), and five beats were required for numerical convergence. Accordingly, the total computational cost required for 10 000 patterns of multi‐current effects would be over 70 million core hours.

In the present study, we overcame the problem of long computational times by utilizing the RIKEN K‐computer with a performance of over 10 petaflops (SPARC64 VIIIfx, 705 024 cores, Fujitsu Ltd., Kawasaki, Japan) (Yonezawa et al., 2011). We varied the extent of block of five ionic currents known to affect arrhythmogenicity incrementally by 10%, including the rapid delayed rectifier potassium current (http://www.guidetopharmacology.org/GRAC/ObjectDisplayForward?objectId=572: 0 to 100%), fast (http://www.guidetopharmacology.org/GRAC/ObjectDisplayForward?objectId=582&familyId=82&familyType=IC: 0 to 40%) and late (I _Na,L: for this current, only 0, 25 and 50% blocks were tested) components of the sodium current, L‐type calcium current (http://www.guidetopharmacology.org/GRAC/ObjectDisplayForward?objectId=529: 0 to 40%), and slow delayed rectifier current (http://www.guidetopharmacology.org/GRAC/ObjectDisplayForward?objectId=560: 0 to 100%), to simulate a total of 9075 patterns of multiple ionic current blocks. For every combination of current block, we simulated the electrophysiological activity of the heart and the associated 12‐lead ECG to create a five‐dimensional map of arrhythmia risk, in which the co‐ordinates of the map represent the extent of block of each current. In addition to the occurrence of arrhythmia, the following ECG indices used for arrhythmia risk assessment were also evaluated: QT interval, T_peak‐T_end interval and J‐T_peak interval (Figure 1).

Figure 1.

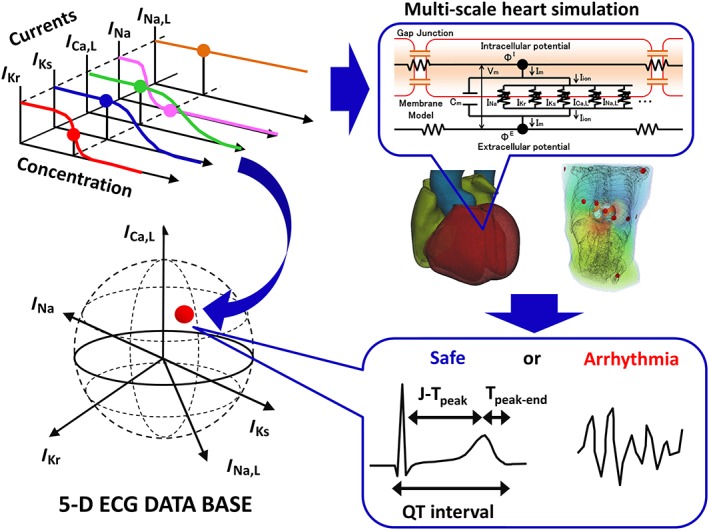
Method. Multiple ionic current‐blocking effects of drugs at each concentration (upper left) was mapped in a five‐dimensional space (lower left). For each point, multi‐scale heart simulation was performed (upper right) to produce a 12‐lead ECG, from which ECG indices or the occurrence of arrhythmia were determined (lower right).

Methods

The same finite element method (FEM) models of the human heart and torso and algorithms that were used in a previous study (Washio et al., 2010; Okada et al., 2011) were used for this study. The details of the model and algorithms are described in Supporting Information Data S1. These models were created from the multi‐detector CT images of a healthy adult volunteer and subdivided into 244 187 136 and 40 038 400 voxels for the heart and torso respectively (Washio et al., 2010; Okada et al., 2011; Okada et al., 2015). Cell models of human ventricular myocytes with different electrophysiological properties (endocardial, M and epicardial) (O'Hara et al., 2011) were implemented to the appropriate FEM node to reproduce the physiological tissue structure of the ventricular wall (Okada et al., 2011). To reproduce the physiological conduction velocity in myocardial tissue, the equations describing the kinetics of the m gate of the Na channel were replaced with those of Ten Tusscher et al. (2004) (similar modification was made in Sanchez‐Alonso et al., 2016). For the rest of the myocyte models, we used the equations and parameters of the original model. The conduction system, including the Purkinje network, was also modelled with specific electrophysiological properties (Stewart et al., 2009). The sites of interaction between the Purkinje network and myocardium (i.e. earliest activation sites) were adjusted to reproduce the normal morphology of QRS waves (Okada et al., 2011).

The following bidomain equations describing the propagation of excitation were solved using the parallel multilevel technique that we have developed (Washio et al., 2010).

$$\begin{array}{l}\mathrm{\beta }\left(C_m\frac{\partial V}{\partial t}+I_{\mathit{ion}}\right)=I_{\mathit{\text{stim}}}^E-\frac{\partial }{\partial x_i}\left(G_{\mathit{ij}}^E\frac{\partial {\varphi }^E}{\partial x_i}\right)\\ \mathrm{\beta }\left(C_m\frac{\partial V}{\partial t}+I_{\mathit{ion}}\right)=I_{\mathit{\text{stim}}}^I-\frac{\partial }{\partial x_i}\left(G_{\mathit{ij}}^I\frac{\partial {\varphi }^I}{\partial x_i}\right)\end{array}$$

where ${\varphi }^E$ and ${\varphi }^I$ are the extracellular and intracellular potentials, respectively; V= ϕ ^I−ϕ ^E is the transmembrane voltage; β is the surface‐to‐volume ratio of the tissue; Cm is the membrane capacitance; t is time; $G_{\mathrm{ij}}^E$ and $G_{\mathrm{ij}}^I$ are the intracellular and extracellular anisotropic conductivity tensors originating from the myocardial fibre structure; x_i and x_j are the tensor notations of the x, y and z coordinates; and I_ion is the sum of ionic transmembrane currents calculated by the human ventricular myocyte model of electrophysiology. Verification of the numerical method is shown in Supporting Information Data S1.

To save computational time, simulations were performed for a heart rate of 1 Hz using only the ventricles. As a preliminary test, we used a longer period, which revealed that, during regular beats with a constant R‐R interval, the system is stable even under the influence of drugs. Accordingly, we determined that a shorter simulation (five beats) could test as many cases as the longer simulation, taking into account the limited computational resource available. ECG indices including the QT interval, T_peak‐T_end and J‐Tpeak were measured in limb lead II of the simulated ECG (Figure 1). The occurrence of arrhythmias was first screened algorithmically by monitoring the deviations in the RR interval or changes in the amplitude of R waves. These observations were then confirmed visually using the ECG findings and the spiral waves in the heart model (Figure 3). In addition to the sustained reentry, we observed non‐sustained ventricular tachycardia in the marginal zone of arrhythmia risk. The extent of block by drugs for each ionic current at specific concentrations (x) was calculated using the following equation, with the concentration at 50% block (IC₅₀) and with a Hill constant (h) taken from the literature (Crumb Jr et al., 2016; Du et al., 2011; Okada et al., 2015).

$$\text{Extent\hspace{0.17em}of\hspace{0.17em}block}=\frac{{10}^{\left(\mathit{\text{logx}}‐{\mathit{\text{logIC}}}_{50}\right)h}}{1+{10}^{\left(\mathit{\text{logx}}‐{\mathit{\text{logIC}}}_{50}\right)h}}$$

Figure 3.

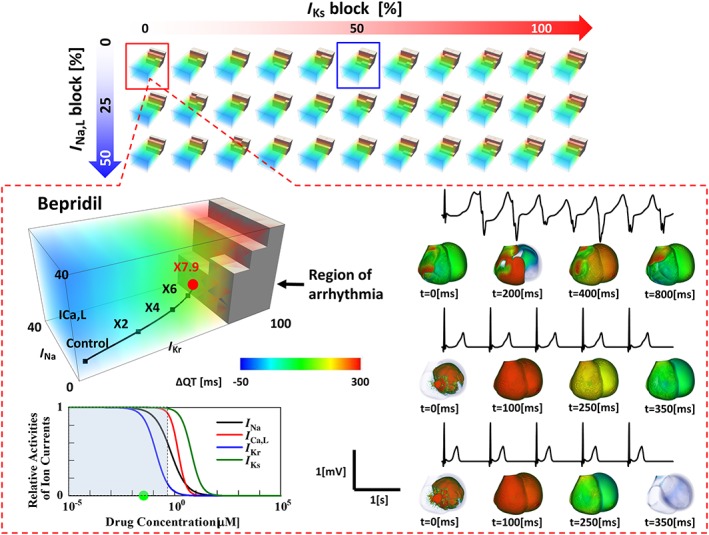
Five‐dimensional hazard map of drug‐induced arrhythmias. Top: Five‐dimensional data are visualized as a cluster of three‐dimensional subspace distributed in a plane with axes of I _Ks block and I _Na,L block. The coordinate system of subspace consists of the extent of block of I _Kr, I _Na and I _Ca,L. Bottom: In each subspace (in this case, I _Ks block = 0% and I _Na,L block = 0%), the dose‐dependent effect of the drug (bepridil) can be traced as a trajectory. The trajectories were generated by functions, and the numbers on them represent the drug concentrations expressed as multiples of ETPC_unbound. The region of arrhythmia is indicated as brown blocks. The inset shows the concentration–block relations of five ion currents. It demonstrates that virtually no inhibitory effects were observed for I _Ks or I _Na,L in the concentration ranges studied (shaded area). ECG changes at various concentrations are shown to the right with the corresponding activation sequence in the heart.

All program codes were written in‐house. They have been registered as intellectual property at the University of Tokyo and thus publicly unavailable.

Data availability

Numerical data are available at Figshare: https://figshare.com/s/dd2bcd2294cdde871066 (doi: https://doi.org/10.6084/m9.figshare.5946739). The data and statistical analysis comply with the recommendations on experimental design and analysis in pharmacology (Curtis et al., 2018).

Nomenclature of targets and ligands

Key protein targets and ligands in this article are hyperlinked to corresponding entries in http://www.guidetopharmacology.org/, the common portal for data from the IUPHAR/BPS Guide to PHARMACOLOGY (Harding et al., 2018), and are permanently archived in the Concise Guide to PHARMACOLOGY 2017/18 (Alexander et al., 2017).

Results

Validation of the model

The O'Hara–Rudy model of the human ventricular myocyte implemented in our heart model has already been validated against human ventricular action potential data (O'Hara et al., 2011; O'Hara and Rudy, 2012). Here, we show the validation at the organ level by comparing the drug‐induced changes in the QT interval predicted by our heart model with the ECG data of normal human subjects (Darpo et al., 2015). In Figure 2, we plotted the simulated and clinically obtained changes in the QT interval (∆QT) as a function of the drug concentrations for five test drugs. Raw data (ECG traces) of these plots can be seen in Supporting Information Figure S2.1. The IC₅₀ and Hill coefficient used for the analyses are shown in Supporting Information Table S2.1. Although we found some discrepancy for http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=2510, the overall simulated changes in the QT interval agreed well with the clinical data. Because the clinical evaluation of ΔQT was made by subtracting the time‐matched ΔQT of the placebo group, the solid lines representing the clinical results do not necessarily cross the origin. Part of the discrepancy between the simulation and clinical results could be attributable to this shift in intercept. Furthermore, uncertainty about the IC₅₀ and Hill coefficient values could be another source of discrepancy because the data used to determine these parameters are highly dependent on the experimental conditions including the voltage protocol (Colatsky et al., 2016). To test this hypothesis, we repeated simulations for quinine while varying the values of these parameters. As shown in Supporting Information Figure S2.2, relations between drug concentration and the QT interval (ΔQTcF) are sensitive to small variations in these two parameters. Good agreement was obtained by changing the IC₅₀ and Hill coefficient by only 10%. These results suggest the importance of standardizing patch clamp protocols for drug screening.

Figure 2.

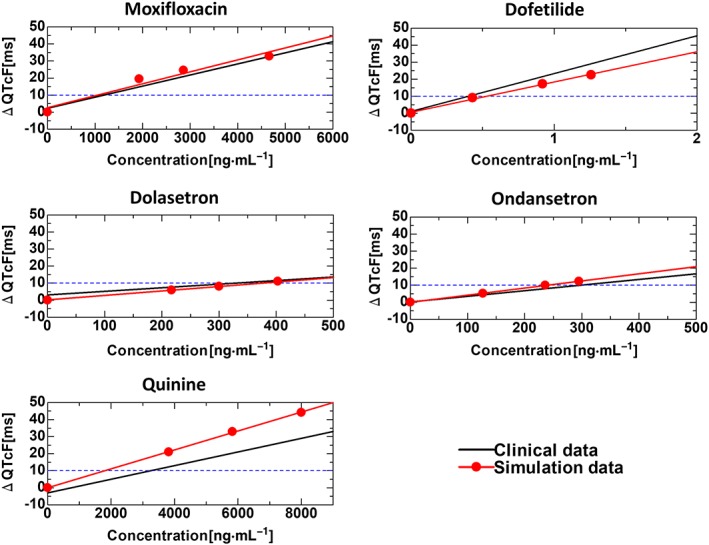
Organ‐level validation of the model. Electrophysiological response of the model was validated against the ECG data of normal human subjects. For five of the test drugs, concentration‐dependent changes in QT intervals (ΔQT) calculated using the model were compared with those from published reports (Darpo et al., 2015). The IC₅₀ and Hill coefficient values for each drug are listed in Supporting Information Table S2.1).

Hazard map

Parallel computing on a K‐computer allowed us to perform 9075 patterns of electrophysiological simulations in 72 600 000 core hours. Because we could not find a method to show a five‐dimensional map in a single panel, we visualized the results in a five‐dimensional presentation composed of three‐dimensional subspaces, in which regions of arrhythmia were superimposed with the QT interval distribution. The selection of the three coordinates in each subspace differed depending on the evaluated drugs based on the following criteria. (i) If three ion currents were affected by the drug, we adopted these ion currents for coordinates. If there were fewer than three, we arbitrarily selected another ion current as the remaining coordinate. (ii) If more than three ion currents were affected, we selected the three most affected ion currents in the concentration range studied. In either case, the statuses of the remaining two currents are parametrically presented by their inhibition rates at the final concentration evaluated. To clearly demonstrate the rationale for selecting the coordinates in each figure, we also showed the concentration–inhibition relation of ion currents for each drug and shaded the range of concentration studied. In each subspace, we clearly observed the region of long QT surrounding the region of arrhythmia, whose margins were modulated by the relative contributions of the three ion currents. Because the concentration–block relationship of each drug was traceable along a trajectory in these spaces, we were able to evaluate ECG changes and arrhythmogenicity (Figure 3) (see Supporting Information Movie S1). Although we computed the 12‐lead ECG for all patterns, only the second limb lead is shown in Figure 3 because of space limitation. The 12‐lead ECGs in Figure 3 are shown in Supporting Information Figure S2.3. The 12‐lead ECGs computed for 9075 patterns will be presented on our website.

We evaluated 26 drugs (Supporting Information Figures 2.4–2.29), for which the IC₅₀ and Hill coefficient of inhibition for five ion currents are available (see Supporting Information Table S2.1 for parameters and references). We attempted to match the results with the risk categories proposed by the Comprehensive Proarrhythmia Assay (CiPA) (Gintant et al., 2016), Redfern et al. (2003), and the QT drug list of CredibleMeds (Woosley et al. [www.CredibleMeds.org]) (Table 1). Among the 13 drugs categorized according to the CiPA, we observed arrhythmias in 4/4 for high‐risk drugs, 4/5 for intermediate‐risk drugs and 0/4 for low‐risk drugs. Among the 16 drugs categorized by Redfern et al., we observed arrhythmias in 3/4 for category 1 (repolarization‐prolonging antiarrhythmic drugs), 4/4 for category 2 (drugs that have been withdrawn or suspended from the market in at least one major regulatory territory due to an unexpected risk of TdP for the condition being treated), 2/2 for category 3 (drugs that have a measurable incidence of TdP in humans or for which numerous case reports exist in the published literature), 0/3 for category 4 (drugs for which there have been isolated reports of TdP in humans) and 1/3 for category 5 (drugs for which there have been no published reports of TdP in humans). Among the 19 drugs categorized by CredibleMeds, we observed arrhythmias in 11/13 for drugs of known risk of TdP, 0/3 for drugs of conditional risk of TdP and 3/3 for drugs of possible risk of TdP. For another seven drugs not in the CredibleMeds list (presumably no‐risk drugs), we observed arrhythmia with only one. In general, the results of simulations agreed well with these risk assessments but were contradictory for some drugs, on which we have some comments. First, in the categorization by Redfern et al., http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=2566 is in category 1, but its incidence of TdP in a clinical trial was quite low (Darpo, 2001). Lawrence et al. (2006) excluded it from the list of category 1 drugs. Second, cibenzoline was categorized as 5 by Redfern et al. and not listed in CredibleMeds, but cases of drug‐induced arrhythmias have been reported with it (De Bruin et al., 2005). http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=83 is reported to be a drug of known risk of TdP in the CredibleMeds risk assessment, but it was judged safe based on the current database. In addition to blocking I _Na, I _Na,L, I _Ca,L and I _Kr, chlorpromazine is known to inhibit the ACh‐mediated potassium current (I _KAch) and the ATP‐sensitive potassium current (I _KATP) (Muller et al., 1991; Okada et al., 2013b), neither of which is implemented in the O'Hara model. The effect of chlorpromazine on these ion currents may lead to arrhythmogenesis. Furthermore, considering that chlorpromazine is classified as an intermediate‐risk drug by CiPA, the occurrence of arrhythmia induced by this drug may require particular conditions.

Table 1.

Risk category of benchmark drugs

Drug name	CiPA risk (Gintant et al., 2016)	Redfern risk (Redfern et al., 2003)	CredibleMeds (Woosley et al. [http://www.CredibleMeds.org])	Prediction by database	Threshold concentration relative to ETPCunbound
Quinidine	High	1	Known risk of TdP	Arrhythmia	0.6
Dofetilide	High	1	Known risk of TdP	Arrhythmia	21.0
Bepridil	High	3	Known risk of TdP	Arrhythmia	7.9
dl‐Sotalol	High	1	Known risk of TdP	Arrhythmia	71
Terfenadine	Intermediate	2	Known risk of TdP	Arrhythmia	865.7
Ondansetron	Intermediate	–	Known risk of TdP	Arrhythmia	23.6
Cisapride	Intermediate	2	Known risk of TdP	Arrhythmia	13
Chlorpromazine	Intermediate	–	Known risk of TdP	Safe	–
Astemizole	Intermediate	2	Known TdP risk	Arrhythmia	182
Ranolazine	Low	–	Conditional risk of TdP	Safe	–
Verapamil	Low	5	–	Safe	–
Mexiletine	Low	–	–	Safe	–
Diltiazem	Low	5	–	Safe	–
Flecainide	–	3	Known risk of TdP	Arrhythmia	3.7
Nilotinib	–	–	Possible TdP risk	Arrhythmia	6.0
Cibenzoline	–	5	–	Arrhythmia	10.6
Sertindole	–	2	Possible TdP risk	Arrhythmia	27.2
Chloroquine	–	–	Known risk of TdP	Arrhythmia	172.4
Moxifloxacin	–	–	Known risk of TdP	Arrhythmia	73.3
Amiodarone	–	1	Known risk of TdP	Safe	–
Amitriptyline	–	4	–	Safe	–
Mibefradil	–	4	–	Safe	–
Propafenone	–	4	–	Safe	–
Quinine	–	–	Conditional risk of TdP	Safe	–
Ritonavir	–	–	Conditional risk of TdP	Safe	–
Saquinavir	–	–	Possible TdP risk	Safe	–

A total of 26 benchmark drugs are listed with their risk categories reported by three independent sources. Predictions made by the current hazard map are shown in columns 5 and 6 along with the threshold concentrations for arrhythmia occurrence. The IC₅₀ and Hill coefficient for each drug are listed in Supporting Information Table S2.1 with their sources.

Finally, we did not observe arrhythmias for three drugs considered to be at conditional risk of TdP by CredibleMeds ‐ quinine, http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=8804, http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=4813 (Woosley et al. [www.CredibleMeds.org]). The precipitating condition for quinine is reported to be hypokalemia. Accordingly, we performed the simulation under a hypokalemic condition (extracellular K⁺ = 2.5 mM) to observe for arrhythmias at 5 times the effective therapeutic plasma concentration (ETPC_unbound). Hypokalemia lowered the arrhythmia threshold of high‐risk drug http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=2604 (Supporting Information Figure S2.30). Ritonavir and saquinavir are classified as drugs with conditional risk of TdP because they reduce the elimination of drugs known to affect QT and induce TdP. These anti‐viral drugs are known to inhibit major isoforms of cytochrome P450 (e.g. http://www.guidetopharmacology.org/GRAC/ObjectDisplayForward?objectId=1337, http://www.guidetopharmacology.org/GRAC/ObjectDisplayForward?objectId=1329), which metabolize many arrhythmogenic drugs, including http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=2342 and http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=2337 (Eagling et al., 1997). Accordingly, the arrhythmogenic risk of ritonavir and saquinavir can be better understood by looking at the effect of quinidine or bepridil at high concentrations rather than evaluating their direct inhibition of the ion current.

Visualization of drug effects in multi‐dimensional spaces provides insight into how interactions among ionic currents affect the arrhythmogenicity and suggests further applications of this database. We compared the concentration–block trajectories of two arrhythmogenic drugs (http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=2608 and quinidine) and a non‐arrhythmogenic drug (amiodarone) obtained from the literature (Darpo, 2001; Redfern et al., 2003; Okada et al., 2015). As shown in Figure 4A (extent of block; I _Na,L = 0, I _Ks = 0, red square in Figure 3), Block of I _Kr strongly attracted the trajectories of quinidine and terfenadine to the region of arrhythmia, whereas concomitant potent block of I _Ca,L appeared to oppose the I _Kr block and to cause amiodarone to remain in the safe region, even at a high concentration. We also observed that the trajectory of quinidine entered the region of arrhythmia at an intermediate concentration (1.94 μM), but it reappeared in the safe region at a higher concentration (4.86 μM). This finding appeared to be consistent with the clinical observation that arrhythmia events occur more frequently at lower concentrations of quinidine (Roden et al., 1986).

Figure 4.

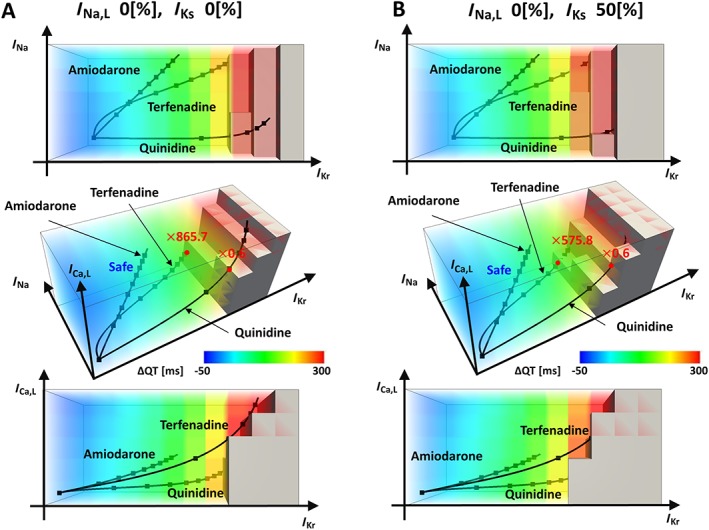
Visualization of drug effects in a hazard map. In each panel, orthogonal projections are shown with a 3D hazard map. (A) Concentration–block relationships of terfenadine, quinidine and amiodarone are shown as trajectories in a subspace at I _Na,L block = 0% and I _Ks block = 0%. (B) Concentration–block relationships of terfenadine, quinidine and amiodarone are shown as trajectories in a subspace at I _Na,L block = 0% and I _Ks block = 50%.

Ionic current blocks are also induced by genetic disorders. Polymorphisms in the gene encoding the I _Ks channel (http://www.guidetopharmacology.org/GRAC/ObjectDisplayForward?objectId=560 are found in Asian populations and sometimes impair the intrinsic current (Kubota et al., 2001). We simulated such a condition in Figure 4B (blue square in Figure 3), in which a 50% reduction of I _Ks channels induced changes in the threshold of arrhythmia for terfenadine (0.252 to 0.167 μM) and in the arrhythmogenicity of quinidine at higher concentrations. This type of information may help doctors customize prescriptions.

The arrhythmogenic risk of a drug can be modified by altering the pharmacological spectrum for currents or co‐administration of specific ionic current blockers. In Figure 5A, we gradually added an inhibitory effect on I _Ca,L to quinidine to ultimately make it a safe drug. The distance between these trajectories and the region of arrhythmia in the multi‐dimensional space can be considered as the safety margin, which varies depending on the condition of individuals. Finally, the significance of I _Na,L in proarrhythmia has been recognized recently, and ranolazine, despite its I _Kr blocking effect, is used as an antiarrhythmic agent (Vicente et al., 2015). To determine how the activities of I _Na,L and I _Kr interact, we observed a subspace with I _Na,L, I _Kr and I_Ca,L coordinates while setting the block of I _Ks and I _Na at 0% (Figure 5B). In clear contrast to quinidine, the trajectory of the ranolazine concentration–block relationship produced a dramatic change with increasing I _Na,L block, thus avoiding arrhythmias. We also found that the arrhythmogenicity of quinidine was also influenced by I _Na,L block.

Figure 5.

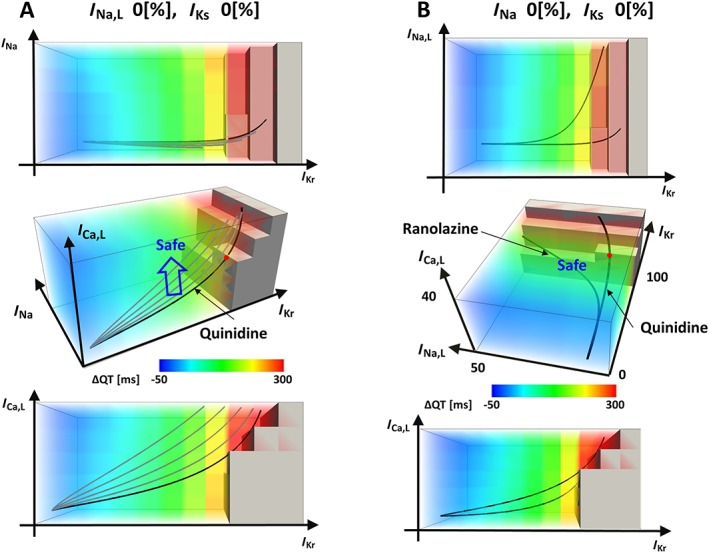
Visualizations of drug effects in hazard map. In each panel, orthogonal projections are shown with a 3D hazard map. (A) Concentration–block relationships of quinidine in a subspace at I _Na,L block = 0% and I _Ks block = 0% are shown. From the original trajectory (thick line), the effect of I _Ca,L block was added gradually to shift the trajectory (blue arrow). (B) The effect of I _Na,L block was visualized for quinidine and ranolazine in a subspace with I _Ca,L, I _Kr and I _Na,L coordinates (I _Na block = 0% and I _Ks block = 0%).

ECG indices for risk assessment

Even in the new paradigm for cardiotoxicity testing, the examination of human ECGs remains a major component. Thus, several ECG indices have been evaluated to determine their utility (Johannesen et al., 2014a; Johannesen et al., 2014b; Sugrue et al., 2015; Vicente et al., 2015; Gintant et al., 2016). In Figure 6A, the occurrence of arrhythmia at each combinatorial state of five ion currents was shown via prolongations of the QT interval, J‐T_peak and T_peak‐T_end. Because these ECG indices could not be determined if arrhythmia developed, the colour codes for these indices were made blank for arrhythmia cases. When I _Kr was extensively blocked, that is, 90–100%, the occurrence of arrhythmia was inevitable, thus demonstrating the strong influence of this ion current. We also found that the strong block of other ionic currents did not induce arrhythmia without moderate to severe I _Kr block. However, in the intermediate range of I _Kr block, the occurrence of arrhythmia was influenced by the activities of other ionic currents in a complex manner. To examine how closely these ECG indices are linked to arrhythmogenicity, we applied a logistic regression analysis to the arrhythmogenicity data, with the extent of the block of each current as a predictor variable, and compared the results with those of multiple linear regression analyses of the QT interval, T_peak‐T_end and J‐T_peak (for details, see Supporting Information Tables S2.2 and 2.3). As shown in Figure 6B, coefficients for regression representing the contribution of each ionic current to arrhythmogenic risk or ECG indices varied not only in their magnitude but also in their signs (plus: facilitatory, minus: inhibitory). However, most notably, the signs of all coefficients were consistent with those of arrhythmogenicity only for J‐T_peak, thus suggesting that similar ionic mechanisms underlie the prolongation of J‐T_peak and arrhythmogenesis. The present results are consistent with those from a recent clinical study demonstrating the superiority of this index in detecting the multi‐channel effect (Johannesen et al., 2014b). We compared the drug induced changes in APD (ΔAPD), QT interval and J‐T_peak for thirteen CiPA test drugs at their IC₅₀ of I _Kr, except for http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=2629 and http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=2298, for which these indices were evaluated at IC₅₀ of I _Na,L and I _Ca,L, respectively, because the effect on I _Kr is absent or present only at very high concentration (Table 2). Drugs categorized as high or intermediate risk are potent I I _Kr blockers and we could not discriminate their risks using either QT interval or J‐T_peak interval. However, for terfenadine with comparable IC₅₀ values for I _Na, I _Ca,L and I _Kr, QT interval was longer than any of the high risk drugs but J‐T_peak was definitely shorter thus accurately reflecting the arrhythmogenic risk. In addition to the ECG indices evaluated in this study, such as QT, T_peak‐T_end and J‐T_peak intervals, the short‐term variability of QT intervals correlated with arrhythmogenicity (Thomsen et al., 2004; Lengyel et al., 2007; Hinterseer et al., 2009; Hinterseer et al., 2010). However, the limitation in the computational resource did not allow us to simulate the number of beats required for this analysis. On the other hand, whereas hERG block showed a predominant effect on QT interval prolongation, the risk of arrhythmia was significantly decreased by I _Ca,L block. Such differing roles of ionic currents may have been the cause of the false positives observed in the QT study.

Figure 6.

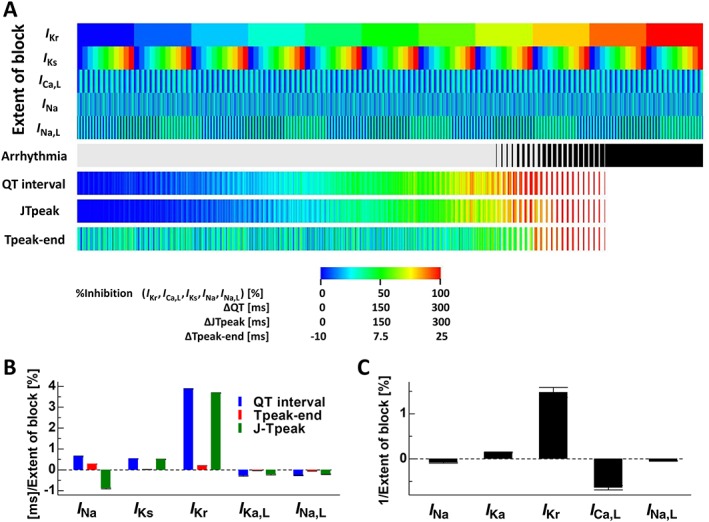
Effects of multiple ionic current blocks on arrhythmogenicity and ECG indices. (A) In the five rows at the top, the extent of block of I _Kr, I _Ks, I _Ca,L, I _Na and I _Na,L is shown in colour. For each combination of ionic current block, the occurrence of arrhythmia is indicated in black (6th row). Prolongations of the QT interval (ΔQT, 7th row), J‐T_peak (ΔJ‐T_peak, 8th row) and T_peak‐T_end (ΔT_peak‐T_end, 9th row) are shown in colour. Colour codes are summarized in the bottom legend. (B) Coefficients of linear regression applied to changes in QT interval, T_peak‐T_end and J‐T_peak. (C) Coefficients of logistic regression applied to the relationship between the occurrence of arrhythmia and ionic current block.

Table 2.

Changes in electrophysiological parameters. For 13 CiPA benchmark drugs, risk categories are shown with changes in APD₉₀ (ΔAPD₉₀), J‐T_peak interval and QT interval observed at IC₅₀ of http://www.guidetopharmacology.org/GRAC/ObjectDisplayForward?objectId=572. Mexiletine and diltiazem were evaluated at IC₅₀ of I _Na,L and I _Ca,L respectively. Further details can be found in Supporting Information Table S2.1.

Drug name	CiPA risk (Gintant et al. 2016)	I Na IC50[μM]	I Ca,L IC50[μM]	I Kr IC50[μM]	I KsIC50 [μM]	I Na,L IC50[μM]	ETPCunbound[μM]	ΔAPD90 [ms]	QT [ms]	JTpeak [ms]
Quinidine	High	24.79	7.731	0.6377	73.33	‐	3.235	88.580	471	356
Dofetildie	High	124.5	184	0.0098	‐	‐	0.0016	92.645	476	361
Bepridil	High	0.6465	1.455	0.1302	6.0312	‐	0.03463	96.815	478	359
dl‐Sotalol	High	‐	‐	356.4	‐	‐	14.68	93.460	477	359
Terfenadine	Intermediate	0.4798	0.8615	0.0985	‐	‐	0.00029	118.725	484	347
Ondansetron	Intermediate	‐	22.551	1.492	‐	19.181	0.3585	88.660	466	355
Cisapride	Intermediate	2.072	4.278	0.0147	‐	‐	0.002579	92.690	476	361
Chlorpromazine	Intermediate	4.536	8.192	1.118	‐	4.56	0.0345	91.150	474	357
Astemizol	Intermediate	1.862	0.9878	0.0281	‐	‐	0.0002878	92.845	476	361
Ranolazine	Low	41.08	118.3	3.927	‐	26.26	2.31	93.295	474	356
Verapamil	Low	4.272	0.3331	0.2013	29.88	‐	0.08797	89.125	452	344
Mexiletine	Low	‐	‐	‐	‐	8.957	2.5032	‐1.710	342	231
Diltiazem	Low	‐	0.112	6.569	‐	‐	0.1275	33.375	330	230

Discussion

To decrease the growing costs of drug discovery, which now threaten world health care by limiting the development of innovative new drugs, the utilization of in silico technologies is encouraged in all stages of R&D. Given the complex nature of arrhythmogenicity, multi‐scale heart simulations associating events at molecular levels with organ‐level electrophysiology would undoubtedly add to the predictability of in silico cardiotoxicity testing. Furthermore, for comparisons with human ECG testing, a solution of bidomain equations of excitation propagation with a realistic torso model is essential. In our attempts to overcome the technical challenge of the huge computational demand (Zemzemi et al., 2013; Sadrieh et al., 2014), we have developed a reliable in silico screening system for cardiotoxicity (Okada et al., 2015).

In the present study, the power of a super computer extended our approach and allowed us to create an exhaustive database of arrhythmogenic risk based on multi‐current activities. Large‐scale, physics‐based simulations have been applied to the development of hazard maps of natural disasters such as earthquakes and floods. To our knowledge, however, this is the first application of such a simulation in biomedicine. We recognize that studies using a single‐cell model of electrophysiology have reported excellent risk prediction (Mirams et al., 2011; Dutta et al., 2017), but comparisons with the clinical data (Figure 2), evaluation of various ECG indices (Figure 6) and examinations of heart morphology (Supporting Information Figure S2.32) can be made only with the multi‐scale simulation. We are aware of those studies examining the ECG changes using one‐dimensional models in which transmural distribution of different cell species – that is, endocardial, mid‐myocardial and epicardial cells – are reproduced (Bottino et al., 2006; Suzuki et al., 2008). In our previous study (Okada et al., 2011), however, we found that not only transmural but also apicobasal, gradients of action potential duration (APD) contributed to physiological T‐wave morphology. This finding is in accord with the clinical study reporting the apicobasal distribution of potassium channels in the human ventricle (Szentadrassy et al., 2005) and suggests the need for a 3D ventricular model for the detailed analysis of ECG indices.

Heart model

To simulate cardiac electrophysiology, not only fibre orientation but also the distribution of cells having different APDs was reproduced in our heart model. The functional role of M‐cells in intact hearts remains a matter of debate (Nattel et al., 2010), and we have tried to resolve the problem using our simulation model. In our previous study (Okada et al., 2011), we exhaustively researched the relation between T‐wave morphology and the distribution of APD and found that only a combination of the transmural gradient (with M‐cells on the endocardial side) and moderate apicobasal gradients produced physiological T waves. Simulated transmural distribution of the APD was similar to that measured in the ventricular wedge preparation from non‐failing human heart (Glukhov et al., 2010), reflecting the transmural expression of potassium channels already described (Soltysinska et al., 2009). The apicobasal APD gradient was also consistent with the heterogeneity of expression levels of potassium ion channels in normal human ventricular myocardium (Szentadrassy et al., 2005). With regard to arrhythmogenesis, in our previous study, we showed that if the entire wall is made up of endocardial, epicardial or M‐cells, we did not observe arrhythmia at up to 10 times the ETPC_unbound of quinidine, whereas we did see arrhythmia at 5 times the ETPC_unbound with the model that included three cell types (Okada et al., 2015). In addition to these observations, we tested cases where the region of M‐cells was increased (from 20 to 70% of the wall volume from the endocardial side (Supporting Information Figure S2.31A‐b), decreased (from 20 to 58% of the wall volume from the endocardial side (Supporting Information Figure S2.31A‐c) or eliminated (Supporting Information Figure S2.31A‐d) from our standard model (from 20 to 64% of the wall volume of the endocardial side (Supporting Information Figure S2.31A‐a). In the case without M‐cells, endocardial cells occupy 0–64% of the wall volume from the endocardial side, and epicardial cells occupy the rest, thus resembling the APD distribution of the classic concept. We found that whereas the alteration of the thickness of M‐cell region only slightly changed the threshold for arrhythmia compared to our standard distribution (Supporting Information Figure S2.31A‐a), the absence of the M‐cells prevented arrhythmias, in spite of the transmural APD gradient. In addition to the role in initiation of arrhythmia by producing early after‐depolarization (EAD), M‐cells may contribute to the evolution of sustained arrhythmia. To test this hypothesis, we applied extra‐stimulus to the right ventricular outflow in models with (Supporting Information Figure S2.31 A‐a) and without, M‐cells (Supporting Information Figure S2.3.1A‐d) and found that sustained arrhythmia was observed only in the model with M‐cells (Supporting Information Figure S2.31B). Altogether, our simulation results suggested that M‐cells located near the endocardium play an essential role in drug‐induced arrhythmia.

This study was intended to assess drug effects in healthy subjects, but the sizes of the heart and body (torso) vary even among healthy subjects, thus potentially influencing the simulation results. Because the torso is a passive conductor, its size and shape do not affect the electrophysiology of the heart. However, detailed analyses of the QT interval and T‐wave morphology, such as T‐peak/T‐end, are possible only with the torso. Regarding heart geometry, we expect that a pathologically dilated or hypertrophied heart with its histological alterations (e.g. fibrosis) and changes in the expression level of ion channels may affect the geometry (Aiba et al., 2010), but analyses of diseased hearts are beyond the scope of this study. We tested the effect of variations in heart size on the effectiveness of three test drugs categorized as high‐risk (bepridil), intermediate‐risk (http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=240) and low‐risk (http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=2406) agents by scaling the model heart to either 80 or 120% of normal while using the same torso model. Although the amplitudes of the ECG waves changed depending on the heart size, changes in heart morphology did not affect the risk assessment, at least within the range tested (Supporting Information Figure S2.32). We also noted that the larger heart caused slight prolongation of the QT interval, but it was mainly due to widening of the QRS complex. The athlete's heart is larger than other normal hearts but has normal function and is thus considered a model for pure morphological changes. According to a recent review on the athlete's heart, although some athletes have abnormal ECG findings, including high voltage, inverted T‐waves, axis deviation, first degree atrioventricular block and QRS prolongation, most arrhythmias on the athletic field are due to undetected structural defects or channelopathies (Walker et al., 2010). These findings are concordant with the current simulation results.

Risk prediction

Theoretically, threshold concentrations obtained for 26 benchmark drugs should reflect the risk level of each drug, but they varied over a wide range. For example, the threshold for terfenadine was 865.7 times ETPC_unbound, a value rarely encountered in the clinical setting. We must note, however, that the electrophysiology of cardiac myocytes is influenced by the tissue concentration of the drug, which is often different from its concentration in circulating plasma. In an experimental study using guinea pigs, Katagi et al. reported that the heart/plasma concentration ratio of terfenadine is about 50 (Katagi et al., 2016). If we assume that the threshold concentration obtained from the current database reflects the tissue concentration, the corresponding plasma concentration would be about 17 times ETPC_unbound. Similarly, heart/plasma concentration ratios in that report estimated the threshold plasma concentration at 28 and 24 times ETPC_unbound for http://www.guidetopharmacology.org/GRAC/LigandDisplayForward?ligandId=7297 and moxifloxacin respectively. However, we admit that such increases in tissue concentration may only reflect the effect of non‐specific binding and not necessarily indicate the greater availability of molecules to the HERG channel. In addition to such pharmacological and physiological issues, other potential reasons may explain the mismatch between the currently obtained threshold concentration and risk level. First, as discussed in the Results section, the ionic current measurements used to determine the IC₅₀ and Hill coefficient vary depending on the experimental conditions and the standardization of the protocol, which is currently a subject of ongoing discussion (Colatsky et al., 2016). In fact, in the case of terfenadine, IC₅₀ values reported in the literature vary over two orders of magnitude (Supporting Information Table S2.4). For instance, if we use the lower value with the concomitant Hill coefficient reported by Friemel's group (2010) instead of those currently used by Okada et al. (2015), the terfenadine concentration at 90% current inhibition goes down to 0.19 μM from the current value of 0.62 μM. To avoid variations in experimental protocol in this study, we adopted the values from papers in which five ionic channels were assayed for many drugs. Second, the problem with the risk categorization also must be taken into consideration. Three lists of risk categories to which we referred in this study assessed the arrhythmogenic risk based on the number or presence of incidence reports – we did not quantitatively analyse the probability of arrhythmogenic events. In a study of a cohort of 197 425 persons using non‐sedating antihistamine drugs, de Abajo et al. found three cases of ventricular arrhythmia among those taking terfenadine. Because of the huge number of prescriptions of this drug, however, the relative risk of terfenadine did not differ from that of other drugs (de Abajo and Rodriguez, 1999). We understand the difficulty associated with intensively assessing every case of arrhythmia that occurs in the real world, but quantitative information on the arrhythmogenic risk of these drugs is critical.

To date, a variety of indices have been proposed for predicting arrhythmogenic risk. Kramer et al. (2013) showed that the use of log(I _Kr IC₅₀/ I _Ca,L IC₅₀) values significantly reduced the number of false‐positive and false‐negative results compared with the hERG assay of 55 test drugs (MICE model). Mirams et al. (2011) reported an accurate classification of torsade‐genic risk by assessing the changes in APD at 90% repolarization (∆APD90) obtained in a single‐cell model of electrophysiology developed by Grandi et al. (2010). We compared the performance of our database with these methods using 13 CiPA test drugs (Table 1). We defined CiPA classifications high and intermediate as TdP(+) and low as TdP(−). For the MICE model, dl‐sotalol and mexiletine were eliminated from the analysis because no significant blocking effect on I _Ca,L was reported. For the Mirams et al. method, we used the Grandi model for 1000 beats under ETPC_unbound of test drugs. The calculated values of these indices are shown in Supporting Information Table S2.5A. We performed ROC analyses for these three methods, including the current database, and calculated the sensitivity, specificity and accuracy for each (Supporting Information Table 2.5B, C, and D). As summarized in Supporting Information Table S2.5, the current database yielded comparable or better results at least for the 13 CiPA test drugs.

Study limitations

Even with more than 9000 patterns of multi‐scale heart simulations achieved by the available computational resources, we could not cover the entire space of the five‐dimensional hazard map. Accordingly, we selected the range of the block for each ion current based on the following reasons. First, the two potassium currents, I _Kr and I _Ks, were studied over the entire range because of their importance in pro‐arrhythmic risk assessment and potent effects on the APD. Second, I _Na block was studied up to 40% because the propagation of excitation in the myocardial tissue was inhibited above this range. Third, in addition to proarrhythmic propensity, the significant negative inotropic effect introduced by the higher degree of I _Ca,L current block is in itself a serious side effect (Ezzaher et al., 1991) and could be a cause of compound attrition – which is why we limited the range of I _Ca,L inhibition to 40%. (iv) Finally, we tested the effect of I _Na,L block at only three levels, because, to date, neither specific inhibitors of I _Na,L nor detailed examinations of its effect on cardiac electrophysiology have been reported. We are planning to fill the remaining vacant spaces, which may contain useful information, during a future simulation study.

Our heart model can reproduce and evaluate the drug effect on gating kinetics of ion channels because the O'Hara–Rudy model of the human ventricular myocyte that we have used, has been validated with ionic current data. However, only the ion current block represented by the change in conductance was taken into account in this study because experimental collection of kinetic data is costly and time‐consuming. Hence, it is rarely used to screen new compounds. Similarly, inclusion of additional ionic currents into the database would augment the reliability of risk assessment. We could evaluate only the five ionic currents in this study even with the computational power of the K‐computer, but the effects of a compound may extend beyond these ionic currents. Further studies dealing with additional ion channels and detailed gating kinetics would surely augment the reliability of our database.

Because of limited computational resources, we simulated only five beats for each case. Studies using a single‐cell model repeated the simulation for 1000 cycles to reach steady state (Dutta et al., 2017). Also, using a ventricular model, Sadriegh et al. showed that the convergence of T‐wave morphology requires more than 100 beats (Sadrieh et al., 2014). In light of these studies, five beats of simulation for each case is not enough to reach steady state, and therefore, the current results may remain at a proof‐of‐concept stage. To have an idea of the number of beats appropriate for assessing arrhythmogenicity, we ran the O'Hara Rudy model for 1000 beats under ETPC_unbound for 13 test drugs. As shown in Supporting Information Figure S2.33, the APDs converged quite rapidly, except for quinidine and diltiazem. Even for these two drugs, however, the APDs reached within 1% of steady‐state values at around 300 beats. We also noted that, at five beats, the APDs were within 2% of steady‐state values for all the test drugs (Supporting Information Figure S2.33B, inset). Although evaluations were made only at ETPC_unbound, these results suggest that the evaluation of arrhythmogenicity is acceptable before reaching steady state (quasi‐steady state). In fact, in recent studies using single‐cell models (Dutta et al., 2017; Kurata et al., 2017), the authors examined the occurrence of EAD at fewer than 1000 beats (quasi‐steady state). Duttas et al. found a strong correlation between their metrics of arrhythmogenicity (net charge constituting the net current during the stimulated beat) analysed at 1000 beats, and the I _Kr reduction threshold for the induction of EAD checked at 100 beats (Dutta et al., 2017). Similarly, Kurata et al. evaluated the occurrence of EAD with 0.5–1.0 min of calculation, whereas they required 5–30 min to achieve steady state. Those numbers are in accordance with the observation by Sadrieh et al. (2014). Taking all these data together, we believe that 100–200 beats are necessary to evaluate arrhythmogenic risk in pharmaceutical research. We hope that the next generation of super‐computers will enable us to create a database based on the simulations of more than 100 beats for each case.

In conclusion, although it required more than 4 days to complete the database by fully using a K‐computer (72 600 000 core hours), the post‐K‐computer project is already underway, and a machine that is 100 times faster will be available in 2020. Therefore, in the near future, the same scale of database may be created in an hour of operation.

This database will be freely available at http://ut-heart.com/. Thus, it can be used not only to assess the risk of drug candidates at any stage of R&D but also to serve as a tool to design a safe drug without resorting to animal or clinical studies. Therefore, this database may constitute a high‐throughput and cost‐saving approach in toxicology (Hamburg, 2011).

Author contributions

J.O., T.Y., J.K, T.F. K.S, S.S. and T.H designed the study and conducted the analysis. J.O., T.W. and T.H. wrote program codes and performed the computations. T.Y., J.K, T.F. and K.S consulted on the study and participated in its design. J.O., S.S. and T.H. wrote the paper.

Conflict of interest

The authors declare no conflicts of interest.

Declaration of transparency and scientific rigour

This http://onlinelibrary.wiley.com/doi/10.1111/bph.13405/abstract acknowledges that this paper adheres to the principles for transparent reporting and scientific rigour of preclinical research recommended by funding agencies, publishers and other organisations engaged with supporting research.

Supporting information

Movie S1 Evaluation of drug effects in a three‐dimensional subspace. Activation sequences in the heart, body surface potential maps, and corresponding electrocardiograms (ECG) are shown at various points along the trajectory representing the concentration‐block relations of bepridil. Concentrations are indicated as multiples of the effective therapeutic plasma concentration (ETPC_unbound).

Figure S1.1 Heart and torso models. A: Morphology of the ventricular model. B: Fiber orientation. Color indicates angles relative to the equatorial plane. C: Transmural distribution of endocardial cells (green), M‐cells (red), and epicardial cells (blue). D: Conduction system. E: Earliest activation sites, where the Purkinje system is coupled to the myocardium (white dots), and activation sequences are seen from the anterior wall (top panel) and posterior wall (bottom panel). Color indicates the local activation time. F: Torso model: body surface with electrocardiographic electrodes (top panel) and major organs (bottom panel).

Figure S1.2 Domains in the model. H: heart domain; B: blood domain; T: tissue domain. ∂H: boundary of heart domain; ∂B: boundary of blood domain; ∂T: boundary of tissue domain.

Figure S1.3 Algorithm for calculating the propagation of excitation and ECG.

Figure S1.4 Tissue models used for verification. A: Top: Model used for the B‐3D problem, Ω: tissue domain. Bottom: Model used for the BB‐3D* problem, Ω: tissue domain; Ω_b: bath domain. Numbers next to the double‐headed arrow indicate size (in mm). B: Tissue model used for the N‐version strategy. S: subdomain for application of stimulation. Numbers next to the double‐headed arrow indicate size (in mm).

Figure S1.5 Verification using the B 3D problem. A: Distribution of the membrane potential (V: left) and extracellular potential (∅_e : right) at the end time (T=1) were compared between simulation results (FE analysis) and exact solutions. B: Errors in membrane potential (V: left) and extracellular potential (∅_e : right) evaluated by the L² spatial norm (red line) and the Soblev H¹ spatial norm (black line) are plotted as functions of the spatial resolution.

Figure S1.6 Verification using the BB 3D* problem. A: Distribution of the membrane potential (V: left) and extracellular potential (∅_e : right) at the end time (T=1) were compared between simulation results (FE analysis) and exact solutions. B: Errors in the membrane potential (V: left) and extracellular potential (∅_e : right) evaluated by the L² spatial norm (red line) and Soblev H¹ spatial norm (black line) are plotted as functions of the spatial resolution.

Figure S1.7 Verification using the N‐version strategy. A: Local activation times simulated with three spatial resolutions (∆x = 0.5 mm, blue line; 0.2 mm, green line; 0.1 mm, red line) are plotted as a function of the distance from the stimulation point. B: Activation time at the end point was simulated using different time steps and spatial resolutions.

Table S1.1 Tissue conductivity.

Table S1.2 Model parameters.

Table S1.3 Definition of the model.

Table S1.4 Definition of the model used for the N‐version benchmark test.

Table S1.5 Model parameters for the N‐version benchmark test.

Table S1.6 Initial state variables of the cell model for the N‐version benchmark test.

Figure S2.1 Effects of drugs on the electrocardiogram at low concentrations. Dose‐dependent changes in QT intervals are shown for five drugs (also plotted in Fig. 2).

Figure S2.2 Influences of IC₅₀ and Hill coefficient on the concentration‐dependent changes in QT intervals (ΔQT) with quinine for I _Kr. Regression lines were obtained by repeating simulations when either increasing or decreasing the IC₅₀ and Hill coefficient (h) by 10%.

Figure S2.3 Effects of bepridil on the 12‐lead electrocardiogram (ECG). The12‐lead ECGs are shown for baseline conditions (left column), at 4× effective therapeutic plasma concentration (ETPC) (middle column), and at 7× ETPC (right column).

Figure S2.4 Arrhythmogenic risk of quinidine. A: The concentration‐block relationship of quinidine is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. The red dot indicates the intersection of the trajectory with the region of arrhythmia. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.5 Arrhythmogenic risk of dofetilide. A: The concentration‐block relationship of dofetilide is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. The red dot indicates the intersection of the trajectory with the region of arrhythmia. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.6 Arrhythmogenic risk of bepridil. A: The concentration‐block relationship of bepridil is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. The red dot indicates the intersection of the trajectory with the region of arrhythmia. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.7 Arrhythmogenic risk of dl‐sotalol. A: The concentration‐block relationship of dl‐sotalol is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. The red dot indicates the intersection of the trajectory with the region of arrhythmia. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.8 Arrhythmogenic risk of terfenadine. A: The concentration‐block relationship of terfenadine is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. The red dot indicates the intersection of the trajectory with the region of arrhythmia. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.9 Arrhythmogenic risk of ondansetron. A: The concentration‐block relationship of ondansetron is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. The red dot indicates the intersection of the trajectory with the region of arrhythmia. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.10 Arrhythmogenic risk of cisapride. A: The concentration‐block relationship of cisapride is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. The red dot indicates the intersection of the trajectory with the region of arrhythmia. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.11 Arrhythmogenic risk of chlorpromazine. A: The concentration‐block relationship of chlorpromazine is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.12 Arrhythmogenic risk of astemizole. Left panel: The concentration‐block relationship of astemizole is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. Right panel: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.13 Arrhythmogenic risk of ranolazine. A: The concentration‐block relationship of ranolazine is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.14 Arrhythmogenic risk of verapamil. A: The concentration‐block relationship of verapamil is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.15 Arrhythmogenic risk of mexiletine. A: The concentration‐block relationship of mexiletine is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.16 Arrhythmogenic risk of diltiazem. A: The concentration‐block relationship of diltiazem is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.17 Arrhythmogenic risk of flecainide. A: The concentration‐block relationship of flecainide is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.18 Arrhythmogenic risk of nilotinib. A: The concentration‐block relationship of nilotinib is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.19 Arrhythmogenic risk of cibenzoline. A: The concentration‐block relationship of cibenzoline is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.20 Arrhythmogenic risk of sertindole. A: The concentration‐block relationship of sertindole is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.21 Arrhythmogenic risk of chloroquine. A: The concentration‐block relationship of chloroquine is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.22 Arrhythmogenic risk of moxifloxacin. A: The concentration‐block relationship of moxifloxacin is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.23 Arrhythmogenic risk of amiodarone. A: The concentration‐block relationship of amiodarone is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.24 Arrhythmogenic risk of amitriptyline. A: The concentration‐block relationship of amytryptiline is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.25 Arrhythmogenic risk of mibefradil. A: The concentration‐block relationship of mibefradil is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.26 Arrhythmogenic risk of propafenone. A: The concentration‐block relationship of propafenone is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.27 Arrhythmogenic risk of quinine A: The concentration‐block relationship of quinine is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.28 Arrhythmogenic risk of ritonavir. A: The concentration‐block relationship of ritonavir is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.29 Arrhythmogenic risk of saquinavir, A: The concentration‐block relationship of saquinavir is shown as a trajectory in the three‐dimensional subspace of the risk map superimposed with the distribution of the QT interval. B: Electrocardiogram (ECG) changes at various concentrations are indicated as multiples of the effective therapeutic plasma concentration. C: Concentration‐inhibition relations of five ion channels are plotted in different colors, indicated above. Shaded area indicates the concentration range evaluated in this sub‐space. Green dots on the abscissa represent ETPC_unbound.

Figure S2.30 Influence of hypokalemia on arrhythmogenic risk. Arrhythmogenic risk of quinine (A) and dofetilide (B) was evaluated under normal and hypokalemic conditions. Electrocardiographic changes at various concentrations of drugs are indicated as multiples of the effective therapeutic plasma concentration under hypokalemic conditions (left panel: extracellular concentration of K⁺ ([K⁺]_o) = 2.5 mM) and normal conditions (right panel: extracellular concentration of K⁺ ([K⁺]_o) = 5.4 mM).

Figure S2.31 Role of M‐cells in arrhythmogenesis. A: Effects of M‐cell distribution. The effects of bepridil were evaluated in models with different M‐cell distributions. (a) M‐cells were distributed 20–64% of the wall volume from the endocardial side. (b) M‐cells were distributed 20–70% of the wall volume from the endocardial side. (c) M‐cells were distributed 20–58% of the wall volume from the endocardial side. (d) Without M‐cells or endocardial cells (0–64% of the wall volume from the endocardial side) or epicardial cells (64–100% of the wall volume from the endocardial side). Top panels show transmural distributions of endocardial cells (green), M‐cells (red), and epicardial cells (blue). Lower panels show ECG lead II at various drug concentrations of bepridil in multiples of ETPC_unboud. B: Role of M‐cells in sustained arrhythmia. Extra‐stimulus was applied to the right ventricular outflow in models with M cells (top panel: model "a" of SFig.2. 31A) and without M‐cells (bottom panel: model "d" of SFig.2. 31A) at 570 ms from the onset of the QRS complex (red arrows) under the addition of bepridil (7.5 times ETPC_unbound).

Figure S2.32 Effect of heart size on arrhythmogenic risk. The effect of heart size was tested for a (A) high‐risk drug (bepridil), (B) intermediate‐risk drug (cisapride), and (C) low‐risk drug (verapamil). Each drug was tested in a small heart (left column), normal heart (middle column), and large heart (right column). The heart was scaled by 80% or 120% of normal, resulting in a left ventricular end‐diastolic volume (LVEDV) of 57 ml (=114×0.8³) or 199 ml (=114×1.2³). Changes in the ECG (limb lead II) at various drug concentrations are shown. Drug concentrations are indicated as multiples of the effective therapeutic plasma concentration.

Figure S2.33 Convergence of action potential durations A. Changes in the action potential durations (APD) during the 1000 cycles of simulations using the O'Hara Rudy model in a control and 13 test drugs at ETPC_unbound. B. Relative deviation from the steady‐state value [(APD90 − APD90_{steady − state})/APD90_{steady − state} × 100]. Inset: Magnified view of the first 10 cycles.

Table S2.1 Parameters of test drugs.

Table S2.2 Multiple linear regression analysis.

Table S2.3 Logistic regression analysis.

Table S2.4 Ranges of IC₅₀ and the Hill coefficient for terfenadine.

Table S2.5 Predictive performance of various methods.

Okada, J. , Yoshinaga, T. , Kurokawa, J. , Washio, T. , Furukawa, T. , Sawada, K. , Sugiura, S. , and Hisada, T. (2018) Arrhythmic hazard map for a 3D whole‐ventricle model under multiple ion channel block. British Journal of Pharmacology, 175: 3435–3452. 10.1111/bph.14357.