Abstract
Since the work of Walter Schottky, it is known that the shot-noise power for a completely uncorrelated set of electrons increases linearly with the time-averaged current. At zero temperature and in the absence of inelastic scattering, the linearity relation between noise power and average current is quite robust, in many cases even for correlated electrons. Through high-bias shot-noise measurements on single Au atom point contacts, we find that the noise power in the high-bias regime shows highly nonlinear behavior even leading to a decrease in shot noise with voltage. We explain this nonlinearity using a model based on quantum interference of electron waves with varying path difference due to scattering from randomly distributed defect sites in the leads, which makes the transmission probability for these electrons both energy and voltage dependent.
It is known from the time of Walter Schottky in 1918,1 that the noise power increases linearly with time averaged current SI = 2e⟨I⟩. In mesoscopic devices, where the Pauli exclusion principle introduces correlations among the electrons, the shot noise drops below this SI value.2 This reduction has been measured experimentally both in 2DEG based point contacts3,4 and metallic point contacts.5 Even here, at zero temperature and in the absence of inelastic scattering, shot noise is known to increase linearly with average current (or applied bias), as given by the expression6−8
| 1 |
where θ is the temperature of the point contact and Tn(EF) is the transmission probability of the nth channel involved in the transport, measured at the Fermi energy EF of the leads. Any deviation from this linearity relation has been attributed to interactions with other degrees of freedom, such as inelastic electron–phonon interaction,9 flicker noise, two level fluctuations,10 heating or nonequilibrium occupation of phonons.11 Setting such deviations apart, the conductance of point contacts is given by the celebrated Landauer’s conductance formula,12 which describes conductance as directly proportional to the sum of the transmission probabilities of the channels involved (G = G0∑Tn(EF)). This sets an upper limit for the maximum conductance for a single channel taking part in transport, equal to the quantum of conductance (G0 = 2e2/h).
These properties for noise and differential conductance hold under quasi equilibrium or in the linear regime, where the transmission probability (T) of a channel is taken as constant, equal to its value at the Fermi energy (EF). In general, the transmission probability of a channel can have both energy and voltage dependence T(E,V). This could bring new pleasant surprises and could also upset current views based on the linear regime. Thanks to a newly developed setup13 we are able to measure noise continuously as a function of bias, up to very high bias, where T cannot be taken as constant and the energy and voltage dependence of T gives rise to highly nonlinear behavior in shot noise. The nonlinearity of shot noise with applied bias can be so strong that it can even lead to negative differential shot noise (NDSN). To understand these nonlinearities, we use a model based on quantum interference of electron waves which take varying paths while being scattered from randomly distributed defect sites in the leads in combination with the usual scattering at the point contact. This quantum interference model leads to energy and voltage dependence of T and qualitatively explains the anomalous experimental noise measurements recorded at high bias.
Measurement Setup
High-bias shot-noise measurements are challenging as 1/f noise or flicker noise increases with the square of the applied bias and so at high bias one is likely to be confronted with a large 1/f noise background over the desired shot noise. This forces us to perform measurements at high frequencies where the 1/f noise decreases. We have developed a new high-frequency shot-noise measurement setup which can measure noise in the MHz frequency range and can record the spectral information.13 This spectral information can be recorded with high speed up to 12 spectra/s. This system is connected to a mechanically controlled break junction setup to study shot noise in metallic point contacts and single-molecule junctions with a high mechanical stability. A schematic of the setup is shown in Figure 1.
Figure 1.
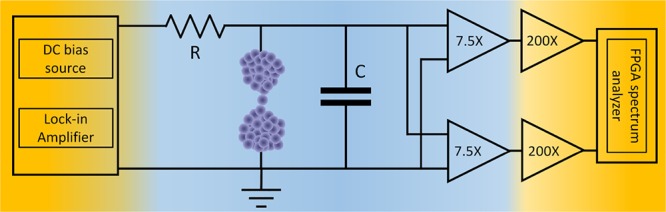
Schematic of the experimental setup. The color gradient shows qualitatively the operating temperature from 300 (orange) to 4.2 K (blue). The setup consists of cryogenic (7.5×) and room temperature amplifiers (200×) together giving 1500 times amplification. The decoupling resistor R is 10 kΩ, and the total stray input capacitance C at the cryogenic amplifier is around 14 pF.
Shot-Noise Measurements
Ballistic single atom point contacts formed between metallic leads have been an important playground to study electronic transport in nanostructures. Both conductance and shot-noise measurements of these contacts have led researchers to understand interesting atomic-scale physics. We start by showing the low-bias shot-noise data data (published earlier by Tewari et al.13), where the usual linear-regime behavior is expected. Figure 2a shows the linearly increasing shot-noise power as we ramp the voltage bias over a metallic point contact. Depending on the strength of the electron–vibron coupling, the electrons could also pass through the contact by inelastically exciting a vibration mode of atoms forming the junction. This opens an additional inelastic channel for the electron transport over the existing elastic channel. This is known to give a kink in the linearly increasing shot-noise power, as shown for a short chain of Au atoms in Figure 2b and is also described in previous work by Kumar et al.9
Figure 2.
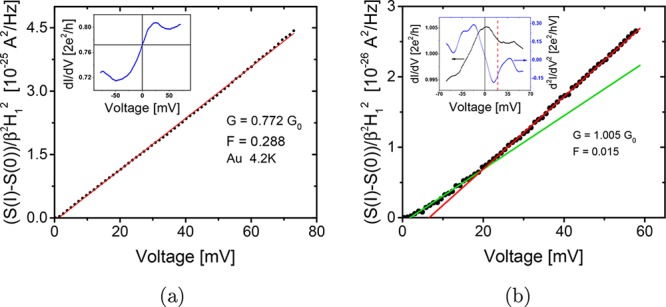
(a) Linearly increasing shot noise with the applied bias over the Au point contact with inset showing the corresponding differential conductance of the contact, (b) Kink in shot noise due to electron phonon interaction close to the vibration mode in Au atomic chain at around 20 meV as seen in the d2I/dV2 shown in the inset.
The results shown in Figure 2 are what we expect for the linear regime where the transmission is almost constant. But when we go to higher bias and the transmission is close to 1, the shot noise measured over single Au atom point contact shows highly nonlinear behavior. A collection of three different examples which we will examine here is shown in Figure 3. These point contacts are formed by opening and closing the mechanically controlled break junctions fitted with a notched 99.99% pure, 200 μm diameter gold wire. In this, every new single atom point contact formed can have a different junction geometry in terms of its atomic configuration of the leads leading to the single atom in the center. Differential conductance measurements are performed before and after the noise measurements to verify the stability of the contact. Figure 3 shows the differential conductance (left) and the excess shot noise (S(I) – S(0)) measured (right) for the three cases.
Figure 3.
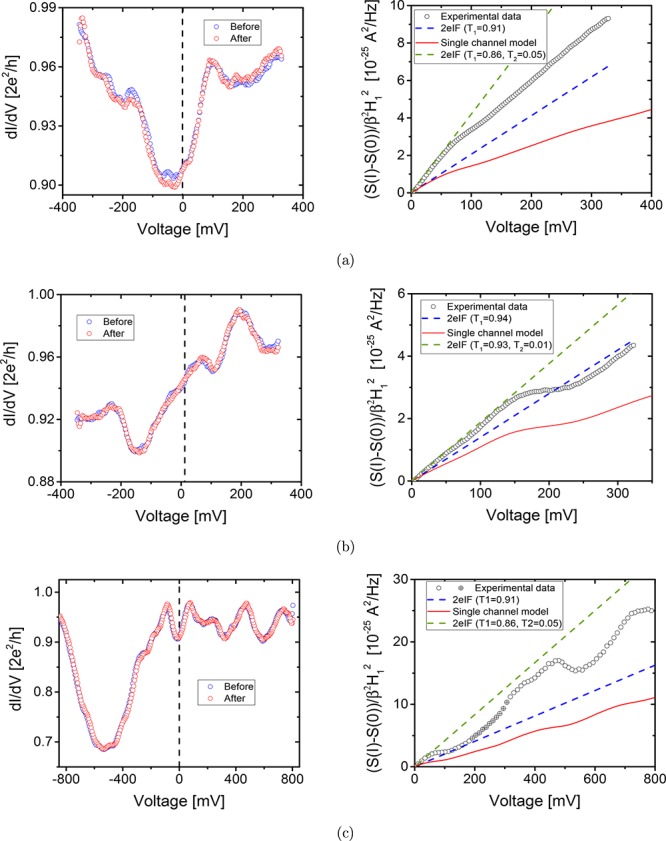
Nonlinear shot-noise data: We show here three examples (a–c) of high-bias shot-noise data. The left graph in each panel shows the differential conductance of the three contacts measured before and after the noise measurement and the right graph shows the corresponding shot-noise data. The experimental noise data is shown with open circles while the modeled noise is shown by red solid curves. The points for which the noise spectra show small deviations from a purely white spectrum are shown with crossed circles.
The three selected examples shown in Figure 3 have differential conductance spectra that are quite different from each other. In example 1 the differential conductance is fairly symmetric and the measured noise (shown with open circles in the right panel of Figure 3a) increases linearly at low bias and then it has a kink around 60 mV followed by a further increase up to 325 mV. This kink can not be due to electron–phonon interaction because the Debey energy for Au is around 14 mV. In example 2 (Figure 3b), the differential conductance is almost antisymmetric about zero bias and the noise shown in the right panel shows a different type of nonlinearity. Here the noise has a staircase like structure, where the noise stagnates at the middle and rises again. Example 3 (Figure 3c) has a very strong asymmetry in the differential conductance of the contact accompanied by even stronger nonlinearity in the shot noise, showing even a region of negative differential shot noise, i.e., a decrease of shot noise with bias. Here the noise is measured up to 800 mV which is much higher than any previous shot-noise measurement done14,15 over metallic point contacts. At these high-bias levels one would expect the noise measurement to become affected by 1/f noise and two-level fluctuations (TLF). Thanks to our FPGA-based spectrum analyzer for the noise, we can identify any deviations from a regular white spectrum (where we apply a threshold of 5% deviation from the mean between 1 and 6 MHz) in our data. This helps us in ensuring that these other noise sources are not the cause of the nonlinearity in shot noise measured at high bias. Previous high-bias shot-noise measurements do not provide access to a spectrum to confirm the white noise character, and we have demonstrated in our previous work13 that such deviations may become very prominent. In the noise plot of Figure 3c, we identified some points with a small nonwhite contribution to the spectra at intermediate bias, for which the white noise part is extracted and the points are shown by crossed circles in the plot. In the next part we will discuss the interpretation we propose for the nonlinear noise based on quantum interference of electronic waves. A discussion on other possible sources of nonlinearity and stability of atomic junctions at such high bias is given at the end.
Quantum Interference Model
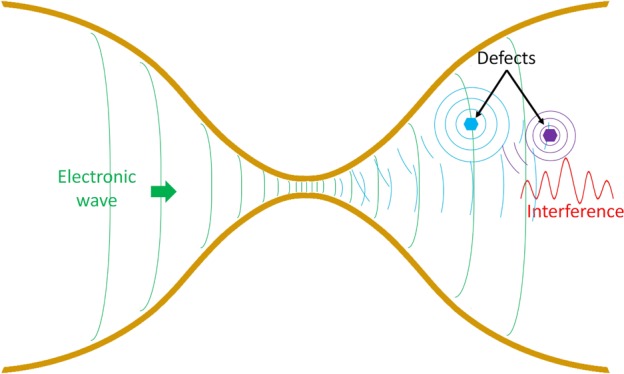
A symmetric differential conductance for positive and negative bias could be expected for a simple point contact studied extensively in quantum transport measurements. However, experiments show that such point contacts can have very commonly a nonsymmetric differential conductance. This asymmetry can be attributed to voltage dependence of transmission as will be explained below based on the Landauer formalism. Quantum interference (QI) of electronic waves due to scattering from defect sites (close to the point contact) can make the transmission voltage dependent. It is known16−18 that such QI in the leads causes strong oscillations in the differential conductance and when the point contact transmission is near unity these oscillations become strongly suppressed. A schematic explaining this QI due to defect scattering is shown in Figure 4a. In the schematic the point contact is shown as a slit in a screen separating the two conductors left and right. Incoming electronic plane waves are shown as blue color wave-fronts. The defects are placed only on the right side of the point contact (or slit) for simplicity. The schematic shows that the electronic waves travel an additional path length on reflecting from the defect as compared to the directly transmitted wave. This creates a phase difference and the two parts of the electronic wave interfere with each other, forming constructive or destructive contributions to the current signal, depending on the position of the defects and energy of incoming beam. Compared to the analysis by Ludoph et al.16,17 our approach differs in two important aspects: (1) We are not interested in ensemble averages but in the effects of individual defects. (2) We will be interested in the large voltage bias regime, beyond lowest-order corrections to the conductance and noise.
Figure 4.
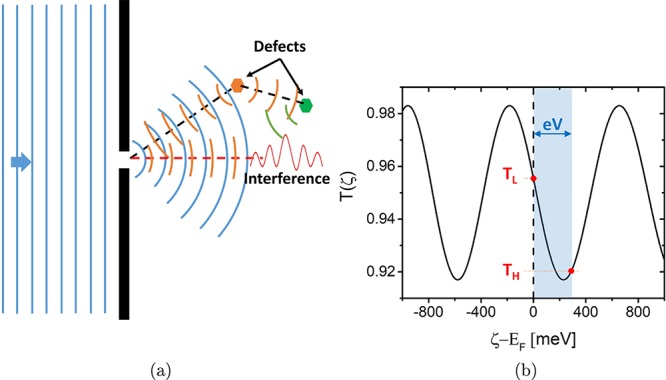
(a) Model based on quantum interference of electronic waves due to scattering from defects in the leads. The point contact is represented as a single slit with defects only shown on the right side. Multiple reflections as shown for the green defect are not taken into account (b) Example of a model transmission for a single defect shown to explain the meaning of TH and TL.
The first case that is considered is that of a single defect at the right side of the contact where the electrons arrive after being accelerated at the contact, and the other case will be added below. Scattering on this defect leads to an interference term in the transmission probability. For an electron that starts from the negative-bias side with initial energy E the transmission takes the form,
| 2 |
where T0 is the transmission that is mainly determined by the properties of the atomic contact itself, here taken to be energy and voltage independent. The amplitude a depends on the distance of the defect and the scattering probability. This amplitude decreases with the distance L between the defect and the contact as L–4, as a result of the solid angle under which the defect is seen from the contact and, after scattering on the return path, the solid angle under which the contact is seen from the defect position. Along its path the scattering partial wave accumulates a phase 2k(E,V)L with respect to the partial wave that is directly transmitted, plus a constant phase ϕ is added,18 which depends on the details of the scattering process. This makes the total transmission both energy and voltage dependent T(E,V).
The wavenumber k(E,V) depends on the total energy (E) of the incoming electron and the voltage drop (V) experienced at the point contact. Because of the acceleration of the electron at the contact site the wavenumber of electrons after the contact will be
| 3 |
So, for multiple defects the transmission takes the form
| 4 |
where Nd is the number of defect sites. A case where multiple defects can sit on either side of the point contact is discussed briefly in the Supporting Information. As the energy (E) and applied bias (V) enter in the above transmission picture only in the combination E + eV/2, we can write the total transmission as a function of a single variable: ζ = E + eV/2. The above total transmission is written for a single channel; for multiple channels one has to use a second index n with transmission of nth channel as Tn(ζ). As the transmission enters as T(1 – T) in shot noise (example eq 1), this energy and voltage dependent transmission causes strong nonlinearities in the shot noise. Important to note is that in the case of quantum interference the transmission takes the form T(E,V) = T(E + eV/2). A more detailed form of T(αE + βV) is not presented in this manuscript but is discussed in detail elsewhere.19 Before going ahead we discuss the assumptions made in the model. (1) We will assume for simplicity that only a single channel is taking part in transport. (2) We assume zero temperature, which helps us in getting rid of the Fermi functions from the integrals as discussed below. This is a reasonable assumption as the experiments shown here are done at liquid helium temperatures, and we work in the regime eV ≫ kBT. (3) Again for simplicity, we assume that the voltage drops entirely over the point contact and not over the defects. This is not a very strong assumption as long as the defects are point like in comparison to the corresponding cross-section of the leads. (4) We leave out any intrinsic energy dependence of the transmission for the metallic point contacts.20 (5) We take the waves to be reflected only once from the defect sites. More than one reflection will reduce the amplitude of the wave significantly.18 (6) We assume the transmission is entirely described by elastic processes. Inelastic scattering on vibration modes of the contact is difficult to incorporate in the simple model we present here without increasing the number of fitting parameters. However, we discuss briefly its effect in the section ‘Analysis of the experimental data’. There we will also discuss which of the above assumptions are the most restrictive ones.
Under these assumptions the total transmission of the system can be taken as given in eq 4 due to QI of electronic waves. Because this transmission is both energy and voltage dependent, we start from the general Landauer expression for time averaged current ⟨I⟩(V) and noise SI(V) for spin degenerate systems.6−8,21,22
| 5 |
| 6 |
As we make the approximation of zero temperature the Fermi functions fL and fR can be
taken as Heaviside functions. On using the Leibniz integration rule
one can write an expression for the differential conductance Gdiff or 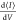 (23,24) starting from eq 5
(23,24) starting from eq 5
| 7 |
which for a single channel becomes
| 8 |
where, 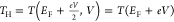 and
and 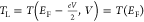 . The meaning of TH and TL is explained in the Figure 4b. Here a simple
model curve T(ζ) is plotted for a single channel
taking only one sine term in eq 4. As a bias voltage is applied, an energy window of width eV centered at EF + eV/2 is opened. TH and TL are the values of the transmission at the
“High” and “Low” side of the window as
shown in the Figure 4b. Note that this figure is applicable for a defect sitting on the
low-bias side(after the point contact). For the other case, TH will remain at zero (i.e., ζ = EF) and TL will be
on the negative side. If there is no voltage dependence of the transmission
(i.e.,
. The meaning of TH and TL is explained in the Figure 4b. Here a simple
model curve T(ζ) is plotted for a single channel
taking only one sine term in eq 4. As a bias voltage is applied, an energy window of width eV centered at EF + eV/2 is opened. TH and TL are the values of the transmission at the
“High” and “Low” side of the window as
shown in the Figure 4b. Note that this figure is applicable for a defect sitting on the
low-bias side(after the point contact). For the other case, TH will remain at zero (i.e., ζ = EF) and TL will be
on the negative side. If there is no voltage dependence of the transmission
(i.e., 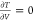 ), then only the width
of the energy window
changes and the total conductance will depend on both TH and TL. In fact it will
be an arithmetic mean of the TH and TL as can be seen from eq 8 and for the case when T has
only energy dependence, one needs to know the T(E) over a window of size eV from EF–eV/2 to EF+eV/2. For the case when the transmission T has both energy and voltage dependence, both the width
of the energy window and its mean will change (see Figure 4b) and the transmission has
to be known over a window of width 2eV from ζ
= −eV to ζ = +eV to
know the complete differential conductance and shot noise from negative
to positive bias. It will be shown below explicitly for the quantum
interference effect (using eq 10 and eq 12)
that both differential conductance and noise will become independent
of the value of TL because of the new
terms coming from the voltage dependence of T. For
the case where defects are placed on the other side, TH will be replaced by TL in
the final expressions. If the transmission is constant or only energy
dependent, then from eq 7, the dI/dV will be symmetric for
the positive and negative bias. Any asymmetry in dI/dV arises from the voltage dependence of the transmission.
The experimentally observed curves for the differential conductance
clearly demonstrate such asymmetry and imply the importance of including
the voltage dependence of T.
), then only the width
of the energy window
changes and the total conductance will depend on both TH and TL. In fact it will
be an arithmetic mean of the TH and TL as can be seen from eq 8 and for the case when T has
only energy dependence, one needs to know the T(E) over a window of size eV from EF–eV/2 to EF+eV/2. For the case when the transmission T has both energy and voltage dependence, both the width
of the energy window and its mean will change (see Figure 4b) and the transmission has
to be known over a window of width 2eV from ζ
= −eV to ζ = +eV to
know the complete differential conductance and shot noise from negative
to positive bias. It will be shown below explicitly for the quantum
interference effect (using eq 10 and eq 12)
that both differential conductance and noise will become independent
of the value of TL because of the new
terms coming from the voltage dependence of T. For
the case where defects are placed on the other side, TH will be replaced by TL in
the final expressions. If the transmission is constant or only energy
dependent, then from eq 7, the dI/dV will be symmetric for
the positive and negative bias. Any asymmetry in dI/dV arises from the voltage dependence of the transmission.
The experimentally observed curves for the differential conductance
clearly demonstrate such asymmetry and imply the importance of including
the voltage dependence of T.
Because the last
term in the expression for the differential conductance
given in eq 8 is an integration
over only energy (E), we can write 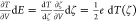 .
.
| 9 |
From eq 8 and 9, the differential conductance can be written as
| 10 |
As we are interested in studying
nonlinear
shot noise, we want to also derive an expression for differential
shot noise 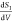 . We define
a function Z(E,V)=T(E,V)(1 – T(E,V)) and making again
the zero-temperature
and single-channel assumptions, we rewrite eq 6 as
. We define
a function Z(E,V)=T(E,V)(1 – T(E,V)) and making again
the zero-temperature
and single-channel assumptions, we rewrite eq 6 as
| 11 |
This expression for noise has the same form as eq 5 for current. Without the need for repeating the exercise we did above for differential conductance, we can immediately write the differential shot noise as
| 12 |
It is important to note the
difference between the above expressions
for conductance and noise with those for the low-bias linear regime,
where we assume constant transmission. In the linear regime, the differential
conductance is given by the Landauer formula, i.e. 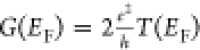 and shot noise is given by SI = 2eIF = 2eVG(EF)F with the Fano
factor F = 1–T(EF). This gives the noise for the linear regime constant
transmission
case as
and shot noise is given by SI = 2eIF = 2eVG(EF)F with the Fano
factor F = 1–T(EF). This gives the noise for the linear regime constant
transmission
case as 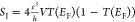 , which, of course,
gives a linear increase
in noise with bias, with complete suppression of noise at transmission
close to T(EF) = 0 and
1. In the quantum interference picture for the nonlinear regime, the
differential conductance eq 10 has close similarity with the linear regime formula, with
the difference that now the transmission should be evaluated at the
high-bias end of the energy window. The expression for shot noise
is however quite different. eq 12 shows the expression for
, which, of course,
gives a linear increase
in noise with bias, with complete suppression of noise at transmission
close to T(EF) = 0 and
1. In the quantum interference picture for the nonlinear regime, the
differential conductance eq 10 has close similarity with the linear regime formula, with
the difference that now the transmission should be evaluated at the
high-bias end of the energy window. The expression for shot noise
is however quite different. eq 12 shows the expression for 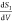 and not SI.
So, here as the transmission will go to 1, the noise is not going
to be zero, but instead the slope of the noise will be zero and we
will see a plateau appearing in the noise curve.
and not SI.
So, here as the transmission will go to 1, the noise is not going
to be zero, but instead the slope of the noise will be zero and we
will see a plateau appearing in the noise curve.
Analysis of the Experimental Data
We start by first taking only a single-channel linear-regime approximation and show the noise (SI = 2eI(1 – T)) with the blue dashed lines for all the three examples in Figure 3, where we have obtained the transmission from the measured differential conductance (T = G[G0]) at zero bias for the three data sets. From here we see that the experimental data suggest the presence of a second channel whose transmission at zero bias can be extracted by fitting the measured noise data with a straight line at low bias (see Supporting Information).This is shown by the green dashed lines in Figure 3 for the three examples and the extracted zero-bias transmission for the second channel (T2) is given in the insets. The second channel has a small transmission, as expected for a Au atomic contact. For metallic atomic contacts the work of Cron et al. has demonstrated quantitative agreement to about 1% accuracy for shot noise at low bias entirely attributed to the Landauer conductance channels.25 Although, we know from this that the three examples we study here are not correctly described by just a single channel, we will first try to use our simple single channel model to understand the measured nonlinearity in the shot noise and then discuss the role of the second channel.
Using eq 10, we can write 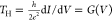 , where G(V) is the differential
conductance (in units of G0) obtained
directly from the experiments. From here we can rewrite eq 12 for the differential shot noise
as
, where G(V) is the differential
conductance (in units of G0) obtained
directly from the experiments. From here we can rewrite eq 12 for the differential shot noise
as
| 13 |
Next, we input the experimentally measured conductance values in eq 13 and integrate these over the whole bias range. The modeled noise thus obtained is shown with solid red curves in Figure 3 in the three examples. In all three examples, the noise reproduces qualitatively the nonlinearities in the experimental data. This is a surprisingly good match considering the assumptions made in the model.
In examples 1 and 2, the model explains the kink and the step structure arising in the noise as an intrinsic property of the contact depending on the position of the defect sites. In example 3, also the modeled noise explains the occurrence of rather complicated nonlinearity in the measured shot noise, although the amplitude of the variations is much smaller, and in particular, the decrease of shot noise with voltage bias observed in the experiments cannot be reproduced. Note that the expression of dSI/dVeq 12 shows that it can never be negative for the current choice of T(E,V). Our model is purely elastic; there are no inelastic effects included and no free parameters used for tweaking the shape of the modeled noise. We are showing here that pure elastic scattering can give large nonlinearities in shot noise and these qualitatively agree with those observed in our experiments. For a better comparison, a plot of the numerical derivative of the measured noise against our model is given in the Supporting Information.
The quantitative mismatch and the fact that our model does not follow the strong nonlinearities such as the negative differential shot noise observed in the experiments are attributed to three main missing ingredients. (1) Inelastic effects are not included in our simple model, but they must play a role at such high bias. We know for contacts with conductance close to 1 G0, the conductance decreases due to inelastic backscattering of electrons. Such effects are not included in the model. (2) The intrinsic energy dependence of the transmission of the point contact itself is ignored (T0 is taken to be constant in eq 4). In reality T0 can be dependent on both energy and voltage as shown by Brandbyge et al.20 (3) The transmission enters in the form T(1–T) in the shot noise, which makes the noise for a channel with T close to 1 very small, and even a small contribution from a second channel with transmission close to zero quickly becomes comparable to the noise of the main channel. Simply adding a constant second channel will add to the noise but will also smooth out the nonlinearities in our model (see Supporting Information). Ideally, we need to include the second channel effect in the quantum interference model, but this goes at the expense of adding many free parameters.
For a complete match one has to find the complete expression for T(E,V) including the inelastic effects, which is not trivial to extract from just shot noise and differential conductance data and further analysis awaits input from theory.
Discussion
In the previous section, we have offered an interpretation for the nonlinear dependence of shot noise on the applied bias. We have seen that, qualitatively, the effects are related to those in the differential conductance, and these are likely due to quantum interference as a result of electrons scattering from defects near the contact. For a quantitative explanation more elaborate models are required, and the observed negative differential noise is particularly exotic. High-bias shot-noise measurements have been reported earlier for Au atomic contacts up to 300 mV in room temperature14 and 250 mV at low temperatures.15 These measurements were performed using a high bandwidth radio frequency (rf) technique, where only the integrated noise is detected by a power detector. The reported nonlinearity in shot noise was shown only as a rise in noise power. In case of the room temperature measurements14 the nonlinear increase in shot noise was attributed to either electron–phonon interaction or local heating of the electronic fluid which crosses the ballistic junction. At low temperature,15 the nonlinear rise was explained using the linear regime Landuaer formalism relations, which in general should not be applicable at high bias as explained above. An occurrence of decrease in shot noise with bias has been reported26 on a n-GaAs MESFET system where due to correlated resonant tunneling (which involves two interacting resonant states) first an enhancement in the shot noise over the Poisson value (2eI) occurs and then a decrease in shot noise with bias. This interpretation is rather specific for this system and is not obviously applicable for noise in metal atomic contacts. Other possible explanations proposed for nonlinearity in shot noise27 are bias-dependent channel mixing and nonequilibrium phonon back-action. A nonequilibrium phonon distribution11 could develop but as a result of the strong coupling to the phonon bath in the Au leads, the nonequilibrium occupation is expected to remain small. Such effects are more important in systems where the vibrons of the system are weakly coupled to the phonon bath of the leads. On the theory side, Lesovik and Loosen28 have shown that the excess noise (S(I) – S(0)) could even become negative for a sharp peak in transmission, close to zero bias, whose width is much smaller than kBT. This is a very rarely occurring possibility and has not been found yet in the experiments.
Joule heating of atomic point contacts at such high bias can also be a concern and has been studied by Nielsen et al.,29 where it was reported that Au atomic contacts could even sustain up to 2 V and more than 150 μA current. Using a semiclassical approach,21,30,31 it has been shown that in the ballistic regime, where the size of the contact is much smaller than the mean free path, the heat carried by electrons under applied bias is dissipated far away in the banks via scattering with phonons. As a result, even at such high bias, the effect of heating remains small, as the electronic temperature in the vicinity of ballistic point contact does not rise much. We measured the global heating effect in our samples by replacing the Au point contact with a standard film resistor of 13 kΩ (close to 1 G0) and recording the noise. From the noise measurement we conclude that the rise in effective temperature for up to 1 V bias over the 13 kΩ resistor, is around 0.075 K which is equivalent to 3.2 × 10–28 A2/Hz in thermal noise.
Conclusion and Outlook
In conclusion, we have performed shot-noise measurements over Au single atom point contacts in the nonlinear regime, even up to 800 mV bias as shown in the third example in Figure 3. These shot noise data show highly nonlinear behavior with applied bias, which has no specific trend and which is different for every different contact. We have shown that these nonlinearities arise due to quantum interference of electronic waves which take multiple paths due to elastic scattering on the defects present in the leads close to the point contact. This makes the transmission probability of the contact energy and voltage dependent, which means that usual assumptions based on the linear regime break down. We can qualitatively explain the main features in the measured nonlinearity. For a fully quantitative description other energy and voltage dependent effects need to be considered due to the intrinsic transmission of the point contact itself, the effect of other channels and the voltage drop over the defect sites. Any inelastic effects, including nonequilibrium phonon back action and backscattering of electrons which could lower the junction conductance is also not included in the model. We have presented experimental data where the nonlinearity is such that the shot noise even decreases with increase in bias. The results presented here suggest control over the position of defects in the vicinity of the point contact could be exploited for designing transmission at will and for achieving desired properties in conductance and noise. This would not be simple to realize for a metallic point contact, but in a predesigned molecular system and mesoscopic systems like 2DEG,32 this is feasible.
Acknowledgments
This work was supported by The Netherlands Organization for Scientific Research (NWO/OCW), as part of the Frontiers of Nanoscience program with Grant Number NF13SAP09. We would also like to acknowledge Dr. Carlos Sabater who contributed in the early stages of the experiments and Dr Rémi Avriller for discussions on the main results.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.8b02176.
The authors declare no competing financial interest.
Supplementary Material
References
- Schottky W. Über spontane Stromschwankungen in verschiedenen Elektrizitätsleiter. Ann. Phys. 1918, 362, 541–567. 10.1002/andp.19183622304. [DOI] [Google Scholar]
- Lesovik G. B. Excess quantum noise in 2D ballistic point contacts. JETP Lett. 1989, 49, 592–594. [Google Scholar]; Lesovik G. B. Pis’ma Zh. Eksp. Teor. Fiz. 1989, 49, 513. [Google Scholar]
- Reznikov M.; Heiblum M.; Shtrikman H.; Mahalu D. Temporal Correlation of Electrons: Suppression of Shot Noise in a Ballistic Quantum Point Contact. Phys. Rev. Lett. 1995, 75, 3340–3343. 10.1103/PhysRevLett.75.3340. [DOI] [PubMed] [Google Scholar]
- Kumar A.; Saminadayar L.; Glattli D. C.; Jin Y.; Etienne B. Experimental Test of the Quantum Shot Noise Reduction Theory. Phys. Rev. Lett. 1996, 76, 2778–2781. 10.1103/PhysRevLett.76.2778. [DOI] [PubMed] [Google Scholar]
- van den Brom H. E.; van Ruitenbeek J. M. Quantum Suppression of Shot Noise in Atom-Size Metallic Contacts. Phys. Rev. Lett. 1999, 82, 1526–1529. 10.1103/PhysRevLett.82.1526. [DOI] [Google Scholar]
- Beenakker C. W. J.; van Houten H. Semiclassical theory of shot noise and its suppression in a conductor with deterministic scattering. Phys. Rev. B: Condens. Matter Mater. Phys. 1991, 43, 12066–12069. 10.1103/PhysRevB.43.12066. [DOI] [PubMed] [Google Scholar]
- Martin T.; Landauer R. Wave-packet approach to noise in multichannel mesoscopic systems. Phys. Rev. B: Condens. Matter Mater. Phys. 1992, 45, 1742–1755. 10.1103/PhysRevB.45.1742. [DOI] [PubMed] [Google Scholar]
- Büttiker M. Scattering theory of current and intensity noise correlations in conductors and wave guides. Phys. Rev. B: Condens. Matter Mater. Phys. 1992, 46, 12485–12507. 10.1103/PhysRevB.46.12485. [DOI] [PubMed] [Google Scholar]
- Kumar M.; Avriller R.; Yeyati A. L.; van Ruitenbeek J. M. Detection of Vibration-Mode Scattering in Electronic Shot Noise. Phys. Rev. Lett. 2012, 108, 146602. 10.1103/PhysRevLett.108.146602. [DOI] [PubMed] [Google Scholar]
- Chen R.; Wheeler P. J.; Natelson D. Excess noise in STM-style break junctions at room temperature. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 85, 235455. 10.1103/PhysRevB.85.235455. [DOI] [Google Scholar]
- Urban D. F.; Avriller R.; Levy Yeyati A. Nonlinear effects of phonon fluctuations on transport through nanoscale junctions. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 82, 121414. 10.1103/PhysRevB.82.121414. [DOI] [Google Scholar]
- Landauer R. Spatial variation of currents and fields due to localized scatterers in metallic conduction. IBM J. Res. Dev. 1988, 32, 306–316. 10.1147/rd.323.0306. [DOI] [Google Scholar]
- Tewari S.; Sabater C.; Kumar M.; Stahl S.; Crama B.; van Ruitenbeek J. M. Fast and accurate shot noise measurements on atomic-size junctions in the MHz regime. Rev. Sci. Instrum. 2017, 88, 093903. 10.1063/1.5003391. [DOI] [PubMed] [Google Scholar]
- Chen R.; Wheeler P. J.; Di Ventra M.; Natelson D. Enhanced noise at high bias in atomic-scale Au break junctions. Sci. Rep. 2015, 4, 4221. 10.1038/srep04221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen R.; Natelson D. Evolution of shot noise in suspended lithographic gold break junctions with bias and temperature. Nanotechnology 2016, 27, 245201. 10.1088/0957-4484/27/24/245201. [DOI] [PubMed] [Google Scholar]
- Ludoph B.; Devoret M. H.; Esteve D.; Urbina C.; van Ruitenbeek J. M. Evidence for Saturation of Channel Transmission from Conductance Fluctuations in Atomic-Size Point Contacts. Phys. Rev. Lett. 1999, 82, 1530–1533. 10.1103/PhysRevLett.82.1530. [DOI] [Google Scholar]
- Ludoph B.; van Ruitenbeek J. M. Conductance fluctuations as a tool for investigating the quantum modes in atomic-size metallic contacts. Phys. Rev. B: Condens. Matter Mater. Phys. 2000, 61, 2273–2285. 10.1103/PhysRevB.61.2273. [DOI] [Google Scholar]
- Untiedt C.; Rubio Bollinger G.; Vieira S.; Agrait N. Quantum interference in atomic-sized point contacts. Phys. Rev. B: Condens. Matter Mater. Phys. 2000, 62, 9962–9965. 10.1103/PhysRevB.62.9962. [DOI] [Google Scholar]
- Tewari S.Molecular electronics: controlled manipulation, noise and graphene architecture. Ph.D. Thesis. Leiden Institute of Physics (LION), Leiden University: 2018. [Google Scholar]
- Brandbyge M.; Kobayashi N.; Tsukada M. Conduction channels at finite bias in single-atom gold contacts. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 60, 17064–17070. 10.1103/PhysRevB.60.17064. [DOI] [Google Scholar]
- Agrait N.; Yeyati A. L.; van Ruitenbeek J. M. Quantum properties of atomic-sized conductors. Phys. Rep. 2003, 377, 81–279. 10.1016/S0370-1573(02)00633-6. [DOI] [Google Scholar]
- Cuevas J. C.; Scheer E.. Molecular electronics: an introduction to theory and experiment; World Scientific: New Jersey, 2010. [Google Scholar]
- Castao E.; Kirczenow G. Theory of nonlinear transport in narrow ballistic constrictions. Phys. Rev. B: Condens. Matter Mater. Phys. 1990, 41, 3874–3877. 10.1103/PhysRevB.41.3874. [DOI] [PubMed] [Google Scholar]
- Zhang G.; Ratner M. A.; Reuter M. G. Is molecular rectification caused by asymmetric electrode couplings or by a molecular bias drop?. J. Phys. Chem. C 2015, 119, 6254–6260. 10.1021/jp5093515. [DOI] [Google Scholar]
- Cron R.; Goffman M. F.; Esteve D.; Urbina C. Multiple-Charge-Quanta Shot Noise in Superconducting Atomic Contacts. Phys. Rev. Lett. 2001, 86, 4104–4107. 10.1103/PhysRevLett.86.4104. [DOI] [PubMed] [Google Scholar]
- Safonov S. S.; Savchenko A. K.; Bagrets D. A.; Jouravlev O. N.; Nazarov Y. V.; Linfield E. H.; Ritchie D. A. Enhanced Shot Noise in Resonant Tunneling via Interacting Localized States. Phys. Rev. Lett. 2003, 91, 136801. 10.1103/PhysRevLett.91.136801. [DOI] [PubMed] [Google Scholar]
- Stevens L. A.; Zolotavin P.; Chen R.; Natelson D. Current noise enhancement: channel mixing and possible nonequilibrium phonon backaction in atomic-scale Au junctions. J. Phys.: Condens. Matter 2016, 28, 495303. 10.1088/0953-8984/28/49/495303. [DOI] [PubMed] [Google Scholar]
- Lesovik G. B.; Loosen R. Negative excess noise in quantum conductors. Z. Phys. B: Condens. Matter 1993, 91, 531–536. 10.1007/BF01316834. [DOI] [Google Scholar]
- Nielsen S. K.; Brandbyge M.; Hansen K.; Stokbro K.; van Ruitenbeek J. M.; Besenbacher F. Current-Voltage Curves of Atomic-Sized Transition Metal Contacts: An Explanation of Why Au is Ohmic and Pt is Not. Phys. Rev. Lett. 2002, 89, 066804. 10.1103/PhysRevLett.89.066804. [DOI] [PubMed] [Google Scholar]
- Sharvin Y. V. A possible method for studying Fermi surfaces. J. Exptl. Theoret. Phys. (U.S.S.R.) 1965, 48, 655–656. [Google Scholar]
- Jansen A. G. M.; Gelder A. P. V.; Wyder P. Point-contact spectroscopy in metals. J. Phys. C: Solid State Phys. 1980, 13, 6073–6118. 10.1088/0022-3719/13/33/009. [DOI] [Google Scholar]
- Topinka M. A.; LeRoy B. J.; Shaw S. E. J.; Heller E. J.; Westervelt R. M.; Maranowski K. D.; Gossard A. C. Imaging Coherent Electron Flow from a Quantum Point Contact. Science 2000, 289, 2323–2326. 10.1126/science.289.5488.2323. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


