Abstract
Chiral metallic nanostructures can generate evanescent fields which are more highly twisted than circularly polarized light. However, it remains unclear how best to exploit this phenomenon, hindering the optimal utilization of chiral electromagnetic fields. Here, inspired by optical antenna theory, we address this challenge by introducing chiral antenna parameters: the chirality flux efficiency and the chiral antenna aperture. These quantities, which are based on chirality conservation, quantify the generation and dissipation of chiral light. We then present a label-free experimental technique, chirality flux spectroscopy, which measures the chirality flux efficiency, providing valuable information on chiral near fields in the far field. This principle is verified theoretically and experimentally with two-dimensionally chiral coupled nanorod antennas, for which we show that chiral near and far fields are linearly dependent on the magnetoelectric polarizability. This elementary system confirms our concept to quantify chiral electromagnetic fields and paves the way toward broadly tunable chiral optical applications including ultrasensitive detection of molecular chirality or optical information storage and transfer.
Keywords: Optical chirality, optical antenna, chirality flux, plasmonics, polarimetry
Chirality, the phenomenon of handedness, is a distinctive property of living matter.1 Molecular chirality arises due to the mirror-symmetric arrangement of otherwise identical compounds. Because the structural differences between these molecules, known as enantiomers, can impact their biochemical function, techniques for selective detection and separation of chiral molecules have been sought.2 Chiral light, such as left- and right-handed circularly polarized plane waves, offers a versatile and noninvasive means to detect molecular chirality.3 However, this approach is intrinsically limited in sensitivity due to the dimensional mismatch between molecules and the wavelength of light,4 which leads to long integration times that hinder applications.5
Recent advances in nanotechnology have enabled the fabrication of chiral metallic nanostructures6 (and achiral nanostructures excited with chiral light7−9) that address the above challenge in two ways. First, their evanescent fields can exceed the chirality of circularly polarized light.10 Second, their spatial extent can better match subwavelength molecular dimensions.11 These two factors can increase detection sensitivity of chiral molecules by orders of magnitude.12−14 Thus, highly chiral evanescent fields offer a promising avenue toward the realization of ultrasensitive on-chip selection and separation of chiral molecules.15−20
However, to move beyond initial demonstrations of highly chiral light, criteria for effectively designing and tailoring nanostructures for the chirality of their fields are needed. This requires methods to characterize nanoscale chiral fields. Probing the near field directly is experimentally challenging with existing techniques.21 Ideally, we would extract information on chiral evanescent fields from far-field measurements,22 but this approach has not yet succeeded.
Optical antenna theory can help resolve this issue. Specifically, just as classical electromagnetic antennas optimize energy transfer between a localized receiver and the free radiation field,23−25 an ideal chiral nanoantenna should enhance the transfer of chiral optical information from a molecule placed in its near field to the far field (Figure 1). Thus, rather than directly probing chiral near fields, an appropriate far-field technique should be sufficient.
Figure 1.
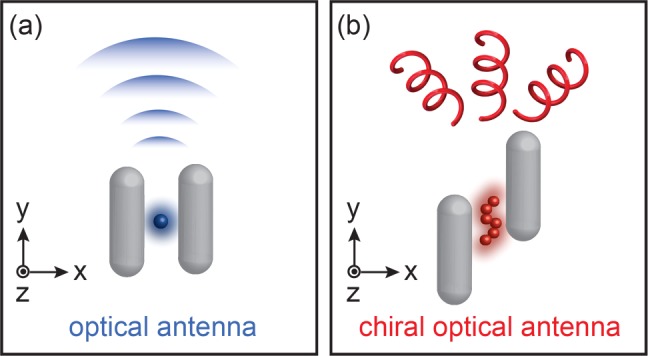
Conceptual illustration of (a) an optical antenna where energy transfer to and from a receiver is enhanced and (b) a chiral optical antenna where the receiver is a chiral molecule and the transfer of chiral optical information to and from the far field is enhanced.
Here, we present a formalism for the optical characterization of chiral nanoantennas inspired by classical antenna theory. We introduce physical quantities, the chirality flux efficiency and the chiral antenna aperture, that enable the quantification of the chiral optical properties of a nanoantenna. We then develop a label-free experimental technique, chirality flux spectroscopy, to measure the chirality flux efficiency and verify our results with both theory and experiment for coupled nanorod dimers with two-dimensional (2D) chirality. We find that the chiral fields of the system are driven by the magnetoelectric polarizability, exhibiting a linear relationship between chirality flux efficiency and the chiral near-field coupling of the two nanorods in the studied regime. Thus, our method provides vital information on chiral near fields that can be accessed in the far field, enabling rational nanoantenna design based on chiral optical fields and the optimal utilization of chiral light in specifically tailored applications.
The handedness of chiral electromagnetic plane waves is determined by the rotation direction around the propagation axis. Locally, this is quantified by the optical chirality density,26 which in its time-averaged form (denoted with an overbar) is
| 1 |
where ω is the angular
frequency and 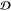 and
and 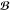 are the
complex amplitudes for the electric
displacement and magnetic fields, respectively, with the asterisk
indicating the complex conjugate. χ̅ is a chiral analogue
to the local density of optical states.27 For a single plane wave, χ̅ reaches its extrema for
circularly polarized light (CPL).28 This
limit (χ̅CPL) can be exceeded by evanescent
waves, due to their theoretically unlimited in-plane spatial frequencies.29 Specifically, a z-decaying
evanescent wave with in-plane wavevector components kx and ky reaches its maximum optical chirality density at
are the
complex amplitudes for the electric
displacement and magnetic fields, respectively, with the asterisk
indicating the complex conjugate. χ̅ is a chiral analogue
to the local density of optical states.27 For a single plane wave, χ̅ reaches its extrema for
circularly polarized light (CPL).28 This
limit (χ̅CPL) can be exceeded by evanescent
waves, due to their theoretically unlimited in-plane spatial frequencies.29 Specifically, a z-decaying
evanescent wave with in-plane wavevector components kx and ky reaches its maximum optical chirality density at
| 2 |
where ε0 is the vacuum permittivity
and 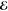 is the
complex electric-field amplitude
with Cartesian components
is the
complex electric-field amplitude
with Cartesian components 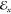 ,
, 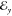 , and
, and 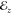 (see
the Supporting Information). Chiral metallic nanostructures, which are effective
generators of chiral evanescent fields,6 therefore offer an accessible route toward chiral sensing.
(see
the Supporting Information). Chiral metallic nanostructures, which are effective
generators of chiral evanescent fields,6 therefore offer an accessible route toward chiral sensing.
Previously, these systems have been characterized using spectroscopic techniques21 designed to evaluate biomolecular structure.30 Most notably, circular dichroism (CD) spectroscopy3,4 measures the differential extinction between illumination with left- and right-handed circularly polarized light. In addition to the conventional extinction approach, variations of CD have been developed on the basis of nonlinear optical response,31 strong optical scattering,32 and fluorescence.33 These have been successfully applied to chiral metallic nanostructures.34−40 Compared to molecules, plasmonic resonances can exhibit CD signal amplitudes that are orders of magnitude higher at ultraviolet, visible, and near-infrared frequencies.41−45 Indeed, geometries to maximize this effect have been proposed.46 Moreover, these signals can be induced or altered by ultraviolet-resonant molecules.47 However, while these spectra provide valuable structural information, their relation to chiral evanescent fields is unclear.22
Instead of alternating the handedness of circularly polarized illumination (as in CD spectroscopy), one can alternatively evaluate the degree of circular polarization of the fields that are emitted or scattered by a chiral sample. Circularly polarized luminescence48 exploits this approach for chiral emitters. Moreover, it has been applied to chiral metallic nanostructures by functionalizing their surface with achiral fluorophores.49,50 Although this strategy can probe chiral near fields, two disadvantages remain: (i) the resulting spectra are convoluted with fluorophore emission51 and (ii) the metal surface must be decorated with fluorescent labels, which can hinder subsequent interactions between the near field and a chiral analyte of interest.
We now introduce an approach that enables the label-free detection of chiral optical fields. By extending optical antenna theory, we can theoretically and experimentally quantify the generation and dissipation of chiral light in terms of parameters that directly relate to the chiral evanescent fields. As optical antenna parameters are derived from energy conservation,29 we base our technique on the analogous conservation law of optical chirality in lossy, dispersive media.22 This requires optical chirality dissipation to balance with the optical chirality flux (see Table 1). Thus, by detecting the degree of circular polarization of the scattered light in the far field, the optical chirality flux can be determined. This then provides information about the chiral near field (see the Supporting Information).
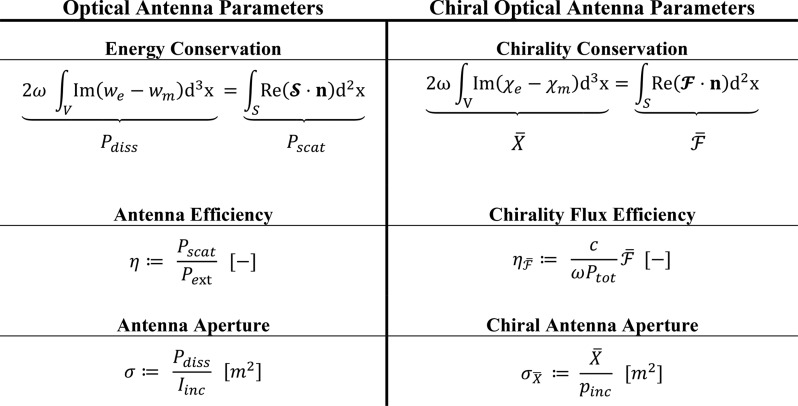
Table 1. Comparison of Optical Antenna Parameters (left) and Chiral Optical Antenna Parameters (right) Based on Their Governing Conservation Laws, Where ω is the Angular Frequency and n Is the Normal Vectora.
In the left column, we and wm are the complex harmonic
electric and magnetic energy densities,22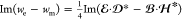 ,
, 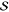 is the
Poynting vector, Pdiss is the dissipated
power, Pscat is the scattered power, Pext = Pdiss + Pscat is
the extinction power, and Iinc is the
incident light intensity. In the right column, χe and χm are the complex harmonic electric and magnetic
optical chirality densities,22
is the
Poynting vector, Pdiss is the dissipated
power, Pscat is the scattered power, Pext = Pdiss + Pscat is
the extinction power, and Iinc is the
incident light intensity. In the right column, χe and χm are the complex harmonic electric and magnetic
optical chirality densities,22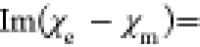
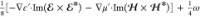
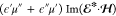 ,
, 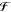 is the
optical chirality flux, c is the speed of light, Ptot is the total power of the outgoing light,
and pinc is the incident power density.
is the
optical chirality flux, c is the speed of light, Ptot is the total power of the outgoing light,
and pinc is the incident power density.
We define two antenna parameters
to characterize chiral nanoantennas,
the chirality flux efficiency 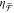 [-] and the chiral antenna aperture
[-] and the chiral antenna aperture 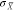 [m2] (see
the Supporting Information for further
details)
[m2] (see
the Supporting Information for further
details)
| 3 |
| 4 |
where c is the speed of light in vacuum and
| 5 |
is the
integral of the optical chirality flux, 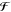 , through
the surface S,22 with
, through
the surface S,22 with
| 6 |
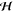 is the complex amplitude of the H field, and Ptot is the total power of
the outgoing light. Further,
is the complex amplitude of the H field, and Ptot is the total power of
the outgoing light. Further,
| 7 |
is the volume-integrated optical chirality dissipation22,69 with
| 8 |
with ϵ = ϵ′ + iϵ″ as the complex permittivity, μ = μ′ + iμ″ as the complex permeability, and χe, χm as the complex harmonic electric and magnetic optical chirality densities.22 Finally, pinc is the incident power density.
While the conventional antenna efficiency quantifies radiative power generation,29eq 3 describes the ability of the antenna to scatter chiral optical fields. Similarly, as the conventional antenna aperture describes power dissipation, related to the absorption cross section,29eq 4 describes the dissipation of chiral optical fields which, for small metallic nanostructures with negligible damping and retardation, can be brought into connection with the near-field optical chirality density.22 The comparison to optical antenna parameters is summarized in Table 1.
We now apply the chiral antenna parameters in eqs 3 and 4 to
an analytical
model of the 2D chiral metallic nanoantenna studied here. In the quasi-static
electric-dipole limit, this system is described by the dipole moment  .52,53 The electric polarizability
is written as αe and the chiral optical properties
are attributed to αc, the coupled magnetoelectric
polarizability.54 Inserting this model
into eqs 1, 3, and 4, we obtain (see the Supporting Information)
.52,53 The electric polarizability
is written as αe and the chiral optical properties
are attributed to αc, the coupled magnetoelectric
polarizability.54 Inserting this model
into eqs 1, 3, and 4, we obtain (see the Supporting Information)
| 9 |
| 10 |
| 11 |
where r and ζ
are the
radial and longitudinal cylindrical coordinates, μ0 is the vacuum permeability, and k is the wavevector
magnitude. Equations 9–11 have several important physical
implications. First, the resonant properties of 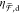 ,
, 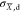 , and χ̅d are linearly
dependent on Re(αc). Due to this proportionality,
the magnetoelectric polarizability αc directly determines
the strength of the chiral optical fields generated. Second, in the
dipole limit, the resonance of
, and χ̅d are linearly
dependent on Re(αc). Due to this proportionality,
the magnetoelectric polarizability αc directly determines
the strength of the chiral optical fields generated. Second, in the
dipole limit, the resonance of 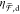 , which is measurable in the far field,
matches the resonance of χ̅d, which describes
the local near fields. Third,
, which is measurable in the far field,
matches the resonance of χ̅d, which describes
the local near fields. Third, 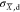 quantifies the ability of the dipolar nanoantenna
to dissipate optical chirality. As predicted by the conservation law
of optical chirality (see the Supporting Information), the resonance with maximum
quantifies the ability of the dipolar nanoantenna
to dissipate optical chirality. As predicted by the conservation law
of optical chirality (see the Supporting Information), the resonance with maximum 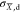 matches that of
matches that of 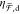 , which is measurable
in the far field.
, which is measurable
in the far field.
We verify our theoretical findings experimentally with 2D chiral nanorod dimers (NRDs) whose dominant properties are dipolar in the studied regime. Figure 2a,b shows scanning-electron micrographs of right- (R) and left-handed (L) NRDs, arranged periodically with an edge-to-edge distance of p = 600 nm (>6 × 104 unit cells). The rod dimensions are 70 nm × 230 nm × 50 nm in x, y, and z (with axes as in Figure 1) to generate sufficient antenna-scattered light. 2D chirality arises due to a ±140 nm vertical and 60 nm horizontal shift (h) between the nanorods in each pair (see the Supporting Information). Nonlinear, multipolar effects arising at small h are negligible.55 The chiral coupling between two metallic nanorods induces a magnetoelectric polarizability,56 and the physical behavior of this system can thus be modeled analytically as a single 2D chiral dipole.
Figure 2.

(a, b) Scanning-electron
micrographs of (a) R-NRD and (b) L-NRD
arrays with a horizontal shift of h = 60 nm and edge-to-edge
distance of p = 600 nm (between outer NRD edges).
The scale bars are 500 nm. (c) Extinction spectrum of the R-NRD array, h = 60 nm. Inset: schematic of an R-NRD unit cell where
∗ denotes the center point (0, 0, 0). (d) The
experimental setup for measuring chirality flux efficiency (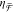 , eq 3). Inset: Schematic
of sample excitation with achiral, linearly
polarized light. While generated chiral evanescent fields decay,
, eq 3). Inset: Schematic
of sample excitation with achiral, linearly
polarized light. While generated chiral evanescent fields decay,  is detected in the far field by analysis
of the scattered degree of circular polarization. For this, the light
is sent through a photoelastic modulator (PEM) and subsequent linear
polarizer (LP). The optical signal is detected by a photomultiplier
tube (PMT) and filtered with a lock-in amplifier at the PEM modulation
frequency.
is detected in the far field by analysis
of the scattered degree of circular polarization. For this, the light
is sent through a photoelastic modulator (PEM) and subsequent linear
polarizer (LP). The optical signal is detected by a photomultiplier
tube (PMT) and filtered with a lock-in amplifier at the PEM modulation
frequency.
The antennas were fabricated by template stripping57 thermally evaporated silver from a structured silicon template onto a glass coverslip, after selective removal of the flat silver deposited around the nanorods58 (see the Supporting Information). An example of the optical extinction spectrum for a specific R-NRD array (h = 60 nm) can be seen on a linear scale in Figure 2c (see the Supporting Information) for x-polarized incident light (axes as in Figure 1). The inset of Figure 2c indicates one R-NRD unit cell with an asterisk marking the center point at (0, 0, 0). The spectrum is broad because in this demonstration we are exploiting a higher-order resonance of the system to increase the scattering signal from the NRDs at visible frequencies.
The principle of chirality flux spectroscopy, our
experimental
technique to measure 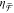 , is shown schematically in Figure 2d. Light from a broadband illumination
source (100 W halogen lamp) is passed through a monochromator and
a linear polarizer (LP) before it is weakly focused [20×, 0.45
numerical aperture (NA) objective] onto the sample. The outgoing signal
is collected with a 10×, 0.3 NA objective. As this study focuses
on single NRD coupling, low NA collection avoids lattice effects arising
at higher angles.50
, is shown schematically in Figure 2d. Light from a broadband illumination
source (100 W halogen lamp) is passed through a monochromator and
a linear polarizer (LP) before it is weakly focused [20×, 0.45
numerical aperture (NA) objective] onto the sample. The outgoing signal
is collected with a 10×, 0.3 NA objective. As this study focuses
on single NRD coupling, low NA collection avoids lattice effects arising
at higher angles.50
Next, a photoelastic modulator (PEM, Hinds Instruments I/FS50) applies quarter-wave retardation to the collected light at 50 kHz, which is subsequently analyzed by another LP. The excitation and collection LPs are aligned precisely ±45° to the PEM optical axis as even minor misalignments can lead to linear birefringence artifacts. A photomultiplier tube (PMT, Hamamatsu R928) then detects the optical signal. The output is fed into a lock-in amplifier (Zurich Instruments, HF2) connected to the electronic signal from the PEM.
The PEM
transforms R- or L-CPL, scattered from the sample, into
linear polarization at ±45° to the PEM axis, leading to
50 kHz modulation after the analyzing LP. In contrast, linear polarization,
predominantly from the excitation beam, is transformed into circular
polarization, which is then modulated at 100 kHz. This polarization-selective
modulation enables the isolated detection of circularly polarized
scattered fields, directly proportional to 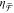 , in a bright-field measurement.
, in a bright-field measurement.
The inset of Figure 2d illustrates how the measurement
of 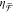 quantifies the ability of a nanoantenna
to generate chiral optical fields. The excitation with achiral, linearly
polarized light is key to this method, as
quantifies the ability of a nanoantenna
to generate chiral optical fields. The excitation with achiral, linearly
polarized light is key to this method, as 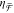 becomes meaningful for a system where the
sample is the only source of chiral optical fields. In this case,
a relationship between chiral near and far fields can be established,
because the chiral light scattered into the far field is a direct
consequence of the rapidly decaying chiral evanescent fields. Specifically,
becomes meaningful for a system where the
sample is the only source of chiral optical fields. In this case,
a relationship between chiral near and far fields can be established,
because the chiral light scattered into the far field is a direct
consequence of the rapidly decaying chiral evanescent fields. Specifically, 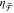 selectively detects the excess of one handedness
of chiral light scattered by the sample, modulated at 50 kHz, while
equal amounts of L- and R-CPL recombine additively to linear polarization, modulated at 100 kHz.
selectively detects the excess of one handedness
of chiral light scattered by the sample, modulated at 50 kHz, while
equal amounts of L- and R-CPL recombine additively to linear polarization, modulated at 100 kHz.
We emphasize that this near-field information is not revealed with CD spectroscopy, in which circularly polarized excitation is used. In that case, the chiral sample’s preferential extinction of one handedness of CPL results in differential amplitudes of L- and R-CPL generating an outgoing elliptical beam (see the Supporting Information).4 Thus, a CD spectrum describes how the sample alters incident chiral light, providing information on chiral geometry,32 but does not reveal its ability to generate chiral fields.
Furthermore, in optical rotatory dispersion (ORD), a spectroscopic technique which is Kramers–Kronig-related to CD,56 a sample is excited with linearly polarized light and the rotation plane of the outgoing elliptical beam is recorded. This effect is related to the net phase retardation experienced by L- and R-CPL when traversing a circularly birefringent medium.30 Thus, ORD is clearly distinct from chirality flux spectroscopy, where polarimetric analysis directly detects an excess of L- or R-CPL in the scattered fields.
We note that
plasmonic quarter-wave plates have been developed
to generate CPL upon linearly polarized excitation.59,60 These systems rely on linear birefringence, where two orthogonal
components of the incident linearly polarized beam obtain a net phase
retardation.30 Linear birefringence does
not occur for our measurement of 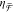 , as our x-polarized excitation
(axes as in Figure 1) experiences a single refractive index. Thus, the chiral fields
detected here result from the nanoantenna’s near-field chiral
coupling or, in other words, intrinsic rather than extrinsic chirality.61,62
, as our x-polarized excitation
(axes as in Figure 1) experiences a single refractive index. Thus, the chiral fields
detected here result from the nanoantenna’s near-field chiral
coupling or, in other words, intrinsic rather than extrinsic chirality.61,62
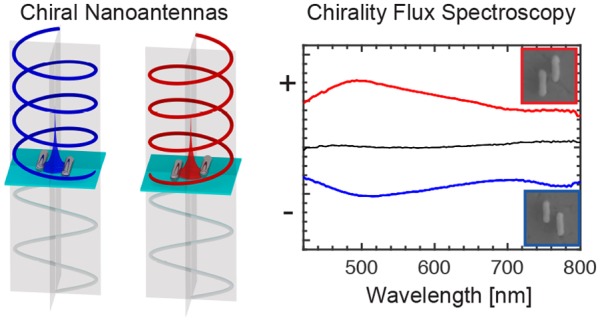
Figure 3a shows
experimental 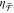 spectra for R-NRDs (red) and L-NRDs (blue),
respectively (h = 60 nm, achiral NRDs in black, see
the Supporting Information). The NRD handedness
determines the sign of the generated chiral optical fields, leading
to mirror-symmetric spectra. These results are well reproduced numerically
in Figure 3b, where
finite-element simulations (COMSOL Multiphysics 5.2) were conducted
with x-polarized plane-wave excitation with periodic
boundary conditions (see the Supporting Information). Amplitude differences between experimental (Figure 3a) and simulated data (Figure 3b) can be attributed to the higher collection
angle in experiment (NA = 0.3, see the Supporting Information). The feature at 600 nm (marked with ∗)
in Figure 3b arises
from the surface lattice resonance of the periodic array (see the Supporting Information). It is not seen in experiment,
presumably due to damping effects and fabrication imperfections.50 By setting the edge-to-edge NRD distance to
600 nm, we sufficiently separate lattice and single-nanoantenna resonances
to distinguish their effects.
spectra for R-NRDs (red) and L-NRDs (blue),
respectively (h = 60 nm, achiral NRDs in black, see
the Supporting Information). The NRD handedness
determines the sign of the generated chiral optical fields, leading
to mirror-symmetric spectra. These results are well reproduced numerically
in Figure 3b, where
finite-element simulations (COMSOL Multiphysics 5.2) were conducted
with x-polarized plane-wave excitation with periodic
boundary conditions (see the Supporting Information). Amplitude differences between experimental (Figure 3a) and simulated data (Figure 3b) can be attributed to the higher collection
angle in experiment (NA = 0.3, see the Supporting Information). The feature at 600 nm (marked with ∗)
in Figure 3b arises
from the surface lattice resonance of the periodic array (see the Supporting Information). It is not seen in experiment,
presumably due to damping effects and fabrication imperfections.50 By setting the edge-to-edge NRD distance to
600 nm, we sufficiently separate lattice and single-nanoantenna resonances
to distinguish their effects.
Figure 3.
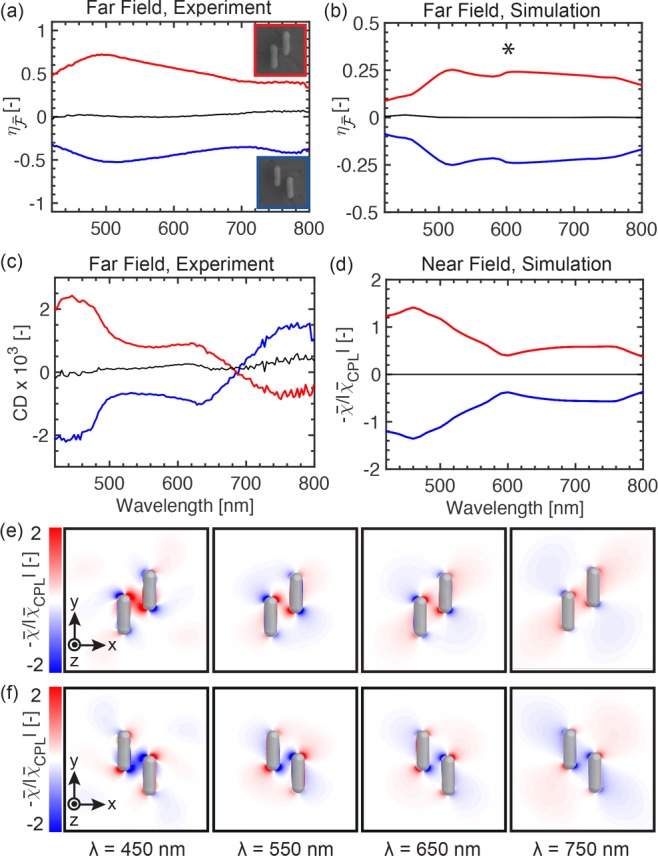
Experimental and simulated analysis of chiral
optical fields for
R-NRDs (red), L-NRDs (blue), and achiral NRDs (black) with h = 60 nm. (a) Experimental chirality flux efficiency (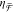 ) spectra. NRDs of opposite handedness show
mirror-symmetric
) spectra. NRDs of opposite handedness show
mirror-symmetric 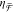 spectra, while achiral NRDs show negligible
spectra, while achiral NRDs show negligible 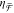 . (b) Simulated
. (b) Simulated 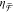 spectra, in good agreement with the experimental
data in part a. Surface lattice effects (marked with ∗) are
not seen in experiment due to damping and fabrication imperfections.
(c) Experimental circular dichroism (CD) spectra, which differ from
spectra, in good agreement with the experimental
data in part a. Surface lattice effects (marked with ∗) are
not seen in experiment due to damping and fabrication imperfections.
(c) Experimental circular dichroism (CD) spectra, which differ from 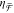 in magnitude, sign, and resonant wavelengths.
(d) Simulated optical chirality enhancement (χ̅/|χ̅CPL|) spectra, evaluated at (0, 0, 0), the center
point between nanorods (see Figure 2c). The spectral properties match those of
in magnitude, sign, and resonant wavelengths.
(d) Simulated optical chirality enhancement (χ̅/|χ̅CPL|) spectra, evaluated at (0, 0, 0), the center
point between nanorods (see Figure 2c). The spectral properties match those of  , where the spectral shift and broadening
in parts a and b are explained by damping, retardation, ensemble effects,
and low NA collection. (e, f) Simulated near-field maps (z = 0 plane, NRD center) of χ̅/|χ̅CPL| for (e) R-NRDs and (f) L-NRDs at various wavelengths (λ),
which further illustrate the trends in part d.
, where the spectral shift and broadening
in parts a and b are explained by damping, retardation, ensemble effects,
and low NA collection. (e, f) Simulated near-field maps (z = 0 plane, NRD center) of χ̅/|χ̅CPL| for (e) R-NRDs and (f) L-NRDs at various wavelengths (λ),
which further illustrate the trends in part d.
For comparison, the experimental setup in Figure 2d was modified to perform CD
measurements
(see the Supporting Information). The resulting
spectra in Figure 3c show that, while both techniques yield characteristic mirror-symmetric
trajectories for R- and L-NRDs, they clearly differ in magnitude,
sign, and resonant wavelengths. The discrepancy between Figure 3a and c verifies that 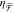 and CD provide different physical information.
and CD provide different physical information.
In Figure 3d, the numerical optical chirality enhancement (χ̅/|χ̅CPL|) of the NRD evanescent fields is plotted versus wavelength. This parameter was evaluated at the NRD center (0, 0, 0) (marked with ∗ in Figure 2c). For both R- and L-NRDs, χ̅/|χ̅CPL| retains the same sign at all wavelengths, with its maximum magnitude at 470 nm. This trend is further confirmed in numerical colormaps of χ̅/|χ̅CPL| (z = 0 plane at NRD center) shown in Figure 3e,f for various wavelengths (λ). Here, the handedness of χ̅/|χ̅CPL| arises due to NRD near-field coupling and changes sign depending on the vertical shift (positive or negative) between the nanorods. This does not occur for the achiral NRDs, where no such excess is present (see the Supporting Information).
Comparing these
results to Figure 3a,b, we find good agreement in the relative magnitude
and sign of χ̅/|χ̅CPL| and 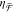 . This confirms the relationship between
. This confirms the relationship between 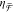 and chiral evanescent fields. However,
differences between χ̅/|χ̅CPL|
and
and chiral evanescent fields. However,
differences between χ̅/|χ̅CPL|
and 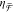 are also observed. These include (i) a
∼50 nm spectral shift and (ii) a broadening between near- and
far-field spectra. Indeed, as with the analogous energy parameters,
(i) and (ii) are plausible effects arising due to damping and retardation
beyond the dipole limit,63 as well as ensemble
effects and low NA collection.64 In contrast,
no such connection can be drawn between χ̅/|χ̅CPL| and the CD spectrum (Figure 3c).
are also observed. These include (i) a
∼50 nm spectral shift and (ii) a broadening between near- and
far-field spectra. Indeed, as with the analogous energy parameters,
(i) and (ii) are plausible effects arising due to damping and retardation
beyond the dipole limit,63 as well as ensemble
effects and low NA collection.64 In contrast,
no such connection can be drawn between χ̅/|χ̅CPL| and the CD spectrum (Figure 3c).
As derived from our theoretical
model, Figure 4 demonstrates
how the magnetoelectric polarizability
αc drives the NRD’s chiral fields, which arise
from plasmonic near-field coupling between two nanorods. Experimental 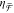 spectra are shown in Figure 4a where the horizontal shift h varies from
60 to 200 nm. We note that different lattice densities
were accounted for by our normalization procedure (see the Supporting Information). R- (red) and L-NRDs
(blue) maintain mirror-symmetric
spectra are shown in Figure 4a where the horizontal shift h varies from
60 to 200 nm. We note that different lattice densities
were accounted for by our normalization procedure (see the Supporting Information). R- (red) and L-NRDs
(blue) maintain mirror-symmetric 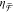 spectra for all h. As h increases
and the nanorod near-field coupling decreases,
the magnitude of
spectra for all h. As h increases
and the nanorod near-field coupling decreases,
the magnitude of 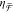 also decreases. Specifically, Figure 4b reveals a linear
trend for the extrema of
also decreases. Specifically, Figure 4b reveals a linear
trend for the extrema of 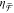 vs h. This was predicted
by our analytical model (eq 9), which states that
vs h. This was predicted
by our analytical model (eq 9), which states that 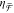 is dependent on the magnetoelectric polarizability
Re(αc) in the 2D chiral dipole limit. In our system,
Re(αc) is linearly related to h,
because the magnetoelectric polarizability is induced by chiral near-field
coupling between nanorods. The relationship between Re(αc) and h can be understood by comparison to
magnetostatics:65 due to plasmon hybridization,66 the plasmon-induced surface charges cause oscillating
currents across the chiral NRD which induce the magnetoelectric dipolar
component. Just as the current density along a circular loop is inversely
proportional to the loop radius, by increasing h in
our chiral NRD system, the effective NRD radius increases and we expect
a decrease in the chiral optical fields, which is well-approximated
as linear in the studied h-regime.
is dependent on the magnetoelectric polarizability
Re(αc) in the 2D chiral dipole limit. In our system,
Re(αc) is linearly related to h,
because the magnetoelectric polarizability is induced by chiral near-field
coupling between nanorods. The relationship between Re(αc) and h can be understood by comparison to
magnetostatics:65 due to plasmon hybridization,66 the plasmon-induced surface charges cause oscillating
currents across the chiral NRD which induce the magnetoelectric dipolar
component. Just as the current density along a circular loop is inversely
proportional to the loop radius, by increasing h in
our chiral NRD system, the effective NRD radius increases and we expect
a decrease in the chiral optical fields, which is well-approximated
as linear in the studied h-regime.
Figure 4.
(a) Experimental chirality
flux efficiency (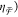 spectra
for R-NRDs (red) and L-NRDs (blue)
for varying horizontal shifts h.
spectra
for R-NRDs (red) and L-NRDs (blue)
for varying horizontal shifts h. 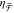 for achiral NRDs is shown at h = 60 nm (black).
Insets: scanning-electron micrographs of a single
NRD in the studied array. (b) Extrema of
for achiral NRDs is shown at h = 60 nm (black).
Insets: scanning-electron micrographs of a single
NRD in the studied array. (b) Extrema of 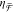 from part a. A linear trend with respect
to h (dashed lines provide linear fits) is observed.
(c) Extrema of simulated χ̅/|χ̅CPL| evaluated at (0, 0, 0) also show a linear trend with
respect to h (dashed lines provide linear fits).
The data in parts b and c verify analytical calculations (eqs 9–11) and reveal that h determines
the magnetoelectric polarizability αc in this system.
(d) Numerical colormaps of χ̅/|χ̅CPL| (z = 0 plane) for R-NRDs further confirm the trends
shown in part c.
from part a. A linear trend with respect
to h (dashed lines provide linear fits) is observed.
(c) Extrema of simulated χ̅/|χ̅CPL| evaluated at (0, 0, 0) also show a linear trend with
respect to h (dashed lines provide linear fits).
The data in parts b and c verify analytical calculations (eqs 9–11) and reveal that h determines
the magnetoelectric polarizability αc in this system.
(d) Numerical colormaps of χ̅/|χ̅CPL| (z = 0 plane) for R-NRDs further confirm the trends
shown in part c.
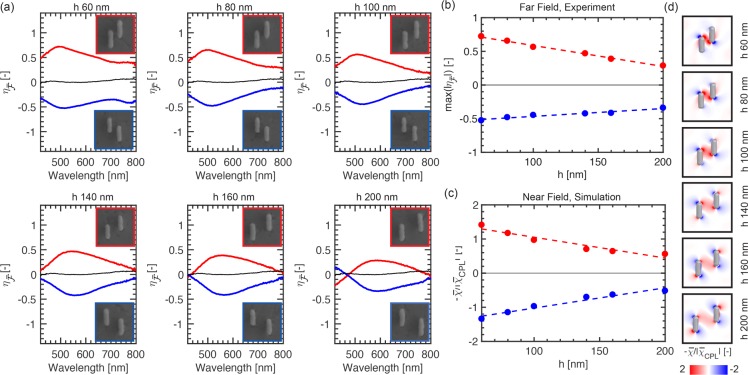
Further, our analytical
model predicts that the chiral near fields
also depend linearly on Re(αc) (eq 11). Indeed, Figure 4c confirms this numerically for χ̅/|χ̅CPL| evaluated at the NRD center (0, 0, 0) (marked
with ∗ in Figure 2c). The decrease in near-field optical chirality with increasing h is further illustrated with numerical colormaps of χ̅/|χ̅CPL| for varying h in Figure 4d. These results allow two important conclusions:
the predominant optical properties of the studied NRD system are dipolar,
and the antenna parameter 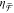 can predict the enhancement of near-field
optical chirality.
can predict the enhancement of near-field
optical chirality.
Finally, we show that the antenna parameters 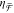 and
and 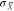 enable broad spectral
tunability of chiral
optical fields. Figure 5a plots experimental
enable broad spectral
tunability of chiral
optical fields. Figure 5a plots experimental 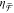 spectra for R-NRDs with varying h. In addition to the decrease of
spectra for R-NRDs with varying h. In addition to the decrease of 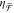 shown in Figure 4, we observe a spectral redshift with increasing h. The experimental wavelengths at which the extrema of
shown in Figure 4, we observe a spectral redshift with increasing h. The experimental wavelengths at which the extrema of 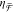 occur, shown with respect to h in Figure 5d, reveal
a linear trend that qualitatively agrees with the simulated
occur, shown with respect to h in Figure 5d, reveal
a linear trend that qualitatively agrees with the simulated 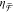 in Figure 5b. Similar
linear shifts have been reported for energy
and have been attributed to changes in the aspect ratio of the structure.55,67 As expected, comparable behavior is found in the chiral near fields
(Figure 5c), evaluated
at the R-NRD center (0, 0, 0) (marked with ∗
in Figure 2c).
in Figure 5b. Similar
linear shifts have been reported for energy
and have been attributed to changes in the aspect ratio of the structure.55,67 As expected, comparable behavior is found in the chiral near fields
(Figure 5c), evaluated
at the R-NRD center (0, 0, 0) (marked with ∗
in Figure 2c).
Figure 5.
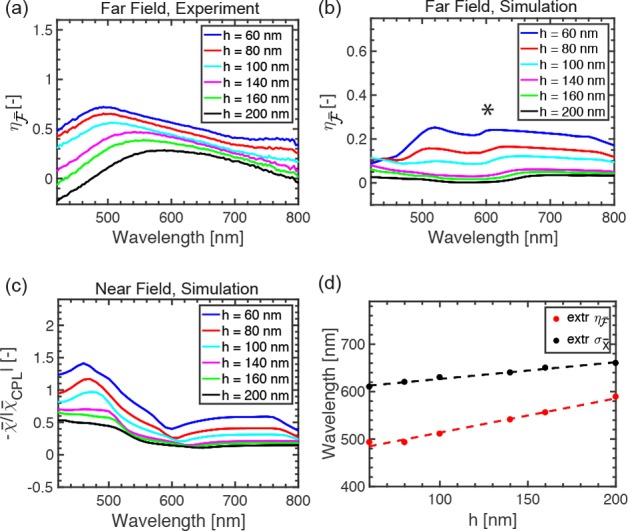
(a) R-NRD experimental
chirality flux efficiency (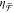 ) spectra for various horizontal shifts h. A redshift is observed with increasing h. (b) Corresponding simulated
) spectra for various horizontal shifts h. A redshift is observed with increasing h. (b) Corresponding simulated 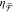 spectra are in agreement with experiments
(* indicates the surface lattice resonance). (c) Simulated χ̅/|χ̅CPL| spectra evaluated at (0, 0, 0) for R-NRDs
replicate far-field trends seen in parts a and b. (d) Extrema of the
dominant feature of experimental
spectra are in agreement with experiments
(* indicates the surface lattice resonance). (c) Simulated χ̅/|χ̅CPL| spectra evaluated at (0, 0, 0) for R-NRDs
replicate far-field trends seen in parts a and b. (d) Extrema of the
dominant feature of experimental 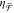 spectra and simulated chiral antenna aperture
(
spectra and simulated chiral antenna aperture
(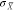 ) spectra for various h (dashed lines provide linear fits). As
) spectra for various h (dashed lines provide linear fits). As 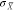 is driven by the surface
lattice resonance,
the redshift is attributed to the increasing surface lattice distance.
The results in part d reveal tunability of chiral fields across the
visible spectrum.
is driven by the surface
lattice resonance,
the redshift is attributed to the increasing surface lattice distance.
The results in part d reveal tunability of chiral fields across the
visible spectrum.
The second antenna parameter 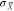 (eq 4) provides further useful chiral optical information.
Due
to chirality conservation (Table 1), the integrated optical chirality dissipation (proportional
to
(eq 4) provides further useful chiral optical information.
Due
to chirality conservation (Table 1), the integrated optical chirality dissipation (proportional
to 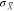 ) is equal to the optical
chirality flux
through the entire surface enclosing the studied structure. Thus,
while we minimize the effect of surface lattice resonances (SLRs)
by evaluating
) is equal to the optical
chirality flux
through the entire surface enclosing the studied structure. Thus,
while we minimize the effect of surface lattice resonances (SLRs)
by evaluating 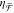 at small angles (SLRs are increasingly
observed at higher angles, as shown in the Supporting Information), the dominant
at small angles (SLRs are increasingly
observed at higher angles, as shown in the Supporting Information), the dominant 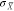 resonances are caused by SLRs in a 2D chiral
system. As we designed our system with an edge-to-edge NRD distance p of 600 nm (see Figure 2c), the effective surface-lattice-resonance wavelength
increases with increasing h, as shown in Figure 5d. The spectral SLR
redshift is also seen in the simulated
resonances are caused by SLRs in a 2D chiral
system. As we designed our system with an edge-to-edge NRD distance p of 600 nm (see Figure 2c), the effective surface-lattice-resonance wavelength
increases with increasing h, as shown in Figure 5d. The spectral SLR
redshift is also seen in the simulated 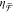 spectra (marked with ∗ in Figure 5b), while damping
and fabrication imperfections suppress this effect in experiment (Figure 5a). Indeed, this
SLR redshift confirms our statement with regard to Figure 3b, where we attributed the
resonance at 600 nm (marked with ∗) to a lattice effect (see
the Supporting Information for further
confirmation). The low-wavelength feature in Figure 5b, which arises with increasing h, can therefore be attributed to a higher-order lattice mode, explaining
its absence in experiment.68 Thus, the
tunability shown in Figure 5d makes it apparent that our combined understanding of
spectra (marked with ∗ in Figure 5b), while damping
and fabrication imperfections suppress this effect in experiment (Figure 5a). Indeed, this
SLR redshift confirms our statement with regard to Figure 3b, where we attributed the
resonance at 600 nm (marked with ∗) to a lattice effect (see
the Supporting Information for further
confirmation). The low-wavelength feature in Figure 5b, which arises with increasing h, can therefore be attributed to a higher-order lattice mode, explaining
its absence in experiment.68 Thus, the
tunability shown in Figure 5d makes it apparent that our combined understanding of 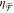 and
and 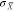 enables the design of
chiral optical fields
across the visible spectrum.
enables the design of
chiral optical fields
across the visible spectrum.
In summary, we introduce the optical
antenna approach to chiral
plasmonics to fully characterize and tune antenna-mediated chiral
light with the chiral antenna parameters 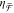 and
and 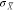 . With chirality flux
spectroscopy, a specifically
designed experimental technique to determine
. With chirality flux
spectroscopy, a specifically
designed experimental technique to determine 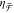 , we show that this approach provides valuable
information on chiral near fields that is accessible in the far field.
We verify this principle with simple 2D chiral coupled nanorod dimers
and find that chiral near and far fields are linearly driven by the
magnetoelectric polarizability. In analogy to energetic enhancement
induced by classical optical antennas, this new approach can lead
to optimized chiral optical applications, where highly chiral evanescent
fields enhance the transmission of chiral information from a chiral
receiver to the free radiation field.
, we show that this approach provides valuable
information on chiral near fields that is accessible in the far field.
We verify this principle with simple 2D chiral coupled nanorod dimers
and find that chiral near and far fields are linearly driven by the
magnetoelectric polarizability. In analogy to energetic enhancement
induced by classical optical antennas, this new approach can lead
to optimized chiral optical applications, where highly chiral evanescent
fields enhance the transmission of chiral information from a chiral
receiver to the free radiation field.
Acknowledgments
We thank H. Eghlidi, B. le Feber, F. Prins, A.-K. Michel, and N. Stricker for insightful discussions. We also thank P. Gutsche for helpful comments, in particular related to the optical chirality dissipation at interfaces. We thank S. A. Meyer for artistic rendering. We thank Y. Fedoryshyn and U. Drechsler for fabrication assistance.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.8b00083.
Experimental methods; derivations of plane- and evanescent-wave optical chirality density and dipole chiral antenna parameters; summary of the conservation law of optical chirality; scanning-electron micrograph images, extinction spectra, and CD spectra for all samples studied; discussion of experimental data analysis; characterization of achiral control samples; numerical methods; discussion of surface-lattice-resonance effects; simulated spectra of the chiral antenna aperture; and numerical geometry optimization (PDF)
Author Contributions
L.V.P. and D.J.N. conceived the project. L.V.P. developed the theory, performed analytical and numerical calculations, designed and built the optical setup, and analyzed the data. L.V.P., P.T., A.S., and E.D.L. carried out the sample fabrication. L.V.P., P.T., and A.S. performed the optical characterization. L.V.P. and D.J.N. wrote the manuscript with input from all authors.
This work was supported by the Swiss National Science Foundation under Award No. 200021-146747. D.J.N. acknowledges partial financial support from the European Research Council under the European Union’s Seventh Framework Program (FP/2007-2013)/ERC Grant Agreement No. 339905 (QuaDoPS Advanced Grant).
The authors declare no competing financial interest.
This paper originally published ASAP on March 23, 2018. Additional changes were made throughout the paper, including a revision to Figure 5 and the addition of reference 52. The revised version was published on May 2, 2018.
Supplementary Material
References
- Richardson G. M.The Foundations of Stereo Chemistry: Memoirs by Pasteur, Van’t Hoff, Lebel and Wislicenus; American Book Co.: New York, 1901. [Google Scholar]
- Hutt A. J.; Tan S. C. Drugs 1996, 52, 1–12. 10.2165/00003495-199600525-00003. [DOI] [PubMed] [Google Scholar]
- Rodger A.; Nordén B.. Circular Dichroism and Linear Dichroism, 1st ed.; Oxford University Press: New York, 1997. [Google Scholar]
- Nakanishi K.; Berova N.; Woody R.. Circular Dichroism : Principles and Applications, 2nd ed.; Wiley-VCH: New York, 2000. [Google Scholar]
- Kelly S. M.; Jess T. J.; Price N. C. Biochim. Biophys. Acta, Proteins Proteomics 2005, 1751, 119–139. 10.1016/j.bbapap.2005.06.005. [DOI] [PubMed] [Google Scholar]
- Hentschel M.; Schäferling M.; Duan X.; Giessen H.; Liu N. Sci. Adv. 2017, 3, e1602735. 10.1126/sciadv.1602735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schäferling M.; Yin X.; Giessen H. Opt. Express 2012, 20, 26326–26336. 10.1364/OE.20.026326. [DOI] [PubMed] [Google Scholar]
- García-Etxarri A.; Dionne J. A. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 87, 235409. 10.1103/PhysRevB.87.235409. [DOI] [Google Scholar]
- Ho C. S.; Garcia-Etxarri A.; Zhao Y.; Dionne J. ACS Photonics 2017, 4, 197–203. 10.1021/acsphotonics.6b00701. [DOI] [Google Scholar]
- Schäferling M.; Dregely D.; Hentschel M.; Giessen H. Phys. Rev. X 2012, 2, 31010. 10.1103/PhysRevX.2.031010. [DOI] [Google Scholar]
- Rotenberg N.; Kuipers L. Nat. Photonics 2014, 8, 919–926. 10.1038/nphoton.2014.285. [DOI] [Google Scholar]
- Hendry E.; Carpy T.; Johnston J.; Popland M.; Mikhaylovskiy R. V.; Lapthorn A. J.; Kelly S. M.; Barron L. D.; Gadegaard N.; Kadodwala M. Nat. Nanotechnol. 2010, 5, 783–787. 10.1038/nnano.2010.209. [DOI] [PubMed] [Google Scholar]
- Tang Y.; Cohen A. E. Science 2011, 332, 333–336. 10.1126/science.1202817. [DOI] [PubMed] [Google Scholar]
- Nesterov M. L.; Yin X.; Schäferling M.; Giessen H.; Weiss T. ACS Photonics 2016, 3, 578–583. 10.1021/acsphotonics.5b00637. [DOI] [Google Scholar]
- Canaguier-Durand A.; Hutchison J. A.; Genet C.; Ebbesen T. W. New J. Phys. 2013, 15, 123037. 10.1088/1367-2630/15/12/123037. [DOI] [Google Scholar]
- McPeak K. M.; van Engers C. D.; Bianchi S.; Rossinelli A.; Poulikakos L. V.; Bernard L.; Herrmann S.; Kim D. K.; Burger S.; Blome M.; Jayanti S. V.; Norris D. J. Adv. Mater. 2015, 27, 6244–6250. 10.1002/adma.201503493. [DOI] [PubMed] [Google Scholar]
- le Feber B.; Rotenberg N.; Kuipers L. Nat. Commun. 2015, 6, 6695. 10.1038/ncomms7695. [DOI] [PubMed] [Google Scholar]
- Tullius R.; Karimullah A. S.; Rodier M.; Fitzpatrick B.; Gadegaard N.; Barron L. D.; Rotello V. M.; Cooke G.; Lapthorn A.; Kadodwala M. J. Am. Chem. Soc. 2015, 137, 8380–8383. 10.1021/jacs.5b04806. [DOI] [PubMed] [Google Scholar]
- Zhao Y.; Saleh A. A. E.; Dionne J. A. ACS Photonics 2016, 3, 304–309. 10.1021/acsphotonics.5b00574. [DOI] [Google Scholar]
- Zhao Y.; Askarpour A. N.; Sun L.; Shi J.; Li X.; Alù A. Nat. Commun. 2017, 8, 14180. 10.1038/ncomms14180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith K. W.; Link S.; Chang W. S. J. Photochem. Photobiol., C 2017, 32, 40–57. 10.1016/j.jphotochemrev.2017.05.004. [DOI] [Google Scholar]
- Poulikakos L. V.; Gutsche P.; McPeak K. M.; Burger S.; Niegemann J.; Hafner C.; Norris D. J. ACS Photonics 2016, 3, 1619–1625. 10.1021/acsphotonics.6b00201. [DOI] [Google Scholar]
- Bharadwaj P.; Deutsch B.; Novotny L. Adv. Opt. Photonics 2009, 1, 438–483. 10.1364/AOP.1.000438. [DOI] [Google Scholar]
- Aćimović S. S.; Kreuzer M. P.; González M. U.; Quidant R. ACS Nano 2009, 3, 1231–1237. 10.1021/nn900102j. [DOI] [PubMed] [Google Scholar]
- Novotny L.; van Hulst N. Nat. Photonics 2011, 5, 83–90. 10.1038/nphoton.2010.237. [DOI] [Google Scholar]
- Tang Y.; Cohen A. E. Phys. Rev. Lett. 2010, 104, 163901. 10.1103/PhysRevLett.104.163901. [DOI] [PubMed] [Google Scholar]
- Joulain K.; Carminati R.; Mulet J.-P.; Greffet J.-J. Phys. Rev. B: Condens. Matter Mater. Phys. 2003, 68, 245405. 10.1103/PhysRevB.68.245405. [DOI] [Google Scholar]
- Bliokh K. Y.; Nori F. Phys. Rev. A: At., Mol., Opt. Phys. 2011, 83, 21803. 10.1103/PhysRevA.83.021803. [DOI] [Google Scholar]
- Novotny L.; Hecht B.. Principles of Nano-Optics, 2nd ed.; Cambridge University Press: Cambridge, U.K., 2012. [Google Scholar]
- Schellman J.; Jensen H. P. Chem. Rev. 1987, 87, 1359–1399. 10.1021/cr00082a004. [DOI] [Google Scholar]
- Simpson G. J. J. Chem. Phys. 2002, 117, 3398–3410. 10.1063/1.1494423. [DOI] [Google Scholar]
- Bustamante C.; Tinoco I.; Maestre M. F. Proc. Natl. Acad. Sci. U. S. A. 1983, 80, 3568–3572. 10.1073/pnas.80.12.3568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turner D. H.; Tinoco I.; Maestre M. J. Am. Chem. Soc. 1974, 96, 4340–4342. 10.1021/ja00820a057. [DOI] [Google Scholar]
- Valev V. K.; Silhanek A. V.; Smisdom N.; De Clercq B.; Gillijns W.; Aktsipetrov O. A.; Ameloot M.; Moshchalkov V. V.; Verbiest T. Opt. Express 2010, 18, 8286–8293. 10.1364/OE.18.008286. [DOI] [PubMed] [Google Scholar]
- Valev V. K.; Baumberg J. J.; De Clercq B.; Braz N.; Zheng X.; Osley E. J.; Vandendriessche S.; Hojeij M.; Blejean C.; Mertens J.; Biris C. G.; Volskiy V.; Ameloot M.; Ekinci Y.; Vandenbosch G. A. E.; Warburton P. A.; Moshchalkov V. V.; Panoiu N. C.; Verbiest T. Adv. Mater. 2014, 26, 4074–4081. 10.1002/adma.201401021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodrigues S. P.; Lan S.; Kang L.; Cui Y.; Cai W. Adv. Mater. 2014, 26, 6157–6162. 10.1002/adma.201402293. [DOI] [PubMed] [Google Scholar]
- Rodrigues S. P.; Cui Y.; Lan S.; Kang L.; Cai W. Adv. Mater. 2015, 27, 1124–1130. 10.1002/adma.201405072. [DOI] [PubMed] [Google Scholar]
- Lu X.; Wu J.; Zhu Q.; Zhao J.; Wang Q.; Zhan L.; Ni W. Nanoscale 2014, 6, 14244–14253. 10.1039/C4NR04433A. [DOI] [PubMed] [Google Scholar]
- Wang L.-Y.; Smith K. W.; Dominguez-Medina S.; Moody N.; Olson J. M.; Zhang H.; Chang W.-S.; Kotov N.; Link S. ACS Photonics 2015, 2, 1602–1610. 10.1021/acsphotonics.5b00395. [DOI] [Google Scholar]
- Smith K. W.; Zhao H.; Zhang H.; Sánchez-Iglesias A.; Grzelczak M.; Wang Y.; Chang W. S.; Nordlander P.; Liz-Marzán L. M.; Link S. ACS Nano 2016, 10, 6180–6188. 10.1021/acsnano.6b02194. [DOI] [PubMed] [Google Scholar]
- Mark A. G.; Gibbs J. G.; Lee T.-C.; Fischer P. Nat. Mater. 2013, 12, 802–807. 10.1038/nmat3685. [DOI] [PubMed] [Google Scholar]
- Cui Y.; Kang L.; Lan S.; Rodrigues S.; Cai W. Nano Lett. 2014, 14, 1021–1025. 10.1021/nl404572u. [DOI] [PubMed] [Google Scholar]
- Han C.; Leung H. M.; Chan C. T.; Tam W. Y. Opt. Express 2015, 23, 33065. 10.1364/OE.23.033065. [DOI] [PubMed] [Google Scholar]
- Hu L.; Tian X.; Huang Y.; Fang L.; Fang Y. Nanoscale 2016, 8, 3720–3728. 10.1039/C5NR08527F. [DOI] [PubMed] [Google Scholar]
- Esposito M.; Tasco V.; Todisco F.; Cuscunà M.; Benedetti A.; Scuderi M.; Nicotra G.; Passaseo A. Nano Lett. 2016, 16, 5823–5828. 10.1021/acs.nanolett.6b02583. [DOI] [PubMed] [Google Scholar]
- Fernandez-Corbaton I.; Fruhnert M.; Rockstuhl C. Phys. Rev. X 2016, 6, 31013. 10.1103/PhysRevX.6.031013. [DOI] [Google Scholar]
- Zhang H.; Govorov A. O. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 87, 75410. 10.1103/PhysRevB.87.075410. [DOI] [Google Scholar]
- Riehl J. P.; Richardson F. S. Chem. Rev. 1986, 86, 1–16. 10.1021/cr00071a001. [DOI] [Google Scholar]
- Meinzer N.; Hendry E.; Barnes W. L. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 88, 41407. 10.1103/PhysRevB.88.041407. [DOI] [Google Scholar]
- Cotrufo M.; Osorio C. I.; Koenderink A. F. ACS Nano 2016, 10, 3389–3397. 10.1021/acsnano.5b07231. [DOI] [PubMed] [Google Scholar]
- Pompa P. P.; Martiradonna L.; Della Torre A.; Della Sala F.; Manna L.; De Vittorio M.; Calabi F.; Cingolani R.; Rinaldi R. Nat. Nanotechnol. 2006, 1, 126–130. 10.1038/nnano.2006.93. [DOI] [PubMed] [Google Scholar]
- Gutsche P; Poulikakos L. V.; Hammerschmidt M.; Burger S.; Schmidt F. Proc. SPIE 2016, 97560X. 10.1117/12.2209551. [DOI] [Google Scholar]
- Sersic I.; Tuambilangana C.; Kampfrath T.; Koenderink A. F. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 83, 245102. 10.1103/PhysRevB.83.245102. [DOI] [Google Scholar]
- Sersic I.; van de Haar M. A.; Arango F. B.; Koenderink A. F. Phys. Rev. Lett. 2012, 108, 223903. 10.1103/PhysRevLett.108.223903. [DOI] [PubMed] [Google Scholar]
- Barron L. D.Molecular Light Scattering and Optical Activity, 2nd ed.; Cambridge University Press: Cambridge, U.K., 2009. [Google Scholar]
- Jain P. K.; El-Sayed M. A. Chem. Phys. Lett. 2010, 487, 153–164. 10.1016/j.cplett.2010.01.062. [DOI] [Google Scholar]
- Yin X.; Schäferling M.; Metzger B.; Giessen H. Nano Lett. 2013, 13, 6238–6243. 10.1021/nl403705k. [DOI] [PubMed] [Google Scholar]
- Nagpal P.; Lindquist N. C.; Oh S.-H.; Norris D. J. Science 2009, 325, 594–597. 10.1126/science.1174655. [DOI] [PubMed] [Google Scholar]
- McPeak K. M.; van Engers C. D.; Blome M.; Park J. H.; Burger S.; Gosálvez M. A.; Faridi A.; Ries Y. R.; Sahu A.; Norris D. J. Nano Lett. 2014, 14, 2934–2940. 10.1021/nl501032j. [DOI] [PubMed] [Google Scholar]
- Zhao Y.; Belkin M. A.; Alù A. Nat. Commun. 2012, 3, 870. 10.1038/ncomms1877. [DOI] [PubMed] [Google Scholar]
- Yu N.; Aieta F.; Genevet P.; Kats M. A.; Gaburro Z.; Capasso F. Nano Lett. 2012, 12, 6328–6333. 10.1021/nl303445u. [DOI] [PubMed] [Google Scholar]
- Plum E.; Fedotov V. A.; Zheludev N. I. J. Opt. A: Pure Appl. Opt. 2009, 11, 074009. 10.1088/1464-4258/11/7/074009. [DOI] [Google Scholar]
- Tian X.; Fang Y.; Sun M. Sci. Rep. 2015, 5, 17534. 10.1038/srep17534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuloaga J.; Nordlander P. Nano Lett. 2011, 11, 1280–1283. 10.1021/nl1043242. [DOI] [PubMed] [Google Scholar]
- Magkiriadou S.; Park J.-G.; Kim Y.-S.; Manoharan V. N. Phys. Rev. E 2014, 90, 062302. 10.1103/PhysRevE.90.062302. [DOI] [PubMed] [Google Scholar]
- Jackson J. D.Classical Electrodynamics, 3rd ed.; John Wiley & Sons, Inc.: New York, NY, 1999. [Google Scholar]
- Nordlander P.; Oubre C.; Prodan E.; Li K.; Stockman M. I. Nano Lett. 2004, 4, 899–903. 10.1021/nl049681c. [DOI] [Google Scholar]
- Link S.; Mohamed M. B.; El-Sayed M. A. J. Phys. Chem. B 1999, 103, 3073–3077. 10.1021/jp990183f. [DOI] [Google Scholar]
- Wang D.; Yang A.; Hryn A. J.; Schatz G. C.; Odom T. W. ACS Photonics 2015, 2, 1789–1794. 10.1021/acsphotonics.5b00546. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.