The application of frequency-domain photoacoustics to temperature-dependent measurements of the Grüneisen parameter in lipids

Abstract

The Grüneisen parameter is an essential factor in biomedical photoacoustic (PA) diagnostics. In most PA imaging applications, the variation of the Grüneisen parameter with tissue type is insignificant. This is not the case for PA imaging and characterization of lipids, as they have a very distinct Grüneisen parameter compared with other tissue types. One example of PA applications involving lipids is the imaging and characterization of atherosclerotic plaques. Intravascular photoacoustic (IVPA) imaging is a promising diagnostic tool that can evaluate both plaque severity and composition. The literature for IVPA has mainly focused on using the difference in absorption coefficients between plaque components and healthy arterial tissues. However, the Grüneisen parameters for lipids and their behavior with temperature have not been well established in the literature. In this study we employ frequency-domain photoacoustic measurements to estimate the Grüneisen parameter by virtue of the ability of this modality to independently measure both the absorption coefficient and the Grüneisen parameter through the use of the phase channel. The values of the Grüneisen parameters of some lipids are calculated as functions of temperature in the range 25–45 °C.

1. Introduction

Biomedical photoacoustics features excellent contrast and functional imaging. The wavelength based optical absorption coefficient of tissue facilitates a variety of photoacoustic (PA) applications in imaging and characterization of tissues. Nevertheless, the PA signal also depends on the Grüneisen parameter and the optical fluence, in addition to the absorption coefficient [1,2]. The foremost subject of biomedical PA functional imaging has been blood, the Grüneisen parameter of which has a very small dependence on hemoglobin concentration [3]. Therefore, its effect on the estimation of parameters such as blood oxygen saturation is minimal. However, the temperature dependence of the Grüneisen parameter has incentivized the use of PA as a tool to monitor tissue temperature [[4], [5], [6], [7], [8], [9]]. On the other hand, knowledge of the Grüneisen parameter is critical for estimating the sensitivity of PA imaging. In fact, one of the effective methods for determining the Grüneisen parameter is via PA measurements [3,10,11]. For instance, the Grüneisen parameter of subcutaneous porcine fat has been measured by the PA method and was reported to be 0.69 at 22 °C [3]. Furthermore, a technique for measuring the Grüneisen parameter was suggested which relied on the time-resolved transient PA signal [12,13]. In this technique the exponential slope of the rising signal edge provides the value of the optical absorption coefficient and the total amplitude yields the Grüneisen parameter. Related to this research, PA has also been employed to measure the acoustic properties, sound speed and ultrasonic attenuation, of tissue and several lipids [[14], [15], [16]].

One of the promising applications of biomedical photoacoustics is the diagnosis of coronary artery disease. This disease is characterized by the narrowing of coronary arterial vessels by atherosclerotic plaques. The buildup of plaque can restrict blood flow and significantly increase the risk of acute coronary events, such as myocardial infarction, due to plaque dislodging and leading to a clog. The early detection of the severity of plaque build-up is an important predictor for patients with atherosclerosis [17]. In addition, assessment tools that allow for direction evaluation of coronary stenosis have better diagnostic value than indirect evaluation tools, such as a stress test [18]. Currently, coronary angiography, intravascular ultrasound (IVUS), and intravascular optical coherence tomography (IV-OCT) are possible diagnostic techniques [19,20]. However, these techniques cannot accurately evaluate the composition or inflammation of plaque to determine its vulnerability [21]. Intravascular photoacoustic (IVPA) imaging is an emerging spectroscopic diagnostic tool that can illuminate the conformation and composition of atherosclerotic plaques [[22], [23], [24], [25], [26], [27], [28], [29]]. In contrast to other techniques such as coronary angiography, IVPA does not require the use of radioactive contrasting dyes. This minimally invasive technique uses the difference in optical absorption coefficients of the various constituents of tissues to characterize their components [27]. For example, Allen et al. [24] have demonstrated the potential of using 1210 nm and 980 nm lasers to differentiate between healthy arterial walls and plaques due to their different absorption coefficients at these two wavelengths.

The Grüneisen parameter is a thermodynamic property that varies with temperature. Tian et al. [30] showed that the Grüneisen parameters of blood and lipids are highly different in their temperature-dependence: the Grüneisen parameter of blood increases with temperature while that of lipids decreases with temperature in the physiological temperature range [30]. The use of the different behavior of the Grüneisen parameter with temperature has been suggested for characterization of atherosclerotic plaques. It has been shown that for the adventitia, the PA signal would increase with temperature, while that for fatty plaque would decrease with increasing temperature [31]. While the spectroscopic feature of IVPA based on differences in absorption coefficients has been extensively studied, the potential of using the difference in the Grüneisen parameter has not been well explored. This can potentially result in the development of novel approaches for the assessment of atherosclerosis. It should be emphasized that the difference between the Grüneisen parameters of healthy tissues and lipids is larger than that of their absorption coefficient differences [24,27], therefore, the effect of this parameter cannot be ignored. One potential way for exploiting this difference is by measuring the photoacoustic (PA) response of atherosclerotic vessels at two different temperatures. For a healthy tissue, the PA signal would increase with temperature while for plaque constituents, such as cholesterol, it would decrease [31]. The change in temperature can be achieved clinically through ultrasound waves, by flushing blood vessels with a low-temperature fluid, or with an endovascular cooling catheter that inserts a balloon filled with a low temperature fluid into the blood vessel [32]. However, the Grüneisen parameters of lipids have not been well established in the literature but have been reported to be between 0.7 and 0.9 [3,10].

In this paper, we investigate the PA method for an estimation of the Grüneisen parameter of lipids. We employ frequency-domain (or Fourier-domain, FD) PA to evaluate the absorption coefficient and the Grüneisen parameter of lipids. The methodology and various techniques of FD-PA for spectroscopic probing and imaging have been discussed before, where the main subject was the evaluation of the blood oxygenation level [[33], [34], [35], [36], [37]]. Furthermore, we report the Grüneisen parameter of some lipids such as mineral oil, castor oil, olive oil, glycerin as well as cholesterol and cholesteryl oleate. The values of Grüneisen parameters of lipids have been reported at room temperature and in the entire physiological temperature range.

2. Theoretical background

The utilization of IVPA is based on the generation of PA signals through irradiation by a laser beam. The pulsed laser creates a transient thermoelastic expansion of the target tissue. This expansion generates a PA wave that is detected by an ultrasonic transducer. The amplitude of the PA signal (p_o) is approximated by [1,2]:

$$p_0\approx \hspace{0.17em}\mathrm{\Gamma }{\mu }_aϜ$$ (1)

where $\Gamma$ is the Grüneisen parameter, ${\mu }_a$ is the absorption coefficient, and $Ϝ$ is the light fluence. The Grüneisen parameter is defined as

$$\hspace{0.17em}\mathrm{\Gamma }=\frac{\beta c_a^2}{C_p}$$ (2)

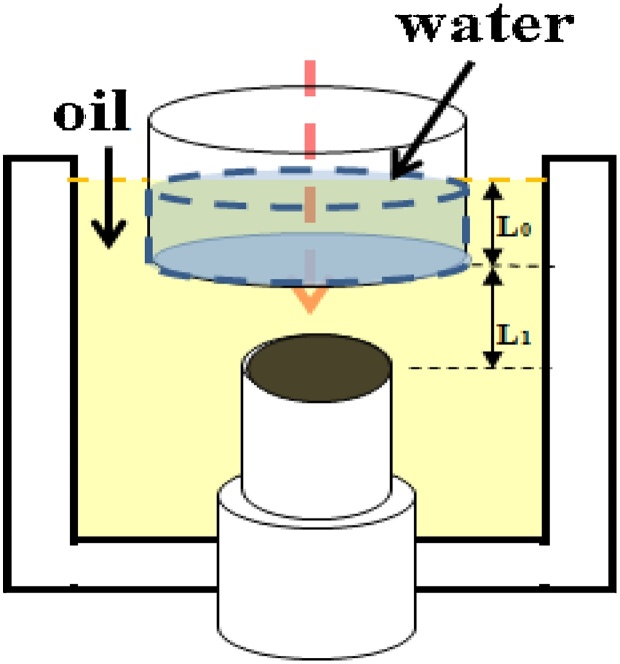
where β is the isobaric volume expansion coefficient, c_a is the sound speed and C_p is the specific heat. Eq. (1) is a very useful approximation for PA functional imaging. However, the direct proportionality of the pressure amplitude to both μ_a and Γ, prevents the estimation of the Grüneisen parameter directly from the PA signal. One solution would be to measure the absorption coefficient independently, for instance, via a purely optical method and use the PA effect to measure the Grüneisen parameter. Another limitation of Eq. (1) is that it does not account for acoustic attenuation. A more rigorous method to relate the absorption coefficient and the PA signal requires a priori knowledge of the geometry and the optical fluence reaching the absorber. It can be shown that the 1D transmission-mode PA pressure spectrum of a two layer material (Fig.1) is given by [38]:

$${\tilde{p}}_a(L_1,f)=\frac{\Gamma e^{-{\mu }_{eff}{L}_0}{e}^{-\alpha (f)L_1}}{\left(1+\frac{{\rho }_s{c}_s}{{\rho }_a{c}_a}\right)}\left(\frac{{\mu }_a({\mu }_a\frac{{\rho }_s{c}_s}{{\rho }_a}+j\omega )}{{\left({\mu }_a{c}_a\right)}^2+{\omega }^2}\right)e^{-j\frac{\omega L_1}{c_a}}{\tilde{I}}_o(f)$$ (3)

where the tilde indicates the Fourier transform operation; ω is the angular frequency, ω = 2πf; c_a (c_s) is the speed of sound in the absorbing liquid and in the interfacial water; ρ_a (ρ_s) is the density of the absorbing liquid (water); μ_a is the absorption coefficient of the absorbing liquid; μ_eff is the effective optical attenuation coefficient of water; α is the acoustic attenuation of oil; L₀ and L₁ are the thickness of the water column and the distance of the transducer from the absorbing liquid (e.g. oil) surface respectively; I_o is the incident laser intensity before attenuation. For a short pulse, negligible acoustic attenuation and approximately similar acoustic impedance of the two liquids, it can be shown that Eq. (3) reduces to Eq. (1). However, in a more general case, the transient detected by the transducer is:

$$V_{tr}(t)=\frac{\Gamma {\mu }_a{e}^{-{\mu }_{eff}{L}_0}}{\left(1+\frac{{\rho }_s{c}_s}{{\rho }_a{c}_a}\right)}\underset{-\infty }{\overset{+\infty }{\int }}\left(\frac{{\mu }_a\frac{{\rho }_s{c}_s}{{\rho }_a}+j\omega }{{\left({\mu }_a{c}_a\right)}^2+{\omega }^2}{e}^{j\omega (t-\frac{L_1}{c_a})}{e}^{-\alpha (f)L_1}{\tilde{I}}_o(f){\tilde{H}}_{tr}\left(f\right)\right)df$$ (4)

where H_tr is the transfer function of the transducer. Eq. (4) helps account for the effect of factors such as the limited bandwidth of the transducer and acoustic attenuation. It should be noticed that acoustic attenuation is also a function of temperature. For a linear frequency modulation (LFM) chirp irradiation, the cross-correlation signal is calculated as follows:

$$R(t)=\frac{\Gamma {\mu }_a{e}^{-{\mu }_{eff}{L}_0}}{2\left(1+\frac{{\rho }_s{c}_s}{{\rho }_a{c}_a}\right)}\left(\frac{\overline{I}{T}_{ch}}{f_2-f_1}\right)\underset{f_1}{\overset{f_2}{\int }}\left(\frac{{\mu }_a\frac{{\rho }_s{c}_s}{{\rho }_a}+j\omega }{{\left({\mu }_a{c}_a\right)}^2+{\omega }^2}{e}^{j\omega (t-\frac{L_1}{c_a})}{e}^{-\alpha (f)L_1}{\tilde{H}}_{tr}\left(f\right)\right)df$$ (5)

where Ῑ is the average laser intensity, T_ch is the chirp duration, and, f₁ and f₂ are the start and end frequencies of the chirp, respectively. Similar to our previous study [35], the relationship between the phase of the cross-correlation signal at the exact delay time corresponding to t = L₁/c_a can be readily calculated:

$$\theta (t=\frac{L_1}{c_a})\approx {\tan }^{-1}\left\{\frac{\underset{f_1}{\overset{f_2}{\int }}\left(\frac{e^{-\alpha (f)L_1}}{\omega }\right)df}{\underset{f_1}{\overset{f_2}{\int }}\left({\mu }_a{c}_s\frac{{\rho }_s}{{\rho }_a}\frac{e^{-\alpha (f)L_1}}{{\omega }^2}\right)df}\right\}={\tan }^{-1}\left\{\frac{{\rho }_a}{{\mu }_a{c}_s{\rho }_s}\frac{\underset{f_1}{\overset{f_2}{\int }}\left(\frac{e^{-\alpha (f)L_1}}{\omega }\right)df}{\underset{f_1}{\overset{f_2}{\int }}\left(\frac{e^{-\alpha (f)L_1}}{{\omega }^2}\right)df}\right\}$$ (6)

Fig. 1.

Schematic of the PA signal generation.

This phase method can be used to directly calculate the absorption coefficient assuming the ratio L₁/c_a is known:

$${\mu }_a\approx \frac{{\rho }_a}{c_s{\rho }_s\tan \left[\theta (t=L_1/c_a)\right]}\frac{\underset{f_1}{\overset{f_2}{\int }}\left(\frac{e^{-\alpha (f)L_1}}{\omega }\right)df}{\underset{f_1}{\overset{f_2}{\int }}\left(\frac{e^{-\alpha (f)L_1}}{{\omega }^2}\right)df}$$ (7)

It is important to note that the phase is not affected by the Grüneisen parameter, therefore the shape of the signal can provide an independent measurement of the absorption coefficient. Then, the amplitude value can be employed independently to obtain the Grüneisen parameter. However, as shown in Eqs. (4), (5), (6), (7), acoustic attenuation is also affecting the amplitude and phase of the PA signal which was neglected in Eq. (1). Acoustic attenuation may be neglected for liquids such as water [35], however, in this work, due to the transmission mode arrangement of the experiments and high viscosity of the oils, acoustic attenuation needs to be considered. Acoustic attenuation of oils is normally described as a power function:

$$\alpha \left(f\right)={\alpha }^{\prime }{f}^n$$ (8)

where n = 2 is consistent with the theoretical model of absorption due solely to viscosity effects [39]. In the frequency range of interest in this paper the mechanism of acoustic absorption mainly consists of thermoviscous effects [39]. Therefore, due to the strong variation of viscosity with temperature, acoustic attenuation also varies with temperature. The values of α΄ and n can be calculated empirically by comparing the acoustic signal transmitted through water versus the liquid or oil under investigation. Knowing the attenuation coefficient of water, the attenuation of oils can be estimated via [14]:

$${\alpha }_{oil}\left(f\right)=-\frac{8.686}{d}\ln \left[\frac{A_{oil}\left(f\right)}{A_{water}\left(f\right)}\right]+{\alpha }_{water}\left(f\right)$$ (9)

3. Experimental set-up

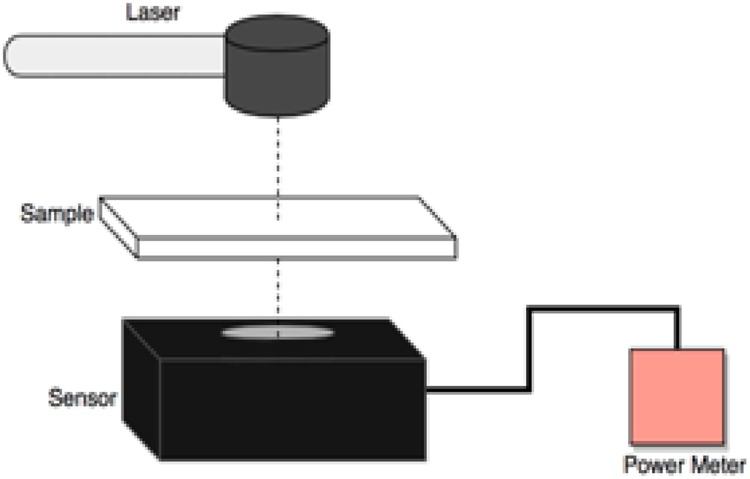
The setup for measuring the absorption coefficients of different materials via a purely optical method is shown in Fig. 2. A handheld optical power meter console (PM200, Thorlabs, NJ, USA) was used with a sensor (S370C, Thorlabs, NJ, USA). A 1210 nm CW laser (LDX Optronics Inc., Maryville, TN, USA) was employed where the samples were 1 mm in thickness placed between two microscopic slides. The absorption coefficients of the samples were then calculated using:

$${\mu }_a=\hspace{0.17em}\frac{1}{\mathcal{l}}\hspace{0.17em}ln\left(\frac{I_0}{I}\right)$$ (10)

where I and I₀ are the laser power through empty microscopic slides and microscopic slides containing the sample, respectively. l is the thickness of the sample. The absorption coefficients of distilled water, mineral oil, olive oil, castor oil, glycerin, cholesterol, and cholesteryl oleate were measured with this setup. The method is very accurate for measurement of transparent materials where the scattering effect is insignificant. For the case of cholesterol, and cholesteryl oleate, the samples were heated to the melting point and then the power attenuation was measured through the samples.

Fig. 2.

Set-up for optical measurement of absorption coefficients.

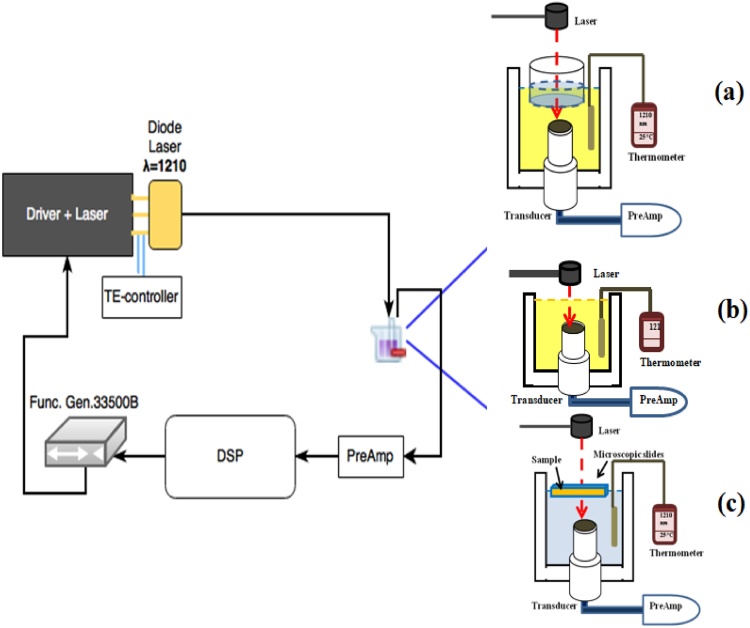
The PA experimental set-up described in this section has been employed to perform measurements in different configurations as demonstrated in Fig. 3. The modulated CW laser emission (1210 nm) described above has been employed to generate the PA signal at 650 mW power. An arbitrary waveform generator (33500B, Agilent Technologies, Inc. Loveland, CO, USA) and a high-frequency driver (VFM10-25, MESSTEC Power Converter GmbH, Germany) were used to modulate the laser diode. The temperature of the laser diode was stabilized by a thermoelectric controller (Arroyo Inst. 5305, San Luis, CA, USA). A focused 3.5 MHz ultrasonic probe was used to detect the PA signal (V382, Panametrics, Olympus, USA). The detected signal was amplified by a preamplifier (Model 5676, Panametrics, Olympus, USA) then digitized by a data acquisition card (NI PXIe 5122, National Instruments, TX, USA). Signal averaging and matched filtering were processed via a NI controller system (NI PXIe-8135, National Instruments, TX, USA).

Fig. 3.

Schematic of the experimental set-up with three different sample configurations in (a), (b), and (c) (see text).

The liquid oil filled a container with the transducer surface at its focal distance from the surface of the oil. The laser beam was directed towards the transducer center from the top of the container. The sample liquid was used in three different configurations. In the first configuration, a plexiglass cylinder filled with water (4 mm height) was located on the surface of the oil where a plastic wrap at the bottom of the cylinder separated the two liquids (Fig. 3(a)). This configuration was employed to measure the absorption coefficient of liquids via the shape of the PA signal. In the second configuration, the surface of the oil was in contact with air (Fig. 3(b)). This configuration was used to measure the change of the PA signal while temperature decreased from 45° to 25 °C. The oil samples and water used in the container in which the sample was immersed were first heated to temperature of ∼50 °C on a hot plate, then added to the containers and allowed to cool down slowly to room temperature while measurements were performed. Room temperature was kept at ∼21 °C. A high accuracy resistance temperature detector thermometer (Omega HH804U, CT, USA) was used to measure the temperature of oil samples. The detailed specifications of the material used as samples in the experiments are reported in Table 1. The third configuration shown in Fig.3(c) was employed to measure the PA signal from a 1-mm layer cholesterol or cholesteryl oleate while temperature decreased from 45° to 25 °C. Due to the high ultrasonic attenuation of cholesterol and cholesteryl oleate, a thin layer was employed to minimize this effect.

Table 1.

Lipid substances used and their specifications.

Material	Manufacturer
Mineral Oil	Rexall, Ontario, Canada
Castor Oil	Castor oil 100%, Rexall, Ontario, Canada
Olive Oil	Rexall, Ontario, Canada
Glycerine	Glycerine 100%, Rexall, Ontario, Canada
Cholesterol 95%	A11470, Alfa Aesar, Ward Hill, MA, USA
Cholesteryl oleate	A11378, Alfa Aesar, Ward Hill, MA, USA

Furthermore, the speeds of sound and acoustic attenuations of the samples were measured using an ultrasonic pitch-catch set-up.

4. Experimental results and discussion

The absorption coefficients of distilled water, mineral oil, castor oil, olive oil and glycerin were measured by the direct optical method at 1210 nm (Fig. 2). These absorption coefficients were found to be constant throughout the experimental temperature range of 25 °C and 45 °C (Table 2). The reported values are not corrected for surface reflectance, but this effect is considered in the calculation of errors. Furthermore, the absorption coefficients of cholesterol and cholesteryl oleate were measured while they were heated to their melting point. Melting these lipids reduced the effect of optical scattering.

Table 2.

The estimated absorption coefficients of samples at 1210 nm.

	${\mu }_a$ at 1210 nm measured optically	${\mu }_a$ at 1210 nm measured via photoacoustic signal
Distilled Water	0.852 ± 0.045 cm−1
Mineral Oil	1.318 ± 0.024 cm−1
Castor Oil	1.100 ± 0.030 cm−1	1.170 ± 0.10 cm−1
Olive Oil	1.164 ± 0.026 cm−1	1.125 ± 0.13 cm−1
Glycerine	0.716 ± 0.038 cm−1	0.85 ± 0.10 cm−1
Cholesterol	1.61 ± 0.12 cm−1
Cholesterol Oleate	1.66 ± 0.16 cm−1

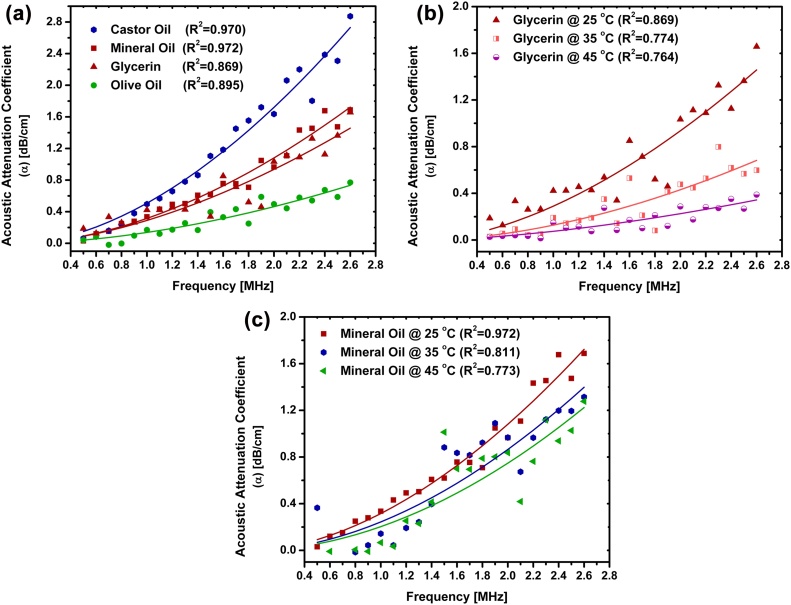
The ultrasound pitch-catch method was used to measure the acoustic attenuation of mineral oil, castor oil, olive oil and glycerin in the frequency range of 500 kHz to 2.6 MHz. These measurements were performed at 25 °C. As shown in Fig. 4(a) the experimental acoustic attenuations were fitted with a power formula (Eq. (8)) using the curve fitting function of MATLAB R2014a (The MathWorks, Inc., MA, USA). The values of speed of sound as well as α at 1 MHz (i.e. α΄) and n are presented in Table 3. For castor oil and olive oil results are very close to the reported values [14]. To account for acoustic attenuation (Eq. (4)), the values of α΄ and n are required in the temperature range of 25–45 °C. The acoustic attenuation of mineral oil and glycerin was measured similarly at 35 and 45 °C and results are shown in Fig. 4(b) and (c). As shown in Ref. [14], for castor oil and olive oil the value of n has a minor variation with temperature while α΄ changes significantly with temperature. Therefore, α΄ (α at 1 MHz) of castor oil and olive oil were measured at 35 and 45 °C while the power factors (n) were assumed to be constant. The constant n through the temperature range of interest can generate an insignificant error for olive oil and an average error of 1.5% in the calculation of α for castor oil in the measurement frequency range [14]. The values of α΄ have been interpolated for the temperature range of 25–45 °C.

Fig. 4.

Acoustic attenuation of (a) mineral oil, castor oil, olive oil and glycerin at 25 °C; (b) mineral oil at 25, 35 and 45 °C; (c) glycerin at 25, 35 and 45 °C. All measurements were performed in the frequency range.0.5–2.6 MHz.

Table 3.

Measured acoustic properties of oils. (* assumed to be constant in the temperature and frequency ranges of interest.).

	SOS [m/s]	α @ 1 MH [dB/cm]	n	α @ 1 MH [dB/cm]	n	α @ 1 MH [dB/cm]	n
	at 25 °C	at 25 °C		at 35 °C		at 45 °C
Mineral Oil	1458 ± 31	0.315 ± 0.049	1.78 ± 0.19	0.244 ± 0.117	1.83 ± 0.61	0.200 ± 0.12	1.88 ± 0.73
Castor Oil	1509 ± 32	0.508 ± 0.083	1.76 ± 0.20	0.356 ± 0.088	1.76*	0.186 ± 0.074	1.76*
Olive Oil	1456 ± 30	0.138 ± 0.043	1.75 ± 0.38	0.105 ± 0.053	1.75*	0.072 ± 0.042	1.75*
Glycerin	1895 ± 38	0.293 ± 0.089	1.69 ± 0.39	0.128 ± 0.062	1.76 ± 0.61	0.074 ± 0.032	1.59 ± 0.55

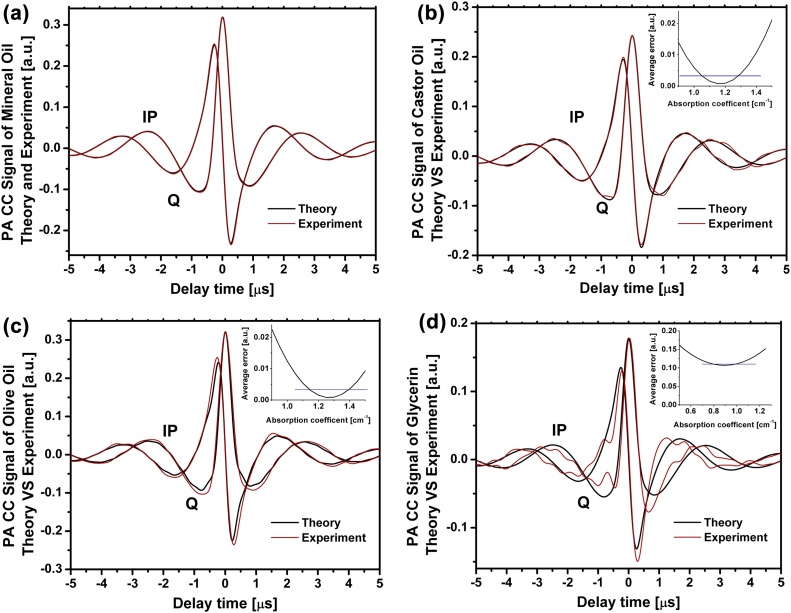
The FD-PA signals of the aforementioned four liquid oils were measured using the set-up shown in Fig. 3(a). The measurements were performed under identical laser fluence and at 25 °C. The height of water layer above the oil (L₀) was 4 mm and the distance between the oil surface and the transducer (L₁) was 23 mm. These distances were kept fixed for all experiments. The laser irradiation was conducted using a LFM chirp sweeping between 300 kHz to 2.6 MHz. The experimental cross-correlation signals from the oil samples were time-gated to eliminate the extra signals induced by the water layer. The mineral oil sample was employed to estimate the Wiener filter representing the dynamics of the transducer and other pieces of instrumentation. As shown in Eq. (7), the delay time should be determined to estimate the absorption coefficient. To avoid the extra unknown (i.e. delay time), theoretical FD-PA signals were calculated for μ_a values between 0.5 and 3 cm⁻¹ with 0.05 cm⁻¹ steps. The FD-PA signals were convolved with the Wiener filter to account for the dynamics of the transducer and other instruments. Then, the error between the theoretical estimate and the experimental signal in the 1 μs range around the peak (approximately corresponding to the FWHM of the signal) was calculated. The minimum error between the theoretical prediction and the experimental signal plus the noise level of the signal provided the best estimate for the μ_a value. The estimated absorption coefficients are reported in Table 2. The experimental PA signals and theoretical estimates as well as calculated errors versus absorption coefficients are shown in Figs. 5(a)–(d). After estimating the absorption coefficient of the samples, the amplitudes of the signals reveal the corresponding Grüneisen parameters. Since signal amplitudes are also affected by acoustic attenuation, employing Eq. (4) with the known transfer function of the transducer can help account for the effect of acoustic attenuation on the PA signal.

Fig. 5.

Theoretical and experimental in-phase (IP) and quadrature (Q) PA cross-correlation signals generated in (a) mineral oil; (b) castor oil; (c) olive oil; and (d) glycerin. The error between the two signals was minimized by adjusting the absorption coefficients.

In the next step, the PA experimental set-up of Fig. 3(b) was used to measure the FD-PA signal and estimate the Grüneisen parameter of lipids in the desired temperature range. Water was employed as a reference to calibrate the PA signals. The temperature dependence of the Grüneisen parameter of water has been discussed extensively in the literature, and has been determined in the temperature range of 4 °C to 100 °C from the following empirical equation [13]:

$$\mathrm{\Gamma }(T)=0.0043+0.0053T$$ (11)

or more accurately [40]:

$$\mathrm{\Gamma }(T)=-0.033+0.007T-0.0000236T^2$$ (12)

To measure the sensitivity of our measurements, we compared the ratio of the FD-PA signal and the Grüneisen parameter (from Eq. (12)) of distilled water as a function of temperature. Given that the set-up remained fixed and laser fluence was kept constant, dividing the PA signals at two different temperatures such as 40 °C and 30 °C can cancel out the ${\mu }_a$ and the fluence (or intensity) terms in Eq. (1):

$$\frac{p\left(40℃\right)}{p\left(30℃\right)}=\frac{\mathrm{\Gamma }\left(40℃\right){\mu }_{a_{water}}Ϝ}{\mathrm{\Gamma }\left(30℃\right){\mu }_{a_{water}}Ϝ}=\frac{\mathrm{\Gamma }\left(40℃\right)}{\mathrm{\Gamma }\left(30℃\right)}$$ (13)

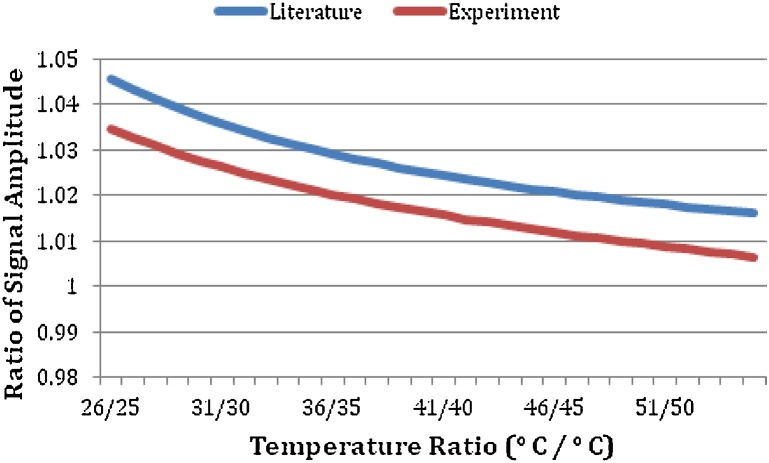
This allows one to calculate the ratio of the PA signal at any two temperatures and use it to calibrate the system. The ratio of the signals at 40 °C and 30 °C was calculated using Eqs. (11) and (12), and was found to be 1.324 and 1.343, respectively. The experimental ratio for the corresponding temperatures was 1.230, which is an error of ∼7.8%. This ratio is independent of instrumentation, laser fluence and absorption coefficient, therefore it is a suitable parameter to assess the accuracy of our measurements. Using Eq. (13), the ratios of measured PA signals of water between 25 °C and 55 °C with 1 °C steps (that is the ratio of the Grüneisen parameters: Γ(T+1°)/Γ(T)) were compared to the empirical formula (Fig. 6). The Grüneisen parameter (Eq. (12)) and the measured ${\hspace{0.17em}\mu }_a$ value for water helped determine the value of laser fluence (F) in the experiment. Knowledge of the value of $Ϝ$ for the experimental system, can be used to measure the Grüneisen parameter of other liquids.

Fig. 6.

Ratio of Γ(T+1°)/Γ(T) in the temperature range of interest.

By measuring the peak PA signals in the temperature range of 25 °C and 45 °C, best quadratic polynomial fits were generated using least squares fitting for water, mineral oil, olive oil, glycerin, and castor oil. The measurements for cholesterol and cholesteryl oleate were made with a thickness of 1 mm and were compared to a mineral oil sample in the experimental set-up of Fig. 3(c). The microscope slide at the bottom of the sample (Fig. 3(c)) reflected part of the acoustic signal, thus it weakened the signal somewhat. However, the signal was still detectable. The least squares fitting and its associated calculations were accomplished using the curve fitting function of MATLAB R2014a (The MathWorks, Inc., MA, USA). Table 4 shows the fitted Grüneisen parameters of the various substances.

Table 4.

The fitted polynomial to the measured Grüneisen parameters of the various substances. (* corrected for acoustic attenuation of oil).

	Best Polynomial Fit	R-squared
Distilled Water	−1.958 × 10-5 × T2+0.002774 × T + 0.005617 $-2.36\hspace{0.17em}\times \hspace{0.17em}{10}^{-5}\hspace{0.17em}{T}^2+0.007\hspace{0.17em}T-0.033\hspace{0.17em}(literature)$	0.9954
Mineral Oil	$-4.855\hspace{0.17em}\times \hspace{0.17em}{10}^{-5}\hspace{0.17em}{T}^2+5.688\hspace{0.17em}\times \hspace{0.17em}{10}^{-5}T+0.7342$ $-4.30\hspace{0.17em}\times \hspace{0.17em}{10}^{-6}\hspace{0.17em}{T}^2-0.00514\hspace{0.17em}T+0.9446$ *	0.9979
Castor Oil	$-0.000121\hspace{0.17em}{\hspace{0.17em}T}^2+\hspace{0.17em}0.01029\hspace{0.17em}T+0.6993$ $-0.0001931\hspace{0.17em}{\hspace{0.17em}T}^2+\hspace{0.17em}0.008389\hspace{0.17em}T+1.012$ *	0.8876
Olive Oil	$-4.196\hspace{0.17em}\times \hspace{0.17em}{10}^{-5}{\hspace{0.17em}T}^2-1.189\hspace{0.17em}{\times \hspace{0.17em}10}^{-3}T+0.9501$ $-3.07\hspace{0.17em}\times \hspace{0.17em}{10}^{-5}{\hspace{0.17em}T}^2-0.003552\hspace{0.17em}T+1.061\hspace{0.17em}*$	0.9936
Glycerine	$-0.8909\hspace{0.17em}\times \hspace{0.17em}{10}^{-5}{\hspace{0.17em}T}^2+8.020\hspace{0.17em}{\times \hspace{0.17em}10}^{-3}T+0.5968$ $-0.0001528{\hspace{0.17em}T}^2-0.00731\hspace{0.17em}T+\hspace{0.17em}0.9885$ *	0.8943
Cholesterol	$2.83\hspace{0.17em}\times \hspace{0.17em}{10}^{-5}{\hspace{0.17em}T}^3-3.011\hspace{0.17em}{\times \hspace{0.17em}10}^{-3}{\hspace{0.17em}T}^2+0.09605\hspace{0.17em}T-0.4476$	0.9893
Cholesterol Oleate	$8.775\hspace{0.17em}\times \hspace{0.17em}{10}^{-4}{\hspace{0.17em}T}^2-0.06828\hspace{0.17em}T+1.911$	0.9855

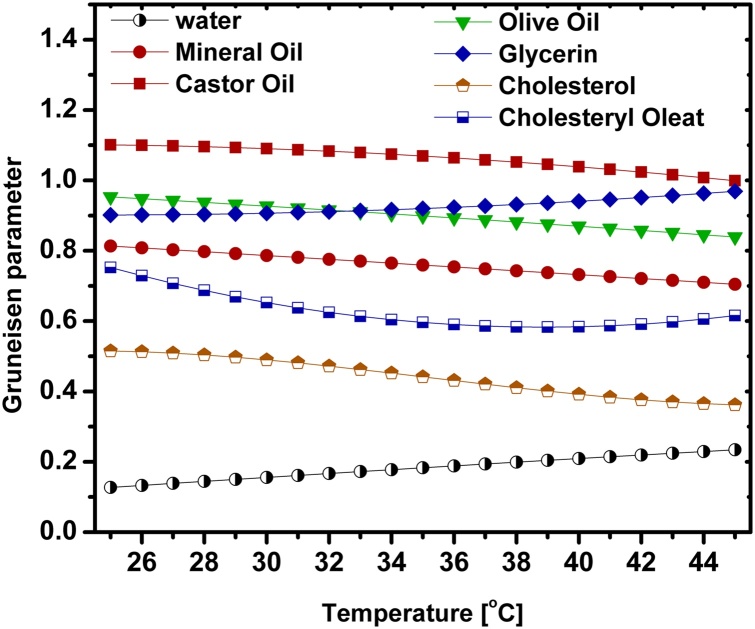
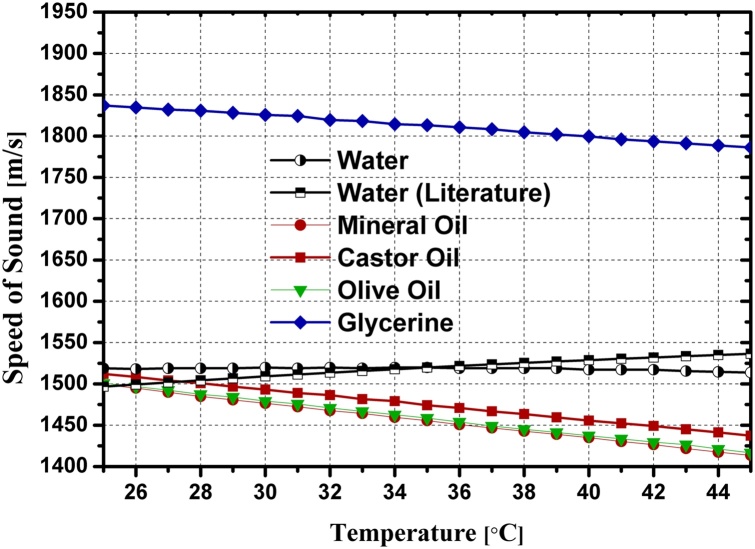
It was mentioned that using Eq. (1) neglects the effect of acoustic attenuation. This effect is crucial as the acoustic attenuation coefficient changes with temperature. Therefore, the measured Grüneisen parameters for oils were corrected for acoustic attenuation (Table 4). It should be clarified that the acoustic attenuation effect on measurements using the configuration of Fig. 3(c) was ignored due to the small thickness of the cholesterol and cholesteryl oleate samples. Also the acoustic attenuation of water was neglected. Fig. 7 shows the resulting Grüneisen parameters of the investigated substances in the temperature range of interest (Table 5). The change in the time delay of the PA signal reveals the speed of sound change with temperature of each sample. With the knowledge between the distance of the surface of the sample and the transducer, the speed of sound was calculated for all substances in the temperature range of 25 °C to 45 °C as a by-product of our measurements (Fig. 8). The measured absorption coefficients for distilled water and mineral oil matched those from the literature [3]. Additionally, the FD-PA system was validated by measuring the ratio of the PA signals at 40 °C and 30 °C and comparing the measured μ_a with the measured value from the purely optical transmission method (Eq. 10).

Fig. 7.

Grüneisen parameters of all samples between 25 °C and 45 °C. Errors measured for mineral oil: 9.4%, castor oil: 13.8%, glycerin: 18.8%, olive oil: 7.5%, cholesterol: 18.1%, and cholesteryl oleate: 23.4%.

Table 5.

Summary of the estimated Grüneisen parameters of the investigated substances in the temperature range.25 °C–45 °C.

	Γ at 25 °C	Γ at 35 °C	Γ at 45 °C
Distilled Water	0.127	0.183	0.234
Mineral Oil	0.813 ± 0.076	0.744 ± 0.070	0.705 ± 0.066
Castor Oil	1.101 ± 0.152	1.069 ± 0.147	0.999 ± 0.138
Olive Oil	0.953 ± 0.071	0.899 ± 0.067	0.839 ± 0.063
Glycerin	0.901 ± 0.169	0.920 ± 0.173	0.969 ± 0.182
Cholesterol	0.515 ± 0.080	0.442 ± 0.069	0.362 ± 0.056
Cholesteryl Oleate	0.753 ± 0.176	0.596 ± 0.139	0.615 ± 0.144

Fig. 8.

Speed of sound in water and in the lipids in the temperature range of interest.

In the case of imaging and characterization of real tissues, one should note that since such tissues are inhomogeneous and contain water and other constituents, optical scattering is significant and tissue physical properties are different from those of their constituents. Due to major optical scattering in real tissues and their inhomogeneous properties, employing the phase method is rather challenging. However, one option for estimating the physical properties (such as the Grüneisen parameter) of real tissues is to use the mass fraction sum of the components [41]. This is based on the fact that the values of the specific heat of water and lipids exhibit very small variation in the 25 to 45 °C temperature range [9]; therefore, the Grüneisen parameter is mainly affected by thermal expansion and the speed of sound. Since the Grüneisen parameters of lipids are much larger than those of other tissue components such as water, their temperature dependence in fat tissues is distinct from other types of tissues. Therefore, it is possible to identify the presence of fat tissues by measuring the changes of the Grüneisen parameter with temperature even if the tissue is not homogeneous or a pure lipid. As an example, the slope of PA efficiency with temperature of in-vitro porcine lard has been investigated elsewhere [9]. This slope, particularly at temperatures below 45 °C, is due to variation in the Grüneisen parameter. The measured slope of PA efficiency for heating porcine lard from 24 to 66 °C was found to be 0.098 mV/°C. To compare the slopes with our estimated Grüneisen parameter variations with temperature, we normalized the slopes by their value at 24 °C (maximum value), which yields the normalized slope of 0.013 °C⁻¹. However, more data are available (Ref. [9], Fig. 4) for cooling from lower temperatures such as 36 °C, 50 °C, and 60 °C. Using the given data values below 45 °C, the average slope was found to be 0.053 mV/°C and the average normalized slope was 0.008 °C⁻¹. The possible reasons for the variation in slopes were explained in detail [9]. The measured Grüneisen parameters in this manuscript yielded the normalized slopes 0.007, 0.005, 0.006, 0.004, 0.015, 0.009 °C⁻¹ for mineral oil, castor oil, olive oil, glycerin, cholesterol and cholesteryl oleate, respectively. It can be seen that the normalized slope of porcine lard is between that of pure cholesterol and mineral oil. In conclusion, the Grüneisen parameter of real fat tissue deviation from that of pure lipids depends on its inhomogeneity and water and fiber contents. Therefore, although there is a large variation of the Grüneisen parameter of real tissues as demonstrated in the case of porcine lard [9], the behavior of the Grüneisen parameter with temperature is still a strong indicator of the presence of lipids.

Another issue that should be addressed here is the thermal relaxation effect during optical-to-thermal energy conversion and heating. Here we should clarify that in CW PA, although the stress confinement condition is not entirely complied with, nevertheless, the thermal confinement assumption is usually valid [38]. To verify the validity of thermal confinement, we can estimate the thermal diffusion length and compare that with the typical optical diffusion length of the probed medium. Thermal diffusion length can be estimated as ${\delta }_T\approx 2\sqrt{D_T\tau }$, where D_T is the thermal diffusivity of the sample and τ is the time scale of laser light irradiation [42]. The time scale can be replaced by 1/f_o, where f_o is the lowest modulated frequency employed, or alternatively τ can be replaced by the chirp duration T_ch. For instance, for olive oil, the thermal diffusivity is 1.46 × 10⁻⁷ m²/s at 20 °C [43]. Therefore, for a chirp duration of 1 ms and modulation frequency range of 0.5–2.6 MHz, the thermal diffusion length is ${\delta }_T\approx 2\sqrt{\frac{D_T}{f_o}}=2\sqrt{\frac{1.46\times {10}^{-7}\raisebox{1ex}{$m$}\!\left/ \!\raisebox{-1ex}{$s$}\right.}{0.5\text{MHz}}}\approx 0.001\text{mm}$ or ${\delta }_T\approx 2\sqrt{D_T{T}_{ch}}=2\sqrt{1.46\times {10}^{-7}\raisebox{1ex}{$m$}\!\left/ \!\raisebox{-1ex}{$s$}\right.\times 1\text{ms}}\approx 0.024\text{mm}$. In both cases the thermal diffusion lengths during one cycle of lowest modulation frequency and during the full chirp are much smaller than the optical diffusion length of the sample which is 1/μ_a = 1/1.164 cm = 10 mm. These estimates show that the effect of thermal diffusion is negligible and the thermal confinement condition is complied with.

Furthermore, since the main subject of this paper, the Grüneisen parameter, is temperature dependent it should be mentioned that the temperature change due to laser heating is very small and doesn’t have a drastic effect on the local temperature. As an example, referring to the available thermodynamic properties of olive oil, its density and specific heat are 913 kg/m³, and 1.8 kJ/kg.K at 20 °C [43]. Therefore, for a chirp duration of 1 ms, laser power of 650 mW, and beam size of 4 mm, the change in the surface temperature of olive oil due to laser light absorption during a full chirp is:

$$\Delta T\approx \frac{{\mu }_a{I}_o{T}_{ch}}{\rho C_p}=\frac{116.4{\text{m}}^{-1}\times \frac{650\times {10}^{-3}\text{W}}{\pi {0.002}^2{\text{m}}^2}\times 0.001\text{s}}{913\frac{\text{kg}}{{\text{m}}^3}\times 1800\frac{\text{J}}{\text{kgK}}}=0.0037°C$$ (14)

This value implies that even after 50 consecutive chirps, their affect on the temperature of the sample will be as low as 0.18 °C. The thermal properties of the other samples used in this study were also very close, therefore, the temperature differences were on the same order of magnitude. In conclusion the above calculations show that both thermal diffusion and local temperature change due to laser irradiation are insignificant in the presented experiments.

In summary, we were able to establish these values for various lipids including mineral oil, olive oil, castor oil, glycerin, cholesterol, and cholesteryl oleate in the temperature range between 25 °C and 45 °C. This study demonstrates the temperature dependent nature of the Grüneisen parameter. Moreover, we noticed diverging trends in the Grüneisen parameter slopes of lipids and non-lipids over the physiological temperature range. These values and trends could potentially result in improvements of accuracy in measurements aiming to differentiate plaque from healthy tissues in a clinical setting. The different behavior of Grüneisen parameters of lipids versus water is consistent with trends in their speed of sound versus temperature, although the relationship is not proportional.

5. Conclusions

Establishing the value of the Grüneisen parameter of various biological tissue constituents allows the quantification of the influence of that parameter on the PA signal as distinct from the absorption coefficient. Based on the results of this study using a single-wavelength laser to measure the difference in the Grüneisen parameters of various lipids and non-lipids, we demonstrated the potential application of FD-IVPA in the differentiation between plaque constituents and healthy arterial tissues. While there exist challenges in the measurement of the Grüneisen parameters of plaque constituents, such as cholesterol, the strength of FD-IVPA lies in the ability of this modality to independently measure both the absorption coefficient and the Grüneisen parameter through the use of the phase channel.

Conflict of interest

The authors declare that there are no conflicts of interest.

Biographies

Simon Liang is a medical student at the University of British Columbia. He received his B.Sc in Physiology from McGill University and an M.Eng degree with a certificate in Healthcare Engineering from University of Toronto. His research interests are medical imaging and vascular diseases.

Bahman Lashkari is a post-doctoral research associate at the CADIFT, University of Toronto where he works on several photoacoustic and ultrasound projects. He received his PhD in the same lab working on frequency-domain photoacoustic imaging (2011). His research interests are in medical imaging and tissue characterization.

Sung Soo Sean Choi received his B.Sc in Biomedical Science from University of Waterloo in 2012 and his M.A.Sc degree in Biomedical Engineering from University of Toronto in 2015. His primary research was to develop a novel cancer diagnostic and monitoring applications using wavelength-modulated photoacoustic spectroscopy. He is now pursuing his PhD in University of Toronto.

Vasilis Ntziachristos is a Professor and Chair for Biological Imaging at Technische Universität München and director of the Institute of Biological and Medical Imaging at Helmholtz Zentrum München. Prior to this appointment he was faculty at Harvard University and the Massachusetts General Hospital. He received his masters and doctorate degrees from the Bioengineering Department of the University of Pennsylvania and the Diploma in Electrical Engineering from the Aristotle University of Thessaloniki, Greece. Professor Ntziachristos serves as chair in international meetings and councils and in the editorial boards of several scientific journals. He has received numerous awards and distinctions, including the Leibniz prize 2013 and the Erwin Schrödinger prize 2011. His main research interests involve the development of optical and opto-acoustic methodologies for probing physiological and molecular events in tissues using non-invasive methods.

Andreas Mandelis is a Full Professor of Mechanical and Industrial Engineering; Electrical and Computer Engineering; and the Institute of Biomaterials and Biomedical Engineering, University of Toronto. He is the Director of the Center for Advanced Diffusion-Wave Technologies (CADIFT). He is the author and co-author of more than 330 scientific papers in refereed journals and 180 scientific and technical proceedings papers. He is the Editor-in-Chief of the International Journal of Thermophysics and an editor of the Journal of Biomedical Optics, Journal of Applied Physics, and Optics Letters.